An extension of high-order Kou's method for solving nonlinear systems and its stability analysis

1.   Introduction

Nonlinear problems are a hot topic in modern mathematics, attracting the attention of many researchers. Problems in fields such as economics, physics, chemistry, and fluid dynamics can be transformed into nonlinear equation systems. The solution of nonlinear equation systems is difficult to discover, and this problem can be solved using some numerical methods ^[1,2,3]. Chen et al. proposed the alternating direction implicit (ADI) compact differential scheme, which reduces the CPU time of two-dimensional problems ^[4]. Yang et al. proposed an efficient compact finite difference method ^[5,6,7] for solving nonlinear equations and an orthogonal Gauss collocation method (OGCM) ^[8] for solving systems of partial differential equations.

Therefore, in-depth research on numerical methods for solving nonlinear systems has important practical significance ^[9]. In solving nonlinear systems, we can obtain approximate solutions with the help of various iterative methods. Multi-point iterative methods ^{[10,11,12,13]} are an effective class of methods for solving nonlinear equation systems.

Wang et al. achieved research results in the study of multi-point iterative methods, such as local convergence analysis ^[14,15,16] and fractal theory-based investigations of iterative methods^[17,18]. Cordero et al. studied the three-step iterative method ^[19,20] for solving nonlinear equations.

Newton's iterative method ^[21] is one of the most famous iterative methods

where $S : D\subseteq \mathbb{R}^{n}\longrightarrow \mathbb{R}^{n}$ and the inverse of the Jacobian matrix $S'(x_{n})$ is ${S'(x_{n})^{-1}}$.

On the basis of Newton's method, Potra-Pták ^[22] proposed a third-order iterative method

These methods $(1.2)$ have the advantage of not needing to compute second-order derivatives.

Cordero et al.^[23] proposed an iterative method using division difference instead of the traditional Jacobi matrix

where $\eta_h(x) = x - \tau_h J_S^{-1}(x) S(x)$ and the parameters $A_h$ satisfy $\sum_{h = 1}^{m} A_h = 1.$ Considering $\tau_1 = 0$, the following iterative method is obtained:

Kou et al. ^[24] proposed an iterative method for solving nonlinear equations with convergence of at least third order

where $\gamma\in \mathbb{R}$. Let $S[x_{n}, y_{n}] = \frac{S(y_{n})-S(x_{n})}{y_{n}-x_{n}}$ and $\frac{S(x_n)^2}{S'(x_n)(s(x_n) - S(y_n))}$ can be represented as$\frac{S(x_{n})}{S[x_{n}, y_{n}]}$. We obtain an iterative method (1.6) for solving nonlinear systems. The iterative method (1.5) can be represented as

where

$\gamma\in \mathbb{R}$ is a real parameter.

The contents of this paper are as follows: Section 2 analyzes the order of convergence of the extended iterative method (1.6). In Section 3, we adopt the Möbius conjugacy map to convert the iterative method (1.6) to a rational operator and examine the fixed points and critical points for this rational operator in depth. The parameter space is constructed and some specific parameters are chosen in the parameter space. Section 4 compares the iterative method (1.6) with other iterative methods through numerical experiments. Section 5 shows some fractal diagrams. We verify that the expanded method has optimal stability and convergence for the parameter $\gamma = 0$.

2.   An expanded iterative method

We prove the convergence order for the iterative method (1.6) with the following theorem.

Theorem 1. Let $S:D\subseteq \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ be a sufficiently differentiable function from an open convex set $D$ and let $x^{*}\in D$ denote the solution of $S (x) = 0$ that makes $S'$ continuous and nonsingular at $x^{*}$. The error equation of the iterative method (1.6) is

When the parameter $\gamma = -1$, the iterative method is fourth-order convergent and the error expression is

Proof. Let $C^{(n)} = \frac{1}{n!} S'(x^{*})^{-1} S^{(n)}(x^{*}), i\geq2$ and $e^{(n)} = x^{(n)}-x^{*}.$ Expanding $S$ in terms of the Taylor's series on $x^{*}$, we get

According to the equation $S'(x^{(n)})^{-1} S'(x^{(n)}) = I$, we can calculate the inverse of $S'(x^{(n)})$ :

where

Now, using(2.3)–(2.5), we get

Taylor expansion of $S(y^{(n)})$ at $x^{*}$ gives

and we have

In the iterative method (1.6), a first-order difference quotient operator is introduced, which can be regarded as a mapping relationship $S[x, y]:D \times D \subset \mathbb{R}^n \times \mathbb{R}^n \to L(\mathbb{R}^n)$,

By performing Taylor expansion on $S'(x + \rho d)$ at point $x$, we can obtain the following results:

According to

the following conclusion can be reached:

where

Based on the equation $S[x^{(n)}, y^{(n)}]^{-1} S[x^{(n)}, y^{(n)}] = I$, the inverse of $S[x^{(n)}, y^{(n)}]^{-1}$ is

Therefore, one has

The error equations for the iterative method (1.6) give us

The equation above shows that the iterative method converges at least to the third order. In particular, when the parameter $\gamma = -1$, the error equation is as follows:

When the parameter $\gamma = 1$, the method (1.6) is a fourth-order convergent method with the following iteration format:

where

□

3.   Study of complex dynamic behavior

Fractal theory ^[25,26] can be used to study the stability and convergence of iterative methods. To visualize the convergence of the proposed iterative approach, fractal maps are constructed for a variety of nonlinear functions. Such methods have been employed in numerous research studies for practical applications. Lee et al.^[27] studied a dynamic view of a class of single-parameter optimal eighth-order multi-root finders under Riemannian ball Möbius conjugate mappings using fractal knowledge. The complex dynamic behavior can be used for exploring the relevant properties of rational operators connected with iterative methods, which are the unique characteristics of rational operators closely connected with iterative methods, as demonstrated by the Möbius conjugate mappings on Riemann spheres. A thorough study of the behavior of the complex dynamics at fixed points allows us to perform a careful analysis of the stability of rational operators. A parameter space that was constructed by the critical point provides us with a reference to have a better idea of the stability in the iterative method, thus enabling us to pick more appropriate parameter values to make iterative methods more stable.

An in-depth study of the method's (1.6) complex dynamic behavior is presented in this section. First, we need to construct rational operators related to the iterative method (1.6).

3.1.   Rational operator

Now, we will analyze the iterative method (1.5) in the context of quadratic polynomial dynamics. The rational operator can be constructed on an arbitrary nonlinear function by a principle based on Riemann ball dynamics ^[28] and the scalar theorem ^[29]. Therefore, a rational operator for quadratic polynomials is designed.

Theorem 2. Let $E(x) = (x-m)(x-a)$ be some arbitrary polynomial of quadratic form, where $m$ and $a$ are its roots. The corresponding rational operator $D_e(x; \gamma)$ of the family in (1.5) applied to $E(x)$ is

Proof. Applying the iterative method (1.5) in $E(x)$, we obtain a rational function $B_e$ associated only with $m$, $a$, and $\gamma$. Next, we construct a rational function $B_e$ by applying the Möbius transform in $B_e$ with the

The properties of the conjugate mappings are as follows (see^[30]):

We can get

and

□

According to the theorem above, we find that the expressive form of the rational operator $D_e(x; \gamma)$ rests on the choice of the parameter value $\gamma$. Furthermore, it is known that $B_e(x)$ and $D_e(x; \gamma)$ are conjugate to each other, and thus the expression for $D_e(x; \gamma)$ contains only the parameter $\gamma$. The form of $D_e(x, \gamma)$ is affected by the parameter $\gamma$, so it is only necessary to explore its relation to $\gamma$. When $\gamma$ is $-1$ or $0$, the expressions of $D_e(x; \gamma)$ will be further simplified by factorizing $D_e(x; \gamma)$ as follows:

and

3.2.   Analysis of iterative methods for fixed points

In this section, the fixed points and the stability of the rational operator $D_e(x; \gamma)$ are analyzed. The particular value of the parameter $\gamma$ will determine the number of fixed points and their stability.

where

and

From solving the equation $D_e(x)-x = 0$, we know that the fixed points include $x = 0, x = \infty, x = 1$, and the roots of the polynomial $\lambda(x) = 1 + 4 x -(-6 + \gamma) x^2 + 4 x^3 + x^4$.

Here, $x = 0$ and $x = \infty$ are the free points and fixed points of the parameter $\gamma$, respectively. Varying values of the parameter $\gamma$ lead to different expressions for the iterative method (1.6). So, for the number of strange fixed points for different values of the parameter, we have Theorem 3.

Theorem 3. For $\lambda(x)$ and $\vartheta(x)$, we have

● If $\gamma = 0$, $(1+x)^3$ is the common factor of the polynomial $\lambda(x)$ and $\vartheta (x)$. In this case, the operator $D_e(x)$ exhibits one unique strong fixed point, namely $x = 1$.

● If $\gamma = 9$, the operator $D_e(x)$ has four strange fixed points, namely $x = -4.79129, x = -0.208712$, the complex number $x = -0.5+ 0.866025i$ and $x = 0.5-0.866025i\ $.

● If $\gamma = 1$, in this case, the operator $D_e(x)$ exhibits two strange fixed points namely $x = -2.61803, x = -0.381966$.

● If $\gamma = 16$, in this case, the operator $D_e(x)$ exhibits four strange fixed points namely $x = -5.82843, x = 1$ (with multiplicity 2) and $x = -0.171573$.

● If $\gamma$ satisfies $(\gamma-1)(\gamma+1)(\gamma-(-1)^{\frac{1}{3}})(\gamma-(-1)^{\frac{2}{3}})\neq0$, the operator $D_e(x)$ has nine strange fixed points: $\ x = 1$ and the eight roots of the polynomial $\lambda(x) = 0$. Then the operator $D_e(x)$ will have five strange fixed points: in addition to $x = 1$, there are four other roots of the polynomial $\lambda (x) = 0$.

Proof. ● With $\lambda (x) = 0$ and $\vartheta (x) = 0$, we can get

Suppose that $x\in C$ is some root such that $\lambda (x) = 0$ and $\vartheta (x) = 0$. Linking these two multinomial equations, we are in a position to remove the parameter $\gamma$, giving us the equation $(1 + x)(1 + x + x^2) = 0$. From $(1 + x) = 0$ or $(1 + x + x^2) = 0$, we get $x = -1$ or $(-1)^{\frac{1}{3}}$ or $x = (-1)^{\frac{2}{3}}$. The common factorization of $\lambda (x) = 0$ and $\vartheta (x) = 0$ is $(1+x)$. As we substitute $x = -1$ for $\lambda (x; -1)$ and $\vartheta (x; -1)$, we get the parameter $\gamma = 0$. So for the operator $D_e(x; 0)$, there is now one anomaly in the fixed points.

● The remainder of the proof is consistent with the approach outlined earlier. □

Theorem $3$ allows us to conclude that the maximum number of fixed points is $5$, while the minimum is $1$. The stability of strange fixed points is discussed below. We first need to calculate the first-order derivatives of the iterative method's rational operator $D_e(x; \gamma)$ with regard to the parameter $\gamma$. The first-order derivatives of $D_e(x; \gamma)$ are computed as follows:

where

The stability characteristics of the fixed points described above are discussed in detail next. With $x = 1$, for the stability of any parameter value $\gamma$ : $\forall \delta \in \mathbb{C} \setminus \left\lbrace -8 \right\rbrace$, the following conclusions are obtained:

1) The point $x$ is repulsive when $|\frac{24}{8 + \gamma}| > 1$;

2) The point $x$ is attractive when $|\frac{24}{8 + \gamma}| < 1$;

3) The point $x$ is parabolic when $|\frac{24}{8 + \gamma}| = 1$;

4) The point $x$ is a superattracting point when $|\frac{24}{8 + \gamma}| \neq 0$.

Proof. This follows from Eq (3.1):

where

and

Substituting $x = 1$ into (3.15), we acquire $D_e'(1;\gamma) = \frac{24}{8+\gamma}$. It is easy to obtain $|\frac{24}{8 + \gamma}| = 1 \Leftrightarrow |24| = |8 +\gamma|$. Let $\gamma = x + iy$ and $(\gamma \in \mathbb{C})$. Then the following equation holds: $(x + 8)^2 + y^2 = 24^2$. Therefore, $|D_e'(1;\gamma)| > 1 \Leftrightarrow |\gamma + 8| < 24$.

The strange fixed point is the root of $x = 1$ and the polynomial $\lambda (x) = \ 1 + 4 x -(-6 + \gamma) x^2 + 4 x^3 + x^4$. The roots of $\lambda (x)$ are denoted as ${\lambda}_i (x)$, for any $i$ ranging from $1$ to $4$. For $\gamma$ satisfying $x(x-1)\neq0$, we have the following:

● If $x = 1$, taking parameter values in the region $[-35, 20]\times[-25, 25]$, it is a point of attraction.

● ${\lambda}_1 (x)$ is exclusive and independent of the value of the parameter $\gamma$.

● ${\lambda}_2(x)$, ${\lambda}_3(x)$, and ${\lambda}_4(x)$ act as attractors for the value of $\gamma$ within the small region of the complex plane $[-10, 12.5] \times[0.96, 0.98]$, $[-2.58, 2.56] \times[-10.96, 12.98]$, $[-1.58, 1.56]\times[-2.06, 1.98]$.

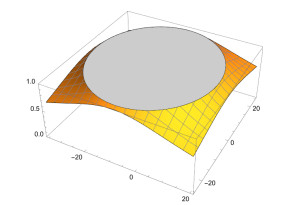
Figure 1 displays the stability regions when x = 1. The repulsive region is depicted as a gray area, while the attractive region is shown as a gold area. When the selected parameter value is inside the disk, a behaves as a repelling point, while a becomes an attractor when the $\gamma$ value is outside the disk. We are generally more attentive to values inside the disk. Figures 1 and 2 illustrate the stability characteristics of the strange fixed points for the operator $D_e(x; \gamma)$.

3.3.   Analysis of the critical points $D_e(x; \gamma)$ for iterative methods

On the basis of the definition of critical point, the critical point of the operator $D_e(x; \gamma)$ is found through solving the equation $D_e'(x; \gamma) = 0$. Clearly, the critical points of the operator are $0$ and $1$, and these are closely related to the roots of the quadratic polynomial $E(x) = (x-m)(x-a)$. Apart from this, the other critical points are considered to be defined as free critical points. The following theorem shows what happens when number of free critical points changes with various values of the parameter $\gamma$.

Theorem 4. If $D_e'(x; \gamma) = 0$, then $x = -1$ and $\delta(x) = 0$ correspond to a free critical point.

● The parameter $\gamma$ takes the value of 0 when $x = -1, \delta(x) = (1+x)^4$, then the rational operator $D_e(x; \gamma)$ has four free critical points, which are $x = -1\ $ (with multiplicity 4).

● The value of parameter $\gamma$ is -8 when $x = 1$, $\varsigma(x) = (1+x)^4-8(1+x^4)$, then the rational operator $D_e(x; \gamma)$ has two free critical points, which are $x = -0.714286-0.699854 i$ and $x = -0.714286+0.699854i$.

● The value of the parameter $\gamma$ is 1 when $x = (-1)^\frac{2}{3}$, $\varsigma(x) = (1+x)^4+(1+x^4)$, at which point, the rational operator $D_e(x; \gamma)$ has four free critical points, which are $x = -1$ (with multiplicity 2) and $x = 0$ (with multiplicity 2).

● For any $\gamma(\gamma+8)(\gamma-9)(\gamma-1)$ that is not equal to 0, we can learn that there are four free critical points.

$cr_1 = \frac{-1}{1+\gamma}-\tau-\frac{1}{2}\sqrt{\Omega-\xi-\Delta-\Gamma};$

$cr_2 = \frac{-1}{1+\gamma}-\tau+\frac{1}{2}\sqrt{\Omega-\xi-\Delta-\Gamma};$

$cr_3 = \frac{-1}{1+\gamma}+\tau-\frac{1}{2}\sqrt{\Omega-\xi-\Delta+\Gamma};$

$cr_4 = \frac{-1}{1+\gamma}+\tau+\frac{1}{2}\sqrt{\Omega-\xi-\Delta+\Gamma};$

where $\tau = \frac{\sqrt{-\gamma+\gamma^2}}{\sqrt{2}\sqrt{1+2\gamma+\gamma^2}}; \xi = \frac{6}{1+\gamma}; \Delta = \frac{2+2\gamma}{1+\gamma}; \Gamma = \frac{\sqrt{1+2\gamma+\gamma^2}(\frac{-64}{(1+\gamma)^3}+\frac{96}{(1+\gamma)^2}-\frac{32}{1+\gamma})}{4\sqrt{2}\sqrt{-\gamma+\gamma^2}}; \Omega = \frac{8}{(1+\gamma)^2}.$ In spite of the large number of free critical points, however, they are not completely independent of each other, but they are interconnected and together influence the dynamical behavior of the iterative method, as $cr_1 = \frac{1}{cr_2} and \ cr_3 = \frac{1}{cr_4}.$

Proof. Under the assumption that $x \in \mathbb{C}$ indicates certain values of $\delta(x) = 0$ if we $\varrho (x) = 0$, and combine these two equations, by eliminating the parameter $\gamma$, we get $\frac{(1+x)^3(-1+x^3)}{x^3} = 0$, which can be reduced to $(1+x)^3(-1+x^3) = 0$. It follows that $(1+x)^3$ and $(-1+x^3)$, which can be a common factorization of $\delta(x) = 0$ and $\varrho(x) = 0$. As a result, substituting $x = -1$ for $\delta(x) = 0$ and $\varrho(x) = 0$ gives the parameter $\gamma = 0$, at which point $\frac{\delta(x)}{\varrho(x)} = -2$, and there are four critical points. The equation $(-1 + x^3) = 0$ is solved to solve for $x = 1, x = -(-1)^\frac{1}{3}$ and $x = (-1)^\frac{2}{3}$. The equation $(-1 + x^3) = 0$ is then solved to solve for $\gamma = 1$ and $\gamma = -8$. There are four critical points in $D_e'(x) = \frac{6x^2(1+x)^2}{(1+2x)^2}$ when $\gamma = 1$. When $\gamma = -8$, $D_e'(x) = \frac{-3x^2(1+x)^2(7+10x+7x^2)}{(1+4x+7x^2)^2}$ has two critical points. □

3.4.   Study of parameter spaces and dynamical planes

The dynamic plane $H$ and the parameter plane $Q$ are plotted and used to visualize the dynamical behavior associated with the iterative method (1.6). In the process of plotting the parameter plane, each $\gamma$-value is located in the same connected region of the parameter space, resulting in a series of subsets of methods (1.6) with similar dynamic behavior. Thus, more stable regions can be identified in the parameter plane, allowing us to extract more members with stability from the family of iterative methods (1.6).

$Q = \{\gamma\in \mathbb{C}$ : the free critical point $cr$ whose orbit converges to $\kappa_q \in \widetilde{C}$ under the influence of the operator $D_e(x; \gamma) \}$.

$H = \{x\in \mathbb{C}$ : for a given $\gamma\in Q$, the orbital of $x\left(\gamma \right)$ tends towards a certain number $\kappa_h \in \widetilde{C}$ under the action of $D_e(x; \gamma)\}$.

3.4.1.   Parameter spaces

By Theorem 3, there are, at most, three free independent critical points that can be observed. Furthermore, we recognize that $x = -1$ is actually the mapping point of the fixed point $x = 1,$ and this critical point does not show a distinctive feature on the parameter plane. Thus, we can distinguish two unique parameter planes that each carry complementary information.

When analyzing the free critical point $cr_1$ (or $cr_2$) as the starting point for a series of iterative methods (1.6) associated with a particular complex value, we color the complex plane according to the convergence properties of the different methods. The corresponding point is labeled in red in the complex plane if the iterative method (1.6) converges to zero. If the convergence is to a non-zero value, then it will be marked in blue. For all other cases, points will be marked green. Figure 3 depicts the parameter plane for the iterative method with the initial point set to $cr_1$. The figure is generated within the range of $\gamma$ values $[-40, 20]\times [-30, 30]$ and $[-5, 5]\times [-5, 5]$, using a grid of $1000 \times 1000$ points and computed with $50$ iterations for each point. Figure 3b provides a more detailed presentation of the situation in Figure 3(a). In Figures 3 and 4, it is observed that the red region represents the iterative method converging to $0$, the blue region represents convergence to infinity, and the green region indicates convergence to $0$. In this final parameter selection process, we should try to avoid using green parameter values and prioritize red or blue parameter values to ensure the stability of the iterative process.

3.4.2.   Dynamic planes

The iterative method (1.6) has a dynamic plane influenced by the parameter $\gamma$, and the regions are marked with different colors. The region where the initial point converges to $0$ we color orange, and the region that converges to infinity is marked blue. The region is green if the initial point converges to the fixed point $x = 1$. Black regions indicate no convergence to any root if the initial point converges to black. Additionally, the iteration track is set to red. The dynamic planes are built on a $400 \times 400$ point grid, with each point undergoing an iterative process of up to $20$ iterations. In Figure 5, the parameter planes that correspond to some specific parameter values are shown. When $\gamma = 0,$ the blue and orange regions are the only ones, indicating that the initial points converge only to $0$ and infinity. This parameter value is therefore considered to be a desirable value to take. For $\gamma = -8$ and $\gamma = 1,$ some black regions appear in Figure 5, and the initial values of these black regions do not converge to any root, suggesting that these parameter values are not ideal choices.

Figure 6: Dynamic planes for special parameter values $\gamma$. We have selected the parameter values that satisfy the condition $\lvert 8 + \gamma \rvert > 24$ and divided these values into two subsets; a group of smaller values, specifically $\gamma = 20, 30,$ and a larger group of values including $\gamma = 1300, 1340, -1500.$ A related graphical presentation can be found in Figure 6. We plot $\gamma = -7000, 10,000;$ refer to Figure 7.

The dynamic plane shows only orange and blue as stable parameter regions. The larger the absolute value of the parameter, the more complex the structure on the dynamic plane tends to be. Putting these observations into context, it is possible to conclude that the corresponding iterative method shows better stability when $\gamma = 0.$

4.   Numerical experiments

In this section, we conduct a series of numerical experiments aimed at verifying the theoretical convergence and stability predictions made in previous sections for the method (2.17)(XM). The iterative methods (2.17) (XM) are compared with Homeier's method (HM) ^[31] and Chun's method (CM)^[32] for solving some nonlinear equations. Then two numerical experiments are carried out to solve the nonlinear systems.

Homeier's method (HM) ^[31]:

where $y^{(n)} = x^{(n)}-S'(x^{(n)})^{-1}S(x^{(n)})$.

Chun's method ^[32]:

where $y^{(n)} = x^{(n)}-S'(x^{(n)})^{-1}S(x^{(n)})$.

Within Tables 1 and 2, the time column demonstrates the computing time, the $x_0$ column labels the starting point in the iterative process, ACOC ^[33] denotes the approximate convergence order.

We use six nonlinear equations mentioned in references ^[34,35] for the in-depth study.

Additionally, we explore population growth patterns^[36]: population dynamics are analyzed by means of a first-order linear ordinary differential equation as follows:

where $c$ stands for a constant birth rate and s stands for a constant migration rate. $P(x)$ is used to represent the total population size at any random time point $x$. By solving the linear differential equation, we can get its generalized solution

By $P_{0}$, we denote the initial population size. Examining and exploring the multiple possible values of the parameters and combining them with the initial conditions provided in the literature ^[37], we can accurately calculate the birth rate by using the nonlinear equation below:

$s_6(x) = 1564-1000e^{x}-\frac{435}{x}(e^{x}-1), \varepsilon\approx0.1009979328831604$.

Here, $c = k$ represents the ideal birth rate we wish to determine.

Example 1. Take the nonlinear system

where $x_1$ and $x_2$ are the unknowns in the nonlinear system (4.5).

Example 2. Take the nonlinear the system of equations for the Hammerstein equation, which plays a crucial role in nonlinear integral equations:

where $x\in \mathbb{C}[0, 1], x, t\in[0, 1]$. The kernel function $M$ is

A system of nonlinear equations is formed by discretization and solved (4.6) by approximating the integral in Eq (4.6) by the Gauss-Legendre product method.

Here, $t_{j}$ and $w_{j}$ are the nodes in the Gauss-Legende product method and the weights. Denote the approximation of $s(t_{j})$ as $x_{i}, i = 1, \ldots, 7$

where

According to Table 1, the iterative method (1.6) has high computational accuracy. Compared with other methods, the iterative method (1.6) takes less time for calculation. In Table 2, different values of stabilization parameters such as $\gamma = 0, \gamma = 1$ and $\gamma = 9,$ are chosen, and the iterative method (1.6) has better convergence. Tables 3 and 4 are numerical experiments for solving nonlinear systems.

5.   Fractal results

This section draws fractal graphs for different iterative methods used to solve the nonlinear equation ${S_1}(x) = x^2-1$. The iterative methods we compare include AM (when parameter $\gamma = 0$, iterative method (1.6) is defined as AM), K2 (when parameter $\gamma = -1$, iterative method (1.6) is defined as K2), Solaiman's method (MH), and Kou's method (KW).

Solaiman's method ^[38] (MH):

Kou's method ^[39] (KW) :

where $y^{(n)} = x^{(n)}+S'(x^{(n)})^{-1}S(x^{(n)})$.

We created a $500 \times 500$ point grid to generate images in the region $\mathbb{D} = [-5, 5]\times[-5, 5]$. The maximum number is 25 iterations. Blue, red, and yellow areas respectively, converge to the roots of the polynomials, whereas areas that do not converge within the maximum number of iterations are in black. The number of iterations is indicated by the brightness of the colors. For example, regions with fewer iterations show brighter colors. From the fractal maps, method AM showed better convergence than the other methods. Therefore, the iterative method (AM) has better convergence and stability than the other methods.

6.   Conclusions

The paper investigates the complex dynamic behavior exhibited by Kou's extended iterative method, which is used to solve systems for nonlinear equations. Strange fixed points and critical points of the iterative method (1.6) are intensively studied. We found the relevant parameter plane and select some parameter values for further analysis. Some unique parameter planes with values such as $\gamma = 0, -1$ and $9$ are observed. By observing the parameter plane and the dynamic plane, we discover the parameter $\gamma = 0$ to have good stability. Numerical experiments and dynamic analyses both agree with each other, verifying the accuracy of the conclusion. We will study the iterative methods with higher convergence and their stability in the future.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgements

This research was supported by Educational Commission Foundation of Liaoning Province of China (No. LJ212410167008), the Key Project of Bohai University (No. 0522xn078), and the "14th Five-Year Plan" Project of Liaoning Province Education Science (No. JG24EB014).

Conflict of interest

The authors declare there are no conflicts of interest.