1.
Introduction
In order to meet new requirements, waveforms must be rethought. This involves incorporating improved features such as lower latency, complexity, power efficiency, quicker data rates, and higher security [1,2]. The filter bank multicarrier (FBMC) modulation is anticipated to address the drawbacks of orthogonal frequency division multiplexing (OFDM). However, despite being under development since the 1960s [3,4], FBMC is not widely used, primarily due to its complex implementation. While FBMC is well known for its superior spectrum efficiency and requiring less precise synchronization compared to OFDM, this advantage stems from its unique system design. In the FBMC system, each subcarrier is filtered, resulting in increased spectral efficiency. Consequently, guard bands are not always necessary for FBMC. Offset quadrature amplitude modulation–based filter bank multicarrier (FBMC-OQAM), an enhanced version of FBMC [5], utilizes quadrature amplitude modulation (QAM) symbols where the in-phase and quadrature components are separated by a half-symbol time. Here, OQAM stands for offset QAM.
One method to enhance the reliability of a communication system is through channel coding. This technique introduces redundancy into the transmitted data, thereby boosting its resilience against errors caused by interference or noise. However, it is important to note that while channel coding increases error resistance, it may also lead to higher bandwidth requirements and increased system complexity.
There are several commonly used channel codes in digital communication, such as error-correcting codes, forward error correction (FEC), convolutional codes, block codes, and turbo codes. Turbo codes, in particular, have gained popularity due to their effectiveness in enhancing communication reliability. Recent works [6,7] have explored precoding schemes to further improve the performance of turbo codes when combined with FBMC modulation. In [6], a novel precoding technique based on a pruned discrete Fourier transform (DFT) combined with one-tap scaling was proposed, offering reduced out-of-band emissions and maintaining a favorable peak-to-average power ratio without requiring a cyclic prefix. Additionally, Wang et al. [7] introduced a non-sinusoidal orthogonal transformation–based data-compressed transmission technique to address FBMC's bi-orthogonality and remove imaginary interference. These advancements, along with the integration of machine learning (ML) approaches and Alamouti code, demonstrate the potential for enhancing FBMC performance in conjunction with multiple-input multiple-output (MIMO) techniques.
Erdal Arikan first suggested polar codes as channel codes in 2009 [8]. The channel polarization theorem, which asserts that every memoryless, binary-input channel can be divided into parallel good and bad channels, is the foundation of polar coding. Polar codes are designed to leverage this concept by allocating parity bits to the bad channels and data bits to the good channels. Consequently, polar codes can achieve high error-correction performance using simple decoding techniques.
While the bit error rate (BER) performance of polar-coded FBMC-OQAM across a multipath fading channel has been investigated [9,10], the results obtained were not comprehensive due to the use of fixed code rate and codeword length values. To the best knowledge of the authors, polar-coded FBMC-OQAM over various channel models has not yet been investigated. Therefore, this research aimed to fill specific knowledge gaps regarding the performance of polar-coded multicarrier systems in various channels.
This paper's contributions encompass the following aspects: First, it conducts a rigorous performance analysis of FBMC-OQAM systems employing polar codes for error correction. This analysis is conducted across two distinct channel environments: additive white Gaussian noise (AWGN) and Nakagami-m channels, providing insights into the system's behavior and robustness in different scenarios. Additionally, the paper contributes to the field by comparing the performance of the proposed FBMC-OQAM system with polar codes against state-of-the-art systems, notably turbo-coded FBMC-OQAM. This comparative analysis offers valuable perspectives on the efficacy and efficiency of the proposed approach, aiding in the advancement of communication system design.
The paper is organized as follows: Section 2 presents a literature review, Section 3 discusses FBMC-OQAM, Section 4 describes the channel codes, Sections 5, 6, 7, and 8 cover turbo codes, Nakagami-m flat fading channel, code interleaving, and simulation results, respectively, and Section 9 concludes the paper.
2.
Literature review
Numerous works have examined the performance of polar codes. Some of them compare it to other channel coding schemes with specific decoding and encoding algorithms, while others compare the performance of the code with different construction and decoding algorithms [8,11,12,13]. In this section, we will discuss works related to polar code construction and decoding algorithms, as well as their connection to FBMC modulation.
Polar coding, introduced by the authors in [8], aims to meet minimal encoding and decoding complexity criteria while achieving capacity-achieving codes for symmetric binary-input discrete memoryless channels (B-DMCs). Various well-known and effective techniques for constructing polar codes in the presence of an AWGN channel are discussed in [8,11]. BER results for the code-creation algorithms are presented in [12], along with complete pseudocode implementations of all construction algorithms. In their simulations, the modulation system employed is binary phase shift keying (BPSK). The study's results demonstrate that the BER performance of all construction approaches is nearly identical, leading the authors to conclude that researchers should prioritize ease of implementation without sacrificing performance. Notably, polar encodings exist in systematic variants [11], which have been shown in the aforementioned articles to be more effective in error correction.
When block fading channels are present, two methods have been suggested to enhance the code's performance. The first technique involves using a code interleaver, which causes code words to appear random and noisy by permuting them to spread out after burst faults [12]. The second method utilizes the transmitter side's channel information (CI) to create the code. Specifically, this method generates the code based on the channel state information (CSI) of the transmitter. However, as demonstrated in [14], this approach to polar code creation for fading channels requires complex numerical optimization processes, in contrast to the first method. It is important to note that the first decoder on the list is the successive cancellation decoder (SCD), which is essential for all more advanced decoders that outperform others.
Among the works that have been examined are those comparing different state-of-the-art coding techniques with the polar coding system. The three most important performance factors for evaluating a channel coding scheme are its BER performance, error floor performance, and implementation complexity. The hardware resource requirements and energy consumption of a particular channel coding scheme are determined by its implementation complexity, primarily related to the decoder [15]. In [14], the hardware efficiency and BER performance of polar codes are compared with turbo and low-density parity check (LDPC) codes. The study compared three polar decoding algorithms—the successive cancellation (SC), successive cancellation list (SCL), and belief propagation (BP) decoders. The authors concluded that polar codes might exhibit lower hardware efficiency, primarily due to the inferior performance of simple implementation complexity algorithms (BP and SC) compared to turbo and LDPC. Low throughput is a concern with polar codes using the SCL decoder, although they demonstrate comparable error correction performance with LDPC. The authors suggested that increasing the SCL decoder's throughput could enhance the effectiveness of polar code implementation.
The authors of [5] examined the BER performance of polar-coded multicarrier modulation in the presence of both AWGN and fading channels. They selected a code word length of N = 1024 and a coding rate of R = 0.5. Employing both BP and SC varieties of polar decoding algorithms, they found that polar-coded multicarrier modulation with BP consistently outperformed turbo-coded multicarrier modulation systems when using 4-QAM as the modulation order. However, it should be noted that their findings might have differed if they had considered different code word lengths (N) and code rates.
Additionally, the authors of [8] investigated the performance of polar-coded multicarrier modulation in the presence of various multipath channels. Similar to the previous study, they utilized a fixed code word length (N) of 1024 and a coding rate (R) of 0.5. However, they employed SCL decoders instead of SC/BP decoders. Their research revealed no coding gain for polar codes compared to convolutional codes, contradicting several other findings. For instance, reports in the literature [5,14] suggest that the error-correcting performance of polar codes with SCL is comparable, if not superior, to that of turbo and LDPC codes.
The research conducted on FBMC modulation sheds light on its performance characteristics and comparisons with OFDM in various scenarios. In one study [16], the authors delved into the BER performance of FBMC-OQAM systems over Rayleigh flat fading channels, particularly examining the impact of phase offset on BER. They found that any phase deviation during user detection can significantly impair FBMC-OQAM system performance. Another investigation [17] explored FBMC-OQAM systems with different modulation levels, focusing on BER analysis using the zero-forcing (ZF) method for signal detection. Their findings showcased that employing ZF in FBMC-OQAM systems can lead to lower BER values. Additionally, OFDM systems are known to suffer from high peak-to-average power ratio (PAPR) values and computational challenges due to Fast Fourier Transform (FFT) operations. A comparison study [18] between OFDM and FBMC for MIMO systems revealed that OFDM offers robustness against interference and lower error rates but exhibits a high PAPR. On the other hand, FBMC demonstrates superior spectral efficiency through optimized power spectral density (PSD). To address the PAPR issue in FBMC, a novel technique [19] involving clipping and filtering (CF) alongside adaptive PAPR reduction strategies was proposed. This method effectively mitigates interference and enhances system performance, though it is noted that conventional PAPR reduction methods are computationally demanding. In summary, these studies provide insights into the performance characteristics of FBMC modulation, its comparison with OFDM, and potential techniques to mitigate its drawbacks, such as high PAPR values.
The investigation conducted in [20] introduces low-complexity polyphase network FBMC (PPN-FBMC) receivers designed for upcoming 5G systems. It explores the application of the sliding window equalizer method in scenarios with multiple paths and improves overall system performance through the utilization of hopping discrete Fourier transform (HDFT) and overlapped window adjustments. Nevertheless, this research faces challenges related to significant computational complexity and issues encountered in environments with multiple propagation paths. Conversely, the research conducted in [21] focuses on developing channel estimation and equalization strategies aimed at mitigating inter-carrier interference and inter-symbol interference. It creates a 2D channel model specifically for OQAM-FBMC systems, resulting in a noteworthy enhancement of 3–5 dB in channel estimation precision and a substantial four orders of magnitude decrease in equalization requirements.
3.
FBMC-OQAM
Utilizing QAM symbols with in-phase and quadrature components separated by a half-symbol time, FBMC-OQAM is a variant of FBMC [5]. Offset QAM is known as OQAM. In FBMC-OQAM, offset OQAM processing is employed to operate at the highest efficiency possible. This processing technique increases spectrum efficiency by 15%–35% [22]. Fast Fourier Transform (FFT) modules can be used to develop FBMC-OQAM transceivers. There are two options for quickly implementing FBMC-OQAM: frequency spreading FBMC (FS-FBMC) and poly-phase network filter bank multicarrier (PPN-FBMC). In this study, we will concentrate on FS-FBMC [5,23]. The type of prototype filter used significantly impacts the performance of FBMC systems [23]. First, it affects the out-of-band (OOB) emission by determining the system's PSD. Second, it affects the inherent interference of the FBMC-OQAM system. Internal interference can degrade pilot symbols, thereby affecting channel estimations [24,25,26]. Therefore, when selecting prototype filter types, it is essential to choose filters that produce minimal OOB emission and inter-symbol interference (ISI).
The prototype filter is characterized by the overlapping factor K, which is the ratio between the length of the impulse response and the multicarrier symbol period. The overlapping factor K also specifies the number of multicarrier symbols that overlap in time. K is always a positive number. The FS-FBMC transceiver requires a larger kN-sized inverse FFT (IFFT) and FFT than OFDM and PPN-FBMC for a total of N subcarriers. This requirement is due to FS-FBMC's wider frequency range. Larger IFFT and FFT sizes enable FS-FBMC to utilize the spectrum more effectively and perform better in the presence of interference.
The evaluation of the traditional single-tap receiver in FBMC-OQAM in comparison to the FS receiver in FBMC-OQAM has been examined in order to comprehend the impact of coding on the performance of these structures in [27]. Studies show that coding can have an impact on the performance of both structures. Within the FBMC-OQAM framework, particular emphasis was placed on the FS receiver for its potential to excel and surpass the traditional single-tap receiver. This is due to variables such as filter length in the time domain and channel dispersion. The efficiency of the FS receiver within FBMC-OQAM was recognized, particularly in relation to varying FFT sizes and their effects on performance across specific channels.
The FBMC/OQAM modulated signal can be described by the following equation:
where j=√2−1, Sk[m] is the mth QAM symbol of the kth subcarrier, and p[n] represents the prototype filter. The ejπ2k introduces orthogonality between the neighboring subcarriers.
The signal that was received can be modeled as follows [28,29]:
where h[n] is the multipath impulse response, w[n] is the additive noise, and * stands for the convolution operator.
At the receiver side, after applying the FFT algorithm to recover the transmitted QAM symbols, the received signal is first passed through a receiver filter bank. Since the received signal is in the frequency domain, the filtering process involves multiplying the received signal R[k] with the frequency coefficients 𝐻𝑘 of the prototype filter. The estimated received QAM symbol can be [6]:
where r[n] denotes the received signal. The total number of subcarriers employed in the system is N, Hk represents the frequency response of a specific prototype filter, K represents the overlapping factor, and the index k' stands for frequency domain index. The terms e−j2πKN and e−jπ2(k+1) are known as phase de-rotation factors. The phase de-rotation factors reverse the effect of the phase rotation factors in Eq (1).
This study used a frequency-spreading filter bank multicarrier (FS-FBMC) receiver, ^Sk[m], to represent the output QAM symbols, as seen from Eq (3). These symbols are complex-valued, and hence ^Sk[m] has two terms (i.e., imaginary and complex).
4.
Channel codes
4.1. Polar codes
In order to achieve the capacity of binary symmetric channels, the first channel-coding technique to do so was polar codes, which were first introduced by Erdal Arikan in 2009. Polar codes have been selected by the third-generation partnership project (3GPP) as error-correcting codes for the 5G new radio (NR) control channels [30]. They belong to the family of block codes [8]. The channel coding scheme—channel polarization—as well as the encoding and decoding techniques that are considered essential and will be used in the simulation are covered in the following sections.
4.1.1. Polar encoding
A (E, Q) polar code represents a block code rate R = Q/E, where E is an integer power of 2. (2nwheren>0) represents the code word length, and Q(Q≤E) represents the number of information or message bits. The equation for the E size polar transform is given in [6] as:
where GE is the code generator matrix of size E×E, whereas n=log2E. ⊗ represents the Kronecker product that produces a block matrix by taking two matrices. Thus, the generator matrix GE is nth Kronecker power of G2. From (4–5), it can be inferred that the 2×2 G2 is the essential kernel of all polar codes of any length E. The input to the generator matrix is a vector uE1=(u1,u2,u3……….uE). This input vector, u1, also contains the E-Q frozen bits. The output row vector of the generator matrix is given in [6] as:
where BE is called the permutation matrix, which is defined in [6] recursively as: BE=RE(I2⊗BE╱2), where I2 is a 2×2 identity matrix. The RE matrix is a reverse shuffle permutation matrix when multiplied by the input vector uE1, the odd-numbered components are copied in the first E/2 outputs, and the even-numbered inputs are copied in the last E/2 outputs. The effect of the reverse reshuffle permutation matrix, RE, is as follows:
4.1.2. Polar decoding
For long code lengths, polar codes decoded by a SCD may attain the capacity of the B-DMC [8]. The SCD decoder is just one of many enhanced versions available, with the SCD algorithm being a key component. Additionally, there are other polar decoding algorithms known to the authors, including SCL [31], successive cancellation flip (SCF) [32], belief propagation (BP) [33], and sphere decoding (SD) [34].
In FBMC, the calculation of the log-likelihood ratio (LLR) is influenced by interference, noise, and various other factors. It is crucial to accurately account for interference, noise, and other influencing factors when modifying the likelihood function to effectively address these effects. An equation for the LLR, which considers interference and noise, can be derived by incorporating the joint probability distribution of the received signal conditioned on the transmitted signal.
In the successive cancellation decoding, the ith estimate of ui or (ˆuii) depends on both the received vectors yE1 and the previously estimated ˆui−1i. The corresponding ˆuii is chosen based on its LLR, which is represented as follows [8]:
The hard decision of ˆuii is then found in the manner shown below [8]:
Based on the encoding graph of polar coding, the LLR of ˆuii can be computed recursively, as described in [8]. Let us define two new functions g(a,b,k) and f(a,b,k):
where a and b are real numbers (a,b∈R) and k∈{0,1}. g(a,b,k) and f(a,b,k) are mapping functions
5.
Turbo codes
Turbo codes, a kind of parallel concatenated convolutional codes (PCCC), were first discussed by Berrou et al. in 1993 [35]. The Shannon limit, which is the theoretical upper bound of error-correction performance for a given channel, was the motivation behind the development of turbo codes. Using two or more convolutional codes simultaneously and combining their outputs using an interleaver is the fundamental concept behind turbo codes. The bit errors are essentially randomized by the interleaver, which makes them easier for the decoder to fix. Similar to PCCC, turbo codes entail iterative decoding of the incoming data using the Bahl-Cocke-Jelinek-Raviv (BCJR) algorithm [33]. Turbo codes can reach error-correction performance close to the Shannon limit with minimal complexity, as shown by [35], making them appropriate for use in practical applications. Due to their great error-correction capacity and low complexity, turbo codes have since become widely utilized in a variety of communication systems, including wireless communication systems and satellite communication systems [35].
5.1. Turbo encoder
Utilizing an interleaver between two or more concurrent concatenated convolutional encoders forms the foundation of turbo encoding [36]. The first convolutional encoder interleaves the input data before encoding it. Subsequently, the output of the first encoder is interleaved once more before being encoded by the second convolutional encoder. This second encoder's output is then sent through the channel. The error-correction ability of the code is enhanced by the use of multiple encoders and interleaving, making it more resistant to noise and other channel imperfections.
Let C1 and C2 be the names of the two constituent convolutional codes. The generating polynomials for these codes are 𝑔1 (𝐷) and 𝑔2 (𝐷). Using the input data 𝑢, the encoder for C1 generates the parity sequence 𝑝1. In a similar manner, the encoder for C2 accepts 𝑢 and outputs 𝑝2. The encoding procedure can be expressed mathematically as:
The turbo codeword c is formed by the interleaved sequences of parity 𝑝1 and p2. The goal of the interleaving is to decorrelate errors that the channel introduced. The interleaved parity sequences p1 and p2 are combined with the original data u to generate the turbo codeword c.
5.2. Turbo decoder
A soft-input soft-output maximum a posteriori (MAP) algorithm is used to decode turbo-encoded data. This algorithm looks for the most likely transmission sequence given the received data and any prior knowledge of the transmitted sequence [37]. The MAP algorithm calculates the likelihood of each possible sent sequence given the received data through an iterative process. This technique employs a trellis to represent every possible communicated sequence, calculating each sequence's likelihood by summing the probabilities of all the paths leading to it. Unlike hard-decision decoding, which produces a single binary value for each bit level, the MAP algorithm achieves soft-decision decoding, providing a set of likelihood values for each bit in the decoded sequence.
A probability distribution can be estimated using the MAP estimation technique based on observed data. Estimating the most likely transmitted message from the noisy signal received is crucial for decoding. This is formulated using Bayes' theorem:
The posterior probability of the message transmitted given the signal received is denoted by P (u/r). The likelihood function, P(r/u), is the probability of receiving the signal r, provided that u was transmitted. P(u) represents the prior probability of the sent message, indicating any preconceived notions or knowledge prior to the observation of the received signal. P(r), sometimes referred to as the evidence or marginal likelihood, is the probability of receiving the signal r.
MAP decoding entails using the soft information received to determine the most likely transmitted message. To do this, one must maximize the posterior probability P (u/r) over all feasible transmitted messages. Soft information is sent between the decoding graph's check nodes, which stand in for parity checks, and variable nodes, which represent bits, as the decoding process moves forward. The reliability of estimations of the transmitted message bits is improved by this information exchange. Iterative MAP decoding is frequently used to improve soft estimates. In each iteration, the soft information is usually updated using the current estimates, and the sent message is then re-estimated using the updated soft information. The iterative process continues until a stopping condition is satisfied, such as reaching the maximum number of iterations.
6.
Nakagami-m flat fading channel
The fading of wireless channels is frequently modeled using the Rayleigh and Rician distributions. However, the Nakagami-m distribution is more adaptable and often provides a better fit to experimental data, as it can mimic a wider variety of fading conditions compared to the Rayleigh and Rician distributions [38].
The likelihood that a random variable is less than or equal to a specific threshold, given that the random variable has a particular mean, variance, and fading parameter, is the Nakagami-m distribution. The fading severity is determined by the fading parameter, m, where a Rayleigh distribution corresponds to m = 1, and a Rician distribution corresponds to m = ∞.
The probability density function (PDF) of the received signal envelope when the Nakagami-m fading channel is present is provided in [38,39]:
The Nakagami-m fading model is widely used in communication systems because of its adaptability in representing various fading scenarios, from moderate to intense circumstances. The parameter 'm' plays a crucial role in determining the severity of fading: lower values of 'm' indicate more intense fading, while higher values suggest less severe conditions. Understanding the significance of 'm' in FBMC-OQAM systems is essential for developing resilient communication strategies tailored to specific channel attributes. This understanding enhances system performance across diverse channel conditions.
7.
Code interleaving
Bursty errors are errors that occur one after another. Many communication systems experience this type of error. Although various algorithms are designed to address these issues, a common practice is to spread out the errors, so they appear randomly to the channel decoder. This process is known as interleaving, which involves a permutation of indices.
The most straightforward type of interleaver is one with a random permutation sequence.
8.
Results and discussion
During simulations, the channel models exhibit varying characteristics, ranging from noisy to fading conditions. Specifically, the fading phenomenon manifests as non-deterministic in nature, with the Nakagami-m fading channel representing a prominent type within this category.
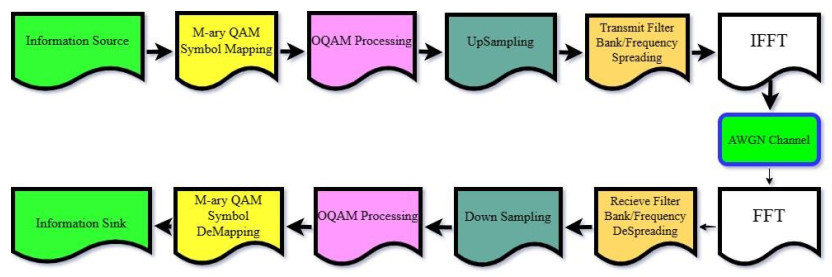
In the simulation, the FBMC-OQAM transceiver depicted in Figure 1 has been employed. Various channel environments have been engaged for the simulations.
Polar codes necessitate accurate channel statistics for the efficient positioning of the message bit. Consequently, the identification of the optimal channel for transmitting the message bits may be inaccurate when the channel characteristics are unknown, resulting in a decline in performance. The methodology adopted in this study involves the utilization of the polar code construction technique, originally intended for the AWGN channel but exhibiting suboptimal performance in fading channels. To address this challenge, a random code interleaver has been implemented.
In polar code constructions, only powers of two are permissible. When conducting a comparison between polar and turbo codes, the sizes of the turbo equivalents that are considered comparable are established by identifying the power of two that is in closest proximity to the lengths of the polar codes. Consequently, although the code rates may not be identical, they exhibit a significant degree of resemblance, with the code lengths employed in the comparisons remaining consistent.
When assessing BER values, the number of runs considered is frequently dictated by various factors, including the desired level of statistical confidence, the computational resources at hand, and the intricacy of the simulation configuration. Numerous simulation trials (commonly falling within the range of hundreds to thousands) are routinely conducted in scholarly investigations to ensure the statistical validity of the findings. For this particular examination, 200 runs were included in the analysis.
8.1. Uncoded FBMC-OQAM over AWGN channel
In this simulation scenario, an uncoded FBMC-OQAM-modulated signal described in Table 1 was passed through an AWGN channel. The receiver then demodulated the received signal, compared it to the transmitted data, and determined the number of error bits. The simulation results, shown in Figure 3, indicate that the BER of the FBMC-OQAM system in the presence of the AWGN channel closely follows the theoretical BER data for 16-QAM modulation. This suggests that the simulation's result validates the correctness of the system model.
8.2. The effect of random interleaver on the performance of polar-coded FBMC-OQAM
The effect of random interleavers on the performance of polar-coded FBMC-OQAM has been investigated in this subsection. Polar codes are known to require accurate channel statistics to determine the best split channels for message bits. However, the polar code used in this simulation was designed for the AWGN channel, which may result in suboptimal performance. To improve the error-correcting performance of polar code, a random code interleaver has been employed. The results for the AWGN channel and for m = 1 (Rayleigh fading channel) with or without interleaving are reported in Figure 4. The simulation results showed that a system with code interleavers had additional coding gain over the uninterleaved system in the presence of the AWGN channel, as validated by equation (16). At BER = 10-3, the system with code interleaver had an additional 0.75 coding gain, while at BER = 10-4, the gain was 1 dB. Similarly, in the presence of the Nakagami-m fading channel, the system with code interleaver had a 1 dB coding gain advantage over the uninterleaved system at BER = 10-3, while at BER = 10-4, the gain advantage was 2 dB. The results clearly showed that the system with code interleavers outperformed the uninterleaved system. Overall, this study demonstrated that random interleaving can improve the performance of polar-coded FBMC-OQAM systems. The results suggest that code interleaving can be used as a simple and effective technique to enhance the error-correcting performance of polar codes in various channel conditions.
8.3. Polar-coded FBMC-OQAM over AWGN channel with different code rates
The simulation scenario involves the transmission of the FBMC-OQAM modulated signal over an AWGN channel with polar codes, as outlined in Table 1. The channel coding parameters utilized in this simulation are detailed in Table 2, encompassing factors such as the lengths of information words (Q) and code words (E). Figure 5 illustrates the system block diagram and showcases the BER performance, revealing a notable enhancement in the BER curves upon the application of polar codes to the system. The coding gain, presented in Table 4, signifies the improvement achieved by employing polar codes at various coding rates in the FBMC-OQAM system. It quantifies the disparity between the BER of the coded system and that of the uncoded system, with the table demonstrating that the coding gain escalates with decreasing coding rates. This trend can be attributed to the augmented redundancy in the transmit block associated with lower coding rates, thereby bolstering the error correction capability of the system.
8.4. Polar-coded FBMC-OQAM over AWGN channel with different frame lengths
The influence of code length on the efficacy of the polar-coded FBMC-OQAM scheme operating across the AWGN channel has been examined, revealing a discernible impact under different block sizes. The symbol parameters of FBMC-OQAM are detailed in Table 1, while the coding attributes of the channel are presented in Table 3. The analysis depicted in Figure 6 illustrates that augmenting the code length leads to a marginal enhancement in bit error rate (BER) performance. This enhancement, however, is deemed inconsequential, given that transitioning from E = 512 to E = 1024 merely yields an additional 0.25 dB in coding gain at BER = 10-3 and approximately 0.75 dB at BER = 10-5. Consequently, the findings from the simulation validate the notion that elongated code lengths hold the potential to enhance system performance.
8.5. Performance of polar-coded FBMC-OQAM over Nakagami-m fading channel
This simulation analyzes the performance of polar-coded FBMC-OQAM systems in Nakagami-m channels with m values of 0.5, 1, and 2, while maintaining Ω = 1 for all cases. The frame length and channel codes are E = 1024 and R = 1/3, respectively, in all cases. Figure 7 displays the BERs of coded and uncoded systems. From Figure 7, it is evident that increasing the fading parameter (m) for a given value of Ω leads to a reduction in the error rate, as validated by equation (15). Additionally, the polar-coded system consistently outperforms the uncoded system in terms of error rate. For instance, when the fading parameter is m = 2, the coded system requires an Eb/No of about 5.5 dB and 6.25 dB to achieve a bit error rate of 10-3 and 10-4, respectively. In contrast, the uncoded system reaches that level at 11.5 and 13.5 dB, resulting in 6 dB and 7.25 dB coding gains at those error probabilities. However, the coding gain achieved in the Nakagami-m channel is small compared to that achieved in the AWGN channel. Table 5 illustrates the coding gain achieved for different fading parameters, with the coding gain decreasing as the severity of the channel increases (as m decreases). Specifically, for m = 0.5, no coding gain is achieved due to the application of polar codes. This indicates that the fading process reduces the error-correcting capability of polar codes. When m = 0.5, it signifies severe fading conditions without a line-of-sight component, coupled with rapid fluctuations in signal strength. In such scenarios, there is typically no coding gain observed. The reason behind this is the extreme variability in signal strength, which can overwhelm the error-correction capabilities of coding schemes. In other words, the errors introduced by the fading channel may be so pronounced that they overshadow any potential performance enhancement that could be provided by error-correcting codes. Therefore, in situations characterized by m = 0.5 or similar extreme fading conditions, relying solely on error-correcting codes for improving performance may not yield significant benefits.
8.6. Performance comparison between polar-coded and turbo-coded FBMC-OQAM over AWGN channel
Figure 8 illustrates the BER performance of polar-coded and turbo-coded FBMC-OQAM systems at a rate of 1/3. For small block lengths of E = 512 and E = 516, polar codes performed nearly as well as turbo codes, with a coding gain only 0.5 dB below that of the turbo-coded system at a BER of 10-3. Nevertheless, turbo codes exhibited faster improvement in performance than polar codes for longer frame sizes. For instance, at a frame size of E = 1024 and a BER of 10-3, the turbo code held a coding gain advantage of 1 dB over the polar-coded system. These findings suggest that while polar codes can excel for small block lengths, turbo codes may be preferable for longer frame sizes in FBMC-OQAM systems with a rate of 1/3.
8.7. Performance comparison between polar-coded and turbo-coded FBMC-OQAM over Nakagami-m fading channel
Figure 9 depicts the bit error rate (BER) performance of FBMC-OQAM systems employing polar and turbo codes. It is evident from the illustration that both coding techniques demonstrate nearly identical performances. In the case of m = 1, the coding gain associated with polar codes is marginally lower than that of turbo codes, by less than 1 dB. This observation implies that in scenarios where a heightened coding gain is sought, turbo coding may prove to be a more advantageous selection over polar coding. Conversely, for m = 0.5, both coding methods showcase practically indistinguishable error performances. Hence, in this specific modulation scheme, it is apparent that both polar and turbo coding options are capable of providing comparable error-correction capabilities.
9.
Conclusions
The error rates of polar-coded FBMC-OQAM in various channel conditions (noisy and fading channels) were carefully examined in this work. Moreover, the error performance of polar-coded MCM systems was compared with that of turbo-coded MCM systems. The implementation of polar codes on FBMC-OQAM systems in the presence of noisy and fading channels was observed from the simulation results to produce a significantly enhanced bit error rate (BER). The gains achieved by polar codes are comparable to those of other cutting-edge channel coding systems, particularly turbo codes. Polar codes exhibit superior error correction performance in the presence of the AWGN channel and shorter block lengths compared with turbo codes. However, they perform similarly for medium-sized code words. The performance of polar codes does not increase rapidly with codeword size, unlike turbo codes, as evidenced in the data, where the coding gain of polar codes is inferior to that of turbo codes by Eb/No = 1 dB. Furthermore, using random code interleavers might result in an increase in coding gain of up to 0.75 dB in AWGN and 2 dB in fading channels. To conduct a more comprehensive analysis of polar-coded FBMC-OQAM, future researchers in this field can expand their research to include SCL decoders, which can achieve even better error-correcting performance.
Author contributions
Tadele A. Abose, Fanuel O. Ayana: Writing ‒ original draft, Writing ‒ review & editing; Thomas O. Olwal: Writing ‒ review & editing; Yihenew W. Marye: Writing ‒ original draft. All authors: Conceptualization, Methodology, Software, Validation, Investigation. All authors have read and agreed to the published version of the manuscript.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad:










