Efficient time second-order SCQ formula combined with a mixed element method for a nonlinear time fractional wave model

1.   Introduction

A large number of fractional partial differential equation (FPDE) models have been found in many fields of science and engineering, such as fractional wave model ^[1,2,3,4,5], fractional diffusion model ^[6,7,8,9,10], fractional FitzHugh-Nagumo monodomain model ^[11], fractional water wave model ^[12,13], fractional Maxwell model ^[14,15], fractional Allen-Cahn model ^[16], fractional constitutive model ^[17] and fractional Fokker-Planck model ^[18]. With the continuous developments of scholars' research on FPDE models, the important fractional wave equations studied by theoretical or numerical methods ^[1,2,3,4,5] have received a lot of attention. However, as scholars know that due to the existing of the fractional derivative, their exact solutions for fractional wave equations are hard to be found by some theoretical methods. So, numerical solutions of fractional wave models are studied by designing efficient numerical algorithms, such as finite element method ^{[2,19,20,21,22]}, meshless method ^[3], finite difference method ^{[23,24,25,26,27,28,29,30,31,32,33]}, spectral method ^[34,35] and collocation method ^[36,37]. In this article, we focus on the following wave model with a nonlinear term and a high-order Caputo time fractional derivative

where $\Omega = (a, b)$ is an open space domain and $J = (0, T]$ with $0 < T < \infty$ is a time interval. The source term $d(x, t)$ is a known smooth function, the nonlinear term satisfies $f(u)\in C^2(R)$ with $f(0) = 0$, and the Caputo fractional derivative is defined by

The fractional wave model (1.1), which describe many physical phenomena including nerve conduction and wave propagation, can be degenerated into the pseudo-hyperbolic equation for $\beta = 1$ and the hyperbolic wave equation for $\beta = 2$, respectively. In ^[38], Wang et al. developed a mixed element method with an $L2$-$1_{\sigma}$ formula for solving the fractional wave model (1.1) with the time Caputo fractional derivative, which was proposed by improving the $H^1$-Galerkin mixed element method ^{[39,40,41,42,43,44]}. The improved mixed element method can approach three unknown functions simultaneously. However, in ^[38], the optimal theory error result for the auxiliary variable $v$ depends on the parameter $\frac{\beta-1}{2}$, from which the optimal estimate result of $\|v(t_n)-v_h^n\|$ cannot abtained by choosing any fractional parameter $\beta\in (1, 2)$.

In this article, we develop a fully discrete mixed finite element scheme, where the mixed element method is used to approximate the space direction and the generalized BDF2-$\theta$ ^[45] that is a shifted convolution quadrature (SCQ) method ^[46] is applied to the approxiamtion of the time direction at any time $t_{n-\theta}$. Based on the formulated fully discrete mixed element method with a second-order SCQ formula, we prove the stability and derive optimal error estimates for three unknown functions. More importantly, with a comparison to the theory error results in ^[38], we can obtain the optimal error result in $L^2$-norm for the auxiliary variable $v$ at time $t_n$ by choosing the shifted parameter $\theta = 0$. Finally, we implement two numerical examples to verify our optimal theory results.

The rest of the article is outlined as follows: In Section 2, the fully discrete scheme based on the combination between a mixed element method and an SCQ formula (generalized BDF2-$\theta$) is derived; In Section 3, the stability is proven by using useful lemmas; The optimal error estimates for the fully discrete scheme are derived in Section 4. Two experiments, in Section 5, are conducted to further confirm our theoretical results. Finally, in the last section we give the conclusions and advancements.

Throughout the article, we denote by $C$ a positive generic constant which is free of time and space meshes, and may be changed at different occurrences.

2.   Fully discrete scheme

By setting the parameter $\alpha = \beta-1$ and an auxiliary variable $v = \frac{\partial u}{\partial t}$ as shown in ^[38], we get

Further, by introducing the other auxiliary variable $\sigma = \frac{\partial v}{\partial x}$, we can rewrite the model ($1.1$) as the following coupled system with the low order space-time derivatives

For the fully discrete scheme, we first divide time interval $[0, T]$ by the nodes $t_n = n\tau$ $(n = 0, 1, 2, ..., N)$ with the time step length size $\tau = T/N$, where $t_n$ satisfy $0 = t_0 < t_1 < t_2 < \cdots < t_N = T$, $N$ is a positive integer. Setting $\phi^ n = \phi(\cdot, t_n)$, the generalized BDF2-$\theta$ (See ^[45]) for the Caputo fractional differential operator with $\alpha\in(0, 1]$ at time $t_{n-\theta}$ is

The convolution weights $\{\omega^{(\alpha)}_j\}^{\infty}_{j = 0}$ are the coefficients of the following generating function with the relation $\omega^{(\alpha)}(\xi) = \sum_{j = 0}^{\infty}\omega^{(\alpha)}_j \xi^j,$

For the convenience of application in calculation, we provide the relationship among these convolution weights $\{\omega^{(\alpha)}_j\}^{\infty}_{j = 0}$.

Lemma 2.1. (See ^[45]) The convolution weights $\omega_k^{(\alpha)}$ for the generalized BDF2-$\theta$ can be arrived at by the recursive formula

For the term $\frac{ \partial v(t_{n-\theta})}{\partial x}$, we have the following formula

Now, by combining Eqs (2.2), (2.3) with (2.5), we have

where

Based on Eq (2.6), the mixed weak formulation is to find $(u^n, v^n, \sigma^n)\in L^2 \times H^1_0\times H^1$, such that

where $g(u^{n-\theta}) = f'(u^{n-\theta}), I_{0}^{n-\theta}\sigma = \tau\Big{(}\frac{1}{2}\sigma^{0}+\sum\limits_{k = 1}^{n-2}\sigma^{k}+(1-\frac{\theta}{2})\sigma^{n-1} +\frac{1}{2}(1-\theta)\sigma^{n}\Big{)}, R^{n-\theta}_{4} = g(u^{n-\theta})(\int_{0}^{t_{n-\theta}}\sigma dt-I_{0}^{n-\theta}\sigma) = O(\tau^2)$.

Setting $(\bar{u}^n, \bar{v}^n, \bar{\sigma}^n) \in L^2 \times H^1_0\times H^1$ be the time approximate solutions of $(u^n, v^n, \sigma^n)$, we have

For formulating the fully discrete mixed element scheme, we provide the following mixed finite element spaces

where $\mathbb{P}^s$ the set of polynomials of $x$ with the degree of $s \in \mathbb{N}$. Based on Eq (2.7), we obtain the mixed element scheme. That is to find $(u_h^n, v_h^n, \sigma_h^n)\in L_h\times V_h\times H_h \subset L^2 \times H^1_0\times H^1$, such that

Remark 2.2. 1) For implementing the computation based on the system (2.9), we need to consider the following case for $n = 1$. For this case, we only need to take the semi-discrete approximation of the nonlinear term

and the fully discrete approximation

2) Now, we illustrate how to derive the Eq (2.7)$(c)$. We multiply Eq (2.6)$(c)$ by $-\frac{\partial \chi}{\partial x}$, and then make the inner product on the space domain $\bar{\Omega} = [a, b]$. Taking the first term as an example, we deduce it in detail. By the integration by part, we obtain for $v\in H_0^1(\Omega)$

which also shows that $\chi$ only needs to belong to $H^1(\Omega)$. For this problem, readers can also see other references ^[39,40,41].

Remark 2.3. 1) In Ref ^[45], one can see that the generalized BDF2-$\theta$ is given by

where $\Psi^{\alpha, n}_\tau \phi$ and $\mathcal{S}^{\alpha, n}_{\tau, k}$ are called the convolution part and the starting part, respectively. If we only consider the model with a sufficiently smooth exact solution, the starting part will disappear. For this problem, readers can see the detailed illustrations in ^[45]. Here, we just study the case without the starting part.

2) Readers can know easily from many references that the following relationship between the Caputo fractional derivative and the Riemann-Liouville derivative holds

which imply that if initial values $\phi^{(j)}(0) = 0$, the equality $^{RL}_0D_t^{\alpha}\phi(t) = ^{C}_0D_t^{\alpha}\phi(t)$ holds. In this article, the Caputo fractional derivative $^{C}_0D_t^{\alpha}\phi(t)$ is written as $\frac{\partial^\alpha \phi(t)}{\partial t^\alpha}$.

3.   Lemmas and stability

Now we need to introduce some useful lemmas for the next analysis.

Lemma 3.1. (See ^[45]) For series $\{\phi^m\}$ $m\geq 2$, we have

with

In addition, we have

where $\theta \in [0, \frac12]$.

Proof. Here, we just need to take $\theta = \frac\alpha2$, and then follow the derived process as in ^[47] to get the result.

Lemma 3.2. (See ^[45])Let $\omega^{(\alpha)}_k$ be the coefficients of generating function $\omega^{(\alpha)}(\xi)$ and the parameter $\theta$ satisfies $0 \leq \theta \leq \min \{\alpha, \frac{1}{2}\}$, where $\alpha \in (0, 1)$. Then we have for any vector $(\phi^0, \phi^1, \cdots, \phi^{n})\in \mathbb{R}^{n+1}$

Lemma 3.3. (See ^[45]) With the shifted parameter $\theta \leq \frac{1}{2}$ and $\phi^0 = 0$, we have for any vector $(\phi^1, \phi^2, \cdots, \phi^n)\in \mathbb{R}^n$

where $v^{m-\theta}\doteq(1-\theta)v^m+ \theta v^{m-1}.$

Without loss of generality, we will analyze the stability of the numerical scheme Eq (2.9) for the case of the source term $d(x, t) = 0$.

Theorem 3.4. For the fully discrete system (2.9), the following stability holds

where $C$ is a positive constant independent on mesh parameters $\tau$ and $h$.

Proof. In Eq (2.9)$(a)$, we take $w_{h} = u^{n}_{h}$, use Eq (3.1) and Cauchy-Schwarz inequality as well as Young inequality to get for $n\geq 2$

Sum Eq (3.7) for $j = 2$ to $n$, and use Eqs (3.2) and (3.3) to arrive at

Letting $\psi_{h} = v^{n-\theta}_{h}$ in Eq (2.9)$(b)$, using Cauchy-Schwarz inequality as well as Young inequality, noting that $v^{n-\theta}_{h}\in V_h\subset H_0^1$ and making use of Poincaré inequality, we have

In Eq (2.9)$(c)$, we set $\chi_{h} = \sigma^{n}_{h}$, replace $n$ with $k$ and sum for $k = 2$ to $n$ to get

Use Hölder inequality as well as Young inequality to arrive at

Multiplying Eq (3.11) by $4\tau$ and using Young inequality as well as triangle inequality, we have

Now we only need to estimate the case for $n = 1$. Similar to the processes of Eqs (3.8) and (3.12), we easily derive

and

Combining Eqs (3.8), (3.12), (3.13) with (3.14), we have

Combining Lemmas 3.2–3.3, Eqs (3.9), (3.15) with (3.16), we have

Use Gronwall lemma to finish the proof.

4.   Optimal error analysis

In this section, we obtain an error estimate for the numerical scheme Eq (2.9). To facilitate the analysis, we first introduce three projection operators with the corresponding estimate inequalities.

Lemma 4.1. Define an $L^2$-projection operator $\Lambda_{h}:L^{2}(\Omega)\rightarrow L_{h}$ by

with an estimate inequality

Lemma 4.2. (See ^[41]).Define an elliptic projection operator $\Upsilon_{h}: H^{1}_{0}(\Omega)\rightarrow V_{h}$, such that

with an estimate inequality

Lemma 4.3. (See ^[41]) Define a Rize projection operator $\Pi_{h}:H^{1}(\Omega) \rightarrow H_{h}$ by

where $\mathcal{A}(\bar{\sigma}, \phi)\doteq \Big{(}\frac{\partial\bar{\sigma}}{\partial x}, \frac{\partial\phi}{\partial x}\Big{)}+\lambda(\bar{\sigma}, \phi)$ and $\mathcal{A}(\phi, \phi) \geq \mu_{0}\|\phi\|^{2}_{1}, \mu_{0} > 0$is a constant. Further, the estimate inequality holds

Theorem 4.4. With $\Lambda_{h}\bar{u}(0) = \bar{u}_h^0$, $\Upsilon_{h}\bar{v}(0) = \bar{v}_h^0$ and $\Pi_{h}\bar{\sigma}(0) = \bar{\sigma}_h^0$, there exists a positive constant $C$ independent of $(h, \tau)$ such that

Proof. For convenience, we write errors as

Subtract Eq (2.9)$(a)$ from Eq (2.8)$(a)$, set $\omega_{h} = \vartheta^{n}$, apply the projection Eq $(4.1)$ and use Cauchy-Schwarz inequality and Young inequality to obtain

Replace $n$ by $m$, sum from $m = 2$ to $n$, and use Lemmas 3.1 to have

Subtract Eq (2.9)$(b)$ from Eq (2.8)$(b)$, take $\psi_h = \xi^{n-\theta}$ and apply projection Eq (4.3) to get

Use Cauchy-Schwarz inequality, Young inequality and Poincaré inequality to arrive at

Subtract Eq (2.9)$(c)$ from Eq (2.8)$(c)$, choose $\chi_h = \delta^{n}$, apply projection Eq (4.5) and use Hölder inequality as well as Young inequality to get

Replace $n$ by $m$ and sum for $m = 2$ to $n$ to arrive at

Noting that the similar method in ^[45,48], we have

and

Multiply Eq (4.13) by $4\tau$, and combine Lemmas 4.1 and 4.3 with Eqs (4.14) and (4.15) to arrive at

Combining Eqs (4.16), (4.9) with (4.11), we have the estimate

For the case $n = 1$, we use a similar derivation to Eq (4.17) to get

Combining Eq (4.17) with (4.18) and using Gronwall inequality, we have

Apply Lemmas 3.2–3.3 and combine Eqs (4.2), (4.4), (4.6) with triangle inequality to arrive at

Combining Eq (4.20) with triangle inequality, we have

which implies that we finish the proof.

5.   Numerical tests

In this section, we will consider two numerical examples based on the linear element to validate our optimal theory results. In numerical experiments, we need to use the recursive formula provided in Lemma 2.1.

5.1.   Example 1

In this test, we calculate the convergence rate in time and space. By taking the space domain $\bar\Omega = [0, 1]$ and the time domain $[0, 1]$, the nonlinear term $f(u) = u^2$ and the source term

with given initial and boundary conditions in Eq (1.1), we can validate easily that the exact solution is $u = t^3\sin\pi x$.

In Table 1, with fixed space step length size $h = \frac{1}{1000}$ and changed time step length parameters $\tau = \frac{1}{10}, \frac{1}{14}, \frac{1}{18}$, we arrive at the approximating time second-order convergence rate in $L^2$-norm for three functions based on different parameters $\beta = 1.3, 1.5, 1.7$ and $\theta = 0.1, 0.2, 0.3$. Similarly, by choosing the same parameters $\beta$ and $\theta$ as the ones in Table 1 with space-time step length parameters $\tau = \frac{1}{2000}$ and $h = \frac{1}{10}, \frac{1}{30}, \frac{1}{50}$, we calculate the approximating a priori error results with the second-order convergence rate in Table 2. The data computed in Tables 1 and 2 show the optimal convergence results are achieved by using our method.

5.2.   Example 2

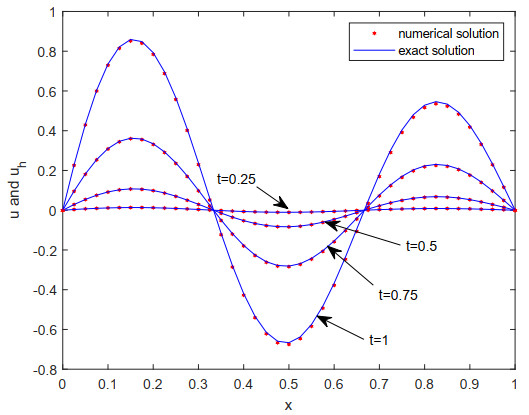
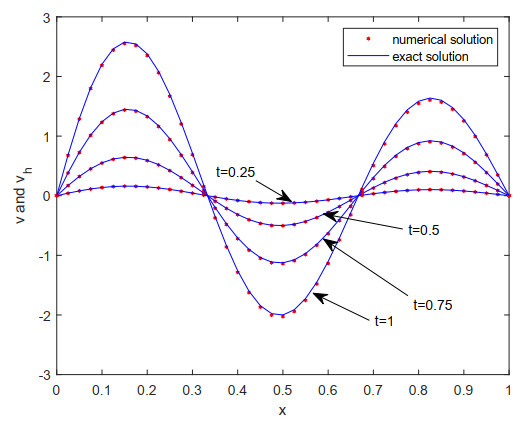
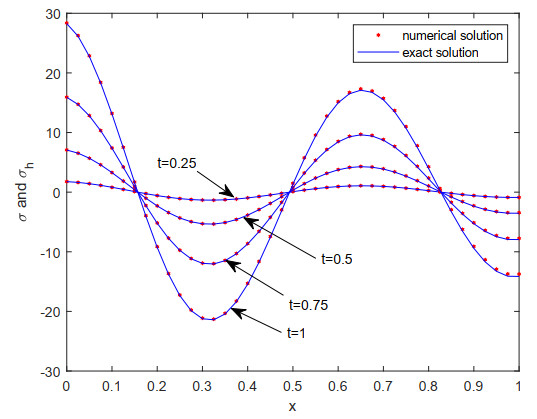
In this numerical example, we consider the same space-time domain and the nonlinear term as shown in the first example, and choose the exact solution $u = t^3\frac{\sin(3\pi x)}{x+1}$ with the corresponding source term. By choosing the space parameter $h = 1/30$, time step length size $\tau = 1/200$, fractional parameter $\beta = 1.7$ and shifted parameter $\theta = 0.3$, we obtain the comparison in Figures 1–3 between the figures of numerical solutions and the figures of exact solutions at $t = 0.25, 0.5, 0.75, 1$, from which one can visually see the approximation effect.

Remark 5.1. 1) From these two examples, readers can see that the linear basis functions for three finite element spaces are used. In this article, the presented time second-order fully discrete mixed finite element scheme is derived by combining Pani's space $H^1$-mixed element method with a time second-order SCQ formula, so it also does not need to meet the LBB condition. Further, the degrees with $k$, $m$ and $r$ of three polynomial basis functions can be freely selected.

2) By introducing two auxiliary variables, the original problem is transformed into a low order coupled system in space-time directions. In this case, many efficient numerical approximation schemes in time for solving this system can be constructed. From the computational point of view, there are some small differences among them. However, the related technical difficulty of theoretical analysis by using different approximation technique is even a big difference, which will bring many challenges to researchers. For example, in this article, the positive definite property is used for analyzing the stability and error estimate, which differs from the iterative technique shown in ^[38].

6.   Conclusions and advancements

From the data computed by our fully discrete SCQ mixed element method, one can see clearly that the convergence orders for both space and time are optimal, which is in agreement with our theory result. With a comparison to the standard Galerkin finite element method for directly solving the studied fractional wave model, the advantage of this method is that three unknown functions can be approximated simultaneously. However, the computing time problem is its limitations, which urges us to further study the fast computing technology based on this method.

In the future, we will extend this method to solve multidimensional fractional wave models and multi-term time fractional wave equations ^[49], and consider other SCQ formulas ^[46,50] and their numerical theories.

Acknowledgments

Authors thank four anonymous reviewers and editors very much for their valuable comments and suggestions for improving our work. This work is supported by the National Natural Science Foundation of China (12061053, 12161063), Natural Science Foundation of Inner Mongolia (2020MS01003, 2021MS01018), Young Innovative Talents Project of Grassland Talents Project, Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (NMGIRT2207) and Scientific Research Projection of Higher Schools of Inner Mongolia (NJZY21266).

Conflict of interest

The authors declare there is no conflicts of interest.