Maturity level of environmental management in the pulp and paper supply chain

1.   Introduction

In 1986, Barnsley ^[1] introduced the concept of the fractal interpolation functions (FIFs) as continuous functions interpolating a given set of data points. Following this, an iterative process for interpolating data that sat on a discrete closed subset of $\mathbb R^n$ was introduced by Dubuc ^[2,3] and a general construction was given by Massopust ^[4]. This construction is based on the Read-Bajraktarevic operator for the FIFs. More precisely, FIFs are generated by an iterated function system (IFS) and arise as fixed points of the Read-Bajraktarevic operator defined on suitable function space. Several authors were interested in the study of many significant properties of FIFs including calculus, dimension, smoothness, stability, perturbation error, and more (^[5,6,7]). The problem of the existence of FIF returns to the study of the existence and uniqueness of some fixed points on the fractal space, and the most widely studied FIFs are based on the Banach fixed point theorem. Recently, many researchers have studied the existence of FIFs by using different well-known results obtained in the fixed point theory, like Rakotch and Matkowski's theorems ^[9,10,11], Geraghty's theorem ^[12] and so on.

Fractal interpolation has found applications in the field of image segmentation, image analysis, image compression and signal processing (^[13,14]). In particular, uniformly sampled signal is required for the discrete wavelet transform computation when we consider the multifractal analysis to study the heart rate variability ^[15]. In order to gain more flexibility in natural-shape generation or in image compression, a new class of IFSs were introduced and were called RIFS ^[16,17]. The RIFS use elements of stochastic processes, which can provide more flexible methods since they involve local IFS ^[18,19]. It induces recurrent fractal interpolation functions (RFIFs) which main advantage is that they are not self-similar and they reflect only local similarities in contrast to the FIFs induced by the standard IFSs. Some properties of RFIFs, including statistical properties ^[20,21] and box dimension ^[22], have been studied (see also ^[17,23]). However, only RFIF, whose existence is ensured by the Banach fixed point theorem, has been considered.

In this paper, we aim to construct non-affine RFIFs using Geraghty contractions. Therefore, we present in the next section some results on RIFS and we give new conditions on the existence of the attractor of a new class of RIFS. These results will be explored in the third paragraph to define a new class of RFIF using Gheraghty contractions. Section four will be devoted to the study of the normalized root mean square errors of time series related to the vaccination of COVID-19 using RFIF, and we compare them with the obtained results on the FIF.

2.   RIFS

2.1.   Preliminary results on RIFS

Let $(\mathcal X, d)$ be a complete, locally compact metric space and $w_j : \mathcal X\rightarrow \mathcal X$, for $j = 1, \ldots, n$ are self-mappings on $\mathcal X$. We define $P = (p_{ij})$ to be an irreducible $n\times n$ row stochastic matrix associated to these maps, i.e.,

and for any $1\leq i, j\leq n$, there exists a sequence $i_1$, $i_2, \ldots, i_k$ with $i_1 = i$ and $i_k = j$ such that

A RIFS consists of an IFS $(\mathcal X, w_i, i = 1, \ldots, n)$ together with a matrix $P$ as defined above. They have their origins in the work of Barnsley and Demko ^[24] and have been developed by Barnsley et al. ^[17]. In fact, they are a natural generalization of the IFS that permits them to construct fractals as fixed points of some operators on complete metric spaces ^[16,25].

A RIFS is, in essence, a Markov chain with $n$ states. Given an initial set that is transformed through the mapping $w_i$, we should say that the chain is in state $i$. The value $p_{ij}$ is the transition probability from state $i$ to state $j$. That is, assuming that the mapping $w_i$ has been employed at the previous iteration, the probability of selecting the map $w_j$ for the next iteration is given by $p_{ij}$. The motivation underlying the necessary properties, that matrix $(p_{ij})$ should satisfy becomes apparent as a consequence of the Markov chain rationale. The first condition given by (2.1) ensures that the chain must be stochastic, that is, at every state the transition probabilities to any other state should sum up to one. The second one (2.2) means that the chain is irreducible. Namely, that we may transfer from any state of the chain to any other state. Therefore, we can be sure that, given sufficient time, all the mappings of the RIFS will be used. Otherwise, if $P$ is reducible, it is possible that some of the mappings of the RIFS will be rendered useless.

Remark 1. An IFS with probabilities $\{ \mathcal X, w_1, \ldots, w_n, p_1, \ldots, p_n\}$ ^[16] provides a simple example of an RIFS $\{ \mathcal X, w_1, \ldots, w_n, (p_{ij})_{1\leq i, j\leq n}\}$ when $p_{ij} = p_j$, for all $i, j\in\{1, \ldots, n\}$. In addition, if $p_1 = p_2 = \cdots = p_n : = p$, then the RIFS reduces to the usual IFS denoted simply by $(\mathcal X, w, p)$. Therefore, RIFSs provide more flexibility so that their attractors need not exhibit the self-similarity or self-tiling properties characteristic of IFS attractors.

Let ${\mathcal H}$ be the set of all nonempty compact subsets of $\mathcal X$. We define the Hausdorff metric $h$ by

with

Then ^[16], the space $({\mathcal H}, h)$ is complete, and compact whenever $\mathcal X$ is compact. Let $\{ \mathcal X, w_1, \ldots, w_n, (p_{ij})_{1\leq i, j\leq n}\}$ be a RIFS and let $W_{ij}: {\mathcal H}\to {\mathcal H}$ be defined as

Now, consider the space ${\mathcal H}^n = {\mathcal H}\times\cdots\times {\mathcal H}$ endowed with the metric $\tilde{h}$ defined as

and let $W : {\mathcal H}^n\to {\mathcal H}^n$ be given by

Thus,

where $I(i) = \big\{1\leq j\leq n\; \ p_{ji} > 0\big\}$, for $i = 1, \ldots, n$.

Example 1. We consider ${\mathbb I} = \Big\{ [0, 1]^2, w_i, 1 = 1, \ldots, 4\Big\}$ the RIFS equipped with the mappings

If we consider the transition matrix

then, the function $W$ is defined by

Now, let $A = (A_1, A_2, A_3, A_4)^T \in {\mathcal H}^4$ be an initial point and assume that $A_i$ was generated by applying the mapping $w_i$ to an unknown set for each $i = 1, 2, 3, 4$, then $W(A)$ is computed as

Therefore, only the maps $w_j$ with positive transition probabilities, i.e., $p_{ij } > 0$ can be applied to the set $A_i$. In particular, only the map $w_3$ is applied to $A_1$.

2.2.   Existence of attractor for a new class of RIFS

Although the Banach fixed point theorem is the most useful tool for the existence (and uniqueness) of attractors of IFS, there are numerous results in the literature related to some generalizations of the Banach principle that give sufficient conditions for the existence of a contractive fixed point (see for example ^[26,27,28]).

Definition 1. 1) Let $(X, \rho)$ be a metric space. If for some function $\varphi :(0, \infty)\rightarrow (0, \infty)$ and a self-map $f$, we have :

then we say that $f$ is a $\varphi$-contraction.

2) If $f$ is a $\varphi$-contraction for some function $\varphi : (0, \infty)\to (0, \infty)$ such that for any $t > 0$, $\alpha(t) = \frac{\varphi(t)}{t} < 1$ and the function $t\mapsto \frac{\varphi(t)}{t}$ is nonincreasing (so-called Geraghty I) (or nondecreasing (Geraghty II), or continuous (Geraghty III)), then we call such a function a Geraghty contraction.

It is easy to see that each Banach contraction is a Geraghty contraction. It suffices to consider the function $\varphi(t) = \alpha t$, for some $0\leq \alpha < 1$. Furthermore, the notions of Geraghty I and III contractions coincide when the metric space $(X, \rho)$ is compact ^[28].

Theorem 1. ^[26] Let $(X, \rho)$ be a complete metric space and $f : X\rightarrow X$ be a Geraghty contraction then there is a unique fixed point $x_\infty\in X$ of $f$, and for each $x\in X$, $\lim\limits_{n\rightarrow +\infty}f^n(x) = x_\infty$.

Theorem 2. Assume that $w_i: \mathcal X\to \mathcal X$, for $i = 1, \ldots, n$ are Geraghty contractions of a RIFS, then there exists a unique set $A = (A_1, \ldots, A_n)$, called the attractor of the RIFS, such that $W(A) = A$ and

We identify $A$ to the union of all $A_i$, that is, $A = \bigcup\limits_{i = 1}^nA_i.$

Proof. Let $\varphi:(0, \infty)\to(0, \infty)$ be a nondecreasing function satisfying $\frac{\varphi(t)}{t} < 1$ for all $t > 0$, and $t\mapsto\frac{\varphi(t)}{t}$ is nonincreasing (or nondecreasing, or continuous), such that

Then, we have

Hence, the Hutchinson operator $W$ is a Geraghty contraction and has a unique fixed compact set (Theorem 2.1). Using (2.3), this means that there exists $n$ compact subsets $A_i$, for $i = 1, \ldots, n,$ such that $A = (A_1, \ldots, A_n)$ and

□

An RIFS $\{ \mathcal X, w_1, \ldots, w_n, (p_{ij})_{1\leq i, j\leq n}\}$ is said to satisfy the open set condition (OSC) if there exists bounded nonempty open sets $U_1, U_2, \ldots, U_n$ with the property that

When the RIFS satisies the OSC, we can compute the Hausdorff dimension of the attractor generated by the system. In fact, the attractor's Hausdorff dimension reflects how space-filling or complex the attractor is. Calculating the Hausdorff dimension of the attractor is a common method of quantifying its complexity. The condition (2.5) is satisfied in the case of RFIF in section three. It prevents the interpolated curve or fractal from collapsing into itself or having degenerate, overlapping segments. It ensures that the points used for interpolation are well separated and distinct, allowing for the generation of a meaningful and nondegenerate fractal or curve.

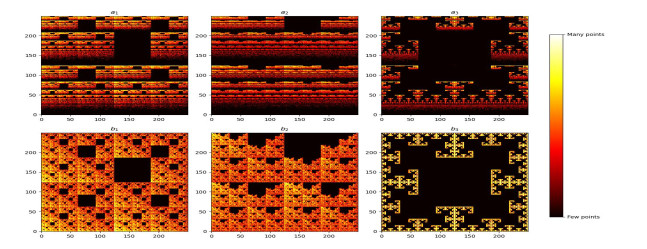
Example 2. This example involves four transformations that take the square into itself. For $1\leq i\leq 4$, the range of $w_i$ is the quadrant of the square labeled $i$. If the transition probability $p_{ij}$ is zero, no points on the attractor lie in the sub-quadrant labeled $ij$. While the structure of the attractor of the RIFS depends only on whether or not $p_{ij}$ is nonzero and not on the values of the $p_{ij}$s, the coloring and texture of the image can be controlled through the probability values (see ^[16] for more details). To illustrate that, different choices for the transition probabilities are considered. Let us consider again the mappings $w_i, i = 1, 2, 3, 4$ defined in Example 1. To construct the attractor, we apply one map of the IFS to a random selected point. Then, at each step, we apply a new map according to the probabilities of the transition of the matrix. In Figure 1 (a1, a2 and a3), we illustrate the attractors of RIFS equipped respectively with the following transition matrices :

Now, we consider $\widetilde {\mathbb I} = \Big\{ [0, 1]^2, \widetilde w_i, i = 1, \ldots, 4\Big\}$, the RIFS equipped with the mappings

where $\beta = 0.01$. These mappings are Geraghty contractions since they satisfy

with $\varphi(t) = \frac{t}{1+\beta t}$ (this fact can be proved using Lemma 1). The attractors of $\widetilde {\mathbb I}$, equipped with the transition matrices $P_1$, $P_2$ and $P_3$, are illustrated in Figure 1 (b1, b2 and b3), respectively.

3.   RFIFs

For $n\geq 2$, let $\{(x_i, y_i)\in \mathbb R^2, \ i = 0, \ldots, n\}$ be a given data set, where $x_0 < x_1 < \ldots < x_n$ and $y_i\in[a, b]$ for all $i = 0, \ldots, n$. For $i = 1, \ldots, n$, we set $I = [x_0, x_n]$ and $I_i = [x_{i-1}, x_i]$. For each interval $I_i$, we define $D_i = [x_{l(i)}, x_{r(i)}]$, with $l(i), r(i)\in\{0, \ldots, n\}$ such that $l(i) < r(i)$ and $x_{r(i)}-x_{l(i)} > x_i-x_{i-1}$. For each $i = 1, \ldots, n$, we consider $L_i :[x_{l(i)}, x_{r(i)}]\rightarrow [x_{i-1}, x_i]$ as the homeomorphism given by $L_i(x) = a_ix+b_i$ and $F_i: D_i\times \mathbb R\rightarrow \mathbb R$ as continuous mappings satisfying

Assume that $F_i$ is k-Lipschitz with respect to the first variable and a Geraghty contraction with respect to the second variable; that is

where $k\geq 0$ and $\varphi :(0, \infty)\rightarrow (0, \infty)$ is a nondecreasing function such that, for any $t > 0$, $\alpha(t): = \frac{\varphi(t)}{t} < 1$ and the function $\alpha$ is nonincreasing (or nondecreasing, or continuous). We define $w_i:D_i\times \mathbb R\rightarrow I_i\times \mathbb R$ by $w_i(x, y) = (L_i(x), F_i(x, y))$. Set $I(i) = \{j\in\{1, \ldots, n\}\; \ I_j\subset D_i\}$.

The proof of the following lemma mimics that of [9, Theorem 3.7] and [12, Theorem 3.3].

Lemma 1. There exists a metric $d_\theta$ in $I\times[a, b]$ equivalent to the Euclidean metric, such that for all $i = 1, \ldots, n$, the mappings $w_i$ defined above, are Geraghty contractions with respect to $d_\theta$.

Proof. We define a metric $d_\theta$ on $I\times[a, b]$ by

where $\theta$ is a real number that is specified in the sequel. Then, for all $(x, y), (x', y')\in I\times[a, b]$, we have:

with $a = \max\limits_{1\leq i\leq n}|a_i|$. Set $\theta: = \frac{1-a}{2(k+1)}$, then $0 < \theta < 1$ and $0 < a+\theta k+\theta < 1$. Moreover, for $t > 0$, let $\beta(t): = \max(a+\theta k+\theta, \frac{\varphi(t)}{t})$. Then, $\beta :(0, \infty)\rightarrow [0, 1)$ is a nonincreasing (or nondecreasing, or continuous), since $t\mapsto\frac{\varphi(t)}{t}$ is a nonncreasing (or nondecreasing, or continuous). Furthermore, we obtain:

where $d((x, y), (x', y')): = |x-x'|+|y-y'|$. Since $0 < \theta < 1$, then, for all $(x, y)\neq(x', y')$, we have:

Thus,

If $\beta : (0, \infty)\rightarrow [0, 1)$ is nonncreasing, then

If $\beta : (0, \infty)\rightarrow [0, 1)$ is nondecreasing, then

where $\beta': (0, \infty) \rightarrow [0, 1)$ is a nondecreasing function defined as $\beta'(t): = \beta(\theta^{-1}t)$.

If $\beta : (0, \infty)\rightarrow [0, 1)$ is continuous, then

where $\beta'' : (0, \infty) \rightarrow [0, 1)$ is a continuous function defined as $\beta''(t) : = \max_{x\in[t, \theta^{-1}t]} \beta(x)$. Hence, $w_i$ are Geraghty contractions in $(I\times[a, b], d_\theta)$. Moreover, we have:

That is, $d_\theta$ is equivalent to the Euclidean metric on $I\times[a, b]$. In particular, $(I\times[a, b], d_\theta)$ is a complete metric space. □

Denote by $C(I)$ the set of continuous functions $f : I = [x_0, x_n]\rightarrow [a, b]$. Let $C^*(I)$ be the set of continuous functions on $I$ that pass through the interpolation points; that is

Then, $C(I)$ and $C^*(I)$ are complete metric spaces with respect to the uniform metric $\rho$ defined by

Define the Read-Bajraktarevic operator $T$ on $C^*(I)$ by

It is easy to verify that $Tf$ is continuous on $I$ and that $Tf(x_i) = y_i$, for all $i = 0, \ldots, n$.

Our main result in this section is given by the following theorem. This extends [17, Corollaries 3.5] and [17, Corollaries 3.7] and the results given in ^[9,12] regarding the existence of FIF defined with Rakotch and Geraghty contractions.

Theorem 3. For $n\geq 2$, let $\{(x_i, y_i); \ i = 0, \ldots, n\}$ be a given data set and let $\{D_i\times \mathbb R, w_i; \ i = 1, \ldots, n\}$ be the RIFS constructed above. Then, there exists a unique function $\tilde{f}\in C(I)$ such that $\tilde{f}(x_i) = y_i$, for all $i = 0, \ldots, n$. Moreover, let $G_i$ be the graph of the restriction of $\tilde{f}$ to $I_i$, then $G = (G_1, \ldots, G_n)$ is the attractor of the RIFS $\{D_i\times \mathbb R, w_i; \ i = 1, \ldots, n\}$, i.e.,

Furthermore, the RFIF $\tilde{f}$ satisfies the functional equation

Proof. Let's first notice that the RIFS $\{D_i\times \mathbb R, w_i; \ i = 1, \ldots, n\}$ has a unique attractor by Lemma 1 and Theorem 2.1. Moreover, for $f, g\in C^*(I)$, we have:

Since, for each $i\in\{1, \ldots, n\}$ and every $x\in I_i$, we have:

then, we obtain :

Thus, $T$ is a Geraghty contraction and has a unique fixed point $\tilde{f}\in C^*(I)$, i.e. there exists a unique continuous function $\tilde{f}$ that interpolates the points $(x_i, y_i)$, $i = 0, \ldots, n$ and satisfies

Moreover, let $G$ be the graph of $f$ and let $G_i$ be the graph of the restriction of $f$ to $I_i$, for $i = 1, \ldots, n$, then,

Furthermore, we have:

Hence, $(G_1, \ldots, G_n)$ is the invariant set of $W$, i.e., the attractor of the RIFS $\{D_i\times \mathbb R, w_i; \ i = 1, \ldots, n\}$, and we have:

□

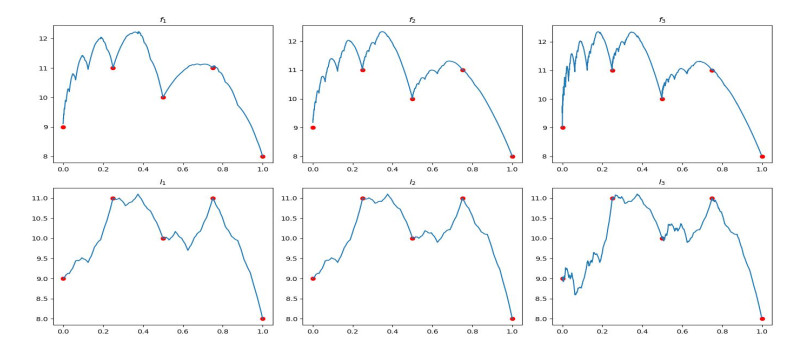
Example 3. Considering the interpolation data

we illustrate the RFIFs corresponding to $\widetilde {\mathbb I}$ equipped with the transition matrices $P_1$, $P_2$ and $P_3$ given in Example 2 in Figure 2 (l1–l3), respectively. The subsequent figure (f1–f3) illustrates the RFIF equipped with affine transformations of Example 1 with the same respective transition matrices so that,

4.   Application

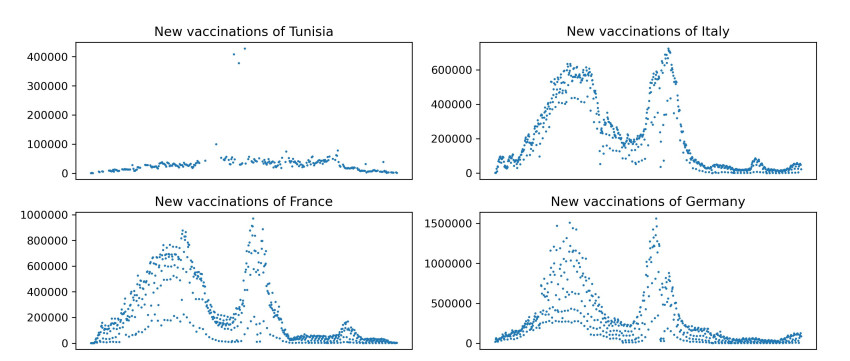
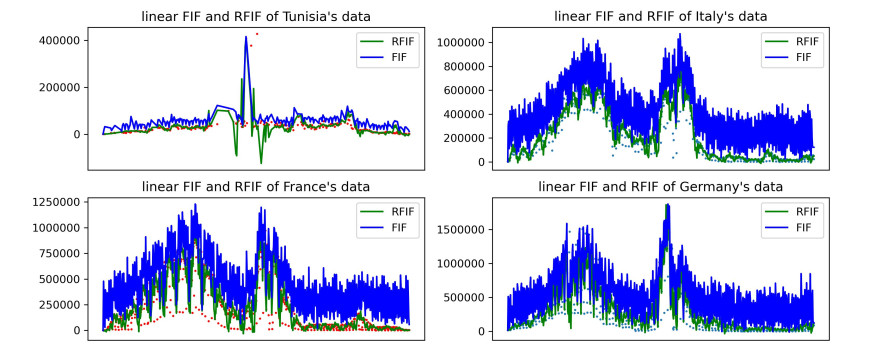
In this section, we will compare RFIF with the classical FIF technique in terms of error rates of the time-series representing the daily vaccinations data. We can show that the fractal interpolation method gives lower error rates than the cubic splines, which is often used to avoid the problem of Runge's phenomenon ^[29]. For this, we collect (from the website ourworldindata.org) daily vaccination data from the following four countries: Germany, Italy, Tunisia and France (see Table 1). As seen in Figure 3, the irregularities of this data is very visible and the reconstruction of the curve from the point of view of fractal interpolation is significantly relevant. This can be an effective way to recover missing information due to insufficient testing, and to analyze the complexity of the evolution of COVID-19 given the importance of vaccination data for each day. In addition, the variations of the FIF incorporate the behavior of the data (see Figure 4). Two methods of fractal interpolation namely linear interpolation, where

as well as fractal interpolation defined by Geraghty contractions, with

are considered.

A common way of measuring the quality of the fit of the interpolation is the normalized root mean square error (NRMSE), which is a statistical error indicator that facilitates the comparison between datasets with different scales and ensures a more universal measure of comparison. There exists various different methods of RMSE normalizations, and we will use

where $y_i$ is the $i$th observation of $y$, $\hat{y}_i$ is the predicted $y$ value given by the interpolation technique and $n$ is the number of total data considered.

In Table 2, we present the results obtained for different parameters $\alpha$ and $\beta$ concerning the daily vaccination data of France. The parameters $\alpha$ and $\beta$ have been chosen arbitrarily. We can see that the RFIF is less sensitive to parameter change compared to the FIF which has big differences in the NMRSE for the various parameter values. This may be explained by the fact that other parameters are involved in the RFIF, namely, the coefficients of the stochastic matrix. Even though we did not get relevant information on the evolution of the disease, we can see the fractal structure of the epidemic curve. Moreover, the presence of parameters $\alpha$ and $\beta$ help to get a wide variety of mappings for approximating problems. The obtained values show a slight improvement when the recurrent fractal interpolation is deployed. Nevertheless, there are still questions about optimal values of the entries of the stochastic matrix that can be managed to determine an optimal choice of the intervals $D_i$ (as defined in Section 3), as well as optimal choice of $\beta$ (as given in ^[13,30] for the choice of the vertical scaling factor) so that the obtained curves fit as closely as possible to the real values.

5.   Conclusions

RIFS can be seen as improvements of the notion of IFS and were introduced in order to gain more flexibility in natural-shape generation and image compression. In this paper, we gave new conditions on the existence of the attractor of a new class of RIFS based on the condition of Geraghty contractions. Consequently, we constructed a new class of RFIF.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [GRANT 4413].

Conflict of interest

The authors declare no conflict of interest.