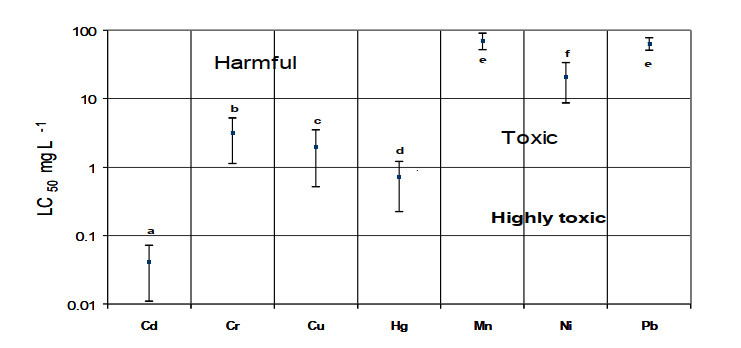
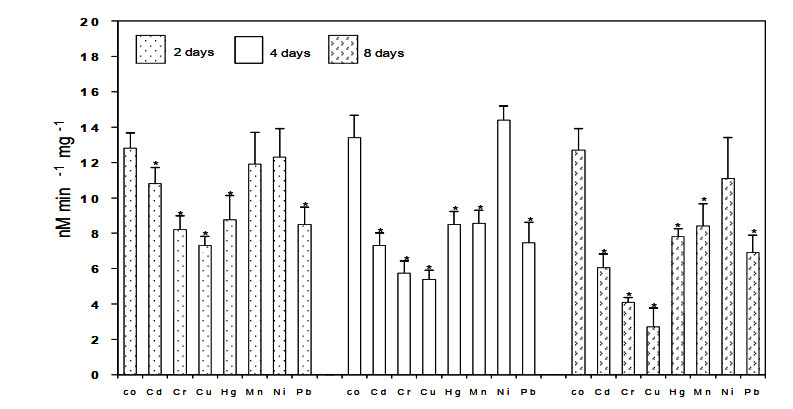
The toxic effect of cadmium, chromium, copper, mercury, manganese, nickel and lead on adult Acanthocyclops americanuscopepods was evaluated to determine the sensitivity of this species to these metals. Toxicity tests were carried out to determine the LC50, after which bioassays were carried out with environmentally relevant sublethal concentrations in order to measure oxidative damage to cell membranes as well as neurotoxic effects. Cadmium was the most toxic metal and manganese was the least harmful. Copper had the greatest oxidative effect (lipid peroxidation) and nickel had the least effect. A 3% to 79% drop was observed in acetylcholinesterase (AchE) activity, with copper causing the greatest inhibitory effect. A. americanus sensitivity to cadmium, manganese and lead was similar to that recorded for Daphnia magna neonates, but the copepods were less sensitive to chromium, copper, mercury and nickel. The response of A. americanus to exposure to metals makes it possible to propose it as a test organism to evaluate the presence and effect of these elements, particularly cadmium, manganese and lead, in toxicity studies, and possibly for monitoring purposes.
1.
Introduction
The realm of heat source estimation concerning encapsulated chips affixed to printed circuit boards (PCBs) stands as a vital field of inquiry within the electronics industry. As the dimensions of electronic devices consistently shrink while integration escalates, comprehending the intricacies of heat generation and dissipation mechanisms within these systems is of paramount importance. The pursuit of accurately estimating heat generation on encapsulated chips holds significance for a multitude of reasons, encompassing the enhancement of thermal management tactics, mitigation of thermal failure risks, and the optimization of overall system performance.
Multiple factors come into play when considering the influence on heat source in encapsulated chips. Among these factors are the electrical and thermal characteristics of both the chip and the encapsulating materials, in addition to the design and arrangement of the PCB. Within the realm of research, a diversity of methodologies has been employed to estimate heat source in encapsulated chips. These approaches span numerical simulation techniques, like the analysis of inverse problems, and experimental strategies, such as the utilization of infrared thermal imaging and thermocouple measurements.
Inverse problem techniques have found application within electronics packaging systems for the purpose of estimating chip heat sources [1,2,3,4,5]. Leveraging this estimation approach facilitates precise quantification of heat source magnitudes, subsequently enhancing the broader realm of electronic thermal management.
As an illustration, Krane et al. [5] employed a least-squares algorithm to ascertain both the magnitude and positioning of heat sources within an electronics system. Their investigation revealed that the fine-grid method exhibits computational expediency surpassing that of the coarse-grid alternative, all while maintaining a negligible compromise on overall accuracy. It's important to note that the Inverse Heat Conduction Problem (IHCP) studies cited earlier did not incorporate air velocity as a factor in their mathematical models. Consequently, a more lifelike scenario, encompassing the coupled heat conduction and convection conditions encountered by chips mounted on a PCB, remains an unexplored avenue.
The CGM [6] stands as an iterative algorithm rooted in gradients and self-regularization. What sets it apart from alternative techniques is its lack of necessity for a priori insights into the functional structure of the unknown variables, rendering it adept at producing dependable estimates for these enigmatic quantities. The robust capabilities of the CGM make it especially fitting for tackling the intricacies of function estimation within three-dimensional inverse problems, particularly those unfolding in irregular domains. Notably, despite its prowess, such problems have remained relatively less explored within the existing literature [7,8,9,10].
Huang et al. [7] delved into a three-dimensional inverse problem aimed at estimating the heat flux applied to the surface of a drilling tool during the drilling process. This estimation was driven by simulated time-dependent temperature distributions captured by sensors embedded onto the drilling surfaces. The outcomes of this investigation underscore the prowess of the gradient method in furnishing dependable estimates, all achieved without the need for foreknowledge regarding the functional nature of the enigmatic functions in play. Notably, the analysis revealed an initial increase in applied heat flux over time owing to escalating torque, followed by a subsequent decline until the point of workpiece penetration.
In another study, Huang and Lee [8] undertook an IHCP using the CGM. Their focus was on the simultaneous estimation of six hitherto unknown internal surface heat fluxes within a square internal combustion chamber. The estimation process hinged on simulated surface temperature measurements. The outcomes of their efforts showcased the feasibility of accurate estimations when dealing with error-free temperature readings. Notably, the maximum relative error for the estimated heat fluxes remained below 3.3%. Furthermore, the study concludes that even in the presence of substantial measurement errors, dependable estimates of internal surface heat fluxes are attainable.
Huang and He [9] undertook the examination of an inverse heat transfer problem, aiming to deduce the elusive spatially varying surface heat flux using the conjugate gradient method (CGM). The veracity of the inverse solutions was substantiated through an array of numerical simulations, encompassing diverse inlet air velocities and plate thicknesses. In addition, an assessment of the impact of measurement errors on the inverse solutions was undertaken. The authors arrived at the conclusion that due to the ill-posed nature intrinsic to the inverse problem, the precision of the estimated heat flux diminishes as the plate thickness increases.
A recent study by Huang and Zhong [10] has undertaken an exploration of an inverse problem, harnessing the potential of the CGM, with the objective of deducing the heat source for a solitary encapsulated chip. This endeavor relied on simulated temperature measurements. Notably, their investigation revolved around the challenging context of conjugated heat transfer conditions. Their study holds the distinction of being the inaugural instance of such an investigation within existing literature. Through a series of numerical experiments, their findings illuminated the potency of the CGM as a robust optimization tool that is well-suited for addressing the intricacies of the three-dimensional inverse heat transfer problem.
In practical scenarios, encapsulated chips are consistently affixed to printed circuit boards (PCBs) to serve functional purposes. Consequently, the real-world context demands the simultaneous estimation of heat generation across multiple chips. Building upon the groundwork laid by Huang and Zhong [10], we aspire to broaden the scope of inquiry. Specifically, our focus lies in extending the investigations to encompass the concurrent estimation of numerous spatially dependent heat sources attributed to chips mounted on a PCB.
The ongoing investigation centers around addressing the 3-D steady-state inverse heat transfer problem using the CGM algorithm. This approach involves a transformative process that divides the problem into two distinct sub-problems, specifically the sensitivity and adjoint problems. The validity of using the CGM in this inverse problem will be examined by estimating multiple heat sources with various inlet velocities and simulated error temperature measurements.
2.
Materials and methods
2.1. The direct problem
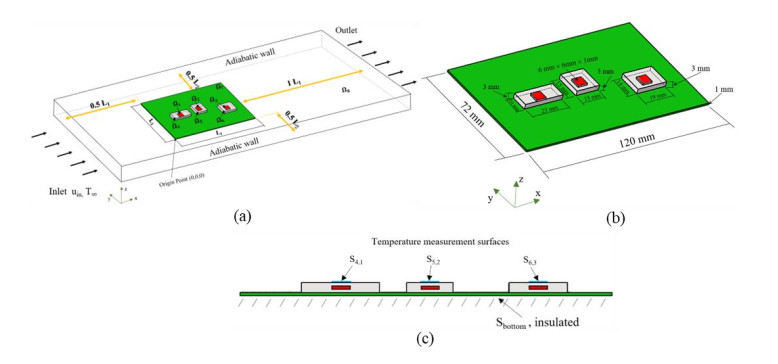
Three unknown spatial-dependent volumetric heat generations of encapsulated chips mounted on a PCB are estimated in this study based on the technique of inverse problems. Ω is a domain of computational and it consists of eight subdomains Ωi, i = 1 to 8. The solid domains include Ω1 to Ω7, where Ω1, Ω2 and Ω3 represent three chips, Ω4, Ω5 and Ω6 represent the encapsulation materials for three chips, and Ω7 is a PCB, while the air domain is indicated as Ω8. The domain of computation considered in this work is given in Figure 1(a), while Figure 1(b) and 1(c) indicate the 3-D and side view of the physical geometry considered in the present study, respectively. Since conjugate heat transfer is considered in the present inverse model, thus it is classified as an Inverse Heat Conduction-Convection Conjugated Problem (IHCCCP).
In solid domains, there exist three volumetric heat generations ψ(Ω1), ψ(Ω2) and ψ(Ω3) for three chips, and an insulation condition is applied on the bottom surface of the PCB, Sbottom. An incompressible inlet air enters the computational domain Ω with velocity uin and ambient temperature T∞, and a perfect thermal contact condition applied to all interfacial surfaces of Ω.
The partial differential equations for the considered direct problem can be given below:
(Ⅰ) Solid domains (Ωi, i = 1 to 7 and s = 1 to 3):
where ki denotes the thermal conductivity of the solid regions, and ψ(Ωs) is the heat source in Ωs. Here δ(∙) is the Dirac delta function, and s = 1 to 3 indicates the number of source positions.
An insulation condition is plied to the bottom wall of the PCB.
Therefore, seven equations are in solid domains Ωi.
(Ⅱ) Air domain (Ω8):
In Ω8, the differential equations for continuity, momentum and energy equations can be obtained as:
where U = {u, v, w} with Uin = uin and T8,in = T∞ and k8 represents the thermal conductivity of air.
(Ⅲ) Interface conditions (SΩi∩Ωj,i≠j):
A perfect thermal contact condition is applied to all the interface surfaces of Ω :
The commercial package CFD-ACE+ (by ESI-CFD Inc., 2020). is utilized to compute the solutions of the above direct problem.
2.2. The inverse problem
For the inverse problem examined in this work, volumetric heat sources ψ(Ω1), ψ(Ω2), and ψ(Ω3) are considered unknown and are functions of space. In addition, temperature readings for S4,1, S5,2, and S6,3 are considered available. These surfaces are the perpendicular projection areas of chips Ω1, Ω2, and Ω3 on the top surfaces of S4, S5 and S6, respectively, and they are illustrated in Figure 1(c).
Let the simulated temperature measurements on Ss+3,s, s = 1 to 3, be denoted by Ym(Ss+3,s), m = 1 to M. The procedure for this IHCCCP is as follows: by utilizing the abovementioned temperature measurements Ym(Ss+3,s), predict the three unknown volumetric heat sources ψ(Ω1), ψ(Ω2) and ψ(Ω3).
The following cost function is thus defined and minimized for obtaining the estimation of three sources:
where Tm(Ss+3,s) are the computed temperatures on Ss+3,s with estimated sources for the exact sources.
2.3. The conjugate gradient method for minimization
The following CGM [11] is used to minimize the cost function J[ψ(Ωs)] and then to estimate unknown volumetric heat generations ψ(Ωs):
where βsn and J′n(Ωs) can be obtained based on the solutions of the following sensitivity and adjoint problems.
2.3.1. The sensitivity problem
Given that the predicament at hand entails three enigmatic volumetric heat sources, denoted as ψ(Ωs), where s ranges from 1 to 3, the derivation of the sensitivity problem necessitates a sequential approach. This involves perturbing a solitary unknown heat source at a time, enabling the isolation and analysis of each distinct unknown in the context of the larger conundrum.
The sensitivity problems are derived from the foundational direct problem as delineated by Eq (1), employing the subsequent approach. For s = 1, it is assumed that when ψ(Ω1) undergoes a variation Δψ(Ω1), while ψ(Ω2) and ψ(Ω3) remain unchanged, and T(Ωi) is perturbed by ΔT1(Ωi). Then, replacing ψ(Ω1) by ψ(Ω1)+Δψ(Ω1) and T(Ωi) by T(Ω)+ ΔT1(Ωi) in the direct problem, subtracting from the resulting expressions in the direct problem and neglecting the second-order terms, the following sensitivity problem for the first sensitivity function ΔT1(Ωi) is obtained as:
(Ⅰ) Solid domains (Ωi, i = 1 to 7):
where an insulation condition is applied to the base surface Sbottom:
(Ⅱ) Air domain (Ω8):
All the thermal parameters considered in this work are assumed to be constants, i.e. it is a linear problem; therefore, Eqs (3) and (4) need to be solved only once in the direct problem at the first iteration, and these solutions can be used for the remaining iterations. In Ω8, the energy equation for the sensitivity function can be derived as:
The inlet conditions for the first sensitivity function can be obtained as Uin = uin and ΔTi,in = 0.
(Ⅲ) Interface conditions (SΩi∩Ωj,i≠j):
The interface conditions on the interface surfaces are given below:
Similarly, for s = 2 and 3, two additional groups of sensitivity equations for sensitivity functions ΔT2(Ωi) and ΔT3(Ωi) are derived below in the solid domain (Ωi, i = 1 to 7):
The sensitivity functions in the air domain are the same as those given in Eq (13). In addition, the boundary condition (14) is also applied to all the interface surfaces of Eqs (15) and (16). To obtain the expression for the calculation of step size βsn, an alternative form of cost function J(ψsn+1) at iteration n+1 must be derived.
The computed temperatures Tm(Ss+3,s) that occur in Eq (7) should be functions of ψ1, ψ2, and ψ3. However, because the measured temperatures Ym(S4,1), Ym (S5,2), and Ym (S6,3) were affected mostly by ψ1, ψ2, and ψ3, respectively, the cost function can be approximately expressed as:
Equation (18) is subjected to linearization through a Taylor series expansion. As a result of this process, we ultimately arrive at:
βsn can then be obtained by minimizing Eq (18) with respect to βsn; thereafter, the following expression can be obtained:
2.3.2. The adjoint problems
The following procedure is performed to derive the adjoint problem: For s = 1, the adjoint functions λ1(Ωi), i = 1 to 7, and λ1(Ω8) are multiplied to Eqs (1) and (5), respectively, and are integrated over the Ωi domains. The expressions are then added to the right-hand side of Eq (7) to obtain a new cost function J[ψ(Ωs)]:
The variation of Eq (20) ΔJ1 can be derived by perturbing ψ(Ω1) by ψ(Ω1)+Δψ(Ω1) and T(Ωi)+ΔT1(Ωi) in Eq (21), while ψ(Ω2) and ψ(Ω3) remain unchanged, subtracting from Eq (20) and neglecting the higher-order terms. The expression given below is obtained
In Eq (21), the domain integral terms are reformulated based on Green's second identity; the boundary and interface conditions of the sensitivity problems are used, and then ΔJ1 is allowed to approach zero. The vanishing of the integrands containing ΔT1 leads to the following adjoint problem λ1(Ωi):
(Ⅰ) Solid domain (Ωi, i = 1 to 7):
(Ⅱ) Air domain (Ω8):
The inlet conditions are Uin = uin and λ1,in(Ω8) = 0, and U and P are computed from Eqs (3) and (4).
(Ⅲ) Interface conditions (SΩi∩Ωj,i≠j):
The perfect thermal contact condition is used to all the interface surfaces of Ω, except for S4,1, S5,2 and S6,3.
The interface conditions on S4,1, S5,2 and S6,3 are given as:
on Ss + 3,s,s=1 to 3. Clearly, extra heat source terms exist on S41, S52 and S63 in the interface surfaces of the adjoint problem.
Finally, the following integral term remains:
The functional increment can be defined as [11]:
The comparison of Eqs (27) and (28) yields the gradient of the cost function:
Similarly, for s = 2 and 3, two sets of adjoint equations for adjoint functions λ2(Ωi) and λ3(Ωi) can be derived, and it is found that they are all identical to λ1(Ωi); therefore, the adjoint equations need to be solved only once. Finally, the following two gradient equations for ψ(Ω2) and ψ(Ω3) are obtained:
The residual between the computed and simulated measured temperatures can be approximated by:
here σ represents the standard deviation of the temperature readings. Substituting the above temperature residual expression into Eq (7), the following stopping criterion value ε, based on the discrepancy principle [11], can be obtained
3.
Results
A 3-D inverse problem using the technique of function estimation is investigated in the present study to determine the distribution of unknown strength of heat generations ψ(Ω1), ψ(Ω2), and ψ(Ω3) of three chips mounted on a PCB with the CGM.
Three silicon chips with k = 124 W/(m-K) and lengths Lx = Ly = 6 mm and Lz = 1 mm were filled with CEL-9200, k = 0.97 W/(m-K) [12], and they were mounted on a PCB with dimensions of 120 mm ×72 mm ×1 mm and k = 0.2 W/(m-K). The sizes (in mm) of the three encapsulated chips in the x, y and z directions are 25×10×3, 15×15×3 and 19×14×3, respectively. The computational domain of the present work is given in Figure 1(a), where uin denotes the inlet air velocity and T∞ = 300 K represents the ambient air temperature. The chips are very thin in this work, therefore it is reasonable to assume that ψ(Ωs) = ψ(x, y) for the numerical experiments.
The center point temperature Tcenter of chip 2 with ψ(Ωs) = 31250 W/m3, uin = 2 m/s and T∞ = 300 K was calculated using the four grid numbers of 162,468,239,162,416,832 and 529,280 as 326.7 K, 341.3 K, 342.5 K and 342.7 K, respectively. It is clear that the error of Tcenter in chip 2 between the grid numbers 416,832 and 529,280 was only 0.058%; therefore, grid numbers of 416,832 were considered for the computations.
The exact temperature readings, Yexact, with random errors, ωσ, were used to simulate the measurement data Y:
here, the symbol ω represents a randomly generated number, facilitated through the IMSL subroutine DRNNOR (by Perforce Software Inc., 2021), encompassing a range from -2.576 to 2.576, corresponding to a 99% confidence bound.
An advantage of using the CGM to compute an inverse problem is the ability to arbitrarily choose the values of initial guesses; therefore, the initial guess for the heat sources is chosen as a small number, ψ(Ωs)0 = 1 W/m3, for all numerical experiments in the present study.
The unknown heat generations ψ(Ω1), ψ(Ω2) and ψ(Ω3) are considered as:
where ψ(Ω1) is assumed to be a constant heat source, and the heat source distributions for ψ(Ω2) and ψ(Ω3) are assumed to be two inclined planes.
The 3-D plots for the exact ψ(Ω2) and ψ(Ω3) are given in Figure 2(a) and 2(b), respectively, and contour plots for ψ(Ω1), ψ(Ω2) and ψ(Ω3) are given in Figure 3(a)–3(c), respectively. The grid sizes of the chip are taken as 20 and 20 in the x and y directions, respectively; thus a total of M = 400 unknown discretized values of heat source are to be estimated at each chip, and 400 temperature readings are needed on Ss+3,s surfaces.
First, inverse estimates are executed using σ = 0.0, uin = 2 m/s, T∞ = 300 K and ψ(Ω1)0 = ψ(Ω2)0 = ψ(Ω3)0 = 1 W/m3. Contour plots of the simulated exact measurement temperatures Y(Ss+3,s), s = 1 to 3, with σ = 0.0 are presented in Figure 4(a)–4(c), respectively. Figure 5(a) and 5(b) illustrate the temperature distributions of air and encapsulated chips on the measurement and bottom surfaces, respectively. Since the magnitude of heat generation varies for chips, the resultant temperatures of the air and encapsulated chips also vary. In addition, because of the motion of air, the air temperatures will be higher in the downstream regions of chips than at the inlet, and the temperatures of the encapsulated chips are higher on the bottom surface than on the measurement surface.
Figure 6(a) illustrates the progression of convergence concerning the number of iterations. It is readily apparent that the cost function experiences a decrease, ultimately converging to 0.0003 after 50 iterations. This trend also underscores that the estimated heat sources exhibit swift convergence towards the precise heat generations, facilitated by the rapid rate of convergence observed over the initial iterations. Subsequent to this swift convergence, the ensuing iterations are employed to meticulously refine and optimize the estimated heat sources within a localized context.
It is observed that the values for constant heat generation ψ(Ω1) can be estimated accurately in only 3 iterations. This result implies that if all the heat generations of chips are constants or nearly constants, which is the case for practical applications, the iteration numbers required to obtain converged estimates should be very small, and it makes the algorithm very efficient in practice.
The estimated 3-D ψ(Ω2) and ψ(Ω3) are given in Figure 2(a) and Figure 2(b), respectively, the contour plots of ψ(Ω1), ψ(Ω2) and ψ(Ω3) are plotted in Figure 3(a)–3(c), respectively, and the corresponding estimated temperatures T(Ss+3,s), s = 1 to 3, are presented in Figure 4(a)–4(c), respectively. The figures indicated that using σ = 0.0, the exact and estimated values are nearly the same for both the heat generations and temperatures.
The computed errors for the estimated temperatures ERR1, s and estimated heat generations ERR2, s are summarized in Table 1 and are defined below.
The influence of temperature readings with errors on heat source estimations ψ(Ω1), ψ(Ω2) and ψ(Ω3) is one of the major concerns for inverse problems and is examined now. The error of the temperatures readings is first considered as σ = 0.01 and then increased to σ = 0.05. The estimation of three heat sources can be obtained after 9 and 8 iterations for σ = 0.01 and 0.05, respectively, and the estimated ψ(Ω1), ψ(Ω2) and ψ(Ω3) are shown in Figure 7(a)–7(c), respectively, for σ = 0.01 and 0.05. The errors ERR1, s and ERR2, s are also summarized in Table 1. These results indicate that the heat generation estimates remain reliable when error readings are considered.
To illustrate the estimated heat generations more clearly, the exact and estimated ψ(Ω1), ψ(Ω2), and ψ(Ω3), at the midpoint of the x position of each chip with y positions varied, are plotted in Figure 8(a)–8(c), respectively. If the measurement errors are increased, the estimates may become poor, but they will be reliable, although the unknown heat source can be replicated accurately for errorless measurements.
In order to validate the proposed algorithm and investigate the impact of the inlet air velocity on the estimated heat generation, it was increased to uin = 4 m/s when σ was set to 0.0. The graph in Figure 6(b) depicts the cost function against the number of iterations for errorless measurements. After 50 iterations, the objective function J decreases to 0.0002, illustrating that the estimated heat source rapidly converges towards the averaged exact heat source in the initial iterations, with the remaining iterations serving to fine-tune it locally.
The estimated contour plots of ψ(Ω1), ψ(Ω2) and ψ(Ω3) are given in Figure 9(a)–9(c), respectively, and the measured and estimated temperatures Y(Ss+3,s) and T(Ss+3,s) are given in Figure 10(a)–10(c) for chip 1, chip 2, and chip 3, respectively. Comparing Figures 4 and 10 shows that a higher air velocity will result in lower surface temperatures of encapsulated chips.
Furthermore, a striking resemblance between the precise and estimated values of both temperature and heat generation was noted. This observation was supported by the analysis of average errors, denoted as ERR1, s and ERR2, s, which are succinctly presented in Table 1. The inverse estimation of heat generations for inexact measurements, σ = 0.01 and 0.05, are also conducted, and the estimated results are listed in Table 1.
Similarly, to compare the exact and estimated heat generations more clearly, the exact and estimated ψ(Ω1), ψ(Ω2), and ψ(Ω3) with uin = 4 m/s at the center point of the x positions of each chip and varying the y position are illustrated in Figure 8(a)–8(c). Again, the heat generations can be reproduced well for σ = 0, but increasing the measurement errors results in acceptable estimates. These results indicate that the air velocities considered in this work have an insignificant influence on the estimated results; in addition, the estimates are reliable when considering error measurements.
Based on the results of the above numerical experiments, it can be concluded that the unknown magnitude of spatially dependent heat generations of multiple chips mounted on a PCB are accurately estimated in this work, and if the temperature measurements are exact or inexact, the inverse solutions remain reliable.
4.
Conclusions
By employing simulated surface-temperature data, we adeptly delved into the realm of a 3-D steady-state inverse heat transfer problem, successfully unraveling the enigma of unknown volumetric heat sources attributed to multiple encapsulated chips adorning a PCB. The linchpin of this investigation lay in the adept utilization of the CGM optimization algorithm. Notably, the CGM's distinct advantage stems from its capacity to obviate the need for presupposing a particular functional form for the heat source. This attribute renders it exceptionally suited for addressing the intricate domain of function-estimation problems, wherein arbitrary initial conjectures for the heat sources are often the norm. It's pertinent to highlight that, while the CGM has formerly been harnessed to unravel inverse problems associated with either heat conduction or heat convection, this study represents its virgin application within the context of the inverse heat transfer problem. Rigorous evaluation ensued through the analysis of multiple test cases, spanning varying heat generations across each chip, an array of inlet velocities, and the inclusion of diverse measurement errors. Notably, simulation results consistently underscored the reliability of CGM-derived estimations for the heat generation of multiple chips, even when confronted with escalating air velocities and measurement inaccuracies. An example of this reliability emerges in the form of the maximum ERR2, 2, which stood resolutely below 3.5412% for σ = 0.05 and uin = 4 m/s. Emanating from the findings of these meticulous numerical experiments, the study culminates with the resounding verdict that the CGM, a potent optimization tool, aptly serves as the key to unlock the solutions to the complex 3-D steady-state inverse heat transfer problem.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The research was funded by the National Science and Technology Council of Taiwan, under Grant NSTC-112-2221-E-006-140-MY3.
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad: