Distributed generation integration optimization using fuzzy logic controller

Santosh Kumar Sharma; D. K. Palwalia; Vivek Shrivastava; Santosh Kumar Sharma; D. K. Palwalia; Vivek Shrivastava

doi:10.3934/energy.2019.3.337

AIMS Energy

2019, Volume 7, Issue 3: 337-348. doi: 10.3934/energy.2019.3.337

Previous Article Next Article

Research article Topical Sections

Distributed generation integration optimization using fuzzy logic controller

Rajasthan Technical University, India

Received: 03 February 2019 Accepted: 10 May 2019 Published: 06 June 2019

Distributed generators (DGs) are connected near load centers and integrated to grid for optimum power system operations. The challenging task for integration of DGs is the proper size and location, due to random character of generation and energy consumption. The objective of the research is to provide the proper size and location of DGs to optimize the voltage profile and reduction in active and reactive power losses. Optimization of distributed generators is performed through fuzzy logic controllers at Ramchandrapura 33/11 kV, 69 bus radial distribution substation, Kota, India. Fuzzy logic controller provides possible solution on selection of distributed generators on the basis of voltage profile of the bus and the impedance of the branch connected DGs at consumer’s end. Forward or backward sweep methodology is used to optimize the load flow analysis for calculation of real and reactive power losses and voltage profile with and without implementation of distributed generators. Proposed approach provides a possible solution for efficient integration of DGs.

Keywords:

Citation: Santosh Kumar Sharma, D. K. Palwalia, Vivek Shrivastava. Distributed generation integration optimization using fuzzy logic controller[J]. AIMS Energy, 2019, 7(3): 337-348. doi: 10.3934/energy.2019.3.337

Related Papers:

[1]	Akash Talwariya, Pushpendra Singh, Mohan Lal Kolhe, Jalpa H. Jobanputra . Fuzzy logic controller and game theory based distributed energy resources allocation. AIMS Energy, 2020, 8(3): 474-492. doi: 10.3934/energy.2020.3.474
[2]	Rabyi Tarik, Brouri Adil . Ant colony optimization algorithm and fuzzy logic for switched reluctance generator control. AIMS Energy, 2022, 10(5): 987-1004. doi: 10.3934/energy.2022045
[3]	Hari Charan Nannam, Atanu Banerjee . A novel control technique for a single-phase grid-tied inverter to extract peak power from PV-Based home energy systems. AIMS Energy, 2021, 9(3): 414-445. doi: 10.3934/energy.2021021
[4]	Ryuto Shigenobu, Oludamilare Bode Adewuyi, Atsushi Yona, Tomonobu Senjyu . Demand response strategy management with active and reactive power incentive in the smart grid: a two-level optimization approach. AIMS Energy, 2017, 5(3): 482-505. doi: 10.3934/energy.2017.3.482
[5]	Ahsan Iqbal, Ayesha Ayoub, Asad Waqar, Azhar Ul-Haq, Muhammad Zahid, Syed Haider . Voltage stability enhancement in grid-connected microgrid using enhanced dynamic voltage restorer (EDVR). AIMS Energy, 2021, 9(1): 150-177. doi: 10.3934/energy.2021009
[6]	Nagaraj C, K Manjunatha Sharma . Fuzzy PI controller for bidirectional power flow applications with harmonic current mitigation under unbalanced scenario. AIMS Energy, 2018, 6(5): 695-709. doi: 10.3934/energy.2018.5.695
[7]	Mohamed G Moh Almihat . An overview of AC and DC microgrid energy management systems. AIMS Energy, 2023, 11(6): 1031-1069. doi: 10.3934/energy.2023049
[8]	Alex Borodin, Elena Streltsova, Zahid Mamedov, Irina Yakovenko, Irina Mityshina, Artem Streltsov . Fuzzy-Logical model for analysis of sustainable development of fuel and energy complex enterprises. AIMS Energy, 2023, 11(5): 974-990. doi: 10.3934/energy.2023046
[9]	Shafiuzzaman Khan Khadem, Malabika Basu, Michael F. Conlon . Capacity enhancement and flexible operation of unified power quality conditioner in smart and microgrid network. AIMS Energy, 2018, 6(1): 49-69. doi: 10.3934/energy.2018.1.49
[10]	Habibullah Fedayi, Mikaeel Ahmadi, Abdul Basir Faiq, Naomitsu Urasaki, Tomonobu Senjyu . BESS based voltage stability improvement enhancing the optimal control of real and reactive power compensation. AIMS Energy, 2022, 10(3): 535-552. doi: 10.3934/energy.2022027

Abstract

Abbreviations: DGs: Distributed Generators; FLC: Fuzzy Logic Controllers; RBF: Reserve Breadth First; BF: Breadth First; PLR: Power Loss Reduction; VI: Voltage Indexing; k: Starting Node; j: End Node; P_k: Active Power at K^th Node; P_j: Active Power at J^th Node; P_{l, j}: Active Loads Connected at J^th Node; R_kj: Connected Resistance Between K^th & J^th Bus; Q_k: Reactive Power at K^th Node; Q_j: Reactive Power at J^th Node; Q_{l, j}: Reactive Loads Connected at J^th Node; X_kj: Connected Reactance Between K^th & J^th Bus; V_j: Voltage Magnitude at J^th Bus; V_k: Voltage Magnitude at K^th Bus; P_OF: Objective Function of Active Power; V_L: Voltage Index; W_p: Weighting Factor of Total Power Loss; W_v: Weighting Factor of Voltage Index; P_loss: Active Power Loss; MVA_b: Base MVA; P_{loss, DG}: Power Loss Through DGs

1. Introduction

The electric grid is mainly consists of large power units and centrally controlled. According to the reports (June, 2018) of Central Electricity Authority India, 67% of electricity is being generated from fossil fuels based power plants. These plants generate reliable electricity but the potential of sources are limited ^[1,2]. Electricity demand is increasing continuously and grid needs to supply the extra amount of electricity from renewable energy sources. Distributed generators (DGs) are small modular power generating technologies and storage systems which provide possible solution by generating electricity near consumer ends ^[3,4,5]. Grids are plagued with unreliable services and are struggling to upgrade power systems to keep up with high demand growth rates ^[6]. There becomes a significant amount of electricity losses in transmission and distribution networks due to inefficient appliances of consumers, lack of smart technologies, inefficient dispensation and routing of electrical energy, unreliable monitoring and communication and lack of mechanism to store electrical energy.

DGs installation is suggested in several research articles. Some of the leading energy generating countries increasing the installation capacity of DGs to make competitive with our existing system. They play virtual impact in power system advancement. Around 20% of recently installed generating units are from renewable energy sources all over the world ^[7,8,9]. DGs affect the load flow and voltage profile of the network. Place and capacity of DGs are essential to manage the losses and to maintain the voltage profile in allowable limits ^[10,11]. Following outcome are observed from the literature review:

● Energy generation through conventional methods are having huge amount of environmental effect.

● DGs installation capacity, proper size, suitable location and their optimization are challenging tasks.

● Modeling of suspicions in consumption and intermittent nature of the DGs make the integration complex.

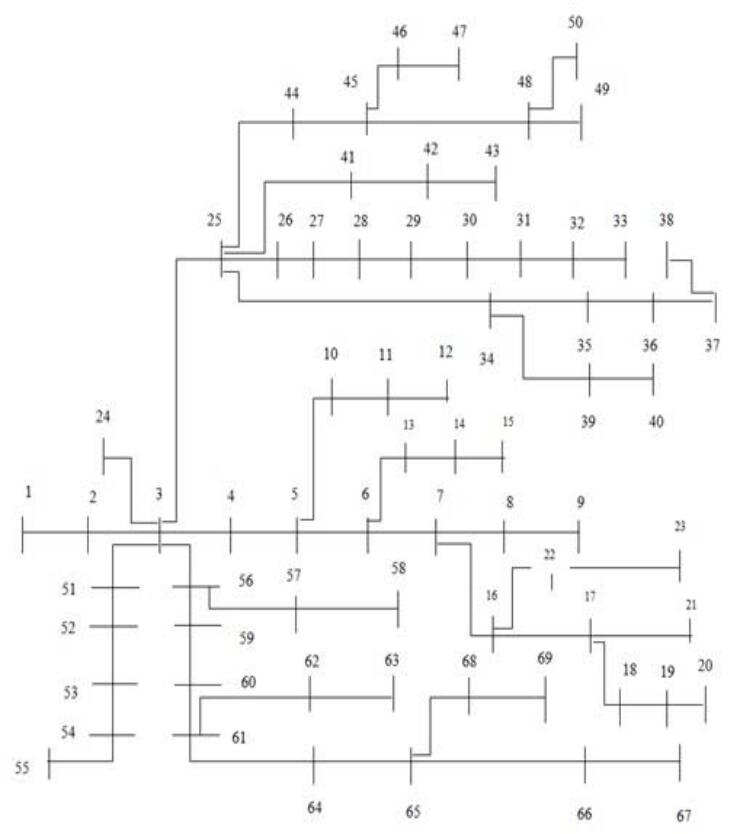
In this paper a 69 bus radial distribution system located at Ramchandrapura feeder, Kota Rajasthan is analyzed. It is 33/11 kV, supplied 69 nodes radial distribution network as shown in Figure 1. Load flow is analyzed by forward or backward sweep method. Load flow analysis is important for optimization of real power losses, reactive power losses, voltage magnitude and phase angle. It is a useful tool for power system planning. Backward or forward sweep method calculated the mentioned variable by scheduling the order of the busses ^[12,13]. DGs are integrated with the help of fuzzy logic controllers (FLC). FLC is an important tool which works on priority concept to find-out the most suitable location of DGs, maintains the voltage profile and reduce losses ^[14,15]. The major contributions of this paper can be summarized as follows:

Figure 1. 69 Bus Ramchandrapura, Kota, India, Radial distribution network.

DownLoad: Full-Size Img PowerPoint

● Increase the penetration level of DGs near load centers.

● Load flow analysis is performed by backward or forward sweep method providing the voltage magnitude, reactive and active power losses.

● Proper size and location of energy generated through DGs are provided by FLC and manage the voltage profile of the busses and reduce the reactive and active power losses.

● To optimize the DGs, fuzzy logic controller is used.

Rest of the paper is organized as follow: The problem of existing Ramchandrapura grid is mathematically evaluated by backward or forward sweep method. It provides the real and reactive energy losses and voltage index in section 2. An algorithm of FLC is provided in section 3, section 4 provides the simulation results of the study and research paper is concluded in section 5.

2. Problem description

2.1. Load flow

Radial structure of distribution network with large number of busses and high R/X ratio with significant voltage drop, load flow analysis with conventional gauss siedel, newton raphson, fast decoupled method may have problems to converge for distribution networks and required large number of iterations. The probable solution is provided by backward or forward sweep analysis, as the mentioned method use the order of the busses connected for calculation of real or reactive power, voltage profile and phase angle ^[16].

Reverse Breadth First (RBF) shorts the branch impedances in descending order which is used for backward sweep operation. If impedance of branches is shorted in ascending order, the result is known as Breadth First (BF) and used for forward sweep operations.

2.1.1. Backward sweep

Power flow is obtained in backward sweep by considering the parameters of previous iteration. The active power flow P_k of branch kj from node k to node j is calculated in backward sweep from end bus in (1) and reactive power flow Qk of branch kj from node k to node j is calculated by (2):

$P_{k} = P_{j}+P_{l, j}+R_{k j} \frac{P_{j}^{\prime 2}-Q_{j}^{\prime 2}}{\left|V_{j}\right|^{2}}$

(1)

${Q_k} = {Q_j} + {Q_{l, j}} + {X_{kj}}\frac{{P_j^{'2} - Q_j^{'2}}}{{{{\left| {{V_j}} \right|}^2}}}$

(2)

where, P'_j = P_j + P_{l, j}; P_{l, j} is defined as the load connected at bus j; P_j is the effective real power at bus 'j'.

2.1.2. Forward sweep

Forward sweep is used to calculate the voltage at each bus starting from source bus. In forward sweep real power of the branch is taken by the value calculated in backward sweep and remains constant. Voltage of bus 'k' is $\mathrm{V}_{\mathrm{k}}\left\lfloor\right.$ δ_k and voltage of bus 'j' is $\mathrm{V}_{\mathrm{j}}\left\lfloor\right.$ δ_j, than the branch impedance Z_ij = R_ij + X_ij. Voltage at k^th bus by (3):

${{\rm{V}}_{\rm{k}}} = {\left[ {V_j^2 - 2\left( {{P_j}{R_{jk}} + {Q_j}{X_{jk}}} \right) + \left( {R_{jk}^2 + X_{jk}^2} \right)\frac{{\left( {P_j^2 - Q_j^2} \right)}}{{V_j^2}}} \right]^{\mathit{\boldsymbol{1/2}}}}$

(3)

2.2. Objective function

Objective function of the research paper is to minimize the active and reactive power losses in (4) and (5) respectively:

$P_{O F} = min \left[\left(W_{p} \times P_{l o s s, p u}\right)+\left(W_{v} \times V_{L}\right)\right]$

(4)

$Q_{O F} = min \left[\left(W_{q} \times Q_{l o s s, p u}\right)+\left(W_{v} \times V_{L}\right)\right]$

(5)

where, P_OF is the objective function for active power, Q_OF is the objective function for reactive power, P_{loss, pu} is the total active power losses in per unit, Q_{loss, pu} is the total reactive power losses in per unit, V_L is the voltage index, W_p & W_v are the weighting factor for total power losses and voltage index, represents the importance of objectives. It is usually assumed between zero to one for W_p or W_q and addition with weighting factor of voltage index is unity as in (6):

$0 \leq W_{p} ~~or~~ W_{q} \leq 1, \& W_{p}+W_{v} = 1$

(6)

If distributed generators alleviate a particular objective to overcome a defined problem, weighting factor of the component is increased.

2.3. Power losses

Centralized generated power is transmitted through transmission lines and distribution networks to consumers to fulfill their demand. Huge amount of power loss occurs as I²R losses in particular line. Total active power losses of system is defined in (7):

$P_{l o s s} = \sum _{k = 1}^{n} I_{k}^{2} R_{k}$

(7)

where, I_k is the magnitude of current in ampere and R_k is the resistance in ohm of k^th bus, n is the number of buses in radial system. Total active power losses depend upon the current flow through the branch and resistance of the branch. Power loss due to integration of DGs is calculated in per unit system in base MVA between zero to one by (8):

$P_{loss, p u} = \frac{P_{loss}}{M V A_{b}}$

(8)

Power loss Reduction (PLR) by installing DGs at distribution feeder is calculated by (9) and in percentage by (10):

$PLR = {P_{loss}} - {P_{loss, DG}}$

(9)

$PLR(\% ) = \frac{{{P_{loss}} - {P_{loss, DG}}}}{{{P_{loss}}}}X\;100$

(10)

where, P_{loss, DG} is the real power loss after installing distributed generators.

2.4. Voltage index (VI)

The voltage index defines as the distance from reference point to the point where system will marginally stable. If the voltage is instable, it causes the voltage collapse. Mathematical calculation of voltage index helps the utilities to reduce the chances of voltage collapse or introduce an automatic scheme to turn on or off the DGs to prevent collapse. Voltage indexing is calculated by steady state power flow analysis at every bus of the distributed network (11) ^[17].

$V I_{k} = \frac{1}{n} \sum _{k = 1}^{n} \frac{V_{k}-V_{k, D G}}{V_{k}}$

(11)

where, V_k is the voltage of k^th bus before installing of DGs and V_{k, DG} is the voltage at k^th bus after installation of DGs.

3. Fuzzy logic control based DG integration

Fuzzy logic controller (FLC) is a method to figure out the behavior of the system. Fuzzy logic controllers have mainly three operations. First is fuzzification, which converts the input data in suitable linguistic values. Second is decision making, which makes the decision on the basis of defined rules. Third is defuzzification, which converts the outcomes into the system understandable data. Mamdani based fuzzy logic controller is used to control the complex and non-linear systems which is having the advantage that if changes happen in between the process, it is not required to change in the whole system from the initial condition ^[18].

In this paper, first input variable is the power capacity of distributed generators in per unit and second variable is impedance of line connecting DGs to consumers, while least real power losses and constant voltage indexing are the output variables.

Where, x₁, x₂, x₃, …., x_n ∈ U input fuzzy set and y₁, y₂, ….., y_n ∈ V output fuzzy sets. Rules for FLC are based on two input variables and output shows the priority to assign DGs as outcome (12).

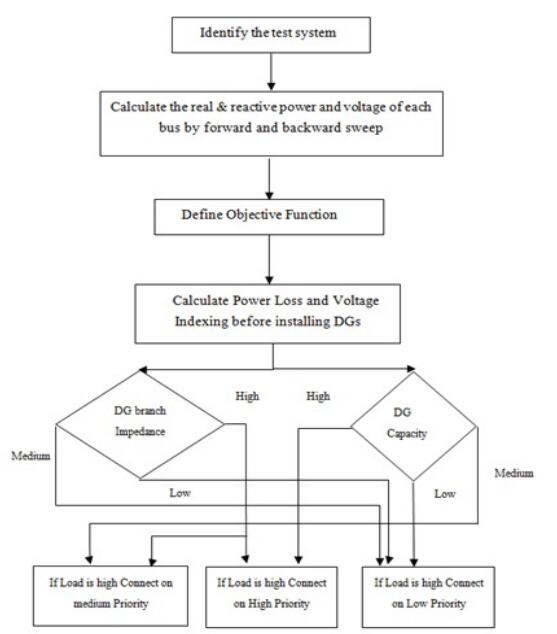
$P_{V} = max \left(V I_{k}\right)+min \left(R_{k d g}+X_{k d g}\right)$

(12)

Output set equation defines that the priority of DGs installation is based on two factors maximum voltage indexing of k bus and minimum impedance of line connected DGs to that bus. Algorithm of the proposed fuzzy logic controller is shown in Figure 2, where relation between two input sets of voltage magnitude and impedance of branch connecting the DGs with radial feeder is shown. FLC rules for decision making are shown in Table 1, having two inputs, subdivided in three sections low, medium and high for voltage magnitude and branch impedance. DG integration priority is high during high capacity and low impedance of line connecting DG to specified bus will be preferred for integration.

Figure 2. Flowchart of DG integration with fuzzy logic controller.

DownLoad: Full-Size Img PowerPoint

Table 1. Rules based for proposed fuzzy logic controller.

DG Power Generation Capacity	Impedance of Line	DG Integration Priority
Low	Low	Low
Low	Medium	Low
Low	High	Low
Medium	Low	Medium
Medium	Medium	Low
Medium	High	Low
High	Low	High
High	Medium	Medium
High	High	Low

| Show Table

DownLoad: CSV

4. Results

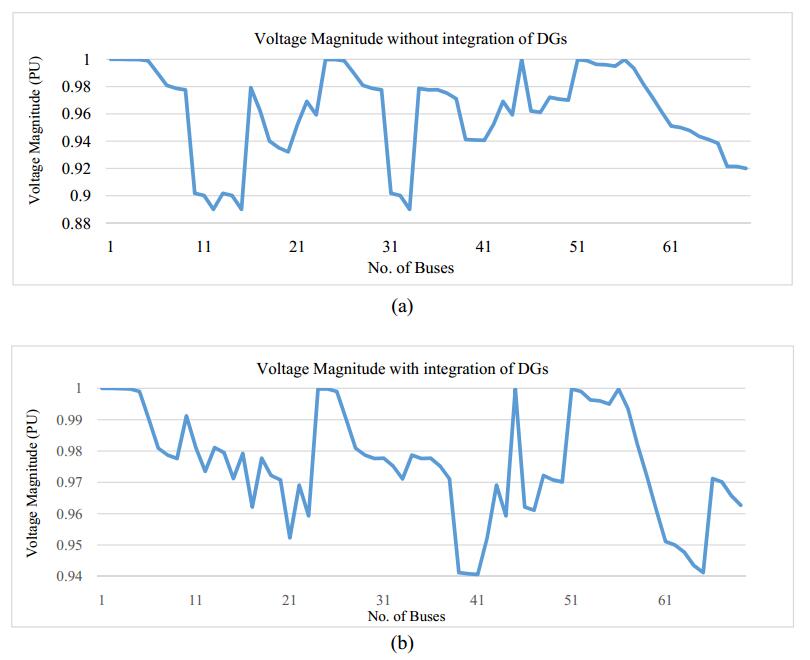
Ramchandrapura, Kota, India, 8 MVA, 33/11 kV radial distribution network is taken into consideration for integration of 5 MW all day power generation capacity of distributed generators. Forward backward sweep method is used for load flow analysis before and after the integration of DGs. Fuzzy logic controller is used for integration of DG through which the proper size and location is optimized. DG capacity represents the requirement of improving the voltage profile at particular node and impedance of line as mentioned in Table 1 which are the input variables for FLC and DG priority is the output variable. DG capacity is high between 3 MW to 5 MW, medium from 1 MW to 3 MW and low when less than 1 MW. Branch impedance is also categorized in three subsets of low, medium and high based on the I²R losses to integrate the DG at particular node. Low I²R losses are preferred for DG integration. Figure 3 denoted the voltage magnitude with or without integration of DGs in per unit. Without integration of DGs voltage magnitude is varied between 1.0 pu to 0.89 pu. DGs are integrated through FLC which improved the voltage magnitude between 1.0 pu to 0.9406 pu. Average pu voltage magnitude is increased from 0.960 pu to 0.9755 pu.

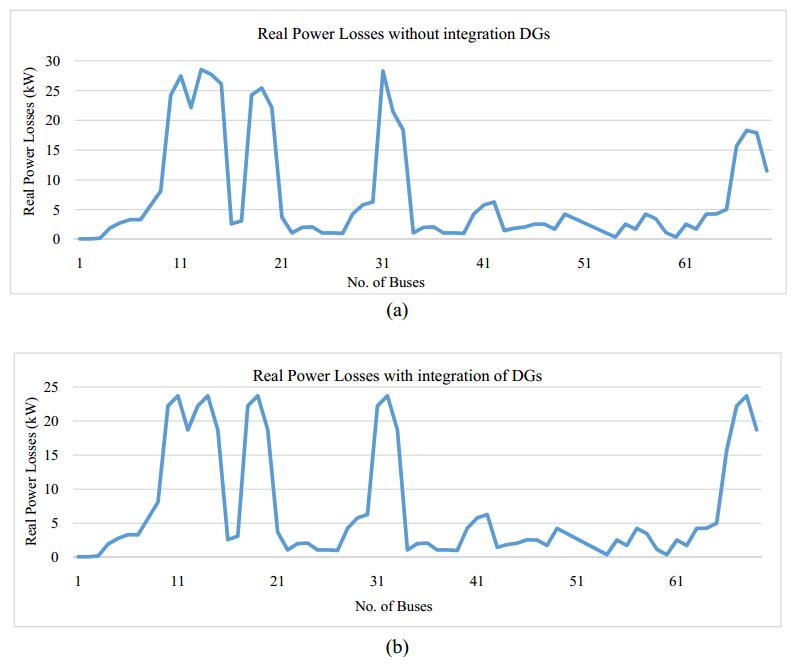
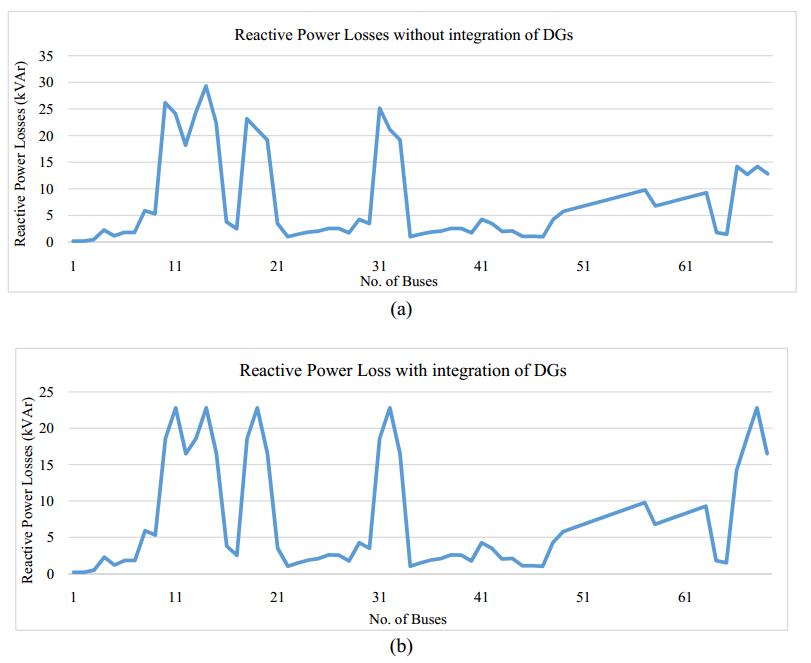
Figure 3. Voltage magnitude of 69 Bus Ramchandrapura, Kota, radial distribution network (a) without DGs integration (b) with DGs integration.

DownLoad: Full-Size Img PowerPoint

Backward sweep method is used for the calculation of real and reactive power losses in load flow analysis and with and without integration of DGs. DGs are being integrated through FLC and reduce the total real and reactive power losses. Real power losses reduced from 501.35 kW to 480.47 kW by integration of DGs. Maximum real power drop is reduced from 28.55 kW to 23.7 kW and average real power losses reduced from 7.26 kW to 6.96 kW by integration of DGs shown in Figure 4. Total reactive power losses reduced from 531.12 kVAr to 507 kVAr, maximum reactive power losses reduced from 29.31 kVAr to 22.8 kVAr and average reactive power losses are reduced from 7.70 kVAr to 7.35 kVAr as shown in Figure 5.

Figure 4. Real Power Losses of Ramchandrapura, Kota, distribution network (a) without integration of DGs (b) with integration of DGs.

DownLoad: Full-Size Img PowerPoint

Figure 5. Reactive power losses of Ramchandrapura, Kota, distribution network (a) without integration of DGs (b) with integration of DGs.

DownLoad: Full-Size Img PowerPoint

Table 2. Comparative study of real and reactive power losses with or without integration of DGs is shown in Table 2.

	Real Power Without Integration of DGs	Real Power With Integration of DGs	Reactive Power Without Integration of DGs	Reactive Power With Integration of DGs
Average Power	7.26 kW	6.96 kW	7.70 kVAr	7.35 kVAr
Maximum Power	28.54 kW	23.7 kW	29.31 kVAr	22.8 kVAr
Total Power	501.34 kW	480.46 kW	531.12 kVAr	507.52 kVAr

| Show Table

DownLoad: CSV

4. Conclusion

Energy consumption at consumer end is increasing day by day and to maintain the balance between generation and consumption, new generating units are required to be installed. Fossil fuels emit harmful gasses in the environment need the solution from renewable energy sources. Distributed generators connected near load centers provide solution of energy enhancement and energy losses through conventional methods. This research paper optimizes a real system existing in Ramchandrapura, Kota, India. Voltage drop and real and reactive power losses at each node is calculated by forward-backward sweep method of load flow analysis. By the integration of distributed generators, real and reactive power losses are reduced and voltage profile is maintained. Fuzzy logic controller is used to optimize the problem and to integrate the DGs with the grid. FLC is implemented on priority basis as decided by voltage drop and impedance of connecting branches. Simulation results of Ramchandrapura, Kota 69 bus radial distribution network shows better results with integration of DGs at proper location. Voltage profile is improved by implementing DGs and reduces the real and reactive power losses. Before implementing FLC, minimum voltage is 0.89 pu is improved by FLC to 0.94 pu. Active power using FLC is reduced from 501.35 kW to 480.47 kW and reactive power losses reduced from 531.12 kVAr to 507 kVAr. Results show that FLC improved the performance of the system by improving voltage profile and real or reactive power losses. In future this system will be able to implement on other existing systems to improve the performance.

Acknowledgements

Authors are thankful to authorities of JVVNL Kota, India, for providing the data of Ramchandrapura, Kota feeder and for the valuable support.

Conflict of Interest

No conflict of interest.

References

[1]	Government of India, Ministry of Power Central Electricity Authority, New Delhi. Available from: http://www.cea.nic.in/reports/monthly/executivesummary/2018/exe_summary-05.pdf .
[2]	Singh P, Kothari DP, Singh M (2014) Interconnected distribution network for the integration of distributed energy resources. Res J Appl Sci, Eng Technol 7: 240–250. doi: 10.19026/rjaset.7.247
[3]	Abu-Mouti FS, El-Hawary ME (2011) Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm. IEEE Trans Power Delivery 26: 2090–2101. doi: 10.1109/TPWRD.2011.2158246
[4]	Akash T, Santosh KS, Pushpendra S, et al. (2018) Smart grid development in India with challenges and opportunities: Execution with game theory. Int J Tech Res Sci 3: 122–128.
[5]	Akash T, Santosh KS, Pushpendra S, et al. (2018) Game theory: demand side management with DG's and storage units. Int J Tech Res Sci 3: 129–133.
[6]	Mahari A, Babaei E (2012) Optimal DG placement and sizing in distribution systems using imperialistic competition algorithm. In 2012 IEEE 5th India international conference on power electronics (IICPE).
[7]	Syahputra R, Soesanti I, Ashari, M (2016) Performance enhancement of distribution network with DG integration using modified PSO algorithm. J Electr Syst 12: 1–19.
[8]	Talwariya A, Sharma D, Pandey AK, et al. (2016) An execution of smart grid with game theory. In 2016 International Conference on Recent Advances and Innovations in Engineering (ICRAIE) 1–4.
[9]	Sharma D, Talwariya A, Pandey A, et al. (2017) Shrouded problems of solar power plant and recommendations. Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore 1–5.
[10]	Prabhu JAX, Sharma S, Nataraj M, et al. (2016) Design of electrical system based on load flow analysis using ETAP for IEC projects. In Power Systems (ICPS), 2016 IEEE 6^th International Conference 1–6.
[11]	Talwariya A, Singh P, Kolhe M (2019) A stepwise power tariff model with game theory based on Monte-Carlo simulation and its applications for household, agricultural, commercial and industrial consumers. Int J Electr Power Energy Syst 111: 14–24. doi: 10.1016/j.ijepes.2019.03.058
[12]	Talwariya A, Sharma SK, Singh P, et al. (2018) A game theory approach for energy tariff and demand side management. International Conference on Recent Advancement and Innovations in Engineering (ICRAIE), Jaipur, India, 1–4.
[13]	Rupa JM, Ganesh S (2014) Power flow analysis for radial distribution system using backward/forward sweep method. Inter J Electr, Comput, Electron Commun Eng 8: 1540–1544.
[14]	Abdel-Akher M (2013) Voltage stability analysis of unbalanced distribution systems using backward/forward sweep load-flow analysis method with secant predictor. IET gener, transm distrib 7: 309–317. doi: 10.1049/iet-gtd.2012.0360
[15]	Hasanien HM, Matar M (2015) A fuzzy logic controller for autonomous operation of a voltage source converter-based distributed generation system. IEEE Trans Smart grid 6: 158–165. doi: 10.1109/TSG.2014.2338398
[16]	Huang SJ, Gu PH, Su WF, et al. (2015) Application of flower pollination algorithm for placement of distribution transformers in a low-voltage grid. In 2015 IEEE international conference on industrial technology (ICIT) 1280–1285.
[17]	Freitas W, Vieira JCM, Morelato A, et al. (2006) Comparative analysis between synchronous and induction machines for distributed generation applications. IEEE Trans Power Syst 21: 301–311. doi: 10.1109/TPWRS.2005.860931
[18]	Alajmi BN, Ahmed KH, Finney SJ, et al. (2011) Fuzzy-logic-control approach of a modified hill-climbing method for maximum power point in micro-grid stand-alone photovoltaic system. IEEE trans power Electron 26: 1022–1030. doi: 10.1109/TPEL.2010.2090903

This article has been cited by:

1.	K. Moloi, Y. Hamam, J. A. Jordaan, 2020, Optimal Location of DGs Into the Power Distribution Grid for Voltage and Power Improvement, 978-1-7281-6746-6, 1, 10.1109/PowerAfrica49420.2020.9219938
2.	Mahmoud G. Hemeida, Salem Alkhalaf, Al-Attar A. Mohamed, Abdalla Ahmed Ibrahim, Tomonobu Senjyu, Distributed Generators Optimization Based on Multi-Objective Functions Using Manta Rays Foraging Optimization Algorithm (MRFO), 2020, 13, 1996-1073, 3847, 10.3390/en13153847
3.	Virendra Sharma, Lata Gidwani, Optimistic use of battery energy storage system to mitigate grid disturbances in the hybrid power system, 2019, 7, 2333-8334, 688, 10.3934/energy.2019.6.688
4.	Olusayo A. Ajeigbe, Josiah L. Munda, Yskandar Hamam, Towards maximising the integration of renewable energy hybrid distributed generations for small signal stability enhancement: A review, 2020, 44, 0363-907X, 2379, 10.1002/er.4864
5.	Leonid Vishnevsky, Igor Voytetsky, Taisiya Voytetskaya, 2019, Marine Electrical Power Plant Dynamic Modes Evaluation Using a Fuzzy Inference System, 978-1-7281-2810-8, 1, 10.1109/CPEE47179.2019.8949175
6.	Shiva Pujan Jaiswal, Vivek Shrivastava, D.K. Palwalia, Opportunities and challenges of PV technology in power system, 2021, 34, 22147853, 593, 10.1016/j.matpr.2020.01.269
7.	Fevrier Valdez, Oscar Castillo, Prometeo Cortes-Antonio, Patricia Melin, Cengiz Kahraman, A survey of Type-2 fuzzy logic controller design using nature inspired optimization, 2020, 39, 10641246, 6169, 10.3233/JIFS-189087
8.	Adedayo Owosuhi, Yskandar Hamam, Josiah Munda, Maximizing the Integration of a Battery Energy Storage System–Photovoltaic Distributed Generation for Power System Harmonic Reduction: An Overview, 2023, 16, 1996-1073, 2549, 10.3390/en16062549
9.	Rudresh B. Magadum, G. B. Ramesh, Mohsin A. Mulla, 2023, Chapter 67, 978-981-19-3950-1, 891, 10.1007/978-981-19-3951-8_67
10.	Virendra Sharma, Kavita Rawat, Gaurav Jain, Nishant Agrawal, Shaaz Rizvi, Prabhat Kumar, 2021, Hybrid SPV & Fuel-Cell power optimization by Battery Storage System for utility network load with & without Grid, 978-1-6654-3402-7, 1, 10.1109/ICRAIE52900.2021.9703810
11.	Rudresh B. Magadum, Vadiraj A. Kulkarni, Abhaykumar D. Janaj, Madhusudan S, Shivanand D. Hirekodi, Vani P. Datar, 2024, Fuzzy Knowledge Based Controller for Multiple Distributed Generators Placement, 979-8-3503-1755-8, 1, 10.1109/ICICACS60521.2024.10498610
12.	Avinash Deshpande, Sateesh N. Dodamani, Rudresh B. Magadum, 2025, Chapter 13, 978-981-97-6709-0, 155, 10.1007/978-981-97-6710-6_13

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Energy

1.8 3.8

Metrics

Article views(6418) PDF downloads(1833) Cited by(12)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Energy

Distributed generation integration optimization using fuzzy logic controller

Related Papers:

Abstract

1. Introduction

2. Problem description

2.1. Load flow

2.1.1. Backward sweep

2.1.2. Forward sweep

2.2. Objective function

2.3. Power losses

2.4. Voltage index (VI)

3. Fuzzy logic control based DG integration

4. Results

4. Conclusion

Acknowledgements

Conflict of Interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Problem description

2.1. Load flow

2.1.1. Backward sweep

2.1.2. Forward sweep

2.2. Objective function

2.3. Power losses

2.4. Voltage index (VI)

3. Fuzzy logic control based DG integration

4. Results

4. Conclusion

Acknowledgements

Conflict of Interest

References

AIMS Energy

Distributed generation integration optimization using fuzzy logic controller

Related Papers:

Abstract

1. Introduction

2. Problem description

2.1. Load flow

2.1.1. Backward sweep

2.1.2. Forward sweep

2.2. Objective function

2.3. Power losses

2.4. Voltage index (VI)

3. Fuzzy logic control based DG integration

4. Results

4. Conclusion

Acknowledgements

Conflict of Interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Problem description

2.1. Load flow

2.1.1. Backward sweep

2.1.2. Forward sweep

2.2. Objective function

2.3. Power losses

2.4. Voltage index (VI)

3. Fuzzy logic control based DG integration

4. Results

4. Conclusion

Acknowledgements

Conflict of Interest

References