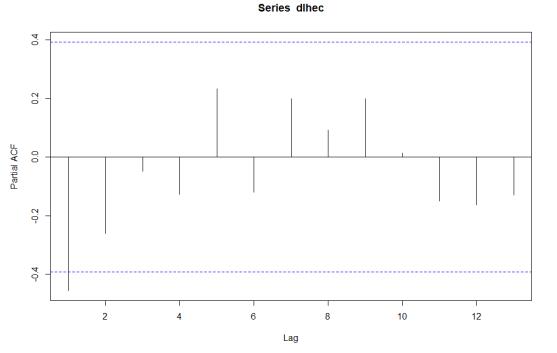
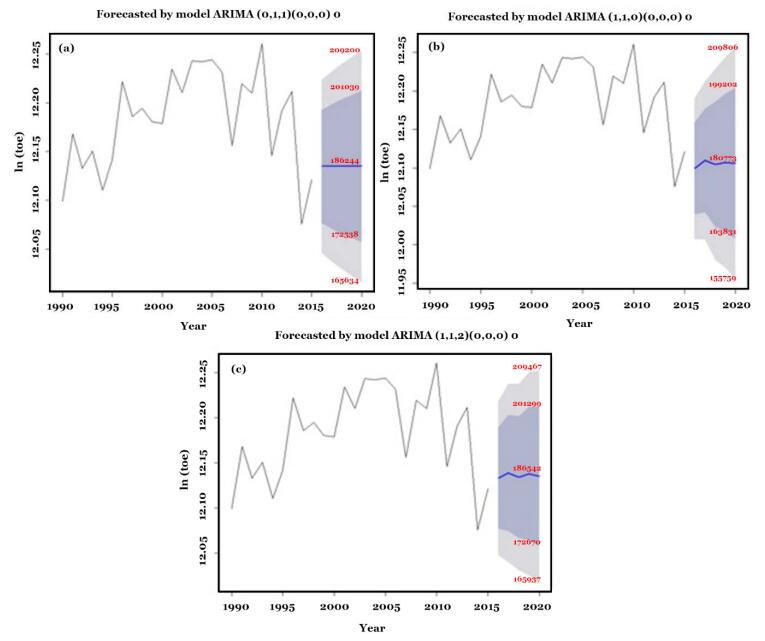
Accurate estimation of the energy need and consumption is considered as one of the most important basis of the economy worldwide. It is also of high importance to mitigate the adverse effects of the release of CO2 (e.g., climate change) from conventional energy sources by using renewable energies, as recommended by European commission. Thus, in this study a forecast regarding the residential energy consumption of the household sector in countries belonging to the Euro area was executed. To proceed with this prediction, time related data from 1990 till 2015 along with Auto Regressive Integrated Moving Average (ARIMA) model were applied. ARIMA model was considered due to possessing the ability of providing accurate results while being able to receive stationary and non-stationary data. The obtained results from the analysis clarified that ARIMA (0,1,1) model is the most accurate model to undertake such prediction as the amount of RMSE achieved was 0.097. This comparison was accomplished by considering the ARIMA (0,1,0) and ARIMA (1,1,2) models as their amounts regarding RMSE were respectively 0.1068149 and 0.0975575. The results indicate that the amount of the energy predicted to be consumed in household sector in EU area is estimated to be 186244 toe (tonne of oil equivalent) which shows a drop in the energy consumption in Euro area probably due to the increase in the energy efficiency especially in recent years.
1.
Introduction
Symbiotic relationships play a crucial role in the study of ecological systems and have gained substantial attention among evolutionary biologists for their frequent involvement in the coevolutionary dynamics between interacting organisms. In addition to well-known symbiotic relationships like mutualism, competition and predator/prey interactions, there are three other types, i.e., commensalism, amensalism and synnecrosis, that have received comparatively less attention from researchers. Amensalism, receiving less attention than commensalism, involves one species adversely affecting another's fitness without gaining any apparent benefit [1] For instance, Xi et al. [2] noted that grassland caterpillars will trigger a death-feigning anti-predator response if grasshoppers suddenly appear. Moreover, by leaping to seek food, the grasshopper may negatively affect the foraging efficiency of the caterpillars, but the behavior of caterpillars has no effect on the grasshopper. Therefore, the two species form an amensalism relationship. The interaction of ibex and weevils feeding on the same type of shrub serves as another illustration of amensalism. Although the presence of the weevil has minimal impact on food availability, the presence of ibex significantly reduces weevil populations. Ibex consume substantial amounts of plant matter, inadvertently ingesting the weevils along with it [3]. According to Veiga et al.[4] the relationships witnessed between honey bees (Apis mellifera) and wasps in the tropical ecosystems of East Africa could be described by amensalism concerning nesting spaces. The experiment's results revealed that wasps refrained from using nest boxes that had been inhabited by bees in the prior breeding season. In contrast, honeybees displayed a tendency to take over these nest boxes, regardless of whether they were previously occupied by wasps. This behavior showcases a clear instance of amensalism, as there was no recorded occurrence of wasps occupying a nest box previously utilized by bees. For a deeper ecological context regarding species amensalism, refer to [3,5,6,7,8] and the related references within those sources.
Although scientists and researchers have extensively investigated amensalism in ecological systems in recent decades, the first mathematical model was put forward by Sun in 2003 [9]. In 2008, Zhu et al. [10] employed the method of vector field analysis to study the following model:
where x and y represent the density of the first and second species at time t, respectively, a1 and b1 stand for the intrinsic growth rates and the intensity of competition of x, a2 and c2 stand for the intrinsic growth rates and the intensity of competition of y. Additionally, c1 represents the strength of the interspecific competition, indicating how much impact the second species has on the first species. By analyzing the equilibrium points in system (1.1), they obtained the following result:
Theorem A (1) If a1c1<a2c2, then the boundary fixed points B(0,a2c2) is globally stable.
(2) If a1c1>a2c2, then the unique positive fixed point A(a1c2−c1a2b1c2,a2c2) is globally stable.
The model (1.1) exhibits simple dynamical behavior as the Theorem A indicates that the system does not generate bifurcation. In recent years, researchers have extensively studied the dynamical behaviors of the amensalism model (1.1) in different scenarios. Several mathematical models have been explored, considering the well-known Allee effect in [11,12,13,14,15]. For instance, Wei et al. [11] proposed an amensalism model with a weak Allee effect and observed saddle-node bifurcations. Luo et al. [12] presented the global dynamics of a two-species Holling-II amensalism system with a nonlinear growth rate by incorporating the Allee effect on the first species. Similarly, some interesting works using non-monotonic functional responses have been presented in [6,16,18]. Amensalism relationships among different species have also been incorporated into the study of harvesting models [19,20]. Under the Michaelis-Menten type harvesting in the first species, Liu et al. [19] investigated the complex dynamics of an amensalism system. Zhao et al. [20] found that incorporating Menten-type harvesting in the second species within the amensalism system leads to notably richer dynamics. These dynamics include scenarios where the extinction of the first species persists or where the approach toward the steady-state occurs at a slower rate. Similar to the above, amensalism models incorporating prey refuge have emerged as a prominent area of research [19,21,22,24].
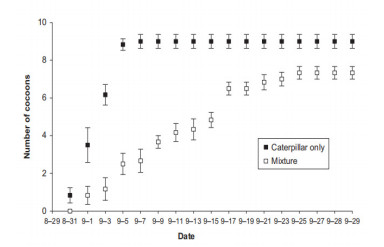
In ecological systems, direct killing in the predation process significantly influences the common symbiosis relationships, i.e., mutualisms, competition and predator/prey interactions. Besides direct killing, the psychological fear induced in the prey due to predation risk also indirectly impacts the breeding rate of the prey. This indirect effect, termed the fear effect, exerts a substantial impact throughout the prey's life cycle, amplifying the complexity of their ecological dynamics. In their experiment involving song sparrows, Zanette et al. [25] observed a 40% reduction in the breeding rate due to the induced fear of predation risk. In another independent study, Elliott et al.[26] reported that Drosophila melanogaster exhibits anti-predator behaviors upon exposure to Mantid odor, displaying reduced activity across both breeding and non-breeding seasons. Meanwhile, Wang et al. [27] presented a mathematical model for prey-predator dynamics, incorporating the fear risk. They disclosed that heightened fear levels might stabilize the ecosystem by preventing the occurrence of periodic oscillations in the population. For more information about predator-prey models with fear effects, see [28,29,30] and references cited therein. The fear effect is not limited to only common symbiosis relationships like mutualism, competition and predator/prey interactions. It has also been observed in commensalism and amensalism types of symbiosis. For example, Xi et al. [2] studied the number of cocoons formed by grassland caterpillars in the presence or absence of grasshoppers and obtained Figure 1. From Figure 1, it can be clearly observed that the fear of grasshoppers by caterpillars can lead to a decline in species numbers. Ogada [31] have highlighted that the presence of large herbivorous mammals in African savanna habitats has resulted in a reduction of the canopy area of trees, as well as a decrease in grass cover by 8% and forb cover by 33%. However, the canopy serves as a crucial habitat and food source for birds in this particular East African savanna ecosystem. Thus, the sizable herbivore has exerted a significant influence on avian behavior and growth, particularly in relation to foraging habits, rates of maturation, chances of survival, reproductive capacity and dietary resources. As a result, the overall diversity of bird species has experienced a decline of approximately 30%. This decline may be interpreted as the fear induced by large herbivores in the East African savanna ecosystem, resulting in reduced avian birth rates. Consequently, developing models that can effectively explain this phenomenon is imperative. However, no scholarly investigations have taken into account the impact of the fear effect on the amensalism system.
Recently, discrete-time models have attracted considerable attention due to their rich and complex dynamic behaviors and have been explored extensively [18,30,32]. However, there needs to be more emphasis on investigating discrete-time amensalism systems. In 2022, Zhou et al. [21] investigated the following discrete amensalism systems:
They studied the stability and attractivity of the equilibrium point of system (1.2) and obtained the following results:
Theorem B (1) If 0<α≤2, 0<c<δαγ, 0<γ<2 or α>2, δ(α−2)γ<c<δαγ, 0<γ<2, then the positive equilibrium point E∗3(x∗3,γδ) is local stability.
(2) If 0<γ<2, 0<α−cγδ<ln2+1, then the positive equilibrium point E∗3(x∗3,γδ) is globally attractive.
Obviously, system (1.2) is the discrete form of model (1.1). In system (1.1), according to Theorem A (2), when a positive equilibrium point exists, it is global stability. This also implied that no matter what the initial conditions are, the solution will eventually converge to the positive equilibrium point. While for discrete system (1.2), Theorem B shows that the conclusion of the stability of the positive equilibrium point can only be obtained under stricter conditions than Theorem A. Additionally, model (1.2) undergoes flip bifurcation at the boundary equilibrium points E1, E2 and the positive equilibrium point E∗3 [21]. This is a dynamic phenomenon that does not exist in the continuous system (1.1), Hence, the investigation of discrete models is highly valuable due to their propensity for exhibiting intricate dynamic phenomena that surpass those observed in continuous models.
Subsequently, Zhou et al.[32] investigated a discrete amensalism system with the Beddington-DeAngelies functional response and Allee effect, and they found that the Allee effect causes the system to take longer trajectories to reach its stable steady-state solution. So far, to the best of our knowledge, there has been no research conducted on the discrete amensalism system with the fear effect by researchers.
Motivated by prior research, we assume that the birth rate of the first species will be reduced by the fear of the second species. We multiply the birth rate of the first species by a decreasing function G(k,y) related to the size of the second species. Based on observations in the biological world, the fear function G(k,y) proposed by Wang et al. [27] must satisfy the following requirements:
where k represents the level of fear and y is the species density. Note that G(k,y)=1/(1+ky) meets the above requirements and 1/(1+ky) is now widely applied in [33,34,35].
Accordingly, on the basis of system (1.1), considering the above assumption, we introduce the fear effect to the first species, resulting in the formulation of the following amensalism model:
where e1 and e2 represent the birth and death rates of the first species and 1/(1+ky) represents the fear effect function. It is to be noted that without the fear effect (k=0), the above model (1.3) will degenerate to the amensalism model (1.1). For the convenience of analysis, with the transformation x=ˉx/b1, y=ˉy/c2, t=ˉt, after dropping the bars, system (1.3) becomes
where k=k1/c2 and c=c1/c2. The numerical simulations in [36] show that when the step size gets bigger in Euler's scheme, both period-doubling and Neimark-Sacker bifurcation happen. This means that the numerical approach for discretization is not accurate. In order to address this shortcoming, the method of piecewise constant arguments was established. Based on the findings in [37,38], the method of piecewise constant arguments is indeed a preferable solution for the discretization of continuous models. Hence, using the method of piecewise constant arguments proposed by Jiang and Rogers [39], similar to the modeling method in [32], we can obtain the following discrete-time model:
Obviously, the initial conditions (x0,y0) for (1.5) are in R2+. In a discrete amensalism ecological model with the fear effect, what kind of dynamical behavior does it exhibit? Does the stability of the equilibrium point change compared to a continuous system (1.1)? Does a new bifurcation happen compared to a discrete system (1.2)? What effects do fear effects have on the system? We will conduct a detailed investigation to answer these questions.
The layout of the paper is as follows: In Section 2, we analyze the relevant properties of the fixed points. Section 3 investigates bifurcation phenomena and considers the chaos control method. Then, in Section 4, we use numerical simulations to validate the feasibility of the obtained results. Finally, a brief discussion is provided at the end of the paper.
2.
Analysis of fixed points
2.1. The existence of equilibria
Note that fixed points are determined by the following system of equations:
Obviously, system (1.5) always has four fixed points: E0(0,0), E1(0,a2), E2(e1−e2,0) and E∗((e1−e2−ke2a2−ka22c−a2c)/(1+ka2),a2). The fixed points E2 and E∗ are non-negative if e2<e1 and e1>(a2k+1)(a2c+e2) are satisfied, respectively. There are two fixed points in region A of Figure 2(a): E0 and E1. There are three fixed points in region B: E0, E1 and E2. There are four fixed points in region C: E0, E1, E2 and E∗.
2.2. The local stability of equilibria
The Jacobian matrix of system (2.1) is calculated as follows:
where M=exp(e1/(1+ky)−e2−x−cy) and N=exp(a2−y).
Next, we analyze the local stability of the equilibria according to the above Jacobian matrix.
Theorem 2.1. E0(0,0) is
1) a source if 0<e2<e1;
2) a saddle if 0<e1<e2;
3) non-hyperbolic if e1=e2.
Proof. For the equilibrium E0(0,0), the Jacobian matrix is
with eigenvalues λ1=exp(e1−e2)>0 and λ2=exp(a2)>1. Thus, E0(0,0) is a source if 0<e2<e1, a saddle if 0<e1<e2 and non-hyperbolic if e1=e2. The proof is completed.
Theorem 2.2. The local stability of E1(0,a2) is described below:
1) a sink if 0<e1<(a2k+1)(a2c+e2) and 0<a2<2;
2) a source if e1>(a2k+1)(a2c+e2) and a2>2;
3) non-hyperbolic if e1=(a2k+1)(a2c+e2) or a2=2;
4) a saddle if one of the conditions holds:
(a) 0<e1<(a2k+1)(a2c+e2) and a2>2;
(b) e1>(a2k+1)(a2c+e2) and 0<a2<2.
Proof. The Jacobian matrix of system (2.1) at E1(0,a2) is given by
Consequently, two eigenvalues are λ1=exp(e1/(1+ka2)−e2−ca2)>0 and λ2=1−a2<1. Hence, if 0<e1<(a2k+1)(a2c+e2) and 0<a2<2, then we have 0<λ1<1 and |λ2|<1. Therefore, E1(0,a2) is a sink. The proofs of (2–4) are similar to (1) and are omitted here. The topological classification of E1 is presented in Figure 2(b).
Theorem 2.3. E2(e1−e2,0) is
1) a source if e1>e2+2;
2) a saddle if 0<e1<2+e2;
3) non-hyperbolic if e1−e2=2.
Proof. For the equilibrium E2(e1−e2,0), the Jacobian matrix is
Obviously, the two eigenvalues are λ1=1−e1+e2=1−(e1−e2)<1 and λ2=exp(a2)>1. If e1−e2>2, i.e., λ1<−1, then |λ1|>1 and |λ2|>1, implying that E2(e1−e2,0) is a source. Therefore, (1) holds. The proof processes of (2) and (3) are similar, we omit the details here. Thus, E2 is always unstable. This completes the proof.
For E∗(x∗,a2), the Jacobian matrix is as follow:
where λ1=1−x∗=1−(e1−(1+a2k)(e2+ca2))/(1+ka2)<1 and λ2=1−a2<1. Note that when 0<c<(e1−e2(1+ka2))/(1+ka2)a2≜˜c and 0<e2<e1/(1+ka2)−2≜e∗∗2. In addition, we can verify c1<˜c. Then,
where c1=(e1−(2+e2)(1+ka2))/(1+ka2)a2. Moreover, if e∗∗2<e2<e1/(1+ka2) and 0<c<˜c, then 1−x∗∈(−1,1). Therefore, the following result can be obtained immediately.
Theorem 2.4. Suppose that 0<c<˜c. Then, the topological classifications of the unique positive fixed point E∗(x∗,a2) is given by Table 1.
2.3. Global attractivity of positive equilibrium point
In this section, we consider the global asymptotic stability of the equilibrium point with the help of Lemmas 3–5 from [30] and Lemmas 2.1 and 2.2 from [40].
Theorem 2.5. Suppose that 0<a2<2, 0<k∗∗<k<k∗ holds and E∗(x∗,a2) is globally attractive, i.e.,
where k∗=e1−e2−ca2(e2+ca2)a2 and k∗∗=e1−ln2−1−e2−ca2(ln2+1+e2+ca2)a2.
Proof. According to Lemma 4 in [30], if 0<a2<2 holds, then
For sufficiently small ε, there exists an integer N1, such that for all n>N1,
From Lemma 2.1 and 2.2 in [40], we obtain:
Now, we consider the following system:
Apparently, x∗1=x∗ is the positive equilibrium point of the system. Suppose {x1(n)} is any positive solution of system (1.5). From Lemma 3 in [30], if 0<e1−(1+ka2)(e2+ca2)<2, we know that limn→∞x1(n)=x∗. Thus, we only need to prove that
Assume that
Therefore, our main goal is to prove limn→∞k1(n)=0.
The first equation of (1.5) is equivalent to
Then, x1(n)exp[θ1(n)k1(n)] is between x1(n) and x(n), and here θ1(n)∈[0,1].
It follows from (2.5) that
Obviously,
holds. Thus, according to Lemma 2.1 and 2.2 in [40], it immediately follows that:
Setting ε→0 in the above inequalities leads to
Hence, taking an integer N2>N1, for ξ>0 small enough, when n≥N2, the following inequality holds:
Assume
Now, let
Therefore,
The following equation can be obtained:
Considering λε1<1, then limn→+∞k1(n)=0, i.e., limn→+∞[x(n)−x1(n)]=0 is established if λ1<1. Since
λ1<1 is equivalent to 1−Q1>−1, i.e.,
Hence, Theorem 3.1 is proved.
2.4. Global attractivity of boundary equilibrium
Now, we discuss the global attractivity of E1 with the help of Lemma 6 and 7 from [30].
Theorem 2.6. Assuming that k>k∗, 0<a2<2 holds, and E1(0,a2) is globally attractive, i.e.,
Proof. The proof of limn→∞y(n)=a2 follows the same process as the one in Theorem 2.5 above, so it is omitted here. Next, we prove that limn→∞x(n)=0.
Consider the auxiliary equation:
combined with the second equation of system (1.5), for all i∈N, we have
According to the Theorem 2.6, we have e11+ka2−e2a2<c, i.e.,
Therefore, the following inequality holds:
where s and h are positive numbers. Then,
and there exist δ>0 such that
From (2.11)–(2.14), we have
Summing up the above formulas, we can get:
Then,
According to Lemma 2.1 in [40] and y(n+1)≤y(n)exp(a2−y(n)), it holds that:
Therefore, taking an integer N2>N1, for ε>0, when n≥N2, y(n)≤exp(a2−1)+ε:=M is established. So, the inequality (2.15) is equivalent to
Thus,
Therefore, if we want to prove limn→∞x(n)=0, we only need to prove
Assume that
Therefore, we can convert what we need to prove into the proof limn→∞k2(n)=0.
By a similar process of proof as in Theorem 2.5, we have that when
limn→∞k2(n)=0 holds. Combining condition (2.11) and condition (2.16), we have that limn→∞x(n)=0 holds when e1/(1+ka2)−e2−ca2<0. Hence, Theorem 2.6 is proved.
3.
Bifurcation analysis
Based on the above proofs, it becomes evident that the system (1.5) exhibits several bifurcation types at its fixed points. In the subsequent discussion, we will examine these potential bifurcations by employing the center manifold [41] and bifurcation theory [42,43].
3.1. Flip bifurcation at E1(0,a2), E2(e1−e2,0)
Theorem 2.2 states that if a2=2 and e1≠(1+a2k)(ca2+e2) holds, then one of the eigenvalues of E1(0,a2) is -1 and another one is neither 1 nor –1. These requirements suggest that all parameters belong to the set TA:
At this point, the central manifold of system (1.5) at E1(0,a2) is x=0. Therefore, the restricted system of (1.5) to it is:
f′(a2)=−1 is obvious, so it can be seen that a flip bifurcation occurs at E1(0,a2). Figure 3(a) depicts the bifurcation diagram about E1.
Based on conclusion (4) of Theorem 2.3, we obtain that all parameters belong to the set TB:
We can easily know that the central manifold of system (1.5) at E2(e1−e2,0) is y=0. So the restricted system of (1.5) to it is:
Thus, we have g′(e1−e2)=−1. Figure 3(b) depicts the bifurcation diagram about E2. Moreover, as illustrated in Figure 3, the maximum Lyapunov exponents (MLE) for(a), (b) are depicted in (c) and (d), respectively.
3.2. Flip bifurcation at E∗(x∗,a2)
According to Theorem 2.4, if e∗1=(1+ka2)(2+e2+a2c), then at E∗(x∗,a2), one eigenvalue is -1 and another one is neither 1 nor -1, These conditions imply that all parameters belong to the set Fc:
If the condition of (e∗1,e2,k,c,a2)∈Fc is satisfied, flip bifurcation may occur. Thus, suppose δ is a bifurcation parameter satisfying ‖δ‖≪1. Then, system (1.5) can be expressed as follows:
First, we transform E∗ to the origin by using the transformation u=x−x∗,v=y−a2 and then utilize Taylor expansion, turning the mapping (3.1) into
where
and
Next, we use the invertible transformation:
Equation (3.2) can be rewritten as
where
and
According to the central manifold theorem, there exists a central limit Wc1(0,0,0), which can be expressed as
where
Based on (3.3), Y=h(X,δ) must satisfy:
By calculation, we obtain t1=t2=t3=0. Thus, the map (3.3) can be written as :
where
Then, we have:
Consequently, the following conclusions can be drawn.
Theorem 3.1. If (e∗1,e2,k,c,a2)∈Fc, then the system (1.5) undergoes flip bifurcation at E∗(x∗,a2). (see Figure 7)
3.3. Transcritical bifurcation at E0(0,0)
According to Theorem 2.1, if e1=e2, then at E0(0,0), one eigenvalue is 1 and another one is neither 1 nor -1. These conditions mean that all of the parameters are in the set Fd:
Taking e1 as the bifurcation parameter and setting η as the disturbance parameter, the map is as follows:
Next, a Taylor expansion is performed at the origin. Then, (3.5) becomes
where
Setting the approximate central mainfold Wc2(0,0,0) of (3.6) as
for x and η sufficiently small. By a simple coefficient comparison, we can obtain h1=h2=h3=0. Therefore, the map on the center manifold is:
By simple compulation, we have:
Hence, we draw the following conclusion about transcritical bifurcation.
Theorem 3.2. If (e1,e2,k,c,a2)∈Fd, then system (1.5) experiences transcritical bifurcation at E0(0,0).
3.4. Chaos control
Considering that the flip bifurcation may lead to chaos, in this section, we focus on controlling the generation of chaos. Combined with the method of hybrid control, the related control system (1.5) is expressed as follows:
where ρ∈(0,1). The Jacobian matrix of E∗(x∗,a2) in the control system (3.7) is as follows:
Its eigenvalues are λ1=1−ρ(e1−(1+a2k)(ca2+e2))/(1+ka2)<1 and λ2=1−ρa2<1, respectively. Hence, we have the following outcome:
Theorem 3.3. The controlled system (1.5) is locally asymptotically stable at E∗(x∗,a2) when
4.
Numerical examples and discussions
In this section, we will illustrate the accuracy of relevant conclusions and explore the influence of the fear effect on the system through numerical simulations.
Example 1. (the effect of fear effect on E1)
1) Given the values (e1,a2,e2,c,k)=(1,1.7,0.4,0.3,0.1), it can be observed that (a2k+1)(a2c+e2)=1.06, which is larger than e1. Additionally, it is known that 0<a2<2. Consider the three sets of initial values: (0.3,0.8), (0.6,0.2) and (1.2,0.7). As depicted in Figure 5(a), it can be observed that E1 exhibits local asymptotic stability. The correctness of the result of Theorem 3 is affirmed. Furthermore, to investigate the impact of the fear effect on the local stability of E1, we varied the parameter k from 0.1 to 5. The findings are depicted in Figure 5(b). It can be observed that the presence of fear induces an increase in the local stability of E1, thereby expediting the process of extinction for the first species.
2) Given the values (e1,e2,c,k)=(4,0.5,1,2) and the condition a2>2, we observe that e1=4<(a2k+1)(a2c+e2). satisfying condition (3) of Theorem 2.2 and indicating that E1 is unstable at this particular moment. Next, we select a2 as the bifurcation parameter to investigate the impact of a2 on the system. As depicted in Figure 6, when the value of a2 grows, the first species will undergo extinction, whereas the second species will experience a state of chaos. Furthermore, the aforementioned conditions fail to meet the requirements stated in Theorem 2.6, namely the conditions for achieving global stability of E1. Therefore, this example also provides additional evidence about the plausibility of the conditions outlined in Theorem 2.6.
Example 2. (the fear effects on the first species)
Case 1: Assuming that the second species is global stability, i.e., 0<a2<2
When the value of k is set to 0.3, Figure 7(a) illustrates periodic-2, 4 and 8 orbits. To provide a more intuitive observation of periodic orbits and chaotic sets, we present the phase diagrams corresponding to each stage of Figure 7(a) for six different values of e1: 2,3.25,3.6,4.1,4.2,4.3. (as shown in Figure 8). The first species exhibits stability when e1 falls between 0 and 3.25, becoming unstable when e1 exceeds 3.25. It is observed that with an increase in the birth rate, the initial species exhibits instability or even chaotic behavior. In this study, our goal is to investigate the impact of the fear effect on the first species under conditions of chaos. We set the parameter e1 to a value of 4.3 and utilize the bifurcation parameter k. The stability of E∗(x∗,a2) is observed to be dependent on the value of k. Specifically, E∗(x∗,a2) is unstable for 0<k<0.65 and stable for k>0.65. The analysis of Figure 7(b) reveals that the fear effect significantly contributes to preserving stability in the first species, especially when the second species achieves global stability.
Case 2: Assuming that the second species is chaos, i.e., a2>2.
When a2>2, the second species exhibits chaotic behavior, leading to the following scenarios. In this chaotic state, it is observed that the fear effect no longer has the effect of stabilizing the first species. Moreover, with the increase of the parameter k, the density of the first species decreases, eventually leading to its extinction when k>k∗.
Figure 10 depicts the effect of the parameters e1 and k, as well as the parameters a2 and k, on the bifurcation.
Furthermore, when the parameter k is set to zero, a comparison between system (1.1) and system (1.5) reveals that the variable a1 in system (1.1) corresponds to the difference between e1 and e2 in system (1.5). Additionally, both b1 and c2 in system (1.1) assume a value of 1 in system (1.5). Consequently, when the parameter values of system (1.5) are set to (a2,c,e2,e1)=(3,0.2,0.3,2.3), it corresponds to the parameter values of system (1.1) being (a2,c1,a1,c2,b1)=(3,0.2,2,1,1). At this time, it is observed that a1/c1>a2/c2. According to the findings of Theorem A, it can be deduced that the positive equilibrium point in system (1.1) is globally stable. However, the positive equilibrium point in system (1.5) is unstable, and there exists a potential for flip bifurcation. Consequently, the discrete model exhibits more intricate dynamical behavior in comparison to the continuous model.
Example 3. (the effect of fear effect on E∗)
We examine the stability of the positive equilibrium point E∗(x∗,a2). The parameters are assigned values of (a2,e2,c,e1)=(0.5,1,0.2,3), and the initial values (x0,y0) are set to (0.4,0.3), (0.5,0.8) and (1.1,0.6) accordingly. Based on the conditions stated in Theorem 2.5, it can be concluded that when k∈(0.07,3.4545), the positive equilibrium point E∗(x∗,a2) is globally stable. To verify the feasibility of Theorem 2.5, we select k=2, as depicted in Figure 12(a). It can be observed that at this value of k, the equilibrium point E∗ remains globally stable. Furthermore, in order to investigate the effect of the fear effect on the global stability of E∗, we chose k=4. The results show that the fear effect affects the global stability of the positive equilibrium point and reduces the density of the first species. This reduction in density eventually leads to the extinction of the first species.
The values assigned to (a2,e2,c,e1) are (1,0.5,0.3,4). For this set of parameters, the values of k∗∗ and k∗ are 0.60 and 4, respectively. We will use k as the bifurcation parameter to investigate the influence of k on the stability of E∗. At this time, the second species is stable. Combined with Figure 13(a), we can see that when k∗∗<k<k∗, E∗ is stable; when k>k∗, the first species becomes extinct. Therefore, we can conclude that an appropriate value of k promotes the convergence of the first species from a chaotic state to stability.
Additionally, examining the two trajectories shown in Figure 13(b) with k=0 and k=1 makes it clear that, as k increases, the solution approaches a stable state within shorter trajectories. This observation underscores the notion that an appropriate level of fear might confer advantages to species, enabling them to acclimate more effectively to changes in the surrounding environment.
Example 4. (Effect of fear effect on the stability of the system)
We proceed to investigate the influence of the fear effect on the system through numerical simulations. The chosen parameter values for this analysis are (e1,a2,e2,c)=(2,1,0.3,0.2). The density distribution of the first species, denoted as x, and the second species, denoted as y, for varying values of k is illustrated in Figure 14. In this analysis, we examine two scenarios: one where the system exhibits a fear effect (k≠0) and another where there is no fear effect (k=0). Furthermore, we categorize the presence of the fear effect into several levels, specifically k=0.3,k=0.5,k=1,k=3,k=5. It was observed that an increase in the fear effect parameter k reduced the density of the first species and had no effect on the second species. However, it enhances the local stability of the first species and diminishes the frequency of oscillations. As the intensity of fear increases, the local stability of the first species will diminish, resulting in the prolonged period required to attain equilibrium. Moreover, a higher value of k leads to the extinction of the first species.
Example 5. The bifurcation parameter for the chaotic region is denoted as k, while the remaining parameter values are established as follows: the values of the variables (e1,a2,e2,c) are as follows: e1=4.3, a2=1, e2=0.3, c=0.2, the given system, denoted as Eq (3.7), can be expressed as:
Based on the observation of Figure 7, it is evident that for values of k within the range of 0<k<0.5, the first species undergoes a chaotic state. Therefore, we select certain values of k such as k=0.20,0.25,0.30,0.35,0.40,0.45. By utilizing Theorem 3.3, in conjunction with Table 2, we can determine the range of values for ρ when 0.2≤k≤0.5.
Figure 15(a), (b) show that chaos control is effective.
5.
Summary and discussion
Through numerical simulations, we find that when the fear effect k changes, the dynamic behaviors of the system will also change accordingly. We summarize the impact of the fear effect k on the system in Table 3:
Additionally, through numerical simulations, we have observed some intuitively understandable phenomena:
1) Compared with the model (1.1) studied by Sun [9], considering the discrete amensalism model (1.5) with fear effect on the first species, the stability of the positive equilibrium point in model (1.5) changes, and the dynamic behavior will become more complicated. For example, transcritical bifurcation and flip bifurcation appear.
2) Compared to system (1.2), the trajectory of system (1.5) reaches its stable steady-state solution more rapidly as the fear effect increases. However, the first species will go extinct more quickly with an increasing fear effect.
3) The dynamic behavior of system (1.5) is different from that of system (1.2). For example, there is a flip bifurcation at the boundary equilibrium point and the positive equilibrium point, but there is also a transcritical bifurcation at E0(0,0), which is not seen in system (1.2). The presence of a transcritical bifurcation indicates that system (1.5) has some plasticity and adaptability to change from one stable state to another in the face of external changes or stresses. This adaptability helps species adapt more quickly to changes in their environment.
4) Zhou [21] did not study the global attractivity of the boundary equilibrium point of system (1.2). However, we notice that the boundary equilibria of system (1.5) is also globally attractive and its attractivity depends on the fear effect k, which means that the second species is stable and the extinction of the first species depends on the fear effect.
5) By observing Figure 1, Xi et al. [2] can only conclude that the fear effect will reduce the density of species. However, they have not conducted in-depth research on how the fear effect will be affected if it gradually increases. Through numerical simulation, it is not difficult to find if the fear effect is large enough to cause the extinction of the first species.
Finally, we must point out that an appropriate model usually takes functional responses into account, and the recent paper [18] explored the dynamical behavior of amensalism system with Beddington- DeAngelies functional response. However, no scholars have yet explored the influence of the fear effect on the dynamical behavior of amensalism system with Beddington-DeAngelies functional response, which will be further investigated in our subsequent work.
Use of AI tools declaration
The authors declare that they have not used artificial intelligence tools in the creation of this article.
Acknowledgments
The authors would like to thank four anonymous reviewers for their valuable comments, which greatly improved the final expression of the paper.
Conflict of interest
The authors declare that there is no conflict of interest.
Appendix
Lemma 3 Let f(u)=uexp(α−βu), where α and β are positive constants, then f(u) is nondecreasing for u∈(0,1β].
Lemma 4 Assume that sequence {un} satisfy un+1=unexp(α−βun), n∈N, where α and β are positive constants and u(0)>0. Then
(i) if α<2, then limn→+∞u(n)=αβ.
(ii) if α≤1, then u(n)≤1β,n=2,3,....
Lemma 5 Suppose that function f,g:Z+×[0,+∞)→[0,+∞) satisfy f(n,x)≤g(n,x)(f(n,x)≥g(n,x)) for n∈Z+ and x∈[0,+∞) and g(n,x) is nondecreasing with respect to x. If {x(n)} and {u(n)} are the solutions of the following difference equations
respectively, and x(0)≤u(0)(x(0)≥u(0)), then
Lemma 2.1 Assume that {x(k)} satisfies x(k)>0 and
where a(k) and b(k) are non-negative sequences bounded above and below by positive constants. Then
where au=supn∈N{a(n)},bl=infn∈N{b(n)}.
Lemma 2.2 Assume that {x(k)} satisfies
lim supk→+∞x(n)≤x∗, and x(N0)>0, where a(k) and b(k) are non-negative sequences bounded above and below by positive constants and N0∈N. Then
where al=infn∈N{a(n)},bu=supn∈N{b(n)}.









 DownLoad:
DownLoad: