Sensitivity analysis-based control strategies of a mathematical model for reducing marijuana smoking

Atta Ullah; Hamzah Sakidin; Shehza Gul; Kamal Shah; Yaman Hamed; Maggie Aphane; Thabet Abdeljawad; Atta Ullah; Hamzah Sakidin; Shehza Gul; Kamal Shah; Yaman Hamed; Maggie Aphane; Thabet Abdeljawad

doi:10.3934/bioeng.2023028

AIMS Bioengineering

2023, Volume 10, Issue 4: 491-510. doi: 10.3934/bioeng.2023028

Previous Article Next Article

Research article Special Issues

Sensitivity analysis-based control strategies of a mathematical model for reducing marijuana smoking

1.
Mathematical and Statistical Sciences, Institute of Autonomous System, Department of Fundamental & Applied Sciences, Universiti Teknologi PETRONAS, 32610, Seri Iskandar, Perak Darul Ridzuan, Malaysia
2.
Department of Mathematics and Sciences, Prince Sultan University, Riyadh 11586, Saudi Arabia
3.
Department of Mathematics, University of Malakand, Chakdara Dir(L), Khyber Pakhtunkhwa, Pakistan
4.
Department of Mathematics and Applied Mathematics, School of Science and Technology, Sefako Makgatho Health Sciences University, Ga-Rankuwa, South Africa

Received: 10 October 2023 Revised: 14 November 2023 Accepted: 15 November 2023 Published: 18 December 2023

The aim of the current study is to reduce marijuana use among the general population. Because marijuana is an illegal narcotic with numerous negative health effects, it continues to pose a severe threat to public health in emerging nations. In this article, a modified mathematical model of the non-users, experimental users, recreational users, and addict's (NERA) model for marijuana consumption is established by incorporating a new compartment that represents the individuals who are being moved to jail by police intervention. The overall population of humans is divided into five main components: the non-smoker's compartment, experimental smoker's compartment, recreational smoker's compartment, addicted smoker's compartment, and prisoner's compartment. The novelty of this work is to modify the NERA model for marijuana consumption and validate the modified model. Furthermore, with the help of sensitivity analysis, control strategies for marijuana consumption in the population are addressed. The invariant region and the basic reproductive number (R₀) are those parts that are needed for the validation of the proposed model. For the numerical simulation of the given model, the 4th-order Runge Kutta method will be used with the help of MATLAB to examine how the control strategies will play a role in marijuana consumption.

Keywords:

Citation: Atta Ullah, Hamzah Sakidin, Shehza Gul, Kamal Shah, Yaman Hamed, Maggie Aphane, Thabet Abdeljawad. Sensitivity analysis-based control strategies of a mathematical model for reducing marijuana smoking[J]. AIMS Bioengineering, 2023, 10(4): 491-510. doi: 10.3934/bioeng.2023028

Related Papers:

[1]	Fırat Evirgen, Fatma Özköse, Mehmet Yavuz, Necati Özdemir . Real data-based optimal control strategies for assessing the impact of the Omicron variant on heart attacks. AIMS Bioengineering, 2023, 10(3): 218-239. doi: 10.3934/bioeng.2023015
[2]	Sarbaz H. A. Khoshnaw, Kawther Y. Abdulrahman, Arkan N. Mustafa . Identifying key critical model parameters in spreading of COVID-19 pandemic. AIMS Bioengineering, 2022, 9(2): 163-177. doi: 10.3934/bioeng.2022012
[3]	Honar J. Hamad, Sarbaz H. A. Khoshnaw, Muhammad Shahzad . Model analysis for an HIV infectious disease using elasticity and sensitivity techniques. AIMS Bioengineering, 2024, 11(3): 281-300. doi: 10.3934/bioeng.2024015
[4]	Mehmet Yavuz, Waled Yavız Ahmed Haydar . A new mathematical modelling and parameter estimation of COVID-19: a case study in Iraq. AIMS Bioengineering, 2022, 9(4): 420-446. doi: 10.3934/bioeng.2022030
[5]	Daniel Borchert, Diego A. Suarez-Zuluaga, Yvonne E. Thomassen, Christoph Herwig . Risk assessment and integrated process modeling–an improved QbD approach for the development of the bioprocess control strategy. AIMS Bioengineering, 2020, 7(4): 254-271. doi: 10.3934/bioeng.2020022
[6]	Bashdar A. Salam, Sarbaz H. A. Khoshnaw, Abubakr M. Adarbar, Hedayat M. Sharifi, Azhi S. Mohammed . Model predictions and data fitting can effectively work in spreading COVID-19 pandemic. AIMS Bioengineering, 2022, 9(2): 197-212. doi: 10.3934/bioeng.2022014
[7]	Sarbaz H. A. Khoshnaw, Azhi Sabir Mohammed . Computational simulations of the effects of social distancing interventions on the COVID-19 pandemic. AIMS Bioengineering, 2022, 9(3): 239-251. doi: 10.3934/bioeng.2022016
[8]	Prasantha Bharathi Dhandapani, Dumitru Baleanu, Jayakumar Thippan, Vinoth Sivakumar . On stiff, fuzzy IRD-14 day average transmission model of COVID-19 pandemic disease. AIMS Bioengineering, 2020, 7(4): 208-223. doi: 10.3934/bioeng.2020018
[9]	Norliyana Nor Hisham Shah, Rashid Jan, Hassan Ahmad, Normy Norfiza Abdul Razak, Imtiaz Ahmad, Hijaz Ahmad . Enhancing public health strategies for tungiasis: A mathematical approach with fractional derivative. AIMS Bioengineering, 2023, 10(4): 384-405. doi: 10.3934/bioeng.2023023
[10]	Lakshmi N Sridhar . Integration of bifurcation analysis and optimal control of a molecular network. AIMS Bioengineering, 2024, 11(2): 266-280. doi: 10.3934/bioeng.2024014

Abstract

1. Introduction

Modeling is a field that requires both creative thinking and in-depth familiarity with all the available applied mathematics approaches. The techniques implemented to solve the resulting mathematical problems must be properly linked to the model's design by using the model in its application [1]. Marijuana misuse has emerged as one of the major problems facing the planet in the early modern era. In both traditional and digital media, marijuana misuse is frequently covered. The rise in substance abuse can have a detrimental effect on communities, the economy and health. People, communities, and the nation are all seriously harmed by this disorder, particularly those who are younger. The state has made several efforts at implementing substance abuse prevention programs, including the control of trafficking in illicit substances and the protection of drug consumption in the population. The ability to combat substances and defeat the proliferation of substances is necessary for the future of an Indonesian nation free from marijuana [2]. The following factors could realistically make cannabis use more likely to cause severe respiratory problems. Cannabis is known to cause visceral peritoneum inflammatory cell hypertrophy and the destruction of multicellular epithelial cells in the airways, alterations that may increase the risk of chronic infections of the respiratory tract [3]. Also, tetrahydrocannabinol may suppress the immune system, which could make chronic respiratory tract infections more likely [4],[5].

Cannabis is usually infected with harmful microorganisms [6],[7], and use of the drug can cause changes in mental state [8], hyperemesis [9] and inhalation events. Studies on the connection between cannabis use and chronic respiratory illnesses are scarce. Compared to something that is not cannabis, yet another tiny investigation discovered that marijuana users had a considerably higher regularity of hard respiratory infection episodes [10] and a considerably higher percentage of outpatient services for lung diseases illness but not hospitalization rates. Our goal was to assess the relationship between marijuana use and much more severe, chronic respiratory symptom outcomes, as defined by hospitalizations for respiratory-related causes, utilizing a connected survey questionnaire and healthcare public records [11]. Cannabis, sometimes known as marijuana, was long regarded as an illegal substance. Marijuana has been decriminalized or allowed for therapeutic or recreational use in many regions of the world. Its use has rapidly increased because of this shift in mentality. 183 million people worldwide are thought to have consumed marijuana in 2014 [12], and 22 million individuals in 2016 matched the criteria for marijuana addiction [13]. Moreover, the percentage of US citizens over 12 years old who have used marijuana in the past year climbed steadily from 11% in 2002 to 18% in 2019, according to the National Survey on Drug Use and Health from 2002 to 2019 [14].

Marijuana usage has become more prevalent, especially among teenagers and young people; approximately 36% of 12th graders and 43% of college students were shown to have used the drug in the previous year. Marijuana is presently the most prevalent illegal drug in the world and is cultivated and manufactured in virtually every nation. An estimated 180.6 million individuals used marijuana worldwide in 2011, representing 3.9% of the entire adult population aged between 15 and 64 years [15]. At the same time, there is data indicating that in the United States, the strength of cannabis items, as measured by the concentration of the main psychoactive element of marijuana, Tetrahydrocannabinol (THC), has been gradually rising from around 4% in 1995 to 15% in 2018 [16].

Marijuana has been designated as a type I drug under US law since 1970, which means it is one of a group of substances, medications or compounds with a high potential for abuse and no recognized medicinal uses [17]. Despite the fact that marijuana is still considered an illicit narcotic by US law, there seems to be a growing consensus among the general public that using it does not represent a serious health risk [18], as a result, access to it should not be restricted or outlawed [19].

The expanding frequency with which this plant's putative therapeutic benefits have been reported in the press, the numerous states with laws allowing its medical use and the vigorous media campaign in its support all have the potential to influence public perception. The authorization of manufacturing and controlled sales for non-medical use, not only in one nation (Uruguay) but also in two US states (Colorado and Washington) [20], without any proof of the long-term safety of its usage, is what makes it most startling. Cannabis sativa, the plant from which marijuana is derived, has more than 400 components of the terpenoid and flavonoid types as well as its own chemical compounds, known as cannabinoids, of which more than 60 are biologically active [21],[22].

Due to cannabidiol's potential to counteract the euphoric effects of THC, the medicinal impacts of cannabis depend on the ratio of THC to cannabidiol, with a 1:1 ratio offering the best therapeutic outcomes with the least number of adverse reactions [23]. Moreover, the method of ingestion affects the pharmacological activity, the process of digestion and the oxidation of the various cannabinoids [24].

Cannabinoids can be taken by mouth, applied in a specific area using lidocaine, or inhaled, and they can be synthetically produced or naturally derived from the cannabis plant. THC is accumulated in fat deposits because its easily pass through the lips and is slowly released into the bloodstream until it is entirely removed from the body, a procedure that may require up to 5 weeks [25],[26]. Because of this, consuming large quantities of weed can cause its effects to last for a long time. Only a few clinical settings have currently approved the use of marijuana as a medication. This is how the FDA (Food and Drug Administration, USA) authorized it for use in AIDS and underweight patients to promote hunger and manage the vomiting and nausea brought on by radiation therapy or chemotherapy. Two synthetic THC derivatives approved for direct use are dronabinol and lidocaine [27].

What level of proof is now available to back up these uses and show that they are safe? In terms of the management of nausea in people with cancer, a mutagenic effect [28] revealed that cannabidiol–but not nabilone–has superior anti-nausea outcomes to commonly prescribed medications like neuroleptics. However, the authors need to be careful when thinking about this because only a few patients were part of the study as the authors can take a limited number of people. Cannabinoids are not advised as a first-line therapy for treating nausea in cancer sufferers, even though they could play a role as a supplemental therapy [29] and despite considering the accessibility of effective antiemetic medicines that have been produced [30]. According to a current systematic study, there is no proof that cannabis is effective or safe for usage in individuals with AIDS [31].

The studies do not allow for solid conclusions to be drawn regarding the efficacy of synthetic cannabis for the therapies of muscle tension and cluster headaches in neurological disorders, and any possible advantage is likely to be modest, while the possible adverse reactions are frequent and long-term protection has not yet been proven [29].

Small healthcare institutions, substantial distortion risks and minimal outcomes in terms of advantages over potential negative effects are typical limitations of all these trials. Given the ample clinical-epidemiological information about the negative impacts created over time by consuming or breathing marijuana, particularly in teenagers, the recreational use of marijuana differs significantly from its potential medical application [32].

This is most likely caused by a variety of factors, including the various forms and dosages used for each type of use. Research on the therapeutic benefits of marijuana has been conducted using artificial sublingual versions at controlled and set concentrations of the active ingredient (for the few proposed studies of the medicinal use of inhaled marijuana, there are no established doses) [21]. On the other hand, when used recreationally, all the explosive components of a plant's leaf are consumed through inhalation or aspiration, with no set or predetermined quantity of any one of them, like how there is clear guidance for the daily doses required for therapeutic use to produce the anticipated positive benefits, there is none for recreational use in terms of a possibly healthy daily dosage. In fact, thanks to more advanced growth techniques, the “effectiveness” of marijuana products has been constantly rising [33],[34]. There is a lot of research showing how using marijuana recreationally has negative psychological effects. Consuming marijuana is known to significantly increase the risk of addiction, particularly in teenagers as well as people who consume it frequently [35]. Also, there is concern that it affects how the brain develops normally. Since these mechanisms are retained on average until the age of 21 [36], cannabinoid receptors are essential for brain growth and maturation, particularly during the teenage years [37].

Other research has connected initial and regular marijuana use to a higher hazard of “rising” to other “harder” illegal substances as well as the emergence of psychological illnesses like depression and anxiety–but particularly to a higher risk of psychotic episodes–particularly among individuals with genetic susceptibility [38]–[40] and mood disorders [19]. Despite the fact that many other components, both mentally and physically, cohabit in every single one of these recent cases, it is almost impossible to establish a direct causative link between marijuana use and the outcomes. Moreover, short-term negative impacts have been discussed, including altered recent history, uncoordinated movement and poor judgement [23].

The fact that there is a direct correlation between bloodstream levels of cannabis and drunken driving performance [41],[42] and the risk of deadly road crashes has been recently connected to marijuana usage [43]. Last but not least, early research has linked marijuana usage to peripheral artery disease, heart attack and brain hemorrhage [44],[45]. But how does marijuana use impact the way you breathe recreationally? It is helpful to contrast marijuana use with the model of tobacco use in respect of the makeup of the smoke produced during combustion and the method or mode in which this drug is smoked to better comprehend the adverse impact of inhaling cannabis on the lungs. Except for the trace amount of caffeine, the smoke produced by burning marijuana leaves is composed of an elaborate combination of chemical compounds, including sodium hydroxide, nitrosamines, naphthalene, hydrocyanic acid, benzopyrene, phenols, benzotriazole and others [46]. Cannabis smoke also contains cannabinoids, which are compounds that are unique to marijuana. When smoking cannabis, the method of inhaling is distinct from that of tobacco users. In the first instance, smoking takes place in less time, with greater combustion efficiency and with longer and more profound breaths [47].

The American Academy of Pediatrics (AAP) acknowledges the insufficient information available to guide recommendations for clinicians regarding marijuana use. In 2018, the AAP recommended a prohibition on marijuana consumption while nursing due to the lack of data on its effects on infant behavior. However, the statement did not address whether marijuana use should be considered a drug interaction for breastfeeding or whether expressed milk from mothers who use recreational marijuana should be used to feed premature infants [48]. A mathematical model known as the NERA model was created by Dauhoo et al. to represent the dynamics of marijuana consumption in a particular community. The approach makes a distinction between drug smokers and non-smokers, classifying marijuana smokers as either addicted, recreational or experimental. The NERA model considers both marijuana use and demographic dynamics [49].

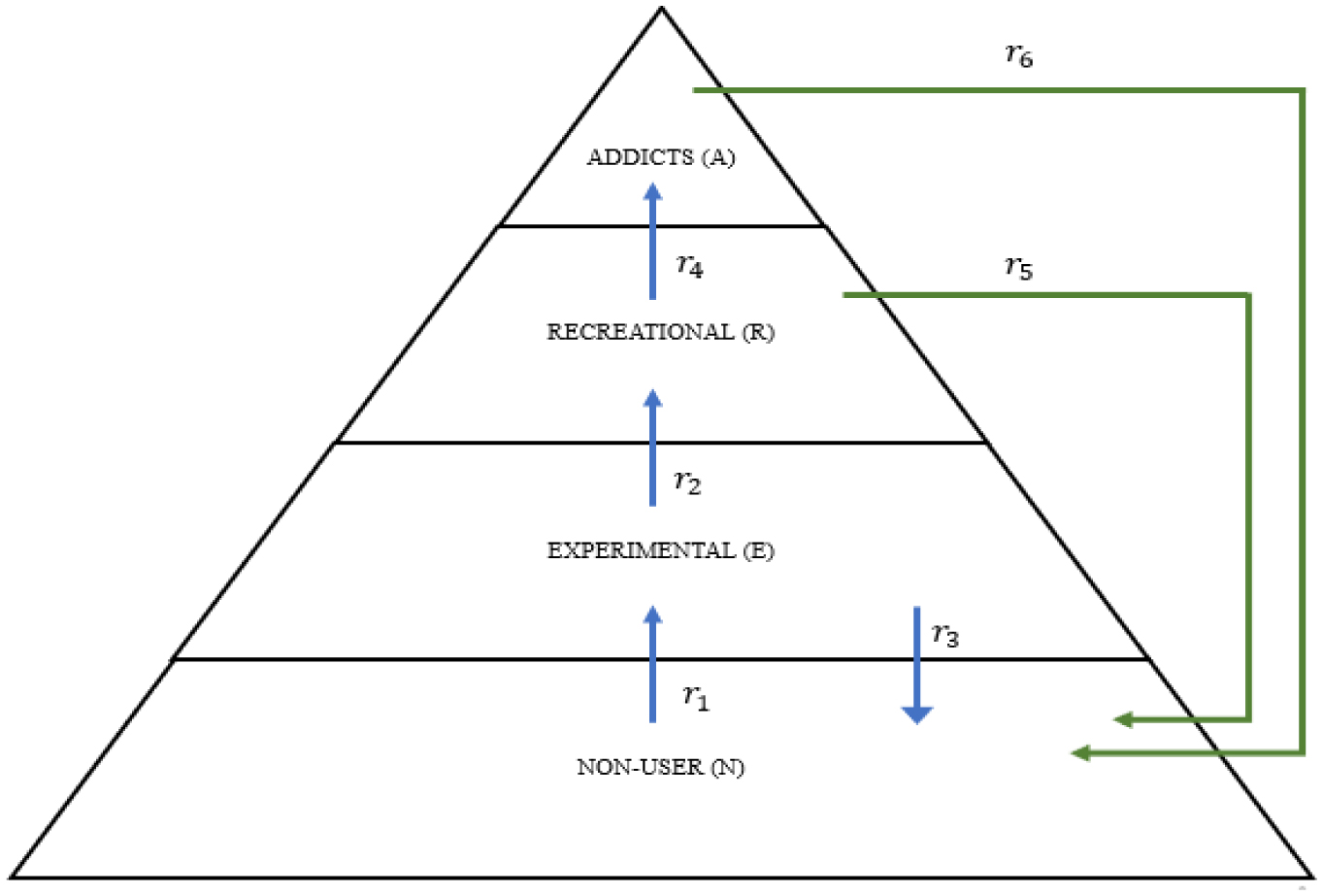
The NERA model was updated by Ginoux et al. to include the predator-prey concept, where drug users are predators and non-users are prey. The model is stochastic and considers the relationships between different groups, with individuals potentially switching between groups. The model is a useful tool for studying the social dynamics of drug use and addiction. Based on the concepts of predator-prey relationships, the factors that cause fluctuations in the number of participants in a group can be referred to as one group preying on another. In this scenario, non-users are the prey for three groups: experimental smokers (E), recreational smokers (R) and addicted smokers (A). Addicted smokers (A) are predators of all recreational smokers (R) and non-users (N), while experimental users (E) prey on both recreational smokers (R) and non-smokers (N). There are two types of functional responses that affect the development of prey (non-users) and predators (experimental, recreational, and addicted users). If there are no predators, the growth of prey (N) should be limited for stabilization and the saturation of the predator population (as the concentration of predators can impact other predator groups) should also be considered to prevent destabilization [50]. The set of differential algorithms that follows is recognized as the Dauhoo model, often referred to as the NERA model, and its mathematical framework are presented in Equation (1). Additionally, the schematic representation of the existing model is shown in Figure 1.

$\begin{array}{l} \dot{N} = β - (β + r_{1} E + r_{1} R) N + r_{3} E + r_{5} R + r_{6} A, \\ \dot{E} = - (β + r_{3} - r_{1} N + r_{2} R) E + r_{1} N R, \\ \dot{R} = - (β + r_{4} + r_{5} - r_{2} E) R, \\ \dot{A} = r_{4} R - (β + r_{6}) A . \end{array}$ (1)

Figure 1. Schematic representation of the existing model [49].

DownLoad: Full-Size Img PowerPoint

2. Model formulation

The process of translating our understanding of a natural system into a mathematical form is known as model formulation. Construction of a conceptual model and its expression into mathematical equations are the two processes involved. We start by choosing the key components (state variables) and the flows that describe the exchange of matter, energy or momentum between them. We demonstrate that the conceptual model equations simply express the rate of change of the state variables as the sum of all flows that enter minus all flows that leave the compartment based on the conservation principle.

In this section, we develop a modified version of the NERA model by incorporating a new compartment that represents smokers who are being moved to jail due to police intervention; this compartment is critical in the community's prevention of marijuana smoking. The total human population is represented by N(t), this population size is divided into two main categories, marijuana users and non-users (S_N). Individuals in non-smoking compartments may be attracted by smokers. Furthermore, marijuana smokers are subdivided into four different compartments, which represent different stages of smoking approaching to be addicted. These compartments are the “experimental smoker's compartment (S_E)”, “recreational smoker's compartment (S_R)”, “addicted smoker's compartment (S_A)” and “prisoner's or arrested smoker's compartment (S_P)”. Individuals in the experimental smoker's compartment are those who interact with recreational individuals, are affected by them and try to smoke marijuana as an experiment for the first time. Those who engage in social interactions with addicts and are influenced by them are classified as recreational smokers because they start using marijuana for pleasure. At some point, both recreational and experimental users of marijuana will develop addictions because of their consistent, slow-burning use of the drug.

The individuals who are addicted play a crucial part in the model because they interact with non-users and encourage them to use drugs and engage in other illegal actions. The arrested compartment is made up of people who were moved from the addicted compartment to jail due to police intervention. Furthermore, we will discuss in the next part the descriptions of the parameters that will be used in the proposed model. The parameter Ş denotes the population's birth rate, and a represents the percentage of the casual class (smokers) who have an impact on non-smokers (susceptible). The percentage of affected individuals who moves to the category of casual smokers after the interaction with addicted individuals is represented by the parameter a₁. The ratio of affected users who become non-users again because of advice of elders or religious scholars is represented by the parameter a₃. The parameter a₂ represents the influence rate of addicted smokers on susceptible (non-smokers). The percentage of addicted people who return to susceptible (non-smokers) because of their restricted surroundings is denoted by the parameter a₄. The ratio of those who are only somewhat hooked going up to the highly addicted class is known as m₁. The parameter m₂ is the proportion of habitual smokers who are imprisoned. The percentage of those individuals who were in jail, have completed their jail sentences and go back to susceptible class is denoted by the parameter m₃. After some time, some of them go back to the addicted compartment with the ratio α₂, while others return to the sensitive compartment. The death ratio encountered by police is denoted by the parameter e, and the human death rate from natural causes is represented by µ.

2.1. The dynamical concept representing the modified model

We define our parameters in Table 1 (all of which are genuine and positive). For clarity of use, we standardize population to 1. To do this, we establish a collection of dependent variables (S_N, S_E, S_R, S_A, and S_P) such that (S_N) = the percentage of non-smokers in the community, (S_E) = the percentage of experimental smokers in the community, (S_R) = the percentage of recreational smokers in the community, (S_A) = the percentage of addicts in the community and (S_P) = the percentage of prisoners in the community, where all the above-discussed classes are presented in Equation (2). Furthermore, the schematic representation of the modified model is shown in Figure 2.

$S_{N} + S_{E} + S_{R} + S_{A} + S_{P} = 1.$ (2)

Figure 2. Schematic representation of the modified model [51].

DownLoad: Full-Size Img PowerPoint

${\begin{matrix} \dot{S_{N}} = Ş - (a S_{R} - a_{2} S_{A} + µ) S_{N} + a_{3} S_{E} + a_{4} S_{R} + m_{3} (1 - α_{2}) S_{P}, \\ \begin{matrix} \dot{S_{E}} = a S_{R} S_{N} - (a_{1} + a_{3} + µ) S_{E}, \\ \dot{S_{R}} = a_{2} S_{A} S_{N} + a_{1} S_{E} - (m_{1} + a_{4} + µ) S_{R}, \\ \dot{S_{A}} = m_{1} S_{R} + m_{3} α_{2} S_{P} - (m_{2} + e + µ) S_{A}, \end{matrix} \\ \dot{S_{P}} = m_{2} S_{A} - (m_{3} + µ) S_{P} . \end{matrix}$ (3)

The parameter descriptions are listed in Table 1.

Table 1. Meanings of the parameters.

Symbols	Parameters definitions	Values	References
Ş	Population's birth rate	0.0015875 day⁻¹	[52]
a	The percentage of the casual class (smokers) who have an impact on non-smoker's (susceptible)	0.446 day⁻¹	[49]
a₁	The ratio of affected persons who switch to the category of casual smokers	0.5 day⁻¹	[49]
a₂	The influence rate of addicted smokers on susceptible	0.001201 day⁻¹	[51]
a₃	The ratio of afflicted individuals who become susceptible again because of advice	0.17 day⁻¹	[49]
a₄	The percentage of addicted people who return to susceptible (non-smokers) because of their limited surroundings	0.002 day⁻¹	[49]
m₁	The ratio of those who are only somewhat hooked going up to the highly addicted class	0.025 day⁻¹	[49]
m₂	The proportion of habitual smokers who are in jail	0.22 day⁻¹	Assumed
m₃	The percentage of those individuals who finish their jail duration	0.0157871 day⁻¹	Assumed
α₂	The percentage of convicts who eventually return to the addicted compartment	0.03 day⁻¹	Assumed
e	The death ratio encountered by police	0.0005 day⁻¹	Assumed
µ	Natural death rate of human population	0.066 day⁻¹	[52]

| Show Table

DownLoad: CSV

2.2. A review of the suggested model

In this section, we covered the invariant region, the basic reproduction number R₀ and model characteristics, including marijuana-free equilibrium (MFE).

2.2.1. Invariant region

The presented mathematical model is related to the live human population. Hence, we assumed all the state variables and parameters utilized in the suggested model are always non-negative at time t = 0. This includes the dynamics of the entire human population, where the complete population is shown by the differential equation below [53],[54]:

$P = S_{N} + S_{E} + S_{R} + S_{A} + S_{P} .$ (4)

Equation (4) is solved to obtain.

$\dot{P} = Ş - µ P - e S_{A} [53] .$ (5)

Equation (5) gives us.

$\dot{P} \leq Ş - µ P [53] .$ (6)

By solving Equation (6), we get

$P \leq P (0) e^{- µ t} + \frac{Ş}{µ} (1 - e^{- µ t}) \Rightarrow P \leq \frac{Ş}{µ} when t ⤑ \infty [53] .$ (7)

We assert the following conclusion in consideration of the analysis above.

2.2.2. Proposition

The region of the suggested model, as described by

$ℳ = [(S_{N}, S_{E}, S_{R}, S_{A}, S_{P}) ε R_{+}^{5}, P \leq \frac{Ş}{µ}] .$ (8)

2.3. Basic reproduction number

Reproductive number, R₀, refers to the number of secondary addictions that a single primary addiction can cause in an entirely non-smoking population. The following generation matrix [55]–[57] discovers the reproduction number as

$R_{0} = ρ (F V^{- 1}) [58, 59],$ (9)

where ρ determines the spectral radius. Moreover, f possesses the Jacobian $ℐ_{f} = F$ .

$f = (\begin{matrix} f_{1} \\ f_{2} \\ f_{3} \end{matrix}) = (\begin{matrix} a S_{R} S_{N} \\ a_{2} S_{A} S_{N} \\ 0 \end{matrix}),$ (10)

The column in Equation (10) represents the people who develop addiction.

$F = (\begin{matrix} \frac{\partial (f_{1})}{\partial (S_{E})} & \frac{\partial (f_{1})}{\partial (S_{R})} & \frac{\partial (f_{1})}{\partial (S_{A})} \\ \frac{\partial (f_{2})}{\partial (S_{E})} & \frac{\partial (f_{2})}{\partial (S_{R})} & \frac{\partial (f_{2})}{\partial (S_{A})} \\ \frac{\partial (f_{3})}{\partial (S_{E})} & \frac{\partial (f_{3})}{\partial (S_{R})} & \frac{\partial (f_{3})}{\partial (S_{A})} \end{matrix}) = (\begin{matrix} 0 & a S_{N} & 0 \\ 0 & 0 & a_{2} S_{N} \\ 0 & 0 & 0 \end{matrix}) [58] .$ (11)

For convenience of writing, Equation (11) is written as follows:

$F = {(\begin{matrix} 0 & n_{1} & 0 \\ 0 & 0 & n_{2} \\ 0 & 0 & 0 \end{matrix})}_{(M F E)} [34, 58] .$ (12)

$ℐ_{v} = V$ is the Jacobian of v.

Where:

$V = (\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \end{matrix}) = (\begin{matrix} - (a_{1} + a_{3} + µ) S_{E} \\ a_{1} S_{E} - (m_{1} + a_{4} + µ) S_{R} \\ m_{1} S_{R} - (m_{2} + µ) S_{A} \end{matrix}),$ (13)

In Equation (13), the column of matrix V displays the individuals who join or leave the harmed class, excluding those who are from the non-smokers class.

$V = (\begin{matrix} \frac{\partial (v_{1})}{\partial (S_{E})} & \frac{\partial (v_{1})}{\partial (S_{R})} & \frac{\partial (v_{1})}{\partial (S_{A})} \\ \frac{\partial (v_{2})}{\partial (S_{E})} & \frac{\partial (v_{2})}{\partial (S_{R})} & \frac{\partial (v_{2})}{\partial (S_{A})} \\ \frac{\partial (v_{3})}{\partial (S_{E})} & \frac{\partial (v_{3})}{\partial (S_{R})} & \frac{\partial (v_{3})}{\partial (S_{A})} \end{matrix}),$ (14)

$V = (\begin{matrix} - (a_{1} + a_{3} + µ) & 0 & 0 \\ b & - (m_{1} + a_{4} + µ) & 0 \\ 0 & m_{1} & - (m_{2} + µ) \end{matrix}) [58, 60],$ (15)

For convenience of writing, Equation (15) is written as follows:

$V = {(\begin{matrix} - Q_{1} & 0 & 0 \\ a_{1} & - Q_{2} & 0 \\ 0 & m_{1} & - Q_{3} \end{matrix})}_{(M F E)} .$ (16)

Following are the dominating eigenvalues of (FV⁻¹) and R₀:

$R_{0} = \sqrt{((a * M * a_{1}) / (Q_{1} * Q_{2}))},$ (17)

$R_{0} = \sqrt{\frac{a a_{1} Ş}{µ (a_{1} + a_{3} + µ) (m_{1} + a_{4} + µ)}} .$ (18)

2.3.1. Biological interpretation of R₀.

According to Equation (18), here, a represents the percentage of the casual class (smokers) who have an impact on non-smokers (susceptible), while a₁ is the ratio of affected (experimental) persons who switch to the category of casual smokers. Due to the high influence rate of marijuana smokers on susceptible persons, the term aa₁Ş of R₀, suggests that some members of the vulnerable (non-smokers) class will start smoking marijuana and thereby join the marijuana smoking group. As a result, aa₁Ş implies that marijuana is being transferred from smoker individuals to susceptible (non-smoker) individuals. The other components (parameters) included in R₀ only specify the intensity of R₀. R naught has the threshold property, which means that if R₀ > 1, the disease may cause a high number of new infections, whereas if R₀ < 1, each infected individual creates, on average, less than one secondary case over its lifespan as infectious. Therefore, the epidemic will progressively vanish. In an epidemic situation, determining the accurate R₀ is essential because it guides subsequent control measures and may be compared to the efficient reproductive number after interventions [61]. In other words, the system dynamics indicates that, if R₀ < 1 the number of infectious individuals monotonically converges to zero. Conversely, if R₀ exceeds 1, the individual initially rises before eventually diminishing, underscoring that R₀ is equal to 1 serves as a distinct threshold, determining whether the disease will be dying out or lead to an epidemic [62].

2.4. Sensitivity analysis of R₀

The ratio of the relative change in the variable to the corresponding difference in the parameter is known as the normalized advance sensitive indices of a variable in relation to a parameter. The sensitive indices can also be constructed via partial derivatives when the variable is a differentiable function of the parameter [63].

2.4.1. Definition

The generalized forward-sensitive indices of R₀, which differ from one another with respect to the parameter Þ, are defined as

$Υ_{Þ}^{R_{0}} = \frac{\partial R_{0}}{\partial Þ} \times \frac{Þ}{R_{0}} [58] .$ (19)

Using the Definition (2.4.1), the sensitivity indices for each parameter are shown in Table 2.

Table 2. Indices for parameter sensitivity.

Parameters	Values	Sensitivity indexes
a₄	0.002	−0.0032
a₃	0.17	−0.1164
m₁	0.025	−0.4006
µ	0.066	−0.6372
a₁	0.5	+0.1575
a	0.446	+0.5000
Ş	0.0015875	+0.5000

| Show Table

DownLoad: CSV

3. Control strategies

In this section, we discussed the sensitive behaviors of the parameters that are used in the model. The present value of a parameter is exactly proportional to the initial speed of transmission R₀, if it has a positive sensitivity index, such as the sensitivity index of the human birth rate Ş, which is +0.5000. The value of the parameter is inversely proportional to the rate of initial transmission of marijuana, R₀, when the parameter has a negative sensitivity index, such as the sensitivity index of the human death ratio, which is −0.6372.

A high value for a parameter will contribute more significantly to the transmission of marijuana than if its sensitivity index is low. Despite having high sensitivity indices, certain parameters, such as the natural death rate and the birth rate of the human, cannot be changed.

Here we construct five major parameters that are most sensitive: a is the percentage of the recreational class (S_R) who have an impact on non-smokers (susceptible), a₁ is the ratio of experimental (S_E) persons who switch to the category of recreational smokers (S_R), a₃ is the ratio of afflicted individuals who become susceptible (non-smokers) again because of advice, a₄ is the percentage of addicted people who return to susceptible because of their limited surroundings and m₁ is the ratio of those who are only somewhat hooked going up to the highly addicted class. The control techniques shown in Table 3 indicate the highest possible values for these initiatives.

Table 3. The values of the parameters for various strategies.

Strategies	m₁	a	a₁	a₃	a₄
Strategy-1	0.045	0.00345	0.03	0.027	0.0042
Strategy-2	0.215	0.000511	0.002	0.367	0.0621
Strategy-3	0.025	0.446	0.5	0.17	0.002

| Show Table

DownLoad: CSV

4. Results and discussion

The following generated figures represent the results of the indicated strategies. As this study is connected to the human population, the human population cannot be negative. Hence, we have assumed certain positive initial values for each compartment, such as S_N(0) = 1000, S_E(0) = 20, S_R(0) = 20, S_A(0) = 20 and S_P(0) = 10. With the help of MATLAB, we use the fourth order Runge Kutta (RK4) method for the numerical simulation of the developed strategies, as the RK4 method has several advantages, making it a widely used numerical technique for solving ordinary differential equations (ODEs). The numerical technique most frequently used to calculate an estimate at each step of the sequences is RK4. Three approaches are used to solve the ten ODEs of the first-order equation with boundary conditions. The RK4 approach is superior in every scenario across every field, according to comparison data in [64]. Meanwhile, [65] showed RK5 and RK8 are less efficient than RK4 since RK4 involves less computational time to compute truncation global error in the numerical solution.

RK4 often provides more accurate solutions, especially for ODEs with complex behaviors. This method is generally more stable than some other numerical methods for solving ODEs. It can handle a wide range of ODEs without encountering stability issues, making it suitable for various applications. RK4 is versatile and applicable to a broad class of ODEs. It can be used for both stiff and non-stiff systems. In some applications, RK4 has been observed to better conserve energy compared to simpler methods. This is an important consideration in simulations of physical systems where energy conservation is a crucial property.

A few limitations of the RK4 method are as follows: This method can accumulate numerical errors over time. For problems with rapidly changing behavior, higher-order methods or adaptive step-size control may be more suitable to maintain accuracy because the Rk4 method may require small step sizes. Extending RK4 to higher-order ODEs can be complex, often requiring the transformation of higher-order equations into equivalent first-order systems. This complexity may make other methods more straightforward for higher-order problems [66].

Figure 3. Graphical representation of Strategy 1.

DownLoad: Full-Size Img PowerPoint

Figure 4. Graphical representation of Strategy 2.

DownLoad: Full-Size Img PowerPoint

Figure 5. Graphical representation of Strategy 3.

DownLoad: Full-Size Img PowerPoint

4.1. Result of strategy 1

As a result of Strategy 1, marijuana smoking can be controlled in 23 months. Figure 3A shows that the experimental compartment of individuals converges to zero in 150 days with the recovery of 480 individuals. The compartment of recreational smokers moves to zero in 165 days with the recovery of 120 individuals, as shown in Figure 3B. The addicted class converges to zero in 196 days with the recovery of 46 persons, as shown in Figure 3C. The prisoners class moves to zero in 197 days, along with the recovery of 10 individuals, as shown in Figure 3D.

4.2. Result of Strategy 2

Using this strategy, marijuana use can be reduced over a period of around 19 months. In 83 days, the density of experimental smokers (Figure 4A) decreases to zero. Figure 4B illustrates how the density of recreational smokers decreases to zero in 120 days. According to Figure 4C, the density of smokers who are hooked decreases to zero in 187 days. Additionally, Figure 4D represents the convict's class, which is reduced to zero in 190 days. Moreover, with the recovery of 95, 133, 198 and 35 individuals respectively, these categories are coming to an end.

4.3. Result of Strategy 3

With the use of this effective strategy, marijuana use can be decreased in around 22 months. Figure 5A illustrates how the density of experimental smokers can be controlled in 146 days. The outcome of the recreational class, which can be managed in 175 days, is shown in Figure 5B. Figure 5C shows the results for the addicted class using this approach, which can be controlled in 169 days, and Figure 5D shows the results for the prisoner's class, which can be controlled in 199 days. Furthermore, with the recovery of 1000, 641, 102 and 157 individuals respectively, these compartments can be controlled.

4.4. Comparison between strategies of the modified model

In this section, the author compares the proposed strategies for controlling marijuana smoking. Strategy 1 can recover 4.20 individuals per day, Strategy 2 can recover 3.49 individuals per day and Strategy 3 can recover 11.9 individuals per day. The numerical result of these strategies for its comparison is constructed in Figure 6.

Figure 6. The stacked bar chart illustrates the comparison of the proposed strategies.

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In this study, the author modified the NERA model by incorporating a new compartment called prisoner's class. The mentioned class is a realistic one, and due to missing this class, it is very difficult to reduce and recover the number of marijuana smokers in the population. For this mathematical framework, the author used a system of first-order non-linear ordinary differential equations. Furthermore, the invariant region, basic reproduction number and sensitivity analysis were addressed for different purposes. The invariant region is the part of the methodology that was solved for the validation of the modified model. For the initial rate of transmission of marijuana smoking, the basic reproduction number was carried out and sensitivity analysis helps us find out the most sensitive parameters that are involved in marijuana transmission. Finally, the authors have constructed three strategies for reducing marijuana smoking using the most sensitive (targeted) parameters. After numerical simulation, the author achieves the result that Strategy 3 is more effective than the other two strategies, as shown in Figure 6. Comparatively, the effective strategy of the modified model is also more rapidly convergent than the existing model. Due to this achievement, the proposed study concludes that the modified model is more significant than the earlier model. In the upcoming study, the author can employ novel techniques called optimal control problem and threshold conditions so that marijuana smoking can be expected to control at minimum cost and time.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first and third authors are thankful to Universiti Teknologi PETRONAS for providing postgraduate assistantships, and Prince Sultan University is appreciated for support through TAS research lab.

Conflicts of interest

We declare that this work is original, and the content has not been published elsewhere or submitted for publication elsewhere. All the authors contributed significantly and agree with the content of the manuscript, and we declare that there is no conflict of interest in this research.

Author Contributions:

Atta Ullah: conceptualization, methodology, investigation, and visualization. Writing an original draft, reviewing, and editing; Hamzah Sakidin: supervision, conceptualization, investigation, review, and editing; Shehza Gul: conceptualization, methodology, investigation, visualization, review, and editing; Kamal Shah: supervision, conceptualization, investigation visualization, review, and editing; Yaman Hamed: supervision, conceptualization, methodology, investigation, visualization, review, and editing; Maggie Aphane: investigation, visualization, and review; Thabet Abdeljawad: investigation, visualization, and review.

References

[1]	Algahtani OJ, Zeb A, Zaman G, et al. (2015) Mathematical study of smoking model by incorporating campaign class. Wulfenia 22: 205-216.
[2]	Leong DP, Teo KK, Rangarajan S, et al. (2018) World Population Prospects 2019. Department of Economic and Social Affairs Population Dynamics. New York (NY): United Nations; 2019 (https://population.un.org/wpp/Download/, accessed 20 September 2020). The decade of healthy ageing. Geneva: World Health Organization. World 73: 362k2469.
[3]	Fligiel SEG, Roth MD, Kleerup EC, et al. (1997) Tracheobronchial histopathology in habitual smokers of cocaine, marijuana, and/or tobacco. Chest 112: 319-326. https://doi.org/10.1378/chest.112.2.319
[4]	BALDWIN GC, Tashkin DP, Buckley DM, et al. (1997) Marijuana and cocaine impair alveolar macrophage function and cytokine production. Am J Respir Crit Care Med 156: 1606-1613. https://doi.org/10.1164/ajrccm.156.5.9704146
[5]	Shay AH, Choi R, Whittaker K, et al. (2003) Impairment of antimicrobial activity and nitric oxide production in alveolar macrophages from smokers of marijuana and cocaine. J Infect Dis 187: 700-704. https://doi.org/10.1086/368370
[6]	Naz H, Dumrongpokaphan T, Sitthiwirattham T, et al. (2023) A numerical scheme for fractional order mortgage model of economics. Results Appl Math 18: 100367. https://doi.org/10.1016/j.rinam.2023.100367
[7]	Alrabaiah H, Ullah Z, Ahmad I, et al. Iterative investigation of korteweg–de vries equation using ab derivative in caputo sense (2023). https://doi.org/10.1142/s0218348x23400959
[8]	Moore THM, Zammit S, Lingford-Hughes A, et al. (2007) Cannabis use and risk of psychotic or affective mental health outcomes: a systematic review. Lancet 370: 319-328. https://doi.org/10.1016/s0140-6736(07)61162-3
[9]	Vozoris NT, Zhu J, Ryan CM, et al. (2022) Cannabis use and risks of respiratory and all-cause morbidity and mortality: a population-based, data-linkage, cohort study. BMJ Open Respir Res 9: e001216. https://doi.org/10.1136/bmjresp-2022-001216
[10]	Tashkin DP, Coulson AH, Clark VA, et al. (1987) Respiratory symptoms and lung function in habitual heavy smokers of marijuana alone, smokers of marijuana and tobacco, smokers of tobacco alone, and nonsmokers. Am Rev Respir Dis 135: 209-216. https://doi.org/10.1378/chest.78.5.699
[11]	Polen MR, Sidney S, Tekawa IS, et al. (1993) Health care use by frequent marijuana smokers who do not smoke tobacco. West J Med 158: 596. https://doi.org/10.1007/978-1-4615-1907-2_99
[12]	Merz F (2018) United nations office on drugs and crime: world drug report 2017. 2017. SIRIUS-Zeitschr Strateg Anal 2: 85-86. https://doi.org/10.1515/sirius-2018-0016
[13]	Degenhardt L, Charlson F, Ferrari A, et al. (2018) The global burden of disease attributable to alcohol and drug use in 195 countries and territories, 1990–2016: a systematic analysis for the global burden of disease study 2016. Lancet Psychiatry 5: 987-1012. https://doi.org/10.1016/s2215-0366(18)30337-7
[14]	Al Juboori R, Subramaniam DS, Hinyard L (2022) Understanding the role of adult mental health and substance abuse in perpetrating violent acts: In the presence of unmet needs for mental health services. Int J Ment Health Addiction 21: 1-9. https://doi.org/10.1007/s11469-022-00778-1
[15]	Lee J, Thrul J (2021) Trends in opioid misuse by cigarette smoking status among US adolescents: Results from national survey on drug use and health 2015–2018. Prev Med 153: 106829. https://doi.org/10.1016/j.ypmed.2021.106829
[16]	Testai FD, Gorelick PB, Aparicio HJ, et al. (2022) Use of marijuana: effect on brain health: a scientific statement from the American Heart Association. Stroke 53: e176-e187. https://doi.org/10.1161/str.0000000000000396
[17]	Beutler JA, Marderosian AH (1978) Chemotaxonomy of Cannabis I. Crossbreeding between Cannabis sativa and C. ruderalis, with analysis of cannabinoid content. Econ Bot 32: 387-394. https://doi.org/10.1007/bf02907934
[18]	Di Forti M, Morgan C, Dazzan P, et al. (2009) High-potency cannabis and the risk of psychosis. Br J Psychiatry 195: 488-491. https://doi.org/10.1192/bjp.bp.109.064220
[19]	Mousavi SE, Bozorgian A (2020) Investigation the kinetics of CO₂ hydrate formation in the water system+ CTAB+ TBAF+ ZnO. Int J New Chem 7: 195-219. https://doi.org/10.33945/sami/ecc.2020.4.10
[20]	Ellis RJ (2009) Smoked medicinal cannabis for neuropathic pain in HIV: a randomized, crossover clinical trial. Neuropsychopharmacology 34: 672-680. https://doi.org/10.1038/npp.2008.120
[21]	Russo E (2001) Cannabinoids in pain management: Study was bound to conclude that cannabinoids had limited efficacy. BMJ 323: 1249-1250. https://doi.org/10.1136/bmj.323.7323.1249
[22]	Russo EB (2008) Cannabinoids in the management of difficult to treat pain. Ther Clin Risk Manag 4: 245-259. https://doi.org/10.2147/tcrm.s1928
[23]	Cascini F, Aiello C, Di Tanna GL (2012) Increasing delta-9-tetrahydrocannabinol (Delta-9-THC) content in herbal cannabis over time: systematic review and meta-analysis. Curr Drug Abuse Rev 5: 32-40. https://doi.org/10.2174/1874473711205010032
[24]	Savaki HE, Cunha J, Carlini EA, et al. (1976) Pharmacological activity of three fractions obtained by smoking cannabis through a water pipe. Bull Narc 28: 49-56. https://doi.org/10.1007/978-3-642-51624-5_39
[25]	Samimi A, Zarinabadi S, Bozorgian A (2021) Optimization of corrosion information in oil and gas wells using electrochemical experiments. Int J New Chem 8: 149-163. https://doi.org/10.33945/sami/jcr.2020.2.5
[26]	Izadi M, Yüzbaşı Ş, Ansari KJ (2021) Application of Vieta–Lucas series to solve a class of multi-pantograph delay differential equations with singularity. Symmetry 13: 2370. https://doi.org/10.3390/sym13122370
[27]	Tashkin DP, Gliederer F, Rose J, et al. (1991) Tar, CO and Δ9-THC delivery from the 1st and 2nd halves of a marijuana cigarette. Pharmacol Biochem Behav 40: 657-661. https://doi.org/10.1016/0091-3057(91)90378-f
[28]	Aldington S, Williams M, Nowitz M, et al. (2007) Effects of cannabis on pulmonary structure, function and symptoms. Thorax 62: 1058-1063. https://doi.org/10.1136/thx.2006.077081
[29]	Bloom JW, Kaltenborn WT, Paoletti P, et al. (1987) Respiratory effects of non-tobacco cigarettes. Br Med J (Clin Res Ed) 295: 1516-1518. https://doi.org/10.1136/bmj.295.6612.1516
[30]	Sadr MB, Bozorgian A (2021) An overview of gas overflow in gaseous hydrates. J Chem Rev 3: 66-82. https://doi.org/10.22034/jcr.2021.118870
[31]	Cruickshank EK (1976) Physical assessment of 30 chronic cannabis users and 30 matched controls. Ann N Y Acad Sci 282: 162-167. https://doi.org/10.1111/j.1749-6632.1976.tb49895.x
[32]	Tashkin DP, Simmons MS, Sherrill DL, et al. (1997) Heavy habitual marijuana smoking does not cause an accelerated decline in FEV1 with age. Am J Respir Crit Care Med 155: 141-148. https://doi.org/10.1164/ajrccm.155.1.9001303
[33]	Tashkin DP, Reiss S, Shapiro BJ, et al. (1977) Bronchial effects of aerosolized Δ9-tetrahydrocannabinol in healthy and asthmatic subjects. Am Rev Respir Dis 115: 57-65. https://doi.org/10.1007/978-1-4613-4286-1_8
[34]	Din A, Li Y, Liu Q (2020) Viral dynamics and control of hepatitis B virus (HBV) using an epidemic model. Alexandria Eng J 59: 667-679. https://doi.org/10.1016/j.aej.2020.01.034
[35]	McNulty W, Usmani OS (2014) Techniques of assessing small airways dysfunction. Eur Clin Respir J 1: 25898. https://doi.org/10.3402/ecrj.v1.25898
[36]	Roth MD, Arora A, Barsky SH, et al. (1998) Airway inflammation in young marijuana and tobacco smokers. Am J Respir Crit Care Med 157: 928-937. https://doi.org/10.1164/ajrccm.157.3.9701026
[37]	Bozorgian A (2021) Exergy analysis for evaluation of energy consumptions in hydrocarbon plants. Int J New Chem 8: 329-344. https://doi.org/10.22034/ijnc.2020.123715.1105
[38]	US Department of Health and Human Services.The benefits of smoking cessation. A report of the surgeon general (DHHS publication no. CDC 90-8416) (1990) .
[39]	Khan H, Alzabut J, Shah A, et al. (2023) On fractal-fractional waterborne disease model: A study on theoretical and numerical aspects of solutions via simulations. Fractals 2023: 2340055. https://doi.org/10.1142/s0218348x23400558
[40]	Khan H, Ahmed S, Alzabut J, et al. (2023) A generalized coupled system of fractional differential equations with application to finite time sliding mode control for Leukemia therapy. Chaos Solitons Fractals 174: 113901. https://doi.org/10.1016/j.chaos.2023.113901
[41]	Bozorgian A (2020) Investigation of hydrate formation phenomenon and hydrate inhibitors. J Eng Ind Res 1: 99-110. https://doi.org/10.22034/ijnc.2020.123715.1105
[42]	Din A, Li Y, Khan T, et al. (2020) Mathematical analysis of spread and control of the novel corona virus (COVID-19) in China. Chaos Solitons Fractals 141: 110286. https://doi.org/10.1016/j.chaos.2020.110286
[43]	Tashkin DP (2015) The respiratory health benefits of quitting cannabis use. Eur Respir Soc 46: 1-4. https://doi.org/10.1183/09031936.00034515
[44]	Bozorgian A, Ghanavati B (2020) Removal of copper II from industrial effluent with beta zeolite nanocryst. https://doi.org/10.22034/pcbr.2022.328704.1213
[45]	Ahmed S, Azar AT, Tounsi M (2022) Design of adaptive fractional-order fixed-time sliding mode control for robotic manipulators. Entropy 24: 1838. https://doi.org/https://doi.org/10.3390/e24121838
[46]	Rabipour S, Abdulkareem Mahmood E, Afsharkhas M (2022) Medicinal use of marijuana and its impacts on respiratory system. J Chem Lett 3: 86-94. https://doi.org/10.22034/jchemlett.2022.347365.1072
[47]	Biehl JR, Burnham EL (2015) Cannabis smoking in 2015: a concern for lung health?. Chest 148: 596-606. https://doi.org/10.1378/chest.15-0447
[48]	Ryan SA, Ammerman SD, O'Connor ME, et al. (2018) Marijuana use during pregnancy and breastfeeding: implications for neonatal and childhood outcomes. Pediatrics 142: e20181889. https://doi.org/10.1542/peds.2018-1889
[49]	Dauhoo M, Korimboccus B, Issack S (2013) On the dynamics of illicit drug consumption in a given population. IMA J Appl Math 78: 432-448. https://doi.org/10.1093/imamat/hxr058
[50]	Ginoux JM, Naeck R, Ruhomally YB, et al. (2019) Chaos in a predator–prey-based mathematical model for illicit drug consumption. Appl Math Comput 347: 502-513. https://doi.org/10.1016/j.amc.2018.10.089
[51]	Ullah A, Sakidin H, Gul S, et al. (2023) Sensitivity analysis-based validation of the modified NERA model for improved performance. J Adv Res Appl Sci Eng Technol 32: 1-11. https://doi.org/10.37934/araset.32.3.111
[52]	Zamir M, Zaman G, Alshomrani AS (2016) Sensitivity analysis and optimal control of anthroponotic cutaneous leishmania. PloS one 11: e0160513. https://doi.org/10.1371/journal.pone.0160513
[53]	Zamir M, Abdeljawad T, Nadeem F, et al. (2021) An optimal control analysis of a COVID-19 model. Alexandria Eng J 60: 2875-2884. https://doi.org/10.1016/j.aej.2021.01.022
[54]	Liu P, Din A, Zarin R (2022) Numerical dynamics and fractional modeling of hepatitis B virus model with non-singular and non-local kernels. Results Phys 39: 105757. https://doi.org/10.1016/j.rinp.2022.105757
[55]	Zamir M, Zaman G, Alshomrani AS (2017) Control strategies and sensitivity analysis of anthroponotic visceral leishmaniasis model. J Biol Dyn 11: 323-338. https://doi.org/10.1080/17513758.2017.1339835
[56]	Zamir M, Sultana R, Ali R, et al. (2015) Study on the threshold condition for infection of visceral leishmaniasis. Sindh Univ Res J 47: 619-622.
[57]	Liu P, Huang X, Zarin R, et al. (2023) Modeling and numerical analysis of a fractional order model for dual variants of SARS-CoV-2. Alexandria Eng J 65: 427-442. https://doi.org/10.1016/j.aej.2022.10.025
[58]	Zamir M, Nadeem F, Alqudah MA, et al. (2022) Future implications of covid-19 through mathematical modeling. Results Phys 33: 105097. https://doi.org/10.1016/j.rinp.2021.105097
[59]	Madhusudanan V, Srinivas MN, Murthy BSN, et al. (2023) The influence of time delay and Gaussian white noise on the dynamics of tobacco smoking model. Chaos Solitons Fractals 173: 113616. https://doi.org/10.1016/j.chaos.2023.113616
[60]	Bushnaq S, Shah K, Tahir S, et al. (2022) Computation of numerical solutions to variable order fractional differential equations by using non-orthogonal basis. AIMS Math 7: 10917-10938. https://doi.org/10.3934/math.2022610
[61]	Guo X, Guo Y, Zhao Z, et al. (2022) Computing R0 of dynamic models by a definition-based method. Infect Dis Model 7: 196-210. https://doi.org/10.1016/j.idm.2022.05.004
[62]	Van den Driessche P (2017) Reproduction numbers of infectious disease models. Infect Dis Model 2: 288-303. https://doi.org/10.1016/j.idm.2017.06.002
[63]	Rodrigues HS, Monteiro MTT, Torres DFM (2013) Sensitivity analysis in a dengue epidemiological model. Conference Papers in Mathematics 2013: 1-7. https://doi.org/10.1155/2013/721406
[64]	Ahmad N, Charan S, Singh VP (2015) Study of numerical accuracy of Runge-Kutta second, third and fourth order method. Int J Comput Math Sci 4: 111-118.
[65]	Islam MA (2015) Accurate solutions of initial value problems for ordinary differential equations with the fourth order Runge Kutta method. J Math Res 7: 41. https://doi.org/10.5539/jmr.v7n3p41
[66]	Aida M (2022) Fourth-order runge-kutta method for solving applications of system of first-order ordinary differential equations. Enhanced Knowl Sci Technol 2: 517-526. https://doi.org/10.1007/s40995-017-0258-1

This article has been cited by:

1.	Atta Ullah, Hamzah Sakidin, Shehza Gul, Kamal Shah, Yaman Hamed, Thabet Abdeljawad, Mathematical model with sensitivity analysis and control strategies for marijuana consumption, 2024, 10, 26668181, 100657, 10.1016/j.padiff.2024.100657
2.	Mudassar Iqbal, Nooraini Zainuddin, Hanita Daud, Ramani Kanan, Hira Soomro, Rahimah Jusoh, Atta Ullah, Iliyas Karim Khan, A modified basis of cubic B-spline with free parameter for linear second order boundary value problems: Application to engineering problems, 2024, 36, 10183647, 103397, 10.1016/j.jksus.2024.103397
3.	Atta Ullah, Hamzah Sakidin, Kamal Shah, Yaman Hamed, Thabet Abdeljawad, A mathematical model with control strategies for marijuana smoking prevention, 2024, 32, 2688-1594, 2342, 10.3934/era.2024107
4.	Jalal Al Hallak, Mohammed Alshbool, Ishak Hashim, Amar Nath Chatterjee, Implementing Bernstein Operational Matrices to Solve a Fractional‐Order Smoking Epidemic Model, 2024, 2024, 1687-9643, 10.1155/2024/9141971

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Bioengineering

Metrics

Article views(1176) PDF downloads(64) Cited by(4)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Bioengineering

Sensitivity analysis-based control strategies of a mathematical model for reducing marijuana smoking