Listen to the radio and go on field trips: A study on farmers' attributes to opt for extension methods in Northwest Ethiopia

1.   Introduction

Images provide an important means of transferring statistical information is online. When plain images are transmitted directly online, they will be vulnerable to various cyber-attacks such as stealing and tampering, which may cause huge losses to the owner of the images. Therefore, image encryption plays an important effect in ensuring the security of information ^[1,2,3,4], which also progresses the study of cryptography. At present, there have been a wide range of secure and effective data encryption technologies proposed by cryptographic experts ^[5,6,7], such as DES ^[8], AES ^[9], RSA, and RC6. However, most of the existing algorithms are designed for textual information, which is compounded by some inherent disadvantages in the encryption of images, such as time lag and low efficiency. Besides, these algorithms ignore the relationship between the adjacent image's pixels. Consequently, it is easy for the image information to be leaked in case of pixel statistics attack. Moreover, it is practically difficult for traditional encryption algorithms to meet the requirements on security and speed simultaneously. Therefore, it is necessary to develop a secure, efficient and fast encryption algorithm suitable for multimedia information, so as to achieve the real-time encryption of files, sounds, images and other sorts of multimedia information, which has attracted widespread attention for research at present.

Since the discovery of the correlation between chaos theory and cryptography, chaos theory has been attracting increased attention from many cryptographic researchers ^[10,11]. There are many chaos' properties that meet the requirements of cryptography technology, such as random-like, deterministic, non-periodic, non-convergent and initial value sensitivity ^[12,13,14]. Apart from that, the desirable cryptographic characteristics of chaos can be taken advantage of to construct an excellent image encryption system. Chaotic encryption technology relies on the chaotic sequences generated by chaotic systems to encrypt information, which brings about such advantages as the ease of implementation, the robustness to attack, and the high level of applicability. Up to now, there have been many articles published on chaotic cryptography and its applications, exploring how chaotic systems can be applied to generate the chaotic sequences that meet various requirements, which is a problem that the cryptographers of all countries aim to resolve. In 1989, Matthews proposed a stream cipher encryption scheme based on Anamorphic Logistic mapping, as described in ^[15], with the concept of "chaotic cryptography'' first proposed to attract widespread attention. According to the exact developmental process of encryption technology, the schemes of image encryption using chaotic systems can be classified into three categories. The first one is the scheme of image encryption using low-dimensional simple chaotic system. The second is the scheme of image encryption using high-dimensional complex chaotic system. The last one is the scheme of image encryption combining chaotic system with other methods.

Matthews designed an encryption algorithm that can make use of the chaotic sequences derived by \label{OLE_LINK2}Logistic mapping, the security of which is completely reliant on the generated chaotic sequences, including the parameters, the number of iterations, and the initial conditions of Logistic mapping. Subsequently, two-dimensional Baker mapping was performed in ^[16] to construct Bernoulli permutation, and to develop the symmetric product cryptography algorithm and pseudo random number generator for image encryption. However, it is difficult to ensure its operating efficiency due to a terrific amount of visual data referred. In this respect, block-oriented symmetric cryptography is considered an effective solution ^[17]. It relies on Kolmogoroff flows and shift registers to scramble the small blocks of data after image segmentation. Then, with parameters introduced into the chaotic system, the encrypted blocks can be expanded, and substitution operations are performed. This scheme proves advantageous over other encryption systems in security and efficiency. To sum up, above is the representative scheme of image encryption using a low-dimensional simplified chaotic system.

Compared with those chaotic systems which is low-dimensional, high-dimensional, and the positive Lyapunov exponents of which exceed 1, is more complex in structure, involving multiple system variables and multiple system parameters. Besides, the high-dimensional attractors generated exhibit more complex dynamic behaviors ^[18]. In other words, the time series produced by high-dimensional chaotic systems are more irregular and unpredictable, while the algorithm's key space designed according to them is much larger than the key space of the encryption algorithm developed on the basis of low-dimensional chaotic mapping ^[19,20], which makes it more suitable for image encryption. With the attempt made by many scholars to combine multiple chaotic maps, high-dimensional chaotic systems, and hyperchaotic systems, the focus of study has shifted to the second type of image encryption technologies. In ^[21], the chaotic sequences were generated by Cat mapping to scramble the pixels of the image at the bit level. Then, Logistic mapping was performed to change the positions and gray values of scrambled pixels through bitwise diffusion. To improve the operating efficiency of the encryption algorithm, a method of changing the position and distribution of image pixels was proposed on the basis of chaotic Henon mapping and Lorenz mapping in ^[22]. However, it involves only the scrambling process while ignoring the substitution or diffusion process, which exposes the geometric features of plaintext images. To solve this problem, a color image encryption scheme was designed in ^[23], with the Logistic mapping sequence used to disrupt the pixel position of the image, and to replace the gray value of the image with the Henon mapping sequence. In ^[24], the popularized 3D Cat map was used to scramble the position of image pixels, while another sequence obtained from the map was adopted to build a real-time secure symmetric encryption scheme by confusing the relationship between the encrypted image and the plaintext image for multiple times. These algorithms are common in creating a sufficiently large key space to counter brute force attacks. With the advancement of computer technology and cryptanalysis technology, there are various image encryption algorithms deciphered in succession on the basis of low and high-dimensional chaotic systems and hyperchaotic systems, which meet challenges to the existing methods of encryption. For example, the improved CKBA algorithm of image encryption proposed in ^[25] was deciphered by C. Li et al. through attack ^[26] known and selected plaintext. They adopted the same scheme to decipher the image encryption algorithm using the hyperchaotic system proposed in ^[27].

The third category is the image encryption scheme combining chaotic systems with other methods, the representative of which is the image encryption technology that integrates the chaotic system with DNA coding technology. In ^[28], such operations as elongation, truncation, deletion, insertion and sequence transformation in the DNA sequence processing method were performed to encode the pixel position of plaintext image, while two-dimensional Logistic chaos mapping was carried out to scramble and replace the pixel position and gray value of the encoded image. This algorithm is not only sensitive to key and easy to implement, but also robust to statistical attacks. In ^[29], the plaintext image was first encoded into a DNA sequence. Then, the chaotic mapping sequence was used to replace the encoded image data, thus obtaining the encrypted image.

Despite plenty of chaotic cryptographic schemes proposed by experts and scholars to date, the theory of chaotic cryptography is still immature. For example, these schemes prove secure only through experiments, with no rigorous mathematical proof available. Therefore, it remains challenging but worthwhile to conduct study on chaotic cryptography. The listed references are all based on finite-dimensional chaotic systems to implement encryption algorithms. However, due to the development of AI, the parameters of finite-dimensional chaotic systems can be simulated through intercepted chaotic sequences. Therefore, the implementation of encryption by finite-dimensional chaotic systems no longer has good security. We present an algorithm of image encryption using the double delay Lorenz system, which provides a safe, reliable and efficient feasible scheme for image encryption. The advantages of the encryption algorithm are as follows: First, because of the infinite dimension of the delay chaotic system, the randomness is stronger and it is more difficult to be simulated by AI technology, so the security efficiency of the encryption algorithm is guaranteed. Second, the time-delay and the location of time-delay make the key space expand further. Finally, the simple implementation of the algorithm makes the image encryption more efficient.

The structure of this article is as follows. The first part briefly introduces the research status of image encryption technology. The second part discusses the Hopf bifurcation and stability of Lorenz system with double delay. The third part adapts the double time-delay Lorenz system to encrypt the digital image. The fourth part verifies the encryption effect by mathematical software. Finally, the conclusion is drawn.

2.   Double time-delay Lorenz system

In respect of secret communication, the value of a chaotic system is directly proportional to its behavioral complexity. Therefore, the Lorenz-like systems ^{[30,31,32,33,34,35]} are unable to meet the requirements, which prompts scholars to create the new chaotic systems whose dynamic behaviors are difficult to predict, such as hyper chaos system, multiple-wing chaotic system and Lorenz system, etc. These chaotic systems demonstrate more desirable chaos characteristics and higher complexity, many of which are applied in the chaos encryption technology to produce satisfactory outcomes of encryption, while ensuring security. A typical example of them is the time-delay Lorenz system developed on the basis of Lorenz system. However short its time-delay is, the state space of the system is infinitely dimensional, as is the solution space of it. That is to say, there are an infinite number of roots for the characteristic equation of the corresponding linearized system. Being fundamentally different from ordinary Lorenz systems in various respects, the time-delay Lorenz system shows completely different dynamic behaviors, thus leading to high complexity. At present, there are some scholars who have also developed time-delay Lorenz systems for application in encryption algorithms. Their system equations are similar to Eq (2.1) below:

where $x$, $y$, and $z$ represent the variables of state, $a$, $b$, $c$ denote the parameters of system, and $\tau (>0)$ refers to a time-delay constant. It is always assumed that the impact of time-delay in the system is always unchanged, which means the $\tau (>0)$ value is a constant. In fact, the understanding of time-delay chaotic systems must be improved. As the basic characteristic of dynamic behaviors of time-delay chaotic systems, the evolution of the system over time depends not only on the current state but also on the status in the past or the future. Besides, the previous or future impact of the system in other dimensions is not necessarily the same. Therefore, in this paper, our consideration is given to the dynamic behaviors of time-delay chaotic systems when the time-delay varies, for their application in encryption.

The state equation of double time-delay Lorenz system is expressed as follows:

where ${\tau _1}(>0)$ and ${\tau _2}(>0)$ represent constant time-delay. The system(2.2) consists of 6 terms in total, including 4 linear terms and 2 nonlinear terms. Compared with other chaotic or hyperchaotic systems, this system is simpler in structure and easier to achieve by circuit, which makes it applicable in the practice of secure communication. Known as the double time-delay Lorenz system, a functional differential dynamical system is constructed by applying double time-delay to the state variables. There are different choices available over time-delay applying positions, and 8 positions with $P_8^2$ different forms of combination. Therefore, this structure is effectively a secure means of encrypting communication. In this paper, one of these structures is adopted as the method of encryption, as shown in the Eq (2.2). Our main contribution of this paper is to linearize the double time-delay Lorenz system and analyze the distribution of the characteristic equation's roots after linearization. Besides, the system's stability at the zero equilibrium point and Hopf bifurcation conditions are determined. Finally, it is used to the technology of image encryption, thus making the outcomes of encryption satisfactory.

The parameters of system are set as

The equilibrium points meets the conditions as follows:

According to Eq (2.3), system (2.2) has three equilibrium points, i.e.

The system's stability at the equilibrium point is discussed and the following theorems are proposed.

Theorem 1. Assume ${\tau _1} = {\tau _2} = 0$, then system (2.2) is unstable at the point $(\sqrt{bc}, \sqrt{bc}, b)$.

Proof. At the point $(\sqrt{bc}, \sqrt{bc}, b)$, the system's Jacobian matrix is expressed as:

The characteristic equation is presented as:

Equation (2.5) can be converted into:

where ${p_1} = a{e^{ - \lambda {\tau _1}}} + c$, ${p_2} = ac{e^{ - \lambda {\tau _1}}} - ab{e^{ - \lambda {\tau _2}}} + ab + bc$, ${p_3} = abc({e^{ - \lambda {\tau _1}}} - {e^{ - \lambda {\tau _2}}} + 2)$.

When ${\tau _1} = {\tau _2} = 0$, Eq (2.6) can be transformed into:

As for the conditions $a > 0$, $b < 0$, $c > 0$, $2abc < 0$. Therefore, by the Routh-Hurwitz criterion, a positive real part will be appeared in the eigenvalue of Eq (6). When ${\tau _1} = {\tau _2} = 0$, system (2.2) is unstable at the point $(\sqrt {bc}, \sqrt {bc}, b)$. □

Given the invariance under the transformation of $S:(x, y, z) \to (-x, -y, z)$, which means there is symmetry for z, system (2.2) is unstable at the point $(-\sqrt{bc}, -\sqrt{bc}, b)$.

Next, the system's stability at point $(0, 0, 0)$ will be discussed. It is easy to identify the linearized system (2.2) at the point $(0, 0, 0)$.

Based on system (2.8), the Jacobian matrix is expressed as:

According to the Jacobian matrix, the characteristic equation can be presented as:

Equation (2.10) can be converted into:

where ${p_1} = a{e^{ - \lambda {\tau _1}}} + c$, ${p_2} = ac{e^{ - \lambda {\tau _1}}} - ab{e^{ - \lambda {\tau _2}}}$, ${p_3} = - abc{e^{ - \lambda {\tau _2}}}$.

When ${\tau _1} = {\tau _2} = 0$, Eq (2.11) can be transformed into:

As for the conditions, $a > 0$, $b < 0$, $c > 0$, therefore, $- abc > 0$, $ac - ab > 0$ and $a + c > 0$. By Routh-Hurwitz criterion, negative real part will appeared in all characteristic roots of the above equation. When ${\tau _1} = {\tau _2} = 0$, system (2.2) is asymptotically and locally stable at the point $(0, 0, 0)$.

3.   Hopf bifurcation analysis of double time-delay Lorenz

A discussion followed will be conducted about the preconditions for the Hopf bifurcation's existence at the equilibrium point. It is assumed that the root of the characteristic Eq (2.11) is $\lambda = \rho + i\omega$, $\rho \in R$, $\omega \in R$. To satisfy the conditions of Hopf bifurcation, there must be conjugated pure imaginary roots in Eq (2.11). Let $\rho = 0$, so that the Equation below can be obtained as:

By substituting Eq (3.1) into Eq (9), and separating the imaginary and real parts, the stability change of the static solution will occur, i.e.,

The impact caused by time-delay variation on the system bifurcation will be discussed below.

3.1.   Identical time-delay

As ${\tau _1} = {\tau _2} = \tau$, Eq (3.2) can be converted into:

where $p = ac - ab$, $q = abc$.

The following steps will be done on the Eq (3.3). After squaring both sides and adding them, Eq (3.4) can be obtained.

The following conclusions can be obtained for Eq (3.4).

Lemma 1. If $a > 0$, $b < 0$, $c > 0$, one or more positive real root appears in the set of roots of the Eq (3.4).

Proof. Let $u = {\omega ^2}$, so that Eq (3.4) can be transformed into:

It is assumed that

Equation (3.6) can be transformed into:

Therefore,

$g(0) = - {q^2} < 0$, $\mathop {\lim }\limits_{u \to + \infty } g(u) = + \infty$

According to the function zero existence theorem, at least one real number ${u_0} \in (0, + \infty)$ appears that makes $g({u_0}) = 0$. Therefore, Eq (3.5) has one or more positive real root. As $u = {\omega ^2}$, Eq (3.4) has one or more positive real root.

Supposed that a real root of Eq (3.4) is ${\omega _0}$, then Eq (3.4) has a pure imaginary root $i{\omega _0}$. Also, the following equation can be obtained.

By substituting $\omega = {\omega _0}$ into Eq (3.8), the $\tau$ value is obtained as:

Therefore, Eq (3.3) has a solution $({\omega _0}, {\tau _k})$, which means that a pair of conjugate pure imaginary roots $\lambda = \pm i{\omega _0}$ appear on the Eq (3.3) when $\tau = {\tau _k}$. □

Suppose ${\tau _0} = \min \{ {\tau _k}\}$, then $\tau = {\tau _0}$ is the minimum value according to the pure imaginary root $\lambda = \pm i{\omega _0}$ of Eq (2.12). Following that, the lemma can be obtained.

Lemma 2. If $a > 0$, $b < 0$, $c > 0$, $\tau = {\tau _0}$, then a dual pure imaginary roots $\lambda = \pm i{\omega _0}$ appears in the set of roots of Eq (3.1).

Suppose the eigen roots of Eq (2.4) $\lambda (\tau) = \alpha (\tau) + i\omega (\tau)$ satisfy the condition that $\alpha ({\tau _k}) = 0$ and $\omega ({\tau _k}) = {\omega _0}$, then the transversal conditions are determined as follows.

Lemma 3. If $a > 0$, $b < 0$, $c > 0$, and $g'(\omega _0^2) > 0$, then $\frac{{d{\mathop{\rm Re}\nolimits} \lambda (\tau)}}{{d\tau }}\left| {_{\tau = {\tau _k}} > } \right.0$.

Proof. when ${\tau _1} = {\tau _2} = \tau$, Eq (2.11) can be converted into:

Taking the both sides' derivative of Eq (3.10) using $\tau$, the following equation can be obtained.

According to Eq (3.10), Eq (3.12) can be obtained as follows:

By introducing Eq (3.12) into Eq (3.11), Eq (3.13) can be obtained.

As ${\tau _k} = i{\omega _0}$, so that

When $\tau = {\tau _0}$, Eq (3.10) has a pure imaginary root $i{\omega _0}$. By substituting it into Eq (3.10), the following equation can be obtained.

As ${e^{ - i{\omega _0}{\tau _0}}} = \cos {\omega _0}{\tau _0} - i\sin {\omega _0}{\tau _0}$, so $\left| {{e^{ - i{\omega _0}{\tau _0}}}} \right| = 1$. Then,

That is to say,

By combining Eq (3.15) and (3.17), the following equation can be obtained.

As $Sign[{\mathop{\rm Re}\nolimits} (\frac{{d\lambda }}{{d\tau }}\left| {_{\tau = {\tau _k}}} \right.)] = Sign\{ {\mathop{\rm Re}\nolimits} [{(\frac{{d\lambda }}{{d\tau }})^{ - 1}}\left| {_{\tau = {\tau _k}}} \right.]\}$, the lemma is proved. □

Therefore, according to Lemma 3.3, the following conclusions can be reached.

Theorem 2. If $a > 0$, $b < 0$, $c > 0$, and $g'(\omega _0^2) > 0$, then

1. When $\tau \in [0, {\tau _0})$, system (2.2) is asymptotically stable at the point $O(0, 0, 0)$;

2. When $\tau > {\tau _0}$, system (2.2) is unstable at the point $O(0, 0, 0)$;

3. When $\tau = {\tau _k}(k = 0, 1, 2, \cdots)$ Hopf bifurcation occurs at the point $O(0, 0, 0)$ in the system (2.2), and $\tau = {\tau _k}(k = 0, 1, 2, \cdots)$ is the Hopf bifurcation value.

3.2.   Different time-delays

For the sake of ensuring the Hopf bifurcation with two different delays and the stability of system (2.2), there are two extremes of Eq (2.11) considered, respectively. Since both ${\tau _1}$ and ${\tau _2}$ are greater than 0, the delay boundary case is considered, i.e., ${\tau _1} = 0$ or ${\tau _2} = 0$. With one of the time-delays fixed, an analysis is conducted as to the other time-delays' impact on the stability and the Hopf bifurcation using Rouche theorem. The advantage of this method is that, the impact of the two time-delays on Hopf bifurcation and its stability can be analyzed according to the assumption that ${\tau _1}$ is fixed and ${\tau _2}$ is regarded as a variable dependent on ${\tau _1}$. Then, the following process is conducted. First of all, it is set that ${\tau _2} = 0$, the system (2.2) with a time-delay ${\tau _1}$ is analyzed, and the stability interval of ${\tau _1}$ is obtained using Rouche theorem, with ${\tau _1}$as the bifurcation parameter. On this basis, negative real part appears in all the roots of Eq (2.11). Second, system (2.2) is analyzed at the stability interval of ${\tau _1}$, and the Rouche theorem is applied to analyze the stability and Hopf bifurcationof the system, with ${\tau _2}$ as the bifurcation parameter. Notably, the stability interval of ${\tau _2}$ is determined by ${\tau _1}$, so that the area encircled by ${\tau _1}$ and ${\tau _2}$ represents the stability interval of system (2.2).

When ${\tau _1} = 0$, Eq (2.11) can be transformed into:

where ${p_1} = a + c$, ${p_2} = ac - ab{e^{ - \lambda {\tau _2}}}$, ${p_3} = - abc{e^{ - \lambda {\tau _2}}}$. Equation (3.19) is converted into:

where ${q_1} = ac$, ${q_2} = ab$, ${q_3} = abc$, ${q_4} = a + c$. After squaring both sides and summing them, Eq (3.19) can be obtained as follows:

By Eq (3.21), the following conclusions can be obtained.

Lemma 4. If $a > 0$, $b < 0$, $c > 0$, one or more positive real root appears in the set of roots of Eq (3.21).

Proof. Let $u = {\omega ^2}$, then Eq (3.21) can be converted into

Assume,

Then, Eq (3.23) can be converted into:

Therefore,

$h(0) = - q_3^2 < 0$, $\mathop {\lim }\limits_{u \to + \infty } h(u) = + \infty$

According to the function zero existence theorem, there is one or more real number ${u_0} \in (0, + \infty)$ that makes $g({u_0}) = 0$. Therefore, Eq (3.23) has one or more positive real root. Since $u = {\omega ^2}$, Eq (3.21) has one or more positive real root.

Assume Eq (3.21) has a real root ${\omega _0}$, so that $i{\omega _0}$ is a pure imaginary root of Eq (3.10). Also, Eq (3.25) can be obtained.

By substituting $\omega = {\omega _0}$ into Eq (3.25), $\tau$ is obtained as:

Therefore, $({\omega _0}, {\tau _{2k}})$ is the solution to Eq (3.25), which means that Eq (3.19) has a couple of conjugate pure imaginary roots $\lambda = \pm i{\omega _0}$ when the time-delay is $\tau = {\tau _{2k}}$. □

Suppose ${\tau _{20}} = \min \{ {\tau _{2k}}\}$, then the $\tau = {\tau _{20}}$ is the minimum value when Eq (3.19) has pure imaginary root $\lambda = \pm i{\omega _0}$. The following lemma can be obtained.

Lemma 5. If $a > 0$, $b < 0$, $c > 0$, ${\tau _2} = {\tau _{20}}$, ${\tau _1} = 0$, then a couple of pure imaginary roots $\lambda = \pm i{\omega _0}$ appears in the set of roots of Eq (3.19).

Suppose that the eigen roots $\lambda (\tau) = \alpha ({\tau _{1k}}) + i\omega ({\tau _{1k}})$ of Eq (3.19) satisfy the condition that $\alpha ({\tau _{1k}}) = 0$ and $\omega ({\tau _{1k}}) = {\omega _0}$, the following transversal conditions are presented.

Lemma 6. If $a > 0$, $b < 0$, $c > 0$, ${\tau _2} = {\tau _{20}}$, ${\tau_1} = 0$ and $h'(\omega _0^2) > 0$, then $\frac{{d{\mathop{\rm Re}\nolimits}\lambda ({\tau _2})}}{{d{\tau _2}}}\left| {_{\tau = {\tau _{2k}}} > } \right.0$.

Proof. When ${\tau _2} = {\tau _{20}}$, ${\tau _1} = 0$, Eq (3.19) can be transformed into:

The derivative of both sides of Eq (3.27) with respect to ${\tau _2}$ is taken to obtain Eq (3.28).

According to Eq (3.27), Eq (3.29) can be obtained.

By substituting Eq (3.29) into Eq (3.28), Eq (3.30) can be obtained.

Since ${\tau _{2k}} = i{\omega _0}$, so that

When ${\tau _1} = {\tau _{20}}$, Eq (3.27) has pure imaginary roots $i{\omega _0}$, which can be substituted into Eq (3.27) to obtain Eq (3.32).

As ${e^{ - i{\omega _0}{\tau _{10}}}} = \cos {\omega _0}{\tau _{10}} - i\sin {\omega _0}{\tau _{10}}$, so that $\left| {{e^{ - i{\omega _0}{\tau _{10}}}}} \right| = 1$. Then,

That is to say,

By combining Eq (3.32) and (3.34), the following equation can be obtained.

Since $Sign[{\mathop{\rm Re}\nolimits} (\frac{{d\lambda }}{{d{\tau _1}}}\left| {_{\tau = {\tau _{1k}}}} \right.)] = Sign\{ {\mathop{\rm Re}\nolimits} [{(\frac{{d\lambda }}{{d{\tau _1}}})^{ - 1}}\left| {_{\tau = {\tau _{1k}}}} \right.]\}$, so that it is proved validly.

Similarly, let ${\tau _2} = 0$, with ${\tau _1}$ as the running parameter, then ${\mathop{\rm Re}\nolimits} [{(\frac{{d\lambda }}{{d{\tau _2}}})^{ - 1}}\left| {_{\tau = {\tau _{2k}}}} \right.] > 0$ can also be proved validly. □

Therefore, according to Lemma 3.6, the following conclusions can be reached.

Theorem 3. The conclusions can be drawn for Eq (3.19) as follows.

1. If $a > 0$, $b < 0$, $c > 0$ and $h'(\omega _0^2) > 0$, then negative real part appears in all characteristic roots of Eq (3.19), when ${\tau _1} \in {\tau _{10}}$. Besides, when ${\tau _1} > {\tau _{10}}$, Eq (3.19) has one or more root with positive real parts.

2. If $a > 0$, $b < 0$, $c > 0$ and $h'(\omega _0^2) > 0$, with system from stable to unstable there are k transitions.

Next, considering that Eq (2.11) has ${\tau _2}$ in its stability interval and ${\tau _1}$ is deemed as the parameter, the following lemma is proposed.

Lemma 7. If negative real part appears in the eigenroots of Eq (3.19), then there is ${\tau _1}({\tau _2}) > 0$ thus making negative real part appear in all the eigenroots of Eq (3.19) when ${\tau _1} \in [0, {\tau _1}({\tau_2}))$.

Proof. Notably, Eq (3.19) has no roots with a non-negative real part, nor does Eq (2.11) has any roots with a non-negative real part when ${\tau _1} = 0$. Given that ${\tau _1}$ is the parameter, it is apparent that the left-hand side of Eq (2.11) is analytic with respect to ${\tau _1}$ and $\lambda$.

Similar to the proof of lemma in Literature ^[36], it is supposed that

where $a$, $b$, $c$, $d$, ${\tau _1}$, ${\tau _2}$ represent the real numbers, ${\tau _1} \ge 0$ and ${\tau _2} \ge 0$. Thus, when ${\tau _1}$ varies, there may be change in the sum of the multiplicity in the right half plane zeros only if one of its zero points appears or crosses the imaginary axis.

With this conclusion applied, it is worth noting that no non-negative real part appears in the roots of Eq (2.11) when ${\tau _1} = 0$. Therefore, it can be concluded that there is ${\tau _{10}}$ that makes negative real part appears in all the characteristic roots of Eq (2.11) when ${\tau _1} \in [0, {\tau _{10}})$.

Based on a summary of the aforementioned lemma, it can be known that the following theorem is the sufficient condition for the characteristic Eq (2.11) to have negative real parts. □

Theorem 4. For ${\tau _2} \in [0, {\tau _{20}})$, there is ${\tau _1}({\tau _2}) > 0$ that makes negative real part appear in all the characteristic roots of Eq (2.11) when ${\tau _1} \in [0, {\tau _1}({\tau _2}))$.

When ${\tau _1} = 0$, it is obtained that ${\tau _2} = {\tau _{20}}$ and $\omega = {\omega _0}$. Therefore, the solution to Eq (3.2) is ${\tau _1}({\tau _{20}}) = 0$. According to this relation, ${\tau _1}({\tau _2})$ can be deduced. Then, Eq (3.2) can be converted into:

where ${u_1} = a\omega _0^2$, ${u_2} = ac{\omega _0}$, ${u_3} = abc$, ${u_4} = ab{\omega _0}$, ${u_5} = - c\omega _0^2$, ${u_6} = \omega _0^3$. Thus, ${\tau _1}({\tau _2})$ can be obtained.

Then, ${\tau _{1k}}$ can be obtained.

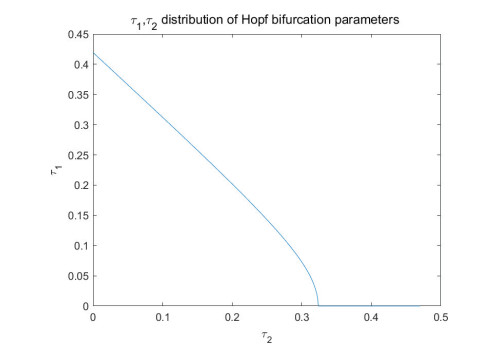
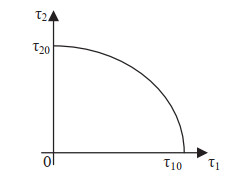
Based on Eq (3.38) as mentioned above, the relationship of ${\tau _1}({\tau _2})$ can be obtained. Figure 1 shows the distribution of ${\tau _1}$ and ${\tau _2}$ for the double time-delay Lorenz system.

In Figure 1, ${\tau _{20}} = \frac{1}{{{\omega _0}}}\arccos (\frac{{{q_2}({q_1}\omega _0^2 - \omega _0^4) - {q_3}{q_4}\omega _0^2}}{{q_3^2 + q_2^2\omega _0^2}})$, ${\tau _{10}} = \frac{1}{{{\omega _0}}}\arccos (\frac{{{u_1}{u_5} + {u_2}{u_6} - ({u_1}{u_3} - {u_2}{u_4})\cos ({\omega _0}{\tau _{20}}) - ({u_2}{u_3} + {u_1}{u_4})\sin ({\omega _0}{\tau _{20}})}}{{u_1^2 + u_2^2}})$. Since $\frac{{d{\mathop{\rm Re}\nolimits} \lambda ({\tau _1})}}{{d{\tau _1}}}\left| {_{\tau = {\tau _{1k}}} > } \right.0$ and ${\mathop{\rm Re}\nolimits} [{(\frac{{d\lambda }}{{d{\tau _2}}})^{ - 1}}\left| {_{\tau = {\tau _{2k}}}} \right.] > 0$, they have the same bifurcation direction, the following theorem is deduced.

Theorem 5. The distribution of ${\tau _1}$ and ${\tau _2}$ of the system (2.2) are obtained from Eqs (3.28) and (3.38), forming $k = 0, 1, 2, \cdots$transition regions that range from stable to unstable regions. The stable and unstable regions are segmented by a curve, which is determined by Eq (3.38). It can be drawn the conclusions as follows:

1. The stable region of the system (2.2) is the region below the curve, which represents the value of the gradually stable parameters ${\tau _1}$ and ${\tau _2}$;

2. The unstable region of the system (2.2) is the region above the curve, which represents the value of the unstable parameters ${\tau _1}$ and ${\tau _2}$, as well as the conditions for the system (2.2) to enter chaos.

3. The region above the curve is the Hopf bifurcation value of the system, at which the Hopf bifurcation of the system (2.2) occurs.

4.   Experimental simulation

The experimental simulation falls into the case of same delay and the case of different delay, respectively demonstrating the bifurcation of double time-delay chaotic systems.

4.1.   Double time-delay chaotic system with same delay

Since the system's parameters $a > 0$, $b < 0$, $c > 0$, we might as well to take $a = 10$, $b = - 4$, $c = 2.5$ to carry out the numerical simulation of dual time-delays chaotic system. Subsequently, the dual time-delays system can be transformed as:

A mathematical software is used to achieve the results: Eq (3.4)'s positive real root ${\omega _0} = 10.6785$, so it is easy to obtain $g'(\omega _0^2) = {\rm{1}}{\rm{.5403}} \times {10^4} > 0$, and in Eq (3.9), ${\tau _0} = 0.1120$. Accordingly, Theorem 3.1 can be concretized into the corollary below.

Corollary 1. If $a > 0$, $b < 0$, $c > 0$, and $g'(\omega _0^2) > 0$, then

1. When $\tau \in [0, 0.1120)$, the system (4.1) is asymptotically stable at the point $O(0, 0, 0)$;

2. When $\tau > 0.1120$, the system (4.1) is unstable at the point $O(0, 0, 0)$;

3. When ${\tau } = 0.1120 + 0.1873k\pi (k = 0, 1, 2, 3, \cdots)$ i.e., the Hopf bifurcation value of the system(4.1), the Hopf bifurcation occurs at the point $O(0, 0, 0)$, thus creating the limit cycle.

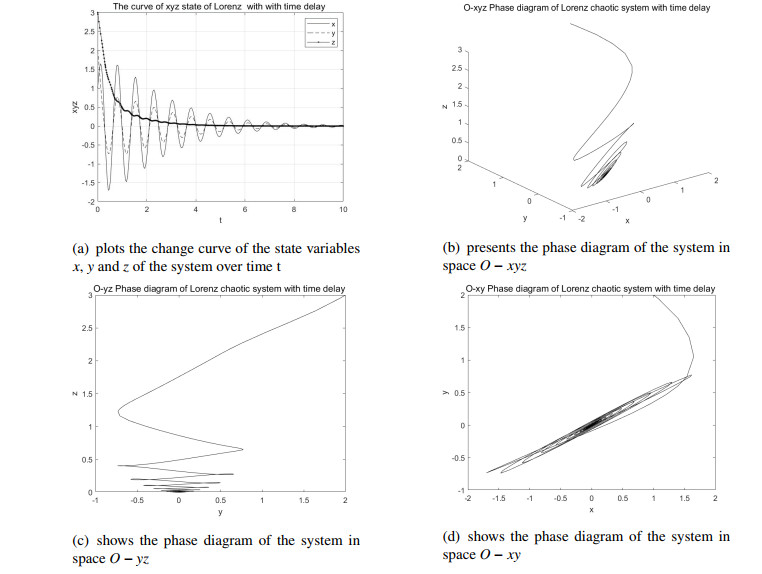
Next, the mathematical software is used to draw the system's phase diagram and the system's trajectory diagram when time-delays $\tau$ are different (Figures 2–4), which indicates the correctness of the results.

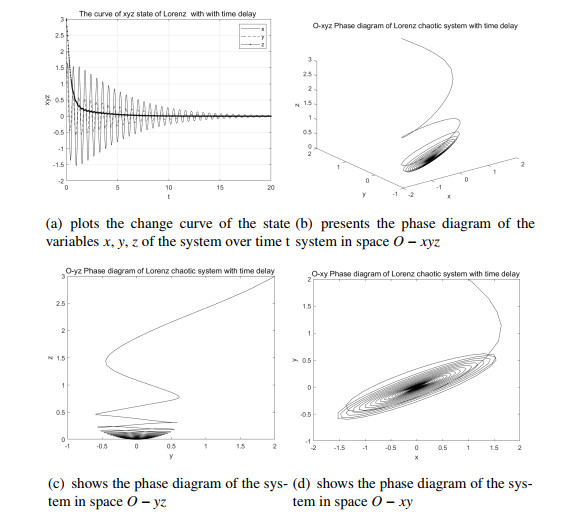
According to Figure 2, when $\tau = 0.11$, the $x$, $y$, $z$ value tends to approach the point $O(0, 0, 0)$ with the passage of time $t$, so the system (4.1) is asymptotically stable at the point $O(0, 0, 0)$.

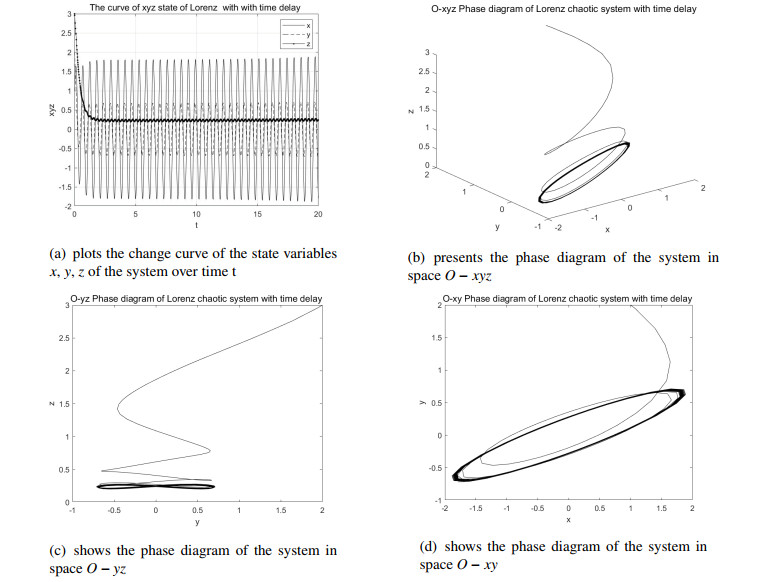
According to Figure 3, when $\tau = 0.1120$, the $x$, $y$, $z$ value of the system (4.1) keep a periodic oscillation forever with the increase of t, and the limit cycles appeared in $O - xyz$ space, which indicates that the Hopf bifurcation occurs at the point $O(0, 0, 0)$.

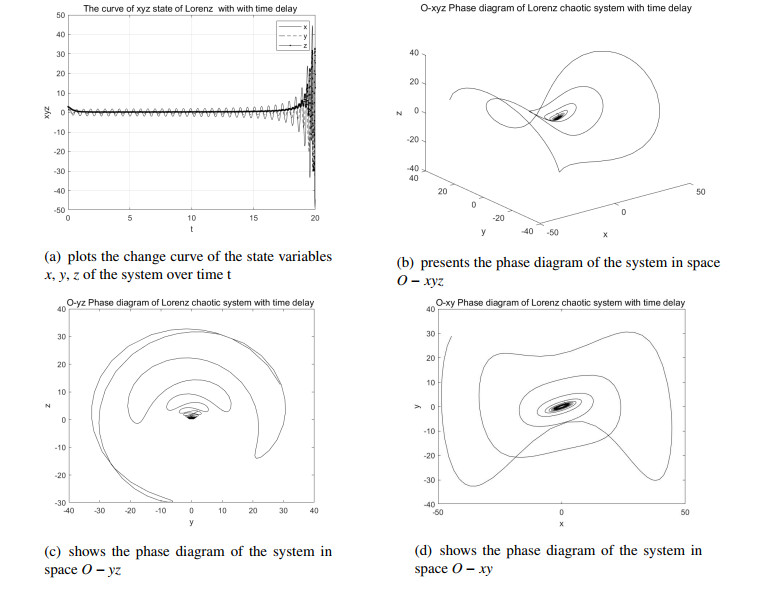
According to Figure 4, the $x$, $y$, $z$ value is gradually away from the point over t, which means that the system (4.1) is unstable at the point $O(0, 0, 0)$ when $\tau = 0.1125$.

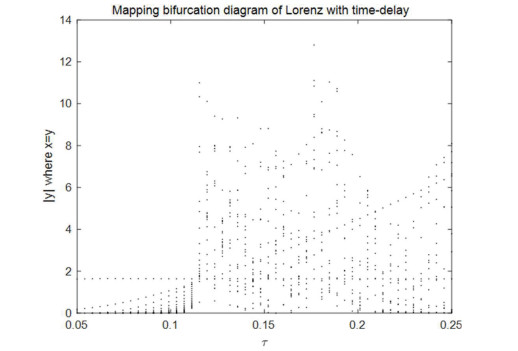
The bifurcation diagram of system can be drawn as the $\tau$ affecting the bifurcation of system, as shown in Figure 5. It can be seen that the system bifurcates at $\tau = 0.1120$ from Figure 5, by which our conclusion also can be verified.

4.2.   Double time-delay chaotic system with different delays

Since the conditions $a > 0$, $b < 0$, $c > 0$, we might as well to take $a = 10$, $b = - 4$, $c = 2.5$ to carry out the numerical simulation of the double time-delays chaotic system.

To determine the value of bifurcation parameters of the system (4.2), the bifurcation conditions of the system (4.2) should be calculated first with single time-delay. Thus, ${\tau _1} = 0$, ${\tau _2} \ne 0$,

The software of mathematics is used to obtain the following results, i.e., Eq (3.21)'s positive real root ${\omega _0} = 3.7458$, so it is easy to obtain $h'(\omega _0^2) = {\rm{2}}{\rm{.5972}} \times {10^3} > 0$, and in Eq (3.20), ${\tau _{20}} = 0.4703$. Accordingly, Theorem 3.4 can be concretized into the corollary as follows.

Corollary 2. If $a > 0$, $b < 0$, $c > 0$ and $h'(\omega _0^2) > 0$, then

1. When ${\tau _{20}} \in [0, 0.4703)$, the system (4.3) is asymptotically stable at the point $O(0, 0, 0)$;

2. When ${\tau _{20}} > 0.4703$, the system (4.3) is unstable at the point $O(0, 0, 0)$;

3. When ${\tau _{2k}} = 0.4703 + 0.5339k\pi (k = 0, 1, 2, 3, \cdots)$, i.e., the Hopf bifurcation value, i.e., the system (4.3) creates the limit cycle at the point $O(0, 0, 0)$.

When the intervals of ${\omega _0}$ and ${\tau _2}$ are obtained, for any one ${\tau _{20}} \in [0, 0.4703)$, the value ${\tau _1}$ can be calculated by Eq (3.21), because it depends on ${\tau _2}$. It is shown in Figure 6 that the value distribution of ${\tau _1}$ and ${\tau _2}$ of the system (4.3)is displayed. According to Theorem 3.4, the system (4.3) is asymptotically stable at the area below the curve, the system (4.3) is unstable at the area above the curve, and the system is in a chaos state on the value of curve, namely, the system (4.3) enters the Hopf bifurcation.

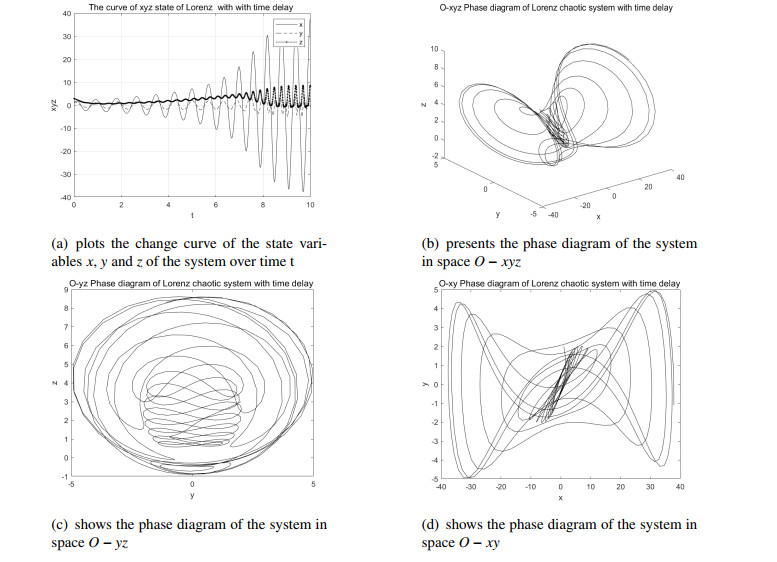
Next, the software of mathematics is used to draw the dual time-delays Lorenz system's trajectory diagram and the dual time-delays Lorenz system's phase diagram over t when the values of ${\tau _1}$ and ${\tau _2}$ are different (Figures 7–9), which proves the correctness of the results.

According to Figure 7, when ${\tau _1} = 0.1$, ${\tau _2} = 0.2$, the $x$, $y$ and $z$ values of the system (4.3) get close to the point $O(0, 0, 0)$ over t, so the system (4.3) is asymptotically stable at the equilibrium point $O(0, 0, 0)$.

According to Figure 8, when ${\tau _2} = 0.2190$ and ${\tau _1} = 0.1801$, the $x$, $y$ and $z$ value of the system (4.3) always keep periodic oscillations with the increase of time, and limit cycles appear in $O - xyz$ space, which indicates that the system (4.3) bifurcates at the point $O(0, 0, 0)$.

According to Figure 9, the $x$, $y$ and $z$ values of the system are gradually away from the equilibrium point over t, that is to say, when ${\tau _1} = 0.1521$ and ${\tau _2} = 0.29$, the system (4.3) is unstable at the point $O(0, 0, 0)$.

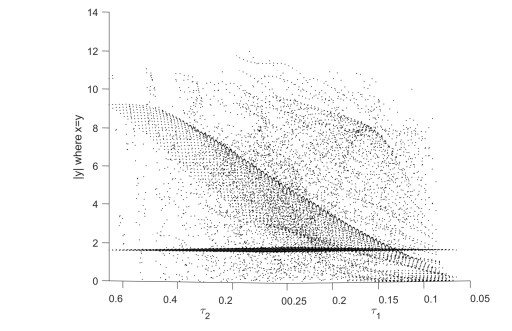
With double time-delays, the system has more complex chaotic phenomena. When ${\tau _1}$ is within the interval [0.05, 0.25] and ${\tau _2}$ is within the interval [0.05, 0.65], the bifurcation diagram of the system can be drawn with the changes of ${\tau _1}$ and ${\tau _2}$. Figure 10 shows that the system is in a stable state in the enclosed region of ${\tau _1}$ and ${\tau _2}$, the system is in the state of Hopf bifurcation on the boundary of the enclosed region, and the system is in the chaotic states in other regions.

5.   Image encryption scheme

At present, scrambling and diffusion are the basic operations of image encryption. Scrambling aims to change the position of pixelof original image using a certain mathematical formula, reduce the correlation between adjacent pixels and generate meaningless ciphertext images, which scrambles and encrypts the original image. However, this operation does not change the value of pixel of original image. The original image still has different statistical characteristics, which is vulnerable to attack and has low security. The scrambling methods mainly include affine transform, Arnold transform, Rubik's Cube transform, Knight-tour, etc. Diffusion aims to modify the pixels of the original image in a way that can be reversed and then reduce the characteristics of statistics of the original image. Thus, the encryption method combining scrambling and diffusion can more effectively encrypt the image.

Chaotic systems are favored by cryptographers for scrambling and diffusion in image encryption because of their pseudo-random and initial value sensitivity. The common chaotic systems were consisted of Logistic mapping, Tent mapping, Henon mapping, Lorenz and Lorenz-like mapping. The chaotic systems produce large keyspace and have strongly adaptive key flows and high security. However, as indicated by the deep research on chaos theories, some low-dimensional chaotic systems have some problems (e.g., simple structure and periodic window), which indicates that the pseudo-random sequences came from the mentioned chaotic systems have weak anti-attack ability and are easy to be cracked. Thus, these chaotic systems cannot ensure the security of the encryption of image. To solve this problem, we produce a double-time-delay chaotic system, which produces pseudo-random sequences with good randomness, wide ranges and no window. Since a double-time-delay chaotic system can replace Logistic mapping chaotic systems with weak dynamic characteristics and narrow chaos range, it can ensure the security of the encryption algorithm.

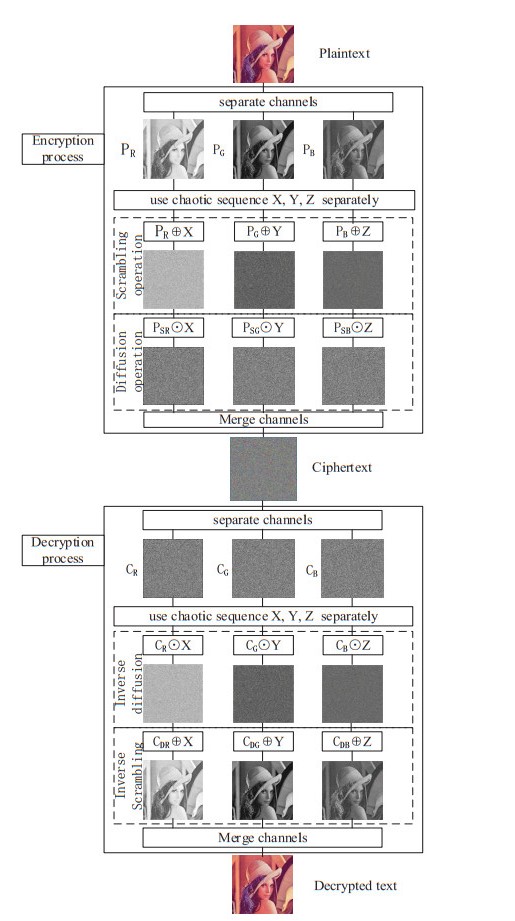
5.1.   Image encryption and decryption process

According to Figure 11, the dual time-delay Lorenz system generates the pseudo-random sequence $(X, Y, Z)$ and then the sequence for scrambling and diffusion is used to the image encryption and decryption process.

5.1.1.   Pseudo-random sequences are generated by time-delay chaotic systems

Time-delay chaotic systems have essential differences with non-time-delay chaotic systems in numerous aspects, and their dynamic behaviors are completely different and show significantly complex phenomena. The basic characteristic of the time-delay chaotic systems is that the evolution of the systems over time is dependent of their current and past states, which is usually referred to as the lag-type time-delay dynamics system. This type of dynamic system is the infinite-dimensional dynamical system usually described by delay-delay differential equations. No matter how small the delay is, the state space of the system is infinite-dimensional, and the solution space is infinite-dimensional, i.e., the characteristic equation of the corresponding linearized system has an infinite number of roots. Before encryption and decryption, a dual time-delay chaotic system is adopted to produce three pseudo-random sequences $(X, Y, Z)$ simultaneously, corresponding to encryption and decryption operations after the color image separation channel. Thud, the keyspace will be larger than that of the previous chaotic systems. The keyspace will comprise three chaotic system parameters, two time-delay values and interception positions of three pseudo-random sequences. If the image size is $M \times N \times 3$, the number of pseudo-random sequences produced by the chaotic system with time-delay will be far higher than $M \times N$. To be specific, M and N denote the horizontal and vertical pixel values of the image, respectively.

5.1.2.   Encryption method

Overall, an encryption algorithm consists of diffusion and scrambling. At the scrambling stage, the pseudo-random sequence is ranked in an order of ascending, and the position of pixel of the plaintext image is transformed in accordance with the sorted sequence to confuse the pixel position of the plaintext image. At the diffusion stage, the matrix is built using the intercepted sequence and multiplied by the scrambled pixel matrix to obtain the pixel matrix of encrypted image.

For a color plaintext image $P$, with a size of $M \times N \times 3$, 3 represents the channels' number of the color image, and P will fall into three layers (${P_R}$, ${P_G}$ and ${P_B}$) according to the channels. Scrambling and diffusion operations are conducted to the respective layer. With ${P_R}$ as an example, the image matrix ${P_R}$ is expanded into a vector according to rows or columns, which is denoted as $A$. Using the sequence $X$ generated by the dual time-delay chaotic system, the following operations are conducted:

1. Intercept $M \times N$ numbers at the given position parameter $d$, $X$, and form $\{ {x_i}, i = 1, 2, \cdots, MN\}$; the respective element of $\{ {x_i}\}$ is rounded by Eq (5.1).

2. Arrange $\{ {x_i}\}$according to an ascending order and remove the repetitions, substract the set $\{ 1, 2, 3, \cdots, MN\}$, and arrange the achieved results in an ascending order and add to the end of $\{ {x_i}\}$.

3. Exchange the positions of $A({x_i})$ and $A({x_{MN - i + 1}})$. After the scrambling operation, the vector after scrambling is expressed as ${P_{SR}}$.

Next, the pseudo-random sequence $X$ is used to diffuse the image matrix which is scrambled from original image. The diffusion operation of the scrambled image matrix is carried out using Eq (5.2), and the inverse operation is Eq (5.3). In this way, the scrambling and diffusion operations are completed.

In general, the encryption algorithm can be summarized below:

5.1.3.   Decryption method

For the decryption process, it can be regarded as the inverse process of encryption, as presented below:

5.2.   Analysis of experimental results and algorithm performance

The Lena color image with a size of $512 \times 512 \times 3$ serves as a test object to validate the algorithm. The dual time-delay Lorenz system above is used to produce pseudo-random sequences to encrypt and decrypt the image. The number of sequence elements produced by the dual time-delay chaotic system is significantly higher than the size number of the color image, and these elements are used for fixed storage. A certain number of elements is intercepted according to the positional parameters in the sequence and participated in the scrambling and diffusion operations. The parameters and initial values of the dual time-delay Lorenz system are $a = 10$, $b = - 4$, $c = 2.5$, ${\tau _1} = 0.1521$, ${\tau _2} = 0.29$, $x(t) = 1$, $y(t) = 2$, $z(t) = 3$, respectively. At this time, the dynamic behavior of the double delays chaotic system is highly complex, and it is in a chaotic state. After 300 points of the generated sequence, a random sequence is taken, so the position parameter $d \ge 300$. The encryption algorithm's performance is evaluated using histogram analysis, correlation coefficient analysis of adjacent pixels, keyspace analysis, key sensitivity analysis, NPCR and UACI analysis.

5.2.1.   Histogram

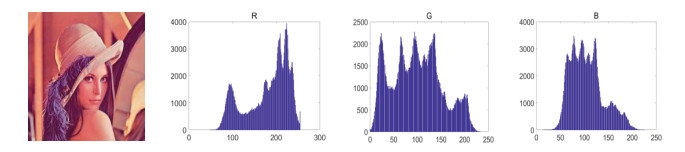
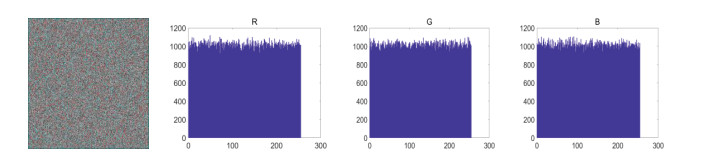
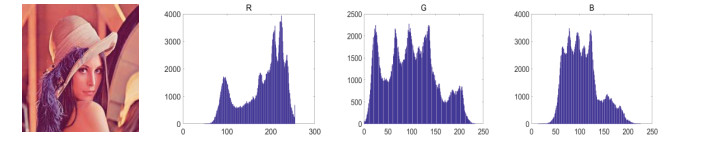
Figure 12 shows the R, G and B pixel histogram of the plaintext image; Figure 13 shows the R, G and B pixel histogram of the encrypted image; Figure 14 illustrates the R, G and B pixel histogram of the decrypted image.

According to Figure 11, the distributions of R, G and B channels' pixel values of the plaintext image show obvious rules of statistics, and the pixel values of the original image have a significant change curve. After scrambling and expansion, the pixel values of ciphertext images are evenly distributed within each grayscale interval (Figure 13), i.e., the frequency of each pixel in the encrypted image is significantly close. Besides, the information of three channels is basically the same, so the attack cannot be carried out with the use of statistical means. According to Figure 14, the distributions of R, G, and B channels' pixel values of the plaintext image are basically the same as those of the image after decryption, which indicates that the decryption effect is high, and the plaintext image can be recovered without being affected by the decryption algorithm. As indicated by the results above, the information of the plaintext image is effectively diffused, and the encryption algorithm can effectively resist statistical attacks.

5.2.2.   Correlation coefficients of adjacent pixels

Pearson correlation coefficient is capable of effectively measuring the dependence of two adjacent sequences in a certain direction. Next, the correlation coefficient of the image before and after encryption will be determined by Eq (5.4):

Where $n(\sum\limits_{i = 1}^n {{x_i}{y_i}}) - (\sum\limits_{i = 1}^n {{x_i}})(\sum\limits_{i = 1}^n {{y_i}})$ denotes the sample variance, $n(\sum\limits_{i = 1}^n {x_i^2}) - {(\sum\limits_{i = 1}^n {{x_i}})^2}$ and $n(\sum\limits_{i = 1}^n {y_i^2}) - {(\sum\limits_{i = 1}^n {{y_i}})^2}$ represent the sample standard deviation of the sequences ${X_j}$ and ${Y_j}$, $(j = 1, 2, \cdots, m - 1)$, respectively. Correlation coefficient $r$ is a critical indicator that reflects the performance of an encryption algorithm. In general, the correlation coefficients between adjacent pixels can be calculated from the horizontal, vertical and diagonal directions using Eq (5.4). When the coefficients are calculated from the horizontal direction, $m$ is the number of rows of the encrypted image; when the coefficients are calculated from the vertical direction, $m$ is the number of columns of the encrypted image; when the coefficients are calculated from the diagonal direction, $m$ is the number of diagonals of the encrypted image. Table 1 lists the calculation results.

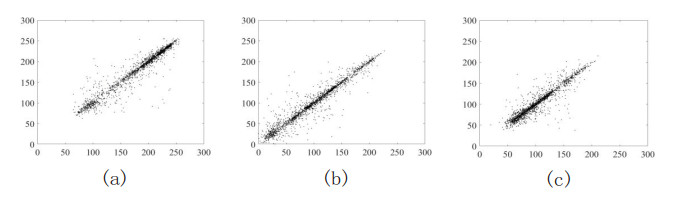
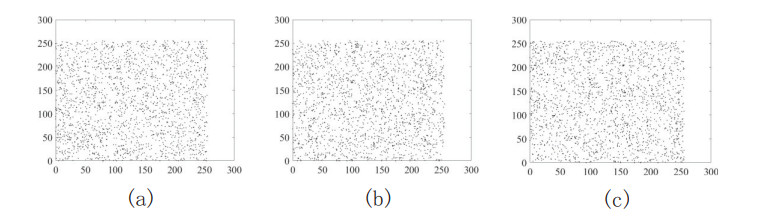
According to Table 1, the correlation coefficients of the encrypted image on vertical, horizontal and diagonal lines approach zero in the implementation of encryption under the mapping of the double time-delays Lorenz system, whereas these results are general. In order to analyze the correlation between any two adjacent pixels more specifically, the correlation between plaintext images and encrypted images in different directions is described using scatter plots. Figure 15 shows the correlation coefficient results of Lena images in the horizontal, vertical and diagonal directions. Figure 14 shows the correlation coefficient results of encrypted images in the horizontal, vertical and diagonal directions.

According to Figure 15, in plaintext images, there is a significant correlation between any two adjacent pixels in different directions. However, according to Figure 16, the correlation between adjacent pixels corresponded by the encrypted image approaches 0. To be specific, the correlation coefficients change from 0.9002, 0.9412 and 0.9423 to 0.0122, 0.0012 and 0.0025, respectively. Thus, the encryption algorithm eliminates the correlation between the adjacent pixels of the plaintext image, so an attacker cannot obtain any information of the plaintext image through correlation analysis.

5.2.3.   Keyspace

The keyspace elements of the encryption and decryption algorithm consist of the parameters of time-delay Lorenz system $a$, $b$, $c$, initial conditions $x(t)$, $y(t)$, $z(t)$, double time-delays ${\tau _1}$, ${\tau _2}$, double time-delays position parameters, as well as position parameters of intercepting sequences. Using MATLAB, 96-bits storage system parameters, initial values and dual time-delays are required, and the rest of keyspace can be stored with 64- bit integer. The position of parameters is the position relation of double time-delays ${\tau _1}$, ${\tau _2}$ in the Lorenz system, and different position relations express a double time-delay chaotic system. As indicated by Eq (4.2), the time-delay parameters can be placed on 8 position vectors, so the position parameter will be $P_8^2$. Moreover, the pseudo-random sequence interception positions are three random values, respectively, representing the positions' value on different vectors. Accordingly, the number of all the combinations of this cryptosystem is significantly higher than 2$^{256}$. This form of encryption algorithm has sufficient keyspace to resist brute force attacks.

5.2.4.   Key sensitivity

Key sensitivity is recognized as another significant indicator to measure the image encryption algorithm's performance. Encryption algorithms with prominent performance should generally be sensitive to keys, so cryptanalysts cannot crack them by repeated trials. The sensitivity here reveals that the decryption algorithm cannot recover the plaintext image or acquire the relevant information of the plaintext image even after a small modification of any element in the keyspace. In other words, only when a completely correct key is employed can the plaintext image be recovered by a decryption algorithm. Figure 17 presents the image (17(b)) obtained by decryption with a correct key, the image (17(c)) obtained by decryption with a wrong time-delay parameter ${\tau _1}$ and the image (17(d)) obtained by intercepting position parameters in the direction of wrong pseudo-random sequence$x$ under the double time-delays ${\tau _1} = 0.1521$, ${\tau _2} = 0.29$.

According to Figures 17(c) and 17(b), when the parameters of the double-time-delay Lorenz system change slightly and other keys are adopted correctly, the decryption algorithm can neither recover and obtain the plaintext image nor acquire any information of the plaintext image. According to Figures 17(d) and 17(c), the decryption algorithm cannot acquire any information of the plaintext image when the position parameters intercepted by the pseudo-random sequence are changed, or other keys remain unchanged. This is because the small changes of system parameters and the changes of sequence interception positions generally cause a completely different chaotic matrix $B$, so the matrix $A$ determined by $A = CB$ is overall inconsistent with the correct scrambling matrix. Thus, the decryption algorithm cannot recover the plaintext image.

5.2.5.   NPCR and UACI

The unified averaged changed intensity (UACI) and The number of changing pixel rate (NPCR) are two indicators applied for measuring the diffusion effect of encryption algorithms. NPCR compares the number of the changed elements in the pixel matrix corresponding to the original image and the encrypted image to ensure that sufficient elements in the pixel matrix are changed, while UACI reflects the average change in the value of pixel of the corresponding position of the plaintext image and the encrypted image. They are defined below respectively:

where,

$A$ denotes the pixel matrix of the plaintext image, with $M$ and $N$ as its number of rows and columns, respectively, and ${A_{SD}}$ represents the pixel matrix of the encrypted image. For two random images, the expected values of NPCR and UACI are 96.6094% and 33.4635%, respectively ^[37]. The NPCR and UACI values of the encrypted image approach their respective expected values, which indicates that the information of the plaintext image is well diffused into the encrypted image. Accordingly, it would be futile for an attacker to attempt to acquire information about the plaintext image through a differential attack.

The NPCR and UACI values of the encrypted image can be calculated according to Eqs (5.5) and (5.6). The calculation results are shown in Table 2.

According to Table 2, the mean NPCR and UACI values of the encrypted image are 99.5905% and 33.0183%, respectively, both of which are significantly close to the expected value. To gain better NPCR and UACI values, we need to only increase the number of columns in the substitution matrix A. At this point, the size of the required chaotic matrix B will increase, so the information of the plaintext image will be better diffused into the encrypted image. Accordingly, the algorithm can resist differential attacks effectively.

5.2.6.   Correlation comparison between adjacent pixels of encrypted images

The degree of reduction in the correlation coefficient between adjacent pixels in encrypted images is an important indicator to measure the security of encryption algorithms. We attempt to demonstrate the security of the proposed algorithm by comparing it with other encryption algorithms. The image encryption schemes involved in the comparison include image encryption schemes ^[37] using multi chaotic systems, image encryption schemes ^[25,38] using bit level scrambling and diffusion, image encryption schemes ^[17] using generalized Arnold mapping, image encryption schemes ^[28] using DNA sequence operation, and image encryption schemes ^[39] using cyclic shift and XOR operation. The correlation coefficients between adjacent pixels in encrypted images under different schemes are shown in Table 3. Specifically, by averaging the correlation coefficients of the pixel matrices in the R, G, and B channels, the correlation coefficient results in each direction can be obtained.

According to Table 3, in the comparison of the correlation coefficients of adjacent pixels, the proposed algorithm has the smallest correlation coefficient in vertical and horizontal directions. In the diagonal direction, besides Zahra's results, the proposed encryption method is capable of reducing the correlation between encrypted image's adjacent pixels. In the three directions, after the average absolute value of the results of all the algorithms is taken, it can be found that the proposed algorithm is the optimal.

The Stanford Cars dataset are used as a test object to verify the encryption efficiency of the algorithm. The Cars dataset contains 16, 185 images of 196 types of vehicles. The specific encryption time is shown in Table 4. According to Table 4, the proposed algorithm has good encryption efficiency in processing large data sets.

6.   Conclusions

In this paper, a safe, reliable and efficient image encryption algorithm is provided using the Lorenz system with double time-delays, since chaotic systems with time delay are infinite dimensional and have more complex dynamic behavior, which is difficult to be simulated by AI technology. The bifurcation condition of the system is analyzed by means of bifurcation study, and the critical value of the bifurcation parameter with time delay is given. When the system enters the chaotic state, the pseudo-random sequence of the system is intercepted, and the color image is encrypted by means of scrambling and diffusion. Through the index analysis, the algorithm has good qualities: simple scheme structure, large key space, low computational complexity, strong resistance to statistical attacks and differential attacks, high key sensitivity, and easy implementation. Although the double time-delays Lorenz system has complex dynamic behavior and can ensure the security of the algorithm by generating chaotic sequences with strong randomness, the generation and calculation of the sequence takes a long time, so the generated sequences of the double time-delays Lorenz system can be stored in advance and then randomly intercepted to achieve real-time encryption.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Some of the authors of this publication are also working on these related projects: Jiangsu Science and Technology Think Tank Youth Talent Program under grant no.2023(JSKJZK2023068).

Conflict of interest

The authors declare there is no conflict of interest.