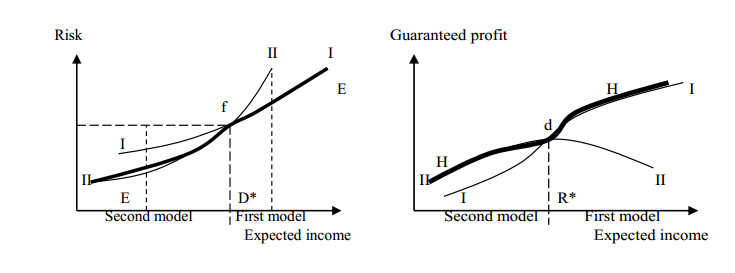
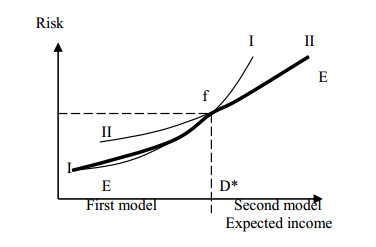
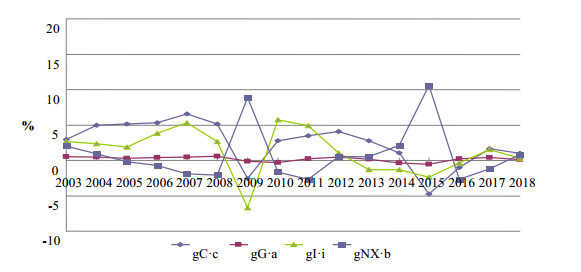
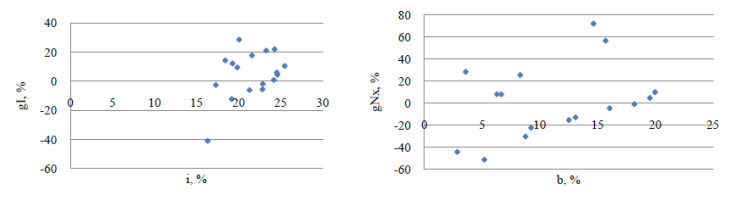
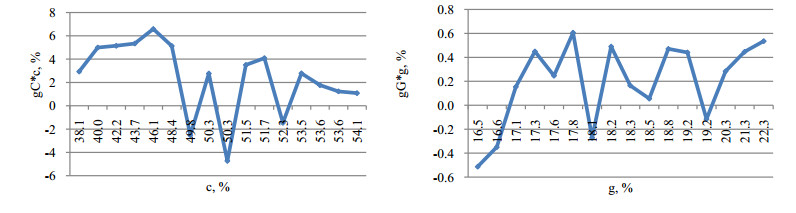
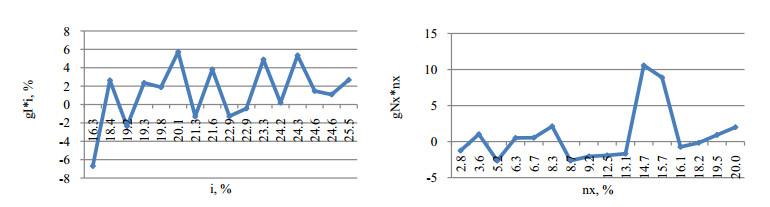
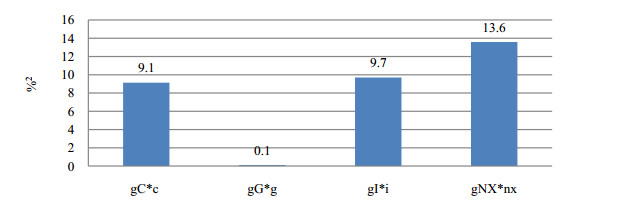
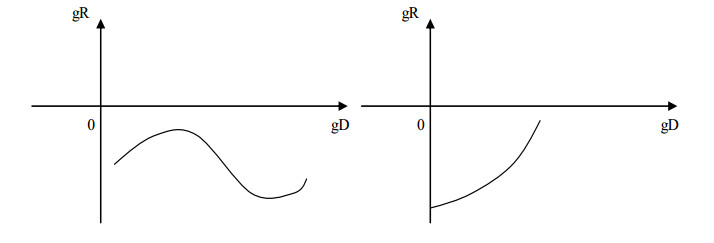
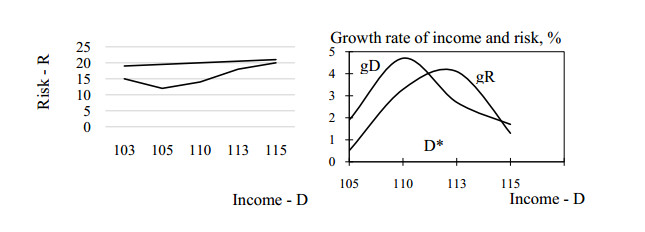
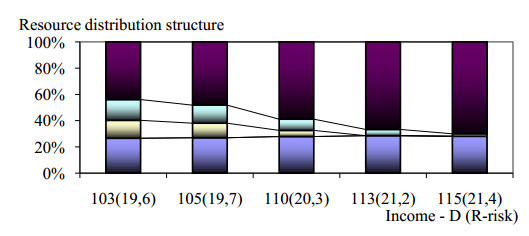
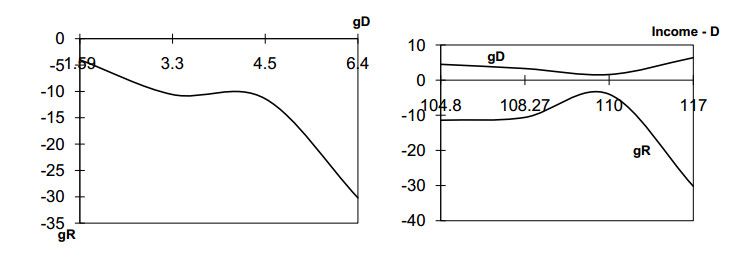
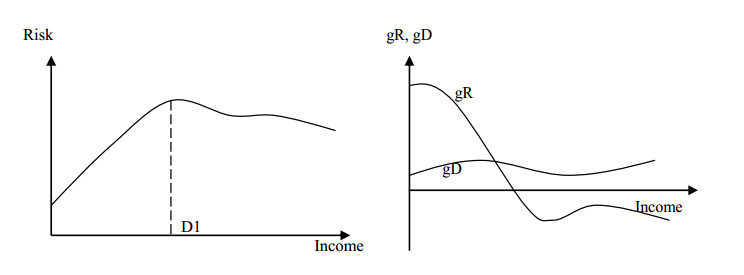
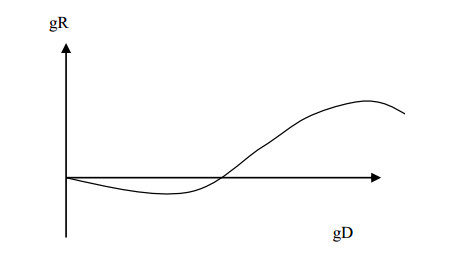
The purpose of the research is to carry out the structural analysis of income and risk dynamics when considering the problem of economic growth, to obtain and apply the structural formula to assess the contribution of GDP elements to growth rate. The methodological basis of the research consists of the theory of economic growth and structural analysis, optimization methods and computer simulation (algorithmization) models of maximizing income and minimizing the total risk of N objects of the economic system. The implementation of the two stages of the research allowed us to establish that for the Russian economy the main contribution to the growth rate in the period 2003–2018 was made by gross consumption, but not by investment spending. The result of computer simulation of optimization models—maximizing income and minimizing risk is that the solution to the problem of structural choice can be an assessment of the dynamics of income and risk at a characteristic point in which different resource allocation structures give the same combination of income and risk. However, the growth rate of income and risk in the characteristic point will certainly be different, and the most acceptable option is to choose the structure that gives a positive growth rate of income and a negative growth rate of risk. This circumstance makes a significant addition to the developed macroeconomic and structural policy measures, which should be oriented not only to some static targets, but also to the impact on the dynamics of the relevant aggregated parameters—income and risk.
1.
Introduction
In this survey we review a PDE approach to the study of fine properties of functions of bounded deformation (BD), which was recently developed by the authors. In particular, we will show how this approach allows to characterize the structure of the singular part of the symmetrized derivative and also to recover some known structure properties of these functions in an easier and more robust way.
Functions of bounded deformation are fundamental in the analysis of a large number of problems from mechanics, most notably in the theory of (linearized) elasto-plasticity, damage, and fracture; we refer to [3,41,49,50,55,70,71,74,75] and the references contained therein. A common feature of these theories is that the natural coercivity of the problem only yields a-priori bounds in the L1-norm of the symmetrized gradient
of a map u:Ω⊂Rd→Rd. As L1 is not reflexive, such L1-norm bounds do not allow for the selection of weakly converging subsequences. This issue is remedied by enlarging L1 to the space of finite Radon measures, where now a uniform bound on the total variation norm permits one to select a weakly* converging subsequence.
Given an open set Ω⊂Rd with Lipschitz boundary, the space BD(Ω) of functions of bounded deformation is then the space of functions u∈L1(Ω;Rd) such that the distributional symmetrized derivative
is (representable as) a finite Radon measure, Eu∈M(Ω;Rd×dsym), where Rd×dsym denotes the space of d×d symmetric matrices. The space BD(Ω) of functions of bounded deformation is a (non-reflexive) Banach space under the norm
where |Eu| denotes the total variation measure of Eu.
One particularly important feature of BD-maps is that the symmetrized derivative Eu may contain a singular part, i.e., a measure that is not absolutely continuous with respect to Lebesgue measure. This may, for instance, correspond to concentrations of strain in the model under investigation. As we will show in the sequel, the allowed "shapes" of these concentrations are quite restricted, merely due to the fact that they occur in a symmetrized gradient. These rigidity considerations play a prominent role in the analysis of a model, for instance, in the integral representation and lower semicontinuity theory for functionals defined on BD and in the characterization of Young measures generated by symmetrized gradients.
1.1. Fine structure results
The study of the fine structure of BD-maps started in the PhD thesis of Kohn [49], and was then systematically carried out by Ambrosio–Coscia–Dal Maso in [3]; further recent results on the fine properties of BD can be found in [10,22,43,68] and the references therein. Classically, the analysis of the space BD(Ω) has been modelled on the analysis of the space of functions of bounded variation, BV(Ω;Rℓ), i.e., those functions u∈L1(Ω;Rℓ) such that the distributional derivative Du can be represented as a finite Borel measure, Du∈M(Ω;Rℓ×d), where Rℓ×d is the space of ℓ×d matrices. The theory of BV-maps in multiple dimensions goes back to De Giorgi [23] and has become a fundamental tool in the Calculus of Variations and in Geometric Measure Theory.
Starting from the seminal works of Federer, [33], we now have a complete understanding of the fine structure of BV-maps, which we summarize in the following, see [5] for details and proofs. For a vector Radon measure μ∈M(Rd;Rn) we write μ=μa+μs for its Lebesgue–Radon–Nikodým decomposition with respect to Lebesgue measure. Denoting by |μ| the total variation measure of μ, we call
the polar vector, whose existence for |μ|-almost every x is ensured by the Besicovitch differentiation theorem (see [5,Theorem 2.22]). We then have the following (amalgamated) structure result in BV:
Theorem 1.1. For u∈BVloc(Rd;Rℓ), we can decompose Du as
Here:
(i) Dau=∇uLd is the absolutely continuous part of Du (with respect to Lebesgue measure). Its density ∇u∈L1loc(Ω;Rℓ×d) is the approximate gradient of u, which satisfies for Ld-almost every x that
(ii) Dju is the jump part of Du. It is concentrated on a countably rectifiable Hd−1 σ-finite set Ju, where it can be represented as
Here, νJu is normal to Ju and u± are the traces of u on Ju in positive and negative νJu-direction, respectively (note that the product (u+−u−)⊗νJu does not depend on the choice of the orientation), and (a⊗b)ij:=aibj is the tensor product of the vectors a and b.
(iii) Dcu is the Cantor part of Du. It vanishes on every Hd−1 σ-finite set. Furtheremore, for |Dcu|-almost all x there are a(x)∈Rℓ and b(x)∈Rd such that
In particular, |Du|≪Hd−1, that is, |Du| is absolutely continuous with respect to the (d−1)-dimensional Hausdorff measure Hd−1. Furthermore, if one denotes by Cu the set of approximate continuity points of u, i.e., those x for which there exists a λ(x)∈Rℓ such that
and by Su:=Rd∖Cu the set of approximate discontinuity points, then
The above structural results are fundamental in the study of many variational problems involving functions of bounded variation. In particular, (ⅲ) above is known as Alberti's rank-one theorem, a key structural result for BV-maps first proved in [1] (see also [54] for a recent, more streamlined proof). It entails strong constraints on the type of possible singularities for Du, see Corollary 3.1 below.
The proofs of all these properties of BV-maps rely heavily on the connection between functions of bounded variation and sets of finite perimeter and on the fine properties of such sets [5,53]. This link is expressed by the Fleming–Rishel coarea formula [34]: For all u:Rd→R it holds that
where both equalities are to be understood in the sense of measures.
Clearly, BV⊂BD, but it has been known since the work of Ornstein [61] that the inclusion is strict (however, see [18,22,38,39] for interesting recent results on partial converses under additional assumptions). More precisely, one can show that for all N∈N there exists a map u∈W1,∞0(B1;Rd) (where B1:=B1(0) is the unit ball in Rd) such that
see [20,48,61] and also [67,Theorem 9.26]. This implies that a Korn inequality of the form
fails for p = 1 (while it is true for all p\in (1, +\infty), see [74]). Furthermore, no analogue of the coarea formula is known in \mathrm{BD} and this prevents the application of several techniques used to establish Theorem 1.1. Nevertheless, several results have been obtained and the analogues of the first two points of Theorem 1.1 have been known for many years [3,49]:
Theorem 1.2. For u\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) we can decompose Eu as
Here:
(i) E^a u = \mathcal{E} u \, \mathcal{L}^d is the absolutely continuous part of Eu. Its density \mathcal{E} u\in \mathrm{L}^1_ \mathrm{loc}(\Omega; \mathbb{R}^{d \times d}_\mathrm{sym}) is the approximate symmetrized gradient of u, which satisfies for \mathcal{L}^d-almost every x that
(ii) E^j u is the jump part of Eu. It is concentrated on a countably rectifiable \mathcal{H}^{d-1} \sigma-finite set J_u, where it can be represented as
Here, \nu_{J_u} is normal to J_u and u^\pm are the traces of u on J_u in positive and negative \nu_{J_u}-direction, respectively, and (a\odot b)_{ij}: = \frac{1}{2}(a \otimes b + b \otimes a) is the symmetric tensor product of the vectors a, b .
(iii) E^c u is the Cantor part of Eu. It vanishes on every \mathcal{H}^{d-1} \sigma-finite set.
In particular, |E u|\ll \mathcal{H}^{d-1}.
Concerning the trace, we remark that there exist two bounded linear trace operators onto \mathcal{H}^{d-1} -rectifiable sets, giving the one-sided traces u^\pm , see Theorem II.2.1 of [75] and also [10,16].
Despite the clear similarity between Theorem 1.1 and Theorem 1.2, some parts are missing. The analogue of the first statement in (1.1) is currently unknown and only partial results are available. This is one of the major open problems in the theory of BD-maps:
Conjecture 1.3. For all u\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) it holds that \mathcal{H}^{d-1}(S_u\setminus J_u) = 0 .
We remark that the following weaker statement was proved in [3]: If u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) , then |Ev|(S_u \setminus J_u) = 0 for all v \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) ; in particular, |E^s u|(S_u \setminus J_u) = 0 .
On the other hand, the analogue of Alberti's rank-one theorem has recently been established by the authors [28]:
Theorem 1.4. Let u\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d). Then, for |E^s u|-almost every x there are vectors a(x), b(x) \in \mathbb{R}^d such that
Note that for the jump part the above theorem is already contained in Theorem 1.2 (ii) and the real difficulty lies in dealing with the Cantor part of Eu. Like Alberti's rank one theorem, Theorem 1.4 allows to deduce some quite precise information on the structure of the singularities of Eu, see Section 3.2 below. The picture is however still less complete than in the BV-case, see Conjecture 3.4.
1.2. A new approach to study singularities
The failure of a coarea-type formula makes the approach used in [3] unsuitable for the proof of Theorem 1.4. The strategy followed in [28] is instead based on a new point of view combining Harmonic Analysis techniques with some tools from Geometric Measure Theory. This approach is heavily inspired by the ideas of Murat and Tartar in the study of compensated compactness [59,60,72,73] and has been introduced in this context for the first time in the PhD thesis of the second author [63].
The core idea is to "forget" about the map u itself and to work with Eu only. This is enabled by the fact that symmetrized derivatives are not arbitrary measures (with values in \mathbb{R}^{d \times d}_\mathrm{sym} ), but that they satisfy a PDE constraint, namely the Saint-Venant compatibility conditions: If the measure \mu = (\mu_{jk}) is the symmetrized derivative of some u\in \mathrm{BD}(\Omega) , i.e., \mu = Eu , then, by direct computation,
For d = 3 this constraint can be written as the vanishing of a double application of the matrix-curl, defined as the matrix-valued differential operator
where \epsilon_{ilk} denotes the parity of the permutation \{1, 2, 3\}\to\{i, l, k\} . Hence, we will write the above equations (for all dimensions) in shortened form as
and say that \mu is " {\rm Curl}~{\rm Curl}~ -free". This PDE-constraint furthermore contains all the information about symmetrized derivatives, as {\rm Curl}~{\rm Curl}~ -freeness is both necessary and sufficient for a measure to be a BD-derivative locally, this is (a modern version of) the Saint-Venant theorem, see for instance [6].
Once this point of view is adopted, it is then natural to try to understand the structure of the singular part of PDE-constrained measures. More precisely, given a linear homogeneous operator
where A_\alpha \in \mathbb{R}^{m\times n}, \alpha = (\alpha_1, \ldots, \alpha_d) \in (\mathbb{N} \cup \{0\})^d is a multi-index, and \partial^\alpha: = \partial^{\alpha_1}_1\cdots\partial^{\alpha_d}_d, we say that an \mathbb{R}^n-valued (local) Radon measure \mu\in \mathcal{M}_ \mathrm{loc}(\Omega; \mathbb{R}^n) is \mathcal{A}-free if it satisfies
Note that since A_\alpha \in \mathbb{R}^{m\times n} this is actually a system of equations. A natural question is then to investigate the restrictions imposed on the singular part \mu^s of \mu by the differential constraint.
To answer to this question, we first note that there are two trivial instances: If \mathcal{A} = 0, then no constraint is imposed. Conversely, if \mathcal{A} is elliptic, i.e., if its symbol
is injective, then by the generalized Weyl lemma, \mu is smooth and thus no singular part is possible.
In view of the above considerations it is natural to conjecture that the presence of singularities is related to the failure of ellipticity. This failure is measured by the wave cone associated to \mathcal{A}, first introduced by Murat and Tartar in the context of compensated compactness [59,60,72,73]:
The main result of [28] asserts that this cone is precisely what constrains the singular part of \mu, see also [26] and the surveys [25,30] for other applications of these results.
Theorem 1.5. Let \mu\in \mathcal{M}(\Omega; \mathbb{R}^n) be an \mathcal{A}-free measure, i.e.,
Then, for |\mu^s|-almost all x,
In the case \mathcal{A} = {\rm Curl}~{\rm Curl}~ we obtain by direct computation, see [37,Example 3.10(e)], that for M\in \mathbb{R}^{d \times d}_\mathrm{sym} , \xi \in \mathbb{R}^d ,
which gives
Thus,
Hence, Theorem 1.5 implies Theorem 1.4. We remark that in the two-dimensional case \mu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^2; \mathbb{R}^{2 \times 2}) we moreover have
where {\rm curl}~ \, (\nu_1, \nu_2) : = \partial_2 \nu_1 - \partial_1 \nu_2 is the classical (scalar-valued) curl in two dimensions, applied row-wise.
Note also that if \mathcal{A} \colon \mathbb{R}^{\ell\times d} \to \mathbb{R}^{\ell\times d \times d} is the d-dimensional row-wise {\rm curl}~-operator defined via
one easily computes that
Hence, Theorem 1.5 also provides a new proof of Alberti's rank one theorem.
Furthermore, we mention that in [7] similar (more refined) techniques were used to recover the dimensional estimates and rectifiability results on the jump parts of BV- and BD-maps; we will discuss these results in Section 3.3.
1.3. Outline of the paper
In Section 2 we start by showing some rigidity statements for maps whose symmetrized gradient is constrained to lie in a certain set. Parts of these result will be used later, but most importantly, we believe that they will give the reader a feel for how the differential constraint characterizing Eu can be used to understand BD-maps. In Section 3 we give a sketch of the proof of Theorem 1.4 and we outline how the improvements in [7] give (optimal) dimensionality and rectifiability estimates. We also investigate the implications of Theorem 1.4 on the structure of singularities of \mathrm{BD} -maps. Finally, in Section 4 we present, mostly without proofs, some applications of the above results to the study of weak* lower semicontinuity of integral functionals, relaxation, and the characterization of Young measures generated by sequences of symmetrized gradients.
2.
Rigidity
Before we come to more involved properties of general \mathrm{BD} -maps, we first investigate what can be inferred by using only elementary rigidity arguments. Besides being useful in the next section, these arguments are also instructive since they show the interplay between the {\rm Curl}~{\rm Curl}~-free condition and some pointwise properties, which is the main theme of this survey. Furthermore, the rigidity theorem, Theorem 2.10, will be used to study tangent measures later. Much of the discussion follows [64,Section 4.4]. To make some proofs more transparent we start presenting the results in the two-dimensional case, where, however, all interesting effects are already present. At the end of the section we deal with the general case.
A rigid deformation is a skew-symmetric affine map \omega \colon \mathbb{R}^d \to \mathbb{R}^d , i.e., u is of the form
The following lemma is well-known and will be used many times in the sequel, usually without mentioning. We reproduce its proof here because the central formula (2.1) will be of use later.
Lemma 2.1. The kernel of the linear operator E \colon \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) \to \mathcal{M}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}_ \mathrm{sym}^{d \times d}) given by
is the space of rigid deformations.
Proof. It is obvious that E u vanishes for a rigid deformation u . For the other direction, let u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) with Eu = 0 . Define
Then, for all i, j, k = 1, \ldots, d , we have, in the sense of distributions,
As Du = Eu + Wu , this entails that Du is a constant, hence u is affine, and it is clear that it in fact must be a rigid deformation.
It is an easy consequence of the previous lemma that any u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) with Eu = S \mathcal{L}^d , where S \in \mathbb{R}_ \mathrm{sym}^{d \times d} is a fixed symmetric matrix, is an affine function. More precisely, u(x) = u_0 + (S+\Xi)x for some u_0 \in \mathbb{R}^d and \Xi \in \mathbb{R}_ \mathrm{skew}^{d \times d} .
Next, we will consider what can be said about maps u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) for which
with a fixed matrix P \in \mathbb{R}^{d \times d}_\mathrm{sym} and a measure \nu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}). As we already saw in (1.4), a special role is played by the symmetric rank-one matrices, a \odot b for a, b \in \mathbb{R}^d . We recall that those matrices can be characterized in terms of their eigenvalues:
Lemma 2.2. Let M \in \mathbb{R}_ \mathrm{sym}^{d \times d} be a non-zero symmetric matrix.
(i) If {\rm rank}~ M = 1 , then M = \pm a \odot a = \pm a \otimes a for a vector a \in \mathbb{R}^d .
(ii) If {\rm rank}~ M = 2 , then M = a \odot b for vectors a, b \in \mathbb{R}^d if and only if the two (non-zero, real) eigenvalues of M have opposite signs.
(iii) If {\rm rank}~ M \geq 3 , then M cannot be written as M = a \odot b for any vectors a, b \in \mathbb{R}^d .
Proof. Ad (i). Every rank-one matrix M can be written as a tensor product M = c \otimes d for some vectors c, d \in \mathbb{R}^d \setminus \{0\} . By the symmetry, we get c_i d_j = c_j d_i for all i, j \in \{1, \ldots, d\} , which implies that the vectors c and d are multiples of each other. We therefore find a \in \mathbb{R}^d with M = \pm a \otimes a .
Ad (ii). Assume first that M = a \odot b for some vectors a, b \in \mathbb{R}^d . Clearly, M maps {\rm span}~\{a, b\} to itself and it is the zero map on the orthogonal complement, hence we may assume that d = 2.
Take an orthogonal matrix Q \in \mathbb{R}^{2 \times 2} such that QMQ^T is diagonal. We compute
whence we may always assume without loss of generality that M is already diagonal,
where \lambda_1, \lambda_2 \neq 0 are the two eigenvalues of M . Writing this out componentwise, we get
As \lambda_1, \lambda_2 \neq 0 , also a_1, a_2, b_1, b_2 \neq 0 , and hence
Thus, \lambda_1 and \lambda_2 must have opposite signs.
For the other direction, by transforming as before we may assume again that M is diagonal:
where \{v_i\}_i is an orthonormal basis of \mathbb{R}^d. Since {\rm rank}~ M = 2 , we know that only two of the \lambda_i are non-zero. Hence, we can assume d = 2 and M to be diagonal, M = \bigl(\begin{smallmatrix} \lambda_1 & \\ & \lambda_2 \end{smallmatrix} \bigr) , and that \lambda_1 and \lambda_2 do not have the same sign. Then, with \gamma : = \sqrt{-\lambda_1/\lambda_2} , we define
For \lambda_1 > 0 , \lambda_2 < 0 say (the other case is analogous),
and therefore
This proves the claim.
Ad (iii). This is trivial.
In the remainder of this section, we will investigate in more detail two-dimensional BD-maps with fixed polar. First, note that if u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) , the map \tilde u(x): = Q^{T}u(Qx), where Q\in \mathbb{R}^{d\times d}, satisfies
Hence, without loss of generality we may assume that P in (2.2) is diagonal.
In the case d = 2 , according to Lemma 2.2 we have three non-trivial cases to take care of, corresponding to the signs of the eigenvalues \lambda_1 , \lambda_2 ; the trivial case \lambda_1 = \lambda_2 = 0 , i.e., P = 0 , was already settled in Lemma 2.1.
First, consider the situation that \lambda_1, \lambda_2 \neq 0 and that these two eigenvalues have opposite signs. Then, from (the proof of) Lemma 2.2, we know that P = a \odot b ( a \neq b ) for
The result about solvability of (2.2) for this choice of P is:
Proposition 2.3 (Rigidity for P = a \odot b ). Let P = \bigl(\begin{smallmatrix} \lambda_1 & \\ & \lambda_2 \end{smallmatrix} \bigr) = a \odot b , where \lambda_1, \lambda_2 \in \mathbb{R} have opposite signs. Then, there exists a map u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^2) solving the differential equation
if and only if \nu is of the form
where \mu_1, \mu_2 \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}) . In this case,
with \omega a rigid deformation and H_1, H_2 \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) satisfying H_1' = \mu_1 and H_2' = \mu_2 .
Here, the notation \mu_1(\mathrm{d} x \cdot a) denotes the measure \gamma \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^2) that acts on Borel sets B \subset \mathbb{R}^2 as
where a^\perp is a unit vector with a \cdot a^\perp = 0 (which is unique up to orientation). Likewise for \mu_2(\mathrm{d} x \cdot b) . Notice also that, since a and b are linearly independent, we could absorb the rigid deformation r into H_1 and H_2 .
Proof. By the chain rule in \mathrm{BV} (see [5,Theorem 3.96]), it is easy to deduce that all u of the form (2.3) satisfy (2.2) with P = a \odot b , that is, Eu = P\nu with \nu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^2; \mathbb{R}) .
For the other direction, we choose Q to be an invertible matrix sending \{ \mathrm{e}_1, \mathrm{e}_2\} to \{a, b\} and instead of u work with \tilde u(x): = Q^{T}u(Qx) , for which
with \tilde{\nu} \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^2; \mathbb{R}) . In the following we write simply u in place of \tilde{u} .
We will use a slicing result [3,Proposition 3.2], which essentially follows from Fubini's theorem: If for \xi \in \mathbb{R}^2 \setminus \{0\} we define
then the result in loc. cit. states
We have Eu = \sqrt{2} (\mathrm{e}_1 \odot \mathrm{e}_2) \nu , so if we apply (2.4) for \xi = \mathrm{e}_1 , we get
where we wrote u = (u_1, u_2) . This yields \partial_1 u_1 = 0 distributionally, whence u_1(x) = H_2(x_2) for some H_2 \in \mathrm{L}_ \mathrm{loc}^1(\mathbb{R}) . Analogously, we find that u_2(x) = H_1(x_1) with H_1 \in \mathrm{L}_ \mathrm{loc}^1(\mathbb{R}) . Thus, we may decompose
and it only remains to show that H_1, H_2 \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) . For this, fix \eta \in \mathrm{C}_c^1(\mathbb{R}; [-1, 1]) with \int \eta \; \mathrm{d} t = 1 and calculate for all \varphi \in \mathrm{C}_c^1(\mathbb{R}; [-1, 1]) by Fubini's Theorem,
So, with K : = {\rm supp}~ \varphi \times {\rm supp}~ \eta ,
for all \varphi \in \mathrm{C}_c^1(\mathbb{R}) with \|{ \varphi}\|_\infty \leq 1 , hence H_1 \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) . Likewise, H_2 \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) , and we have shown the proposition.
In the case \lambda_1 \neq 0 , \lambda_2 = 0 , i.e., P = \lambda_1 (\mathrm{e}_1 \odot \mathrm{e}_1) , one could guess by analogy to the previous case that if u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^2) satisfies Eu = P\nu for some \nu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}) , then u and \nu should only depend on x_1 up to a rigid deformation. This, however, is false, as can be seen from the following example.
Example 2.4. Consider
Then, u satisfies E u = Pg \, \mathcal{L}^d , but neither u nor g only depend on x_1 .
The general statement reads as follows.
Proposition 2.5 (Rigidity for P = a \odot a ). Let P = \bigl(\begin{smallmatrix} \lambda_1 & \\ & 0 \end{smallmatrix} \bigr) = \lambda_1 (\mathrm{e}_1 \odot \mathrm{e}_1) . Then, there exists a map u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^2) solving the differential equation
if and only if \nu is of the form
where \mu, \gamma\in \mathcal{M}_ \mathrm{loc}(\mathbb{R}) . In this case,
with \omega a rigid deformation and H \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) , \mathcal{P} \in \mathrm{W}^{1, \infty}_ \mathrm{loc}(\mathbb{R}) with \mathcal{P}' \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) satisfying H' = \mu and \mathcal{P}" = \gamma .
Proof. The necessity is again a simple computation.
For the sufficiency, assuming by a mollification argument that u is smooth, there exists g \in \mathrm{C}^\infty(\mathbb{R}^2) such that
We have from (2.1) that
Thus,
This gives that (W u)_{12} and hence also \partial_2 g depend on the first component x_1 of x only, \partial_2 g(x) = p(x_1) say. Define
and observe that \partial_2 h = 0 . Hence we may write h(x) = h(x_1) and have now decomposed g as
This gives the claimed decomposition in the smooth case. The general case follows by approximation.
Finally, we consider the case where the eigenvalues \lambda_1 and \lambda_2 are non-zero and have the same sign. Then, P \neq a \odot b for any a, b \in \mathbb{R}^2 by Lemma 2.2. Define the differential operator
and notice that whenever a function g \colon \mathbb{R}^2 \to \mathbb{R} satisfies \mathcal{A}_P g = 0 distributionally, the function \tilde g(x_1, x_2): = g(\sqrt{|{\lambda_2}|} x_1, \sqrt{|{\lambda_1}| }x_2) is harmonic (recall that \lambda_1, \lambda_2 have the same sign). In particular, by Weyl's lemma, g is smooth.
Proposition 2.6 (Rigidity for P \neq a \odot b ). Let P = \bigl(\begin{smallmatrix} \lambda_1 & \\ & \lambda_2 \end{smallmatrix} \bigr) , where \lambda_1, \lambda_2 \in \mathbb{R} have the same sign. Then, there exists a map u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^2) solving the differential equation
if and only if \nu satisfies
Moreover, in this case both \nu and u are smooth.
Proof. First assume that g \in \mathrm{C}^\infty(\mathbb{R}^2) satisfies \mathcal{A}_P g = 0 . Define
and observe
Hence, there exists f \in \mathrm{C}^\infty(\mathbb{R}^2) with \nabla f = F , in particular
Put
We calculate (we apply the curl row-wise), using (2.5),
Let u \in \mathrm{C}^\infty(\mathbb{R}^2; \mathbb{R}^2) be such that \nabla u = \mathcal{U} . Then, as distributions, E u = P g .
For the other direction, it suffices to show that Eu = P\nu for some \nu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^2) implies \mathcal{A}_P \nu = 0 . The smoothness of u, \nu then follows from Weyl's lemma as remarked above. Since d = 2 we can exploit (1.5) to get that
so that the claim follows.
Remark 2.7. Note that the key point in the above lemma is that whenever Eu = P\nu with P\ne a\odot b for any a, b \in \mathbb{R}^2 , the fact that Eu is {\rm curl}~{\rm curl}~-free implies that the measure \nu is actually a solution of an elliptic PDE, namely (2.6). This is also the key fact underlying the proof of Theorem 1.4 in the next section.
Remark 2.8 (Comparison to gradients). Proposition 2.6 should be contrasted with the corresponding situation for gradients. If u \in \mathrm{W}_ \mathrm{loc}^{1, 1}(\mathbb{R}^2; \mathbb{R}^2) satisfies
and {\rm rank}~ P = 2 , then necessarily u is affine, a proof of which can be found, for instance, in [65,Lemma 3.2] (this rigidity result is closely related to Hadamard's jump condition, also see [11,Proposition 2], [24,Lemma 1.4], [58,Lemma 2.7] for related results). Notice that this behavior for the gradient is in sharp contrast to the behavior for the symmetrized gradient, as can be seen from the following example.
Example 2.9. Let
Then, one can check that g is harmonic (corresponding to \mathcal{A}_P g = \Delta g = 0 ) and u satisfies \mathcal{E} u = Pg . So, the fact that P cannot be written as a symmetric tensor product does not imply that any solution to the differential inclusion \mathcal{E} u \in {\rm span}~ \{P\} must be affine. However, as noted in Remark 2.7, g is still "rigid" (in a weaker sense) since it has to satisfy an elliptic PDE.
We conclude this section with the following general version of the rigidity statements in every dimension; the proofs of (ⅰ), (ⅱ) follow the same (elementary) strategy as above, whereas in (ⅲ) we see the first instance of an approach via the Fourier transform.
Theorem 2.10. Let u\in \mathrm{BD}_ \mathrm{loc} (\mathbb{R}^d) and assume that
for a fixed matrix P \in \mathbb{R}^{d \times d}_\mathrm{sym} and a (signed) measure \nu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}) . Then:
(i) If P = a \odot b for some a, b \in \mathbb{R}^d with a \ne \pm b, then there exist two functions H_1, H_2\in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}), a vector v \in {\rm span}~\{a, b\}^\perp, and a rigid deformation \omega such that
(ii) If P = \pm a \odot a for some a \in \mathbb{R}^d , then there exist a function H\in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}), an orthonormal basis \{v_2, \ldots, v_j\} of {\rm span}~\{a\}^\perp, functions \mathcal{P}_j\in \mathrm{W}^{1, \infty}_ \mathrm{loc}(\mathbb{R}) with \mathcal{P}'_j\in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) ( j = 2, \ldots, d ), and a rigid deformation \omega such that
(iii) If P \neq a \odot b for any a, b \in \mathbb{R}^d , then u and \nu are smooth.
Proof. Ad (i). By regularization we can assume that u is smooth and that
Recall from (2.1) that for Wu : = \frac{1}{2} (Du - Du^T) we have
We assume without loss of generality that a = \mathrm{e}_1 and b = \mathrm{e}_2. Then,
From this we readily deduce that \partial_j g = \mathrm{const} for j = 3, \ldots, d and, applying the curl to the first equation, that
Hence, we can write
where h_1, h_2 \in \mathrm{C}^\infty(\mathbb{R}) and v is orthogonal to {\rm span}~\{ \mathrm{e}_1, \mathrm{e}_2\}.
We may compute that for the u given in (ⅰ) with H_i defined via H_i' = h_i , i = 1, 2 (the shift of H_i is arbitrary and can later be absorbed into the rigid deformation r ) and a : = \mathrm{e}_1 , b : = \mathrm{e}_2 , we have that \mathcal{E} u = 2(a\odot b) g with the g above. Thus, by Lemma 2.1, we conclude that our u must have this form (we absorb a rigid deformation into \omega ).
Ad (ii). We assume that P = \mathrm{e}_1 \odot \mathrm{e}_1 and we argue as above to deduce that
and \nabla (Wu)_{ij} = 0 if i, j \geq 2. This implies that
for suitable functions p_j \in \mathrm{C}^\infty(\mathbb{R}). Hence,
for some h \in \mathrm{C}^\infty(\mathbb{R}) . Again, defining H via H' = h and \mathcal{P}_j via \mathcal{P}_j'' = p_j , we obtain for the u given in (ⅱ) that \mathcal{E} u = 2(\mathrm{e}_1 \odot \mathrm{e}_1)g with g as above. We conclude as before via Lemma 2.1.
Ad (iii). Let L : = {\rm span}~\{P\} and denote by \mathbf{P} \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R}^{d \times d}_\mathrm{sym} the orthogonal projection onto the orthogonal complement L^\perp of L . For every smooth cut-off function \rho \in \mathrm{C}^\infty_c(\mathbb{R}^d; [0, 1]) with \rho \equiv 1 on a bounded open set U \subset \mathbb{R}^d , the function w : = \rho u satisfies
So,
with p = d/(d-1) by the embedding \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) \hookrightarrow \mathrm{L}^{d/(d-1)}_ \mathrm{loc}(\Omega; \mathbb{R}^d) [75].
Applying the Fourier transform (which we define for an integrable function w via \hat{w}(\xi) : = \int w(x) \mathrm{e}^{2\pi \mathrm{i} x \cdot \xi} \; \mathrm{d} x ) to both sides of (2.9) and considering \mathbf{P} to be identified with its complexification (that is, \mathbf{P}(A+ \mathrm{i} B) = \mathbf{P}(A) + \mathrm{i} \mathbf{P}(B) for A, B \in \mathbb{R}^{d \times d}_\mathrm{sym} ), we arrive at
Here, we used that for a symmetrized gradient one has
The main point is to show (see below) that we may "invert" \mathbf{P} in the sense that if
for some w \in \mathrm{W}^{1, p}(\mathbb{R}^d; \mathbb{R}^m) , R \in \mathrm{L}^p(\mathbb{R}^d; L^\perp) , then
for some family of linear operators \mathbf{M}(\xi) \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R}^{d \times d}_\mathrm{sym} that depend smoothly and positively 0 -homogeneously on \xi .
We then infer from the Mihlin multiplier theorem (see for instance [44,Theorem 5.2.7]) that
So, also using \rho \mathcal{E} u = \mathcal{E} w - u \odot \nabla \rho , we get the estimate
for some constant C > 0 . In particular, by Korn's inequality (1.2), u \in \mathrm{W}_ \mathrm{loc}^{1, p}(\Omega; \mathbb{R}^d) \subset \mathrm{L}^{p^*}(\Omega; \mathbb{R}^d) for p^* : = dp/(d-p) if d < p and p^* = \infty if p > d ). We can now iterate ("bootstrap") via (2.9) (which we also need to differentiate in order to get bounds on derivatives) to conclude that u is smooth.
It remains to show (2.11). Notice that \mathbf{P}(a \odot \xi) \neq 0 for any a \in \mathbb{C}^m \setminus \{0\} , \xi \in \mathbb{R}^d \setminus \{0\} by the assumption on P. Thus, for some constant C > 0 we have the ellipticity estimate
The (complexified) projection \mathbf{P} \colon \mathbb{C}^{m \times d} \to \mathbb{C}^{m \times d} has kernel L^{ \mathbb{C}} : = {\rm span}~_{ \mathbb{C}} L (the complex span of L ), which in the following we also denote just by L . Hence, \mathbf{P} descends to the quotient
and [\mathbf{P}] is an invertible linear map. For \xi \in \mathbb{R}^d \setminus \{0\} let
be a \mathbb{C} -basis of \mathbb{C}^{m \times d} with the property that the matrices G_{d+1}(\xi), \ldots, G_{d^2-1}(\xi) depend smoothly on \xi and are positively 1 -homogeneous in \xi , that is, G_{d+1}(\alpha \xi) = \alpha G_{d+1}(\xi) for all \alpha \geq 0 . Furthermore, for \xi \in \mathbb{R}^d \setminus \{0\} denote by \mathbf{Q}(\xi) \colon \mathbb{C}^{m \times d} \to \mathbb{C}^{m \times d} the (non-orthogonal) projection with
If we interpret \mathrm{e}_1 \odot \xi, \ldots, \mathrm{e}_d \odot \xi, G_{d+1}(\xi), \ldots, G_{d^2-1}(\xi) as vectors in \mathbb{R}^{d^2} and collect them into the columns of the matrix X(\xi) \in \mathbb{R}^{d^2 \times (d^2-1)} , and if we further let Y \in \mathbb{R}^{d^2 \times (d^2-1)} be a matrix whose columns comprise an orthonormal basis of L^\perp , then, up to a change in sign for one of the G_l 's, there exists a constant c > 0 such that
Indeed, if \det (Y^T X(\xi)) was not uniformly bounded away from zero for all \xi \in \mathbb{S}^{d-1} , then by compactness there would exist a \xi_0 \in \mathbb{S}^{d-1} with \det (Y^T X(\xi_0)) = 0 , a contradiction. We can then write \mathbf{Q}(\xi) explicitly as
This implies that \mathbf{Q}(\xi) depends positively 0 -homogeneously and smoothly on \xi \in \mathbb{R}^d \setminus \{0\} . Also \mathbf{Q}(\xi) descends to the quotient
which is now invertible. It is not difficult to see that \xi \mapsto [\mathbf{Q}(\xi)] is still positively 0 -homogeneous and smooth in \xi \neq 0 (by utilizing the basis given above). Since \hat{w}(\xi) \odot \xi \in {\rm ran}~\mathbf{Q}(\xi) , we have
where [\hat{w}(\xi) \odot \xi] designates the equivalence class of \hat{w}(\xi) \odot \xi in \mathbb{C}^{m \times d} / L . This fact in conjunction with \widehat{ \mathcal{E} w}(\xi) = (2\pi \mathrm{i}) \, \hat{w}(\xi) \odot \xi allows us to rewrite (2.10) in the form
or equivalently as
The multiplier \mathbf{M}(\xi) \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R}^{d \times d}_\mathrm{sym} for \xi \in \mathbb{R}^d \setminus \{0\} is thus given by
which is smooth and positively 0 -homogeneous in \xi . Consequently, we have shown the multiplier equation (2.11).
3.
Singularities
In this section we sketch the proof of Theorem 1.4 and present some of its implications concerning the structure of singularities that can occur in BD-maps. We will also outline how this type of argument allows one to recover the dimensionality results in Theorem 1.2.
3.1. Proof sketch of Theorem 1.4
To simplify the proof and to expose the main ideas as clearly as possible we assume again that we are working in dimension d = 2. Our argument for BD-maps here is a bit more direct than the original one in [28] and does not use Fourier analysis. We also make the connection to the rigidity results of Section 2 explicit. This stresses the crucial argument, namely to exploit the ellipticity contained in the condition \frac{ \mathrm{d} \mu}{ \mathrm{d} |{\mu}|}(x_0) \notin \Lambda_{ \mathcal{A}}. Let us also note that by using the slicing properties of BD-maps [3,Proposition 3.4] and by arguing as in [1] (see also [24,Section 2]) one can recover the theorem in any dimension from this particular case.
We assume by contradiction that the set
satisfies |E^s u|(E)>0. We now want to zoom in around a generic point x_0\in E. To this end we recall the notion of tangent measure: For a vector-valued Radon measure \mu \in \mathcal{M}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}^n) and x_0 \in \mathbb{R}^d , a tangent measure to \mu at x_0 is any (local) weak* limit in the space \mathcal{M}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}^n) of the rescaled measures
for some sequence r_k \downarrow 0 of radii and some sequence c_k > 0 of rescaling constants. The definition of the push-forward T^{x_0, r_k}_\# \mu here expands to
We denote by {\rm Tan}(\mu, x_0) the set of all possible tangent measures of \mu at x_0. It is a remarkable theorem of Preiss [62] (see, e.g., [67,Proposition 10.5] for a proof in our notation) that for every measure \mu, {\rm Tan}(\mu, x_0) contains at least one non-zero measure for |{\mu}|-almost every x_0. Furthermore, at |{\mu}|-almost all points x_0 ,
see [67,Lemma 10.4]. If one assumes that |E^su|(E)>0, it then follows by elementary arguments from measure theory, see, e.g., [28,Proof of Theorem 1.1] that there exists at least one point x_0\in E and a sequence of radii r_k \downarrow 0 such that the following properties hold:
(ⅰ) \lim\limits_{k\to \infty} \frac{|E^a u|(B_{r_k}(x_0))}{|E^s u|(B_{r_k}(x_0))} = 0 ;
(ⅱ) \lim\limits_{k\to \infty} \, \rlap{-} \smallint _{B_{r_k}(x_0)} \biggl|\frac{ \mathrm{d} Eu }{ \mathrm{d} |Eu|}(x)-\frac{ \mathrm{d} Eu }{ \mathrm{d} |Eu|}(x_0)\bigamma| \; \mathrm{d}|E^s u|(x) = 0 ;
(ⅲ) there exists a positive Radon measure \sigma \in {\rm Tan}(|{E^s u}|, x_0) with \sigma \perp B_{1/2} \neq 0 ( B_{1/2} : = B_{1/2}(0) ) and such that
(ⅳ) P: = \frac{ \mathrm{d} Eu}{ \mathrm{d} |Eu|}(x_0)\ne a \odot b for any a, b \in \mathbb{R}^d .
Define
We have the following Poincaré-type inequality in BD, proved in [75]:
Thus, we conclude that there exists a sequence of rigid deformations \omega_k and a map v\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^2) such that
and v satisfies
and \sigma = |{Ev}| is a positive measure. By Proposition 2.6, \sigma is smooth. Unfortunately, this is however not in contradiction with \sigma \in {\rm Tan}(|E^su|, x_0)\setminus\{0\} , since there are purely singular measures having only Lebesgue-absolutely continuous measures as tangents at almost all points, see [62,Example 5.9 (1)]. In order to prove the theorem we thus have to exploit the ellipticity mentioned in Remark 2.7 in a more careful way.
Let us assume without loss of generality that P = \bigl(\begin{smallmatrix} 1 & \\ & 1 \end{smallmatrix}\bigr), so that \mathcal{A}_P defined in Proposition 2.6 is the Laplace operator. By recalling that
we can use (1.5) to get, cf. (2.6),
Furthermore, by combining (ⅰ) and (ⅱ) above it is not hard to check that
We now take a cut-off function \varphi \in \mathrm{C}_c^\infty(B_1;[0, 1]) with \varphi \equiv 1 on B_{1/2}. Exploiting the identity (in the sense of distributions)
which is valid for any smooth function \varphi and any measure \nu, we get, using (3.2), that
where Z_K, R_k, and S_k are measures supported in B_1 and satisfying
We apply \Delta^{-1} to both sides of the above equation to get
where
and K_1 is a constant-coefficient polynomial in the second derivatives of K_3. In particular, K_1 is a Calderón–Zygmund kernel and (see [44,69])
By this and standard estimates [44,69], one easily sees that the sequences (K_2 \star R_k)_k and (K_3 \star R_k)_k are strongly precompact in \mathrm{L}^1, and that
Furthermore, one easily checks that K_1 \star Z_k \to 0 in the distributional sense. It is then straightforward to combine the above facts with the positivity of \sigma_k (see [28,Lemma 2.2] for details) to deduce that also the sequence (\varphi\sigma_k)_k is precompact in \mathrm{L}^1, whereby
This is, however, in contradiction with \sigma being absolutely continuous (which follows from Proposition 2.6) and \sigma_k being singular. Indeed, if we let G_k be the null set where \sigma_k is concentrated, we obtain that
which is impossible.
3.2. Local structure of singularities
As we mentioned in the introduction, Alberti's rank-one theorem, Theorem 1.1 (ⅲ), implies a strong constraint on the possible behaviors of singularities of BV-maps. In particular, even at points x_0 \in \Omega around which u \in \mathrm{BV}(\Omega; \mathbb{R}^m) has a Cantor-type (e.g. fractal) structure, the "slope" of u has a well-defined direction. This is made precise in the following important consequence of Alberti's theorem.
Corollary 3.1. Let u \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}^d; \mathbb{R}^\ell) . Then, at |{D^s u}| -almost every x_0 every tangent measure \sigma \in {\rm Tan}(D^s u, x_0) is b -directional for some direction b \in \mathbb{S}^{d-1} in the sense that
for all bounded Borel sets B \subset \mathbb{R}^d and all v \in \mathbb{R}^d orthogonal to b .
For the proof see for instance [67,Corollary 10.8].
Combining Theorem 1.4 with Theorem 2.10 one can obtain some structural information on tangent measures for \mathrm{BD} maps. In fact, also exploiting the decomposition (3.1), which involves only positive measures after the fixed polar, the structure results of Theorem 2.10 can be improved for tangent measures.*
*We gratefully acknowledge Adolfo Arroyo-Rabasa for pointing this out to us.
Theorem 3.2. Let u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) . Then, at all point such that |{E^s u}| -almost every x_0 the following holds: for all \sigma \in {\rm Tan}(|E^su|, x_0) there exists w\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) such that
where a, b \in \mathbb{R}^d are such that
Moreover:
(i) If a \neq \pm b , then there exist two functions H_1, H_2\in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) such that
(ii) If a = \pm b , then there exist a function H\in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) such that
Proof. Given a tangent measure \sigma \in {\rm Tan}(|E^su|, x_0) , by arguing as in the proof of Theorem 1.4, one gets a sequence r_k \downarrow 0 and a sequence of rigid deformations \omega_k such that the maps
converge to a map w \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) with
By Theorem 1.4,
for some a, b \in \mathbb{R}^d . Thus, case (i) or case (ii) of Theorem 2.10 applies. Assume for instance a\ne \pm b.
Then,
and, by (2.7),
First, we observe that we may assume \omega = 0 since we may just subtract it from w .
We claim that since \sigma is a positive measure and v \in {\rm span}~\{a, b\}^\perp, this implies that v = 0, so that the conclusion holds. To prove the claim, assume without loss of generality that a = \mathrm{e}_3, b = \mathrm{e}_2 and that v = \alpha \mathrm{e}_1 with \alpha \ge 0. Let \varphi\in \mathrm{C}^0_c(\mathbb{R}^{d-1};[0, 1]), \psi \in \mathrm{C}^0_c([0, 1];[0, 1]) and let t\in \mathbb{R}. By integrating \sigma against \varphi(x')\psi (x_1-t) (x = (x_1, x')) we get
Since the first term on the right hand side of the above equation is independent of t, by letting t\to -\infty we get that \alpha = 0, which is the desired conclusion. In the same way, if a = \pm b, one uses Theorem 2.10 (ⅱ), (2.8), and the positivity of \sigma to conclude in a similar way.
Note that according to the preceding result the structure of possible tangent BD-maps can be quite complicated. However, if we additionally know x_0 \in J_u, as a consequence of the structural Theorem 1.2 we obtain that the tangent map at this point has a much simpler structure, namely
for some w^\pm \in \mathbb{R}^d and n \in \mathbb{S}^{d-1} (in fact, n = \nu_{J_u} ); in particular, w is one-directional.
At a generic point we can still prove that there is always at least one one-directional tangent measure. Indeed, one has the following result, proved in [29,Lemma 2.14]:
Theorem 3.3 (Very good singular blow-ups). Let u \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) . Then, at |{E^s u}| -almost every x_0 there exist \sigma \in {\rm Tan}(|E^su|, x_0) and w\in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) such that
where a, b \in \mathbb{R}^d are such that
and
Here, \{\xi, \eta\} = \{a, b\}, G \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) , and A \colon \mathbb{R}^d \to \mathbb{R}^d is an affine map.
Sketch of the proof. The idea of the proof is to start with a tangent map w as in Theorem 3.2 and to take a further blow-up in order to end up in the above situation and to appeal to a theorem of Preiss that tangent measures to tangent measures are tangent measures, see [56,Theorem 14.16]. One needs to distinguish two cases:
In the case where H_1'(x\cdot b) and H_2'(x\cdot a) do not have singular parts, one simply takes a Lebesgue point of both of them and blows up around that point. Thus one finds an affine tangent map. In the case where H_1'(x\cdot b) has a singular part, one easily checks that D^s H_1(x\cdot a) is singular with respect to H_2'(x\cdot a) and hence, taking a suitable blow-up, one again ends up with a w of the desired form.
We refer to [29,Lemma 2.14] for the details.
Note that in the above theorem one cannot decide a-priori which of the two directions a, b will appear in the second blow-up. Furthermore, it can happen that the roles of a and b differ depending on the blow-up sequence. In view of the analogy with the rectifiable part, where only one-directional measures are seen as possible tangent measures, one might formulate the following conjecture:
Conjecture 3.4. For |{E^su}|-almost all x_0, the conclusion of Theorem 3.3 holds for every tangent measure \sigma\in {\rm Tan}(E^su, x_0).
Note that if verified, this statement would imply that the structure of the Cantor part (which can be thought of as containing "infinitesimal" discontinuities) is essentially the same as the jump part (which contains macroscopic discontinuities).
3.3. Dimensionality and rectifiability
In [7] it was shown that the approach used to prove Theorem 1.5 can be extended to recover some information about dimensionality and rectifiability of \mathcal{A}-free measures. Indeed, it turns out that if an \mathcal{A}-free measure \mu charges a "low-dimensional" set, then its polar vector \frac{ \mathrm{d}\mu}{ \mathrm{d} |\mu|} has to satisfy a strong constraint at |{\mu}| -almost every point in this set. To state this properly, let us introduce the following family of cones:
where \mathbb A(\xi) is defined in (1.3) and {\rm Gr}(h, d) is the Grassmannian of h-planes in \mathbb{R}^d. Note that
We also recall the definition of the h-dimensional integral geometric measure, see [56,Section 5.14],
where \gamma_{h, d} is the Haar measure on the Grassmannian. The main result of [7] is the following, see [7,Theorem 1.3]:
Theorem 3.5 (Dimensional restrictions on polar). Let \mu \in \mathcal{M}(\Omega; \mathbb{R}^m) be \mathcal{A} -free and let E \subset \mathbb{R}^d be a Borel set with \mathcal I^{h}(E) = 0 for some h\in \{1, \ldots, d\}. Then,
Note that for h = d this theorem coincides with Theorem 1.5. The following is a straightforward corollary, see [7,Corollary 1.4]:
Corollary 3.6 (Dimensionality). Let \mathcal{A} and \mu be as in Theorem 3.5 and assume that \Lambda^h_{ \mathcal{A}} = \{0\} for some h \in \{1, \ldots, d\}. Then,
In particular,
and thus
where
By combining the above corollary with the Besicovitch–Federer rectifiability criterion, see [33,Section 3.3.13], one obtains that for an \mathcal{A}-free measure its h -dimensional parts are rectifiable whenever \Lambda^{h}_{ \mathcal{A}} = \{0\}. Recall that for a positive measure \sigma its h-dimensional upper density at a point x is defined as
We then have, see [7,Theorem 1.5]:
Theorem 3.7 (Rectifiability). Let \mathcal{A} and \mu be as in Theorem 3.5 and assume that \Lambda^{h}_{ \mathcal{A}} = \{0\}. Then, the set \{\theta^*_h(|\mu|) = +\infty\} is |\mu| -negligible and \mu \perp \{\theta^{*}_{h}(|\mu|)>0\} is concentrated on an h-rectifiable set R, that is,
where \lambda : R \to \mathbb{R}^{m} is \mathcal{H}^h -measurable.
The above results also imply a new proof of the rectifiability of the (d-1)-dimensional part of derivatives of BV-maps and of symmetrized derivatives of BD-maps. Indeed, it suffices to notice that, by direct computations,
This recovers item (ⅱ) in Theorems 1.1 and 1.2. We refer the reader to [7] for a more detailed discussion.
4.
Integral functionals and Young measures
In this section we consider integral functionals of the form
where \Omega is a bounded Lipschitz domain, f \colon \Omega \times \mathbb{R}^{d \times d}_\mathrm{sym} \to [0, \infty) is a Carathéodory integrand (Lebesgue measurable in the first argument and continuous in the second argument) with linear growth at infinity, that is,
and the subspace \mathrm{LD}(\Omega) of \mathrm{BD}(\Omega) consists of all BD-maps such that Eu is absolutely continuous with respect to Lebesgue measure (i.e., E^s u = 0 ).
Recall that a sequence (u_j) is said to weak*-converge to u in \mathrm{BD}(\Omega), in symbols u_j \overset{*}\rightharpoonup u , if u_j \to u strongly in \mathrm{L}^1(\Omega; \mathbb{R}^d) and Eu_j \overset{*}\rightharpoonup Eu in \mathcal{M}(\Omega; \mathbb{R}_{\rm sym}^{d\times d}) . Moreover, (u_j) converges strictly or area-strictly to u if u_j \overset{*}\rightharpoonup u in \mathrm{BD}(\Omega) and additionally |{Eu_j}|(\Omega) \to |{Eu}|(\Omega) or \langle Eu_j \rangle(\Omega) \to \langle Eu \rangle(\Omega) , respectively. Here, for u \in \mathrm{BD}(\Omega) , we define the (reduced) area functional \langle Eu \rangle(\Omega) as
Since \mathrm{LD}(\Omega) is area-strictly dense in \mathrm{BD}(\Omega) (by a mollification argument, see, e.g., Lemma 11.1 in [67] for the corresponding argument for the density of \mathrm{W}^{1, 1}(\Omega) in the space \mathrm{BV}(\Omega) ), one can show the following result, whose proof is completely analogous to the BV-case; see, for instance, Theorem 11.2 in [67].
Proposition 4.1. Let f \colon \overline{{\Omega}} \times \mathbb{R}^{d \times d}_\mathrm{sym} \to [0, \infty) be continuous and such that the (strong) recession function
exists. Then, the area-strictly continuous extension of the functional \mathcal{F} defined in (4.1) onto the space \mathrm{BD}(\Omega) is
Note that, clearly, f^\infty is positively 1 -homogeneous in A , that is f^\infty(x, \alpha A) = \alpha f^\infty(x, A) for all \alpha \geq 0 . Moreover, the existence of f^\infty entails that f has linear growth at infinity.
While the above result gives a way to extend \mathcal{F} to all of \mathrm{BD}(\Omega) , at least for some integrands, in general neither \mathcal{F} nor \overline{ \mathcal{F}} admit a minimizer. Usually, this occurs if \overline{ \mathcal{F}} is not weakly* lower semicontinuous. In this situation we define the relaxation \mathcal{F}_{*} of \mathcal{F} onto \mathrm{BD}(\Omega) as
Our first task is to identify \mathcal{F}_{*} as an integral functional, which will entail a suitable (generalized) convexification of the integrand.
4.1. Symmetric-quasiconvexity
The appropriate generalized convexity notion related to symmetrized gradients is the following: We call a bounded Borel function f \colon \mathbb{R}_ \mathrm{sym}^{d \times d} \to \mathbb{R} symmetric-quasiconvex if
where D \subset \mathbb{R}^d is any bounded Lipschitz domain (the definition is independent of the choice of D by a covering argument). Similar assertions to the ones for quasiconvex functions hold, cf. [31,13]. In particular, if f has linear growth at infinity, we may replace the space \mathrm{W}_0^{1, \infty}(D; \mathbb{R}^d) in the above formula by \mathrm{W}_0^{1, 1}(D; \mathbb{R}^d) or \mathrm{LD}_0(D) ( \mathrm{LD} -functions with zero boundary values in the sense of trace), see Remark 3.2 in [13].
Using one-directional oscillations, one can prove that if the function f \colon \mathbb{R}_ \mathrm{sym}^{d \times d} \to \mathbb{R} is symmetric-quasiconvex, then it holds that
whenever A, B \in \mathbb{R}_ \mathrm{sym}^{d \times d} with B - A = a \odot b for some a, b \in \mathbb{R}^d and \theta \in [0, 1] , cf. Proposition 3.4 in [37] for a more general statement in the framework of \mathcal{A} -quasiconvexity.
If we consider \mathbb{R}_ \mathrm{sym}^{d \times d} to be identified with \mathbb{R}^{d(d+1)/2} and f \colon \mathbb{R}_ \mathrm{sym}^{d \times d} \to \mathbb{R} with \tilde{f} \colon \mathbb{R}^{d(d+1)/2} \to \mathbb{R} , then the convexity in (4.3) implies that \tilde{f} is separately convex (i.e., convex in every entry separately) and so, f is locally Lipschitz continuous, see for example Lemma 2.2 in [12]. If additionally f has linear growth at infinity, then loc. cit. even implies that f is globally Lipschitz continuous.
Notice that from Fatou's lemma we get that the recession function f^\infty , if it exists, is symmetric-quasiconvex whenever f is; this is completely analogous to the situation for ordinary quasiconvexity. Hence, f^\infty is also continuous on \mathbb{R}_ \mathrm{sym}^{d \times d} in this situation.
We mention that non-convex symmetric-quasiconvex functions with linear growth at infinity exist. One way to construct such a function (abstractly) is the following: We define the symmetric-quasiconvex envelope SQf \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R} \cup \{-\infty\} of a locally bounded Borel-function f \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R} as
where A \in \mathbb{R}^{d \times d}_\mathrm{sym} . Clearly, SQf \leq f . Furthermore, if f has p -growth, we may replace the space \mathrm{W}_0^{1, \infty}(B_1; \mathbb{R}^d) by \mathrm{W}_0^{1, p}(B_1; \mathbb{R}^d) via a density argument.
Just as for the classical quasi-convexity one can show the following, cf. [37,Proposition 3.4]:
Lemma 4.2. For a continuous function f \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to [0, \infty) with p -growth, p \in [1, \infty) , the symmetric-quasiconvex envelope SQf is symmetric-quasiconvex.
We then have the following class of symmetric-quasiconvex, but not convex, functions:
Lemma 4.3. Let F \in \mathbb{R}_ \mathrm{sym}^{d \times d} be a matrix that cannot be written in the form a \odot b for any a, b \in \mathbb{R}^d and let p \in [1, \infty) . Define
Then, SQh(0) > 0 and the symmetric-quasiconvex envelope SQh is not convex (at zero).
We sketch here the proof since it is quite illuminating and shows a connection to the wave cone of the {\rm Curl}~{\rm Curl}~ -operator.
Proof of Lemma 4.3. The key point is to show that SQh(0) > 0 . Then, if SQh were convex,
a contradiction.
To prove that SQh(0) > 0 we argue by contradiction and assume the existence of a sequence of maps (\psi_j) \subset \mathrm{W}_0^{1, \infty}(B_1; \mathbb{R}^d) such that
In particular,
By mollification, we can assume that the \psi_j are smooth and we extend them by zero to \mathbb{R}^d. This allows one to employ the Fourier transform like in the proof of Theorem 2.10 (ⅲ). Recall that for a symmetrized gradient one has
We let L: = {\rm span}~{F} and we denote by \mathbf{P} the orthogonal projection onto L^\perp (identified with its complexification). We have already seen in (2.11) that we may "invert" \mathbf{P} in the sense that if
for some w \in \mathrm{W}^{1, p}(\mathbb{R}^d; \mathbb{R}^m) , R \in \mathrm{L}^p(\mathbb{R}^d; L^\perp) , then
for some family of linear operators \mathbf{M}(\xi) \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R}^{d \times d}_\mathrm{sym} that depend smoothly and positively 0 -homogeneously on \xi . Then we conclude as follows:
For p = 2 , Plancherel's identity \|{g}\|_{ \mathrm{L}^2} = \|{\hat{g}}\|_{ \mathrm{L}^2} together with (4.6) implies
But then h(\mathcal{E} \psi_j) \to |{F}| in \mathrm{L}^1(B_1) , contradicting (4.5). Thus, SQh(0) > 0 .
For p \in (1, \infty) , we may apply the Mihlin multiplier theorem (see for instance [44,Theorem 5.2.7]) to get analogously that
which is again at odds with (4.5).
For p = 1 , we only have the weak-type estimate
see [44,Theorem 5.2.7]. This in particular implies that, up to a subsequence, it holds that \mathcal{E} \psi_j \to 0 almost everywhere. On the other hand, by the trivial estimate
in conjunction with (4.6) we deduce that |{ \mathcal{E} \psi_j}| is equiintegrable. By Vitali's theorem, \mathcal{E} \psi_j\to 0 in \mathrm{L}^1 and we conclude as above.
An alternative way to show that SQh(0)>0 would be to rely on the following generalization of the Ball–James theorem [11] on approximate rigidity for the two-state problem.
Theorem 4.4. Let p \in [1, \infty) and A, B\in \mathbb{R}_ \mathrm{sym}^{2 \times 2} be such that B-A\ne a \odot b for any a, b \in \mathbb{R}^2 . Let (\psi_j) \subset \mathrm{W}_0^{1, \infty}(B_1; \mathbb{R}^d) be a sequence of maps such that
Then, up to a subsequence, either \mathcal{E} \psi_j\to A or \mathcal{E} \psi_j\to B in \mathrm{L}^p.
Indeed, applying the above lemma to \{A, B\} = \{-F, F\}, one obtains that either \mathcal{E} \psi_j \to F or \mathcal{E} \psi_j \to -F in \mathrm{L}^p, in contradiction with the fact that
which follows from the zero trace assumption on \psi_j\in \mathrm{W}_0^{1, \infty}(B_1; \mathbb{R}^d).
Theorem 4.4 can in fact be proved in the more general context of \mathcal{A}-free measures; we refer the reader to [27] (which is based on the techniques of [28]). For the case of first-order operators \mathcal{A} , this result is also proved in [19].
Let us also remark that recently there has been a detailed investigation into symmetric polyconvexity, see [15].
4.2. Relaxation
We now consider the question raised at the beginning of this section, namely to identify the relaxation \mathcal{F}_* of \mathcal{F} . First results in this direction for functions in \mathrm{BD}(\Omega) , but without a Cantor part (i.e., the singular part E^s u originates from jumps only and does not contain Cantor-type measures), were proved in [13,14,32,42].
The first lower semicontinuity theorem applicable to the whole space \mathrm{BD}(\Omega) was proved in [64] by employing the results of Section 2 together with a careful analysis of tangent measures and (iterated) tangent Young measures (see Section 4.5 below). That work, however, left open the question of relaxation, where more information on the structure of the singular part is required. In this context, we refer to [4,36], where this question is treated for BV-maps via Alberti's rank-one theorem (and Corollary 3.1), and to [65], which shows that Alberti's rank-one theorem is not necessary to prove weak* lower semicontinuity in BV (without a full relaxation theorem). In \mathrm{BD}, a first intermediate relaxation result was obtained in [8] and an essentially optimal version was finally proved in [51], see Theorem 4.5 below.
A challenge in the formulation of a relaxation theorem is that it involves passing to the symmetric-quasiconvex hull SQf of the integrand (defined in (4.4)), but in general the (strong) recession function (SQf)^\infty does not exist; in this context, we refer to [57,Theorem 2] for a counterexample. Thus, we need a more general notion of recession function: For any f \in \mathrm{C}(\overline{{\Omega}} \times \mathbb{R}^{d \times d}_\mathrm{sym}) with linear growth at infinity we can always define the generalized recession function f^\# \colon \overline{{\Omega}} \times \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R} via
which again is always positively 1 -homogeneous and the linear growth at infinity of f suffices for f^\# to take only real values. In other works, f^\# is usually just called the "recession function" (and denoted by " f^\infty "), but here the distinction to between f^\# and f^\infty is important. It is elementary to prove that f^\#(x, \, \cdot\, ) is upper semicontinuous. For a convex function f , always f^\# = f^\infty . We refer to [9] for a more systematic approach to recession functions and their associated cones.
As mentioned before, the following relaxation result is proved in [51]:
Theorem 4.5. Let \Omega\subset\mathbb{R}^d be a bounded Lipschitz domain and let f \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to[0, \infty) be a continuous function such that there exist constants 0 < c\leq C , for which the inequality
holds. Then, the weak* relaxation of the functional \mathcal{F} in \mathrm{BD}(\Omega) is given by
In particular, \mathcal{F}_* is weakly* lower semicontinuous on \mathrm{BD}(\Omega) .
The proof of this theorem proceeds by the blow-up method, see e.g., [35,36], and exploits Theorem 1.4 as well as the existence of very good blow-ups from Theorem 3.3.
We also note that [17] establishes a general integral representation theorem for the relaxed functional \mathcal{F}_* .
We conclude this section by noting that the previous discussion applies to functionals whose integrand depends only on the symmetric part of the gradient. However, it is not hard to construct an integrand f \colon \mathbb{R}^{d \times d}\to \mathbb{R}, which depends on the full matrix, but for which
In this case the corresponding integral functional \mathcal{F} will be coercive only on BD and one would like to study the relaxed functional \mathcal{F}_{*}. This has been achieved in some specific cases when E^c u = 0, see [21,40], but in the general case not much is known, see the discussion in [21,Section 7].
4.3. Generalized Young measures
In the remainder of this survey we consider a more abstract approach to the theory of integral functionals defined on \mathrm{BD} , namely through the theory of generalized Young measures. These objects keep track of all oscillations and concentrations in a weakly* converging sequence of measures; here, we will apply this to the symmetrized derivatives (Eu_j) of a weakly*-converging sequence of BD-maps (u_j) \subset \mathrm{BD}(\Omega) . Our presentation follows [2,29,52,64,67], where also proofs and examples can be found.
Let, as usual, \Omega \subset \mathbb{R}^d be a bounded Lipschitz domain. For f \in \mathrm{C}(\overline{{\Omega}} \times \mathbb{R}^N) and g \in \mathrm{C}(\overline{{\Omega}} \times \mathbb{B}^N) , where \mathbb{B}^N denotes the open unit ball in \mathbb{R}^N , we let
Define
In particular, f \in \mathbf{E}(\Omega; \mathbb{R}^N) has linear growth at infinity with growth constant C = \|{Rf}\|_{ \mathrm{L}^\infty(\Omega \times \mathbb{B}^N)} . Furthermore, for all f \in \mathbf{E}(\Omega; \mathbb{R}^N) , the (strong) recession function f^\infty \colon \overline{{\Omega}} \times \mathbb{R}^N \to \mathbb{R} , defined in (4.2), exists and takes finite values. It can be shown that in fact f \in \mathrm{C}(\overline{{\Omega}}; \mathbb{R}^N) is in the class \mathbf{E}(\Omega; \mathbb{R}^N) if and only if f^\infty exists in the sense (4.2).
A (generalized) Young measure \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) on the open set \Omega \subset \mathbb{R}^d with values in \mathbb{R}^N is a triple \nu = (\nu_x, \lambda_\nu, \nu_x^\infty) consisting of
(ⅰ) a parametrized family of probability measures (\nu_x)_{x \in \Omega} \subset \mathcal{M}_1(\mathbb{R}^N) , called the oscillation measure;
(ii) a positive finite measure \lambda_\nu \in \mathcal{M}_+(\overline{{\Omega}}) , called the concentration measure; and
(ⅲ) a parametrized family of probability measures (\nu_x^\infty)_{x \in \overline{{\Omega}}} \subset \mathcal{M}_1(\mathbb{S}^{N-1}) , called the concentration-direction measure,
for which we require that
(ⅳ) the map x \mapsto \nu_x is weakly* measurable with respect to \mathcal{L}^d , i.e., the function x \mapsto \langle {f(x, \, \cdot\, ), \nu_x} \rangle is \mathcal{L}^d -measurable for all bounded Borel functions f \colon \Omega \times \mathbb{R}^N \to \mathbb{R} ;
(ⅴ) the map x \mapsto \nu_x^\infty is weakly* measurable with respect to \lambda_\nu ; and
(ⅵ) x \mapsto \langle {|{ \, \cdot\, }|, \nu_x} \rangle \in \mathrm{L}^1(\Omega) .
The duality pairing between f \in \mathbf{E}(\Omega; \mathbb{R}^N) and \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) is given as
The weak* convergence \nu_j \overset{*}\rightharpoonup \nu in \mathbf{Y}(\Omega; \mathbb{R}^N) \subset \mathbf{E}(\Omega; \mathbb{R}^N)^* is then defined with respect to this duality pairing. If (\gamma_j) \subset \mathcal{M}(\overline{{\Omega}}; \mathbb{R}^N) is a sequence of measures with \sup_j |{\gamma_j}|(\overline{{\Omega}}) < \infty , then we say that the sequence (\gamma_j) generates a Young measure \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) , in symbols \gamma_j \overset{\mathbf{Y}}{\to} \nu , if for all f \in \mathbf{E}(\Omega; \mathbb{R}^N) it holds that
Also, for \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) we define the barycenter as the measure
The following is the central compactness result in \mathbf{Y}(\Omega; \mathbb{R}^N) :
Lemma 4.6 (Compactness). Let (\nu_j) \subset \mathbf{Y}(\Omega; \mathbb{R}^N) be such that
Then, (\nu_j) is weakly* sequentially relatively compact in \mathbf{Y}(\Omega; \mathbb{R}^N) , i.e., there exists a subsequence (not relabeled) such that \nu_j \overset{*}\rightharpoonup \nu and \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) .
In particular, if (\gamma_j) \subset \mathcal{M}(\overline{{\Omega}}; \mathbb{R}^N) is a sequence of measures with \sup_j |{\gamma_j}|(\overline{{\Omega}}) < \infty as above, then there exists a subsequence (not relabeled) and \nu \in \mathbf{Y}(\Omega; \mathbb{R}^N) such that \gamma_j \overset{\mathbf{Y}}{\to} \nu .
4.4. BD-Young measures
A Young measure in \mathbf{Y}(\Omega; \mathbb{R}_ \mathrm{sym}^{d \times d}) is called a BD-Young measure, \nu \in \mathbf{BDY}(\Omega) , if it can be generated by a sequence of BD-symmetrized derivatives. That is, for all \nu \in \mathbf{BDY}(\Omega) there exists a (necessarily norm-bounded) sequence (u_j) \subset \mathrm{BD}(\Omega) with Eu_j \overset{\mathbf{Y}}{\to} \nu . When working with \mathbf{BDY}(\Omega) , the appropriate space of integrands is \mathbf{E}(\Omega; \mathbb{R}_ \mathrm{sym}^{d \times d}) since it is clear that both \nu_x and \nu_x^\infty only take values in \mathbb{R}_ \mathrm{sym}^{d \times d} whenever \nu \in \mathbf{BDY}(\Omega) . It is easy to see that for a BD-Young measure \nu \in \mathbf{BDY}(\Omega) there exists u \in \mathrm{BD}(\Omega) satisfying Eu = [\nu] \perp \Omega ; any such u is called an underlying deformation of \nu .
The following results about BD-Young measures are proved in [52,64,67] (the references [52,67] treat BV-Young measures, but the proofs adapt line-by-line).
Lemma 4.7 (Good generating sequences). Let \nu \in \mathbf{BDY}(\Omega) .
(i) There exists a generating sequence (u_j) \subset \mathrm{BD}(\Omega) \cap \mathrm{C}^\infty(\Omega; \mathbb{R}^d) with Eu_j \overset{\mathbf{Y}}{\to} \nu .
(ii) If additionally \lambda_\nu(\partial \Omega) = 0 , then the u_j from (i) can be chosen to satisfy u_j|_{\partial \Omega} = u|_{\partial \Omega} , where u \in \mathrm{BD}(\Omega) is any underlying deformation of \nu .
The proof of this result can be found in [52,Lemma 4].
4.5. Tangent Young measures
In order to carry out blow-up constructions involving Young measures, we will need localization principles for these objects, one at regular and one at singular points. These results should be considered complements to the theory of tangent measures and thus the Young measures obtained in the blow-up limit are called tangent Young measures.
Define \mathbf{BDY}_ \mathrm{loc}(\mathbb{R}^d) by replacing \mathbf{Y}(\Omega; \mathbb{R}_ \mathrm{sym}^{d \times d}) and \mathrm{BD}(\Omega) by their respective local counterparts. When working with \mathbf{BDY}_ \mathrm{loc}(\mathbb{R}^d) , the appropriate space of integrands is \mathbf{E}_c(\mathbb{R}^d; \mathbb{R}_ \mathrm{sym}^{d \times d}) , i.e., the set of all functions in \mathbf{E}(\mathbb{R}^d; \mathbb{R}_ \mathrm{sym}^{d \times d}) with (uniformly) compact support in the first argument.
The following two results are proved in [64]:
Proposition 4.8 (Localization at regular points). Let \nu \in \mathbf{BDY}(\Omega) be a BD-Young measure. Then, for \mathcal{L}^d -almost every x_0 \in \Omega there exists a regular tangent Young measure \sigma \in \mathbf{BDY}_ \mathrm{loc}(\mathbb{R}^d) satisfying
In particular, for all bounded open sets U \subset \mathbb{R}^d with \mathcal{L}^d(\partial U) = 0 , and all h \in \mathrm{C}(\mathbb{R}^{d \times d}) such that the recession function h^\infty exists in the sense of (4.2), it holds that
Proposition 4.9 (Localization at singular points). Let \nu \in \mathbf{BDY}(\Omega) be a BD-Young measure. Then, for \lambda_\nu^s -almost every x_0 \in \Omega , there exists a singular tangent Young measure \sigma \in \mathbf{BDY}_ \mathrm{loc}(\mathbb{R}^d) satisfying
In particular, for all bounded open sets U \subset \mathbb{R}^d with (\mathcal{L}^d + \lambda_\sigma)(\partial U) = 0 and all positively 1 -homogeneous g \in \mathrm{C}(\mathbb{R}_ \mathrm{sym}^{d \times d}) it holds that
4.6. Good blow-ups for Young measures
By exploiting the results in Section 3, in particular Theorem 3.3, one can show that for almost all singular points of a BD-Young measure there is a tangent Young measure such that the underlying deformation has a one-directional structure, see [29,Lemma 2.14].
Theorem 4.10 (Very good singular blow-ups). Let \nu \in \mathbf{BDY}(\Omega) be a BD-Young measure. Then, for \lambda_\nu^s -almost every x_0 \in \Omega , there exists a singular tangent Young measure \sigma \in \mathbf{BDY}_ \mathrm{loc}(\mathbb{R}^d) such that [\sigma] = Ew for some w \in \mathrm{BD}_ \mathrm{loc}(\mathbb{R}^d) of the form
Here, \xi, \eta \in \mathbb{R}^d \setminus \{0\} , G \in \mathrm{BV}_ \mathrm{loc}(\mathbb{R}) , and A \colon \mathbb{R}^d \to \mathbb{R}^d is an affine map.
We remark that the previous result also holds for (possibly non-BD) Young measures \nu \in \mathbf{Y}(\Omega; \mathbb{R}^{d \times d}_\mathrm{sym}) with the property that [\nu] \perp \Omega = Eu for some u \in \mathrm{BD}(\Omega) .
Using the previous theorem, the main result of [29] characterizes completely all BD-Young measures:
Theorem 4.11. Let \nu \in \mathbf{Y}(\Omega; \mathbb{R}^{d \times d}_\mathrm{sym}) be a (generalized) Young measure. Then, \nu is a BD-Young measure, \nu \in \mathbf{BDY}(\Omega) , if and only if there exists u \in \mathrm{BD}(\Omega) with [\nu] \perp \Omega = Eu and for all symmetric-quasiconvex h \in \mathrm{C}(\mathbb{R}_ \mathrm{sym}^{d \times d}) with linear growth at infinity, the Jensen-type inequality
holds at \mathcal{L}^d -almost every x \in \Omega .
This result is the generalization to BD of the so-called Kinderlehrer–Pedregal theorem characterizing classical Young measures (i.e., \lambda_\nu = 0 ) generated by sequences of gradients [45,46] and the characterization of generalized sequences generated by BV-derivatives, first established in [52] and refined in [47,66].
We remark that the use of the generalized recession function h^\# can in general not be avoided since, as discussed above, not every symmetric-quasiconvex function with linear growth at infinity has a (strong) recession function (and one needs to test with all those; but see [48,Theorem 6.2] for a possible restriction on the class of test integrands).
Note that the above theorem does not impose any constraint on the singular part (i.e., \lambda_\nu^s and the corresponding \nu_x^\infty ) of the Young measure \nu , except for the fact that the barycenter [\nu] 's polar is of the form a\odot b at almost every singular point (which follows by the existence of an underlying deformation and Theorem 1.4). It is a remarkable fact that this is enough to also ensure the validity of the following singular Jensen-type inequality:
Theorem 4.12. For all \nu \in \mathbf{BDY}(\Omega) and for all symmetric-quasiconvex h \in \mathrm{C}(\mathbb{R}_ \mathrm{sym}^{d \times d}) with linear growth at infinity, it holds that
at \lambda_\nu^s -almost every x \in \Omega .
The key step to proving the preceding theorem is a surprising convexity property of 1 -homogeneous symmetric-quasiconvex functions at matrices of the form a \odot b proved by Kirchheim–Kristensen in [48]:
Theorem 4.13. Let h^\infty \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R} be positively 1 -homogeneous and symmetric-quasiconvex. Then, h^\infty is convex at every matrix a \odot b for a, b \in \mathbb{R}^d , that is, there exists an affine function g \colon \mathbb{R}^{d \times d}_\mathrm{sym} \to \mathbb{R} with
Proof of Theorem 4.12. We first establish the following general claim: Let \mu \in \mathcal{M}_1(\mathbb{R}^{d \times d}_\mathrm{sym}) be a probability measure with barycenter [\mu] : = \langle {{\rm id}, \mu} \rangle = a \odot b for some a, b \in \mathbb{R}^d , and let h \in \mathrm{C}(\mathbb{R}^{d \times d}_\mathrm{sym}) be positively 1 -homogeneous and symmetric-quasiconvex. Then,
Indeed, by the preceding theorem, h is actually convex at matrices a \odot b , that is, the classical Jensen inequality holds for measures with barycenter a \odot b , such as our \mu . This shows the claim.
If \nu = (\nu_x, \lambda_\nu, \nu_x^\infty) \in \mathbf{BDY}(\Omega) , then there is a u \in \mathrm{BD}(\Omega) such that
so at \lambda_\nu^s -almost every x \in \Omega we have by Theorem 1.4 that [\nu_x^\infty] = a(x) \odot b(x) for some a(x), b(x) \in \mathbb{R}^d . Thus, applying the claim above to \nu_x^\infty immediately yields the singular Jensen-type inequality.
Together, Theorems 4.11 and 4.12 have the following remarkable interpretation: While there are constraints on the oscillations and concentrations making up the absolutely continuous part of a BD-Young measure \nu , the concentrations in the singular part are totally unconstrained besides the requirement that [\nu_x^\infty] \, (\lambda_\nu^s \perp \Omega)(\mathrm{d} x) = E^s u for some u \in \mathrm{BD}(\Omega) . In particular, any probability measure \mu \in \mathcal{M}(\mathbb{R}^{d \times d}_\mathrm{sym}) with barycenter [\mu] = \langle {{\rm id}, \mu} \rangle = a \odot b for some a, b \in \mathbb{R}^d occurs as the concentration-direction measure of a BD-Young measure.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme, grant agreement No 757254 (SINGULARITY).
Conflict of interest
The authors declare no conflict of interest.














 DownLoad:
DownLoad: