Sustainable production model with stochastic machine breakdown using smart manufacturing under circular economy

1.   Introduction

Most manufacturing firms have started producing green products in technical and scientific fields. A manager of a manufacturing industry accepts challenges arising in producing good quality green products and attempts to achieve the better provision of services. However, long-run green-production processes can sometimes experience internal or external problems, causing the manufacturing machine to stop. In such cases, the main task of the managers is to restart the machine as soon as possible. However, in such situations, the produced green products can contain defects. Moreover, in the current highly competitive business situation, managers need to ensure good and consistent product quality. The make-to-order (MTO) production process needs the manufacturer to maintain the system costs. Here MTO policy indicates that the manufacturing process starts after receiving the order from the retailer. MTO production process exacerbates machine failure situations for sudden starting the manufacturing process. After the on-hand green inventory is completely delivered to the retailer, the machine is started again if it is completely repaired or waiting for completion, and this policy is known as a no-resumption (NR) policy. In other situations, the production process is resumed after machine repair is performed without focusing on the completion of the produced green products; this is known as abort resumption (AR) policy ^[34]. Corrective maintenance implies repairing the machine that had previously stopped suddenly, and the time required for repair is known as the corrective maintenance time. To prevent machine failure, the machine is fully checked after the completion of the production process; this is known as preventive maintenance. All manufacturers must be aware of both the aforementioned important concepts. It is preferable if manufacturing sector follows preventive maintenance though the machine breakdown situations may not occur frequently. Generally, models of economic order quantity and economic production quantity focus on the production of perfect green products. However, a realistic model may not always be able to produce such products. As a result, the system needs an inspection policy that separates low-quality (or defective) green products from the rest. Usually, a human or machine performs the inspection and may not be able to perform the separation process with complete accuracy, i.e., an error may arise. This error could be of two types: Type-I and Type-II. Type-I errors occur when a non-defective green product is rejected for being defective; conversely, Type-II errors occur when a defective green product is accepted as non-defective ^[19]. To improve the company's brand image, the manager needs to decrease Type-II errors in a supply chain management (SCM) model. By using inspection, the production process is cleared from defective products. This process needs investments to clean and dispose of the unusable green products. The perfect green products are supplied to the market by different transportation mediums. During transportation, the system emits different greenhouse gases (GHGs).

Global warming results in climate changes including changes in temperature, soil moisture, precipitation, and sea level. The main causes of global warming are the emissions of GHGs, particularly (CO$_2$), which is directly or indirectly emitted by human being. Many approaches, such as agreed emissions targets, emissions trading schemes, and carbon tax, are proposed to reduce CO$_2$ emissions ^[31,33]. The environmental problem presented by GHG emissions is calculated in terms of the equivalence factor of CO$_2$ (in short CO$_2$e or CO$_2$eq); managers of manufacturing plants admit to the occurrence of emissions in SCM models. CO$_2$e is emitted during the manufacture as well as transportation of products, and this emission increases every day ^[45]. Therefore, the key question to any industry is how these emissions can be controlled. To decrease carbon emissions, various regional carbon caps are decided worldwide for accepting some cost in the scale of carbon emissions ^[29]. To consider this cost, the manufacturer's total cost must be increased. As the general criteria for a manufacturer is to minimize the total production cost, the system is essentially aimed at decreasing the carbon emission cost, i.e., CO$_2$e. In this study, the carbon emissions cost is calculated by assuming both the fixed and variable types in the integrated green inventory model. The reusable and eco-friendly products are generally known as green products and these products has increasing demand nowadays. Again, the transportation of perfect green products in the system involves many different policies such as single-setup-single-delivery, single-setup-multi-delivery (SSMD), and multi-setup-multi-delivery (MSMD), among which the SSMD is a more usable policy. During the transportation of green products, the transportation cost is introduced in the system, and most of the supply chain is completed by assuming fixed and variable transportation cost. The container capacity and distance-dependent transportation cost is a realistic scenario in the transportation sector ^[46]. Allowing these things, the model's main focus is to find economic and environmental solutions, which are shown in the numerical and case study sections. Maintaining the product quality reduces the wastage green products and shows economical benefit in the model. Similarly, the model studies the environmental effects by calculating the GHG emissions from the production and transportation process. Now the motivation of the study is as follows:

● The main challenge for any industry manager is how to maintain and increase the product quality and quantity for the goodwill of the company within a random machine failure. With failure or no failure, the system must maintain the machine correctly and preventively.

● Including SSMD transportation schedule and MTO production policy, any industry manager tries to minimize the system's expenditure.

● For the environmental issues, there are always exist challenges how to minimize the bad environmental things for any government. That's why the industry manager calculated the total amount of GHGs emitted from the production as well as the transportation schedule.

2.   Literature review

The study ^[34] discussed the use of NR policy in the case of machine breakdown along with maintaining the product quality through inspection policy. The safety stock was utilized to cater to the system's additional demand. In the machine breakdown, the demand in corrective maintenance time was fulfilled by the produced products as well as additional stock (safety stock). The authors of ^[24] briefly proposed a product's safety stock and safety factor. The study ^[41] proposed warehouse maintenance with smart technology. The manuscript of ^[4] discussed a preventive maintenance policy in a energy-enabled production system. Various risks are presented within the sustainable supply chain model for manufacturing or others. The risks were mitigated by assuming several strategies within the model ^[28]. Supply chain risk was discussed by ^[22] for short life-time products.

Mostly, less emergency conservative product manufacturing industries follow MTO production process. The MTO policy indicates that the manufacturer commences production after receiving an order from a retailer in an economic manufacture quantity (EMQ) model. The authors in ^[34] introduced the EMQ model to determine low-quality (defective) products, and the behavior of such products was described in ^[30]. The authors of ^[43] introduced a manufacturing system, where defective rate of produced products was a random variable and the defective products were reworked. How the manufacturing process was utilised in the model of ^[12] to get high technology products. The authors of ^[19] examined the integrated model's inspection errors and learning effect. The errors in the inspection much arrived in the human inspection than the automation (inspection done by machine) policy and that's why the authors ^[37] introduced automation policy in a smart production system. The authors ^[23] was elaborated the learning effect and inspection errors in a supply chain to identify actual defective products. The authors of ^[32] recently introduced a flexible production system within the green investment in a multi-retailer SCM.

Several authors have investigated both the fixed and variable transportation costs in the SSMD policy. For example, the models ^[10] and ^[46] formulated a three-echelon supply chain model considering these transportation costs. Model ^[26] proposed that the transportation cost was a power function of delivery quantity. The study ^[36] considered remanufacturing process for reworking defective products with an additional investment. A multi-stage complex production system was discussed by ^[38] for quality maintenance and increased the company's brand image. The authors of ^[25] determined the amount of deteriorate products from the system and used remanufacturing for environmental factors. The vendor or buyer may not always be reliable; therefore, their behavior was focused on in the model ^[17].

To ensure good environmental health, production industries and transport companies are controlled the reduction of carbon emissions in their production and transportation processes. The authors in ^[48] proposed that production industries and transportation companies must extract CO$_2$ from used energies in various fuels of sustainable food production system. A green supply chain was proposed to minimize carbon emissions in the model ^[14] and ^[21]. According to the SSMD policy, the carbon emissions are increased with the increase of shipment number and transported product quantities. The carbon emissions in an imperfect production system were discussed by ^[47]. The manuscript ^[3] said low carbon emissions with respect to imperfect and damaged products. The warranty policy for shortages and the investment for the improvement of quality was discussed by ^[20]. The studies ^[2] proposed SCM models, in which carbon emissions were calculated through product deterioration in the retention of on-hand inventory and product transportation. The authors of ^[8] focused on the environmental factors based on waste vegetable oil collection and solved a Heuristic algorithm. The study ^[39] discussed the pricing strategies for substitutable products. These pricing strategies were elaborated under centralized and decentralized SCM model within the model ^[44]. A three-echelon closed-loop-supply chain was discussed by ^[42] within the carbon footprint environment and game strategies solved the model. The authors of ^[15] designed closed-loop-supply chain through transportation schedule within various echelon. Another thing is outsourcing, which is introduced at the manufacturer or retailer to deliver some products or services towards a smooth business process. The supply chain with outsourcing criteria was introduced by ^[5] under the capacity exibility and reservation. Within the manufacturing system, the outsourcing criteria was described by ^[27]. The authors of ^[16] elaborated the sustainable transportation within outsourcing environment through eco-logistic transportation schedule. The authors of ^[13] were elaborated the carbon emission within the online-to-offline supply chain through controlling the lead time.

Usually, the manufacturing sector tries to reduces GHGs from the production process though they are producing green products. Similarly, the transportation sector reduces GHGs to transport the products. The total amount of GHGs emissions and their costs related to the emissions are calculated in the model. Normally, the manufacturer is always trying to produce a perfect (good or high-quality) product but for various problems (labour issue, strike, long-run production process) occur and it starts to produced imperfect (defect or low-quality) products in the production process. An inspection is needed to cleaned the production process from the imperfect products but human inspection may arises errors during inspection. As inspection and inspection errors are considered in this study. Again, the smooth production process may shut down due to sudden unexpected problems. At this situation, the safety stock of products can save to fill up the existing demand of the system. In the transportation process, the transportation cost is more realistic when it depends on the container's capacity and distance between destinations. From the authors' contribution Table 1, it is seen that, these research gaps are not fulfilled till now and by assuming all of these research gaps. The authors propose a manufacturer–retailer two-echelon model, wherein container and distance-dependent transportation cost are focused on. Using this model, the total carbon emissions during manufacturing and transportation processes can be minimized. In long-term production processes, problems in any machinery or other factors can cause the system to breakdown suddenly; therefore, corrective maintenance is performed as early as possible. During corrective maintenance, the delivery of green products to the market continues as usual until stocks last. A scenario is considered in which the model is divided into three subcases based on the stock of green products. These cases are discussed based on the preventive maintenance time required when the machine does not stop production. The inspection process is conducted throughout the production run, and the errors in this process are considered simultaneously. Section 3 presents the problem definition, notation, and assumptions made in the study. Model description, solution methodology, numerical study, and conclusions are discussed in Sections 4, 5, 6 and 7, respectively. Table 1 lists some of the authors' contributions to major keywords and Table 4 is described the changes of major cost parameters via sensitivity analysis table.

3.   Problem definition, notation, and assumptions

The proposed model is described as the problem definition. The assumptions and notation for the study are described in this section.

3.1.   Problem definition

This study emphasizes a imperfect production model which produces green products. An inspection process is setup for finding the defective products from the production system to clean the system. The inspection errors of Type-I and Type-II are appears in the system as human works inspection process. Meanwhile, a machine breakdown occurs at a random time during the production time $t_1$. The corrective maintenance is considered for repairing the machine based on the three cases: repairing is completed before the delivery process is started, repairing time belongs to the duration of the delivery time, and repairing time goes beyond the delivery time duration. Products are transported through SSMD policy and depends upon the number of containers and number of shipments. The GHG emissions from the transportation system is considered in this study. A comparison between machine breakdown and without machine breakdown situation is discussed. The without machine breakdown situation requires preventive maintenance to prevent the machine breakdown at a random time.

3.2.   Notation

The listed notation in Table 6 are used in this study to develop the model and the table is given in Appendix.

3.3.   Assumptions

Every time customers need their own satisfaction to select a cloth. That's why the cloth industry manager is agreed to satisfy customers' demand via MTO policy. The manager collects customers' orders through their size and selected cloth then he starts the manufacturing process. The assumptions are based on the clothes (green product) manufacturing industry and the assumptions are elaborated in the following manner.

${1)}$ This model is an integrated model of green inventory between manufacturer and retailer. In the green production process, the manufacturer produces a single-type of green products. Both perfect and defective green products are produced during the production period of $[0, t_1]$. By discarding the imperfect green products, the production process is cleaned and this gives a high impact of the companies' brand image on the customers ^[30].

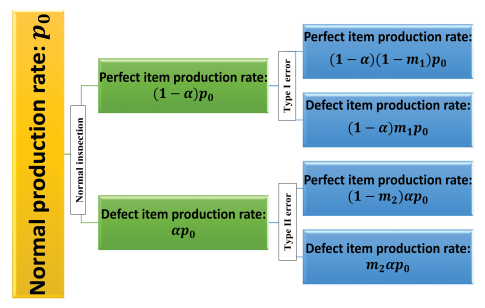
${2)}$ Due to the errors in the human inspection, two types of inspection errors occur within the inspection process, namely, Type-I error $(m_1\%)$ and Type-II error $(m_2\%)$. By considering inspection errors, the exact production rate of a perfect green product is $\{(1-\alpha)(1-m_1)+\alpha m_2\}p_0 = u_1p_0 = p$ and the production rate of defective green product is $(p_0-p) = (1-u_1)p_0$ according to Figure 1, where $u_1 = \{(1-\alpha)(1-m_1)+\alpha m_2\}$ ^[19].

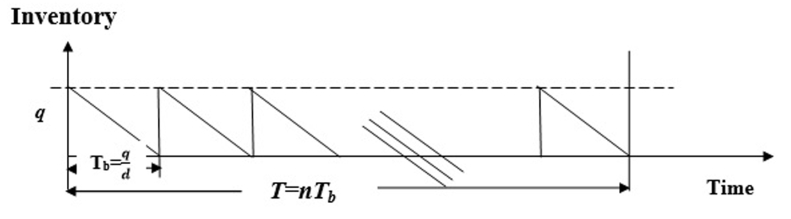
${3)}$ For maintenance of the brand image of the company, the manufacturer delivers only perfect green products to the retailer in a small quantity, $q (q\leq pt_1)$, for a fixed period $T_b = \frac{q}{d}$, where $d (d\leq q)$ is the retailer's annual demand.

${4)}$ More holding cost is essential to hold more products at a time. All green products are produced based on the retailer's order to reduce the holding cost, and products are transported in small quantities equally. Thus, the model follows MTO policy and the transportation process follows SSMD policy. The retailer transports some products to the customer's home based on their demands by requiting a suitable outsourcing home delivery agency ^[26,27].

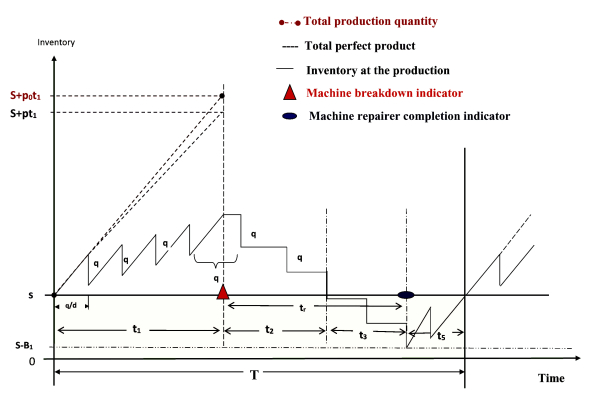
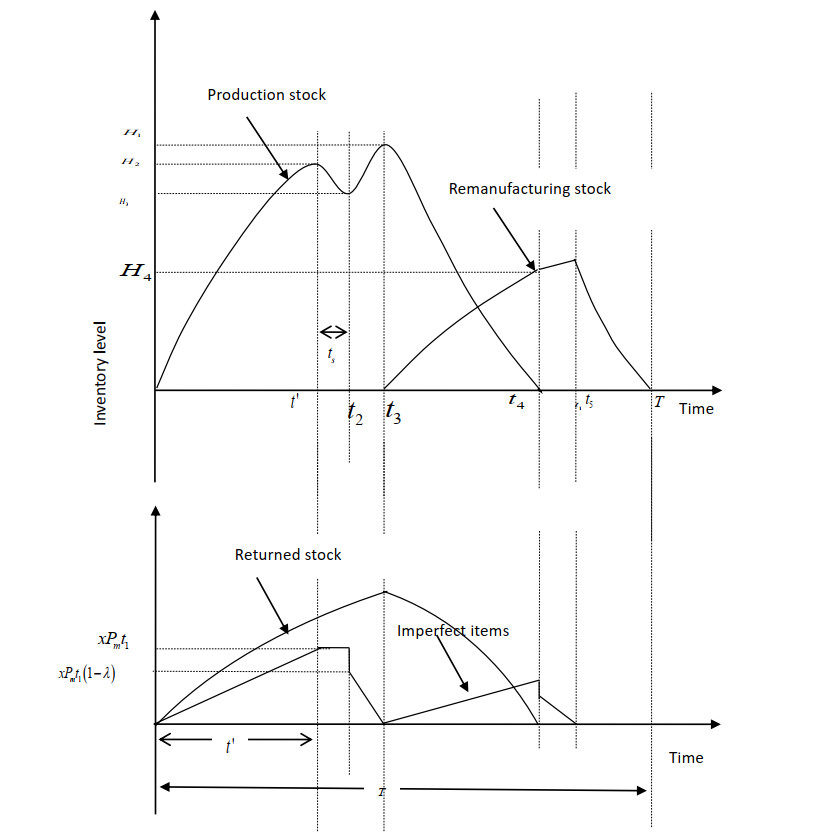
${5)}$ For the long-run production process, a machine can breakdown at any random time. When random machine breakdown occurs in the production process $(t_1 < \frac Q p)$, the model is developed considering three subcases based on corrective repair time $(t_r)$ and the time required to finish the produced/stored green products. The First subcase occurs when $t_r\leq t_2 = \frac {t_1(p-d)} d$. As there exists additional stock $S$, the next subcases are assumed when $t_2 < t_r\leq \frac {t_1(p-d)+S} d$ and $\frac {t_1(p-d)+S} d < t_r < \infty$ ^[18,34].

${6)}$ To prevent machine failure, the manufacturer checks the machine after it satisfies the ordering quantity $(t_1 = \frac Q p)$ such that the machine is at rest. At this point, the manufacturer commences preventive maintenance for the machine. Similar to those in the aforementioned case, three subcases are considered based on preventive maintenance time $t_p$ and product finished time ^[4].

${7)}$ In the SSMD transportation policy, the shipment number is always a positive integer; therefore, the shipment number is fixed by using the nearest integer function $([\triangle])$. This function is required for insufficient produced green products in machine breakdown situations. The shipment number for the First subcase is $n_1 = [\frac {pt_1} {q}]$. For the Second subcase, let $B_1(\leq S)$ be the downward green inventory at the safety stock level; then, the shipment number is $n_2 = [\frac {pt_1+B_1} q]$. In the Third subcase, the manufacturer delivers the produced and safety stock of green products by $n_4 = [\frac {S+pt_1} q]$ shipments.

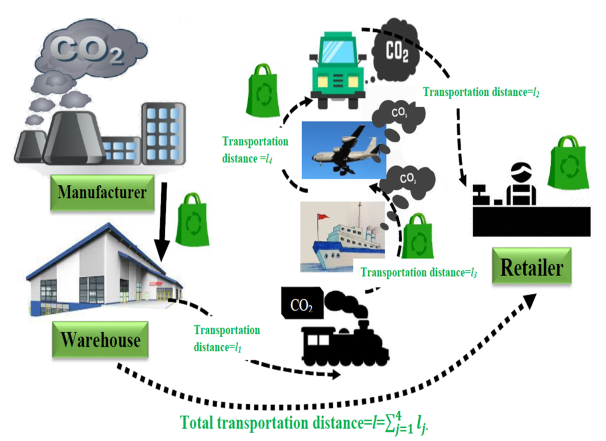
${8)}$ The transportation cost is required for transporting the products, which depends on the container's capacity ($\gamma$) and distance between the manufacturer and retailer ($l$). To deliver unit quantity, $q$, $\frac q {\gamma}$ containers per shipment are required, and the total of $\frac {nq} {\gamma}$ containers are required for the entire cycle time of $T$. Therefore, the total transportation cost is $\frac {lc_tnq} {\gamma}$ ^[46].

${9)}$ During the production and transportation processes, some GHGs are emitted owing to using fossil fuels and expending of other energies. For the production of per unit green product, the GHGs emission is $GHG_p = \sum_{1}^{3} e_i GE_i$ ^[33].

${10)}$ The GHGs emit in the transportation schedule and different amounts for different transportation mediums such as truck, train, ocean bridge, air, or others. Mainly, these four mediums are used to transport the products. Therefore, we assume the total traveling distance ($l$) covered by a truck, train, ocean barge. The distances of different mediums are assumed to be represented by $l_1$, $l_2$, $l_4$, and $l_5$, respectively. Thus, $l = \sum l_j$. Therefore, GHGs emissions and energy consumption are described as $GHG_T = \sum\limits_{j = 1}^{4}l_{j}GT_j$ ^[7].

4.   Model description

This manuscript proposes a two-echelon supply chain model for an one manufacturer (upper echelon) and one retailer (lower echelon). After the retailer's order (lot size $Q_0$) is received, the manufacturer commences the production at rate $p_0$, and no revised stock exists to meet immediate demands (i.e., MTO production policy). The safety stock is used only when finished the produced products though uncompleted the corrective maintenance. During a long-term production process, some problems arise, producing defective green products. The human's inspection process then conducts for the entire production period [$0, t_1$] within all produced items $(p_0t_1)$. At rate $\alpha$, the production rates of defective and perfect products are represented as $\alpha p_0$ and $(1-\alpha)p_0$ for the production uptime $[0, t_1]$. Owing to the inspection errors, the actual production rates of perfect and defective products are calculated to be $(1-\alpha)(1-m_1)p_0$ and $(1-\alpha)m_1p_0$, respectively (according to the Figure 1) in the perfect production rate of $(1-\alpha)p_0$. Similarly, the actual production rates of perfect and defective products are $\alpha m_2p_0$ and $(1-m_2)\alpha p_0$, respectively in the defect production rate of $\alpha p_0$. Therefore, the total perfect and defect production rates are $p = \{(1-\alpha)(1-m_1)+\alpha m_2\}p_0 = u_1p_0$ and $\{(1-\alpha)m_1+(1-m_2)\alpha \}p_0 = (1-u_1)p_0$, respectively, where $u_1 = (1-\alpha)(1-m_1)+\alpha m_2$.

All the perfect green products are sent to the retailer at small quantities of $q$ for a fixed period $T_b = q/d$ [see the Figure 2], where $d (\leq p)$ is the annual demand rate for the retailer; the unusable green products are wasted (disposed) of at some cost $C_2$. By considering these inspection and its errors, the production process is cleaned from the defective wastage products. In the production process of the time period $[0, t_1]$, the machine shuts down randomly during the production process. We elaborate on this in the following text by considering the cases with $(t_1 < Q/p)$ and without $(t_1 = Q/p)$ machine breakdown.

4.1.   First case: With machine breakdown ($t_1 < Q/p$)

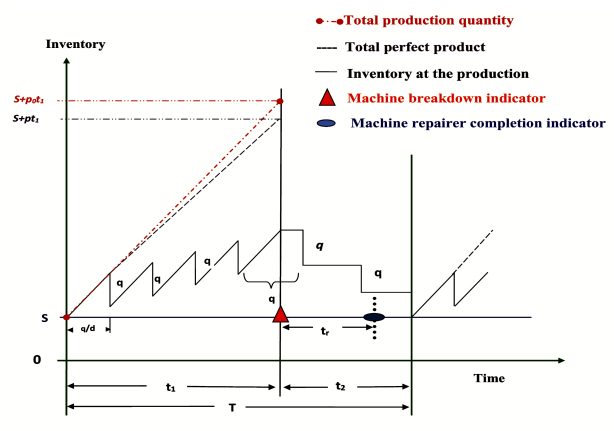
Machine breakdown occurs randomly in the production uptime of $(0, t_1)$, resulting in the sudden requirement for initiation of machine repair. Let $t_r$ be the machine repair time. By considering whether the repair time ($t_r$) is lesser or greater than the production downtime $t_2( = \frac {t_1(p-d)} d)$, three subcases are described, which are reached when $t_r\leq t_2$, $t_2 < t_r\leq \frac {t_1(p-d)+S} d$, and $\frac {t_1(p-d)+S} d < t_r < \infty$, respectively, where $S$ is the safety stock for the manufacturer. The following common costs are presented for any of the three subcases.

Here, $c_r$ and $t_r$ are the unit time machine repair charge and machine repair time, respectively. Then, the machine repair cost $c_rt_r$ is applied throughout the case. The retailer is agreed to home delivery of some products ($\omega \%$) according to the customer's requirement, and a third-party local transportation agency performs the delivery process. To perform this, the third-party's work is included in the outsourcing, and the amount to perform this is included in outsourcing cost. Total outsourcing cost $o_c\omega q$ is applied within the model, where unit product outsourcing cost is $o_c$. For production time $t_1$, the total inspection and its related cost, which is the sum of inspection cost $(C_0p_0t_1)$, inspection errors cost $(C_3(1-\alpha)m_1p_0t_1+C_4\alpha m_2p_0t_1)$, and disposal cost $(C_2(p_0t_1-pt_1))$ are calculated as

where $u_2 = C_0+C_3\alpha m_2+C_4(1-\alpha)m_1+C_2(1-u_1)$.

The total delivery cost is obtained by multiplying the delivery cost per container ($c_t$), distance between manufacturer and retailer ($l$), number of shipments ($n$), and total number of containers per shipment ($\frac q \gamma$). Therefore, the total delivery cost is $\frac{lc_tnq} \gamma$ for $n$ shipment. The carbon emissions cost is calculated from the production and transportation processes. Let $e_i$ and $GE_i$ be the useable nonrenewable energy in unit energy (megajoule (MJ) or others) and GHG emissions factor for nonrenewable energy reduction/extraction in the unit of kg for equivalence CO$_2$ (kg.CO$_2$e), respectively, for a unit of green product produced, where $i$ refers to the index number for the use of electricity $(i = 1)$, natural gas $(i = 2)$ and coal $(i = 3)$. Thus, the total GHG emissions or energy extraction for a green product is $GHG_p = \sum\limits_{i = 1}^{3} e_i GE_i$. As $c_p$ is the carbon price for a unit kg of CO$_2$e (kg.CO$_2$e) GHGs, the cost is $c_pGHG_p = c_p\sum e_i GE_i$ for a produced green product. Let $GT_j$ represent the GHG emissions and energy consumption for a unit distance of transporting a shipment of green product by truck $(j = 1)$, train $(j = 2)$, ocean barge $(j = 3)$ and air $(j = 4)$. For transporting shipment quantity $q$ to the retailer, let $l_{j}$ represent the distance for traveling via truck, train, ocean barge and air; therefore, $l = \sum l_{j}$ is the total distance between vendor and retailer. Therefore, the total GHG emissions for a shipment quantity being transported to the retailer is $GHG_T = \sum\limits_{j = 1}^{4} l_{j}GT_j$. As $c_p$ is the carbon price, the total GHG emissions cost is $c_pGHG_T = c_p\sum l_{j}GT_j$. Thus, the total GHG emissions cost is $p_0t_1c_p\sum e_i GE_i+nc_p\sum l_{j}GT_j$, where the total produced green product is $p_0t_1$ for production uptime $t_1$, and $n$ is the shipment number (see Figure 3).

4.1.1.   First subcase: $t_r\leq t_2$

In this subcase, the corrective maintenance of the nonfunctioning machine is completed before the already-produced perfect green products are delivered. Let $n_1$ be the number of shipments required to deliver the entire perfectly produced green inventory $(pt_1)$ to the retailer in equal quantities of $q$ which does not cause interference in the safety stock quantity of $(S)$. Thus, the shipment number is described by $n_1 = [pt_1/q]$, where $[\triangle]$ is the nearest integer function, and $pt_1$ is approximately equal to $n_1q$, for which the last shipment contains some excess or lack of green product compared to the normal delivery quantity $q$. Here, the cycle times of the retailer and manufacturer are $T_b = \frac q d$ and $T = n_1T_b = \frac {n_1q} d = \frac {pt_1} d$, respectively. Figure 4 shows the on-hand green inventory for the manufacturer ($I_1^v$), which is calculated by subtracting the area formed by the safety stock and production graph [i.e., $(S+p_0t_1)T-p_0t_1^2/2$] and the delivery graph (i.e., $T_b\{q+2q+...+(n_1-1)q\} = \frac {qT(n_1-1)} 2$) in the cycle period of $T$. Thus,

The per unit production cost $(p_c)$ is applicable to all the produced green products $(p_0t_1)$ in production time $t_1$. Thus, the total production cost is $p_cp_0t_1$. Hence, the total cost for the manufacturer is the sum of the setup cost ($A_1$), machine repair cost $(c_rt_r)$, production cost ($p_cp_0t_1$), holding cost ($h_1I_1^v$), inspection and its related costs $(I_c(t_1))$, delivery cost ($\frac {lc_tn_1q} {\gamma}$), and carbon emissions cost ($p_0t_1c_p\sum e_i GE_i+n_1c_p\sum l_{j}GT_j$). Per unit time, the total cost for the manufacturer is given by

where $T = n_1T_b = \frac {n_1q} {d} = \frac {pt_1} {d}$ and $\frac {n_1} T = \frac {d} q$.

Again, the retailer handles quantity $q$ for period $T_b$ and therefore, the total inventory is obtained from an area calculation by the retailer [See the Figure 2] and this is $\frac {qT_b} 2$ for a shipment. Consequently, the on-hand green inventory for the retailer is calculated as $I_1^b = \frac {n_1qT_b} {2} = \frac {qT} 2$. Thus, the total cost to the retailer includes the total handling cost ($n_1A_2$), outsourcing cost ($n_1o_c\omega q$), and increased holding cost ($h_2-h_1$), where the retailer pays the excess holding cost. Therefore,

From Eqs (4.1) and (4.2), the total integrated green inventory cost per unit time is calculated as

As $m_1$ and $m_2$ are random variables, the expected total cost per unit time for the First subcase is

where $E[u_1] = (1-\alpha)(1-E[m_1])+\alpha E[m_2]$ and $E[u_2] = C_0+C_3(1-\alpha)E[m_1]+C_4\alpha E[m_2]+C_2(1-E[u_1])$.

4.1.2.   Second subcase: $t_2 < t_r\leq \frac {t_1(p-d)+S} d$

Although the produced perfect green products ($pt_1$) are sell out completely in this subcase, the machine correction process is not completed. Let $B_1(<S)$ be the sell-out quantity from the safety stock in time $t_3$, required to mitigate the shortage in this situation. Therefore, the total delivery quantities are $pt_1+B_1 (<Q+S)$ and the machine repair time is $t_r = t_2+t_3 = \frac {t_1(p-d)+B_1} d$, where $B_1 = dt_3$. Let the shipment number is $n_2 = [\frac {pt_1+B_1} q]$. Therefore, $n_2q$ is approximately equal to $(pt_1+B_1)$, where the last shipment contains a quantity of approximately $q$. Assume that the delivered safety-stock quantity, $B_1$, is accounted for after the machine is started, with the simultaneous fulfillment of demand. Let $t_5$ be the time to fulfil quantity $B_2$, i.e., $B_2 = (p-d)t_1$, and the demanded quantity $dt_5$ is delivered via $n_3$ shipments. This implies that during production time $t_5$, the produced perfect green products are as $B_1+n_3q = B_1+dt_5$; therefore, $B_1+n_3q = B_1+dt_5 = pt_5$. The cycle time is calculated as $T = (n_2+n_3)T_b = n_2T_b+t_5$, where $n_3T_b = t_5$, i.e., $n_3 = \frac {dt_5} q$. Therefore, the total cycle time is calculated as $T = t_1+t_2+t_3+t_5 = n_2T_b+t_5 = \frac {pt_1+B_1} {d}+\frac {B_1} {(p-d)} = \frac {pt_1+B_1+dt_5} {d}$. In this entire case, $t_r = t_2+t_3 = \frac {t_1(p-d)+B_1} d$, $T-t_5 = \frac {pt_1+B_1} d$, and $\frac {n_2+n_3} T = \frac {d} {q}$. Therefore, from Figure 5, the on-hand green inventory for the manufacturer is given by

Here, the additional produced green products are represented by $p_0t_5$, and the total produced green products are represented by $p_0(t_1+t_5)$. Therefore, the production, inspection, and variable carbon emissions cost are applicable to all the produced quantities, $p_0(t_1+t_5)$. Thus, the total cost for the manufacturer is the sum of the setup cost ($A_1$), machine repair cost $(c_rt_r)$, production cost ($p_cp_0(t_1+t_5)$), holding cost ($h_1I_2^v$), inspection and its related cost ($I_c(t_1+t_5)$), delivery cost $\big(\frac {lc_tq(n_2+n_3)} {\gamma}\big)$, and carbon emissions cost ($p_0t_1c_p\sum e_i GE_i+(n_2+n_3)c_p\sum l_{j}GT_j$). Therefore, the total cost for the manufacturer per unit time is given by

where $t_r = \frac {t_1(p-d)+B_1} d$ and $t_5 = \frac {B_1} {p-d}$.

Furthermore, the retailer handles only shipment quantity $q$ for the whole period, $T_b$. The retailer receives the good-quality green product quantities through $n_2+n_3$ shipments. Therefore, the total green inventory of the retailer is $\frac {qT_b} 2$ for a shipment; consequently, the on-hand green inventory is $I_2^b = \frac {(n_2+n_3)qT_b} {2} = \frac {qT} {2}$. Thus, the total cost for the retailer is the sum of the total handling cost ($(n_2+n_3)A_2$), outsourcing cost ($(n_2+n_3)o_c\omega q$) and increased carrying cost ($h_2-h_1$) that is payable by the retailer. Therefore, the total cost for the retailer per unit time is

From Eqs (4.4) and (4.5), the total integrated green inventory cost per unit time is

where $t_5 = \frac {B_1} {p-d}$. As $m_1$ and $m_2$ are random variables, the expected total cost per unit time for the Second subcase is

where $E[u_1] = (1-\alpha)(1-E[m_1])+\alpha E[m_2]$, $E[u_2] = C_0+C_3(1-\alpha)E[m_1]+C_4\alpha E[m_2]+C_2(1-E[u_1])$, and $t_5 = \frac {B_1} {p-d}$.

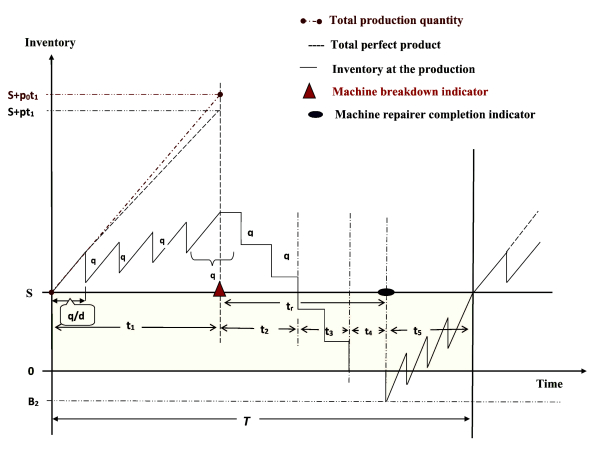
4.1.3.   Third subcase: $\frac {t_1(p-d)+S} d < t_r < \infty$

In this subcase, machine repair time $(t_r)$ is greater than the time needed for expanding the sales of all produced green products and safety stock, $(t_2+t_3)$. Let $t_4 = t_r-t_2-t_3$; then, some additional demand is generated even though there is no stock of green products. Thus, the system analyzes the shortage situations and assumes the shortage amount to be $B_2$ during the demand in $t_4$ time. To smoothly continue business, the manufacturer tries to mitigate the shortage by supplying $n_5$ shipment quantities, i.e., $n_5q = B_2 = dt_4$. Let $n_4 = [\frac {S+pt_1} q]$ be the shipment number required for selling out the produced green products as well as safety stock. After the sales are completed at $t_1+t_2+t_3$ time, $d(t_1+t_2+t_3) = n_4q = pt_1+S$ and $t_r = t_2+t_3+t_4 = \frac {t_1(p-d)+S+B_2} d$. As the system follows the NR policy, it is assumed here that demand for $B_2+S$ quantities are fulfilled by immediately starting the production after machine repair, and the demand in the production process $(dt_5)$ is fulfilled by time $t_5$ through $n_6$ shipments, i.e., $B_2+S+dt_5 = pt_5$ and $dt_5 = n_6q$. Therefore, the cycle time is calculated as $T = \Sigma _{1}^{5} t_i = (n_4+n_5)T_b+t_5 = \frac {n_4q+n_5q} d+t_5 = \frac {pt_1+S+B_2+dt_5} {d}$, $\frac {n_4+n_5+n_6} T = \frac d q$, and $pt_1+S = n_4q = d(t_1+t_2+t_3) = d(T-t_4-t_5) = dT-B_2-dt_5$. As shown in Figure 6, the on-hand green inventory $(I_3^v)$ and the amount of shortage $(I_s^v)$ for the manufacturer over the total cycle time $T$ are given by

In this subcase, the produced green items are represented as $p_0(t_1+t_5)$. The inspection and its related cost throughout the production time $(t_1+t_5)$ are calculated as $I_c(t_1+t_5) = u_2p_0(t_1+t_5)$; similarly, the production cost is $p_cp_0(t_1+t_5)$. Therefore, the total cost for the manufacturer is the sum of the setup cost ($A_1$), machine repair cost $(c_rt_r)$, production cost ($p_cp_0(t_1+t_5)$), holding cost ($h_1I_3^v$), shortage cost ($c_sI_s^v$), inspection and its related cost $I_c(t_1+t_5)$, delivery cost ($\frac {lc_tq(n_4+n_5+n_6)} {\gamma}$), and carbon emissions cost ($p_0c_p(t_1+t_5)\sum e_{i}GE_i+c_p(n_4+n_5+n_6)\sum l_{j}GT_j)$. Thus, the total cost for the manufacturer per unit time is given by

where the machine repair time is $t_r = \frac {t_1(p-d)+S+B_2} d$ and $t_5 = \frac {B_2+S} {p-d}$.

Again, the retailer handles green product quantity $q$ for the entire period $T_b$, received through $(n_4+n_5+n_6)$ shipments. Therefore, the total green inventory by the retailer is $\frac {qT_b} 2$ for a shipment, and consequently, the on-hand green inventory is $I_3^b = \frac {(n_4+n_5+n_6)qT_b} {2} = \frac {qT} {2}$. Thus, the total cost for the retailer is the sum of total handling cost ($(n_4+n_5+n_6)A_2$), outsourcing cost ($(n_4+n_5+n_6)o_c\omega q$), and increased echelon value ($h_2-h_1$) for holding green inventory. Therefore, the total cost per unit time is

From the Eqs (4.7) and (4.8), per unit time, the total integrated inventory cost is

where $t_5 = \frac {B_2+S} {p-d}$. As $m_1$ and $m_2$ are random variables, then the expected total cost per unit time for the Third subcase is

where $E[u_1] = (1-\alpha)(1-E[m_1])+\alpha E[m_2]$, $E[u_2] = C_0+C_3(1-\alpha)E[m_1]+C_4\alpha E[m_2]+C_2(1-E[u_1])$, and $t_5 = \frac {B_2+S} {p-d}$.

4.1.4.   General subcase: First, Second and Third subcases

The expected total cost functions ($ETC_1, ETC_2$, and $ETC_3$) are given by Eqs (4.3), (4.6), and (4.9) for the First, Second, and Third subcases, respectively. By considering $B_1 = 0$ and $t_r = \frac {t_1(p-d)} d$ in expression $ETC_2(q, t_1)$ of Eq (4.6), this coincides with expression $ETC_1(q, t_1)$ in 4.3. Similarly, the substitution of $B_2 = 0$, $t_5 = \frac {S} {p-d}$, and $S = B_1$ in expression $ETC_3(q, t_1)$ of Eq (4.9) coincides with expression $ETC_2(q, t_1)$ of Eq (4.6). Thus, the expected total cost function, $ETC_3(q, t_1)$, represents the more general form among three expressions. The solution methodology and all other discussions are described based on the general expected cost function in Eq (4.9).

4.2.   Second case: Without machine breakdown ($t_1=Q/p$)

Suppose machine breakdown does not occur in the production process. In this case, the system produces the ordering lot size quantity of $Q_0$ with production uptime $t_1 = Q_0/p_0 = Q/p$, where $Q$ is the actual number of perfect green products in the system. Here, the preventive maintenance could be applied to the machine, which reaches the rest stage after producing the total lot size. Based on the preventive maintenance time $(t_p)$ and the green production downtime of $t_2$, the three subcases are similar to those described in Section 4.1. The subcases are $t_p\leq t_2 = \frac {Q(p-d)} {pd}$, $t_2 < t_p\leq \frac {Q(p-d)+pS} {pd}$, and $\frac {Q(p-d)+pS} {pd} < t_p < \infty$. From the previous discussion, the Third subcase is the most general case among all three subcases; therefore, the preventive maintenance was applied to the Third subcase. By setting $t_1 = Q/p$ in the expected cost function of Eq (4.9) and replacing corrective maintenance charge $c_r$ with the preventive maintenance charge $c_p$, the system gives the total expected cost per unit time as follows:

where preventive maintenance time $t_p = \frac {Q(p-d)+p(S+B_2)} {pd}$. In addition, here, $E[u_1] = (1-\alpha)(1-E[m_1])+\alpha E[m_2]$, $E[u_2] = C_0+C_3(1-\alpha)E[m_1]+C_4\alpha E[m_2]+C_2(1-E[u_1])$, and $t_5 = \frac {B_2+S} {p-d}$.

5.   Solution methodology

As $m_1$ and $m_2$ are random variables, let their corresponding probability density functions (PDFs) are $f(m_1)$ and $f(m_2)$. Therefore, the following expectation values are used in the whole model.

As $m_1$ and $m_2$ represent the expressions of $u_1$ and $u_2$, the expected values are calculated as

and these are fixed with respect to the decision variables for this model, i.e., the derivatives of $E[u_1]$ and $E[u_2]$ with respect to variables $q$, $t_1$, and $Q$ are always zero. The next subsections of the solution procedure are described based on Eq (4.9) for the First subcase described in 4.1 (with machine breakdown) and Eq (4.10) for the Second subcase described in 4.2 (without machine breakdown).

5.1.   With machine breakdown

Proposition 1: The general cost function (4.9) is minimized if $\frac {2d(A_2+c_f)} {q^3}\times \frac {h_1\{p(2-E[u_1])-d\}} {E[u_1]} > \frac {h_1^2p^2B_2^2} {4(pt_1+S+B_2+dt_5)^4}$.

Proof. The classical optimization technique is discussed with respect to general cost function (4.9). Now, partial differentiation is performed on Eq (4.9) with respect to decision variables $q$ and $t_1$ as follows:

For the necessary conditions required for classical optimizations, expressions $\frac {\partial ETC_3(q, t_1)} {\partial q}$ and $\frac {\partial ETC_3(q, t_1)} {\partial t_1}$ are equated to zero, and stationary points $q = q^*$ and $t_1 = t_1^*$ are considered as the roots of the following equations:

These partial derivatives at this stationary point are again partially differentiated to obtain the following results:

Here, $\frac {\partial^2 ETC_3(q, t_1)} {\partial q^2} > 0$ and $\frac {\partial^2 ETC_3(q, t_1)} {\partial t_1^2} > 0$. In addition, the following is reviewed for global minimization at stationary point $(q^*, t_1^*)$

where $\frac {2d(A_2+c_f)} {q^3}\times \frac {h_1\{p(2-E[u_1])-d\}} {E[u_1]} > \frac {h_1^2p^2B_2^2} {4(pt_1+S+B_2+dt_5)^4}$. This shows that the expected total cost function in Eq (4.9) reaches the global minimum at $(q^*, t_1^*)$, and this point is obtained by solving Eqs (5.1) and (5.2).

5.2.   Without machine breakdown

Proposition 2: Globally minimize the expected total cost function Equation (4.10) if $\frac {2d(A_2+c_f)} {q^3}\times \frac {h_1\{p(2-E[u_1])-d\}} {u_1(Q+S+B_2+dt_5)} > \frac {h_1^2B_2^2} {4(Q+S+B_2+dt_5)^4}$.

Proof. Partially differentiate Eq (4.10) with respect to $q$ and $Q$ as follows:

By equating expressions $\frac {\partial ETC_4(q, Q)} {\partial q}$ and $\frac {\partial ETC_4(q, Q)} {\partial Q}$ to zero, stationary points $q = q^*$ and $Q = Q^*$ are considered the default values in Eqs (5.3) and (5.4). Partially differentiate these equations again to obtain the following result at that stationary point.

Here, $\frac {\partial^2 ETC_4(q, Q)} {\partial q^2} > 0 \hbox{ & } \frac {\partial^2 TC_4(q, Q)} {\partial Q^2} > 0$. Moreover, check whether the following holds for global minimization at stationary point $(q^*, Q^*)$

where $\frac {2d(A_2+c_f)} {q^3}\times \frac {h_1\{p(2-E[u_1])-d\}} {u_1(Q+S+B_2+dt_5)} > \frac {h_1^2B_2^2} {4(Q+S+B_2+dt_5)^4}$. This shows that the expected total cost function in Eq (4.10) reaches a global minimum at $(q^*, Q^*)$, which is obtained by solving Eqs (5.3) and (5.4).

Here, Eq (4.10) shows the general total expected cost function. Similarly, the global minimization at optimal points $q = q^*$ and $Q = Q^*$ must satisfy the following equations.

6.   Numerical study

The validation of this model is verified by the following two examples. The useful optimum results are shown using tables; finally, the case study is described to analyze the real data.

6.1.   Example 1

The considered parametric values are described as follows, where some supported parametric values are obtained from the research by ^[40]. The values are $d = 30$ units/order, $p_0 = 40$ units/day, $A_1 = \$50$/setup, $A_2 = \$5$/shipment, $p_c = \$10$/unit, $h_1 = \$0.08$/unit, $h_2 = \$0.1$/unit, $S = 400$ units, $\alpha = 5\%$, $E[m_1] = 0.01$, $E[m_2] = 0.04$, $C_0 = \$0.1$/unit, $C_2 = \$1$/unit, $C_3 = \$0.023$/unit, $C_4 = \$0.01$/unit, $\omega = 40\%$, $o_c = \$2.3$/unit outsource product, $c_t = \$0.7$/shipment/container, $\gamma = 5$ units, $l = 1780$ km, $e_1 = 90$ MJ/unit product, $e_2 = 130$ MJ/unit product, $e_3 = 200$ MJ/unit product, $GE_1 = 0.2$ kg.CO$_2$e/MJ, $GE_2 = 0.26$ kg.CO$_2$e/MJ, $GE_3 = 0.32$ kg.CO$_2$e/MJ, $c_p = \$0.004$/kg.CO$_2$e, $l_1 = 150$ km, $l_2 = 310$ km, $l_3 = 520$ km, $l_4 = 800$ km, $GT_1 = 0.15$ kg.CO$_2$e/km, $GT_2 = 0.018$ kg.CO$_2$e/km, $GT_3 = 0.03$ kg.CO$_2$e/km, and $GT_4 = 0.024$ kg.CO$_2$e/km. The numerical example of this model is based on two main cases: with and without machine breakdown. Each case has three subcases, which are represented in the tabular format.

6.1.1.   With machine breakdown

The numerical experiment in the case of machine breakdown includes the previous parametric values along with the following parametric values of corrective maintenance cost ($c_r$), corrective maintenance time ($t_r$), downtime of green inventory ($B_1$), shortages ($B_2$), and shortage cost ($c_s$). The optimal results for the First, Second, and Third subcases are listed in Table 2 and simultaneously the results are graphically shown in Figure 7 within the machine breakdown situation.

The First subcase shows that corrective maintenance time $(t_r) = 5$ days is lesser than inventory downward time $(t_2) = \frac {t_1^*(p-d)} d = 6.13$ days; i.e., the machine repair time is lesser than the time required for completing green production. Next, in the Second subcase, $t_r = \frac {t_1^*(p-d)+S+B_1} d = 2.43$ days, which is greater than $t_2 = \frac {t_1^*(p-d)} d = 2.03$ days; i.e., the machine repair time is greater than the time for finishing the green production. In the Third subcase, $t_r = \frac {t_1^*(p-d)+S+B_2} d = 39.97$ days is greater than $t_2+t_3 = \frac {t_1^*(p-d)+S} d = 35.97$ days; i.e., the machine repair time is greater than the time for finishing production of green products as well as safety stock.

Here normal production rate is $p_0 = 40$ units/day and per day the defective products are calculated as $p_0-p = 2.3$ units. At the optimum production time (days), First, Second, and Third subcases are presented the defective green products as $2.3\times 23.88 = 54.92$ units, $2.3\times 7.93 = 18.24$ units, and $2.3\times 88.2 = 202.86$ units, respectively. These unusable defective green products reduce the brand image of the company due to unsatisfied feedback from the customers. Thus, by disposing of these wastage green products, the production system is cleaned.

6.1.2.   Without machine breakdown

This section provides a numerical example for the case in which the machine breakdown does not occur by considering the general case, i.e., Third subcase. Along with the previous parametric values and preventive maintenance cost of $c_p = \$120$, the shortage green products at $B_2 = 200$ units and $c_s = \$100$ give the minimum expected total cost of $ETC_4(q^*, Q^*) = \$7,568.34$ for the optimal delivery quantity of $q^* = 56.19$ units and expected order lot size of $Q_0^* = Q^*/E[u_1] = 2,130.16$ units, where the perfect lot size is $Q^* = 2,130.31$ units. Therefore, in this case, the wastage unusable green products are approximately 130 units and the production system is cleaned by discarding these defective products. Here, preventive repair time $t_p = \frac {Q^*(p-d)+p(S+B_2)} {pd} = 34.5$ days is greater than time $t_2+t_3 = 27.89$ days. The graphical representations for this case is shown in Figure 8.

6.2.   Example 2

In this example, we consider the following parametric values: $d = 300$ units/order, $p_0 = 700$ units/month, $A_1 = \$200$/setup, $A_2 = \$25$/shipment, $p_c = \$12$/unit, $h_1 = \$0.09$/unit, $h_2 = \$0.11$/unit, $S = 100$ units, $\alpha = 5\%$, $E[m_1] = 0.02$, $E[m_2] = 0.04$, $C_0 = \$0.02$/unit, $C_2 = \$0.8$/unit, $C_3 = \$0.03$/unit, $C_4 = \$0.02$/unit, $\omega = 30\%$, $o_c = \$40$/unit outsource product, $c_t = \$0.7$/ shipment/ container, $\gamma = 15$ units, $l = 1360$ miles, $e_1 = 90$ ft-Ibs/unit product, $e_2 = 130$ ft-Ibs/unit product, $e_3 = 200$ ft-Ibs/unit product, $GE_1 = 0.2$ kg.CO$_2$e/ft-Ib, $GE_2 = 0.26$ kg.CO$_2$e/ft-Ib, $GE_3 = 0.32$ kg.CO$_2$e/ft-Ib, $c_p = \$0.004$/kg.CO$_2$e, $l_1 = 150$ miles, $l_2 = 310$ miles, $l_3 = 400$ miles, $l_4 = 500$ miles, $GT_1 = 0.15$ kg.CO$_2$e/mile, $GT_2 = 0.018$ kg.CO$_2$e/mile, $GT_3 = 0.03$ kg.CO$_2$e/mile, and $GT_4 = 0.024$ kg.CO$_2$e/mile. The optimal results for this example are listed in Table 3, where three subcases and the last case are described separately. The expected optimal lot size is $Q_0^* = Q/E[u_1]$.

Similarly, here the normal production rate is $p_0 = 700$ units/month and per month the defective products are calculated as $p_0-p = 46.9$ units. At the optimum production time (months), First, Second, and Third subcases are presented the defective green products as $46.9\times 2.28 = 106.9$ units, $46.9\times 1.99 = 93.3$ units, and $46.9\times 3.01 = 141$ units, respectively for machine breakdown situations. Again, for the without machine breakdown situations, the defective green products are $(1-E[u_1])Q_0^* = 22.4$ units. Thus, by disposing of these wastage green products, the production system is cleaned.

6.3.   Sensitivity analysis

From Table 4 of the sensitivity analysis, the following statements are declared in Example 6.1. The percentage of the expected total cost of various cases are changed with the change in the parameter values by $-50\%$, $-25\%$, $25\%$, and $50\%$.

${1)}$ The change of all parameter values from negative to positive shows a simultaneous change in the resultant expected total cost. However, $ETC_2$ and $ETC_3$ have no convergent result for $+50\%$ change in $h_1$ and $-50\%$ and $-25\%$ in $h_2$. In addition, expression $ETC_4$ from Eq (4.10) does not show a convergent result for the change in parameters $h_1$ and $h_2$. Furthermore, $ETC_4$ does not converge for $-50\%$ and $-25\%$ changes in $A_1$ and $c_s$, $+50\%$ in $p_c$, $+25\%$ in carbon price ($c_p$), and $+50\%$ in $c_p$. All the expected total cost functions are more sensitive to parameter change from negative to positive values; this is good for industries in terms of investment reduction. Between the setup cost to the manufacturer ($A_1$) and handling cost to the retailer ($A_2$), the latter is more sensitive.

${2)}$ The percentage of change of the parameters is directly proportional to the green production cost ($p_c$), delivery cost ($c_t$), and outsourcing cost. This implies that with cost reduction, the total expected cost reduces, which is beneficial to manufacturing industries. The delivery cost is more sensitive than the green production cost.

${3)}$ Among all the expressions in Eqs (4.3), (4.6), (4.9) and (4.10), $ETC_4$ in Eq (4.10) is the most sensitive, as it does not provide any convergence results for the change in various parameters. Here, the delivery cost is the most sensitive among all the parameters.

${4)}$ From the above explanation, the industry manager is always watching the parametric values for which range the cost function can get a convergent and better result. The minimization problem gets better timing for corrective and preventive maintenance. There is another decision for the retailer that how much product can be distributed through outsourcing mode to get a better finding.

6.4.   Case study

Generally, the collected data from any realistic situation are irregular, and normalization is required for the probabilistic function. The data are normalized using the sample mean, standard deviation, and histogram to give PDFs of $f(m_1)$ and $f(m_2)$. Accordingly, the expectation values of the Type-I errors $E(m_1)$ and Type-II errors $E(m_2)$ are obtained; finally, the values of $E(u_1)$ and $E(u_2)$ are obtained. The data, used in this study, are taken from a company, situated in West Bengal, India. The company does not transport products via ocean barge and air; therefore, $l_3 = 0$ and $l_4 = 0$. That is, the travailing distance is $460$ km, and their green products do not fall short (i.e., $B_2 = 0$) when preventive maintenance is performed. Using the following data, the optimal result is listed in Table 5: parametric values are $d = 300$ units/order, $p_0 = 700$ units/month, $A_1 = \$200$/setup, $A_2 = \$25$/shipment, $p_c = \$12$/unit, $h_1 = \$0.09$/unit, $h_2 = \$0.11$/unit, $S = 100$ units, $\alpha = 5\%$, $E[m_1] = 0.02$, $E[m_2] = 0.04$, $C_0 = \$0.02$/unit, $C_2 = \$0.8$/unit, $C_3 = \$0.03$/unit, $C_4 = \$0.02$/unit, $\omega = 30\%$, $o_c = \$40$/unit outsource product, $c_t = \$0.7$/shipment/container, $\gamma = 15$ units, $l = 460$ km, $e_1 = 90$ joule/unit product, $e_2 = 130$ joule/unit product, $e_3 = 200$ joule/unit product, $GE_1 = 0.2$ kg.CO$_2$e/joule, $GE_2 = 0.26$ kg.CO$_2$e/joule, $GE_3 = 0.32$ kg.CO$_2$e/joule, $c_p = \$0.004$/kg.CO$_2$e, $l_1 = 150$ km, $l_2 = 310$ km, $GT_1 = 0.15$ kg.CO$_2$e/km, and $GT_2 = 0.018$ kg.CO$_2$e/km. In Table 5, the three subcases and last case are described separately. The expected optimal lot size is $Q_0^* = Q/E[u_1]$. The realistic result in the enterprise is similar to that of the model in Table 5. The company accepts the model and followed the proposal of this research. The use of this realistic data could achieve better results that those obtained in Example 2 in Section 6.2.

6.5.   Comparative study

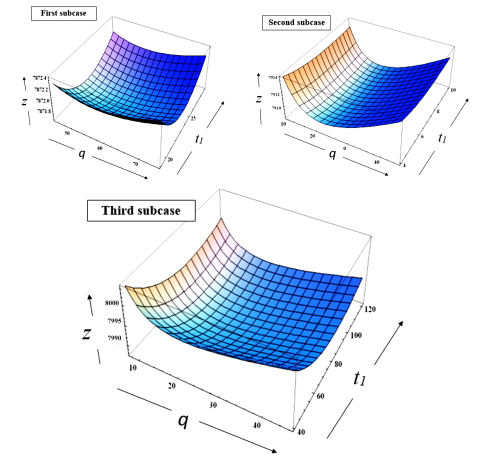
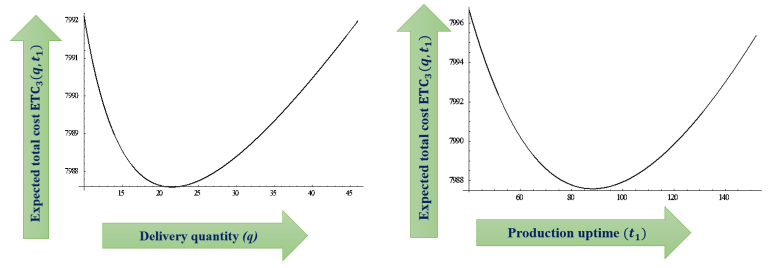
This section presents the relationship between the expected total cost and decision variables. As previously discussed, the Third subcase is the general subcase among all three subcases in the case of machine breakdown. The expected total cost for the Third subcase is considered in the discussion in this section. Figure 9 plots the expected total cost for the general subcase (i.e., Eq (4.9)) versus the decision variables. Here, the cost function increases or decreases depending on variables and shows a convex curve, with other parameters fixed.

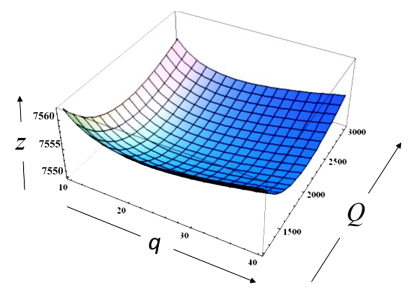
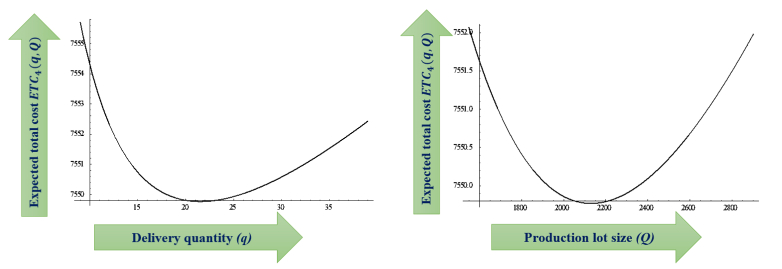
Similarly, Eq (4.10) presents the expected total cost in the case without machine breakdown, as plotted in Figure 10 against decision variables; the curve is convex. This figure is advantageous for obtaining the optimal values of decision variables.

6.6.   Managerial insights

The sensitivity analysis and comparative study provide many significant managerial insights for improving the manufacturer's industrial processes. In any situation that means machine breakdown and no breakdown situations, the industry manager gets convergence results, which are gloriously accepted from the case study discussion. The question regarding how the manufacturer controls the manufacturing process for obtaining the minimum system cost can be answered straightforward: by obtaining any of the subcases or the last case---whichever is applicable. The numerical study results are obtained as $\$7,871.67$–$\$7,987.6$ for the three subcases and $\$7,549.77$ for the Second case. This shows that the Second case, in which the machine breakdown does not occur, is the best case for the manufacturer, who could take the decision of resolving the machine breakdown situation; i.e., the manufacturer tries to compensate for the machine breakdown in the manufacturing process. From the subcases, cost in the First subcase is less than the cost in the Second subcase, which in turn is less than the cost in the Third subcase. Thus, the manufacturer would try to start the machine as soon as possible in the case of breakdown.

The sensitivity analysis shows that the expected total cost greatly impacts the transportation cost. To achieve a better result, the manufacturer may minimize the transportation cost. In any situation, there may arrive some imperfect products within the system. The industry's brand image maintains and increases by discarding those imperfect products from the system. Errors in the inspection process are overcome to obtain the best result.

7.   Conclusions

This study introduced a supply chain model between a manufacturer and a retailer for a single type of green product by employing the MTO policy. The manufacturer produced both high- and low-quality green products and determined the defective green products through an inspection process. However, the human inspection processes might not always be reliable, mainly resulting in two types of errors: Type-I and Type-II errors. These errors were discussed based on the quality of the inspected green products in this model. By assuming the presence of these two types of errors, the authors calculated the quantities of perfect green products and discarded the imperfect wastage green products. In this way, the production process was cleaned from waste products and grew up the company's brand image. The inspection and related costs were calculated from inspection process, along with the cost for those inspection errors and disposal costs. During the production process, the machine might fail, and an immediate corrective repair might be applied. The cost of that corrective maintenance was included in the proposed model. However, the machine might not fail during the whole production process in a specific cycle; therefore, preventive maintenance might be performed to ensure its good performance in the next cycle. This was similar in the Second case 4.2, in which the additional stock of green products was distributed to the market after the production was finished. These two cases were divided into three subcases depending on the time required for maintenance and delivery of finished green products. The general case was discussed in detail in this manuscript, and a classical optimization technique was utilized among these subcases. The model followed the SSMD policy for delivering green products to the market. The transportation cost was depended on the capacity of the container and distance between manufacturer and retailer. During production and transportation processes, the system introduced GHGs, including CO$_2$, which affected the environment. The GHG was calculated by the CO$_2$e (or CO$_2$eq) [kg]. The emitted GHG was calculated separately for the production and transportation processes. Green-product transportation might not be via a unit mode, thus this study discussed four types of transportation modes. The total emitted GHGs in the transportation process was calculated by adding the emissions of all the transportation modes. If in case the mode does not fall under any of the four types mentioned in the model, it could be omitted by simply considering the distance traveled as zero. Finally, the total GHG emissions cost was calculated, including emission for both production and transportation processes. The expected total cost contained inspection and its related cost, transportation costs, outsourcing cost, and carbon emission costs. Among the many discussed cases, we used the general results for the model and globally optimized the general cost function by using a classical analytic method. Finally, results for numerical and sensitivity analyses for some parameters were obtained.

The limitation of this research is that the machine could break down at a random time; however, this was not considered as a random variable in this study. The machine repair and preventive maintenance times depend on the produced products, available safety stock, and shortage of green products, which were not considered in this model; this can be overcome by extending the model by assuming time as a random variable.

In the future, the model can be extended using multiple types of green products, an inspection of an out-of-control system, and occurrences of multiple machine breakdowns. Here, outsourcing is considered reliable; this is another limitation of the model, anyone can extend the model by assuming unreliable outsourcing criteria. A new direction can be obtained by considering the deterioration criteria for green products ^[11]. The model can be extended by considering stock-dependent holding cost and demand within trade-credit policy ^[9]. In addition, various other environmental issues for different countries within integrated management system can be considered in the model of ^[1] along with different methodology ^[35]. The unreliable batch will modify that model ^[6], and along this directions, the model may be extended.

Acknowledgments

The Work is supported by the National Research Foundation of Korea (NRF) grant, funded by the Korea Government (MSIT) (NRF-2020R1F1A1064460).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix