Citation: Dora Luz Castro-López, Macarena Trujillo, Enrique Berjano, Ricardo Romero-Mendez. Two-compartment mathematical modeling in RF tumor ablation: New insight when irreversible changes in electrical conductivity are considered[J]. Mathematical Biosciences and Engineering, 2020, 17(6): 7980-7993. doi: 10.3934/mbe.2020405
| [1] | Rui Zhang, Shuicai Wu, Weiwei Wu, Hongjian Gao, Zhuhuang Zhou . Computer-assisted needle trajectory planning and mathematical modeling for liver tumor thermal ablation: A review. Mathematical Biosciences and Engineering, 2019, 16(5): 4846-4872. doi: 10.3934/mbe.2019244 |
| [2] | Xiaoru Wang, Hongjian Gao, Shuicai Wu, Tao Jiang, Zhuhuang Zhou, Yanping Bai . Numerical evaluation of ablation zone under different tip temperatures during radiofrequency ablation. Mathematical Biosciences and Engineering, 2019, 16(4): 2514-2531. doi: 10.3934/mbe.2019126 |
| [3] | Salman Lari, Hossein Rajabzadeh, Mohammad Kohandel, Hyock Ju Kwon . A holistic physics-informed neural network solution for precise destruction of breast tumors using focused ultrasound on a realistic breast model. Mathematical Biosciences and Engineering, 2024, 21(10): 7337-7372. doi: 10.3934/mbe.2024323 |
| [4] | Nilay Mondal, Koyel Chakravarty, D. C. Dalal . A mathematical model of drug dynamics in an electroporated tissue. Mathematical Biosciences and Engineering, 2021, 18(6): 8641-8660. doi: 10.3934/mbe.2021428 |
| [5] | J. A. López Molina, M. J. Rivera, E. Berjano . Electrical-thermal analytical modeling of monopolar RF thermal ablation of biological tissues: determining the circumstances under which tissue temperature reaches a steady state. Mathematical Biosciences and Engineering, 2016, 13(2): 281-301. doi: 10.3934/mbe.2015003 |
| [6] | Urszula Ledzewicz, Shuo Wang, Heinz Schättler, Nicolas André, Marie Amélie Heng, Eddy Pasquier . On drug resistance and metronomic chemotherapy: A mathematical modeling and optimal control approach. Mathematical Biosciences and Engineering, 2017, 14(1): 217-235. doi: 10.3934/mbe.2017014 |
| [7] | Avner Friedman, Harsh Vardhan Jain . A partial differential equation model of metastasized prostatic cancer. Mathematical Biosciences and Engineering, 2013, 10(3): 591-608. doi: 10.3934/mbe.2013.10.591 |
| [8] | María J. Rivera, Juan A. López Molina, Macarena Trujillo, Enrique J. Berjano . Theoretical modeling of RF ablation with internally cooled electrodes: Comparative study of different thermal boundary conditions at the electrode-tissue interface. Mathematical Biosciences and Engineering, 2009, 6(3): 611-627. doi: 10.3934/mbe.2009.6.611 |
| [9] | Weirui Lei, Jiwen Hu, Yatao Liu, Wenyi Liu, Xuekun Chen . Numerical evaluation of high-intensity focused ultrasound- induced thermal lesions in atherosclerotic plaques. Mathematical Biosciences and Engineering, 2021, 18(2): 1154-1168. doi: 10.3934/mbe.2021062 |
| [10] | Rebeccah E. Marsh, Jack A. Tuszyński, Michael Sawyer, Kenneth J. E. Vos . A model of competing saturable kinetic processes with application to the pharmacokinetics of the anticancer drug paclitaxel. Mathematical Biosciences and Engineering, 2011, 8(2): 325-354. doi: 10.3934/mbe.2011.8.325 |
Computer modeling has been widely used to study temperature distributions during radiofrequency (RF) tumor ablation (RFA). Up to now, this method involved solving an electrical-thermal coupled problem using a mathematical framework based on the Laplace equation to solve the electrical problem and the Pennes' equation for the thermal problem. The first computer models mimicked an RFA on non-tumor tissue, i.e. the tissue sub-domain was assumed to be homogeneous and constituted by a 'single compartment' [1,2,3]. Computer modeling was later used to explore temperature distributions in tumors with non-healthy tissue properties, for which two-compartment models were proposed: one compartment (or sub-domain) representing the tumor and the other the healthy tissue. Some two-compartment models considered a tumor with a cylindrical shape [4,5], while others assumed a spherical shape [6,7,8] or a two-layer setup [9]. About the RF applicator, some studies considered a multi-prong [6,7] while others modeled a single-needle RF applicator as the Cool-tip model [10,11,12].
The reason for two-compartment models was the experimental evidence that found that tumor electrical conductivity (σ) at RF frequencies is higher than that of healthy tissue. For instance, Haemmerich et al [13] measured σ at 1 MHz in in vivo tissues and reported mean values of 0.461 S/m for healthy liver and 0.523 S/m for tumor tissue. Prakash et al [14] reported mean values of 0.271 S/m for healthy ex vivo liver tissue and 0.471 S/m for tumor tissue (at 1 MHz). Haemmerich et al [15] reported mean values of 0.26 S/m for healthy liver and 0.504 S/m for tumor tissue (at 460 kHz) and Laufer et al [16] reported mean values of 0.15 S/m for healthy liver and 0.25 S/m for tumor tissue (at 400 kHz). This data hence suggested that RF power could be preferentially deposited in the tumor. In fact, the simulations conducted with two-compartment models showed more effective tumor destruction (in terms of temperature reached and coagulation zone volume) than those conducted with homogeneous (single compartment) models [10,11].
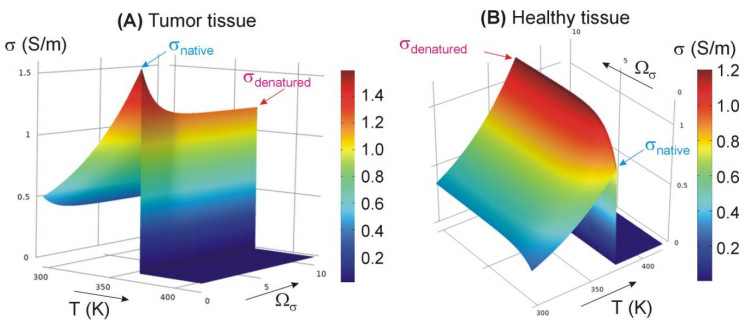
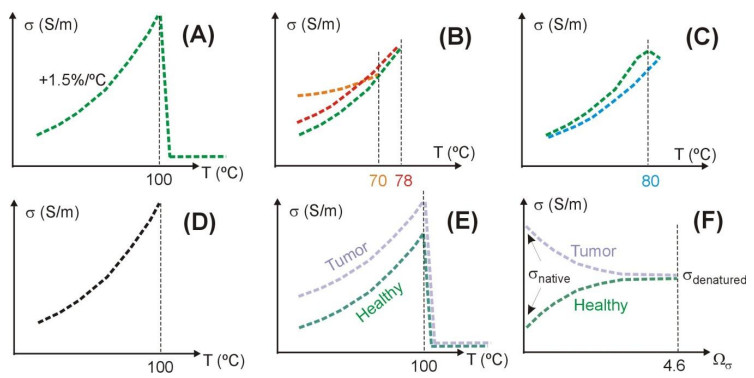
All the two-compartment models proposed to date have considered a change of σ exclusively dependent on temperature, based on an increase up to 100 ℃ (e.g. +1.5%/℃) and then a drop of several orders of magnitude to mimic the water loss associated with vaporization at this temperature (see Figure 1A) [4,5,6,7]. These models therefore did not consider irreversible changes of σ due to the accumulated thermal damage reported for non-tumor (i.e. healthy) tissues subjected to hyperthermic heating [17,18,19,20]. For instance, Pop et al [17] characterized the change of σ in ex vivo kidney at 460 kHz during and after heating at constant temperature (with target values between 48 and 78 ℃) and separated the changes in σ due to the reversible temperature effect (with a rate of +1.62%/℃) from the permanent structural effect, which was modeled by an Arrhenius model. In general, they observed that in the samples heated to between 64.3 and 71.2 ℃, during cooling σ dropped to a higher value than for native tissue (as suggested by the orange line in Figure 1B). In this context, the adjective native refers to tissue that has not undergone heating, as opposed to denatured, which has been subjected to heating. Interestingly, Pop et al also reported 'aberrant' behavior in samples heated to 78.5 ℃, in which σ fell during cooling to a lesser value than samples heated to 71.2 ℃ or lower (as suggested by the red line in Figure 1B). This behavior was associated with tissue desiccation, since the measurements were made after slow heating for several minutes.
Zurbuchen et al [18] measured σ at 470 kHz in ex vivo and in vivo liver samples subjected to heating and observed a plateau around 80 ℃ (see green line in Figure 1C) and a return to the initial σ value after cooling (as suggested by the blue line in Figure 1C). Suspecting that the plateau was due gradual tissue desiccation at slow heating, Macchi et al [19] measured σ at 480 kHz in ex vivo liver samples and compared changes in σ with temperature at fast and slow heating rates. They found that with fast heating the plateau disappeared and σ rose gradually to 100 ℃ (maximum temperature used in their experiments), therefore returning almost to the starting point in Figure 1A (see black line in Figure 1D). These authors conducted RFA simulations considering different mathematical expressions to model the dependence of σ, ranging from those that only take temperature into account (as shown in Figure 1A) to those that included accumulated thermal damage at slow (Figure 1C) and fast (Figure 1D) heating rates. Interestingly, they did not find any large differences in terms of coagulation zone volume, although it should be remembered that they only simulated up to the first roll-off (impedance jump to 300 Ω). Macchi's study did not measure values of post-heating σ, i.e. during cooling. These results were later confirmed by Deas Yero et al [20], who measured σ at 500 kHz in ex vivo liver samples subjected to slow and fast heating.
If the studies on irreversible changes in σ with temperature in healthy tissues are not abundant, there is even less data on what occurs in tumor tissues. To our knowledge, only Haemmerich et al [15] reported σ values at 500 kHz in tumor tissue before and after ablation. Although these values were taken from a single patient, it is remarkable that while the healthy tissue σ was considerably lower than in the tumor before ablation (in agreement with other studies [13,14,15,16]), the difference between tumor and healthy tissue σ was greatly reduced after ablation. Although this finding may seem irrelevant, we think that it would be reasonable from a physical point of view to imagine that the difference in σ values of healthy tissue and tumor could be smaller after ablation because the two tissue types 'tend towards a similar physiological state', which is that of heat-induced necrotized tissue. If this were true, the advantage of tumor over surrounding healthy tissue in terms of improved electrical conduction would not be sustained throughout several minutes of ablation, but would only exist before tumor ablation. Our goal was thus to explore how temperature distribution and coagulation zone size computed from a two-compartment model could vary in the case of including simultaneously reversible changes due to temperature, as suggested in Figure 1E, and irreversible changes due to thermal coagulation as suggested in Figure 1F (where σ could be modulated by an Arrhenius function Ωσ, as previously done by Macchi et al [19] in case of homogeneous tissue) in the specific case of assuming that the differences in σ between healthy and tumor tissue disappear as tissue passes from native state to denatured state.
As in most two-compartment models, the electrical conductivities (σ) of healthy and tumor tissue were considered to be different, as has been reported in some experimental studies [13,14,15,16]. We used the values reported by Haemmerich et al [15]: 0.26 S/m for healthy liver and 0.504 S/m for tumor tissue (assumed to be taken at room temperature, 22 ℃).
The reversible change of σ associated with temperature was modeled using a piecewise function Φ(T) (as shown in Figure 1E) characterized by an increase of +1.5%/℃ until 100 ℃, followed by a reduction of two orders of magnitude between 100 and 101 ℃, and a constant value thereafter. This allows modeling the tissue desiccation associated with vaporization [19]. To sum up, the reversible change of σ with temperature was expressed as:
| σ(T)=σnative⋅Φ(T) | (1) |
where σnative is the electrical conductivity of healthy or tumor tissue at 22 ℃. On the other hand, the irreversible changes associated with the heating for each σ were modeled by assuming that both σnative (tumor and healthy tissue) tend towards an identical value (σdenatured) as the ablation progresses (as shown in Figure 1F). We assumed a σdenatured value equal to the mean value between the two σnative i.e. 0.38 S/m (at 21℃). To model the change from σnative to σdenatured we used an Arrhenius model as proposed by Pop et al [17], which determines the first-order kinetic rate for the irreversible changes in electrical conductivity. The parameter Ωσ represents the expected fraction of cells unaffected by irreversible changes, and is computed as follows:
| Ωσ(T,t)=Aσ∫t0e−ΔEσR⋅T(τ)dτ | (2) |
where Aσ is the frequency factor (6×1034 s-1), ΔEσ is the activation energy for the irreversible reaction (2.38×105 J/mol), R is the universal gas constant (8.314 J/mol·K) and T(τ) is the absolute temperature (K) as a function of time. The values of Aσ and ΔEσ were taken from [17] and were those of ex vivo kidney tissue (none are available for liver). The parameter Ωσ (associated with irreversible changes) was combined with Eq. 1 (associated with reversible changes) to obtain a full expression for changes of σ:
| σ(T,Ωσ)=[σnative+(σdenatured−σnative)⋅(1−e−Ωσ)]⋅e0.015(T−Tref) | (3) |
where Tref is the temperature at which the values of σnative and σdenatured were considered (22 ℃). Figure 2 shows the change of σ with temperature (reversible changes) and Ωσ (irreversible changes) both for healthy and tumor tissues.
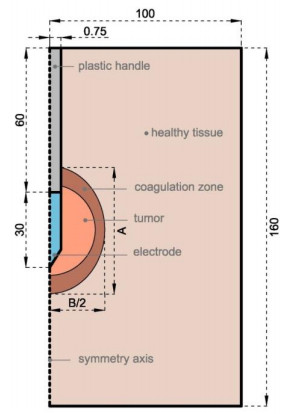
A two-compartment model was built and solved by the Finite Element Method using Comsol Multiphysics software (Burlington, MA, USA). The geometry of the problem was represented by a 2D axis symmetric model, which consisted of a cylindrical subdomain mimicking healthy liver tissue and a spherical subdomain mimicking tumor with different diameters (2, 3 and 4 cm) (see Figure 3). It also included a 3-cm 17G RF Cool-Tip applicator placed in the center of the tumor. The dispersive electrode was modeled as an electrical boundary condition V = 0 on all the outer boundaries except the symmetry axis. The internal cooling of the active electrode was modeled by setting a constant temperature of 10 ℃, while temperature was 37 ℃ on all the outer boundaries except the symmetry axis. The model was based on a coupled electric-thermal problem in which the governing equation for thermal problem was the Bioheat Equation:
| ρc∂T∂t=∇⋅(k⋅∇T)−ρbcbω(T−Tb)+Qm+QRF | (4) |
where ρ is tissue density, c tissue specific heat, T temperature, k tissue thermal conductivity, ρb blood density, cb blood specific heat, Tb body temperature (37 ℃), ω blood perfusion coefficient (at temperature Tb), Qm metabolic heat generation per unit volume (which can be negligible compared to other terms), and QRF heat source term due RF energy. Eq. (4) was applied to each region of the model by substitution of the appropriate properties. To calculate QRF we solved the electrical problem, which for RFA can be calculated by:
| QRF=→J⋅→E=σ|→E|2=σ|−∇V|2 | (5) |
where →J is the current density vector (A/m2), →E electrical field vector (V/m), σ electrical conductivity (S/m) and V voltage (V). We used quasi-static approximation to solve the electrical problem where conduction currents were assumed to dominate compared to displacement currents. The electric voltage was computed by solving the equation [14]:
| ∇⋅(σ∇V)=0 | (6) |
Table 1 shows the values of the properties of the materials [15,21]. The accumulated thermal damage is the effect of exposing it to a high temperature for a prolonged time. A traditional way to predict the probability of irreversible thermal damage is the Arrhenius reaction rate model (as done in Eq. (2)) in which the parameter Ω is related with the expected cellular survival fraction and is computed as follows:
| Material | ρ (kg/m3) | σ (S/m) | c (J/kg·K) | k (W/m·K) | ω (1/s) |
| Healthy tissue | 1080 | 0.26 | 3455 | 0.502 | 0.016 |
| Tumor | 1045 | 0.504 | 3760 | 0.5 | 0.009 |
| Blood | 1046 | - | 3639 | - | - |
| Metal (electrode) | 8000 | 7.4·106 | 480 | 18 | - |
| Plastic (insulated trocar) | 70 | 10-5 | 1045 | 0.026 | - |
| ρ: density, σ: electrical conductivity, c: specific heat, k: thermal conductivity, ω: blood perfusion. Tissue properties assessed at 37 ℃ (see text for more details related to σ thermal dependence). | |||||
DownLoad:
CSV
| Ω(T,t)=A∫t0e−ΔER⋅T(τ)dτ | (7) |
where A is the frequency factor (7.39·1039 s-1), ΔE is the activation energy for the irreversible damage reaction (2.557·105 J/mol), and R is the universal gas constant (8.314 J/mol·K). The parameters A and ΔE were taken from [10]. A value Ω = 4.6 (99% cell death probability) was used to compute the coagulation zone volume. Note that although Ωσ and Ω have the same type of mathematical formulation (both are Arrhenius models), the former models the irreversible changes in tissue σ, while the latter models the vital state of the tissue.
We assumed that blood perfusion ceased once tissue was destroyed. This cessation was simulated by a first order kinetic model [7]:
| ω(T,t)=ω0⋅e−Ω(T,t) | (8) |
where ω0 is the blood perfusion coefficient at temperature Tb.
In order to compare the two formulations (Eq. (1) vs. Eq. (3)), we conducted computer simulations with models: the one that considers only irreversible changes in σ (Model 1) vs. the one that also considers irreversible changes (Model 2). The computer simulations mimicked a controlled-impedance pulsed protocol as described in [22]. Basically, a constant voltage of 90 V is applied until the impedance exceeds a threshold of 100 Ω (roll-off). The voltage is then discontinued for 15 s, and the initial voltage value is reapplied. This is repeated every time a roll-off occurs for a total duration of 12 min, after which the computer simulates a 10 min cooling period in order to include the thermal latency and the subsequent enlargement of the coagulation zone [23]. The isoline Ω = 4.6 was used to compute the axial (A) and transverse (B) diameters of the coagulation zone (see Figure 3).
The models were verified in terms of mesh size, time-step and outer dimensions as described in [22]. The value of the maximum temperature reached in the tissue at the end of the ablation was used as a control parameter and a difference of less than 0.5% as a criterion between simulations.
Models 1 and 2 were verified in terms of spatial (mesh size) and time (time-step) discretization, along with the outer dimensions. Convergence tests were conducted to verify that the values used in the computer model represented the RFA with sufficient accuracy. The meshing size at the electrode-tissue interface was ~0.003 mm and at the point furthest from the active electrode was ~16 mm. The optimal time-step was ~0.5 s and the number of triangular elements ranged from 1300 to 1550, depending on the tumor size.
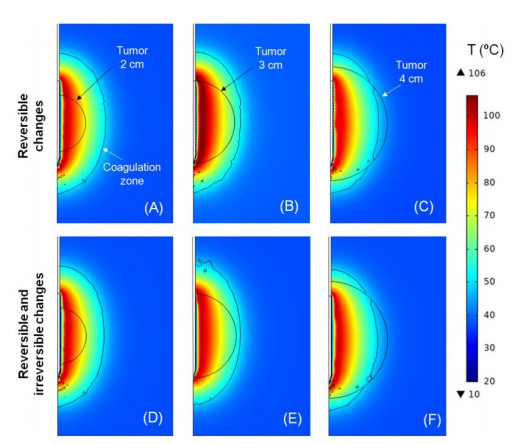
Table 2 shows the axial and transverse diameters of the coagulation zone computed from the model considering only reversible changes of σ and from the model including also irreversible changes. The differences between both models were 0.1 and 0.2 cm for axial and transverse diameters, respectively. This small difference between the results predicted by both models is also reflected in the marked similarity between the temperature distributions computed, as shown in Figure 4. There were hardly any differences between the number of roll-offs during RFA predicted by both models (29-32).
| Tumor diameter (cm) | Axial diameter (cm) | Transverse diameter (cm) | |||
| Model 1 | Model 2 | Model 1 | Model 2 | ||
| 2 | 5.0 | 5.1 | 3.6 | 3.4 | |
| 3 | 5.2 | 5.3 | 3.7 | 3.5 | |
| 4 | 5.0 | 5.1 | 3.4 | 3.6 | |
DownLoad:
CSV
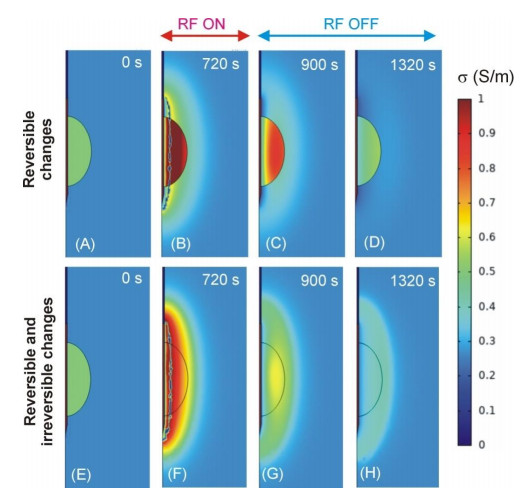
Due to the intricate mathematical formulation developed to model the reversible and irreversible changes in σ during RFA (see Eq (3) and Figure 2), it was crucial to check that each point of the domain (including tumor and healthy tissue) behaved as expected. In this regard, Figure 5 shows the evolution of the spatial distribution of σ at the beginning of the RFA (0 s), just after RF power application (720 s) and at two times during the cooling period following the cessation of RF power (900 and 1320 s). As expected from a two-compartment model, at the initial time both models clearly show different σ values for the tumor and healthy tissue (see Figure 5A and 5 E). These are the values of tissue that has not undergone ablation, i.e. σnative. In both models, a desiccated tissue area is clearly visible surrounding the electrode at the end of ablation (720 s). This is a narrow strip (blue in Figure 5B and Figure 5F), representing the extremely low values of reversible σ changes. Interestingly, at the same time, the model that only includes reversible changes (Figure 5B) is seen to keep a high σ value in the entire tumor sub-domain (red), while this does not occur in the model that also includes the irreversible changes (Figure 5F). During the cooling phase (i.e. when the RF power has been switched off), the σ values in healthy tissue and tumor are seen to return to their initial values in the reversible change-only model (see Figure 5C and 5D). The small differences just around the active electrode are due to the electrode cooling effect. However, in the model with irreversible changes it can be seen how the σ values in tumor and tissue tend to equalize in the areas affected by coagulation (they tend to value σdenatured) and in fact they never return to their initial values (Figure 5G and 5H).
Despite the current absence of experimental data on the variations in σ values of healthy and tumor tissue during and after RF-induced heating, we proposed a new mathematical formulation to be included in two-compartment RFA models in order to include both reversible and irreversible changes in σ. Using the currently available values and assuming the difference between σ values of healthy and tumor tissue disappear as tissue passes from native state to denatured state (due to thermal coagulation) we conducted simulations to assess how a two-compartment model would predict coagulation zone volume when considering or ignoring irreversible σ changes. Our results show that after 12-minutes of RFA the results in terms of coagulation zone size are almost identical by both including and excluding irreversible changes. In other words, the coagulation zone size predicted by two-compartment RFA models is very similar if irreversible σ changes are either considered or ignored. This result is in agreement with that reported by Macchi et al [19], who found that the simulation results of constant power RFA on homogeneous tissue were almost identical for the different ways of modeling σ (both including and ignoring irreversible changes), although they argued that the Arrhenius-based model (which takes the irreversible changes into account) would be the most suitable since it automatically adjusts the σ value according to the thermal history. Our conclusions could obviously be different as new experimental values of σ become available for healthy and tumor tissue subjected to heating. Meanwhile, our contribution proposes a new model and checks its performance in a specific ablation case. The new formulation could also be applied to other models of other electromagnetic hyperthermic techniques focused on tumor ablation in which tissue electrical conductivity plays a relevant role [24], such as microwave ablation, or even to mathematical models based on other types of energy such as HIFU [25], since it is possible that other tissue characteristics (e.g. related with the fluid transport in the tissue [26,27]) have the same behavior as that hypothesized here for electrical conductivity, i.e. that normal and pathological tissue tend to have the same characteristics once coagulated.
Furthermore, the concept of a two-compartment model could be extended to ablation of other substrates (not just tumor), i.e. a generic model based on a central zone that mimics pathological tissue (target) and another surrounding zone that mimics healthy tissue, e.g. RF ablation of cardiac arrhythmias [28], in which the substrate causing the arrhythmia could be an area with differentiated electrical properties [29]. If we assume that the difference in σ values between healthy cardiac tissue and the ablation target (arrhythmogenic focus, post-infarct scar, etc.) will be smaller after ablation, the conclusions of the present study could have implication for more general two-compartment models. The concept of two-compartment model could also be applied to any RFA technique in which the target area has been doped with nanostructures [30,31,32]. Note that the properties of the zone 'seeded with nanostructures' could maintain different properties than the unseeded zones once both have been coagulated, in which case our conclusions would not be valid.
The study's main limitation is hence a certain amount of speculation in assuming that the σ values of tumor and healthy tissue will tend to equalize when they are subjected to RF-induced heating. In spite of this limitation, our contribution is to propose a novel mathematical formulation to model combinations of reversible and irreversible σ changes. The second limitation was using kidney data [17] to build the Arrhenius function (Eq. (2)) that modeled irreversible σ changes in both healthy and tumor tissue (no liver or tumor data are currently available). The third is the lack of experimental validation for the proposed models, which is shared by all the two-compartment models proposed to date [4,5,6,7,8,9,10,11,12], due to the complexity of ablating tumor tissue under controlled conditions of size, position, electrical and thermal characteristics, etc. We also must recognize that the differences in coagulation zone size between models that include or ignore irreversible σ changes may not be so small under other ablation settings (duration, power).
Our two-compartment model took the differences in σ into account exclusively since it determines how electrical power is spatially deposited in the tissue. In fact, the development of a two-compartment model was motivated by the experimental evidence that tumor σ at RF frequencies is higher than that of healthy tissue, which suggests that targeting potency within the tumor would have a positive effect. However, we should point out that thermal properties (such as specific heat and thermal conductivity) could also show differences between tumor and healthy tissue and so could be included in future two-compartment models.
Finally, it is important to point out that our model was based on the Bioheat Equation. This equation assumes an infinite speed of heat transmission, which limits its use in some cases where large amounts of heat are applied to the tissues for very short times, as usually occurs in laser applications in which a change in the formulation is necessary, for example using the hyperbolic heat equation with a single or dual phase lag formulation. The time fractional approach has also been considered as an alternative formulation for heat transmission in tissues such as the cornea, which are also usually treated by laser. However, the RFA application conditions in the range of time and temperature gradients do not hinder the continued use of the Bioheat equation, so that the results do not change with these alternative formulations. Another assumption of the Bioheat Equation is that it assumes a uniform perfusion ratio and does not differentiate between blood and tissue, regardless of the direction of blood flow. A review of the models applied to hyperthermia treatments can be found in Andreozzi et al [33]. As there are currently no results that show a significant difference between the results obtained with the alternative models and those obtained with the Bioheat Equation, we here used the Bioheat Equation as the model.
This work analyzes the temperature distribution and coagulation zone size computed by a two-compartment radiofrequency ablation (RFA) model when including simultaneously reversible changes in the tissue electrical conductivity (σ) due to temperature and irreversible changes due to thermal coagulation. The computer simulations showed that the differences between both models were only 0.1 and 0.2 cm for axial and transverse diameters, respectively. This suggests that irreversible changes of electrical conductivity do not have a significant impact in terms of coagulation zone size on two-compartment RFA models, which means the mathematical framework of the two-compartment models for tumor RFA could be simplified.
This work was supported by the National Council of Science and Technology (CONACYT, México) through a scholarship grant to Dora Luz Castro-López, CVU registration Nº 446604; and by the Spanish Ministerio de Ciencia, Innovación y Universidades under "Programa Estatal de I+D+i Orientada a los Retos de la Sociedad", Grant Nº "RTI2018-094357-B-C21".
The authors have no conflicts of interest or financial disclosures to make relevant to this submission.
| [1] |
D. Haemmerich, S. T. Staelin, S. Tungjitkusolmun, F. T. Lee Jr, D. M. Mahvi, J. G. Webster, Hepatic bipolar radio-frequency ablation between separated multiprong electrodes, IEEE Trans. Biomed. Eng., 48 (2001), 1145-1152. doi: 10.1109/10.951517
|
| [2] |
D. Haemmerich, L. Chachati, A. S. Wright, D. M. Mahvi, F. T. Lee Jr, J. G. Webster, Hepatic radiofrequency ablation with internally cooled probes: Effect of coolant temperature on lesion size, IEEE Trans. Biomed. Eng., 50 (2003), 493-500. doi: 10.1109/TBME.2003.809488
|
| [3] | I. A. Chang, U. D. Nguyen, Thermal modeling of lesion growth with radiofrequency ablation devices, Biomed. Eng. Online, 3 (2004), 27. |
| [4] | Z. Liu, S. M. Lobo, S. Humphries, C. Horkan, S. A. Solazzo, A. U. Hines-Peralta, et al., Radiofrequency tumor ablation: insight into improved efficacy using computer modeling, AJR Am. J. Roentgenol., 184 (2005), 1347-1352. |
| [5] | S. M. Lobo, Z. J. Liu, N. C. Yu, S. Humphries, M. Ahmed, E. R. Cosman, et al., RF tumour ablation: computer simulation and mathematical modelling of the effects of electrical and thermal conductivity, Int. J. Hyperth., 21 (2005), 199-213. |
| [6] | T. W. Sheu, C. W. Chou, S. F. Tsai, P. C. Liang, Three-dimensional analysis for radio-frequency ablation of liver tumor with blood perfusion effect, Comput. Methods Biomech. Biomed. Eng., 8 (2005), 229-240. |
| [7] |
D. Haemmerich, B. J. Wood, Hepatic radiofrequency ablation at low frequencies preferentially heats tumour tissue, Int. J. Hyperth., 22 (2006), 563-574. doi: 10.1080/02656730601024727
|
| [8] | M. Ahmed, Z. Liu, S. Humphries, S. N. Goldberg, Computer modeling of the combined effects of perfusion, electrical conductivity, and thermal conductivity on tissue heating patterns in radiofrequency tumor ablation, Int. J. Hyperth., 24 (2008), 577-588. |
| [9] |
D. Haemmerich, D. J. Schutt, RF ablation at low frequencies for targeted tumor heating: In vitro and computational modeling results, IEEE Trans. Biomed. Eng., 58 (2011), 404-410. doi: 10.1109/TBME.2010.2085081
|
| [10] |
G. Zorbas, T. Samaras, Parametric study of radiofrequency ablation in the clinical practice with the use of two-compartment numerical models, Electr. Biol. Med., 32 (2013), 236-243. doi: 10.3109/15368378.2013.776435
|
| [11] |
B. Zhang, M. A. Moser, E. M. Zhang, Y. Luo, H. Zhang, W. Zhang, Study of the relationship between the target tissue necrosis volume and the target tissue size in liver tumors using two-compartment finite element RFA modelling, Int. J. Hyperth., 30 (2014), 593-602. doi: 10.3109/02656736.2014.984000
|
| [12] |
M. Jamil, E. Y. Ng, Quantification of the effect of electrical and thermal parameters on radiofrequency ablation for concentric tumor model of different sizes, J. Therm. Biol., 51 (2015), 23-32. doi: 10.1016/j.jtherbio.2015.03.002
|
| [13] |
D. Haemmerich, S. T. Staelin, J. Z. Tsai, S. Tungjitkusolmun, D. M. Mahvi, J. G. Webster, In vivo electrical conductivity of hepatic tumours, Physiol. Meas., 24 (2003), 251-260. doi: 10.1088/0967-3334/24/2/302
|
| [14] | S. Prakash, M. P. Karnes, E. K. Sequin, J. D. West, C. L. Hitchcock, S. D. Nichols, et al., Ex vivo electrical impedance measurements on excised hepatic tissue from human patients with metastatic colorectal cancer, Physiol. Meas., 36 (2015), 315-328. |
| [15] |
D. Haemmerich, D. J. Schutt, A. W. Wright, J. G. Webster, D. M. Mahvi, Electrical conductivity measurement of excised human metastatic liver tumors before and after thermal ablation, Physiol. Meas., 30 (2009), 459-466. doi: 10.1088/0967-3334/30/5/003
|
| [16] |
S. Laufer, A. Ivorra, V. E. Reuter, B. Rubinsky, S. B. Solomon, Electrical impedance characterization of normal and cancerous human hepatic tissue, Physiol. Meas., 31 (2010), 995-1009. doi: 10.1088/0967-3334/31/7/009
|
| [17] |
M. Pop, A. Molckovsky, L. Chin, M. C. Kolios, M. A. Jewett, M. D. Sherar, Changes in dielectric properties at 460 kHz of kidney and fat during heating: importance for radio-frequency thermal therapy, Phys. Med. Biol., 48 (2003), 2509-2525. doi: 10.1088/0031-9155/48/15/317
|
| [18] | U. Zurbuchen, C. Holmer, K. S. Lehmann, T. Stein, A. Roggan, C. Seifarth, et al., Determination of the temperature-dependent electric conductivity of liver tissue ex vivo and in vivo: Importance for therapy planning for the radiofrequency ablation of liver tumours, Int. J. Hyperth., 26 (2010), 26-33. |
| [19] |
E. G. Macchi, M. Gallati, G. Braschi, E. Persi, Dielectric properties of RF heated ex vivo porcine liver tissue at 480 kHz: measurements and simulations, J. Phys. D Appl. Phys., 47 (2014), 485401. doi: 10.1088/0022-3727/47/48/485401
|
| [20] |
D. D. Yero, F. G. Gonzalez, D. Van Troyen, G. A. E. Vandenbosch, Dielectric properties of ex vivo porcine liver tissue characterized at frequencies between 5 and 500 kHz when heated at different rates, IEEE Trans. Biomed. Eng., 65 (2018), 2560-2568. doi: 10.1109/TBME.2018.2807981
|
| [21] | E. Ewertowska, R. Quesada, A. Radosevic, A. Andaluz, X. Moll, F. G. Arnas, et al., A clinically oriented computer model for radiofrequency ablation of hepatic tissue with internally cooled wet electrode, Int. J. Hyperth., 35 (2019), 194-204. |
| [22] |
M. Trujillo, J. Bon, M. J. Rivera, F. Burdio, E. Berjano, Computer modelling of an impedance-controlled pulsing protocol for RF tumour ablation with a cooled electrode, Int. J. Hyperth., 32 (2016), 931-939. doi: 10.1080/02656736.2016.1190868
|
| [23] | R. M. Irastorza, M. Trujillo, E. Berjano, How coagulation zone size is underestimated in computer modeling of RF ablation by ignoring the cooling phase just after RF power is switched off, Int. J. Numer. Method Biomed. Eng., 33 (2017), 10.1002/cnm.2869. |
| [24] |
B. Zhang, M. A. Moser, E. M. Zhang, Y. Luo, W. Zhang, Numerical analysis of the relationship between the area of target tissue necrosis and the size of target tissue in liver tumours with pulsed radiofrequency ablation, Int. J. Hyperth., 31 (2015), 715-725. doi: 10.3109/02656736.2015.1058429
|
| [25] | M. Mohammadpour, B. Firoozabadi, Numerical study of the effect of vascular bed on heat transfer during high intensity focused ultrasound (HIFU) ablation of the liver tumor, J. Therm. Biol., 86 (2019), 102431. |
| [26] | A. Andreozzi, M. Iasiello, P. A. Netti, A thermoporoelastic model for fluid transport in tumour tissues, J. R Soc. Interf., 16 (2019), 20190030. |
| [27] | A. Andreozzi, M. Iasiello, P. A. Netti, Effects of pulsating heat source on interstitial fluid transport in tumour tissues, J. R Soc. Interf., 17 (2020), 20200612. |
| [28] |
M. Iasiello, A. Andreozzi, N. Bianco, K. Vafai, The porous media theory applied to radiofrequency catheter ablation, Int. J. Numer. Methods Heat Fluid Flow, 30 (2019), 2669-2681. doi: 10.1108/HFF-11-2018-0707
|
| [29] | Y. Salazar, R. Bragos, O. Casas, J. Cinca, J. Rosell, Transmural versus nontransmural in situ electrical impedance spectrum for healthy, ischemic, and healed myocardium, IEEE Trans. Biomed. Eng., 51 (2004), 1421-1427. |
| [30] |
M. Qiu, A. Singh, D. Wang, J. Qu, M. Swihart, H. Zhang, P. N. Prasad, Biocompatible and biodegradable inorganic nanostructures for nanomedicine: Silicon and black phosphorus, Nano Today, 25 (2019), 135-155. doi: 10.1016/j.nantod.2019.02.012
|
| [31] | Z. Xie, T. Fan, J. An, W. Choi, Y. Duo, Y. Ge, et al., Emerging combination strategies with phototherapy in cancer nanomedicine, Chem. Soc. Rev., 2020 Jun 22. |
| [32] | M. Luo, T. Fan, Y. Zhou, H. Zhang, L. Mei, 2D black phosphorus-based biomedical applications, Adv. Funct. Mater., 29 (2019), 1808306. |
| [33] |
A. Andreozzi, L. Brunese, M. Iasielllo, C. Tucci, G. P. Vanoli, Modeling heat transfer in tumors: A review of thermal therapies, Ann. Biomed. Eng., 47 (2019), 676-693. doi: 10.1007/s10439-018-02177-x
|
| 1. | Jorge Yaulema, Jose Bon, M. Carmen Gómez-Collado, Juan José Pérez, Enrique Berjano, Macarena Trujillo, Switching Monopolar Mode for RF-Assisted Resection and Superficial Ablation of Biological Tissue: Computational Modeling and Ex Vivo Experiments, 2020, 8, 2227-9717, 1660, 10.3390/pr8121660 | |
| 2. | Eugenio J Sánchez-Muñoz, Enrique Berjano, Ana González-Suárez, Computer simulations of consecutive radiofrequency pulses applied at the same point during cardiac catheter ablation: Implications for lesion size and risk of overheating, 2022, 220, 01692607, 106817, 10.1016/j.cmpb.2022.106817 | |
| 3. | Ana González-Suárez, Juan J. Pérez, Ramiro M. Irastorza, Andre D'Avila, Enrique Berjano, Computer modeling of radiofrequency cardiac ablation: 30 years of bioengineering research, 2022, 214, 01692607, 106546, 10.1016/j.cmpb.2021.106546 | |
| 4. | Junren Ran, Martin Ostoja-Starzewski, Temperature and state-dependent electrical conductivity of soft biological tissue at hyperthermic temperatures, 2024, 41, 0265-6736, 10.1080/02656736.2024.2422509 |
Figures(5) / Tables(2)
Dora Luz Castro-López, Macarena Trujillo, Enrique Berjano, Ricardo Romero-Mendez. Two-compartment mathematical modeling in RF tumor ablation: New insight when irreversible changes in electrical conductivity are considered[J]. Mathematical Biosciences and Engineering, 2020, 17(6): 7980-7993. doi: 10.3934/mbe.2020405
| Material | ρ (kg/m3) | σ (S/m) | c (J/kg·K) | k (W/m·K) | ω (1/s) |
| Healthy tissue | 1080 | 0.26 | 3455 | 0.502 | 0.016 |
| Tumor | 1045 | 0.504 | 3760 | 0.5 | 0.009 |
| Blood | 1046 | - | 3639 | - | - |
| Metal (electrode) | 8000 | 7.4·106 | 480 | 18 | - |
| Plastic (insulated trocar) | 70 | 10-5 | 1045 | 0.026 | - |
| ρ: density, σ: electrical conductivity, c: specific heat, k: thermal conductivity, ω: blood perfusion. Tissue properties assessed at 37 ℃ (see text for more details related to σ thermal dependence). | |||||
DownLoad:
CSV
| Tumor diameter (cm) | Axial diameter (cm) | Transverse diameter (cm) | |||
| Model 1 | Model 2 | Model 1 | Model 2 | ||
| 2 | 5.0 | 5.1 | 3.6 | 3.4 | |
| 3 | 5.2 | 5.3 | 3.7 | 3.5 | |
| 4 | 5.0 | 5.1 | 3.4 | 3.6 | |
DownLoad:
CSV
| Material | ρ (kg/m3) | σ (S/m) | c (J/kg·K) | k (W/m·K) | ω (1/s) |
| Healthy tissue | 1080 | 0.26 | 3455 | 0.502 | 0.016 |
| Tumor | 1045 | 0.504 | 3760 | 0.5 | 0.009 |
| Blood | 1046 | - | 3639 | - | - |
| Metal (electrode) | 8000 | 7.4·106 | 480 | 18 | - |
| Plastic (insulated trocar) | 70 | 10-5 | 1045 | 0.026 | - |
| ρ: density, σ: electrical conductivity, c: specific heat, k: thermal conductivity, ω: blood perfusion. Tissue properties assessed at 37 ℃ (see text for more details related to σ thermal dependence). | |||||
| Tumor diameter (cm) | Axial diameter (cm) | Transverse diameter (cm) | |||
| Model 1 | Model 2 | Model 1 | Model 2 | ||
| 2 | 5.0 | 5.1 | 3.6 | 3.4 | |
| 3 | 5.2 | 5.3 | 3.7 | 3.5 | |
| 4 | 5.0 | 5.1 | 3.4 | 3.6 | |
