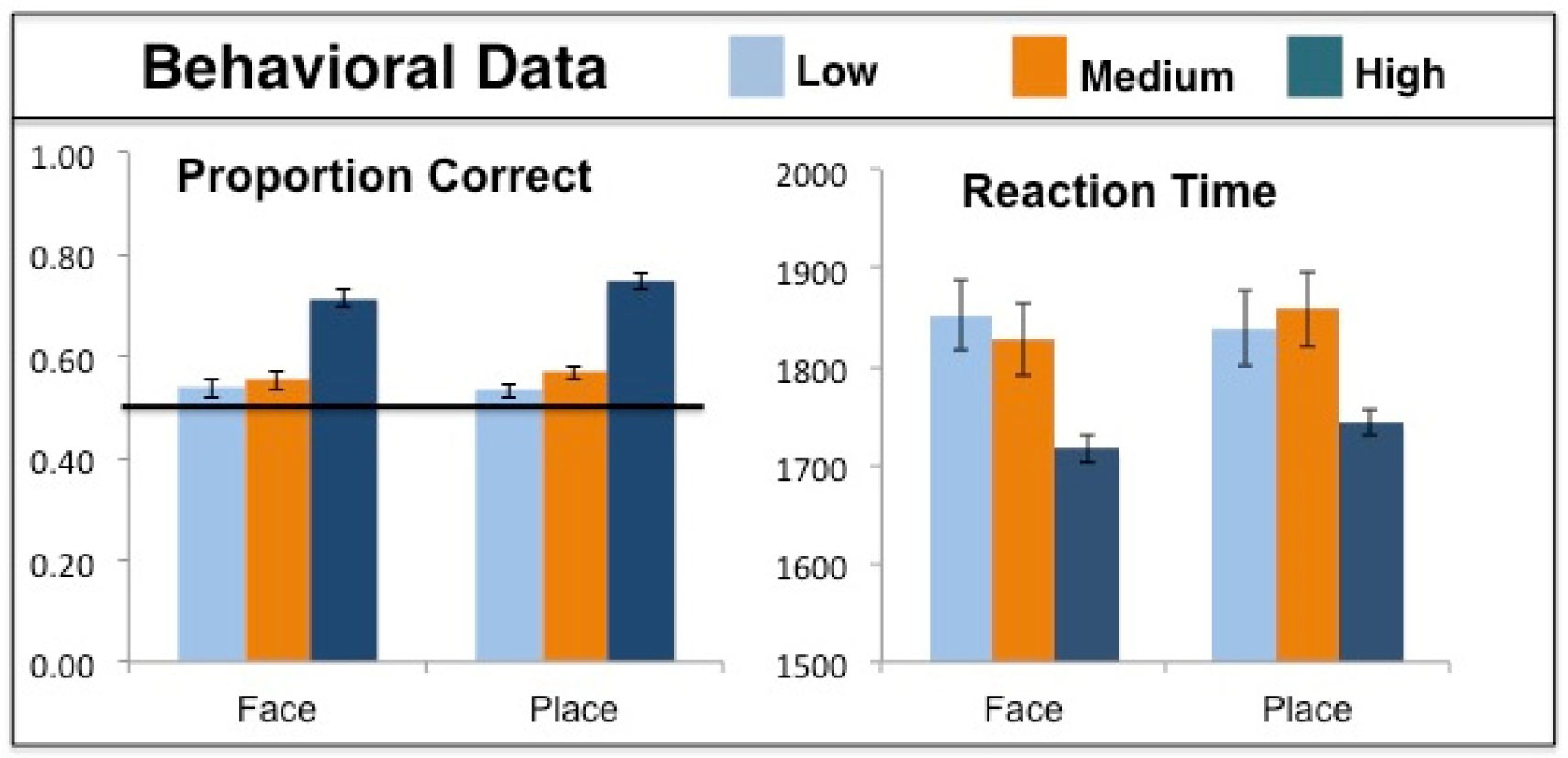
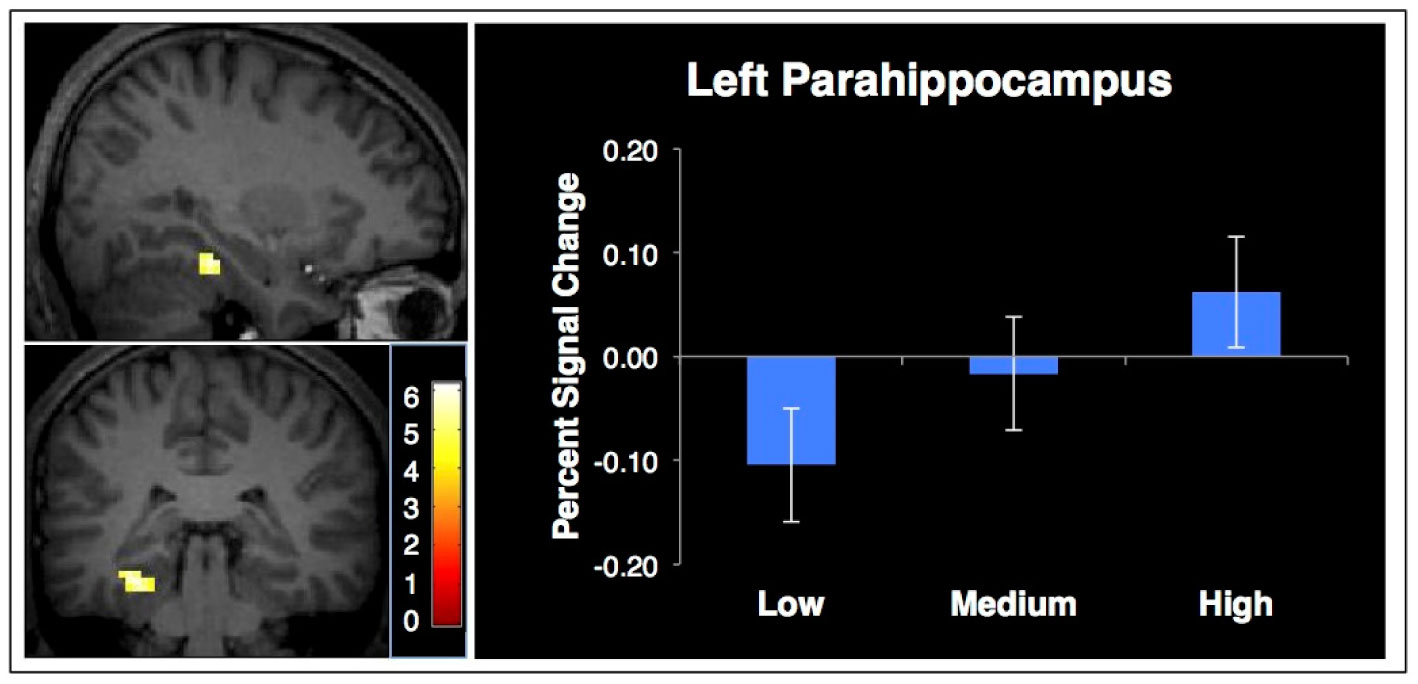
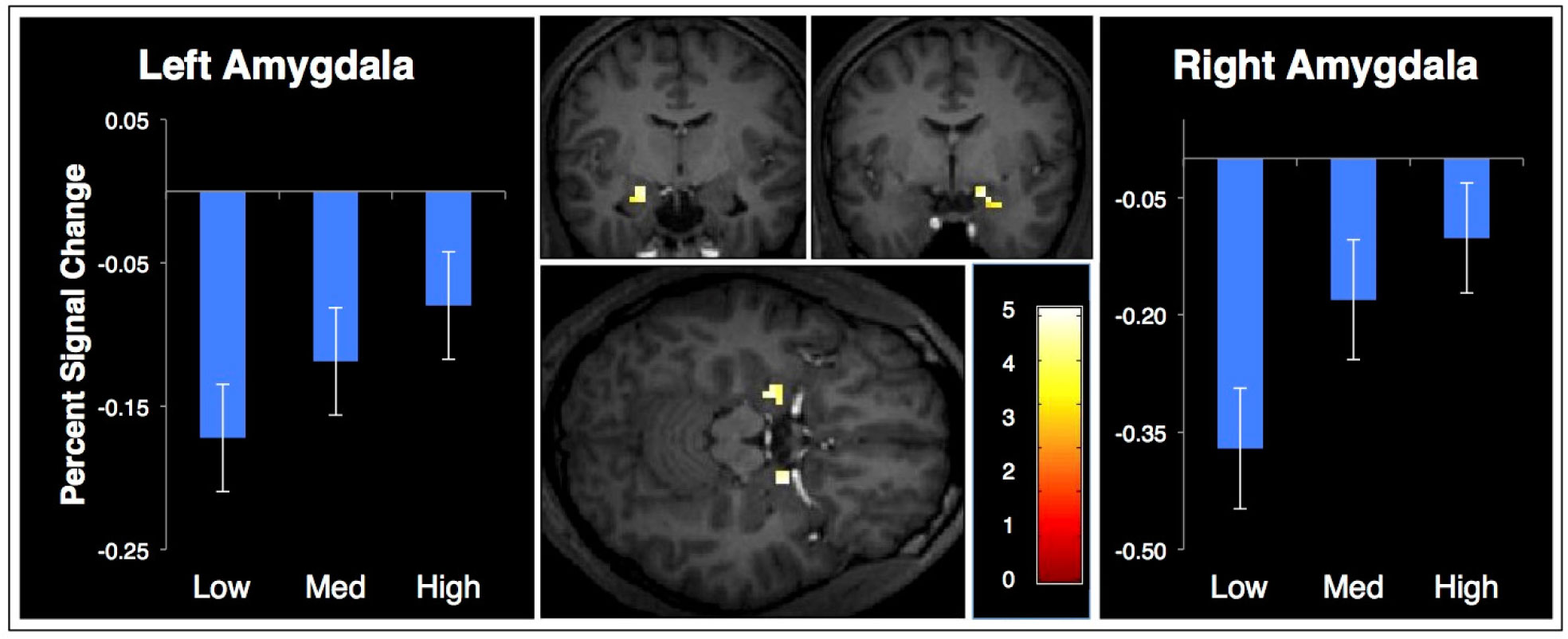
Many theories of episodic memory posit that the subjective experience of recollection may be driven by the activation of stimulus-specific cortical regions during memory retrieval. This study examined cortical activation during associative memory retrieval to identify brain regions that support confidence judgments of source memory in stimulus-specific ways. Adjectives were encoded with either a picture of a face or a scene. During a source memory test, the word was presented alone and the participant was asked if the word had been previously paired with a face or a scene. We identified brain regions that were selectively active when viewing pictures of scenes or faces with a separate localizer scan. We then identified brain regions that were differentially activated to words during the source memory test that had been previously paired with faces or scenes, masked by the localizer activations, and examined how those regions were modulated by the strength of the source memory. Bilateral amygdala activation tracked source memory confidence for faces, while parahippocampal cortex tracked source memory confidence for scenes. The magnitude of the activation of these domain-specific perceptual-processing brain regions during memory retrieval may contribute to the subjective strength of episodic recollection.
1.
Introduction
The predator-prey system is one of the most important systems for studying the interaction of two species in ecology. Predator-prey systems have important mathematical consequences because they describe ecosystem dynamics and the interactions of diverse species. These systems assist in the estimation of population dynamics by depicting the interaction between predators and prey using mathematical equations. Furthermore, they can inform ecologists by providing insights into the complex interactions between various species within an ecosystem. This knowledge can then be used to develop strategies aimed at the conservation of biodiversity and the effective management of resources [1]. Lotka [2] and Volterra [3] established a fundamental predator-prey system consisting of two species. Over time, several scholars have made modifications to this system to offer a more realistic explanation and improve understanding, as it fails to account for numerous real-world scenarios and complexities. To increase the predator-prey dynamic's authenticity, several ecological principles have been incorporated. These principles include the Allee effect, functional response, refuge-seeking behavior, cannibalism, harvesting impact, and interactions between predators and prey that are mediated by fear [4,5,6,7,8,9,10,11,12].
Numerous researchers have utilized the logistic map to illustrate the prey's growth [13,14,15,16]. Nonetheless, there is a lack of research on the stability analysis of a discrete predator-prey system that takes into account the growth of the prey using a Ricker map [17,18,19]. The logistic map in a one-dimensional population growth model is given by $ x_{n+1} = rx_n(1-\frac{x_n}{k}) $, while the Ricker map is defined as $ x_{n+1} = rx_n e^{1-\frac{x_n}{k}} $. One evident unrealistic feature of the logistic map is that $ 1-\frac{x_n}{k} $ is negative for $ x_n > k $, implying that large populations become negative at the next time step. In contrast, the Ricker map is preferable, as large values of $ x_n $ result in extremely small (but still positive) values of $ x_{n+1} $. Thus, if a population exceeds its carrying capacity, it will fall to extremely low levels, while some of the population survives. Another advantage of the Ricker map is that the exponential component $ e^{1-\frac{x_n}{k}} $ provides a nonlinear response to population density changes, mimicking instances where prey populations might face abrupt declines due to predation pressure.
It is typical to represent dynamical systems in one of two ways when modeling them: i) either as continuous-time systems [20], which are described using differential equations, ii) or as discrete-time systems, which are described by difference equations. Throughout the years, scholars have conducted thorough investigations into the nonlinear dynamic properties exhibited by continuous systems. Recently, numerous researchers have paid significant attention to discrete-time systems [21,22,23,24,25,26,27]. This is because discrete systems are much more effective at facilitating nonoverlapping generations than continuous systems. Discrete-time systems have the advantage of making numerical solutions easy to obtain. The study in [28] describes a precise discrete-time analytical (DTA) signal processing method for estimating frequency and phasor that works well with real-time computing requirements. The study in [29] is primarily concerned with determining ways to compute state and output bounding sets for uncertain discrete-time systems with pointwise-bounded, persistent inputs. The authors in [30] proposed the k-symbol discrete-time fractional Lozi system (FLS). Several critical dynamics of these systems are examined. They also investigate the necessary and sufficient requirements for stable and asymptotically stable k-symbol fractional dynamical systems. Furthermore, substantial research suggests that discrete-time systems may display more complex dynamics than corresponding continuous-time systems [31,32,33,34,35,36,37,38,39,40].
There are two distinct approaches to obtaining a discrete system. One way is to start with a continuous system and then use different techniques, such as the Euler technique [41,42,43,44,45] and the piecewise constant argument method [46,47,48,49,50,51], to turn it into a discrete system. On the other hand, we begin the analysis directly with the discrete system. Hamada et al. [52] studied the following discrete predator-prey system with the Ricker-type growth function:
where $ x_n $ denotes prey density, $ y_n $ is predator density, $ r $ is the intrinsic growth rate of the prey, $ k $ is the environmental carrying capacity of prey, and $ b x_n y_n $ and $ d x_n y_n $ represent the predator-prey confrontation, respectively, which are useful for predators and harmful for prey. The parameters $ r, k, b, $ and $ d $ are positive constants.
To enhance their chances of survival and minimize predation risks, prey species often engage in active refuge-seeking behaviors. This phenomenon has a significant impact on the dynamics of predator-prey interactions because it acts as a crucial mechanism in the preservation and mitigation of the extinction risk that prey species face. Gonzalez-Olivares and Ramos-Jiliberto [53] presented prey refuges in a simple predator-prey system. Ma et al. [54] investigated the dynamic behaviors of a predator-prey system, considering the mutual interference of a predator and a prey refuge. Chen et al. [55] investigated the prey refuge in a Leslie-Gower predator-prey model. Molla et al. [56] investigated the stability and Hopf bifurcation of the predator-prey system with refuge on prey. Numerous researchers have conducted extensive research on the refuge effect and acquired some fascinating results [57,58,59,60,61,62,63]. According to literature studies, the change in prey refuge positively affects prey density and negatively influences predator density. For instance, increasing prey refuge leads to a rise in the prey population, while decreasing prey refuge results in a decrease in the prey population. Negative influence signifies an inverse correlation, with one quantity increasing as the other decreases. Moreover, it has both stabilizing and destabilizing effects. Our work supports previous studies [64,65,66] by demonstrating that both prey and predators benefit from a moderate refuge level.
Thus, motivated by the above discussion, we naturally want to know: When a refuge effect is added to the prey population in system (1.1), what will happen to the dynamical properties? Hence, we extend the system (1.1) by adding the refuge effect to the prey population. Thus, the following modified system is obtained:
Here $ (1-m)x_n $ represents the quantity of prey available for predation, where $ 0 < m < 1 $ is the protection rate of the prey refuge for prey.
The remainder of the paper is formatted as follows: Section 2 investigates the presence and topological classification of fixed points. Section 3 explores the period-doubling (PD) and Neimark-Sacker (NS) bifurcation analysis at the positive fixed point. Section 4 applies two control methods to regulate bifurcations and chaos. To verify and describe the theoretical results, Section 5 presents some numerical examples. Section 6 discusses the influence of refuge on system (1.2). Lastly, our analysis is summarized in Section 7.
2.
Topological classification of fixed points
Understanding the stability of fixed points is critical in a predator-prey system. These fixed points depict equilibrium states in which predator and prey populations have reached a balance. Analyzing their stability allows us to forecast the long-term behavior of these ecological systems and provide insight into how different elements influence the overall dynamics of the ecosystem.
2.1. Existence of fixed points
Proposition 2.1. For system (1.2), we have three types of fixed points:
1) The trivial fixed point $ E_0 = (0, 0) $ always exists.
2) The predator-free fixed point $ E_1 = (k(ln(r)+1), 0) $ exists if $ r > \frac{1}{e} $.
3) The coexistence fixed point $ E_2 = \bigg(\frac{1}{d(1-m)}, \frac{re^{1-\frac{1}{kd(1-m)}}-1}{b(1-m)}\bigg) $ exists if $ r > e^{-1+\frac{1}{kd(1-m)}} $.
Proof. To determine the fixed points of system (1.2), we need to solve
From Eq (2.2), it follows that either $ y = 0 $ or $ x = \frac{1}{d(1-m)} $. Substituting $ y = 0 $ into Eq (2.1), we obtain
From Eq (2.3), it follows that either $ x = 0 $ or $ x = k(ln(r)+1) $. Next, substituting $ x = \frac{1}{d(1-m)} $ into Eq (2.1), we obtain
□
2.2. Stability of fixed points
The eigenvalues of the Jacobian matrix help determine the stability of fixed points. If $ \xi_1, \xi_2 $ are eigenvalues of the Jacobian matrix, then $ (x, y) $ is a sink (locally asymptotically stable (LAS)) when $ |\xi_1| < 1 $ along with $ |\xi_2| < 1 $. The fixed point $ (x, y) $ is a source when $ |\xi_1| > 1 $ along with $ |\xi_2| > 1 $. The fixed point $ (x, y) $ is a saddle point (SP) when $ |\xi_1| < 1 \wedge |\xi_2| > 1 $ (or $ |\xi_1| > 1 \wedge |\xi_2| < 1 $). Moreover, the fixed point $ (x, y) $ is a non-hyperbolic point (NHP) when the absolute value of either $ \xi_1 $ and $ \xi_2 $ is one. Classifying the positive fixed point directly using eigenvalues is not easy. Thus, we employ the following result:
Lemma 2.2. [67]
Consider the quadratic function $ \Lambda(\xi) = \xi^2+K_1\xi+K_0 $. Suppose that $ \Lambda(1) > 0 $. If $ \xi_1 $ and $ \xi_2 $ both satisfy the equation $ \Lambda(\xi) = 0 $, then
1) $ |\xi_1| < 1 $ along with $ |\xi_2| < 1 $ if $ \Lambda(-1) > 0 \wedge K_0 < 1 $,
2) $ |\xi_1| < 1 \wedge |\xi_2| > 1 $ (or $ |\xi_1| > 1 \wedge |\xi_2| < 1 $) if $ \Lambda(-1) < 0 $,
3) $ |\xi_{1, 2}| > 1 $ if $ \Lambda(-1) > 0 \wedge K_0 > 1 $,
4) $ |\xi_2|\neq 1 \wedge \xi_1 = -1 $ if $ \Lambda(-1) = 0 \wedge K_1 \neq 0, 2 $,
5) $ \xi_1, \xi_2 \in \mathbb{C} $ along with $ |\xi_{1, 2}| = 1 $ if $ K_1^2-4K_0 < 0 \wedge K_0 = 1 $.
Through simple computations, one can obtain that:
Proposition 2.3. The trivial fixed point $ E_0 $ is a
1) LAS if $ 0 < r < \frac{1}{e} $,
2) SP if $ r > \frac{1}{e} $,
3) NHP if $ r = \frac{1}{e} $.
Proof. We obtain
The diagonal entries $ \xi_1 = 0 $ and $ \xi_2 = e r > 0 $ are the eigenvalues $ J(E_0) $. Clearly $ |\xi_1| < 1 $ and
□
Proposition 2.4. The fixed point $ E_1 $ is
1) LAS if $ \frac{1}{e} < r < min\{e, e^{\frac{1}{dk(1-m)}-1}\} $,
2) source if $ r > max\{e, e^{\frac{1}{dk(1-m)}-1}\} $,
3) SP if $ mix\{e, e^{\frac{1}{dk(1-m)}-1}\} < r < max\{e, e^{\frac{1}{dk(1-m)}-1}\} $,
4) NHP if any one of the following satisfies:
(i) $ r = e $,
(ii) $ r = e^{\frac{1}{dk(1-m)}-1} $.
Proof. We obtain
The eigenvalues of $ J(E_0) $ are $ \xi_1 = -ln(r) $ and $ \xi_2 = dk(1-m)(1+ln(r)) > 0 $. One can see that
Similarly, we obtain
□
Next, we classify the positive fixed point $ E_2 $ of system (1.2) using the Jacobian matrix $ J(x, y) $ and Lemma 2.2.
Theorem 2.5. The positive fixed point
1) $ E_2 $ is LAS if any one of the following satisfies:
(i) $ d < \frac{1}{k(1-m)} $ and
$ e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg) < r < -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg), $
(ii) $ \frac{1}{k(1-m)} < d < \frac{2}{k(1-m)} $ and
$ r < min \bigg\{e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg), -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg)\bigg\} $,
(iii) $ d > \frac{2}{k(1-m)} $ and
$ -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) < r < e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg), $
2) $ E_2 $ is an SP if one of the following satisfies:
(i) $ d < \frac{2}{k(1-m)} $ and $ r > -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) $,
(ii) $ d > \frac{2}{k(1-m)} $ and $ r < -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) $,
3) $ E_2 $ is a source if any one of the following satisfies:
(i) $ d > \frac{2}{k(1-m)} $ and
$ r > max \bigg\{e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg), -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg)\bigg\}, $
(ii) $ \frac{1}{k(1-m)} < d < \frac{2}{k(1-m)} $ and
$ e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg) < r < -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg), $
(iii) $ d < \frac{1}{k(1-m)} $ and
$ r < min \bigg\{e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg), -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg)\bigg\} $,
4) $ E_2 $ is NHP and experiences PD bifurcation if
$ r = -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) $ and
$ d \neq \frac{2}{k(1-m)}, \ r \neq 2dk(1-m)e^{-1-\frac{1}{d k (-1+m)}}, \ 4dk(1-m)e^{-1-\frac{1}{d k (-1+m)}}. $
5) $ E_2 $ is NHP and experiences NS bifurcation if
$ r = e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg), d \neq \frac{1}{k(1-m)} $ and $ 0 < r < 4dk(1-m)e^{-1-\frac{1}{d k (-1+m)}} $.
Proof. We obtain
The corresponding characteristic polynomial is
where
It can be obtained through calculations that
It is easy to see that the positivity of the $ y $-coordinate of $ E_2 $ implies that $ \Lambda(1) > 0 $. By setting $ \Lambda(-1) = 0 $, one can obtain that:
By setting $ \Lambda(0) = 1 $, one can obtain that:
By setting $ K_1\neq 0, 2 $, we obtain that:
Next, by setting $ K_1^2-4K_0 < 0 $ and $ K_0 = 1 $, we obtain that:
□
The fixed point categorizations in a discrete-time predator-prey model possess distinct ecological interpretations. A sink represents a state of steady coexistence, a saddle shows a state of intermittent stability, an unstable source implies unexpected shifts in population, and non-hyperbolic points hint at complicated and difficult-to-predict interactions. Understanding these categorizations assists ecologists in comprehending the stability and dynamics of predator-prey interactions, which are vital for efficient ecosystem management and conservation.
3.
Bifurcation analysis
This section is dedicated to conducting a thorough investigation of PD and NS bifurcation in system (1.2) at $ E_2 $. To get a comprehensive examination of bifurcation analysis, we suggest the readers to [68,69,70,71,72,73,74,75,76,77,78,79,80,81]. These bifurcations signify important changes in the dynamics of the system, providing insights into situations in which minor changes to parameters result in major changes in the dynamics of predator-prey interactions. Additionally to enhance our understanding of ecosystem dynamics, knowing the roles of PD and NS bifurcations also makes it easier to develop efficient conservation and management methods to maintain the long-term coexistence of predator and prey populations.
3.1. PD bifurcation
In this section, we investigate the PD bifurcation at $ E_2 $ under condition 4) stated in Theorem 2.5. By introducing a minimal perturbation $ \delta $ ($ |\delta|\lll 1 $) to the bifurcation parameter $ r $ in system (1.2), the resulting system is obtained:
Assume that $ u_n = x_n-\frac{1}{d(1-m)}, \ v_n = y_n-\frac{(r+\delta) e^{1-\frac{1}{kd(1-m)}}-1}{b(1-m)} $. After substituting the value of $ r = -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) $, the system (3.1) is simplified to
where
Next, the system (3.2) is diagonalized through the consideration of the following transformation:
Upon applying the mapping (3.3), the system (3.2) undergoes the alteration as follows:
where
Next, we determine the center manifold denoted by $ Q^C $ for the system (3.4) at the origin, in a close neighborhood to $ \delta = 0 $. Using the center manifold theorem, we can derive the following approximate expression for the center manifold $ Q^C $:
where
where $ \xi = \frac{3+3 d k (-1+m)}{2+d k (-1+m)} $. As a result, the system (3.4) is limited to $ Q^C $ in the manner as follows:
For the function (3.5) to go through PD bifurcation, the following two quantities must possess nonzero values:
Based on the aforementioned study, the following result is obtained:
Theorem 3.1. Assume that condition 4) of Theorem 2.5 is satisfied. The system (1.2) experiences PD bifurcation at $ E_2 $ if $ l_1, l_2 $ given in (3.6) and (3.7) are nonzero and $ r $ changes in a close neighborhood of $ r = -3e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-2+d k (1-m)}\bigg) $. Moreover, if $ \ l_2 > 0 $ (respectively $ l_2 < 0 $), then a period-2 orbit of the system (1.2) emerges and it is stable (respectively, unstable).
The above result demonstrates how small changes may produce a significant change in the system's behavior, resulting in a doubling of population oscillation periods. This result discloses an important component of the predator-prey relationship, revealing a transition point in the ecosystem from orderly and predictable cycles to chaotic and unpredictable dynamics.
3.2. NS bifurcation
In this section, we investigate the NS bifurcation at $ E_2 $ under condition (5) stated in Theorem 2.5. By introducing a minimal perturbation $ \delta $ ($ |\delta|\lll 1 $) to the bifurcation parameter $ r $ in system (1.2), the resulting system is obtained:
Assume that $ u_n = x_n-\frac{1}{d(1-m)}, \ v_n = y_n-\frac{(r+\delta) e^{1-\frac{1}{kd(1-m)}}-1}{b(1-m)} $. After substituting the value of $ r = e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg) $, the system (3.8) is simplified to
where
The characteristic equation of the linearized system (3.9) is
where
The solutions of (3.10) are
Moreover, we obtain
Additionally, it is required that $ \xi_{1, 2}^i \neq 1 $ when $ \delta = 0 $ for $ i = 1, 2, 3, 4, $ which corresponds to $ \alpha(0) \neq -2, 2, 0, 1 $. We obtain
Moreover, $ \alpha(0) \neq -2, 0, 1 $ is equivalent to
Next, to change (3.9) into normal form at $ \delta = 0 $, we use the following similarity transformation:
Upon application of the mapping (3.13), the system (3.9) takes the following form:
where
Next, we need the following discriminatory value $ L $ to be not zero to make sure that system (1.2) undergoes NS bifurcation.
where
Therefore, the result derived from the above analysis is as follows:
Theorem 3.2. Suppose that condition 5) of Theorem 2.5 is satisfied. If the condition (3.12) is satisfied and $ L $ given in (3.15) holds a nonzero value, then system (1.2) experiences NS bifurcation at $ E_2 $ as long as $ r $ varies in a close neighbourhood of $ r = e^{-1-\frac{1}{d k (-1+m)}}\bigg(\frac{d k (1-m)}{-1+d k (1-m)}\bigg) $. Furthermore, in instances where $ L $ is negative (alternatively, positive), the NS bifurcation encountered in system (1.2) at $ E_2 $ is categorized as supercritical (subcritical), giving rise to the presence of a unique closed invariant curve originating from $ E_2 $ that is attracting (repelling).
The above result illustrates that, under certain conditions, the predator-prey system experiences an NS bifurcation at point $ E_2 $. This finding indicates a transition in the ecosystem from simple to more complex patterns, resulting in the presence of consistent, non-repeating cycles. Understanding the NS bifurcation enables ecologists to identify the start of enduring, nonlinear fluctuations in the ecosystem, hence facilitating the assessment of long-term population dynamics and ecological stability.
4.
Chaos control
In a predator-prey model, real-world factors serve as control parameters, influencing population dynamics. Environmental changes, such as changes in vegetation or landscape, have an impact on both predators and prey by influencing shelter, food availability, and reproductive success. Introducing a competitor species influences both populations, whether it be new prey for the predator or a competing predator for the prey. Human activities such as hunting rules, conservation initiatives, and harvesting have a direct impact on population size and relationships. Climate elements, such as temperature and precipitation, operate as control variables, influencing birth, mortality, and migration patterns.
Control theory may be employed to control population dynamics in a predator-prey model. It is possible to avoid overpopulation and the extinction of species by maintaining a sustainable and balanced ecosystem by the adjustment of factors such as hunting limits or habitat protection. White-tailed deer populations in the US are managed by hunting limitations to minimize overpopulation and habitat destruction [82]. The Great Barrier Reef Marine Park Authority in Australia prioritizes coral ecosystem maintenance and habitat protection for marine biodiversity [83]. Community-based natural resource management in Namibia promotes sustainable activities like controlled hunting, benefitting wildlife and livelihoods [84]. These examples demonstrate how hunting limitations and habitat conservation affect ecological balance and biodiversity globally.
The objective of control theory is to create management plans that guarantee the populations of prey and predators will coexist in the long run. Bifurcations and unstable oscillations have historically been thought of negatively in mathematical biology since they harm the biological population's ability to reproduce. One can create a controller that may alter the bifurcation characteristics for some non-linear systems to obtain certain desired dynamical properties and manage chaos under the impact of PD and NS bifurcations. There are several strategies for chaos control in a discrete-time system. This section focuses on two different types of control strategies: state feedback control and hybrid control approaches. Both methods are effective in controlling bifurcation and chaos. The hybrid control method is easy to implement. The controlled system in the hybrid control method preserves the fixed points of the original system, while in feedback control, the controlled system may preserve only one fixed point at which we want to control bifurcation and chaos. There is only one control parameter $ \rho \in (0, 1) $ in the hybrid control method, while there are two control parameters ($ \kappa_1, \kappa_2 \in \mathbb{R} $) in the feedback control method.
4.1. Feedback control method
The feedback control technique [85,86] involves transforming the chaotic system into a piecewise linear system to derive an optimal controller that reduces the upper limit. Subsequently, the optimization issue is performed subject to specified constraints. The aforementioned technique is employed to achieve stabilization of chaotic orbits located at an unstable fixed point inside the system (1.2). The controlled system under consideration for this purpose is as follows:
where $ U_n = \kappa_1 \bigg(x_n-\frac{1}{d(1-m)}\bigg)+\kappa_2 \bigg(y_n-\frac{re^{1-\frac{1}{kd(1-m)}}-1}{b(1-m)}\bigg) $ is the feedback controlling force, $ \kappa_1 $ and $ \kappa_2 $ are feedback gains. Through simple calculations, it is obtained that for system (4.1), we have
The matrix $ J(E_2) $ has the following characteristic equation:
where
Let $ \xi_1 $ and $ \xi_2 $ are the roots of (4.3), then we have
The marginal stability lines may be found by solving the systems of equations $ \xi_1 = \pm 1 $ and $ \xi_1 \xi_2 = 1 $. These conditions ensure that $ |\xi_{1, 2}| < 1 $. Assume that $ \xi_1 \xi_2 = 1 $, then Eq (4.5) implies that
Next, we take $ \xi_1 = 1 $ and utilizing Eqs (4.4) and (4.5), we obtain
Next, we take $ \xi_1 = -1 $ and utilizing Eqs (4.4) and (4.5), we obtain
The stable eigenvalues are enclosed within the triangular region bounded by $ L_1, L_2 $, and $ L_3 $.
4.2. Hybrid control method
The hybrid control technique [87] is a method that combines state feedback and parameter modification to stabilize unstable periodic orbits contained in the system's chaotic attractor. As a result, the regulated system retains its stability over a wide variety of parameters. We take the following controlled system:
where $ \rho \in (0, 1) $. The parameter $ \rho $, acting like a control parameter, balances the impact of the original system (1.2) with the modified system (4.9). If the value of $ \rho $ becomes negative, it might indicate the reverse impact of the original system (1.2). Conversely, if $ \rho $ exceeds $ 1 $, it could indicate an amplified effect of the original system (1.2) beyond its natural influence, perhaps leading to unrealistic or unworkable consequences in the modified system (4.9). The same fixed points are shared by systems (4.9) and (1.2). We obtain
with corresponding characteristic polynomial
where
Theorem 4.1. The fixed point $ E_2 $ of the system (4.9) is LAS if
Remark 4.2. These control strategies aim to mitigate bifurcation and chaos in the system (1.2). The mathematical equations in systems (4.1) and (4.9) define parameters $ \kappa_1, \kappa_2 $ and $ \rho $ in the context of control techniques. It is important to note that these specific control methods may not have direct, established parallels in current ecological models or practices. Our approach introduces theoretical modifications, and we acknowledge the need for further research and practical applications within the field of mathematical ecology to fully validate these methods.
5.
Numerical examples
In this section, we will corroborate our theoretical findings for system (1.2) by numerical simulations. These numerical simulations will include bifurcation diagrams, phase portraits, time series plots, and maximum Lyapunov exponent (MLE) graphs. We have used MATHEMATICA for computations and MATLAB for graphs.
5.1. Bifurcation analysis varying $ r $
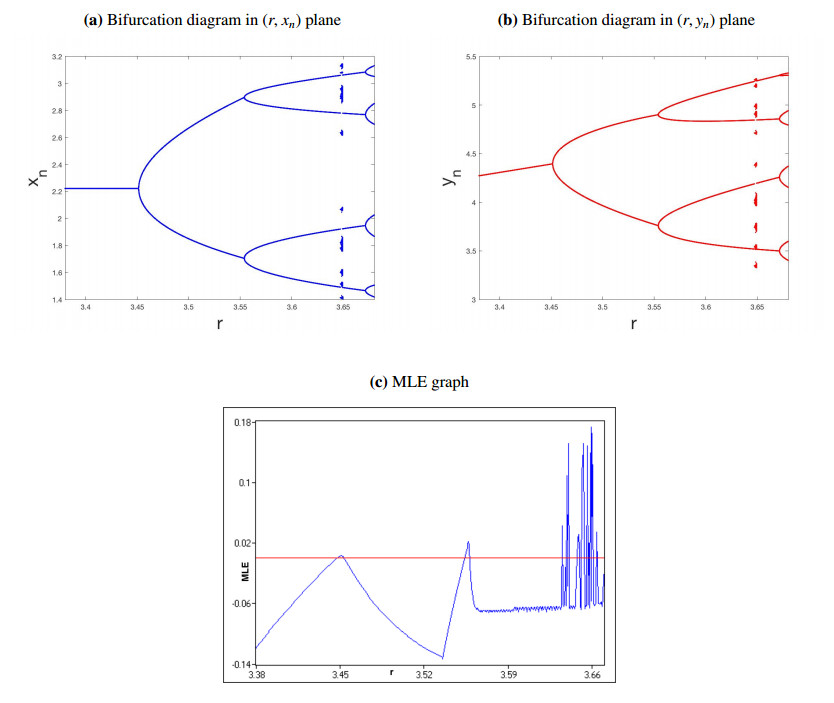
We assume that $ k = 2.5, b = 1.3, m = 0.5, d = 0.9, x_0 = 2.25, y_0 = 4.45, r \in [3.38, 3.68] $, then, system (1.2) goes through PD bifurcation when $ r \approx 3.451523 $. The positive fixed point is obtained as $ E_2 = (2.222222, 4.395604) $. The eigenvalues of $ J(E_2) $ are $ \xi_1 = -1 $ and $ \xi_2 = -0.428571 $ with $ |\xi_2| \neq 1 $. For these parametric values, we obtain
Thus, we obtain
The bifurcation diagrams of system (1.2) are given in Figure 1(a), (b), while the MLE is plotted in Figure 1(c).
Next, consider $ k = 2.5, b = 1.3, m = 0.5, d = 1.5, x_0 = 1.3, y_0 = 1.7 $ and varying $ r \in[1.1, 2.1] $. The system (1.2) goes through NS bifurcation at $ r \approx 1.343762 $ and has the positive fixed point $ E_2 = (1.333333, 1.758242) $. The eigenvalues of $ J(E_2) $ are $ \xi_{1, 2} = 0.428571\pm 0.903508 i $ with $ |\xi_{1, 2}| = 1 $. Moreover, some careful calculations give
Thus, it is obtained that $ L = -0.078752 < 0 $, which proves the correctness of Theorem 3.2. Bifurcation diagrams are depicted in Figure 2(a), (b), while the MLE is plotted in Figure 2(c). The presence of negative MLEs indicates the presence of chaotic areas.
Next, Figure 3(a)–(h) shows phase portraits of system (1.2) for various various values of $ r $. One can observe that $ E_2 $ is LAS for $ r < 1.343762 $ but loses stability at $ r \approx 1.343762 $ when the system (1.2) goes through NS bifurcation. For $ r \geq 1.343762 $, an invariant curve emerges from $ E_2 $, the radius of which grows as $ r $ grows. Some $ 5-, 10- $ periodic orbits are also plotted in Figure 3(d), (f), Finally, we obtain a strange chaotic attractor given in Figure 3(h).
5.2. Bifurcation analysis and chaos control varying $ m $
We assume that $ r = 3.5, k = 2.5, b = 1.3, d = 0.9, x_0 = 1.95, y_0 = 4.50, m \in [0.42, 0.52] $, then, system (1.2) experiences both NS bifurcation and PD bifurcation as $ m $ varies in small neighborhoods of $ m_1 \approx 0.424620 $ and $ m_2 \approx 0.495050 $, respectively. The bifurcation diagrams of system (1.2) are given in Figure 4(a), (b), while the MLE is plotted in Figure 4(c). The presence of negative MLEs indicates the existence of stable fixed points or stable periodic windows, whereas positive MLEs indicate the presence of chaotic areas. Furthermore, the phase portraits of system (1.2) are given in Figure 5(a)–(h) for various values of the parameter $ m $. One can observe that system (1.2) experiences NS bifurcation for small values of refuge. At the NS bifurcation point, an invariant closed curve emerges, representing a repeating pattern in predator-prey populations. Moreover, the system experiences PD bifurcation for large values of refuge. At the PD bifurcation point, the system (1.2) transitions from stable behavior to periodic oscillations, and subsequently, the period of these oscillations doubles.
The existence of two critical values, $ m_1 $ and $ m_2 $, suggests a threshold behavior in the system (1.2). When $ m $ is less than $ m_1 $, the positive fixed point $ E_2 $ is unstable, implying that predator-prey interaction is too skewed in favor of the predators, and the prey population cannot sustain itself. Similarly, when $ m $ is greater than $ m_2 $, then $ E_2 $ is also unstable, indicating that too much refuge availability disrupts the predator-prey balance. This suggests that a moderate level of refuge is beneficial for both predator and prey populations.
The efficacy of the hybrid control approach will next be evaluated. We assume $ \rho = 0.96, r = 3.5, k = 2.5, b = 1.3, d = 0.9, x_0 = 1.95, y_0 = 4.50 $ and vary $ m $ for the controlled system (4.9). If $ 0.405045 < m < 0.500983 $, the positive fixed point $ E_2 $ is LAS. The controlled system's bifurcation diagrams, and Figure 6(a), (b) show that the bifurcation has been postponed in the controlled system (4.9).
Next, we aim to evaluate the efficacy of the feedback control technique. Considering $ r = 3.5, k = 2.5, b = 1.3, d = 0.9 $, and $ m = 0.515 $, as well as the initial conditions $ x_0 = 1.95 $ and $ y_0 = 4.50 $ for the controlled system (4.1), the marginal stability lines are as follows:
and
Figure 7(a) depicts the stability region bounded by lines $ L_1, L_2 $, and $ L_3 $ for system (4.1). The fixed point $ E_2 $ of system (1.2) is shown to be unstable for the given parametric values. The controlled system (4.1) is examined with feedback gains $ \kappa_1 = -2.95 $ and $ \kappa_2 = -1.20 $. Figure 7 illustrates the graph of $ x_n $ as shown in Figure 7(c), $ y_n $ as shown in Figure 7(d), and the phase portrait as presented in Figure 7(b) for the system (4.1). Therefore, it may be deduced that the use of the feedback control methodology seems to be effective in controlling bifurcation and chaos.
6.
Influence of refuge effect
Trivial fixed point $ E_0 = (0, 0) $ and boundary fixed point $ E_1 = (k(ln(r)+1), 0) $ are independent of refuge effect $ m $. The positive fixed point $ E_2 = \bigg(\frac{1}{d(1-m)}, \frac{re^{1-\frac{1}{kd(1-m)}}-1}{b(1-m)}\bigg) $ is dependent on refuge effect $ m $. We assume that $ r = 3.5, k = 2.5, b = 1.3, d = 0.9 $. Then, in Table 1, we observe that the density of prey population increases as refuges used by prey increases, while that of predators first increases and then decreases with prey refuges. The same is observed in Figure 8. When the number of prey using refuges is sufficiently large, our findings indicate that the prey population will exceed its maximum environmental carrying capacity, leading to the extinction of predators. Furthermore, the examination of stability and bifurcation demonstrates that an appropriate amount of refuge is advantageous for the populations of both predators and prey.
7.
Conclusions
The refuge effect plays a crucial role in determining the stability of predator-prey interactions in an ecosystem. In a predator-prey system, such a refuge could be a physical space, a habitat, or any resource that protects the prey. In this paper, we present and study the complex dynamics of a discrete-time predator-prey system with the refuge effect. The presence and stability of fixed points are investigated. Moreover, a thorough analysis of local bifurcations at the positive fixed point is conducted. The study illustrates that the system (1.2) goes through both PD and NS bifurcation. Moreover, the presence of a positive MLE guarantees the existence of chaos in the system (1.2). Feedback control and hybrid control approaches are used to control bifurcation and chaos. Consequently, effective control is achieved for both types of bifurcation across an extensive range of parameters. Furthermore, numerical simulations are executed to demonstrate the theoretical results that were previously presented. These simulations use several visual representations, including bifurcation diagrams, MLE graphs, phase portraits, and time series plots.
It is observed that a positive fixed point is stable if the refuge parameter $ m $ lies in an optimal range $ m_1 < m < m_2 $. When $ m $ is less than $ m_1 $, the positive fixed point $ E_2 $ is unstable, implying that predator-prey interaction is too skewed in favor of the predators, and the prey population cannot sustain itself. Similarly, when $ m $ is greater than $ m_2 $, then $ E_2 $ is also unstable, indicating that too much refuge availability disrupts the predator-prey balance. This suggests that a moderate level of refuge is beneficial for both predator and prey populations.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare there is no conflict of interest.
Acknowledgments
This work was supported by Research Funding from Youjiang Medical University for Nationalities, Baise, China under Grant numbers yy2020bsky050 & yy2023rcky002, the National Natural Science Foundation of China under Grant number 62162063, and the Scientific Research and Technology Development Program of Guangxi, China under Grant number 2021AC19308. The funding bodies did not play any role in the design of the study and in writing the manuscript.









 DownLoad:
DownLoad: