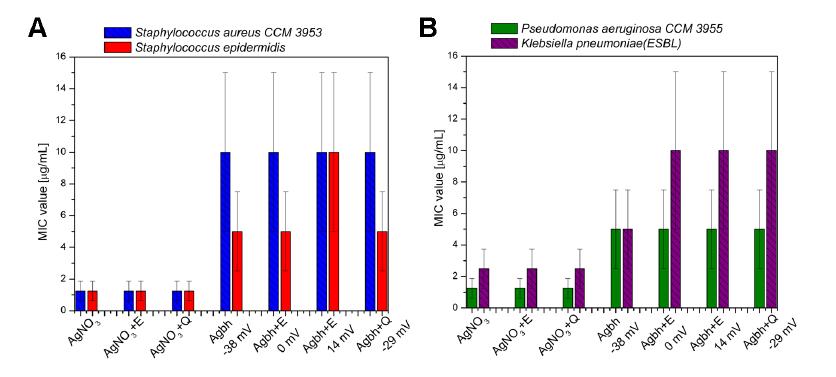
1. Introduction
Since the publication of the seminal paper [11] mathematical compartmental models are widely used to describe infectious diseases dymanics in large populations (see, for example [9], [4], [2] and [8]). It is well accepted that once an infected individual comes into contact with an unaffected population, the disease will spread by contact with the infectious individuals. Compartmental models divide the population into compartments characterizing the spread of the diseases and letters are used to denote the number of individuals in each compartment. Usually, the size of the population to be studied is $N$, $S$ is the number of susceptible individuals and the number of infectious individuals is $I$. The letter $R$ is also used to denote the number of those who recover from the disease or, as in [11], those who are removed from the disease by death or by recovery. The nature of the disease as well the reason why the models are studied may dictate the need for different compartments to be included. For example, SEIR models are used for diseases where infected individuals do not become immediately infectious; they are considered to be exposed to the disease and placed in compartment $E$, being moved to the $I$ compartment only after some latent period of time.
The basic reproduction number, $R_0$, measures the transmission potential of a disease (see, for example, [10]). It is defined as "the expected number of secondary cases produced by a single (typical) infection in a completely susceptible population". From the mathematical point of view, it is an important concept when dealing with the dynamic systems defined by the compartmental models (SIR model, SEIR models, etc) because of its relevance to the stability of the equilibrium points. Indeed, there is a vast literature devoted to the stability analysis of such models; in this respect we refer the reader to [4] [2] and [8] (to name but a few!) and references within. Recently one has witnessed an increasing interest on applications of optimal control to such models (see [17], [13], [18], [1], [12], [6] and [16]). This comes as no surprise since optimal control theory has been a successful tool in the design of different control strategies for dynamic systems in general ([20]).
Many papers on optimal control applied to epidemiology propose $L^2$ costs (see, for example, [17] and [1]). One reason for this is that a closed form of the optimal control may be obtained, a form that facilitates the numerical verification of the solution (although, by itself, it does not guarantees that the solution is the optimal one since it usually depends on the multipliers). On the other hand, it has been argued that $L^1$ costs are appropriated to biological systems while those with $L^2$ costs are not ([13]). This reasoning may explain the attention optimal control problems with $L^1$ costs have recently gained; see, for example, [13], [12] and [16].
In this paper we focus on optimal control problems to control, via vaccination, the spread of a disease described by a SEIR model. We follow closely the approach in [16]: we consider $L^1$ costs, we solve the problems numerically applying the direct method, we use known software packages, and we present numerical solutions that satisfy necessary optimality conditions with high accuracy. Notably, and differing from [16], we work with a normalized SEIR model.
The normalized SEIR model differs from the usual SEIR model since the variables are fractions of the whole population instead of the number of individuals in each compartment. The theoretical and numerical treatment involving the latter model is usually done as if the variables are continuous and not integers; treating such variables as integers would demand the use of integer programming what is known to be very heavy computationally. When we turn to normalized models the variables are, by nature, continuous. In the literature, normalized models are common when the total population is assumed to remain constant during the time frame under study. This is not our case; here we normalize a SEIR model that incorporates exponential natural birth and death, as well as disease-caused death (similarly to what is done in [14]). As far as optimal control is concerned, normalizing such model brings out some new issues related to the choice of costs and the introduction of non standard constraints, questions we discuss here when comparing optimal control for normalized and not normalized SEIR models.
Herein, we refer to the SEIR model, where the variables $S$, $E$, $I$ and $R$ denote the number of individuals in each compartment, as the classical SEIR model as opposed to the normalized SEIR model.
We emphasize that we do not concentrate on any particular disease. Rather, our aim is to illustrate how previously proposed optimal control formulations can be handled by this new model, when different scenarios are considered. Taking into account that the set of parameters for the population in [16], based on [17], are not to be found in today's world, we use different population's parameters closed related to some European countries.
Like other models in epidemiology, SEIR models represent only a rough approximation of reality. However, they provide new insights into the spreading of diseases and, when optimal control is applied, new insight on different vaccination policies.
This paper is organized in the following way. In Section 2 we introduce an optimal control problem with $L^1$ cost involving the classical SEIR model and its "normalized" counterpart. A brief description of our numerical methods as well as the tables with the set of parameters used in our simulation are presented in Section 3. Numerical methods give a helping hand for the discussion on the pros and cons of optimal control problems with classical and normalized models presented in Section 4. This discussion highlights the need for a criterious choice of cost. In Sections 5 and 6, we solve our optimal control problem numerically partially validating our solution using the maximum principle and the computed multipliers. Conclusions follow in the last section of this paper.
2. Optimal control problems for SEIR models with $L^1$ cost
The SEIR model is a compartmental model well accepted as modelling some infectious diseases. At each instant $t$, $S(t)$, $E(t)$, $I(t)$, and $R(t)$ denote the number of individuals in the susceptible, exposed, infectious and recovered compartments. The total population is $N(t) = S(t) + E(t) + I(t) + R(t)$. We assume that our population has exponential natural birth rate $b$ and death rate $d$ and that that all newborns are susceptible to the diseases. The disease transmission is described by the parameters $f$, denoting the rate at which the exposed individuals become infectious, $g$, denoting the rate at which infectious individuals recover, $a$, denoting the death rate due to the disease and $c$, denoting the disease incidence coefficient of horizontal transmission (vertical transmission is not considered). The rate of transmission of the disease is $c\frac{I(t)}{N(t)}$. For simplicity the parameters $a$, $b$, $c$, $d$ and $f$ are assumed to be constants. For more information about such model we refer the reader to [2], [10], [17] and references within.
Optimal control techniques for SEIR models allow the study of different vaccines policies; different policies are confronted in [17] and [1] where the minimizing cost is $L^2$, and in [16], covering the case of $L^1$ cost. As in the aforementioned works we assume that only susceptible people is vaccinated (implying that it is possible to distinguish between exposed and susceptible individuals) and that the vaccine is effective so that all vaccinated susceptible individuals become immune. Let $u(t)$ represent the percentage of the susceptible individuals being vaccinated per unit of time. Taking all the above considerations into account we are led to the following dynamical system (see [17]):
|
$
˙S(t)=bN(t)−dS(t)−cS(t)I(t)N(t)−u(t)S(t),S(0)=S0,
$
|
(1)
|
|
$
˙E(t)=cS(t)I(t)N(t)−(f+d)E(t),E(0)=E0,
$
|
(2)
|
|
$
˙I(t)=fE(t)−(g+a+d)I(t),I(0)=I0,
$
|
(3)
|
|
$
˙N(t)=(b−d)N(t)−aI(t),N(0)=N0,
$
|
(4)
|
where $S_0$, $E_0$, $I_0$ and $N_0$ are nonnegative initial conditions.
For some $\bar u\geq 0$, we impose the following control constraint to $u$:
|
$
\label{control-constraint}
0 \leq u(t) \leq \bar u \;\;\;\; a.e. \; t \in [0,T] ,
$
|
(5)
|
where $T$ represents the period of time under consideration. The recovered population is related to the total population by $N(t) = S(t) + E(t) + I(t) + R(t)$. Hence, $R(t) = N(t) -S(t) - E(t) - I(t)$ which gives the differential equation
|
$
\label{Rdifeq}
\dot R(t) = g I(t)-dR(t)+u(t)S(t) , \;\;\;\; R(0) = R_0 .
$
|
(6)
|
Here, the aim of applying optimal control to SEIR models is to control the spreading of the disease with some minimum financial cost. The cost should then be a weighted sum of the society financial costs of having, at each time, $I(t)$ infected individuals and the cost of the vaccination effort what is mathematical translated as (7). This leads to the $L^1$ cost as in [16]:
|
$
\label{L1-objective}
J_C(X,u)= \int_0^{T} \left( AI(t)+Bu(t)\right)~dt,
$
|
(7)
|
where $X=(S,E,I,N)$ and $A>0$, $B>0$ are weight parameters related with financial costs.
Throughout this paper we refer to the optimal control problem of minimizing $J_1(X,u)$ over all $X \in W^{1,1}([0,T]:\mathbb{R}^4)$ and all piecewise continuous functions $u:[0,T]\to \mathbb{R}$ satisfying (1)-(6) and (5) as the classical and basic optimal control problem:
|
$\nonumber
(P) \left\{
Minimize∫T0(AI(t)+Bu(t)) dtsubject to˙S(t)=bN(t)−dS(t)−cS(t)I(t)N(t)−u(t)S(t),S(0)=S0,˙E(t)=cS(t)I(t)N(t)−(f+d)E(t),E(0)=E0,˙I(t)=fE(t)−(g+a+d)I(t),I(0)=I0,˙N(t)=(b−d)N(t)−aI(t),N(0)=N0,u(t)∈[0,ˉu] for a. e.t∈[0,T], with ˉu∈]0,1].
\right.
\nonumber
$
|
Next, we associate $(P)$ with a normalized optimal control problem. Normalizing models are obtained considering the percentage of the total population to be $1$ at each instant $t$. Then, defining
|
$
s(t)=\frac{S(t)}{N(t)}, \;\;\;\; e(t)=\frac{E(t)}{N(t)},\;\;\;\; i(t)=\frac{I(t)}{N(t)}, \;\;\;\; r(t)=\frac{R(t)}{N(t)} ,
$
|
(8)
|
we have
|
$
s(t)+e(t)+i(t)+r(t)=1\text{ for all }t.
$
|
(9)
|
Notice that $s(t)$ is the percentage of the population in compartment $S(t)$, $e(t)$ is the percentage of the population in compartment $E(t)$, $i(t)$ is the percentage of the population in compartment $I(t)$ and $r(t)$ be the percentage of the population in compartment $R(t)$. The normalized counterpart of (1)-(6) is then:
|
$
˙s(t)=b−cs(t)i(t)−bs(t)+ai(t)s(t)−u(t)s(t),
$
|
(10)
|
|
$
˙e(t)=cs(t)i(t)−(f+b)e(t)+ai(t)e(t),
$
|
(11)
|
|
$
˙i(t)=fe(t)−(g+a+b)i(t)+ai2(t),
$
|
(12)
|
|
$
˙r(t)=gi(t)−rb(t)+ai(t)r(t)+u(t)s(t).
$
|
(13)
|
Remarkably, the dead rate parameters do not appear in this model (a feature we discuss in Remark 1 below). It is a simple matter to see that due to (9) we can discard equation (13), allowing us to reduce the number of differential equations from the normalized SEIR model (10)-(13).
Now we are faced with the choice of the cost for the normalized model. Taking into account that the main aim is to control or to eliminate the disease from the population under study, different costs is may be considered, reflecting different concerns.
The choice of the cost for $(P)$ is based on the need to define vaccine policies to minimize some social and financial burden of the disease into the population. The cost $J_C$ for $(P)$ captures two easily recognized social and financial costs that the infectious disease imposes on a society; the burden of having people infected among the population, translated in $J_C$ as $AI(t)$, and the burden of vaccination to combat the spreading of the diseases, translated in $J_C$ as $Bu(t)$. Noteworthy, the weights $A$ and $B$ can be easily changed to reflect different scenarios.
An almost straightforward translation of this reasoning to our normalized model yields $J_n(x,u)=\displaystyle\int_0^T (\rho i(t)+u(t))~dt,$ where $x=(s,e,i)$ is now the state variable and $\rho$ a parameter reflecting different weights on $i$ and $u$. Numerically speaking, this cost is clearly different to $J_C$ since its two terms are now both percentages while $J_C$ has a weighted sum of two distinctive amounts. Not surprising, some simple tuning of $\rho$ may lead to similar results specially in situations where the total population $N$ does not vary much and, in particular, when the total population remains constant. However, $J_n$ demands that the cost of infected people should be calculated in terms of the percentage of people infected instead of using the number of infected people as in $J_C$, something that depends on the economic practices.
We postpone this discussion of the introduction of different costs to future research and we proceed now with the cost $J_n$ above for our normalized model. Putting all together we are led to the normalized basic optimal control problem:
|
$\nonumber
(P_{n}) \left\{
Minimize∫T0(ρi(t)+u(t)) dtsubject to˙s(t)=b−cs(t)i(t)−bs(t)+ai(t)s(t)−u(t)s(t),s(0)=s0,˙e(t)=cs(t)i(t)−(f+b)e(t)+ai(t)e(t),e(0)=e0,˙i(t)=fe(t)−(g+a+b)i(t)+ai2(t),i(0)=i0,u(t)∈[0,ˉu] for a. e.t∈[0,T], with ˉu∈]0,1].
\right.
\nonumber
$
|
Note that the dynamics is of the form $\dot{x}(t)=f(x(t))+g(x(t))u$, with $x=(s,\;e,\;i)$ and appropriate functions $f(x)$ and $g(x)$.
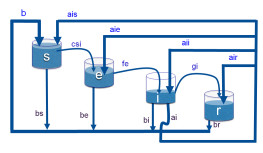
Remark 1. A word of caution regarding the way the system (10)-(13) is viewed. We cannot interpret the dynamics between these new compartments in the same way as with the classical model. Indeed, in equation (10) the term $+ai(t)s(t)$ does not mean that those who died of the disease become susceptible as if reborn in a different compartment. Instead, this dynamical model can be better understood using fluid analogies in the following way. Consider a system with four tanks with the same amount of water circulating between them. At each instant $t$ the total amount of water in the system is constant but the level of water in each tank varies. This analogy is presented in Figure 1 assuming that $u(t)=0$. As mentioned before, $(P_n)$ does not depend on the parameter $d$. This happens because the normal dead rate is equal for any compartment and thus it does not affect the distribution of population into compartments. On the other hand, the birth rate works as if feeding the susceptible compartment.
We will discuss pros and cons of $(P)$ and $(P_n)$ using numerical solutions. Before that, however, we need to briefly present some remarks on the numerical tools and to describe the set of parameters used in our simulations.
3. Numerical methods and data for simulations
Optimal control problems can be solved numerically by direct or indirect methods. Here, we opt to use the direct method (for a description these two methods see, for example, [19]): first the problem is discretized and the subsequent optimization problem is then solved using software packages with large scale nonlinear continuous optimization solvers. In this work all the simulations were made with the Applied Modelling Programming Language (AMPL), developed by [7], and interfaced to the Interior-Point optimization solver IPOPT, developed by [21]. Alternatively, the optimization solver WORHP (see [3]) can also be interfaced with AMPL. We refer the reader to [16] and references within for more information on software for optimal control problems.
The application of the Maximum Principle to problems in the form of $(P)$ (the control appearing linearly in the dynamics and the cost and with box control constraints) yields that the solution is a concatenation of bang-bang arcs and$/$or singular arcs. That is the case of $(P_n)$ and $(P)$. When the optimal control is bang-bang, sufficient second order optimality conditions (SSC) can be checked numerically; SSC as described in [15] and [19] can be checked with high accuracy using the control package NUDOCCCS. Alternatively they can also be tested with AMPL interfaced with IPOPTS or with WORHP.
In all the computations we consider the time horizon to be 20 years: thus $T=20$. The parameters characterizing the population and the disease are in table 1. These parameters do not correspond to any specific population or diseases. In fact, $f$, $a$ and $g$ are equal to those in [17], while $c$ is adapted from the corresponding values in [17]. As for $b$ and $d$, these are closely related to birth rates and death rate in European countries. The disease parameters correspond to a devastating disease as one can see either by calculating the reproduction number, which is higher than 1 (see [10]) or by solving the classical SEIR system ((1)-(6)) with $u(t)=0$. In the next section, and when convenient, we use different parameters but this will be clearly stated. The values of the initial conditions follow those in [17]: for classical SEIR models they are presented at table 2 together with the parameters $A$ and $B$ of the objective functional. The initial conditions for the normalized problem $(P_n)$ are presented at table 3.
Table 1. Parameters for SEIR models.
| Parameter |
Description |
Value |
| b |
Natural birth rate |
0.01 |
| d |
Death rate |
0.0099 |
| c |
Incidence coefficient |
1.1 |
| f |
Exposed to infectious rate |
0.5 |
| g |
Recovery rate |
0.1 |
| a |
Disease induced death rate |
0.2 |
| T |
Number of years |
20 |
Table 2. Initial Conditions and cost parameters for problems with classical SEIR model.
| Parameter |
Description |
Value |
| A |
weight parameter |
1 |
| B |
weight parameter |
2 |
| S0 |
Initial susceptible population |
1000 |
| E0 |
Initial exposed population |
100 |
| I0 |
Initial infected population |
50 |
| R0 |
Initial recovered population |
15 |
| N0 |
Initial population |
1165 |
Table 3. Initial Conditions and cost parameters for problems with classical SEIR model normalized model.
| Parameter |
Description |
Value |
| s0 |
Percentage of initial susceptible population |
0.858 |
| e0 |
Percentage of initial exposed population |
0.086 |
| i0 |
Percentage of initial infected population |
0.043 |
4. Comparison $(P)$ with $(P_n)$
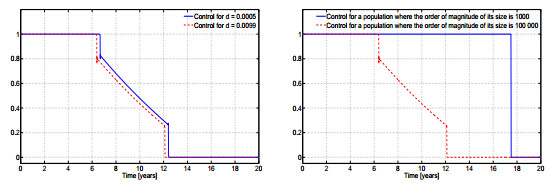
The problem $(P)$ is sensitive to the dimension of the population. For example, the solution changes when we merely perturb the dead rate parameter, $d$, or when the initial values $S_0$, $E_0$, $I_0$ and $R_0$ are multiplied by a given positive constant. The first situation is illustrated in the left graph of Figure 2, where the optimal control for a problem $(P)$ with $d=0.0099$ is shown together with the optimal control for a problems with $d=0.0005$; although the profile of the optimal control is the same, the switching times do change. Sensitivity of $(P)$ to different initial values is illustrated in the right graph of Figure 2. For a smaller population the optimal control is of the bang-singular-bang type whereas, for a larger population it is bang-bang. In both cases, the percentages of susceptible, exposed and infected initial individuals is the same. Clearly, the cost is in the core of sensitivity of $(P)$ with respect to the size of the initial population and also with respect to different death rates.
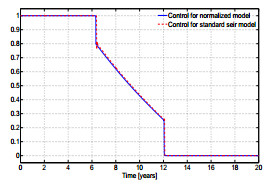
Although the two problem $(P)$ and $(P_n)$ are different, we can get $(P_n)$ to produce approximately the same solutions of $(P)$ as mentioned above. To do so, we need to choose the parameter $\rho$ in $J_n$ to be $\rho=\dfrac{A\times \pi}{B}$, where $A$ and $B$ are the weights of $I(t)$ and $u(t)$ and $\pi$ is an average of the total population during $T$. An example is shown in 3. Observe that if the total population remains almost constant, we can choose $\pi=N_0$.
Clearly, the reason why $(P)$ and the $(P_n)$, with parameters associated to $(P)$, differ resides on the cost. As mentioned before, the cost of $J_n$, introduced in section 2 as an adaptation of $J_C$, requires a fresh approach. Indeed, $(P_n)$ demands that the "financial" cost be expressed in terms of percentages and not numbers of individuals.
When considering problem $(P_n)$, we are mainly concerned on how the total population is distributed into compartments. Because of the nature of the percentages we use, both the total number of the population as well as the dead rate are simply not there. The problem $(P_n)$ may be useful to simulate the same disease acting on different sized populations but with similar birth rates. Observe also, that if needed, when solving $(P_n)$ numerically we can keep track of the changes of the total the population by adding the differential equation $\dot{N}(t)=(b-d)N(t)-ai(t)N(t)$ to our code. This does not cause any change on the optimal control since the solution does not depend on $N$. While $(P_n)$ has the advantage of covering different populations in one go, it does not always subsumes or replaces $(P)$. For example, the situation when one seeks vaccination policies when the total number of vaccines available are bounded (as in [17]) is tailored for the classical model $(P)$. Mixed constraints like those introduced in [1], i.e., of the form
|
$
u(t)S(t)\leq V_0,
\label{eq:restricao}
$
|
(14)
|
can be mathematically translated to normalized models but they loose their meaning. However, this drawback may be overcome by considering $u(t)\in [0,\bar{u}]$, for a suitable contant $\bar{u}<1$. This technique was also used in [16], for $(P)$, as numerical simulations shows that the results obtained by using this strategy are similar to the solutions obtained by using the restriction described in (14).
5. Solution of $(P_n)$
We now focus on the Maximum Principle for the problem $(P_n)$. The Hamiltonian given by
|
$H(x,\;p,\;u)=pf(x)+pg(x)u-\lambda(\rho i+u),$
|
for appropriated $f$ and $g$, $x=(s,e,i)$ and where $p(t)= \left(p_s(t),p_e(t), p_i(t)\right) \in \mathbb{R}^3$ denotes the adjoint variable. Let $(x^*,u^*) \in W^{1,\infty}\times L^\infty$ be an optimal solution to $(P_n)$. Then the maximum principle [5] asserts the existence of a scalar $\lambda\geq 0$ and an absolutely continuous function $p$ such that the following conditions are satisfied almost everywhere:
(ⅰ) $\max \{|p(t)|:t\in[0,T]\}+\lambda>0$ (nontriviality condition)
(ⅱ) $\dot{p}(t)=-H_x[t]=\langle p(t),f_x[t]+g_x[t]u^*(t)\rangle -\lambda (0,\;0, \;\rho)$ (adjoint condition),
(ⅲ) $H(x^*(t),p(t),u^*(t))=\displaystyle\max_u \{H(x^*(t),p(t),u(t))\::\: 0\leq u \leq \bar{u}\}$ (maximization of the Hamiltonian),
(ⅳ) $p(T)=0$ (transversality condition).
Since $(P_n)$ does not have final time constraints on the states, it is well known that the above conditions hold with $\lambda=1$. Set $\phi (t)=H_u[t]=\langle p(t), g[t]\rangle -1$. This is called the switching function and it is of help to deduce a characterization of the optimal control $u^*$ from (ⅰ)-(ⅳ) which we proceed to do next.
It is a simple matter to see that condition (ⅲ) is equivalent to
|
$
\phi (t)u^*(t)=\displaystyle\max\limits_u \{\phi (t)u(t)\::\: 0\leq u \leq \bar{u}\}.
$
|
(15)
|
It follows that $u^*$ is bang-bang in an interval $I\subset [0, T]$, if the switching function $\phi$ has a finite number of isolated zeros at which the control switches between $0$ and $\bar u$. If $\phi$ is zero on an interval, then $u^*$ is singular, i.e.,
|
$
u^*(t)= \left\{
ˉu, if ϕ(t)>0,0, if ϕ(t)<0,singular, if ϕ(t)=0.
\right.
\label{eq:sis_sing_sem_restr}
$
|
(16)
|
In terms of the data of $(P_n)$ the adjoint condition (ⅱ) reads
|
$
-\dot{p}_s(t)\;\;\;\; = (ai(t)-ci(t)-b-u(t))p_s(t)+ci(t)p_e(t),
$
|
(17)
|
|
$
-\dot{p}_e(t) \;\;\;\;= (ai(t)-b-f)p_e(t)+fp_i(t),
$
|
(18)
|
|
$
-\dot{p}_i(t) \;\;\;\; = (as(t)-cs(t))p_s(t)+(cs(t)+ae(t))p_e(t)+\nonumber \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2ai(t)-a-b-g)p_i(t)-\rho.
$
|
(19)
|
Also, we have
|
$
\phi(t)=-1-p_s(t)s(t).
$
|
(20)
|
Since our computations show that a singular arc appear, let us assume that $\phi(t)=0$ for $t$ in an interval $I\subset [0,T]$ and check if we can obtain formulas for the singular controls. We work in the region1
1Since the initial condition belong to the interior of $\mathcal{R}$ and $\bar u\in ]0,1]$, this statement is easily verified numerically.
|
${ \mathcal{R}}:=\left\{(s,e,i)\in\mathbb{R}^3:~s\geq 0,~e\geq 0, ~ i\geq 0\right\}$
|
and so we deduce that
|
$\phi(t)=0 \text{ implies that }p_s(t) = -\frac{1}{s(t)}< 0.$
|
In the interior of the singular interval we have $\dfrac{d \phi}{dt}=0$ and $\dfrac{d^2 \phi}{dt}=0$. Now
|
$\dfrac{d\phi}{dt}=cs(t)i(t)p_e(t)-bp_s(t)=0$
|
implies that that $p_e = \frac{-b}{cs^2(t)i(t)} \leq 0$. Since
|
$
d2ϕdt=aci(t)2pe(t)s(t)−aci(t)pe(t)s(t)−bci(t)pe(t)s(t)+cfe(t)pe(t)s(t)−cgi(t)pe(t)s(t)−c2i(t)2pe(t)s(t)−ci(t)pe(t)s(t)u(t)+2bci(t)pe(t)+cfi(t)pe(t)s(t)−cfi(t)s(t)pi(t)+abi(t)ps(t)−bci(t)ps(t)−b2ps(t)−bps(t)u(t),
$
|
(21)
|
depends on the control variable $u$, we say that the singular control (if it exists) is of order one. Moreover, since $p_s(t) \leq 0$ and $p_e(t) \leq 0$, we have
|
$\dfrac{d }{d u}\left(\dfrac{d^2 \phi}{d t}\right)=-ci(t)p_e(t)s(t)-bp_s(t)>0.$
|
Thus the strict Generalized Legendre-Clebsch Condition (GLC) holds and we can solve $\dfrac{d^2 \phi}{d t}=0$ with respect to the control variable to get
|
$
using(x,p)=c(−c+a)s(t)i(t)2pe(t)ci(t)pe(t)s(t)+bps(t)+cefs(t)pe(t)−b2ps(t)ci(t)pe(t)s(t)+bps(t)+((((−a−b+f−g)s(t)+2b)pe(t)−fs(t)pi(t)−bps(t))c+abps(t))i(t)ci(t)pe(t)s(t)+bps(t)
$
|
(22)
|
It is important to observe that the above expression for singular controls depends on the multipliers. Since we do not establish that the multipliers are unique, we can only expect to use (22) to validate numerical findings but not to prove to optimality. In fact, to prove optimality of computed solution we need to check numerically sufficient conditions. Unfortunately, there are no numerically verifiable sufficient conditions for problems with singular arcs.
6. Numerical solutions for $(P_n)$
We now present and discuss the results of our simulations for $(P_n)$. Recall that we use the data in table 1 and 3. We treat three different cases:
● Case 1: $\bar u=1$ and $\rho=500$,
● Case 2: $\bar u=1$ and $\rho=10$,
● Case 3: $\bar u=0.2$ and $\rho=500$.
In the first two cases the computed optimal control exhibits a bang-singular-bang structure while in the last one the optimal control is bang-bang. For all the three cases we present graphs with the computed controls and trajectories. As in [16] and to keep the exposition short, we do not present the graphs of the multipliers but we give their computed initial values, and we also present the final states, the costs and the switching times
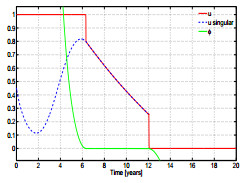
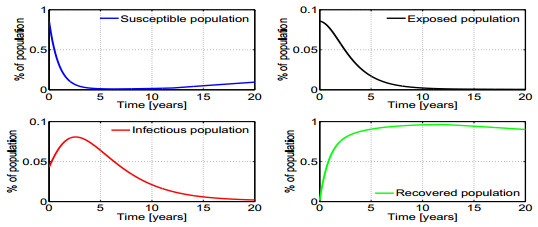
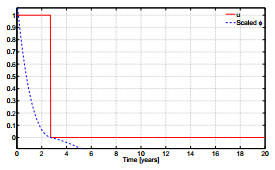
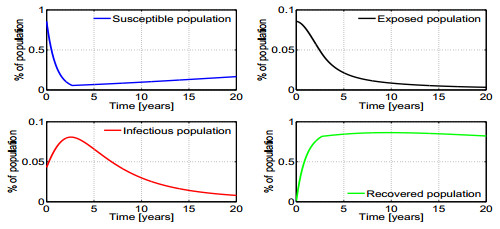
Case 1. Taking $\bar u$ to be $1$ depicts the situation when all the susceptible population can be vaccinated. The results of the simulations are shown in figures 4 and 5. In Fig. 4 we show that the numeric optimal control and switching function, $\phi$, satisfy (16) while the computed singular control (22) coincides with the computed optimal control $u^*$. The optimal trajectories are presented in Fig. 5.
Numerical results for Case 1: $J=327.15,\;\;\; t_1 = 6.4, \;\;\; t_2 = 12.07,$
|
$
s(T)=0.095341,e(T)=0.00051104,i(T)=0.0020380,ps(0)=−126.5,pe(0)=−2253,pi(0)=−3219.
$
|
Case 2. The results of the simulations are shown in figures 6 and 7. In figure 6 the optimal control, $u^*$, and the switching function, $\phi$, are presented. As expected, $u^*=1$ and $u^*=0$ when, respectively, $\phi(t)>0$ and $\phi<0$. The optimal trajectories for the state are presented in figure 7.
Numerical results for case 2: $J=10.181,\;\;\; t_1 = 2.71,$
|
$
s(T)=0.16598,e(T)=0.0033060,i(T)=0.0079433,ps(0)=−377.0,pe(0)=−5137,pi(0)=−7081.
$
|
When we go from case 1 to case 2, the optimal control goes from singular to bang-bang. This is because when we decrease the value of $\rho$, the weight of the control in the cost increases.
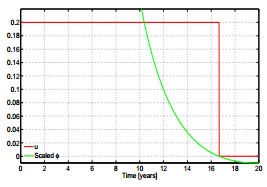
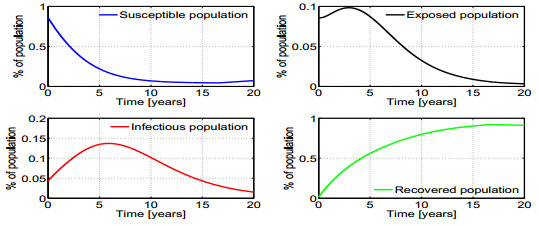
Case 3. While keeping $\rho=500$, we now consider that only $20\%$ of the susceptible people are eligible to be vaccinated, i.e., $\bar{u}=0.2$. Results of the simulations are illustrated in figures 8 and 9. In Fig. 8 the optimal vaccinate rate, $u^*$, and the switching function, $\phi$, are presented. As expected, $u^*(t)=\bar u=0.2$ and $u^*=0$ when, respectively, $\phi>0$ and $\phi<0$. The trajectories for the state are presented in Fig. 9. The profile of the optimal control is bang-bang. The control becomes equal to zero at instant $t_1 = 16.67$.
Numerical results for case 3: $J=806.12, \;\;\; t_1 = 16.67,$
|
$
s(T)=0.071623,e(T)=0.0031999,i(T)=0.015275,ps(0)=−1025,pe(0)=−4692,pi(0)=−6872.
$
|
6.1. Approximation for optimal control
If the control is bang-bang as in case 2 and 3 second order sufficient conditions may be checked numerically as described in [15] and [16]. Here we refrain from engaging in such discussion to keep the exposition short. Here we compute numerically the switching times using the so called induced optimization problem as in [15]. Recall that the switching times are the points $t_{s1}$ at which the optimal control changes from one bound to another.
Implementing the induced optimization problem with AMPL for case 2, with $\rho=10$ and $\bar{u}=1$ and denoting by $t_{s1}$ and $J_s$ the computed switching time and cost, we get $t_{s1}=t_1=2.71$ and $J_s=10.183$ which in contrast with $J=10.181$ is a good approximation.
For case 3, with $\rho=500$ and $\bar{u}=0.2$, we have $t_{s1}=16.63<t_1=16-67$ while we get get a match for the cost $J_s=J=806.12$.
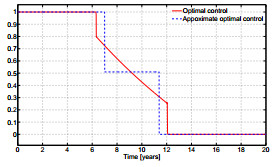
We now turn to case 1 where the computed control $u^*$ is of the form of Bang-Singular-Bang. As discussed in [16], singular controls may be hard to implemented in practice. To remedy this, [16] proposes to approximate the singular control by a constant value $ \tilde{u}$. Here we do as in [16] to calculate the switching times defining the singular interval $t_{s1}$ and $t_{s2}$, the value $0\leq \tilde{u} \leq 1$ and the corresponing cost for case 1 where $\rho=500$ and $\bar{u}=1$. Using the arc parametrization method described in [15], now implemented in AMPL code, we obtain $t_{s1}=7$, $t_{s2}=11.5$, $\tilde{u} = 0.55$ with cost $J_s = 326.12$ a value very close to the previous $J = 327.15$. Figure 10 a comparison between $u^*$ and $u_{apr}$ is shown.
7. Conclusion
We studied the optimal control of an epidemiological normalized SEIR model using a $L^1$-type objectives. We extracted information about the optimal solution from the Maximum Principle. In particular, we determined a closed form for the singular controls. Numerical NP solvers were applied to the discretized problem enabling us to compute optimal control solutions that match the necessary conditions, in particular, the switching conditions and forms for the singular controls.
Moreover, we confronted this problem with the one previously studied in [16] where the so called classical SEIR model is used. The normalized model may cover in one single problem populations of different size and it is defined with what may be seen as a more realistic cost. Because of the use of normalized model, the solution of $(P_n)$ is dictated by the distribution of the population into the three different compartments and the disease characteristics. On the other hand, the normalized model has the disadvantage of not allowing the analysis of certain real situations that cannot be translated by percentages, such as when there is a limited stock of vaccine at a non-constant population. Our discussion of these two problems highlights their differences and the need for a criterion choice of cost, a challenging and relevant subject in optimal control for biomathematics problems.
8. Acknowledgments
The authors would like to thank Prof. Helmut Maurer for numerous and enlightening discussions on this topic as well as his help in writing up AMPL codes for the problems reported here. Thanks are due to the anonymous referees whose many comments and suggestions greatly improved this paper.
The financial support of FEDER funds through COMPETE and Portuguese funds through the Portuguese Foundation for Science and Technology (FCT), within the FCT project PTDC/EEI-AUT/1450/2012—FCOMP-01-0124-FEDER-028894, PTDC/EEI-AUT/2933/2014, TOCCATTA -funded by FEDER funds through COMPETE2020 -POCI and FCT as well as POCI-01-0145-FEDER-006933 -SYSTEC -funded by FEDER funds through COMPETE2020 – Programa Operacional Competitividade e Internacionalização (POCI) – and by national funds through FCT -Fundação para a Ciência e a Tecnologia, are gratefully acknowledged.









 DownLoad:
DownLoad: