1. Introduction
Methods to evaluate the soundness of a structure against inherent defects include the Boiler and Pressure Vessel Code Section XI from ASME (American Society of Mechanical Engineers) [1] and the JSME (Japan Society of Mechanical Engineers) Codes for Nuclear Power Generation Facilities [2]. For the soundness of welded joints, WES2805 (Japanese Welding Engineering Society) [3] and BS7910 (British Standard) [4] are representative codes. These types of codes are called FFS (Fitness-for-Service) codes and have been established as national standards in many countries [5]. In FFS standards, a normalization process for defects is important because real defects have various and complicated shapes, making it impossible to assess the individual stress intensity factor. Coalescence judgements are also important for multiple defects located in close proximity. In many codes, coalescence judgments are incorporated. In the case that multiple cracks are located in adjacent positions, the probability of fracture or fatigue is likely to increase, and defect size must be estimated to be larger than in the case of a single crack. In each standard, the judgment for interaction is assessed mainly by two steps. One is the judgment of alignment for cracks in different parallel plane to be treated as co-planar cracks. Second is the judgment for coalescence for two co-planar cracks to be regarded as one larger crack. It is interesting that these procedures are varied by countries or technical fields. Although an entirely detailed description is impossible due to limitations of space, here some characteristic points of several standards will be described on the basis of the organization by Hasegawa et al. [6]. For the alignment condition, constant critical distance between parallel planes, 12.5mm, is adopted in ASME, JSME and HPIS. On the other hand, the critical distance is varied with the size of cracks in BS and WES. For example, two surface cracks which is having semi-circular shape is assumed, critical distance is double of the radius of the size of crack in BS and same size in WES (1997) and one and a half times in WES (2007). Thus there is the case the FFS assessment result will vary substantially by the difference of using standards. Coalescence judgment condition of co-planar cracks is also varied by standards. If semi-elliptical surface cracks are assumed in same plane, the critical proximity distance which is needed to be coalesced is determined by crack representative length in all standards. However, which length is used for the judgment is different from standards. The depth of the crack is used in ASME, JSME and HPIS and length is used in BS and WES. Furthermore, BS has characteristic judgement rule, that is, critical proximity distance is varied by the aspect ratio of the cracks. Revised WES (2007) based on this study also has similar characteristic rule.
In general, the stress intensity factor (K value) is used for the establishment of such judgment conditions. In past investigations, an interaction effect has been reported for through-thickness multiple cracks that are regularly located in plane [7,8,9] and parallel [10,11]. The interaction of surface cracks has also been investigated. In general, the profile of the K value of a surface crack is much changed by its aspect ratio, so the interaction of two close cracks becomes more complicated. Several typical problems have been studied so far, including multiple surface cracks located on one line [12,13,14,15,16,17,18] and those that are located in parallel but on different planes [19]. However, a quantitative interaction condition has not yet been developed.
Considering such background, some of the authors investigated the increase of K value in the most important situation for welded joints, that is, two surface cracks locate in close position in order to improve the coalescence judgment criterion of WES [20,21]. By these findings and more discussion, for more simplification of criterion considering wide use and the confirmation of the absence of unsafe case WES was revised in 2007. In this paper, K calculations of various combinations of cracks are re-arranged and new calculations for the discussion of revision of WES2805 are shown. Finally a coalescence criterion was clarified especially for brittle fracture. Furthermore, the appropriateness of the coalescence judgement in new WES2805 (in which the findings of this study were already introduced) is investigated.
2. Method
In order to quantify the amount of interaction of two close cracks, finite element method is used as same as the previous researches. The calculations are conducted using ABAQUS (ver. 6.5.1) [22], which is a general-purpose commercial finite element code. The analysis was conducted under elastic conditions under the normal materialconstants of the steel at ambient temperature, that is, the Young’s modulus, E, is set to be 206 GPa and the Poisson’s ratio, ν, is 0.3. Uniform tensile stress, σ0 is assumed as loading condition and set to be 100 MPa. The stress intensity factor, K value was calculated by conversion from a contour integral around the crack tip, i.e., the J-integral value in three modes (opening, in-plane shear and out-of-plane shear) was first calculated and then converted to the K value by equation (1-1) to (1-3) [23], where the integral path is a sufficiently outer contour for which the contour independence is confirmed and the J integral shows a constant value. To perform a finite element calculation, it is necessary to create a finite element mesh. For the accurate calculation of the K value, it is important to allocate finely divided meshes around the crack tip. Used model and meshes are explained separately in the case of surface cracks and that of through thickness cracks.
2.1. Surface Cracks
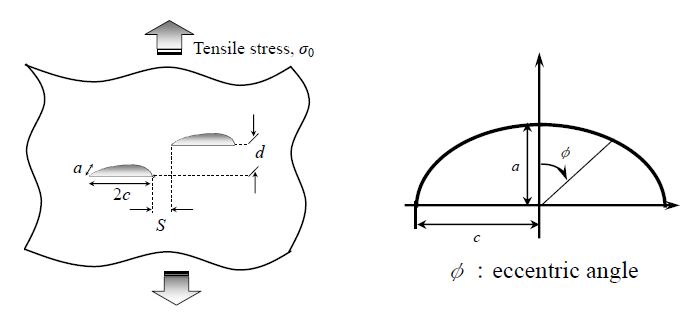
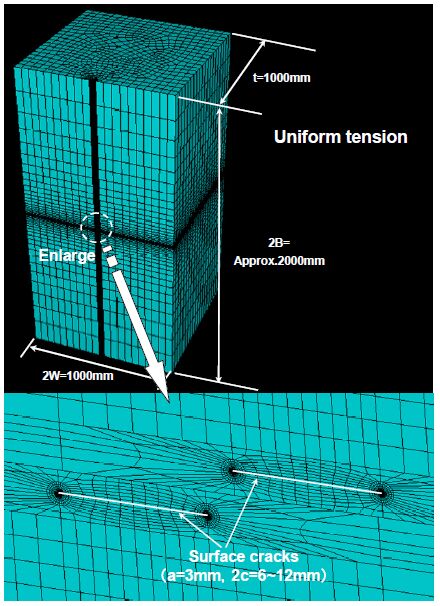
Figure 1 shows the crack face plane of a single crack that was handled in this manner. In general, the mesh division of a three-dimensional curved crack tip entails a high degree of difficulty, so there is a greater difficulty in producing a model with multiple cracks located at arbitrary positions in different planes (Figure 2), and when the variable S (the distance between two crack tips) is negative, that is, the overlapping condition, it becomes still more difficult. Therefore, when there are multiple cracks, the unit block (referred to as a part) including a surface crack that was created in accordance with the method proposed by Kamaya et al. [19] was copied to the required position, and then they were non-node-covalently bonded. This time, each node position on the joint surface does not necessarily coincide with that on another part; however, the node set on both joint surfaces continues to exist on a single surface. The deformation of both parts is calculated as each face attempts to not be separated (surface to surface features of ABAQUS). In this manner, complex meshing tasks including a plurality of surface cracks can be replaced by a relatively simple task of creating and joining multiple parts of the unit meshes of a single crack. An example of a mesh that is created in this manner is shown in Figure 3. Cracks having a complex mesh are very close, without the interaction of two mesh divisions. Ordinary type 8-Node quadratic isoparametric element is used in the analysis.
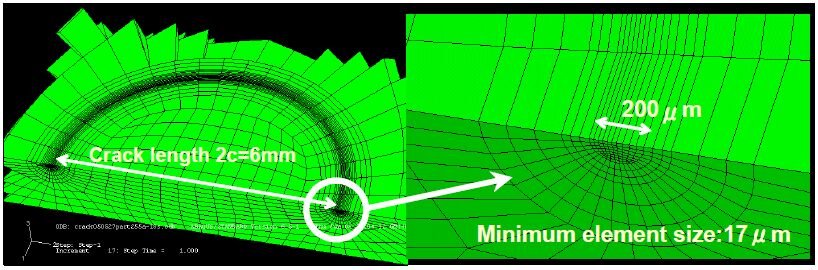
In the finite element method, it is necessary to create a finite object even for an infinite problem. The reported solutions for high-precision surface cracks assume that each crack is in a semi-infinite plate. Hence, a rectangular solid with dimensions of 2W, 2B and t, as shown in Figure 3, was produced, where W, B, and t are all sufficiently longer than the crack length. According to Kamaya et al. [19], by decreasing each of the three parameters, the crack length to width ratio, c/W, the crack length to the analysis model length ratio c/B and the crack depth to analysis model thickness ratio, a/t, and the calculated K value are asymptotic to the solution of the semi-infinite plate model. It can be concluded that by reducing the values to c/W = 0.2, c/B = 0.1 and a/t = 0.08, the model is approximated to a semi-infinite plate. This time, the planes of each crack is set to be perpendicular to the face of the object and the crack of length 2c is equal to 6~12 mm and the crack depth a is 3 mm, whereas the size of the model 2W = t is approximately 1000 mm and 2B is approximately 2000 mm, so that size parameters are calculated, c/W = 0.012~0.024, c/B = 0.006~0.012, and a/t = 0.003, and it is concluded that the size is sufficient to represent a semi-infinite plate.
2.2. Through Thickness Crack
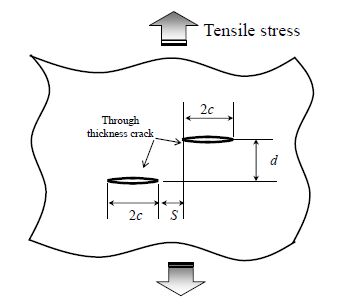
In order to evaluate the extreme high aspect ratio (a/c) condition of the surface cracks, through thickness cracks is modelled in FEM analysis as shown in Figure 4. Two dimensional analyses are conducted by using four nodes-square shape elements accordance with plane strain assumption. Mesh division is easy and unnecessary to use non-node-covalently bonded as surface crack problems. In this study this condition of through thickness cracks is referred as a/c = ∞ considering the consistency from the investigation of surface cracks.
2.3. Verification of Numerical Analysis
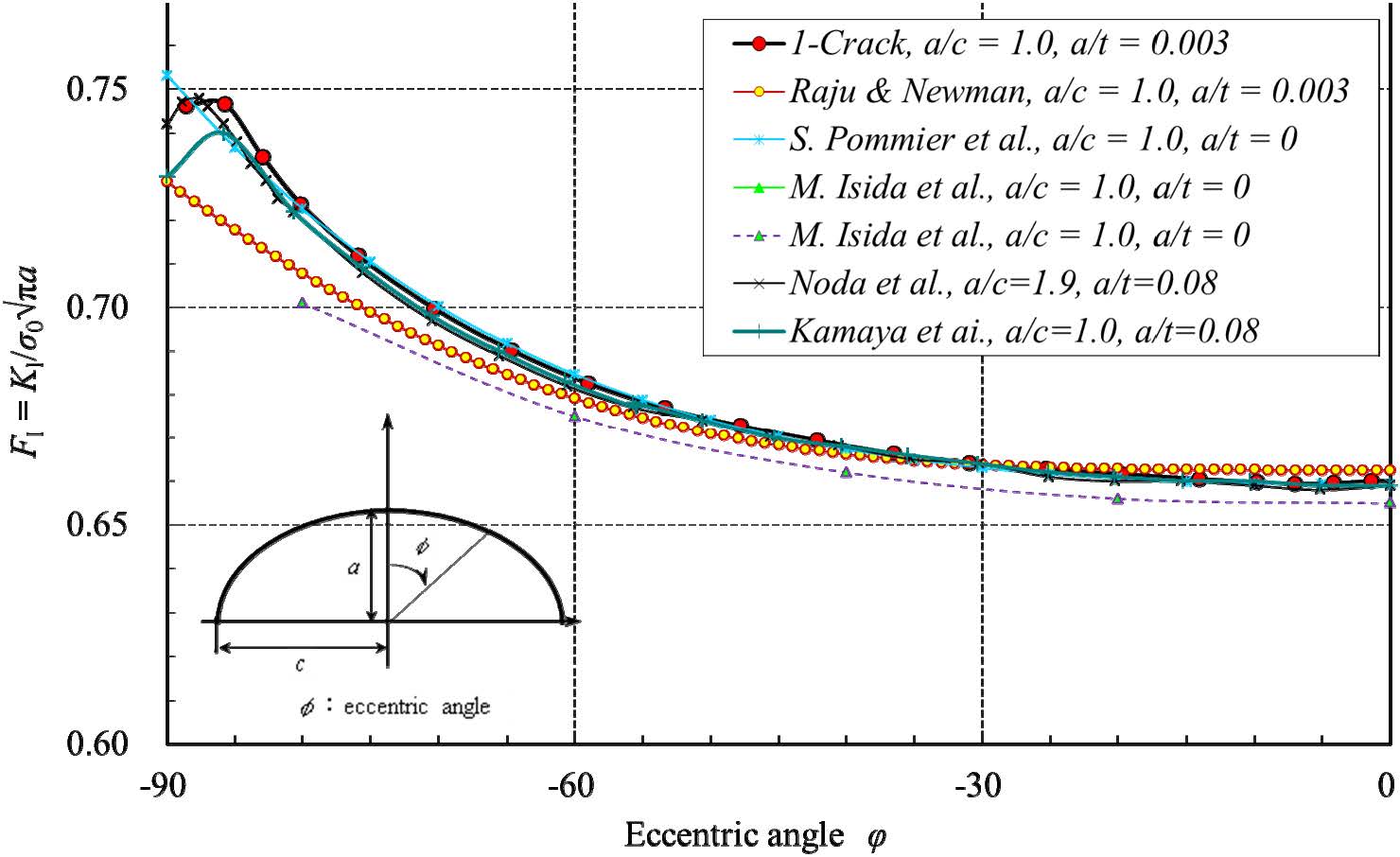
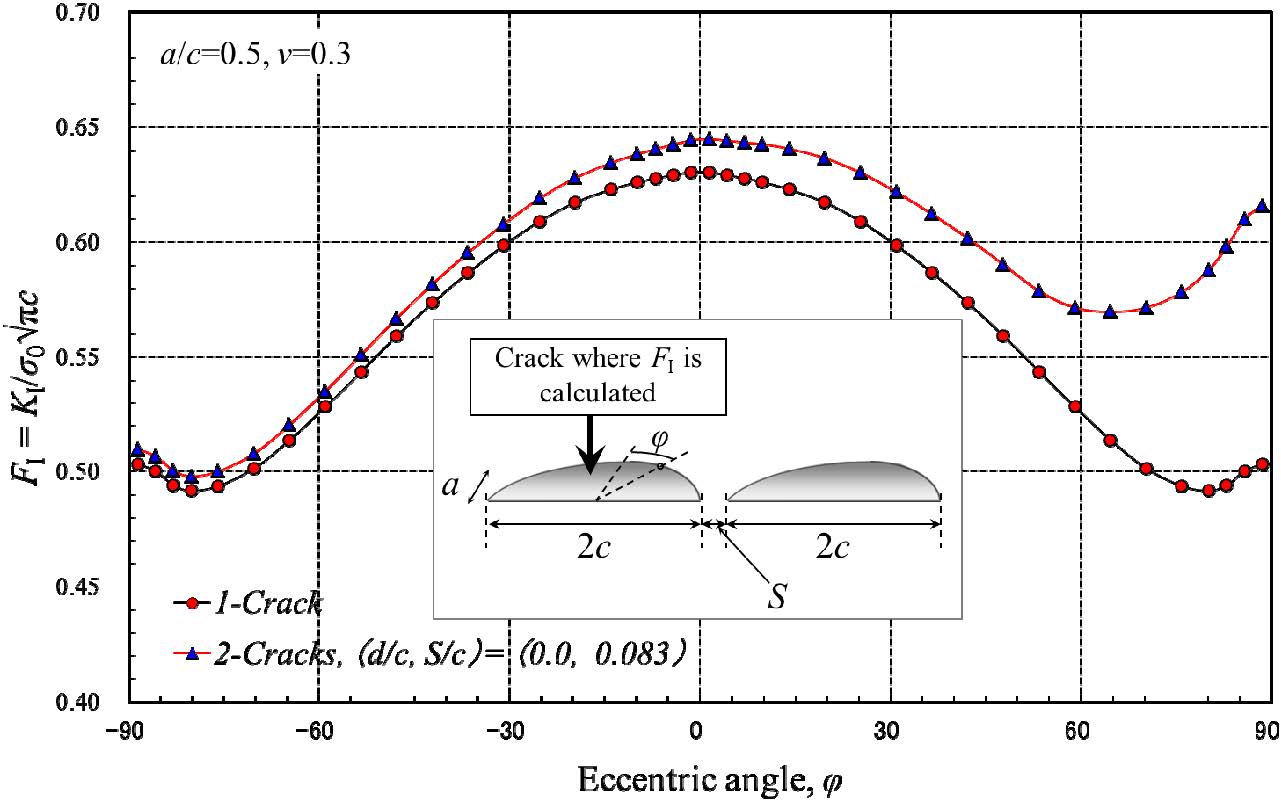
As the analysis of the K values using the finite element method is dependent on the analysis conditions, for example, the element division method, it is essential to verify the analytical accuracy by using an authenticsolution result. Here, to validate the analysis accuracy, the K value of a surface crack that exists alone was to be verified by previous literatures in which a high-accuracy solution was reported. The analysisresults of the case of a semicircular shape, a = c = 3 mm are shown in Figure 4. The KI value is shown as a dimensionless parameter, the FI value, by equation (2-1). If only one crack exists under remote uniform stress, both of KII and KIII are zero. However, if two cracks are closely located in different planes, KII and KIII become to have the positive value. In this section, in order to investigate fracture modes which are needed to be discussed, non-dimensional stress intensity factor, FII, FIII are also introduced as shown in equations (2-2) and (2-3), where σ0 is the uniform tensile stress. Here, there is a need for caution as FII, FIII are different from the commonly used non-dimensional parameter. However, authors think that FII, FIII can be used for the comparison of the strength of the each stress intensity factor directly.
In Figure 5, the results of previous analyses by Newman et al. [24], Noda et al. [25], Kamaya et al. [19], Pommier et al. [26] and Ishida et al. [27] are also shown. The analytical result of this study shows good agreement with that of Noda et al. [25], who analyzed in specific detail the surface portion by the body force method. The analytical results of Noda et al. [25] have a superior feature in that 3 or more digits of precision have been appended.
A similarverification was necessary for a through thickness crack. It is clearly shown in previous paper by authors [20] that the analytical result by the finite element method shows quite good agreement with the theoretical value.
2.4. Importance of Aspect Ratio of a Surface Crack
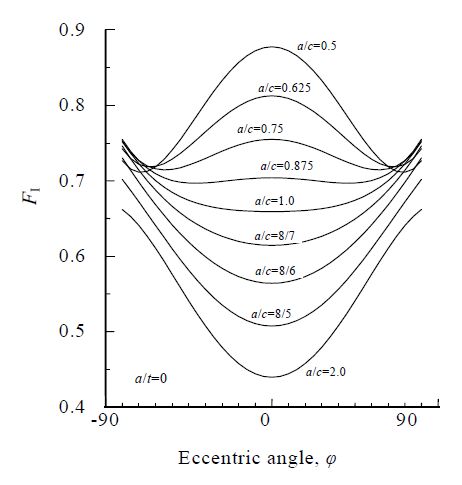
For the calculation of the K value of a semi-elliptical surface crack, it is important to assess the aspect ratio of the crack. Figure 6 shows the relationship between the aspect ratio and the K value distribution of a single crack by Pommier et al. [26]. In the case where the aspect ratio a/c of the crack is large (deep in the thickness direction), the K value at the end of the surface crack is increased. If it is small (shallow in the thickness direction), the deepest point shows the maximum K value. In discussing an increase in the K value in the case where two surface cracks approach, it is not sufficient to evaluate only the rise in the K value at the closest point, but the maximum K values in the case of a single crack and multiple cracks should also be discussed. Therefore, by calculating the K values in all nodes at the crack tip, the increase in the maximum value was assessed. This is because the maximum K point for multiple cracks is not necessarily at the end or the deepest portion. Additionally, for example, if the aspect ratio a/c is small, although the K value at the proximal end certainly increases even if the surface cracks come closer, it can be assumed that the maximum point is still at the deepest part, and the influence of the interaction that should be taken into account is small.
In this study, as mentioned previously, the ratio of the maximum K values of a single crack and multiple cracks are discussed by varying the aspect ratio of the crack across 4 levels (a/c = ∞, 1.0, 0.75, 0.5), and then the proximity position and the increase in the K value is investigated. The criterion for the interaction was to proceed with the consideration of a K value increase of greater than 10%.
3. Results
3.1. Expression of Proximity Position
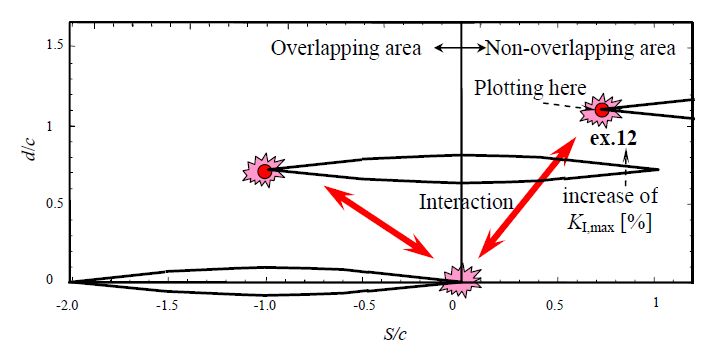
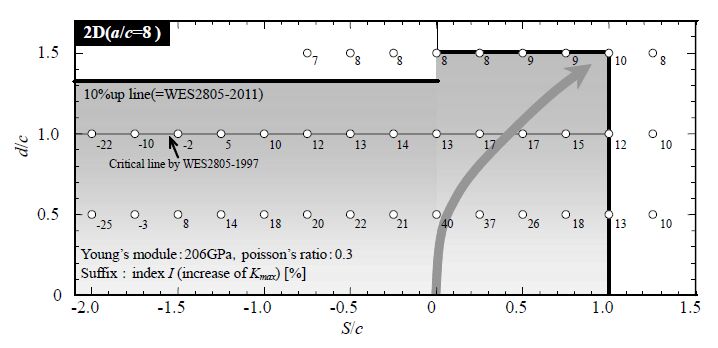
In order to discuss the interaction of two close surface cracks having same shape, the positional relationship of two cracks having same shape is expressed based on the coordination of crack tips from the appearance of surface side directly. As shown schematically in Figure 7, one side of crack tips is firstly positioned to the original point. When second crack is considered, the crack tip position which becomes face-to-face is plotted as the expression of the relationship between two surface cracks. In expressing the dimensionless quantities of the proximity distance, S/c and the inter-planar distance d/c were used as the vertical and horizontal axes, respectively. The plot shows the calculation performed at a point in the coordinate system, and the suffix numbers show the index I as the ratio of the maximum value of KI (Mode I stress intensity factor) in the case of a single crack, [KI, max]single (although there is no maximum or minimum of the concept in the case of through-thickness cracks), to that in the case of multiple cracks, [KI, max]double. In sum, I is the percentage increase in the maximum KI value calculated by equation (3). In this study, the interaction criterion which should be coalesced to one large crack was set to be I = 10%. In this study only mode I is focused. This is because the other stress intensity factor is not considered to be picked up as described in Section 3.2.
|
I=([KI,max]double[KI,max]single−1)×100
|
(3)
|
3.2. Fracture Mode for Assessment
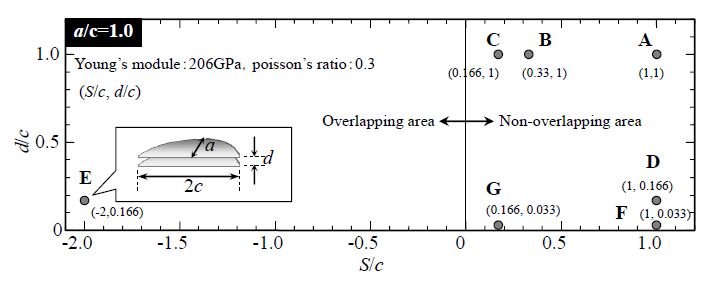
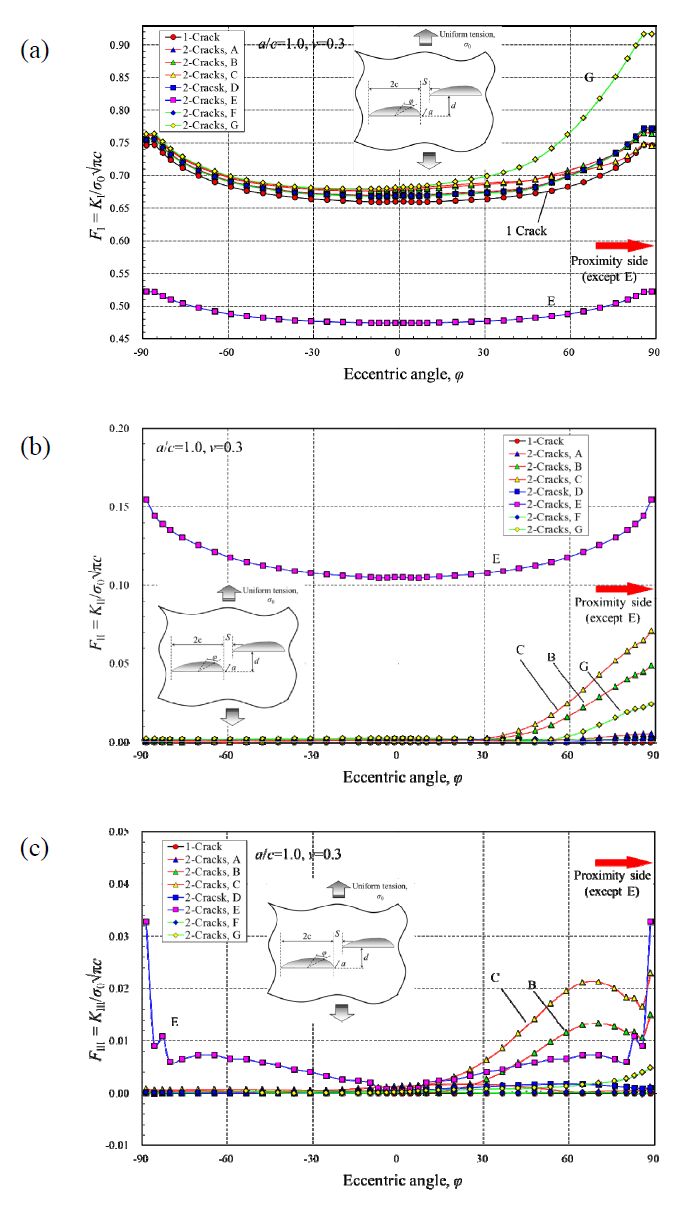
To evaluate the interaction in the stress intensity factor when the cracks are present in different planes, as shown in Figures 2 and 3, the stress intensity factor of the shear mode, as well as the opening mode, is clarified. In this study, checking the interaction situation in the three modes for a representative position condition, the mode that has to be investigated is shown. To study the interaction of two identical cracks that are adjacent in the present study, we thought it is beneficial to study a crack shape in which the maximum KI value is at the end of the crack front, so a semi-elliptical crack with an aspect ratio a/c = 1.0 was considered. Considering the case of two cracks with the same dimensions in adjacent positions, their positional relationship is shown in Figure 8. The conditions investigated in this section are the 7 points of A~G in Figure 8. The change in the K value in each mode was expressed by the eccentric angle in Figure 9. It is revealed that Mode I has a significantly greater K value than the others, so the remaining two modes can be ignored.
3.3. Interaction for Two Close Cracks
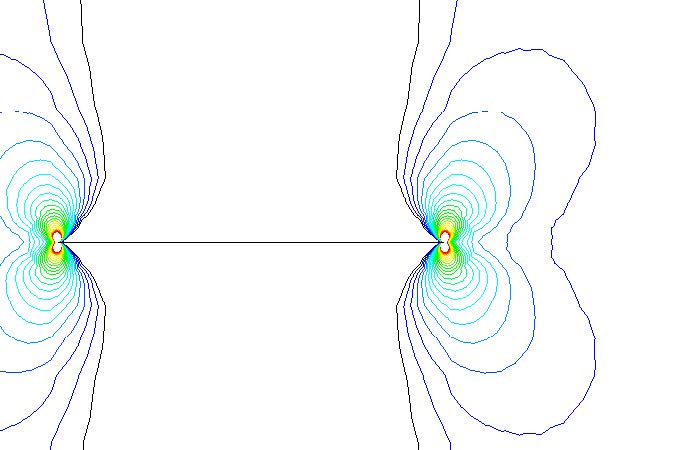
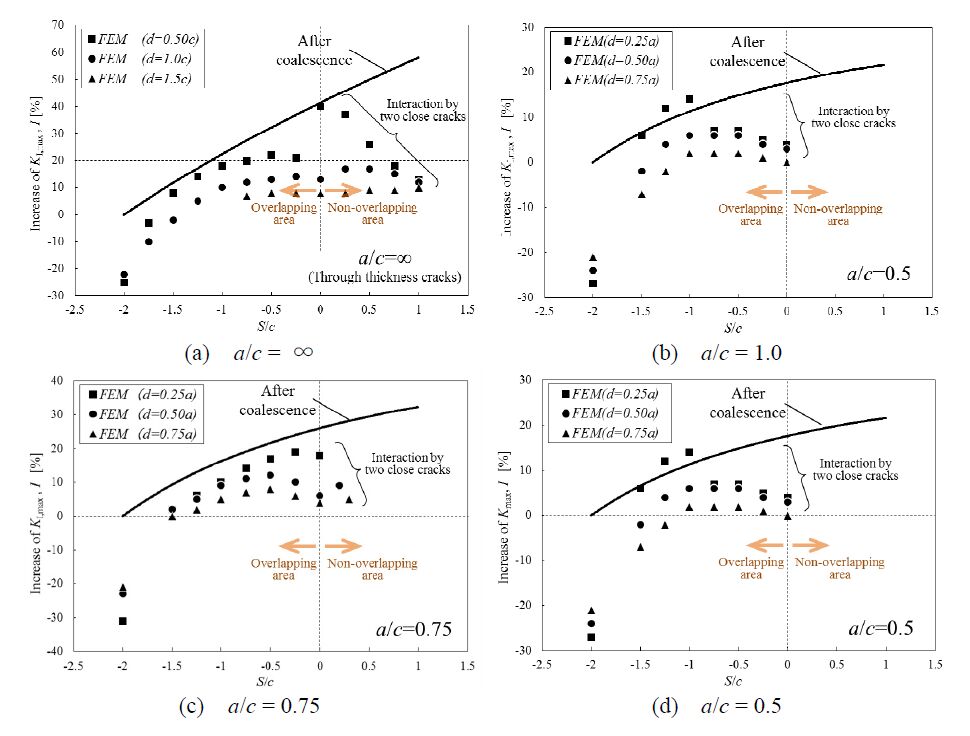
Figure 10 shows the calculation results of the case of a/c = ∞ as an example. As described in Figure 7, a positive S/c value means that the two cracks do not overlap. When index I is considered in this figure, as the inter-planar distance d/c increases, the interaction amount generally shows a downward trend. However, it is important to note that the maximum interaction point is not necessarily close to the vertical axis, which means that the distance S/c would be equal to zero, but rather the maximum interaction point is moved to a point of distance S/c that becomes larger as the inter-planar distance d/c is increased. This maximum point is considered to correspond to the ridge when drawing stress contours for a single crack (Figure 11). That is, the interaction effect is considered to be maximized when the crack tip of the other surface crack is located at a point corresponding to the ridge of the stress contours. If the interaction is judged as a rectangular solid in the region of S/c≥0 for this example (a/c = ∞), the critical region is S/c≤1.0 and d/c≤1.5 by the interpolated calculations. These criteria for through-thickness cracks are wider than those of WES2805-1997 and were adopted in the revision of WES2805 in 2007 and 2011.
If S/c is negative, the cracks are located in overlapping positions. Even in this situation, it is clearly shown that the interaction amount becomes smaller at a greater inter-planar distance. The interaction amount decreases to less than zero as the crack approaches the completely overlapping situation, that is, S/c = −2.0, and finally at the condition of S/c = −2.0 and d/c = 1.0, the interaction amount of each crack drops to −22% [20].
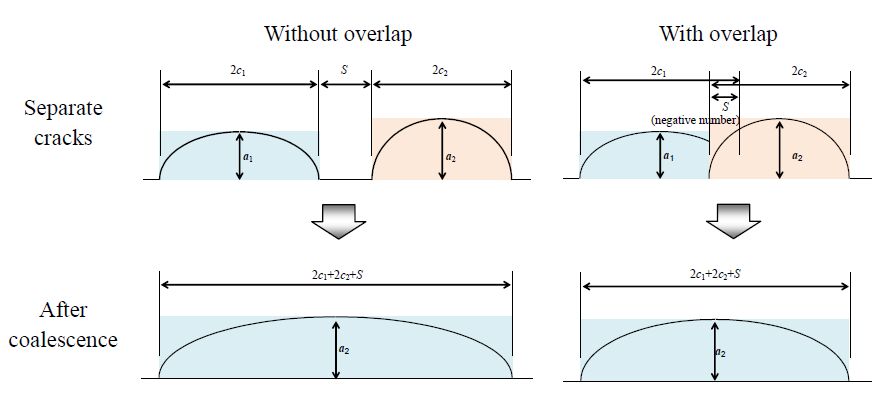
In the region of the S/c < 0, if the interaction criterion which should be coalesced to one large crack is referred to the inter-planar distance, d/c, d/c≤1.0 in the case of a/c = ∞. Although it is possible to determine the rectangular critical region as being the same as in the condition of S/c≥0, in this study, only the d/c criterion is adopted, independent of theS/c value. This is because over-conservatism can be avoided when the cracks are located in an overlapping relationship, taking into account that the coalescence procedure adopts an envelope size (Figure 12) for multiple cracks. Finally, the interaction cri terion which should be coalesced to one large crack can be expressed as the bold line in Figure 9.
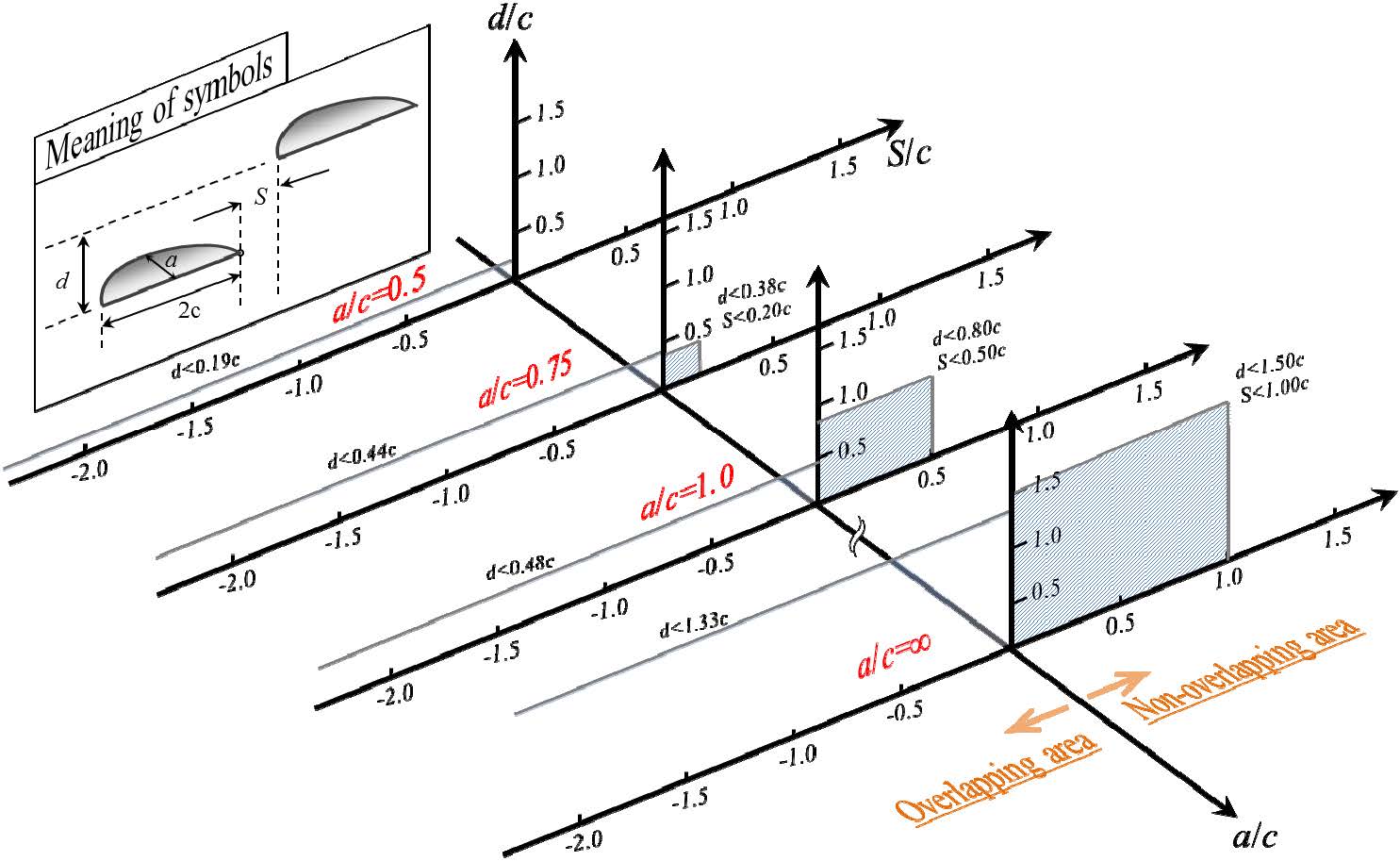
The interaction criterion which should be coalesced to one large crack for the other a/c conditions was also determined by FEM analysis results in a similar way. The result that includes all conditions of a/c is shown in Figure 13. This shows that two cracks with a small a/c condition rarely show interaction. The reason is that the deepest point of the crack with a small a/c condition is the maximum K point, as shown in section 4. Figure 14 shows the interacting situation for very close cracks with a/c = 0.5, which indicates that the increase in the K value at the deepest point is not as much as that on the edge. However, the maximum point remains in the deepest point even in this very close case. Even in the case of a/c = 0.75, which is almost the same value as between the edge point and the deepest point, the interaction region is so limited in the S/c≥0 region.
4. Discussion
The interaction judgment conditions by the finite element method can be obtained as shown in Figure 13 for each aspect ratio of the crack. In the study of Murakami et al. [13], it was revealed that the K values of a surface crack with a finite a/c value monotonically changes and asymptotically approaches that of the through crack. Hence, a similar tendency is assumed to be maintained for this time interaction conditions, and the results of the surface cracks and through cracks can be thought to have a continuous relationship.
4.1. Non-Overlapping Condition
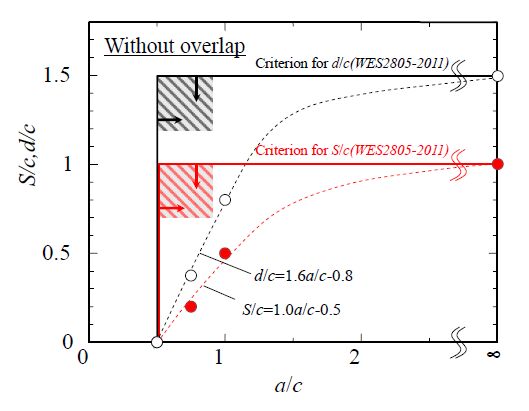
First, by extracting the critical S/c and d/c value from non-overlapping area in Figure 13, the interaction critical point in the case of S/c ≧ 0 is plotted as a/c as a vertical axis variable, so the region where coalescence is needed can be recognized in Figure 15. It can be seen from this figure that there is no interaction region in the condition of a/c < 0.5. Figure 15 also includes the simplified linear part for such interaction conditions. This relationship can be approximately denoted by equations (4) and (5) for the inter-planar distance d/c and the proximity distance S/c, respectively. If a/c = ∞critical d/c is 1.5 and critical S/c is 1. As explained in previous paragraph, these (Equations (4) and (5) and plots in a/c = ∞ condition should be continuously connected so the interaction region becomes representable as a region that is smaller than the dotted line drawn in Figure 15. These critical conditions became reference data for revision activity of WES2805-2011 published by the Japanese Welding Engineering Society. Finally furthersimplified conditions described as a bold line and arrows in Figure 15 is adopted in the revision. It is clearly shown that the revised WES2805 specification includes much conservatism, especially in the small a/c region. These conservative judgment rules are to avoid complexity and enhance ease-of-use as a fitness for service standard. However, adoption of the judgement that cracks with lower aspect ratio than 0.5 do not need to consider the interaction is quite new and it seems a major advance.
|
d≦1.6a−0.8c(0.5<a/c≦1.5)
|
(4)
|
|
S≦1.0a−0.5c(0.5<a/c≦1.5)
|
(5)
|
4.2. Overlapping Condition
In the case of S/c < 0, which is the overlapping condition, the critical interacting condition is expressed in a similar way. The approximate critical limit is shown as a dotted line, including the linear part in Figure 16, which is a function of the aspect ratio and independent of S. The linear part can be described as equation (6). In the revised WES2805, the critical condition d≤1.5c was adopted as a simplified criterion the same as in the non-overlapping condition. This also includes the conservatism as in the non-overlapping condition. However in overlapping condition, the effect of coalescence treatment is so limited that this conservatism is not thought to come to an issue.
4.3. Change of K Values by Coalescence Process
Two cracks that satisfy the critical conditions for the interaction are advance through the coalescence process, as shown in Figure 12, which includes some safety margin, as described in the previous section. In this section, it is determined if the increase of KI, max in one coalesced crack compared with one original crack is larger than that of two closely interaction cracks. Figure 17 shows a comparison of the increase of KI, max between one coalesced crack and two cracks in close proximity. Figure 17(a)-(d) correspond to the cases of a/c = ∞, 1.0, 0.75 and 0.5, respectively.
In this study, in the case of a surface crack, the inter-plane distance is changed to 0.25a, and in the case of through thickness cracks, the proximity distance between them is changed to 0.50c. In most cases, the increase of KI, max by the coalescence process exceeds for two interacting cracks. It is intuitive that if the proximity distance is very short, the increase in the KI, max value will rise. Especially in the case of cracks separated by a negligible distance, there may be a large K value at the close side, but brittle fracture generates propagation to combine the two cracks, and then the driving force of the crack is assumed to be able to relax. This means that the increases in the KI, max values at a very close position do not need to be considered. Here, it has been shown that the increase in KI, max in two close cracks almost match with the increase in KI, max by the coalescence process when the proximity position relationship shows a symbol “■” in Figure 17.
Inter-plane distance of “■”:
・Case(a), through-thickness cracks: d = 0.5c;
・Case(b)-(d), surface cracks: d = 0.25a.
When the cracks are located in closer proximity than these distances, the coalescence process will result in a prediction that is overly dangerous by WES2805. However, these inter-plane distances are sufficientlyshort, so the possibility of a brittle crack propagating in a direction different from that of the adjacent crack from the KI, max point is considered to be extremely low. By these considerations, it can be concluded that this envelope process of coalescence provides a prediction that errs on the side of safety.
5. Conclusions
The K value increases due to the interaction of two surface cracks/two through cracks of the same length located in any of the positional relationships were obtained by the finite element method. As a result of a study focusing on the aspect ratio of the crack, the following conclusions were revealed.
(1) The positional relationship in which the mutual interaction is increased is related to the distribution of the stress contours of the crack tip, not necessarily the point at which the proximity distance is zero.
(2) In the case of the positional relationship of no overlap (S/c ≧ 0), the interaction region is greatly affected by the aspect ratio of the cracks. As the shape in the thickness direction becomes deeper, the interaction region increases, and it becomes closer to the interaction conditions of the through-thickness crack. Additionally, in the case of cracks that are shallow in the thickness direction where a/c ≦ 0.5, the interaction is little seen because the maximum KI, max position is in the deepest part.
(3) The interaction criterion which should be coalesced to one large crack can be divided into the positional relationship of no overlap (S/c≥0) and overlap (S/c < 0). The region that is judged to be needed to coalesce (a KI, max rise of 10 percent) is approximately notated in Figures 15 and 16.
(4) These findings were introduced to an FFS standard, WES2805, established by the Japanese Welding Engineering Society (JWES) through some simplification, that is, d≤1.5c for overlapping cracks and [d < 1.5c and S < 1.0c and a/c≥0.5] for non-overlapping cracks. The coalescence procedure adopts the envelope size (Figure 12) of two cracks.
(5) As a result of the investigation of the safety margin for the coalescence process, it is shown that in the case of close cracks that must be considered to initiate brittle fracture without a short crack to connect two cracks, the increase in KI, max is always higher in one coalesced crack than in two close cracks.
Acknowledgement
The authors wish to acknowledge Iron and Steel Division in Japanese Welding Engineering Society for dedicated discussions of this study.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: