The selection problem for some first-order stationary Mean-field games

1.   Introduction

Mean-field games (MFG) model systems with many rational noncooperative players, describe the player's optimal strategies and determine the statistical properties of their distribution. These games are often determined by a system of a Hamilton-Jacobi equation coupled with a transport or Fokker-Planck equation. In the study of stationary Hamilton-Jacobi equations, a standard method to obtain a solution is to consider the vanishing discount problem. This was the strategy used originally in [31] in the study of homogenization problems. For second-order MFG, the existence of a solution for the discounted problem was shown, for example, in [20] and [8] and for first-order MFG in [16] in the sense of weak solutions and in [3] using variational methods. In the second-order case, the vanishing discount limit was studied in [4]. In the first-order case, the theory is not as much developed and the vanishing discount limit has not been examined previously. Here, our goal is to study the limit behavior as $\epsilon\to 0$ of the following discounted first-order stationary mean-field game.

Problem 1. Let ${\mathbb{T}}^d$ be the $d$-dimensional flat torus identified with $[0, 1]^d$. Let $V: {\mathbb{T}}^d \to {\mathbb{R}}$, $V\in C^{1, \alpha}( {\mathbb{T}}^d)$, $g:[0, \infty) \to {\mathbb{R}}\cup\{-\infty\}$, {$g\in C^{1, \alpha}((0, +\infty))$, with $g$ strictly increasing, and fix a discount rate, $\epsilon>0$. Find $u^ \epsilon, m^ \epsilon : {\mathbb{T}}^d \to {\mathbb{R}}$ with $m^ \epsilon (x){\geqslant} 0$ such that

We say that $(u^\epsilon, m^\epsilon)$ is a classical solution of the preceding problem if $u^\epsilon \in C^{2, \alpha}( {\mathbb{T}}^d)$ and $m^\epsilon \in C^{1, \alpha}( {\mathbb{T}}^d)$ with $m^\epsilon{\geqslant} 0$. As we show in Proposition 3.1, $m^\epsilon$ cannot vanish, hence, $m^\epsilon>0$. As in the case of Hamilton-Jacobi equations, we expect that, as $\epsilon\to 0$, the solutions of (1.1) converge, maybe through subsequences after adding a suitable constant to $u^\epsilon$, to a solution of the following first-order MFG.

Problem 2. With $g$, $V$ as in Problem 1, find $u, m: {\mathbb{T}}^d \to {\mathbb{R}}$ with $m{\geqslant} 0$ and ${\overline{H}}\in {\mathbb{R}}$ such that

Because (1.2) is invariant under addition of constants to $u$, we can prescribe the additional normalization condition

According to [16] (also see [17]), Problem 2 admits weak solutions under suitable polynomial growth conditions of $g$, see Corollary 6.3 in [16]. Here, in Section 7, under a different set of hypothesis and using a limiting argument, we establish the existence of solutions for Problem 2. A natural question in the analysis of the limit $\epsilon\to 0$ is the selection problem; that is, whether the sequence $(u^ \epsilon, m^ \epsilon)$ converges (not just whether a subsequence converges) and if so, what is the limit among all possible solutions of (1.2). This matter is our main focus here.

For Hamilton-Jacobi equations, the discounted problem corresponds to the following control problem. Let ${\bf x}(t) \in {\mathbb{R}}^d$ be the state of an agent at the time $t$. This agent can change its state by choosing a control ${\bf v} \in L^{\infty}([0, \infty), {\mathbb{R}}^d)$. Thus, its trajectory, $\bf{x}(t)$, is determined by $\dot{\bf{x}}\rm(t) = \bf{v}\rm(t)$, with initial condition ${\bf x}(t) = x\in {\mathbb{T}}^d$. The agent selects the control to minimize the cost functional

for a given Lagrangian, $L: {\mathbb{T}}^d \times {\mathbb{R}}^d \to {\mathbb{R}}$. The value function, $u^ \epsilon$, is given by

where the infimum is taken over ${\bf v}\in L^\infty([0, +\infty), {\mathbb{R}}^d)$.

The Hamiltonian, $H: {\mathbb{T}}^d \times {\mathbb{R}}^d \to {\mathbb{R}}$, corresponding to this control problem is the Legendre transform of $L$; that is,

Under standard coercivity and convexity assumptions on $L$, $u^ \epsilon$ is the unique viscosity solution of the discounted Hamilton-Jacobi equation,

For coercive Hamiltonians, the results in [31] give that $\epsilon u^ \epsilon$ is uniformly bounded and that $u^\epsilon$ is equi-Lipschitz for $\epsilon>0$. Thus, $u^ \epsilon-\min_{ {\mathbb{T}}^d}u^ \epsilon$ uniformly converges to a function, $u$, along subsequences, as $\epsilon \to 0$. Moreover, $\epsilon u^ \epsilon$ converges to a constant $-\tilde{H}$. By stability of viscosity solutions, $(u, \tilde{H})$ solves the ergodic Hamilton-Jacobi equation

where the unknowns are $u: {\mathbb{T}}^d \to {\mathbb{R}}$ and $\tilde{H} \in {\mathbb{R}}$. However, the solution of (1.3) may not be unique. Hence, the solution constructed above could depend on the particular subsequence used to extract the limit. The study of the selection problem was started in [19] using the discounted Mather measures introduced in [2]. The main convergence result was established in [5]. Subsequently, several authors investigated and extended those ideas in [1], [26], [27], and [34]. Recently, the case of non-convex Hamiltonians was addressed in [21].

In MFGs, we consider a large population of agents where each agent seeks to optimize an objective function. Here, however, the running cost depends on statistical information about the players, encoded in a probability density, $m: {\mathbb{T}}^d\times [0, \infty)\to {\mathbb{R}}$. In the model discussed here, the Lagrangian is $\hat{L}(x, p) = \frac{1}{2}|p|^2-V(x)+g(m)$ and each agent seeks to minimize the functional

Now, we suppose that the value function, $u^ \epsilon: = \inf_{{\bf v}}\hat{J, }$ is smooth. Then, $u^ \epsilon$ solves the first equation in (1.1) and the optimal control is given by ${\bf v}(t) = -Du^ \epsilon({\bf x}(t))$. Because the players are rational, they use this optimal control. Here, $\epsilon$ represents the rate at which players quit the game, which occurs at independent and memoryless times. Furthermore, new players join the game randomly at a rate $\epsilon$, as can be seen by looking at the right-hand side of the second equation in (1.1). Then, in the stationary configuration, the density, $m$, is determined by the second equation in (1.1). Without an inflow of players, the only non-negative solution is trivial, $m = 0$.

The theory for second-order stationary MFG is now well developed and in many cases the existence of smooth solutions can be established, see for example [25], [24], [35], or [8]. For logarithmic nonlinearities, the existence of smooth solutions was proven in [9]. However, this is a special case; as shown in Section 2, for first-order MFG, the existence of smooth solutions may not hold (see also a detailed discussion in [23] and [22]). Thus, in general, we need to consider weak solutions, see [7] or [16] for an approach using monotone operators and [3] for a variational approach.

One of the difficulties of first-order stationary MFG is the lack of regularizing terms in both the Hamilton-Jacobi equation and in the transport equation. Nonetheless, the MFG system behaves somewhat like an elliptic equation. Here, we explore this effect and obtain conditions under which Problem 1 has classical solutions. These conditions are given in the following two assumptions.

Assumption 1. $g$ and $V$ satisfy that $g^{-1}\big(g(1)-\mathrm{osc}_{x \in {\mathbb{T}}^d}V(x)\big)>0$.

Assumption 2. There exist constants $C_1>0$, $C_2>0$ and $\beta \in {\mathbb{R}}$ such that for all $z > 0$,

Assumption 3. $\lim_{z\to +\infty} g(z) = +\infty.$

For $\beta{\geqslant} -1$, Assumption 2 imples the preceding assumption. This is not the case for $\beta<-1$.

An example that satisfies the preceding assumptions is the following:

where $d = 1$ and $V$ is extended by periodicity to ${\mathbb{R}}$. The preceding two assumptions are used to obtain lower bounds on the density and can be interpreted as follows. Because $g$ is increasing agents want to avoid crowded areas and prefer areas with low density. However, if the oscillation of the potential is large, the trade-off between a low-density area with high potential and a high-density area with low potential may not pay-off. Hence, the control of the oscillation of $V$ given in Assumption 1 implies that no point is totally avoided by the agents.

As we mentioned previously, the two preceding assumptions imply the existence of a classical solution for Problem 1 as stated in the following theorem.

Theorem 1.1. Suppose that Assumptions 1-3 hold. Then, for each $\epsilon>0$, Problem 1 has a unique classical solution $(u^ \epsilon, m^ \epsilon)$ with $m^ \epsilon>0$.

The proof of this theorem is given in Section 5 using a continuation method combined with the a priori estimates in Section 3 and the DeGiorgi-Nash-Moser argument outlined in Section 4. As a corollary of the preceding theorem, we obtain our first convergence result.

Corollary 1.2. Suppose that Assumptions 1-3 hold. Then, Problem 2 has a unique classical solution $(u, m, \bar H)$, with $m>0$ and $\int_{ {\mathbb{T}}^d} u dx = 0$. Furthermore, let $(u^ \epsilon, m^ \epsilon)$ solve Problem 1. Then

The proof of this corollary is given at the end of Section 5.

For second-order MFGs, the vanishing discount problem for mean-field games was addressed in [4]. Inspired by the approach there, we consider the following formal asymptotic expansion

for the solution of Problem 1. Using this expansion in (1.1), assuming that $(u, m, \lambda)$ solves Problem 2, and matching powers of $\epsilon$, we obtain the following problem that determines the terms $\lambda$, $v$, and $\theta$ in (1.4). To simplify the presentation, we discuss the case of $C^\infty$- solutions.

Problem 3. Let $g$ be as in Problem 1 with $g\in C^\infty$ and let $(u, m)$ be $C^\infty$- solutions of Problem 2 with $m>0$ and $\int u = 0$. Find $v, \theta: {\mathbb{T}}^d \to {\mathbb{R}}$ and $\lambda \in {\mathbb{R}}$ such that

Remark 1.3. The normalization condition $\int u dx = 0$ is required for the uniqueness of the constant $\lambda$. Given a solution of (1.5), by adding a constant $\kappa$ to $u$ and subtracting $\kappa$ to $\lambda$, we produce another solution.

The existence of a solution to the preceding problem is established in Proposition 6.5 in Section 6. In that section, we prove the following improved asymptotic rate of convergence.

Theorem 1.4. Suppose Assumption 2 holds. Let $(u^ \epsilon, m^ \epsilon)$ and $(u, m, \bar H)$, with $m>0$ and $\int u = 0$, be classical solutions of, respectively, Problems 1 and 2. Let $(v, \theta, \lambda)$ be the corresponding classical solution to Problem 3. Then,

Remark 1.5. The preceding theorem remains valid if we replace Assumption 2 with the weaker condition that for any $z_0>0$ there exists $\gamma(z_0)>0$ such that

for all $z>z_0$.

In the last section of the paper, Section 7, we investigate the asymptotic behavior of $(u^ \epsilon, m^ \epsilon)$ as $\epsilon \to 0$. Here, we work with weak solutions in the sense of the definition below, and we consider the case where uniqueness of solution for Problem 2 may not hold. In this case, we replace Assumption 1 and 2 the following assumption that still allows the existence of solutions to be established.

Assumption 4. There exist positive constants, $c_1, c_2{\geqslant} 0$, and a positive real number, $\alpha$, such that

for all $m>0$.

Remark 1.6. From the preceding hypothesis, we obtain that there exist positive constants $\tilde c_1, \tilde c_2$ and $C$ such that

Of course, if Assumption 1 does not hold, we cannot ensure the existence of smooth solutions to Problem 1. Nonetheless, the existence of weak solutions for Problem 1 was proven in [16].

Closely related existence results are also addressed in [3]. The results in [16] requires less restrictive assumptions, albeit at the price of not having the uniqueness result from [3]. For a comparison between these two notions of weak solutions, we refer the reader to [16]. More precisely, we consider the following result.

Theorem 1.7 (from [16]). Suppose that Assumption 4 holds and $\alpha>\frac{d-4}{2}$ if $d{\geqslant} 8$. Then, Problem 1 has a weak solution $(m^\epsilon, u^\epsilon)$ as follows. There exists a constant $C$, independent of $\epsilon$ such that

1. $m^\epsilon{\geqslant} 0$ and $\int_{ {\mathbb{T}}^d} m^\epsilon dx = 1$,

2. $\|(m^\epsilon)^{\frac{\alpha+1}{2}}\|_{W^{1, 2}( {\mathbb{T}}^d)}{\leqslant} C$,

3. $\|u^ \epsilon-\int_{ {\mathbb{T}}^d} u^ \epsilon dx \|_{W^{1, 2}( {\mathbb{T}}^d)}{\leqslant} C$,

4. $\left|\epsilon \int_{ {\mathbb{T}}^d} u^ \epsilon dx\right|{\leqslant} C$,

5. $\|(m^\epsilon)^{\frac{\alpha+1} 2}Du^\epsilon\|_{BV( {\mathbb{T}}^d)}{\leqslant} C$.

Moreover,

in the sense of distributions, with

almost everywhere. Furthermore,

in the sense of distributions and almost everywhere.

We note that in [16], the specific form of Hamiltonian $H(x, p) = \frac{1}{2}|p|^2+V(x)$ was crucial to get the existence solutions with the properties above. Similar techniques applied to Problem 2 yield the existence of a number ${\overline{H}}$ and functions $(m, u)$ satisfying estimates 1-3 and 5 in Theorem 1.7 such that

in the sense of distributions, with

almost everywhere. Furthermore,

in the sense of distributions and almost everywhere.

When classical solutions are not available, we need to work with regular weak solutions, as defined next.

Definition 1.8. A pair $(m^\epsilon, u^\epsilon)$ is a regular weak solution of Problem 1 if it satisfies (1.6), (1.7) and (1.8) in the preceding theorem and, in particular, the same estimates 1-5 with the same constants. Similarly, a triple $(u, m, {\overline{H}})$ is a regular weak solution of Problem 2 if it satisfies (1.9), (1.10), (1.11) and the estimates 1-5 in the preceding theorem with the same constants.

In Section 7, Proposition 7.1, we consider a sequence of regular weak solution of Problem 1 and show that, by extracting a subsequence if necessary, it converges to a regular weak solution of Problem 2. In particular, this approach gives the existence a regular weak solution for Problem 2.

Our selection result for regular weak solutions, proven in Section 7, is the following theorem.

Theorem 1.9. Suppose that Assumption 4 holds and $\alpha>\frac{d-6}{d+2}$ if $d>6$. Let $(u^ \epsilon, m^ \epsilon)$ be a regular weak solution of Problem 1. Suppose that $\langle u^ \epsilon \rangle \rightharpoonup \bar{u}$ in $H^1( {\mathbb{T}}^d)$ and that $m^ \epsilon\rightharpoonup \bar{m}$ weakly in $L^{1}( {\mathbb{T}}^d)$. Let $(u, m)$ be a regular weak solution of Problem 2. Then,

and $\bar m = m$. Moreover, we have

where

The proof of the preceding theorem relies on ideas from Aubry-Mather theory introduced in [19]. The paper ends with a short example that illustrates the preceding result.

2.   Lack of uniqueness

Here, we examine the uniqueness of solutions of (1.2). First, we use the uniqueness method by Lasry-Lions [29] to show that the probability density, $m$, is unique. Thus, failure of uniqueness for (1.2) requires multiplicity of solutions, $u$, of the Hamilton-Jacobi equation. Second, we revisit an example from [23], where uniqueness does not hold. This example serves to illustrate the selection principle derived in Section 7.

2.1.   Lasry-Lions method

The monotonicity argument introduced by Lasry-Lions (see, [28] or the lectures [30]), can be used to prove the uniqueness of solution for MFGs in the time-dependent case and gives the uniqueness of $m$ in the stationary problem. Here, we apply this technique to Problem 2. Let $(u_1, m_2, \bar{H}_1)$ and $(u_2, m_2, \bar{H}_2)$ be classical solutions of (1.2). Then,

Now, we multiply the first equation by $(m_1-m_2)$ and the second equation by $(u_1-u_2)$. Next, subtracting the resulting identities and integrating by parts, we obtain

Accordingly, $m_1 = m_2 = m$ on ${\mathbb{T}}^d$ because $g$ is strictly increasing. Moreover, $Du_1 = Du_2$ on $m>0$. Hence, classical solutions $(u, m, \bar{H})$ of (1.2) with $m>0$ are unique up to an additive term in $u$. Uniqueness may fail if $m$ vanishes, as we show in Section 2.2. A similar proof gives that (2.1) holds for the solutions of (1.1). By Lemma 1, $m^ \epsilon$ is positive. Hence, classical solutions of Problem 1 are unique.

2.2.   An explicit example

Here, we show two distinct regular weak solutions to (1.2). In the example below, the existence of a unique smooth solutions fails and $m$ vanishes at an interval.

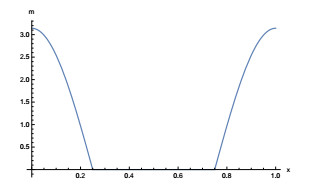
Let $g(m) = m$, $d = 1,$ and $V(x) = \pi \cos (2\pi x)$. Then, (1.2) becomes

From the second equation in (2.2), $mu_x = c$ for some constant. We claim that, $mu_x = 0$. Indeed, if $c\neq 0$, $u_x = \frac{c}{m}$. This is not possible because $\int_{ {\mathbb{T}}} u_x dx = 0$. Thus, $u$ is constant on the set $m>0$. From the first equation in (2.2) and taking into account that $\int_{ {\mathbb{T}}} m dx = 1$, we have $\bar{H} = 0$ and, thus,

The preceding expression vanishes in an interval, as can be seen in Figure 1.

On the other hand, from the first equation in (2.2), we see that $u\in H^1( {\mathbb{T}}^1)$ is a regular weak solution if $u$ satisfies

and

For example, We set the functions $\tilde u$ and $\hat u$ by

and

where $\chi$ is the characteristic function. Then, we observe that $(\hat{u}, m, 0)$ and $(\tilde{u}, m, 0)$ satisfy (2.3) and (2.4). Thus, $(\tilde u, m, {\overline{H}})$ and $(\hat u, m, {\overline{H}})$ are regular weak solutions.

3.   Preliminary estimates

In this section, we establish preliminary a priori estimates for solutions of Problem 1. To simplify the notation, we denote by $(u, m)$ a solution of Problem 1, instead of $(u^ \epsilon, m^ \epsilon)$. Here, we seek to establish bounds for $(u, m)$ that are uniform in $\epsilon$. Accordingly, the bounds in this section depend only on the data, $g$, $V$, and $d$ but not on $\epsilon$ nor on the particular solution. First, we show that $m$ is a probability; that is, nonnegative and its integral is 1. Next, we establish a lower bound and higher integrability for $m$. Finally, we prove Lipschitz bounds for $u$, which give the regularity of the solutions in the one-dimensional case. The higher dimensional case requires further estimates that are addressed in the following section.

Proposition 3.1. Let $(u, m)$ be a classical solution of Problem 1. Then, for every $x\in {\mathbb{T}}^d$, $m(x)> 0$ and

Proof. First, we show the positivity. Suppose that $x_0\in {\mathbb{T}}^d$ is such that $m(x_0) = \min_{x\in {\mathbb{T}}^d} m(x) = 0$. At this point, the second equation in (1.1) becomes

However, the left-hand side is $0$, which is a contradiction. To check (3.1), we integrate the second equation in (1.1) and use integration by parts. Then, we see that

Thus, we get the conclusion.

Next, we get a uniform lower bound for $m$.

Proposition 3.2. Suppose that Assumption 1 holds. Then, there exists a constant, $C>0,$ such that for any classical solution, $(u, m)$ of Problem 1, we have

Proof. First, we bound $\| \epsilon u\|_{L^{\infty}( {\mathbb{T}}^d)}$. Let $\tilde{x} \in {\mathbb{T}}^d$ be a minimum point of $u$. At this point, $Du(\tilde{x}) = 0$ and $\Delta u(\tilde{x}) {\geqslant} 0$. From the second equation in (1.1), we get

Since $m$ is positive, $\Delta u(\tilde{x})< \epsilon$ and, thus, $m(\tilde{x}){\geqslant} 1$. Because $g$ is increasing, it follows from the first equation in (1.1) that

Next, let $\hat{x} \in {\mathbb{T}}^d$ be a maximum point of $u$. By an analogous argument, we get

Thus, $\| \epsilon u\|_{L^\infty( {\mathbb{T}}^d)} {\leqslant} C$.

Now, we address the lower bound for $m$. By the first equation in (1.1) and (3.2), for all $x \in {\mathbb{T}}^d$, we have

Using Assumption 1, we get the lower bound for $m$.

In the following Lemma, we give an upper bound for $m$.

Lemma 3.3. Suppose that Assumptions 1 and 2 hold. Then, there exists a constant, $C>0,$ such that for any classical solution, $(u, m),$ of Problem 1, we have

Proof. First, we multiply the first equation in (1.1) by $(1-m)$ and the second equation in (1.1) by $u$. Integrating by parts and adding the resulting identities, we have

Using Assumption 2, we get

On the other hand, in light of Proposition 3.2, there exists $0<m_0<m(x)$ for all $x \in {\mathbb{T}}^d$. Furthermore, Assumption 2 guarantees that for all $t{\geqslant} m_0$,

Therefore, combining the preceding inequalities with (3.4), we obtain (3.3).

In the next proposition, we establish that $u$ is Lipschitz continuous and get uniform bounds for $m$ using a technique introduced in [9].

Proposition 3.4. Suppose that Assumptions 1 and 2 hold. Then, there exists a constant $C>0$ such that for any classical solution, $(u, m),$ of Problem 1, we have

Proof. At first, we show the case $d = 1$. Multiplying the first equation by $m_{xx}$ and the second by $u_{xx}$, we obtain

Next, we subtract these equations and integrate by parts to get

using a weighted Cauchy-Schwarz inequality with $\delta >0$. Because $m$ is bounded by below, taking $\delta>0$ sufficiently small, $\|m_x\|_{L^2( {\mathbb{T}})}$ and $\|u_{xx}\|_{L^2( {\mathbb{T}})}$ are bounded. In view of (3.3), we get the desired result.

Next, we discuss the case $d{\geqslant}2$. Take $p {\geqslant} \beta$. Multiplying the second equation in (1.1) by $\mathrm{div}(m^pDu)$, we obtain

Differentiating the first equation in (1.1), we get

Next, we rewrite the right-hand side of (3.5) as follows:

using (3.6) in the last line. Combining (3.7) and (3.5), we obtain

where the last inequality follows from a weighted Cauchy inequality with $\delta>0$ and $\beta$ is the exponent in Assumption 2. For $\delta$ sufficiently small, there exists $C$ that does not depend on $p$, such that

where the last inequality is a consequence of $\int_{ {\mathbb{T}}^d}m = 1$ and $p+\beta+2>p+1$.

For $d>2$, $2^* = \frac{2d}{d-2}$ is the Sobolev conjugated exponent to $2$; if $d = 2$, we use the convention that $2^*$ is an arbitrarily large real number. Using Sobolev's inequality and (3.8), we gather that

Thus, there exists a positive constant $C>0$ such that for all $q{\geqslant} \beta+1$,

Next, we take $1<\theta<2^*/2$ and define $r_n = \theta^n+\beta+1$. In view of (3.3), $\|m\|_{r_0}$ is bounded. Now we observe that $\frac{r_n}{r_{n+1}} <\frac{2}{2^*}$. Thus, for each $n \in {\mathbb{N}}$, there exists $0<\alpha_n<1$ satisfying

By Hölder's inequality and the above estimate with $q+1 = r_n$, we obtain

Iterating the prior inequality, we get

The right-hand side is bounded uniformly in $n \in {\mathbb{N}}$ because

Hence, $\|m\|_\infty$ is bounded. According to the first equation in (1.1), and using the bound for $\epsilon u$ in Proposition 3.2, we obtain that $\|Du\|_\infty$ is also bounded.

When $d = 1$, we can get additional estimates for $Du$ and $m$, as shown in the next proposition. The case $d{\geqslant} 2$ is discussed in the next section.

Proposition 3.5. Suppose that Assumption 1 holds. Let $d = 1$. Then, there exists a constant $C>0$ such that for any classical solution, $(u, m),$ of Problem 1, we have

Proof. Differentiating the first equation in (1.1)and multiplying by $m$, we get

Solving the second equation in (1.1) for $mu_{xx}$ and substituting in the above identity, we have

Because $m$ is bounded by below, the denominator in the preceding expression does not vanish. Thus, from the previous Proposition, the right-hand side is bounded. Accordingly, $\|m_x\|_{L^{\infty}( {\mathbb{T}})}$ is bounded. Returning to the second equation (1.1), we see that $\|u_{xx}\|_{L^{\infty}( {\mathbb{T}})}$ is bounded. Returning to (3.9), we see that $\|m\|_{C^{1, \alpha}( {\mathbb{T}})}$ is bounded. Thus, from the second equation in (1.1), we gather that $\|u_x\|_{C^{1, \alpha}( {\mathbb{T}})}$ is bounded.

4.   Estimates in higher dimensions

Now, we obtain additional estimates for the solutions of (1.1) in the case $d{\geqslant}2$. As in the previous section, to simplify the notation, we omit the $\epsilon$ in $(u^ \epsilon, m^ \epsilon)$ and denote by $(u, m)$ a solution of Problem 1. First, by solving the first equation in (1.1) for $m$, we get

Next, replacing the resulting expression into the second equation in (1.1), we obtain

Here, we apply the DeGiorgi-Nash-Moser regularity method to (4.1) to obtain our estimates.

We begin by selecting $k$ with $1{\leqslant} k {\leqslant} d$. Differentiating (4.1) with respect to $x_k$, we conclude that $v = u_{x_k}$ solves

where

and $\delta_{ij} = 1$ if $i = j$ and $\delta_{ij} = 0$ otherwise. Because of Propositions 3.2 and 3.4, there exists a constant, $C>0$, such that for any classical solution, $u$, of (4.1), we have $\| \epsilon u\|_{\infty} +\|Du\|_{\infty} {\leqslant} C$. Hence, we get

Moreover, using again Propositions 3.2 and 3.4, we see that there exists a constant $\lambda>0$ such that for all $\xi \in {\mathbb{R}}^d$, we have

Next, we prove that $v$ is Hölder-continuous and, thus, get higher regularity for $u$.

Proposition 4.1. Suppose that Assumptions 1 and 2 hold. Let $d{\geqslant}2$. Then, there exist constants, $C>0$ and $0<\alpha<1$, such that for any classical solution, $u$, of (4.1), we have

Proof. Take $R>0$. Let $v$ solve (4.2). Write $v = z+w$ where $z$ is a solution of

in $B_{2R}$ and $z = 0$ on $\partial B_{2R}$. Therefore, $w$ solves

in $B_{2R}$ with $w|_{B_{2R}} = v$.

We begin by establishing the following claim.

Claim 1. For $d>2$, there exists a constant, $C>0$, that depends only on the bounds in (4.4) such that

Remark 4.2. If $d = 2$, we get $\| z \|_{L^\infty(B_{2R})} {\leqslant} \bar{C}R^\kappa$, for any $\kappa<\frac 1 2$. This difference is due to the exponent $2^*$ in dimension $2$ being replaced by an arbitrarily large constant. The argument that follows needs to be adapted accordingly, namely the bound in (4.8) below, but the key steps remain unchanged. This case will be omitted.

Let $k{\geqslant}0$. By multiplying (4.5) by $(z-k)^+$ and integrating by parts, we get

Set

It suffices to prove that we can choose a constant $C>0$ satisfying $|A(CR)| = 0$. Because $(z-k)^+_{x_i} = 0$ on $A(k)^C$ and $(z-k)^+_{x_i} = z_{x_i}$ on $A(k)$, we obtain from (4.7) that

In view of (4.4) and the bounds in (4.3), we get

Next, using Sobolev's inequality and taking into account that $(z-k)^+ = 0$ on $\partial B_{2R}$, we conclude that, for any $h>k$,

Combining the two preceding estimates, we obtain

Next, we take a sequence $k_n = M\left(1-\frac 1 {2^n}\right)$, where

Using the above estimate, we obtain

We now prove by induction that

where $\mu = \frac{2^*}{\frac{2^*}{2}-1}$. The case $n = 0$ is clear. Assume our claim holds for some $n$, we have to check that it holds for $n+1$. We have

using our choice for $M$ and $\mu$.

Finally, by considering the limit $n \to \infty$, we get $|A(M)| = 0$. If $d>2$, we have

Thus, we get Claim 1.

Next, using the ellipticity bounds in (4.4), we apply the DeGiorgi-Nash-Moser estimate (see, [18], Theorem $8.22$) to (4.6) to establish the following claim.

Claim 2. We have

for some constant $0<\eta<1$, where we denoted

Combining the two preceding claims, we obtain the following estimate:

Claim 3. There exist constants $C>0$ and $0<\alpha<1$ such that for all $0<R<1$, we have

Set

where $\alpha$ satisfies $0<\alpha<-\frac{\log \eta}{\log 4}$.

Here, we prove by induction that there exist $\mu>1$ satisfying

for some sufficiently large $M>0$. We choose $\mu$ satisfying

and then we choose $M> \frac{2}{4^\alpha}\|v\|_{L^\infty( {\mathbb{T}}^d)}$ and such that

The prior choice of $M$ is possible due to (4.11).

For $n = 0$, $M_0 {\leqslant} \frac{2}{4^\alpha}\|v\|_{L^\infty( {\mathbb{T}}^d)}{\leqslant} M$. Next, we assume that (4.10) holds for some $n{\geqslant} 0$ and verify that it also holds for $n$ replaced by $n+1$. Using (4.9), we have that

Using the defining property of $M$, (4.12), we get (4.10).

Finally, for $0<R<1$, combining (4.9) and (4.10), we obtain

which establishes the claim.

Claim 4.

Due to Claim 3, we get $\|Du\|_{C^{0, \alpha}( {\mathbb{T}}^d)} {\leqslant} C$. Since (4.2) is a uniformly elliptic equation and the Hölder-norm of the coefficients is bounded. Therefore, it follows from Schauder's estimate that $\|Dv\|_{C^{0, \alpha}( {\mathbb{T}}^d)} {\leqslant} C$. Hence, we conclude that $\|Du\|_{C^{1, \alpha}( {\mathbb{T}}^d)}{\leqslant} C$.

5.   Existence of solution for the discounted problem

Here, we prove the existence of a classical solution for (1.1), using the continuation method. In this Section, we suppose Assumption 1-3.

5.1.   Setting

A key difficulty is that $g^{-1}$ may not always defined on the whole real line. Thus, to perform the continuation method, we modify $g$ as follows. We consider the case where $\lim_{z\to 0}g(z) <-\infty$. We begin by selecting $m_0 \in {\mathbb{R}}$ satisfying $0<m_0<\min \{1, g^{-1}(g(1)-\mathrm{osc}V)\}$. Then, we define an increasing funcion $h:(0, \infty) \to {\mathbb{R}}$ satisfying $g{\geqslant} h$, $h(z) \to -\infty$ as $z \to 0$ and Assumption 2. Let $\eta$ be a decreasing smooth function satisfying

Now, we consider

where

Because $f:(0, \infty) \to {\mathbb{R}}$ is increasing and surjective, we can define its inverse $f^{-1}: {\mathbb{R}} \to (0, \infty)$. Moreoever, $f{\leqslant} g$ on $(0, m_0]$, and $f = g$ on $[m_0, +\infty)$. As (1.1) and (4.1) are equivalent, and (5.1) is equivalent to

We check that $f$ satisfies both Assumption 1 and Assumption 2. Indeed, because $f^{-1}$ is positive, $f^{-1}(f(1)-\mathrm{osc} V)>0$. Next, we see that for all $z>0$,

Finally, since $g{\geqslant} h$ and $\eta$ is decreasing, we have

Thus, we obtain the estimates in Section 3 and 4 for (5.1) and (5.2). In the case $\lim_{z \to 0} g(z) = -\infty$, we can omit this resetting.

Remark 5.1. Replacing $g$ by $f$, we modify the behavior of $g(z)$ as $z \to 0$, to define its inverse on the whole real line. However, thanks to the lower bound for $m^ \epsilon$ in Proposition 3.2, the above does not change the solution. Indeed, any classical solution $(u^ \epsilon, m^ \epsilon)$ to (5.1) solves (1.1) as shown in the proof of Theorem 1.1.

Remark 5.2. Without Assumption 3, we need to modify $g(z)$ as $z \to +\infty$, in addition to the preceding changes. However, this is more complicated because the upper bound for $m^ \epsilon$ is more qualitative than the lower bound. On the other hand, typical examples of $g$ are power or logarithm functions which satisfy Assumption 3.

5.2.   Continuation method

Here, we show the existence of classical solution to (5.2), using the continuation method. We begin by defining an operator, $J: C^{2, \alpha}( {\mathbb{T}}^d) \times [0, 1] \to C^{0, \alpha}( {\mathbb{T}}^d)$, by

We set

We claim that $\Lambda = [0, 1]$. First, we observe that $0\in \Lambda$. In fact, for $u_0 \equiv \epsilon^{-1}f(1)$, we have $J(u_0, 0) = 0$. Accordingly, $\Lambda$ is non-empty. Thus, it suffices to check that $\Lambda$ is relatively open and closed in $[0, 1]$, to get $\Lambda = [0, 1]$. In the next proposition, we verify that $\Lambda$ is a closed set.

Proposition 5.3. Consider the setting of Problem 1 and suppose that Assumptions 1-3 hold. Let $\Lambda$ as in (5.3). Then, $\Lambda$ is relatively closed in $[0, 1]$.

Proof. Fix a sequence $\lambda_n \in \Lambda$ converging to $\lambda\in [0, 1]$ as $n \to \infty$. We must show that $\lambda \in \Lambda$. For that, take $u_{\lambda_n}$ satisfying $J(u_{\lambda_n}, \lambda_n) = 0$. Proceeding as in Section 3 and Section 4, replacing $g$ and $V$ by $f$ and $\lambda_n V$ respectively, we get bounds for $\{ u_{\lambda_n} \}_{n \in {\mathbb{N}}}$. In particular, the a priori bounds in Proposition 3.5 (for $d = 1$) or Proposition 4.1 (for $d>1$) guarantee that there exists a subsequence of $\{ u_{\lambda_n} \}_{n \in {\mathbb{N}}}$ converging to some $u \in C^{2, \alpha}( {\mathbb{T}}^d)$. By passing to the limit, we conclude that $J(u, \lambda) = 0$. Accordingly, $\lambda \in \Lambda$.

Now, we show that $\Lambda$ is relatively open. For each $\lambda \in \Lambda$, let $u_\lambda\in C^{2, \alpha}( {\mathbb{T}}^d)$ solve $J(u_\lambda, \lambda) = 0$ and set

We consider the linearization of $J$ around this solution and define $L_\lambda: C^{2, \alpha}( {\mathbb{T}}^d) \to C^{0, \alpha}( {\mathbb{T}}^d)$ for $\phi \in C^{2, \alpha}( {\mathbb{T}}^d)$ by

Lemma 5.4. Consider the setting of Problem 1. Let $u_\lambda\in C^{2, \alpha}( {\mathbb{T}}^d)$ solve $J(u_\lambda, \lambda) = 0$ and let $L_\lambda$ be given by (5.4). Then, $L_\lambda$ is an isomorphism between $C^{2, \alpha}( {\mathbb{T}}^d)$ and $C^{0, \alpha}( {\mathbb{T}}^d)$.

Proof. We must prove that for any $\xi \in C^{0, \alpha}( {\mathbb{T}}^d)$, the equation

has a unique solution, $\phi \in C^{2, \alpha}( {\mathbb{T}}^d)$. We define $B_\lambda: H^1( {\mathbb{T}}^d) \times H^1( {\mathbb{T}}^d) \to \mathbb{R}$ by

Note that if $v$ and $w$ are smooth, $B_\lambda$ becomes $B_\lambda [v, w] = (L_\lambda(v), w)_{L^2}$. Using Hölder inequality, we see that $B_\lambda$ is bounded. Now, using Riesz's Representation Theorem, we see that there exists a bounded linear operator $A: H^1( {\mathbb{T}}^d) \to H^1( {\mathbb{T}}^d)$ such that $B_\lambda [v, w] = (Av, w)$ for all $w \in H^1( {\mathbb{T}}^d)$. We divide the rest of the proof in the following three claims.

Claim 1. There exists a constant, $c>0,$ such that $\|Av\|_{H^1( {\mathbb{T}}^d)} {\geqslant} c\|v\|_{H^1( {\mathbb{T}}^d)}$ for all $v\in H^1( {\mathbb{T}}^d)$.

We establish this claim by contradiction. For that, suppose that there exists $\{v_n\}_{n\in {\mathbb{N}}} \subset H^1( {\mathbb{T}}^d)$ with $\|v_n\|_{H^1( {\mathbb{T}}^d)} = 1$ and $Av_n \to 0$. Then,

Next, we have

Since $m_\lambda$ and $(f^{-1})'$ are positive, we see that $Dv_n \to 0$ and $\epsilon v_n+Du_\lambda \cdot Dv_n \to 0$ in $L^2( {\mathbb{T}}^d)$. Hence, we can construct a subsequence $\{v_{n_k}\}_{k\in {\mathbb{N}}}$ satisfying $v_{n_k} \to 0$ in $H^1( {\mathbb{T}}^d)$, which contradicts $\|v_n\|_{H^1( {\mathbb{T}}^d)} = 1$.

Claim 2. The range of $A$, $R(A)$, is closed and $R(A) = H^1( {\mathbb{T}}^d)$.

Take a sequence $\{z_n\}_{n\in {\mathbb{N}}} \subset R(A)$ that converges to $z \in E$. To prove the first part of the claim, we begin by showing that $z \in R(A)$. For that, take $w_n \in H^1( {\mathbb{T}}^d)$ satisfying $z_n = Aw_n$. From the preceding claim, it follows that $\{w_n\}_{n\in {\mathbb{N}}}$ is a Cauchy sequence converging to some $w\in H^1( {\mathbb{T}}^d)$. By the continuity of $A$, we have $z = Aw$. Thus, $z \in R(A)$.

Next, to establish the last part of the claim, suppose that $R(A) \neq H^1( {\mathbb{T}}^d)$. In this case, there exists a non-zero vector, $v \in R(A)^\perp$. Then, we get

This contradicts $v \neq 0$.

Claim 3. (5.5) has a unique solution $\phi \in C^{2, \alpha}( {\mathbb{T}}^d)$.

To prove this last claim, we define a bounded linear functional, $T:H^1( {\mathbb{T}}^d) \to {\mathbb{R}},$ by

The Riesz Representation Theorem guarantees that there exists a unique $\hat{w} \in H^1( {\mathbb{T}}^d)$ satisfying $T(w) = (\hat{w}, w)$ for all $w \in H^1( {\mathbb{T}}^d)$. Taking $\phi = A^{-1}\hat{w}$, we get

that is, $\phi \in H^1( {\mathbb{T}}^d)$ is the unique weak solution of (5.5). Because (5.5) is a uniformly elliptic equation and the coefficients belong to $C^{0, \alpha}( {\mathbb{T}}^d)$, we conclude that $\phi \in C^{2, \alpha}( {\mathbb{T}}^d)$.

To finish the proof of Theorem 1.1 we verify that $\Lambda$ is relatively open. This is achieved in the next proposition.

Proposition 5.5. Consider the setting of Problem 1 and suppose that Assumptions 1-3 hold. Let $\Lambda$ as in (5.3). Then, $\Lambda$ is relatively open in $[0, 1]$.

Proof. By the preceding lemma, Lemma 5.4, we can apply the implicit function theorem (see [6]) to the operator $J$ to conclude that $\Lambda$ is open. Therefore, for any $\lambda \in \Lambda$, there exists $\delta>0$ such that for any $\hat{\lambda} \in ({\lambda}-\delta, {\lambda}+\delta)$, we can find $\hat{u} \in C^{2, \alpha}( {\mathbb{T}}^d)$ such that $J(\hat u, \hat \lambda) = 0$.

By combining the previous results, we prove Theorem 1.1 as follows.

Proof of Theorem 1.1. Since $1\in \Lambda$, there exists a classical solution $u^ \epsilon$ for (5.2). Take $m^ \epsilon = f^{-1}( \epsilon u^ \epsilon+\frac{1}{2}|Du^ \epsilon|^2+V)$. Then, $(u^ \epsilon, m^ \epsilon)$ solves (5.1). Arguing as in Proposition 3.2, from (5.1) we obtain that $m^ \epsilon {\geqslant} f^{-1}\left( f(1)-\mathrm{osc}V \right)$. By the definition of $f$, noting that $m_0<1$, we obtain that for all $x\in {\mathbb{T}}^d$

Because $g(m^ \epsilon) = f(m^ \epsilon)$ on ${\mathbb{T}}^d$, $(u^ \epsilon, m^ \epsilon)$ solves (1.1).

The identity (2.1) gives that (1.1) has a unique classical solution. Indeed, let $(u^ \epsilon_1, m^ \epsilon_1)$ and $(u^ \epsilon_2, m^ \epsilon_2)$ be classical solutions to (1.1). Then,

Now, we multiply the first equation by $(m^ \epsilon_1-m^ \epsilon_2)$ and the second equation by $(u^ \epsilon_1-u^ \epsilon_2)$. Next, subtracting the resulting identities and integrating by parts, we obtain

Accordingly, $m^ \epsilon_1 = m^ \epsilon_2$ on ${\mathbb{T}}^d$ because $g$ is strictly increasing. Moreover, $Du^ \epsilon_1 = Du^ \epsilon_2$ on $m>0$. In view of positivity of $m^ \epsilon$, we see $Du^ \epsilon_1 = Du^ \epsilon_2$ on ${\mathbb{T}}^d$. Hence, from the first equation in (1.1), $u^ \epsilon_1 = u^ \epsilon_2$ on ${\mathbb{T}}^d$.

Finally, we show that under Assumptions 1 and 2, we have the convergence of the solutions of (1.1).

Proof of Corollary 1.2. The estimates in Section 3 and 4 do not depend on $\epsilon$. Therefore, we can extract a subsequence $\epsilon_j$ such that $\epsilon_j u^{ \epsilon_j}$ converges uniformly to a constant $-\bar{H}$ and $(u^{ \epsilon_j}-\int_{ {\mathbb{T}}^d}u^{ \epsilon_j} dx , m^{ \epsilon_j})$ converges to some $(u, m)$ in $C^{2, \alpha}\times C^{1, \alpha}$. Therefore, $(u, m, \bar{H})$ solves (1.2). By the results in Section 2, $m$ and $\bar{H}$ are uniquely determined. Accordingly, the limit of $\epsilon_j u^{ \epsilon_j}$ and $m^{ \epsilon_j}$ does not depend on the subsequence. Because of Proposition 3.2, we have that $m>0$. Thus, there exists a unique solution, $(u, m, \bar{H})$ of (1.2) satisfying the additional condition $\int_{ {\mathbb{T}}^d} u dx = 0$.

6.   Refined asymptotics

Now, we investigate the asymptotic behavior of $\{u^ \epsilon - { {\overline{H}}}/ \epsilon\}_{ \epsilon>0}$ and prove Theorem 1.4, thus improving the converge results in Corollary 1.

First, to address Problem 3, we consider the linearized discounted problem that we state now.

Problem 4. Let $g$ be as in Problem 1 with $g\in C^\infty$ and let $(u, m)\in C^\infty ( {\mathbb{T}}^d)\times C^\infty( {\mathbb{T}}^d)$ solve Problem 2 with $m>0$. Suppose that $\epsilon>0$. Given $A, B \in C^\infty( {\mathbb{T}}^d)$, find $v^ \epsilon, \theta^ \epsilon: {\mathbb{T}}^d \to {\mathbb{R}}$ such that

Proposition 6.1. Suppose Assumption 2 holds. Then, Problem 4 has a unique weak solution $(v^ \epsilon, \theta^ \epsilon)\in H^1( {\mathbb{T}}^d)\times L^2( {\mathbb{T}}^d)$.

Proof. Because $m>0$, Assumption 2 (or the alternative assumption in Remark 1.5) gives that $g'(m)$ is bounded by below. From the first equation in (6.1), we get

Using the previous expression for $\theta^ \epsilon$ in the second equation in (6.1), we obtain

Therefore, it suffices to show that (6.3) has a weak solution. For that, we define a bilinear form, $K:H^1( {\mathbb{T}}^d)\times H^1( {\mathbb{T}}^d)\to {\mathbb{R}}$, by

Because $m$ and $u$ are smooth with $g'(m)$ bounded by below, we see that $K$ is a bounded bilinear form. Moreover, for all $\phi \in H^1( {\mathbb{T}}^d)$,

Hence, $K$ is coercive. Thus, applying the Lax-Milgram theorem, we see that (6.3) has a unique weak solution, $v^\epsilon\in H^1( {\mathbb{T}}^d)$. Then, using (6.2) and taking into account that $g'(m)$ is bounded by below, we obtain a weak solution $\theta^ \epsilon\in L^2( {\mathbb{T}}^d)$.

Proposition 6.2. Let $(v^ \epsilon, \theta^ \epsilon)\in H^1( {\mathbb{T}}^d)\times L^2( {\mathbb{T}}^d)$ be a weak solution of Problem 4. Then, there exists a constant $C>0$ independent of $\epsilon$ such that

Proof. We multiply the first equation in (6.1) by $\theta^ \epsilon$ and the second one by $v^ \epsilon$. Next, we subtract the resulting expressions to get

Integrating by parts, we obtain

Using Poincaré's inequality, we conclude that

Hence, taking into account that $m$ is bounded by below,

Arguing analogously, we obtain

Hence, by (6.4),

Combining the preceding inequality with (6.4), we have the estimate

Finally, the first equation in (6.1) yields

Next, we bootstrap higher regularity for $(v^ \epsilon, \theta^ \epsilon)$.

Proposition 6.3. Let $(v^ \epsilon, \theta^ \epsilon)$ be a weak solution of Problem 4. Fix $h\in \{1, 2, , ..., d\}$ and let $z = v^ \epsilon_{x_h}$. Then, for each $k\in {\mathbb{N}}$, there exists a constant $C_k>0$ such that

Proof. We begin by rewriting (6.3) as

Next, we fix $h \in \{1, 2, ..., d\}$ and let $z = v^ \epsilon_{x_h}$. Differentiating the preceding equation with respect to $x_h$, we obtain

where

and

By the previous proposition, we know that

Furthermore, we have the estimates

and

Let $k{\geqslant} 0$. Multiplying (6.5) by $z$ and integrating by parts, we get

Because of the uniform ellipticity of $a^{ij}$, we get

Hence,

Therefore,

and

The conclusion follows by iterating this argument for higher derivatives.

Proposition 6.4. Let $(v^ \epsilon, \theta^ \epsilon)$ be a weak solution of Problem 4. Then, for each $k\in {\mathbb{N}}$, there exists a constant $C_k>0$ such that

In particular, $(v^ \epsilon, \theta^ \epsilon)$ is a classical solution of (6.1).

Proof. Differentiating the first equation in (6.1), we get

The above implies

Iterating the preceding steps, we get the result.

Proposition 6.5. For $\epsilon>0$, let $(v^ \epsilon, \theta^ \epsilon)$ be a weak solution of Problem 4 and assume that

for some constant $C>0$. Then, there exists a solution $(v, \theta, \lambda)$ of Problem 3 and, for each $k\in {\mathbb{N}}$,

Proof. By the previous estimates on the solutions of Problem 4, we can choose a subsequence such that $\epsilon v^ \epsilon \to -\lambda$, $\theta^ \epsilon \to \theta$ and $v^ \epsilon -\int v^ \epsilon \to v$. Clearly, $(v, \theta, \lambda)$ solves (1.5). Because the solution to (1.5) is unique, the limit is independent of the particular sequence. Therefore, $(v^ \epsilon, \theta^ \epsilon)$ converges to $(v, \theta)$.

Finally, we present the proof of Theorem 1.4.

Proof of Theorem 1.4. Fix $k\in {\mathbb{N}}$ and set

where $\hat{C_k}$ is to be chosen later. For $(v, \theta)\in E_k$, we find $(\hat{v}, \hat{\theta})$ solving (6.1), where

and

Because,

we obtain

We can choose $\hat{C_k}$ such that, for $\epsilon$ small enough, the right-hand side is less than $\hat{C_k}$. Then, it holds that $(v, \theta) \to (\hat{v}, \hat{\theta})$ has a fixed point $(v^ \epsilon, \theta^ \epsilon)$. We remark that $( \epsilon v^ \epsilon+u+\frac{\bar{H}}{ \epsilon}, m+ \epsilon \theta^ \epsilon)$ solves (1.1) and therefore it is equal to $(u^ \epsilon, m^ \epsilon)$. Hence, by the previous proposition, for suitably large $k$, as $\epsilon \to 0$,

7.   Convergence and selection

Now, we investigate the behavior of $(u^ \epsilon, m^ \epsilon)$ as $\epsilon \to 0$ in the case where Problem 2 may have multiple solutions; that is, when Assumptions 1 and 2 do not hold. We are interested in which of the solutions of Problem 2 arise as a limit of solutions of Problem 1. Without Assumptions 1 and 2, smooth solutions may not exist. Therefore, we need to work with weak solutions. For Problem 1, weak solutions were shown to exist in [16]. In Section 7.1, we review those existence results and use them to show the existence of a solution for Problem 2. Then, in Section 7.2, we construct certain measures on phase space that generalize Mather measures. Next, in Section 7.3, we prove our main selection result, Theorem 1.9. We end the paper with a discussion of an explicit example, in Section 7.4.

7.1.   Regular weak solutions

We begin this section by proving the following result on the stability of regular weak solutions. In particular, since the estimate of regular weak solutions of Problem 1 was proved in [16], we obtain the existence of regular weak solutions for Problem 2.

Proposition 7.1. Suppose that Assumption 4 holds and $\alpha>\frac{d-4}{d}$ if $4<d$. Let $(m^\epsilon, u^\epsilon)$ be a regular weak solution of Problem 1. Assume that $m^\epsilon\rightharpoonup m$ weakly in $L^1( {\mathbb{T}}^d)$, $u^\epsilon -\int u^ \epsilon dx \rightharpoonup u$ weakly in $W^{1, 2}( {\mathbb{T}}^d)$, and that $\epsilon \int u^\epsilon \mathit{\mbox{}}dx\to - {\overline{H}}$. Then, $(m, u, {\overline{H}})$ is a regular weak solution of Problem 2.

Proof. Properties 1 and 3 in Theorem 1.7 are immediate; that is,

From Property 2, we conclude that, through a subequence $(m^\epsilon)^{\frac{\alpha+1}{2}}$, converges weakly in $W^{1, 2}$ to a function $\eta(x)$. Moreover, by Rellich-Kondrachov theorem, $(m^\epsilon)^{\frac{\alpha+1}{2}}\to \eta$ in $L^2( {\mathbb{T}}^d)$ and extracting a further sequence if necessary also almost everywhere. Therefore, $m^\epsilon\to \eta^{\frac{2}{\alpha+1}} = m$ almost everywhere. Accordingly $(m^\epsilon)^{\frac{\alpha+1}{2}}$ converges to $m^{\frac{\alpha+1}{2}}$ weakly in $W^{1, 2}( {\mathbb{T}}^d)$, strongly in $L^2( {\mathbb{T}}^d)$ and almost everywhere. Consequently

Next, we examine Property 5 in Theorem 1.7. By compactness, $(m^\epsilon)^{\frac{\alpha+1} 2}Du^\epsilon$ converges weakly in BV, through a subsequence, to a function $\psi\in BV$ with $\|\psi\|_{BV( {\mathbb{T}}^d)}{\leqslant} C$. Because $(m^\epsilon)^{\frac{\alpha+1} 2}$ converges to $m^{\frac{\alpha+1} 2}$ strongly in $L^2( {\mathbb{T}}^d)$ and $Du^\epsilon$ converges weakly to $Du$ in $L^2( {\mathbb{T}}^d)$, we have for any $\varphi\in C^\infty( {\mathbb{T}}^d)$

Therefore,

Finally, we address the limit properties corresponding to (1.6), (1.7) and (1.8). We take a smooth function, $\varphi\in C^\infty( {\mathbb{T}}^d)$, multiply (1.8) by $\varphi$ and integrate. Because

we have

Because of Rellich-Kondrachov theorem

for any $q<2^*$. In particular, for $\alpha$ in the range of Assumption 4 this implies $m^\epsilon\to m$ strongly in $L^2( {\mathbb{T}}^d)$. Using the weak convergence of $u^\epsilon$ in $W^{1, 2}( {\mathbb{T}}^d)$ we conclude that

Next, we select a smooth non-negative function, $\varphi{\geqslant} 0$, multiply (1.6) by $\varphi$, and integrate in ${\mathbb{T}}^d$. We have

Moreover, by convexity

Finally, we observe that

For any $\alpha>0$, we can select $p$ and $p'$ such that $\frac 1 p+\frac 1 {p'}+1$, $p (\alpha-1)<\frac{2^*}{2} (\alpha+1)$, and $p'<\frac{2^*}{2} (\alpha+1)$. Next, we estimate

Therefore, since $\|m^\epsilon-m\|_{L^{p'}}\to 0$, we conclude that

Proposition 7.2. Suppose that Assumption 4 holds. Let $(m^\epsilon, u^\epsilon)$ be a regular weak solution of Problem 1. Then, there exists a constant $C>0$ independent of $\epsilon$ such that

Proof. Because of properties 1 and 2 in Theorem 1.7, Assumption 4 implies that

Then, (7.1) follows by integrating (1.7).

Remark 7.3. If Assumptions 4 holds, a similar estimate holds for regular weak solutions $(m, u, {\overline{H}})$ of Problem 2. Namely, there exists a constant $C>0$ such that

7.2.   Mather measures

We begin by introducing a class of phase-space probability measures called Mather measures, see [32] and [33]. These measures were introduced in the context of Lagrangian mechanics and later used to examine the properties of Hamilton–Jacobi equations in [12,13,14,15] and in [10,11]. In the context of the selection problem, generalized Mather measures were first used in [19]. As previously, we suppose that Assumption 4 holds. Accordingly, we work with regular weak solutions of Problems 1 and 2.

Fix a regular weak solution $(u^ \epsilon, m^ \epsilon)$ of Problem 1 and a regular weak solution $(u, m)$ of Problem 2. Next, we rewrite (1.1) as

where $W^ \epsilon(x) = V(x)-g(m^ \epsilon)$ and, assuming without loss of generality that ${\overline{H}} = 0$, we rewrite (1.2) as

where $W(x) = V(x)-g(m)$.

Proposition 7.4. Suppose that Assumption 4 holds. Let $(u^\epsilon, m^\epsilon)$ be a regular weak solution of Problem 1. Let $L^ \epsilon = \frac{1}{2}|v|^2-W^ \epsilon(x)$ with $W^ \epsilon(x) = V(x)-g(m^ \epsilon)$. Consider the phase-space measure, $\mu^ \epsilon$, the $\epsilon$-Mather measure, determined by

for all $\phi\in C( {\mathbb{T}}^d\times {\mathbb{R}}^d)$. Then, $\mu^ \epsilon$ satisfies the discounted holonomy condition

for all $\varphi\in C^1( {\mathbb{T}}^d)$. Moreover, we have

Proof. Because (1.8) holds in the sense of distributions, the discounted holonomy condition for $\mu^ \epsilon$, (7.2), follows immediately. Next, recall that if $m^\epsilon$ is an integrable non-negative function then $L^2_{1+m^\epsilon}( {\mathbb{T}}^d)$, the space of all measurable functions $f: {\mathbb{T}}^d\to {\mathbb{R}}$ that satisfy

is a Hilbert space. Moreover, if $\eta_\delta$ is a standard mollifier, we have

in $L^2_{1+m^\epsilon}( {\mathbb{T}}^d)$. Due to (1.6) and (1.7), we have

Accordingly, because of (7.2), we have

Taking the limit $\delta\to 0$, we obtain

Taking into account the definition of $L^\epsilon$ and using the identities (1.7) and (7.4), we conclude that

Remark 7.5. From (7.2) and (7.3), we conclude that $\mu^ \epsilon$ is a discounted Mather measure with trace ${{{\rm{d}}}} x$ in the sense of the definition in [19].

Similarly, for Problem 2, we have the following result.

Proposition 7.6. Suppose that Assumption 4 holds. Let $(u, m, {\overline{H}})$ be a regular weak solution of Problem 2. Assume without loss of generality that ${\overline{H}} = 0$. Let $L = \frac{1}{2}|v|^2-W$ with $W(x) = V(x)-g(m)$. Consider the phase-space measure, $\mu$, the Mather measure, determined by

for all $\phi\in C( {\mathbb{T}}^d\times {\mathbb{R}}^d)$. Then, $\mu$ satisfies the holonomy constraint

for all $\varphi\in C^1( {\mathbb{T}}^d)$. Moreover

Proof. The proof is analogous to the one of Proposition 7.4

7.3.   Selection

The goal of this section is to prove Theorem 1.9 and, hence, establish a selection criterion for the limit of $u^ \epsilon$ and prove the convergence of $m^\epsilon$. Our proof is inspired by the one in [19].

Proof of Theorem 1.9. Let $(u^ \epsilon, m^ \epsilon)$ be a regular weak solution of Problem 1. Suppose that $u^ \epsilon -\int u^ \epsilon dx \rightharpoonup \bar{u}$ in $H^1( {\mathbb{T}}^d)$ and that $m^ \epsilon\rightharpoonup \bar{m}$ weakly in $L^{1}( {\mathbb{T}}^d)$. Note that due to the bounds in Theorem 1.7, we have that $m^ \epsilon\to \bar m$ strongly in $L^p$ for $p<\frac{2^*}{2}(\alpha+1)$. Let $(u, m)$ be a regular weak solution of Problem 2. Let $\mu^ \epsilon$ and $\mu$ be the Mather measure constructed in the previous section in Propositions 7.4 and 7.6.

For any $v \in {\mathbb{R}}^d$ and almost every $x \in {\mathbb{T}}^d$, we have

where $W^ \epsilon$ is as in Proposition 7.4. Consider a standard mollifier $\eta_\delta$, and let $p = D(\eta_\delta*u)$. Then, for $v \in {\mathbb{R}}^d$ and almost every $x \in {\mathbb{T}}^d$,

where $W$ is as in Proposition 7.6. Integrating the left-hand side of the preceding expression with respect to $\mu^ \epsilon$ and using the holonomy condition, (7.2), and (7.3), we obtain

Next, we integrate the right-hand side of (7.5) and use Jensen's inequality to obtain

taking into account (1.9). Because $W\in L^{\frac{\alpha+1}{\alpha}}( {\mathbb{T}}^d)$, $\eta_\delta*W\to W$ in $L^{\frac{\alpha+1}{\alpha}}( {\mathbb{T}}^d)$ as $\delta\to 0$. Therefore, taking into account that $m^\epsilon\in L^{\alpha+1}( {\mathbb{T}}^d)$, we have

as $\delta\to 0$. Therefore, combining (7.5), (7.6), and (7.7), and by considering the limit $\delta \to 0$, we conclude that

On the other hand, we observe that, for all $v\in {\mathbb{R}}^d$ and almost every $x \in {\mathbb{T}}^d$,

Integrating with respect to $\mu$ and proceeding in a similar manner, we obtain

Next, from (7.8), we gather

Finally, from (7.9), we get

Adding the above two inequalities, we obtain

By Sobolev's inequality, we have $\langle u^ \epsilon \rangle, \langle u \rangle \in L^{2^*}( {\mathbb{T}}^d)$, uniformly in $\epsilon$. Moreover, $m, m^\epsilon\in L^{\frac{2^*}{2}(\alpha+1)}( {\mathbb{T}}^d)$, uniformly in $\epsilon$. In the range of $\alpha$, we observe $m, m^\epsilon\in L^{(2^*)'}( {\mathbb{T}}^d)$, where $(2^*)'$ is the Hölder's conjugate of $2^*$. Therefore, $\int \langle u^ \epsilon \rangle m dx$ and $\int \langle u \rangle m^ \epsilon dx$ are bounded uniformly in $\epsilon$. Consequently, the first term in the left-hand side of (7.10) converges to 0. Hence, we obtain (1.12). Moreover, because the second term is non-negative, we conclude by the monotonicity of $g$ that

Hence, (1.13) holds.

7.4.   An explicit example

Finally, in this subsection, we present an application of our selection criterion. We consider the following discount problem:

Thus $d = 1$, $V(x) = \pi \cos(2\pi x)$, and $g(m) = m$. The associated limit problems of (7.11) is (2.2) in Section 2.2. By Theorem 1.7, there exists a regular weak solution $(u^ \epsilon, m^ \epsilon)\in H^1( {\mathbb{T}}^1)\times H^1( {\mathbb{T}}^1)$, of (7.11). We note that $u^ \epsilon -\int_{ {\mathbb{T}}^d} u^ \epsilon dx$ converges along subsequence weakly in $H^1( {\mathbb{T}}^1)$. In view of Proposition 7.1, the limit is a regular weak solution of (2.2). However, regular weak solutions for (2.2) are not unique, as we show in Section 2.2.

By (1.13), we get the following result:

Proposition 7.7. Let $(u^ \epsilon, m^ \epsilon)$ be regular weak solution of (7.11). Suppose that $u^ \epsilon-\int u^ \epsilon dx \to \bar{u}$ as $\epsilon \to 0$ weakly in $H^1( {\mathbb{T}}^1)$. Let $(u, m)$ be any regular weak solution of (2.2). Then,

Using the above criterion, we can show that $u^ \epsilon-\int_{ {\mathbb{T}}^1} u^ \epsilon dx$ fully converges weakly in $H^1( {\mathbb{T}}^1)$ sense and we can detect the unique limit of $u^ \epsilon -\int_{ {\mathbb{T}}^1} u^ \epsilon dx$, as we show now.

Proposition 7.8. Let $\tilde u\in H^1( {\mathbb{T}}^1)$ be determined by

and $\tilde u(0) = 0$. Then $\tilde u$ is the unique minimizer of $\int_{ {\mathbb{T}}^1} \langle u\rangle m \mathit{\mbox{}} dx$ over all regular weak solutions $u$ of (2.2).

Proof. Let $u$ be any regular weak solution of (2.2). Because the quantities

$\int_{ {\mathbb{T}}^1} \langle u\rangle m \mbox{ }dx$ is invariant by addition of a constant to $u$, we can assume $u(0) = \tilde u(0) = 0$, without loss of generality. Moreover, because of (2.3) and by periodicity, we have $u(x) = \tilde u(x) = 0$ for $x\in [0, 1/4]\cup[3/4, 1]$. Then,

Hence, it suffices to discuss the quantities of $-\int_{ {\mathbb{T}}^1} u\mbox{ }dx$.

Because of (2.4), we can see that $\tilde u(x) {\geqslant} u(x)$ in $x\in [1/4, 1/2]$. On the other hand, it holds that $\tilde u(x) {\geqslant} u(x)$ in $x\in [1/2, 3/4]$. Indeed, suppose that there exists $x_0 \in [1/2, 3/4]$ and solution $u_0$ such that $\tilde u(x_0) < u_0(x_0)$. Then, it follows from (2.4) that $u_0(3/4)>\tilde u(3/4) = 0$, which is a contradiction. Thus, $\tilde u(x){\geqslant} u(x)$ for $x\in {\mathbb{T}}^1$ and we see $\int_{ {\mathbb{T}}^1}\tilde u\mbox{ }dx{\geqslant} \int_{ {\mathbb{T}}^1}u\mbox{ }dx$.

Acknowledgments

The authors thank anonymous referees for their careful reading of our manuscript and their many insightful comments and suggestions.