Emergent behaviors of Lohe Hermitian sphere particles under time-delayed interactions

1.   Introduction

Emergent dynamics of a many-body system is ubiquitous in classical and quantum systems, e.g., aggregation of bacteria [38, 39], flocking of birds [2], schooling of fish, synchronization of fireflies and neurons [7, 34, 41, 42] and hand clapping of people in a concert hall, etc. For surveys and books, we refer to [1, 2, 4, 16, 19, 35, 36, 40, 42]. In this paper, we continue studies begun in [8, 24] on the emergent dynamics of the LHS model. The LHS model corresponds to the complex counterpart of the Lohe sphere(LS) model which has been extensively studied in previous literature [11, 26, 32, 33, 37, 43]. The LHS model is the first-order aggregation model describing continuous-time dynamics of particle's position on the Hermitian unit sphere $\mathbb{HS}^{d-1} : = \Big \{ z = ([z]_1, \cdots, [z]_d)\in \mathbb C^d:\; \|z \| : = \sqrt{\sum_{\alpha = 1}^{d} |[z]_\alpha|^2} = 1 \Big \}$ with $d \geq 1$. Here we denote the $\alpha$-th component of the complex vector $z\in \mathbb C^d$ as $[z]_\alpha$ which is consistent with earlier notation in [23]. As a warmup for our discussion, we briefly introduce the LHS model with time-delayed interactions.

Let $z_j = ([z_j]_1, \cdots, [z_j]_d) \in \mathbb C^d$ be a position of the $j$-th Hermitian Lohe particle on the Hermitian unit sphere, and interaction weight between the $j$-th and $k$-th particle is denoted by the real value $a_{jk} \in \mathbb R$. Then, the temporal dynamics of $z_j$ is governed by the Cauchy problem to the LHS model with a uniform time-delay $\tau > 0$:

where $z_k^{\tau}(t) : = z_k(t-\tau)$, $\varphi_j = \varphi_j(t)$ is a bounded continuous function of $t$, $\Omega_j$ is a $d\times d$ skew-Hermitian matrix and $(a_{ik}) \in \mathbb R^{N \times N}$ is a symmetric matrix whose components are all positive. Before we continue further, we introduce

A global well-posedness of system (1) can be done by combining a local well-posedness from the standard Cauchy-Lipschitz theory in [25, 28] and a priori uniform bound in Lemma 2.1. In the absence of time-delay with $\tau = 0$, emergent dynamics of the LHS model was investigated in [8, 24] in which several sufficient frameworks were proposed for complete and practical aggregations. In this paper, we are interested in the following simple question:

"Under what conditions on system parameters $\kappa_0, \kappa_1, \tau$, network topology $(a_{ij})$ and initial data set $\{ \varphi_j \}$, can we verify the emergence of collective behaviors of the LHS with time-delay?"

This question has been already addressed for other low-rank aggregation models (rank-1: vectors or rank-2: matrices), to name a few, the Lohe sphere model [9, 10], the Lohe matrix model [18]. Throughout the paper, we set

Next, we recall several induced concepts on the emergent dynamics of tensors [23, 24] in the following definition.

Definition 1.1. Let $\{z_i \}$ be a global solution to (1).

1. Complete aggregation occurs asymptotically if the ensemble diameter $D(Z)$ tends to zero asymptotically:

2. Practical aggregation (with respect to time-delay) occurs asymptotically if the ensemble diameter $D(Z)$ satisfies

3. Practical aggregation (with respect to time-delay and coupling strength $\kappa_0$) occurs asymptotically if the ensemble diameter $D(Z)$ satisfies

Then, it is easy to see that complete aggregation implies practical aggregation. In the absence of time-delay $\tau = 0$, emergent dynamics for (1) has been extensively studied in [24] (see Section 2.3). Thus, main point of this paper is to analyze the effect of time-delayed interactions in the emergent dynamics of (1). For notational simplicity, we set

The main results of this paper are threefold. First, we consider the following setting:

In this case, system (1) becomes

When the coupling gain pair $(\kappa_0, \kappa_1)$ is close to the SL coupling gain pair, i.e.,

system (2) can be rewritten as follows (see Section 3):

Our first set of results is concerned with the complete aggregation of (3) (see Theorem 3.1 and Theorem 3.6). We assume that system parameters and initial data satisfy

For the complete aggregation, we introduce a Lyapunov functional:

where $\gamma$ is a constant to be determined later. Then, in Section 3, we show that $\mathcal{E}_{ij}(t)$ satisfies the energy estimate (see Section 3.2.2):

for some positive constant $\beta$. By Barbalat's lemma [3], the above estimate leads to the complete aggregation (see Theorem 3.6):

Now, our second set of result deals with the practical aggregation with respect to time-delay (Theorem 4.1). We assume that system parameters and initial data satisfy

Then, the practical aggregation (with respect to the size of time-delay) emerges:

Our final set of result is concerned with the practical aggregation with respect to both time-delay and free flow matrix $\Omega_j$ (Theorem 4.7). For system (1), we assume that system parameters satisfy

Note that for any unit complex vectors $z_i^0$ and $z_j^0$, we have

Thus, relations (4) implies restriction on initial diameter and network structure:

For all-to-all network structure with $a_{ij} = 1$, the R.H.S. of (5) becomes

which is true for any initial data. Then, the practical aggregation (with respect to time-delay and coupling strength $\kappa_0$) emerges:

Note that although we imposed the initial condition on $\varphi_j(t)$ for a time-strip $-\tau\leq t\leq 0$, we require that the initial condition depends on the initial data at $t = 0$ for practical aggregation estimate in Theorem 4.7.

The rest of paper is organized as follows. In Section 2, we present conservation laws for the LHS model with time-delay, its reduction to other aggregation models, and review previous results on the emergent dynamics for the LHS model without time-delay and LS model with a time-delay. In Section 3, we provide a sufficient framework for the complete aggregation when the coupling gain pair is close to that of SL coupling gain pair. In Section 4, we provide a sufficient framework leading to the practical aggregation under a general setting. Finally, Section 5 is devoted to a brief summary of main results and some open problems.

2.   Preliminaries

In this section, we discuss two conservation laws of the LHS model with time-delay and its reduction to other aggregation models, and review previous results on the emergent dynamics for the LHS model.

2.1.   Conservation laws

In this subsection, we study conservation laws associated with (1).

Lemma 2.1. (Conservation of modulus) Let $\{z_j\}$ be a global solution to (1) with initial data satisfying $\|\phi_j(t)\| = 1$ for $-\tau \leq t \leq 0$, $j \in \mathcal{N}$. Then, the modulus of $z_j$ satisfies

i.e., the Hermitian sphere $\mathbb{HS}^{d-1}$ is a positively invariant set for (1).

Proof. We use $(a_{jk}) \in \mathbb R^{N \times N}$ and sesquilinearity of the inner product to find

Below, we estimate the terms ${\mathcal I}_{1i}$ with $1\leq i\leq 6$ one by one.

$\bullet$ Case A (Estimates on ${\mathcal I}_{11} + {\mathcal I}_{12}$): Since $\Omega_j$ is skew-Hermitian, we have

$\bullet$ Case B (Estimates on ${\mathcal I}_{13} + {\mathcal I}_{14}$): We use $\langle z_j, z_k^{\tau} \rangle = \overline{\langle z_k^{\tau}, z_j \rangle}$ to see that

$\bullet$ Case C (Estimates on ${\mathcal I}_{15} + {\mathcal I}_{16}$): Similar to Case B, one has

Finally we combine all the estimates in Cases A, B, and C to obtain

This yields

Remark 1. Note that the symmetry of $a_{ij}$ plays no role in the conservation of modulus.

Lemma 2.2. (Propagation of real-valuedness) Suppose that $\{\Omega_j\}$ and initial data set $\{ \varphi_j \}$ satisfy the relations:

for all $j\in\mathcal{N}$ and $-\tau\leq t\leq 0$, and let $\{z_j\}$ be a solution to system (1). Then $z_j$ is a real-valued state, i.e.,

Proof. This follows from the standard uniqueness theory of time-delayed ordinary differential equations [25, 28]

2.2.   Reduction to aggregation models

In this subsection, we discuss the reductions of (1) to the Lohe sphere model and the Kuramoto model. Suppose that initial data set $\{\varphi_j \}$ satisfy

for all $j\in\mathcal{N}$ and $-\tau\leq t\leq 0$. Then, it follows from Lemma 2.1 and Lemma 2.2 that

In this case, the coupling terms in the R.H.S. of (1) become

We set

Then the real-valued state $x_j \in \mathbb R^d$ satisfies the LS model with time-delay [10]:

where $\Omega_j$ is a $d\times d$ skew-symmetric matrix for all $j$. Emergent dynamics of system (7) has been studied in [9]. To see the reduction to the Kuramoto model, we also set

Again, we substitute the ansatz (8) into (6) to derive the Kuramoto model with time-delay [21, 22]:

The emergent dynamics of (9) has been extensively studied in literature, for example, complete synchronization for the mean-field model [5], complete synchronization [12, 15, 29], critical coupling strength for complete synchronization [17]. In summary, one has the following diagram:

On the other hand, the emergent dynamics of Lohe type matrix models has also been investigated in literature, e.g., sufficient conditions for complete aggregations [6, 14], mean-field approach for quaternion's collective dynamics [13], generalized Lohe sphere model on Riemannian manifolds [20], a gradient flow approach for the Lohe matrix model [27], conserved quantities and non-abelian generalization of the Kuramoto model [30, 31, 32] etc.

2.3.   Previous results

In this subsection, we present two results on the emergent dynamics of the LHS model without a time-delay and the Lohe sphere model with time-delay which correspond to the special cases for (1).

First, we consider the LHS model with zero time-delay case with $\tau = 0$ over the complete network with $a_{ik} = 1$ for all $i$ and $k$. Under these setting, system (1) becomes

For emergent dynamics of (10), we introduce an order parameter as a modulus of $z_c$ and state diameter:

where $z_c$ is the centroid of all $z_i$:

On the other hand, we consider (11) with a zero free flow:

where $w_c: = \frac{1}{N}\sum\limits_{k = 1}^Nw_k$.

Then the emergence of complete aggregation and solution splitting property of (10) can be summarized in the following proposition.

Proposition 1. [24] Suppose that coupling gains, free flows and initial data satisfy

where $\Omega$ is a skew-Hermitian matrix with size $(d+1)\times(d+1)$. Let $\{z_j \}$ be a global solution to (10). Then, the following assertions hold.

1. Complete aggregation emerges asymptotically:

2. Solution splitting property holds:

where $w_j$ is a solution to (12).

Proof. For a detailed proof, we refer to Theorem 4.1 of [24].

Second, we consider the Lohe sphere model on the unit sphere in $\mathbb R^{d}$ under the influence of time-delay:

Proposition 2. [10] Suppose that the system parameters and initial data satisfy

where $\|\cdot\|_{\infty}$ is defined by $\|\Omega\|_{\infty} : = \max_{i,j}|\Omega_{ij}|$, and $\varphi(t) : = (\varphi_1(t), \cdots, \varphi_N(t))$. Also, let $\{x_j \}$ be a global solution to $(13)$. Then, we have

Proof. For a proof, we refer to Theorem 3.1 of [10].

3.   Emergence of complete aggregation

In this section, we provide an emergent dynamics of (1) under the following setting:

Note that this case corresponds to the same free flow and complete network topology. Then system (1) becomes

In the following two subsections, we study complete aggregation in which coupling gains satisfy the following relations:

In Section 2.3 of [8], the authors reduced the vector version of the Stuart-Landau model to the LHS model with the special pair of coupling gains. From this process, Stuart-Landau(SL) coupling gain pair and close-to SL coupling gain pair were naturally obtained. For the convenience of the reader who wants to know how the SL coupling appears from the generalized Stuart-Landau model in $\mathbb C^{d+1}$, we added a brief explanation in Appendix A.

3.1.   SL coupling gain pair

In this subsection, we consider the emergent behavior of (14) for the Stuart-Landau gain pair. In this case, the coupling term can be simplified as follows: on $\mathbb{HS}^{d-1}$,

Finally, we combine (14) and (15) to get

Theorem 3.1. Suppose system parameters and initial data set $\varphi_j$ satisfy

and let $\{ z_j \}$ be a global solution to (16). Then, the complete aggregation emerges asymptotically:

Proof. We leave its proof in Section 3.1.2.

Remark 2. (1) The SL coupling gain pair case can be reduced to the Lohe sphere model with time-delay treated in [9, 10].

(2) Due to technical difficulties, we can not obtain analytical results for the exponential decay of the LHS model with $\tau>0$, however, numerical simulations seem to suggest an exponential aggregation as in the Lohe sphere case without time-delay (see Figure 3.1).

3.1.1.   A priori estimates

In the part, we provide four lemmas for the emergent dynamics of (16) following the strategy in [10].

Lemma 3.2. Let $\{z_j\}$ be a global solution to (16). Then we have

for all $i, j\in\mathcal{N}$ and $t\geq s+\tau$.

Proof. We set

Then, it satisfies

It follows from $(16)_1$ and (17) that

This yields

On the other hand, we have

We combine (19) and (20) to obtain

Finally, relation (21) and $|\langle z, w\rangle|\leq \|z\|\cdot\|w\|$ yield desired estimate.

Lemma 3.3. Let $\{z_j\}$ be a global solution to (16). Then we have following relation for suitable positive numbers $s,u,t$:

Proof. Note that

We integrate (18) on the interval $[t-u, t]$ and take the inner product of the resulting relation and $z_i(t) - z_j^s(t)$ as in [10] to find

For an emergent dynamics, we introduce a modified ensemble diameter as follows:

Lemma 3.4. Let $\{z_j\}$ be a global solution to (16). Then, the functional (22) satisfies

Proof. In Lemma 3.3, we set $s = \tau$ and take $s, u = \tau$. Since inequalities in Lemma 3.3 and Lemma 3.4 are similar to estimates in Lemma 4.1 and 4.2 in [10], we can derive the same result. The only difference is that we have terms involving real parts, but it can be estimated in the same way as [10] since

We set

In order to control the term $\|z_c^\tau - z_c^{2\tau}\|^2$ appearing in Lemma 3.4, we give the following estimate for $\Delta_{z_j}^\tau$.

Lemma 3.5. Let $\{z_j\}$ be a global solution to (16). Then, the functional $\Delta_{z_j}^\tau$ satisfies

Proof. Note that

This yields

Now we are ready to provide a proof of our first main result.

3.1.2.   Proof of Theorem 3.1

In this part, we present our first result on the complete aggregation by combining all the estimates in Lemma 3.2 - Lemma 3.5 in two steps. We will briefly sketch the proof, since in the next section, we will provide more general statement and its proof.

$\bullet$ Step A (Existence of a trapping set): First, we claim

Proof. We first estimate $D^{0,\tau}(t)$ in an interval $[-\tau, 2\tau]$. Next, we define a set

and proceed the proof using Lipschitz continuity of $D^{0,\tau}(t)$ in order to show $\sup\mathcal{T} = \infty$.

Note that

This yields

$\bullet$ Step B (Key step): We claim

For this, we define a Lyapunov functional $\mathcal{E}$: for $Z = (z_1, \cdots , z_N)$,

where $\gamma$ is a positive constant. Then, one has

Here, for the computation of $\frac{d}{dt}\|z_i - z_j\|^2$, we used Lemma 3.2 with $s = 0$, and the fact that $\mathrm{Re}\langle z_i + z_j, z_c^\tau \rangle > \frac{7}{4}$ when $D^{0,\tau}(t) <\frac{1}{2}$(see the proof of Lemma 3.4).

By applying Young's inequality, we have

Now we set $\gamma = \frac{\kappa_0}{N}$ to get

since $N \geq 3$. This leads to

Using the boundedness of $\|\dot{z}_j\|$ for all $j$, we can apply Barbalat's lemma to obtain the desired result.

3.2.   Close-to-SL coupling gain pair

In this subsection, we consider the situation in which the coupling gain pair is close to Stuart-Landau coupling gain pair:

Note that

We substitute $\kappa_1 = \tilde{\kappa}- \frac{\kappa_0}{2}$ into (23) to get

By straightforward calculation, one has

For the second inequality (25), we use the triangle inequality,

and similar arguments in the proof of Lemma 3.3 to derive

Theorem 3.6. Suppose system parameters and initial data satisfy

where $\mathcal{C}_1: = 2 \left(\frac{N-1}{N}\right)\cdot(\kappa_0+|\tilde{\kappa}|)$, and let $\{z_j\}$ be a global solution to (24). Then complete aggregation emerges asymptotically:

Proof. We leave its detailed proof in Section 3.2.2.

3.2.1.   Basic estimates

In this part, we provide several a priori estimates.

Lemma 3.7. Let $\{z_j\}$ be a global solution to (24). For $t \geq 2\tau$, we have following inequality:

Proof. We set $s = \tau$ in the inequality (25) to find

In the inequality (26), we set

to get

For a fixed $t$, there exist $i_t$ and $j_t$ such that

Then, for $t \geq 2\tau$, one has

Hence, one has

Lemma 3.8. Let $\{z_j\}$ be a global solution to (24). Then, one has

3.2.2.   Proof of Theorem 3.6

Suppose system parameters and initial data satisfy

and let $\{z_j\}$ be a solution of system (24). Then, the proof consists of two steps.

$\bullet$ Step A (Existence of a trapping set): We claim

Proof of (28): We follow the same arguments as in [10]. For this, we divide the estimate into three time intervals:

$\diamond$ Step A.1 (Estimate in the time-interval $[0,\tau]$): By triangle inequality, we have

$\diamond$ Step A.2 (Estimate in the time-interval $[\tau, 2\tau]$): Similar to Step A, we use triangular inequality to get

However, since

one has

Therefore, we give

$\diamond$ Step A.3 (Estimate in the time-interval $[2\tau, \infty)$): By (27), one has

Here, we used

for $N\geq3$.

Next we claim:

For a proof, we define a set $\mathcal{T}$ as

and proceed the proof using Lipschitz continuity of $D^{0,\tau}(t)$ as in [10]. The only difference is the estimate of $\frac{d}{dt}D^{0,\tau}(t)$. By direct estimates, one has

Hence, it follows from $|\tilde{\kappa}|<\frac{9}{256}\kappa_0$ that

In this way, we verified claim (28).

$\bullet$ Step B (Zero convergence of modified diameter): We claim

The proof is similar to Theorem 3.1 of [10] with a slight difference. We present main steps that involve such differences. We put $s = 0$ in (25) to get

Next, we define a Lyapunov functional $\mathcal{E}_{ij}$ for $Z = (z_1, \cdots , z_N)$ and $i, j\in\mathcal{N}$:

where $\gamma$ is a positive constant. Then, one has

By Young's inequality, we have

Now, we set

Then, we have

For $N \geq 3$ and $|\tilde{\kappa}| < \frac{1}{16}\kappa_0$, we have

Here we set

to obtain

This yields

which is equivalent to

It follows from definition of $\mathcal{E}_{ij}$ that

Finally, we have

By letting $t\to\infty$, one has

It follows from the boundedness of $\|\dot{z}_j\|$ for all $j$ that

This means $\|z_i(s)-z_j(s)\|$ is uniformly continuous. Hence, we can apply Barbalat's lemma to obtain the desired estimate (29).

4.   Emergence of practical aggregation

In this section, we study the practical aggregation of the LHS model.

4.1.   Complete network topology

In this subsection, we set

In this case, system (1) becomes

For handy notation, we set

Our third main result is concerned with the practical aggregation. Recall that

Theorem 4.1. Suppose coupling gains and initial data satisfy

and let $\{z_j\}$ be a global solution to (24). Then, system (24) exhibits the practical synchronization:

Proof. We leave its proof in Section 4.1.2.

4.1.1.   Basic estimates

In this part, we provide several lemmas to be crucially used in the proof of Theorem 4.1.

Lemma 4.2. Let $\{z_j\}$ be a global solution to (31). Then, $G_{ij}$ satisfies

Proof. By direct calculation, one has

Lemma 4.3. Let $A\in \mathbb C^{d\times d}$ and $v\in \mathbb C^{d}$ be given matrix and vector, respectively. Then, one has

where $\|\cdot\|$ is a vector norm in $\mathbb C^d$ and $\|\cdot\|_F$ is the Frobenius norm defined by $\|A\|_F : = \sqrt{tr(A^\dagger A)}$.

Proof. We set the componentwise form of $A$ and $v$ as follows:

where $1\leq \alpha,\beta,\gamma\leq d$. By the Cauchy-Schwarz inequality, we have

Thus, one has

and this yields the desired result.

Lemma 4.4. Let $\{z_j\}$ be a global solution to (30). Then $L_{ij}$ in (31) satisfies

where the positive constant $\mathcal{C}_2$ is given by

Proof. By the Cauchy-Schwarz inequality, we have

Note that $\|z_j\| = 1$. By Lemma 3.8, we have

Lemma 4.5. Let $\{z_j\}$ be a global solution to (30). Then, $|L_{ij}|$ satisfies

Proof. We use (30) to get

Thus, we have

Note that

So we have

Note that the last two terms of the right hand side in above equation goes to zero as $\tau$ goes to $0$.

$\bullet$ Step A: Note that

By Lemma 4.4, we have for any $i$,

Since $L_{ii} = 0$, one has

$\bullet$ Step B: Next, we analyze the term

In the sequel, we estimate $A_i,\; i = 1,2$ as follows.

$\bullet$ (Estimate of $A_2$): By direct estimate, one has

On the other hand, note that

$\bullet$ (Estimate of $A_1$): Similarly, by Lemma 4.4, one has

Thus, we have

In (32), we combine all the estimate (33) and (34) to find

and

$\bullet$ Step C: Finally, we analyze the term

By direct calculation, we have

Note that

and so

$\bullet$ Step D: We collect all the estimates in Step A - Step C to find

We set

Then, for each time $t$, there exists $i_t$ and $j_t$ by which the maximum is attained, i.e.

Now we want to obtain the dynamics of $L(t)$.

Lemma 4.6. Let $\{z_j\}$ be a global solution to (24). Then, the functional $L(t)$ in (35) satisfies

Proof. It follows from Lemma 4.5 and the fact that $|L_{ci}| \leq L(t)$, we have

Note that

Since $|L_{ci}^{\tau}| \leq |L_{ci}| + \mathcal{C}_2\tau \leq L(t) + \mathcal{C}_2\tau$, we have

Hence we obtain the desired estimate:

4.1.2.   Proof of Theorem 4.1

Consider a quadratic polynomial

Now we study the practical aggregation as $\tau\searrow0$. Here we fix the other variables. Let us assume that $2|\kappa_1|<\kappa_0$. Then for a sufficiently small $\tau$, there are two roots of $f(x) = 0$.

Note that the discriminant $D_\tau$ of $f(x)$ is given explicitly as

Note that the constant term $(1- \frac{2|\kappa_1|}{\kappa_0})^2$ is positive by the assumption so that

so $D_\tau$ is positive as $\tau$ tends to 0. Now, for $\tau \ll 1$, we denote two roots by $x_-(\tau)$ and $x_+(\tau)$ with $x_-(\tau)\leq x_+(\tau)$. Then we have following property from the phase portrait:

We also obtain

4.2.   General network topology

In this subsection, we will study practical aggregation of the system (1). Here we set network topology as $\{a_{ij}\}$ with $a_{ij} \geq 0$, for all $i,j \in \mathcal{N}$.

Theorem 4.7. Let $\{z_j\}$ be a global solution to (36) with the following initial condition:

Then, system (36) exhibits the practical aggregation:

Proof. We leave its proof in Section 4.2.2

4.2.1.   Basic estimates

In this part, we provide several a priori estimates to be used in the proof of Theorem 4.7.

Lemma 4.8. Let $\{z_j\}$ be a global solution to (36). Then $G_{ij}$ in (31) satisfies

Proof. By definition of $G_{ij} = \langle z_i, z_j \rangle$, one has

which yields the desired estimate.

Lemma 4.9. Let $\{z_j\}$ be a global solution to (36). Then, one has

where the positive constant $\mathcal{C}_3$ is given by

Proof. By the Cauchy-Schwarz inequality, we have

On the other hand, we have

Now, we set

Then, we have

We set

Then by direct calculation, we get the following lemma.

Lemma 4.10. Let $\{z_j\}$ be a global solution to (36). Then $|L_{ij}|$ satisfies

Proof. We use (36) to find

Thus, we have

In the sequel, we prove each term in the R.H.S. of the above relation.

$\bullet$ Step A: By direct calculation, one has

$\bullet$ Step B: We set

Then, one has

$\bullet$ Step C: We set

$\bullet$ Step D: Note that

$\bullet$ Step E: We collect all the estimates in Step A - Step D to get

4.2.2.   Proof of Theorem 4.7

Recall that

Then, for each time $t$, there exists $i_t$ and $j_t$ by which the maximum is attained:

Then by Lemma 4.10, one has

Then, we have

Now, we set

This yields

If we impose following conditions:

we obtain

Since the roots of

can be expressed as

If we combine this expression, under the condition (38) we have

By similar arguments with previous result, we have desired estimate.

5.   Conclusion

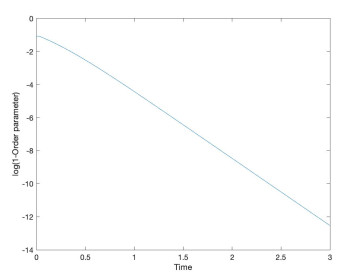
In this paper, we have proposed several sufficient frameworks leading to complete aggregation and practical aggregation in terms of initial data, coupling gains and size of time-delay for the LHS model with time-delayed interactions. The LHS model is a complex counterpart of the LS model, and it describes the continuous-time dynamics of the Lohe Hermitian sphere particles on the unit Hermitian sphere. For the SL coupling gain pair with $\kappa_1 = -\frac{\kappa_0}{2}$, the LHS model on $\mathbb C^d$ can be rewritten as the LS model on $\mathbb R^{2d}$. When the coupling gain pair is close to that of the SL coupling gain pair and the corresponding linear flows are the same, we show that the LHS flow with a time-delay tends to complete aggregation asymptotically for some admissible class of initial data and system parameters. For a general network, we also provided a sufficient framework for practical aggregation to the LHS model with respect to time-delay. Even for the LS model on the unit sphere in Euclidean space, the complete aggregation is not known in previous literature, except some weak aggregation estimates such as practical aggregation. We leave this interesting issue for a future work.

Appendix A.   Derivation of the SL coupling.

We begin with the generalized Stuart-Landau model on $\mathbb C^{d+1}$:

where $z_j\in \mathbb C^{d+1}$ for all $j\in\mathcal{N}$, $\Omega$ is a skew-Hermitian matrix with the size $(d+1)\times (d+1)$ and $I_{d+1}$ is the identity matrix with the size $(d+1)\times (d+1)$. Now, we substitute the ansatz:

into (39) to see

Then, $\langle w_j, (40) \rangle$ implies

where we used the fact that $\| w_j \| = 1$.

If we take the real part of (41), one has

where we used the relations:

Now, we combine (40) and (42) to get

Similarly, we impose $r_j\equiv1$ on (43) to obtain

If we put $\kappa_0 = \kappa$ and $\kappa_1 = -\frac{\kappa}{2}$ into the LHS model, then we get the above system. Therefore, the SL coupling gain pair $(\kappa_0, \kappa_1) = \left(\kappa, -\frac{\kappa}{2}\right)$ can be obtained by the generalized Stuart-Landau model.