Sharp interface limit in a phase field model of cell motility

1.   Introduction

The problem of cell motility has been a classical subject in biology for several centuries. It dates back to the celebrated discovery by van Leeuwenhoek in the 17th century who drastically improved the microscope to the extent that he was able to observe motion of single celled organisms that moved due to contraction and extension. Three centuries later this problem continues to attract the attention of biologists, biophysicists and, more recently, applied mathematicians. A comprehensive review of the mathematical modeling of cell motility can be found in [27].

This work is motivated by the problem of motility (crawling motion) of eukaryotic cells on substrates. The network of actin (protein) filaments (which is a part of the cytoskeleton in such cells) plays an important role in cell motility. We are concerned with cell shape dynamics, caused by extension of the front of the cell due to polymerization of the actin filaments and contraction of the back of the cell due to detachment of these filaments. Modeling of this process in full generality is at present a formidable challenge because several important biological ingredients (e.g., regulatory pathways [27]) are not yet well understood.

In recent biophysical studies several simplified phase field models of cell motility have been proposed. Simulations performed for these models demonstrated good agreement with experiments (e.g., [40,38] and references therein). Recall that phase field models are typically used to describe the evolution of an interface between two phases (e.g., solidification or viscous fingering). The key ingredient of such models is an auxiliary scalar field, which takes two different values in domains describing the two phases (e.g., 1 and 0) with a diffuse interface of a small width. An alternative approach to cell motility involving free boundary problems is developed in [22,34,5,33,32].

We consider the coupled system of parabolic PDEs, which is a modified version of the model from [40] in the diffusive scaling ($t\mapsto \varepsilon^2 t$, $x \mapsto \varepsilon x$):

where

The unknowns here are the scalar phase field function $\rho_\varepsilon$ and the orientation vector $P_\varepsilon$; $\Omega$ is a bounded domain in $\mathbb{R}^2$, $\lambda_\varepsilon$ is the Lagrange multiplier responsible for preservation of volume. We study solutions of system (1)-(3) in the sharp interface limit, when the parameter $\varepsilon>0$ (which is, loosely speaking, the width of the interface) tends to zero.

While system (1)-(3) represents a modified version of the model from [40], the main features of the original model are preserved. First, the volume preservation constraint in [40] is imposed by introducing a penalization parameter into the double well potential. In (1)-(2) the volume preservation is enforced by the (dynamic) Lagrange multiplier $\lambda_\varepsilon$ given by (3). Both ways of introducing volume preservation are equivalent in the sharp interface limit, see [1,2,8]. Second, for technical simplicity we dropped two terms in the original equation for the orientation field $P$. One of them, responsible for a stronger damping in the phase $\rho_\varepsilon \sim 0$, can be added to (2) without any qualitative changes, while the second one, the so-called $\gamma$-term, leads to an enormous technical complication, even existence is very hard to prove. Ref. [40] qualifies this term as a symmetry breaking mechanism, which is important for initiation of motion, however it is observed in [40] that self-sustained motion occurs even without $\gamma$-term (page 3 in [40]). Third, our study reveals another symmetry breaking mechanism in (1)-(2), emanated from asymmetry of the potential $W(\rho)$ (see Subsection 1.2). That is, the effect of $\gamma$-term is replaced, to some extent, by asymmetry of the potential $W$. Note that symmetry of potential $W(\rho)=W(1-\rho)$ reflects an idealized view that the two phases $\rho\sim 0$ and $\rho\sim 1$ are equivalent resulting in the symmetric profile of the interface with respect to interchanging of the phases. In the model under consideration the phase $\rho\sim 1$ corresponds to the cell interior and $\rho\sim 0$ outside the cell, therefore the phases are not equivalent and it is natural to assume that the potential $W$ is asymmetric.

Heuristically, system (1)-(3) describes the motion of a interface caused by the competition between mean curvature motion (due to stiffness of interface) and the push of the orientation field on the interface curve. The main issue is to determine the influence of this competition on the qualitative behavior of the sharp interface solution. The parameter $\beta>0$ models this competition which is why it plays a key role in the analysis of system (1)-(3).

1.1.   Techniques

Recall the Allen-Cahn equation which is at the core of system (1)-(3),

where $W^\prime(\rho)$ is the derivative of a double equal well potential $W(\rho)$. We suppose that

e.g. $W(\rho)=\frac{1}{4}\rho^2(\rho-1)^2$. Equation (4) was introduced in [3] to model the motion of the phase-antiphase boundary (interface) between two grains in a solid material. Analysis of (4) as $\varepsilon \to 0$ leads to the asymptotic solution that takes values $\rho_\varepsilon\sim 0$ and $\rho_\varepsilon\sim 1$ in the domains corresponding to two phases separated by an interface of width of order $\varepsilon$, the so-called sharp interface. Furthermore, it was shown that this sharp interface obeys mean curvature motion. Recall that in this motion the normal component of the velocity of each point of the surface is equal to the mean curvature of the surface at this point. This motion has been extensively studied in the geometrical community (e.g., [19,21,18,7] and references therein). It also received significant attention in PDE literature. Specifically [12] and [13] established existence of global viscosity solutions (weak solutions) for the mean curvature flow. Mean curvature motion of the interface in the limit $\varepsilon \to 0$ was formally derived in [15], [36] and then justified in [14] by using the viscosity solutions techniques. The limit $\varepsilon\to 0$ was also studied for a stochastically perturbed Allen-Cahn equation (4) in [23,29].

Solutions of the stationary Allen-Cahn equation with the volume constraint were studied in [26] by $\Gamma$-convergence techniques applied to the stationary variational problem corresponding to (4). It was established that the $\Gamma$-limiting functional is the interface perimeter (curve length in 2D or surface area in higher dimensions). Subsequently in the work [35] an evolutionary reaction-diffusion equation with double-well potential and nonlocal term that describes the volume constraint was studied. The following asymptotic formula for evolution of the interface $\Gamma$ in the form of volume preserving mean curvature flow was formally derived in [35]:

where $V$ stands for the normal velocity of $\Gamma(t)$ with respect to the inward normal, $\kappa$ denotes the curvature of $\Gamma(t)$, $|\Gamma(t)|$ is the curve length. Formula (6) was rigorously justified in the radially symmetric case in [9] and in the general case in [11].

Three main approaches to the study of asymptotic behavior (sharp interface limit) of solutions of phase field equations and systems have been developed.

When a comparison principle for solutions applies, a PDE approach based on viscosity solutions techniques was successfully used in [14,4,17,24] and other works. This approach can not be applied to the system (1)-(3), because

● equations (1)-(2) are coupled through spatial gradients,

● equation (1) contains the nonlocal (volume preservation) term $\lambda_\varepsilon$ given by (3).

Another technique used in such problems is $\Gamma$-convergence (see [37,23] and references therein). This technique also does not work for the system (1)-(3). The standard Allen-Cahn equation (4) is a gradient flow (in $L^2$ metric) with Ginzburg-Landau energy functional, which is why one can use the $\Gamma$-convergence approach. However, there is no energy functional such that problem (1)-(3) can be written as a gradient flow.

When none of the above elegant tools apply, one can use direct construction of an asymptotic expansion followed by its justification via energy bounds [28]. In Allen-Cahn type problems it typically requires a number of terms (e.g., at least five in [11]) in the expansion. In this work we use some ingredients of this technique. We construct an asymptotic formula (see e.g., (65)) with just two terms: the leading one with the only unknown location of the interface and the corrector vanishing in the limit $\varepsilon \to 0$. This representation is supplemented with an additional condition that the unknown term in the corrector is orthogonal to the eigenfunction of the Allen-Cahn operator linearized around its standing wave (see (66)). This condition defines the interface location implicitly (in a "weak form", via an integral identity) but it allows us to apply a Poincaré type inequality (142) in derivation of necessary bounds for the corrector. This representation leads to a reduction of the coupled system to a single singularly perturbed non-linear PDE which for $\varepsilon \to 0$ provides the sharp interface limit. This approach is rigorously justified in the 1D model problem, however we believe that this justification can be carried out in the 2D problem (1)-(3). For small $\beta$ it is implemented via the contraction mapping principle; for large $\beta$ it requires more subtle stability analysis of a semigroup generated by a nonlinear nonlocal operator.

1.2.   Main results

The main objectives of this work are: prove well-posedness of (1)-(3), reveal the effect of the coupling in (1)-(2) on the sharp interface limit, study qualitative behavior of system (1)-(2) versus values of the parameter $\beta$.

The first main result, Theorem 1, demonstrates that there is no finite time blow up and that the sharp interface property of the initial data propagates in time. Theorem 1 establishes existence of solutions to problem (1)-(3) on the time-interval $[0, T]$ for any $T>0$ and sufficiently small $\varepsilon$, $\varepsilon <\varepsilon_0(T)$. It also shows that a sharp (width $\varepsilon$) interface at $t=0$ remains sharp for $t \in (0, T)$. This is proved by combining a maximum principle with energy type bounds.

To study how coupling of equations (1)-(2) along with the nonlocal volume constraint (3) affect the sharp interface limit we use formal asymptotic expansions following the method of [15]. In this way we derive the equation of motion for the sharp interface,

where $c_0$ is a constant determined by the potential $W(\rho)$ and the function $\Phi(V)$ is a given function (obtained by solving (31)).

The parameter $\beta$ in (2) can be thought of as the strength of coupling in system (1)-(3). If $\beta$ is small, then (1) and (7) can be viewed as a perturbation of Allen-Cahn equation with volume preserving term and curvature driven motion (6), respectively. Results of the work [25], which addresses (7) for small (subcritical) values of $\beta$, show that curves evolving according to (7) behave similarly to those satisfying (6): they become close to circles quite fast exhibiting a little shift compared with curvature driven motion. On the other hand, if $\beta$ is not small evolution of sharp interface changes dramatically. In this case the function $c_0V-\Phi_{\beta}(V)$ is no longer invertible and one can expect quite complicated behavior of the interface curve. As the first step to study this case, it is natural to look for solutions for (1)-(3) with steady motion. We can predict existence of such solutions based on our results for a 1D analogue of (1)-(3). We prove that in the 1D case there exist traveling wave solutions with nonzero velocities, provided that $\beta$ is large enough and the potential $W(\rho)$ has certain asymmetry, e.g. $W(\rho)=\frac{1}{4}\rho^2(\rho-1)^2(\rho^2+1)$. Existence of such traveling waves is consistent with experimental observations of motility on keratocyte cells which exhibit self-propagation along the straight line maintaining the same shape over many times of its length [22].

Heuristically, for traveling waves with nonzero velocity, say $V_\varepsilon>0$, the push of $P_\varepsilon$ on the front edge of the interface must be stronger than its pullback on the rear edge. This asymmetry in $P_\varepsilon$ comes forth with an asymmetry of $W(\rho)$. We show that the velocity $V=V_\varepsilon$ solves simultaneously equations $c_0V=\Phi_\beta(V)-\lambda$ and $-c_0V=\Phi_\beta(-V)-\lambda$, up to a small error. These equations are obtained in the sharp interface limit on the front and rear edges of the interface, respectively; $-\Phi_\beta(-V)$ and $-\Phi_\beta(V)$ represent in these equations, loosely speaking, the push (and pullback) of $P_\varepsilon$ on the front and rear edges. Then eliminating $\lambda$ one derives $2 c_0 V=\Phi_\beta(V)-\Phi_\beta(-V)$, this yields the only solution $V=0$ unless the potential has certain asymmetry (for symmetric potentials, e.g., $W(\rho)=\frac{1}{4}\rho^2(\rho-1)^2$, one has $\Phi_\beta(V)=\Phi_\beta(-V)$). Theorem 2 justifies the equation $2 c_0 V=\Phi_\beta(V)-\Phi_\beta(-V)$ for velocities of traveling waves in the sharp interface limit $\varepsilon\to 0$. Its proof is based on Schauder's fixed point theorem.

Finally, we study the 1D model parabolic problem without any restrictions on $\beta$, where the effects of curvature and volume preservation are mimicked by a given forcing term $F(t)$. As already mentioned the main technical trick here is to introduce a special (two term) representation of solutions which allows us to reduce the study of the interface velocity to a single singularly perturbed nonlinear equation. Linearization of this equation and spectral analysis of the corresponding generator lead to a notion of stable and unstable velocities. The main result here, Theorem 6, can be informally stated as follows. If the interface velocity $V_{\varepsilon}$ belongs to the domain of stable velocities it keeps varying continuously obeying the law $c_0V_\varepsilon(t)=\Phi_\beta(V_\varepsilon(t))-F(t)+o(1)$ until it becomes unstable (if so). This theoretical result is supplemented by numerical simulations which show that interface velocities exhibit jumps and reveal existence of a hysteresis loop. Note that velocity jumps were also observed in [40]. More precisely, the onset of cell motion was attributed to the subcritical instability (see Fig. 3 and discussion below this figure on page 5 in [40]) which is a typical example of hysteresis [39]. Our stability analysis also predicts that stationary solutions of (1)-(3) with circular shape of the phase field functions are unstable in the case of asymmetric potentials and large enough $\beta$. This conjecture is based on the fact that zero velocity is unstable in this case (see Remark 7).

The paper is organized as follows. Section 2.1 is devoted to the well-posedness of the problem (1)-(3). In Section 2.2 the equation for the interface motion (7) is formally derived. Section 3 deals with traveling wave solutions. Section 4 contains the rigorous justification of the sharp interface limit in the context of the model 1D problem. Some results obtained in this manuscript were announced in [6] without proofs.

2.   Well-posedness of the problem and formal derivation of the sharp interface limit

2.1.   Bounds for the solution of (1)-(2) with $\varepsilon$-transition layer on finite time intervals

In this section we consider the system (1)-(3) supplemented with the Neumann and the Dirichlet boundary conditions on $\partial \Omega$ for $\rho_\varepsilon$ and $P_\varepsilon$, respectively,

Introduce the following energy-type functionals

Assyme that system (1)-(2) is supplied with initial data that satisfy:

and

The first condition (10) is a weakened form of a standard condition $0\leq \rho_\varepsilon(x, 0)\leq 1$ for the phase field variable. If $\lambda_\varepsilon \equiv 0$, then the maximum principle implies $0\leq \rho_\varepsilon(x, t)\leq 1$ for $t>0$. The presence of nontrivial $\lambda_\varepsilon$ leads to an "extended interval" for $\rho_\varepsilon$.¹ The second condition (11) means that at $t=0$ the function $\rho_\varepsilon$ has the structure of an "$\varepsilon$-transition layer", that is, the domain $\Omega$ consists of three subdomains: one where $\rho_\varepsilon\sim 1$ (inside the cell), another where $\rho_\varepsilon \sim 0$ (outside the cell), and they are separated by a transition layer of width $\varepsilon$ (a diffusive interface). Furthermore, it can be shown that the magnitude of the orientation field $P_\varepsilon$ is small everywhere except the $\varepsilon$-transition layer (see (19)).

¹ The exponent $1/4$ in (10) can be replaced by any positive number less than $1/2$ as will be seen in the proof the next theorem.

Theorem 1. (Bounds on finite time intervals) If the initial data $\rho_\varepsilon(x, 0)$, $P_\varepsilon(x, 0)$ satisfy (10) and (11), then for any $T>0$ the solution of (1)-(2) $\rho_\varepsilon$, $P_\varepsilon$ with boundary conditions (8) exists on the time interval $(0, T)$ for sufficiently small $\varepsilon>0$, $\varepsilon<\varepsilon_0(T)$. Moreover, $-\varepsilon^{1/4}\leq \rho_\varepsilon (x, t)\leq 1+\varepsilon^{1/4}$ and

where $C$ is independent of $t$ and $\varepsilon$.

Remark 1. This theorem implies that if the initial data are well-prepared in the sense of (10)-(11), then for $0<t <T$ the solution exists and has the structure of an $\varepsilon$-transition layer. Moreover, the bound on initial data (10) remains true for $t>0$. While it relies on a maximum principle argument, it also requires additional estimates on $\lambda_\varepsilon$ as seen from (14) below. Note also that in the proof below the interval of existence of the solution extends to $[0, T_\varepsilon]$, where $T_\varepsilon$ can be estimated from below by $C_0|\log \varepsilon|$. However, energy bounds (12) are proved only for $T_\varepsilon=O(1)$.

Remark 2. A solution of (1)-(2) is understood as follows

and equations (1) and (2) hold in $H^{-1}(\Omega)$ for almost all $t\in [0, T]$.

Proof. First multiply (1) by $\partial_t \rho_\varepsilon$ and integrate over $\Omega$:

Here we used the fact that, due to (3), the integral of $\partial_{t}\rho_{\varepsilon}$ over $\Omega$ is zero and thus

Next, using the maximum principle in (1) we get:

Let $T_\varepsilon>0$ be the maximal time such that

and from now on assume that $t\leq T_\varepsilon$.

Using (13), (15) and integrating by parts we obtain

We proceed by deriving an upper bound for the integral in the right hand side of (16). By (1) we have

The following bounds are obtained by routine application of the Cauchy-Schwarz and Young's inequalities. For the sum of the first three terms in (17) we get,

Since $(W^\prime(\rho_\varepsilon))^2\leq C W(\rho_\varepsilon)$ we also have

Finally, in order to bound $I_5$ we first derive,

then

Thus,

and using this inequality, (17) and (15) in (16), then substituting the resulting bound in (13) we obtain, for sufficiently small $\varepsilon$,

Now we obtain a bound for the last two terms in (18). Taking the scalar product of (2) with $2k P_\varepsilon+4|P_\varepsilon|^2 P_\varepsilon$, $k>0$, integrating over $\Omega$ and using (15) we get

We chose $k:=C_1+1$ to obtain

Finally, introducing $G_\varepsilon=E_\varepsilon+\int_\Omega(4k|P_\varepsilon|^2+|P_\varepsilon|^4)\, dx$, by (18) and (19) we have the differential inequality,

with a constant $C>0$ independent of $\varepsilon$. Considering the bounds on the initial data and assuming that $\varepsilon$ is sufficiently small, one can easily construct a bounded supersolution $\tilde G$ of (20) on $[0, T]$ such that $\tilde G(0)\geq G_\varepsilon$. We now have, $G_\varepsilon\leq C$ on $[0, T_\varepsilon]$ for sufficiently small $\varepsilon$. By (14) and (17) we then conclude that $T_\varepsilon$ in (15) actually coincides with $T$ when $\varepsilon$ is small. The theorem is proved.

2.2.   Formal derivation of the sharp interface equation (7)

In this section we formally derive equation (7) for the 2D system (1)-(2). While the derivation is analogous to the single Allen-Cahn equation (e.g., [36], [11]), the gradient coupling in (1)-(2) results in a nonlinear term that modifies the mean curvature motion.

Assume that that initial data $\rho_{\varepsilon}(x, 0)$ converge to the characteristic function of a smooth subdomain $\omega_0\subset \Omega$ as $\varepsilon\to 0$. Next we want to describe the evolution of the interface $\Gamma(t)=\partial \omega_t$ with $t$, where $\omega_t$ is the support of $\mathop {\lim }\limits_{\varepsilon \to 0} {\rho _\varepsilon }(x, t)$. We will assume that the initial data coincide with initial values of asymptotic expansions for $\rho_\varepsilon$ and $P_\varepsilon$ to be constructed below.

Let $X_0(s, t)$ be a parametrization of $\Gamma(t)$. In a vicinity of $\Gamma(t)$ the parameters $s$ and the signed distance $r$ to $\Gamma(t)$ will be used as local coordinates, so that

The inverse mapping to $x=X(r, s, t)$ is given by

where in the formula for $r$ we choose $+$ if $x\in \omega_t$ and $-$, if $x\notin \omega_t$. Recall that $\Gamma(t)$ is the limiting location of interface as $\varepsilon \to 0$. Next we seek $\rho_\varepsilon$ and $P_{\varepsilon}$ in the following forms in local coordinates $(r, s)$:

Introduce asymptotic expansions in local coordinates:

Now, substitute (22)-(24) into (1) and (2). Collecting terms with likewise powers of $\varepsilon$ ($\varepsilon^{-2}$ and $\varepsilon^{-1}$) and equating them to zero we successively get,

and

where $\kappa(s, t)$ is the curvature of $\Gamma_0(t)$ and $V_0(t):=-\partial_t r$ is the limiting velocity. The curvature $\kappa$ appears in the equation when one rewrites the Laplace operator in (1) in local coordinates $(r, s)$.

It is well-known that there exists a standing wave solution $\theta_0(z)$ of (25) which tends to $1$ as $z\to \infty$ and to $0$ as $z\to-\infty$, respectively. Moreover, all derivatives of the function $\theta_0(z)$ exponentially decay to $0$ as $|z|\to\infty$ and $\theta_0'(z)$ is an eigenfunction of the linearized Allen-Cahn operator $\mathcal{L}u:=-u"+W"(\theta_0)u$ corresponding to the eigenvalue $0$. Then multiplying (26) by $\theta_0'(z)$ and integrating over $z$ we are lead to the solvability condition for (26)

Next we obtain the formula for $\lambda_0(t)$. It follows from (3) that $\int_{\Omega}\partial_t \rho_{\varepsilon}=0$. Substitute expansion (22) for $\rho_{\varepsilon}$ into $\int_{\Omega}\partial_t \rho_{\varepsilon}=0$ and take into account the fact that

Thus, in order to satisfy the condition $\int_{\Omega}\partial_t \rho_{\varepsilon}=0$ to the leading order, $V_0(s, t)$ must have

Using this fact and integrating (28) with respect to $s$ with the weight $|\frac{\partial }{\partial s}X_0(s, t)|$, we get

Finally, the unique solution of (27) is given by $\Psi_0(z, s, t)=\psi(z, V_0(s, t))\upsilon (s, t)$ where $\psi=\psi(z, V)$ is the unique (bounded) solution of

The representation $\Psi_0(z, s, t)=\psi(z;V_0(s, t))\upsilon (s, t)$ yields

where we have also taken into account the linearity of (30) in $\beta$. Now substitute (31) and (29) into equation (28) to conclude the derivation of sharp interface equation (7).

3.   Traveling waves in 1D

In this section we study special solutions of system (1)-(2) in the 1D case. Specifically, we look for traveling waves (traveling pulses). Therefore it is natural to switch to the entire space $\mathbb{R}^1$ setting. We show that, not surprisingly, there are nonconstant stationary solutions, standing waves. However, we prove that apart from standing waves there are true traveling waves when the parameter $\beta$ is large enough and the potential $W(\rho)$ has certain asymmetry, e.g. $W(\rho)=\frac{1}{4}(\rho^2+\rho^4)(\rho-1)^2$, see also the discussion in Remark 4.

We are interested in (localized in some sense) solutions of (1)-(2) with $\rho_{\varepsilon} =\rho_{\varepsilon}(x-Vt)$, $P_{\varepsilon}=P_{\varepsilon}(x-Vt)$. They satisfy the following stationary equations with unknown constant velocity $V$ and constant $\lambda$:

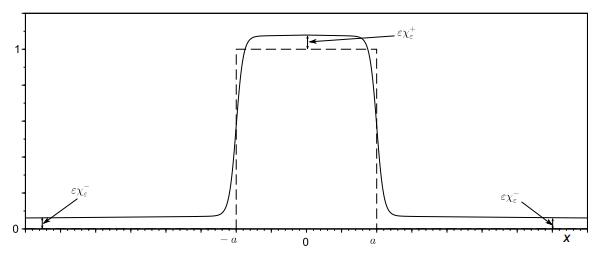
Let us postulate an ansatz for the phase field function $\rho_\varepsilon$. Given $a>0$, we look for solutions of (32)-(33) for sufficiently small $\varepsilon>0$ with $\rho_\varepsilon$ having the form

where

constants $\chi^{-}_\varepsilon$ and $\chi^{+}_\varepsilon$ are the smallest (in absolute value) solutions of $W^\prime(\varepsilon\chi^{-}_\varepsilon)=\varepsilon\lambda$ and $W^\prime(1+\varepsilon\chi^{+}_\varepsilon)=\varepsilon\lambda$, respectively, and $u$ is the new unknown function vanishing at $\pm\infty$. The role of the constant $\chi^{-}_\varepsilon$ in (34) is to amend the first term of the representation so that $u$ decays at $\pm \infty$. Similarly, $\chi^{+}_\varepsilon$ is introduced to end up with $u$ which is exponentially close to one in $(-a, a)$ away from points $\pm a$ (see also Fig. 1).

Substitute representation (34) in (32)-(33) to find after rescaling the variable $y:=x/\varepsilon$ and rearranging terms,

and

Note that the ansatz (34) yields the characteristic function of the interval $(-a, a)$ in the limit $\varepsilon\to 0$, provided that $u=u_\varepsilon$ remains bounded. In this sense we seek solutions with localized profiles of the phase field function $\rho_\varepsilon$. The idea of the construction of traveling wave solutions is based on the observation that solvability of the above equations (35) and (36) can be handled by local analysis near the points $\pm a$. Indeed, setting $z=y+a$ (35)-(36) and keeping only leading order terms we (formally) obtain

Resolve the second equation to obtain $P_\varepsilon(z)=\psi(z, V)$, then solvability of the first equation (recall that $\partial_z^2\theta_0^\prime(z)-W^{\prime\prime}(\theta_0(z))\theta_0^\prime(z)=0$) requires that $c_0V=\Phi_\beta(V)-\lambda$, where we have used (31). Similarly, local analysis near the point $a$ leads to the equation $-c_0V=\Phi_\beta(-V)-\lambda$. Thus, we have reduced the infinite dimensional system (35)-(36) to a two dimensional one.

In order to transform the above heuristics into a rigorous analysis we reset (35)-(36) as a fixed point problem. To this end rewrite (35) in the following form, introducing auxiliary functions ${\theta}_\varepsilon^{(1)}(y)=\theta_0^\prime(y+a/\varepsilon)+\theta_0^\prime(a/\varepsilon-y)$ and $\theta_\varepsilon^{(2)}(y)=\theta_0^\prime(y+a/\varepsilon)-\theta_0^\prime(a/\varepsilon-y)$,

where

and

Note that the operator $\mathcal{Q}_\varepsilon$ in the left hand side of (37),

has two eigenfunctions $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(2)}$ corresponding to the zero eigenvalue.

Lemma 1. Let $v_\varepsilon$ be any function from $H^1(\mathbb R)$ orthogonal to both $\theta^{(1)}_{\varepsilon}$ and $\theta^{(2)}_{\varepsilon}$ in $L^2(\mathbb R)$. Assume also that $f_\varepsilon:=\mathcal{Q}_{\varepsilon} v_\varepsilon$ belongs to $L^2(\mathbb R)$. Then for sufficiently small $\varepsilon$

with $C$ independent of $\varepsilon$ and $v_\varepsilon$.

Proof. Multiplying $\mathcal{Q}_\varepsilon v_\varepsilon$ by $v_\varepsilon$ in $L^2(\mathbb R)$ and representing $v_\varepsilon$ as $v_\varepsilon=\theta_\varepsilon^{(1)} w_\varepsilon$ (note that $\theta_\varepsilon^{(1)}>0$) we derive

where the latter equality is obtained via integrating by parts, and the term with $H_\varepsilon$ vanishes thanks to orthogonality of $v_\varepsilon$ to $\theta^{(2)}_\varepsilon$. Thus

The statement of Lemma 1 immediately follows if we prove the following inequality

with $C$ independent of $\varepsilon$ and $v_\varepsilon$. Indeed, using (42) in (41) we get

and combining (43) with

yields (39).

To prove (42) we use the Poincaré inequality (see Appendix A)

with a constant $C$ independent of $\varepsilon$ and

Due to orthogonality of $\theta_\varepsilon^{(1)} w_\varepsilon$ to $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(1)}$, we have

Thanks to the exponential decay of $\theta_0'$, $\theta_0'(y)\leq \alpha_0 e^{-\kappa |y|}$ (see, e.g., [28]), it follows that

for sufficiently small $\varepsilon$ and $r>0$ independent of $\varepsilon$. Combining (45) and (44) we obtain (42), the Lemma is proved.

Proposition 1. For sufficiently small $\varepsilon$ the operator $\mathcal{Q}_\varepsilon^\ast$ adjoint to $\mathcal{Q}_\varepsilon$ (with respect to the scalar product in $L^2(\mathbb{R})$) has two eigenfunctions $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(3)}=\theta_\varepsilon^{(2)}+q_\varepsilon$ corresponding to the zero eigenvalue, with $\|q_\varepsilon\|_{H^1}=o(\varepsilon)$. Moreover the equation $\mathcal{Q}_\varepsilon u=f$ has a solution if and only if $f\in L^2(\mathbb{R})$ is orthogonal to the eigenfunctions $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(3)}$ of $\mathcal{Q}_\varepsilon^\ast$.

Proof. Given $f\in L^2(\mathbb{R})$, consider the equation $\mathcal{Q}_\varepsilon u=f$ rewriting it in the form

Since $W^{\prime\prime}(0)>0$, the equation $\partial_y^2u-W^{\prime\prime}(0)u=\tilde f$ has the unique solution $u=G\tilde f$ for every $\tilde f\in L^2(\mathbb{R})$ with a bounded resolving operator $G:L^2(\mathbb{R}) \to L^2(\mathbb{R})$. Moreover, by applying the operator $G$ to (46) we reduce this equation to $u+Ku =Gf$, where $K$ is a compact operator (this can be easily shown using the properties of the function $\theta_0$). Thus we can apply the Fredholm theorem to study the solvability of (46). Note that $\mathcal{Q}_\varepsilon$ does not have other eigenfunctions corresponding to the zero eigenvalue besides $\theta_\varepsilon^{(1)}$ and ${\theta}_\varepsilon^{(2)}$. Indeed, existence of such an eigenfunction $v_\varepsilon$ orthogonal to $\theta_\varepsilon^{(1)}$, ${\theta}_\varepsilon^{(2)}$ in $L^2(\mathbb{R})$ and normalized by $\int v^2_\varepsilon dy=1$ would contradict (41) derived in the proof of Lemma 1.

Consider now the eigenfunction $\theta^{(3)}_\varepsilon$ of $\mathcal{Q}_\varepsilon^\ast$ orthogonal to $\theta^{(1)}_\varepsilon$, and represent it as $\theta^{(3)}_\varepsilon =\theta^{(2)}_\varepsilon +q_\varepsilon$ with $q_\varepsilon$ orthogonal to both $\theta^{(1)}_\varepsilon$ and $\theta^{(2)}_\varepsilon$. Then combining the equality

with Lemma 1 we obtain that $\|q_\varepsilon\|_{H^1}=o(\varepsilon)$ as $\varepsilon\to 0$.

Let us consider now for a given $u\in H^1(\mathbb{R})$, $V$ and $\lambda$ a solution $P_\varepsilon$ of (35), assuming that $\varepsilon$ is sufficiently small and $\|u\|_{H^1}\leq M$, $|\lambda|\leq M$, $|V|\leq M$ for some finite $M$. We represent $P_\varepsilon$ in the form

and observe that $B_\varepsilon$ can be estimated as follows,

Now consider $u$ in the left hand side of (37) as an unknown function to write down the solvability condition

Calculate leading terms of (48) for small $\varepsilon$ taking into account the fact that

and

where $O(\varepsilon^2)$ in (49) and (50) stand for functions whose $L^\infty$-norm is bounded by $C\varepsilon^2$. Note also that integrals

tend to zero, when $\varepsilon \to 0$. Thus (48) can be rewritten as

where functions $\tilde \Phi_1$, $\tilde \Phi_2$ and their first partial derivatives in $V$ and $\lambda$ are uniformly bounded by some constant depending on $M$ only. Note that if $V_0$ is a nondegenerate root of the equation $2c_0V=\Phi_\beta(V)-\Phi_\beta(-V)$ then for sufficiently small $\varepsilon$, in a neighborhood of $V_0$ and $\lambda_0=\frac{1}{2}(\Phi_\beta(V_0)+\Phi_\beta(-V_0))$ there exists a unique pair $V_\varepsilon(u)$ and $\lambda_\varepsilon(u)$ solving (51) and depending continuously on $u$.

Theorem 2. (Existence of traveling waves) Assume that the equation $2c_0V=\Phi_\beta(V)-\Phi_\beta(-V)$ has a nondegenerate root $V_0$. Then for sufficiently small $\varepsilon$ there exists a function $u_\varepsilon$, with $\|u_\varepsilon\|_{H^1}\leq C$ and $C$ being independent of $\varepsilon$, a function $P_\varepsilon$ and constants $V=V_\varepsilon$, $\lambda=\lambda_\varepsilon$ such that $\rho_\varepsilon$ given by (34) and $P_\varepsilon$ are solutions of (32)-(33). Moreover, the velocity $V_\varepsilon$ and the constant $\lambda_\varepsilon$ converge to $V_0$ and $\lambda_0:=\frac{1}{2}(\Phi_\beta(V_0)+\Phi_\beta(-V_0))$ as $\varepsilon\to 0$.

Proof. Consider the mapping $u\mapsto \mathcal{Q}_\varepsilon^{-1}G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$, where $\lambda_\varepsilon=\lambda_\varepsilon(u)$ and $V_\varepsilon=V_\varepsilon(u)$ solve (51), and $P_\varepsilon$ is the solution of (36) with $V=V_\varepsilon$ and $\lambda=\lambda_\varepsilon$. The operator $\mathcal{Q}_\varepsilon$ has two eigenfunctions $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(2)}$ corresponding to the zero eigenvalue, we choose $v:=\mathcal{Q}_\varepsilon^{-1}G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ to be orthogonal to $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(2)}$ in $L^2(\mathbb{R})$. Then the following holds. If $\|u\|_{H^1}\leq M$, then $\|\mathcal{Q}_\varepsilon^{-1}G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)\|_{H^1}\leq M$ for large $M$ and sufficiently small $\varepsilon$. Indeed, by virtue of Lemma 1 it suffices to find an appropriate bound for the norm $\|G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)\|_{L^2}$. Considering formula (38) for $G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ observe that the only third line and terms $V_\varepsilon\partial_y\phi_\varepsilon$ and $P_\varepsilon\partial_y\phi_\varepsilon$ in the second line have non vanishing norm in $L^2(R)$ as $\varepsilon\to 0$. Moreover, these norms can be bounded by $C +\varepsilon C_1(M)$ with $C$ independent of $M$, while the norm of other therms can be estimated by $\varepsilon C_2(M)$. Thus $\|G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)\|_{L^2}\leq C +\varepsilon C_3(M)$ and using Lemma 1 we obtain

with $C_4$ independent of $M$. It remains to choose $M>C_4$ to conclude that

for sufficiently small $\varepsilon$.

Also, the mapping $u\mapsto \mathcal{Q}_\varepsilon^{-1}G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ is continuous in $H^1$. Thus, we can apply the Schauder fixed point theorem provided we establish the compactness of the mapping under consideration. To this end we consider a subset of functions $u$ which decay exponentially with their first derivatives:

We claim that for some $M>0$ and $r>0$ the solution $v$ of the equation $\mathcal{Q}_\varepsilon v=G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ (orthogonal to $\theta_\varepsilon^{(1)}$ and $\theta_\varepsilon^{(2)}$) belongs to $\mathcal{K}_{M, r}$ for every $u\in \mathcal{K}_{M, r}$, when $\varepsilon$ is sufficiently small. Indeed, the required bound for the norm of $v$ in $H^1(\mathbb{R})$ is already established. It remains to prove that $v$ and $\partial_y v$ decay exponentially when $|y|\geq 2a/\varepsilon$. To this end we observe first that

with $C>0$ independent of $M$ and $\varepsilon$, and $r_1>0$ depending on $M$ only. The proof of (53) is carried out in two steps. First, we multiply (36) by $P_\varepsilon$, integrate on $\mathbb{R}$ and apply the Cauchy-Schwarz inequality. As a result we get $\|P_\varepsilon\|_{L^\infty}\leq C\|P_\varepsilon\|_{H^1}\leq C_1(1+\varepsilon M)$. Second, observe that the function $\theta_0^\prime(y)$ decays exponentially when $y\to\pm\infty$. Therefore there exists $C_2 \geq C_1(1+\varepsilon M)$ and $r_1>0$ such that the functions $P_{\pm}(y):=\pm C_2 e^{-r_1(|y|-2 a/\varepsilon)}$ satisfy

This yields pointswise bounds $-C_2 e^{-r_1(|y|-2a/\varepsilon)}\leq P_\varepsilon(y)\leq C_2 e^{-r_1(|y|-2a/\varepsilon)}$ for all $y\leq -2a/\varepsilon$ and $y\geq 2a/\varepsilon$. Next using (53) in the equation $\mathcal{Q}_\varepsilon v=G(\lambda, V, P_\varepsilon, u )$ and arguing similarly one can establish that $|v|\leq C(1+\varepsilon C_1(M))e^{-r_2(|y|-2a/\varepsilon)}$ for $|y|\geq 2a/\varepsilon$. Finally, taking an integral from $-\infty$ to $y$ (or from $y$ to $+\infty$) of the equation $\mathcal{Q}_\varepsilon v=G(\lambda, V, P_\varepsilon, u )$ we get the required bound for $\partial_y v$ on $(-\infty, -2a/\varepsilon]$ (or $[2a/\varepsilon, +\infty)$).

Thus the image of the convex closed set $\mathcal{K}_{M, r}$ under the mapping

is contained in $\mathcal{K}_{M, r}$. Also, the equation $\mathcal{Q}_\varepsilon v=G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ provides the following bound $|\partial_y^2 v|\leq C(|u|, |\partial_y u|, |v|, |\partial_y v|)$ while $|u|$, $|v|$, $|\partial_y u|$ and $|\partial_y v|$ have pointwise bounds with decay estimates for large $y$, both $u$ and $v$ being elements of $\mathcal{K}_{M, r}$. This implies that the mapping $u\mapsto \mathcal{Q}_\varepsilon^{-1}G(\lambda_\varepsilon, V_\varepsilon, P_\varepsilon, u)$ is compact on $\mathcal{K}_{M, r}$ (in the topology of $H^1(\mathbb{R})$). Thus there exists a fixed point of this mapping in $\mathcal{K}_{M, r}$. Since the principal part $0=\Phi_\beta(V)+\Phi_\beta(-V)-2\lambda$ and $2c_0V=\Phi_\beta(V)-\Phi_\beta(-V)$ of the system (51) is nondegenerate in the neighborhood of $V_0$ and $\lambda_0$, we have $V_\varepsilon\to V_0$ and $\lambda_\varepsilon\to \lambda_0$ as $\varepsilon \to 0$.

Remark 3. Note that $V_0=0$ and $\lambda_0=\Phi_\beta(0)$ are always solutions of the principal part of the system (51). Moreover one can establish a traveling wave (in fact standing wave) solution with $V_\varepsilon$ equal to zero exactly, by following the line of Theorem 2 but considering subspace of even functions $u\in H^1(\mathbb{R})$. The existence of nontrivial traveling waves (with nonzero velocities) is granted by Theorem 2 in the case when the equation $2c_0V=\Phi_\beta(V)-\Phi_\beta(-V)$ has a nonzero (nondegenerate) root. Such a solution does not exist for the standard potential $W(\rho)=\frac{1}{4}\rho^2(\rho-1)^2$, in this case $\Phi_\beta(V)=\Phi_\beta(-V)$ for all $V$ due to the fact that $\theta_0^\prime$ is an odd function. However, if the potential has two equally deep wells but possesses certain asymmetry, e.g. $W(\rho)=\frac{1}{4} (\rho^2+\rho^4)(\rho-1)^2$, we have $\Phi_\beta(V)>\Phi_\beta(-V)$ for $V>0$, so that nontrivial solutions of $2c_0V=\Phi_\beta(V)-\Phi_\beta(-V)$ do exist for sufficiently large $\beta$, $\beta>\beta_{\rm critical}$. The plot of the function $\Phi_\beta(V)$ for $\beta=1$ and $W(\rho)=\frac{1}{4}(\rho^2+\rho^4)(\rho-1)^2$ is depicted in Fig. 2, as well as the corresponding standing wave.

Remark 4. As already mentioned, nontrivial traveling waves appear in the case when $W(\rho)$ has certain asymmetry, that, in particular, makes the derivative $\Phi_\beta^\prime(V)$ of $\Phi_\beta(V)$ positive at $V=0$. The function $\Phi_\beta(V)$ depends on the potential $W(\rho)$ in a complex way. Its derivative at $V=0$ is given by $\Phi'_{\beta}(0)=\beta \int (\theta_0')^2 \psi_V(y) dy$ with $\psi_V(y)$ solving $(-\partial_y^2+I)^2\psi_V=\theta_0"$. The following representation $\psi_V(y)=\int e^{-|y-z|}(1+|y-z|)\theta_0^{''}(z)dz$ can be obtained in a standard way by using fundamental solution, so that

where $y(\theta_0)=\int\limits_{1/2}^{\theta_0}\dfrac{d\theta_0}{\sqrt{2W(\theta_0)}}$ (this relation between $y$ and $\theta_0$ follows from the equation $\theta_0'=\sqrt{2W(\theta_0)}$ obtained by multiplication of $\theta_0"=W'(\theta_0)$ by $\theta_0'$ and integration with respect to $y$). On the other hand, $\Phi_{\beta}$ is a bounded function, therefore if the right hand side of (54) is positive, then for sufficiently large $\beta$ there are non-zero solutions of equation $2c_0V=\Phi_{\beta}(V)-\Phi_{\beta}(-V)$.

In order to have more insight about this dependence assume that the diffusion coefficient in equation (2) for $P_\varepsilon$ is given by $\delta\varepsilon$, where $\delta$ is a positive parameter independent of $\varepsilon$. This leads to redefining $\Phi_\beta(V)$ as follows,

One can write down an asymptotic expansion of $\psi$ and its derivative $\psi_V$ with respect to $V$ at $V=0$ for sufficiently small $\delta>0$

Then we have

which yields, after integrating by parts and using the relations $(\theta^\prime)^2=2W(\theta)$, $\theta^{\prime\prime}=W^\prime(\theta)$,

The integral in (55) can be interpreted as a measure of asymmetry of the potential $W(\rho)$, and nontrivial traveling waves emerge if this integral is positive and

4.   Sharp interface limit in 1D model problem

The equation of motion (7) formally derived in Subsection 2.2 exhibits qualitative changes for large values of the parameter $\beta$. This is indicated, in particular, by the fact that the equation

may have multiple roots $V$. Note that combining the curvature and integral (constant) terms in (7) yields the equation of the form (56) with

In this Section we analyze a 1D analogue of the original model and rigorously derive a law of motion in the sharp interface limit. For given $F(t)\in C[0, T]$ we consider bounded solutions of the system

Analysis of the 1D problem (57)-(58) is a necessary step for understanding the original problem (1)-(2). Observe that motion of the interface in the 2D system (1)-(2) occurs in the normal direction, and therefore it is essentially one-dimensional. Thus, the 1D model (57)-(58) is anticipated to capture the main features of (1)-(2). The effects of curvature and mass conservation in (7) are modeled by a given function $F(t)$. We believe that qualitative conclusions obtained for the 1D problem (57)-(58) apply for the 2D model (1)-(2).

We study the asymptotic behavior of solutions to the system (57)-(58) as $\varepsilon\to 0$ with "well-prepared" initial data for $\rho_\varepsilon$,

where $\theta_0$ is a standing wave solution of the Allen-Cahn equation (25) such that $\theta_0(z)\to 0$ as $z\to-\infty$ and $\theta_0(z)\to 1$ as $z\to+\infty$. We seek $\rho_\varepsilon$ in the form

The $x_{\varepsilon}(t)$ in (60) can be viewed as a location of the interface. Remark 5 explains that a choice of $x_\varepsilon$ is not unique, however it is well defined in the limit $\varepsilon\to 0$.

The main goal of this Section is to prove that $x_{\varepsilon}(t)$ converges as $\varepsilon\to 0$ to $x_0(t)$, whose velocity $V_0(t)=\dot{x}_0(t)$ solves the sharp interface equation

where $\Phi(V)$ is the known nonlinear function given by (31). This equation can be formally obtained in the limit $\varepsilon \to 0$ as in the Section 2.2.

Next for reader's convenience we summarize key steps of the asymptotic analysis of (57)-(58):

(ⅰ) Choice of a special representation. The function $\rho_{\varepsilon}$ is represented in the form

where $\theta_0$ and $\chi_\varepsilon$ are known, and $u_{\varepsilon}$, $Q_\varepsilon$ are the new unknown functions. Existence of $x_{\varepsilon}(t)$ with estimates on $u_{\varepsilon}$ uniform in $\varepsilon$ and $t$ are established in Section 4.2.

(ⅱ) Reduction of the system to a single equation. The unknown function $u_{\varepsilon}$ is eliminated by showing that the third term in representation (62) is small. Next, we split $Q_{\varepsilon}$ into two parts, $Q_{\varepsilon}=A_{\varepsilon}+B_{\varepsilon}$, where $B_{\varepsilon}$ depends on $u_{\varepsilon}$ but is small, and $A_{\varepsilon}$ does not depend on $u_\varepsilon$. Thus, the original system (57)-(58) is reduced to

Taking the limit $\varepsilon\to 0$ in the system (63)-(64) is non-trivial because of the product term $V_{\varepsilon}(t)\partial_y A_{\varepsilon}$.

(ⅲ) Analysis of reduced problem. For sufficiently small $\beta$ we prove that $x_{\varepsilon}(t)\to x_0(t)$ as $\varepsilon\to 0$ by the contraction mapping principle. For larger $\beta$, system (63)-(64) further reduces to a singularly perturbed non-linear non-local equation. The limiting transition in this equation is based on the stability analysis of the semigroup generated by the linearized operator.

4.1.   Asymptotic representation for $\rho_{\varepsilon}$

In order to pass to the limit $\varepsilon \to 0$ in (57)-(58) we further specify $v_{\varepsilon}$ in (60). Namely, we introduce the representation

with the new unknown function $u_{\varepsilon}$ satisfying

and $\chi_{\varepsilon}(y, t)$ defined by

where $\chi^+$ and $\chi^-$ are solutions of the following ODEs

with the initial data $\chi^+_{\varepsilon}(0)=F(0)/W^{\prime\prime}(1)$ and $\chi^-_{\varepsilon}(0)=F(0)/W^{\prime\prime}(0)$.

The idea of the decomposition of the lower order term in (60) into two parts is suggested by the observation that it is the most important to control behavior of $\rho_\varepsilon$ in the vicinity of the interface. So, ideally we would like to localize the analysis by considering functions that are negligibly small outside the interface. However, the right hand side $F(t)$ prevents $\rho_\varepsilon$ from being localized. The function $\chi_\varepsilon$ absorbs this nonlocal part of $\rho_\varepsilon$: the new unknown function $u_\varepsilon$ decays at infinity and, therefore, it allows one to work in Sobolev spaces on $\mathbb R$. Note that the standard ODE methods yield the following bounds

moreover, thanks to the continuity of $F(t)$ and a particular choice of the initial values $\chi^{\pm}_\varepsilon(0)$ we have

Finally, we set $Q_\varepsilon(y, t):=P_\varepsilon(x_\varepsilon+\varepsilon y, t)$.

Remark 5. The choice of $x_\varepsilon$ in the representation (60) is not unique, e.g. its perturbation with a term of order $\varepsilon^2$ still leads to an expansion of the form (60). We introduced the additional orthogonality condition (66) which implicitly specifies $x_\varepsilon(t)$. This condition allows us to use Poincaré type inequalities (see Appendix A) when deriving various bounds for $u_\varepsilon$. If the initial value of $u_\varepsilon$ in the expansion (65) does not satisfy (66), it can be fixed by perturbing the initial value $x_\varepsilon(0)=0$ with a higher order term. Indeed, this amounts to solving the equation

If $\|v_\varepsilon\|_{L^2}\leq C$ then the latter equation has a solution $x_\varepsilon(0)$ and $|x_\varepsilon(0)|=o(\varepsilon)$.

4.2.   Reduction of the system to a single equation

The following theorem justifies the expansions (65) and will be used to obtain a reduced system for unknowns $x_\varepsilon(t)$ and $Q_\varepsilon(y, t)$ by eliminating $u_{\varepsilon}$.

Theorem 3. (Validation of representation (65)-(66)) Let $\rho_{\varepsilon}$ and $P_{\varepsilon}$ be solutions of problem (57)-(58) with initial data $\rho_\varepsilon(x, 0)=\theta_0(x/\varepsilon)+\varepsilon v_\varepsilon(x/\varepsilon)$ and $P_{\varepsilon}(x, 0)=p_\varepsilon (\frac{x}{\varepsilon})$, where

and

Then there exists $x_{\varepsilon}(t)$ such that the expansion (65)-(66) holds with $\|u_{\varepsilon}(\cdot, t)\|_{L^2}~\leq C$ for $t\in [0, T]$.

Proof. Step 1. (coupled system for $u_\varepsilon$, $Q_\varepsilon$ and $V_\varepsilon:=\dot x_\varepsilon$) Note that the maximum principle applied to (57) yields $\|\rho_\varepsilon\|_{L^\infty}\leq C$. This bound in conjunction with (68) allow one to write down the expansion

where $\xi_\varepsilon$ and $\overline{\xi}_\varepsilon$ are some bounded functions (while $\xi_\varepsilon$ and $\overline{\xi}_\varepsilon$ depend on $\theta_0$, $\chi_\varepsilon$ and $u_\varepsilon$, this dependence is omitted for brevity). Then substituting the expansion (65) into equation (57) leads to

This equation is coupled with that for $Q_\varepsilon$

Finally, considering the solution $\rho_\varepsilon$ as a given function we differentiate (65) in time, multiply by $\theta_0^\prime(y)$ and integrate in $y$ over $\mathbb R$ to obtain the equation for $V_\varepsilon$. Thanks to (66) we get

Note that if we obtain a uniform in $t$ a priori bound of the form $\|u_\varepsilon\|_{L^2}\leq C$ with $C$ independent of $\varepsilon$, (74) can be resolved with respect to $\dot x_\varepsilon=V_\varepsilon$ to come up with a well posed system (72)-(74).

Step 2. (energy estimates for $u_{\varepsilon}$ and $Q_\varepsilon$) Represent $u_\varepsilon$ as $u_{\varepsilon}=\theta_0^\prime w_{\varepsilon}$, then multiply the equation (72) by $u_{\varepsilon}$ and integrate in $y$ over $\mathbb R$. Since

and

we get

where $R_1=\partial_y^2\chi_\varepsilon +\dfrac{W^\prime(\theta_0)-W^\prime(\theta_0+\varepsilon \chi_{\varepsilon})}{\varepsilon}-\varepsilon^2\dfrac{\partial \chi_{\varepsilon }}{\partial t}$. Due to the construction of $\chi_\varepsilon$ we have, $\|R_1\|_{L^2}\leq C$ with $C$ independent of $\varepsilon$ and $t$. Also, by a Poincaré type inequality (see Appendix A)

with $C_{\theta_0}>0$ independent of $u_\varepsilon$. Thus (75) implies that

where we have also used the interpolation inequality $\int |u|^4dy\leq C\|u\|_{H^1}\|u\|_{L^2}^3$ which yields $\int |u|^4dy\leq C(\|u\|_{H^1}^2+\|u\|_{L^2}^6)$. Next we derive differential inequalities

by multiplying (73) by $Q_\varepsilon$ and $\partial^2_y Q_\varepsilon$, and integrating on $\mathbb{R}$.

Step 3. (uniform bound for $\|u_\varepsilon\|_{L^2}$) We show that differential inequalities (76)-(78) imply that $\|u_\varepsilon\|^2_{L^2}$ remains uniformly bounded on $[0, T]$ when $\varepsilon>0$ is small. To this end fix $M>\max\{1, \|u_\varepsilon(\, \cdot\, , 0)\|^2_{L^2}\}$, to be specified later, and consider the first time $t=\overline t\in (0, T)$ when $\|u_\varepsilon(\, \cdot\, , t)\|^2_{L^2}$ reaches $M$ (if any). We have, $\|u_\varepsilon(\, \cdot\, , t)\|^2_{L^2}<M$ on $(0, \overline{t})$ and

It follows from (77) that $\|Q_\varepsilon\|^2_{L^2}\leq C+C\varepsilon^2 M-\varepsilon\frac{d}{dt} \|Q_\varepsilon\|^2_{L^2}$; the same bound also holds for $\|\partial_y Q_\varepsilon\|^2_{L^2}$. Substitute these bounds in (76) and integrate from $0$ to $\overline{t}$ to conclude that

with a constant $C$ independent of $\overline{t}$, M and $\varepsilon$. Now integrate (78) from $0$ to $t$, in view of (80) this results in the following pointwise inequality

for all $t \in(0, \overline{t})$. Also, Gronwall's inequality applied to (77) yields

We substitute the latter two bounds into (76) and consider the resulting inequality at $t=\overline{t}$. In view of (79) we have that $\|u(\, \cdot\, , \overline{t})\|_{L^2}\leq\|u(\, \cdot\, , \overline{t})\|_{H^1}$ and

where $C$ is independent of $\overline{t}$, M and $\varepsilon$. Thus, taking $M$ bigger than

e.g. $M:=2\overline{M}$, and considering sufficiently small $\varepsilon>0$ we see that $\|u(\, \cdot\, , \overline{t})\|_{L^2}^2<M$. This shows that $\|u(\, \cdot\, , \overline{t})\|_{L^2}^2<M$ on $[0, T]$, and the Theorem is proved.

Note that as a bi-product of the above proof we obtained the integral bound

which plays an important role in the following derivation of a reduced system for $V_\varepsilon$ and $Q_\varepsilon$.

The special form of the representation (65) (cf. (66)) together with estimates of Theorem 3 and (81) allow us to derive a system of the form (63)-(64) for $V_\varepsilon$ and $Q_\varepsilon$. To this end multiply (72) by $\theta_0^\prime(y)$ and integrate in $y$ over $\mathbb R$, this results in

where $A_\varepsilon$ is the solution of

with the initial condition $A_\varepsilon(y, 0)=p_\varepsilon(y)$($=Q_\varepsilon(y, 0)$) and

with $\tilde \xi_\varepsilon$ being a bounded function (as well as ${\xi}_\varepsilon$ and $\overline{\xi}_\varepsilon$). It follows from (69) that $\tilde{o}_\varepsilon$ uniformly converges to $0$ as $\varepsilon\to 0$ ($|\tilde{o}_\varepsilon|\leq C\varepsilon$ if $F$ is Lipschitz or $W^{\prime\prime}(0)=W^{\prime\prime}(1)$). Next we show that $\mathcal{O}_{\varepsilon}(t)$ is bounded in $L^{\infty}(0, T)$ uniformly in $\varepsilon$.

Proposition 2. Let conditions of Theorem 3 be satisfied, then $\mathcal{O}_{\varepsilon}(t)$ introduced in (84) is bounded uniformly in $t\in [0, T]$ and $\varepsilon$.

Proof. By Theorem 3 the first term in (84) is bounded. To estimate the remaining terms represent $Q_\varepsilon$ as $Q_\varepsilon=A_\varepsilon+B_\varepsilon$, where $B_\varepsilon$ solves

with zero initial condition. Multiply this equation by $B_\varepsilon$ and integrate on $\mathbb{R}$, then multiply (85) by $\partial^2_y B_\varepsilon$ and integrate on $\mathbb{R}$ to obtain

After integrating these inequalities from $0$ to $t$ we make use of (81) to derive $\|B_\varepsilon\|_{H^1}^2\leq C\varepsilon$. Also, Gronwall's inequality applied to (86) yields $\|B_\varepsilon\|_{L^2}^2\leq C\varepsilon^2$. Similarly, in order to bound $\|A_\varepsilon\|_{L^2}$ and $\|\partial_y A_\varepsilon\|_{L^2}$ we first get

then apply Gronwall's inequality to conclude that $\|A_\varepsilon\|_{H^1}^2\leq C$. Thus,

From now on $\tilde{\mathcal{O}}_\varepsilon$, $\tilde o_\varepsilon$ and ${\mathcal{O}}_\varepsilon$ are regarded as given functions in the reduced system (82)-(83), and their influence on the behavior of the system is small. Observe that taking the formal limit as $\varepsilon \to 0$ in the system (82)-(83) leads to (61). Indeed, the formal limit as $\varepsilon\to 0$ in (83) is nothing but (30) whose unique solution is $\psi(y;V(t))$. Then substituting this function into the limit of (82) yields (61).

4.3.   Sharp interface limit for small $\beta$ by contraction mapping principle

The following Theorem establishes the sharp interface limit for sufficiently small $\beta$. We assume that initial data $P_\varepsilon(\varepsilon y, 0)=A_\varepsilon(y, 0)$ are bounded in $L^2(\mathbb{R})$ by a constant $C$ independent of $\varepsilon$:

Theorem 4. (Sharp Interface Limit for subcritical $\beta$) Let $A_{\varepsilon}$, $V_{\varepsilon}$ be solution of the reduced system (82)-(83) with $\tilde{\mathcal{O}_{\varepsilon}}, \mathcal{O}_{\varepsilon}\in L^{\infty}(0, T)$ and $\tilde o_\varepsilon$ converging to $0$ in $L^\infty(0, T)$ as $\varepsilon\to 0$. Assume also that (87) holds. Then there exists $\beta_0>0$ (e.g., $\forall$ $0< \beta_0<2/\max\{\|(\theta_0^\prime)^2\|_{L^2}, \sqrt{c_0}\}$) such that for $0\leq\beta<\beta_0$

where $V_0$ is the unique solution of (61).

Proof. Step 1. (Study of the boundary layer at $t=0$). We show that the function $\eta_{\varepsilon}(y, t)=A_\varepsilon(y, t)-\psi(y, V_0(0) )$ behaves as a boundary layer at $t=0$. Since $\psi$ satisfies $\partial_y^2\psi+V_0(0)\partial_y\psi-\psi=\beta\theta_0^\prime$, $c_0V_0(0)=\int (\theta_0')^2 \psi dy-F(0)$ and $A_\varepsilon$, $V_\varepsilon$ solve (82)-83, we have

Multiply (89) by $\eta_\varepsilon$ and integrate on $\mathbb{R}$,

Note that $\|\partial_y \psi\|_{L^2}^2+\|\psi\|_{L^2}^2=-\beta\int\theta_0^\prime\psi dy$, therefore $\|\partial_y \psi\|_{L^2}^2\leq \beta^2\| \theta_0^\prime\|_{L^2}^2/4=\beta^2 c_0/4$. Thus, if $\beta \|(\theta^\prime)^2\|_{L^2}<2$, then for sufficiently small $\varepsilon$ and $0<t<\sqrt{\varepsilon}$ we have

with some $\omega>0$ independent of $\varepsilon$. Now apply Gronwall's inequality to (90) to obtain that

in particular,

Step 2. (Resetting of (82)-(83) as a fixed point problem). Consider an arbitrary $V\in L^\infty(\sqrt{\varepsilon}, T)$ and define $\mathcal{F}_{\varepsilon}:L^{\infty}(\sqrt{\varepsilon}, T)\mapsto L^{\infty}(\sqrt{\varepsilon}, T)$ by

where $A$ is the unique solution of

on $\mathbb{R}\times (\sqrt{\varepsilon}, T]$ and $\tilde{\eta}_\varepsilon$ solves

Note that thanks to (91),

It follows from the construction of $\mathcal{F}_\varepsilon$ that $V_\varepsilon$ is a fixed point of this mapping. Next we prove that, for sufficiently small $\beta$, $\mathcal{F}_\varepsilon$ is a contraction mapping. Consider $V_1, V_2\in L^{\infty}(\sqrt{\varepsilon}, T)$ and let $A_1$, $A_2$ be solutions of (93)-(94) with $V=V_1$ and $V=V_2$, respectively. The function $\bar{A}:=A_1-A_2$ solves the following problem

Multiplying equation (96) by $\bar{A}$ and integrating in $y$ we get

On the other hand every solution $A$ of (93)-(94), in particular $A_2$, satisfies

Indeed, multiplying (93) by $A$ and integrating in $y$ we get

which yields $\varepsilon\frac{d}{dt}\|A\|^2_{L^2}+\|A\|^2_{L^2}\leq c_0\beta^2$, the latter inequality in turn implies that $\|A\|^2_{L^2}\leq \|\psi\|^2_{L^2}e^{-t/\varepsilon}+\beta^2c_0(1-e^{-t/\varepsilon})$ for $t\in[\sqrt{\varepsilon}, T]$. Observing that $\|\psi\|_{L^2}^2\leq\beta^2c_0$, we are led to (99).

Substitute now (99) in (98) to conclude that

Thus, for $\beta<2/\sqrt{c_0}$, $\mathcal{F}_{\varepsilon}$ is a contraction mapping.

Step 3. Since $V_\varepsilon$ is a fixed point of the mapping $\mathcal{F}_{\varepsilon}$, we have

Thus,

It remains to prove that

Step 4. (Proof of (102)). First, we approximate $V_0(t)$, which can be a non-differentiable function, by a smooth function. Namely, construct $V_{0\varepsilon}(t)\in C^1[0, T]$, e.g., as a mollification of $V_0(t)$, such that

Let $A$ be the solution of (93)-(94) with $V=V_0(t)$. Consider $D_\varepsilon(y, t):=A(y, t)-\psi(y, V_{0\varepsilon}(t))$, it satisfies the following equality

on $\mathbb{R}\times (\sqrt{\varepsilon}, \infty)$. Since the right hand side of (104) converges to $0$ in $L^\infty([0, T], L^2(\mathbb{R}))$ and the norm of initial values $\|D_\varepsilon(y, \sqrt{\varepsilon})\|_{L^2}= \|\psi(y, V_0(0))-\psi(y, V_{0\varepsilon}(\sqrt{\varepsilon}))\|_{L^2}\to 0$ as $\varepsilon\to 0$, we have

Finally, since $\int (\theta_0^\prime)^2\psi(y, V_{0\varepsilon})dy=c_0V_0+F(t)+O(|V_{0\varepsilon}-V_0|)$ we see that

Then combining (95), (103) and (105) we establish (102), and the Theorem is proved.

4.4.   Sharp interface limit for arbitrary $\beta$ via stability analysis

4.4.1.   Reduction to a stability problem

For larger $\beta$ the contraction principle no longer applies and both analysis and the results become more complex. Here the stability analysis of the semigroup generated by a non-local non self-adjoint operator is used in place of the contraction mapping principle.

In the case where $\beta$ is not small, solutions of (61) are no longer unique, see Fig. 3. However, the original PDE problem (57)-(58) (as well as the reduced system (82)-(83) has the unique solution. This indicates that analysis for large $\beta$ must be complemented by a criterion of how to select the limiting solution of equation (61) among all solutions of this equation.

As a first step, we neglect terms $\varepsilon\tilde{\mathcal{O}}_{\varepsilon}(t)$, $\varepsilon\mathcal{O}_{\varepsilon}(t)$ and $\tilde o_\varepsilon(t)$ in the reduced system (82)-(83) and study the system

(in (106)-(107), $f_\varepsilon$ replaces $A_\varepsilon$ from (82)-(83)). Substitute (106) into (107) to rewrite the (106)-(107) as a single equation

In the limit $\varepsilon\to 0$ this equation (formally) leads to the PDE

Taking the formal limit is justified below for passing from (108) to (109).

Remark 6. Equation (108) is a singular perturbation of (109) and both equations are non-autonomous. It is well-known that singular limit problems, including non-autonomous equations, can be reduced to the analysis of large time behavior of autonomous equations. To illustrate this, recall a standard example of an ODE with a small parameter $\varepsilon$ from [20],

Assume that there exists the unique root $\phi(t)$ of $\mathcal{F}$, i.e., $0=\mathcal{F}(\phi(t), t), \;t\in[0, T]$. Then the singular limit $\phi(t)=\lim\limits_{\varepsilon\to 0}z_{\varepsilon}(t)$ holds provided that $\phi(t)$ is a stable root, i.e., all solutions $u(\tau)$ of an autonomous problem $\frac{du(\tau)}{d\tau}=\mathcal{F}(u(\tau), t)$ ($t$ is fixed) converge to the large time limit $\phi(t)$: $\mathop {\lim }\limits_{\tau \to \infty } u(\tau ) = \phi (t).$ Note that the problem (110) has two time scales: a slow time $t$ and a fast time $\tau$. Also the large-time limit corresponds to $\tau \to \infty$ for a fixed parameter $t$.

Note that the equivalence of singular and large-time limits is straightforward for the singularly perturbed autonomous problems ($\mathcal{F}$ does not depend on $t$ in (110)). In this case, the simple rescaling

reduces the singular limit problem to a problem of stability of steady state.

To justify the transition from (108) to (109) we introduce three time scales: slow, fast, and intermediate. More precisely, we employ the following three step procedure: (Ⅰ) partition the interval $[0, T]$ by segments of length $\sqrt{\varepsilon}$ on which the equation (108) is "almost" autonomous ($F(t)$ is "almost" constant on each of these intervals); (Ⅱ) on the first interval $(0, \sqrt{\varepsilon})$, by appropriate scaling $\tau=t/\varepsilon$ and stability analysis find large-time asymptotics $\tau\to\infty$ (here we used equivalence of singular and large-time limits for autonomous equations); (Ⅲ) use the asymptotics found in (Ⅱ) as initial conditions for the next interval $(\sqrt{\varepsilon}, 2\sqrt{\varepsilon})$, repeat step (Ⅱ) on this interval, and continue to obtain global asymptotics on $[0, T]$. A crucial ingredient here is an exponential stability of the linearized problem which prevents accumulating of errors (see bound (124) in Lemma 2).

4.4.2.   Spectral analysis of the linearized operator

Rescale the "fast" time $\tau=t/\varepsilon$ in the unknown $f_\varepsilon$ in (108) and "freeze" time $t$ in $F(t)$ (as described in step (Ⅱ) above)

here $t\in[0, T]$ is considered to be a fixed parameter. Steady states of (111) are solutions of (109). Let $f_0$ be such a solution, we define its velocity by

then $f_0(y)=\psi(y, V_0)$, where $\psi(y;V)$ is defined in (30). Linearizing equation (111) around $f_{0}$ we obtain

where $\mathcal{T}(V):L^2(\mathbb R)\mapsto L^2(\mathbb R)$ is a linear operator parameterized by $V\in \mathbb{R}$ and given by

Operator $\mathcal{T}(V)$ is a perturbation of a local operator $\mathcal{A}(V) f:= -\partial_y^2 f -V \partial_y f + f$ by a non-local rank one operator $\mathcal{P}(V)f= -\partial_y\psi(y, V)\frac{1}{c_0}(f, (\theta_0^\prime)^2)_{L^2}$, where $(\, \cdot\, , \, \cdot\, )_{L^2}$ stands for the standard inner product in $L^2(\mathbb{R})$. The spectrum $\sigma(\mathcal{A}(V))$ of operator $\mathcal{A}(V)$ is described by the following straightforward proposition.

Proposition 3. The spectrum $\sigma(\mathcal{A}(V))$ consists only of its essential part:

The spectrum $\sigma(\mathcal{T}(V))$ of $\mathcal{T}(V)$ is described in

Theorem 5. (On spectrum of the linearized operator) Consider the part $\sigma_p(\mathcal{T}(V))$ of the spectrum $\sigma(\mathcal{T}(V))$ laying in $\mathbb C\backslash \sigma_{\text{ess}}(\mathcal{A})$. Then $\sigma_p(\mathcal{T}(V))$ is given by

Moreover, all $\lambda$ from $\sigma_{\text{p}}(\mathcal{T}(V))$ are eigenvalues with finite algebraic multiplicities, and geometric multiplicity one.

Proof. We suppress dependence of $\mathcal{A}, \mathcal{T}$, and $\eta$ on $V$ for brevity. Consider $\lambda \notin \sigma_{\text{ess}}(\mathcal{A}) \cup\sigma_p(\mathcal{T})$ and $g\in L^2(\mathbb R)$. There exists the solution $f$ of

which can be represented as

Eliminate $(f, (\theta_0^\prime )^2)_{L^2}$ from the latter equation to find that

Thus, if $\lambda\notin\left\{\lambda\in \mathbb{C}; ((\mathcal{A}-\lambda)^{-1}\partial_y\psi, (\theta_0^\prime )^2)_{L^2}= c_0 \right\}\cup \sigma_{\text{ess}}(\mathcal{A})$, then $\lambda$ belongs to the resolvent set of $\mathcal{T}$.

Now suppose that $\lambda\in \sigma_p(\mathcal{T}(V))$. Then $((\mathcal{A}-\lambda)^{-1}\partial_y\psi, (\theta_0^\prime )^2)_{L^2}= c_0$ and by Fredholm's theorem applied to (115), $\lambda$ is an eigenvalue of finite multiplicity. Let $f$ be a corresponding eigenfunction, then by (115) we have

Take the scalar product of this equality with $(\theta_0^\prime)^2$ to conclude that $\lambda \in \sigma_p(\mathcal{T})$ if and only if

and $(\mathcal{A}-\lambda)^{-1} \partial_y\psi$ is the unique (up to multiplication by a constant) eigenfunction.

Thus, Theorem 5 reduces the study of the part of the spectrum $\sigma_p(\mathcal{T})=\sigma(\mathcal{T})\setminus \sigma_{\text{ess}}(\mathcal{A})$ of operator $\mathcal{T}(V)$ to the equation (116). Next, using the obtained characterization of the $\sigma_p(\mathcal{T})$ we study the stability of $\mathcal{T}$.

Proposition 4. If $\Phi^\prime_\beta(V)\geq c_0$, then there exists a real non positive eigenvalue $\lambda\in \sigma_p(\mathcal{T}(V))$.

Proof. Consider the function $\zeta(\lambda):= \left((\mathcal{A}(V)-\lambda)^{-1}\partial_y\psi, (\theta_0')^2\right)_{L^2}$ for real $\lambda\in (-\infty, 0]$. We claim that $\zeta(0)=\Phi^\prime(V)$. Indeed, differentiate (30) to find that

where $\psi_{V}$ denotes the partial derivative of $\psi$ in $V$. Thus

On the other hand it is easy to see that $\zeta(\lambda)\to 0$ as $\lambda\to-\infty$, consequently $\zeta(\lambda)=c_0$ for some $\lambda\in (-\infty, 0]$. By Theorem 5 this $\lambda$ is a non positive eigenvalue of $\mathcal{T}(V)$.

Def 1. Define the set of stable velocities $\mathcal{S}$ by

where $\mathcal{T}(V)$ is the linearized operator given by (114).

Remark 7. In the case of 2D sytem (1)-(3) one can expect (yet to be proved) that there exist standing wave solutions with circular symmetry when $\Omega$ is a disk. However our preliminary reasonings show that these solutions are not stable if $\Phi_\beta^\prime(0)>c_0$ (this latter inequality holds for asymmetric potentials $W(\rho)$ and sufficiently large $\beta$). This conjecture originates from the fact that zero velocity and its small perturbations does not belong to the set of stable velocities as shown in Proposition 4.

Proposition 4 implies that the inequality

is a necessary condition for stability of $V$. We hypothesize that (118) is also a sufficient condition, and therefore (118) describes the set $\mathcal{S}$, that is,

To support our hypothesis we consider $W(\rho)=\frac14\rho^2(\rho-1)^2$. In this case, the set $\left\{V\in\mathbb R: \;\Phi'_\beta(V)< c_0\right\}$ is the complement to the open interval $(V_{\text{min}}, V_{\text{max}})$, where $V_{\text{min}}$ and $V_{\text{max}}$ are the local maximum and minimum, respectively (see Fig. 3 and the sketch of $c_0V-\Phi_\beta(V)$ in Fig. 4). Numerical simulations clearly show that (119) holds. We can also rigorously prove that there exist such $V_1$ and $V_2$ that the set of stable velocities $\mathcal{S}$ is non-empty and, moreover, contains the compliment to the open interval $(V_1, V_2)$. This is done by means of Fourier analysis which allows us to rewrite (116) as an integral equation for a complex number $\lambda$. Details are relegated to Appendix B.

4.4.3.   Main result for 1D interface limit

In this subsection we formulate the main result on the 1D sharp interface limit in the system (57)-(58) for arbitrary $\beta>0$. Introduce the following conditions:

(C1) Let $V_0 \in \mathcal{S}$ solve $c_0V_0- \Phi_\beta(V_0)=F(0)$ and let $[0, T_\star]$ be a time interval such that there exists $V(t)\in \mathcal{S}$ a continuous solution of

(C2) Assume that $P_{\varepsilon}(x, 0)=p_{\varepsilon}(x/\varepsilon)$ and $\|p_\varepsilon(\, \cdot\, )-\psi(\, \cdot\, , V_0)\|_{L^2}< \delta$ with a small constant $\delta>0$ independent of $\varepsilon$ (the function $\psi=\psi(y;V_0)$ is defined by (30)).

Theorem 6. (Sharp Interface Limit for all $\beta$) Let $x_{\varepsilon}$ be as in Theorem 3 and assume that conditions (C1) and (C2) hold along with the conditions of Theorem 3. Then $x_{\varepsilon}(t)$ converges to $x_0(t)$ in $C^1[0, T_\star]$, where $V(t):= \dot{x}_{0}(t)$ is the solution of (120) as defined in (C1).

Theorem 6 justifies the sharp interface equation (120) for any $\beta$. Its proof consists of two steps: (ⅰ) reduction to a single equation (nonlinear, singularly perturbed) which is done in Section 4.2 and (ⅱ) passage to the limit in this equation based on stability analysis presented below, which is the main ingredient of the proof.

Remark 8. Condition (C2) is crucial to determine the solution branch in the case if $V_0$ is not a unique solution of (120).

Proof of Theorem 6. Rewrite (82)-(83) in the form of the single PDE

Recall that $\tilde{\mathcal{O}}_{\varepsilon}(t)$ and ${\mathcal{O}}_{\varepsilon}(t)$ are uniformly bounded functions, $\tilde {o}_\varepsilon(t)$ tends to $0$ uniformly on $[0, T_{\ast}]$ as $\varepsilon\to 0$. We next pass to the limit in equation (121) using exponential stability (established in (127)) of the semigroup corresponding to the linearized operator. The following local stability result plays the crucial role in the proof.

Lemma 2. There exist $\omega>0$ and $\delta>0$ such that if

then for any $0<r<1$ and sufficiently small $\varepsilon$, $\varepsilon<\varepsilon_0 (T_\ast)$, the function $\eta_\varepsilon(y, t, \tau)=A_{\varepsilon}(y, t+\varepsilon \tau)-\psi(y, V(t))$ satisfies

for $0\leq \tau \leq \frac{1}{\varepsilon^r}$. The constants $\omega, \delta$ and $C$ in are independent of $t$, $\tau$ and $\varepsilon$.

This Lemma shows that if the initial data are at distance at most $\delta$ from $\psi$ (in the $L^2$-norm), then the solution $A_\varepsilon(y, t+\varepsilon \tau)$ approaches $\psi$ exponentially fast in $\tau$ (first term in the RHS of (123)) with a deviation that is bounded from above independently of $t$ (described by the second and the third terms in the RHS of (123)). The conclusion of Theorem 6 immediately follows from this Lemma. Indeed, consider the time interval $(0, t_1)$, $t_1:=\sqrt{\varepsilon}$. Then by Lemma 2 we obtain

where $m$ denotes the modulus of continuity of $F$ on $[0, T_\star]$. Choose $\varepsilon$ small enough so that $\log\frac{1}{\varepsilon}\leq \frac{\omega}{2}\sqrt{\varepsilon}$ and the right hand side of (124) is bounded by $\delta$. Similarly, for intervals $(t_1, t_2)$, where $t_2:=2\sqrt{\varepsilon}$, $(t_2, t_3$, where $t_3:=3\sqrt{\varepsilon}$, etc., we obtain

To complete the proof of Theorem 6 we again use Lemma 2 to bound $\|A_{\varepsilon}(\, \cdot\, , t)-\psi(\, \cdot\, , V(t))\|^2_{L^2}$ for $t\in (t_i, t_{i+1})$, $i=1, 2\dots$.

Proof of Lemma 2. As in the first step of the proof of Theorem 4, consider the function $\eta_{\varepsilon}(y, \tau):=A_{\varepsilon}(y, t+\varepsilon\tau)-\psi(y, V(t))$, hereafter $t$ is considered as a fixed parameter. It follows from (121) and (30) that $\eta_{\varepsilon}$ satisfies the following PDE

where

Introduce the semigroup operator $e^{-\mathcal{T}\tau}, \tau>0$ in $L^2(\mathbb R)$, then by Duhamel's principle

where $R_\varepsilon (y, \tau)$ denotes the right hand side of (125).

In order to proceed with the proof of Lemma 2 we first prove exponential stability of the semigroup $e^{-\mathcal{T}t}$ and establish its consequences in the following

Lemma 3. There exists $\omega>0$ such that

(ⅰ) the following inequality holds

where $\|e^{-\mathcal{T}\tau}\|$ stands for the operator norm of $e^{-\mathcal{T}\tau}$ in $L^2(\mathbb R)$;

(ⅱ) for every $g(y, t)$,

with a constant $C$ independent of $g$.

Moreover, constants $\omega$, $M$ and $C$ can be chosen independently of $t$ (recall that $\mathcal{T}=\mathcal{T}(V(t))$ depends on $t$).

Proof of Lemma 3. Step 1. (proof of (ⅰ)). For every fixed $V\in \mathcal{S}$, it follows from Gerhardt-Prúss theorem (see, e.g., [16,31]) that (127) holds with some constants $M$ and $\omega>0$. However, for later use we need a stronger result, we prove that these constants can be chosen independently of $V=V(t)$ for $t\in[0, T_\ast]$. To this end we establish the following bound

with constants $\omega>0$, $\varphi_0>0$ and $C$ all independent of $t\in [0, T_\ast]$. Then Theorem I.7.7 from [30] yields the inequality $\|e^{-(\mathcal{T}(V(t))-\omega)\tau}\|\leq M$ for $\tau>0$ with constants $\omega>0$ and $M$ independent of $t$, and this latter inequality is equivalent to (127).

Set $\mathcal{T}^\prime(t, \omega):=\mathcal{T}(V(t))-\omega$ and $\mathcal{A}^\prime(t, \omega):=\mathcal{A}(V(t))-\omega$. To prove (129) we first derive by Fourier analysis,

where $\overline{\varphi}=\frac{1}{2}\arctan \frac{1}{\max_t |V(t)|}$, constant $C$ is independent of both $t\in [0, T_\ast]$ and $0\leq\omega<1/2$. Next we make use of the representation (cf. Theorem 5)

where $\mu(\lambda;t, \omega)=c_0- \left((\mathcal{A}^\prime(t, \omega)-\lambda)^{-1}\partial_y \psi, (\theta_0^\prime)^2\right)_{L^2}$.

It follows from (130) that the family of holomorphic functions $\mu(\cdot;t, \omega):\Pi_{\overline{\varphi}}\to \mathbb C$ satisfies $|\mu|>1/2$ everywhere but on a fixed bounded subset $K$ of $\Pi_{\overline{\varphi}}$ which is independent of $0\leq \omega\leq 1/2$ and $t\in [0, T_{\ast}]$. On the other hand the functions $\mu(\lambda;t, \omega)$ are uniformly bounded in $\{\lambda\in\mathbb{C};\, {\rm Re} \lambda<1/4\}$ and they depend continuously on $t$ and $\omega$. Now taking into account the fact that $V(t)\in \mathcal{S}$ for all $t\in [0, T_{\ast}]$ we show that $|\mu(\lambda;t, 0)|\geq \mu_0$ when $\lambda \in K$ and $|\text{Re}\lambda|\leq 2\omega$ for some $1/2\geq\mu_0>0$ and $1/2\geq \omega>0$. Indeed, otherwise there is a sequence $t_k\to t_0$, $\lambda_k\to \lambda_0$ such that $\text{Re}\lambda_0=0$ and $\mu(\lambda_k;t_k, 0)\to 0$. Then, by Montel's theorem, up to extracting a subsequence $\mu(\lambda_k;t_k, 0)\to\mu(\lambda_0;t_0, 0)$, but $\mu(\lambda_0;t_0, 0)\neq 0$ as $V(t_0)\in \mathcal{S}$ (cf. proof of Theorem 5). Thus there are $\varphi_0>0$ ($\varphi_0\leq\overline{\varphi}$) such that $|\mu(\lambda;t, \omega)|\geq \mu_0$ for $\lambda\in \Pi_{\varphi_0}$. Using this fact and inequality (130) to bound terms in in (131) we get (129), and therefore (127) holds for some $\omega>0$ and $M$, both being independent of $t$. This result immediately yields (128) for $k=0$.

Step 2. (proof of (ⅱ)). To prove (128) for $k=1$ consider first $\tau\geq 1$ and show that

The idea here is to establish a short time parabolic regularization property. Consider $f:=e^{-\mathcal{T}s}\partial_y g$, it can be represented as $f=\partial_y v$ with $v$ solving

In a standard way, multiplying (133) by $v$ and integrating in $y$ we get

Then an application of Gronwall's inequality yields the uniform bound

Using this bound in (135) we derive

It follows that $\|\partial_y v(\, \cdot\, , s_0)\|_{L^2}\leq C_1\|g\|_{L^2}$ for some $0<s_0\leq 1$. Then by the semigroup property we have

where we have used (127). The bound (132) being established, we conclude with the estimate

To complete the proof of (128) consider

(if $\tau<1$, we set $g(y, \tau^\prime)\equiv 0$ for $\tau^\prime<0$).It follows from the definition of $\tilde{f}$ that $\tilde{f}(y)=\tilde{v}(1, y)$, where $v$ solves

Multiply equation (137) by $v$ and integrate in $y$ to obtain

Now apply Gonwall's inequality. As a result we get

Thus

Combining (139) with (136) completes the proof of Lemma 3.

Now we apply Lemma 3 to (126) to obtain the bound

for $0\leq\tau\leq 1/\varepsilon^r$ ($0<r<1$), where $C_\ast$ depends only on $F(t)$ and $T_{\ast}$ and $\delta_\varepsilon=C(\max_{s\in [t, t+\varepsilon \tau]}\left(|F(t)-F(s)|^2+\tilde o_\varepsilon^2(s)\right) +\varepsilon^2)$. Let $\alpha(\tau)$ be the right hand side of (140). Consider $s\in [0, \tau]$, by (140) we have

and $\alpha(0)=2M^2\|\eta_\varepsilon(\, \cdot\, , 0)\|_L^2$. Choosing an arbitrary $q$ from the interval

we see that the function $\overline{\alpha}(s):=q e^{-\omega s/2}+2\delta_\varepsilon(\tau)/\omega$ satisfies for sufficiently small $\varepsilon$ the differential inequality

Therefore, if $\alpha(0)\leq \overline{\alpha}(0)=q+2\delta_\varepsilon(\tau)/\omega$, then $\alpha(s)\leq \overline{\alpha}(s)$ $\forall$ $0\leq s \leq \tau$. Thus we have proved that

provided that $\|\eta_\varepsilon(\, \cdot\, , 0)\|_{L^2}\leq \delta$ with $0<\delta<\sqrt{q}/(\sqrt{2}M)$. This concludes the proof of Lemma 2 and Theorem 6.

4.5.   Numerical observations. Hysteresis loop

In view of the above analysis the equation(61) for large $\beta$ may have many solutions of quite complicated structure (e.g., discontinuous). Therefore, we need to introduce a criterion for selection of the "correct" solutions that are limiting solutions to the problem with $\varepsilon>0$. This is analogous, e.g. to viscosity solutions of Allen-Cahn when physical solutions are obtained (by regularization) in the sharp interface limit $\varepsilon\to 0$, [14].

We now introduce such a criterion based on numerical observations and suggested by the stability analysis depicted in Fig. 4. Define the left velocity interval $\mathcal{B}_{\text{L}}:=(-\infty, V_{\min}]$ and the right velocity interval $\mathcal{B}_{\text{R}}:=[V_{\max}, \infty)$ for stable velocities $V$.

Assume for simplicity of presentation that function $F(t)\in C[0, T]$ is strictly increasing. Then the solution of (61) is chosen based on the following two criteria

(Cr1) if $V(0)\in \mathcal{B}_L$, there is a unique $V(t)\in\mathcal{B}_L$ satisfying (61) for all $t\in[0, T]$. Note that this $V(t)$ is the only solution which is continuous and never enters the "forbidden" interval $[V_{\min}, V_{\max}]$

(Cr2) if $V(0)\in \mathcal{B}_R$, then for any $t\in[0, T]$ the solution $V(t)$ of (61) is chosen in the right velocity interval $\mathcal{B}_R$, unless it is impossible ($F(t)>F_{\min}$, where $F_{\min}$ is defined in Fig. 4). In the latter case $V(t)$ is chosen from the left velocity interval $\mathcal{B}_L$.

Intuitively, evolution of the sharp interface velocity can be described as follows. Consider for example the left part of Figure 4 left. As time evolves, the velocity increases along the right green branch until it reaches $V_{\max}$, then it jumps (along the horizontal red dashed line) to the solution of (61) on the left green branch, and continues increasing along this branch.

Finally, numerical simulations show that the criterion (Cr2) predicts hysteresis in the system (61). Consider two forcing terms corresponding to the right and the left parts of Fig. 4:

and $\beta=150$. For $t\in [0,1]$ both $F_{\downarrow}(t)$ and $F_{\uparrow} (t)$ have the same values but in the opposite order in time $t$. Fig. 5 (left) depicts the solution of equation (61) according to to the criteria (Cr1) and (Cr2). The red and blue branches coincide when $F~\notin~[F_{\min}, F_{\max}]$. Moreover, a surprising hysteresis loop is observed when $F\in [F_{\min}, F_{\max}]$.

We also performed numerical simulations for the original PDE system (57)-(58) for $\rho_{\varepsilon}(x, 0)=\theta_0(x/\varepsilon)$, $P_{\varepsilon}(x, 0)=\theta_0'(x/\varepsilon)$, $\varepsilon=0.01$, and defining $\varepsilon$-interface $x_{\varepsilon}(t)$ as a number such that $\rho_{\varepsilon}(x_{\varepsilon}(t), t)\approx 0.5 (\rho_{\varepsilon}(+\infty, t)+\rho_{\varepsilon}(-\infty, t))$. The branches corresponding to $F_\downarrow$ and $F_{\uparrow}$ are depicted in Fig. 5 (right). The same hysteresis is observed which justifies numerically the above criteria.

Appendix A. Auxiliary inequalities

It is well known (see, e.g., [28]) that under conditions (5) on the potential $W(\rho)$ the corresponding standing wave $\theta_0$ satisfies, for some $\alpha_0>1$,

where ${{\kappa }_{\pm }}=2\sqrt{{W}''((1\pm 1)/2)}$. In the case of the symmetric potential $W(\rho)=\frac14 \rho^2(\rho-1)^2$, $\kappa_-=\kappa_+$ and the standing wave $\theta_0$ is explicitly given by $\theta_0(y)=\frac{1}{2}(1+\tanh\frac{y}{2\sqrt{2}})$.

Theorem 7. (Poincaré inequality) The following inequality holds

where

Proof. Step 1. (Friedrich's inequality). Let $u\in C^1(\mathbb R)$ satisfy $u(0)=0$. Then we show that the inequality

holds with $C_F$ independent of $u$. Indeed,

Thus,

Dividing this inequality by $\left(\int_{0}^{\infty} (\theta_0^\prime)^2u^2 dy\right)^{1/2}$, and than taking square of both sides we get

Similarly we obtain

Then adding (145) to (145) yields (144).

Step 2. We prove the Poincaré inequality (142) by contradiction. Namely, assume that there exists a sequence $v_n\in C^1(\mathbb R)\cap L^{\infty}(\mathbb R)$ such that

Apply Friedrich's inequality (144) to functions $v_n(y)-v_n(0)$:

On the other hand,

Hence,

which contradicts the normalization $\int (\theta_0^\prime)^2 v_n^2 dy=1$. The Theorem is proved.

Corollary 1. Let $u\in H^1(\mathbb{R})$, then

with a constant $C$ independent of $u$.

Proof. Recall that standing waves $\theta_0$ of the Allen-Cahn equation along with (141) satisfy

for some $\alpha_1>0$. Then applying Theorem 7 to $v=u/\theta_0^\prime$ and using density of $C^1(\mathbb{R})$ in $H^1(\mathbb{R})$ one derives (147).

Appendix B. On spectral properties of operator $\mathcal{T}$ in the case $W(\rho)=\frac{1}{4}\rho^2(\rho-1)^2$

In this appendix we study the set of stable of velocities $\mathcal{S}$, i.e., the set of such $V\in \mathbb R$ that the point spectrum of the linearized operator $\mathcal{T}(V)$ defined by (114) lies in the right half of the complex plane. We restrict ourselves here to the case $W(\rho)=\frac14 \rho^2(\rho-1)^2$.

Theorem 5 implies that if $\text{Re}\lambda\leq 0$, then $\lambda$ solves the equation (116). Though (116) is a scalar equation with respect to $\lambda\in \mathbb C$, the evaluation of its left hand side requires solution of the PDE (30). By means of Fourier analysis, we can avoid solving the PDE and rewrite (116) in the form

where $\tilde{\theta_0'}$ and ${\widetilde{(\theta_0')^2}}$ are Fourier transforms of $\theta_0'$ and $(\theta_0')^2$, respectively. In the case $W(\rho)=\frac14 \rho^2(1-\rho)^2$:

Introduce $\chi(k):=-\frac{\beta\pi \sqrt{2}}{12} k^2 (2k^2+1)\text{csch}^2 (\sqrt{2}\pi k)$, then equation (148) becomes

Next, consider $\lambda=\lambda_r+i\lambda_i$. Denote by $\mathcal{H}_\lambda(k)$ the integrand in (150) and rewrite it in the form

where $\mu=1-\lambda_r$.

Proposition 5. (ⅰ) Assume $V<\sqrt{2}$. If $\Phi'_\beta(V)<c_0$, then all eigenvalues $\lambda \in \sigma_p(\mathcal{T}(V))$ have positive real part, $\text{Re}\lambda>0$.

(ⅱ) There exists $\bar{V}>0$ such that for all $V>\bar{V}$ all eigenvalues of $\mathcal{T}(V)$ have positive real part.

Remark 9. Condition $V<\sqrt{2}$ is a technical assumption in the proof which guarantees that integral (153) is negative. However, numerical simulations show that integral (153) is negative for all $V$.

Proof. Part (ⅰ). First, assume $0<|V|<\sqrt{2}$. We prove that if $\lambda=\lambda_r+i\lambda_i$ with $\lambda_r<1$ ($\mu>0$) is a root of equation $\zeta(\lambda)=1$, then $\lambda_i=0$. In particular, the condition $\lambda_r<1$ guarantees that $\lambda\notin \sigma_{\text{ess}}(\mathcal{A}(V))$.

Rewrite the imaginary part of $\zeta(\lambda_r+i\lambda_i)$:

Since the numerator is the difference between $(V^2-2)k^2$ and a positive expression, we obtain $\text{Im}\zeta(\lambda)\neq 0$ for $\lambda_i \neq 0$.

Take $\lambda_i=0$ and rewrite the real part of $\zeta(1-\mu)$:

The function $\text{Re}\zeta(1-\mu)$ is obviously monotone for $\mu>0$. Indeed, denote by $\Psi_k(\mu)$ the term of integrand in (151) which depends on $\mu$:

Compute $\Psi'_k(\mu)$:

If $|V|<\sqrt{2}$, then $\Psi'_{k}(\mu)<0$, which proves the monotonicity of $\text{Re}\zeta(1-\mu)$.

Finally, assume by contradiction that $\beta c_0^{-1}\Phi(V)<1$, but there exists an eigenvalue $\lambda_0$ with zero or negative real part, $\text{Re}\lambda_0\leq 0$. Then $\zeta(\text{Re}\lambda_0)=\zeta(\lambda_0)\leq\zeta(0)<1$ that contradicts $\zeta(\lambda)=1$.

Consider $V\leq 0$. Then $\text{Re}\zeta(\lambda_0)\leq 0$. Indeed, observe that $\text{Re}\zeta(\lambda_0)$ equals to

The integral in (153) is negative or zero and, thus, cannot be equal to $1$, so equality (116) does not hold and, in particular, there does not exist eigenvalues with negative real part. Thus, part (ⅰ) is proved.

Part (ⅱ) follows immediately from (153).

Appendix C. The original model from [40]

In this appendix we present the original phase-field model for the motion of a keratocyte cell on a substrait introduced in [40]. It consists ofequations for the phase-field $\rho$ and the orientation vector $P$:

Coefficients $D_{\rho}$ and $D_{P}$ describe diffusion of $\rho$ and $P$; $\alpha$ and $\beta$ are the actin protrusion and polymerization strengths; $\tau_1$ and $\tau_2$ are decay rates for $P$ (depolymerization) inside and outside the cell; $\gamma$ is the strength of myosin motors. The second term in the right hand side of (154) is defined as follows $W'(\rho) = \rho(\delta-\rho)(1-\rho)$ where

Here $\mu$ is stiffness of the volume constraint, $V_0$ is the initial area of cell, and $\sigma$ describes contraction due to actin bundles. In this model, the area penalization is introduced via parameter $\delta$ in the double well potential $W(\rho)$ as in the well-known Belousov-Zhabotinskii model [10,24]. A dimensionless parameter $\sigma$ describes contractility due to bundles; in [40] this parameter ranges from 0 to 0.7 (see Table 1 in [40]). For the sake of simplicity in this work we considered the case $\sigma=0$ only.

Acknowledgments

The authors are grateful to I. Aronson and F. Ziebert for useful discussions on the phase field model of cell motility introduced in their paper. The authors wish to thank M. Mizuhara who assisted in the proof-reading of the manuscript.