New wave behaviors and stability analysis for magnetohydrodynamic flows

Shengfang Yang; Huanhe Dong; Mingshuo Liu; Shengfang Yang; Huanhe Dong; Mingshuo Liu

doi:10.3934/nhm.2024040

Networks and Heterogeneous Media

2024, Volume 19, Issue 2: 887-922. doi: 10.3934/nhm.2024040

Previous Article Next Article

Research article Special Issues

New wave behaviors and stability analysis for magnetohydrodynamic flows

College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China

Received: 30 July 2024 Revised: 21 August 2024 Accepted: 29 August 2024 Published: 04 September 2024

The Lie symmetry analysis and generalized Riccati equation expansion methods were performed on the inviscid and viscous incompressible magnetohydrodynamic equations. Using the Lie symmetry analysis method, symmetries and similarity reductions of (2 + 1)- and (3 + 1)-dimensional magnetohydrodynamic equations were derived. Different forms of trigonometric function solutions and rational solutions were obtained, which yielded periodic solutions, single soliton solutions, and lump solutions. Furthermore, using the generalized Riccati equation expansion method, we obtained abundant new solutions of magnetohydrodynamic equations, including kink, kink-like, breather, and interaction solutions. Moreover, the stability of magnetohydrodynamic equations was investigated from both qualitative and quantitative perspectives. The exact solutions and stability analysis could provide accurate mathematical descriptions and theoretical basis for numerical analysis and regulation of magnetohydrodynamic systems.

Keywords:

Citation: Shengfang Yang, Huanhe Dong, Mingshuo Liu. New wave behaviors and stability analysis for magnetohydrodynamic flows[J]. Networks and Heterogeneous Media, 2024, 19(2): 887-922. doi: 10.3934/nhm.2024040

Related Papers:

[1]	Jinyi Sun, Weining Wang, Dandan Zhao . Global existence of 3D rotating magnetohydrodynamic equations arising from Earth's fluid core. Networks and Heterogeneous Media, 2025, 20(1): 35-51. doi: 10.3934/nhm.2025003
[2]	Tong Li . Qualitative analysis of some PDE models of traffic flow. Networks and Heterogeneous Media, 2013, 8(3): 773-781. doi: 10.3934/nhm.2013.8.773
[3]	Georges Bastin, Jean-Michel Coron, Brigitte d'Andréa-Novel . On Lyapunov stability of linearised Saint-Venant equations for a sloping channel. Networks and Heterogeneous Media, 2009, 4(2): 177-187. doi: 10.3934/nhm.2009.4.177
[4]	Zhongyi Huang . Tailored finite point method for the interface problem. Networks and Heterogeneous Media, 2009, 4(1): 91-106. doi: 10.3934/nhm.2009.4.91
[5]	Seung-Yeal Ha, Hansol Park, Yinglong Zhang . Nonlinear stability of stationary solutions to the Kuramoto-Sakaguchi equation with frustration. Networks and Heterogeneous Media, 2020, 15(3): 427-461. doi: 10.3934/nhm.2020026
[6]	Leonid Berlyand, Mykhailo Potomkin, Volodymyr Rybalko . Sharp interface limit in a phase field model of cell motility. Networks and Heterogeneous Media, 2017, 12(4): 551-590. doi: 10.3934/nhm.2017023
[7]	Yacine Chitour, Guilherme Mazanti, Mario Sigalotti . Stability of non-autonomous difference equations with applications to transport and wave propagation on networks. Networks and Heterogeneous Media, 2016, 11(4): 563-601. doi: 10.3934/nhm.2016010
[8]	Farman Ali Shah, Kamran, Dania Santina, Nabil Mlaiki, Salma Aljawi . Application of a hybrid pseudospectral method to a new two-dimensional multi-term mixed sub-diffusion and wave-diffusion equation of fractional order. Networks and Heterogeneous Media, 2024, 19(1): 44-85. doi: 10.3934/nhm.2024003
[9]	Ken-Ichi Nakamura, Toshiko Ogiwara . Periodically growing solutions in a class of strongly monotone semiflows. Networks and Heterogeneous Media, 2012, 7(4): 881-891. doi: 10.3934/nhm.2012.7.881
[10]	Michael Herty, Lorenzo Pareschi, Mohammed Seaïd . Enskog-like discrete velocity models for vehicular traffic flow. Networks and Heterogeneous Media, 2007, 2(3): 481-496. doi: 10.3934/nhm.2007.2.481

Abstract

1. Introduction

Magnetohydrodynamic (MHD) equations are composed of Euler (or Navier-Stokes) equations and Maxwells equations, which are mainly used to describe the complex interactions between conductive fluids and electromagnetic fields. They are widely applied in plasma ^[1], astrophysical research ^[2,3], controlled thermonuclear fusion ^[4], and new industrial technologies ^[5]. The study of exact solutions for magnetohydrodynamics systems can provide possible ideas for finding the global smooth solutions of the Navier-Stokes equation. However, compared with the Navier-Stokes equation, MHD equations contain additional nonlinear and coupling terms for velocity and magnetic fields, which makes their research more challenging.

The qualitative stability analysis of MHD systems has been widely studied. Qin et al. ^[6] investigated the exponential stability of the global solution of (1 + 1)-dimensional compressible MHD equations. Suo et al. ^[7] studied the well-posedness of (2 + 1)-dimensional incompressible MHD equations with horizontal dissipation. Wang et al. ^[8] proved the stability of the global weak solution of (3 + 1)-dimensional incompressible MHD equations when the norms of the initial data are bounded by the minimal value of the viscosity coefficients. Li et al. ^[9] studied the convergence stability of local solutions for (3 + 1)-dimensional compressible viscous MHD equations. Xu et al. ^[10] studied the stability of local solutions to (3 + 1)-dimensional barotropic compressible MHD equations with vacuum. In the quantitative analysis, the complex nonlinearity and strong coupling of MHD equations make it difficult to seek the analytical solutions by some classical methods, such as the bilinear method ^[11], Darboux transformation method ^[12,13], Backlund transformation method ^[14], Lie symmetry analysis method ^[15,16,17], non-local symmetry analysis method ^[18,19], and Riemann-Hilbert method ^[20,21]. The quantitative calculations on MHD equations mainly focused on constructing specific forms of exact solutions or numerical solutions. Nevertheless, analytical solutions can provide an accurate mathematical description and theoretical basis for analysis and regulation of MHD systems, which has aroused widespread research interest. Donato et al. ^[22] studied exact solutions of (1 + 1)-dimensional MHD equations by Lie group analysis. Dorodnitsyn et al. ^[23] explored symmetries of plane one-dimensional MHD flows in the mass Lagrangian coordinates. Liu et al. ^[24] derived exact solutions of (2 + 1)-dimensional incompressible and barotropic MHD equations by Lie symmetry analysis. Xia et al. ^[25] studied group invariant solutions of (2 + 1)-dimensional incompressible ideal MHD equations by Lie symmetry method. Picard et al. ^[26] obtained some exact solutions of (3 + 1)-dimensional ideal MHD equations based on Lie group theory. Considering the physical significance of MHD equations and importance of analytical calculation, more diverse forms of exact solutions of MHD equations deserve to be further studied.

As powerful tools for solving nonlinear equations, symmetry analysis ^{[15,16,17,18,19]} and the simplest equation methods ^[27] demonstrate special advantages in handling nonlinear terms in dynamical systems. For instance, Zhao et al. ^[15] studied the Heisenberg equation from the perspective of statistical physics by Lie symmetry analysis. Ali et al. ^[16] obtained new exact invariant solutions of (3 + 1)-dimensional variable coefficients Kudryashov-Sinelshchikov equation by Lie symmetry analysis. Adeyemo et al. ^[17] explored closed-form solutions of integrable (2 + 1)-dimensional Boussinesq equation by Lie symmetry reductions. Ren et al. ^[18] derived interaction solutions of modified Kadomtsev-Petviashvili equation by nonlocal symmetry reductions. Vitanov et al. ^[27] investigated the role of the simplest equations in obtaining exact and approximate solutions of nonlinear partial differential equations. The Lie symmetry analysis method simplifies problems by finding the invariance of differential equations, and transforms the original equations into a more easily solvable form through symmetry transformations. This method provides powerful tools for solving nonlinear problems with complex structures. The generalized Riccati equation is an important auxiliary equation with rich special solutions. This makes the generalized Riccati equation mapping method an effective direct method for constructing the solitary wave solutions, the periodic solutions and the rational solutions for MHD equations. In this paper, using the Lie symmetry analysis method and generalized Riccati equation expansion method, we obtain new solutions with various forms of MHD equations. The major contributions of this article are listed as follows:

(1) Based on symmetry analysis and generalized Riccati equation expansion methods, the complex nonlinear and strongly coupled terms in MHD equations are technically handled. Different forms of new solutions are derived, which can describe various wave behaviors for MHD flows. Some of the solutions can be reduced to exact solutions for Euler or Navier-Stokes equations when magnetic fields vanish, which may provide references for the research on global solutions for Navier-Stokes equations.

(2) The stability of solutions for MHD equations is analyzed from both qualitative and quantitative perspectives based on the obtained solutions.

(3) The new solutions, wave behaviors, and stability analysis provide accurate mathematical descriptions and theoretical basis for numerical analysis and regulation of MHD systems.

The rest of the paper is organized as follows: The transformations for MHD equations are given in Section 2. In Section 3, the exact solutions of inviscid and viscous (2 + 1)-dimensional MHD equations are obtained by the Lie symmetry analysis method and generalized Riccati equation expansion method. In Section 4, inviscid and viscous (3 + 1)-dimensional MHD equations are further studied. In Section 5, the stability of MHD equations is studied from qualitative and quantitative perspectives. Finally, some conclusions are drawn in Section 6.

2. Preliminaries

The flow of conducting fluid in a magnetic field is governed by the following incompressible MHD equations ^[28], which are a combination of Euler (or Navier-Stokes) equations of fluid dynamics and Maxwell's equations of electromagnetism. The set of equations express the conservation of mass, momentum and the interaction of the flow with the magnetic field. Consider (2 + 1)- and (3 + 1)-dimensional incompressible MHD equations ^[28]

$\begin{equation} \left\{ \begin{aligned} & {{\mathbf{U}}_{t}}-\nu \Delta \mathbf{U}+(\mathbf{U}\cdot \nabla )\mathbf{U}+\nabla p+\kappa \mathbf{B}\times \operatorname{curl}\mathbf{B} = \mathbf{0}, \\ & {{\mathbf{B}}_{t}}+\eta \operatorname{curlcurl}\mathbf{B}-\operatorname{curl}(\mathbf{U}\times \mathbf{B})+\nabla r = \mathbf{0}, \\ & \operatorname{div}\mathbf{U} = 0, \ \operatorname{div}\mathbf{B} = 0, \end{aligned} \right. \end{equation}$

(2.1)

where $\mathbf{U}$ is fluid velocity, $p$ is hydrodynamic pressure, $\mathbf{B}$ is magnetic induction, $r$ is magnetic pressure. The physical parameters $\nu$ , $\mu$ and $\sigma$ represent kinematic viscosity, magnetic permeability and electric conductivity, respectively. $\eta = \frac{1}{\mu \sigma }$ , $\kappa = \frac{1}{\mu }$ . Substituting equations

$\begin{aligned} &\mathbf{B}\times \operatorname{curl}\mathbf{B} = \frac{1}{2}\nabla (\vert\mathbf{B}{{\vert}^{2}})-(\mathbf{B}\cdot \nabla )\mathbf{B} , \ \operatorname{curlcurl}\mathbf{B} = -\Delta \mathbf{B}, \\ &\operatorname{curl}(\mathbf{U}\times \mathbf{B}) = (\mathbf{B}\cdot \nabla )\mathbf{U}-(\mathbf{U}\cdot \nabla )\mathbf{B}, \end{aligned}$

into (2.1), the incompressible MHD equations (2.1) can be rewritten as

$\begin{equation} \left\{ \begin{aligned} & {{\mathbf{U}}_{t}}-\nu \Delta \mathbf{U}+(\mathbf{U}\cdot \nabla )\mathbf{U}+\nabla p+\kappa [\frac{1}{2}\nabla (\vert\mathbf{B}{{\vert}^{2}})-(\mathbf{B}\cdot \nabla )\mathbf{B}] = \mathbf{0}, \\ & {{\mathbf{B}}_{t}}-\eta \Delta \mathbf{B}-(\mathbf{B}\cdot \nabla )\mathbf{U}+(\mathbf{U}\cdot \nabla )\mathbf{B}+\nabla r = \mathbf{0}, \\ & \operatorname{div}\mathbf{U} = 0, \ \operatorname{div}\mathbf{B} = 0. \\ \end{aligned} \right. \end{equation}$

(2.2)

3. New wave behaviors of $(2 + 1)$ -dimensional MHD flows

Denote $\mathbf{x} = (x, y)$ , $\mathbf{U} = ({{u}_{1}}(t, \mathbf{x}), {{u}_{2}}(t, \mathbf{x}))$ , $\mathbf{B} = ({{b}_{1}}(t, \mathbf{x}), {{b}_{2}}(t, \mathbf{x}))$ in (2.2). (2 + 1)-dimensional MHD equations can be given as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}-\nu ({{u}_{1xx}}+{{u}_{1yy}})+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}})+\kappa ({{b}_{2}}{{b}_{2x}}-{{b}_{2}}{{b}_{1y}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}-\nu ({{u}_{2xx}}+{{u}_{2yy}})+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}})+\kappa ({{b}_{1}}{{b}_{1y}}-{{b}_{1}}{{b}_{2x}})+{{p}_{y}} = 0, \\ & {{b}_{1t}}-\eta ({{b}_{1xx}}+{{b}_{1yy}})-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-\eta ({{b}_{2xx}}+{{b}_{2yy}})-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}})+{{r}_{y}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}} = 0, \ {{b}_{1x}}+{{b}_{2y}} = 0. \end{aligned} \right. \end{equation}$

(3.1)

3.1. Lie symmetry analysis of MHD equations

The vector field of system (3.1) can be expressed as

$\begin{equation} \underline{V} = {{\zeta }_{1}}\frac{\partial }{\partial t}+{{\zeta }_{2}}\frac{\partial }{\partial x}+{{\zeta }_{3}}\frac{\partial }{\partial y}+{{\phi }_{1}}\frac{\partial }{\partial {{u}_{1}}}+{{\phi }_{2}}\frac{\partial }{\partial {{u}_{2}}}+{{\varphi }_{1}}\frac{\partial }{\partial {{b}_{1}}}+{{\varphi }_{2}}\frac{\partial }{\partial {{b}_{2}}}+{{\psi }_{1}}\frac{\partial }{\partial p}+{{\psi }_{2}}\frac{\partial }{\partial r}, \end{equation}$

(3.2)

where ${{\zeta }_{i}}$ ( $i = 1, 2, 3$ ), ${{\phi }_{j}}$ , ${{\varphi }_{j}}$ , ${{\psi }_{j}}$ ( $j = 1, 2$ ) are undetermined coefficients about $t$ , $\mathbf{x}$ , $\mathbf{U}$ , $\mathbf{B}$ , $p$ , $r$ . It follows from second-order prolongation $p{{r}^{(2)}}\underline{V}(\Delta){{\vert}_{\Delta = 0}} = 0$ that

$\begin{equation} \begin{aligned} & {{\phi }^{t}_{1}}-\nu ({{\phi }^{xx}_{1}}+{{\phi }^{yy}_{1}})+{{\phi }_{1}}{{u}_{1}}_{x}+{{u}_{1}}{{\phi }^{x}_{1}}+{{\phi }_{2}}{{u}_{1}}_{y}+{{u}_{2}}{{\phi }^{y}_{1}}+\kappa ({{\varphi }_{2}}{{b}_{2x}}+{{b}_{2}}{{\varphi }^{x}_{2}}-{{\varphi }_{2}}{{b}_{1}}_{y}-{{b}_{2}}{{\varphi }^{y}_{1}})+{{\psi }^{x}_{1}} = 0, \\ & {{\phi }^{t}_{2}}-\nu ({{\phi }^{xx}_{2}}+{{\phi }^{yy}_{2}})+{{\phi }_{1}}{{u}_{2}}_{x}+{{u}_{1}}{{\phi }^{x}_{2}}+{{\phi }_{2}}{{u}_{2y}}+{{u}_{2}}{{\phi }^{y}_{2}}+\kappa ({{\varphi }_{1}}{{b}_{1y}}+{{b}_{1}}{{\varphi }^{y}_{1}}-{{\varphi }_{1}}{{b}_{2}}_{x}-{{b}_{1}}{{\varphi }^{x}_{2}})+{{\psi }^{y}_{1}} = 0, \\ & {{\varphi }^{t}_{1}}-\eta ({{\varphi }^{xx}_{1}}+{{\varphi }^{yy}_{1}})-{{\varphi }_{1}}{{u}_{1}}_{x}-{{b}_{1}}{{\phi }^{x}_{1}}-{{\varphi }_{2}}{{u}_{1}}_{y}-{{b}_{2}}{{\phi }^{y}_{1}}+{{\phi }_{1}}{{b}_{1x}}+{{u}_{1}}{{\varphi }^{x}_{1}}+{{\phi }_{2}}{{b}_{1}}_{y}+{{u}_{2}}{{\varphi }^{y}_{1}}+{{\psi }^{x}_{2}} = 0, \\ & {{\varphi }^{t}_{2}}-\eta ({{\varphi }^{xx}_{2}}+{{\varphi }^{yy}_{2}})-{{\varphi }_{1}}{{u}_{2}}_{x}-{{b}_{1}}{{\phi }^{x}_{2}}-{{\varphi }_{2}}{{u}_{2}}_{y}-{{b}_{2}}{{\phi }^{y}_{2}}+{{\phi }_{1}}{{b}_{2x}}+{{u}_{1}}{{\varphi }^{x}_{2}}+{{\phi }_{2}}{{b}_{2}}_{y}+{{u}_{2}}{{\varphi }^{y}_{2}}+{{\psi }^{y}_{2}} = 0, \\ & {{\phi }^{x}_{1}}+{{\phi }^{y}_{2}} = 0, \ {{\varphi }^{x}_{1}}+{{\varphi }^{y}_{2}} = 0. \end{aligned} \end{equation}$

(3.3)

3.1.1. Inviscid MHD equations

Choosing $\nu = \eta = 0$ and $\kappa = 1$ in Eq (3.1), the inviscid MHD equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}})+({{b}_{2}}{{b}_{2x}}-{{b}_{2}}{{b}_{1y}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}})+({{b}_{1}}{{b}_{1y}}-{{b}_{1}}{{b}_{2x}})+{{p}_{y}} = 0, \\ & {{b}_{1t}}-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}})+{{r}_{y}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}} = 0, \ {{b}_{1x}}+{{b}_{2y}} = 0. \\ \end{aligned} \right. \end{equation}$

(3.4)

Solving (3.3) with $\nu = \eta = 0$ and $\kappa = 1$ , the coefficient functions of vector field $\underline{V}$ can be obtained as

$\begin{equation} \begin{aligned} & {{\zeta }_{1}} = 2{{C}_{1}}t+{{C}_{2}}, \ {{\zeta }_{2}} = {{C}_{0}}x-{{C}_{12}}y+{{f}_{1}}(t)+{{C}_{3}}, \ {{\zeta }_{3}} = {{C}_{12}}x+{{C}_{0}}y+{{f}_{2}}(t)+{{C}_{4}}, \\ & {{\phi }_{1}} = ({{C}_{0}}-2{{C}_{1}}){{u}_{1}}-{{C}_{12}}{{u}_{2}}+{{f}^{\prime }_{1}}(t), \ {{\phi }_{2}} = {{C}_{12}}{{u}_{1}}+({{C}_{0}}-2{{C}_{1}}){{u}_{2}}+{{f}^{\prime }_{2}}(t), \\ & {{\varphi }_{1}} = ({{C}_{0}}-2{{C}_{1}}){{b}_{1}}-{{C}_{12}}{{b}_{2}}, \ {{\varphi }_{2}} = {{C}_{12}}{{b}_{1}}+({{C}_{0}}-2{{C}_{1}}){{b}_{2}}, \\ & {{\psi }_{1}} = 2({{C}_{0}}-2{{C}_{1}})p-x{{f}{{^{\prime \prime}_{1}}}}(t)-y{{f}{{^{\prime \prime }_{2}}^{ }}}(t)+\alpha (t), \ {{\psi }_{2}} = 2({{C}_{0}}-2{{C}_{1}})r+\beta (t), \\ \end{aligned} \end{equation}$

(3.5)

where ${{C}_{0}}, {{C}_{1}}, {{C}_{2}}, {{C}_{3}}, {{C}_{4}}$ and ${{C}_{12}}$ are arbitrary constants. ${{f}_{1}}(t), {{f}_{2}}(t), \alpha (t)$ and $\beta (t)$ are arbitrary functions related to $t$ only. When ${{C}_{2}} = 1$ , ${{C}_{3}} = {{\bar{v}}_{1}}$ , ${{C}_{4}} = {{\bar{v}}_{2}}$ , ${{C}_{0}} = {{C}_{1}} = {{C}_{12}} = {{f}_{1}}(t) = {{f}_{2}}(t) = 0$ ,

$\begin{equation} \begin{aligned} \underline{V}& = ({{C}_{2}}\frac{\partial }{\partial t}+{{C}_{3}}\frac{\partial }{\partial x}+{{C}_{4}}\frac{\partial }{\partial y})+\alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r} = \frac{\partial }{\partial t}+{{{\bar{v}}}_{1}}\frac{\partial }{\partial x}+{{{\bar{v}}}_{2}}\frac{\partial }{\partial y}+\alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r}. \\ \end{aligned} \end{equation}$

(3.6)

The characteristic equation is

$\begin{equation} \frac{dt}{1} = \frac{dx}{{{{\bar{v}}}_{1}}} = \frac{dy}{{{{\bar{v}}}_{2}}} = \frac{d{{u}_{1}}}{0} = \frac{d{{u}_{2}}}{0} = \frac{d{{b}_{1}}}{0} = \frac{d{{b}_{2}}}{0} = \frac{dp}{\alpha (t)} = \frac{dr}{\beta (t)}. \end{equation}$

(3.7)

It follows from (3.7) that corresponding invariants are

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{1}} = x-{{{\bar{v}}}_{1}}t, \ {{{\bar{\zeta }}}_{2}} = y-{{{\bar{v}}}_{2}}t, \ {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{u}_{2}}, \ {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{b}_{1}}, \\ & {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{b}_{2}}, \ Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -p+\int{\alpha (t)dt, }\ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -r+\int{\beta (t)dt.} \\ \end{aligned} \end{equation}$

(3.8)

Substituting (3.8) into (3.4), reduced equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{{\bar{v}}}_{1}}{{F}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}+{{F}_{1}}{{F}_{1{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}+{{G}_{2}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}-{{Q}_{{{{\bar{\zeta }}}_{1}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{F}_{2}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{F}_{1}}{{F}_{2{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{G}_{1}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}-{{G}_{1}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}-{{Q}_{{{{\bar{\zeta }}}_{2}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{G}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}-{{G}_{1}}{{F}_{1{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}+{{F}_{1}}{{G}_{1{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}-{{R}_{{{{\bar{\zeta }}}_{1}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{G}_{2}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{G}_{2{{{\bar{\zeta }}}_{2}}}}-{{G}_{1}}{{F}_{2{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{F}_{1}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{G}_{2{{{\bar{\zeta }}}_{2}}}}-{{R}_{{{{\bar{\zeta }}}_{2}}}} = 0, \\ & {{F}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{F}_{2{{{\bar{\zeta }}}_{2}}}} = 0, \ {{G}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{G}_{2{{{\bar{\zeta }}}_{2}}}} = 0. \\ \end{aligned} \right. \end{equation}$

(3.9)

It can be obtained that (3.10)–(3.12) are three kinds of solutions for (3.9).

Case 1. Sin/cos-type solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{\cos }^{2}}({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{\cos }^{2}}({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{2}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -\sin ({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})\cos ({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -\sin ({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})\cos ({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{1}}, \\ & Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{{\bar{v}}}_{1}}\sin (-2{{{\bar{\zeta }}}_{1}}+2{{{\bar{\zeta }}}_{2}})-\frac{\cos (-4{{{\bar{\zeta }}}_{1}}+4{{{\bar{\zeta }}}_{2}})}{8}+m, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = n, \\ \end{aligned} \right. \end{equation}$

(3.10)

where $m$ and $n$ are arbitrary constants.

Case 2. Sech-type solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{\operatorname{sech}}^{2}}({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{\operatorname{sech}}^{2}}({{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}})-{{{\bar{v}}}_{2}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{c}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -{{c}_{1}}, \ Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = m, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = n, \\ \end{aligned} \right. \end{equation}$

(3.11)

where ${{c}_{1}}$ is arbitrary constant.

Case 3. Rational solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -\frac{{{c}_{2}}{{{\bar{\zeta }}}_{2}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = \frac{{{c}_{2}}{{{\bar{\zeta }}}_{1}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = -\frac{{{c}_{3}}{{{\bar{\zeta }}}_{2}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = \frac{{{c}_{3}}{{{\bar{\zeta }}}_{1}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \\ & Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = \frac{{{c}_{2}}(2{{{\bar{\zeta }}}_{1}}{{{\bar{v}}}_{2}}-2{{{\bar{\zeta }}}_{2}}{{{\bar{v}}}_{1}}+{{c}_{2}})}{2(\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2})}+m, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = \frac{{{c}_{3}}({{{\bar{\zeta }}}_{1}}{{{\bar{v}}}_{2}}-{{{\bar{\zeta }}}_{2}}{{{\bar{v}}}_{1}})}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}+n, \\ \end{aligned} \right. \end{equation}$

(3.12)

where ${{c}_{2}}$ and ${{c}_{3}}$ are arbitrary constants. Substituting (3.8) into (3.10)–(3.12), respectively, we obtain that (3.13)–(3.15) are three kinds of solutions for $(2 + 1)$ -dimensional MHD equations (3.4).

Case 1. Sin/cos-type solution.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\cos }^{2}}[x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{1}}, \ {{u}_{2}} = {{\cos }^{2}}[x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{2}}, \\ &{{b}_{1}} = \sin [x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]\cos [x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{1}}, \\ &{{b}_{2}} = \sin [x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]\cos [x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{1}}, \ r = -n+\int{\beta (t)dt}, \\ &p = {{\bar{v}}_{1}}\sin [(2{{\bar{v}}_{1}}-2{{\bar{v}}_{2}})t-2x+2y]+\frac{\cos [(4{{{\bar{v}}}_{1}}-4{{{\bar{v}}}_{2}})t-4x+4y]}{8}-m+\int{\alpha (t)dt}.\\ \end{aligned} \end{equation}$

(3.13)

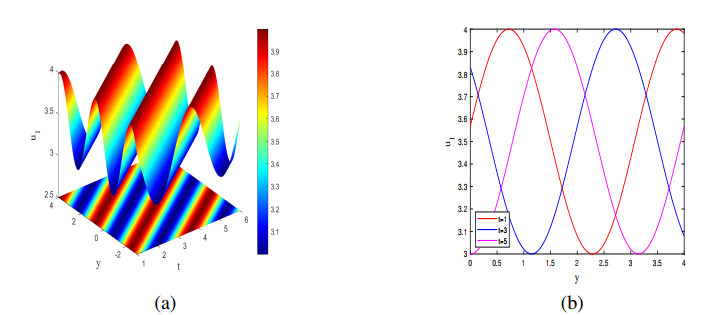
Setting ${{\bar{v}}_{1}} = 3, {{\bar{v}}_{2}} = 4$ and $x = 6$ for ${{u}_{1}}$ in (3.13), we obtain of periodic solution ${{u}_{1}}$ as follows.

Figure 1. (a) The evolution of periodic solution via (3.13), (b)

$u_1$ (

$t$ = 1, 3, 5).

DownLoad: Full-Size Img PowerPoint

From solution (3.13) and Figure 1, it can be seen that the solution exhibits periodic characteristics over time and space. The physical significance of the solution mainly includes the following points:

(ⅰ) Periodic solution can be used to analyze the stability of MHD system. If the MHD system can reach periodic solutions, it usually means that the system can achieve stability under certain conditions.

(ⅱ) Periodic solution can describe oscillatory phenomena in the MHD system, such as periodic changes in magnetic fields, periodic fluctuations in fluid velocity, etc.

(ⅲ) In industry, such as magnetohydrodynamic power generation, periodic flow can improve power generation efficiency. By optimizing the periodic solution, more efficient power generation equipment can be designed.

Case 2. Sech-type solution.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\operatorname{sech}}^{2}}[x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{1}}, \ {{u}_{2}} = {{\operatorname{sech}}^{2}}[x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}})t]+{{\bar{v}}_{2}}, \\ &{{b}_{1}} = {{c}_{1}}, \ {{b}_{2}} = {{c}_{1}}, \ p = -m+\int{\alpha (t)dt}, \ r = -n+\int{\beta (t)dt}. \end{aligned} \end{equation}$

(3.14)

Setting ${{\bar{v}}_{1}} = 1$ and ${{\bar{v}}_{2}} = 2$ for ${{u}_{1}}$ in (3.14), we obtain of single soliton solution ${{u}_{1}}$ as follows.

Figure 2. The evolution of a single soliton solution via (3.14) (

$t = 1, \ 4, \ 7$ , respectively).

DownLoad: Full-Size Img PowerPoint

From Figure 2, it can be seen that the velocity is constant in certain domains of space. Moreover, the velocity is induced to a sudden rise until it reaches a maximum value. As a stable wave form, the characteristics of solitons emerge from the collective behavior of nonlinear media. Solitons play an important role in the study of MHD waves due to their unique properties and applications in various physical contexts. The importance of solitons in the main problem mostly includes the following points:

(ⅰ) As a special wave phenomenon, solitons can form stable wave structures in plasmas. In controlled thermonuclear fusion research, soliton waves can be used to describe some wave phenomena in plasma, which has potential application value for achieving and maintaining the stability of fusion plasma.

(ⅱ) Solitons can maintain their shape and amplitude is unchanged during propagation. This property is important for understanding and predicting some wave propagations in MHD flow.

(ⅲ) Solitons can help explain some phenomena in MHD flow, such as the localized structure of magnetic fields and the dynamic behavior of magnetic domain walls.

Case 3. Rational solution.

$\begin{equation} \begin{aligned} & {{u}_{1}} = \frac{{{c}_{2}}(y-{{{\bar{v}}}_{2}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{u}_{2}} = -\frac{{{c}_{2}}(x-{{{\bar{v}}}_{1}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \\ & {{b}_{1}} = \frac{{{c}_{3}}(y-{{{\bar{v}}}_{2}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{b}_{2}} = -\frac{{{c}_{3}}(x-{{{\bar{v}}}_{1}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \\ & p = -\frac{{{c}_{2}}[2(x-{{{\bar{v}}}_{1}}t){{{\bar{v}}}_{2}}-2(y-{{{\bar{v}}}_{2}}t){{{\bar{v}}}_{1}}+{{c}_{2}}]}{2[{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}]}-m+\int{\alpha (t)dt}, \\ & r = -\frac{{{c}_{3}}[(x-{{{\bar{v}}}_{1}}t){{{\bar{v}}}_{2}}-(y-{{{\bar{v}}}_{2}}t){{{\bar{v}}}_{1}}]}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}-n+\int{\beta (t)dt}. \\ \end{aligned} \end{equation}$

(3.15)

Setting ${{\bar{v}}_{1}} = 1, {{\bar{v}}_{2}} = 1, {{c}_{2}} = 1$ and $x = 2$ for ${{u}_{1}}$ in (3.15), we obtain lump (c.f. for solution ${{u}_{1}}$ as follows.

Figure 3. (a) The evolution of lump solution via (3.15), (b) Overview of

$u_1$ .

DownLoad: Full-Size Img PowerPoint

From Figure 3, it can be seen the flow have the characteristics of spatial and temporal localization. Lump solution corresponds to the emergent phenomenon of energy focusing in a specific region or time point. The amplitude of peak and valley is several times higher than the surrounding background height. The scale transformation of the lump has already been processed in mathematics. Actually, shock wave may be seen and local instability may occur in reality.

Remark 3.1. (1) If $b_1 = b_2 = 0$ and $r = 0$ in (3.14) and (3.15), then (3.14) and (3.15) reduce to exact solutions for (2 + 1)-dimensional Euler equation.

(2) Since $\omega = \frac{\partial {{u}_{2}}}{\partial x}-\frac{\partial {{u}_{1}}}{\partial y}\ne 0$ in (3.13) and (3.14) and $\omega = \frac{\partial {{u}_{2}}}{\partial x}-\frac{\partial {{u}_{1}}}{\partial y} = 0$ in (3.15), it can be concluded that (3.13) and (3.14) correspond to rotational flow. Additionally, (3.15) corresponds to inrotational flow.

3.1.2. Viscous MHD equations

Without loss of generality, choosing $\nu = \eta = \kappa = 1$ in Eq (3.1), the viscous MHD equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}-({{u}_{1xx}}+{{u}_{1yy}})+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}})+({{b}_{2}}{{b}_{2x}}-{{b}_{2}}{{b}_{1y}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}-({{u}_{2xx}}+{{u}_{2yy}})+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}})+({{b}_{1}}{{b}_{1y}}-{{b}_{1}}{{b}_{2x}})+{{p}_{y}} = 0, \\ & {{b}_{1t}}-({{b}_{1xx}}+{{b}_{1yy}})-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-({{b}_{2xx}}+{{b}_{2yy}})-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}})+{{r}_{y}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}} = 0, \ {{b}_{1x}}+{{b}_{2y}} = 0. \\ \end{aligned} \right. \end{equation}$

(3.16)

Solving (3.3) with $\nu = \eta = \kappa = 1$ , the coefficient functions of vector field $\underline{V}$ can be obtained as

$\begin{equation} \begin{aligned} & {{\zeta }_{1}} = 2{{C}_{1}}t+{{C}_{2}}, \ {{\zeta }_{2}} = {{C}_{1}}x-{{C}_{12}}y+{{f}_{1}}(t)+{{C}_{3}}, \ {{\zeta }_{3}} = {{C}_{12}}x+{{C}_{1}}y+{{f}_{2}}(t)+{{C}_{4}}, \\ & {{\phi }_{1}} = -{{C}_{1}}{{u}_{1}}-{{C}_{12}}{{u}_{2}}+{{f}^{\prime }_{1}}(t), \ {{\phi }_{2}} = {{C}_{12}}{{u}_{1}}-{{C}_{1}}{{u}_{2}}+{{f}^{\prime }_{2}}(t), \\ & {{\varphi }_{1}} = -{{C}_{1}}{{b}_{1}}-{{C}_{12}}{{b}_{2}}, \ {{\varphi }_{2}} = {{C}_{12}}{{b}_{1}}-{{C}_{1}}{{b}_{2}}, \\ & {{\psi }_{1}} = -2{{C}_{1}}p-x{{f}{{^{\prime \prime}_{1}}}}(t)-y{{f}{{^{\prime \prime}_{2}}}}(t)+\alpha (t), \ {{\psi }_{2}} = -2{{C}_{1}}r+\beta (t). \\ \end{aligned} \end{equation}$

(3.17)

Case 1. When ${{C}_{1}} = {{C}_{2}} = {{C}_{3}} = {{C}_{4}} = {{C}_{12}} = {{f}_{1}}(t) = {{f}_{2}}(t) = 0$ , $\underline{V} = \alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r}.$

The corresponding invariants are

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{0}} = t, \ {{{\bar{\zeta }}}_{1}} = x, \ {{{\bar{\zeta }}}_{2}} = y, \ {{F}_{1}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{2}}) = -{{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{1}}) = -{{u}_{2}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{0}}, \ {{{\bar{\zeta }}}_{2}}) = -{{b}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{1}}) = -{{b}_{2}}. \\ \end{aligned} \end{equation}$

(3.18)

Substituting invariants (3.18) into (3.16), and solving the reduced equations,

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{g}_{1}}{{e}^{-t}}\cos y, \text{ }\ {{u}_{2}} = {{g}_{2}}{{e}^{-t}}\cos x, \ {{b}_{1}} = {{g}_{3}}{{e}^{-t}}\cos y, \ {{b}_{2}} = {{g}_{4}}{{e}^{-t}}\cos x, \\ &p = \frac{[-\cos (2y){{g}^{2}_{3}{g}_{4}}+2{{g}^{3}_{4}}\sin^{2} x+4{g}_{3}({{g}^{2}_{2}}-{{g}^{2}_{4}})\sin x\sin y]{{e}^{-2t}}}{4{{g}_{4}}}+m(t), \ r = n(t), \end{aligned} \end{equation}$

(3.19)

is a sin/cos-type solution for MHD equations (3.16), where ${{g}_{1}}{{g}_{4}}-{{g}_{2}}{{g}_{3}} = 0$ . $m(t)$ and $n(t)$ are arbitrary functions related to $t$ only. Setting ${{g}_{1}} = 1$ for ${{u}_1}$ in (3.19), we obtain of solution ${{u}_{1}}$ as follows.

Figure 4. (a) The evolution of periodic solution via (3.19), (b)

$u_1$ (

${t}$ = 0.2, 0.5, 0.8).

DownLoad: Full-Size Img PowerPoint

From Figure 4, it can be seen that as time increases, the shape and direction of the velocity remain unchanged, but the amplitude decreases.

Case 2. When ${{C}_{2}} = 1$ , ${{C}_{i}} = {{C}_{12}} = {{f}_{1}}(t) = {{f}_{2}}(t) = \alpha (t) = \beta (t) = 0\ ({i} = 0, 1, 3, 4), \ \underline{V} = \frac{\partial }{\partial t}.$

The characteristic equation is

$\begin{equation} \frac{dt}{1} = \frac{dx}{0} = \frac{dy}{0} = \frac{d{{u}_{1}}}{0} = \frac{d{{u}_{2}}}{0} = \frac{d{{b}_{1}}}{0} = \frac{d{{b}_{2}}}{0} = \frac{dp}{0} = \frac{dr}{0}. \end{equation}$

(3.20)

The corresponding invariants are

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{1}} = x, \ {{{\bar{\zeta }}}_{2}} = y, \ {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = {{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = {{u}_{2}}, \\&{{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = {{b}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = {{b}_{2}}, \ Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = p, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}) = r. \\ \end{aligned} \end{equation}$

(3.21)

Substituting invariants (3.21) into (3.16), and solving the reduced equations,

$\begin{equation} \begin{aligned} & {{u}_{1}} = {{\operatorname{sech}}^{2}}(x+iy), \ {{u}_{2}} = i{{\operatorname{sech}}^{2}}(x+iy), \\ & {{b}_{1}} = {{\operatorname{sech}}^{2}}(x+iy), \ {{b}_{2}} = i{{\operatorname{sech}}^{2}}(x+iy), \ p = m, \ r = n, \\ \end{aligned} \end{equation}$

(3.22)

is a sech-type solution for MHD equations (3.16). Using symmetry

$\underline{V} = t\frac{\partial }{\partial x}+t\frac{\partial }{\partial y}+\frac{\partial }{\partial {{u}_{1}}}+\frac{\partial }{\partial {{u}_{2}}},$

solution (3.22) can further generate the following invariant solution

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t))+\varepsilon , \ {{u}_{2}} = i{{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t))+\varepsilon , \\ &{{b}_{1}} = {{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t)), \ {{b}_{2}} = i{{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t)), \ p = m(t), \ r = n(t), \end{aligned} \end{equation}$

(3.23)

where $\varepsilon$ is arbitrary constant.

Remark 3.2. (1) The lump solution (3.15) for inviscid MHD equations (3.4) also satisfies the viscous MHD equations (3.16).

(2) If $b_1 = b_2 = 0$ and $r = 0$ in (3.23), then (3.23) reduces to exact solutions for (2 + 1)-dimensional Navier-Stokes equation.

(3) Since $\omega = \frac{\partial {{u}_{2}}}{\partial x}-\frac{\partial {{u}_{1}}}{\partial y}\ne 0$ in (3.19) and $\omega = \frac{\partial {{u}_{2}}}{\partial x}-\frac{\partial {{u}_{1}}}{\partial y} = 0$ in (3.23), it can be concluded that (3.19) corresponds to rotational flow. Moreover, (3.23) corresponds to inrotational flow.

3.2. Generalized Riccati equation expansion method for MHD equations

As an important method of simplest equation methods, the generalized Riccati equation method ^[29,30] provides a powerful mathematical tool to deal with the complex nonlinear and strong coupling terms in MHD equations. Using traveling wave transformation,

$\begin{equation} \zeta = {{k}_{2}}x+{{k}_{3}}y-{{k}_{1}}t, \end{equation}$

(3.24)

equations (3.1) are transformed into following ordinary differential equations (ODEs) as

$\begin{equation} \left\{ \begin{aligned} & -{{k}_{1}}{{u}_{1\zeta }}-\nu ({{k}^{2}_{2}}{{u}_{1\zeta \zeta }}+{{k}^{2}_{3}}{{u}_{1\zeta \zeta }})+({{k}_{2}}{{u}_{1}}{{u}_{1\zeta }}+{{k}_{3}}{{u}_{2}}{{u}_{1\zeta }})+\kappa ({{k}_{2}}{{b}_{2}}{{b}_{2\zeta }}-{{k}_{3}}{{b}_{2}}{{b}_{1\zeta }})+{{k}_{2}}{{p}_{\zeta }} = 0, \\ & -{{k}_{1}}{{u}_{2\zeta }}-\nu ({{k}^{2}_{2}}{{u}_{2\zeta \zeta }}+{{k}^{2}_{3}}{{u}_{2\zeta \zeta }})+({{k}_{2}}{{u}_{1}}{{u}_{2\zeta }}+{{k}_{3}}{{u}_{2}}{{u}_{2\zeta }})+\kappa ({{k}_{3}}{{b}_{1}}{{b}_{1\zeta }}-{{k}_{2}}{{b}_{1}}{{b}_{2\zeta }})+{{k}_{3}}{{p}_{\zeta }} = 0, \\ & -{{k}_{1}}{{b}_{1\zeta }}-\eta ({{k}^{2}_{2}}{{b}_{1\zeta \zeta }}+{{k}^{2}_{3}}{{b}_{1\zeta \zeta }})-({{k}_{2}}{{b}_{1}}{{u}_{1\zeta }}+{{k}_{3}}{{b}_{2}}{{u}_{1\zeta }})+{{k}_{2}}{{u}_{1}}{{b}_{1\zeta }}+{{k}_{3}}{{u}_{2}}{{b}_{1\zeta }}+{{k}_{2}}{{r}_{\zeta }} = 0, \\ & -{{k}_{1}}{{b}_{2\zeta }}-\eta ({{k}^{2}_{2}}{{b}_{2\zeta \zeta }}+{{k}^{2}_{3}}{{b}_{2\zeta \zeta }})-({{k}_{2}}{{b}_{1}}{{u}_{2\zeta }}+{{k}_{3}}{{b}_{2}}{{u}_{2\zeta }})+{{k}_{2}}{{u}_{1}}{{b}_{2\zeta }}+{{k}_{3}}{{u}_{2}}{{b}_{2\zeta }}+{{k}_{3}}{{r}_{\zeta }} = 0, \\ & {{k}_{2}}{{u}_{1\zeta }}+{{k}_{3}}{{u}_{2\zeta }} = 0, \ {{k}_{2}}{{b}_{1\zeta }}+{{k}_{3}}{{b}_{2\zeta }} = 0. \end{aligned} \right. \end{equation}$

(3.25)

Suppose that the solution of ODEs (3.25) can be expressed as a polynomial of $\phi (\zeta)$ as

$\begin{equation} \begin{aligned} & {{u}_{1}} = \sum\limits_{i = 0}^{{{N}_{1}}}{{{a}_{i}}{{\phi }^{i}}(\zeta )}, \ {{u}_{2}} = \sum\limits_{i = 0}^{{{N}_{2}}}{{{m}_{i}}{{\phi }^{i}}(\zeta )}, \ {{b}_{1}} = \sum\limits_{i = 0}^{{{N}_{3}}}{{{n}_{i}}{{\phi }^{i}}(\zeta )}, \\ & {{b}_{2}} = \sum\limits_{i = 0}^{{{N}_{4}}}{{{s}_{i}}{{\phi }^{i}}(\zeta )}, \ p = \sum\limits_{i = 0}^{{{N}_{5}}}{{{l}_{i}}{{\phi }^{i}}(\zeta )}+l(t), \ r = \sum\limits_{i = 0}^{{{N}_{6}}}{{{q}_{i}}{{\phi }^{i}}(\zeta )}+q(t), \\ \end{aligned} \end{equation}$

(3.26)

where ${{a}_{i}}, {{m}_{i}}, {{n}_{i}}, {{s}_{i}}, {{l}_{i}}, {{q}_{i}}$ are undetermined constants and ${{a}_{{{N}_{1}}}}, {{m}_{{{N}_{2}}}}, {{n}_{{{N}_{3}}}}, {{s}_{{{N}_{4}}}}\ne 0$ . $l(t)$ and $q(t)$ are arbitrary functions related to $t$ only. $\phi (\zeta)$ satisfies the generalized Riccati equation

$\begin{equation} {\phi }'(\zeta ) = {{\xi }_{0}}+{{\xi }_{1}}\phi (\zeta )+{{\xi }_{2}}{{\phi }^{2}}(\zeta ), \end{equation}$

(3.27)

where ${{\xi }_{0}}, {{\xi }_{1}}$ and ${{\xi }_{2}}$ are arbitrary constants with ${{\xi }_{2}}\ne 0$ . We choose ${{N}_{1}} = {{N}_{2}} = {{N}_{3}} = {{N}_{4}} = {{N}_{5}} = {{N}_{6}} = 2$ with can balance the highest order of the derivative and nonlinear terms in ODEs.

3.2.1. Inviscid MHD equations

When $\nu = \eta = 0$ and $\kappa = 1$ in ODEs (3.25), substituting (3.26) and (3.27) into (3.25), collecting the coefficients of ${{\phi }^{i}}(\zeta)$ and setting them to be zeros, we obtain

$\begin{equation} \begin{aligned} & {{a}_{0}} = {{a}_{0}}, {{a}_{1}} = {{a}_{1}}, {{a}_{2}} = {{a}_{2}}, {{k}_{1}} = {{k}_{1}}, {{k}_{2}} = {{k}_{2}}, {{k}_{3}} = {{k}_{3}}, {{l}_{1}} = {{l}_{1}}, {{l}_{2}} = -\frac{{{n}^{2}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}{2{{k}^{2}_{3}}}, \\ &{{m}_{0}} = \frac{-{{a}_{0}}{{k}_{2}}+{{k}_{1}}}{{{k}_{3}}}, {{m}_{1}} = -\frac{{{a}_{1}}{{k}_{2}}}{{{k}_{3}}}, {{m}_{2}} = -\frac{{{k}_{2}}{{a}_{2}}}{{{k}_{3}}}, {{n}_{0}} = -\frac{{{k}^{2}_{3}}{{l}_{1}}}{{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}, {{n}_{1}} = {{n}_{1}}, \\ &{{n}_{2}} = 0, {{q}_{1}} = 0, {{q}_{2}} = 0, {{s}_{0}} = \frac{{{k}_{2}}{{k}_{3}}{{l}_{1}}}{{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}, {{s}_{1}} = -\frac{{{k}_{2}}{{n}_{1}}}{{{k}_{3}}}, {{s}_{2}} = 0. \\ \end{aligned} \end{equation}$

(3.28)

Substituting (3.28) and the general solutions of (3.27) (c.f. ^[29]) into (3.26), it can be obtained following four kinds of solutions for the (2 + 1)-dimensional inviscid MHD equations.

Case 1. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} > 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the tanh-type solution can be obtained as follows.

(3.29)

where $\zeta = {{k}_{2}}x+{{k}_{3}}y-{{k}_{1}}t.$ Setting ${{a}_{0}} = -1, {{a}_{1}} = -7, {{a}_{2}} = 1, {{k}_{1}} = 3, {{k}_{2}} = 1, {{k}_{3}} = -1, {{\xi }_{0}} = 1, {{\xi }_{1}} = 3$ and ${{\xi }_{2}} = 1$ for $u_1$ in (3.29), we obtain of kink solution ${{u}_{1}}$ as follows.

Figure 5.

$u_1$ (

$t = 2, \ 4, \ 6$ , respectively).

DownLoad: Full-Size Img PowerPoint

In particular, when ${{\xi }_{0}} = 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ , the sinh-cosh-type solution can be obtained as follows

(3.30)

where $C$ is arbitrary constant. Setting ${{a}_{0}} = 4, {{a}_{1}} = -10, {{a}_{2}} = -8, {{k}_{1}} = -4, {{k}_{2}} = -16, {{k}_{3}} = -2, {{\xi }_{0}} = 0,$ ${{\xi }_{1}} = 1, {{\xi }_{2}} = 1, C = 1$ and $x = 1$ for $u_1$ in (3.30), we obtain of anti-kink-like solution ${{u}_{1}}$ as follows.

Figure 6. (a)

$u_1$ , (b)

$u_1$ (

${t}$ = 1, 2, 3).

DownLoad: Full-Size Img PowerPoint

The kink and kink-like solutions can be understood as a macroscopic stable structure generated from the field dynamics at the microscale. They manifest as a rapid change or discontinuity in some field at the macro level.

Case 2. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} < 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the tan-type solution can be obtained as follows.

$\begin{eqnarray} {{u}_{1}}& = &\frac{4{{a}_{0}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{a}_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ && +\frac{{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ {{u}_{2}}& = &\frac{4{{\xi }^{2}_{2}}(-{{a}_{0}}{{k}_{2}}+{{k}_{1}})+2{{a}_{1}}{{k}_{2}}{{\xi }_{1}}{{\xi }_{2}}-{{k}_{2}}{{a}_{2}}{{\xi }^{2}_{1}}}{4{{k}_{3}}{{\xi }^{2}_{2}}}-\frac{{{k}_{2}}{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{k}_{3}}{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta )\\ &&+\frac{{{k}_{2}}({{a}_{2}}{{\xi }_{1}}-{{a}_{1}}{{\xi }_{2}})}{2{{k}_{3}}{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}} \tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ {{b}_{1}}& = &-\frac{2{{k}^{2}_{3}}{{l}_{1}}{{\xi }_{2}}+{{n}^{2}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{1}}}{2{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{2}}}+\frac{{{n}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ {{b}_{2}}& = &\frac{2{{k}_{2}}{{k}^{2}_{3}}{{l}_{1}}{{\xi }_{2}}+{{k}_{2}}{{n}^{2}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{1}}}{2{{k}_{3}}{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{2}}}-\frac{{{k}_{2}}{{n}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{k}_{3}}{{\xi }_{2}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ). \end{eqnarray}$

Case 3. When ${{\xi }_{1}} = {{\xi }_{0}} = 0$ and ${{\xi }_{2}}\ne 0$ , the rational solution can be obtained as follows

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{a}_{0}}-\frac{{{a}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{a}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{u}_{2}} = \frac{-{{a}_{0}}{{k}_{2}}+{{k}_{1}}}{{{k}_{3}}}+\frac{{{a}_{1}}{{k}_{2}}}{{{k}_{3}}({{\xi }_{2}}\zeta +C)}-\frac{{{a}_{2}}{{k}_{2}}}{{{k}_{3}}({{\xi }_{2}}\zeta +C){{}^{2}}}, \\ &{{b}_{1}} = -\frac{{{k}^{2}_{3}}{{l}_{1}}}{{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}-\frac{{{n}_{1}}}{{{\xi }_{2}}\zeta +C}, \ {{b}_{2}} = \frac{{{k}_{2}}{{k}_{3}}{{l}_{1}}}{{{n}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}+\frac{{{k}_{2}}{{n}_{1}}}{{{k}_{3}}({{\xi }_{2}}\zeta +C)}.\text{ } \end{aligned} \end{equation}$

(3.31)

3.2.2. Viscous MHD equations

When $\nu = \eta = \kappa = 1$ in ODEs (3.25), Substituting (3.26) and (3.27) into (3.25), we obtain

$\begin{equation} \begin{aligned} & {{a}_{0}} = {{a}_{0}}, {{a}_{1}} = {{a}_{1}}, {{a}_{2}} = {{a}_{2}}, {{k}_{1}} = {{k}_{1}}, {{k}_{2}} = {{k}_{2}}, {{k}_{3}} = -i{{k}_{2}}, {{l}_{1}} = \frac{((-{{a}_{0}}+i{{m}_{0}}){{k}_{2}}+{{k}_{1}}){{a}_{1}}}{{{k}_{2}}}, \\ &{{l}_{2}} = \frac{((-{{a}_{0}}+i{{m}_{0}}){{k}_{2}}+{{k}_{1}}){{a}_{2}}}{{{k}_{2}}}, {{m}_{0}} = {{m}_{0}}, {{m}_{1}} = -i{{a}_{1}}, {{m}_{2}} = -i{{a}_{2}}, {{n}_{0}} = {{n}_{0}}, {{n}_{1}} = {{n}_{1}}, {{s}_{2}} = 0, \\ &{{n}_{2}} = 0, {{q}_{1}} = \frac{((-{{a}_{0}}+i{{m}_{0}}){{n}_{1}}-(i{{s}_{0}}-{{n}_{0}}){{a}_{1}}){{k}_{2}}+{{n}_{1}}{{k}_{1}}}{{{k}_{2}}}, {{q}_{2}} = -{{a}_{2}}(i{{s}_{0}}-{{n}_{0}}), {{s}_{0}} = {{s}_{0}}, \ {{s}_{1}} = -i{{n}_{1}}. \\ \end{aligned} \end{equation}$

(3.32)

Substituting (3.32) and general solutions of (3.27) (c.f. ^[29]) into (3.26), it can be obtained that (3.33)–(3.40) are four kinds of solutions for (2 + 1)-dimensional viscous MHD equations.

Case 1. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} > 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tanh-type solution can be obtained.

(3.33)

In particular, when ${{\xi }_{0}} = 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ , the following sinh-cosh-type solution can be obtained.

(3.34)

Setting ${{a}_{1}} = 2, {{a}_{2}} = -2, {{m}_{0}} = -1, {{k}_{1}} = 1, {{k}_{2}} = -1, {{\xi }_{0}} = 0, {{\xi }_{1}} = -2, {{\xi }_{2}} = -14, C = 1$ and $x = 1$ for ${{u}_{2}}$ in (3.34), we obtain breather (c.f. ) for solution ${{u}_{2}}$ as follows.

Figure 7. (a) The evolution of Akhmediev breaher solution via

$\vert{{u}_{2}} \vert$ , (b) Overview of

$\vert{{u}_{2}} \vert$ , (c)

$\vert {{u}_{2}} \vert(t = 1, 2, 3)$ .

DownLoad: Full-Size Img PowerPoint

From , the breather appears to be localized in the $t$ -axis direction, and periodic in the $y$ -axis direction. It corresponds to a type of nonlinear wave where energy is concentrated in a local oscillation manner. The breather solutions can serve as a carrier of energy transfer during the propagation process, and the characteristics of this energy transfer are related to the macroscopic behavior in emergent phenomena.

Case 2. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} < 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tan-type solution can be obtained.

$\begin{eqnarray} &&\begin{aligned} {{u}_{1}} = &\frac{4{{a}_{0}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{a}_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(3.35)

$\begin{eqnarray} &&\begin{aligned} {{u}_{2}} = &{m}_{0}+\frac{i(2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}+\frac{i({{a}_{2}}{{\xi }_{1}}-{{a}_{1}}{{\xi }_{2}})}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & -\frac{i{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(3.36)

$\begin{eqnarray} &&{{b}_{1}} = \frac{2{{n}_{0}}{{\xi }_{2}}-{{n}_{1}}{{\xi }_{1}}}{2{{\xi }_{2}}}+\frac{{{n}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \end{eqnarray}$

(3.37)

$\begin{eqnarray} &&{{b}_{2}} = {s}_{0}+\frac{i{{n}_{1}}{{\xi }_{1}}}{2{{\xi }_{2}}}-\frac{i{{n}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ). \end{eqnarray}$

(3.38)

Setting ${{a}_{1}} = -12, {{a}_{2}} = 2, {{m}_{0}} = 1, {{k}_{1}} = -6, {{k}_{2}} = 1, {{\xi }_{0}} = -2, {{\xi }_{1}} = -2, {{\xi }_{2}} = -1$ and $x = 1$ in (3.36), we obtain for breather solution ${{u}_{2}}$ as follows.

Figure 8. (a) The evolution of Kuznetsov-Ma breaher solution via

$\vert {{u}_{2}} \vert$ , (b) Overview of

$\vert {{u}_{2}} \vert$ , (c)

$\vert {{u}_{2}} \vert$ (

$y = 1, 1.5, 2$ ).

DownLoad: Full-Size Img PowerPoint

From , the breather appears to be localized in the $y$ -axis direction, and periodic in the $t$ -axis direction, which corresponds to a nonlinear local wave that oscillates periodically in time.

Case 3. When ${{\xi }_{1}} = {{\xi }_{0}} = 0$ and ${{\xi }_{2}}\ne 0$ , the following rational solution can be obtained.

$\begin{eqnarray} &&{{u}_{1}} = {{a}_{0}}-\frac{{{a}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{a}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{u}_{2}} = {{m}_{0}}+\frac{i{{a}_{1}}}{{{\xi }_{2}}\zeta +C}-\frac{i{{a}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \end{eqnarray}$

(3.39)

$\begin{eqnarray} &&{{b}_{1}} = {{n}_{0}}-\frac{{{n}_{1}}}{{{\xi }_{2}}\zeta +C}, \ {{b}_{2}} = {{s}_{0}}+\frac{i{{n}_{1}}}{{{\xi }_{2}}\zeta +C}. \end{eqnarray}$

(3.40)

4. New wave behaviors of (3 + 1)-dimensional MHD flows

Denote $\mathbf{x} = (x, y, z)$ , $\mathbf{U} = ({{u}_{1}}(t, \mathbf{x}), {{u}_{2}}(t, \mathbf{x}), {{u}_{3}}(t, \mathbf{x}))$ , $\mathbf{B} = ({{b}_{1}}(t, \mathbf{x}), {{b}_{2}}(t, \mathbf{x}), {{b}_{3}}(t, \mathbf{x}))$ in (2.2), the component form of the (3 + 1)-dimensional MHD equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}-\nu ({{u}_{1xx}}+{{u}_{1yy}}+{{u}_{1zz}})+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}}+{{u}_{3}}{{u}_{1z}})+\kappa ({{b}_{2}}{{b}_{2x}}+{{b}_{3}}{{b}_{3x}}-{{b}_{2}}{{b}_{1y}}-{{b}_{3}}{{b}_{1z}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}-\nu ({{u}_{2xx}}+{{u}_{2yy}}+{{u}_{2zz}})+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}}+{{u}_{3}}{{u}_{2z}})+\kappa ({{b}_{1}}{{b}_{1y}}+{{b}_{3}}{{b}_{3y}}-{{b}_{1}}{{b}_{2x}}-{{b}_{3}}{{b}_{2z}}+{{p}_{y}} = 0, \\ & {{u}_{3t}}-\nu ({{u}_{3xx}}+{{u}_{3yy}}+{{u}_{3zz}})+({{u}_{1}}u_{3x}^{{}}+{{u}_{2}}{{u}_{3y}}+{{u}_{3}}{{u}_{3z}})+\kappa ({{b}_{1}}{{b}_{1z}}+{{b}_{2}}{{b}_{2z}}-{{b}_{1}}{{b}_{3x}}-{{b}_{2}}{{b}_{3y}})+{{p}_{z}} = 0, \\ & {{b}_{1t}}-\eta ({{b}_{1xx}}+{{b}_{1yy}}+{{b}_{1zz}})-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}}+{{b}_{3}}{{u}_{1z}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}}+{{u}_{3}}{{b}_{1z}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-\eta ({{b}_{2xx}}+{{b}_{2yy}}+{{b}_{2zz}})-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}}+{{b}_{3}}{{u}_{2z}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}}+{{u}_{3}}{{b}_{2z}})+{{r}_{y}} = 0, \\ & {{b}_{3t}}-\eta ({{b}_{3xx}}+{{b}_{3yy}}+{{b}_{3zz}})-({{b}_{1}}{{u}_{3x}}+{{b}_{2}}{{u}_{3y}}+{{b}_{3}}{{u}_{3z}})+({{u}_{1}}{{b}_{3x}}+{{u}_{2}}{{b}_{3y}}+{{u}_{3}}{{b}_{3z}})+{{r}_{z}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}}+{{u}_{3z}} = 0, \ {{b}_{1x}}+{{b}_{2y}}+{{b}_{3z}} = 0. \\ \end{aligned} \right. \end{equation}$

(4.1)

4.1. Lie symmetry analysis of MHD equations

The vector field of the system (4.1) can be expressed as

$\begin{equation} \begin{aligned} \underline{V} = &{{\zeta }_{1}}\frac{\partial }{\partial t}+{{\zeta }_{2}}\frac{\partial }{\partial x}+{{\zeta }_{3}}\frac{\partial }{\partial y}+{{\zeta }_{4}}\frac{\partial }{\partial z}+{{\phi }_{1}}\frac{\partial }{\partial {{u}_{1}}}+{{\phi }_{2}}\frac{\partial }{\partial {{u}_{2}}}+{{\phi }_{3}}\frac{\partial }{\partial {{u}_{3}}}\\ &+{{\varphi }_{1}}\frac{\partial }{\partial {{b}_{1}}}+{{\varphi }_{2}}\frac{\partial }{\partial {{b}_{2}}}+{{\varphi }_{3}}\frac{\partial }{\partial {{b}_{3}}}+{{\psi }_{1}}\frac{\partial }{\partial p}+{{\psi }_{2}}\frac{\partial }{\partial r}, \end{aligned} \end{equation}$

(4.2)

where ${{\zeta }_{i}}$ ( $i = 1, 2, 3, 4$ ), ${{\phi }_{j}}$ , ${{\varphi }_{j}}$ ( $j = 1, 2, 3$ ) and ${{\psi }_{k}}$ ( $k = 1, 2$ ) are undetermined coefficients about $t$ , $\mathbf{x}$ , $\mathbf{U}$ , $\mathbf{B}$ , $p$ and $r$ . It follows from the second-order prolongation $p{{r}^{(2)}}\underline{V}(\Delta){{\vert}_{\Delta = 0}} = 0$ that

$\begin{eqnarray} &&\begin{aligned} &{{\phi }^{t}_{1}}-\nu ({{\phi }^{xx}_{1}}+{{\phi }^{yy}_{1}}+{{\phi }^{zz}_{1}})+{{\phi }_{1}}{{u}_{1}}_{x}+{{u}_{1}}{{\phi }^{x}_{1}}+{{\phi }_{2}}{{u}_{1}}_{y}+{{u}_{2}}{{\phi }^{y}_{1}}+{{\phi }_{3}}{{u}_{1}}_{z}+{{u}_{3}}{{\phi }^{z}_{1}}\\ &+\kappa ({{\varphi }_{2}}{{b}_{2x}}+{{b}_{2}}{{\varphi }^{x}_{2}}+{{\varphi }_{3}}{{b}_{3x}}+{{b}_{3}}{{\varphi }^{x}_{3}}-{{\varphi }_{2}}{{b}_{1}}_{y}-{{b}_{2}}{{\varphi }^{y}_{1}}-{{\varphi }_{3}}{{b}_{1}}_{z}-{{b}_{3}}{{\varphi }^{z}_{1}})+{{\psi }^{x}_{1}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.3)

$\begin{eqnarray} &&\begin{aligned} & {{\phi }^{t}_{2}}-\nu ({{\phi }^{xx}_{2}}+{{\phi }^{yy}_{2}}+{{\phi }^{zz}_{2}})+{{\phi }_{1}}{{u}_{2}}_{x}+{{u}_{1}}{{\phi }^{x}_{2}}+{{\phi }_{2}}{{u}_{2y}}+{{u}_{2}}{{\phi }^{y}_{2}}+{{\phi }_{3}}{{u}_{2z}}+{{u}_{3}}{{\phi }^{z}_{2}}\\ &+\kappa ({{\varphi }_{1}}{{b}_{1y}}+{{b}_{1}}{{\varphi }^{y}_{1}}+{{\varphi }_{3}}{{b}_{3y}}+{{b}_{3}}{{\varphi }^{y}_{3}}-{{\varphi }_{1}}{{b}_{2}}_{x}-{{b}_{1}}{{\varphi }^{x}_{2}}-{{\varphi }_{3}}{{b}_{2}}_{z}-{{b}_{3}}{{\varphi }^{z}_{2}})+{{\psi }^{y}_{1}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.4)

$\begin{eqnarray} &&\begin{aligned} & {{\phi }^{t}_{3}}-\nu ({{\phi }^{xx}_{3}}+{{\phi }^{yy}_{3}}+{{\phi }^{zz}_{3}})+{{\phi }_{1}}{{u}_{3}}_{x}+{{u}_{1}}{{\phi }^{x}_{3}}+{{\phi }_{2}}{{u}_{3}}_{y}+{{u}_{2}}{{\phi }^{y}_{3}}+{{\phi }_{3}}{{u}_{3}}_{z}+{{u}_{3}}{{\phi }^{z}_{3}}\\ &+\kappa ({{\varphi }_{1}}{{b}_{1z}}+{{b}_{1}}{{\varphi }^{z}_{1}}+{{\varphi }_{2}}{{b}_{2z}}+{{b}_{2}}{{\varphi }^{z}_{2}}-{{\varphi }_{1}}{{b}_{3}}_{x}-{{b}_{1}}{{\varphi }^{x}_{3}}-{{\varphi }_{2}}{{b}_{3y}}-{{b}_{2}}{{\varphi }^{y}_{3}})+{{\psi }^{z}_{1}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.5)

$\begin{eqnarray} &&\begin{aligned} & {{\varphi }^{t}_{1}}-\eta ({{\varphi }^{xx}_{1}}+{{\varphi }^{yy}_{1}}+{{\varphi }^{zz}_{1}})-{{\varphi }_{1}}{{u}_{1}}_{x}-{{b}_{1}}{{\phi }^{x}_{1}}-{{\varphi }_{2}}{{u}_{1}}_{y}-{{b}_{2}}{{\phi }^{y}_{1}}-{{\varphi }_{3}}{{u}_{1}}_{z}\\ &-{{b}_{3}}{{\phi }^{z}_{1}}+{{\phi }_{1}}{{b}_{1x}}+{{u}_{1}}{{\varphi }^{x}_{1}}+{{\phi }_{2}}{{b}_{1}}_{y}+{{u}_{2}}{{\varphi }^{y}_{1}}+{{\phi }_{3}}{{b}_{1}}_{z}+{{u}_{3}}{{\varphi }^{z}_{1}}+{{\psi }^{x}_{2}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.6)

$\begin{eqnarray} &&\begin{aligned} & {{\varphi }^{t}_{2}}-\eta ({{\varphi }^{xx}_{2}}+{{\varphi }^{yy}_{2}}+{{\varphi }^{zz}_{2}})-{{\varphi }_{1}}{{u}_{2}}_{x}-{{b}_{1}}{{\phi }^{x}_{2}}-{{\varphi }_{2}}{{u}_{2}}_{y}-{{b}_{2}}{{\phi }^{y}_{2}}-{{\varphi }_{3}}{{u}_{2}}_{z}\\ &-{{b}_{3}}{{\phi }^{z}_{2}}+{{\phi }_{1}}{{b}_{2x}}+{{u}_{1}}{{\varphi }^{x}_{2}}+{{\phi }_{2}}{{b}_{2}}_{y}+{{u}_{2}}{{\varphi }^{y}_{2}}+{{\phi }_{3}}{{b}_{2}}_{z}+{{u}_{3}}{{\varphi }^{z}_{2}}+{{\psi }^{y}_{2}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.7)

$\begin{eqnarray} &&\begin{aligned} &{{\varphi }^{t}_{3}}-\eta ({{\varphi }^{xx}_{3}}+{{\varphi }^{yy}_{3}}+{{\varphi }^{zz}_{3}})-{{\varphi }_{1}}{{u}_{3}}_{x}-{{b}_{1}}{{\phi }^{x}_{3}}-{{\varphi }_{2}}{{u}_{3}}_{y}-{{b}_{2}}{{\phi }^{y}_{3}}-{{\varphi }_{3}}{{u}_{3}}_{z}\\ &-{{b}_{3}}{{\phi }^{z}_{3}}+{{\phi }_{1}}{{b}_{3x}}+{{u}_{1}}{{\varphi }^{x}_{3}}+{{\phi }_{2}}{{b}_{3}}_{y}+{{u}_{2}}{{\varphi }^{y}_{3}}+{{\phi }_{3}}{{b}_{3}}_{z}+{{u}_{3}}{{\varphi }^{z}_{3}}+{{\psi }^{z}_{2}} = 0, \\ \end{aligned} \end{eqnarray}$

(4.8)

$\begin{eqnarray} && {{\phi }^{x}_{1}}+{{\phi }^{y}_{2}}+{{\phi }^{z}_{3}} = 0, \ {{\varphi }^{x}_{1}}+{{\varphi }^{y}_{2}}+{{\varphi }^{z}_{3}} = 0. \end{eqnarray}$

(4.9)

4.1.1. Inviscid MHD equations

Choosing $\nu = \eta = 0$ and $\kappa = 1$ in equations (4.1), the inviscid MHD equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}}+{{u}_{3}}{{u}_{1z}})+({{b}_{2}}{{b}_{2x}}+{{b}_{3}}{{b}_{3x}}-{{b}_{2}}{{b}_{1y}}-{{b}_{3}}{{b}_{1z}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}}+{{u}_{3}}{{u}_{2z}})+({{b}_{1}}{{b}_{1y}}+{{b}_{3}}{{b}_{3y}}-{{b}_{1}}{{b}_{2x}}-{{b}_{3}}{{b}_{2z}})+{{p}_{y}} = 0, \\ & {{u}_{3t}}+({{u}_{1}}u_{3x}^{{}}+{{u}_{2}}{{u}_{3y}}+{{u}_{3}}{{u}_{3z}})+({{b}_{1}}{{b}_{1z}}+{{b}_{2}}{{b}_{2z}}-{{b}_{1}}{{b}_{3x}}-{{b}_{2}}{{b}_{3y}})+{{p}_{z}} = 0, \\ & {{b}_{1t}}-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}}+{{b}_{3}}{{u}_{1z}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}}+{{u}_{3}}{{b}_{1z}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}}+{{b}_{3}}{{u}_{2z}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}}+{{u}_{3}}{{b}_{2z}})+{{r}_{y}} = 0, \\ & {{b}_{3t}}-({{b}_{1}}{{u}_{3x}}+{{b}_{2}}{{u}_{3y}}+{{b}_{3}}{{u}_{3z}})+({{u}_{1}}{{b}_{3x}}+{{u}_{2}}{{b}_{3y}}+{{u}_{3}}{{b}_{3z}})+{{r}_{z}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}}+{{u}_{3z}} = 0, \ {{b}_{1x}}+{{b}_{2y}}+{{b}_{3z}} = 0. \\ \end{aligned} \right. \end{equation}$

(4.10)

Solving (4.3)–(4.9) with $\nu = \eta = 0$ and $\kappa = 1$ , the coefficient functions of vector field $\underline{V}$ can be obtained as

$\begin{eqnarray} && {{\zeta }_{1}} = 2{{C}_{1}}t+{{C}_{2}}, \ {{\zeta }_{2}} = {{C}_{0}}x-{{C}_{12}}y-{{C}_{13}}z+{{f}_{1}}(t)+{{C}_{3}}, \\ && {{\zeta }_{3}} = {{C}_{12}}x+{{C}_{0}}y-{{C}_{23}}z+{{f}_{2}}(t)+{{C}_{4}}, \ {{\zeta }_{4}} = {{C}_{13}}x+{{C}_{23}}y+{{C}_{0}}z+{{f}_{3}}(t)+{{C}_{5}}, \\ &&{{\phi }_{1}} = ({{C}_{0}}-2{{C}_{1}}){{u}_{1}}-{{C}_{12}}{{u}_{2}}-{{C}_{13}}{{u}_{3}}+{{f}^{\prime }_{1}}(t), \ {{\phi }_{2}} = {{C}_{12}}{{u}_{1}}+({{C}_{0}}-2{{C}_{1}}){{u}_{2}}-{{C}_{23}}{{u}_{3}}+{{f}^{\prime }_{2}}(t), \\ && {{\phi }_{3}} = {{C}_{13}}{{u}_{1}}+{{C}_{23}}{{u}_{2}}+({{C}_{0}}-2{{C}_{1}}){{u}_{3}}+{{f}^{\prime }_{3}}(t), \ {{\varphi }_{1}} = ({{C}_{0}}-2{{C}_{1}}){{b}_{1}}-{{C}_{12}}{{b}_{2}}-{{C}_{13}}{{b}_{3}}, \\ && {{\varphi }_{2}} = {{C}_{12}}{{b}_{1}}+({{C}_{0}}-2{{C}_{1}}){{b}_{2}}-{{C}_{23}}{{b}_{3}}, \ {{\varphi }_{3}} = {{C}_{13}}{{b}_{1}}+{{C}_{23}}{{b}_{2}}+({{C}_{0}}-2{{C}_{1}}){{b}_{3}}, \\ && {{\psi }_{1}} = 2({{C}_{0}}-2{{C}_{1}})p-x{{f}^{\prime \prime }_{1}}(t)-y{{f}^{\prime \prime }_{2}}(t)-z{{f}^{\prime \prime }_{3}}(t)+\alpha (t), \ {{\psi }_{2}} = 2({{C}_{0}}-2{{C}_{1}})r+\beta (t). \end{eqnarray}$

When ${{C}_{2}} = 1$ , ${{C}_{3}} = {{\bar{v}}_{1}}$ , ${{C}_{4}} = {{\bar{v}}_{2}}$ , ${{C}_{5}} = {{\bar{v}}_{3}}$ , ${{C}_{0}} = {{C}_{1}} = {{C}_{12}} = {{C}_{13}} = {{C}_{23}} = 0$ , ${{f}_{1}}(t) = {{f}_{2}}(t) = 0$ ,

$\begin{equation} \begin{aligned} \underline{V}& = ({{C}_{2}}\frac{\partial }{\partial t}+{{C}_{3}}\frac{\partial }{\partial x}+{{C}_{4}}\frac{\partial }{\partial y}+{{C}_{5}}\frac{\partial }{\partial z})+\alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r} \\ & = \frac{\partial }{\partial t}+{{{\bar{v}}}_{1}}\frac{\partial }{\partial x}+{{{\bar{v}}}_{2}}\frac{\partial }{\partial y}+{{{\bar{v}}}_{3}}\frac{\partial }{\partial z}+\alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r}. \\ \end{aligned} \end{equation}$

(4.11)

The characteristic equation is

$\begin{equation} \frac{dt}{1} = \frac{dx}{{{{\bar{v}}}_{1}}} = \frac{dy}{{{{\bar{v}}}_{2}}} = \frac{dz}{{{{\bar{v}}}_{3}}} = \frac{d{{u}_{1}}}{0} = \frac{d{{u}_{2}}}{0} = \frac{d{{u}_{3}}}{0} = \frac{d{{b}_{1}}}{0} = \frac{d{{b}_{2}}}{0} = \frac{d{{b}_{3}}}{0} = \frac{dp}{\alpha (t)} = \frac{dr}{\beta (t)}. \end{equation}$

(4.12)

It follows from (4.12) that corresponding invariants are

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{1}} = x-{{{\bar{v}}}_{1}}t, \ {{{\bar{\zeta }}}_{2}} = y-{{{\bar{v}}}_{2}}t, \ {{{\bar{\zeta }}}_{3}} = z-{{{\bar{v}}}_{3}}t, \ {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{u}_{2}}, \\ & {{F}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{u}_{3}}, \ {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{b}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{b}_{2}}, \ {{G}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{b}_{3}}, \\ & Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -p+\int{\alpha (t)dt, }\ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -r+\int{\beta (t)dt.} \end{aligned} \end{equation}$

(4.13)

Substituting (4.13) into (4.10), reduced equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{{\bar{v}}}_{1}}{{F}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{F}_{1{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{F}_{1{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}+{{F}_{3}}{{F}_{1{{{\bar{\zeta }}}_{3}}}}+{{G}_{2}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}+{{G}_{3}}{{G}_{3{{{\bar{\zeta }}}_{1}}}}\\ &-{{G}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}-{{G}_{3}}{{G}_{1{{{\bar{\zeta }}}_{3}}}}-{{Q}_{{{{\bar{\zeta }}}_{1}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{F}_{2}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{F}_{2{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{F}_{2{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{F}_{3}}{{F}_{2{{{\bar{\zeta }}}_{3}}}}+{{G}_{1}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}+{{G}_{3}}{{G}_{3{{{\bar{\zeta }}}_{2}}}}\\ &-{{G}_{1}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}-{{G}_{3}}{{G}_{2{{{\bar{\zeta }}}_{3}}}}-{{Q}_{{{{\bar{\zeta }}}_{2}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{F}_{3}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{F}_{3{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{F}_{3{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{F}_{3{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{F}_{3{{{\bar{\zeta }}}_{2}}}}+{{F}_{3}}{{F}_{3{{{\bar{\zeta }}}_{3}}}}+{{G}_{1}}{{G}_{1{{{\bar{\zeta }}}_{3}}}}+{{G}_{2}}{{G}_{2{{{\bar{\zeta }}}_{3}}}}\\ &-{{G}_{1}}{{G}_{3{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{G}_{3{{{\bar{\zeta }}}_{2}}}}-{{Q}_{{{{\bar{\zeta }}}_{3}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{G}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{G}_{1{{{\bar{\zeta }}}_{3}}}}-{{G}_{1}}{{F}_{1{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{F}_{1{{{\bar{\zeta }}}_{2}}}}-{{G}_{3}}{{F}_{1{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{G}_{1{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{G}_{1{{{\bar{\zeta }}}_{2}}}}\\ &+{{F}_{3}}{{G}_{1{{{\bar{\zeta }}}_{3}}}}-{{R}_{{{{\bar{\zeta }}}_{1}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{G}_{2}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{G}_{2{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{G}_{2{{{\bar{\zeta }}}_{3}}}}-{{G}_{1}}{{F}_{2{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{F}_{2{{{\bar{\zeta }}}_{2}}}}-{{G}_{3}}{{F}_{2{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{G}_{2{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{G}_{2{{{\bar{\zeta }}}_{2}}}}\\ &+{{F}_{3}}{{G}_{2{{{\bar{\zeta }}}_{3}}}}-{{R}_{{{{\bar{\zeta }}}_{2}}}} = 0, \\ & {{{\bar{v}}}_{1}}{{G}_{3}}_{{{{\bar{\zeta }}}_{1}}}+{{{\bar{v}}}_{2}}{{G}_{3{{{\bar{\zeta }}}_{2}}}}+{{{\bar{v}}}_{3}}{{G}_{3{{{\bar{\zeta }}}_{3}}}}-{{G}_{1}}{{F}_{3{{{\bar{\zeta }}}_{1}}}}-{{G}_{2}}{{F}_{3{{{\bar{\zeta }}}_{2}}}}-{{G}_{3}}{{F}_{3{{{\bar{\zeta }}}_{3}}}}+{{F}_{1}}{{G}_{3{{{\bar{\zeta }}}_{1}}}}+{{F}_{2}}{{G}_{3{{{\bar{\zeta }}}_{2}}}}\\ &+{{F}_{3}}{{G}_{3{{{\bar{\zeta }}}_{3}}}}-{{R}_{{{{\bar{\zeta }}}_{3}}}} = 0, \\ & {{F}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{F}_{2{{{\bar{\zeta }}}_{2}}}}+{{F}_{3{{{\bar{\zeta }}}_{3}}}} = 0, \ {{G}_{1}}_{{{{\bar{\zeta }}}_{1}}}+{{G}_{2{{{\bar{\zeta }}}_{2}}}}+{{G}_{3{{{\bar{\zeta }}}_{3}}}} = 0. \\ \end{aligned} \right. \end{equation}$

(4.14)

It can be obtained that (4.15)–(4.17) are three kinds of solutions for (4.14).

Case 1. Sin-cos-type solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\cos }^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{1}}, \\ & {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\cos }^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{2}}, \\ & {{F}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\cos }^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{3}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\sin (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})\cos (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{1}}, \\ & {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\sin (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})\cos (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{1}}, \\ & {{G}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\sin (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})\cos (2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{1}}, \\ &\begin{aligned} Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = &-\frac{3{{{\bar{v}}}_{1}}\sin (-4{{{\bar{\zeta }}}_{1}}+2{{{\bar{\zeta }}}_{2}}+2{{{\bar{\zeta }}}_{3}})}{2}-\frac{3\cos (-8{{{\bar{\zeta }}}_{1}}+4{{{\bar{\zeta }}}_{2}}+4{{{\bar{\zeta }}}_{3}})}{16}+m, \\ \end{aligned}\ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = n, \\ \end{aligned} \right. \end{equation}$

(4.15)

where $m$ and $n$ are arbitrary constants.

Case 2. Sech-type solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\operatorname{sech}}^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\operatorname{sech}}^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{2}}, \\ & {{F}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{\operatorname{sech}}^{2}}(2{{{\bar{\zeta }}}_{1}}-{{{\bar{\zeta }}}_{2}}-{{{\bar{\zeta }}}_{3}})-{{{\bar{v}}}_{3}}, \ {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\frac{1}{2}({{c}_{1}}+{{c}_{2}}), \\ & {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{c}_{1}}, \ {{G}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{c}_{2}}, \ Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = m, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = n, \\ \end{aligned} \right. \end{equation}$

(4.16)

where ${{c}_{1}}$ and ${{c}_{2}}$ are arbitrary constants.

Case 3. Rational solution.

$\begin{equation} \left\{ \begin{aligned} & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\frac{{{c}_{3}}{{{\bar{\zeta }}}_{2}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = \frac{{{c}_{3}}{{{\bar{\zeta }}}_{1}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{F}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{c}_{5}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -\frac{{{c}_{4}}{{{\bar{\zeta }}}_{2}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = \frac{{{c}_{4}}{{{\bar{\zeta }}}_{1}}}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}, \ {{G}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = -{{c}_{6}}, \\ & Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = \frac{{{c}_{3}}(2{{{\bar{\zeta }}}_{1}}{{{\bar{v}}}_{2}}-2{{{\bar{\zeta }}}_{2}}{{{\bar{v}}}_{1}}+{{c}_{3}})}{2(\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2})}+m, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = \frac{{{c}_{4}}({{{\bar{\zeta }}}_{1}}{{{\bar{v}}}_{2}}-{{{\bar{\zeta }}}_{2}}{{{\bar{v}}}_{1}})}{\bar{\zeta }_{1}^{2}+\bar{\zeta }_{2}^{2}}+n, \\ \end{aligned} \right. \end{equation}$

(4.17)

where ${{c}_{3}}, {{c}_{4}}, {{c}_{5}}$ and ${{c}_{6}}$ are arbitrary constants. Substituting (4.13) into (4.15)–(4.17), respectively, we obtain that (4.18)–(4.20) are three kinds of solutions for (3 + 1)-dimensional MHD equations (4.10).

Case 1. Sin-cos-type solution.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\cos }^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{1}}, \\ &{{u}_{2}} = {{\cos }^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{2}}, \\ &{{u}_{3}} = {{\cos }^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{3}}, \\ &{{b}_{1}} = \sin [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]\cos [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{1}}, \\ &{{b}_{2}} = \sin [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]\cos [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{1}}, \\ &{{b}_{3}} = \sin [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]\cos [2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{1}}, \\ &\begin{aligned}p = &\frac{3{{{\bar{v}}}_{1}}\sin [(4{{{\bar{v}}}_{1}}-2{{{\bar{v}}}_{2}}-2{{{\bar{v}}}_{3}})t-4x+2y+2z]}{2}\\ &+\frac{3\cos [(8{{{\bar{v}}}_{1}}-4{{{\bar{v}}}_{2}}-4{{{\bar{v}}}_{3}})t-8x+4y+4z]}{16}-m+\int{\alpha (t)dt}, \end{aligned}\\ &r = -n+\int{\beta (t)dt}.\\ \end{aligned} \end{equation}$

(4.18)

Case 2. Sech-type solution.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\operatorname{sech}}^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{1}}, \\ & {{u}_{2}} = {{\operatorname{sech}}^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{2}}, \\ &{{u}_{3}} = {{\operatorname{sech}}^{2}}[2x-y-z-(2{{\bar{v}}_{1}}-{{\bar{v}}_{2}}-{{\bar{v}}_{3}})t]+{{\bar{v}}_{3}}, \\ & {{b}_{1}} = \frac{1}{2}({{c}_{1}}+{{c}_{2}}), \ {{b}_{2}} = {{c}_{1}}, \ {{b}_{3}} = {{c}_{2}}, \ p = -m+\int{\alpha (t)dt}, \ r = -n+\int{\beta (t)dt}.\\ \end{aligned} \end{equation}$

(4.19)

Setting ${{\bar{v}}_{1}} = -2, {{\bar{v}}_{2}} = -4, {{\bar{v}}_{3}} = -1, y = -2$ and $x = 2$ for ${{u}_{1}}$ in (4.19), we obtain of solution ${{u}_{1}}$ as follows.

Figure 9. (a) The evolution of single soliton solution

$u_1$ , (b)

$u_1$ (

$z$ = 1, 2, 3).

DownLoad: Full-Size Img PowerPoint

Case 3. Rational solution.

$\begin{equation} \begin{aligned} & {{u}_{1}} = \frac{{{c}_{3}}(y-{{{\bar{v}}}_{2}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{u}_{2}} = -\frac{{{c}_{3}}(x-{{{\bar{v}}}_{1}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{u}_{3}} = {{c}_{5}}, \\ & {{b}_{1}} = \frac{{{c}_{4}}(y-{{{\bar{v}}}_{2}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{b}_{2}} = -\frac{{{c}_{4}}(x-{{{\bar{v}}}_{1}}t)}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}, \ {{b}_{3}} = {{c}_{6}}, \\ & p = -\frac{{{c}_{3}}[2{(x-{{{\bar{v}}}_{1}}t)}{{{\bar{v}}}_{2}}-2{(y-{{{\bar{v}}}_{2}}t)}{{{\bar{v}}}_{1}}+{{c}_{3}}]}{2[{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}]}-m+\int{\alpha (t)dt}, \\ &r = -\frac{{{c}_{4}}[{(x-{{{\bar{v}}}_{1}}t)}{{{\bar{v}}}_{2}}-{(y-{{{\bar{v}}}_{2}}t)}{{{\bar{v}}}_{1}}]}{{{(x-{{{\bar{v}}}_{1}}t)}^{2}}+{{(y-{{{\bar{v}}}_{2}}t)}^{2}}}-n+\int{\beta (t)dt}.\\ \end{aligned} \end{equation}$

(4.20)

Remark 4.1. (1) If $b_1 = b_2 = b_3 = 0$ and $r = 0$ in (4.19) and (4.20), then (4.19) and (4.20) reduce to exact solutions for (3 + 1)-dimensional Euler equation.

(2) Since $\omega = \nabla \times \mathbf{U}\ne \mathbf{0}$ in (4.18) and (4.19) and $\omega = \nabla \times \mathbf{U} = \mathbf{0}$ in (4.20), it can be concluded that (4.18) and (4.19) correspond to rotational flow. Additionally, (4.20) corresponds to inrotational flow.

4.1.2. Viscous MHD equations

Without loss of generality, choosing $\nu = \eta = \kappa = 1$ in Eq (4.1), the viscous MHD equations can be obtained as

$\begin{equation} \left\{ \begin{aligned} & {{u}_{1t}}-({{u}_{1xx}}+{{u}_{1yy}}+{{u}_{1zz}})+({{u}_{1}}u_{1x}^{{}}+{{u}_{2}}{{u}_{1y}}+{{u}_{3}}{{u}_{1z}})+({{b}_{2}}{{b}_{2x}}+{{b}_{3}}{{b}_{3x}}-{{b}_{2}}{{b}_{1y}}-{{b}_{3}}{{b}_{1z}})+{{p}_{x}} = 0, \\ & {{u}_{2t}}-({{u}_{2xx}}+{{u}_{2yy}}+{{u}_{2zz}})+({{u}_{1}}u_{2x}^{{}}+{{u}_{2}}{{u}_{2y}}+{{u}_{3}}{{u}_{2z}})+({{b}_{1}}{{b}_{1y}}+{{b}_{3}}{{b}_{3y}}-{{b}_{1}}{{b}_{2x}}-{{b}_{3}}{{b}_{2z}})+{{p}_{y}} = 0, \\ & {{u}_{3t}}-({{u}_{3xx}}+{{u}_{3yy}}+{{u}_{3zz}})+({{u}_{1}}u_{3x}^{{}}+{{u}_{2}}{{u}_{3y}}+{{u}_{3}}{{u}_{3z}})+({{b}_{1}}{{b}_{1z}}+{{b}_{2}}{{b}_{2z}}-{{b}_{1}}{{b}_{3x}}-{{b}_{2}}{{b}_{3y}})+{{p}_{z}} = 0, \\ & {{b}_{1t}}-({{b}_{1xx}}+{{b}_{1yy}}+{{b}_{1zz}})-({{b}_{1}}{{u}_{1x}}+{{b}_{2}}{{u}_{1y}}+{{b}_{3}}{{u}_{1z}})+({{u}_{1}}{{b}_{1x}}+{{u}_{2}}{{b}_{1y}}+{{u}_{3}}{{b}_{1z}})+{{r}_{x}} = 0, \\ & {{b}_{2t}}-({{b}_{2xx}}+{{b}_{2yy}}+{{b}_{2zz}})-({{b}_{1}}{{u}_{2x}}+{{b}_{2}}{{u}_{2y}}+{{b}_{3}}{{u}_{2z}})+({{u}_{1}}{{b}_{2x}}+{{u}_{2}}{{b}_{2y}}+{{u}_{3}}{{b}_{2z}})+{{r}_{y}} = 0, \\ & {{b}_{3t}}-({{b}_{3xx}}+{{b}_{3yy}}+{{b}_{3zz}})-({{b}_{1}}{{u}_{3x}}+{{b}_{2}}{{u}_{3y}}+{{b}_{3}}{{u}_{3z}})+({{u}_{1}}{{b}_{3x}}+{{u}_{2}}{{b}_{3y}}+{{u}_{3}}{{b}_{3z}})+{{r}_{z}} = 0, \\ & {{u}_{1x}}+{{u}_{2y}}+{{u}_{3z}} = 0, \ {{b}_{1x}}+{{b}_{2y}}+{{b}_{3z}} = 0. \\ \end{aligned} \right. \end{equation}$

(4.21)

Solving (4.3)–(4.9) with $\nu = \eta = \kappa = 1$ , the coefficient functions of vector field $\underline{V}$ can be obtained as

$\begin{equation} \begin{aligned} & {{\zeta }_{1}} = 2{{C}_{1}}t+{{C}_{2}}, \ {{\zeta }_{2}} = {{C}_{1}}x-{{C}_{12}}y-{{C}_{13}}z+{{f}_{1}}(t)+{{C}_{3}}, \\ & {{\zeta }_{3}} = {{C}_{12}}x+{{C}_{1}}y-{{C}_{23}}z+{{f}_{2}}(t)+{{C}_{4}}, \ {{\zeta }_{4}} = {{C}_{13}}x+{{C}_{23}}y+{{C}_{1}}z+{{f}_{3}}(t)+{{C}_{5}}, \\ & {{\phi }_{1}} = -{{C}_{1}}{{u}_{1}}-{{C}_{12}}{{u}_{2}}-{{C}_{13}}{{u}_{3}}+{{f}^{\prime }_{1}}(t), \ {{\phi }_{2}} = {{C}_{12}}{{u}_{1}}-{{C}_{1}}{{u}_{2}}-{{C}_{23}}{{u}_{3}}+{{f}^{\prime }_{2}}(t), \\ & {{\phi }_{3}} = {{C}_{13}}{{u}_{1}}+{{C}_{23}}{{u}_{2}}-{{C}_{1}}{{u}_{3}}+{{f}^{\prime }_{3}}(t), \ {{\varphi }_{1}} = -{{C}_{1}}{{b}_{1}}-{{C}_{12}}{{b}_{2}}-{{C}_{13}}{{b}_{3}}, \\ & {{\varphi }_{2}} = {{C}_{12}}{{b}_{1}}-{{C}_{1}}{{b}_{2}}-{{C}_{23}}{{b}_{3}}, \ {{\varphi }_{3}} = {{C}_{13}}{{b}_{1}}+{{C}_{23}}{{b}_{2}}-{{C}_{1}}{{b}_{3}}, \\ & {{\psi }_{1}} = -2{{C}_{1}}p-x{{f}^{\prime \prime }_{1}}(t)-y{{f}^{\prime \prime }_{2}}(t)-z{{f}^{\prime \prime }_{3}}(t)+\alpha (t), \ {{\psi }_{2}} = -2{{C}_{1}}r+\beta (t). \\ \end{aligned} \end{equation}$

(4.22)

Case 1. ${{C}_{1}} = {{C}_{2}} = {{C}_{3}} = {{C}_{4}} = {{C}_{5}} = {{C}_{12}} = {{C}_{13}} = {{C}_{23}} = {{f}_{1}}(t) = {{f}_{2}}(t) = 0$ , $\underline{V} = \alpha (t)\frac{\partial }{\partial p}+\beta (t)\frac{\partial }{\partial r}.$

For invariants

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{0}} = t, \ {{{\bar{\zeta }}}_{1}} = x, \ {{{\bar{\zeta }}}_{2}} = y, \ {{{\bar{\zeta }}}_{3}} = z, \\ & {{F}_{1}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{2}}) = -{{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{1}}) = -{{u}_{2}}, \ {{F}_{3}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{3}}) = -{{u}_{3}}, \\ & {{G}_{1}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{2}}) = -{{b}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{1}}) = -{{b}_{2}}, \ {{G}_{3}}({{{\bar{\zeta }}}_{0}}, {{{\bar{\zeta }}}_{3}}) = -{{b}_{3}}. \\ \end{aligned} \end{equation}$

(4.23)

Substituting invariants (4.23) into (4.21), and solving the reduced equations,

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{g}_{1}}{{e}^{-t}}\cos y, \ {{u}_{2}} = {{g}_{2}}{{e}^{-t}}\cos x, \ {{u}_{3}} = {{c}_{7}}, \\ & {{b}_{1}} = {{g}_{3}}{{e}^{-t}}\cos y, \ {{b}_{2}} = {{g}_{4}}{{e}^{-t}}\cos x, \ {{b}_{3}} = {{c}_{8}}, \\ & p = \frac{[-\cos (2y){{g}^{2}_{3}{g}_{4}}+2{g}^{3}_{4}sin^{2}x+4{g}_{3}({{g}^{2}_{2}}-{{g}^{2}_{4}})\sin x\sin y]{{e}^{-2t}}}{4{{g}_{4}}}+m(t), \ r = n(t), \\ \end{aligned} \end{equation}$

(4.24)

is a sin/cos-type solution for MHD equations (4.21), where ${{g}_{1}}{{g}_{4}}-{{g}_{2}}{{g}_{3}} = 0.\ {{c}_{7}}$ and ${{c}_{8}}$ are arbitrary constants. $m(t)$ and $n(t)$ are arbitrary functions related to $t$ only.

Case 2. ${{C}_{2}} = 1$ , ${{C}_{i}} = {{C}_{12}} = {{C}_{13}} = {{C}_{23}} = {{f}_{j}}(t) = \alpha (t) = \beta (t) = 0\ ({i} = 1, 3, 4, 5, {j} = 1, 2, 3), \ \underline{V} = \frac{\partial }{\partial t}.$

The corresponding invariants are

$\begin{equation} \begin{aligned} & {{{\bar{\zeta }}}_{1}} = x, \ {{{\bar{\zeta }}}_{2}} = y, \ {{{\bar{\zeta }}}_{3}} = z, \ Q({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = p, \ R({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = r, \\ & {{F}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{u}_{1}}, \ {{F}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{u}_{2}}, \ {{F}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{u}_{3}}, \\&{{G}_{1}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{b}_{1}}, \ {{G}_{2}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{b}_{2}}, \ {{G}_{3}}({{{\bar{\zeta }}}_{1}}, {{{\bar{\zeta }}}_{2}}, {{{\bar{\zeta }}}_{3}}) = {{b}_{3}}.\\ \end{aligned} \end{equation}$

(4.25)

Substituting invariants (4.25) into (4.21), and solving the reduced equations,

$\begin{equation} \begin{aligned} & {{u}_{1}} = {{\operatorname{sech}}^{2}}(x+iy), \ {{u}_{2}} = i{{\operatorname{sech}}^{2}}(x+iy), \ {{u}_{3}} = {{c}_{9}}, \ p = m, \\ &{{b}_{1}} = {{\operatorname{sech}}^{2}}(x+iy), \ {{b}_{2}} = i{{\operatorname{sech}}^{2}}(x+iy), \ {{b}_{3}} = {{c}_{10}}, \ r = n, \\ \end{aligned} \end{equation}$

(4.26)

is a sech-type solution for MHD equations (4.21), where ${{c}_{9}}$ and ${{c}_{10}}$ are arbitrary constants. Using symmetry $\underline{V} = t\frac{\partial }{\partial x}+t\frac{\partial }{\partial y}+t\frac{\partial }{\partial z}+\frac{\partial }{\partial {{u}_{1}}}+\frac{\partial }{\partial {{u}_{2}}}+\frac{\partial }{\partial {{u}_{3}}}$ , solution (4.26) can further generate the following invariant solution,

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t))+\varepsilon , \ {{u}_{2}} = i{{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t))+\varepsilon , \\ & {{u}_{3}} = {{c}_{9}}+\varepsilon, \ {{b}_{1}} = {{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t)), \ {{b}_{2}} = i{{\operatorname{sech}}^{2}}(x-\varepsilon t+i(y-\varepsilon t)), \\ & {{b}_{3}} = {{c}_{10}}, \ p = m(t), \ r = n(t).\\ \end{aligned} \end{equation}$

(4.27)

Remark 4.2. (1) The lump solution (4.20) for inviscid MHD equations (4.10) also satisfies the viscous MHD equations (4.21).

(2) If $b_1 = b_2 = b_3 = 0$ and $r = 0$ in (4.27), then (4.27) reduces to exact solutions for (3 + 1)-dimensional Navier-Stokes equation.

(3) Since $\omega = \nabla \times \mathbf{U}\ne \mathbf{0}$ in (4.24) and $\omega = \nabla \times \mathbf{U} = \mathbf{0}$ in (4.27), it can be concluded that (4.24) corresponds to rotational flow. Moreover, (4.27) corresponds to inrotational flow.

4.2. Generalized Riccati equation expansion method for MHD equations

Using traveling wave transformation $\zeta = {{k}_{2}}x+{{k}_{3}}y+{{k}_{4}}z-{{k}_{1}}t$ , Eq (4.1) are transformed into following ODEs as

$\begin{equation} \left\{ \begin{aligned} & -{{k}_{1}}{{u}_{1\zeta }}-\nu ({{k}^{2}_{2}}{{u}_{1\zeta \zeta }}+{{k}^{2}_{3}}{{u}_{1\zeta \zeta }}+{{k}^{2}_{4}}{{u}_{1\zeta \zeta }})+{{k}_{2}}{{u}_{1}}{{u}_{1\zeta }}+{{k}_{3}}{{u}_{2}}{{u}_{1\zeta }}+{{k}_{4}}{{u}_{3}}{{u}_{1\zeta }}\\ &+\kappa ({{k}_{2}}{{b}_{2}}{{b}_{2\zeta }}+{{k}_{2}}{{b}_{3}}{{b}_{3\zeta }}-{{k}_{3}}{{b}_{2}}{{b}_{1\zeta }}-{{k}_{4}}{{b}_{3}}{{b}_{1\zeta }}) +{{k}_{2}}{{p}_{\zeta }} = 0, \\ & -{{k}_{1}}{{u}_{2\zeta }}-\nu ({{k}^{2}_{2}}{{u}_{2\zeta \zeta }}+{{k}^{2}_{3}}{{u}_{2\zeta \zeta }}+{{k}^{2}_{4}}{{u}_{2\zeta \zeta }})+{{k}_{2}}{{u}_{1}}{{u}_{2\zeta }}+{{k}_{3}}{{u}_{2}}{{u}_{2\zeta }}+{{k}_{4}}{{u}_{3}}{{u}_{2\zeta }}\\ &+\kappa ({{k}_{3}}{{b}_{1}}{{b}_{1\zeta }}+{{k}_{3}}{{b}_{3}}{{b}_{3\zeta }}-{{k}_{2}}{{b}_{1}}{{b}_{2\zeta }}-{{k}_{4}}{{b}_{3}}{{b}_{2\zeta }}) +{{k}_{3}}{{p}_{\zeta }} = 0, \\ & -{{k}_{1}}{{u}_{3\zeta }}-\nu ({{k}^{2}_{2}}{{u}_{3\zeta \zeta }}+{{k}^{2}_{3}}{{u}_{3\zeta \zeta }}+{{k}^{2}_{4}}{{u}_{3\zeta \zeta }})+{{k}_{2}}{{u}_{1}}{{u}_{3\zeta }}+{{k}_{3}}{{u}_{2}}{{u}_{3\zeta }}+{{k}_{4}}{{u}_{3}}{{u}_{3\zeta }}\\ &+\kappa ({{k}_{4}}{{b}_{1}}{{b}_{1\zeta }}+{{k}_{4}}{{b}_{2}}{{b}_{2\zeta }}-{{k}_{2}}{{b}_{1}}{{b}_{3\zeta }}-{{k}_{3}}{{b}_{2}}{{b}_{3\zeta }})+{{k}_{4}}{{p}_{\zeta }} = 0, \\ & -{{k}_{1}}{{b}_{1\zeta }}-\eta ({{k}^{2}_{2}}{{b}_{1\zeta \zeta }}+{{k}^{2}_{3}}{{b}_{1\zeta \zeta }}+{{k}^{2}_{4}}{{b}_{1\zeta \zeta }})-({{k}_{2}}{{b}_{1}}{{u}_{1\zeta }}+{{k}_{3}}{{b}_{2}}{{u}_{1\zeta }}+{{k}_{4}}{{b}_{3}}{{u}_{1\zeta }})\\ &+{{k}_{2}}{{u}_{1}}{{b}_{1\zeta }}+{{k}_{3}}{{u}_{2}}{{b}_{1\zeta }}+{{k}_{4}}{{u}_{3}}{{b}_{1\zeta }}+{{k}_{2}}{{r}_{\zeta }} = 0, \\ & -{{k}_{1}}{{b}_{2\zeta }}-\eta ({{k}^{2}_{2}}{{b}_{2\zeta \zeta }}+{{k}^{2}_{3}}{{b}_{2\zeta \zeta }}+{{k}^{2}_{4}}{{b}_{2\zeta \zeta }})-({{k}_{2}}{{b}_{1}}{{u}_{2\zeta }}+{{k}_{3}}{{b}_{2}}{{u}_{2\zeta }}+{{k}_{4}}{{b}_{3}}{{u}_{2\zeta }})\\ &+{{k}_{2}}{{u}_{1}}{{b}_{2\zeta }}+{{k}_{3}}{{u}_{2}}{{b}_{2\zeta }}+{{k}_{4}}{{u}_{3}}{{b}_{2\zeta }}+{{k}_{3}}{{r}_{\zeta }} = 0, \\ & -{{k}_{1}}{{b}_{3\zeta }}-\eta ({{k}^{2}_{2}}{{b}_{3\zeta \zeta }}+{{k}^{2}_{3}}{{b}_{3\zeta \zeta }}+{{k}^{2}_{4}}{{b}_{3\zeta \zeta }})-({{k}_{2}}{{b}_{1}}{{u}_{3\zeta }}+{{k}_{3}}{{b}_{2}}{{u}_{3\zeta }}+{{k}_{4}}{{b}_{3}}{{u}_{3\zeta }})\\ &+{{k}_{2}}{{u}_{1}}{{b}_{3\zeta }}+{{k}_{3}}{{u}_{2}}{{b}_{3\zeta }}+{{k}_{4}}{{u}_{3}}{{b}_{3\zeta }}+{{k}_{4}}{{r}_{\zeta }} = 0, \\ & {{k}_{2}}{{u}_{1\zeta }}+{{k}_{3}}{{u}_{2\zeta }}+{{k}_{4}}{{u}_{3\zeta }} = 0, \ {{k}_{2}}{{b}_{1\zeta }}+{{k}_{3}}{{b}_{2\zeta }}+{{k}_{4}}{{b}_{3\zeta }} = 0. \\ \end{aligned} \right. \end{equation}$

(4.28)

Suppose that the solution of ODEs (4.28) can be expressed as a polynomial of $\phi (\zeta)$ as follows.

$\begin{equation} \begin{aligned} & {{u}_{1}} = \sum\limits_{i = 0}^{{{N}_{1}}}{{{a}_{i}}{{\phi }^{i}}}(\zeta ), \ {{u}_{2}} = \sum\limits_{i = 0}^{{{N}_{2}}}{{{m}_{i}}{{\phi }^{i}}}(\zeta ), \ {{u}_{3}} = \sum\limits_{i = 0}^{{{N}_{3}}}{{{d}_{i}}{{\phi }^{i}}}(\zeta ), \ {{b}_{1}} = \sum\limits_{i = 0}^{{{N}_{4}}}{{{n}_{i}}{{\phi }^{i}}}(\zeta ), \\ & {{b}_{2}} = \sum\limits_{i = 0}^{{{N}_{5}}}{{{s}_{i}}{{\phi }^{i}}}(\zeta ), \ {{b}_{3}} = \sum\limits_{i = 0}^{{{N}_{6}}}{{{f}_{i}}{{\phi }^{i}}}(\zeta ), \ p = l(t)+\sum\limits_{i = 0}^{{{N}_{7}}}{{{l}_{i}}{{\phi }^{i}}}(\zeta ), \ r = q(t)+\sum\limits_{i = 0}^{{{N}_{8}}}{{{q}_{i}}{{\phi }^{i}}}(\zeta ), \\ \end{aligned} \end{equation}$

(4.29)

where ${{a}_{i}}, {{m}_{i}}, {{d}_{i}}, {{n}_{i}}, {{s}_{i}}, {{f}_{i}}, {{l}_{i}}, {{q}_{i}}$ are undetermined constants and ${{a}_{{{N}_{1}}}}$ , ${{m}_{{{N}_{2}}}}$ , ${{d}_{{{N}_{3}}}}$ , ${{n}_{{{N}_{4}}}}$ , ${{s}_{{{N}_{5}}}}$ , ${{f}_{{{N}_{6}}}}\ne 0$ . $l(t)$ and $q(t)$ are arbitrary functions related to $t$ only. $\phi (\zeta)$ satisfies Eq (3.27). We choose ${{N}_{1}} = {{N}_{2}} = {{N}_{3}} = {{N}_{4}} = {{N}_{5}} = {{N}_{6}} = {{N}_{7}} = {{N}_{8}} = 2$ with can balance the highest order of the derivative and nonlinear terms in ODEs.

4.2.1. Inviscid MHD equations

When $\nu = \eta = 0$ and $\kappa = 1$ in ODEs (4.28), substituting (4.29) and (3.27) into (4.28), we collect the coefficients of ${{\phi }^{i}}(\zeta)$ and set them to be zeros, we obtain

$\begin{equation} \nonumber \begin{aligned} & {{a}_{0}} = {{a}_{0}}, {{a}_{1}} = {{a}_{1}}, {{a}_{2}} = {{a}_{2}}, {{d}_{0}} = {{d}_{0}}, {{d}_{1}} = {{d}_{1}}, {{d}_{2}} = {{d}_{2}}, {{f}_{0}} = {{f}_{0}}, {{f}_{1}} = {{f}_{1}}, {{f}_{2}} = 0, \\ &{{k}_{1}} = {{k}_{1}}, {{k}_{2}} = {{k}_{2}}, {{k}_{3}} = {{k}_{3}}, {{k}_{4}} = {{k}_{4}}, {{l}_{1}} = \frac{(-{{k}^{2}_{2}}-{{k}^{2}_{3}}-{{k}^{2}_{4}}){{f}_{0}}{{f}_{1}}}{{{k}^{2}_{2}}+{{k}^{2}_{3}}}, {{l}_{2}} = -\frac{{{f}^{2}_{1}}({{k}^{2}_{2}}+{{k}^{2}_{3}}+{{k}^{2}_{4}})}{2({{k}^{2}_{2}}+{{k}^{2}_{3}})}, \\ &{{m}_{0}} = \frac{-{{a}_{0}}{{k}_{2}}-{{k}_{4}}{{d}_{0}}+{{k}_{1}}}{{{k}_{3}}}, {{m}_{1}} = \frac{-{{a}_{1}}{{k}_{2}}-{{k}_{4}}{{d}_{1}}}{{{k}_{3}}}, {{m}_{2}} = \frac{-{{k}_{2}}{{a}_{2}}-{{k}_{4}}{{d}_{2}}}{{{k}_{3}}}, {{n}_{0}} = {{n}_{0}}, \\ &{{n}_{1}} = \frac{{{f}_{1}}{{k}_{2}}{{k}_{4}}}{-{{k}^{2}_{2}}-{{k}^{2}_{3}}}, {{n}_{2}} = 0, {{q}_{1}} = 0, {{q}_{2}} = 0, {{s}_{0}} = \frac{-{{k}_{4}}{{f}_{0}}-{{k}_{2}}{{n}_{0}}}{{{k}_{3}}}, {{s}_{1}} = \frac{{{f}_{1}}{{k}_{3}}{{k}_{4}}}{-{{k}^{2}_{2}}-{{k}^{2}_{3}}}, {{s}_{2}} = 0. \end{aligned} \end{equation}$

Combined with the general solutions of (3.27) (c.f. ^[29]), it folllows from (4.29) that (4.30)–(4.38) are four kinds of solutions for (3 + 1)-dimensional inviscid MHD equations.

Case 1. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} > 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tanh-type solution can be obtained.

$\begin{eqnarray} &&\begin{aligned} {{u}_{1}} = &\frac{4{{a}_{0}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{a}_{2}}{{\xi }_{1}}-{{a}_{1}}{{\xi }_{2}}}{2{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ &+\frac{{{a}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{4{{\xi }^{2}_{2}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.30)

$\begin{eqnarray} &&\begin{aligned} {{u}_{2}} = &\frac{4{{\xi }^{2}_{2}}(-{{a}_{0}}{{k}_{2}}-{{d}_{0}}{{k}_{4}}+{{k}_{1}})+2{{\xi }_{1}}{{\xi }_{2}}({{k}_{2}}{{a}_{1}}+{{d}_{1}}{{k}_{4}})-{{\xi }^{2}_{1}}({{k}_{2}}{{a}_{2}}+{{d}_{2}}{{k}_{4}})}{4{{k}_{3}}{{\xi }^{2}_{2}}} \\ & +\frac{{{\xi }_{2}}({{a}_{1}}{{k}_{2}}+{{d}_{1}}{{k}_{4}})-{{\xi }_{1}}({{k}_{2}}{{a}_{2}}+{{d}_{2}}{{k}_{4}})}{2{{k}_{3}}{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & -\frac{{{k}_{2}}{{a}_{2}}+{{d}_{2}}{{k}_{4}}}{4{{k}_{3}}{{\xi }^{2}_{2}}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}){{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.31)

$\begin{eqnarray} &&\begin{aligned} {{u}_{3}} = &\frac{4{{d}_{0}}{{\xi }^{2}_{2}}-2{{d}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{d}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{-{{d}_{1}}{{\xi }_{2}}+{{d}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & +\frac{{{d}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{4{{\xi }^{2}_{2}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.32)

$\begin{eqnarray} &&\begin{aligned} {{b}_{1}} = &\frac{2{{n}_{0}}{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})+{{f}_{1}}{{k}_{2}}{{k}_{4}}{{\xi }_{1}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}+\frac{{{f}_{1}}{{k}_{2}}{{k}_{4}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.33)

$\begin{eqnarray} &&\begin{aligned} {{b}_{2}} = &\frac{-2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})({{k}_{4}}{{f}_{0}}+{{k}_{2}}{{n}_{0}})+{{k}^{2}_{3}}{{f}_{4}}{{f}_{1}}{{\xi }_{1}}}{2{{k}_{3}}{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}+\frac{{{k}_{3}}{{f}_{4}}{{f}_{1}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \end{aligned} \end{eqnarray}$

(4.34)

$\begin{eqnarray} &&{{b}_{3}} = \frac{2{{f}_{0}}{{\xi }_{2}}-{{f}_{1}}{{\xi }_{1}}}{2{{\xi }_{2}}}-\frac{{{f}_{1}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2{{\xi }_{2}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \end{eqnarray}$

(4.35)

where $\zeta = {{k}_{2}}x+{{k}_{3}}y+{{k}_{4}}z-{{k}_{1}}t.$

Setting ${{a}_{0}} = 6, {{a}_{1}} = 6, {{a}_{2}} = -2,$ ${{d}_{0}} = 1, {{d}_{1}} = -3, {{d}_{2}} = -2, {{k}_{1}} = 2,$ ${{k}_{2}} = -4, {{k}_{3}} = 1, {{k}_{4}} = 1, {{\xi }_{0}} = -1,$ ${{\xi }_{1}} = -2, {{\xi }_{2}} = 3, y = 1$ and $t = 5$ in (4.31), we obtain of kink solution ${{u}_{2}}$ as follows.

Figure 10. (a) $u_2$ , (b) $u_2$ ( $z$ = 4, 5, 6).

DownLoad: Full-Size Img PowerPoint

In particular, when ${{\xi }_{0}} = 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ , the following sinh-cosh-type solution can be obtained.

$\begin{equation} \begin{aligned} &\begin{aligned} {{u}_{1}} = &{{a}_{0}}-\frac{{{a}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{{{a}_{2}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \\ \end{aligned}\\ &\begin{aligned} {{u}_{2}} = &\frac{-{{a}_{0}}{{k}_{2}}-{{d}_{0}}{{k}_{4}}+{{k}_{1}}}{{{k}_{3}}}+\frac{({{a}_{1}}{{k}_{2}}+{{d}_{1}}{{k}_{4}}){{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{k}_{3}}{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}\\ &-\frac{({{k}_{2}}{{a}_{2}}+{{d}_{2}}{{k}_{4}}){{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{k}_{3}}{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \\ \end{aligned}\\ &\begin{aligned} {{u}_{3}} = {{d}_{0}}-\frac{{{d}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{{{d}_{2}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \\ \end{aligned}\\ &{{b}_{1}} = {{n}_{0}}+\frac{{{f}_{1}}{{k}_{2}}{{k}_{4}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}, \\ &{{b}_{2}} = \frac{-{{k}_{4}}{{f}_{0}}-{{k}_{2}}{{n}_{0}}}{{{k}_{3}}}+\frac{{{k}_{3}}{{k}_{4}}{{f}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{({{k}^{2}_{2}}+{{k}^{2}_{3}}){{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}\text{, }\\ &{{b}_{3}} = {{f}_{0}}-\frac{{{f}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}\text{. } \end{aligned} \end{equation}$

(4.36)

Setting ${{a}_{0}} = 2, {{a}_{1}} = -2, {{a}_{2}} = -\frac{12}{7}, {{d}_{0}} = -10, {{d}_{1}} = 12, {{d}_{2}} = 3, {{k}_{1}} = -14, {{k}_{2}} = -7, {{k}_{3}} = -2,$ ${{k}_{4}} = -2, {{\xi }_{0}} = 0, {{\xi }_{1}} = 1, {{\xi }_{2}} = -\frac{1}{2}, y = 1, C = 1$ and $x = 5$ in $u_2$ in (4.36), we obtain of kink-like solution ${{u}_{2}}$ as follows.

Figure 11. (a) $u_2$ , (b) $u_2$ ( $z$ = 4, 5, 6).

DownLoad: Full-Size Img PowerPoint

Case 2. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} < 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tan-type solution can be obtained.

$\begin{equation} \begin{aligned} &\begin{aligned} {{u}_{1}} = &\frac{4{{a}_{0}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{a}_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned}\\ &\begin{aligned} {{u}_{2}} = &\frac{4{{\xi }^{2}_{2}}(-{{a}_{0}}{{k}_{2}}-{{d}_{0}}{{k}_{4}}+{{k}_{1}})+2{{\xi }_{1}}{{\xi }_{2}}({{a}_{1}}{{k}_{2}}+{{d}_{1}}{{k}_{4}})-{{\xi }^{2}_{1}}({{k}_{2}}{{a}_{2}}+{{k}_{4}}{{d}_{2}})}{4{{k}_{3}}{{\xi }^{2}_{2}}} \\ & +\frac{-{{\xi }_{2}}({{a}_{1}}{{k}_{2}}+{{d}_{1}}{{k}_{4}})+{{\xi }_{1}}({{k}_{2}}{{a}_{2}}+{{k}_{4}}{{d}_{2}})}{2{{k}_{3}}{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & -\frac{{{k}_{2}}{{a}_{2}}+{{k}_{4}}{{d}_{2}}}{4{{k}_{3}}{{\xi }^{2}_{2}}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}){{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned}\\ &\begin{aligned} {{u}_{3}} = &\frac{4{{d}_{0}}{{\xi }^{2}_{2}}-2{{d}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{d}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{d}_{1}}{{\xi }_{2}}-{{d}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{d}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned}\\ &\begin{aligned} {{b}_{1}} = \frac{2{{n}_{0}}{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})+{{f}_{1}}{{k}_{2}}{{k}_{4}}{{\xi }_{1}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}-\frac{{{f}_{1}}{{k}_{2}}{{k}_{4}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned}\\ &\begin{aligned} {{b}_{2}} = \frac{-2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})({{k}_{4}}{{f}_{0}}+{{k}_{2}}{{n}_{0}})+{{k}^{2}_{3}}{{k}_{4}}{{f}_{1}}{{\xi }_{1}}}{2{{k}_{3}}{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}-\frac{{{k}_{3}}{{k}_{4}}{{f}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}({{k}^{2}_{2}}+{{k}^{2}_{3}})}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \end{aligned}\\ &{{b}_{3}} = \frac{2{{f}_{0}}{{\xi }_{2}}-{{f}_{1}}{{\xi }_{1}}}{2{{\xi }_{2}}}+\frac{{{f}_{1}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2{{\xi }_{2}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ). \end{aligned} \end{equation}$

(4.37)

Case 3. When ${{\xi }_{1}} = {{\xi }_{0}} = 0$ and ${{\xi }_{2}}\ne 0$ , the following rational solution can be obtained.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{a}_{0}}-\frac{{{a}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{a}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{u}_{2}} = \frac{-{{a}_{0}}{{k}_{2}}-{{d}_{0}}{{k}_{4}}+{{k}_{1}}}{{{k}_{3}}}+\frac{{{a}_{1}}{{k}_{2}}+{{d}_{1}}{{k}_{4}}}{{{k}_{3}}({{\xi }_{2}}\zeta +C)}-\frac{{{a}_{2}}{{k}_{2}}+{{d}_{2}}{{k}_{4}}}{{{k}_{3}}({{\xi }_{2}}\zeta +C){{}^{2}}}, \\ &{{u}_{3}} = {{d}_{0}}-\frac{{{d}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{d}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{b}_{1}} = {{n}_{0}}+\frac{{{f}_{1}}{{k}_{2}}{{k}_{4}}}{({{k}^{2}_{2}}+{{k}^{2}_{3}})({{\xi }_{2}}\zeta +C)}, \\ &{{b}_{2}} = \frac{-{{k}_{4}}{{f}_{0}}-{{k}_{2}}{{n}_{0}}}{{{k}_{3}}}+\frac{{{k}_{3}}{{k}_{4}}{{f}_{1}}}{({{k}^{2}_{2}}+{{k}^{2}_{3}})({{\xi }_{2}}\zeta +C)}, \ {{b}_{3}} = {{f}_{0}}-\frac{{{f}_{1}}}{{{\xi }_{2}}\zeta +C}. \end{aligned} \end{equation}$

(4.38)

4.2.2. Viscous MHD equations

When $\nu = \eta = \kappa = 1$ in ODEs (4.28), substituting (4.29) and (3.27) into (4.28), we obtain

$\begin{equation} \nonumber \begin{aligned} & {{a}_{0}} = {{a}_{0}}, {{a}_{1}} = {{a}_{1}}, {{a}_{2}} = {{a}_{2}}, {{d}_{0}} = {{d}_{0}}, {{d}_{1}} = \frac{i{{a}_{1}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{{k}_{2}}}, {{d}_{2}} = \frac{i{{a}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{{k}_{2}}}, {{f}_{0}} = {{f}_{0}}, \\ &{{f}_{1}} = {{f}_{1}}, {{f}_{2}} = {{f}_{2}}, {{k}_{1}} = {{k}_{1}}, {{k}_{2}} = {{k}_{2}}, {{k}_{3}} = {{k}_{3}}, {{k}_{4}} = i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}, {{m}_{0}} = {{m}_{0}}, {{m}_{1}} = \frac{{{a}_{1}}{{k}_{3}}}{{{k}_{2}}}, \\ &{{m}_{2}} = \frac{{{a}_{2}}{{k}_{3}}}{{{k}_{2}}}, {{n}_{0}} = {{n}_{0}}, {{n}_{1}} = \frac{{{f}_{1}}{{k}_{2}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, {{n}_{2}} = \frac{{{f}_{2}}{{k}_{2}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, {{s}_{0}} = {{s}_{0}}, {{s}_{1}} = \frac{{{f}_{1}}{{k}_{3}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, \\ \end{aligned} \end{equation}$

$\begin{equation} \nonumber \begin{aligned} &{{s}_{2}} = \frac{{{f}_{2}}{{k}_{3}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, {{l}_{1}} = \frac{{{a}_{1}}(-{{a}_{0}}{{k}_{2}}-i{{d}_{0}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}-{{m}_{0}}{{k}_{3}}+{{k}_{1}})}{{{k}_{2}}}, \\ &{{l}_{2}} = -\frac{{{a}_{2}}(i({{a}_{0}}{{k}_{2}}+{{m}_{0}}{{k}_{3}}-{{k}_{1}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}-{{d}_{0}}({{k}^{2}_{2}}+{{k}^{2}_{3}}))}{i{{k}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, \\ & {{q}_{1}} = -\frac{(-{{a}_{1}}{{n}_{0}}+{{f}_{1}}{{d}_{0}}){{k}_{2}}-{{k}_{3}}{{s}_{0}}{{a}_{1}}}{{{k}_{2}}}+\frac{({{a}_{0}}{{f}_{1}}+{{a}_{1}}{{f}_{0}}){{k}^{2}_{2}}-{{f}_{1}}(-{{m}_{0}}{{k}_{3}}+{{k}_{1}}){{k}_{2}}+{{f}_{0}}{{a}_{1}}{{k}^{2}_{3}}}{i{{k}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}, \\ & {{q}_{2}} = -\frac{(-{{a}_{2}}{{n}_{0}}+{{f}_{2}}{{d}_{0}}){{k}_{2}}-{{k}_{3}}{{s}_{0}}{{a}_{2}}}{{{k}_{2}}}+\frac{({{a}_{0}}{{f}_{2}}+{{a}_{2}}{{f}_{0}}){{k}^{2}_{2}}-{{f}_{2}}(-{{m}_{0}}{{k}_{3}}+{{k}_{1}}){{k}_{2}}+{{f}_{0}}{{a}_{2}}{{k}^{2}_{3}}}{i{{k}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}. \end{aligned} \end{equation}$

Combined with general solutions of (3.27) (c.f. ^[29]), it follows from (4.29) that (4.39)–(4.52) are four kinds of solutions for (3 + 1)-dimensional viscous MHD equations.

Case 1. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} > 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tanh-type solution can be obtained.

$\begin{eqnarray} &&\begin{aligned} {{u}_{1}} = &\frac{4{{a}_{0}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}}+\frac{{{a}_{2}}{{\xi }_{1}}-{{a}_{1}}{{\xi }_{2}}}{2{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & +\frac{{{a}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{4{{\xi }_{2}}^{2}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \text{ } \\ \end{aligned} \end{eqnarray}$

(4.39)

$\begin{eqnarray} &&\begin{aligned} {{u}_{2}} = &\frac{4{{m}_{0}}{{k}_{2}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{k}_{3}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{k}_{3}}{{\xi }^{2}_{1}}}{4{{k}_{2}}{{\xi }^{2}_{2}}}\\ &+\frac{{{k}_{3}}(-{{a}_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }_{1}})}{2{{k}_{2}}{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & +\frac{{{a}_{2}}{{k}_{3}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{4{{k}_{2}}{{\xi }^{2}_{2}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \text{ } \\ \end{aligned} \end{eqnarray}$

(4.40)

$\begin{eqnarray} &&\begin{aligned} {{u}_{3}} = &{{d}_{0}}+\frac{i(-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{4{{k}_{2}}{{\xi }^{2}_{2}}}\\ &+\frac{i{{a}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{4{{k}_{2}}{{\xi }^{2}_{2}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta )\\ & +\frac{i({{a}_{2}}{{\xi }_{1}}-{{a}_{1}}{{\xi }_{2}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{2{{k}_{2}}{{\xi }^{2}_{2}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) , \\ \end{aligned} \end{eqnarray}$

(4.41)

$\begin{eqnarray} &&\begin{aligned} {{b}_{1}} = &{{n}_{0}}+\frac{-2{{f}_{1}}{{k}_{2}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{k}_{2}}{{\xi }^{2}_{1}}}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}} \\ &+\frac{{{k}_{2}}(-{{f}_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }_{1}})}{i2{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & +\frac{{{f}_{2}}{{k}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \text{ }\\ \end{aligned} \end{eqnarray}$

(4.42)

$\begin{eqnarray} &&\begin{aligned} {{b}_{2}} = &{{s}_{0}}+\frac{-2{{f}_{1}}{{k}_{3}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{k}_{3}}{{\xi }^{2}_{1}}}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}} +\frac{{{k}_{3}}(-{{f}_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }_{1}})}{i2{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ) \\ & +\frac{{{f}_{2}}{{k}_{3}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ), \text{ } \\ \end{aligned} \end{eqnarray}$

(4.43)

$\begin{eqnarray} &&\begin{aligned} {{b}_{3}} = &\frac{4{{f}_{0}}{{\xi }^{2}_{2}}-2{{f}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}} +\frac{-{{f}_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{{{\xi }_{1}}^{2}-4{{\xi }_{2}}{{\xi }_{0}}}\tanh (\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta )\\ &+\frac{{{f}_{2}}({{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}})}{4{{\xi }_{2}}^{2}}{{\tanh }^{2}}(\frac{\sqrt{{{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}}}}{2}\zeta ). \end{aligned} \end{eqnarray}$

(4.44)

Setting ${{a}_{1}} = -1, {{a}_{2}} = 2, {{d}_{0}} = 1, {{k}_{1}} = 1, {{k}_{2}} = 1, {{k}_{3}} = 1, {{\xi }_{0}} = 2, {{\xi }_{1}} = -6, {{\xi }_{2}} = 3$ and $y = 1$ in (4.41), we obtain for solution ${{u}_{3}}$ as follows.

Figure 12. (a) The evolution of interaction solution between anti-kink and solition wave via $\vert{{u}_{3}} \vert(t = 1)$ , (b) Overview of $\vert {{u}_{3}} \vert(t = 1)$ , (c) $\vert {{u}_{3}} \vert(t = 1, 2, 3, z = 1)$ .

DownLoad: Full-Size Img PowerPoint

In particular, when ${{\xi }_{0}} = 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ , the following sinh-cosh-type solution can be obtained.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{a}_{0}}-\frac{{{a}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{{{a}_{2}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \\ &\begin{aligned} {{u}_{2}} = &{{m}_{0}}-\frac{{{a}_{1}}{{k}_{3}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{k}_{2}}{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{{{a}_{2}}{{k}_{3}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{k}_{2}}{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \end{aligned}\\ &\begin{aligned} {{u}_{3}} = &{{d}_{0}}-\frac{i{{a}_{1}}{{\xi }_{1}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{k}_{2}}{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{i{{a}_{2}}{{\xi }^{2}_{1}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{k}_{2}}{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \text{ } \end{aligned}\\ &\begin{aligned} {{b}_{1}} = &{{n}_{0}}-\frac{{{f}_{1}}{{k}_{2}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{i{{\xi }_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}+\frac{{{f}_{2}}{{k}_{2}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{i{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}, \end{aligned}\\ &\begin{aligned} {{b}_{2}} = &{{s}_{0}}-\frac{{{f}_{1}}{{k}_{3}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{i{{\xi }_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}\text{+}\frac{{{f}_{2}}{{k}_{3}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{i{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}\text{, } \end{aligned}\\ &{{b}_{3}} = {{f}_{0}}-\frac{{{f}_{1}}{{\xi }_{1}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}{{{\xi }_{2}}[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}\text{+}\frac{{{f}_{2}}{{\xi }^{2}_{1}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )]}^{2}}}{{{\xi }^{2}_{2}}{{[\sinh ({{\xi }_{1}}\zeta )+\cosh ({{\xi }_{1}}\zeta )+C]}^{2}}}.\\ \end{aligned} \end{equation}$

(4.45)

Case 2. When ${{\xi }^{2}_{1}}-4{{\xi }_{2}}{{\xi }_{0}} < 0$ and ${{\xi }_{1}}{{\xi }_{2}}\ne 0$ (or ${{\xi }_{0}}{{\xi }_{2}}\ne 0$ ), the following tan-type solution can be obtained.

(4.46)

$\begin{eqnarray} &&\begin{aligned} {{u}_{2}} = &\frac{4{{m}_{0}}{{k}_{2}}{{\xi }^{2}_{2}}-2{{a}_{1}}{{k}_{3}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{k}_{3}}{{\xi }^{2}_{1}}}{4{{k}_{2}}{{\xi }^{2}_{2}}} +\frac{{{k}_{3}}({{a}_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }_{1}})}{2{{k}_{2}}{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{a}_{2}}{{k}_{3}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{k}_{2}}{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.47)

$\begin{eqnarray} &&\begin{aligned} {{u}_{3}} = &{{d}_{0}}+\frac{i(-2{{a}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{a}_{2}}{{\xi }^{2}_{1}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{4{{k}_{2}}{{\xi }^{2}_{2}}}+\frac{i{{a}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{4{{k}_{2}}{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta )\\ &+\frac{i({{a}_{1}}{{\xi }_{2}}-{{a}_{2}}{{\xi }_{1}})\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{2{{k}_{2}}{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) , \\ \end{aligned} \end{eqnarray}$

(4.48)

$\begin{eqnarray} &&\begin{aligned} {{b}_{1}} = &{{n}_{0}}+\frac{{{k}_{2}}(-2{{f}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }^{2}_{1}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}} +\frac{{{k}_{2}}({{f}_{1}}{{\xi }_{2}}-{{f}_{2}}{{\xi }_{1}})}{i2{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{f}_{2}}{{k}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.49)

$\begin{eqnarray} &&\begin{aligned} {{b}_{2}} = &{{s}_{0}}+\frac{{{k}_{3}}(-2{{f}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }^{2}_{1}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}} +\frac{{{k}_{3}}({{f}_{1}}{{\xi }_{2}}-{{f}_{2}}{{\xi }_{1}})}{i2{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{k}_{3}}{{f}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{i4{{\xi }^{2}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ), \\ \end{aligned} \end{eqnarray}$

(4.50)

$\begin{eqnarray} &&\begin{aligned} {{b}_{3}} = &\frac{4{{f}_{0}}{{\xi }^{2}_{2}}-2{{f}_{1}}{{\xi }_{1}}{{\xi }_{2}}+{{f}_{2}}{{\xi }^{2}_{1}}}{4{{\xi }^{2}_{2}}} +\frac{{{f}_{1}}{{\xi }_{2}}-{{f}_{2}}{{\xi }_{1}}}{2{{\xi }^{2}_{2}}}\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}\tan (\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ) \\ & +\frac{{{f}_{2}}(4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}})}{4{{\xi }^{2}_{2}}}{{\tan }^{2}}(\frac{\sqrt{4{{\xi }_{2}}{{\xi }_{0}}-{{\xi }^{2}_{1}}}}{2}\zeta ). \end{aligned} \end{eqnarray}$

(4.51)

Case 3. When ${{\xi }_{1}} = {{\xi }_{0}} = 0$ and ${{\xi }_{2}}\ne 0$ , the following rational solution can be obtained.

$\begin{equation} \begin{aligned} &{{u}_{1}} = {{a}_{0}}-\frac{{{a}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{a}_{2}}}{({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{b}_{1}} = {{n}_{0}}-\frac{{{f}_{1}}{{k}_{2}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}({{\xi }_{2}}\zeta +C)}+\frac{{{f}_{2}}{{k}_{2}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}{{({{\xi }_{2}}\zeta +C)}^{2}}}, \\ &{{u}_{3}} = {{d}_{0}}-\frac{i{{a}_{1}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{{k}_{2}}({{\xi }_{2}}\zeta +C)}+\frac{i{{a}_{2}}\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}}{{{k}_{2}}({{\xi }_{2}}\zeta +C){{}^{2}}}, \ {{u}_{2}} = {{m}_{0}}-\frac{{{a}_{1}}{{k}_{3}}}{{{k}_{2}}({{\xi }_{2}}\zeta +C)}+\frac{{{a}_{2}}{{k}_{3}}}{{{k}_{2}}({{\xi }_{2}}\zeta +C){{}^{2}}}, \text{ }\\ &{{b}_{2}} = {{s}_{0}}-\frac{{{f}_{1}}{{k}_{3}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}({{\xi }_{2}}\zeta +C)}+\frac{{{f}_{2}}{{k}_{3}}}{i\sqrt{{{k}^{2}_{2}}+{{k}^{2}_{3}}}{{({{\xi }_{2}}\zeta +C)}^{2}}}\text{, }\ {{b}_{3}} = {{f}_{0}}-\frac{{{f}_{1}}}{{{\xi }_{2}}\zeta +C}+\frac{{{f}_{2}}}{{{({{\xi }_{2}}\zeta +C)}^{2}}}.\\ \end{aligned} \end{equation}$

(4.52)

Setting ${{a}_{1}} = 2i, {{a}_{2}} = i, {{d}_{0}} = -2, {{k}_{1}} = 3, {{k}_{2}} = -2, {{k}_{3}} = -2, {{\xi }_{0}} = 0, {{\xi }_{1}} = 0, {{\xi }_{2}} = -1, C = 1, z = 2$ and $x = -15$ for ${{u}_{3}}$ in (4.52), we obtain for bright–dark soliton solution ${{u}_{3}}$ as follows.

Figure 13. (a) $\vert {{u}_{3}} \vert$ , (b) $\vert {{u}_{3}} \vert$ ( $t$ = 1, 2, 3).

DownLoad: Full-Size Img PowerPoint

5. Stability of MHD flows

5.1. Qualitative analysis

We analyze the continuous dependence of solution for MHD equations (2.2) on initial data, or namely the stability of MHD equations (2.2) from a qualitative perspective.

Lemma 5.1. ^[31] For $q\in[2, \infty)$ , there exists $C > 0$ such that for $f\in H^{1}(\mathbb{R}^2)$ ,

$\begin{equation} \left\| {f} \right\|_{L^{q}(\mathbb{R}^2 )}^{q}\le C\left\| {{f}} \right\|_{{{L}^{2}(\mathbb{R}^2 )}}^2\left\| {\nabla{{{f}}}} \right\|_{{{L}^{2}(\mathbb{R}^2 )}}^{q-2}. \end{equation}$

(5.1)

Lemma 5.2. ^[32] For $p \in [2, 6]$ , there exists $C > 0$ such that for $g\in H^{1}(\mathbb{R}^3)$ ,

$\begin{equation} \left\| {g} \right\|_{L^{p}(\mathbb{R}^3 )}^{p}\le C\left\| {{g}} \right\|_{{{L}^{2}(\mathbb{R}^3 )}}^{{(6-p)}/{2}\;}\left\| {\nabla{{{g}}}} \right\|_{{{L}^{2}(\mathbb{R}^3 )}}^{{(3p-6)}/{2}\;}. \end{equation}$

(5.2)

Theorem 5.3. For $n = 2, 3$ , if the initial data ${\mathbf{U}_{0}}, {\mathbf{B}_{0}}\in {{({{L}^{2}}({{\mathbb{R}}^{n}}))}^{n}}$ , then the solutions $(\mathbf{U}, \mathbf{B})$ for the (2 + 1)- and (3 + 1)-dimensional MHD equations (2.2) with periodic boundary condition at infinity depend on the initial data continuously in ${{({{L}^{2}}({{\mathbb{R}}^{n}}))}^{n}}$ .

Proof. Let $({\mathbf{U}_{1}}, {\mathbf{B}_{1}})$ and $({\mathbf{U}_{2}}, {\mathbf{B}_{2}})$ be two solutions to MHD equations (2.2) with initial data ${\mathbf{U}_{0}}, {\mathbf{B}_{0}}\in {{({{L}^{2}}({{\mathbb{R}}^{n}}))}^{n}}$ . Set $\tilde{\mathbf{U}} = {\mathbf{U}_{1}}-{\mathbf{U}_{2}}$ , $\tilde{\mathbf{B}} = {\mathbf{B}_{1}}-{\mathbf{B}_{2}}$ , $\tilde{p} = {{p}_{1}}-{{p}_{2}}$ , $\tilde{r} = {{r}_{1}}-{{r}_{2}}$ , then $(\tilde{\mathbf{U}}, \tilde{\mathbf{B}})$ is the solution to the following system,

$\left\{\begin{array}{l} \tilde{\mathbf{U}}_t-\nu \Delta \tilde{\mathbf{U}}+((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{U}_{1}}+({\mathbf{U}_{2}}\cdot \nabla) \tilde{\mathbf{U}})\kappa((\tilde{\mathbf{B}}\cdot \nabla) {\mathbf{B}_{1}}+({\mathbf{B}_{2}}\cdot \nabla) \tilde{\mathbf{B}})+\nabla \tilde{p}\\ +\frac{1}{2}\kappa\nabla(\vert\mathbf{B}_1{{\vert}^{2}}-\vert\mathbf{B}_2{{\vert}^{2}}) = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.3)\\ \tilde{\mathbf{B}}_t-\eta \Delta \tilde{\mathbf{B}}+((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{B}_{1}}+({\mathbf{U}_{2}}\cdot \nabla) \tilde{\mathbf{B}})-((\tilde{\mathbf{B}}\cdot \nabla) {\mathbf{U}_{1}}+({\mathbf{B}_{2}}\cdot \nabla) \tilde{\mathbf{U}})+\nabla\tilde{r} = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.4)\\ \operatorname{div}\ \tilde{\mathbf{U}} = 0, \ \operatorname{div}\ \tilde{\mathbf{B}} = 0. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.5) \end{array}\right.$

Case 1. $n = 2$ .

It follows from H $\ddot{\text{o}}$ lder inequality and Lemma 5.1 that

$\begin{equation} -((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{U}_{1}}, \tilde{\mathbf{U}})\le {{\left\| \nabla {\mathbf{U}_{1}} \right\|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{4}}}^{2}\le C_0{{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{{}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{{}}, \end{equation}$

(5.6)

$\begin{equation} ((\tilde{\mathbf{B}}\cdot \nabla) {\mathbf{U}_{1}}, \tilde{\mathbf{B}})\le {{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{4}}}^{2}\le C_0{{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{{}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{{}}, \end{equation}$

(5.7)

$\begin{equation} ((\tilde{\mathbf{B}}\cdot \nabla) {\mathbf{B}_{1}}, \tilde{\mathbf{U}})\le {{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}{{\| {\tilde{\mathbf{B}}} \|}_{{{L}^{4}}}}{{\| {\tilde{\mathbf{U}}} \|}_{{{L}^{4}}}}\le C_0{{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{\frac{1}{2}}, \end{equation}$

(5.8)

$\begin{equation} -((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{B}_{1}}, \tilde{\mathbf{B}})\le {{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}{{\| {\tilde{\mathbf{U}}} \|}_{{{L}^{4}}}}{{\| {\tilde{\mathbf{B}}} \|}_{{{L}^{4}}}}\le C_0{{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{\frac{1}{2}}. \end{equation}$

(5.9)

Take $L^{2}$ inner product of (5.3) with ${\tilde{\mathbf{U}}}$ and (5.4) with ${\tilde{\mathbf{B}}}$ , respectively. Without loss of generality, choose $\nu = \eta = \kappa = 1$ in (5.3) and (5.4). Since

$\begin{equation} (({\mathbf{U}_{2}}\cdot \nabla) \tilde{\mathbf{U}}, \tilde{\mathbf{U}}) = 0, \ \ (({\mathbf{U}_{2}}\cdot \nabla) \tilde{\mathbf{B}}, \tilde{\mathbf{B}}) = 0, \ \ (({\mathbf{B}_{2}}\cdot \nabla )\tilde{\mathbf{B}}, \tilde{\mathbf{U}})+(({\mathbf{B}_{2}}\cdot \nabla) \tilde{\mathbf{U}}, \tilde{\mathbf{B}}) = 0, \end{equation}$

(5.10)

and

$\begin{equation} (\nabla (\tilde{p}+\frac{1}{2}\kappa(\vert\mathbf{B}_1{{\vert}^{2}}-\vert\mathbf{B}_2{{\vert}^{2}})), \tilde{\mathbf{U}}) = 0, \ \ (\nabla \tilde{r} , \tilde{\mathbf{B}}) = 0, \end{equation}$

(5.11)

using (5.6)–(5.11), we have

$\begin{equation} \begin{aligned} & \frac{d}{dt}(\left\| \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+\left\| \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2})+2\left\| \nabla \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+2\left\| \nabla \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2} \\ \le & C{{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{{}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{{}}+C {{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{{}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{{}}\\ +&2C{{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{\frac{1}{2}}. \end{aligned} \end{equation}$

(5.12)

where $C = 2{{C}_{0}}$ . It follows from Young inequality and (5.12) that

$\begin{equation} \begin{aligned} & \frac{d}{dt}(\left\| \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+\left\| \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2})+2\left\| \nabla \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+2\left\| \nabla \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2} \\ \le & \frac{{{C}^{2}}}{2}\left( \left\| \nabla {\mathbf{U}_{1}} \right\|_{{{L}^{2}}}^{2}+\left\| \nabla {\mathbf{B}_{1}} \right\|_{{{L}^{2}}}^{2} \right)\left( \left\| {\tilde{\mathbf{U}}} \right\|_{{{L}^{2}}}^{2}+\left\| {\tilde{\mathbf{B}}} \right\|_{{{L}^{2}}}^{2} \right)+\left(\left\| \nabla \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+\left\| \nabla \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2}\right). \end{aligned} \end{equation}$

(5.13)

Using Gr $\ddot{\text{o}}$ nwall's inequality, $\left\| {\tilde{\mathbf{U}}} \right\|_{{{L}^{2}}}^{2}+\left\| {\tilde{\mathbf{B}}} \right\|_{{{L}^{2}}}^{2}\le M{{ (\left\| {\tilde{\mathbf{U}}} \right\|_{{{L}^{2}}}^{2}+\left\| {\tilde{\mathbf{B}}} \right\|_{{{L}^{2}}}^{2}) \vert }_{t = {{t}_{0}}}}.$ Then, solution $(\mathbf{U}, \mathbf{B})$ for (2 + 1)-dimensional MHD equations (2.2) with periodic boundary condition at infinity depends on the initial data continuously in ${{({{L}^{2}}({{\mathbb{R}}^{2}}))}^{2}}$ .

Case 2. $n = 3$ .

It follows from H $\ddot{\text{o}}$ lder inequality and Lemma 5.2 that

$\begin{equation} -((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{U}_{1}}, \tilde{\mathbf{U}})\le {{\left\| \nabla {\mathbf{\mathbf{U}}_{1}} \right\|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{3}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{6}}}\le C_0{{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{{\frac{1}{2}}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{{\frac{3}{2}}}, \end{equation}$

(5.14)

$\begin{equation} ((\tilde{\mathbf{B}}\cdot \nabla ){\mathbf{U}_{1}}, \tilde{\mathbf{B}})\le {{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{3}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{6}}}\le C_0{{\| \nabla {\mathbf{U}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{\frac{3}{2}}. \end{equation}$

(5.15)

$\begin{equation} ((\tilde{\mathbf{B}}\cdot \nabla) {\mathbf{B}_{1}}, \tilde{\mathbf{U}})\le {{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}{{\| {\tilde{\mathbf{B}}} \|}_{{{L}^{3}}}}{{\| {\tilde{\mathbf{U}}} \|}_{{{L}^{6}}}}\le C_0{{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{B}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}, \end{equation}$

(5.16)

$\begin{equation} -((\tilde{\mathbf{U}}\cdot \nabla) {\mathbf{B}_{1}}, \tilde{\mathbf{B}})\le {{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}{{\| {\tilde{\mathbf{U}}} \|}_{{{L}^{3}}}}{{\| {\tilde{\mathbf{B}}} \|}_{{{L}^{6}}}}\le C_0{{\| \nabla {\mathbf{B}_{1}} \|}_{{{L}^{2}}}}\| {\tilde{\mathbf{U}}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{U}} \|_{{{L}^{2}}}^{\frac{1}{2}}\| \nabla \tilde{\mathbf{B}} \|_{{{L}^{2}}}. \end{equation}$

(5.17)

Using Young inequality with $\varepsilon$ , without loss of generality, choosing $\nu = \eta = \kappa = 1$ in (5.3) and (5.4), there exists $\varepsilon < \frac{2}{3}$ such that

$\begin{aligned} &\frac{d}{dt}( \left\| \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+\left\| \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2})+2\left\| \nabla \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+2\left\| \nabla \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2} \\ \le & C(\varepsilon )(\left\| \nabla {\mathbf{U}_{1}} \right\|_{{{L}^{2}}}^{4}+\left\| \nabla {\mathbf{B}_{1}} \right\|_{{{L}^{2}}}^{4})(\left\| {\tilde{\mathbf{U}}} \right\|_{{{L}^{2}}}^{2}+\left\| {\tilde{\mathbf{B}}} \right\|_{{{L}^{2}}}^{2})+3 \varepsilon (\left\| \nabla \tilde{\mathbf{U}} \right\|_{{{L}^{2}}}^{2}+\left\| \nabla \tilde{\mathbf{B}} \right\|_{{{L}^{2}}}^{2}). \end{aligned}$

Similarly, using Gr $\ddot{\text{o}}$ nwall's inequality, it can be obtained that solution $(\mathbf{U}, \mathbf{B})$ for (3 + 1)-dimensional MHD equations (2.2) with periodic boundary condition at infinity depends on the initial data continuously in ${{({{L}^{2}}({{\mathbb{R}}^{3}}))}^{3}}$ .

5.2. Quantitative analysis

Next, we further analyze the stability of MHD equations (2.2) combining with the exact solutions obtained above from a quantitative perspective, which provide an accurate mathematical description for the stability of MHD systems. Denote ${\bar{\mathbf{U}}} = \mathbf{U}+\mathbf{U}'$ , $\bar{\mathbf{B}} = \mathbf{B}+\mathbf{B}'$ , where $\mathbf{U}', \mathbf{B}'$ are disturbances to the velocity and magnetic field, respectively. $(\mathbf{U}, \mathbf{B})$ and $(\bar{\mathbf{U}}, \bar{\mathbf{B}})$ are solutions before and after being affected by disturbances, respectively. Therefore $\mathbf{U}', \mathbf{B}'$ satisfy the following system

$\left\{\begin{array}{l} {\mathbf{U}'_t}-\nu \Delta {\mathbf{U}'}+(({\mathbf{U}'}\cdot \nabla) {\mathbf{U}}+(({\mathbf{U}+\mathbf{U}'})\cdot \nabla) {\mathbf{U}'})-\kappa(({\mathbf{B}'}\cdot \nabla) {\mathbf{B}}+(({\mathbf{B}+\mathbf{B}'})\cdot \nabla) {\mathbf{B}'})\\ +\nabla {p}'+\frac{1}{2}\kappa\nabla(-\vert\mathbf{B}{{\vert}^{2}}+\vert\mathbf{B}+\mathbf{B}'{{\vert}^{2}}) = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.18)\\ {\mathbf{B}'_t}-\eta \Delta {\mathbf{B}'}+(({\mathbf{U}'}\cdot \nabla) {\mathbf{B}}+(({\mathbf{U}+\mathbf{U}'})\cdot \nabla) {\mathbf{B}'})-(({\mathbf{B}'}\cdot \nabla) {\mathbf{U}}+(({\mathbf{B}+\mathbf{B}'})\cdot \nabla) {\mathbf{U}'})\\ +\nabla{r}' = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.19)\\ \operatorname{div}{\mathbf{U}'} = 0, \ \operatorname{div}{\mathbf{B}'} = 0. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(5.20) \end{array}\right.$

We select several obtained exact solutions of MHD system to study the impact of disturbances on stability of the system.

Case 1. Harmonic disturbance.

The initial disturbance is

${{{u}'_{1}}}({{t}_{0}}, x, y) = A_1\cos (\frac{2\pi }{w_1}(x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}}){{t}_{0}})), \ \ {{{u}'_{2}}}({{t}_{0}}, x, y) = A_2\cos (\frac{2\pi }{w_2}(x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}}){{t}_{0}})),$

where $A_1, \ A_2$ are amplitude of disturbance waves. We analyze the behavior of $u_1$ , $u_2$ in (3.13) after being affected by disturbances ${{{u}'_{1}}}({{t}}, x, y)$ , ${{{u}'_{2}}}({{t}}, x, y)$ . Set $A_i = 0.1, w_i = 5\ (i = 1, 2)$ , the evolution of $u_1+{u'_{1}}$ can be displayed intuitively as following ( $u_2+{u'_{2}}$ is similar).

Figure 14. (a) $u_1+{u'_{1}}$ , (b) $u_1+{u'_{1}}$ ( $t$ = 1, 3, 5).

DownLoad: Full-Size Img PowerPoint

From , it can be seen that with the evolution of time, the amplitude of $\mathbf{U}$ under the influence of the harmonic disturbance is limited. The solutions $(\mathbf{U}, \mathbf{B})$ for the (2 + 1)-dimensional MHD equations (2.2) depend on the initial data continuously in ${{({{L}^{2}}({{\mathbb{R}}^{2}}))}^{2}}$ , which is also consistent with the conclusion of qualitative analysis.

Case 2. Bell shaped solitary wave disturbance.

The initial disturbance is

${{{u}'_{1}}}({{t}_{0}}, x, y) = A_1\operatorname{sech} (\frac{2\pi }{w_1}(x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}}){{t}_{0}})), \ \ {{{u}'_{2}}}({{t}_{0}}, x, y) = A_2\operatorname{sech} (\frac{2\pi }{w_2}(x-y-({{\bar{v}}_{1}}-{{\bar{v}}_{2}}){{t}_{0}})),$

where $A_1, \ A_2$ are amplitude of disturbance waves. We analyze the behavior of $u_1$ , $u_2$ in (3.14) after being affected by disturbances ${{{u}'_{1}}}({{t}}, x, y)$ , ${{{u}'_{2}}}({{t}}, x, y)$ . Set $A_i = 0.1, w_i = 5(i = 1, 2)$ , the evolution of $u_1+{u'_{1}}$ can be displayed intuitively as following ( $u_2+{u'_{2}}$ is similar).

Figure 15. $u_1+{u'_{1}}$ ( $t = 1, \ 4, \ 7$ , respectively).

DownLoad: Full-Size Img PowerPoint

From , it can be seen that the amplitude of $\mathbf{U}$ under the influence of the Bell shaped solitary wave disturbance has increased but is limited. The velocity $\mathbf{U}$ under the influence of Bell shaped solitary wave disturbance is stable.

6. Conclusions

In this paper, several novel classes of solutions and stability analysis are presented for MHD flows. When the magnetic field vanishes, some of the exact solutions can be reduced to solutions of Euler or Navier-Stokes equation. Through Lie symmetry analysis and the generalized Riccati equation expansion method, the MHD system achieves order reduction and dimensionality reduction, and the complex nonlinear and strongly coupled terms in fluid dynamics systems are handled technically. The Lie group of transformations and the similarity reductions of (2 + 1)- and (3 + 1)-dimensional inviscid and viscous MHD equations are studied. The exact solutions with rich forms are obtained, which can describe certain solition-like surface waves, such as periodic solution, single soliton solution, and lump solution. The mechanisms of rotational and irrotational fluids are analyzed. Furthermore, using the generalized Riccati equation expansion method, we obtain miscellaneous traveling wave solutions, including kink, kink-like, anti-kink-like, breather, and interaction solutions. In addition, the continuous dependence of solutions for MHD equations for initial values is studied from qualitative and quantitative perspectives.

Compared with the related work, the novelty of this paper lies in that we consider the problem from multiple perspectives and obtain new exact solutions. For instance, Dorodnitsyn et al. ^[23] studied (1 + 1)-dimensional inviscid MHD flows in the mass Lagrangian coordinates, while we studied from the perspective of both inviscid and viscous of (2 + 1)- and (3 + 1)-dimensional MHD equations. Liu et al. ^[24] obtained analytical solutions of (2 + 1) -dimensional inviscid incompressible MHD equations by Lie symmetry analysis. Picard et al. ^[26] obtained some exact solutions of (3 + 1)-dimensional inviscid MHD equations by the symmetry reduction method. We used Lie symmetry analysis as well as generalized Riccati equation expansion methods to study both inviscid and viscous of (2 + 1)- and (3 + 1)-dimensional MHD equations. Moreover, based on the study, we obtain new exact solutions with richer forms. Xia et al. ^[25] used the Lie symmetry method to obtain some exact solutions of (2 + 1)-dimensional incompressible ideal MHD equations. Cheung et al. ^[33] obtained bounded soliton solutions of (2 + 1)-dimensional incompressible MHD equations. However, we obtain some new exact solutions for both inviscid and viscous of (2 + 1)- and (3 + 1)-dimensional MHD equations, such as lump solutions, kink solutions, kink-like solution, breather solutions, and interaction solution between anti-kink and solition. Ayub et al. ^[34] studied solitary wave solutions for two-dimensional viscous incompressible MHD flow regarding space evolution, while we studied from the perspective of both inviscid and viscous of (2 + 1)- and (3 + 1)-dimensional MHD flows, which consider both time and space evolution.

The exact solutions we obtain can correspond to different physical behaviors for MHD flows. For instance, solitons can maintain their shape and thier amplitude is unchanged during propagation. This property is important for understanding and predicting some wave propagations in MHD flow. Soliton waves can be used to describe some wave phenomena in plasma, which has potential application value for achieving and maintaining the stability of fusion plasma. Periodic solutions can describe some periodic oscillation phenomena in MHD flow. Lump solution can correspond to waves that are localized in time and space, while the amplitude of peak and valley is several times higher than the surrounding background height. Breather solutions can explain MHD flow that exhibits periodicity in certain direction and locality in other directions. The kink and kink-like solutions can manifest as a rapid change or discontinuity in some fields at the macro level. Considering the physical significance and the importance of studying analytical solutions of MHD equations, compressible case and MHD systems with other factors such as time-dependent density and Coriolis force deserve to be further studied.

Author contributions

Shengfang Yang worked on conceptualization, writing-original draft, formal analysis, software. Huanhe Dong worked on conceptualization, resources, validation, supervision. Mingshuo Liu worked on methodology, writing-review & editing, formal analysis, validation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. 12105161, 12305003).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	F. Haas, A magnetohydrodynamic model for quantum plasmas, Phys. Plasmas, 12 (2005), 062117. https://doi.org/10.1063/1.1939947 doi: 10.1063/1.1939947
[2]	X. Zhou, Y. Shen, D. Yuan, R. Keppens, X. Zhao, L. Fu, et al., Resolved magnetohydrodynamic wave lensing in the solar corona, Nat. Commun., 15 (2024), 3281. https://doi.org/10.1038/s41467-024-46846-z doi: 10.1038/s41467-024-46846-z
[3]	P. Kumar, V. M. Nakariakov, J. T. Karpen, K. S. Cho, Direct imaging of magnetohydrodynamic wave mode conversion near a 3D null point on the sun, Nat. Commun., 15 (2024), 2667. https://doi.org/10.1038/s41467-024-46736-4 doi: 10.1038/s41467-024-46736-4
[4]	B. Zohuri, Plasma Physics and Controlled Thermonuclear Reactions Driven Fusion Energy, Albuquerque, New Mexico, USA: Springer, 2016. https://doi.org/10.1007/978-3-319-47310-9
[5]	R. Yousofvand, S. Derakhshan, K. Ghasemi, M. Siavashi, MHD transverse mixed convection and entropy generation study of electromagnetic pump including a nanofluid using 3D LBM simulation, Int. J. Mech. Sci., 133 (2017), 73–90. https://doi.org/10.1016/j.ijmecsci.2017.08.034 doi: 10.1016/j.ijmecsci.2017.08.034
[6]	Y. Qin, X. Liu, X. Yang, Global existence and exponential stability for a 1D compressible and radiative MHD flow, J. Differ. Equations, 253 (2012), 1439–1488. https://doi.org/10.1016/j.jde.2012.05.003 doi: 10.1016/j.jde.2012.05.003
[7]	X. Suo, Q. Jiu, Global well-posedness of 2D incompressible Magnetohydrodynamic equations with horizontal dissipation, Discrete Contin. Dyn. Syst. - Ser. A., 42 (2022), 4523–4253. https://doi.org/10.3934/dcds.2022063 doi: 10.3934/dcds.2022063
[8]	Y. Wang, K. Wang, Global well-posedness of the three dimensional magnetohydrodynamics equations, Nonlinear Anal. Real World Appl., 17 (2014), 245–251. https://doi.org/10.1016/j.nonrwa.2013.12.002 doi: 10.1016/j.nonrwa.2013.12.002
[9]	Y. P. Li, W. A. Yong, The zero Mach number limit of the three-dimensional compressible viscous magnetohydrodynamic equations, Chin. Ann. Math. Ser. B, 36 (2015), 1043–1054. https://doi.org/10.1007/s11401-015-0918-4 doi: 10.1007/s11401-015-0918-4
[10]	Q. M. Xu, X. Zhong, Local well-posedness to the three-dimensional barotropic compressible magnetohydrodynamic equations with vacuum, J. Math. Phys., 62 (2021), 031501. https://doi.org/10.1063/5.0039481 doi: 10.1063/5.0039481
[11]	W. X. Ma, Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Differ. Equations, 264 (2018), 2633–2659. https://doi.org/10.1016/j.jde.2017.10.033 doi: 10.1016/j.jde.2017.10.033
[12]	L. Y. Ma, H. Q. Zhao, S. F. Shen, W. X. Ma, Abundant exact solutions to the discrete complex mKdV equation by Darboux transformation, Commun. Nonlinear Sci. Numer. Simul., 68 (2019), 31–40. https://doi.org/10.1016/j.cnsns.2018.07.037 doi: 10.1016/j.cnsns.2018.07.037
[13]	X. Xin, Y. Liu, Y. Xia, H. Liu, Integrability, Darboux transformation and exact solutions for nonlocal couplings of AKNS equations, Appl. Math. Lett., 119 (2021), 107209. https://doi.org/10.1016/j.aml.2021.107209 doi: 10.1016/j.aml.2021.107209
[14]	M. M. A. Qurashi, D. Baleanu, M. Inc, Optical solitons of transmission equation of ultra-short optical pulse in parabolic law media with the aid of Backlund transformation, Optik, 140 (2017), 114–122. https://doi.org/10.1016/j.ijleo.2017.03.109 doi: 10.1016/j.ijleo.2017.03.109
[15]	Z. Zhao, B. Han, Lie symmetry analysis of the Heisenberg equation, Commun. Nonlinear Sci. Numer. Simul., 45 (2017), 220–234. https://doi.org/10.1016/j.cnsns.2016.10.008 doi: 10.1016/j.cnsns.2016.10.008
[16]	M. R. Ali, R. Sadat, Lie symmetry analysis, new group invariant for the (3 + 1)-dimensional and variable coefficients for liquids with gas bubbles models, Chin. J. Phys., 71 (2021), 539–547. https://doi.org/10.1016/j.cjph.2021.03.018 doi: 10.1016/j.cjph.2021.03.018
[17]	O. D. Adeyemo, C. M. Khalique, Closed-form solutions and conserved quantities of a new integrable (2 + 1)-dimensional Boussinesq equation of nonlinear sciences, Int. J. Nonlinear Sci. Numer. Simul., 24 (2023), 2801–2821. https://doi.org/10.1515/ijnsns-2020-0288 doi: 10.1515/ijnsns-2020-0288
[18]	B. Ren, Interaction solutions for mKP equation with nonlocal symmetry reductions and CTE method, Phys. Scr., 90 (2015), 065206. https://doi.org/10.1088/0031-8949/90/6/065206 doi: 10.1088/0031-8949/90/6/065206
[19]	Y. Li, H. Hu, Nonlocal symmetries and interaction solutions of the Benjamin-Ono equation, Appl. Math. Lett., 75 (2018), 18–23. https://doi.org/10.1016/j.aml.2017.06.012 doi: 10.1016/j.aml.2017.06.012
[20]	Y. Li, J. Li, R. Wang, Multi-soliton solutions of the N-component nonlinear Schrödinger equations via Riemann-Hilbert approach, Nonlinear Dyn., 105 (2021), 1765–1772. https://doi.org/10.1007/s11071-021-06706-7 doi: 10.1007/s11071-021-06706-7
[21]	X. F. Zhang, S. F. Tian, J. J. Yang, The Riemann-Hilbert approach for the focusing Hirota equation with single and double poles, Anal. Math. Phys., 11 (2021), 1–18. https://doi.org/10.1007/s13324-021-00522-3 doi: 10.1007/s13324-021-00522-3
[22]	A. Donato, F. Oliveri, Reduction to autonomous form by group analysis and exact solutions of axisymmetric MHD equations, Math. Comput. Modell., 18 (1993), 83–90. https://doi.org/10.1016/0895-7177(93)90216-L doi: 10.1016/0895-7177(93)90216-L
[23]	V. A. Dorodnitsyn, E. I. Kaptsov, R. V. Kozlov, S. V. Meleshko, One-dimensional MHD flows with cylindrical symmetry: Lie symmetries and conservation laws, Int. J. Non-Linear Mech., 148 (2023), 104290. https://doi.org/10.1016/j.ijnonlinmec.2022.104290 doi: 10.1016/j.ijnonlinmec.2022.104290
[24]	M. S. Liu, H. H. Dong, On the existence of solution, Lie symmetry analysis and conservation law of magnetohydrodynamic equations, Commun. Nonlinear Sci. Numer. Simul., 87 (2020), 105277. https://doi.org/10.1016/j.cnsns.2020.105277 doi: 10.1016/j.cnsns.2020.105277
[25]	S. Xia, Z. Wang, Lie symmetries, group invariant solutions and conservation laws of ideal MHD equations, J. Appl. Anal. Comput., 12 (2022), 1959–1986. https://doi.org/10.11948/20210410 doi: 10.11948/20210410
[26]	P. Y. Picard, Some exact solutions of the ideal MHD equations through symmetry reduction method, J. Math. Anal. Appl., 337 (2008), 360–385. https://doi.org/10.1016/j.jmaa.2007.03.100 doi: 10.1016/j.jmaa.2007.03.100
[27]	N. K. Vitanov, On modified method of simplest equation for obtaining exact and approximate solutions of nonlinear PDEs: The role of the simplest equation, Commun. Nonlinear Sci. Numer. Simul., 16 (2011), 4215–4231. https://doi.org/10.1016/j.cnsns.2011.03.035 doi: 10.1016/j.cnsns.2011.03.035
[28]	G. D. Zhang, X. He, X. Yang, A fully decoupled linearized finite element method with second-order temporal accuracy and unconditional energy stability for incompressible MHD equations, J. Comput. Phys., 448 (2022), 110752. https://doi.org/10.1016/j.jcp.2021.110752 doi: 10.1016/j.jcp.2021.110752
[29]	Z. Li, X. Zhang, New exact kink solutions and periodic form solutions for a generalized Zakharov-Kuznetsov equation with variable coefficients, Commun. Nonlinear Sci. Numer. Simul., 15 (2010), 3418–3422. https://doi.org/10.1016/j.cnsns.2010.01.003 doi: 10.1016/j.cnsns.2010.01.003
[30]	H. U. Rehman, A. R. Seadawy, S. Razzaq, S. T. R. Rizvi, Optical fiber application of the Improved Generalized Riccati Equation Mapping method to the perturbed nonlinear Chen-Lee-Liu dynamical equation, Optik, 290 (2023), 171309. https://doi.org/10.1016/j.ijleo.2023.171309 doi: 10.1016/j.ijleo.2023.171309
[31]	X. Huang, Y. Wang, Global strong solution with vacuum to the two dimensional density-dependent Navier-Stokes system, SIAM J. Math. Anal., 46 (2014), 1771–1788. https://doi.org/10.1137/120894865 doi: 10.1137/120894865
[32]	J. Li, Z. Xin, Global Existence of Regular Solutions with Large Oscillations and Vacuum, Berlin Heidelberg: Springer Cham, 2016. https://doi.org/10.1007/978-3-319-10151-4_58-1
[33]	K. L. Cheung, Exact solutions for the two-dimensional incompressible magnetohydrodynamics equations, Appl. Math. Sci., 8 (2014), 5915–5922. http://doi.org/10.12988/ams.2014.48641 doi: 10.12988/ams.2014.48641
[34]	K. Ayub, M. Y. Khan, Q. M. Ul-Hassan, M. Ashraf, M. Shakeel, Soliton formations for magnetohydrodynamic viscous flow over a nonlinear stretching sheet, Pramana, 91 (2018), 1–7. https://doi.org/10.1007/s12043-018-1652-8 doi: 10.1007/s12043-018-1652-8

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Networks and Heterogeneous Media

1.2 1.8

Metrics

Article views(779) PDF downloads(41) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(15)

Networks and Heterogeneous Media

New wave behaviors and stability analysis for magnetohydrodynamic flows

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. New wave behaviors of $(2 + 1)$ -dimensional MHD flows

3.1. Lie symmetry analysis of MHD equations

3.1.1. Inviscid MHD equations

3.1.2. Viscous MHD equations

3.2. Generalized Riccati equation expansion method for MHD equations

3.2.1. Inviscid MHD equations

3.2.2. Viscous MHD equations

4. New wave behaviors of (3 + 1)-dimensional MHD flows

4.1. Lie symmetry analysis of MHD equations

4.1.1. Inviscid MHD equations

4.1.2. Viscous MHD equations

4.2. Generalized Riccati equation expansion method for MHD equations

4.2.1. Inviscid MHD equations

4.2.2. Viscous MHD equations

5. Stability of MHD flows

5.1. Qualitative analysis

5.2. Quantitative analysis

6. Conclusions

Author contributions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Networks and Heterogeneous Media

New wave behaviors and stability analysis for magnetohydrodynamic flows

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. New wave behaviors of (2+1) (2 + 1) -dimensional MHD flows

3.1. Lie symmetry analysis of MHD equations

3.1.1. Inviscid MHD equations

3.1.2. Viscous MHD equations

3.2. Generalized Riccati equation expansion method for MHD equations

3.2.1. Inviscid MHD equations

3.2.2. Viscous MHD equations

4. New wave behaviors of (3 + 1)-dimensional MHD flows

4.1. Lie symmetry analysis of MHD equations

4.1.1. Inviscid MHD equations

4.1.2. Viscous MHD equations

4.2. Generalized Riccati equation expansion method for MHD equations

4.2.1. Inviscid MHD equations

4.2.2. Viscous MHD equations

5. Stability of MHD flows

5.1. Qualitative analysis

5.2. Quantitative analysis

6. Conclusions

Author contributions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3. New wave behaviors of $(2 + 1)$ -dimensional MHD flows