Assessing contamination sources and environmental hazards for potentially toxic elements and organic compounds in the soils of a heavily anthropized area: the case study of the Acerra plain (Southern Italy)

1.   Introduction

Jellyfish plays an important role in the marine ecosystems as a keystone species and a potential resource for human consumption ^[1]. The amount of jellyfish has been significantly increasing in many waters since 1980s ^[2]. Jellyfish can be found in many regions worldwide such as Japan ^[3], the China Seas ^[4], the Mediterranean Sea ^[5], Taiwan ^[6], Southampton Water and Horsea Lake, England ^[7]. It can survive in a wide range of water temperatures $ (0- 36\; ^{\circ}C) $ and salinities $ (3- 36\%) $ ^[8,9].

Jellyfish has a complex life history with several different phases: planula, polyp, strobila, ephyra and medusa ^[10]. The polyp and medusa are two main stages of the life cycle of jellyfish. Medusae are dioecious, the sperm combines with egg to form a planula, which normally settles to the bottom and then occur metamorphosis of planula into tentacles-ring polyp (or scyphistoma) ^[11]. For Aurelia aurita jellyfish, the scyphistoma produces external outgrowths asexually by budding, the vitally asexual reproduction of polyp ($ 94\% $), stolon ($ 5\% $) and podocysts ($ 1\% $) ^[3]. The scyphistoma changes into strobila (strobilating polyp) through strobilation, which is asexual reproduction by division into segments developing into ephyra. After liberating from strobila, the ephyra becomes adult medusa. In addition, strobila reverts into the initial scyphistoma ^[11]. Since jellyfish has a distinct mobility patterns in different phases of its life history, it is interesting to take these facts into account for model formulation.

Temperature has a great effect on variations of jellyfish populations ^[12] as the asexual reproduction rate and strobilation rate depend on the functions of temperatures ^[11]. Global warming has affected the increase of jellyfish populations because it might cause the distribution, growth, and ephyrae production of medusae ^[13]. The rapid strobilation might be proceeded at the warmer temperature, but the continuous high temperature results in the fewer budding and increased mortality ^[6]. Hence the population explosions of polyps and medusae might be caused at the appropriate increase of temperature, but rising temperatures lead to the decreased populations.

Many approaches for jellyfish have been developed to discuss the nature of the correlations between environmental indices and population abundance ^[6,14]. In particular, mathematical modeling is one of the important tools in analyzing the dynamical properties in aquatic systems. In ^[15], Oguz et al. presented food web model with an anchovy population and bioenergetics-based weight growth model governed by system of differential equations. In ^[16], Melica et al. conducted that the dynamics of polyps population by the logistic model. In ^[11], Xie et al. proposed the following two-dimensional dynamic model of scyphozoan jellyfish:

where $ P(t) $ and $ M(t) $ are the population sizes of polyps and medusae at time $ t $, respectively. For system (1.1), by using the Bendixson-Dulac's negative criterion and Poincare-Bendixson Theorem, the conditions for the global asymptotical stability of the equilibria $ E_0 $, $ E_1 $ and $ E^* $ are given. The effects of temperature, substrate and predation on the population sizes of scyphozoan were investigated by numerical simulations.

Although multiple progresses have been seen in the above work of ^[11], for system (1.1), it is assumed that each population preserves an equal density dependent rate and each individual has the same opportunity to compete for their common resources during the whole life history. Unfortunately, this is not realistic due to the life history of jellyfish which has a diverse mobility body structures in different stages. The immature stages of jellyfish are much weaker than the mature stages and so they cannot compete for their common resources. Jellyfish reaches maturity after surviving the immature stages. Therefore, it is realistic and interesting for us to construct the stage-structured jellyfish model that exhibits a diversity between these different stages.

Recently, population dynamic models with stage structure and time delays have attracted more attention from authors ^{[17,18,19,20,21,22,23,24]}. For instance, Aiello and Freedman proposed a stage-structured model of single species containing of the immature and mature stages and using a discrete time delay taken from birth to maturity ^[18]. Liu et al. showed that the global stability for the two competitive Lotka-Volterra system with time delay that denotes the time taken from birth to maturity. They proposed that the stage structure is one of the main reasons that cause permanence and extinction for the two competitive system ^[23]. There have been an increasing interest and progress in the study of the above stage-structured models which assume all individuals are in the same species that require the analogous amount of time to become mature at the same age. Unlike birds and mammals, jellyfish species have the different mobility shapes in the distinctive stages of its life cycle. Thus, the previous methods and techniques cannot be applied exactly to our system because we classify the single species jellyfish into two-stage structure. Mathematically, the proposed model has two delay terms and the equations are matched with each other, which is not similar with the previous models ^[18,23,24].

In this paper, we will propose a time-delayed jellyfish model with stage structure and will investigate how the stage structure parameters and temperature affect the dynamical behaviors of system (2.2). Our main purpose is to study the population dynamics of jellyfish for the largest surviving probability as well as for final population numbers. To find the largest surviving probability, we will take the global asymptotical behaviors of the model by applying the monotone dynamical properties (for reference, see ^[25] and [26,p. 90]).

This paper is organized as follows: in Section 2, we propose the model and show that the solutions are positiveness and ultimately bounded. The main results of this paper are presented in Section 3. In Section 4, we perform numerical simulations to explore the effects of two delays and temperature on the dynamics. Section 5 is the brief discussion of our results.

2.   Model description and preliminaries

2.1.   Model formulating

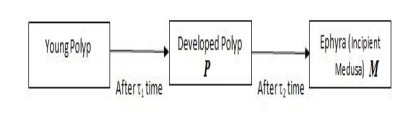
The life history of jellyfish is divided into two main stages; polyp and medusa. The larval stage of polyp is planula and the elementary phase of medusa is ephyra. Let $ P(t) $ and $ M(t) $ be the population size or number of polyps and medusae at time $ t $, respectively. The model is based on the following assumptions and the diagram in Figure 1:

$ \rm(A1) $ $ \tau_1 $ is the length of the stage from the young polyp to the mature polyp. The immature polyp reproduces asexually at time $ t-\tau_1 $ and surviving from time $ t-\tau_1 $ to $ t $ is $ e^{-(d_1+d_2)\tau_1} $.

$ \rm(A2) $ $ \tau_2 $ is the time lag taken from the developed polyp to ephyra (incipient medusa), i.e., the developed polyp reaches ephyra after surviving this stage. Denote $ \tau = \max\lbrace{\tau_1, \tau_2}\rbrace $.

$\rm (A3) $ Its maturity is denoted by $ \tau = \max\lbrace{\tau_1, \tau_2}\rbrace, \tau > 0 $.

$ \rm(A4) $ Each population competes for their common resources.

$ \rm(A5) $ Each population has its own natural death rate, the mortality of polyp is varied by the factors of silt coverage or nudibranch consumption while that of medusa is because of different types of predators.

By the preceding assumptions, we get the following polyp-medusa population with stage structure:

As pointed out in ^[11], $ \alpha(T) $ denotes the asexual reproduction rate affected by temperature, involving budding, stolon and podocyst et al., $ s_1 $ is the survival and metamorphosis rate of planula, $ \gamma $ represents the sexual reproduction rate, $ b_1 $ and $ b_2 $ denote the density-dependent rates of polyps and medusae respectively, $ s_2 $ is the survival and development rate of ephyra, $ \beta(T) $ is the strobilation rate affected by temperature and $ n $ is strobilation times. Assuming that the death rate of the immature population is proportional to the existing immature population with proportionality constants $ d_i > 0 $, i = 1, 2, 3, 4. The loss of polyp is either due to natural death rate $ d_1 $ or due to the factors of silt coverage $ d_2 $ and $ \tau_1 $ is the time taken from the immature polyp to the mature one; thus $ e^{-(d_1+d_2)\tau_1} $ is the survival probability of each immature polyp to reach the mature one. The death of medusa is either from natural fatality rate $ d_3 $ or because of the predations $ d_4 $ and $ \tau_2 $ is the time length between the developed polyp and ephyra (incipient medusa); thus $ e^{-(d_3+d_4)\tau_2} $ is the survival rate of each developed polyp to reach the ephyra (incipient medusa) population. As it takes a few days in the larval stage of jellyfish life, the permanence and extinction criteria for the stage structured model are independent in this larval stage.

For the goal of simplicity, we denote $ a = \alpha(T), $ $ b = s_1\gamma, $ $ d = d_1+d_2 $, $ c = s_2\beta(T)n, $ $ d_* = d_3+d_4 $. Thus the following system can be obtained from system (2.1).

where $ \zeta_1 = d\tau_1 $ and $ \zeta_2 = d_*\tau_2 $. Denote $ \zeta_1 $ and $ \zeta_2 $ the degrees of the stage structure.

Let $ X = \mathcal{C}([-\tau, 0], \mathbb{R}^2) $ be the Banach space of all continuous function from $ [-\tau, 0] $ to $ \mathbb{R}^2 $ equipped with the supremum norm, where $ \tau = \max\lbrace{\tau_1, \tau_2}\rbrace $. By the standard theory of functional differential equations (see, for example, Hale and Verduyn Lunel ^[27]), for any $ \psi\in\mathcal{C}([-\tau, 0], \mathbb{R}^2) $, there exists a unique solution $ Y(t, \psi) = (P(t, \psi), M(t, \psi)) $ of system (2.2); which satisfies $ Y_0 = \psi $.

For system (2.2), we consider the initial conditions to either the positive cone $ X^+ = \{\psi\in X|\mbox{ $\psi_i(\theta)\ge 0$ for all $\theta\in[-\tau, 0]$, $i = 1, 2$ }\} $ or the subset of $ X^+ $ of functions which are strictly positive at zero, $ X_0^+ = \lbrace{\psi\in X^+|\psi_i(0) > 0, i = 1, 2}\rbrace $.

2.2.   Positivity and boundedness of solutions

Lemma 2.1. For equation

where $ a, b, c, d_*, B > 0 $, $ \tau = \max\lbrace{\tau_1, \tau_2}\rbrace, \tau > 0 $ and $ \overline{W}(0) > 0 $ and $ \overline{W}(\theta)\ge 0 $, $ \theta\in[-\tau, 0] $, we have: $ \lim_{t\to\infty}\overline{W}(t) = \frac{2d_*ae^{-\zeta_1}+2bce^{-\zeta_2}}{d_*B} $ if $ d_*ae^{-\zeta_1}+bce^{-\zeta_2} > 0 $.

Proof. By using the similar argument of Lu et al. [28,Proposition 1], we will prove that $ \overline{W}(t) > 0 $, for all $ t\ge0 $. Otherwise, there exists some constant $ \acute{t}_0 > 0 $ such that $ \min \lbrace{\overline{W}(\acute{t}_0)}\rbrace = 0. $ Let $ t_0 = \inf \lbrace{\acute{t}_0: \overline{W}(\acute{t}_0) = 0}\rbrace. $ Then we have that $ \min \lbrace{\overline{W}(t_0)} = 0\rbrace $ and $ \min \lbrace{\overline{W}(t)}\rbrace > 0 $, $ \forall t \in [0, t_0) $. From system (2.3), we have

Incorporation initial conditions and Eq (2.4), we get $ \overline{W}(t_0) > 0 $, contradicting $ \min \lbrace{\overline{W}(t_0)}\rbrace = 0 $. Consequently, $ \overline{W}(t) > 0 $ for all $ t \ge 0 $.

Let $ \overline{W}^* = \frac{2d_*ae^{-\zeta_1}+2bce^{-\zeta_2}}{d_*B} $ denotes the unique positive equilibrium of system (2.3). Denote $ u(t) = \overline{W}(t)-\overline{W}^* $, thus system (2.3) takes the form as

Constructing the Lyapunov functional

we have

which is negative definite and $ \left.\frac{dV}{dt}\right|_{(2.5)} = 0 $ if and only if $ u = 0 $. By Lyapunov-LaSalle invariance principle ([29,Theorem 2.5.3]), we get $ \lim_{t\to\infty}\overline{W}(t) = \overline{W}^* = \frac{2d_*ae^{-\zeta_1}+2bce^{-\zeta_2}}{d_*B} $, this proves Lemma 2.1.

Lemma 2.2. Given system (2.2), then:

(I) Under the initial conditions, all the solutions of system (2.2) are positive for all $ t\ge 0 $.

(II) Solutions of system (2.2) are ultimately bounded.

Proof. (I) We start with proving the positivity of solutions by using the similar argument of Lu et al. [28,Proposition 1]. We will prove that $ P(t) > 0 $, $ M(t) > 0 $ for $ t\ge 0 $. Otherwise, there exists some constant $ \tilde{t}_0 > 0 $ such that $ \min\lbrace{P(\tilde{t}_0), M(\tilde{t}_0)\rbrace = 0} $. Let $ t_0 = \inf\lbrace{\tilde{t}_0:P(\tilde{t}_0) = 0, M(\tilde{t}_0) = 0}\rbrace $. Then we have that $ \min\lbrace{P(t_0), M(t_0)}\rbrace = 0 $ and $ \min\lbrace{P(t), M(t)}\rbrace > 0 $, $ \forall t\in[0, t_0) $. From system (2.2), we have

Incorporation initial conditions and Eq (2.6), we obtain $ P(t_0) > 0 $ and $ M(t_0) > 0 $, contradicting $ \min\lbrace{P(t_0), M(t_0)}\rbrace = 0 $. Consequently, $ P(t) > 0 $, $ M(t) > 0 $ for all $ t\ge 0 $.

(II) We show that the boundedness of solutions as follows.

Let $ W = \frac{d_*}{b}P+M $. By system (2.2), we have

where $ B: = \min{\{\frac{bb_1}{d_*}, b_2}\} $.

where $ -2((\frac{d_*}{b}P)^2+M^2)\le -(\frac{d_*}{b}P+M)^2 $.

Consider the equation

By using Lemma 2.1 and Comparison Theorem, we get

$ \limsup_{t\to\infty}W(t)\le \frac{2d_*ae^{-\zeta_1}+2bce^{-\zeta_2}}{d_*B} $, which implies $ P(t) $ and $ M(t) $ are ultimately bounded. This completes the proof of Lemma 2.2.

2.3.   Existence of equilibria

The equilibria $ (P, M) $ of system (2.2) satisfies the following system

System (2.2) has the equilibria $ E_0 = (0, 0) $ for all parameter values and $ E_1 = (\frac{ae^{-\zeta_1}-d}{b_1}, 0) $ if $ ae^{-\zeta_1}-d > 0 $ and $ c = 0 $.

Since Eq (2.8) can be rewritten as

When $ PM\neq 0 $, from Eq (2.9) it follows that

Further, substituting $ P = \frac{(d_*+b_2M)M}{ce^{-\zeta_2}} $ into Eq (2.10) and we get

Set

thus $ F(M) $ is a decreasing function of $ M $ for any $ M > 0 $.

Noting that the continuity and monotonicity of $ F(M) $ and that $ F(+\infty) < 0 $, furthermore since one can get $ F(0) > 0 $ provided that

hold true, therefore we conclude that system (2.2) admits a unique positive equilibrium given Eq (2.11) is satisfied.

3.   Stability and global attractiveness

The purpose of this section is to study the global stability of system (2.2).

3.1.   Stability

Now we consider the local stability of the equilibria. The characteristic equation of system (2.2) takes the form as follows;

where

Lemma 3.1. Suppose that $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $, then the equilibrium $ E_0 = (0, 0) $ of system (2.2) is locally asymptotically stable.

Proof. The characteristic equation of system (2.2) at the equilibrium $ E_0 $ is as follows:

To show that it is asymptotically stable under assumption $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $, we just need to prove that the solutions of the characteristic equation $ C(\lambda) = 0 $ must have negative real parts. Let $ \lambda = u+iv $, where $ u $ and $ v $ are real numbers. Denote

Substituting $ \lambda $ by $ u+iv $ into Eq (3.1)

Then

Assume that $ u\ge 0 $, then we get

Hence

From Eq (3.2), we obtain

Hence Eq (3.3) contradicts to the assumption $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $, thus $ u < 0 $, which means $ \lambda $ must have negative real parts. This proves Lemma 3.1.

Lemma 3.2. Suppose that $ ae^{-\zeta_1}-d > 0 $ and $ c = 0 $, then the equilibrium $ E_1 = (\frac{ae^{-\zeta_1}-d}{b_1}, 0) $ of system (2.2) is locally asymptotically stable.

Proof. The characteristic equation of system (2.2) at the equilibrium $ E_1 $ is

Then $ \lambda = -d_* $ is a negative root of the equation $ X(\lambda) = 0 $. Let $ \lambda-d+2ae^{-\zeta_1}-ae^{-\zeta_1-\lambda\tau_1} = 0 $; then if the root is $ \lambda = u+iv $, we have $ u+2ae^{-\zeta_1}-d-ae^{-\zeta_1-u\tau_1}\cos(v\tau_1) = 0 $. Assume that $ u\ge 0 $, then $ u+2ae^{-\zeta_1}-d-ae^{-\zeta_1-u\tau_1}\cos(v\tau_1)\ge ae^{-\zeta_1}-d > 0 $ is a contradiction, hence $ u < 0 $. This shows that all the roots of $ X(\lambda) = 0 $ must have negative real parts, and therefore $ E_1 $ is locally asymptotically stable. This proves Lemma 3.2.

Lemma 3.3. Suppose that $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $ and $ c\neq0 $, then the equilibrium $ E^* = (P^*, M^*) $ of system (2.2) is locally asymptotically stable.

Proof. The characteristic equation of system (2.2) at the equilibrium $ E^* $ is

To show that it is asymptotically stable under $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $, we just need to prove that the solutions of the characteristic equation must have negative real parts. Let $ \lambda = u+iv $ where $ u $ and $ v $ are real numbers. Denote

Substituting $ \lambda $ by $ u+iv $ into the above equation.

Then

Assume that $ u\ge 0 $, then we get

Hence

By Eq (3.5), we get

By assumption $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $, which is a contradiction, thus $ u $ must be negative real parts. This completes the proof of Lemma 3.3.

3.2.   Global attractiveness

Before the details, we will present the notion from the literature ^[25]. We define

by $ x_t(\theta) = x(t+\theta), \forall \theta\in[-\tau, 0] $. Consider a delay system

for which uniqueness of solutions is assumed, $ x(t, \psi) $ designates the solution of Eq (3.6) with initial condition $ x_0 = \psi $ $ (\psi\in\mathcal{C}) $.

A non-negative equilibrium $ v = (v_p, v_m)\in \mathbb{R}^2 $ of system (2.2) is said to be globally attractive if $ Y(t)\to v $ as $ t\to\infty $, for all admissible solutions $ Y(t) $ of system (2.2). We say that $ v $ is globally asymptotically stable if it is stable and globally attractive.

System (2.2) is written as Eq (3.6),

Observe that system (2.2) is cooperative, i.e., $ Df_i(\psi)\varphi\ge 0 $, for all $ \psi, \varphi\in X^+ $ with $ \varphi_i(0) = 0, i = 1, 2 $. This implies that $ f $ satisfies quasi-monotonicity condition [26,p. 78]. Typically, in population dynamics the stability of equilibria is closely related to the algebraic properties of some kinds of competition matrix of the community. Denote

For convenience, we shall refer to $ N = A+D $ as the (linear) community matrix:

Since $ D\ge 0 $, the matrix $ N $ in Eq (3.8) is called cooperative. If $ D $ is irreducible, then the matrix $ N $ in Eq (3.8) is also irreducible; in this case, system (2.2) is called an irreducible system [26,p. 88], and the semiflow $ \psi\mapsto Y_t(\psi) $ is eventually strongly monotone. $ f = (f_1, f_2)^T:\mathbb{R}^2 \to \mathbb{R}^2 $ is strictly sublinear, i.e., for any $ P\gg 0, M\gg 0 $ and any $ \alpha\in(0, 1), $

Cooperative $ DDEs $ satisfying these sublinearity conditions have significant properties [30,Proposition 4.3].

Recall that the stability modulus of square matrix $ N $ in Eq (3.8), denoted by $ s(N) $, is defined by $ s(N) = \max \{Re \lambda:\mbox{ $\lambda$ is an eigenvalue of $N$ }\rbrace $. If the matrix $ N $ in Eq (3.8) has nonnegative off diagonal elements and is irreducible, then $ s(N) $ is a simple eigenvalue of the matrix $ N $ with a (componentwise) positive eigenvector (see, e.g., [31,Theorem A.5]).

The matrix $ N $ in Eq (3.8) is

then we can easily get the following:

$ s(N) > 0 $ if and only if $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $ and $ s(N) < 0 $ if and only if $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $.

Definition 3.4. ^[32] A square matrix $ A = [a_{ij}] $ with non-positive off diagonal entries, i.e., $ a_{ij}\le 0 $ for all $ i\neq j $, is said to be an M-matrix if all the eigenvalues of $ A $ have a non-negative real part, or equivalently, if all its principal minors are non-negative, and $ A $ is said to be a non singular M-matrix if all the eigenvalues of $ A $ have positive real part, or, equivalently, if all its principal minors are positive.

Theorem 3.5. Suppose that $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $, then the equilibrium $ E_0 $ of system (2.2) is globally asymptotically stable.

Proof. Let $ P(t, l) $, $ M(t, k) $ be the solutions of system (2.2) with $ P(0+\theta, l) = l $, $ M(0+\theta, k) = k $ for $ \theta\in[-\tau, 0] $. Note that $ f_1(l) = l[-d+b+ae^{-\zeta_1}-b_1l] < 0 $ for $ l > 0 $ sufficiently large and $ f_2(k) = k[-d_*+ce^{-\zeta_2}-b_2k] < 0 $ for $ k > 0 $ sufficiently large. Hence we can easily conclude that all admissible solutions of system (2.2) are bounded [26,Corollary 5.2.2]. We have $ s(N) < 0 $ if and only if $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $. By the assumption $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} < 0 $, we observed that it is equivalent to having $ -N $ a non singular M-matrix. Since matrix $ -N $ is a non singular M-matrix, there exists the equilibrium $ v = (v_p, v_m)\in \mathbb{R}^2, v > 0, $ such that $ Nv < 0 $, hence we get

Let $ P(t)\ge 0 $, $ M(t)\ge 0 $ be solutions of system (2.2). Denote $ y_p(t) = \frac{P(t)}{v_p} $ and $ y_m(t) = \frac{M(t)}{v_m} $, thus system (2.2) takes the form as

It suffices to prove that $ (L_p, L_m): = \limsup_{t\to\infty} (y_p(t), y_m(t)) = (0, 0) $. Let $ L_p: = \limsup\lbrace{y_p(t)}\rbrace $, $ L_m: = \limsup\lbrace{y_m(t)}\rbrace $, $ \tilde{L}: = \max\lbrace{L_p, L_m}\rbrace $ and suppose that $ \tilde{L} > 0 $. From Eq (3.9), we can choose $ \varepsilon > 0 $ such that

Let $ T > 0 $ be such that $ y_p(t)\le \tilde{L}+\varepsilon $, $ y_m(t)\le \tilde{L}+\varepsilon $ for all $ t > T-\tau $ and the cases of $ y_p(t) $ and $ y_m(t) $ are separated as eventually monotone and not eventually monotone. By [26,Proposition 5.4.2], if $ y_p(t) $ and $ y_m(t) $ are eventually monotone, then $ y_p(t)\to \tilde{L} $ and $ y_m(t)\to \tilde{L} $ as $ t\to \infty $ for $ t\ge T $ and we obtain

Since $ \gamma_p < 0 $ and $ \gamma_m < 0 $, these imply that $ \lim_{t\to \infty} (y_p(t), y_m(t)) = -\infty $, which is impossible. By using the similar argument of Aiello and Freedman [18,Theorem 2], if $ y_p(t) $ and $ y_m(t) $ are not eventually monotone, there is a sequence $ t_n\to\infty $ such that $ y_p(t_n)\to \tilde{L}, $ $ y'_p(t_n) = 0 $ and $ y_m(t_n)\to \tilde{L}, $ $ y'_m(t_n) = 0 $. We obtain (3.11) with $ t $ replaced by $ t_n $, again a contradiction. This proves $ \lim_{t\to \infty} (y_p(t), y_m(t)) = (0, 0) $. Using Lemma 3.1, we complete the proof of Theorem 3.5.

Theorem 3.6. Suppose that $ ae^{-\zeta_1}-d > 0 $ and $ c = 0 $, then the equilibrium $ E_1 $ of system (2.2) is globally asymptotically stable.

Proof. If $ c = 0 $, the second equation of system (2.2) becomes

For the independent subsystem (3.12), it is obvious that $ \lim_{t\to \infty} M(t) = 0 $.

Then the first equation of system (2.2) becomes

Let $ \varepsilon > 0 $ be sufficiently small and $ L > 0 $ be sufficiently large such that $ \varepsilon\le P(t)\le L $, $ t\in[-\tau, 0] $, and

Let $ P_\varepsilon(t) $ and $ P_L(t) $ be the solutions of Eq (3.13) with $ P_\varepsilon(t) = \varepsilon $ and $ P_L(t) = L $ for $ t\in[-\tau, 0] $. From the monotone properties of the equation ^[26], the function $ P_\varepsilon(t) $ is increasing and $ P_L(t) $ is decreasing for $ t\ge 0 $ and

It therefore follows that

because the only equilibrium of the equation between $ \varepsilon $ and $ L $ is $ \frac{ae^{-\zeta_1}-d}{b_1} $. Using Lemma 3.2, we complete the proof of Theorem 3.6.

Lemma 3.7. Suppose there is a positive equilibrium $ (P^*, M^*) $ of system (2.2), and that $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $ and $ c\neq 0 $. Then all solutions $ P(t, \psi_1) $, $ M(t, \psi_2) $ of system (2.2) with $ \psi_i\in X_0^+, i = 1, 2 $ satisfy $ \liminf_{t\to\infty}(P(t, \psi_1), M(t, \psi_2))\ge (P^*, M^*) $.

Proof. For $ (P^*, M^*) $ an equilibrium of system (2.2), we have

Denote $ \bar{P}(t) = \frac{P(t)}{P^*} $ and $ \bar{M}(t) = \frac{M(t)}{M^*} $ in system (2.2), and dropping the bar for simplicity, we get

For the solutions $ P(t) = P(t, \psi_1) $ and $ M(t) = M(t, \psi_2) $ of Eq (3.15) with $ \psi_i\in X_0^+ $ for $ i = 1, 2 $, we first claim that $ (l_p, l_m): = \liminf_{t\to\infty}(P(t), M(t)) > (0, 0) $. Otherwise, there exist $ \delta\in(0, 1) $ and $ t_0 > \tau $ such that $ \tilde{l} = \min\lbrace{(P(t), M(t)):t\in[0, t_0]}\rbrace $ and $ \tilde{l} < \delta $. By using Eq (3.14),

But these are not possible. Since the definition of $ t_0 $, $ P'(t_0)\le 0 $ and $ M'(t_0)\le 0 $.

Next we prove that $ (l_p, l_m)\ge(1, 1) $. Choose $ \tilde{l} = \min \lbrace{l_p, l_m}\rbrace $ and suppose that $ \tilde{l} < 1 $. Let $ T > 0 $ and $ \varepsilon > 0 $ be chosen so that $ P(t)\ge \tilde{l}-\varepsilon $ and $ M(t)\ge \tilde{l}-\varepsilon $ for all $ t > T-\tau $.

By [26,Proposition 5.4.2], if $ P(t) $ and $ M(t) $ are eventually monotone, then $ P(t)\to \tilde{l} $ and $ M(t)\to \tilde{l} $ and for $ t\ge T $, we have

leading to $ P(t)\to \infty $ and $ M(t)\to \infty $ as $ t\to \infty $, contradicting $ \tilde{l} < 1 $. By using the similar argument of Aiello and Freedman [18,Theorem 2], if $ P(t) $ and $ M(t) $ are not eventually monotone, there is a sequence $ t_n\to \infty $ such that $ P(t_n)\to \tilde{l}, $ $ P'(t_n) = 0 $ and $ M(t_n)\to \tilde{l}, $ $ M'(t_n) = 0 $. For $ t_n\ge T $, we obtain the above inequalities $ t_n $ instead of $ t $, which yield that $ 0 = P'(t_n)\ge n_p $ and $ 0 = M'(t_n)\ge n_m $, again contradicting $ \tilde{l} < 1 $. This proves that $ \tilde{l}\ge 1 $.

Theorem 3.8. Suppose that $ (ae^{-\zeta_1}-d)d_*+bce^{-\zeta_2} > 0 $ and $ c\neq 0 $, then the equilibrium $ E^* $ of system (2.2) is globally asymptotically stable.

Proof. For $ (P^*, M^*) $ of system (2.2), after the changes $ P(t)\mapsto \frac{P(t)}{P^*} $ and $ M(t)\mapsto \frac{M(t)}{M^*} $, consider system (3.15) with positive equilibrium $ (1, 1)\in \mathbb{R}^2 $. In view of Lemmas 3.3 and 3.7, we only need to prove that $ (L_p, L_m): = \limsup_{t\to \infty}(P(t), M(t))\le (1, 1) $ and any positive solution $ P(t) $, $ M(t) $ of Eq (3.15).

For the sake of contradiction, suppose that $ \tilde{L} = \max \lbrace{L_p, L_m}\rbrace > 1 $. Choose $ \varepsilon > 0 $ and $ t > \tau $, such that $ P(t)\le \tilde{L}+\varepsilon $ and $ M(t)\le \tilde{L}+\varepsilon $ for all $ t > T-\tau $ and

Separating the cases of $ P(t) $ and $ M(t) $ eventually monotone and not eventually monotone, and reasoning as in the proofs of Theorem 3.5 and Lemma 3.7, we obtain a contradiction, thus $ \tilde{L}\le 1 $. Finally we get $ \lim_{t\to \infty}(P(t), M(t)) = (P^*, M^*) $. Using Lemma 3.3, we complete the proof of Theorem 3.8.

Remark 1. Note that when $ \tau_1 = \tau_2 = 0 $, system (2.2) becomes system (1.1). Theorems 4–6 in ^[11] are the corresponding results of Theorems 3.5, 3.6 and 3.8 for system (2.2), respectively. Our main results not only extend the results in ^[11] but also generalize the related results into the stage-structured system with two delays. But the proof methods of our results are quite different to those in ^[11].

4.   Numerical simulations

In this section, we numerically simulate the dynamics of system (2.2) for a range of parameters which are the same as those in ^[11]. In this paper, we add the values of two delays $ \tau_1 $ and $ \tau_2 $ from ^[10,33]. The parameters are given in Table 1.

Values signatured by $ ^{a} $ are from experimental data with unit innovation and those signatured by $ ^{b} $ are estimated from references.

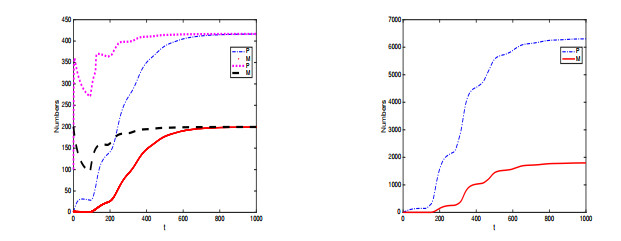
The left figure of Figure 2 shows that the positive equilibrium $ E^* $ of system (2.2) is globally asymptotically stable under different initial values. The left figure and right figure of Figure 2 take the parameters data 1 and data 2, respectively. Figure 2 shows that the population sizes change with respect to environmental indices but do not depend on the initial values. The population explosion occurs even though the initial values $ (P = 0, M = 2) $ are small (see the right figure of Figure 2). The numbers of two stages in the right figure of Figure 2 are larger than those in the left figure of Figure 2 because the reproduction is high while the destructions and competitions are low in the right figure of Figure 2. The trajectories of the right figure of Figure 2 finally tend towards a higher population level up to 10–15 times than the trajectories in the left figure of Figure 2 (in the corresponding Figure 3 of ^[11], the populations of Figure 3(b) is higher 30–50 times than Figure 3(a)) although the initial values $ (0, 2) $ are of equal values.

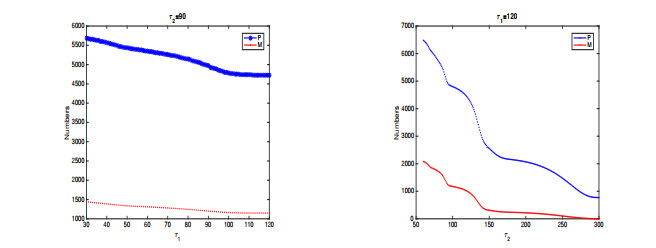
Based on data 2, Figure 3 illustrates how time delays affect the population dynamics. In the left figure of Figure 3, we fix the delay $ \tau_2 $ as the best fit value and increase the delay $ \tau_1\in [30,120] $. We find that the populations are slightly fallen over the longer period $ \tau_1 $ (see the left figure of Figure 3). This is because of the lack of needed temperature and resources and so the asexual reproduction period is long, and the results of the population are low. When we fix the delay $ \tau_1 $ and change the delay $ \tau_2 $ from $ 60 $ to $ 300 $, the populations are significantly decreased over the longer period $ \tau_2 $ (see the right figure of Figure 3). Overall, Figure 3 can be seen that the peaks of population abundance occur at the small $ \tau_1 $ and $ \tau_2 $ while the longer maturation periods may be responsible for the lower populations.

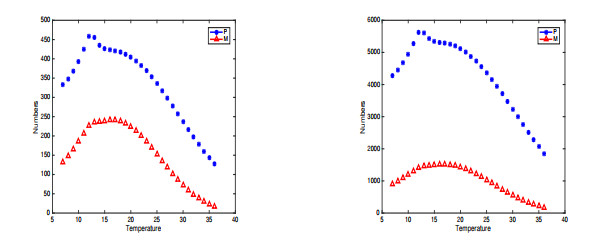
Figure 4 depicts the effect of temperature $ T\in [7,36] $ on the populations. Temperature is the impact factor that affects the asexual reproduction and strobilation of the jellyfish. In ^[11], Xie et al. presented that

In Figure 4, the numbers of polyp reach a peak at $ 12.5\; ^{\circ}C $, which correlates with the maximum budding rate of experimental data ^[14] and then gradually declined over the high temperature. From $ 12.5\; ^{\circ}C $ to $ 16.8\; ^{\circ}C $ is the maximum level of the number of medusae which is different from the experimental result $ 15\; ^{\circ}C $ ^[14]. Figure 4 reveals that an appropriate increase of temperature might cause a large increase in the number of populations but the rise of temperatures would result in the fewer populations. Comparing the corresponding Figure (4d) in ^[11] with the right figure of Figure 4 in this paper, we find out that we can exactly see the peak populations due to the stage structure and can exactly know the effects of temperature on the population dynamics because the temperature is considered up to $ 36\; ^{\circ}C $ in this paper.

5.   Discussion

In this paper, we propose and analyze a delayed jellyfish model with stage structure, which is an extension of ODE model studied by Xie et al. in ^[11]. We have investigated how the phenomena of budding and strobilation influence the population dynamics of the jellyfish population. $ \tau_1 $ stands the time needed from the stage of the young polyp to the developed polyp and $ \tau_2 $ stands the time taken from the mature polyp to ephyra (incipient medusa). We have developed the systematic analysis of the model in both theoretical and numerical ways.

We have proved the global stability of the equilibria under suitable conditions. Our results not only extend but also improve some related results of literature ^[11]. Our Theorems 3.5, 3.6 and 3.8 straightly extend the corresponding Theorems 4–6 in ^[11], respectively. Comparing the corresponding Theorems 4–6 in ^[11] for the ODE system (1.1) with Theorem 3.5, 3.6 and 3.8 for system (2.2), we find out that there are two extra terms $ e^{-d\tau_1} $ and $ e^{-d_*\tau_2} $ in our permanence and extinction criteria, i.e., the surviving probability of each immature population to develop into mature, which obtains due to the stage structure. From our results, we find that the jellyfish population will be extinct in the large immature mortality rate $ d, d_* $ or the long maturation $ \tau_1, \tau_2 $. Thus we may suggest that the proper increases of $ d\tau_1 $ and $ d_*\tau_2 $ have a negative effect of jellyfish population.

Biologically, our results suggest that (i) jellyfish species go extinct if the survival rate of polyp during cloning and the survival rate of the incipient medusa during strobilation are less than their death rates; (ii) polyps will continue and there is no complement from polyp to medusa if the survival rate of polyp during cloning is larger than its death rate and the temperature is not enough to strobilate; (iii) both polyp and medusa will survive in a certain ideal environment and our result converges to the positive constant when the survival rate of polyp during cloning and the survival rate of the incipient medusa during strobilation are larger than their death rates.

Besides the above systematic theoretical results, we have performed the numerical simulations to support the theoretical results. Our numerical results suggest that the positive equilibrium is globally asymptotically stable under distinctive initial values and the population sizes don't deal with the initial values but they change with respect to environmental factors. In Figures 3 and 4, our results suggest that the abundance in population occurs at the smaller periods $ \tau_1 $ and $ \tau_2 $ whereas the longer periods $ \tau_1 $ and $ \tau_2 $ will lower the peak population of polyp and medusa. In addition to the problem due to increasing $ \tau_1 $ and $ \tau_2 $, the increase of temperatures might cause the outburst of the population dynamics. If there is much higher temperature, the population rate leads to decline. Since temperature has a great impact on jellyfish population, it is interesting for one to consider the populations under the relevance to temperature. We leave this interesting problem as our future work.

Acknowledgments

We would like to take this chance to thank the editor and the anonymous referees for their very valuable comments, which led to a significant improvement of our previous versions. The authors would like to thank Dr. Zhanwen Yang for his warm help on the numeric simulations. Z. Win, B. Tian and S. Liu are supported by the Natural Science Foundation of China (NSFC) (No. 11871179, 11771374, 91646106).

Conflict of interest

All authors declare no conflicts of interest in this paper.