Stage duration distributions and intraspecific competition: a review of continuous stage-structured models

1.   Introduction

Single species population dynamics are governed by the growth rate, which is further determined by the survival and reproduction of its individuals. Both the survival and reproduction rates differ from individual to individual, depending on age, body mass, etc. Trivially speaking, individuals in the reproductive stage directly contribute to the birth rate, and the survival rates vary by life stages. In combination, variations in demographic rates among individuals should be appropriately incorporated into a population growth model. Instead of considering excessively detailed demographic characteristics in laboratory or field experiments, it would be more practical in some cases to lump individuals with similar characteristics together in a specific life stage. On the other hand, ignoring the variations among different stages can lead to misleading predictions on population dynamics ^[1]; therefore, stage-structured models are proposed as an ideal tool to describe population growth, which take a balance between the model complexity and model performance. Usually, individuals in the same stage can be assumed to undergo an identical development time (a mean development delay) while omitting variances in stage durations. However in some scenarios, the time an individual takes in a specific life stage is not uniformly distributed. For example, some eggs hatch (e.g., become larvae in some insects) before other eggs laid at the same time ^[1], and a non-uniform (non-Dirac) distribution for the stage duration should be considered when grouping age-stratified individuals together in a stage. To describe the heterogeneity in development, various distributions for stage durations have been fitted from the stage-frequency data obtained from monitoring cohorts through time, including gamma, Weibull, log-normal, logistic and other distributions ^[2]. For example, the widely used gamma distribution with a positive integer shape parameter $n$ and rate parameter $n\lambda > 0$ has the following probability density function

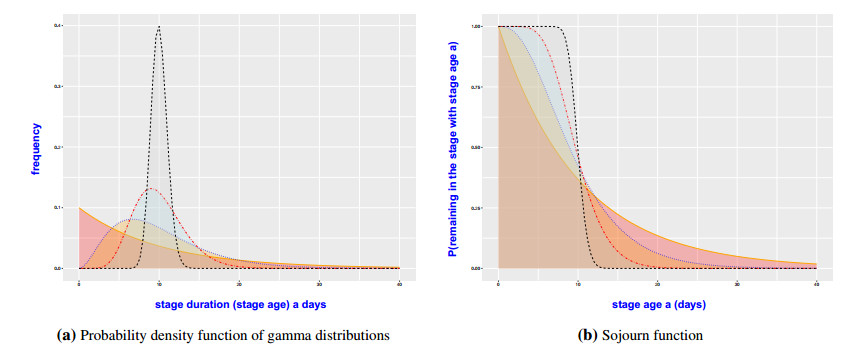
This special gamma distribution is also called an Erlang distribution as the shape parameter $n$ is a positive integer. The mean value and variance of this distribution are $\frac{1}{\lambda}$ and $\frac{1}{n\lambda^2}$. It has been fitted to the stage-frequency data ^[2,3] for different species. When $n = 1$, it becomes an exponential distribution. Taking the limit case when $n$ goes to infinity, it becomes the Dirac distribution (also called Dirac $\delta$-distribution). Different probability density functions are illustrated in Figure 1(a) for a mean duration fixed at $\frac{1}{\lambda} = 10$ days. In this case, the probability of an individual with the stage age $a$ remaining in the particular stage is presented in Figure 1(b).

Competition occurs when two or more individuals of the same or different populations negatively affect each other, striving for limited resources such as food, water, territory, sunlight and mates ^[4]. There are two different types of competition: intraspecific competition which occurs between individuals of the same species and interspecific competition which occurs between individuals of different species. The logistic growth model incorporates the density-dependent population growth rate due to intraspecific competition, and describes the sigmoid growth curve for a single species. Many generalized forms of the logistic equation have been proposed to fit the observed growth phenomena; examples include, the Richards model for species growth ^[5] and epidemic data ^[6], and a more generalized logistic growth model ^[7,8]. When individual movement in a spatial habitat is considered, the Fisher-KPP equation ^[9] for a continuous spatial domain and multi-patch logistic questions can be formulated ^[10]. The spatial dynamics can be investigated and the maximal total population problem can be further studied ^[11,12,13]. After almost a century of research, the competitive interaction continues to fascinate researchers who want to understand its role in shaping the population dynamics of a single species and engaging species in a community.

The main focus here is on stage-structured models of individuals of the same species competing for the same resources in an ecosystem (e.g. food or living space). However, it should be noted that the stage-structured modeling idea for single population growth has been widely employed in other research areas, such as for disease transmission with various infectious period distributions ^{[14,15,16,17,18]} and stage-dependent exposure ^[19], spatial population dynamics in continuous ^[20] and discrete ^[21] habitats, within-host virus dynamics to account for the stages of the viral life cycle before viral production ^[22], the immune responses of T cell life stages ^[23] and the waning of the immunity of a vaccinated individual ^[24].

In this manuscript, two basic modeling approaches based on integral equations and partial differential equations, are reviewed in Section 2. Both frameworks are further reduced into ordinary differential equations with or without a time delay under further Dirac and gamma distribution assumptions on the development time, respectively. Further remarks on advantages and inherent limitations are briefly discussed in the same section. Section 3 is devoted to presenting recent modeling studies, in particular those by Stephen A. Gourley and collaborators, when the mean stage duration and survival probability are regulated by population density due to intraspecific competition. Section 4 concludes the manuscript by discussing some related problems on the topic.

2.   Two physiologically-structured modeling approaches

In this section, we will review two basic structured modeling frameworks ^[25] based on integral equations and partial differential equations. The main focus will be on reducing the models under gamma and Dirac distribution assumptions for stage progression. Without loss of generality, we consider the simplest case when there are two stages, denoted as immature (pre-reproductive) and mature (reproductive) stages with population sizes $I(t)$ and $M(t)$, respectively. The sojourn functions $P_I(a)$ and $P_M(a)$ describe the probabilities that a living individual remains in immature and mature stages for $a$ units of time (stage age $a$), respectively, and satisfy the following properties: (ⅰ) $0 \leq P_X(a) \leq 1$; (ⅱ) $P_X(a)$ is nonincreasing on $a$; (ⅲ) $\int_{0}^{\infty} P_X(a)da < {\infty}$, where $X = I$, $M$. Please note that we assume the function $P_X(a)$ is differentiable, with the derivative $P'_{X}(a)$ applied for the ease of notational simplicity. When it is not differentiable, the Riemann integrals should be represented as Riemann-Stieltjes integrals; rigorous treatments can be found in ^[26]. Further interesting biological indices can be derived from this sojourn function ^[26], such as (ⅰ) the mean sojourn time in stage $X$ (mean duration of the stage) can be directly computed as $D = \int_0^{\infty}P_X(a)da$; (ⅱ) the expected remaining sojourn times at the stage age $s$ would be $D(s) = \frac{1}{P_X(s)}\int_s^{\infty}P_X(\eta)d\eta$ and $D = D(0)$; (ⅲ) the average expectation of the remaining sojourn (duration) $E = \frac{\int_0^{\infty}aP_X(a)da}{\int_0^{\infty}P_X(a)da}$; (ⅳ) the variance of the stage duration is $V = D(2E-D)$.

Population dynamics are intuitively dependent on the stage duration distributions $P_X(a)$; the Dirac and gamma distributions will be further discussed in more details. By default, the term "age" represents the chronological age of an individual. In this section, the stage-specific age will be used in some arguments, instead of the chronological age, to measure the time since entering the stage (also called the age within stage). Taking a mature individual with the chronological age $\eta$ who matures at the chronological age $s$ as an example, this individual develops to the mature stage at $I$-stage age $s$ and has $M$-stage age $\eta-s$.

2.1.   Structured population model in an integral form

Individuals in the immature stage $I$ at a time $t$ include those born at a previous time $s$, surviving to the time $t$ with the survival probability $\Pi_I(t-s)$ and staying in the stage with the probability $P_I(t-s)$, as well as those introduced at the initial time but remaining alive and in the stage. These arguments lead to the following integral form for the population size of immatures:

Here the birth rate $B(M(t))$ at a time $t$ is a function of the population size of the reproductive stage $M(t)$. The number of immatures that were introduced at the initial time and stay in the stage is

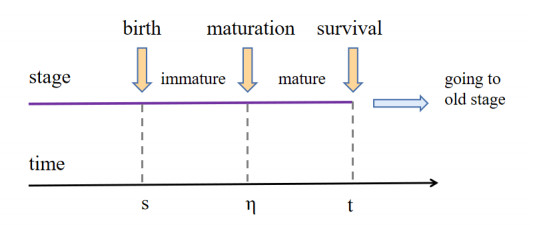
The dynamic evolution of the matured population size $M(t)$ can be depicted in Figure 2 in consideration of birth, survival and stage progression from the previous $I$ stage, as well as the development to a consequential old stage. Individuals in the mature stage $M$ at time $t$ include (ⅰ) those entering the stage at time $\eta$, surviving in the stage with the survival probability $\Pi_{M}(t-{\eta})$ and staying in the stage with stage distribution function $P_M(t-\eta)$, and (ⅱ) those mature individuals staying in the stage from the initial time or those developed from initially introduced immatures ($M_0(t)$ in Eq (2.2)). Please note that individuals entering the $M$-stage at time $\eta$ have $M$-stage age $t-{\eta}$. Furthermore, individuals entering to the mature stage at time $\eta$ are exactly those born at time $s\leq \eta$, surviving through the immature stage with the probability $\Pi_{I}({\eta}-{s})$ and maturing at the time $\eta$ at rate $-P_{I}^{'}({\eta}-{s})$ (these individuals entering the mature stage have the $I$-stage age $\eta-s$). Here, we should mention that the development rate for immature individuals with $I$-stage age $a$ is given by the derivative $-P_{I}^{'}(a)$. This term in the form of the probability density function can be derived from the following observations: An individual leaves $I$-stage and enters to the $M$-stage during the age interval $(a, a+\Delta a)$ with the probability $P_I(a) - P_I(a+{\Delta}a)$. Taking the limit when $\Delta a$ goes to zero, the individuals with $I$-stage age $a$ develop to $M$-stage at the rate $-P_{I}^{'}(a)$. These arguments give rise to the following equation

The term $M_0(t)$ can be expressed as

with $M(0)P_M(t)\Pi_M(t)$ capturing the number of remaining mature individuals introduced at time $0$ and $I(0)\int_{0}^{t}\Pi_I(u)(-P_{I}^{'}(u))\Pi_M(t-u)P_M(t-u)du$ measuring the number of mature individuals developed from immatures introduced at time $0$. On the other hand, if we introduce the following term to represent the maturation rate at time $\eta$

then we can rewrite the Eqs (2.2) and (2.3) to obtain

If one regards the maturation rate as the "birth rate" to the mature stage, then $M(t)$ in Eq (2.5) takes a similar form as $I(t)$ in Eq (2.1). We would like to remark that the stage-structured models in integral form go back to Lotka ^[27]. The model derivation was rigorously presented in [26,Chapter 13] upon careful consideration of the movement through a stage and the stage contents, stage input and stage outputs, which also relaxes the differentiability assumption on $P_I(a)$ by using Stieltjes integrals.

Since the stage duration distribution is the main focus of the current study, we take simple exponential distributions for the survival functions $\Pi_I(a)$ and $\Pi_M(a)$, that is

for individuals staying with the stage age $a$ in the $I$-stage and $M$-stage, respectively. The parameters $\mu_I$ and $\mu_M$ denote the death rates in immature and mature stages. When the stage duration distributions take some ecologically justified functions, the integral stage-structured model (2.1) and (2.2) can be rewritten into ordinary differential equations with/without time delays. In the following subsections, gamma and Dirac distributions will be discussed. However, we should mention that other stage length distributions would be more appropriate in some scenarios: for example, the distribution of the time duration spanning infection to disease death is better fitted by a lognormal distribution than by a gamma distribution ^[28] or Weibull distributions. More interesting investigations into log-normally distributed stage durations can be found in ^[28] and [26,Section 12.8].

2.1.1.   Gamma stage duration distribution

Assuming the stage duration follows a gamma distribution, then the probabilities of an individual with the stage age $a$ remaining in each stage are given by

and

with shape and rate parameter sets $(n, n\lambda)$ and $(m, m\gamma)$ respectively. It should be highlighted that the age $a$ is not the chronological age, but the stage-specific age for the actual amount of time an individual has been alive in the $I$- and $M$-stages respectively.

With the exponential survival probability for immatures, we have

Substituting (2.7) into the equation of $I(t)$ (Eq (2.1)) gives

where

with $I_{j0}(t) = I(0) {e}^{-({\mu}_{I}+n\lambda)t} \frac{({n}{\lambda}t)^{j-1} }{(j-1)!}$. Using these sub-stage variables $I_j(t)$, a differential equation system can be derived as follows by taking the derivative of each $I_j(t)$ with respect to $t$:

and for $2\leq j\leq n$,

Note that the probability density function for the gamma distribution $P_{I}(t)$ satisfies

The maturation rate in (2.4) becomes

The equation for the mature stage (2.5) can be rewritten as

with

Similar arguments as those for $I_j(t)$ lead to a series of equations for variables of mature individuals in each sub-stage:

Therefore, by introducing sub-stage variables $I_j(t)$ and $M_i(t)$, a closed ordinary differential equation model can be derived from the integral form given by (2.1) and (2.2) when the stage duration distributions follow the gamma distributions in (2.7) and (2.8):

2.1.2.   Dirac stage duration distribution

The Dirac stage distribution is suitable to describe the case when individuals entering a specific stage together are assumed to undergo an identical development time that is equal to the mean development delay while the variances in the stage duration are omitted ^[2]. For the convenience of illustration, we simply assume that $P_M(\xi)\equiv 1$ for all $M$-stage ages $\xi$, that is, the mature individuals, if alive, will always stay in the stage. The probability function for immature stage duration with a mean value $\tau$ can be expressed as

This means that alive individuals with $I$-stage age smaller than $\tau$ remain in the $I$-stage, while those with an age larger than $\tau$ develop to $M$-stage. Please note that ${P}_{I}(a)$ is not differentiable. However, for notational simplicity, we use the concept of Dirac delta function $\delta(x)$ to represent its probability density function. Arguments to deal with non-differentiable sojourn functions can be found in [26,Chapter 13]. We consider the case when $t > \tau$ (by resetting the initial timing), and therefore, all immature individuals introduced at time $0$ will either die or develop to the $M$-stage after time $t$, that is $I_0(t) = 0$ for all $t > \tau$. The assumption $t > \tau$ also implies $M_0(t) = e^{-\mu_Mt} M(0)+I(0)e^{-(\mu_I\tau+\mu_M(t-\tau))}$. Then we have,

which can be written into a differential equation

Then, Eq (2.2) for $M(t)$ now becomes

Please note that $\delta(\cdot)$ is the corresponding Dirac delta function. Taking the derivative of $M(t)$, we obtain

2.1.3.   Basic reproduction number and initial growth rate

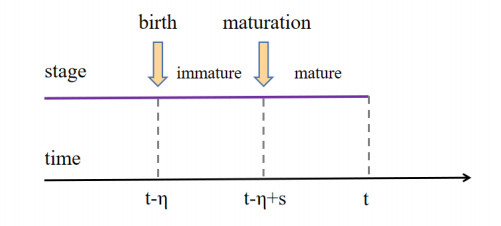
The integral form can be written as other equivalent forms according to different biological arguments on stage progression, birth and survival. If we consider the stage progression of individuals as illustrated in Figure 3, then the integral form of (2.2) can be written as

with $M_0(t)$ given in (2.3). In this expression, the integral term accounts for individuals with the chronological age $\eta$ at time $t$ (i.e., those born at a previous time $t-\eta$ with $\eta\in [0, t]$) and successfully entering and staying in the $M$-stage alive.

It is easy to obtain the net reproduction number $\mathcal{R}_{0}$ with the following renewal argument for the Volterra integral form (see ^[29]). In fact, if we assume the population size is very small and the density-dependent regulations on the birth rate function $B(M(t))$ can be ignored, then the birth rate at time $t$ can be approximated as

with a constant per-capita birth rate $b$. Let

then we have the following Volterra integral form for the population size of the $M$-stage

The net reproduction number in demography can be defined as

Suppose $P_{I}(x)$ takes the gamma distribution function given by (2.7) and $P_M(x) = 1$. By taking the exponential survival probability (2.6), we have

which implies that

For the simple case that the immature stage duration follows an exponential distribution with the mean duration $1/\lambda$, namely $P_I(a) = {e}^{-{\lambda}{a}}$, then

When ${P}_{I}(a)$ takes the Dirac distribution with the mean duration $\tau$ and $P_M(a)\equiv 1$ as those in Section 2.1.2, we have

and therefore,

By seeking the solution to the following characteristic equation (Euler-Lotka equation)

one can determine the initial growth rate (also called intrinsic growth rate or Malthusian parameter ^[30]). Let $f(r) = \int_{0}^{\infty} e^{-r\eta}\Phi(\eta) d{\eta}$, and assume there exists a real number $\hat{r}$ such that $1\leq f(\hat{r}) < \infty$ (for most biological models, we may always find such a negative $\hat{r}$). Then it is interesting to observe the following facts: (ⅰ) $f(r)$ is a nonincreasing and continuous function of $r$, (ⅱ) $f(\hat{r})\geq 1$ and (ⅲ) $\lim\limits_{r\to \infty}f(r) = 0$. Therefore, the above equation $f(r) = 1$ admits a unique real root $r = r_0\in [\hat{r}, \infty)$, which is the intrinsic growth rate. Using the identity that $\mathcal{R}_{0} = f(0)$ and the monotonicity of $f(r)$, it is evident that the sign of $r_0$ is the same as that of $\mathcal{R}_{0}-1$. Furthermore, the monotonicity $f(r)$ and uniqueness of the real root to the equation $f(r) = 1$ facilitate the design of efficient numerical algorithms, such as the bisection method algorithm, to compute the initial growth rate.

2.2.   Structured model with partial differential equations

Assume $u(a, t)$ and $v(\xi, t)$ are the population densities of immature and mature individuals at time $t$ with stage-specific ages $a$ and $\xi$, respectively. Then the sizes of the populations in the immature and mature stages can be expressed as

where ${P}_{I}(a)$ and ${P}_{M}(\xi)$ represent the probability functions of individuals with the stage-age $a$ staying in the immature and mature stages, respectively. On the other hand, the following partial differential equation, originally proposed by McKendrick ^[31] and widely used in recent studies such as ^{[25,32,33,34]}, can be employed to describe the dynamics of age-dependent variables

and

with natural death rates $\mu_I$ and $\mu_M$ in each stage.

It is reasonable to assume that the density of the immatures $u(0, t)$ with age $0$ at time $t$ is exactly the birth rate, that is

The density of mature individuals with $M$-stage age $0$ at time $t$ is that of immature individuals developing to the $M$-stage at time $t$, that is

where $-P'_I(a)$ represents the development rate for immature individuals with $I$-stage age $a$, as discussed in Section 2.1.

2.2.1.   Gamma stage duration distribution

When the stage duration follows gamma distributions as given by (2.7) and (2.8), we have

By introducing the sub-stage population densities described in Subsection 2.1.1:

and

the immature population size and the matured population size can be represented as

Differentiating $I_j(t)$ and $M_i(t)$ and using (2.11) and (2.12), we can obtain a stage-structured model in ordinary differential equation form, which is same as system (2.10).

2.2.2.   Dirac stage duration distribution

In this subsection, we assume the stage distribution follows a Dirac distribution. Similar to those in Subsection 2.1.2, we assume $P_M(\xi)\equiv 1$ for all $M$-stage ages $\xi$ and that the distribution function for the immature stage has a mean duration $\tau$. In this case,

and the number of immature $I(t)$ and mature $M(t)$ individuals can be expressed as

respectively. Therefore, (2.11) gives

Similarly, we have the following equation for the matured population size $M(t)$:

It remains to find the maturation rate $u(\tau, t)$, which can be achieved by integration along characteristics. Let $V^s(t) = u(t-s, t)$, then we have

and $V^s(t) = e^{-\mu_I(t-t_0)}V^s(t_0)$. If $t\geq \tau$, setting $s = t-\tau$ and $t_0 = t-\tau$ gives

If $t < \tau$, let $s = t-\tau$ and $t_0 = 0$, then

Therefore, the stage-structured population dynamics with a Dirac distribution for immature stage duration can be described by two sets of systems on different time intervals:

and

It should be noted that the variable $M(t)$ can be decoupled from the whole model system. Moreover, a scalar delay differential equation (the second equation of (2.13)) would be sufficient to reflect the long-term dynamics of the mature stage ^[35] under the conditions of a suitable initial value specified for $M(\theta)$ with $\theta\in [-\tau, 0]$.

2.3.   Remarks on two modeling approaches and reduced differential counterparts

In Subsections 2.1 and 2.2, two modeling approaches for physically structured population growth are presented in the form of an integral system (Eqs (2.1) and (2.2)) and a partial differential system (Eqs (2.11) and (2.12)). The relationship between the integral equation approach and the partial differential equation approach was established in [26,Chapter 13]. When the stage duration follows a gamma distribution, both modeling frameworks can be reduced into a system of ordinary differential equations, while a system of delay differential equations can be derived when the stage distribution follows a Dirac distribution. The reduction, without losing relevant growth information, makes it easier to investigate the population dynamics. The possibility of reducing a physiologically structured population model, such as those in Section 2.1, to an ordinary differential equation model has been investigated ^[36].

The integral system can be naturally formulated by applying ecological arguments for birth, stage progression and survival. Furthermore, the net reproduction of the population growth can be intuitively derived by using the integral equation nature of the system, with each term having clear biological interpretations. Moreover, the initial growth rate can be easily defined with the help of the linearized system, and its existence and uniqueness can be established through the use of simple mathematical arguments. As a byproduct, the important relationship between the net reproduction number $\mathcal{R}_0$ and the initial growth rate $r_0$ can be easily established: the sign of $\mathcal{R}_0-1$ is the same as that of $r_0$.

It should be noted that a generalized birth function $B(M(t))$ was assumed in the last two subsections, as it can easily accommodate the density-dependent self-regulation on the birth rate. However, the density-independence assumptions are imposed for the survivorship and stage-to-stage progression. When it is necessary to relax the density-independence assumptions on the stage-progression function $P_X(t)$ and survivorship $\Pi_X(t)$ for the immature ($X = I$) and mature ($X = M$) stages, it may become challenging to propose appropriate probability functions. In this sense, the integral framework may not be a convenient way to describe the structured population size when more complicated density-dependent self-regulation is considered, as will be demonstrated by the model (2.14) presented later and those reviewed in the coming Section 3. Furthermore, an integral system can also be derived from a state-structured partial differential equation when the related survival and stage-progression functions can be formulated from the corresponding evolution system ^[37].

To conclude this section, we show that the age-structured partial differential system can be extended to accommodate the density-dependent survivorship due to intra specific competition when the gamma distribution is assumed. In this scenario, Eqs (2.11) and (2.12) can be revised to account for excess density-dependent mortality rate due to competition:

where functions $f(\cdot)$ and $g(\cdot)$ represent the excess death rates due to intraspecific competition, dependent on total population sizes of the respective stage. Differentiating each sub-stage variable in Section 2.2.1 for immatures $I_j(t)$, we have

and

Similarly, for the sub-stages of mature individuals, we have

and

In summary, when intraspecific competition induces excess mortality in immatures and the immature stage duration follows a gamma distribution, an ordinary differential system can be reformulated from the age-structured partial differential equation modeling approach:

3.   Stage structured model with Dirac distribution and intraspecific competition

This section is devoted to reviewing some population models with an assumed Dirac distribution for immature stage duration and intraspecific competition. In particular, we are interested in presenting different types of models that can be formulated under various assumptions on the effect of immature competition.

3.1.   Excess mortality due to competition among the same age cohort

Considering the competition between immatures of the same age, Gourley and Liu ^[38] explored the following evolution equation for the population density $u(a, t)$ for age $a$ at time $t$

In this model, the competitive effects between immatures are given by a nonlinear function $T(u(a, t))$, which describes the influence of intraspecific competition among the immature individuals due to limited living space and resources. The competition among mature individuals is not taken into account.

By taking a similar arguments as those in Subsection 2.2.2, $M(t)$-equation can be written as

To close this equation, it is essential to obtain the explicit form of the maturation rate $u(\tau, t)$, which can be found by applying integration along characteristics. By introducing the function $u^{\xi}(a) = u(a, a+\xi)$, the authors obtained

which implies that

hence,

Here, $u^{\xi}(0) = u(0, \xi) = B(M(\xi))$. Choosing $a = \tau$ and $\xi = t-\tau$, the maturation rate $u(\tau, t)$ at time $t > \tau$ can be solved explicitly from

Since the function $T$: $(0, \infty) \rightarrow \mathbb{R}_{+}$ may be nonlinear, it is impossible to obtain an explicit expression $u(\tau, t) = Q(B(M(t-\tau)))$ to illustrate the relationship between the maturation rate $u(\tau, t)$ at time $t$ and the birth rate $B(M(t-\tau))$ at time $t-\tau$. However, this relationship $y = Q(x)$ can be implicitly defined by

Moreover, the function $y = Q(x)$ is well-defined as $T(\cdot)$ is nonnegative and nondecreasing. Then

With this kind of competition in consideration, the authors of ^[38] show that all solutions are bounded for any birth function $B(\cdot)$. Linearizing the model at a boundary equilibrium gives verifiable and biologically interpretable conditions for its stability. In what follows, we will present several models of this type.

3.1.1.   Case when $T(u(a, t))=\beta_I (u(a, t))^{2}$

By specifying the nonlinear function as $T(u(a, t)) = \beta_I (u(a, t))^{2}$ in (3.1), Liu, Röst and Gourley ^[39] investigated the following model

where $\beta_I$ denotes the effect of intraspecific competition among immature individuals. In this case, it is possible to write down the function given by (3.2) explicitly. In fact, the new variable $u^{\xi}(a) = u(a, a+\xi)$ satisfies

which takes the form of a Bernoulli differential equation, with the solution explicitly given by

Therefore, when $t > \tau$, setting $a = \tau$ and $\xi = t-\tau$ gives $u^{t-\tau}(0) = u(0, t-\tau) = B(M(t-\tau))$ and

With this special nonlinear function $T(u(a, t)) = \beta_I (u(a, t))^{2}$, the long-term dynamics of $M(t)$ can be described by the following delay differential equation:

3.1.2.   Alternative formulation for a delayed logistic equation

Arino, Wang and Wolkowicz ^[40] derived a model by applying a different approach with the aid of survival arguments for those being alive at time $t-\tau$ that is still alive at time $t$ by using the following evolution equation

By the technique of separation of variables and integration from $t-\tau$ to $t$, they obtained

Putting this density-dependent term into a logistic equation with a birth rate $\gamma$, the authors formulated an alternative logistic delay differential equation with a time delay $\tau$:

It is shown that the population dies out when the delay is too large. The existence of a positive equilibrium, and its relationship with parameter values are further illustrated in ^[40].

3.1.3.   Alternative formulation for a distributed delayed logistic equation

Using a similar argument as that in ^[40], Lin, Wang and Wolkowicz ^[41] formulated a logistic equation with distributed delays. The time delay is distributed according to a kernel function $k(s)$ by using a mean delay $\tau$, that is:

Then the discrete delay logistic-type equation (3.4) can be extended to the following one:

The delay kernel can take a variety of functions, such as the Dirac delta function, a uniform distribution, gamma distribution and tent distribution. When the kernel function is Dirac delta function, Eq (3.5) is exactly the discrete delay case described by Eq (3.4). A threshold result for survival and extinction was established in ^[41]: the global attractivity of the unique positive equilibrium and the zero equilibrium are established under different parameter regimes.

3.2.   Excess mortality due to competition among the same stage

Considering the excess mortality due to intraspecific competition between individuals at the same life stage, Fang, Gourley and Lou ^[42] assumed the Dirac distribution described by immatures for the model (2.14), copied as follows for easy reference:

In this case, the number of individuals in each stage are

Differential equations for two variables $I(t)$ and $M(t)$ when $t > \tau$ can be derived as

where $u(0, t) = B(M(t))$ and $u(\infty, t) = 0$. The maturation rate $u(\tau, t)$ can be explicitly solved by integration along characteristics, as follows:

It should be highlighted that (3.6) explicitly couples both variables $I(t)$ and $M(t)$ together, which is different from the previous scalar delay differential equations for the population size at the mature stage (such as those in Subsections 2.1.2 and 2.2.2, and Subsection 3.1). Furthermore, since the maturation rate $u(\tau, t)$ is a decreasing function of $I$ as the function $f(\cdot)$ is assumed to be increasing, there are novel challenges in the theoretical analysis. In particular, the stability analysis of the equilibria becomes difficult due to the strong coupling of two state variables. A generic convergence result is established for small delays by using monotone dynamical systems theory and exponential ordering ^[42].

3.2.1.   Age-dependent larval competition model

Another larval competition model was proposed and studied by Liu, Röst and Gourley ^[39], which follows

In this model, $\epsilon$ characterizes the intensity of population competition among the immature individuals, and $p(\overline{a}, a)$ is an adjustable parameter to describe various competition types: (ⅰ) $p(\overline{a}, a)$ being a constant if an immature individual is likely to compete with all other immature individuals with the same competitive pressure, regardless of age; (ⅱ) $p(\overline{a}, a) = 0$ as $\overline{a} < a$, implying that an immature individual only competes with older individuals; (ⅲ) $p(\overline{a}, a) = \delta (\overline{a}-a)$ with a Dirac delta function $\delta(\cdot)$ if competition occurs among individuals of the same age, which was considered in (3.3).

To transform the model into an ordinary differential equation form with time delay, it is essential to find the maturation rate $u(\tau, t)$ by using the evolution of immature population density described by (3.7). It seems impossible to obtain explicit solutions for general cases, and the authors in ^[39] applied perturbation theory to seek the solution of the following two specific forms:

with $u_0(0, t) = B(M(t))$ and $u_1(0, t) = 0$. Integrating (3.7) along characteristics gives the maturation rate $u(\tau, t)$ when $t > \tau$, and two alternative models for the mature population $M(t)$ are given by

and

This model, proposed under the simple assumption that an individual larva experiences competition from other larvae during development, poses rich dynamics. In particular, the existence of multiple co-existing equilibria is shown in some parameter regimes.

3.3.   Stage distribution regulated by population density

When the duration of staying in the immature stage is regulated by the population density, it would be more convenient to use another variable $x$ called "state" ^[30], which generalizes the concept of the age, to describe the population density evolution. Based on the fact that maturation can be measured to some extent by state, the maturity of an individual occurs when its state $x$ achieves a fixed threshold $l$. Let $u(x, t)$ represent the population density of immature individuals of state $x$ at time $t$, then the immature population size $I(t)$ at time $t$ counts all individuals with a state variable $x$ smaller than $l$, that is

This new variable makes it possible to describe the case that the rate of change of the state $x$ with respect to time is not constant, but is dependent on the population density (see Eq (3.8)).

3.3.1.   Size-structured model with decreased development rate due to competition

Assuming all individuals at the immature stage compete for limited resources, which slows their development, Gourley, Liu and Lou ^[43] used the following equation to describe the rate of change for the length variable $x$ at time $t$:

which relies both on time $t$ and on the total number of individuals comprising the immature population $I(t)$. Here, the function $P(t, I)$ is decreasing on the variable $I$ and is dependent on time $t$ to reflect the time-changing environmental impacts on development.

To derive the partial differential equation for $u(x, t)$ to obtain that in (3.1), the authors used the following argument: After a period of ${\delta}t$, an immature individual will have developed a length of ${\delta}x$, namely

which implies that

by a Taylor expansion. Taking the derivative of $I(t)$ and using Eq (3.9), one obtains

where $P(t, I(t))i(0, t)$ denotes the birth rate, that is $P(t, I(t))i(0, t) = B(M(t))$, and $P(t, I(t))i(l, t)$ denotes the maturation rate, which will be calculated according to the birth rate at time $t-\tau(t)$. The term $u(x, t)$ relies on whether $(x, t)$ is above or below the characteristic $x = X(t)$, where

Introducing a parameter $s$ such that $\frac{dt}{ds} = 1$, then $\frac{dx}{ds} = P(t, I(t))$. The parameter $s$ is used to describe the position along a particular characteristic and $s = 0$ corresponds to a boundary.

When $x \geq X(t)$, a characteristic $(x(s), t(s))$ meets the $x$-axis, which implies that $t = 0$ when $s = 0$. Setting $t(0) = 0$ gives $x-x(0) = X(t)$. It follows from (3.9) that

which implies that

thus

When $x \leq X(t)$, a characteristic $(x(s), t(s))$ meets the $x$-axis, which implies that $x(0) = 0$ and $t = s+t(0)$. The corresponding $s$-value for a particular point $(x, t)$ can be defined by

Defining $L(x, t)$ to be the root $s$, which implies that

Therefore,

Hence,

and the corresponding maturation delay $\tau(t) = L(l, t)$ for individuals developing to the mature stage at time $t$ depends on the immature population size $I(t)$ as specified by

The last integral-algebraic equation has a clear biological interpretation: an individual that develops to the mature stage at time $t$ should be born at $t-\tau(t)$ such that the accumulative length increase during the time interval $[t-\tau(t), t]$ attains the critical value $l$. We should mention that similar integral forms to characterize the density-dependent time delay can also be found in other earlier studies, such as ^[44,45,46].

Based on the fact that the variable $x$ remains valid for the immature population, the equation describing the number of individuals at the mature stage can be expressed as

In addition, the size of the immature population $I(t)$ satisfies

Results on the boundedness of solutions and the linear stability of the equilibria are presented in ^[43]. The boundedness of solutions holds even for unbounded birth functions within certain conditions. It is also shown that if an equilibrium is locally stable in the absence of competition among larvae, then the equilibrium is stable in the presence of weak competition.

3.4.   Paused development due to immature competition

Considering extreme cases that the development may be paused due to immature competition, termed as diapause, Brunner, Gourley, Liu and Xiao ^[47] studied the following size growth rate function

with the constant $P_0$. This form implies that the immature individuals develop at a constant rate $P_0$ when their total number is less than $I_c$, while the growth of the immature population is paused due to high competition pressure when its size exceeds $I_c$. Therefore, the change of an immature individual's size can be described as

and the growth rate function is dependent on the immature population size $I(t)$.

Since the occurrence of diapause may increase the maturation time $\tau(t)$ needed, $\tau(t) \geq l/P_0$ with $l$ being the critical size at maturity. As a matter of fact, when $P(\cdot)$ is nonnegative, but not strictly positive everywhere, $\tau(t)$ can be defined as

which reduces to

if $P(\cdot)$ is strictly positive. Based on the integration along characteristics, the delay differential system can be formulated as follows:

When an Allee effect is assumed for the birth rate function $B(\cdot)$, diapause may induce population extinction even for large initial population sizes. Diapause may also introduce periodic solutions that can arise even for a strictly increasing birth function.

4.   Discussion

Development from one life stage to the next takes time while the time spent in each stage may be synchronized or vary between individuals, giving rise to various distributions of development times in each stage for different species. These distributions intuitively can play important roles in the transition rates among different life stages. In this manuscript, two basic modeling frameworks to describe demographic changes of population dynamics, based on integral and partial differential systems, are presented. These models can be reduced to ordinary and delay differential stage-structured models under gamma and Dirac distribution assumptions. It is evident that each framework has its advantages and inherent limitations. In particular, the integral system can be naturally formulated by checking the stage progression of individuals. Furthermore, the net reproduction number and initial growth rate can be explicitly derived from the integral system. However, it becomes challenging to integrate the density-dependent regulations on the stage distribution and survival probabilities in an integral system due to difficulties in formulating appropriate survival probability functions and stage duration distributions. This may be suitably resolved by using structured partial differential equation models. By applying further assumptions to these density-dependent regulations, the partial differential system can be reduced to different forms, and in particular, various delay differential equation models were reviewed in this study.

When the impact of density regulation on immature individual survival and development is negligible, it is evident from Section 2 that the equation for the matured population size is decoupled from the integral system ((2.1) and (2.2)) as the variable accounting for the immature population size does not appear in (2.2). A similar observation can be made regarding the delay differential equation model in Sections 2.1.2 and 2.2.2 when the Dirac distribution is assumed for the stage duration of immatures. From an analytical point of view, this observation makes it possible to analyze the dynamics of the mature stage $M(t)$ first, and then to feed the equation of the immature stage with the dynamic profile $M(t)$. Since the extinction and persistence of the species can be predicted from those of each stage, it would be sufficient to show the extinction/persistence of mature individuals from the decoupled equation for $M(t)$, as analyzed in ^[42] for the case when the immature competition force $f(\cdot) = 0$. When a gamma distribution is assumed for the stage duration of immatures, the maturation rate becomes $n\lambda I_n(t)$ in the system of ordinary differential equations described in Sections 2.1.1 and 2.2.1, which makes it impossible to decouple the variables for mature stages from the whole system at first glance. However, if one revisits the definition of $I_n(t)$ in (2.9), it can be expressed in terms of $M(t)$ with a distributed delay kernel.

Furthermore, a Dirac distribution with an average duration $\tau$ can be approximated by a gamma distribution as shown in (2.7), with $\gamma = 1/\tau$ and a large $n$ (such that the variance of the gamma distribution $\tau^2/n$ is very small), as shown in Figure 1. Intuitively, the delay differential equation model under Dirac distribution assumption would also be approximated by $n$ ordinary differential equations under the gamma distribution assumption for a large $n$. As a matter of fact, this can be rigorously shown by the linear chain trick ^[48], as illustrated in Section 2.2.2 by observing the maturation rate when $t > \tau$ is

In the above expression, $\delta(\cdot)$ is the Dirac-delta function and $P_I(a)$ takes the gamma distribution as in (2.7).

The stage-structured modeling idea in this manuscript can easily accommodate spatial movements of individuals. In particular, when individuals are performing random movements, a reaction-diffusion model with/without time delay can be formulated when the exponential and Dirac distributions are assumed for the stage duration ^[20,49,50]. In particular, a nonlocal delay term can be formulated when the Dirac distribution is assumed and immature individuals move during development. Interested readers may refer to the pioneering model formulations by Stephen Gourley and his collaborators, such as those in ^{[50,51,52,53]}.

Other modeling frameworks, such as matrix population models and individual-based models, are also important tools to incorporate the variation of individual-level demographic characteristics, which are beyond the scope of this review. We refer the interested readers to ^[1,2] for incorporating stage duration distributions in other model forms, such as matrix models and statistical stage-duration distribution models. Further biotic and abiotic factors may also impact the stage duration distributions: for example, the seasonal environmental oscillations can induce seasonal developmental delays and seasonal diapauses, which have been modeled in ^[54,55]. We leave these topics for further investigation.

Acknowledgments

We are very grateful to the anonymous referees for their careful reading and valuable comments, as well as some inspiring references.

Conflict of interest

The authors declare there is no conflict of interest.