Using air thermal time to predict the time course of seedling emergence of Avena sterilis subsp. sterilis (sterile oat) under Mediterranean climate

1.   Introduction

Avena sterilis L. subsp. sterilis is a cereal weed native to an area extending from the Mediterranean up to Pakistan and Kenya. Currently it is introduced into different parts of the world including North and South America, central and northern Europe, south Africa and Australia ^[1]. This weed is tremendously competitive, producing substantial yield losses up to 70 kg grain ha^–1 panicle^–1 m^–2 in wheat ^[2] and exhibits a high fecundity that results in massive soil seed banks ^[3,4]. Because of its high competitiveness, its presence in fields also hampers the recovery of weed diversity and associated ecosystem services ^[5,6]. In conventionally managed cereal fields its control relies mostly on herbicide applications. However, a relatively high number of A. sterilis populations worldwide have developed resistance to one of at least four different mode-of-action herbicide groups ^[7] and thus it has been ranked among the weed species with high risk of development of herbicide resistance ^[8].

The timing of weed control applications is crucial for the implementation of effective Integrated Weed Management (IWM) strategies ^[9]. Control methods (chemical and non-chemical) applied too early or too late result in low control efficacies as they allow the escape of plants that will refill the seed bank for the next season. Therefore, emergence models can give valuable information for an optimal implementation of control measures throughout knowledge of the emergence pattern.

Weed emergence is governed by soil environmental conditions, mainly water availability and temperature ^[10,11]. In this regarding, empirical models based on accumulation of either thermal or hydrothermal time have been developed for many weed species to predict the time course of seedling emergence in crop fields ^[12,13,14]. These models assume that seeds need to accumulate a certain amount of degree days, either independent of water availability in soil (thermal models) or only when water availability is permissive for germination (hydrothermal models). Hydrothermal models are generally more accurate in describing emergence as they include soil water potential in addition to temperature. Nevertheless, they are of limited practical application because water potential is difficult to measure in a reliable way. Modeling based on thermal time is a more realistic approach because soil temperature is easier to collect and prediction using these models appears to be accurate enough ^[12,15]. For instance, Grundy et al. ^[16] developed simple thermal-time-based models to predict the emergence of Chenopodium album and Stellaria media, and Yousefi et al. ^[17] described thermal time models to predict the emergence of Avena fatua and Polygonum aviculare in garlic fields.

Within the species A. sterilis, emergence models have been developed for one of its two subspecies, A. sterilis subsp. ludoviciana (Durieu) Guillet & Magne ^[18,19]. However, to date none has been developed for A. sterilis subsp. sterilis that can provide useful information to growers to improve the efficacy of currently available control measures. Both subspecies are often confused despite their distinctive morphological traits and geographic distribution ^[3,20]. For instance, A. sterilis subsp. ludoviciana is most abundant in Central and North Spain ^[21], being rare in Southern Spain where A. sterilis subsp. sterilis is predominant ^[22]. Apparently, the latter subspecies is more thermophilous than A. sterilis subsp. Ludoviciana ^[21].

Taking into account the great impact that A. sterilis has on cereal crops and the need to decrease both selection pressure on herbicide resistance and the potential range shift resulting from climate change ^[23], this study aimed to develop a predictive model of the time course of seedling emergence in cereal fields based on accumulation of thermal time. Such a model can serve as a tool for farmers and technicians to increase the efficacy of control measures targeting this species.

2.   Materials and methods

2.1.   Experimental design

Data for model setting were collected in a controlled experiment conducted from mid autunm 2007 in an experimental field at La Rabida Campus of the University of Huelva (Huelva, Andalusia, Spain; 37º12ʹ10''N, 6º55ʹ05''W, 23 m a.s.l.). Fifteen 25 × 25 cm plots were randomly established and the soil up to 5 cm deep was replaced by a substrate (2.5 l.). The substrate was a mixture of 50% Kekkilä garden peat, 25% sand, and 25% local sandy clay soil. After autoclave sterilization to suppress viability of existing seeds, the volume of substrate to be added to each plot was thoroughly mixed with 200 seeds of A. sterilis subsp. sterilis and placed on topsoil on 27th November 2007, within the winter cereal sowing season in Southern Spain. Seed losses to soil surface-foraging predators were prevented by placing 2-mm mesh nets over 0.4 m diameter, 0.1 m height PVC fences placed encircling the plots. Numbers of emerged seedlings were recorded and thereafter removed at weekly intervals until end of seedling emergence (mid-April).

Cumulative thermal time in Celsius-based degree days (CTT) was calculated daily as follows ^[24]:

Where Tmean is the daily air mean temperature (℃), Tbase is the lowest temperature at which germination can occur and n is the number of days after sowing. When Tmean < Tbase no thermal time is accumulated. Base temperature (Tb) was set to 0.8 ℃ according to previous results for the co-specific grass weed A. sterilis subsp. Ludoviciana ^[25].

2.2.   Emergence model

Two sigmoid functions, the Gompertz curve and the Weibull cumulative distribution function, commonly used in the weed science literature ^[13], were tested for their ability to represent percentage accumulated emergence (E) of A. sterilis subsp. sterilis as a function of CTT,

Gompertz:

Weibull:

K is the maximum emergence percentage predicted by the model, b is the rate of increase in emergence, m is the point of inflection and d is the parameter determining the asymmetry of the curve. Parameters were estimated by nonlinear regression using the Marquard-Levenberg algorithm with the statistical package SPSS version 20. Goodness-of-fit was determined by calculating the Coefficient of Efficiency (ENS) ^[26]:

Where RMSE is the root-mean-square error and SD is the standard deviation of the observed values. ENS varies between −∞ and 1.0, being 0 < ENS≤1 considered as the acceptable range (Nash and Sutcliffe 1970). In addition, to establish the sense of potential biases, the sum of the residuals (SRES) and the sum of the absolute residuals (SARES) ^[27] were calculated:

where O_i and P_i are observed and predicted cumulative percentage seedling emergence, respectively; ABS is absolute value of the number within parentheses and n is the number of observations. When SRES is small compared to SARES, errors in the model will tend to cancel out. When SRES and SARES are large and SRES is positive, the model tends to underestimate the observed value. On the other hand, when SRES is negative and large in comparison to SARES then the model will tend to overestimate the observed value.

The selection of the most plausible model was performed by comparing the Akaike information criterion corrected for small samples (AICc) ^[28]. The smaller AICc value corresponds to a more plausible model:

where AIC = 2p − 2ln(L), p is the number of parameters, n is sample size and ln(L) is the log-likelihood of the estimated model.

2.3.   Validation

Two validation experiments were performed. A controlled experiment similar to the one described in the model setting section was carried out at Palos de la Frontera (Huelva, Andalusia, south-western Spain, 37°13′40″N, 6°53′36″W, 23m a.s.l) in 2007. The other validation experiment was carried out in a commercial field (durum wheat cv. 'Amilcar') located in Gibraleón (Huelva, Andalusia, south-western Spain, 37°18′36″N, 6°55′05″W; 26 m a.s.l.) in 2008. Both locations have a typical Mediterranean climate, with a mean annual temperature of 16.6 ℃ and mean annual rainfall of 555 mm, mainly distributed between October and April. In the field experiment, seedling emergence data was collected weekly, from crop sowing until the end of seedling emergence by mid-April, from 10 randomly distributed 50 × 50 cm permanent quadrats. Air temperature was obtained from weather stations located less than 5 km from both the experimental and commercial fields. The prediction accuracy of the selected model was evaluated by the coefficient of determination (R²) of the linear regression of predicted against observed emergence.

3.   Results and discussion

An important element for an effective implementation of integrated weed management strategies is the fine-tuning of control timing ^[29]. Usually, seedlings constitute the most sensitive stage of the plant life cycle to disturbance and environmental stress. For weeds exhibiting predictable yearly patterns of seed germination and seedling emergence, such in arable crops and seasonal climates, application of control measures immediately after the target weed population completes emergence is the natural choice. This goal can be accomplished with the aid of accurate-enough predictive models of weed emergence which, in turn, could serve as the basis for the development of decision support systems helping farmers in making weed control decisions ^[30]. This work establishes for the first time a model for the prediction of field emergence of A. sterilis subsp. sterilis that can serve as a first step for the establishment of a decision-making tool for the control of this important weed of winter cereals.

The seedling emergence in the controlled experiments was quite similar, 53.25% (range: 50–57%) and 50.60% (range 46–52.5%) in the Rabida Campus and Palos de la Frontera (validation), respectively. The emergence in Gibraleon (validation field experiment) was 9.9 ± 7.4 seedlings/0.25 cm². The emergence percentages are higher than those established for A. sterilis subps ludoviciana which range between 31% and 46% ^[31].

The two alternative models evaluated, Weibull (ENS = 0.98) and Gompertz (ENS = 0.90), provided a good fit to the data, as indicated by ENS values very close to the optimum (ENS = 1). Nevertheless, the Weibull model was more plausible (AICc = 45.49) than the Gompertz model (AICc = 50.53) to explain the data set. Accordingly, the Weibull model was selected to describe the emergence time course of A. sterilis subsp. sterilis. Moreover, this model showed no appreciable bias, as indicated by a small SRES value (8.73) associated to a much larger SARES value (42.03) and, therefore, model errors tended to cancel out.

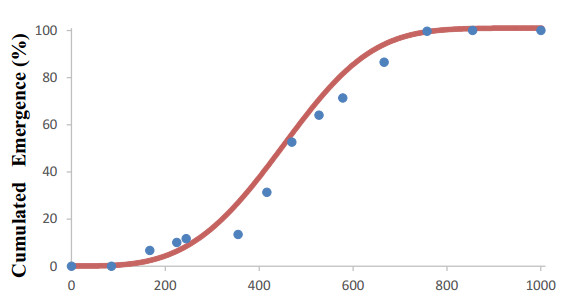
For the Weibull model, the parameter estimates (mean ±standard errors) were k = 100.93 (±2.99), b = 0.002 (±4.8 × 10⁻⁵) and d = 3.43 (±0.32). Therefore, the fitted model was E = 100.93 * (1 – exp (−(0.002 * TT)^3.43)) (Figure 1). According to this model, the onset of emergence takes place at 130 CTT, and 50% and 90% emergence is accomplished at 448 and 632 CTT, respectively. The developed Weibull model based on thermal time offered a good and unbiased description of seedling emergence of A. sterilis subsp. sterilis. Despite the fact that soil moisture is an important environmental factor regulating weed seed germination and seedling emergence in dryland areas, we found that air temperature alone is an accurate predictor of the emergence time course of this species. These results agree with those obtained by Picapietra et al. ^[32] and Grundy and Mead ^[33], who demonstrated the feasibility of using air temperature to predict the emergence patterns of Echinocloa colona and Stellaria media. Thermal time has also been proposed to model the emergence of A. sterilis subsp. ludoviciana. For this latter subspecies, Leguizamon et al. ^[18] found that when soil water availability was not limiting, the Weibull model provided an adequate description of the link between thermal time accumulation and the time course of seedling emergence.

The evaluation test showed high performance of the fitted emergence model. The model presented a very good agreement with the observed seedling emergence pattern in the Gibraleón commercial field (R² = 0.95) and good in the experimental plot in Palos de la Frontera (R² = 0.81) (Figure 2).

The thermal model proposed appears to be robust enough to describe the emergence of A. sterilis subsp. sterilis based on simple thermal time accumulation as shown by the evaluation tests carried out in conditions on southern Spain. Despite this promising result, the model may be not accurate if applied to other areas with different environmental and agronomic conditions ^[34,35,19]. Environmental conditions may influence primary dormancy of seeds, shortening or delaying germination. This variation in dormancy status among seeds in the seed bank introduce uncertainty about the thermal time already accumulated by the seeds. Further research should be focused on model validation under different weather and soil management conditions to render it a valuable tool for farmers in selecting the application timing of control measures targeting this species. Furthermore, integrated into a decision support system ^[30], the model may contribute to the sustainability of weed management in dryland cereal fields and it can be useful to develop more accurate models of the effect of climate change on this species ^[23].

4.   Conclusions

The Weibull thermal model proposed seems to be robust enough to be tested as a predictive tool of A. sterilis emergence in winter cereal fields. Further research should be addressed for a wider validation of the model that can render it a valuable tool for farmers for adequate timing of control measures of A. sterilis. Furthermore, integrated into a decision support system or in climate change models may contribute to the sustainability of weed management in dryland cereal fields.

Acknowledgments

This research was funded by FEDER (European Regional Development Funds) and the Spanish Ministry of Economy and Competitiveness (project AGL2005-0405).

Conflict of interest

All authors declare no conflicts of interest in this paper.