The total variation flow in metric graphs

1.   Introduction and preliminaries

Metric graphs are widely used to model a wide range of problems in chemistry, physics, or engineering, describing quasi-one-dimensional systems such as carbon nano-structures, quantum wires, transport networks, or thin waveguides. Concerning the applications in biology, we can cite, for instance, the recent works ^[15,16]. They are also widely studied in mathematics; see ^[7,20] for an overview.

One of the earliest accounts of a partial differential equation set on a metric graph can be found in the $1980$ work of Lumer (^[17]) on ramification spaces. Since then, the theory has seen considerable developments, due, in particular, to the natural appearance of graphs in the modeling of various physical situations. Among the partial differential equation problems set on metric graphs, one has become increasingly popular: the ones set on quantum graphs. By quantum graphs one usually refers to a metric graph $\Gamma = (V, E)$ equipped with a differential operator $H$ often referred to as the Hamiltonian. The most popular example of a Hamiltonian is $- \Delta$ on the edges with Kirchhoff conditions. The book of Berkolaiko and Kuchment ^[7] provides an excellent introduction to the theory of quantum graphs. In the last years, we have had a great development of other important topics like: the wave equation in metric graphs related with control problems (see survey book ^[14]) and nonlinear quantum graphs associated with the nonlinear evolution equation of Schrödinger type (see the survey paper ^[21]). Now, to our knowledge, there is very little literature on nonlinear evolution problems in metric graphs, such as for the $p$-Laplacian operator.

The aim of this paper is to analyse the initial-boundary value problem associated with the total variation flow in metric graphs. In this regard, we introduce the $1$-Laplacian operator associated with a metric graph. We then proceed to prove existence and uniqueness of solutions of the total variation flow in metric graphs for data in $L^2(\Gamma)$ and to study their asymptotic behaviour, showing that the solutions reach the stationary state in finite time. Furthermore, we obtain explicit solutions.

From the mathematical point of view, the study of the total variation flow in Euclidean spaces was carried out using, as its main tools, the classical theory of maximal monotone operators due to Brezis (^[9]) and the Crandall-Liggett Theorem (^[6,13]), being the energy space the space of function of bounded variation. In order to characterize the solutions, the Green's formula shown by Anzelotti in ^[5] proved to be crucial (see ^[2,3,4] for a survey). The study of a similar problem in the general framework of metric random walk spaces, which have as important particular cases the weighted graphs and nonlocal problems with non–singular kernels, was done in ^[18].

Here, we use similar tools, so we introduce the space of bounded variation functions in metric graphs and we establish a Green's formula in order to characterize the $1$-Laplacian operator in metric graphs. Let me point out the importance of giving an adequate definition of the total variation of a bounded variation function in the context of metric graphs that takes into account its structure and measures the jumps in the vertices.

1.1.   Metric graphs

We recall here some basic knowledge about metric graphs, see for instance ^[7] and the references therein.

A graph $\Gamma$ consists of a finite or countable infinite set of vertices ${\mathrm{V}}(\Gamma) = \{{{{\mathrm{v}}}}_i\}$ and a set of edges ${\mathrm{E}}(\Gamma) = \{{{\bf e}}_j\}$ connecting the vertices. A graph $\Gamma$ is said to be a finite graph if the number of edges and the number of vertices are finite. An edge and a vertex on that edge are called incident. We will denote ${{{\mathrm{v}}}}\in {{\bf e}}$ when the edge ${{\bf e}}$ and the vertex ${{{\mathrm{v}}}}$ are incident. We define ${\mathrm{E}}_{{{{\mathrm{v}}}}}(\Gamma)$ as the set of all edges incident to ${{{\mathrm{v}}}}$, and the degree of ${{{\mathrm{v}}}}$ as $d_{{{\mathrm{v}}}}: = \sharp {\mathrm{E}}_{{{{\mathrm{v}}}}}(\Gamma)$. We define the boundary of $V(\Gamma)$ as

and its interior as

We will assume the absence of loops, since if these are present, one can break them into pieces by introducing new intermediate vertices. We also assume the absence of multiple edges.

A walk is a sequence of edges $\{{{\bf e}}_1, {{\bf e}}_2, {{\bf e}}_3, \dots\}$ in which, for each $i$ (except the last), the end of ${{\bf e}}_i$ is the beginning of ${{\bf e}}_{i+1}$. A trail is a walk in which no edge is repeated. A path is a trail in which no vertex is repeated.

From now on we will deal with a connected, compact and metric graph $\Gamma$:

$\bullet$ A graph $\Gamma$ is a metric graph if

$1)$ each edge ${{\bf e}}$ is assigned with a positive length $\ell_{{{\bf e}}}\in]0, +\infty];$

$2)$ for each edge ${{\bf e}}$, a coordinate is assigned to each point of it, including its vertices. For that purpose, each edge ${{\bf e}}$ is identified with an ordered pair $({\mathrm{i}}_{{{\bf e}}}, {\mathrm{f}}_{{{\bf e}}})$ of vertices, being ${\mathrm{i}}_{{{\bf e}}}$ and ${\mathrm{f}}_{{{\bf e}}}$ the initial and terminal vertex of ${{\bf e}}$ respectively, which has no sense of meaning when travelling along the path but allows us to define coordinates by means of an increasing function

such that, letting $c_{{\bf e}}({\mathrm{i}}_{{\bf e}}): = 0$ and $c_{{\bf e}}({\mathrm{f}}_{{\bf e}}): = \ell_{{{\bf e}}}$, it is exhaustive; $x_{{{\bf e}}}$ is called the coordinate of the point $x\in {{\bf e}}$.

$\bullet$ A graph is said to be connected if a path exists between every pair of vertices, that is, a graph which is connected in the usual topological sense.

$\bullet$ A compact metric graph is a finite metric graph whose edges all have finite length.

If a sequence of edges $\{{{\bf e}}_j\}_{j = 1}^n$ forms a path, its length is defined as $\sum_{j = 1}^n\ell_{{{\bf e}}_j}.$ The length of a metric graph, denoted $\ell(\Gamma)$, is the sum of the length of all its edges. Sometime we identify $\Gamma$ with

Given a set $A \subset \Gamma$, we define its length as

For two vertices ${{{\mathrm{v}}}}$ and $\hat{{{\mathrm{v}}}},$ the distance between ${{{\mathrm{v}}}}$ and $\hat {{{\mathrm{v}}}}$, $d_\Gamma({{{\mathrm{v}}}}, \hat {{{\mathrm{v}}}})$, is defined as the minimal length of the paths connecting them. Let us be more precise and consider $x$, $y$ two points in the graph $\Gamma$.

-if $x, y\in{{\bf e}}$ (they belong to the same edge, note that they can be vertices), we define the distance-in-the-path-${{\bf e}}$ between $x$ and $y$ as

-if $x\in {{\bf e}}_a$, $y\in {{\bf e}}_b$, let $P = \{{{\bf e}}_a, {{\bf e}}_1, \dots, {{\bf e}}_{n}, {{\bf e}}_b\}$ be a path ($n\ge 0$) connecting them. Let us call ${{\bf e}}_{0} = {{\bf e}}_a$ and ${{\bf e}}_{n+1} = {{\bf e}}_b$. Following the definition given above for a path, set ${{{\mathrm{v}}}}_{0}$ the vertex that is the end of ${{\bf e}}_0$ and the beginning of ${{\bf e}}_{1}$ (note that these vertices need not be the terminal and the initial vertices of the edges that are taken into account), and ${{{\mathrm{v}}}}_{n}$ the vertex that is the end of ${{\bf e}}_n$ and the beginning of ${{\bf e}}_{n+1}$. We will say that the distance-in-the-path-$P$ between $x$ and $y$ is equal to

We define the distance between $x$ and $y$, that we will denote by $d_\Gamma(x, y)$, as the infimum of all the distances-in-paths between $x$ and $y$, that is,

We remark that the distance between two points $x$ and $y$ belonging to the same edge ${{\bf e}}$ can be strictly smaller than $|y_{{\bf e}}-x_{{\bf e}}|$. This happens when there is a path connecting them (using more edges than ${{\bf e}}$) with length smaller than $|y_{{\bf e}}-x_{{\bf e}}|$.

A function $u$ on a metric graph $\Gamma$ is a collection of functions $[u]_{{{\bf e}}}$ defined on $]0, \ell_{{{\bf e}}}[$ for all ${{\bf e}}\in {\mathrm{E}}(\Gamma),$ not just at the vertices as in discrete models.

Throughout this work, $\int_{\Gamma} u(x) dx$ or $\int_{\Gamma} u$ denotes $\sum_{{{\bf e}}\in {\mathrm{E}}(\Gamma)} \int_{0}^{\ell_{{{\bf e}}}} [u]_{{{\bf e}}}(x_{{\bf e}})\, dx_{{\bf e}}$. Note that given $\Omega \subset \Gamma$, we have

Let $1\le p\le +\infty.$ We say that $u$ belongs to $L^p(\Gamma)$ if $[u]_{{{\bf e}}}$ belongs to $L^p(]0, \ell_{{{\bf e}}}[)$ for all ${{\bf e}}\in {\mathrm{E}}(\Gamma)$ and

The Sobolev space $W^{1, p}(\Gamma)$ is defined as the space of functions $u$ on $\Gamma$ such that $[u]_{{{\bf e}}}\in W^{1, p}(0, \ell_{{{\bf e}}})$ for all ${{\bf e}}\in {\mathrm{E}}(\Gamma)$ and

The space $W^{1, p}(\Gamma)$ is a Banach space for $1 \le p \le\infty$. It is reflexive for $1 < p < \infty$ and separable for $1 \le p < \infty.$ Observe that in the definition of $W^{1, p}(\Gamma)$ we does not assume the continuity at the vertices.

A quantum graph is a metric graph $\Gamma$ equipped with a differential operator acting on the edges together with vertex conditions. In this work, we will consider the $1-$Laplacian differential operator given by

on each edge.

2.   The total variation flow in metric graphs

In this section we will assume that $\Gamma$ is a finite, compact and connected metric graph. To introduce the total variation flow in the metric graph $\Gamma$, we first need to study the bounded variation functions in $\Gamma$ and to get a Green's formula in $\Gamma$ analogue to the classical Anzellotti Green's formula.

2.1.   BV functions and integration by parts

For bounded variation functions of one variable we follow ^[1]. Let $I \subset {\mathbb R}$ be an interval, we say that a function $u \in L^1(I)$ is of bounded variation if its distributional derivative $Du$ is a Radon measure on $I$ with bounded total variation $\vert Du \vert (I) < + \infty$. We denote by $BV(I)$ the space of all functions of bounded variation in $I$. It is well known (see ^[1]) that given $u \in BV(I)$ there exists $\overline{u}$ in the equivalence class of $u$, called a good representative of $u$, with the following properties. If $J_u$ is the set of atoms of $Du$, i.e., $x \in J_u$ if and only if $Du(\{ x \}) \not = 0$, then $\overline{u}$ is continuous in $I \setminus J_u$ and has a jump discontinuity at any point of $J_u$:

where by simplicity we are assuming that $I = ]a, b[$. Consequently,

Moreover, $\overline{u}$ is differentiable at ${\mathcal L}^1$ a.e. point of $I$, and the derivative $\overline{u}'$ is the density of $Du$ with respect to ${\mathcal L}^1$. For $u \in BV(I)$, the measure $Du$ decomposes into its absolutely continuous and singular parts $Du = D^a u + D^s u$. Then $D^a u = \overline{u}' \ {\mathcal L}^1$. We also split $D^su$ in two parts: the jump part $D^j u$ and the Cantor part $D^c u$.

It is well known (see for instance ^[1]) that

and also,

Obviously, if $u \in BV(I)$ then $u \in W^{1, 1}(I)$ if and only if $D^su \equiv 0$, and in this case we have $Du = \overline{u}' \ {\mathcal L}^1$.

A measurable subset $E \subset I$ is a set of finite perimeter in $I$ if $\chi_E \in BV(I)$, and its perimeter is defined as

From now on, when we deal with point-wise valued $BV$-functions we shall always use the good representative. Hence, in the case $u \in W^{1, 1}(I)$, we shall assume that $u \in C(\overline{I})$.

Given ${{\bf z}} \in W^{1, 2}(]a, b[)$ and $u \in BV(]a, b[)$, by ${{\bf z}} Du$ we mean the Radon measure in $]a, b[$ defined as

Note that if $\varphi \in \mathcal{D}(]a, b[): = C^\infty_c(]a, b[)$, then

which is the definition given by Anzellotti in ^[5].

Working as in ^[5,Corollary 1.6], it is easy to see that

Then, ${{\bf z}} Du$ is absolutely continuous with respect to the measure $\vert Du \vert$, and we will denote by $\theta({{\bf z}}, Du, x)$ the Radom-Nikodym derivative of ${{\bf z}} Du$ with respect to $\vert Du \vert$, that is

Working as in ^[5,Proposition 2.8], we have that if $f \in C^1({\mathbb R})$ is an increasing function, then

The next result was proved in ^[5] in ${\mathbb R}^N$, with $N \geq 2$. We can adapt the proof for $N = 1$. For convenience, we give here the details.

Proposition 2.1. Let ${{\bf z}}_n \in W^{1, 2}(]a, b[)$. If

and

then for every $u \in BV(]a, b[)$, we have

and

Proof. We have

Then,

Thus, to verify that (2.3) holds; that is,

for every $\varphi \in C_c(]a, b[)$, it is sufficient to check this limit for test functions $\varphi \in \mathcal{D}(]a, b[)$. Now, for $\varphi \in \mathcal{D}(]a, b[)$,

which proves (2.3). Let us prove now (2.4). Given $\epsilon > 0$, since $\vert Du \vert$ is a bounded Radon measure, there exists an open subset $U \subset]a, b[$ such that

and for every $\varphi \in \mathcal{D}(]a, b[)$, there exists $N \in {\mathbb N}$ such that

Now, we choose $\varphi \in \mathcal{D}(]a, b[)$ such that $0 \leq \varphi \leq1$, $\varphi \equiv 1$ on $\overline{U}$. Then, by (2.6) and (2.7), for all $n \geq N$, we have

proving (2.4).

We need the following integration by parts formula, which can be proved using a suitable regularization of $u \in BV(I)$ as in the proof of ^[5,Theorem 1.9] (see also Theorem C.9. of ^[2]).

Lemma 2.2. If ${{\bf z}} \in W^{1, 2}(]a, b[)$ and $u \in BV(]a, b[)$, then

Definition 2.3. We define the set of bounded variation functions in $\Gamma$ as

Given $u \in BV(\Gamma)$, for ${{\bf e}} \in E_{{{\mathrm{v}}}}$, we define

For $u \in BV(\Gamma)$, we define

We also write

Obviously, for $u \in BV(\Gamma)$, we have

$BV(\Gamma)$ is a Banach space with respect to the norm

Remark 2.4. Note that we do not include a continuity condition at the vertices as in the definition of the spaces $BV(\Gamma)$. This is due to the fact that, if we include the continuity in the vertices, then typical functions of bounded variation such as the functions of the form $\chi_D$ with $D \subset \Gamma$ such that ${{{\mathrm{v}}}} \in D$, being ${{{\mathrm{v}}}}$ a common vertex to two edges, would not be elements of $BV(\Gamma)$.

By the Embedding Theorem for $BV$-functions (cf. ^[1,Corollary 3.49,Remark 3.30]), we have the following result.

Theorem 2.5. The embedding $BV(\Gamma) \hookrightarrow L^p(\Gamma)$ is continuous for$1\leq p \leq \infty$, being compact for $1 \leq p < \infty$.

We denote

and

$C_c(\Gamma)$ is a Banach space with respect to the norm $\Vert u \Vert_{\infty} = \sup \{ \vert u(x) \vert \ : \ x \in \Gamma \}$, we denote by

the dual of $C_c(\Gamma)$, and we will call the elements of $\mathcal{M}_b(\Gamma)$ Radon measures in $\Gamma$.

Definition 2.6. Given $u \in BV(\Gamma)$, we define $Du: C_c(\Gamma) \rightarrow {\mathbb R}$ as

Note that if $\varphi \in \mathcal{D}(\Gamma)$, then

We have

Therefore, $Du \in \mathcal{M}_b(\Gamma)$ and $\Vert Du \Vert_{\mathcal{M}_b(\Gamma)} \leq \vert D u \vert (\Gamma)$. On the other hand, given $\epsilon > 0$ there exists $\varphi_{{\bf e}} \in C_c ((0, \ell_{{{\bf e}}}))$, with $\Vert \varphi_{{\bf e}} \Vert_\infty \leq 1$ such that

Then, if $\varphi: = \bigoplus_{{{\bf e}} \in E(\Gamma)} \varphi_{{\bf e}} \in C_c(\Gamma)$, we have

Consequently,

Let us point out that, in metric graphs, $\vert D u \vert (\Gamma)(u)$ is not a good definition of the total variation of $u$ since it does not measure the jumps of the function at the vertices. In order to give a definition of the total variation of a function $u \in BV(\Gamma)$ that takes into account the jumps of the function at the vertices, we are going to obtain a Green's formula like the one obtained by Anzellotti in ^[5] for $BV$-functions in Euclidean spaces. In order to do this, we start by defining the pairing ${{\bf z}} Du$ between an element ${{\bf z}} \in W^{1, 2}(\Gamma)$ and a BV function $u$. This will be a metric graph analogue of the classic Anzellotti pairing introduced in ^[5].

Definition 2.7. For ${{\bf z}} \in W^{1, 2}(\Gamma)$ and $u \in BV(\Gamma)$, we define ${{\bf z}} Du: = ([{{\bf z}}]_{{\bf e}}, D[u_{{\bf e}}])_{{{\bf e}} \in E(\Gamma)}$, that is, for $\varphi \in C_c(\Gamma)$,

We have that ${{\bf z}} Du$ is a Radon measure in $\Gamma$ and

By (2.1), we have

If we define

then

Moreover, by (2.2), if $f \in C^1({\mathbb R})$ is a increasing function, then

Given ${{\bf z}} \in W^{1, 2}(\Gamma)$, for ${{\bf e}} \in E_{{{\mathrm{v}}}}$, we define

By Lemma 2.2, we have

Then, if we define

for ${{\bf z}} \in W^{1, 2}(\Gamma)$ and $u \in BV(\Gamma)$, we have the following Green's formula:

We define

For $u \in BV(\Gamma)$ and ${{\bf z}} \in X_0(\Gamma)$, we have the following Green's formula

Proposition 2.8. For $u \in BV(\Gamma)$, we have

Proof. Let $u \in BV(\Gamma)$. Given ${{\bf z}} \in X_0(\Gamma)$ with $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$, applying Green's formula (2.14) and (2.11), we have

Therefore,

On the other hand,

Now, given $(\varphi_{{\bf e}}) \in \mathcal{D}(\Gamma)$, if we define ${{\bf z}}$ such that $[{{\bf z}}]_{{\bf e}} = \varphi_{{\bf e}}$ for all ${{\bf e}} \in E(\Gamma)$, we have ${{\bf z}} \in X(\Gamma)$. Hence, we get

Remark 2.9. By the above result, we have that the energy functional $\mathcal{E}_\Gamma : L^2(\Gamma) \rightarrow [0, + \infty]$ defined by

is convex and lower semi-continuous. Therefore, we could study the gradient flow associated with $\mathcal{E}_\Gamma$ as a possible definition of the total variation flow in metric graphs. However, I would like to point out that this is not the adequate way since the solutions of this gradient flow coincide with the solutions of the Neumann problem at each edge, regardless of the structure of the metric graph. This is the reason for which we are going to introduce our concept of total variation in metric graphs.

We consider now the elements of $W^{1, 2}(\Gamma)$ that satisfies a Kirchhoff condition, that is, the set

Note that if ${{\bf z}} \in X_K(\Gamma)$, then $[{{\bf z}}]_{{\bf e}}({{{\mathrm{v}}}}) = 0$ for all ${{{\mathrm{v}}}} \in \partial V(\Gamma)$. Therefore, for $u \in BV(\Gamma)$ and ${{\bf z}} \in X_K(\Gamma)$, we have the following Green's formula

Now, for ${{{\mathrm{v}}}} \in {\rm int}(V(\Gamma))$, we have

Hence

Therefore, we can rewrite the Green's formula (2.16) as

Remark 2.10. Given a function $u$ in the metric graph $\Gamma$, we say that $u$ is continuous at the vertex ${{{\mathrm{v}}}}$ if

We denote this common value as $u({{{\mathrm{v}}}})$. We denote by $C({\rm int}(V(\Gamma)))$ the set of all functions in $\Gamma$ continuous at the vertices ${{{\mathrm{v}}}} \in {\rm int}(V(\Gamma))$

Note that if $u \in BV(\Gamma) \cap C({\rm int}(V(\Gamma)))$ and ${{\bf z}} \in X_K(\Gamma)$, then by (2.16), we have

We can now give our concept of total variation of a function in $BV(\Gamma)$.

Definition 2.11. For $u \in BV(\Gamma)$, we define its total variation as

We say that a measurable set $E \subset \Gamma$ is a set of finite perimeter if $\chi_E \in BV(\Gamma)$, and we define its $\Gamma$-perimeter as

that is

As a consequence of the above definition, we have the following result.

Proposition 2.12. $TV_\Gamma$ is lower semi-continuous with respect to the convergencein $L^2(\Gamma)$.

As in the local case, we have the following coarea formula relating the total variation of a function with the perimeter of its superlevel sets.

Theorem 2.13 (Coarea formula). For any $u \in L^1(\Gamma)$, let $E_t(u): = \{ x \in \Gamma \ : \ u(x) > t \}$. Then,

Proof. We have

Given ${{\bf z}} \in X_K(\Gamma)$ with $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$, since by Green's formula (2.16)

and having in mind (2.20), we get

Therefore, by (2.19), we obtain that

To prove the other inequality, we can assume that $TV_\Gamma(u) < \infty$ and, consequently, $u \in BV(\Gamma)$. Then, we can find a sequence $u_n \in C^{\infty}(\Gamma)$, such that $u_n \to u$ in $L^1(\Gamma)$ and

Now, taking a subsequence if necessary, we also have that $\chi_{E_t(u_n)} \to \chi_{E_t(u)}$ in $L^1(\Gamma)$ for almost all $t \in {\mathbb R}$. Then, by the lower semi-continuity of ${\rm Per}_\Gamma$ and using the coarea formula for Lipschitz functions, we have

We introduce now

Note that $JV_\Gamma (u)$ measures, in a weighted way, the jumps of $u$ at the vertices.

Proposition 2.14. For $u \in BV(\Gamma)$, we have

If $u \in BV(\Gamma) \cap C({\rm int}(V(\Gamma)))$, then

If $\Gamma$ is linear, that is $d_{{{\mathrm{v}}}} = 2$ for all ${{{\mathrm{v}}}} \in{\rm int}(V(\Gamma))$, then

Proof. The inequality $\vert Du \vert(\Gamma) \leq TV_\Gamma(u)$ is a consequence of Proposition 2.8. Let $u \in BV(\Gamma)$. Given ${{\bf z}} \in X_K(\Gamma)$ with $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$, applying Green's formula (2.17) and (2.11), we have

Therefore,

Suppose now that $u \in BV(\Gamma) \cap C({\rm int}(V(\Gamma)))$. Since $JV_\Gamma (u) = 0$, by (2.23), we have

On the other hand,

Then, since $\mathcal{D}(\Gamma) \subset X_K(\Gamma)$, we have $\vert Du \vert(\Gamma) \leq TV_\Gamma(u)$ and (2.24) holds.

Finally, let us see that (2.25) holds. By (2.26), for any $n \in {\mathbb N}$, we have that there exists $\varphi^n_{{\bf e}} \in C^\infty_c((0, \ell_{{{\bf e}}}))$, $\Vert \varphi^n_{{\bf e}} \Vert_\infty \leq 1$

Let ${\rm supp}(\varphi^n_{{\bf e}}) = [a^n_{{\bf e}}, b^n_{{\bf e}}]$, $0 < a^n_{{\bf e}} < b^n_{{\bf e}} < \ell_{{\bf e}}$. Now, given ${{{\mathrm{v}}}} \in {\rm int}(V(\Gamma))$ and ${{\bf e}} \in E_{{{\mathrm{v}}}} (\Gamma)$, suppose that ${{{\mathrm{v}}}} = {\mathrm{f}}_{{\bf e}}$ and ${\mathrm{i}}_{{\bf e}} \not\in {\rm int}(V(\Gamma))$. Then, we make the following definition: for $n \in {\mathbb N}$ such that $\ell_{{\bf e}} - \frac1n > b^n_{{\bf e}}$,

Suppose now that ${{{\mathrm{v}}}} = {\mathrm{i}}_{{\bf e}}$ and ${\mathrm{f}}_{{\bf e}} \not\in {\rm int}(V(\Gamma))$. In this case, we define, for $n \in {\mathbb N}$ such that $\frac1n < a^n_{{\bf e}}$,

Finally, suppose that ${{{\mathrm{v}}}} = {\mathrm{f}}_{{\bf e}}$ and ${\mathrm{i}}_{{\bf e}} \in {\rm int}(V(\Gamma))$. Then, we define, for $n \in {\mathbb N}$, such that $\frac1n < a^n_{{\bf e}}$ and $\ell_{{\bf e}} - \frac1n > b^n_{\hat{{{\bf e}}}}$,

Then, since $d_{{{\mathrm{v}}}} = 2$ for all ${{{\mathrm{v}}}} \in{\rm int}(V(\Gamma))$, if we define ${{\bf z}}^n$ such that $[{{\bf z}}^n]_{{\bf e}}: = \varphi^n_{{\bf e}} \pm \phi^n_{{\bf e}}$, taking the sign of $\phi^n_{{\bf e}}$ depending on the orientation of ${{\bf e}}$, we have ${{\bf z}}^n \in X_K(\Gamma)$, and

See the next Example for the definition of $\phi^n_{{\bf e}}$ in a particular case.

Hence, we get

Now,

Hence,

Therefore,

Consequently, taking limit as $n \to \infty$, we obtain that

Corollary 2.15. For $u \in BV(\Gamma)$, we have

Then

Proof. Obviously, if $u$ is constant, then $TV_\Gamma(u) = 0$. Suppose that $TV_\Gamma(u) = 0$. By (2.23), we have $\vert Du \vert(\Gamma) = 0.$ Then, $[u]_{{\bf e}} = a_{{\bf e}}$ is constant for all ${{\bf e}} \in E(\Gamma)$. Suppose that $u$ is not constant, then there exist ${{\bf e}}_1, {{\bf e}}_2 \in E(\Gamma)$, with $a_{{{\bf e}}_1} \not = a_{{{\bf e}}_2}$. We have

We can assume that ${{{\mathrm{v}}}} = {\mathrm{f}}_{{{\bf e}}_1} = {\mathrm{i}}_{{{\bf e}}_2} \in {\rm int}(V(\Gamma))$. Then if we take ${{\bf z}} \in W^{1, 2}(\Gamma)$ such that

we have that ${{\bf z}}\in X_K(\Gamma)$ and $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$. Therefore

which is a contradiction and consequently $u$ is constant.

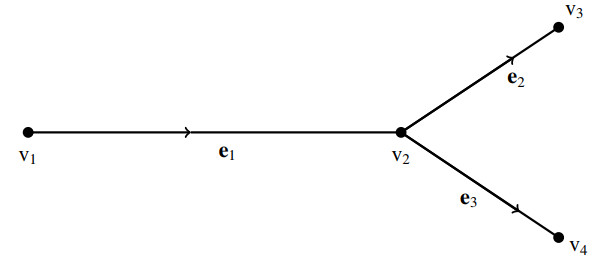
Example 2.16. Consider the linear metric graph $\Gamma$ with four vertices and three edges, $V(\Gamma) = \{{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_3, {{{\mathrm{v}}}}_4 \}$ and $E(\Gamma) = \{ {{\bf e}}_1: = [{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2], {{\bf e}}_2: = [{{{\mathrm{v}}}}_3, {{{\mathrm{v}}}}_2], {{\bf e}}_3: = [{{{\mathrm{v}}}}_3, {{{\mathrm{v}}}}_4] \}$.

Let $u \in BV(\Gamma)$ and suppose that

For $n \in {\mathbb N}$ large enough, we define

and

Then, we have

and

Thus, ${{\bf z}}^n \in X_K(\Gamma)$. Moreover,

and

Therefore,

In the next example we will see that the equality (2.25) does not hold if $u \not\in C({\rm int}(V(\Gamma)))$ or there exists ${{{\mathrm{v}}}} \in{\rm int}(V(\Gamma))$ with $d_{{{\mathrm{v}}}} \geq 3$.

Example 2.17. Consider the metric graph $\Gamma$ with four vertices and three edges, $V(\Gamma) = \{{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_3, {{{\mathrm{v}}}}_4 \}$ and $E(\Gamma) = \{ {{\bf e}}_1: = [{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2], {{\bf e}}_2: = [{{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_3], {{\bf e}}_3: = [{{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_4] \}$.

Let $u: = \chi_{{{\bf e}}_1} - \chi_{{{\bf e}}_2}$. Then,

By Green's formula (2.17), we have

Now, given ${{\bf z}} \in X(\Gamma)$ with $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$, we have $[{{\bf z}}]_{{{\bf e}}_1} ({{{\mathrm{v}}}}_2) = [{{\bf z}}]_{{{\bf e}}_2} ({{{\mathrm{v}}}}_2) + [{{\bf z}}]_{{{\bf e}}_3} ({{{\mathrm{v}}}}_2).$ Hence,

Therefore,

2.2.   The total variation flow in metric graphs

In order to study the total variation flow in the metric graph $\Gamma$ we consider the energy functional $\mathcal{F}_\Gamma : L^2(\Gamma) \rightarrow [0, + \infty]$ defined by

which is convex and lower semi-continuous. Following the method used in ^[2] we will characterize the subdifferential of the functional $\mathcal{F}_\Gamma$.

Given a functional $\Phi : L^2(\Gamma) \rightarrow [0, \infty]$, we define $\widetilde {\Phi}: L^2(\Gamma) \rightarrow [0, \infty]$ as

with the convention that $\frac{0}{0} = \frac{0}{\infty} = 0$. Obviously, if $\Phi_1 \leq \Phi_2$, then $\widetilde {\Phi}_2 \leq \widetilde {\Phi}_1$.

Theorem 2.18. Let $u \in BV(\Gamma)$ and $v \in L^2(\Gamma)$. The following assertions are equivalent:

(i) $v \in \partial \mathcal{F}_\Gamma (u)$;

(ii) there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$ such that

and

(iii) there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$ such that (2.31) holds and

Moreover, $D(\partial \mathcal{F}_\Gamma)$ is dense in $L^2(\Gamma)$.

Proof. Since $\mathcal{F}_\Gamma$ is convex, lower semi-continuous and positive homogeneous of degree $1$, by ^[2,Theorem 1.8], we have

We define, for $v \in L^2(\Gamma)$,

Observe that $\Psi$ is convex, lower semi-continuous and positive homogeneous of degree $1$. Moreover, if $\Psi(v) < \infty$, the infimum in (2.35) is attained, i.e., there exists some ${{\bf z}} \in X_K(\Gamma)$ such that $v = - {{\bf z}}^{\prime}$ and $\Psi(v) = \Vert {{\bf z}} \Vert_{L^\infty(\Gamma)}$. In fact, let ${{\bf z}}_n \in X_K(\Gamma)$ with $v = - {{\bf z}}_n^{\prime}$ for all $n \in {\mathbb N}$, such that $\Psi(v) = \lim_{n \to \infty} \Vert {{\bf z}}_n \Vert_\infty$. We can assume that

We must show that ${{\bf z}}$ satisfies the Kirchhoff condition. Now, by Proposition 2.1, we have that

Fix ${{{\mathrm{v}}}} \in V(\Gamma)$. Applying Green's formula (2.16) to ${{\bf z}}_n$ and $u \in BV(\Gamma)$, we get

Hence, taking $u$ such that $[u]_e({{{\mathrm{v}}}}) = 1$ for all ${{\bf e}}\in {\mathrm{E}}_{{{\mathrm{v}}}}(\Gamma)$ and $[u]_{\hat{{{\bf e}}}} = 0$ if ${{{\mathrm{v}}}} \not\in {\mathrm{E}}_{{{\mathrm{v}}}}(\Gamma)$, we have

Then, taking the limit as $n \to \infty$ and having in mind (2.13), we obtain

Therefore, ${{\bf z}} \in X_K(\Gamma)$ and $\Psi(v) = \Vert {{\bf z}} \Vert_{L^\infty(\Gamma)}$.

Let us see that

We begin by proving that $\widetilde{\mathcal{F}_\Gamma}(v) \leq \Psi(v)$. If $\Psi (v) = +\infty$ then this assertion is trivial. Therefore, suppose that $\Psi (v) < +\infty$. Given $\epsilon > 0$, there exists ${{\bf z}} \in X_K(\Gamma)$ such that $v = - {{\bf z}}^{\prime}$ and $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq \Psi(v) + \epsilon$. Then, for $w\in BV(\Gamma)$, applying Green's formula (2.17) and (2.11), we have

Taking the supremum over $w$ we obtain that $\widetilde{\mathcal{F}_\Gamma}(v) \leq \Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq \Psi(v) + \epsilon$, and since this is true for all $\epsilon > 0$, we get $\widetilde{\mathcal{F}_\Gamma}(v) \leq \Psi(v)$.

To prove the opposite inequality let us denote

Then, by (2.19), we have that, for $v\in L^2(\Gamma)$,

Thus, $\mathcal{F}_\Gamma\leq \widetilde{ \Psi}$, which implies, by ^[2,Proposition 1.6], that $\Psi = \widetilde{\widetilde{\Psi}} \leq \widetilde{ \mathcal{F}_\Gamma}$. Therefore, $\Psi = \widetilde{\mathcal{F}_\Gamma}$, and, consequently, from (2.34), we get

from where the equivalence between (i) and (ii) follows.

To prove the equivalence between (ii) and (iii) we only need to apply Green's formula (2.17).

Finally, by ^[9,Proposition 2.11], we have

from which the density of the domain follows.

We can also prove the following characterization of the subdifferential in terms of variational inequalities.

Proposition 2.19. The following conditions are equivalent:

$(a)$ $(u, v) \in \partial\mathcal{F}_\Gamma$;

$(b)$ $u, v \in L^2(\Gamma)$, $u \in BV(\Gamma)$ and there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}}\Vert_{L^\infty(\Gamma)} \leq 1$ such that $v = -{{\bf z}}^{\prime}$, and for every $w \in BV(\Gamma)$

$(c)$ $u, v \in L^2(\Gamma)$, $u \in BV(\Gamma)$ and there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}}\Vert_{L^\infty(\Gamma)} \leq 1$ such that $v = -{{\bf z}}^{\prime}$, and for every $w \in BV(\Gamma)$

Proof. $(a) \Rightarrow (c)$: By Theorem 2.18, we have that there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$ such that $v = -{{\bf z}}^{\prime}$ and

Then, given $w \in BV(\Gamma)$, multiplying $v = -{{\bf z}}^{\prime}$ by $w -u$, integrating over $\Gamma$ and using Green's formula (2.17), we get

Obviously, $(c)$ implies $(b)$. To finish the proof, let us see that $(b)$ implies $(a)$. If we take $w = u$ in (2.37), we get

and, therefore, by (2.11), we have

Proposition 2.20. For any $v \in \partial \mathcal{F}_\Gamma (u)$ it holds that

and

Proof. Since $v \in \partial \mathcal{F}_\Gamma(u)$, given $w \in BV(\Gamma)$, we have that

so we get (2.39). On the other hand, (2.40) is given in Theorem 2.18.

Definition 2.21. We define the $1$-Laplacian operator in the metric graph $\Gamma$ as

that is, if $u \in BV(\Gamma)$, $v \in L^2(\Gamma)$ and there exists ${{\bf z}} \in X_K(\Gamma)$, $\Vert {{\bf z}} \Vert_{L^\infty(\Gamma)} \leq 1$ such that

and

We have that the Cauchy problem

can be rewritten as the abstract Cauchy problem in $L^2(\Gamma)$,

Since $\mathcal{F}_\Gamma$ is convex and lower semi-continuous in $L^2(\Gamma)$ and $D(\partial \mathcal{F}_\Gamma)$ is dense in $L^2(\Gamma)$ by the Brezis-Komura theory (see ^[9]), we have that for any initial data $u_0 \in L^2(\Gamma)$ there exists a unique strong solution to problem (2.44). Therefore, we have the following existence and uniqueness result.

Theorem 2.22. For any initial data $u_0 \in L^2(\Gamma)$ there exists a unique solution $u(t)$ of the Cauchy problem (2.43), in the sense that $u \in C(0, T; L^2(\Gamma)) \cap W^{1, 1}(0, T; L^2(\Gamma))$ for any $T > 0$, $u(t) \in BV(\Gamma)$ and there exists ${{\bf z}} \in L^\infty(0, T; L^\infty(\Gamma))$, ${{\bf z}}(t) \in X_K(\Gamma)$, $\Vert {{\bf z}}(t) \Vert_{L^\infty(\Gamma)} \leq 1$, for almost all $t \in (0, T)$, such that

and

Definition 2.23. Given $u_0 \in L^2(\Gamma)$, we denote by $e^{t \Delta_1^{\Gamma}}u_0$ the unique solution of problem (2.43). We call the semigroup $\{e^{t\Delta_1^{\Gamma}} \}_{t \geq 0}$ in $L^2(X, \nu)$ the total variational flow in the metric graph $\Gamma$. $

The total variational flow in the metric graph satisfies the mass conservation property.

Proposition 2.24. For $u_0 \in L^2(\Gamma)$,

Proof. By (ii) in Theorem 2.18 and Green's formula (2.16), we have

and

Hence,

and, consequently,

2.3.   Asymptotic behaviour

By (2.28), we have

Since $\mathcal{F}_\Gamma$ is a proper and lower semicontinuous function in $L^2(\Gamma)$ attaining a minimum at the constant zero function and, moreover, $\mathcal{F}_\Gamma$ is even, by ^[12,Theorem 5], we have that there exists $v_0 \in \mathcal{N}(\mathcal{F}_\Gamma)$ such that

Now, having in mind Proposition 2.24, we have

We denote

We will see that the total variational flow in the metric graph $\Gamma$ reaches the mean $\overline{u_0}$ of the initial data $u_0$ in finite time, that is, $T_{ex}(u_0) < \infty$. We will rely on the results proved by Bungert and Burger in ^[10] (see also ^[11]) for the gradient flow of a coercive (in the sense described below), absolutely $1$-homogeneous convex functional defined on a Hilbert space.

Let us recall some notation used in ^[10]. Let $\mathcal{H}$ be a Hilbert space and $J: \mathcal{H} \rightarrow (-\infty, + \infty]$ a proper, convex, lower semi-continuous functional. Then, it is well known (see ^[9]) that the abstract Cauchy problem

has a unique strong solution $u(t)$ for any initial datum $u_0 \in \overline{D(J)}$.

We say that $J$ is coercive, if there exists a constant $C > 0$ such that

where

Clearly, this inequality is equivalent to positive lower bound of the Rayleigh quotient associated with $J$, i.e.,

For $u_0 \in \mathcal{H}_0$, if $u(t)$ is the strong solution of (2.47), we define its extinction time as

In the next result, we summarize the results obtained by Bungert and Burger in ^[10].

Theorem 2.25. Let $J$ be a convex, lower-semicontinuous functional on $\mathcal{H}$with dense domain. Assume that $J$ is absolutely $1$-homogeneous and coercive. For $u_0 \in\mathcal{H}_0$, let $u(t)$ be the strong solution of (2.47). Then, we have

$(i)$ (Finite extinction time)

$(ii)$ (General upper bounds)

$(iii)$ (Sharper bound for the finite extinction)

where

Now we are going to apply Theorem 2.25 to study the asymptotic behaviour of the solutions of the Cauchy problem (2.43).

Obviously, the convex, lower semi-continuous functional $\mathcal{F}_\Gamma$ is absolutely $1$-homogeneous, that is, $\mathcal{F}_\Gamma(\lambda u) = \vert \lambda \vert \mathcal{F}_\Gamma(u)$, for all $\lambda \in {\mathbb R}$ and all $u \in L^2(\Gamma)$. In this case,

Let us see that $\mathcal{F}_\Gamma$ is coercive. In fact, if it weren't we could find a sequence $u_n \in L^2(\Gamma)_0$ such that

Now, by homogeneity, we can asume that $\Vert u_n \Vert_{L^2(\Gamma)} = 1$ for all $n \in {\mathbb N}$, so

By Theorem 2.5, we can assume, taking a subsequence if necessary, that

Then, by the lower semi-continuity of $TV_\Gamma$ (Proposition 2.12), we have $TV_\Gamma(u) = 0$. Then, by (2.28), $u$ is constant. Now, since $u_n \in L^2(\Gamma)_0$,

Therefore, $\Vert u \Vert _{L^2(\Gamma)} = 0$, which is a contradiction since $\Vert u \Vert _{L^2(\Gamma)} = 1.$

If we denote

we have

Then, by Theorem 2.25, we have the following result.

Theorem 2.26. For any $u_0 \in L^2(\Gamma)$, we have

Moreover,

where

Proof. It is a direct application of Theorem 2.25, having in mind that for any constant function $v_0$ and any $u_0 \in L^2(\Gamma)$, we have $\mathcal{F}_{\Gamma}(u_0 + \overline{u_0}) = \mathcal{F}_{\Gamma}(u_0)$ and $\partial \mathcal{F}_{\Gamma}(u_0 + \overline{u_0}) = \partial \mathcal{F}_{\Gamma}(u_0)$ (see ^[10,Proposition A.3]).

To obtain a lower bound on the extinction time, we introduce the following space which, in the continuous setting, was introduced in ^[19]:

and consider in $G_m(\Gamma)$ the norm

Note that, for $v \in G_m(\Gamma)$, we have that there exists ${{\bf z}}_v\in X(\Gamma)$, such that $v = -{{\bf z}}'_v$ and $\Vert v \Vert_{m, *} = \Vert {{\bf z}}_v \Vert_\infty$.

From the proof of Theorem 2.18, for $f \in G_m(\Gamma)$, we have

and, moreover,

The next result is consequence of ^[11,Proposition 6.9]. We give the proof to be self-contained

Theorem 2.27. Given $u_0 \in L^2(\Gamma)$, we have

Proof. If $u(t): = e^{t\Delta^\Gamma_1}u_0$, we have

Then, by Proposition 2.20, we get

2.4.   Explicit solutions

Let us now see that we can compute explicitly the evolution of characteristic functions. First we need to do the computations for the Neumann problem for the total variation flow in an interval $(0, L)$ of ${\mathbb R}$, that is, for the problem

In ^[3], we have proved the existence and uniqueness of solutions to problem (2.55), where the concept of solution is the following. For $u_0 \in L^2(]0, L[)$ we say that $u \in C(0, T; L^2(]0, L[) \cap W^{1, 1}(0, T; L^2(]0, L[)$ is a weak solution of (2.55) if $u(0) = u_0$, $u(t) \in BV((0, L))$ and there exists ${{\bf z}} \in L^\infty(0, T; L^\infty(]0, L[)$, $\Vert {{\bf z}}(t) \Vert_{L^\infty(]0, L[)} \leq 1$, for almost all $t \in]0, T[$, such that

and

Lemma 2.28. Let $0 < a, b, c < L$ and $k > 0$. Then, we have

$(1)$ If $u_0 = k\chi_{(0, a)}$, then the solution of (2.55) is given by

where $T = \frac{ka(L-a)}{L}$, and

$(2)$ If $u_0 = k\chi_{]b, L[}$, then the solution of (2.55) is given by

where $T = \frac{k(L-b)}{L}$, and

$(3)$ Let $0 < k_1 < k_2$. If $u_0 = k_1 \chi_{]0, c[} + k_2 \chi_{]c, L[}$, then the solution of (2.55) is given by

where $T = \frac{(k_2-k_1)c(L-c)}{L}$, and

$(4)$ Assume that $0 < a < b < L$ and also that $L < a+b$. If $u_0 = k\chi_{]a, b[}$, then the solution of (2.55) is given by

where $T_1 = \frac{(b-a)(L-b)}{2L-(a+b)}k$,

where

and

Proof. (1): Given the initial datum $u_0 = \chi_{]0, a[}$ we look for a solution of the form

on some interval $]0, T[$ defined by the inequality $\alpha(t) > \beta(t)$ for $t \in]0, T[$, and $\alpha(0) = k$, $\beta(0) = 0$. Then, we shall look for some ${{\bf z}} \in L^\infty(0, T; L^\infty(]0, L[)$, $\Vert {{\bf z}}(t) \Vert_{L^\infty(]0, L[)} \leq 1$ for almost all $t \in]0, T[$, such that

and

For $0 \leq t \leq T$, we define

Integrating equation (2.59) over $(0, a)$, we obtain

Thus $\alpha'(t) = - \frac{1}{a}$ and, therefore, $\alpha(t) = k - \frac{t}{a}$. Similarly, we deduce that $\beta'(t) = \frac{1}{L -a}$, hence $\beta(t) = \frac{t}{L-a}$. Then, the first $T$ such that $\alpha(T) = \beta(T)$, is given by $T = \frac{ka(L-a)}{L}$. An easy computation shows that (2.62) holds for all $t \in]0, T[$. Finally, if we take ${{\bf z}}(t) = 0$ for $t > T$, we have that

is a solution for $t \geq T.$

The proof of (2) is similar to the proof of (1), taking in this case, for $0 \leq t \leq T$,

(3): We look for a solution of the form

on some interval $]0, T[$ defined by the inequality $\alpha(t) < \beta(t)$ for $t \in]0, T[$, and $\alpha(0) = k_1$, $\beta(0) = k_2$. Working as in the proof of (1), we shall look for some ${{\bf z}} \in L^\infty(0, T; L^\infty(]0, L[)$, with $\Vert {{\bf z}}(t) \Vert_{L^\infty(]0, L[)} \leq 1$ for almost all $t \in]0, T[$ and ${{\bf z}}(t)(0) = {{\bf z}}(t)(L) = 0$, satisfying

and

Then,

Hence, taking, for $0 \leq t \leq T$,

it is easy to see that

and

Therefore, for $0 < t \leq T = \frac{(k_2-k_1)c(L-c)}{L}$, the solution is given by

Moreover,

(4): In this case we look for a solution of the form

on some interval $(0, T)$ defined by the inequality $\alpha(t) < \beta(t)$, $\gamma(t) < \beta(t)$ for $t \in]0, T[$, and $\alpha(0) = \gamma(t) = 0$, $\beta(0) = k$. Working as in the proof of (1), we need to find a vector field ${{\bf z}} \in L^\infty(0, T; L^\infty(]0, L[)$, $\Vert {{\bf z}}(t) \Vert_{L^\infty(]0, L[)} \leq 1$, for almost all $t \in]0, T[$, satisfying

Now, if we take, for $0 \leq t \leq T$,

Hence,

Since we are assuming that $L-b < a$, we have $\alpha(t) < \gamma(t)$. Then, for

we have $\beta(T_1) = \gamma(T_1)$. Hence, for $0 < t \leq T_1$, if

it is easy to see that

and

Therefore, for $0 < t \leq T_1$, $u(t)$ is the solution. Now,

Then, applying (3), we have

where

Finally, for $t > T_2$, the solution in given by

Remark 2.29. Let us point out that it is obtained in ^[8] that for the initial data $u_0 = k_1 \chi_{(a, b)} + k_2 \chi_{(b, L)}$ with $0 < k_1 < k_2$, the solution of (2.55) is given by

for $0 \leq t \leq T_1$, with

We are now going to find an explicit solution in the case of a simpler metric graph in order to see the difference in behaviour with the case of the total variation flow in an interval with Neumann boundary conditions that we have considered in the above result.

Example 2.30. Consider the metric graph $\Gamma$ with three vertices and two edges, that is $V(\Gamma) = \{{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_3 \}$ and $E(\Gamma) = \{ {{\bf e}}_1: = [{{{\mathrm{v}}}}_1, {{{\mathrm{v}}}}_2], {{\bf e}}_2: = [{{{\mathrm{v}}}}_2, {{{\mathrm{v}}}}_3], \}$. Let $0 < a < \ell_{{{\bf e}}_2}$ and assume that $\ell_{{{\bf e}}_1} > \ell_{{{\bf e}}_2} - a$. We are going to find the solution of the total variation flow for the initial datum $u_0: = k \chi_D$, with $k > 0$ and $D: = ({{{\mathrm{v}}}}_2, c_{{{\bf e}}_2}^{-1}(a))$.

We look for solutions of the form:

for all $0 < t \leq T$ such that

Then, we need to find ${{\bf z}}(t) \in X_K(\Gamma)$, with $\Vert {{\bf z}}(t) \Vert_\infty \leq 1$, satisfying:

By (2.25), we can write (2.64) as

Now,

Hence,

and

Thus, if we assume that $[{{\bf z}}]_{{{\bf e}}_2}(a) = -1$, and having in mind that $[{{\bf z}}(t)]_{{{\bf e}}_1} ({{{\mathrm{v}}}}_2) = - [{{\bf z}}(t)]_{{{\bf e}}_2} ({{{\mathrm{v}}}}_2)$, we have that we can rewrite (2.64) as

Now,

and then, (2.64) is equivalent to

Therefore, if $[{{\bf z}}(t)]_{{{\bf e}}_1}({{{\mathrm{v}}}}_2) = [{{\bf z}}(t)]_{{{\bf e}}_1}(\ell_{{{\bf e}}_1}) = 1$, we have that (2.64) holds.

We define

and

Note that

thus ${{\bf z}}(t) \in X_K(\Gamma)$.

On the other hand, integrating in (2.63), we get

Consequently, since $\ell_{{{\bf e}}_1} > \ell_{{{\bf e}}_2} - a$, the solution is given by

and

where

We have

Now, for $t > T_1$, we look for a solution of the form

for all $T_1 < t \leq T _2$ such that

Then, we need to find ${{\bf z}}(t) \in X_K(\Gamma)$, with $\Vert {{\bf z}}(t) \Vert_\infty \leq 1$, satisfying:

By (2.25), we can write (2.66) as

which, having in mind that $[{{\bf z}}(t)]_{{{\bf e}}_1} ({{{\mathrm{v}}}}_2) + [{{\bf z}}(t)]_{{{\bf e}}_2} ({{{\mathrm{v}}}}_2) = 0$, is equivalent to

Then, if $[{{\bf z}}(t)]_{{{\bf e}}_1} ({{{\mathrm{v}}}}_2) = 1$, we have that (2.66) holds.

We define

and

Now, integrating in (2.65), for $T_1 < t \leq T_2$, we get

where $T_2$ is given by

that is,

Consequently, the solution $u(t)$ of the Cauchy problem (2.43) for the initial datum $u_0: = k \chi_D$ is given by

and

where

Moreover, for $t \geq T_2$,

Remark 2.31. Let us point out that in the above example, we see that the solution does not coincide with the solution of the Neumann problem in each edge. However, this happens if we consider that the total variation of a function $u$ is given by $\vert Du \vert (\Gamma)$, in which case it does not take into account the structure of the metric graph.

Example 2.32. Consider the metric graph $\Gamma$ of the example 2.17

Assume that $\ell : = \ell_{{{\bf e}}_2} = \ell_{{{\bf e}}_3}$ and let $0 < a < \ell_{{{\bf e}}_1}$ such that $a < 2 \ell$. We are going to find the solution of the total variation flow for the initial datum $u_0: = k \chi_D$, with $k > 0$ and $D: = (c_{{{\bf e}}_1}^{-1}(a), {{{\mathrm{v}}}}_2)$.

We look for solutions of the form:

for all $0 < t \leq T_1$ such that

Then, we need to find ${{\bf z}}(t) \in X_K(\Gamma)$, with $\Vert {{\bf z}}(t) \Vert_\infty \leq 1$, satisfying:

Now

hence

Since ${{\bf z}}(t) \in X_K(\Gamma)$, $[{{\bf z}}(t)]_{{{\bf e}}_1} ({{{\mathrm{v}}}}_2) = -[{{\bf z}}(t)]_{{{\bf e}}_2} ({{{\mathrm{v}}}}_2) - [{{\bf z}}(t)]_{{{\bf e}}_3} ({{{\mathrm{v}}}}_2)$, thus

Therefore, we can write (2.68) as

On the other hand,

Now,

Thus

Then, if $[{{\bf z}}(t)]_{{{\bf e}}_1}(a) = 1$ and $[{{\bf z}}(t)]_{{{\bf e}}_1}({{{\mathrm{v}}}}_2) = -1$, (2.69) holds.

We define

Now, integrating in (2.67), we get

Consequently, the solution is given by

and

where

since we are assuming that $a < 2 \ell$.

Now, for $t > T_1$, we look for a solution of the form

with

such that

Then, we need to find ${{\bf z}}(t) \in X_K(\Gamma)$, with $\Vert {{\bf z}}(t) \Vert_\infty \leq 1$, satisfying:

and

Now $Du(t) = 0,$ hence

Since ${{\bf z}}(t) \in X_K(\Gamma)$, we have

On the other hand,

Now,

Hence,

Therefore, (2.71) holds, if $[{{\bf z}}(t)]_{{{\bf e}}_1}({{{\mathrm{v}}}}_2) = -1$.

Now, integrating (2.70), for $T_1 \leq t \leq T_2$, we have

Consequently, the solution is given by

and

where

For $t \geq T_2$, we have

Acknowledgments

The author is grateful to Wojciech Górny, Delio Mugnolo and Julián Toledo for stimulating discussions on this paper. The author have been partially supported by the Spanish MCIU and FEDER, project PGC2018-094775-B-100.

Conflict of interest

The author declares no conflict of interest.