A quantum mechanical approach to random X chromosome inactivation

1.   Introduction

In 1961, Mary Lyon proposed for the first time the hypothesis of the random X chromosome inactivation (XCI) in mammalian female cells [1]. This mechanism of gene dosage compensation emerged to guarantee that XX and XY individuals have an equivalent number of X-linked genes [1],[2]. This is accomplished by silencing one of the two X chromosomes (Xs) in females during early development, around the time of implantation, and maintaining it at the following cell divisions and throughout life [3],[4]. This leads to a mosaic of cells with different Xs activated in female tissues [5]. Although this mechanism differs from species to species, it has been found that in eutherian (placental) mammals, the inactivation happens, for the most part, at random [1],[6]. This means that both Xs, paternal and maternal, have equal chances of getting silenced. Conversely, a non-random skewed inactivation is associated with several X-linked syndromes in female carriers [7]–[9].

Despite the vast amount of research conducted for the past half-century on this topic, the choice process - which X remains active - remains unclear. This XCI mechanism is particularly enigmatic since cells manage to perform a random, instantaneous, and mutually exclusive inactivation with a high level of accuracy. Although various models have been proposed to explain the process that cells undergo to accomplish this phenomenon from a classical mechanical approach (e.g.: blocking factor [10],[11], transient X cross communication [12], stochastic process [13], predetermined fate [14], Xist-levels dependent [15]), to this day a consensus is far from being reached [16]. Consequently, this paper proposes a theoretical model that addresses the choice process of XCI through the scope of quantum mechanics in an effort to develop a more comprehensive understanding of this process. This quantum model is, foremost, based on Shrödinger's [17] proposal, whereby quantum mechanical effects occur in biological systems at the atomic level, having a large-scale influence on living beings. This approach has been widely used since then in an effort to explain distinct biological phenomena, such as proton tunneling in enzyme reactions and quantum coherence in photosynthesis light-harvesting efficiency [18]–[21].

In this model, the precise conditions that need to be satisfied for quantum effects to be involved in the X inactivation choice process are described in detail, with the intent to make a compelling case in favor of this approach. It should be kept in mind, nevertheless, that the central quantum concept described here can be applied under different circumstances. This paper makes use of previously published data that have not all necessarily been proven comprehensively, owing in part to the difficulty of designing satisfactory experiments that replicate the in vivo process of X inactivation [16]. Additionally, although the present model was developed with a main human focus, some data found in mice (Mus musculus) research is utilized since most of the experimental knowledge we hold about XCI comes from mouse embryonic stem cells [16],[22],[23]. This is the reason behind employing the mouse-way of writing genetic regions when referring to some of the data (lowercase), instead of the human one (uppercase).

In the first section of this work, the biological and chemical conditions that need to be satisfied for the construction of this model are presented, followed by the actual development of the quantum mechanical model, its suitability to different models and conditions, and its scope and contributions to XCI and quantum biology.

2.   Biological premises

2.1.   Physical pairing

The first condition that needs to be fulfilled, and perhaps the most essential, for this quantum model is a physical contact, or crosstalking as it is known in genetics, between the two X chromosomes. A physical pairing occurs when two homologous chromosomes communicate in trans, which is not uncommon in cells' fate determination. It has been observed in T-cell differentiation, DNA replication, PcG protein silencing, and olfactory receptor choice [24]–[27]. With regards to X chromosome inactivation, despite a few data showing otherwise [13],[28]–[30], it has been widely proven that a physical pairing between the Xs (d ≤ 2 µm), with a half-life of <1.0 hour, is essential for the initiation of the silencing process [12],[31]–[36]. A chaotic choice occurs when there is a loss of communication in trans [11],[34].

The Xs pair up occurs by the X-inactivation center (XIC/Xic), an X-linked region that includes the central regulatory elements for X chromosome inactivation [33],[34],[37]. In mice, the leading non-coding RNAs (ncRNA) during X inactivation are Xist, in charge of designating the inactivated X chromosome by a coating mechanism, and its antisense unit Tsix and Xite, responsible for keeping one of the X chromosomes activated by blocking the up-regulation of Xist [34],[38],[39]. However, although Xist and Xite play a fundamental role in XCI, it may well be argued that Tsix is the central gene regulating the choice process as it undergoes a trans gene-to-gene pair up [11],[34],[36],[39].

When it comes to humans, TSIX does not have the same role as in mice, since it is only active once the X chromosome has already been inactivated [22]. Instead, it has been demonstrated that XIST is the gene responsible for guiding the X inactivation choice process in humans, resulting in a skewed inactivation when it expresses a mutation [23],[40]–[43]. Although the choice process is mediated by several genes and proteins [16],[23],[32],[35], it is adequate to assert that in mice and humans it depends, primarily, on the proper action of Tsix and XIST, respectively. However, the trans gene-to-gene pairing has not been investigated as thoroughly during the human Xs physical pairing as in mice.

Thus, the reason to exhibit the importance of Tsix and XIST in their corresponding species is to enable the assumption that XIST may pair up in a similar trans gene-to-gene manner as Tsix prior to human XCI.

2.2.   XIST point mutation

The full-length transcript of XIST is 19.3 kb [44], which in quantum terms is still too big to obey the rules of quantum mechanics. Thus, it is necessary to scale further down to find the potential originator of the quantum mechanical effect in XCI: the nucleotide bases. This has been done repeatedly in quantum biology since Lowdin's proton tunneling model on gene mutations under the principle that, at this level, the functioning of the nucleotides depends on the dynamics of electrons and protons [45]. This view raises the third biological condition that must be satisfied in this model, which is the capability of a point mutation to influence the gene function of XIST.

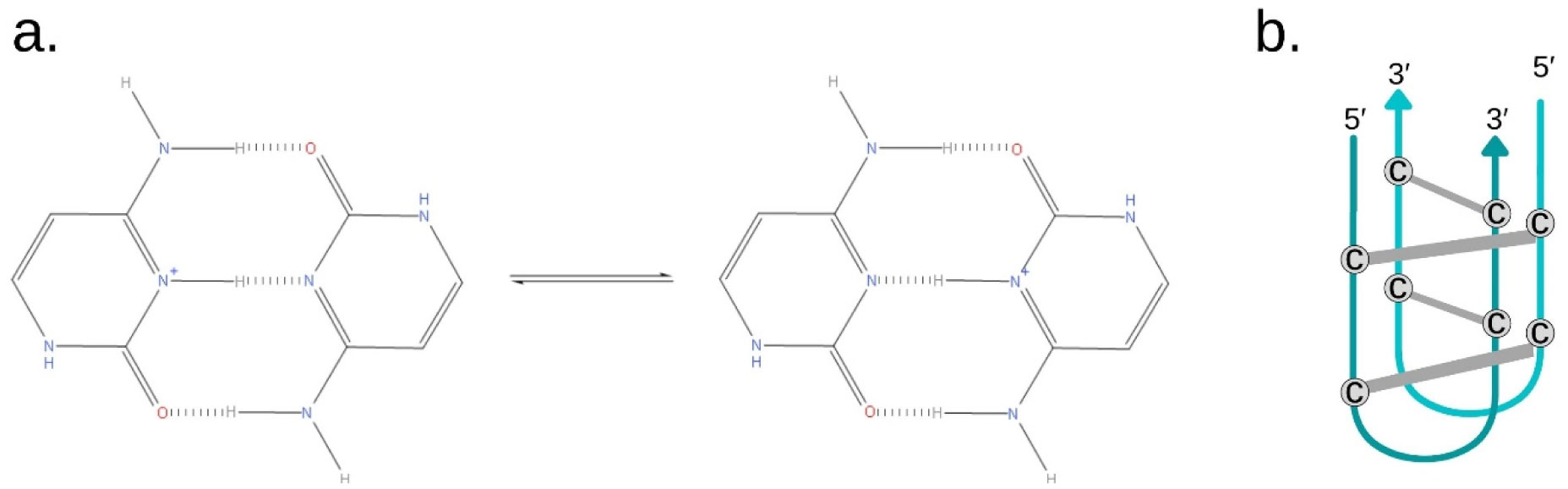
It has been demonstrated that the modification of a single nucleotide in XIST and specifically a base substitution at position −43 in its minimal promoter, occupied typically by a cytosine, impacts the choice process [41],[46]–[48]. In two unrelated families, it was found that a cytosine (C) to guanine (G) mutation at this position demonstrated a preferential inactivation of the X carrying the mutation, ranging from 55: 45 to 95: 5 preference [41]. An explanation of this effect was proposed by Pugacheva et al. [42], establishing that a substitution of a base in the −43 position of XIST regulates the X inactivation due to a CTCF-XIST promoter complex. The CCCTC-binding factor (CTCF), a DNA-binding protein that influences transcription, has been demonstrated to serve as an XIST epigenetic switch during female cell differentiation [49]–[52]. Pugacheva et al. [42], concluded that the C (-43) G mutation enhances the CTCF-XIST binding, activating XIST, thus inactivating the X expressing the mutation (refer to Figure 1).

Chemical premises

2.3.   i-motif pairing

Since the -43-nucleotide position in the XIST minimal promoter may be considered as a pivotal location in the random selection of the active and inactive X, and an XCI system affected by quantum effects needs to be occurring at the bases level, this model proposes that the physical pairing between XISTs could be occurring at this nucleotide position, causing a cytosine-cytosine pair up in an i-motif configuration.

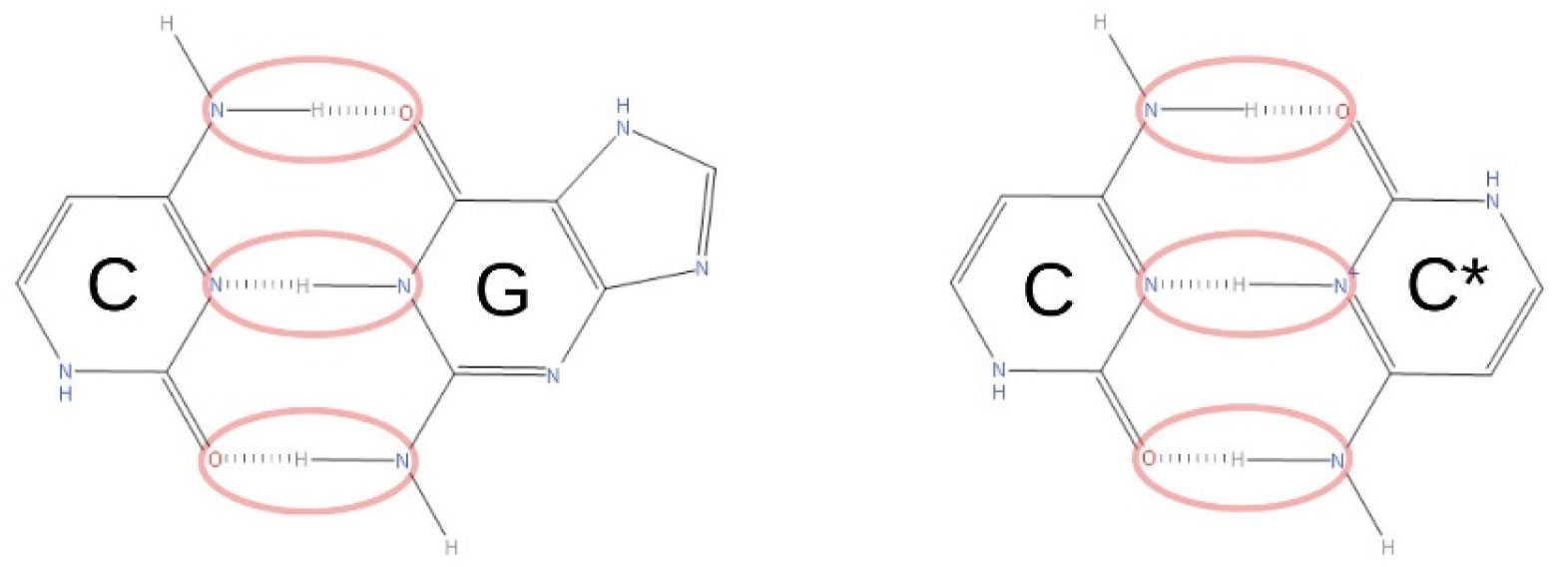
RNA pairing occurs in a wide variety of configurations. Generally, bases in structured RNAs engage in canonical Watson-Crick base pairs (adenine (A) forms base pair with uracil (U) and guanine (G) with cytosine (C)) [53],[54]. However, 40% of the interactions occur in non-canonical ways, which include the i-motif pairing [54]. This is a base interaction that happens intra and intermolecularly, when a cytosine (C) and a protonated cytosine (C*) at the nitrogen in the 3-position, pair by hydrogen bonding, establishing multiple C·C* base pairs, intercalated in an antiparallel orientation [55],[56] (refer to Figure 2).

Although an i-motif structure has not been identified or investigated in XIST, it has been found in human genome [58]–[61], gene promoters [62]–[64], and in the X chromosome [65]. Moreover, several of XIST promoter characteristics at the -43 position make it a fitting candidate to be prone to i-motif pairings. Specifically, its long C-tracts, which provide pairing stability, particularly beyond five, and two thymines following the cytosine section, which operate as capping residues in i-motifs [56],[57],[65] (refer to Figure 1).

2.4.   Cytosine-dependent inactivation

The protonation of one of the cytosines emerging from the i-motif pairing is crucial for the elaboration of this model. This will establish a concrete difference between the two XISTs at a pivotal location just prior to the CTCF binding, which behaves as an XCI switch; thus, here is proposed, resulting in an active and inactive X. This proposal is based on the assumption that when a C to G mutation has been found to skew the X inactivation choice process, it is due to the guanine emulating the chemical structure of the protonated cytosine, which will occur under normal circumstances between non-mutated XISTs–with an electronegative O atom and two positive charged H atoms as shown in Figure 3. This means that, for reasons that will become clear presently, in normal conditions the protonated cytosine will assure a random mutually exclusive choice, while the expression of a G will skew the process by simulating the chemical structure of a C*.

Considering this C*-CTCF interaction as the main factor causing inactivation means that the XIST carrying the protonated C* will activate, designating its X chromosome as the inactive, whereas the second XIST maintaining the canonical C will remain inactive allowing its X to be expressed (Figure 4).

Based on the presented data, this quantum mechanical model is developed under the following biological and chemical premises:

• XISTs undergo a physical pairing, in a similar trans gene-to-gene manner as Tsix, prior to the inactivation of one of the X chromosomes.
• The alteration of a single base in XIST disrupts the CTCF binding, thus, influences the process of choice during XCI.
• The XISTs pair-up occurs in an i-motif configuration.
• The protonation of one of the cytosines, as a result of the i-motif pairing, enhances the CTCF-XIST binding, which in turn activates the XIST, resulting in an activated X.

3.   Quantum mechanics in XCI choice process

3.1.   Cytosine superposition

The hydrogen bonding found in i-motif, occurs by a hemiprotonated N···H···N arrangement [55], which, as shown in Figure 2, means that the hydrogen proton is not attached to a nitrogen of one of the cytosines but instead, the proton hops between the nitrogen of two cytosines.

The proton transfer between AT and GC base pairs and its potential effect on the genome operation has been broadly explored since Löwdin's model [45],[66]. Conversely, this reaction has not been explored enough in i-motif structures [67]. Nonetheless, by means of NMR spectroscopy and a QM approach, Lieblein et al. [57], confirmed the hypothesis that the hemiprotonated N···H···N moiety can be described as an asymmetric double-well potential, in which the shared proton is delocalized causing it to oscillate between the two wells. They found that with low, distance-dependent barriers (maximum height of 6 kcalmol-1), and fast proton transfer rates (minimum transfer rate of 108 s-1) the quantum mechanical phenomenon of tunneling is potentially involved.

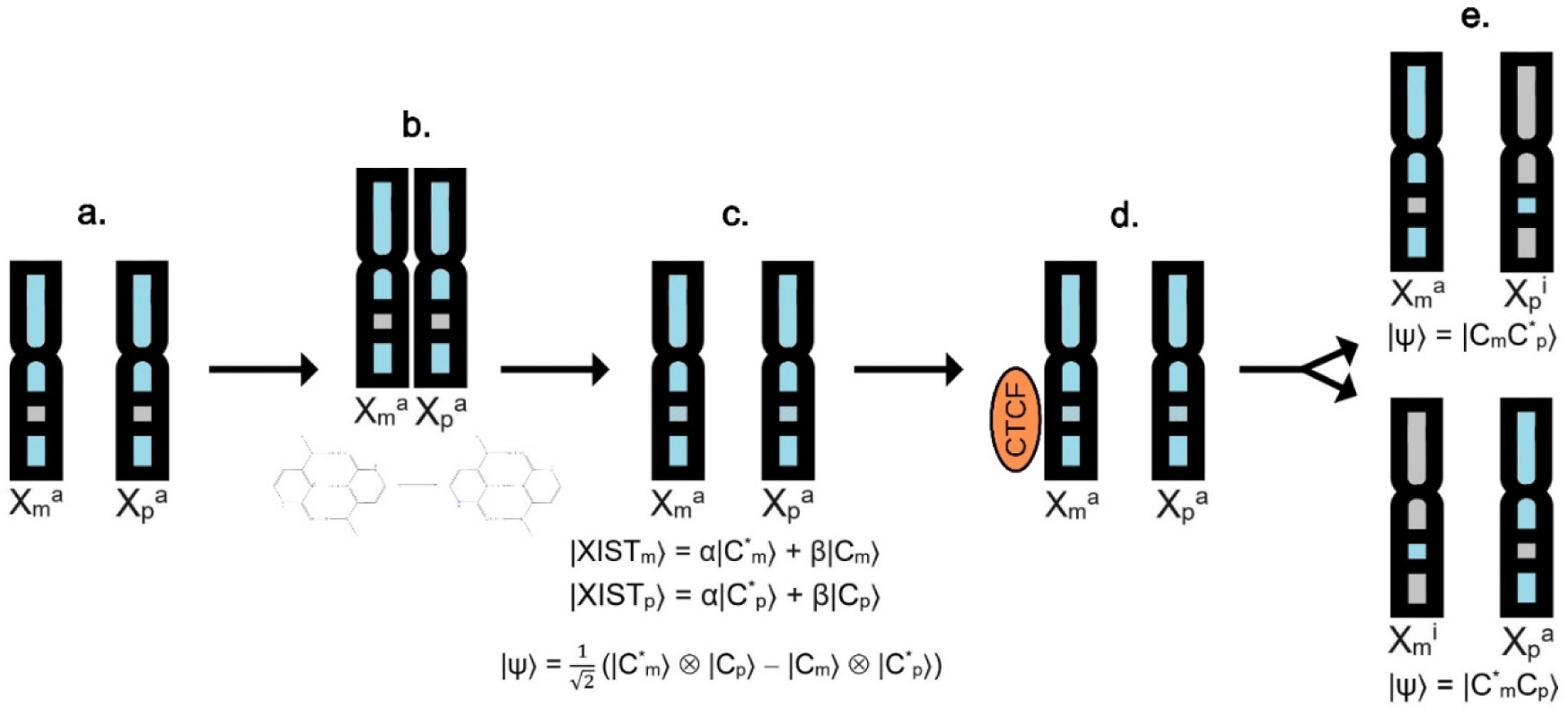
This model suggests that as the physical pairing ceases and the C·C* base pair dismantles, beyond 2.5 Å of N-N distance [57], the H proton, under tunneling effect, loses its definite location and rather, exists in a fuzzy state between both cytosines. As such, each XIST can be described as an independent state vector (|XISTm⟩ and |XISTp⟩), in which its cytosine is found in a coherent superposition of two (orthogonal) basis vectors (|C*⟩ and |C⟩). In other words, at this point maternal and paternal XIST will not carry either a protonated C* or a canonical C, but the probability of projecting both at the same time.

In this description, the sum of the basis vectors is weighted by amplitudes represented as complex numbers (α, β).

This superposition will be maintained until an act of measurement is performed, hence, determining which XIST will be activated. A measurement in the quantum world does not necessarily entail a human act of measuring - and indeed physicists use different definitions - but it can simply be regarded as an interaction between a system and a measuring device.

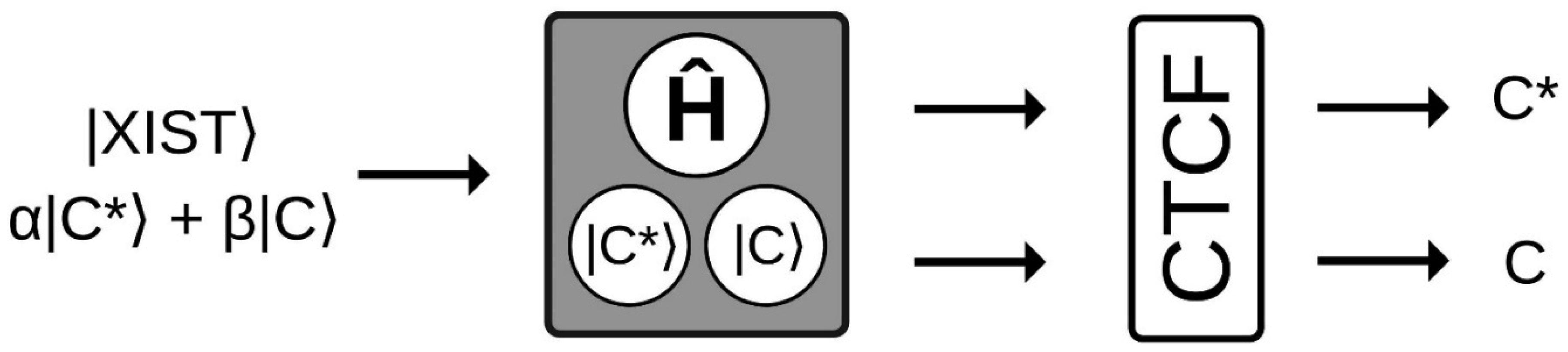
In quantum mechanics the measurable property of a physical system is called an observable, described by a linear operator. In this model, the observable is the H proton position since we can actually detect by a measurement if it is found in the maternal or the paternal cytosine, described by the operator Ĥ. This operator will have a set of eigenstates (|C*⟩ and |C⟩) with associated eigenvalues (C* and C). That is to say, that the measurement of Ĥ yields the result C* when the system is in the state |C*⟩ (hydrogen proton bonding with the cytosine nitrogen), and the result C when the system is in the state |C⟩ (hydrogen bonding proton is absent). No other results are possible for the measured value of Ĥ in the state vectors |XIST⟩.

As mentioned, in order for a measurement to be made-projecting on a single eigenstate, thus collapsing the superposition-a measuring apparatus is needed. In this model, such apparatus is represented by CTCF. Thereby, when the CTCF performs a measurement on a cytosine found in a superposition by binding to it, it unpredictably turns it into one of the eigenstates of the observable (refer to Figure 5).

This measurement will destroy the H proton delocalization enhancing the CTCF-XIST promoter complex in one of the chromosomes, causing its inactivation. This would mean that the CTCF is involved in the choice and inactivation process (refer to Figure 6).

3.2.   Entangled state

Hitherto, the maternal |XISTm⟩ and paternal |XISTp⟩ state vectors have been described as independent systems. Nevertheless, as correlated states, it will be more accurate to describe them as a single composite system.

In fact, the combined system behaves as a Bell state, a maximally entangled superposition of two-particle states, in which the probability of both XISTs to project |C*m⟩|C*p⟩ and |Cm⟩|Cp⟩ are 0, they are either |C*m⟩|Cp⟩ or |Cm⟩|C*p⟩. The state is unfactorizable, it cannot be described separately. The entangled system caused by the delocalized proton will be written as:

Consequently, if CTCF performs a (partial) measurement on any of the XIST, for instance the maternal, and it is found in the |Cm⟩ eigenstate, the state of the paternal XIST must be |C*p⟩. The system collapses in the state |CmC*p⟩. If instead, CTCF measures |C*m⟩ at first, the state of the paternal must be |Cp⟩, collapsing in the |C*mCp⟩ state. After the collapse, the two-particle state is no longer entangled (as described in Figure 6). It is important to point out that this model assumes that the probability of the CTCF to find the proton in either one of the cytosines is equally likely.

4.   Model applications

As mentioned above, although there already are existent models that describe the process cells undergo to achieve X inactivation in-depth, a quantum mechanical approach elucidates the choice process phenomenon in a more probabilistic coherent matter. Nonetheless, this is solely a partial step of the XCI process. Thus, the main goal of this model is to serve as a complementary element to the existing theories, despite some aspects coming into conflict.

4.1.   Pairing

The current models and their variants can be divided into two types: deterministic - the ones that consider the Xs physical pairing as essential for the X inactivation [11],[12], and stochastic–the ones that do not [13],[15]. In this regard, although quantum mechanics is considered stochastic or random by nature, a physical interaction between the chromosomes, during which information can be shared or exchanged, is essential for the feasibility of the present model. Moreover, the fact that an X-to-X pairing is needed for the development of a quantum-based model, reduces its applicability to only diploid cells and not polyploid cases, a factor that is not only explained but also used as evidence in other models [10],[13]. Notwithstanding, an abnormal number of chromosomes is rarely found in mammals, even less so in humans.

4.2.   Nucleotide pairs

To this model, a C-C pair up is required to enable the proton tunneling that could determine which X gets inactivated. Nonetheless, the same principle may be applied to any other base pairing at a pivotal position that gathers similar characteristics as the cytosines pair. For instance, in the XIST-levels dependent model, an A-repeat is considered crucial for a random inactivation [15]. By applying the quantum notion that a proton can be tunneled between adenines establishing a concrete difference within two essential genes for a random inactivation, a quantum mechanical approach could be applied to Royce-Tolland's model.

It is important to note that based on this approach, what disrupts the random X inactivation is the disturbance of the establishment of a delocalized shared proton between two bases and not necessarily a base mutation, i.e., C (-43) G mutation. Hence the occurrence of investigations findings of skewed inactivation patterns without base mutations in the minimal promoter [68]–[71].

4.3.   Measurement apparatus

Although the CTCF is needed and convenient for the elaboration of this model, since it has been experimentally proven to have a great influence on the allelic choice and be nucleotide sensitive, it is not essential for a random X inactivation subjected to quantum mechanical effects. According to Tegmark [72] and Zurek [73], a quantum system can be divided into three subsystems that interact with each other: subject S, detector or measuring apparatus D, and environment E. As proposed, when the C-C* base pair (S) and CTCF (D) interact, the wavefunction collapses projecting a protonated or non-protonated cytosine. Nevertheless, this is not the only course in which a quantum superposition can collapse. The coherence of the H proton superposition could leak out into the environment when the C-C* (S) interacts with the cell environment (E), forcing the stem to yield a classical result, i.e., protonated or non-protonated [73]. That is to say that in the event that CTCF does not bind to XIST immediately after the separation of the physical pairing, as assumed in this work, the quantum mechanical effects described in this model could still occur where the CTCF only acts as a classical molecule engaging with a previously-decohere system.

4.4.   Quantum system

It is deemed necessary to clarify that by explaining how the delocalized H proton shared by the C-C* pair allows the X inactivation mechanism to be described as an entangled state, this paper does not intend to imply that the entire chromosome can be found in a quantum state, a proposal already made by Ogryzko [74], and further developed by Bordonaro & Ogryzko [75], in which the whole cell should be considered to be subject to quantum effects. This is an argument that may well be made taking into account the data found by Mlynarczyk-Evans et al. [14], where the X chromosomes coordinately switch between active and inactive, allowing to describe both Xs to be found in a superposition state until the collapse of the wavefunction yields a definite inactivation. This view, however, goes beyond the scope of the present work. For this model, the approach utilized by Khalili & Mcfadden [76] is used, where “the coupling between fundamental particles and the environment of living cells enables their macroscopic behavior to be determined by quantum rather than classical laws”.

5.   Discussion

5.1.   Contributions to XCI knowledge

One of the main arguments that can be made against this theoretical model is the fact that several conditions need to be fulfilled, which have not always been comprehensively proven and in some cases not even directly investigated. Nonetheless, what this approach successfully demonstrates is how a shared delocalized proton at a key base pair position, can explain a random, instantaneous, and mutually exclusive choice process. This may well occur at a different pair-base, position, or gene to those employed here, as long as the X-X physical pairing occurs. Despite the conflicting arguments that may exist within X inactivation models, including this one, this paper considers, as Patrat et al. [23], that the combination of models is required to progress in the understanding of this phenomenon.

This theoretical approach may be, justifiably, considered reductionist or oversimplified from a strictly biochemical standpoint, since it has been proven that many biological components are responsible for the XCI. Nevertheless, what is intended in this work is to lay aside all of these fundamental biochemical components and their influence in the system, to demonstrate how a very specific and transcendental step of the choice process may be subject to quantum mechanical effects.

Several assumptions proposed here are worth investigating, not only to authenticate this theoretical model but also because of their valuable contributions to a more extensive insight into XCI. Particularly, the potential XIST-XIST pairing occurring prior to human X inactivation, the prospective non-canonical base pairs occurring during X chromosomes crosstalking, such as i-motif, the influence of these non-canonical forms in gene regulators, namely CTCF, and the time CTCF takes to bind to XIST after the Xs pairing.

5.2.   Implications for quantum biology knowledge

The main contributions to the current knowledge of quantum biology in this work are: 1) the potential involvement and relevance of interchromosomal proton tunneling in non-canonical pair bases prior to gene expression, and 2) the introduction of the possibility of transcription factors, such as CTCF, behaving as measurement quantum devices in gene expression. Consequently, this quantum mechanical approach could be applied to other cell differentiation mechanisms where trans-chromosomal pairing occurs.

If quantum mechanics do play such an influential role in a fundamental process of gene expression as presented here, this would contribute to an idea suggested by McFadden [77] in which the quantum world is not only a constituent of our reality but also the cause of it by assisting biological systems to solve evolutionary challenges (e.g.: energy efficiency in enzyme and photosynthesis reactions [18],[19], adaptive mutations [76] and several others currently being investigated [78]–[80]). As a last remark, it is important to note that stochastic effects are found throughout our physical reality without requiring help from the quantum world. Only further research will determine if the randomness found in certain biological systems is related to the probabilistic nature laying at the heart of quantum mechanics.

6.   Conclusions

Biological, chemical, and physical assumptions proposed in this model have yet to be confirmed. However, what this model demonstrates is that when an essential step of the X chromosome inactivation is described as a quantum driven system (i.e., H proton quantum tunneling during interchromosomal pairing), it is possible to reach a more comprehensive explanation of the random, instantaneous, and mutually exclusive XCI choice process. Thus, the relevance of investigating this possibility further.