On a new flexible Lomax distribution: statistical properties and estimation procedures with applications to engineering and medical data

1.   Introduction

The Lomax distribution was introduced to model business data by Lomax ^[1]. It has many applications in various fields such as income, wealth inequality, engineering, medical and biological sciences, lifetime and survival analysis. The Lomax distribution characterization can be defined in a variety of ways. It is a special case of the Pearson type VI distribution, as well as a combination of the exponential and gamma distributions. However, the Lomax distribution does not give a suitable modelling for data with non-monotone failure rates, such as the upside-down bathtub or bathtub then upside down failure rates, which are common in survival and biological studies. The need for extended forms of the Lomax model arises in many applied areas. The probability density function (PDF) for the Lomax distribution with shape parameter $\sigma$ and scale parameter $\tau$, is given by

and the corresponding cumulative distribution function (CDF) is

The Lomax distribution is also known in the literature as the Pareto distribution of second kind. It has many applications in actuarial, biological studies, finance and insurance. It is also able to model the survival times of patients after a heart transplant (see Bain and Engelhardt ^[2]). Although the Lomax distribution has a wide range of applications, it cannot cover bathtub upside down failure formed data. Many authors suggested new forms of the standard Lomax distribution by adding shape parameter(s) to get more flexibility in the PDF and the hazard rate function to overcome this lack of flexibility. Among these studies, Marshall-Olkin extended Lomax distribution proposed by Ghitany et al. ^[3], exponentiated Lomax distribution introduced by Abdul-Moniem and Abdel-Hameed ^[4], beta Lomax distribution by Lemonte and Cordeiro ^[5]. Also, Cordeiro et al. ^[6] introduced gamma Lomax distribution, Tahir et al. ^[7] proposed Weibull Lomax distribution, Al-Zahrani ^[8] also proposed extended Poisson-Lomax distribution and transformed Lomax by Nassar et al. ^[9].

In this study, a new three parameter Lomax distribution which called logarithmic transformed Lomax (LTLo) distribution is introduced by adding a new shape parameter to the CDF in (1.2) based on the method proposed by Pappas et al. ^[10]. Pappas et al. ^[10] introduced a method for generating distributions by adding an extra shape parameter to provide a more flexibility to existing distributions. The proposed method is called Logarithmic Transformed (LT) method. The CDF and the corresponding PDF of the LT method are, respectively, given by

and

where $\bar{G}(x) = 1-G(x)$ and $G(x)$ is the CDF of the baseline distribution. Many authors have used this approach to create new distributions by taking $G(x)$ of any known distribution and applying the method. Al-Zahrani et al. ^[11] proposed a new extension of Weibull extension model and studied its properties. Dey et al. ^[12] studied some properties of this generator and obtained an expansion to the CDF and PDF in (1.3) and (1.4), respectively. They also introduced a generalization for generalized exponential distributions. Eltehiwy ^[13] introduced a logarithmic inverse Lindley distribution by taking the $G(x)$ in (1.3) of the inverse Lindley distribution. We are motivated to propose the LTLo distribution because

1. It contains the Lomax distribution as a sub model.

2. It is suitable for modelling skewed data which may not be properly modelled by other competitive models.

3. It can model monotonically decreasing, upside down and bathtub then upside down hazard rates.

4. As presented in Section 2 that the LTLo distribution can be displayed as a mixture of the Lomax distribution.

5. The analysis of two real data sets show its superiority over other competing distributions namely, Kumaraswamy Lomax (KL), exponentiated Lomax (EL), beta Lomax (BL), gamma-Lomax (GL).

Another motivation to this paper is to see how different classical estimators of the LTLo distribution perform by considering various parameter values and different sample sizes and to draw a guideline for choosing the best estimation method in this case, which may be of deep interest to applied statisticians.

The rest of this article is organized as follows: The LTLo distribution is introduced in Section 2 as well as the expansion of its PDF and CDF. Some statistical properties are derived in Section 3. In Section 4, four methods of estimation are used to estimate the unknown parameters of the LTLo distribution. A simulation study is considered in Section 5 and in Section 6, two real data sets are analyzed. Finally, the paper is concluded in Section 7.

2.   Model description

Let $X$ be a random variable follows the Lomax distribution with PDF and CDF, respectively, given by (1.1) and (1.2), then the PDF of the LTLo distribution can be obtained from (1.4) as

and the corresponding CDF is

The survival and hazard rate functions of the LTLo distribution are, respectively, given by

and

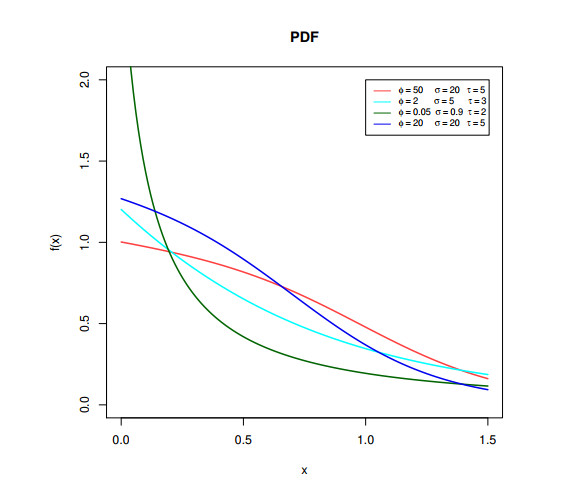
Figure 1 depicts the different shapes of the PDF of the LTLo distribution given by (2.1) by considering different values to the scale and the shape parameters. The new distribution is able to model the right skewed data, as can be seen in Figure 1. Figure 2 also depicts the various shapes of its hazard rate function for various parameter values using $\tau = 1$. Figure 2 shows that the hazard rate function of the LTLo distribution can be decreasing, upside down, and bathtub then upside down shaped.

Now, an useful representation for the LTLo distribution can be obtained. Using the series representation in the form

Applying (2.5) for the PDF in (2.1) gives

where $g(x; (k+1)\sigma, \tau, \phi)$ denotes the PDF of the Lomax distribution with shape parameter $(k+1)\sigma$ and scale parameter $\tau$ and

Different structural properties of the LTLo distribution can be determined using this representation. By integrating (1.1), the CDF of $X$ is given by

where $G(x)$ is the CDF of the Lomax distribution with scale parameter $\tau$ and shape parameter $(k+1)\sigma$.

3.   Properties of the LTLo generator

In this section, some properties of the LTLo distribution are derived, specially quantile function, moments, incomplete moments, conditional moment, entropies and stress-strength.

3.1.   Quantile function and median inactivity time

For the LTLo distribution, the quantile function denoted by $x = Q_{LTLo}(q)$ can be obtained by inverting (2.1) as follows

One can generate $X$ by taking $q$ as a uniform random variable in $(0, 1)$. The skewness and kurtosis measures can be obtained from (3.1) using a well-known relations.

3.2.   Moments

The noncentral moment of the LTLo distribution can be obtained as

where $B(., .)$ is the beta function. It is to be noted that the $r^{th}$ moment of $X$ exists iff $\sigma > r$. In particular the first noncentral moment is the expected value $E(X)$. Also, the variance of the distribution can be obtained as $var(X) = E(X^2)-[E(X)]^2$, where $E(X^2)$ is the second noncentral moments. Based on the first four noncentral moments the skewness and kurtosis can be obtained using the following relations

The following propositions are a description of three different types from moments such as incomplete moments, moment generating function (mgf) and conditional moment.

Prop 1. If $X$ $\sim$ LTLo$(\phi, \sigma, \tau)$, then the incomplete moments of $X$ is given by

where $F_{2:1}\left(.; .;.; .\right)$ is the Gauss hypergeometric function (see Gradshteyn and Ryzhik [14,Formula 9.10]).

The first incomplete moment, $I _{1}(t)$, follows from (3.2) with $n = 1$. The main applications of $I _{1}(t)$ are the Bonferroni and Lorenz curves and the mean deviation.

Prop 2. If $X$ $\sim$ LTLo, then the mgf of $X$ is given by

Prop 3. If $X$ $\sim$ LTLo$(\phi, \sigma, \tau)$, then the conditional moment of $X$ is given by

where

The mean, variance, skewness and kurtosis of the LTLo distribution can be calculated using the expression of the noncentral moments. Figure 3 presents these values for various values of the parameters $\phi$ and $\sigma$ and by considering the scale parameter $\tau$ to be one in all the cases. Figure 3 shows that the skewness of the LTLo distribution is always positive. It can be also noted that the mean, variance, skewness and kurtosis are non-monotonic as the parameters ranging from small to large.

3.3.   Entropy

Entropy is one of the most popular technique that used to measure the uncertainty associated with a random variable and it was originally used in physics. Measuring of entropy is very important role in many areas such as statistics, chemical and biological phenomenon. More entropy is referred to less information that found in a sample. The entropy of a random variable $X$ with density function $f(x)$ is a measure of its uncertainty. The R$\acute{e}$nyi entropy (RE) introduced by R$\acute{e}$nyi ^[15] is defined as

For the LTLo distribution with PDF given by (2.1), the RE can be written as

3.4.   Order statistics

Order statistics have a wide range of uses in statistics, including quality control monitoring, non parametric statistics and reliability. Let $X_1, \ldots, X_n$ be a random sample of size $n$ drawn from a continuous population then the PDF of the the $s^{th}$ order statistic is defined by

where $B(., .)$ is the beta function. Using (2.1) and (2.2), one can obtain

Substituting (3.5) in Eq (3.4), the PDF of $X_{(s)}$ for the LTLo distribution reduces to

The $k-th$ moment of $X_{(s)}$ can be obtained as

A numerical integration technique can be used to obtain (3.6). Let $k = 1$ and by setting $s = 1$ and $n$, one can obtain the expected values of the first and last order statistics, respectively.

3.5.   Probability weighted moments

The $(u, v)^{th}$ probability weighted moments of $X$ following the LTLo distribution is defined by

Based on Eq (3.7), one can obtain

where

3.6.   Residual life and reversed residual life

The $n^{th}$ moment of the residual life can be calculated using a general formula (see Navarro et al. ^[16]).

Based on Eq (2.1) and applying the binomial expansion of $(x-t)^n$, one can obtain

The $n^{th}$ moment of the reversed residual life via the general formula

Based on Eq (2.1) and applying the binomial expansion of $(t-x)^n$, one can obtain

3.7.   Reversed failure rate and mean past life time

Let $T\geq 0$ be a continuous random variable with CDF $F(t)$ and PDF $f(t)$, then the reversed failure rate (RFR) is defined as

For the LTLo distribution, the RFR, say $r(t)$, is obtained as

The first moment of the mean past life time can be obtained via the general formula

For the LTLo distribution, the mean past life time, $S(t)$, is obtained as

The strong mean past life time lies in the framework of the RFR function. It has many reliability properties that provide some applications in survival analysis and reliability. The strong mean past life time can be obtained via the general formula

For the LTLo distribution, the strong mean past life time is derived as

3.8.   Stress-strength

The stress-strength is the measure of the system efficiency which arises quite naturally in the mechanical reliability of a system. Practically, the system fails if and only if the used stress is more than its strength at any time. The concept of the stress-strength has gotten impressive consideration and commonly utilized in numerous engineering applications. Let $Z_1$ and $Z_2$ be two independent random variables with LTLo distributions, respectively. If $Z_1$ represents "stress" and $Z_2$ represents "strength, " then the stress-strength is given by

Using series expansion $\log(\frac{1}{1-y}) = \sum_{k = 1}^{\infty}\frac{y^k}{k}$, $-1\leq y < 1$ in the last equation, one can obtain

Using binomial series expansion in the last equation, one can obtain

4.   Estimation methods

In this section, four estimation methods are considered to estimates the unknown parameters, $\phi, \sigma$ and $\tau$, of the the LTLo distribution.

4.1.   Maximum likelihood estimation

To obtain the maximum likelihood estimates (MLEs), the log-likelihood function of the observations $x_1, \cdots, x_r$ of a random sample of size $r$ from the PDF in (2.1) can be written as follows

For the unknown parameters $\phi, \sigma$ and $\tau$, the MLEs can be obtained by solving the following normal euations

and

To obtain the MLEs of $\phi, \sigma$ and $\tau$, any numerical technique can be implemented for this purpose.

4.2.   Least and weighted least-squares estimation

Let $r$ denotes to the sample size and $X_{(1)} < X_{(2)} < \cdots < X_{(r)}$ be the order statistics from the LTLo distribution, the least square estimators (LSEs) of the unknown parameters $\phi, \sigma$ and $\tau$ can be obtained by minimizing the following function

with respect to unknown parameters $\phi, \sigma$ and $\tau$, where $v_{j} = \frac{j}{n+1}$ or by solving

and

where

and

Similarly, one can obtain the weighted least square estimators (WLSEs) of the unknown parameters $\phi, \sigma$ and $b$, by minimizing

with respect to $\phi, \sigma$ and $\tau$, where $c_{j} = \frac{(r+1)^2(r+2)}{j(n-j+1)}$ or by solving the following three nonlinear equations

and

where $\psi_{1j}, \psi_{2j}$ and $\psi_{3j}$ are given by (4.2)–(4.4).

4.3.   Maximum product of spacings estimation

Let $\Lambda_{i}(\phi, a, \tau)$ be the uniform spacings of a random sample obtained from the LTLo distribution which can be written as

Thus, the maximum product of spacing (MPS) estimators of $\phi, \sigma$ and $\tau$ can be obtained by maximizing the following function

with respect to $\phi, \sigma$ and $\tau$. Another way to obtain these estimates is to solve the following three nonlinear equations

and

where $\psi_{1j}, \psi_{2j}$ and $\psi_{3j}$ are given by (4.2)–(4.4).

5.   Simulation study

In this part, a simulation study is performed to evaluate which estimation method provides the most efficient estimates based on the minimal mean square error criterion, while taking into consideration various parameter values and sample sizes. The selected sample sizes are 20, 50,100,150,200 and 250, and the parameter values are $(\phi, \sigma, \tau) = (2, 2, 2), (1.5, 0.5, 0.8)$ and $(2.5, 1.5, 1)$. For each environment, the procedure is repeated 1000 times, and average estimates and average mean square errors (MSEs) are calculated. It is to be mentioned here that the different estimates are obtained using the quasi-Newton method and all computations in this section and the next section are implemented using MATHCAD program Ver.15. Also, all figures in this paper are developed using R programming language. Tables 1–3 summarize these values. From these tables it is observed that the various estimation methods give asymptotically unbiased estimates, meaning that as the sample size grows, the estimates appear to match the true parameter values. It should also be noted that as the sample size grows, the MSEs for all of the estimates decrease. Furthermore, the simulation results show that in the majority of circumstances, the LSEs have the smallest MSEs.

6.   Real data analysis

Here, we provide an application to two real data sets to show the importance of our new distribution. The first data set (data set I) presents the service times of 63 Aircraft Windshield and measured in 1000 h. These data were considered by Murthy et al. ^[17]. The second data set (data set II) reported by Bekker et al. ^[18], which refers to the survival times (in years) of a group of patients given chemotherapy medication alone. The data set includes the survival times (in years) for 46 patients. The LTLo distribution is fitted to these data using the maximum likelihood method and compare its results with some competitive models namely, KL, EL, BL, GL and Lomax (L) distributions. These distributions have the following PDFs (for $x > 0$):

and

The estimates and the corresponding standard error of estimates of these models are presented in Table 4 for data set I and in Table 5 for data set II. The Kolmogorov-Smirnov (K-S) statistic and its p-value are used to compare the various models with the LTLo model. Tables 4 and 5 also show these statistics for data set I and data set II, respectively. Moreover, the goodness of fit statistics, Akaike information criterion (AIC), consistent Akaike information criterion (CAIC), Bayesian information criterion (BIC), Hannan-Quinn information criterion (HQIC), Anderson-Darling ($A^{*}$) and Cramer-von Mises ($W^{*}$) are also computed and displayed in Table 6 for the two real data sets. Based on these findings, one can conclude that the LTLo distribution perform better than the other competing models, and therefore it should be chosen as the best one. Also, the Q-Q plots for the two data sets are presented in Figure 4 which indicate that the LTLo distribution is a good model to fit these data. The plots of the histogram and the fitted PDF of the LTLo distribution are displayed in Figures 5(a) and 6(a) for data set I and data set II, respectively. On the other hand, the plots of the fitted and the empirical survival functions are displayed in Figures 5(b) and 6(b) for data set I and data set II, respectively. Overall, one can deduce that the LTLo distribution is an acceptable model to fit these data sets. Figure 7 displays the log-likelihood functions of $\phi, \sigma$ and $\tau$ for the two data sets, which indicate that the MLEs are unique. Since the L distribution can be obtained as a special case of the LTLo distribution. Therefore, the likelihood ratio test (LRT) can be considered to test the null hypothesis that the parameter $\phi$ tends to one. The results of the LRT are presented in Table 7 for the two data sets. The results of the LRT show that the LTLo distribution is more appropriate for the given data sets than the traditional L distribution.

The different estimation methods are used to calculate the estimates the LTLo model parameters for the two data sets. These estimates are obtained and presented in Tables 8 and 9 for the data set I and data set II, respectively. The K-S and its p-value are obtained for each method to show which method provides a good fit. The results in Tables 8 and 9 show that the LSEs has the smallest K-S distance with highest p-value. So, it is recommended to use the least square method to estimate the parameters of the LTLo distribution from the two real data sets. Now, the estimates displayed in Table 8 and the moments of the first and last order statistics can be used to estimate the minimum and the maximum of the service times of Aircraft Windshield in 1000 h on average for different sample sizes. These estimates are displayed in Figure 8 for data set I based on the different estimation methods. From Figure 8 and using the least square method one can expect that the minimum service time of Aircraft Windshield is 0.024 1000 h based on a sample of size 160 Aircraft Windshield. Similarly, it is expected to have 6.122 1000 h as a maximum service time of Aircraft Windshield. From data set II and using the same approach, the different estimates of the minimum and the maximum survival times (in years) are displayed in Figure 9 based on different sample sizes. Based on the least square method one can observe from Figure 9 that the expected minimum survival time is 0.0072 year based on a sample of 160 patients, while the expected maximum survival time is 7.109 year.

7.   Conclusions

In this paper, a new extension of Lomax distribution which called logarithmic transformed Lomax distribution has been introduced. The proposed distribution contains one scale and two shape parameters. Its hazard rate function can be decreasing, upside down and bathtub then upside down shaped. The various hazard rate shapes candidate the distribution to use quite effectively in analyzing many life applications. The new statistical properties of the proposed distribution are discussed. Also, the unknown parameters of the proposed distribution are estimated using four different estimation methods. In terms of minimum mean square errors, the performance of the various estimators is compared using a simulation study. The least square estimates outperformed the other suggested approaches in a simulation analysis. Finally, two real data sets for service times of Aircraft Windshield and survival times of a group of patients given chemotherapy medication are examined to demonstrate its usefulness and superiority over some well-known distributions with three or more parameters. Finally, The proposed distribution is used to estimate the minimum and maximum values for the service times of Aircraft Windshield and the survival times of patients given chemotherapy medication. As a future work, one can estimate the entropy, stress-strength, Bonferroni and Lorenz curves of the logarithmic transformed Lomax distribution using complete or censored data.

Acknowledgments

The authors would like to express their thanks to the editor and anonymous referees for useful suggestions and valuable comments. This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-track Research Funding Program.

Conflict of interest

The authors declare there is no conflict of interest in this paper.