Adapted block hybrid method for the numerical solution of Duffing equations and related problems

1.   Introduction

The integration of second-order initial value problems (IVPs) with periodic or oscillatory solutions has attracted the attention of numerical researchers in recent times. Second-order IVPs of the type

whose solutions are periodic in nature and the suitable frequency, $\varsigma$, is roughly known in advance, with $\psi :R \times R^{ 2n} \longrightarrow R^{n}$ a sufficiently differentiable function satisfying the conditions of existence and uniqueness of solution (Wend ^[47,48]), are regularly encountered in sciences and engineering, a list of which is provided in Abdulganiy et al. ^[28] and Jator et al. ^[31].

A special case of the ODEs in Eq (1.1) is the generalized non-linear Duffing oscillator given by

where $\delta, \varphi \in R$ are real constants and $\Gamma \left(t \right)$ is a periodic function, usually a sinusoidal function or its combinations. Most phenomena in our world are described by non-linear equations. Consequently, this makes the study of non-linear oscillators in physics, engineering and other physical sciences of great importance (Liu and Jhao ^[49], and Li et al. ^[62]). Non-linear oscillatory problems are essential tools in physical sciences and other engineering disciplines, and in particular, non-linear differential equations with oscillatory solutions are related to many practical problems such as non-linear stiffness, snap-through mechanism, the pendulum problem, non-linear electric circuit among others (Kovacic and Brennan ^[52], and Razzak ^[30]).

Many interesting methods have appeared in literature for the integration of the general initial-value problems (1.1) and also for the particular Eq (1.2). Some of these methods are based on series solution (Schovanec and White ^[33], and Liu and Jhao ^[49]), variational iteration (Ozis and Yildirim ^[56]), perturbation methods or semi analytic approaches (He ^[43], Belendez et al. ^[38], and Younesian et al. ^[58]), modified differential transformed methods (Nourazar and Mirzabeigy ^[34]), explicit and exact solutions (Marinca and Herisan ^[60], and Gholam-Ali and Emmanuel ^[61]) { and the analytical prediction of the periodic motions of a periodically forced, damped, duffing oscillator through the discrete implicit mappings (Guo and Luo ^[63], and Luo ^[64])}.

From a numerical perspective, some methods have been considered for the integration of Eqs (1.1) and (1.2) either directly or after transforming each of them into a corresponding system of first-order ODEs of the following structure

where $f\mathrm{:}\mathbb{R}\times {\mathbb{R}}^\theta \rightarrow {\mathbb{R}}^\theta$ is a smooth function that satisfies the Lipchitz condition, and $\theta$ is the dimension of the system. Among such methods we find ones with constant coefficients (Lambert ^[41], Jator and Oladejo ^[1], Sunday et al. ^[3], Enright ^[4], Hairer et al. ^[5], Lambert and Watson ^[6], and Jator ^[7]), adapted methods, viz, exponentially fitted methods (Vanden Berghe et al. ^[21], Franco ^[8,9,16,17], Ixaru et al. ^[20], Martín-Vaquero and Vigo-Aguiar ^[22], You and Chen ^[24], Li et al. ^[51], Konguetsof and Simos ^[26], Tsitouras ^[57], and Fang et al. ^[18,19]), and trigonometrically fitted methods (Gautschi ^[10], Neta and Ford ^[11], Neta ^[12], Vigo-Aguiar and Ramos ^[36], Jator et al. ^{[23,27,29,31,35,40]}, Ramos and Vigo-Aguiar ^[32], Monovasilis et al. ^[2], Abdulganiy et al. ^{[28,37,46,53,54,55]}, Senu et al. ^[50], and Samat and Ismail ^[59]).

Most of the numerical methods mentioned are applied in stepwise form that turns out to be incapable of achieving highly accurate results due to the oscillatory features of the solutions.

It is against this background that we propose an adapted block hybrid method (ABHM) with trigonometric coefficients to integrate exactly the IVP in Eq (1.3) when the solutions are in the linear space generated by $\left\lbrace 1, t, t^{2}, t^{3}, \sin \left(\varsigma t \right), \cos \left(\varsigma t \right)\right\rbrace$. This set of basis functions is considered for its ease to be analyzed (Ngwane and Jator ^[23]) and the provision of an improved extension for solving IVPs with periodic results (Coleman and Duxbury ^[15]). Other probable basis functions are enumerated in Nguyen et al. ^[39]. The remaining part of this article is organised as follows: The construction of the proposed ABHM is presented in Section 2. The essential features of the method are illustrated in Section 3, whereas the implementation and some numerical experiments are exemplified in Section 4 to demonstrate the efficiency of the new method. Finally, some concluding comments are provided in Section 5.

2.   Preliminaries

2.1.   Construction of ABHM

In order to integrate the IVP in (1.3) numerically, we proceed by considering that we have a scalar equation and assuming that the exact solution $y \left(t \right)$ can be approximated by a fitted function $I \left(t, u \right)$ which incorporates a parameter $u$. A continuous adapted block hybrid method (CABHM) on the interval $\left[t_{n}, t_{n+2} \right]$ is developed to produce a discrete formula. Three secondary formulas as a by-product via the CABHM are produced too, to form the ABHM. The CABHM has the general form.

where $t_{n+\kappa} = t_n+\kappa h, y_{n+\kappa}\simeq y(t_{n+\kappa}), f_{n+\kappa} = f(t_{n+\kappa}, y_{n+\kappa}), \kappa = 0, v, 1, \mu, 2$, $u = \varsigma h$, and $\varsigma$ is the fitting frequency, $\{v, \mu \} = \{\frac{1}{2}, \frac{3}{2}\}$ are off node points, and $\delta_{0}$, $\delta_{v}$, $\delta_{1}$, $\delta_{\mu }$, $\delta_{2}$ are parameters to be found from the multistep collocation technique, that depend on the parameter frequency, $\varsigma$, and the step length $h = t_{n+1}-t_{n}$.

The exact solution $y \left(t \right)$ is assumed to be approximated by a fitted function defined by

In view of this approximation, we impose that the following system of six equations be satisfied

The theorem that aids the development of the continuous method is stated as follows:

Theorem 1. Let $I \left(t, u \right)$ be the fitting function associated to the set $P_{i} (t) = \{ \mathit{\rm{1, t, }}t^{2}, \; t^{3}, \sin (\varsigma t), \cos (\varsigma t) \}$ and the vector $K = (y_{n}, f_{n}, \; f_{n+v}, \; f_{n+1}, \; f_{n+ \mu }, f_{n+2}) ^{T}$, where $T$ denotes the transpose. Consider the following $6 \times 6$ matrix coefficient of the system in (2.3)

and $W_{i}$ obtained after substituting the $i$-{th} column of W with the vector $K$. If we impose that $I (t, u)$ agrees with the system of six equations in (2.3) then the continuous approximation from which the ABHM will be generated can be written as

Proof. We necessitate that the Eq (2.1) be characterized by the expected fitted function as follows

Substituting Eqs (2.5) and (2.6) into Eq (2.1) yield

We let

so that Eq (2.7) becomes

If we impose the conditions in Eq (2.3) on Eq (2.8), we obtain a system of six equations which is expressed as $W \Lambda = K$, where $\Lambda = \left(\Lambda _{0}, \Lambda _{1}, \Lambda _{2}, \Lambda _{3}, \Lambda _{4}, \Lambda _{5} \right) ^{T}$ is a vector form of six undetermined coefficients that can be obtained by Crammer's rule as follows:

$W_{i}$ is found by substituting the $i$-th column of W by $\Lambda$. Equation (2.8) through the substitution of Eq (2.9) becomes

Remark 1. We emphasize that the equation in (2.10) provides a continuous approximation of the true solution, and has the form of Eq (2.1).

2.2.   Specific of ABHM

We evaluate the equation in (2.1) at $t = t_{n+v}$, $t = t_{n+1}$, $t = t_{n+\mu}$, and $t = t_{n+2}$, respectively, to obtain our proposed method, ABHM, which constitutes three secondary formulas given as

and one primary formula which results in

The coefficients of these formulas are provided in Eqs (2.13)–(2.16) as follows:

Remark 2. It is emphasized that when $u\to 0$, the coefficients of the ABHM may suffer substantial cancellations affecting the calculations. In this situation, the expansion of the coefficients in Taylor's series is usually considered (Lambert ^[41]). The expansion of the coefficients of ABHM in series form up to order $O \left(u^{10} \right)$ are as provided below

Remark 3. According to Lambert ^[41], taking limit when $u\to 0$ in the coefficients in (2.17)–(2.20), a Simpson block hybrid method based on polynomial basis is recovered.

3.   Basic properties of the ABHM

This section discuses the basic properties of the ABHM which include the local truncation error (LTE) and its consequences, zero-stability, convergence and linear stability.

3.1.   Local truncation error of the ABHM and its consequences

In this subsection, the theory of linear operator (Lambert ^[41]) is employed to establish the local truncation errors of the ABHM.

Proposition 1. The local truncation error of each of the 3 secondary formulas for the ABHM is $C_{6}h^{6}(\varsigma ^2 y^{4}(t_n)-y^{(6)}(t_n))+O (h^{7})$, while that of the primary formula has the form $C_{7}h^{7}(\varsigma ^2 y^{5}(t_n)-y^{(7)}(t_n))+O (h^{8})$

Proof. Associate the secondary formulas with linear difference operators ${\mathcal{L}}_{v}\left[y\left(t_n\right); h\right]$, ${\mathcal{L}}_{1}\left[y\left(t_n\right); h\right]$, ${\mathcal{L}}_{\mu}\left[y\left(t_n\right); h\right]$ and the primary formula with the linear difference operator ${\mathcal{L}}\left[y\left(t_n\right); h\right]$ defined respectively by

With the aid of Taylor series, we expand the right hand side of each of the formulas in Eq (3.1) in power of $h$, with the assumption that $y\left(t\right)$ is a sufficiently differentiable function. It is obvious that the first non zero term of each formula in (3.1) is $C_{p+1}$, where $C_{p+1}$ is equivalently written as $C_{6}h^{6}(\varsigma ^2 y^{4}(t_n)+y^{(6)}(t_n))+O (h^{7})$ and $C_{7}h^{7}(\varsigma ^2 y^{5}(t_n)+y^{(7)}(t_n))+O (h^{8})$ for the secondary and primary formulas of ABHM respectively, and $C_{6}$ and $C_{7}$ are their respective error constants.

Corollary 1. The Local truncation errors of the formulas in the ABHM are respectively given by

Consequently, the order p of the ABHM is at least ${\it p} = 5$.

Remark 4. We observe that the local truncation error of ABHM preserves its basis function. This statement follows from the result of the differential equation $y^{(6)}\left(t\right)+{\varsigma }^2y^{(4)}\left(t\right) = 0$ which is a linear combination of the fitted function of ABHM.

Remark 5. Following the definition given by Lambert ^[41], a numerical method is consistent if its order $p > 1$. Since the order of each of the formula of ABHM is greater than 1, then it is consistent.

3.2.   Analysis of convergence of the ABHM

The analysis of convergence of the ABHM is done following the guidelines by Abdulganiy et al. ^[28,46].

Theorem 2. Let $\overline{Y}$ be a vectorial approximation of the true solution vector Y for the system obtained from ABHM given by Eqs (2.11) and (2.12) on the successive block intervals $[t_0, t_2]$, $[t_2, t_4], \cdots, [t_{N-2}, t_N]$, with $N$ even. If $E = (e_1, e_2, \cdots, e_N)^T$ denotes the error vector, where $e_j = y\left(t_j\right)-y_j$, assuming the solution in closed form is several times differentiable on $\left[t_{0}, t_{N} \right]$ and if $\Vert E \Vert = \Vert \overline{Y}-Y \Vert$, then for appropriately small $h$, the ABHM is a convergent method of order five, specifically, $\Vert E \Vert = O \left(h^{5} \right)$.

Proof. Suppose the $N\times N$-matrices of coefficients of the ABHM method are defined as follows:

and the $N$-vector containing the known values given by

We consider the vectors of exact values $Y = (y(t_{v}), y(t_{1}), y(t_{\mu}), \cdots, y(t_N))^{T}$ and $F = (f(t_v, y(t_v)), f(t_1, y(t_1)), f(t_\mu, y(t_\mu)), \cdots, f(t_N, y(t_N)))^{T}$, the vectors of the approximate values $\overline{\mathrm{Y}} = (y_{v}, y_{1}, y_{\mu}, \cdots, y_N)^{T}$ and $\bar{F} = (f_{v}, f_{1}, f_{\mu}, \cdots, f_N)^{T}$, and the vectors of the local truncation errors $L(h) = (L_{v}, L_{1}, L_{\mu}, \cdots, L_N)^{T}$.

The exact form of the system formed by the formulas in Eqs (2.11) and (2.12) along the two-step blocks on the integration intervals is

On the other hand, the system that provides the approximate values may be written as

Subtracting Eq (3.3) from Eq (3.4) we obtain

and having in mind that $E = \ \bar{Y}-Y = (e _{v}, e _{1}, e _{v}, \cdots, e _N)^{T}$, the above equation becomes

We apply the Mean-Value Theorem to obtain $\bar{F}-F = J E$, where $J$ is the Jacobian matrix

and the partial derivatives are applied at intermediate points $\left\{\xi_i\right\}_{i = 1}^N$, which are on each corresponding line joining $\left(x_i, y(x_i)\right)$ to $\left(x_i, y_i\right)$. In view of this, the equation in (3.6) can be written as

Let $\Upsilon$ denotes the matrix $\Upsilon = -\Delta J$. Then we have that

For adequately small $h$, the matrix $\Pi+\Upsilon$ is invertible (see ^[28]). Therefore, if we denote by

and consider the maximum norm, we can obtain after expanding in Taylor series the terms in $\Omega$ that $\|\Omega\| = O(h^{-1})$. Finally, we have that

Therefore, the ABHM is a convergent method of fifth-order.

3.3.   Stability of ABHM

Following Fatunla ^[45], the ABHM can be characterized in the following block matrix form

where $Y_{W+1} = {\left(y_{n+v}, y_{n+1}, y_{n+\mu}, y_{n+2}\right)}^T,$ $Y_{W } = {\left(y_{n-\mu}, y_{n-1}, y_{n-v}, y_n\right)}^T,$ $F_{W+1} = {\left(f_{n+v}, f_{n+1}, f_{n+\mu}, f_{n+2}\right)}^T,$ $F_{W} = {\left(f_{n-\mu}, f_{n-1}, f_{n-v}, f_n\right)}^T$, $I$ is the identity matrix of dimension four, $\otimes$ denotes the Kronecker product of matrices, and $A_{(0)}, A_{(1)}, B_{(0)}, and B_{(1)}$ are $4\times 4$ matrices obtained from the coefficients of the method, and given by

3.3.1.   Zero stability

Zero-stability is a type of stability that deals with the behaviour of a numerical scheme when $h\to 0$.

Definition 1 (Lambert ^[41] and Fatunla ^[42]). A numerical method is zero stable if the modulus of the roots of the first characteristic equation is less than or equal to one and those of modulus one is simple. i.e., $\rho \left(R \right) = \det \left[RA_{ \left(1 \right) }-A_{ \left(0 \right) } \right] = 0 \ and \ \vert R_{i} \vert \leq 1$.

Proposition 2. The ABHM is zero-stable.

Proof. As $h\to 0$ in Eq (3.9), we find out that

which gives the first characteristic equation after normalization as

and consequently, ABHM is zero-stable according to the previous definition.

3.3.2.   Linear stability of ABHM

Applying the ABHM specified by the formulas in (3.9) to the test equation $y' = \lambda y$ and letting $\eta = \lambda h$, yields

where

is called stability matrix which ensures the stability of the ABHM. The stability matrix $M(\eta, u)$ for ABHM has eigenvalues given by$\ \left({\chi }_1, {\chi }_2, {\chi }_3, {\chi }_4\right) = (0, 0, 0, {\chi }_4)$, where ${\chi }_4\left(\eta, u\right) = \frac{\sigma_4\left(\eta, u\right)}{\tau_4\left(\eta, u\right)}$ is the stability function, and $\sigma_4\left(\eta, u\right)$ and $\tau_4\left(\eta, u\right)$ are specified in the appendix.

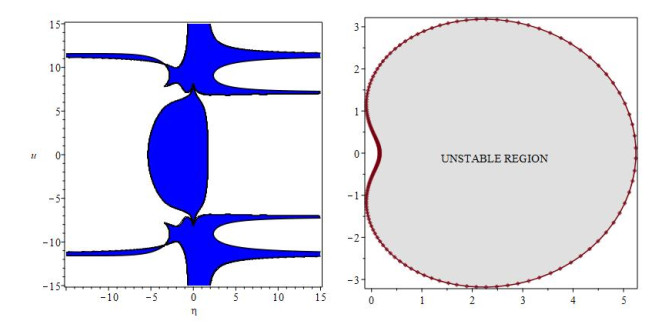
Remark 6. We emphasise that according to the following definitions, the stability function ${\chi }_4$ ensures the stability region of the ABHM.

Definition 2. (Coleman and Ixaru ^[25]). The region of stability of a numerical method for solving (1.3) is the region in the $(\eta, u)$-plane for which $\left|M\left(\eta, u\right)\right|\le 1$.

Definition 3. (Ndukum et al. ^[31]). An ABHM with the coefficients $A_{(0)}\left(u\right)$, $A_{(1)}\left(u\right)$, $B_{(0)}\left(u\right)$, $B_{(1)}(u)$ with the stability function $M\left(\eta, u\right)$ is said to be A-stable at $u = u_0$, if $\left|M \left(\eta, u_0\right)\right| < 1$, for all $\eta\in {\mathbb{C}}^-$.

Remark 7. $A$-stability of ABHM is a property similar to $A$-stability for the orthodox methods which is essential for a numerical integrator to do well on stiff problems.

The stability region of ABHM is plotted in the $\left(\eta, u\right)-$ plane as shown in Figure 1 (Left) whereas Figure 1 (Right) is the region $\left|M \left(z, u\right)\right| < 1$ at $u_0 = \frac{\pi}{9}$ in the complex plane through boundary locus method for which $\eta\in {\mathbb{C}}^-$.

4.   Numerical experiment

The effectiveness of ABHM is established in this section. Four well known Duffing equations in the literature are provided. A written algorithm in Maple 2016.1 is developed for ABHM. The values of the fitting parameters used in the numerical examples were taken from the referenced problems. However, the strategies for the frequency choice considered by ^[36] can be utilized.

In the numerical investigations, we plotted the graphs of the absolute errors obtained using the ABHM to show how the results of the ABHM and exact results agree with the errors. As a measure of accuracy, the graphs of the absolute errors obtained using the ABHM and the exact results are plotted on the same scale, whereas the computational efficiency is measured by the plots of the maximum errors of the results obtained using ABHM against the number of function evaluations (NFE) required by each integrator in comparison with the following listed methods.

ETFFSH5S: Five stage explicit trigonometrically-fitted method of order six in Li et al. ^[51]

ETFFSH6S: Six stage explicit trigonometrically-fitted of method order seven in Li et al. ^[51]

BHTM: Block Hybrid Trigonometrically-Fitted Method in Abdulganiy et al. ^[37]

BHT: Block Hybrid Trigonometrically-Fitted Method in Ngwane and Jator ^[23]

BTDF8: Eighth order block third derivative method in Jator et al. ^[40]

BTDF10: Tenth order block third derivative method in Jator et al. ^[40]

HLMM: A seventh order hybrid linear multistep method in Jator ^[7]

DIRKNNew: New Diagonally Implicit Runge-Kutta Nyström Method for Periodic IVPs in Senu et al. ^[50]

(TFARKN 5(3)): Trigonometrically-Fitted Runge-Kutta-Nyström method in of Fang et al. ^[19]

TFARKN: Trigonometrically-Fitted Adapted Runge-Kutta-Nyström method in Fang et al. ^[18]

EM8: An explicit eight order method in Tsitouras ^[57]

EFRKN: Exponentially Fitted Runge-Kutta-Nyström method in Franco ^[17]

ARK4: Fourth Order and Four stages adapted RK method in Franco ^[17]

ARK3/8: Fourth Order and Four stages adapted RK method in Franco ^[17]

EFRK: Exponentially Fitted Explicit Runge-Kutta Method in Franco ^[8]

IIIb: mixed collocation method of order 6 in Duxbury ^[14]

RK6: The Butcher's sixth-order method given in Hairer et al. ^[5]

MEHM6: The Modified sixth-order Explicit Hybrid Method with four stages derived in Samat and Ismail ^[59]

4.1.   Duffing equations

4.1.1.   Example 1

As our first numerical experiment, we consider the following Duffing equation in the interval [0,100]

whose result in closed form $y \left(t \right) = sn \left(\varsigma t; \frac{k}{ \varsigma } \right)$ represents a periodic motion in terms of the Jacobian elliptic function $sn$, where $\kappa = 0.03$ and $\varsigma = 5$ respectively. In order to compare errors of different methods, we use step lengths $h = \frac{1}{2^{i}}, i = 3, 4, 5, 6.$ The accuracy of the ABHM with respect to the exact solution is provided in Figure 2 (Left) while its efficiency is represented visually in Figure 2 (Middle). In Figure 2 (Right), we plotted the absolute error graph with $h = \frac{1}{32}$ to show the agreement between the exact and the approximate solutions which confirms the accuracy of ABHM with errors less than $10^{-10}$. We see clearly that the proposed method performs better.

4.1.2.   Example 2

In the second example, we consider the following undamped Duffing equation

where $\alpha$ is a forcing term given as $\alpha = 0.01$ in the interval $0\le t\le \frac{33\pi }{4}$, the analytical solution is given as $y \left(t \right) = \cos t$. For the numerical experiment, we select the step-sizes as $h = \frac{\pi}{2^{i}}, i = 1, 2, 3, 4, 5, 6$. The graph of absolute errors between the exact and the approximate solutions agrees with errors less than $10^{-22}$ with $h = \frac{\pi}{2^{6}}$ as shown in Figure 3 (Left). We present the accuracy of the ABHM with $\varsigma = 1$ for different point on the interval of integration in comparison with the exact solution in Figure (Middle) whereas the efficiency curve plotted in Figure 3 (Right) for different step sizes evidently shows that the ABHM outperformed some other numerical methods it compared in recent literature. Figure 4 shows the behaviour of the results of the ABHM in relation to the exact results for a large forcing term $\alpha = 2$. For this, we select $h = \frac{\pi}{2^{6}}$ which reveals same behaviour as $\alpha = 0.01$ with errors less than $10^{-22}$.

4.1.3.   Example 3

The following Undamped Duffing Equation is considered as our third experiment

with $\epsilon = 10^{-10}$ and whose solution in closed form is $y \left(t \right) = \epsilon \sin \left(10t \right) + \cos \left(t \right)$.

With step-size $h = \frac{1}{2^{2}}$, Figure 5 (Left) shows errors less than $10^{-14}$. While Figure 5 (Middle) with step-sizes selected as $h = \frac{1}{2^{i}}, i = 1, 2, 3, 4, 5, 6$ shows the performance of the proposed method with reference to the analytic solution, the plot in Figure 5 (Right) illustrates the superiority of the ABHM over some of the methods it compared.

4.1.4.   Example 4

We consider the non-linear Duffing equation forced by a harmonic function given by

A theoretical solution of this equation obtained by Van Dooren (1974) given by $y \left(x \right) = \phi_{1}\cos \left(\lambda x \right) +\phi_{2}\cos \left(3 \lambda x \right) +\phi_{3}\cos \left(5 \lambda x \right) +\phi_{4}\cos \left(7 \lambda x \right)$ and the suitable initial conditions are $y \left(0 \right) = \phi_{0}, \dot{y} \left(0 \right) = 0$, where $\lambda = 1.01,$ $\xi = 2.0 \times 10^{-3},$ $\phi_{0} = 2.00426728069 \times 10^{-1},$ $\phi_{1} = 2.00179477536 \times 10^{-3},$ $\phi_{2} = 2.46946143 \times 10^{-4},$ $\phi_{3} = 3.04016 \times 10^{-7},$ and $\phi_{4} = 3.74 \times 10^{-10}.$ For this example, we select $\varsigma = 1.01$ as fitting frequency. Whereas the absolute errors of the ABHM are shown in Figure 6 (Left), the correctness of the ABHM with reference to the exact solution is plotted in Figure 6 (Middle). The good performance of ABHM in the interval $\left[0, \frac{20.5\pi }{1.01}\right]$ with step length $h = \frac{1}{2^{i}}, i = 1, 2, 3, 4, 5, 6$ in comparison with some numerical methods in the recent literature is plotted in Figure 6 (Right) respectively.

4.2.   Related problems

As emphasised in section one, besides the Duffing equations, the proposed adapted method in the present study can be used for solving other types of oscillatory problems. We integrate two of such problems to establish the efficiency of the ABHM.

4.2.1.   Example 5

We consider the following well known two body problem

where $r = \sqrt[]{y_{1}^{2}+y_{2}^{2}}$ and whose analytic result is given by $y_{1} \left(t \right) = \dot{y}_{2} \left(t \right)$, $y_{2} \left(t \right) = \sin \left(t \right).$ The problem is considered in the integration interval $0 \leq t \leq 10$ with $\varsigma = 1.$ The absolute errors of the ABHM in terms of agreement with the exact solution are shown in Figure 7 (Left). The numerical accuracy of ABHM is displayed in Figure 7 (Middle), while the graphical illustration of its efficacy in terms of number of functions evaluation and time are shown in Figure 7 (Right) and Figure 8 respectively. Figure 7 (Right) and Figure 8 establish the advantage of ABHM over some of the other numerical integrators in the recent literatures.

4.2.2.   Example 6

Consider the non-linear perturbed system on the range $\left[\text{0, 10} \right]$ with $\epsilon = 10^{-3}$

where

and the solution in closed form is given as $y_{1} \left(x \right) = \epsilon \sin \left(x^{2} \right)+\cos \left(5x \right), y_{2} \left(x \right) = \epsilon \cos \left(x^{2} \right)+\sin \left(5x \right)$. Details of the results given in Figure 9 (Left) and Figure 9 (Middle), and the efficiency curves plotted in Figure 9 (Right), reveal that the ABHM is an efficient numerical integrator for the non-linear perturbed system.

5.   Conclusions

An adapted block hybrid method with trigonometric coefficients that depend on a constant frequency and constant step length for Duffing equations has been considered in this article. The proposed integrator has benefit of being self starting with better accuracy in comparison with the exact solutions. Details of the numerical examples established the superiority of the ABHM on Duffing equations and some related problems over a portion of the existing formulas in the reviewed literature.

Appendix

$\sigma_{{4}} = (22 \eta^{4}+ (6 u^{2}-48)$$\eta^{3}+(-22 u^{2}+48) \eta^{2}+ 48 \eta u^{2} -48 u^{2})$$(\cos (u/2)) ^{4}+ (6 \eta u (\eta^{3}- \frac {22 \eta^{2}}{3}+ 16 \eta- 16) \sin (u/2) -38$$\, \eta^{4}+ (18\, u ^{2}- 80) \eta^{3}+ 6\, \eta^{2} u^{2}- 32 \, \eta \, u^{2}+ 96 \, u^{2})$$(\cos (u/2)) ^{3}+ (-6\, \eta^{2} u (\eta + 8)$$(\eta + 2) \sin (u/2) -6\, \eta^{4}+ 128\, \eta^{3}+ (38\, u ^{2}- 96) \eta^{2} - 16\, \eta \, u^{2})$$(\cos (u/2)) ^{2}+ (-3\, \eta$$\, u (\eta^{3 }- \frac {32\, \eta^{2}}{3} + 16 \, \eta - 32) \sin (u/2) + 38\, \eta^{4}+$$(-12 \, u^{2}+ 80) \eta^{3} - 6\,$$\eta^{2} u^{2}+ 32 \, \eta \, u^{2}- 96\, u^{2}) \cos (u/2) + 3\, \eta^{2} u (\eta + 4) ^{2}$$\sin (u/2) -16\, \eta^{4}- 80$$\, \eta^{3}+ (-16\, u^{2}+ 48)$$\eta^{2}- 32 \, \eta\, u^{2}$$+ 48\, u^{2}$

$\tau_{4} = -6\, \sin (u/2)$$(\cos (u/2) -1) (((11/3\, \eta^{4}+$$(u^{2}+ 8) \eta^{3}+ (11/3\, u^{2}+8)$$\eta^{2} + 8 \, \eta\, u^{2}+ 8\, u^{2}) \cos (u/2) -8/3\, (\eta^{2} + 3\, \eta + 3)$$(\eta^{2} + u^{2})) \sin (u/2) - \eta^{4}$$((\cos (u/2)) ^{2} - 1/2) u)$

Acknowledgments

This work is supported by Foundation of Chongqing Municipal Key Laboratory of Institutions of Higher Education ([2017]3), Foundation of Chongqing Development and Reform Commission (2017[1007]), and Foundation of Chongqing Three Gorges University.

The authors are grateful to Professor Higinio Ramos for carefully reading and correcting the manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.