Analysis of some Katugampola fractional differential equations with fractional boundary conditions

1.   Introduction

The Lyapunov inequality, proved in 1907 by Russian mathematician Aleksandr Mikhailovich Lyapunov ^[1], is very useful in various problems related with oscillation theory, differential and difference equations and eigenvalue problems (see ^{[2,3,4,5,6,7]} and the references therein). The Lyapunov result states that, if a nontrivial solution to the following boundary value problem

exists, where $g$ is a continuous function, then the following inequality

holds. This theorem formulates a necessary condition for the existence of solutions and allows to deduce sufficient conditions for non-existence of solutions to the considered boundary problem.

Recently, the research of Lyapunov-type inequality has gained more and more popularity, because by replacing the classical derivative with some fractional operators allows to model processes exhibiting memory effect. The first work in this direction is due to Ferreira ^[8] in 2013 by using the Riemann-Liouville derivative of order $\alpha\in(1, 2]$. In ^[9] was investigated the Lyapunov-type inequality for the boundary value problem with the Katugampola fractional derivative. In ^[10] was used the Caputo fractional derivative and in ^[11] the Hadamard fractional derivative.

Moreover, together with raising popularity of fractional operators, many modifications of the Lyapunov inequality appeared by changing the boundary conditions, for example $u(a) = u'(b) = 0$ or $u'(a) = u(b) = 0$ (see ^[12,13,14]).

Motivated by the above works, we consider in this paper the Katugampola fractional differential equation under boundary condition involving the Katugampola fractional derivative. We choose this special fractional derivative because it generalizes two other fractional operators, that is the Riemann-Liouville and the Hadamard fractional derivatives and classical derivative of integer order. More precisely, we consider the boundary value problem

where $1 < \alpha\leq 2, \ 0 < \beta\leq 1$ and $g:[a, b] \to \mathbb{R}$ is a continuous function. Thanks to the detailed analysis of the integral equation equivalent to (1.2) we are able to obtain a corresponding Lyapunov-type inequality. After that, we show some applications to present the effectiveness of the new Lyapunov-type inequality. We deduce some existence and non-existence results for the considered problem (1.2) which are very helpful for other researchers in this field. Furthermore, at the end of the article there will be graphs illustrating the applications of the proven theorems.

2.   Preliminaries

In this section, we introduce the definitions and properties of the Katugampola fractional operators which are needed to prove the main results. For more details, we refer to ^[15,16,17].

Definition 2.1. Let $\alpha > 0, \ \rho > 0, \ -\infty < a < b < \infty$. The operators

for $t\in (a, b)$ are called the left-sided and right-sided Katugampola integrals of fractional order $\alpha$, respectively. The operators $I^{\alpha, \rho}_{a+}f$ and $I^{\alpha, \rho}_{b-}f$ are defined for $f\in L^p(a, b), \ p\geq 1.$

Definition 2.2. Let $\alpha > 0, \ \rho > 0, \ n = [\alpha]+1, \ 0 < a < t < b\leq\infty$. The operators

for $t\in (a, b)$ are called the left-sided and right-sided Katugampola derivatives of fractional order $\alpha$, respectively.

The Katugampola derivative generalizes two other fractional operators, by introducing a new parameter $\rho > 0$ in the definition. Indeed, if we take $\rho\rightarrow 1$, we have the Riemann-Liouville fractional derivative, i.e.,

Moreover, if we take $\rho\rightarrow 0^+$, we get the Hadamard fractional derivative, i.e.,

Example 2.3. (^[9]) For $\rho > 0, \ \alpha > 0, \ \lambda > \alpha-1$, we have

The higher order Katugampola fractional operators satisfy the following properties, which were precisely discussed and proven in ^[9,16,17].

Lemma 2.4. (^[16]) Let $\alpha > 0, \ \rho > 0$ and $f\in L[a, b]$ then

Lemma 2.5. (^[16]) Let $\alpha > \beta > 0, \ \rho > 0$ and $f\in L[a, b]$ then

Lemma 2.6. (^[17]) Let $n-1 < \alpha < n, \ n\in\mathbb{N}, \ \rho > 0$ and $f\in L[a, b]$ then

where $\tilde{c}_i$ are real constants.

It is worth to mention that the complex formula for the Katugampola operator is established in ^[18].

3.   Main result

We start with writing problem (1.2) in its equivalent integral form.

Theorem 3.1. Function $u \in C[a, b]$ is a solution to the boundary value problem $(1.2)$ if and only if $u$ is a solution to the integral equation

where the Green function $G$ is given by

Proof. Integrating equation from (1.2) and using Lemma 2.6 we obtain that general solution is of the form

where $c_{1}$ and $c_{2}$ are some real constants. Since $u(a) = 0$, we get $c_2 = 0$. Moreover, differentiating (3.3) in Katugampola sense with $c_2 = 0$, we have

By Example 2.3 and Lemma 2.5 we obtain

Since $D_{a+}^{\beta, \rho}u(b) = 0$, we get

Therefore,

which ends the proof. The below theorem present the properties of the Green function $G$ obtained in (3.2)

Theorem 3.2. Let $\ 0 < a < b < \infty$, $\alpha \in (1, 2]$, $\beta \in (0, 1]$, $\alpha > \beta +1$ and $\rho > 0$. The function $G$ given by $(3.2)$ satisfies the following estimates

$(i)$ $G (t, s)\geq 0$, $t, s \in [a, b]$,

$(ii)$ $\max \limits_{t\in [a, b]}G(t, s) = G(s, s)\leq \frac{4^{\beta}\max\{a^{\rho-1}, \ b^{\rho-1}\}}{\Gamma(\alpha)}\left(\frac{b^{\rho}-a^{\rho}}{4\rho}\right)^{\alpha-1}$, \quad $s \in [a, b]$.

Proof. First we prove the positivity of function $G$. For $t\leq s$ it is obvious, but for $s < t$ we can rewrite function $G$ in the form

Let us see that there is the following estimation

because

Thus the function $G$ is positive also for $s < t$.

(ii) Now, we prove that $G(t, s)\leq G(s, s)$. Firstly, we consider the interval $a\leq t \leq s \leq b$. Differentiating $G$ with respect to $t$ we have

Therefore,

because the function $G$ with respect to $t$ is increasing on the considered interval.

Now, let we take the interval $a \leq s < t \leq b$. Taking the derivative of function $G$ with respect to $t$, we obtain

Note that ${\frac{\partial G}{\partial t} \leq 0}$ because

Therefore,

because the function $G$ is decreasing with respect to $t$ on the considered interval. From (3.4) and (3.5) we get

for $s\in[a, b]$, $t\in [a, b]$. Now let us define a function $f$

In order to find the maximum value of this function, we check the sign of the derivative on the interior $(a, b)$. We have

It follows that $f'(\hat{s}) = 0$ if and only if

It is easily seen that $f'(s) < 0$ for $\hat{s} < s$ and $f'(s) > 0$ for $\hat{s} > s$.

Therefore

It ends the proof. We are ready to state and prove our main results in the Banach space $C[a, b]$ with the maximum norm $||u|| = \max\limits_{t \in[a, b]}|u(t)|$.

Theorem 3.3. If a nontrivial continuous solution of the fractional boundary value problem $(1.2)$ exists, where $g$ is a real and continuous function and $\alpha > \beta+1$, then

Proof. It follows from Theorem 3.1 that solution of the fractional boundary value problem (1.2) satisfies the integral equation (3.1). Thus

Using the estimation of the function $G$ which was obtained in Theorem 3.2 we get

Thus, we have

The proof is completed. In particular, if we chose $\beta = 0$ in Theorem 3.3, we obtain the main theorem of the work ^[9]. Moreover, taking $\alpha = 2, \ \beta = 0,$ and $\rho = 1$ we recover the classical Lyapunov's inequality (1.1).

Due to the fact, that the Katugampola derivative has an additional parameter $\rho$ (which by taking $\rho\rightarrow 0^+$ reduces to the Hadamard fractional derivative and for parameter $\rho = 1$ become the Riemann-Liouville fractional derivative) we get the Lyapunov-type inequality for both the Riemann-Liouville derivative $D^\alpha_{a+}$ and the Hadamard derivative $^{H}{D}^\alpha_{a+}$.

Corollary 3.4. If a nontrivial continuous solution of the fractional boundary value problem

exists, where $g$ is a real and continuous function, then

In particular, if we take, in Corollary 3.4, $\beta = 0$ we obtain the main result of the work ^[10] proved by Ferreiro.

Corollary 3.5. If a nontrivial continuous solution of the fractional boundary value problem

exists, where $g$ is a real and continuous function, then

4.   Applications and examples

In this section, we apply the results on the Lyapunov-type inequalities obtained previously to study the nonexistence of solutions for certain fractional boundary value problems.

Theorem 4.1. If

then $(1.2)$ has no nontrivial solution.

The proof of this theorem is trivial and it is left for the reader.

Example 4.2. Let us consider the following boundary value problem

By Theorem 3.3, if the continuous solution to the problem (4.1) exists, then necessarily

Note, that inequality depends on two parameters $\lambda$ and $\rho$. Taking $\rho = 1$ we obtain $\lambda > 1.2534$, but for $\rho\rightarrow 0^+$ we have $\lambda > 2.1719$. In particular, for $\lambda = 1$, $\rho = 1$ and $\rho\rightarrow 0^+$ the solution to problem (4.1) does not exist. For $\lambda = 2$, the solution does not exist for $\rho\rightarrow 0^+$, but for $\rho = 1$ the solution to (4.1) may exist. Moreover, for $\lambda = 3$ the solution may exist for $\rho = 1$ and $\rho\rightarrow 0^+$.

Let us consider problem (1.2) with $g(t) = \lambda$

If problem (4.2) admits a nontrivial solution $u_\lambda$, we say that $\lambda$ is an eigenvalue of problem (4.2). We have the following result which provides a lower bound of the eigenvalues of problem (4.2).

Corollary 4.3. If $\lambda$ is an eigenvalue of problem (4.2), then

The proof follows immediately from Theorem 3.3.

Furthermore, if

then $\lambda$ is not an eigenvalue of problem (4.2).

Example 4.4. Let us consider problem (4.2) with $\beta = \frac{1}{4}, \ \rho = 1$. If

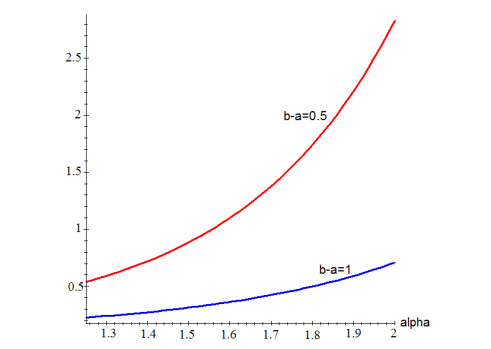
then the solution of the eigenvalue of problem (4.2) does not exist. The plot below shows the upper estimation of $\lambda$ depending on order of considered equation, for which (4.2) does not have a solution. The red line is for cases $b-a = 0.5$, and the blue line is for $b-a = 1$.

Acknowledgements

The authors would like to thank Karolina Szczesiul (student of Faculty of Mathematics and Computer Science of University of Białystok) for the helpful calculations.

Conflict of interest

The authors declare that they have no conflict of interest.