Some new mathematical models of the fractional-order system of human immune against IAV infection

H. M. Srivastava; Khaled M. Saad; J. F. Gómez-Aguilar; Abdulrhman A. Almadiy; H. M. Srivastava; Khaled M. Saad; J. F. Gómez-Aguilar; Abdulrhman A. Almadiy

doi:10.3934/mbe.2020268

Mathematical Biosciences and Engineering

2020, Volume 17, Issue 5: 4942-4969. doi: 10.3934/mbe.2020268

Previous Article Next Article

Research article Special Issues

Some new mathematical models of the fractional-order system of human immune against IAV infection

1.
Department of Mathematics and Statistics, University of Victoria, Victoria, British Columbia V8W 3R4, Canada
2.
Department of Medical Research, China Medical University Hospital, China Medical University, Taichung 40402, China
3.
Department of Mathematics and Informatics, Azerbaijan University, 71 Jeyhun Hajibeyli Street, Baku AZ1007, Azerbaijan
4.
Department of Mathematics, College of Arts and Sciences, Najran University, Najran, Kingdom of Saudi Arabia
5.
Department of Mathematics, Faculty of Applied Science, Taiz University, Taiz, Yemen
6.
CONACyT-Tecnológico Nacional de México/CENIDET, Interior Internado Palmira S/N, Col. Palmira, C. P. 62490, Cuernavaca Morelos, México
7.
Department of Biology, College of Arts and Sciences, Najran University, Najran, Kingdom of Saudi Arabia

Received: 26 May 2020 Accepted: 07 July 2020 Published: 16 July 2020

Fractional derivative operators of non-integer order can be utilized as a powerful tool to model nonlinear fractional differential equations. In this paper, we propose numerical solutions for simulating fractional-order derivative operators with the power-law and exponential-law kernels. We construct the numerical schemes with the help the fundamental theorem of fractional calculus and the Lagrange polynomial interpolation. These schemes are applied to simulate the dynamical fractional-order model of the immune response (FMIR) to the uncomplicated influenza A virus (IAV) infection, which focuses on the control of the infection by the innate and adaptive immunity. Numerical results are then presented to show the applicability and efficiency on the FMIR.

Keywords:

Citation: H. M. Srivastava, Khaled M. Saad, J. F. Gómez-Aguilar, Abdulrhman A. Almadiy. Some new mathematical models of the fractional-order system of human immune against IAV infection[J]. Mathematical Biosciences and Engineering, 2020, 17(5): 4942-4969. doi: 10.3934/mbe.2020268

Related Papers:

[1]	A. M. Elaiw, Raghad S. Alsulami, A. D. Hobiny . Global dynamics of IAV/SARS-CoV-2 coinfection model with eclipse phase and antibody immunity. Mathematical Biosciences and Engineering, 2023, 20(2): 3873-3917. doi: 10.3934/mbe.2023182
[2]	Abdessamad Tridane, Yang Kuang . Modeling the interaction of cytotoxic T lymphocytes and influenza virus infected epithelial cells. Mathematical Biosciences and Engineering, 2010, 7(1): 171-185. doi: 10.3934/mbe.2010.7.171
[3]	Ting Guo, Zhipeng Qiu . The effects of CTL immune response on HIV infection model with potent therapy, latently infected cells and cell-to-cell viral transmission. Mathematical Biosciences and Engineering, 2019, 16(6): 6822-6841. doi: 10.3934/mbe.2019341
[4]	Tahir Khan, Roman Ullah, Gul Zaman, Jehad Alzabut . A mathematical model for the dynamics of SARS-CoV-2 virus using the Caputo-Fabrizio operator. Mathematical Biosciences and Engineering, 2021, 18(5): 6095-6116. doi: 10.3934/mbe.2021305
[5]	Maysaa Al Qurashi, Saima Rashid, Fahd Jarad . A computational study of a stochastic fractal-fractional hepatitis B virus infection incorporating delayed immune reactions via the exponential decay. Mathematical Biosciences and Engineering, 2022, 19(12): 12950-12980. doi: 10.3934/mbe.2022605
[6]	Jiazhe Lin, Rui Xu, Xiaohong Tian . Threshold dynamics of an HIV-1 model with both viral and cellular infections, cell-mediated and humoral immune responses. Mathematical Biosciences and Engineering, 2019, 16(1): 292-319. doi: 10.3934/mbe.2019015
[7]	Cameron Browne . Immune response in virus model structured by cell infection-age. Mathematical Biosciences and Engineering, 2016, 13(5): 887-909. doi: 10.3934/mbe.2016022
[8]	Cuicui Jiang, Kaifa Wang, Lijuan Song . Global dynamics of a delay virus model with recruitment and saturation effects of immune responses. Mathematical Biosciences and Engineering, 2017, 14(5&6): 1233-1246. doi: 10.3934/mbe.2017063
[9]	Maysaa Al Qurashi, Saima Rashid, Ahmed M. Alshehri, Fahd Jarad, Farhat Safdar . New numerical dynamics of the fractional monkeypox virus model transmission pertaining to nonsingular kernels. Mathematical Biosciences and Engineering, 2023, 20(1): 402-436. doi: 10.3934/mbe.2023019
[10]	Xuejuan Lu, Lulu Hui, Shengqiang Liu, Jia Li . A mathematical model of HTLV-I infection with two time delays. Mathematical Biosciences and Engineering, 2015, 12(3): 431-449. doi: 10.3934/mbe.2015.12.431

Abstract

1. Introduction

Mathematical modeling of the spread of infectious diseases has attracted much attention of researchers in various disciplines. The importance of the modeling is that it has become an important tool in understanding the dynamics of diseases and in the decision-making process with regard to rapid intervention programs in controlling and limiting the spread of these diseases ^{[1,2,3,4,5,6,7]}. Until mathematical tools are employed, real-world problems were modeled by means of an abstract model. These mathematical models contain basic variables and relationships corresponding to the observed and recorded phenomena and behavior. Due to the fact that the theory of differential equations is not sufficient to describe and model many real-world and complex problems, the critical importance of fractional differential equations appears in modeling these issues in recent years ^{[8,9,10,11,12,13,14,15,16,17,18]}. Furthermore, owing to its many widespread applications, scientists and researchers have significantly attracted the attention toward fractional differential equations. Accordingly, many models of differential equations containing fractional differentiation and fractional integration have been developed. And the fact that, for many fractional differential equations, it is difficult to find the exact solutions, so it has become very important to develop and update numerical methods so that we can find approximate and numerical solutions to many of these equations ^{[19,20,21,22,23,24,25,26,27,28]}.

The Adams-Bashforth predictor-corrector method has been proposed ^{[29,30,31,32,33,34,35]}, as a great and powerful numerical method which is capable of providing a numerical solution of fractional differential equations. The method can be used for linear as well as nonlinear fractional differential equations.

In this paper, we derive and discuss the numerical solutions of the fractional-order model of the human immune response to influenza A virus (IAV) infection by using the method that was proposed in ^[36], which combines the fundamental theorem of fractional calculus and the two-step Lagrange polynomial. The authors in ^[37] proposed a simplified dynamical model of immune response to uncomplicated influenza A virus (IAV) infection. This model focuses on the control of the infection by the innate and adaptive immunity ^[37]. Zhang et al. ^[38] propped a long review on hostvirus interaction: How host cells defend against Influenza A Virus Infection. They presented a general description on recent work regarding different host cells and molecules facilitating antiviral defenses against IAV infection and how IAVs antagonize host immune responses. Also, Vires et al. ^[39,40,41] discussed in details on the factors for influenza A virus infection, Preserving Virus Motility, IL16 deficiency enhances Th1 and cytotoxic T lymphocyte response against influenza A virus infection. In our paper, we focus on studying the effect of the change of the integer-order derivatives and non-integer derivatives with power and exponential kernels.

The paper is organized as follows. Notations and basic definitions of fractional derivatives are given in Section 2. In Section 3, the classical model of immune response is presented. In Section 4 and 5, the numerical method with power and exponential laws is discussed and illustrated graphically. Finally, conclusions are summarized in Section 6.

2. Preliminaries

In this section, we give some basic definitions and properties of fractional calculus theory ^[2,3,43,44].

Definition 1. If $Y(t)\in L_{1}(a, b)$ , the set of all integrable functions on $(a, b),$ and $\alpha > 0,$ then the Riemann-Liouville fractional integral of order $\alpha,$ denoted by $J^{\alpha}_{a+}$ is defined by

$\begin{eqnarray} J^{\alpha}_{a+}Y(t) = \frac{1}{\Gamma(\alpha)} \int_{a}^{t}(t - \eta)^{\alpha-1}Y(\eta) d\eta. \end{eqnarray}$

(2.1)

Definition 2. For $\alpha > 0,$ the Liouville-Caputo fractional derivative of order $\alpha,$ denoted by $^{ LC}D_{a+}^{\alpha},$ is defined by

$\begin{eqnarray} ^{ \rm{LC}}\mathcal{D}_{a+}^{\alpha}Y(t) = \frac{1}{\Gamma(n - \alpha)}\int_{a}^{t}(t - \eta)^{n-\alpha-1} \mathcal{D}^{n}Y(\eta) d\eta \end{eqnarray}$

(2.2)

$(n-1 \lt \alpha \lt n;\; n\in \mathbb{N} = \{1,2,3,\cdots\}),$

$\begin{eqnarray} ^{ \rm{LC}}\mathcal{D}_{a+}^{\alpha} = D^{\alpha}, \end{eqnarray}$

(2.3)

where $D = \frac{d}{dt}$ .

We next introduce the Caputo-Fabrizio-Caputo fractional integral operator of order $\alpha > 0$ ^[45].

Definition 3. The Caputo-Fabrizio-Caputo derivative operator (CFC) with respect to $t$ , denoted by $^{ CFC}_{\; \; \; \; \; \; 0}D_\eta^{\alpha}$ , is defined by

$\begin{equation} ^{ \rm{CFC}}_{\;\;\;\;\;0}{\mathcal{D}}_\eta^{\alpha} Y(t) = \frac{M(\alpha)}{n-\alpha}\int_{0}^{t} \exp \left(-\frac{\alpha(t-\eta)}{n-\alpha}\right) \mathcal{D}^{n}{Y}(\eta)d\eta \end{equation}$

(2.4)

$(n-1 \lt \alpha \lt n;\; n\in \mathbb{N}),$

where $M(\alpha)$ is a normalization function such that $M(0) = M(1) = 1$ .

Definition 4. Losada and Nieto ^[45] proposed the fractional integral according to the CFC as follows:

$\begin{equation} ^{ \rm{CFC}}J_{0}^{\alpha}Y(t) = \frac{(1-\alpha)}{ M(\alpha)} Y(t)+\frac{\alpha}{ M(\alpha)} \int_{0}^{t}Y(\eta) d\eta. \end{equation}$

(2.5)

3. Classical immune response

3.1. Mathematical formulation

In this section, we will first provide remarkably simple details about the composition and the basis on the model of human immune response to influenza A virus (IVA) infection. For further details and for the history of this virus infection, we refer the reader to the earlier work ^[37].

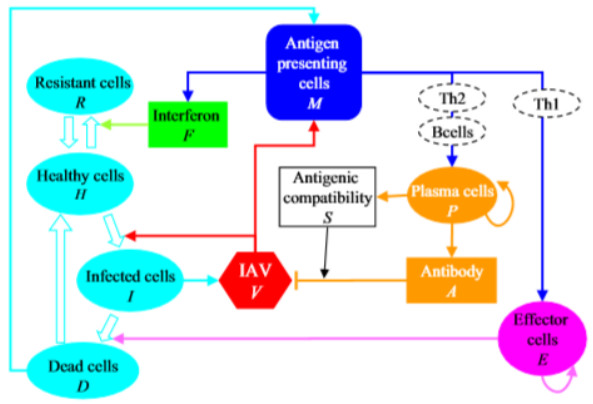
The human immune response model against the IVA infection has been found to be a simplified population dynamic model consisting of the following interactions. Figure 1 shows the schematic representation of interactions included in the model ^[37]. Respiratory system epithelial cells are presumed to be present in one of these four possible states: Healthy (H), infected (I), dead (D), or resistant (R) to infection. Total epithelial cell count (that is, H + I + D + R) is believed to be constant. The particles of the virus (IAV) interact with and infect healthy cells. Once these virus particles die, the infected cells release new virus particles. Proliferation of healthy cells causes regeneration and the proportion of dead cells decreases. APS stimulates interferon a and b (F) production which interacts with healthy cells and converts them to a resistant state. In addition, APS stimulates the proliferation of effector cells (E) which kill the infected cells.

Figure 1. Schematic representation of interactions included in the model. The influenza virus (IAV) is shown as red hexagon, the four different cell types are shown in cyan. Components of adaptive immunity are shown in orange, cellular component of innate immunity in purple, and interferon component in green. Upregulation is represented by lines terminated with arrows and inhibition by lines terminated with bars. The inter-conversion of cell types (cyan) is indicated by dashed arrows. Dashed ovals represent details of the mechanism ignored in this model. Homeostatic maintenance of effector and plasma cell populations are indicated by self-regulating loops ^[37].

DownLoad: Full-Size Img PowerPoint

Finally, they stimulate production of the plasma cell (P). This, in turn, produces antibodies (A) to neutralize the virus. The antigenic compatibility (S) between the virus and the antibodies currently generated by the organism modulates the neutralization. S quantifies the interaction of the antibodies with the virus. In order to illustrate the components of the immune response as shown in Figure 1, we will use the previous interactions to construct a system of ten differential equations describing the dynamics of the main variables.

$\begin{align} \frac{d V}{dt} = \gamma_{V} I -\gamma_{VA} S A V -\gamma_{VH} V H-\alpha_{V} V-\frac{a_{V1} V}{1+a_{V2}V}, \end{align}$

(3.1)

$\begin{align} \frac{d H}{dt} = b_{HD} D(H+R) a_{R} R -\gamma_{HV} V H -b_{HV} F H, \end{align}$

(3.2)

$\begin{align} \frac{d I}{dt} = \gamma_{HV} V H-b_{IE} E I, \end{align}$

(3.3)

$\begin{align} \frac{d M}{dt} = (b_{MD}D+b_{MV}V)(1-M)-a_{M} M, \end{align}$

(3.4)

$\begin{align} \frac{d F}{dt} = (b_{F}M+C_{F}I)-b_{FH} H F-a_{F} F, \end{align}$

(3.5)

$\begin{align} \frac{d R}{dt} = b_{HF} H F-a_{R} R, \end{align}$

(3.6)

$\begin{align} \frac{d E}{dt} = b_{EM} M E-ab{IE} I E+ a_{E} (1-E), \end{align}$

(3.7)

$\begin{align} \frac{d P}{dt} = b_{PM} M P+ a_{P} (1-P), \end{align}$

(3.8)

$\begin{align} \frac{d A}{dt} = b_{A} P-\gamma_{AV} S A V -a_{A} A \end{align}$

(3.9)

and

$\begin{align} \frac{d S}{dt} = r P(1-S). \end{align}$

(3.10)

We impose the following initial conditions:

$\begin{align} & V(0) = v_{0}, \, H(0) = h_{0}, \, I(0) = i_{0}, \, M(0) = m_{0}, \, F(0) = f_{0},\, R(0) = r_{0}, \, E(0) = e_{0},\, P(0) = p_{0}, \, \\ & A(0) = a_{0}, S(0) = s_{0}, \end{align}$

(3.11)

where $V, H, I, M, F, R, E, P, A$ and $S$ are Viral load per epithelial cell, proportion of healthy cells, proportion of infected cells, activated antigen presenting cells per homeostatic level, interferons per homeostatic level of macrophages, proportion of resistant cells, effector cells per homeostatic level, plasma cells per homeostatic level, antibodies per homeostatic level and antigenic distance, respectively.

3.2. Description of the involved parameters

The above parameters are defined in the following table:

Table 1. Description of the involved parameters ^[37].

Parameter	Description
$\gamma_{V}$	Rate constant of influenza A virus (IAV) particles secretion per infected epithelial cells
$\gamma_{VA}$	Rate constant of neutralization of IAV by antibodies
$\gamma_{VH}$	Rate constant of adsorption of IAV by infected epithelial cells
$\alpha_{V}$	Rate constant of nonspecific IAV removal
$a_{V_{1}}$	Rate constant of nonspecific IAV removal
$a_{V_{2}}$	Rate constant of nonspecific IAV removal per cell per CTL as the CTL response sets up
$b_{HD}$	Rate constant of regeneration of epithelial cells
$a_{R}$	Rate constant of epithelial cells virus resistance state decay
$\gamma_{HV}$	Rate constant of epithelial cells infected by IAV
$b_{HF}$	Rate constant of epithelial cells virus resistant state induction
$b_{IE}$	The rate of removal of CTL per infected hepatocyte per CTL
$a_{I}$	Rate constant of infected epithelial cells damage by cytopathicity of IAV
$b_{MD}$	Rate constant of stimulation of antigen presenting cells by dead cells
$b_{MV}$	Rate constant of stimulation of antigen presenting cells by virus particles
$a_{M}$	Rate constant of stimulated state loss of antigen presenting cells
$b_{F}$	Interferon (IFN) production rate per APC
$c_{F}$	Interferon (IFN) production rate per infected cell
$b_{FH}$	Rate constant of epithelial cells that IFN binds
$a_{F}$	Rate constant of IFN's natural decay
$b_{EM}$	Rate constant of stimulation of effector cells
$b_{EI}$	Rate constant of death of effectors by lytic interactions with infected epithelial cells
$a_{E}$	Rate constant of natural death of effector cells
$b_{PM}$	Rate constant of plasma cells production cells
$a_{P}$	Rate constant of natural death of plasma cells
$b_{A}$	Antibody production rate per plasma cells
$\gamma_{AV}$	Rate constant of antibodies which binds to IAV
$a_{A}$	Rate constant of natural death of antibodies
$r$	Rate constant for $S$ variable

| Show Table

DownLoad: CSV

4. Immune response with fractional-order derivatives

In this section, we present a generalization of the numerical schemes proposed in ^[36] for the fractional immune response involving the Liouville-Caputo and Caputo-Fabrizio-Caputo fractional-order derivatives.

The fractional immune response model is obtained by replacing the classical derivative by the operator ${}_{0} D_{t}^{\alpha}$

$\begin{align} {}_{0} D_{t}^{\alpha}V = \gamma_{V} I -\gamma_{VA} S A V -\gamma_{VH} V H-\alpha_{V} V-\frac{a_{V1} V}{1+a_{V2}V}, \end{align}$

(4.1)

$\begin{align} {}_{0} D_{t}^{\alpha} H = b_{HD} D(H+R) a_{R} R -\gamma_{HV} V H -b_{HV} F H, \end{align}$

(4.2)

$\begin{align} {}_{0} D_{t}^{\alpha} I = \gamma_{HV} V H-b_{IE} E I, \end{align}$

(4.3)

$\begin{align} {}_{0} D_{t}^{\alpha} M = (b_{MD}D+b_{MV}V)(1-M)-a_{M} M, \end{align}$

(4.4)

$\begin{align} {}_{0} D_{t}^{\alpha} F = (b_{F}M+C_{F}I)-b_{FH} H F-a_{F} F, \end{align}$

(4.5)

$\begin{align} {}_{0} D_{t}^{\alpha} R = b_{HF} H F-a_{R} R, \end{align}$

(4.6)

$\begin{align} {}_{0} D_{t}^{\alpha}E = b_{EM} M E-ab{IE} I E+ a_{E} (1-E), \end{align}$

(4.7)

$\begin{align} {}_{0} D_{t}^{\alpha} P = b_{PM} M P+ a_{P} (1-P), \end{align}$

(4.8)

$\begin{align} {}_{0} D_{t}^{\alpha} A = b_{A} P-\gamma_{AV} S A V -a_{A} A \end{align}$

(4.9)

and

$\begin{align} {}_{0} D_{t}^{\alpha} S = r P(1-S). \end{align}$

(4.10)

The numerical solution to the system given by Eqs (4.1)–(4.10) is obtained by applying the following numerical algorithms.

4.1. Numerical scheme for fractional immune response in LC sense

Involving the LC derivative, we have

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} V = \gamma_{V} I -\gamma_{VA} S A V -\gamma_{VH} V H-\alpha_{V} V-\frac{a_{V1} V}{1+a_{V2}V}, \end{align}$

(4.11)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} H = b_{HD} D(H+R) a_{R} R -\gamma_{HV} V H -b_{HV} F H, \end{align}$

(4.12)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} I = \gamma_{HV} V H-b_{IE} E I, \end{align}$

(4.13)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} M = (b_{MD}D+b_{MV}V)(1-M)-a_{M} M, \end{align}$

(4.14)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} F = (b_{F}M+C_{F}I)-b_{FH} H F-a_{F} F, \end{align}$

(4.15)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} R = b_{HF} H F-a_{R} R, \end{align}$

(4.16)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} E = b_{EM} M E-ab{IE} I E+ a_{E} (1-E), \end{align}$

(4.17)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} P = b_{PM} M P+ a_{P} (1-P), \end{align}$

(4.18)

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} A = b_{A} P-\gamma_{AV} S A V -a_{A} A \end{align}$

(4.19)

and

$\begin{align} ^{ \rm{LC}}_{0}D_{t}^{\alpha} S = r P(1-S). \end{align}$

(4.20)

Now, by applying the fundamental theorem of fractional calculus on Eqs (4.11)–(4.20), we obtain

$\begin{align} V(t) - V(0) & = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(\gamma_{V} I(\eta) -\gamma_{VA} S(\eta) A(\eta) V(\eta) -\gamma_{VH} V(\eta) H(\eta)-\alpha_{V} V \\ & \quad -\frac{a_{V1} V(\eta)}{1+a_{V2}V(\eta)}\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.21)

$\begin{align} H(t) - H(0) & = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(b_{HD} D\big(H(\eta)+R(\eta)\big) a_{R} R(\eta) -\gamma_{HV} V(\eta) H(\eta) -b_{HV} F(\eta) H(\eta)\Big) \\ &\qquad \cdot (t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.22)

$\begin{align} I(t) - I(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(\gamma_{HV} V(\eta) H(\eta)-b_{IE} E(\eta) I(\eta)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.23)

$\begin{align} M(t) - M(0) & = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(\big(b_{MD}D+b_{MV}V(\eta)\big)\big(1-M(\eta)\big)-a_{M} M(\eta)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.24)

$\begin{align} F(t) - F(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(\big(b_{F}M(\eta)+C_{F}I(\eta)\big)-b_{FH} H(\eta) F(\eta)-a_{F} F(\eta)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.25)

$\begin{align} R(t) - R(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(b_{HF} H(\eta) F(\eta)-a_{R} R(\eta)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.26)

$\begin{align} E(t) - E(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(b_{EM} M(\eta) E(\eta)-ab{IE} I(\eta) E(\eta)+ a_{E} \big(1-E(\eta)\big)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.27)

$\begin{align} P(t) - P(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big( b_{PM} M(\eta) P(\eta)+ a_{P} \big(1-P(\eta)\big)\Big)(t - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.28)

$\begin{align} A(t) - A(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(b_{A} P(\eta)-\gamma_{AV} S(\eta) A(\eta) V(\eta) -a_{A} A(\eta)\Big)(t - \eta)^{\alpha - 1}d\eta \end{align}$

(4.29)

and

$\begin{align} S(t) - S(0) = \frac{1}{\Gamma(\alpha)} \int_{0}^{t} \Big(r P(\eta)\big(1-S(\eta)\big)\Big)(t - \eta)^{\alpha - 1}d\eta. \end{align}$

(4.30)

Equations (4.21)–(4.30) can be reformulated as follows:

$\begin{align} V(t_{n+1}) - V(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(\gamma_{V} I(\eta) -\gamma_{VA} S(\eta) A(\eta) V(\eta) -\gamma_{VH} V(\eta) H(\eta)-\alpha_{V} V \\ &\quad - \frac{a_{V1} V(\eta)}{1+a_{V2}V(\eta)}\Big)(t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.31)

$\begin{align} H(t_{n+1}) - H(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(b_{HD} D\big(H(\eta)+R(\eta)\big) a_{R} R(\eta) -\gamma_{HV} V(\eta) H(\eta) \\ &\quad - b_{HV} F(\eta) H(\eta)\Big) \cdot (t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.32)

$\begin{align} I(t_{n+1}) - I(0) = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \ Big( \gamma_{HV} V(\eta) H(\eta)-b_{IE} E(\eta) I(\eta)\Big)(t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.33)

$\begin{align} M(t_{n+1})- M(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(\big(b_{MD}D+b_{MV}V(\eta)\big)\big(1-M(\eta)\big)-a_{M} M(\eta) \Big),\\ &\qquad \cdot (t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.34)

$\begin{align} F(t_{n+1}) - F(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(\big(b_{F}M(\eta)+C_{F}I(\eta)\big)-b_{FH} H(\eta) F(\eta)-a_{F} F(\eta)\Big)\\ &\qquad \cdot (t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.35)

$\begin{align} R(t_{n+1}) - R(0) = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big( b_{HF} H(\eta) F(\eta)-a_{R} R(\eta)\Big)(t_{m+1}- \eta)^{\alpha - 1}d\eta, \end{align}$

(4.36)

$\begin{align} E(t_{n+1}) - E(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty} \int_{t_{m}}^{t_{m+1}} \Big( b_{EM} M(\eta) E(\eta)-ab{IE} I(\eta) E(\eta)+ a_{E} \big(1-E(\eta)\big)\Big)\\ &\qquad \cdot (t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.37)

$\begin{align} P(t_{n+1}) - P(0) = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big( b_{PM} M(\eta) P(\eta)+ a_{P} \big(1-P(\eta)\big)\Big)(t_{m+1} - \eta)^{\alpha - 1}d\eta, \end{align}$

(4.38)

$\begin{align} A(t_{n+1}) - A(0) & = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(b_{A} P(\eta)-\gamma_{AV} S(\eta) A(\eta) V(\eta) -a_{A} A(\eta)\Big) \\ &\qquad \cdot (t_{m+1} - \eta)^{\alpha - 1}d\eta \end{align}$

(4.39)

and

$\begin{align} S(t_{n+1}) - S(0) = \frac{1}{\Gamma(\alpha)} \sum\limits_{m = 0}^{\infty}\int_{t_{m}}^{t_{m+1}} \Big(r P(\eta)\big(1-S(\eta)\big)\Big)(t_{m+1} - \eta)^{\alpha - 1}d\eta. \end{align}$

(4.40)

Using the two-step Lagrange polynomial interpolation, we obtain

$\begin{align} V(t_{n+1}) & = V(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Big( \Big(\gamma_{V} I(t_{m}) -\gamma_{VA} S(t_{m}) A(t_{m}) V(t_{m})-\gamma_{VH} V(t_{m}) H(t_{m}) \\ &\quad - \alpha_{V} V(t_{m}) - \frac{a_{V1} V(t_{m})}{1+a_{V2}V(t_{m})}\Big)\cdot\int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta \\ &\quad-\Big(\gamma_{V} I(t_{m-1}) -\gamma_{VA} S(t_{m-1}) A(t_{m-1}) V(t_{m-1})-\gamma_{VH} V(t_{m-1}) H(t_{m-1}) \\ &\quad - \alpha_{V} V(t_{m-1}) - \frac{a_{V1} V(t_{m-1})}{1+a_{V2}V(t_{m-1})}\Big) \cdot\int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Big), \end{align}$

(4.41)

$\begin{align} H(t_{n+1}) & = H(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg(\Big(b_{HD} D\big(H(t_{m})+R(t_{m})\big) a_{R} R(t_{m}) \\ &\quad - \gamma_{HV} V(t_{m}) H(t_{m}) - b_{HV} F(t_{m}) H(t_{m})\Big)\cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta \\ &\quad - \Big(b_{HD} D\big(H(\eta)+R(\eta)\big) a_{R} R(\eta) -\gamma_{HV} V(\eta) H(\eta) - b_{HV} F(\eta) H(\eta)\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.42)

$\begin{align} I(t_{n+1}) & = I(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg(\Big( \gamma_{HV} V(t_{m}) H(t_{m})-b_{IE} E(t_{m}) I(t_{m})\Big)\\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big( \gamma_{HV} V(t_{m-1}) H(t_{m-1})-b_{IE} E(t_{m-1}) I(t_{m-1})\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.43)

$\begin{align} M(t_{n+1}) & = M(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg(\Big(\big(b_{MD}D+b_{MV}V(t_{m})\big)\big(1-M(t_{m})\big)-a_{M} M(t_{m}) \Big)\\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(\big(b_{MD}D+b_{MV}V(t_{m-1})\big)\big(1-M(t_{m-1})\big) \\ &\quad -a_{M} M(t_{m-1}) \Big)\cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.44)

$\begin{align} F(t_{n+1}) & = F(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(\big(b_{F}M(t_{m})+C_{F}I(t_{m})\big)-b_{FH} H(t_{m}) F(t_{m})-a_{F} F(t_{m})\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(\big(b_{F}M(t_{m-1})+C_{F}I(t_{m-1})\big) \\ &\quad -b_{FH} H(t_{m-1}) F(t_{m-1})-a_{F} F(t_{m-1})\Big) \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.45)

$\begin{align} R(t_{m+1}) & = \varphi_{1}(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg(\Big(b_{HF} H(t_{m}) F(t_{m})-a_{R} R(t_{m})\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(b_{HF} H(t_{m-1}) F(t_{m-1})-a_{R} R(t_{m-1})\Big) \\ & \qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.46)

$\begin{align} E(t_{m+1}) & = E(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg( \Big( b_{EM} M(t_{m}) E(t_{m})-ab{IE} I(t_{m}) E(t_{m})+ a_{E}\big(1-E(t_{m})\big)\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big( b_{EM} M(t_{m-1}) E(t_{m-1})-ab{IE} I(t_{m-1}) E(t_{m-1}) \\ &\quad + a_{E}\big(1-E(t_{m-1})\big)\Big)\vdots \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg), \end{align}$

(4.47)

$\begin{align} P(t_{n+1}) & = P(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Big( \Big(b_{PM} M(t_{m}) P(t_{m})+ a_{P} \big(1-P(t_{m})\big)\Big) \\ &\qquad \cdot\int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(b_{PM} M(t_{m-1}) P(t_{m-1})+ a_{P}\big(1-P(t_{m-1})\big)\Big) \\ & \qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Big), \end{align}$

(4.48)

$\begin{align} A(t_{n+1}) & = A(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(b_{A} P(t_{m})-\gamma_{AV} S(t_{m}) A(t_{m}) V(t_{m}) -a_{A} A(t_{m})\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(b_{A} P(t_{m})-\gamma_{AV} S(t_{m}) A(t_{m}) V(t_{m}) -a_{A} A(t_{m})\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg) \end{align}$

(4.49)

and

$\begin{align} S(t_{n+1}) & = S(0) + \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(r P(t_{m})\big(1-S(t_{m})\big)\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}}\frac{(\eta - t_{m-1})}{(t_{m+1} - \eta)^{1-\alpha }} d\eta -\Big(r P(t_{m-1})\big(1-S(t_{m-1})\big)\Big) \\ &\qquad \cdot \int_{t_{m}}^{t_{m+1}} \frac{(\eta - t_{m})}{(t_{m+1} - \eta)^{1-\alpha}}d\eta \Bigg) \end{align}$

(4.50)

These integrals are evaluated directly and the numerical solutions of Eqs (4.11)–(4.20) involving the LC derivative are given by

$\begin{align} V(t_{n+1}) & = V(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(\gamma_{V} I(t_{m}) -\gamma_{VA} S(t_{m}) A(t_{m}) V(t_{m})-\gamma_{VH} V(t_{m}) H(t_{m}) \\ &\quad - \alpha_{V} V(t_{m}) - \frac{a_{V1} V(t_{m})}{1+a_{V2}V(t_{m})}\Big)\cdot \chi_{1}(n,m) \\ &\quad -\Big(\gamma_{V} I(t_{m-1}) -\gamma_{VA} S(t_{m-1}) A(t_{m-1}) V(t_{m-1})-\gamma_{VH} V(t_{m-1}) H(t_{m-1}) \\ &\quad - \alpha_{V} V(t_{m-1}) - \frac{a_{V1} V(t_{m-1})}{1+a_{V2}V(t_{m-1})}\Big) \cdot\chi_{2}(n,m) \Bigg), \end{align}$

(4.51)

$\begin{align} H(t_{n+1}) & = H(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg(\Big(b_{HD} D\big(H(t_{m})+R(t_{m})\big) a_{R} R(t_{m}) \\ &\quad - \gamma_{HV} V(t_{m}) H(t_{m}) - b_{HV} F(t_{m}) H(t_{m})\Big)\cdot \chi_{1}(n,m) \\ &\quad - \Big(b_{HD} D\big(H(\eta)+R(\eta)\big) a_{R} R(\eta) -\gamma_{HV} V(\eta) H(\eta) - b_{HV} F(\eta) H(\eta)\Big) \\ &\qquad \cdot \chi_{2}(n,m) \Bigg), \end{align}$

(4.52)

$\begin{align} I(t_{n+1}) & = I(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg( \Big( \gamma_{HV} V(t_{m}) H(t_{m})-b_{IE} E(t_{m}) I(t_{m})\Big) \\ &\qquad \cdot \chi_{1}(n,m)-\Big( \gamma_{HV} V(t_{m-1}) H(t_{m-1})-b_{IE} E(t_{m-1}) I(t_{m-1})\Big) \\ &\qquad \cdot \chi_{2}(n,m)\Bigg), \end{align}$

(4.53)

$\begin{align} M(t_{n+1}) & = M(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n} \Bigg( \Big(\big(b_{MD}D+b_{MV}V(t_{m})\big)\big(1-M(t_{m})\big)-a_{M}M(t_{m}) \Big) \\ &\qquad \cdot \chi_{1}(n,m) -\Big(\big(b_{MD}D+b_{MV}V(t_{m-1})\big)\big(1-M(t_{m-1})\big) \\ &]quad -a_{M} M(t_{m-1}) \Big)\cdot\chi_{2}(n,m) \Bigg), \end{align}$

(4.54)

$\begin{align} F(t_{n+1}) & = F(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(\big(b_{F}M(t_{m})+C_{F}I(t_{m})\big)-b_{FH} H(t_{m}) F(t_{m})-a_{F} F(t_{m})\Big) \\ &\qquad \cdot \chi_{1}(n,m)-\Big(\big(b_{F}M(t_{m-1})+C_{F}I(t_{m-1})\big) \\ &\quad -b_{FH} H(t_{m-1}) F(t_{m-1})-a_{F} F(t_{m-1})\Big) \cdot \chi_{2}(n,m) \Bigg), \end{align}$

(4.55)

$\begin{align} R(t_{m+1}) & = \varphi_{1}(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(b_{HF} H(t_{m}) F(t_{m})-a_{R} R(t_{m})\Big) \\ &\qquad \cdot \chi_{1}(n,m) -\Big(b_{HF} H(t_{m-1}) F(t_{m-1})-a_{R} R(t_{m-1})\Big) \\ & \qquad \cdot \chi_{2}(n,m) \Bigg), \end{align}$

(4.56)

$\begin{align} E(t_{m+1}) & = E(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big( b_{EM} M(t_{m}) E(t_{m})-ab{IE} I(t_{m}) E(t_{m}) \\ &\quad + a_{E} \big(1-E(t_{m})\big)\Big)\cdot\chi_{1}(n,m) -\Big( b_{EM} M(t_{m-1}) E(t_{m-1})-ab{IE} I(t_{m-1}) E(t_{m-1}) \\ &\quad + a_{E} \big(1-E(t_{m-1})\big)\Big)\cdot \chi_{2}(n,m) \Bigg), \end{align}$

(4.57)

$\begin{align} P(t_{n+1}) & = P(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \frac{1}{h \Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(b_{PM} M(t_{m}) P(t_{m})+ a_{P} \big(1-P(t_{m})\big)\Big) \\ &\qquad \cdot \chi_{1}(n,m)-\Big(b_{PM} M(t_{m-1}) P(t_{m-1})+ a_{P} \big(1-P(t_{m-1})\big)\Big) \cdot \chi_{2}(n,m) \Bigg), \end{align}$

(4.58)

$\begin{align} A(t_{n+1}) & = A(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(b_{A} P(t_{m})-\gamma_{AV} S(t_{m}) A(t_{m}) V(t_{m}) -a_{A} A(t_{m})\Big) \\ &\qquad \cdot \chi_{1}(n,m)-\Big(b_{A} P(t_{m})-\gamma_{AV} S(t_{m}) A(t_{m}) V(t_{m}) -a_{A} A(t_{m})\Big)\cdot \chi_{2}(n,m) \Bigg) \end{align}$

(4.59)

and

$\begin{align} S(t_{n+1}) & = S(0) + \frac{h^{\alpha}}{\alpha(\alpha+1)\Gamma(\alpha)} \sum\limits_{m = 0}^{n}\Bigg( \Big(r P(t_{m}) \big(1-S(t_{m})\big)\Big) \\ &\qquad \cdot \chi_{1}(n,m) -\Big(r P(t_{m-1})\big(1-S(t_{m-1})\big)\Big) \chi_{2}(n,m) \Bigg). \end{align}$

(4.60)

$\begin{align} \chi_{1}(n,m)& = \Big((n + 1 - m)^{\alpha}(n -m + 2 + \alpha) - (n - m)^{\alpha}\times (n -m + 2 + 2\alpha) \Big), \end{align}$

(4.61)

$\begin{align} \chi_{2}(n,m) = \Big((n + 1 - m)^{\alpha+1} - (n -m)^{\alpha}(n -m + 1 + \alpha)\Big). \end{align}$

(4.62)

4.2. Numerical scheme for fractional immune response in CFC sense

Considering the CFC derivative, we have

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} V = \gamma_{V} I -\gamma_{VA} S A V -\gamma_{VH} V H-\alpha_{V} V-\frac{a_{V1} V}{1+a_{V2}V}, \end{align}$

(4.63)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha}H = b_{HD} D(H+R) a_{R} R -\gamma_{HV} V H -b_{HV} F H, \end{align}$

(4.64)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} I = \gamma_{HV} V H-b_{IE} E I, \end{align}$

(4.65)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} M = (b_{MD}D+b_{MV}V)(1-M)-a_{M} M, \end{align}$

(4.66)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} F = (b_{F}M+C_{F}I)-b_{FH} H F-a_{F} F, \end{align}$

(4.67)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} R = b_{HF} H F-a_{R} R, \end{align}$

(4.68)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} E = b_{EM} M E-ab{IE} I E+ a_{E} (1-E), \end{align}$

(4.69)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} P = b_{PM} M P+ a_{P} (1-P), \end{align}$

(4.70)

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} A = b_{A} P-\gamma_{AV} S A V -a_{A} A \end{align}$

(4.71)

and

$\begin{align} ^{ \rm{CFC}}_{0}D_{\xi}^{\alpha} S = r P(1-S). \end{align}$

(4.72)

As in the preceding section, by applying the fundamental theorem of fractional calculus, we obtain

$\begin{align} V(t) - V(0) & = \frac{1-\alpha}{M(\alpha)}\Big(\gamma_{V} I(t) -\gamma_{VA} S(t) A(t) V(t) -\gamma_{VH} V(t) H(t)-\alpha_{V} V(t) -\frac{a_{V1} V(t)}{1+a_{V2}V(t)}\Big) \\&\quad + \frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big(\gamma_{V} I(\eta) -\gamma_{VA} S(\eta) A(\eta) V(\eta) -\gamma_{VH} V(\eta) H(\eta)-\alpha_{V} V \\ &\quad - \frac{a_{V1} V(\eta)}{1+a_{V2}V(\eta)}\Big)d\eta, \end{align}$

(4.73)

$\begin{align} H(t) - H(0) & = \frac{1-\alpha}{M(\alpha)}\Big(b_{HD} D\big(H(t)+R(t)\big) a_{R} R(t) -\gamma_{HV} V(t) H(t) -b_{HV} F(t) H(t)\Big) \\ &\quad +\frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big(b_{HD} D\big(H(\eta)+R(\eta)\big) a_{R} R(\eta) -\gamma_{HV} V(\eta) H(\eta) -b_{HV} F(\eta) H(\eta)\Big)d\eta, \end{align}$

(4.74)

$\begin{align} I(t) - I(0) & = \frac{1-\alpha}{M(\alpha)}\Big( \gamma_{HV} V(t) H(t)-b_{IE} E(t) I(t)\Big)\\ &\quad + \frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big( \gamma_{HV} V(\eta) H(\eta)-b_{IE} E(\eta) I(\eta)\Big)d\eta, \end{align}$

(4.75)

$\begin{align} M(t) - M(0) & = \frac{1-\alpha}{M(\alpha)}\Big(\big(b_{MD}D+b_{MV}V(t)\big)\big(1-M(t)\big)-a_{M} M(t)\Big) \\ &\quad +\frac{\alpha}{M(\alpha)}\int_{0}^{t} \Big(\big(b_{MD}D+b_{MV}V(\eta)\big)\big(1-M(\eta)\big)-a_{M} M(\eta)\Big)d\eta, \end{align}$

(4.76)

$\begin{align} F(t) - F(0) & = \frac{1-\alpha}{M(\alpha)}\Big(\big(b_{F}M(t)+C_{F}I(t)\big)-b_{FH} H(t) F(t)-a_{F} F(t)\Big)\\ &\quad + \frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big(\big(b_{F}M(\eta)+C_{F}I(\eta)\big)-b_{FH} H(\eta) F(\eta)-a_{F} F(\eta)\Big)d\eta, \end{align}$

(4.77)

$\begin{align} R(t) - R(0) = \frac{1-\alpha}{M(\alpha)} \Big(b_{HF} H(t) F(t)-a_{R} R(t)\Big) + \frac{\alpha}{M(\alpha)}\int_{0}^{t} \Big(b_{HF} H(\eta) F(\eta)-a_{R} R(\eta)\Big)d\eta, \end{align}$

(4.78)

$\begin{align} E(t) - E(0) & = \frac{1-\alpha}{M(\alpha)} \Big(b_{EM} M(t) E(t)-ab{IE} I(t) E(t)+ a_{E} \big(1-E(t)\big)\Big) \\ &\quad + \frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big(b_{EM} M(\eta) E(\eta)-ab{IE} I(\eta) E(\eta)+ a_{E}\big(1-E(\eta)\big)\Big) d\eta, \end{align}$

(4.79)

$\begin{align} P(t) - P(0) & = \frac{1-\alpha}{M(\alpha)} \Big( b_{PM} M(t) P(t)+ a_{P} \big(1-P(t)\big)\Big) \\ & \quad +\frac{\alpha}{M(\alpha)}\int_{0}^{t} \Big( b_{PM} M(\eta) P(\eta)+ a_{P}\big(1-P(\eta)\big)\Big)d\eta, \end{align}$

(4.80)

$\begin{align} A(t) - A(0) & = \frac{1-\alpha}{M(\alpha)} \Big(b_{A} P(t)-\gamma_{AV} S(t) A(t) V(t) -a_{A} A(t)\Big) \\ & \quad +\frac{\alpha}{M(\alpha)}\int_{0}^{t} \Big(b_{A} P(\eta)-\gamma_{AV} S(\eta) A(\eta) V(\eta) -a_{A} A(\eta)\Big) d\eta, \end{align}$

(4.81)

and

$\begin{align} S(t) - S(0) & = \frac{1-\alpha}{M(\alpha)} \Big(r P(t)\big(1-S(t)\big)\Big)+\frac{\alpha}{M(\alpha)} \int_{0}^{t} \Big(r P(\eta)\big(1-S(\eta)\big)\Big)d\eta, \end{align}$

(4.82)

where $M(\alpha)$ is a normalization function such that $M(0) = M(1) = 1$ .

We now complete the procedure with one equation and, for the remaining equations, we repeat the same procedure to get the final constructions of approximation iteration. First, we let $t = t_{n+1}$

$\begin{align} S(t_{n+1}) - S(0) = \frac{1-\alpha}{M(\alpha)} \Big(r P(t_{n})\big(1-S(t_{n})\big)\Big) +\frac{\alpha}{M(\alpha)} \int_{0}^{t_{n+1}} \Big(r P(\eta)\big(1-S(\eta)\big)\Big)d\eta. \end{align}$

(4.83)

Then $t = t_{n}$ and

$\begin{align} S(t_{n}) - S(0) = \frac{1-\alpha}{M(\alpha)} \Big(r P(t_{n-1})\big(1-S(t_{n-1})\big)\Big) +\frac{\alpha}{M(\alpha)} \int_{0}^{t_{n}} Big(r P(\eta)\big(1-S(\eta)\big)\Big)d\eta. \end{align}$

(4.84)

Thus, in view of Eqs (4.83), (4.84), we obtain

$\begin{align} S(t_{n+1}) & = S(t_{n})+ \frac{1-\alpha}{M(\alpha)}\Bigg( \Big(r P(t_{n})\big(1-S(t_{n})\big)\Big) - \Big(r P(t_{n-1})\big(1-S(t_{n-1})\big)\Big)\Bigg)\\ &\quad + \frac{\alpha}{M(\alpha)} \int_{t_{n}}^{t_{n+1}} \Big(r P(\eta)\big(1-S(\eta)\big)\Big)d\eta. \end{align}$

(4.85)

In view of the Lagrange polynomial interpolation, and by integrating the following expressions, we obtain

$\begin{align} \int_{t_{n}}^{t_{n+1}}\Big(r P(\eta)\big(1-S(\eta)\big)\Big)d\eta & = \frac{3h}{2} \Bigg(\Big(r P(t_{n})\big(1-S(t_{n})\big)\Big)\Bigg) \\ &\quad-\frac{h}{2}\Bigg(\Big(r P(t_{n+1})\big(1-S(t_{n+1})\big)\Big)\Bigg). \end{align}$

(4.86)

After some manipulation, we have the following expression:

$\begin{align} S(t_{n+1}) & = S(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(r P(t_{n})\big(1-S(t_{n})\big)\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(r P(t_{n-1})\big(1-S(t_{n-1})\big)\Big). \end{align}$

(4.87)

Following the same procedure as in the case of LC, we find that

$\begin{align} V(t_{n+1}) & = V(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(\gamma_{V} I(t_{n}) -\gamma_{VA} S(t_{n}) A(t_{n}) V(t_{n})-\gamma_{VH} V(t_{n}) H(t_{n}) \\ &\quad - \alpha_{V} V(t_{n}) - \frac{a_{V1} V(t_{n})}{1+a_{V2}V(t_{n})}\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(\gamma_{V} I(t_{n-1}) -\gamma_{VA} S(t_{n-1}) A(t_{n-1}) V(t_{n-1})-\gamma_{VH} V(t_{n-1}) H(t_{n-1}) \\ & \quad - \alpha_{V} V(t_{n-1}) - \frac{a_{V1} V(t_{n-1})}{1+a_{V2}V(t_{n-1})}\Big). \end{align}$

(4.88)

$\begin{align} H(t_{n+1}) & = H(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{HD} D\big(H(t_{n})+R(t_{n})\big) a_{R} R(t_{n}) \\ &\quad - \gamma_{HV} V(t_{n}) H(t_{n}) - b_{HV} F(t_{n}) H(t_{n})\Big)\\ &\quad - \Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big( b_{HD} D\big(H(t_{n-1})+R(t_{n-1})\big) a_{R} R(t_{n-1}) \\ &\quad - \gamma_{HV} V(t_{n-1}) H(t_{n-1}) - b_{HV} F(t_{n-1}) H(t_{n-1})\Big), \end{align}$

(4.89)

$\begin{align} I(t_{n+1}) & = I(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(\gamma_{HV} V(t_{n}) H(t_{n})-b_{IE} E(t_{n}) I(t_{n})\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(\gamma_{HV} V(t_{n-1}) H(t_{n-1})-b_{IE} E(t_{n-1}) I(t_{n-1})\Big), \end{align}$

(4.90)

$\begin{align} M(t_{n+1}) & = M(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(\big(b_{MD}D+b_{MV}V(t_{n})\big)\big(1-M(t_{n})\big)-a_{M} M(t_{n})\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big( \big(b_{MD}D+b_{MV}V(t_{n-1})\big)\big(1-M(t_{n-1})\big)-a_{M} M(t_{n-1})\Big), \end{align}$

(4.91)

$\begin{align} F(t_{n+1}) & = F(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(\big(b_{F}M(t_{n})+C_{F}I(t_{n})\big)-b_{FH} H(t_{n}) F(t_{n})-a_{F} F(t_{n})\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(\big(b_{F}M(t_{n-1})+C_{F}I(t_{n-1})\big)-b_{FH} H(t_{n-1}) F(t_{n-1}) \\ &\quad - a_{F} F(t_{n-1})\Big), \end{align}$

(4.92)

$\begin{align} R(t_{n+1}) & = R(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{HF} H(t_{n}) F(t_{n})-a_{R} R(t_{n})\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(b_{HF} H(t_{n-1}) F(t_{n-1})-a_{R} R(t_{n-1})\Big), \end{align}$

(4.93)

$\begin{align} R(t_{n+1}) & = R(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{HF} H(t_{n}) F(t_{n})-a_{R} R(t_{n})\Big)\\ &\quad - \Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(b_{HF} H(t_{n-1}) F(t_{n-1})-a_{R} R(t_{n-1})\Big), \end{align}$

(4.94)

$\begin{align} E(t_{n+1}) & = E(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{EM} M(t_{n}) E(t_{n})-ab{IE} I(t_{n}) E(t_{n})+ a_{E} \big(1-E(t_{n})\big)\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(b_{EM} M(t_{n-1}) E(t_{n-1})-ab{IE} I(t_{n-1}) E(t_{n-1})+ a_{E} \big(1-E(t_{n-1})\big)\Big), \end{align}$

(4.95)

$\begin{align} P(t_{n+1}) & = P(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{PM} M(t_{n}) P(t_{n})+ a_{P} \big(1-P(t_{n})\big)\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(b_{PM} M(t_{n-1}) P(t_{n-1})+ a_{P} \big(1-P(t_{n-1})\big)\Big), \end{align}$

(4.96)

and

$\begin{align} A(t_{n+1}) & = A(t_{n})+ \Big(\frac{1-\alpha}{M(\alpha)}+\frac{3\alpha h}{2 M(\alpha)}\Big)\Big(b_{A} P(t_{n})-\gamma_{AV} S(t_{n}) A(t_{n}) V(t_{n}) -a_{A} A(t_{n})\Big)\\ &\quad -\Big(\frac{1-\alpha}{M(\alpha)}+\frac{\alpha h}{2 M(\alpha)}\Big)\Big(b_{A} P(t_{n-1})-\gamma_{AV} S(t_{n-1}) A(t_{n-1}) V(t_{n-1}) -a_{A} A(t_{n-1})\Big). \end{align}$

(4.97)

5. Numerical simulations

In this section, we present numerical simulations of the model given by the systems given by Eqs (4.1)–(4.10), and (4.63)–(4.72). We study the dynamical behavior of the model for variation of the integer-order derivative and non-integer $\alpha$ . The basis of the selection of the parameter values are shown in ^[37]. In our investigation, we have concentrated upon the case that the host has no dead, infected or resistant cells, no interferon molecules, and no activated APC so that $h_{0} = 1, i_{0} = m_{0} = f_{0} = r_{0} = 0)$ . The initial levels of effectors, plasma cells, and antibodies are assumed to be at the homeostatic values (that is, $e_{0} = p_{0} = a_{0} = 1$ ) ^[42]. The initial antigenic compatibility is $s_{0} = 0.1$ and the initial virus particle $v_{0} = 0.01.$ Now our focus is on studying the effect of the change of the integer and non-integer derivatives on the behaviour of the numerical solutions. For the the effects of biological behaviour for this model ^[42].

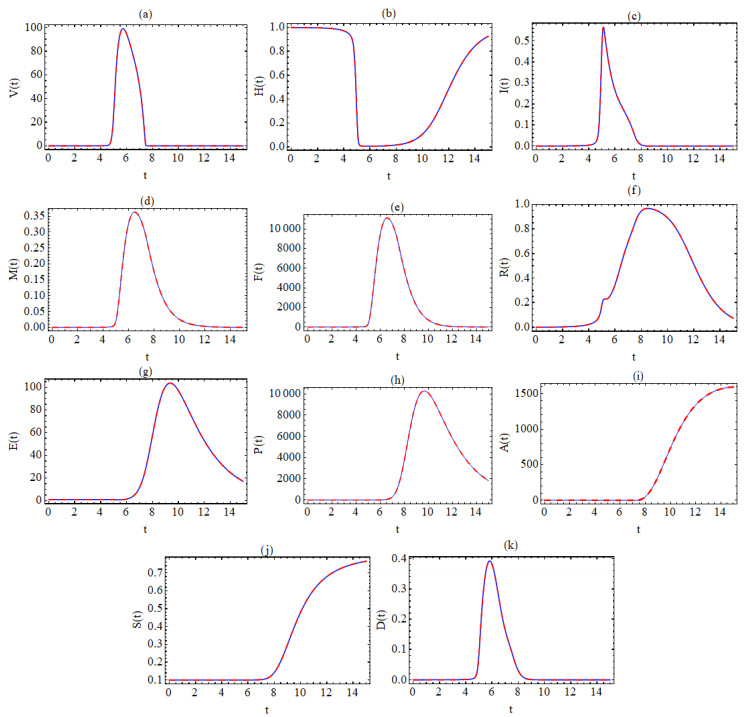
First of all, in , we clarify the comparison between the solutions presented in this paper with those derived by using known numerical methods such as finite difference methods (FDM) in the case of $\alpha = 1$ . Of course, the numerical solutions based on the two operators LC and CFC in the case when $\alpha = 1$ are identical, so the comparison will be done once. We set the initial and parameter values as $v_{0} = 0.01, \, h_{0} = 1, \, i_{0} = 0, \, m_{0} = 0, \, f_{0} = 0, \, r_{0} = 0, \, e_{0} = 1, \, p_{0} = 1, a_{0} = 1, s_{0} = 0.1 \; \gamma_{V} = 510, \gamma_{VA} = 6192/10, \gamma_{VH} = 102/100, \alpha_{V} = 17/10, a_{V_{1}} = 100, a_{V_{2}} = 23000, b_{HD} = 4, a_{R} = 1, \gamma_{HV} = 34/100, b_{HF} = 1/100, b_{IE} = 66/1000, a_{I} = 15/10$ , $b_{MD} = 1, b_{MV} = 37/10000, a_{M} = 1, b_{F} = 250000, c_{F} = 2000, b_{FH} = 17, a_{F} = 8, b_{EM} = 83/10, b_{EI} = 272/100, a_{E} = 4/10, b_{PM} = 115/10, a_{P} = 4/10, b_{A} = 43/1000, \gamma_{AV} = 1462/10, a_{A} = 43/1000$ and $r = 3/100000$ . These initial values and parameters were taken as in ^[37].

Figure 2. Graph of the comparison between the numerical solutions based on LC and CFC operators and the numerical solutions based on FDM for

$\alpha = 1, v_{0} = 0.2, \, h_{0} = 0.1, \, i_{0} = 0.01, \, m_{0} = 0.01, \, f_{0} = 0, \, r_{0} = 0.1, \, e_{0} = 2, \, p_{0} = 0.4, a_{0} = 1, s_{0} = 0.1$

$\gamma_{V} = 510, \gamma_{VA} = 6192/10, \gamma_{VH} = 102/100, \alpha_{V} = 17/10, a_{V_{1}} = 100, a_{V_{2}} = 23000, b_{HD} = 4, a_{R} = 1, \gamma_{HV} = 34/100, b_{HF} = 1/100, b_{IE} = 66/1000, a_{I} = 15/10$ ,

$b_{MD} = 1, b_{MV} = 37/10000, a_{M} = 1, b_{F} = 250000, c_{F} = 2000, b_{FH} = 17, a_{F} = 8, b_{EM} = 83/10, b_{EI} = 272/100, a_{E} = 4/10, b_{PM} = 115/10, a_{P} = 4/10, b_{A} = 43/1000, \gamma_{AV} = 1462/10, a_{A} = 43/1000$ and

$r = 3/100000$ . Red color: LC(CFC) solutions; blue color: FDM solutions.

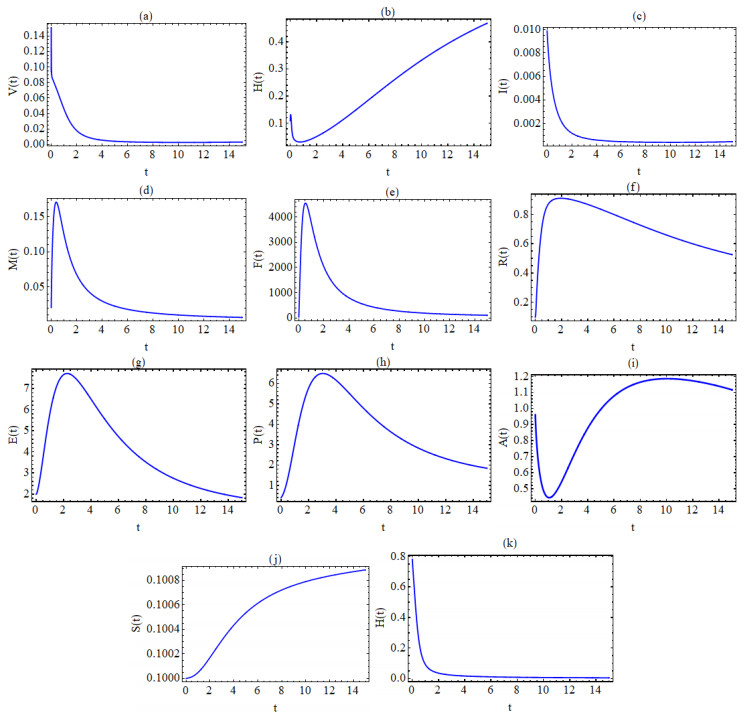
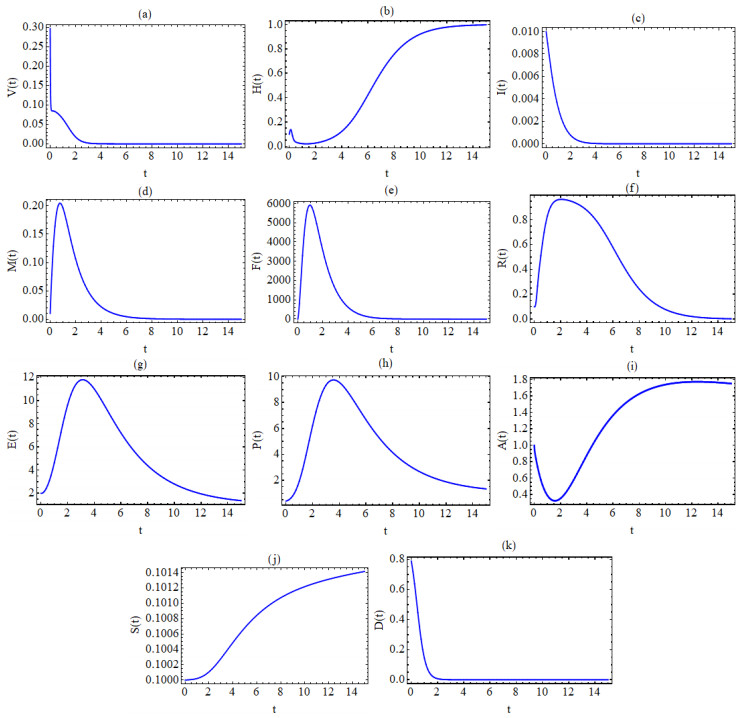
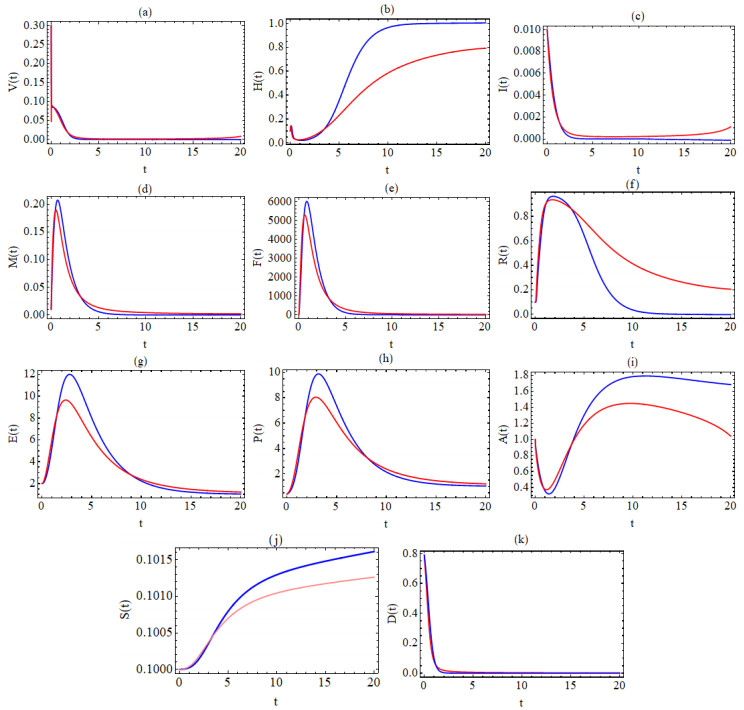
DownLoad: Full-Size Img PowerPoint

From it is clear that our results are consistent with those derived by the known numerical method as well as those with the results in ^[37]. Now we focus on the fraction $\alpha$ values which are the aim of our paper. Figures 2 and illustrate the behavior of the numerical solutions based on the LC and CFC operators, respectively. In the numerical solutions based on the LC operators are displayed against time (days) for the initial values $v_{0} = 0.2, \, h_{0} = 0.1, \, i_{0} = 0.01, \, m_{0} = 0.01, \, f_{0} = 0, \, r_{0} = 0.1, \, e_{0} = 2, \, p_{0} = 0.4, a_{0} = 1, s_{0} = 0.1$ and for the same parameter values as those in Figure 2. In Figure 4 the numerical solutions based on the CFC operator are plotted against time for the similar data as in . shows the behavior of the numerical solutions based onto the LC and CFC operators with $\alpha = 0.9$ .

Figure 3. Graph of the numerical solutions against

$t$ using the LC operator for

$\alpha = 0.8, v_{0} = 0.01, \, h_{0} = 1, \, i_{0} = 0, \, m_{0} = 0, \, f_{0} = 0, \, r_{0} = 0, \, e_{0} = 1, \, p_{0} = 1, a_{0} = 1, s_{0} = 0.1 \; \gamma_{V} = 510, \gamma_{VA} = 6192/10, \gamma_{VH} = 102/100, \alpha_{V} = 17/10, a_{V_{1}} = 100, a_{V_{2}} = 23000, b_{HD} = 4, a_{R} = 1, \gamma_{HV} = 34/100, b_{HF} = 1/100, b_{IE} = 66/1000, a_{I} = 15/10$ ,

$r = 3/100000$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. Graph of the numerical solutions against

$t$ using the CFC operator for

$r = 3/100000$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. Graph of the numerical solutions against

$t$ using the CFC operator for

$\alpha = 0.9, v_{0} = 0.3, \, h_{0} = 1, \, i_{0} = 0, \, m_{0} = 0, \, f_{0} = 0, \, r_{0} = 0, \, e_{0} = 1, \, p_{0} = 1, a_{0} = 1, s_{0} = 0.1 \; \gamma_{V} = 510, \gamma_{VA} = 6192/10, \gamma_{VH} = 102/100, \alpha_{V} = 17/10, a_{V_{1}} = 100, a_{V_{2}} = 23000, b_{HD} = 4, a_{R} = 1, \gamma_{HV} = 34/100, b_{HF} = 1/100, b_{IE} = 66/1000, a_{I} = 15/10$ ,

$r = 3/100000$ . Red color: LC solutions; blue color: CFC solutions.

DownLoad: Full-Size Img PowerPoint

We note from that the two solutions exhibit the same behavior at the time of getting started and also at the steady state as $t$ approaches to a large time.

6. Conclusions

In our present investigation, we have considered the model of immune response to uncomplicated influenza A virus (HIV) infection, the discussion of which was initiated in ^[1]. The novelty of the presented work is in the construction of a new algorithm for the fractional-order system of human immune against HIV infection. To the best our knowledge, this is the first study for this fractional-order model. Here, in this paper, we have replaced the ordinary derivative by the Liouville-Caputo (LC) and Caputo-Fabrizio (CFC) fractional-order derivatives. We have constructed the scheme for these operators according to the fundamental theorem of fractional calculus and the two-step Lagrange polynomials. Numerical simulations are carried out by using these schemes.

The accuracy of the numerical solutions was verified for our usage of the proposed method by closely comparing our numerical solutions with the numerical solutions resulting from the use of the computer program package, Mathematica, and also with those in ^[37]. Excellent agreement has been found. The behavior of the numerical solutions for LC and CFC are also illustrated graphically.

Some useful highlights of our present investigation are being itemized below.

● The proposed methods have many applications and are widely used because of their good properties in the process of approximation.

● The methods used include a numerical technique with high accuracy, which is easy to use for other problems as well.

● The numerical solutions have the same behaviour when the order of the derivative varies from non-integer order to integer order.

● For future work, it is possible to extend these studies to the fractal-fractional derivatives involving different operators.

● For the interest and motivation for further researches on the subject of this paper, we have chosen to cite a number of recently-published related works ^{[4,5,6,25,26,27,46,47,48,49,50,51,52]}.

● These recent works proposed and made use of many different methods and techniques for solving various families of fractional differential equations.

Acknowledgements

J. F. Gómez Aguilar acknowledges the support provided by CONACyT: Cátedras CONACyT para jóvenes investigadores 2014 and SNI-CONACyT.

Conflict of interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

[1]	D. S. Jones, M. J. Plank, B. D. Sleeman, Differential Equations and Mathematical Biology, Chapman & Hall (CRC Press), Baton Roca, Florida, 2010.
[2]	A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies, Elsevier (North-Holland) Science Publishers, Amsterdam, London and New York, 2006.
[3]	H. M. Srivastava, Fractional-order derivatives and integrals: Introductory overview and recent developments, Kyungpook Math. J., 60 (2020), 73-116.
[4]	S. Kumar, A. Ahmadian, R. Kumar, D. Kumar, J. Singh, D. Baleanu, et al., An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets, Mathematics, 8 (2020), 558.
[5]	J. Singh, A. Kilicman, D. Kumar, R. Swroop, F. M. Ali, Numerical study for fractional model of nonlinear predator-prey biological population dynamical system, Therm. Sci., 23 (2019), S2017- S2025.
[6]	S. Aljhani, M. S. Md Noorani, A. K. Alomari, Numerical solution of fractional-order HIV model using homotopy method, Discrete Dyn. Nat. Soc., 2020 (2020), 2149037.
[7]	J. M. Amigó, M. Small, Mathematical methods in medicine: Neuroscience, cardiology and pathology, Philos. Trans. A Math. Phys. Eng. Sci., 375 (2017), 20170016.
[8]	M. A. Khan, S. W. Shah, S. Ullah, J. F. Gómez-Aguilar, A dynamical model of asymptomatic carrier zika virus with optimal control strategies, Nonlinear Anal. Real World Appl., 50 (2019), 144-170.
[9]	M. A. Taneco-Hernández, V. F. Morales-Delgado, J. F. Gómez-Aguilar, Fractional Kuramoto-Sivashinsky equation with power law and stretched Mittag-Leffler kernel, Phys. A, 527 (2019), 121085.
[10]	S. Ullah, M. A. Khan, J. F. Gómez-Aguilar, Mathematical formulation of hepatitis B virus with optimal control analysis, Optim. Control Appl. Methods, 40 (2019), 529-544.
[11]	V. F. Morales-Delgado, J. F. Gómez-Aguilar, K. M. Saad, M. A. Khane, P. Agarwal, Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach, Phys. A, 523 (2019), 48-65.
[12]	V. F. Morales-Delgado, J. F. Gómez-Aguilar, K. M. Saad, R. F. E. Jiméenez, Application of the Caputo-Fabrizio and Atangana-Baleanu fractional derivatives to mathematical model of cancer chemotherapy effect, Math. Methods Appl. Sci., 42 (2019), 1167-1193.
[13]	E. Bonyah, M. A. Khan, K. O. Okosun, J. F. Gómez-Aguilar, Modelling the effects of heavy alcohol consumption on the transmission dynamics of gonorrhea with optimal control, Math. Biosci., 309 (2019), 1-11.
[14]	V. F. Morales-Delgado, J. F. Gómez-Aguilar, M. A. Taneco-Hernándeza, R. F. Escobar-Jiménez, V. H. Olivares-Peregrino, Mathematical modeling of the smoking dynamics using fractional differential equations with local and nonlocal kernel, J. Nonlinear Sci. Appl., 11 (2018), 994- 1014.
[15]	E. Uçar, S. Uçar, N. Özdemir, Z. Hammouch, Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative. Chaos Solitons Fractals, 118 (2019), 300- 306.
[16]	M. A. Khan, Z. Hammouch, D. Baleanu, Modeling the dynamics of hepatitis E via the CaputoFabrizio derivative, Math. Model. Natur. Phenom., 14 (2019), 311.
[17]	J. Hristov, Derivation of the fractional Dodson equation and beyond: Transient diffusion with a non-singular memory and exponentially fading-out diffusivity, Progr. Fract. Differ. Appl., 3 (2017), 1-16.
[18]	K. M. Owolabi, A. Atangana, Numerical simulation of noninteger order system in subdiffusive, diffusive, and superdiffusive scenarios, J. Comput. Nonlinear Dyn., 12 (2017), 031010.
[19]	K. M. Saad, K. M. Khader, J. F. Gómez-Aguilar, D. Baleanu, Numerical solutions of the fractional Fisher's type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods, Chaos, 29 (2019), 023116.
[20]	M. M. Khader, K. M. Saad, Numerical treatment for studying the blood ethanol concentration systems with different forms of fractional derivatives, Int. J. Modern Phys. C., 31 (2020), 1-13.
[21]	K. M. Saad, J. F. Gómez-Aguilar, Coupled reaction-diffusion waves in a chemical system via fractional derivatives in Liouville-Caputo sense, Rev. Mex. Fís., 64 (2018), 539-547.
[22]	K. M. Saad, J. F. Gómez-Aguilar, Analysis of reaction-diffusion system via a new fractional derivative with non-singular kernel, Phys. A, 509 (2018), 703-716.
[23]	K. M. Saad, New fractional derivative with non-singular kernel for deriving Legendre spectral collocation method, Alexandria Eng. J., 2019, forthcoming.
[24]	K. M. Saad, H. M. Srivastava, J. F. Gómez-Aguilar, A fractional quadratic autocatalysis associated with chemical clock reactions involving linear inhibition, Chaos Solitons Fractals, 132 (2020), 109557.
[25]	A. K. Alomari, Homotopy-Sumudu transforms for solving system of fractional partial differential equations, Adv. Differ. Equations, 2020 (2020), 222.
[26]	A. Goswami, J. Singh, D. Kumar, Sushila, An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma, Phys. A, 524 (2019), 563-575.
[27]	J. Singh, D. Kumar, D. Baleanu, On the analysis of fractional diabetes model with exponential law, Adv. Differ. Equations, 2018 (2018), 231.
[28]	K. M. Saad, E. H. F. Al-Shareef, A. K. Alomari, D. Baleanu, J. F. Gómez-Aguilar, On exact solutions for time-fractional Korteweg-de Vries and Korteweg-de Vries-Burgers' equations using homotopy analysis transform method, Chin. J. Phys., 63 (2020), 149-162.
[29]	M. Masjed-Jamei, Z. Moalemi, H. M. Srivastava, I. Area, Some modified Adams-Bashforth methods based upon the weighted Hermite quadrature rules, Math. Methods Appl. Sci., 43 (2020), 1380-1398.
[30]	K. Diethelm, N. J. Ford, A. D. Freed, A predictor-corrector approach for the numerical solution of fractional differential equations, Nonlinear Dyn., 29 (2020), 3-22.
[31]	K. Diethelm, A. J. Ford, A. D. Freed, Detailed error analysis for a fractional Adams method, Numer. Algorithms, 36 (2004), 31-52.
[32]	L. Galeone, R. Garrappa, Fractional Adams-Moulton methods, Math. Comput. Simul., 79 (2008), 1358-1367.
[33]	C. Li, C. Tao, On the fractional Adams method, Comput. Math. Appl., 58 (2009), 1573-1588.
[34]	V. Daftardar-Gejji, H. Jafari, Analysis of a system of non autonomous fractional differential equations involving Caputo derivatives, J. Math. Anal. Appl., 328 (2007), 1026-1033.
[35]	V. Daftardar-Gejji, Y. Sukale, S. Bhalekar, A new predictor-corrector method for fractional differential equations, Appl. Math. Comput., 244 (2014), 158-182.
[36]	A. Atangana, K. M. Owolabi, New numerical approach for fractional differential equations, Math. Model. Nat. Phenom., 13 (2018), 3.
[37]	B. Hancioglua, D. Swigona, G. Clermont, A dynamical model of human immune response to influenza A virus infection, J. Theoret. Biol., 246 (2007), 70-86.
[38]	Y. Zhang, Z. Xu, Y. Cao, Host-Virus Interaction: How Host Cells Defend Against Influenza A Virus Infection, Viruses, 12 (2020), 376.
[39]	E. De Vries, W. Du, H. Guo, C. A. De Haan, Influenza A Virus Hemagglutinin-NeuraminidaseReceptor Balance: Preserving Virus Motility, Trends Microbiol., 28 (2020), 57-67.
[40]	B. Li, S. M. Clohisey, B. S. Chia, B. Wang, A. Cui, T. Eisenhaure, et al., Genome-wide CRISPR screen identifies host dependency factors for influenza A virus infection, Nat. Commun., 11 (2020), 164.
[41]	R. Jia, S. Liu, J. Xu, X. Liang, IL16 deficiency enhances Th1 and cytotoxic T lymphocyte response against influenza A virus infection, Biosci. Trends, 13 (2020), 516-522.
[42]	B. Asquith, C. R. M. Bangham, An introduction to lymphocyte and viral dynamics: The power and limitations of mathematical analysis, Proc. Biol. Sci., 270 (2003), 1651-1657.
[43]	I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Mathematics in Science and Engineering, Academic Press, San Diego, London and Toronto, 1999, 198, 1-340.
[44]	K. S. Miller, B. Ross, An Introduction to Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication, John Wiley and Sons, New York, Chichester, Brisbane, Toronto and Singapore, 1993.
[45]	W. Faridi, M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 73-85.
[46]	H. Singh, H. M. Srivastava, Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials, Appl. Sci., 10 (2020), 2850.
[47]	H. M. Srivastava, H. I. Abdel-Gawad, K. M. Saad, Stability of traveling waves based upon the Evans function and Legendre polynomials, Appl. Sci., 10 (2020), 846.
[48]	H. M. Srivastava, H. Günerhan, B. Ghanbari, Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity, Math. Methods Appl. Sci., 42 (2019), 7210-7221.
[49]	H. M. Srivastava, F. A. Shah, R. Abass, An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation, Russian J. Math. Phys., 26 (2019), 77-93.
[50]	H. M. Srivastava, R. S. Dubey, M. Jain, A study of the fractional-order mathematical model of diabetes and its resulting complications, Math. Methods Appl. Sci., 42 (2019), 4570-4583.
[51]	H. M. Srivastava, H. Günerhan, Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease, Math. Methods Appl. Sci., 42 (2019), 935-941.
[52]	B. Ahmad, M. Alghanmi, A. Alsaedi, H. M. Srivastava, S. K. Ntouyas, The Langevin equation in terms of generalized Liouville-Caputo derivatives with nonlocal boundary conditions involving a generalized fractional integral, Mathematics, 7 (2019), 533.

This article has been cited by:

1.	Mohammad Izadi, H.M. Srivastava, Numerical approximations to the nonlinear fractional-order Logistic population model with fractional-order Bessel and Legendre bases, 2021, 145, 09600779, 110779, 10.1016/j.chaos.2021.110779
2.	Saif Ullah, Sana Zulfiqar, Anum Aish Buhader, Najeeb Alam Khan, Analysis of Caputo-Fabrizio fractional order semi-linear parabolic equations via effective amalgamated technique, 2021, 96, 1402-4896, 035214, 10.1088/1402-4896/abd796
3.	C. J. Zúñiga-Aguilar, J. F. Gómez-Aguilar, H. M. Romero-Ugalde, Hadi Jahanshahi, Fawaz E. Alsaadi, Fractal-fractional neuro-adaptive method for system identification, 2021, 0177-0667, 10.1007/s00366-021-01314-w
4.	P. Veeresha, D.G. Prakasha, Abdel-Haleem Abdel-Aty, Harendra Singh, Emad E. Mahmoud, Sunil Kumar, An efficient approach for fractional nonlinear chaotic model with Mittag-Leffler law, 2021, 33, 10183647, 101347, 10.1016/j.jksus.2021.101347
5.	Hari Mohan Srivastava, Khaled M. Saad, A Comparative Study of the Fractional-Order Clock Chemical Model, 2020, 8, 2227-7390, 1436, 10.3390/math8091436
6.	Hamdy I. Abdel‐Gawad, Ali A. Aldailami, Khaled M. Saad, José F. Gómez‐Aguilar, Numerical solution of q ‐dynamic equations , 2020, 0749-159X, 10.1002/num.22725
7.	H. M. Srivastava, Khaled M. Saad, Numerical Simulation of the Fractal-Fractional Ebola Virus, 2020, 4, 2504-3110, 49, 10.3390/fractalfract4040049
8.	Kashif Ali Abro, Abdon Atangana, José Francisco Gomez-Aguilar, Role of bi-order Atangana–Aguilar fractional differentiation on Drude model: an analytic study for distinct sources, 2021, 53, 0306-8919, 10.1007/s11082-021-02804-3
9.	H. M. Srivastava, I. Area, J. J. Nieto, Power-series solution of compartmental epidemiological models, 2021, 18, 1551-0018, 3274, 10.3934/mbe.2021163
10.	Hassan Khan, J. F. Gómez-Aguilar, A. A. Alderremy, Shaban Aly, Dumitru Baleanu, On the approximate solution of fractional-order Whitham–Broer–Kaup equations, 2021, 35, 0217-9849, 2150192, 10.1142/S021798492150192X
11.	Ebenezer Bonyah, Ali Akgül, On solutions of an obesity model in the light of new type fractional derivatives, 2021, 147, 09600779, 110956, 10.1016/j.chaos.2021.110956
12.	Tahir Khan, The analysis of fractional-order hepatitis B epidemiological model, 2022, 1745-5030, 1, 10.1080/17455030.2022.2120217
13.	Nauman Raza, Zara Hassan, J. F. Gómez-Aguilar, Extraction of new super-Gaussian solitons via collective variables, 2021, 53, 0306-8919, 10.1007/s11082-021-03125-1
14.	Tahir Khan, Roman Ullah, Ali Yousef, Gul Zaman, Qasem M. Al-Mdallal, Yasser Alraey, M. De Aguiar, Modeling and Dynamics of the Fractional Order SARS-CoV-2 Epidemiological Model, 2022, 2022, 1099-0526, 1, 10.1155/2022/3846904
15.	H. M. Srivastava, Rashid Jan, Asif Jan, Wejdan Deebani, Meshal Shutaywi, Fractional-calculus analysis of the transmission dynamics of the dengue infection, 2021, 31, 1054-1500, 053130, 10.1063/5.0050452
16.	Hari M. Srivastava, Jaouad Danane, Analysis of a Stochastic SICR Epidemic Model Associated with the Lévy Jump, 2022, 12, 2076-3417, 8434, 10.3390/app12178434
17.	Babak Shiri, Dumitru Baleanu, A General Fractional Pollution Model for Lakes, 2022, 4, 2096-6385, 1105, 10.1007/s42967-021-00135-4
18.	Hassan Khan, Rasool Shah, J.F. Gómez-Aguilar, Dumitru Baleanu, Poom Kumam, D. Baleanu, D. Kumar, J. Hristov, Travelling waves solution for fractional-order biological population model, 2021, 16, 0973-5348, 32, 10.1051/mmnp/2021016
19.	Xiaolan Liu, Cheng-Cheng Zhu, Hari Mohan Srivastava, Hongyan Xu, Global Stability for a Diffusive Infection Model with Nonlinear Incidence, 2022, 10, 2227-7390, 4296, 10.3390/math10224296
20.	Jianghua Han, Optimization System of Strength and Flexibility Training in Aerobics Course Based on Lagrangian Mathematical Equation, 2022, 0, 2444-8656, 10.2478/amns.2022.2.0169
21.	H. M. Srivastava, Sinan Deniz, A new modified semi-analytical technique for a fractional-order Ebola virus disease model, 2021, 115, 1578-7303, 10.1007/s13398-021-01081-9
22.	Sergio Adriani David, Carlos Alberto Valentim, Amar Debbouche, Fractional Modeling Applied to the Dynamics of the Action Potential in Cardiac Tissue, 2022, 6, 2504-3110, 149, 10.3390/fractalfract6030149
23.	SHU-BO CHEN, SAMANEH SORADI-ZEID, MARYAM ALIPOUR, YU-MING CHU, J. F. GÓMEZ-AGUILAR, HADI JAHANSHAHI, OPTIMAL CONTROL OF NONLINEAR TIME-DELAY FRACTIONAL DIFFERENTIAL EQUATIONS WITH DICKSON POLYNOMIALS, 2021, 29, 0218-348X, 2150079, 10.1142/S0218348X21500791
24.	Tahir Khan, Rahman Ullah, Thabet Abdeljawad, Manar A. Alqudah, Faizullah Faiz, A Theoretical Investigation of the SARS-CoV-2 Model via Fractional Order Epidemiological Model, 2023, 135, 1526-1506, 1295, 10.32604/cmes.2022.022177
25.	Tahir Khan, Saeed Ahmad, Rahman Ullah, Ebenezer Bonyah, Khursheed J. Ansari, The asymptotic analysis of novel coronavirus disease via fractional-order epidemiological model, 2022, 12, 2158-3226, 035349, 10.1063/5.0087253
26.	Dong-Me Li, Bing Chai, Qi Wang, A model of hepatitis B virus with random interference infection rate, 2021, 18, 1551-0018, 8257, 10.3934/mbe.2021410
27.	Hari M. Srivastava, Abedel-Karrem N. Alomari, Khaled M. Saad, Waleed M. Hamanah, Some Dynamical Models Involving Fractional-Order Derivatives with the Mittag-Leffler Type Kernels and Their Applications Based upon the Legendre Spectral Collocation Method, 2021, 5, 2504-3110, 131, 10.3390/fractalfract5030131
28.	Sachin Kumar, Dia Zeidan, Numerical study of Zika model as a mosquito-borne virus with non-singular fractional derivative, 2022, 15, 1793-5245, 10.1142/S1793524522500188
29.	Amit Kumar Saraswat, Manish Goyal, Numerical simulation of time-dependent influenza model with Atangana–Baleanu non-integer order derivative in Liouville–Caputo sense, 2022, 96, 0973-7111, 10.1007/s12043-022-02335-w
30.	Tahir Khan, Roman Ullah, Gul Zaman, Jehad Alzabut, A mathematical model for the dynamics of SARS-CoV-2 virus using the Caputo-Fabrizio operator, 2021, 18, 1551-0018, 6095, 10.3934/mbe.2021305
31.	Fırat EVİRGEN, Esmehan UÇAR, Sümeyra UÇAR, Necati ÖZDEMİR, Modelling Influenza A disease dynamics under Caputo-Fabrizio fractional derivative with distinct contact rates, 2023, 3, 2791-8564, 58, 10.53391/mmnsa.1274004
32.	J.E. Lavín-Delgado, S. Chávez-Vázquez, J.F. Gómez-Aguilar, V.H. Olivares-Peregrino, Eduardo Pérez-Careta, Trajectory tracking of a mobile robot manipulator using fractional backstepping sliding mode and neural network control methods, 2024, 0228-6203, 1, 10.1080/02286203.2024.2371678
33.	Sana Abdulkream Alharbi, Mohamed A. Abdoon, Rania Saadeh, Reima Daher Alsemiry, Reem Allogmany, Mohammed Berir, Fathelrhman EL Guma, Modeling and analysis of visceral leishmaniasis dynamics using fractional‐order operators: A comparative study, 2024, 47, 0170-4214, 9918, 10.1002/mma.10101
34.	Asia Kanwal, Salah Boulaaras, Ramsha Shafqat, Bilal Taufeeq, Mati ur Rahman, Explicit scheme for solving variable-order time-fractional initial boundary value problems, 2024, 14, 2045-2322, 10.1038/s41598-024-55943-4
35.	H.M. Srivastava, 2025, 9780443288142, 1, 10.1016/B978-0-44-328814-2.00007-2

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(5658) PDF downloads(442) Cited by(35)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(5) / Tables(1)

Mathematical Biosciences and Engineering

Some new mathematical models of the fractional-order system of human immune against IAV infection

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Classical immune response

3.1. Mathematical formulation

3.2. Description of the involved parameters

4. Immune response with fractional-order derivatives

4.1. Numerical scheme for fractional immune response in LC sense

4.2. Numerical scheme for fractional immune response in CFC sense

5. Numerical simulations

6. Conclusions

Acknowledgements

Conflict of interests

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Mathematical Biosciences and Engineering

Some new mathematical models of the fractional-order system of human immune against IAV infection

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Classical immune response

3.1. Mathematical formulation

3.2. Description of the involved parameters

4. Immune response with fractional-order derivatives

4.1. Numerical scheme for fractional immune response in LC sense

4.2. Numerical scheme for fractional immune response in CFC sense

5. Numerical simulations

6. Conclusions

Acknowledgements

Conflict of interests

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog