Decay/growth rates for inhomogeneous heat equations with memory. The case of large dimensions

Dedicated to the memory of our good friend Ireneo Peral, whose enthusiasm for mathematics and life will always be a model for us.

1.   Introduction and main results

1.1.   Goal

This paper is part of a project intending to give a precise description (decay/growth rates and profiles) of the large-time behavior of solutions to the Cauchy problem

where $u_0$ and $f(\cdot, t)$ belong to $L^1(\mathbb{R}^N)$. Here, $\partial_t^\alpha$, $\alpha\in(0, 1)$, denotes the so-called Caputo $\alpha$-derivative, introduced independently by many authors using different points of view, see for instance ^{[2,11,13,15,17,20]}, defined for smooth functions by

and $(-\Delta)^\beta$, $\beta\in(0, 1]$, is the usual $\beta$ power of the Laplacian, defined for smooth functions by $(-\Delta)^\beta = \mathcal{F}^{-1}(|\cdot|^{2\beta}\mathcal{F})$, where $\mathcal{F}$ stands for Fourier transform; see for instance ^[21].

Fully nonlocal heat equations like (1.1), nonlocal both in space and time, are useful to model situations with long-range interactions and memory effects, and have been proposed for example to describe plasma transport ^[8,9]; see also ^[3,4,18,22] for further models that use such equations.

When the forcing term $f$ is trivial, a complete description of the large-time behavior of (1.1) was recently given in ^[5,6]; see also ^[16]. Hence, since the problem is linear, it only remains to study the case with trivial initial datum, namely

This task is by far more involved, and this paper represents a first step towards its completion. It is devoted to the obtention of (sharp) decay/growth rates of solutions to (1.2) when the forcing term satisfies

and the spatial dimension is large, $N > 4\beta$. This already involves critical phenomena depending on the values of $p$ and $\gamma$. If $1\le N\le 4\beta$, additional critical phenomena associated to the dimension appear, that make the analysis somewhat different. This case is considered in ^[7]. Notice that we are allowing $\gamma$ to take negative values, so that $\|f(\cdot, t)\|_{L^1(\mathbb{R}^N)}$ may grow with time.

If $f(\cdot, t)\in L^1(\mathbb{R}^N)$ for all $t\ge0$ and $|\mathcal{F}f(\xi, t)|\le C|g(\xi)|$ for some function $g$ such that

then problem (1.2) has a unique bounded classical solution given by Duhamel's type formula

with $Y = \partial_t^{1-\alpha} Z$, where $Z$ is the solution to (1.2) with $f\equiv0$ having a Dirac mass as initial datum; see ^[12,16]. If we only assume $f\in L^\infty_{\rm loc}([0, \infty):L^1(\mathbb{R}^N))$, the function $u$ in (1.4) is still well defined, but it is not in general a classical solution to (1.2). Nevertheless, it is a solution in a generalized sense ^[14,16]. In this paper we will always deal with solutions of this kind, given by (1.4), which are denoted in the literature as mild solutions ^[16,19].

Notation. As is common in asymptotic analysis, $g\asymp h$ will mean that there are constants $\nu, \mu > 0$ such that $\nu h\le g\le \mu h$.

1.2.   The kernel $Y$. critical exponents

Since the mild solution is given by the convolution in space and time of the forcing term $f$ with the kernel $Y$, having good estimates for the latter will be essential for the analysis. Such estimates were obtained in ^[16], and are recalled next.

The kernel $Y$ has a self-similar form,

Its profile $G$ is positive, radially symmetric and smooth outside the origin, and if $N > 4\beta$ satisfies the sharp estimates

In particular, we have the global bound

and, since $|\xi|^{\frac{(N-2)(\alpha-1)}{(2-\alpha)}}\exp(-\sigma|\xi|^{\frac2{2-\alpha}})\le C_\nu|\xi|^{-(N+2\beta)}$ if $|\xi|\ge\nu$, also the exterior bound

Notice that $Y(\cdot, t)\in L^p(\mathbb{R}^N)$ if and only if $p\in [1, p_*)$, where $p_*: = N/(N-4\beta)$. Moreover,

Therefore, $Y\in L_{\rm loc}^1([0, \infty):L^p(\mathbb{R}^N))$ if and only if $p\in [1, p_{\rm c})$, where $p_{\rm c}: = N/(N-2\beta)$. Since the mild solution is given by a convolution of $f$ with $Y$ both in space and time, the threshold value that will mark the border between subcritical and supercritical behaviors will be $p_{\rm c}$, and not $p_*$. In particular, condition (1.3) guarantees that $u(\cdot, t)\in L^p (\mathbb{R}^N)$ for $p\in[1, p_{\rm c})$, but not for $p\ge p_{\rm c}$. Hence, in order to deal with supercritical exponents $p\ge p_{\rm c}$ we need some extra assumption on the spatial behavior of the forcing term. In the present paper we will use two different such extra hypotheses, the pointwise condition

and the integral condition

We do not claim that these conditions are optimal; but they are not too restrictive, and are easy enough to keep the proofs simple.

1.3.   Precedents and statement of results

The only precedent is given in ^[16], where the authors study the problem in the integrable in time case $\gamma > 1$ and prove, for all $p\in [1, \infty]$ if $1\le N < 4\beta$, and for $p\in [1, p_{\rm c})$ if $N\ge 4\beta$, that

In particular, using (1.11) we get the sharp estimate

This result is also valid for the local case, $\alpha = 1$, $\beta = 1$; see for instance ^[1,10] for the case $p = 1$. In this special situation $Y = Z$ is the well-known fundamental solution of the heat equation, whose profile does not have a spatial singularity and belongs to all $L^p$ spaces.

An analogous convergence result is definitely not possible for $\alpha\in(0, 1)$ if $p\ge p_*$, since $Y(\cdot, t)\not\in L^p(\mathbb{R}^N)$ in that case, or if $\gamma\le 1$. Moreover, even in the subcritical range (1.14) only gives a sharp rate and a nontrivial limit profile in the diffusive scale $|x|\asymp t^{\theta}$; see below. Hence we need a different approach.

As we will see, it turns out that, in contrast with the local case, and due to the effect of memory, the decay/growth rates are not the same in different space-time scales. Moreover, the scale that determines the dominant rate depends on the value of the exponent $p$. Our strategy will consist in tackling this difficulty directly by studying separately the rates in exterior regions, $|x|\ge\nu t^\theta$ with $\nu > 0$, compact sets or intermediate regions $|x|\asymp g(t)$ with $g(t)\to\infty$ and $g(t) = o(t^\theta)$. We already found this phenomenon for the Cauchy problem, (1.1) with $f\equiv0$, where the decay rate was $O(t^{-\alpha})$ in compact sets and $O\big(t^{-N\theta\big(1-\frac1p\big)}\big)$ in exterior regions; see ^[5,6].

Our first result concerns exterior regions.

Theorem 1.1 (Exterior regions). Let $f$ satisfy (1.3) and also (1.12) if $p\ge p_{\rm c}$. Let $u$ be the mild solution to (1.2). For all $\nu > 0$ there is a constant $C$ such that

These estimates are sharp.

For $p\in[1, p_{\rm c})$ and $\gamma > 1$ the result follows from (1.14), showing that the behavior in this regions dominates the global behavior in the subcritical case.

We now turn to the behavior in compact sets which, due to the effect of memory, will dominate the global behavior for large values of $p$.

Theorem 1.2 (Compact sets). Let $f$ satisfy (1.3). If $p\ge p_{\rm c}$, assume also (1.13) with $\gamma$ as in (1.3). Let $u$ be the mild solution to (1.2). For every compact set $K$ there exists a constant $C$ such that

These estimates are sharp.

Remark. Note that $q_{\rm c}(p_{\rm c}) = 1$.

As expected, the rates in intermediate regions, between compact sets and exterior regions, are intermediate between the ones in such scales.

Theorem 1.3 (Intermediate regions). Let $f$ satisfy (1.3) and also (1.12) if $p\ge p_{\rm c}$. Let $g(t)\to\infty$ be such that $g(t) = o(t^\theta)$. Let $u$ be the mild solution to (1.2). For all $0 < \nu < \mu < \infty$ there exists a constant $C$ such that

These estimates are sharp.

We also obtain results that connect the behaviors in compact sets and exterior regions, thus getting the (global) decay rate in $L^p(\mathbb{R}^N)$.

Theorem 1.4 (Global results). Assume (1.3), and also (1.12) and (1.13) with $\gamma$ as in (1.3) if $p\ge p_{\rm c}$. Let $u$ be the mild solution to (1.2). There is a constant $C$ such that

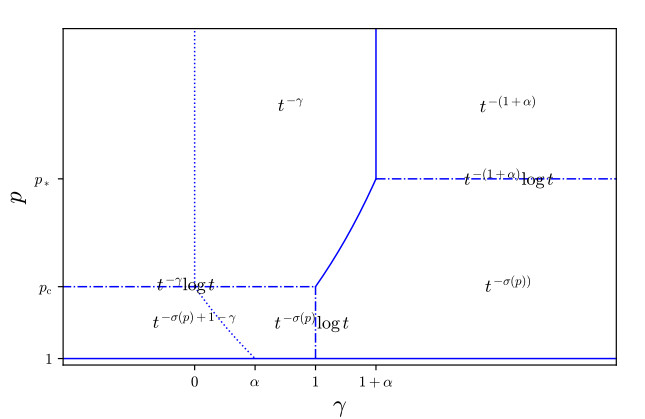
see Figure 1. These estimates are sharp.

Notice that the borderline separating decay and growth is $\gamma = 0$ only for $p\ge p_{\rm c}$. For $p\in [1, p_{\rm c})$ the frontier is given by

see the dotted line in Figure 1. For $p = 1$ this corresponds to $\gamma = \alpha$. An informal explanation for this fact can be found in formula (1.4). We are integrating in time, but $Y(x, t) = \partial^{1-\alpha}_t Z(x, t)$. Hence, it is like if we were integrating $\alpha$ times in time. As for the behavior for the borderline $\gamma$, in general there is neither growth nor decay. The exception is the case $p = p_{\rm c}$, $\gamma = 0$, in which there is a slow logarithmic growth.

Another remarkable fact is that the rates depend on $\gamma$ not only in the non-integrable case $\gamma\le1$, which might have been expected, but also in part of the region $\gamma\in [1, 1+\alpha)$ if $p$ is supercritical.

2.   Exterior region

In this section we prove Theorem 1.1, which gives the behavior of all $L^p$ norms of the mild solution $u$ to (1.2) in exterior regions, $\{(x, t)\in Q:|x|\ge \nu t^\theta\}$, $\nu > 0$.

Proof of Theorem 1.1. The starting point is Duhamel's type formula (1.4). If $p\in[1, p_{\rm c})$, then $Y(\cdot, t)$ belongs to $L^p(\mathbb{R}^N)$. Therefore, using (1.3) and (1.11),

Integration of $\int_0^{\frac t2}(1+s)^{-\gamma}\, {\rm d}s$ gives the result.

We turn now our attention to the case $p\ge p_{\rm c}$, for which we assume also the decay condition (1.12). We have $|u|\le {\rm I}+{\rm II}$, where

We start by estimating ${\rm I}$. Notice that if $|y| < |x|/2$, then $|x-y| > |x|/2$. Thus, if moreover $|x|\ge\nu t^\theta$, there holds that $|x-y|(t-s)^{-\theta} > \nu /2$. Hence, the bound (1.10) yields

Using also (1.3) we arrive at ${\rm I}(x, t)\le C |x|^{-(N+2\beta)}\int_0^t(t-s)^{2\alpha-1}(1+s)^{-\gamma}\, {\rm d}s$, and therefore

and the desired bound for ${\rm I}$ follows.

Now we turn to ${\rm II}$. We choose $\varepsilon\in(0, 1/2)$. Given $x\in\mathbb{R}^N$, $t > 0$, $s\in(0, t)$, we denote $\mathcal{B}(x, t, s) = \{y\in\mathbb{R}^N: |x-y| < |x|^ \varepsilon(t-s)^{\theta(1- \varepsilon)}\}$. Note that for $|x| > \nu t^\theta$ and $y\in(\mathcal{B}(x, t, s))^{\rm c}$ we have $|x-y|(t-s)^{-\theta} > \nu^ \varepsilon$. Therefore, using the estimates (1.9)–(1.10), we have ${\rm II}\le {\rm II}_1+{\rm II}_2$, with

We have, using the decay condition (1.12),

Since $p\ge p_{\rm c}$ and $\varepsilon\in(0, 1/2)$, we have $(N-4\beta \varepsilon)p > N$, and hence

and integration gives the bound in (1.15) for this term.

Finally, since $|x-y|\ge|x|^ \varepsilon(t-s)^{\theta(1- \varepsilon)}$ in $(\mathcal{B}(x, t, s))^{\rm c}$, using the condition (1.3) on $f$,

so that

Now, integration gives the bound.

In order to check that the bound in (1.15) is sharp we choose $f(x, t) = (1+t)^{-\gamma}\chi_{B_1}(x)$. If $t$ is large, $|y| < 1$ and $|x| > \nu t^\theta$, then $|y| < |x|/2$. Hence, $|x|/2 < |x-y| < 3|x|/2$, so that, assuming also that $|x| < \mu t^\theta$ and $0 < s < t/2$,

Thus, since the profile $G$ of $Y$ is positive, under these conditions $Y(x-y, t-s)\ge C(t-s)^{-\sigma_*}$ for some constant $C > 0$, see (1.5), and therefore,

Thus,

which implies the desired lower bound.

3.   Compact regions

In this section we prove Theorem 1.2, which gives the large-time behavior of the $L^p$ norms of the mild solution to (1.3) in compact sets $K$.

Proof of Theorem 1.2. Let $t\ge 1$. We have $|u|\le {\rm I}+{\rm II}$, where

Using the global bound (1.9) for $Y$ we get

Let $q = 1$ if $p\in[1, p_{\rm c})$, $q > q_{\rm c}(p)$ as in (1.13) if $p\ge p_{\rm c}$. Let $r$ satisfy $1+\frac1p = \frac1q+\frac1r$. Then $r\in [1, p_{\rm c})$, and in particular $r\in [1, p_*)$. Thus, for all $t\ge 2$ we have

which implies that $\|{\rm I}(\cdot, t)\|_{L^p(K)}\le C t^{-\min\{\gamma, 1+\alpha\}}$.

In order to bound ${\rm II}$ we take $r\in[1, p_{\rm c})$ as before. Then, using (1.11) we get

which combined with the estimate for ${\rm I}$ yields the result.

In order to prove that estimate (1.16) is sharp we consider $f(x, t) = (1+t)^{-\gamma}\chi_{K+B_1}(x)$, where $K$ is any compact set with measure different from 0. We have

If $x\in K$ and $|x-y| < 1$, then $y\in K+B_1$. Notice that $|x-y| < 1$ and $s < t-1$ imply that $|x-y|(t-s)^{-\theta}\le 1$. Therefore, using the self-similar form (1.5) of $Y$ and the bound from below (1.6) for the profile $G$, for all $x\in K$ we have

for some constant $C > 0$. Thus, no matter the value of $\gamma$, for all $x\in K$ and $t$ large enough,

while if $\gamma > 1$, then

so that $\|u(\cdot, t)\|_{L^p(K)}\ge C t^{-\min\{\gamma, 1+\alpha\}}$.

4.   Intermediate scales

In this section we study the large-time behavior of the $L^p$ norms of the mild solution to (1.3) in regions where $|x|\asymp g(t)$ with $g(t)\to\infty$ such that $g(t) = o(t^\theta)$, which is the content of Theorem 1.3.

Proof of Theorem 1.3. We have $|u|\le {\rm I}+{\rm II}$, where

To estimate ${\rm I}$ we decompose it as ${\rm I} = {\rm I}_1+{\rm I}_2+{\rm I}_3$, where

If $0 < s^\theta < |x|/2 < |y|$, then $|y|s^{-\theta}\ge1$. Therefore, using (1.10) and condition (1.3), if $|x| < \mu g(t)$ with $g(t) = o(t^\theta)$ we have

Thus, $\|{\rm I}_1(\cdot, t)\|_{L^p(\{\nu < |x|/g(t) < \mu\})}\le C t^{-\gamma}g(t)^{2\beta-N(1-\frac1p)}$.

As for ${\rm I}_2$ and ${\rm I}_3$, using the global bound (1.9) for $Y$ and condition (1.3),

Therefore,

Now we turn to ${\rm II}$. We decompose it as ${\rm II}\le {\rm II}_1+{\rm II}_2$, where

We start with the subcritical case $p\in[1, p_{\rm c})$. Notice that if $s^\theta < |y|$, then $|y|s^{-\theta}\ge 1$. Moreover, if $|x| = o(t^\theta)$, then $(|x|/2)^{1/\theta} = o(t)$, and hence $(|x|/2)^{1/\theta} < t/2$ if $t$ is large. Therefore, using the bounds (1.9) and (1.10), we have ${\rm II}_1\le {\rm II}_{11}+{\rm II}_{12}$, where

Using condition (1.3), and remembering that $g(t) = o(t^\theta)$,

On the other hand, from the global bound (1.9),

and therefore, thanks to condition (1.3),

Let now $p\ge p_{\rm c}$. Since $|x-y|\ge|x|/2\ge \nu g(t)/2\to \infty$ as $t\to\infty$, then, thanks to assumption (1.12), we have that $|f(x-y, t-s)|\le C|x|^{-N}(1+t-s)^{-\gamma}$ for all $t$ large. Hence,

Therefore, $\|{\rm II}_{1}(\cdot, t)\|_{L^p(\{\nu < |x|/g(t) < \mu\})}\le C t^{-\gamma}g(t)^{2\beta-N(1-\frac1p)}$ also when $p\ge p_{\rm c}$.

As for ${\rm II}_2$, also when $p\ge p_{\rm c}$, since $|y| < |x|/2$ implies $|x-y| > |x|/2$, using the global estimate (1.9) and the decay condition (1.12),

and hence

Estimate (1.17) follows from the above bounds and the fact that $g(t) = o(t^\theta)$.

To end the proof we have to check that (1.17) is sharp. To this aim we take $f(x, t) = (1+t)^{-\gamma}\chi_{B_1}(x)$. Let $t$ be large enough so that $g(t) > 2/\nu$. If $\nu g(t) < |x| < \mu g(t)$ and $|x-y| < 1$,

Under these assumptions, if $s\in (0, (\nu g(t)/2)^{1/\theta})$, then $|y|s^{-\theta}\ge |y|/(\nu g(t)/2)\ge 1$. Therefore, if $g(t) = o(t^\theta)$, using (1.5) and the estimates from below in (1.7)–(1.8), and performing the change of variables $s = \tau g(t)^{1/\theta}$, we arrive at

Therefore,

On the other hand, under the assumptions leading to (4.6), if moreover $s\in(t/2, t)$ and $t$ is large enough, we have $|y| < 2\mu g(t) < (t/2)^\theta < s^\theta$. Thus, using the estimate from below in (1.6),

Hence,

Estimates (4.7)–(4.8) show that (1.17) is sharp.

5.   Estimates in $\mathbb{R}^N$

In this section we establish the behavior of the global $L^p(\mathbb{R}^N)$ norms of the mild solution to (1.2), Theorem 1.4.

Proof of Theorem 1.4. Due to the results of theorems 1.1 and 1.2, it is enough to show that the estimates are true in some region of the form $\{R\le |x|\le \delta t^\theta\}$ with $R, \delta > 0$.

We have $|u|\le{\rm I}+{\rm II}$, with ${\rm I}$ and ${\rm II}$ as in (4.1). The term ${\rm I}$ is further decomposed as ${\rm I} = {\rm I}_1+{\rm I}_2+{\rm I}_3$, with ${\rm I}_j$, $j\in\{1, 2, 3\}$ as in (4.2). Since $|x| < \delta t^\theta$ in the region we are interested in, taking $\delta\in (0, 2^{1-\theta})$, then $(|x|/2)^{1/\theta} < t/2$. Therefore, reasoning as in Section 4, we obtain (4.3)–(4.4), from where

We conclude that

To analyze ${\rm II}$ we decompose it as ${\rm II} = {\rm II}_1+{\rm II}_2$, where ${\rm II}_1$ and ${\rm II}_2$ are as in (4.5). We start with the subcritical case $p\in [1, p_{\rm c})$. Using (1.3) and (1.11),

Let now $p\ge p_{\rm c}$. If $|y| < |x|/2$ and $|x| > R$, then $|x-y|\ge|x|/2\ge R/2$. Hence, taking $R$ large enough so that (1.12) holds outside $B_{R/2}$, we have that $|f(x-y, t-s)|\le C|x|^{-N}(1+t-s)^{-\gamma}$. Hence, reasoning as in Section 4,

and we get,

The above estimates together with theorems 1.1 and 1.2 yield the result.

Acknowledgments

This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 777822. Carmen Cortázar supported by FONDECYT grant 1190102 (Chile). Fernando Quirós supported by Ministerio de Economía y Competitividad (Spain), through project MTM2017-87596-P, and by Ministerio de Ciencia e Innovación (Spain), through project ICMAT-Centro de excelencia "Severo Ochoa", CEX2019-000904-S. Noemí Wolanski supported by CONICET PIP 11220150100032CO 2016-2019, ANPCyT PICT2016-1022, UBACYT 20020150100154BA and MathAmSud 13MATH03 (Argentina).

Conflict of interest

The authors declare no conflict of interest.