($2n-3$)-fault-tolerant Hamiltonian connectivity of augmented cubes $AQ_n$

1.   Introduction

Interconnection networks are of particular interest in the study of parallel computing systems. An interconnection network can be modeled as a graph $G = (V, E)$, where $V$ expresses the vertex set and $E$ expresses the edge set. Exploring the structures of $G$ is essential for designing a suitable topology for such an interconnection network. Topology structure has a crucial impact on the overall performance of the network. It determines the physical distribution of network nodes/links and the connection relationship between them. It also determines the number of hops in message transmission and the length of links per hop. Therefore, the topology has a great influence on the delay and power consumption. In addition, because the topology determines the number of available transmission paths between nodes, it also affects the distribution of network traffic, network bandwidth and transmission performance.

The hypercube $Q_n$ is one of the most prevalent interconnection networks among all the popular parallel network topologies that possess properties such as logarithmic diameter, high symmetry, linear bisection width. The $n$-dimensional augmented cube $AQ_n$ is an outstanding variation of the hypercube $Q_n$. It possesses many of the favorable properties of $Q_n$ as well as some embedded properties not found in $Q_n$. Much research has been conducted on this type of augmented cube, and it appears frequently in the literatures ^{[1,3,4,12,13,14,16,20,22]}.

In the last several years, the path embedding problem has become one of the most-studied graph embedding problems, appearing prolifically in the literatures^[5,6,10,14]. The fault-tolerant path embedding problem has also been the subject of frequent investigation, as is evident in the literatures ^{[3,4,7,11,10,22,23,24]}.

A path (or cycle) is considered a Hamiltonian path (or Hamiltonian cycle) if it passes through every vertex of graph G once and only once. A graph is said to be Hamiltonian if it contains at least one Hamiltonian cycle. One of the most challenging contemporary problems in graph theory is identifying a necessary and sufficient condition for a graph to be considered Hamiltonian. A graph $G$ is regarded as Hamiltonian connected if for any pair of distinct vertices $u$ and $v$, a Hamiltonian path $P_{uv}$ exists. Hamiltonian paths and cycles have applicability for practical problems such as online optimization of complex, flexible manufacturing systems ^[25], wormhole routing ^[26], deadlock-free routing and broadcasting algorithms ^[27]. Applicability for such problems have been a driving force for the study of networks embedded with Hamiltonian paths.

In large interconnection networks, vertices(or edges) show a propensity for faultiness. This faultiness demands attention, as fault-tolerance serves as an important index of a network's stability. A graph $G$ can be said to be $k$-fault-tolerant Hamiltonian connected if $G-F$ remains Hamiltonian connected for any $F\subset V(G)\cup E(G)$ with $|F|\leq k$.

Hsu et al.^[3] proved that $AQ_n(n\geq1)$ is Hamiltonian-connected. They also showed that $AQ_n$ is ($2n-3$)-fault-tolerant Hamiltonian and ($2n-4$)-fault-tolerant Hamiltonian connected for $n\geq4$ even when faulty elements occur. Soon after, Wang et al.^[4] proved that $AQ_n$ is ($2n-5$)-fault-tolerant Panconnected for $n\geq3$. We improved this result and showed that if $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq 2n-4$, then for any two distinct error-free vertices $u$ and $v$ with distance $d$, there exists an error-free path $P_{uv}$ of length $l$ with $max\{d+2, 4\} \leqslant l \leqslant 2^n-f_v-1$ in $AQ_n-F$($n\geq4$)^[22].

In this paper, we show that for any two distinct error-free vertices $u$ and $v$, there exists a fault-free Hamiltonian path $P_{uv}$ that joins vertices $u$ and $v$ with the exception of $(u, v)$, which is a weak vertex-pair in $AQ_n-F$($n\geq4$) under the assumption that $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq 2n-3$.

The rest of this paper is outlined as follows. Section 2 introduces the definitions and properties of the augmented cubes $AQ_n$. In Section 3, we investigate some lemmas of $AQ_n$ to be used in our proofs. Section 4 proves the main theorem. Finally, Section 5 concludes the paper.

2.   The definition and properties of $AQ_n$

In this section, we will introduce the definition of $AQ_n$ and basic properties used in this paper.

Definition 2.1. The $n$-dimensional augmented cube $AQ_n$, proposed by Choudum and Sunitha^[16], can be defined recursively as follows.

$AQ_1$ is a complete graph $K_2$ with vertex set $\{0, 1\}$. For $n\geq 2$, $AQ_n$ is obtained by taking two copies of the augmented cube $AQ_{n-1}$ denoted by $^0AQ_{n-1}$ and $^1AQ_{n-1}$, and adding $2\times 2^{n-1}$ edges between the two copies as follows.

Let $V(^0AQ_{n-1}) = \{ 0x_{n-1}\ldots x_2x_1 | x_i \in \{0, 1\}\}$ and $V(^1AQ_{n-1}) = \{1x_{n-1}\ldots x_2x_1 | x_i \in \{0, 1\}\}$. A vertex $x\in V(^0AQ_{n-1})$ is adjacent to a vertex $y\in V(^1AQ_{n-1})$ if and only if either:

(1) $x_i = y_i$ for $1\leq i\leq n-1$; in this case, $xy$ is called a hypercube edge and we set $x = y^{h_n}$ or $y = x^{h_n}$, or

(2) $x_i = \overline{y_i}$ for $1\leq i\leq n-1$; in this case, $xy$ is called a complement edge and we set $x = y^{c_n}$ or $y = x^{c_n}$.

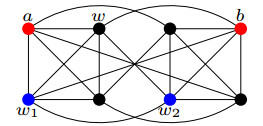
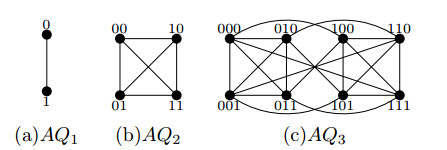
And an edge between $x = x_nx_{n-1}\ldots x_i\ldots x_2x_1$ and $y = x_nx_{n-1}\ldots\overline{x_i}\ldots x_2x_1$($x_i \in \{0, 1\}$, $2\leq i\leq n$) is called an $i$-dimensional hypercube edge, setting $x = y^{h_i}$ or $y = x^{h_i}$, an edge between $x = x_nx_{n-1}\ldots x_i\ldots x_2x_1$ and $y = x_nx_{n-1}\ldots\overline{x_i}\ldots \overline{x_2x_1}$($x_i \in \{0, 1\}$, $1\leq i\leq n$) is called an $i$-dimensional complement edge, setting $x = y^{c_i}$ or $y = x^{c_i}$. For any vertex $u$ in $AQ_n$, we use $u^h$ to denote $u^{h_n}$ and use $u^c$ to denote $u^{c_n}$. Examples of the augmented cubes $AQ_1$, $AQ_2$ and $AQ_3$ are shown in Figure 1(a)–(c), respectively.

$AQ_n$ is $(2n-1)$-regular that has, naturally, $2^n$ vertices. For the sake of simplicity, we write this as $L =$$^0AQ_{n-1}$ and $R =$$^1AQ_{n-1}$. Let $N_{AQ_n}(x)$ express the set of vertices which are incident to vertex $x$ and $E_{AQ_n}(x)$ express the set of edges which are incident to vertex $x$. For each vertex $x\in V(L)$(or $V(R)$), let $N_L(x)$(or $N_R(x)$) express the set of vertices adjacent to $x$ in $V(L)$(or $V(R)$), $E^C$ signify the set of edges joining $L$ to $R$ and $E_L(x)({\rm or}\ E_R(x))$ serve as the set of edges which are incident to vertex $x$ in $L({\rm or}\ R)$.

For two distinct vertices $u$ and $v$ in $G$, a path $P_{uv}$ from vertex $u$ to vertex $v$ of length $k$ is a sequence of different vertices $(x_0, x_1, \ldots, x_k)$, where $x_0 = u$, $x_k = v$, $x_{i-1}x_i\in E(G)$ for each $i = 1, 2, \ldots, k$, and $k$ is the number of edges in $P_{uv}$, called the length of $P_{uv}$. The distance between vertices $u$ and $v$, denoted by $d_{uv}$, is the length of a shortest path from vertex $u$ to vertex $v$ in $G$.

Let $P_{uv} = (u, u_1, u_2, \cdots, u_{k-1}, v)$ be a path from vertex $u$ to vertex $v$. A subsequence $(u_i, u_{i+1}, \cdots, u_j)$ of $P_{uv}$ is called a subpath of $P_{uv}$, denoted by $P_{uv}(u_i, u_j)$. We can write $P_{uv} = (u, u_1, \cdots, u_{i}, P_{uv}(u_i, u_j), u_j, \cdots u_{k-1}, v)$. A cycle is a path $P_{uv}$ with $u = v$. We use $C = (u, u_1, u_2, \cdots, u_{k-1}, u)$ to denote a cycle containing vertex $u$.

We first give the useful definitions and properties about $AQ_n$ as follows.

Proposition 2.1. Let $uv$ be an edge in $AQ_n$($n\geq2$) ^[4]. If $uv$ is not an $(n-1)$-dimensional complement edge, then $u^h$, $u^c$, $v^h$ and $v^c$ are all distinct. Otherwise, $u^h = v^c$, $u^c = v^h$.

Proposition 2.2. For any two distinct vertices $u$ and $v$ of $AQ_n$, we have $|(N_{AQ_n}(u)\cup E_{AQ_n}(u))\cap (N_{AQ_n}(v)\cup E_{AQ_n}(v))|\leq 5$.

Proof. Let $m$ be the adjacent vertex of vertex $u$. Then

If there exists at least one common adjacent vertex between any two distinct vertices $u$ and $v$ of $AQ_n$, then $d_{uv}\leq2$. We divided to the following two cases to prove.

Case 1. $d_{uv} = 1$.

Case 1.1. $v = u^{c_i}$($1\leq i\leq n$). Then $v = u_nu_{n-1}\cdots u_{i+1}\bar{u}_i\bar{u}_{i-1}\cdots \bar{u}_2\bar{u}_1$.

$m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i+1}}, u^{c_{i-1}}, u^{h_{i}}, u^{h_{i+1}}\}$ for $2\leq i\leq n-1$, $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i+1}}, u^{h_{i+1}}\}$ for $i = 1$, $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i-1}}, u^{h_{i}}\}$ for $i = n$.

Case 1.2. $v = u^{h_i}$($2\leq i\leq n$). Then $v = u_nu_{n-1}\cdots u_{i+1}\bar{u}_iu_{i-1}\cdots u_2u_1$.

$m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i-1}}, u^{c_{i}}\}$ for $2\leq i\leq n$.

Case 2. $d_{uv} = 2$.

Case 2.1. $v = u^{c_ic_k}$($1\leq i < k\leq n$, $k\neq i+1$). Then $v = u_nu_{n-1}\cdots u_{k+1}\bar{u}_{k}\bar{u}_{k-1}\cdots \\\bar{u}_{i+1}u_iu_{i-1}\cdots u_2u_1$. $m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i}}, u^{c_{k}}, u^{h_{k}}, u^{h_{i+1}}\}$ for $k = i+2$ and $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i}}, u^{c_{k}}\}$ for $k\neq i+2$.

Case 2.2. $v = u^{c_ih_k}$($1\leq i < k\leq n$, $k\neq i+1$). Then $v = u_nu_{n-1}\cdots u_{k+1}\bar{u}_{k}u_{k-1}\cdots u_{i+1}\bar{u}_i\bar{u}_{i-1}\cdots \bar{u}_2\bar{u}_1$. $m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i}}, u^{h_{k}}, u^{c_{k}}, u^{h_{i+1}}\}$ for $k = i+2$ and $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{c_{i}}, u^{h_{k}}\}$ for $k\neq i+2$.

Case 2.3. $v = u^{h_ih_k}$($2\leq i < k\leq n$). Then $v = u_nu_{n-1}\cdots u_{k+1}\bar{u}_{k}u_{k-1}\cdots u_{i+1}\bar{u}_iu_{i-1}\\ \cdots u_2u_1$. $m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{h_{i}}, u^{h_{k}}, u^{c_{i-1}}, u^{c_{k}}\}$ for $k = i+1$ and $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{h_{i}}, u^{h_{k}}\}$ for $k\neq i+1$.

Case 2.4. $v = u^{h_ic_k}$($2\leq i < k\leq n$). Then $v = u_nu_{n-1}\cdots u_{k+1}\bar{u}_{k}\bar{u}_{k-1}\cdots\bar{u}_{i+1}u_i\bar{u}_{i-1}\\\cdots \bar{u}_2\bar{u}_1$. $m\in N(v)$ if and only if

Then $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{h_{i}}, u^{c_{k}}, u^{c_{i-1}}, u^{h_{k}}\}$ for $k = i+1$ and $N_{AQ_n}(u)\cap N_{AQ_n}(v) = \{u^{h_{i}}, u^{c_{k}}\}$ for $k\neq i+1$.

Combining the above cases, we have that $|N_{AQ_n}(u)\cap N_{AQ_n}(v)|\leq4$. If $uv\in E(AQ_n)$, then $|(N_{AQ_n}(u)\cup E_{AQ_n}(u))\cap (N_{AQ_n}(v)\cup E_{AQ_n}(v))|\leq 5$. If $uv\notin E(AQ_n)$, then $|(N_{AQ_n}(u)\cup E_{AQ_n}(u))\cap (N_{AQ_n}(v)\cup E_{AQ_n}(v))|\leq 4$. Hence, we have $|(N_{AQ_n}(u)\cup E_{AQ_n}(u))\cap (N_{AQ_n}(v)\cup E_{AQ_n}(v))|\leq 5$.

Definition 2.2. Let $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F| = 2n-3$. If $AQ_n-F$ include a vertex $w$ with $N_{AQ_n-F}(w) = \{w_1, w_2\}$, then $w$ is considered a weak 2-degree vertex and $(w_1, w_2)$ is considered a $w$-weak vertex pair(or a weak vertex pair, for short).

Take $F = \{a, b\}$ for an example, we know that $w$ is a weak 2-degree vertex and $(w_1, w_2)$ is a weak vertex-pair in $AQ_3-F$(See Figure 2).

Because it is impossible for any error-free path $P_{w_1w_2}$ of length $l$ with $l\geq3$ to contain the weak 2-degree vertex $w$, no error-free Hamiltonian path that joins vertices $w_1$ and $w_2$ exists in $AQ_n-F$. Fortunately, at most one weak $2$-degree vertex $w$ and at most one $w$-weak vertex-pair exist in $AQ_n-F(n\geq5)$ for any $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F| = 2n-3$. We shall provide proof of this fact in Proposition 2.3.

Definition 2.3. If $(w_1, w_2)$ is not a weak vertex-pair for arbitrary vertex $w\in V(AQ_n-F)$, then $(w_1, w_2)$ is called a normal vertex pair.

Proposition 2.3. Let $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq 2n-1$$(n\geq6)$. Then there exists at most one vertex $z\in V(AQ_n-F)$ such that $d_{AQ_n-F}(z)\leq 2$.

Proof. Assume that there exist two vertices $z_1, z_2$ such that $d_{AQ_n-F}(z_1)\leq 2$ and $d_{AQ_n-F}(z_2)\leq 2$. Since $AQ_n$ is a $(2n-1)$-regular graph, we have $|F\cap(N_{AQ_n}(z_1)\cup E_{AQ_n}(z_1))|\geq 2n-3$ and $|F\cap(N_{AQ_n}(z_2)\cup E_{AQ_n}(z_2))|\geq 2n-3$.

By Proposition 2.2, $|(N_{AQ_n}(z_1)\cup E_{AQ_n}(z_1))\cap (N_{AQ_n}(z_2)\cup E_{AQ_n}(z_2))|\leq 5$. Then $|F\cap(N_{AQ_n}(z_1)\cup E_{AQ_n}(z_1))|$+$|F\cap(N_{AQ_n}(z_2)\cup E_{AQ_n}(z_2))|$-$|F\cap (N_{AQ_n}(z_1)\cup E_{AQ_n}(z_1))\cap (N_{AQ_n}(z_2)\cup E_{AQ_n}(z_2))|\geq 2(2n-3)-5$=$4n-11 > 2n-1(n\geq6)$, a contradiction to $|F|\leq 2n-1$.

Hence, at most one vertex $z\in V(AQ_n-F)$ exists in $AQ_n-F$ such that $d_{AQ_n-F}(z)\leq 2$ for any $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq 2n-1$. By Proposition 2.3, we can obtain the Corollary 2.1 as follows.

Corollary 2.1. Let $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq2n-3$. Then at most a weak $2$-degree vertex $w$ and at most a $w$-weak vertex-pair exist in $AQ_n-F(n\geq6)$.

3.   Some lemmas

Denote $F^L = F\cap L$, $F^R = F\cap R$, $F^C = F\cap E^C$, $F_v = F\cap V(AQ_n)$, $F_e = F\cap E(AQ_n)$, $F_v^L = V(L)\cap F^L$, $F_v^R = V(R)\cap F^R$, $f_v = |F_v|$, $f_v^L = |F_v^L|$, $f_v^R = |F_v^R|$.

We need the following lemmas.

Lemma 3.1. $AQ_n(n\geq3)$ is $(2n-4)$-fault-tolerant Hamiltonian connected and ($2n-3$)-fault-tolerant Hamiltonian ^[3].

Lemma 3.2. If $|F^L| = 2n-3(n\geq6)$, then for arbitrary vertex-pair $(u, v)$ with $u, v\in V(L)$, there exist two faulty elements $x_1, x_2\in F^L$ such that $(u, v)$ is a normal vertex-pair in $L-(F^L-\{x_1, x_2\})$.

Proof. We use the following two cases to prove.

Case 1. $(u, v)$ is a $w$-weak vertex pair in $L-F^L$. Then $d_{L-F^L}(w) = 2$ and $|F^L\cap (N_L(w)\cup E_L(w))| = 2n-5$. By Proposition 2.3, $w$ is the unique vertex in $L-F^L$ with $d_{L-F^L}(w)\leq 2$.

So, we can choose two elements $x_1, x_2\in F^L\cap (N_L(w)\cup E_L(w))$. Let $F^L_1 = F^L-\{x_1, x_2\}$, then $d_{L-F^L_1}(w) = 4$. Hence, $(u, v)$ is a normal vertex pair in $L-F^L_1$.

Case 2. $(u, v)$ is a normal vertex pair in $L-F^L$. Let vertex $z\in L-F^L$ with the least degree.

Case 2.1. $\delta(L-F^L) = 0$, then $F^L\subset N_L(z)\cup E_L(z)$, $d_{L-F^L}(z) = 0$.

Case 2.1.1. $z\in \{u, v\}$. Assume that $u = z$(When $v = z$, the same proofs apply).

By Proposition 2.3, $u$ is the unique vertex in $L-F^L$ with $d_{L-F^L}(u)\leq 2$. Then $(u, v)$ is a normal vertex-pair in $L-(F^L-\{x_1, x_2\})$ for arbitrary two elements $x_1, x_2$ of $F^L$.

Case 2.1.2. $z\notin \{u, v\}$.

By Proposition 2.3, $z$ is the unique vertex in $L-F^L$ with $d_{L-F^L}(z)\leq 2$. There exist two elements $x_1, x_2\in F^L\cap (N_L(z)\cup E_L(z))$ with $x_1, x_2\notin \{uz, vz\}$. Let $F^L_1 = F^L-\{x_1, x_2\}$, then $d_{L-F^L_1}(z) = 2$ and $N_{L-F^L_1}(z)\neq\{u, v\}$. Hence, $(u, v)$ is a normal vertex pair in $L-F^L_1$.

Case 2.2. $\delta(L-F^L) = 1$. Then $|F^L\cap (N_L(z)\cup E_L(z))| = 2n-4$ and $d_{L-F^L}(z) = 1$.

By Proposition 2.3, $z$ is the unique vertex in $L-F^L$ with $d_{L-F^L}(z)\leq 2$. There exist two elements $x_1, x_2\in F^L\cap (N_L(z)\cup E_L(z))$. Let $F^L_1 = F^L-\{x_1, x_2\}$, then $d_{L-F^L_1}(z) = 3$. Then $(u, v)$ is a normal vertex pair in $L-F^L_1$.

Case 2.3. $\delta(L-F^L)\geq2$.

Then $(u, v)$ is a normal vertex-pair in $L-(F^L-\{x_1, x_2\})$ for arbitrary two elements $x_1, x_2$ of $F^L$.

The Lemma holds.

By a similar argument to Lemma 3.2, we can get the following Lemma.

Lemma 3.3. If $|F^L| = 2n-4(n\geq6)$, then for arbitrary vertex-pair $(u, v)$ with $u, v\in V(L)$, there is a faulty element $x\in F^L$ such that $(u, v)$ is a normal vertex-pair in $L-(F^L-\{x\})$.

Lemma 3.4. Let $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq2$ and $x, y, z, w$ be four distinct vertices in $AQ_n(n\geq4)$. Then two disjoint paths $P_{xy}$, $P_{zw}$ such that $V(P_{xy})\cup V(P_{zw}) = V(AQ_n-F)$ will exist.

Proof. We prove the lemma by induction on $n\geq 4$. The induction basis for $n = 4$ holds by computer program. Suppose that the lemma holds for $n-1$ with $n\geq 5$, then we must show the lemma holds for $n$.

Case 1. $x, y, z, w\in V(L)$.

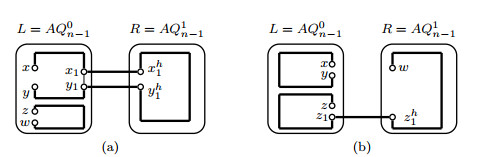
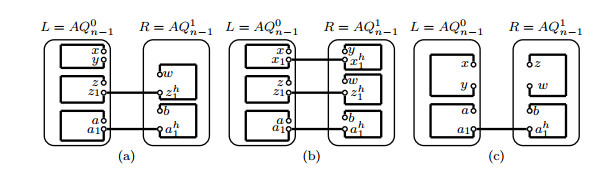
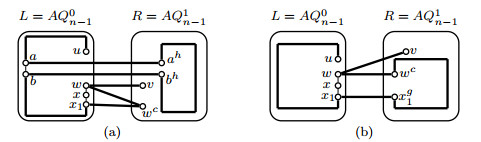
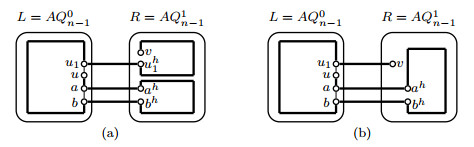
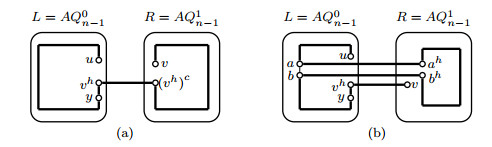
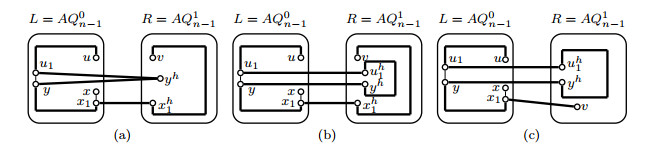
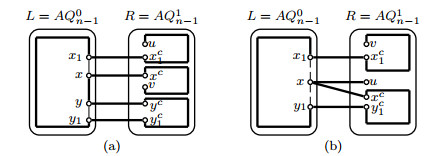
By induction hypothesis, two disjoint paths $P_{xy}$, $P_{zw}$ with $V(P_{xy})\cup V(P_{zw}) = V(L-F^L)$ exist in $L-F^L$. Assume that $|V(P_{xy})|\geq |V(P_{zw})|$. Then $\frac{|V(P_{xy})|}{2}\geq \lceil\frac{2^n-2}{2}\rceil/2\geq 7$($n\geq5$). Since $|F|\leq2$, we can choose an edge $x_1y_1\subset E(P_{xy})$ such that $x^h_1, y^h_1, x_1x^h_1, y_1y^h_1\notin F$. By Lemma 3.1, a Hamiltonian path $P_{x^h_1y^h_1}$ will exist in $R-F^R$. Let $P^{1}_{xy} = (x, P_{xy}(x, x_1), x_1, x_1^h, P_{x^h_1y^h_1}, y^h_1, y_1, P_{xy}(y_1, y), y)$. Then $P^{1}_{xy}, P_{zw}$ are two desired paths in $AQ_n-F$(see Figure 3(a)).

Case 2. $x, y, z\in V(L)$, $w\in V(R)$.

Since $|E^C|-12 = 2^n-12\geq 20(n\geq5)$, an error-free edge $z_1z_1^h$ can be chosen form $E^C$ such that $z_1\notin \{x, y, z\}$, $z_1^h\neq w$ and $z_1, z_1^h\notin F$. By induction hypothesis, two disjoint paths $P_{xy}$, $P_{zz_1}$ with $V(P_{xy})\cup V(P_{zz_1}) = V(L-F^L)$ exist in $L-F^L$. By Lemma 3.1, we can find a Hamiltonian path $P_{z_1^hw}$ in $R-F^R$. Let $P_{zw} = (z, P_{zz_1}, z_1, z_1^h, P_{z_1^hw}, w)$. Then $P_{xy}, P_{zw}$ are two desired paths in $AQ_n-F$(see Figure 3(b)).

Case 3. $x, y\in V(L)$, $z, w\in V(R)$.

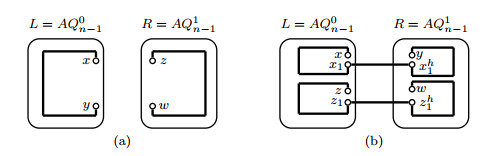
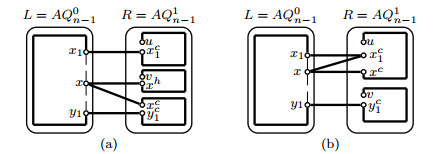
By Lemma 3.1, we can find a Hamiltonian path $P_{xy}$ in $L-F^L$ and a Hamiltonian path $P_{zw}$ in $R-F^R$. Then $P_{xy}, P_{zw}$ are two desired paths in $AQ_n-F$(see Figure 4(a)).

Case 4. $x, z\in V(L)$, $y, w\in V(R)$.

Since $|E^C|-12 = 2^n-12\geq 20(n\geq5)$, there are two error-free disjoint edges $x_1x_1^h, z_1z_1^h$ such that $x_1, z_1\notin \{x, z\}$, $x^h_1, z_1^h\notin \{y, w\}$ and $x_1, x^h_1, z_1, z_1^h\notin F$. By induction hypothesis, two disjoint paths $P_{xx_1}$, $P_{zz_1}$ with $V(P_{xx_1})\cup V(P_{zz_1}) = V(L-F^L)$ exist in $L-F^L$ and two disjoint paths $P_{x_1^hy}$, $P_{z_1^hw}$ with $V(P_{x_1^hy})\cup V(P_{z_1^hw}) = V(R-F^R)$ exist in $R-F^R$. Let $P_{xy} = (x, P_{xx_1}, x_1, x_1^h, P_{x_1^hy}, y)$, $P_{zw} = (z, P_{zz_1}, z_1, z_1^h, P_{z_1^hw}, w)$. Then $P_{xy}, P_{zw}$ are two desired paths in $AQ_n-F$(see Figure 4(b)).

The lemma holds.

Lemma 3.5. Let $x, y, z, w, a, b$ be six distinct vertices in $AQ_n(n\geq4)$. Then there exist three disjoint paths $P_{xy}$, $P_{zw}$, and $P_{ab}$ such that $V(P_{xy})\cup V(P_{zw})\cup V(P_{ab}) = V(AQ_n)$.

Proof. We prove the lemma by induction on $n\geq 4$. The induction basis for $n = 4$ holds by computer program. Suppose the lemma holds for $n-1$ with $n\geq 5$, then we must show the lemma holds for $n$.

Case 1. $x, y, z, w, a, b\in V(L)$.

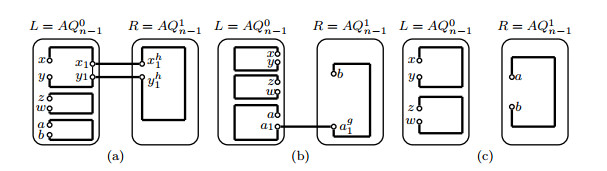
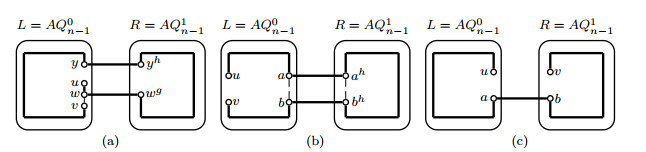
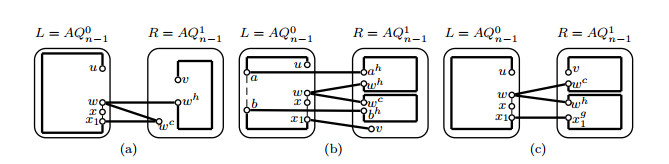
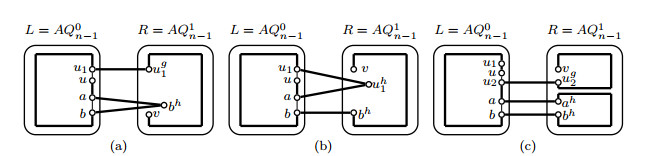
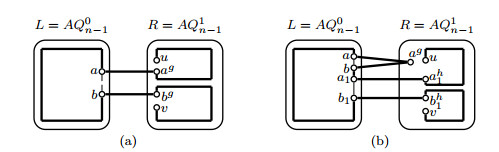
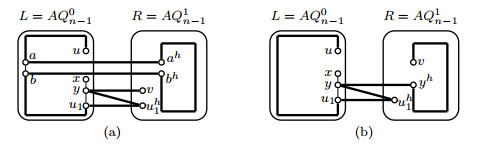
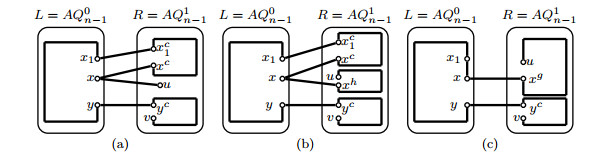
By induction hypothesis, three disjoint paths $P_{xy}$, $P_{zw}$ and $P_{ab}$ with $V(P_{xy})\cup V(P_{zw})\cup V(P_{ab}) = V(L)$ will exist in $L$. Let $x_1y_1\in E(P_{xy})$. By Lemma 3.1, a Hamiltonian path $P_{x^h_1y^h_1}$ can be found in $R$. Let $P^{1}_{xy} = (x, P_{xy}(x, x_1), x_1, x_1^h, P_{x^h_1y^h_1}, y^h_1, y_1, P_{xy}(y_1, y), y)$. Then $P^{1}_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 5(a)).

Case 2. $x, y, z, w, a\in V(L)$, $b\in V(R)$.

Choose a vertex $a_1$ from $V(L)-\{x, y, z, w, a\}$ such that there exists a vertex $a^g_1\in\{a^h_1, a^c_1\}$ with $a^g_1\neq b$. By induction hypothesis, three disjoint paths $P_{xy}$, $P_{zw}$ and $P_{aa_1}$ with $V(P_{xy})\cup V(P_{zw})\cup V(P_{aa_1}) = V(L)$ will exist in $L$. By Lemma 3.1, a Hamiltonian path $P_{a^g_1b}$ can be found in $R$. Let $P_{ab} = (a, P_{aa_1}, a_1, a^g_1, P_{a^g_1b}, b)$. Then $P_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 5(b)).

Case 3. $x, y, z, w\in V(L)$, $a, b\in V(R)$.

By Lemma 3.4, two disjoint paths $P_{xy}$, $P_{zw}$ with $V(P_{xy})\cup V(P_{zw}) = V(L)$ exist in $L$. By Lemma 3.1, we can find a Hamiltonian path $P_{ab}$ in $R$. Then $P_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 5(c)).

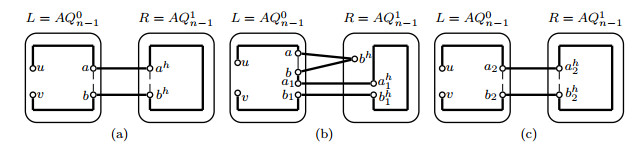
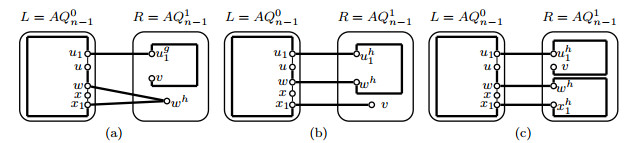
Case 4. $x, y, z, a\in V(L)$, $w, b\in V(R)$.

Since $|E^C|-12 = 2^n-12\geq 20$, there are two disjoint edges $z_1z_1^h, a_1a_1^h$ such that $z_1, a_1\notin \{x, y, z, a\}$ and $z_1^h, a_1^h\notin \{w, b\}$. By induction hypothesis, three disjoint paths $P_{xy}$, $P_{zz_1}$ and $P_{aa_1}$ with $V(P_{xy})\cup V(P_{zz_1})\cup V(P_{aa_1}) = V(L)$ will exist in $L$. And by Lemma 3.4, two disjoint paths $P_{z_1^hw}$, $P_{a_1^hb}$ with $V(P_{z_1^hw})\cup V(P_{a_1^hb}) = V(R)$ will exist in $R$. Let $P_{zw} = (z, P_{zz_1}, z_1, z_1^h, P_{z_1^hw}, w)$ and $P_{ab} = (a, P_{aa_1}, a_1, a_1^h, P_{a_1^hb}, b)$. Then $P_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 6(a)).

Case 5. $x, z, a\in V(L)$, $y, w, b\in V(R)$.

Since $|E^C|-12 = 2^n-12\geq 20$, there are three disjoint edges $x_1x_1^h, z_1z_1^h, a_1a_1^h$ such that $x_1, z_1, a_1\notin \{x, z, a\}$ and $x^h_1, z_1^h, a_1^h\notin \{y, w, b\}$. By induction hypothesis, three disjoint paths $P_{xx_1}$, $P_{zz_1}$ and $P_{aa_1}$ with $V(P_{xx_1})\cup V(P_{zz_1})\cup V(P_{aa_1}) = V(L)$ will exist in $L$ and three disjoint paths $P_{x_1^hy}$, $P_{z_1^hw}$, $P_{a_1^hb}$ with $V(P_{x_1^hy})\cup V(P_{z_1^hw})\cup V(P_{a_1^hb}) = V(R)$ will exist in $R$. Let $P_{xy} = (x, P_{xx_1}, x_1, x_1^h, P_{x_1^hy}, y)$, $P_{zw} = (z, P_{zz_1}, z_1, z_1^h, P_{z_1^hw}, w)$ and $P_{ab} = (a, P_{aa_1}, a_1, a_1^h, P_{a_1^hb}, b)$. Then $P_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 6(b)).

Case 6. $x, y, a\in V(L)$, $z, w, b\in V(R)$.

Since $|E^C|-12 = 2^n-12\geq 20$, there is an edge $a_1a_1^h$ such that $a_1\notin \{x, y, a\}$ and $a_1^h\notin \{z, w, b\}$. By Lemma 3.4, two disjoint paths $P_{xy}$ and $P_{aa_1}$ with $V(P_{xy})\cup V(P_{aa_1}) = V(L)$ will exist in $L$ and two disjoint paths $P_{zw}$ and $P_{a_1^hb}$ with $V(P_{zw})\cup V(P_{a_1^hb}) = V(R)$ will exist in $R$. Let $P_{ab} = (a, P_{aa_1}, a_1, a_1^h, P_{a_1^hb}, b)$. Then $P_{xy}, P_{zw}, P_{ab}$ are three desired paths in $AQ_n$(see Figure 6(c)).

The lemma holds.

4.   Main results

Theorem 4.1. Let $F\subset V(AQ_n)\cup E(AQ_n)$ with $|F|\leq 2n-3$$(n\geq 4)$. Then for arbitrary two different vertices $u$ and $v$ in $AQ_n-F$, there exists an error-free Hamiltonian path $P_{uv}$ except $(u, v)$ is a weak vertex-pair in $AQ_n-F$.

Proof. For $|F|\leq 2n-4$, the theorem holds by Lemma 3.1. We only need to consider $|F| = 2n-3$.

Now, we prove the theorem by induction on $n \geq 4$. The induction basis for $n = 4, 5$ holds by computer program (https://github.com/ZhangHeidi/Hypercubes/blob/master/vcn02.c). Supposing that the theorem holds for $n-1$ with $n\geq6$, we must show the theorem holds for $n$.

We may assume $|F^R| \leq |F^L|$(When $|F^R| \geq |F^L|$, the same proofs apply). Then $|F^R|\leq\lfloor\frac{2n-3}{2}\rfloor\leq n-1$. Notice that $|N_R(x)| = 2n-3$ for any vertex $x\in R$, we have $|N_{R-F^R}(x)|\geq n-2 \geq4$. Thus $R-F^R$ does not contain weak vertex-pairs.

Case 1. $|F^L| \leq 2n-5$.

Case 1.1. $u, v\in V(L-F^L)$ or $u, v\in V(R-F^R)$. Suppose that $u, v\in V(L-F^L)$.

Case 1.1.1. $(u, v)$ is a $w$-weak vertex-pair in $L-F^L$, i.e., $N_{L-F^L}(w) = \{u, v\}$. Since $|N_{L}(w)| = 2n-3$, we have $|F^L| = 2n-5$ and $|F^R|+|F^C| = 2$. Note that $(u, v)$ is a normal vertex-pair in $AQ_n-F$, we can choose a vertex $w^g$ from $\{w^h, w^c\}$ such that $w^g, ww^g\notin F$.

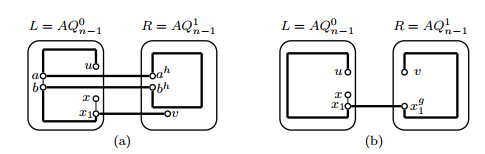
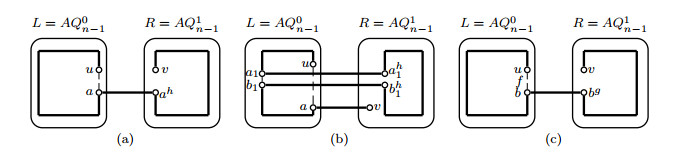
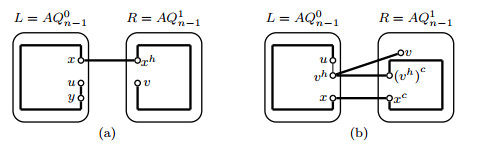
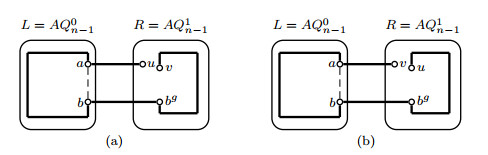
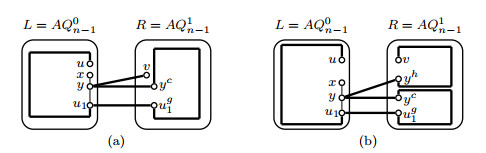
Because $|V(L)-F^L-\{u, w, v\}|\geq2^{n-1}-(2n-5)-3\geq22(n\geq6)$ and $|F^R|+|F^C| = 2$, there is a vertex $y\in V(L)-F^L-\{u, w, v\}$ such that $y^h, yy^h\notin F$ and $y^h\neq w^g$. By Corollary 2.1, $(u, y)$ is a normal vertex-pair in $L-F^L$. By induction hypothesis, a Hamiltonian path $P_{uy}$ exists in $L-F^L$. Notice that $N_{L-F^L}(w) = \{u, v\}$, then $N_{P_{u y}}(w) = \{u, v\}$. Since $|F^R|\leq2\leq 2n-6$, by Lemma 3.1, a Hamiltonian path $P_{w^gy^h}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, w, w^g, P_{w^gy^h}, y^h, y, P_{uy}(y, v), v)$ can therefore be found(see Figure 7(a)).

Case 1.1.2. $(u, v)$ is a normal vertex-pair in $L-F^L$.

Since $|F^L| \leq 2n-5$, by induction hypothesis, a Hamiltonian path $P_{uv}$ exists in $L-F^L$. By $\lfloor\frac{l_{uv}+1}{2}\rfloor-(2n-3) = \lfloor\frac{2^{n-1}-f_v^L}{2}\rfloor-(2n-3)\geq3$, we can choose an edge $ab\in E(P_{uv})$ such that $a^h, b^h, aa^h, bb^h\notin F$. By induction hypothesis, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F^R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uv}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{uv}(b, v), v)$ can therefore be found(see Figure 7(b)).

Case 1.2. $u\in V(L-F^L)$ and $v\in V(R-F^R)$.

According to the definition of $AQ_n$, $|E^C| = 2^n$. Since $|E^C|-2|F| = 2^{n}-2(2n-3)\geq 46$($n\geq 6$), there is an error-free edge $ab\in E^C$ such that $a, b\notin\{u, v\}$, $a, b\notin F$ and $(u, a)$ is a normal vertex-pair in $L-F^L$. By induction hypothesis, a Hamiltonian path $P_{ua}$ in $L-F^L$ and a Hamiltonian path $P_{bv}$ in $R-F^R$ exist. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, b, P_{bv}, v)$ can therefore be found(see Figure 7(c)).

Case 2. $|F^L| = 2n-4$. Then $|F^R|+|F^C| = 1$.

Case 2.1. $u, v\in V(L-F^L)$.

By Lemma 3.3, we can choose an element $f\in F^L$ such that $(u, v)$ is a normal vertex-pair in $L-(F^L-\{f\})$. Let $F_1^L = F^L-\{f\}$. Then $|F_1^L| = 2n-5$. By induction hypothesis, a Hamiltonian path $P_{uv}$ exists in $L-F_1^L$.

Case 2.1.1. $f\in V(P_{uv})\cup E(P_{uv})$.

If $f\in E(L)\cap F^L$, say $f = ab$; if $f\in V(L)\cap F^L$, say $N_{P_{uv}}(f) = \{a, b\}$; let $P_{uv} = (u, P_{uv}(u, a), a, f, b, P_{uv}(b, v), v)$. Suppose that $|\{a^h, b^h, aa^h, bb^h\} \cap F|\leq |\{a^c, b^c, aa^c, bb^c\}\cap F|$.

Case 2.1.1.1. $|\{a^h, b^h, aa^h, bb^h\}\cap F| = 0$.

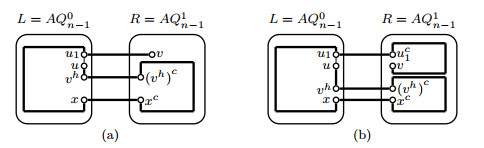
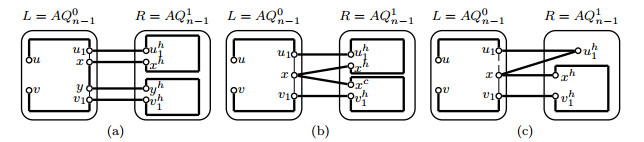
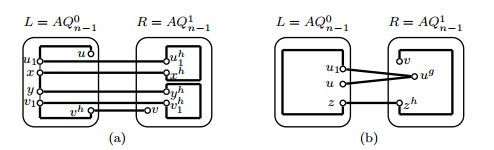
Since $|F^R|\leq1\leq2n-6$, by Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F^R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uv}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{uv}(b, v), v)$ can therefore be found(see Figure 8(a)).

Case 2.1.1.2. $|\{a^h, b^h, aa^h, bb^h\}\cap F| = 1$. Then $|\{a^c, b^c, aa^c, bb^c\}\cap F| = 1$.

Notice that $|F^R|+|F^C| = 1$, we have $\{a^h, b^h, aa^h, bb^h\}\cap F = \{a^c, b^c, aa^c, bb^c\}\cap F$, i.e., $\{a^h, b^h, aa^h, bb^h\} = \{a^c, b^c, aa^c, bb^c\}$. Then by Proposition 2.1, $a = b^{c_{n-1}}$, $a^h = b^c$ and $a^c = b^h$. Suppose that $a^h\in F$, then $b^h\notin F$. Let $a_1b_1\in E(P_{uv})$ with $a_1, b_1\notin \{a, b\}$ and $F^R_1 = F^R+\{b^h\}$. Then $|F^R_1|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a_1^hb_1^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uv}(u, a), a, b^h, b, P_{uv}(b, a_1), a_1, a_1^h, P_{a_1^hb_1^h}, b_1^h, b_1, P_{uv}(b_1, v), v)$ can therefore be found(see Figure 8(b)).

Case 2.1.2. $f\notin V(P_{uv})\cup E(P_{uv})$.

Then an edge $a_2b_2$ can be chosen from $P_{uv}$ with $a_2^h, b_2^h, a_2a_2^h, b_2b_2^h \notin F$. Since $|F^R|\leq1\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a_2^hb_2^h}$ exists in $R-F^R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uv}(u, a_2), a_2, a_2^h, P_{a_2^hb_2^h}, b_2^h, b_2, P_{uv}(b_2, v), v)$ can therefore be found(see Figure 8(c)).

Case 2.2. $u\in V(L-F^L)$ and $v\in V(R-F^R)$.

Case 2.2.1. $|F^L_v|\geq 1$. There is a vertex $x\in F^L_v$. Let $F^L_1 = F^L-\{x\}$, then $|F^L_1| = |F^L|-1 = 2n-5$.

Case 2.2.1.1. $(u, x)$ is a normal vertex-pair in $L-F^L_1$.

By induction hypothesis, a Hamiltonian path $P_{ux}$ exists in $L-F^L_1$. Let $N_{P_{ux}}(x) = x_1$. Since $|F^R|+|F^C| = 1$, there is a vertex $x_1^g\in \{x_1^h, x_1^c\}$ such that $x_1^g, x_1x_1^g\notin F$.

(1) $x_1^g = v$. Choose an edge $ab\in E(P_{ux})$ such that $a^h, b^h, aa^h, bb^h\notin F$ and $a, b\notin \{x, x_1\}$. Let $F_1^R = F^R+\{v\}$. Then $|F_1^R|\leq2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian $P_{uv} = (u, P_{ux}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{ux}(b, x_1), x_1, v)$ can therefore be found(see Figure 9(a)).

(2) $x_1^g\neq v$. Since $|F^R|\leq1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x_1^gv}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux}(u, x_1), x_1, x_1^g, P_{x_1^gv}, v)$ can therefore be found(see Figure 9(b)).

Case 2.2.1.2. $(u, x)$ is a $w$-weak vertex-pair in $L-F^L_1$. Then $N_{L-F^L_1}(w) = \{u, x\}$, i.e., $N_{L-F^L}(w) = u$.

By Corollary 2.1., $(u, w)$ is a normal vertex-pair in $L-F^L_1$. Since $|F^L_1| = 2n-5$, by induction hypothesis, a Hamiltonian path $P_{uw}$ exists in $L-F^L_1$. By $N_{L-F^L_1}(w) = \{u, x\}$, we have $N_{P_{uw}}(w) = \{x\}$. Let $N_{P_{uw}}(x) = \{x_1\}$ with $x_1\neq w$.

(1) $|\{w^h, w^c\}\cap F| = 0$.

(1.1) $v\in \{w^h, w^c\}$, assume that $v = w^h$. If $x_1 = w^{c_{n-1}}$, then by Proposition 2.1, $x_1^h = w^c, x_1^c = w^h$. We can choose an edge $ab\in E(P_{uw})$ such that $a^h, b^h, aa^h, bb^h\notin F$ and $a, b\notin \{w, x, x_1\}$, then $v, w^c\notin \{a^h, b^h\}$. Let $F^R_1 = F^R+\{v, w^c\}$. Then $|F^R_1|\leq3\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{uw}(b, x_1), x_1, w^c, w, v)$ can therefore be found(see Figure 10(a)). If $x_1\neq w^{c_{n-1}}$, then by Proposition 2.1, $x_1^h\neq w^c, x_1^c\neq w^h$. There exists an error-free vertex $x^g_1\in\{x^c_1, x^h_1\}$ such that $x^g_1, x_1x^g_1\notin F$. We have $x^g_1\notin \{w^c, v\}$. Let $F_1^R = F^R+\{v\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x^g_1w^c}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw}(u, x_1), x_1, x_1^g, P_{x^g_1w^c}, w^c, w, v)$ can therefore be found(see Figure 10(b)).

(1.2) $v\notin \{w^h, w^c\}$.

For $x_1 = w^{c_{n-1}}$. By Proposition 2.1, $x_1^h = w^c, x_1^c = w^h$, i.e., $v\notin \{x_1^h, x_1^c\}$. Let $F^R_1 = F^R+\{w^c\}$. Then $|F^R_1|\leq2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{w^hv}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw}(u, x_1), x_1, w^c, w, w^h, P_{w^hv}, v)$ connecting vertices $u$ and $v$ can therefore be found (see Figure 11(a)).

For $x_1\neq w^{c_{n-1}}$. By Proposition 2.1, $x_1^h\neq w^c, x_1^c\neq w^h$. There exists a correct vertex $x^g_1\in\{x^c_1, x^h_1\}$ such that $x^g_1, x_1x^g_1\notin F$. If $x^g_1 = v$, we can choose an edge $ab\in E(P_{uw})$ with $a, b\notin \{w, x, x_1\}$, $a^h, aa^h, b^h, bb^h\notin F$ and $a\neq w^{c_{n-1}}, b\neq w^{c_{n-1}}$. Let $F_1^R = F^R+\{v\}$. Then $|F_1^R|\leq2$. By Lemma 3.4, two disjoint paths $P_{a^hw^h}, P_{w^cb^h}$ with $V(P_{a^hw^h})\cup V(P_{w^cb^h}) = V(R-F_1^R)$ exist in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw}(u, a), a, a^h, P_{a^hw^h}, w^h, w, w^c, P_{w^cb^h}, b^h, b, P_{uw}(b, x_1), x_1, v)$ can therefore be found(see Figure 11(b)). If $x^g_1\neq v$. Since $|F^R|\leq1$, by Lemma 3.4, two disjoint paths $P_{x_1^gw^h}, P_{w^cv}$ with $V(P_{x_1^gw^h})\cup V(P_{w^cv}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw}(u, x_1), x_1, x_1^g, P_{x_1^gw^h}, w^h, w, w^c, P_{w^cv}, v)$ can therefore be found(see Figure 11(c)).

(2) $|\{w^h, w^c\}\cap F| = 1$. Assume that $w^c\in F$. Let $N_{P_{uw}}(u) = \{u_1\}$.

For $x_1 = w^{c_{n-1}}$ or $u_1 = w^{c_{n-1}}$. Assume that $x_1 = w^{c_{n-1}}$, then by Proposition 2.1, $x_1^h = w^c, x_1^c = w^h$ i.e., $x_1^h\in F$. Since $|F^C|+|F^R| = 1$, there exists a correct vertex $u^g_1\in\{u^c_1, u^h_1\}$ such that $u^g_1, u_1u^g_1\notin F$ and $u^g_1\neq v$. Let $F_1^R = F^R+\{w^h\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{u^g_1v}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, w, w^h, x_1, P_{uw}(x_1, u_1), u_1, u_1^g, P_{u^g_1v}, v)$ can therefore be found(see Figure 12(a)).

For $x_1\neq w^{c_{n-1}}$ and $u_1\neq w^{c_{n-1}}$. By Proposition 2.1, $x_1^h\neq w^c, x_1^c\neq w^h$, $u_1^h\neq w^c, u_1^c\neq w^h$. If $v\in \{x_1^h, u_1^h\}$, assume that $v = x_1^h$. Let $F^R_1 = F^R+\{v\}$. Then $|F^R_1|\leq2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{w^hu_1^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, w, w^h, P_{w^hu_1^h}, u_1^h, u_1, P_{uw}(u_1, x_1), x_1, v)$ can therefore be found(see Figure 12(b)). If $v\notin \{x_1^h, u_1^h\}$, since $|F^R|\leq1$, by Lemma 3.4, two disjoint paths $P_{w^hx_1^h}, P_{u_1^hv}$ with $V(P_{w^hx_1^h})\cup V(P_{u_1^hv}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, w, w^h, P_{w^hx_1^h}, x_1^h, x_1, P_{uw}(x_1, u_1), u_1, u_1^h, P_{u_1^hv}, v)$ can therefore be found(see Figure 12(c)).

Case 2.2.2. $|F^L_v| = 0$. A faulty edge $f$ can be chosen from $F^L$ such that $f\notin E_L(v^h)\cup E_L(v^c)$. Otherwise, $F^L\subset E_L(v^h)\cup E_L(v^c)$. Consider the following two cases.

Case 2.2.2.1. There is a faulty edge $f\in F^L$ such that $f\notin E(v^h)\cup E(v^c)$. Let $F_1^L = F^L-f$. Then $|F_1^L| = 2n-5$. By Lemma 3.1, a Hamiltonian cycle $C$ containing vertex $u$ exists in $L-F_1^L$.

(1) $f\notin E(C)$. Let $a\in N_{C}(u)$ with $a, aa^h\notin F$ and $C = (u, P_{ua}, a, u)$.

For $a^h\neq v$, since $|F^R|\leq1$, by Lemma 3.1, a Hamiltonian path $P_{a^hv}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, a^h, P_{a^hv}, v)$ can therefore be found(see Figure 13(a)).

For $a^h = v$, let $F^R_1 = F^R+\{v\}$. Then $|F^R_1|\leq 2\leq2n-6$. Choose an edge $a_1b_1\in E(C)$ such that $a_1^h, b_1^h, a_1a_1^h.b_1b_1^h\notin F$ and $a_1, b_1\notin \{u, a\}$. By Lemma 3.1, a Hamiltonian path $P_{a_1^hb_1^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}(u, a_1), a_1, a_1^h, P_{a_1^hb_1^h}, b_1^h, b_1, P_{ua}(b_1, a), a, v)$ can therefore be found(see Figure 13(b)).

(2) $f\in E(C)$. Let $f = ab$. Consider the following two cases.

(2.1) $f\in E_C(u)$. Let $f = ub$ and $C = (u, P_{ub}, b, u)$. Since $|F^R|+|F^C| = 1$, there is a correct vertex $b^g\in \{b^h, b^c\}$ such that $bb^g\notin F$. Since $f\notin E(v^h)\cup E(v^c)$, $b^g\neq v$. Then by $|F^R|\leq1$ and Lemma 3.1, a Hamiltonian path $P_{b^gv}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ub}, b, b^g, P_{b^gv}, v)$ can therefore be found(see Figure 13(c)).

(2.2) $f\notin E_C(u)$. Let $f = ab$ and $C = (u, P_{ua}, a, b, P_{bu_1}, u_1, u)$. Suppose that $|\{u_1^h, u_1u_1^h, a^h, aa^h, b^h, bb^h\}\cap F|\leq |\{u_1^c, u_1u_1^c, a^c, aa^c, b^c, bb^c\}\cap F|$.

(2.2.1) $|\{u_1^h, u_1u_1^h, a^h, aa^h, b^h, bb^h\}\cap F| = 0$.

For $u_1^h\neq v$, by Lemma 3.4, two disjoint paths $P_{u_1^hv}$, $P_{a^hb^h}$ with $V(P_{u_1^hv})\cup V(P_{a^hb^h}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, a^h, P_{a^hb^h}, b^h, b, P_{bu_1}, u_1, u^h_1, P_{u^h_1v}, v)$ can therefore be found(see Figure 14(a)).

For $u_1^h = v$, let $F^R_1 = F^R+\{v\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, a^h, P_{a^hb^h}, b^h, b, P_{bu_1}, u_1, v)$ can therefore be found(see Figure 14(b)).

(2.2.2) $|\{u_1^h, u_1u_1^h, a^h, aa^h, b^h, bb^h\}\cap F| = 1$. Then $|\{u_1^c, u_1u_1^c, a^c, aa^c, b^c, bb^c\}\cap F| = 1$. Notice that $|F^R|+|F^C| = 1$, we have $\{u_1^h, u_1u_1^h, a^h, aa^h, b^h, bb^h\}\cap F = \{u_1^c, u_1u_1^c, a^c, aa^c, b^c, bb^c\}\cap F$. Then by Proposition 2.1, $a = b^{c_{n-1}}$ or $a = u_1^{c_{n-1}}$ or $b = u_1^{c_{n-1}}$.

For $a = b^{c_{n-1}}$, by Proposition 2.1, $a^h = b^c$ and $a^c = b^h$. Suppose that $a^h\in F$. Then $b^h\notin F$ and $|\{u_1^h, u_1u_1^h, u_1^c, u_1u_1^c\}\cap F| = 0$. It follows that a vertex $u_1^g$ can be chosen from $\{u_1^h, u_1^c\}$ such that $u_1^g\neq v$. Let $F^R_1 = F^R+\{b^h\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{u_1^gv}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, b^h, b, P_{bu_1}, u_1, u_1^g, P_{u_1^gv}, v)$ can therefore be found(see Figure 15(a)).

For $a = u_1^{c_{n-1}}$, by Proposition 2.1, $a^h = u_1^c$ and $a^c = u_1^h$. Suppose that $a^h\in F$. Then $u_1^h\notin F$ and $|\{b^h, bb^h, b^c, bb^c\}\cap F| = 0$. Let $F^R_1 = F^R+\{u_1^h\}$. Then $|F^R_1|\leq 2\leq2n-6$. Notice that $f = ab\notin E(v^h)\cup E(v^c)$, then $v\notin \{b^h, b^c\}$. By Lemma 3.1, a Hamiltonian path $P_{b^hv}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua}, a, u_1^h, u_1, P_{u_1b}, b, b^h, P_{b^hv}, v)$ can therefore be found(see Figure 15(b)).

For $b = u_1^{c_{n-1}}$, by Proposition 2.1, $b^h = u_1^c$ and $b^c = u_1^h$. Assume that $u_1^h\in F$. Then $b^h\notin F$ and $|\{a^h, aa^h, a^c, aa^c\}\cap F| = 0$. Let $u_2 = N_{C}(u)$ with $u_2\neq u_1$. Then $u_2^h, u_2u_2^h, u_2^c, u_2u_2^c\notin F$. Notice that $f = ab\notin E(v^h)\cup E(v^c)$, then $v\notin \{a^h, a^c\}$. If $u_2 = a^{c_{n-1}}$, since $v\notin \{a^h, a^c\}$, then for any vertex $u_2^g\in \{u_2^h, u_2^c\}$ with $u_2^g\neq v$. If $u_2\neq a^{c_{n-1}}$, then there is a vertex $u_2^g\in \{u_2^h, u_2^c\}$ such that $u_2^g\neq v$. Since $|F^R|\leq 1$, by Lemma 3.4, two disjoint paths $P_{a^hb^h}, P_{u_2^gv}$ with $V(P_{a^hb^h})\cup V(P_{u_2^gv}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ub}, b, b^h, P_{b^ha^h}, a^h, a, P_{ua}(a, u_2), u_2, u^g_2, P_{u^g_2v}, v)$ can therefore be found(see Figure 15(c)). If $u_2 = a$, then we use $a^c$ instead of $u_2^g$.

Case 2.2.2.2. $F^L\subset N_L(v^h)\cup E_L(v^c)$. Suppose that $|F^L\cap E_L(v^h)|\geq |F^L\cap E_L(v^c)|$. Let $e_1, e_2\in F^L\cap E_L(v^h)$ and $F_1^L = F^L-\{e_1, e_2\}+\{v^h\}$. Then $|F_1^L| = 2n-5$. Since $|N_L(v^h)| = 2n-3$ and $|F^L| = 2n-4$, there is a correct vertex $y$ such that $y\in N_{L-F^L}(v^h)$.

(1) $u = v^h$. Choose a vertex $x$ from $V(L)-F^L-\{u, v^c, y\}$ with $x^h, xx^h\notin F$ and $x^h\neq v$. Since $|F^L\cap E_L(v^h)|\geq |F^L\cap E_L(v^c)|$ and $F_1^L = F^L-\{e_1, e_2\}+\{v^h\}$, $(x, y)$ is a normal vertex-pair in $L-F_1^L$. By induction hypothesis, a Hamiltonian path $P_{xy}$ exists in $L-F_1^L$. Since $|F^R|\leq 1$, by Lemma 3.1, a Hamiltonian path $P_{x^hv}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, y, P_{yx}, x, x^h, P_{x^hv}, v)$ can therefore be found(see Figure 16(a)).

(2) $u\neq v^h$.

(2.1) $y = u$. Then $u\in N_{L-F^L}(v^h)$. Notice that $F^L\subset N_L(v^h)\cup E_L(v^c)$ and $|F^R|+|F^C| = 1$. Since $(u, v)$ is a normal vertex pair in $AQ_n-F$, we have that $v^h(v^h)^c, (v^h)^c\notin F$. Choose a vertex $x$ from $V(L)-F^L-\{v^h, v^c, y\}$ with $x^c, xx^c\notin F$ and $x^c\neq v$. Since $|F^L\cap E_L(v^h)|\geq |F^L\cap E_L(v^c)|$ and $F_1^L = F^L-\{e_1, e_2\}+\{v^h\}$, $(u, x)$ is a normal vertex-pair in $L-F_1^L$. By induction hypothesis, a Hamiltonian path $P_{ux}$ exists in $L-F_1^L$.

(2.1.1) $v^hv\notin F$. Let $F^R_1 = F^R+\{v\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x^c{(v^h)}^c}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux}, x, x^c, P_{x^c{(v^h)}^c}, {(v^h)}^c, v^h, v)$ can therefore be found(see Figure 16(b)).

(2.1.2) $v^hv\in F$. Let $u_1\in N_{P_{ux}}(u)$. Since $|F^R|+|F^C| = 1$, $u_1^c, u_1u_1^c\notin F$.

If $u_1^c = v$, let $F^R_1 = F^R+\{v\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{{(v^h)}^cx^c}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, v^h, {(v^h)}^c, P_{{(v^h)}^cx^c}, x^c, x, P_{ux}(x, u_1), u_1, v)$ connecting vertices $u$ and $v$ can therefore be found(see Figure 17(a)).

If $u_1^c\neq v$, by $|F^R|\leq 1$ and Lemma 3.4, two disjoint paths $P_{{(v^h)}^cx^c}$, $P_{u_1^cv}$ with $V(P_{{(v^h)}^cx^c})\cup V(P_{u_1^cv}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, v^h, {(v^h)}^c, P_{{(v^h)}^cx^c}, x^c, x, P_{ux}(x, u_1), u_1, u^c_1, P_{u_1^cv}, v)$ can therefore be found(see Figure 17(b)).

(2.2) $y\neq u$. Since $|F^L\cap E_L(v^h)|\geq |F^L\cap E_L(v^c)|$ and $F_1^L = F^L-\{e_1, e_2\}+\{v^h\}$, $(u, y)$ is a normal vertex-pair in $L-F_1^L$. By induction hypothesis, a Hamiltonian path $P_{uy}$ exists in $L-F_1^L$.

If $v^hv\in F$, then ${(v^h)}^c, v^h{(v^h)}^c\notin F$. Since $|F^R|\leq 1$, by Lemma 3.1, a Hamiltonian path $P_{{(v^h)}^cv}$ exists in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uy}, y, v^h, {(v^h)}^c, P_{{(v^h)}^cv}, v)$ can therefore be found(see Figure 18(a)).

If $v^hv\notin F$, then choose an edge $ab\in E(P_{uy})$ with $a^h, b^h, aa^h, bb^h\notin F$ and $v\notin \{a^h, b^h\}$. Let $F^R_1 = F^R+\{v\}$. Then $|F_1^R|\leq2\leq2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uy}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{uy}(b, y), y, v^h, v)$ can therefore be found(see Figure 18(b)).

Case 2.3. $u, v\in V(R-F^R)$.

Notice that $u^h = {(u^c)}^{c_{n-1}}$ and $v^h = {(v^c)}^{c_{n-1}}$. By Proposition 2.2, $|N_L(u^h)\cap N_L(u^c)| = 2$ and $|N_L(v^h)\cap N_L(v^c)| = 2$. Let $N_L(u^h)\cap N_L(u^c) = \{m_1, m_2\}$, $N_L(v^h)\cap N_L(v^c) = \{m_3, m_4\}$, and $F_1^L = \{m_1, m_2, m_3, m_4, u^hu^c, v^hv^c\}$. Since $|F^L| = 2n-4\geq 8(n\geq 6)$, $|F^L-F_1^L|\geq 2$. Then we can choose a faulty element $f$ with $f\in F^L-F_1^L$. Then $|F^L-\{f\}| = 2n-5$. By Lemma 3.1, a Hamiltonian cycle $C$ exists in $L-(F^L-\{f\})$. If $C$ contains $f$, let $C = (a, P_{ab}, b, f, a)$. If $C$ does not contain $f$, let $C = (a, P_{ab}, b, a)$ with $ab\notin \{u^hu^c, v^hv^c\}$. Since $|F^R|+|F^C| = 1$, there is a vertex $a^g\in \{a^h, a^c\}$ and a vertex $b^g\in \{b^h, b^c\}$ with $a^g, b^g, aa^g, bb^g\notin F$. If $|\{a^g, b^g\}\cap\{u, v\}|\geq1$, then by the choice of the above error element $f$, $a\neq b^{c_{n-1}}$, i.e., $a^h, a^c, b^h, b^c$ are all distinct. Since $|F^R|+|F^C| = 1$, we can choose an error-free set $\{a^g, b^g, aa^g, bb^g\}$ such that $|\{a^g, b^g\}\cap\{u, v\}| = 1$. Therefore, we only need to consider the following two cases.

Case 2.3.1. $|\{a^g, b^g\}\cap\{u, v\}| = 0$.

Case 2.3.1.1. $a^g\neq b^g$.

Since $|F^R|\leq1$, by Lemma 3.4, two disjoint paths $P_{ua^g}$, $P_{b^gv}$ with $V(P_{ua^g})\cup V(P_{b^gv}) = V(R-F^R)$ exist in $R-F^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua^g}, a^g, a, P_{ab}, b, b^g, P_{b^gv}, v)$ can therefore be found(see Figure 19(a)).

Case 2.3.1.2. $a^g = b^g$.

Let $F^R_1 = F^R+\{a^g\}$. Then $|F^R_1|\leq2$. Choose an edge $a_1b_1\in E(P_{ab})$ with $a_1, b_1\notin \{a, b\}$, $a^h_1, b^h_1\notin \{u, v\}$ and $a^h_1, b^h_1, a_1a^h_1, b_1b^h_1\notin F$. By Lemma 3.4, two disjoint paths $P_{ua_1^h}$, $P_{b_1^hv}$ with $V(P_{ua_1^h})\cup V(P_{b_1^hv}) = V(R-F_1^R)$ exist in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ua_1^h}, a_1^h, a_1, P_{ab}(a_1, b), b, a^g, a, P_{ab}(a, b_1), b_1, b_1^h, P_{b_1^hv}, v)$ can therefore be found(see Figure 19(b)).

Case 2.3.2. $|\{a^g, b^g\}\cap\{u, v\}| = 1$.

Case 2.3.2.1. $u\in \{a^g, b^g\}$, suppose that $u = a^g$. Let $F^R_1 = F^R+\{u\}$. Then $|F^R_1|\leq 2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{b^gv}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, a, P_{ab}, b, b^g, P_{b^gv}, v)$ can therefore be found(see Figure 20(a)).

Case 2.3.2.2. $v\in \{a^g, b^g\}$, suppose that $v = a^g$. Let $F^R_1 = F^R+\{v\}$. Then $|F^R_1|\leq 2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{ub^g}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, P_{ub^g}, b^g, b, P_{ba}, a, v)$ can therefore be found(see Figure 20(b)).

Case 3. $|F^L| = 2n-3$. Then $|F^R| = |F^C| = 0$.

Case 3.1. $u, v\in V(L-F^L)$. By Lemma 3.2, there exist two elements $f_1, f_2\in F^L$ with $(u, v)$ is a normal vertex-pair in $L-(F^L-\{f_1, f_2\})$. Let $F_1^L = F^L-\{f_1, f_2\}$. Then $|F_1^L| = 2n-5$. By induction hypothesis, a Hamiltonian path $P_{uv}$ exists in $L-F_1^L$ which may or may not include $f_1$ or $f_2$ on it. Removing $f_1$ and $f_2$, path $P_{uv}$ is divided into three, two, or one segments relying on the situations in which $f_1$ and $f_2$ are on $P_{uv}$ or not. For the last two situations, we may arbitrarily delete one or two more edges from $P_{uv}$ to make it into three subpaths. Therefore, we may write the path $P_{uv}$ with these subpaths as $(u, P_{uu_1}, u_1, f_1^{'}, x, P_{xy}, y, f_2^{'}, v_1, P_{v_1v}, v)$.

Case 3.1.1. The length of $P_{xy}$ $l_{xy}\geq1$. By Lemma 3.4, two disjoint paths $P_{u_1^hx^h}$, $P_{y^hv_1^h}$ with $V(P_{u_1^hx^h})\cup V(P_{y^hv_1^h}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uu_1}, u_1, u_1^h, P_{u_1^hx^h}, x^h, x, P_{xy}, y, y^h, P_{y^hv_1^h}, v_1^h, v_1, P_{v_1v}, v)$ can therefore be found(see Figure 21(a)).

Case 3.1.2. The length of $P_{xy}$ $l_{xy} = 0$. Then $x = y$.

Case 3.1.2.1. $x\neq u_1^{c_{n-1}}$ and $x\neq v_1^{c_{n-1}}$. By Proposition 2.1, $x^h\neq u_1^c$, $x^c\neq u_1^h$ and $x^h\neq v_1^c$, $x^c\neq v_1^h$. By Lemma 3.4, two disjoint paths $P_{u_1^hx^h}$, $P_{x^cv_1^h}$ with $V(P_{u_1^hx^h})\cup V(P_{x^cv_1^h}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uu_1}, u_1, u_1^h, P_{u_1^hx^h}, x^h, x, x^c, P_{x^cv_1^h}, v_1^h, v_1, P_{v_1v}, v)$ can therefore be found(see Figure 21(b)).

Case 3.1.2.2. $x = u_1^{c_{n-1}}$ or $x = v_1^{c_{n-1}}$. Assume that $x = u_1^{c_{n-1}}$. By Proposition 2.1, $x^h = u_1^c, x^c = u_1^h$. Let $F_1^R = F^R+\{u_1^h\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x^hv_1^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P^1_{uv} = (u, P_{uu_1}, u_1, u_1^h, x, x^h, P_{x^hv_1^h}, v_1^h, v_1, P_{v_1v}, v)$ can therefore be found(see Figure 21(c)).

Case 3.2. $u\in V(L-F^L)$, $v\in V(R)$.

Case 3.2.1. $|F_v^L|\geq1$. There exists at least one faulty vertex $x\in F^L$.

Let $F^L_1 = F^L-\{x\}$. Then $|F^L_1| = 2n-4$. By Lemma 3.3, there is an element $f_1\in F^L_1$ with $(u, x)$ is a normal vertex-pair in $L-(F^L_1-\{f_1\})$. Let $F^L_2 = F^L_1-\{f_1\}$. Then $|F^L_2| = 2n-5$. By induction hypothesis, a Hamiltonian path $P_{ux}$ exists in $L-F^L_2$ which may or may not include $f_1$ on it. Similar to Case 3.1, we may write the path $P_{ux}$ as $(u, P_{uu_1}, u_1, f_1^{'}, y, P_{yx_1}, x_1, x)$.

Case 3.2.1.1. The length of $P_{yx_1}$ $l_{yx_1}\geq1$.

(1) $y = u_1^{c_{n-1}}$. By Proposition 2.1, $y^h = u_1^c$ and $y^c = u_1^h$.

(1.1) $v\in\{y^h, u_1^h\}$. We may assume that $u_1^h = v$. We have $v\notin \{y^h, x_1^h\}$. Let $F_1^R = F^R+\{y^h\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x_1^hv}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, y^h, y, P_{yx_1}, x_1, x^h_1, P_{x_1^hv}, v)$ can therefore be found(see Figure 22(a)).

(1.2) $v\notin\{y^h, u_1^h\}$.

(1.2.1) $x_1^h\neq v$. By Lemma 3.4, two disjoint paths $P_{u_1^hy^h}$, $P_{x_1^hv}$ with $V(P_{u_1^hy^h})\cup V(P_{x_1^hv}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, u^h_1, P_{u_1^hy^h}, y^h, y, P_{yx_1}, x_1, x^h_1, P_{x_1^hv}, v)$ can therefore be found(see Figure 22(b)).

(1.2.2) $x_1^h = v$. Let $F_1^R = F^R+\{v\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{u_1^hy^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, u^h_1, P_{u_1^hy^h}, y^h, y, P_{yx_1}, x_1, v)$ can therefore be found(see Figure 22(c)).

(2) $y\neq u_1^{c_{n-1}}$. By Proposition 2.1, $y^h\neq u_1^c$ and $y^c\neq u_1^h$. There exists $\{u_1^g, y^g\}\in\{\{u_1^h, y^h\}, \{u_1^c, y^c\}\}$ such that $v\notin \{u_1^g, y^g\}$.

For $x_1^h\neq v$, the proof is similar to (1.2.1) of Case 3.2.1.1.

For $x_1^h = v$, the proof is similar to (1.2.2) of Case 3.2.1.1.

Case 3.2.1.2. The length of $P_{yx_1}$ $l_{yx_1} = 0$. Then $x_1 = y$.

(1) $y = u_1^{c_{n-1}}$. By Proposition 2.1, $y^h = u_1^c$ and $y^c = u_1^h$.

(1.1) $v\in \{y^h, u_1^h\}$. We may assume that $v = y^h$. Choose an edge $ab\in P_{ux}$ with $a, b\notin \{u_1, y, x\}$. Then $v\notin \{a^h, b^h\}$. Let $F_1^R = F^R+\{v, u_1^h\}$. Then $|F_1^R| = 2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}(u, a), a, a^h, P_{a^hb^h}, b^h, b, P_{uu_1}(b, u_1), u_1, u_1^h, y, v)$ can therefore be found(see Figure 23(a)).

(1.2) $v\notin \{y^h, u_1^h\}$. Let $F_1^R = F^R+\{u_1^h\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{y^hv}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, u_1^h, y, y^h, P_{y^hv}, v)$ can therefore be found(see Figure 23(b)).

(2) $y\neq u_1^{c_{n-1}}$. By Proposition 2.1, $y^h\neq u_1^c$ and $y^c\neq u_1^h$. There is a vertex $u_1^g\in \{u_1^h, u_1^c\}$ such that $u_1^g\neq v$.

(2.1) $v\in \{y^h, y^c\}$. We may assume that $v = y^h$. Let $F_1^R = F^R+\{v\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{u_1^gy^c}$ exists in $R-F_1^R$. Let $P_{uv} = (u, P_{uu_1}, u_1, u_1^g, P_{u_1^gy^c}, y^c, y, v)$. An error-free Hamiltonian path $P_{uv}$ can therefore be found(see Figure 24(a)).

(2.2) $v\notin \{y^h, y^c\}$. By Lemma 3.4, two disjoint paths $P_{u_1^gy^c}$, $P_{y^hv}$ with $V(P_{u_1^gy^c})\cup V(P_{y^hv}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, u_1^g, P_{u_1^gy^c}, y^c, y, y^h, P_{y^hv}, v)$ can therefore be found(see Figure 24(b)).

Case 3.2.2. $|F_v^L| = 0$.

Case 3.2.2.1. For any vertex $y\in V(L)$, $|E_L(y)\cap F^L|\leq2$. Since $|F^L| = 2n-3\geq 9(n\geq6)$, we can choose two edges $f_1, f_2\in F^L$ with $f_1, f_2\notin E_L(v^h)\cup E_L(v^c)$ and $f_1, f_2$ do not share the same vertex. Let $F^L_1 = F^L-\{f_1, f_2\}$. Then $|F^L_1| = 2n-5$. We may assume that $v^h\neq u$. By induction hypothesis, there exists a Hamiltonian path $P_{uv^h}$ in $L-F^L_1$ which may or may not include $f_1$ or $f_2$ on it. Removing $f_1$ and $f_2$, path $P_{uv^h}$ is divided into three, two, or one segments relying on the situations in which $f_1$ and $f_2$ are on $P_{uv^h}$ or not. For the last two situations, we may delete one or two more edges which are not incident to vertices $v^h, v^c$ from $P_{uv^h}$ to make it into three subpaths. Therefore, we may write the path $P_{uv^h}$ with these subpaths as $(u, P_{uu_1}, u_1, f_1^{'}, x, P_{xy}, y, f_2^{'}, v_1, P_{v_1v^h}, v^h)$. Let $F^R_1 = F^R+\{v\}$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{u_1^hx^h}$ and $P_{y^hv_1^h}$ with $V(P_{u_1^hx^h})\cup V(P_{y^hv_1^h}) = V(R-F^R_1)$ exist in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, P_{uu_1}, u_1, u_1^h, P_{u_1^hx^h}, x^h, x, P_{xy}, y, y^h, P_{y^hv_1^h}, v_1^h, v_1, P_{v_1v^h}, v^h, v)$ can therefore be found(see Figure 25(a)).

Case 3.2.2.2. A vertex $y$ exists in $L$ with $|E_L(y)\cap F^L|\geq3$.

Let $e_1, e_2, e_3\in E_L(y)\cap F^L$ and $F^L_1 = F^L-\{e_1, e_2, e_3\}+y$. Then $|F^L_1| = 2n-5$.

(1) $y = u$. There is a vertex $u^g\in \{u^h, u^c\}$ with $u^g\neq v$. Let $N_L(u^g) = \{u, u_1\}$ and $z\in V(L)-\{u, u_1, v^h, v^c\}$ with $(u_1, z)$ is a normal vertex-pair in $L-F^L_1$. Then $z^h\neq v$. By induction hypothesis, a Hamiltonian path $P_{u_1z}$ exists in $L-F^L_1$. Let $F^R_1 = F^R+\{u^g\}$. Then $|F^R_1| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{z^hv}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, u^g, u_1, P_{u_1z}, z, z^h, P_{z^hv}, v)$ can therefore be found(see Figure 25(b)).

(2) $y\neq u$.

(2.1) $y\in \{v^h, v^c\}$. We may assume that $y = v^c$. Let $z\in V(L)-\{u, v^h, v^c\}$ with $(u, z)$ is a normal vertex-pair in $L-F^L_1$. Then $z^h\neq v$. By induction hypothesis, a Hamiltonian path $P_{uz}$ exists in $L-F^L_1$. Let $F^R_1 = F^R+\{v\}$. Then $|F^R_1| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{z^h{(v^c)}^h}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, P_{uz}, z, z^h, P_{z^h{(v^c)}^h}, {(v^c)}^h, v^c, v)$ can therefore be found(see Figure 26(a)).

(2.2) $y\notin \{v^h, v^c\}$. Let $z\in V(L)-\{u, y, v^h, v^c\}$ with $(u, z)$ is a normal vertex-pair in $L-F^L_1$ and $z\neq y^{c_{n-1}}$. By Proposition 2.1, $z^h\neq y^c$ and $z^c\neq y^h$. By induction hypothesis, a Hamiltonian path $P_{uz}$ exists in $L-F^L_1$. By Lemma 3.4, two disjoint paths $P_{z^hy^h}$ and $P_{y^cv}$ with $V(P_{z^hy^h})\cup V(P_{y^cv}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P_{uv} = (u, P_{uz}, z, z^h, P_{z^hy^h}, y^h, y, y^c, P_{y^cv}, v)$ can therefore be found(see Figure 26(b)).

Case 3.3. $u, v\in V(R)$.

Case 3.3.1. $|F_v^L|\geq2$. There are at least two vertices $x_1, x_2\in F^L$. Let $F_1^L = F^L-\{x_1, x_2\}$. Then $|F_1^L| = 2n-5$.

Case 3.3.1.1. $(x_1, x_2)$ is a normal vertex-pair in $L-F_1^L$. By induction hypothesis, a Hamiltonian path $P_{x_1x_2}$ exists in $L-F_1^L$. Let $N_{P_{x_1x_2}}(x_1) = x_{11}$ and $N_{P_{x_1x_2}}(x_2) = x_{21}$.

(1) There is a vertex $x^g_{11}\in\{x^h_{11}, x^c_{11}\}$ and a vertex $x^g_{21}\in\{x^h_{21}, x^c_{21}\}$ such that $x^g_{11}, x^g_{21}\notin\{u, v\}$. By Lemma 3.4, two disjoint paths $P_{ux^g_{11}}$, $P_{x^g_{21}v}$ with $V(P_{ux^g_{11}})\cup V(P_{x^g_{21}v}) = V(R)$ exist in $R$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux^g_{11}}, x^g_{11}, x_{11}, P_{x_1x_2}(x_{11}, x_{21}), x_{21}, x^g_{21}, P_{x^g_{21}v}, v)$ can therefore be found(see Figure 27(a)).

(2) For any vertex $x^g_{11}\in\{x^h_{11}, x^c_{11}\}$ and vertex $x^g_{21}\in\{x^h_{21}, x^c_{21}\}$, $\{x^g_{11}, x^g_{21}\} = \{u, v\}$. We assume that $x^g_{11} = u$ and $x^g_{21} = v$. Let $ab\in E(P_{x_1x_2}(x_{11}, x_{21}))$ with $a, b\notin \{x_{11}, x_{21}\}$ and $F_1^R = F^R+\{u, v\}$. Then $|F_1^R| = 2\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{a^hb^h}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, x_{11}, P_{x_1x_2}(x_{11}, a), a, a^h, P_{a^hb^h}, b^h, b, P_{x_1x_2}(b, x_{21}), x_{21}, v)$ can therefore be found(see Figure 27(b)).

(3) $\{x^h_{11}, x^c_{11}\} = \{u, v\}$ and $u, v\notin \{x^h_{21}, x^c_{21}\}$ or $\{x^h_{21}, x^c_{21}\} = \{u, v\}$ and $u, v\notin \{x^h_{11}, x^c_{11}\}$. Assume that $\{x^h_{11}, x^c_{11}\} = \{u, v\}$ and $u, v\notin \{x^h_{21}, x^c_{21}\}$. Let $F_1^R = F^R+\{u\}$. Then $|F_1^R| = 1\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{x^h_{21}v}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, x_{11}, P_{x_1x_2}(x_{11}, x_{21}), x_{21}, x^h_{21}, P_{x^h_{21}v}, v)$ can therefore be found(see Figure 27(c)).

Case 3.3.1.2. $(x_1, x_2)$ is a $w$-weak vertex-pair in $L-F_1^L$, i.e., $F^L\subset N_L(w)\cup E_L(w)$, $|N_{L-F^L}(w)| = 0$ and $N_{L-F_1^L}(w) = \{x_1, x_2\}$. Since $(u, v)$ is a normal vertex-pair in $AQ_n-F$, $|\{w^h, w^c\}\cap \{u, v\}|\leq1$. By Corollary 2.1, $(w, x_2)$ is a normal vertex-pair in $L-F_1^L$. By induction hypothesis, a Hamiltonian path $P_{wx_2}$ exists in $L-F_1^L$. Since $N_{L-F_1^L}(w) = \{x_1, x_2\}$, we have $N_{P_{wx_2}}(w) = x_1$.

(1) $|\{w^h, w^c\}\cap \{u, v\}| = 1$. Suppose that $u\in \{w^h, w^c\}$, say $u = w^h$. Let $N_{P_{wx_2}}(x_1)-w = x_{11}$ and $N_{P_{wx_2}}(x_2) = x_{21}$.

(1.1) $x_{11} = w^{c_{n-1}}$ or $x_{21} = w^{c_{n-1}}$. Suppose that $x_{11} = w^{c_{n-1}}$. By Proposition 2.1, $w^h = x^c_{11}$ and $w^c = x^h_{11}$. There is a vertex $x^g_{21}\in\{x^h_{21}, x^c_{21}\}$ such that $x^g_{21}\neq v$. Let $F^R_1 = F^R+\{u, w^c\}$. Then $|F^R_1| = 2\leq 2n-6$. By Lemma 3.1, an error-free Hamiltonian path $P_{x^g_{21}v}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, w, w^c, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, x^g_{21}, P_{x^g_{21}v}, v)$ can therefore be found(see Figure 28(a)).

(1.2) $x_{11}\neq w^{c_{n-1}}$ and $x_{21}\neq w^{c_{n-1}}$. Then by Proposition 2.1, $x^h_{11}\neq w^c$, $x^c_{11}\neq w^h$ and $x^c_{21}\neq w^h$, $x^h_{21}\neq w^c$.

If $v\in\{x^c_{21}, x^c_{11}\}$, we may assume that $x^c_{21} = v$. Let $F^R_1 = F^R+\{u, v\}$. Then $|F^R_1| = 2\leq 2n-6$. By Lemma 3.1, an error-free Hamiltonian path $P_{w^cx^c_{11}}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, w, w^c, P_{w^cx^c_{11}}, x^c_{11}, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, v)$ can therefore be found(see Figure 28(b)).

If $v\notin\{x^c_{21}, x^c_{11}\}$, let $F^R_1 = F^R+\{u\}$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{w^cx^c_{11}}$, $P_{x^c_{21}v}$ with $V(P_{w^cx^c_{11}})\cup V(P_{x^c_{21}v}) = V(R-F^R_1)$ exist in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, w, w^c, P_{w^cx^c_{11}}, x^c_{11}, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, x^c_{21}, P_{x^c_{21}v}, v)$ can therefore be found(see Figure 28(c)).

(2) $|\{w^h, w^c\}\cap \{u, v\}| = 0$.

(2.1) $x_{11} = w^{c_{n-1}}$ or $x_{21} = w^{c_{n-1}}$. Assume that $x_{11} = w^{c_{n-1}}$. By Proposition 2.1, $w^h = x^c_{11}$ and $w^c = x^h_{11}$.

If at least one vertex of $\{u, v\}$, say $v$, is adjacent to $x_{21}$. Let $F^R_1 = F^R+\{w^c, v\}$. Then $|F^R_1| = 2\leq 2n-6$. By Lemma 3.1, an error-free Hamiltonian path $P_{uw^h}$ exists in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw^h}, w^h, w, w^c, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, v)$ can therefore be found(see Figure 29(a)).

If both of $u$ and $v$ are not adjacent to $x_{21}$. Let $F^R_1 = F^R+w^c$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{uw^h}$, $P_{x^h_{21}v}$ with $V(P_{uw^h})\cup V(P_{x^h_{21}v}) = V(R-F^R_1)$ exist in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw^h}, w^h, w, w^c, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, x^h_{21}, P_{x^h_{21}v}, v)$ can therefore be found(see Figure 29(b)).

(2.2) $x_{11}\neq w^{c_{n-1}}$ and $x_{21}\neq w^{c_{n-1}}$. Then by Proposition 2.1, $x^h_{11}\neq w^c$, $x^c_{11}\neq w^h$ and $x^c_{11}\neq w^h$, $x^h_{11}\neq w^c$.

(2.2.1) There is a vertex $x^g_{11}\in \{x^h_{11}, x^c_{11}\}$ with $x^g_{11}\notin \{u, v\}$ and $x^g_{21}\in \{x^h_{21}, x^c_{21}\}$ with $x^g_{21}\notin \{u, v\}$. By Lemma 3.5, three disjoint paths $P_{uw^h}$, $P_{{w^c}x^g_{11}}$, $P_{x^g_{21}v}$ exist in $R$ with $V(P_{uw^h})\cup V(P_{{w^c}x^g_{11}})\cup V(P_{x^g_{21}v}) = V(R)$. An error-free Hamiltonian path $P_{uv} = (u, P_{uw^h}, w^h, w, w^c, P_{{w^c}x^g_{11}}, x^g_{11}, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, x^g_{21}, P_{x^g_{21}v}, v)$ can therefore be found(see Figure 30(a)).

(2.2.2) $\{x^h_{11}, x^c_{11}\} = \{u, v\}$ and $u, v\notin \{x^h_{21}, x^c_{21}\}$ or $\{x^h_{21}, x^c_{21}\} = \{u, v\}$ and $u, v\notin \{x^h_{11}, x^c_{11}\}$. Assume that $\{x^h_{11}, x^c_{11}\} = \{u, v\}$ and $u, v\notin \{x^h_{21}, x^c_{21}\}$. Let $F_1^R = F^R+\{u\}$. Then $|F_1^R| = 1$. By Lemma 3.4, two disjoint paths $P_{x^h_{21}w^h}$, $P_{w^cv}$ exist in $R-F_1^R$ with $V(P_{x^h_{21}w^h})\cup V(P_{w^cv}) = V(R-F_1^R)$. An error-free Hamiltonian path $P_{uv} = (u, x_{11}, P_{wx_2}(x_{11}, x_{21}), x_{21}, x^h_{21}, P_{x^h_{21}w^h}, w^h, w, w^c, P_{w^cv}, v)$ can therefore be found(see Figure 30(b)).

(2.2.3) $\{x^h_{21}, x^c_{21}, x^h_{11}, x^c_{11}\} = \{u, v\}$. We may assume that $x^h_{21} = u$ and $x^h_{11} = v$. Let $a\in N_{P_{wx_2}}(x_{11})$ with $a\neq x_1$ and $b\in N_{P_{wx_2}}(a)$ with $b\neq x_{11}$.

(2.2.3.1) $a = w^{c_{n-1}}$. Then $a^h = w^c$ and $a^c = w^h$. Let $F_1^R = F^R+\{u, v, w^h\}$. Then $|F_1^R| = 3\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{b^cw^c}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, x_{21}, P_{wx_2}(x_{21}, b), b, b^c, P_{b^cw^c}, w^c, w, w^h, a, x_{11}, v)$ can therefore be found(see Figure 31(a)).

(2.2.3.2) $b = w^{c_{n-1}}$. Then $b^h = w^c$ and $b^c = w^h$. Let $F_1^R = F^R+\{u, v, w^h\}$. Then $|F_1^R| = 3\leq 2n-6$. By Lemma 3.1, a Hamiltonian path $P_{w^ca^c}$ exists in $R-F_1^R$. An error-free Hamiltonian path $P_{uv} = (u, x_{21}, P_{wx_2}(x_{21}, b), b, w^h, w, w^c, P_{w^ca^c}, a^c, a, x_{11}, v)$ can therefore be found(see Figure 31(b)).

(2.2.3.3) $a\neq w^{c_{n-1}}$ and $b\neq w^{c_{n-1}}$. Then $a^h\neq w^c$, $a^c\neq w^h$ and $b^h\neq w^c$, $b^c = w^h$. Let $F_1^R = F^R+\{u, v\}$. Then $|F_1^R| = 2$. By Lemma 3.4, two disjoint paths $P_{b^hw^h}$, $P_{w^ca^h}$ exist in $R-F_1^R$ with $V(P_{b^hw^h})\cup V(P_{w^ca^h}) = V(R-F_1^R)$. An error-free Hamiltonian path $P_{uv} = (u, x_{21}, P_{wx_2}(x_{21}, b), b, b^h, P_{b^hw^h}, w^h, w, w^c, P_{w^ca^h}, a^h, a, x_{11}, v)$ can therefore be found(see Figure 31(c)).

Case 3.3.2. $|F_v^L|\leq1$.

Case 3.3.2.1. For any vertex $x$ with $|E_L(x)\cap F^L|\leq2$. Since $|F^L\cap E(L)|\geq 2n-4\geq 8(n\geq6)$, we can choose two edges $e_1, e_2\notin E_L(u^c)\cup E_L(v^h)\cup E_L(v^c)$. Let $F^L_1 = F^L-\{e_1, e_2\}$. Then $|F^L_1| = 2n-5$. By Lemma 3.1, a Hamiltonian cycle $C$ will exist in $L-F_1^L$ which may or may not include $e_1$ or $e_2$ on it. Removing $e_1$ and $e_2$, cycle $C$ is divided into two, one or zero pieces depending on the cases in which $e_1$ and $e_2$ are on $C$ or not. For the last two cases, we may choose to delete one or two more edges which are not incident to vertices $u^h, u^c, v^h, v^c$ from $C$ to make it into two subpaths. Therefore, we may write cycle $C$ using these subpaths as $(x, e_1^{'}, x_1, P_{x_1y_1}, y_1, e_2^{'}, y, P_{yx}, x)$.

(1) The length of $P_{yx}$ $l_{yx}\geq 1$. Since $|F^R| = 0$, by Lemma 3.5, three disjoint paths $P_{ux_1^c}$, $P_{y_1^cy^c}$, $P_{x^cv}$ exist in $R$ with $V(P_{ux_1^c})\cup V(P_{y_1^cy^c})\cup V(P_{x^cv}) = V(R)$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux_1^c}, x_1^c, x_1, P_{x_1y_1}, y_1, y_1^c, P_{y_1^cy^c}, y^c, y, P_{yx}, x, x^c, P_{x^cv}, v)$ can therefore be found(see Figure 32(a)).

(2) The length of $P_{yx}$ $l_{yx} = 0$. Then $x = y$.

(2.1) $x = u^h$. Let $F^R_1 = F^R+\{u\}$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{x^cy_1^c}$, $P_{x_1^cv}$ with $V(P_{x^cy_1^c})\cup V(P_{x_1^cv}) = V(R-F^R_1)$ exist in $R-F^R_1$. An error-free Hamiltonian path $P_{uv} = (u, x, x^c, P_{x^cy_1^c}, y_1^c, y_1, P_{y_1x_1}, x_1, x_1^c, P_{x_1^cv}, v)$ can therefore be found(see Figure 32(b)).

(2.2) $x\neq u^h$.

(2.2.1) $x\neq x_1^{c_{n-1}}$ and $x\neq y_1^{c_{n-1}}$. By Proposition 2.1, $x^h\neq x_1^c$, $x^c\neq x_1^h$ and $x^h\neq y_1^c$, $x^c\neq y_1^h$. By Lemma 3.5, three disjoint paths $P_{ux_1^c}$, $P_{y_1^cx^c}$ and $P_{x^hv}$ exist in $R$ with $V(P_{ux_1^c})\cup V(P_{y_1^cx^c})\cup V(P_{x^hv}) = V(R)$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux_1^c}, x_1^c, x_1, P_{x_1 y_1}, y_1, y_1^c, P_{y_1^cx^c}, x^c, x, x^h, P_{x^hv}, v)$ can therefore be found(see Figure 33(a)).

(2.2.2) $x = x_1^{c_{n-1}}$ or $x = y_1^{c_{n-1}}$. Suppose that $x = x_1^{c_{n-1}}$. By Proposition 2.1, $x^h = x_1^c$ and $x^c = x_1^h$. Let $F^R_1 = F^R+\{x_1^c\}$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{ux^c}$, $P_{y_1^cv}$ exist in $R-F^R_1$ with $V(P_{ux^c})\cup V(P_{y_1^cv}) = V(R-F^R_1)$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux^c}, x^c, x, x_1^c, x_1, P_{x_1 y_1}, y_1, y_1^c, P_{y_1^cv}, v)$ can therefore be found(see Figure 33(b)).

Case 3.3.2.2. There exists a vertex $x$ with $|E_L(x)\cap F^L|\geq3$. Let $e_1, e_2, e_3\in E_L(x)\cap F^L$ and $F^L_1 = F^L-\{e_1, e_2, e_3\}+x$. Then $|F^L_1| = 2n-5$.

(1) There exists no correct element incident to vertex $x$ in $L-F^L$. Since $(u, v)$ is a normal vertex-pair in $AQ_n-F$, $|N_{AQ_n-F}(x)\cap \{u, v\}|\leq 1$. Choose two different vertices $x_1, y$ from $V(L)-\{x, u^h, u^c, v^h, v^c\}$ with $x_1\neq x^{c_{n-1}}$, $y\neq x^{c_{n-1}}$ and $(x_1, y)$ is a normal vertex-pair in $L-F^L_1$. By induction hypothesis, a Hamiltonian path $P_{x_1y}$ exists in $L-F^L_1$. Notice that $x_1, y\in V(L)-\{x, u^h, u^c, v^h, v^c\}$, then $u, v\notin \{x_1^h, x_1^c, y^h, y^c\}$.

(1.1) $|N_{AQ_n-F}(x)\cap \{u, v\}| = 1$. Assume that $u\in N_{AQ_n-F}(x)$ and $u = x^h$. Let $F^R_1 = F^R+\{u\}$. Then $|F^R_1| = 1$. By Lemma 3.4, two disjoint paths $P_{x^cx_1^c}$, $P_{y^cv}$ exist in $R-F^R_1$ with $V(P_{x^cx_1^c})\cup V(P_{y^cv}) = V(R-F_1^R)$. An error-free Hamiltonian path $P_{uv} = (u, x, x^c, P_{x^cx_1^c}, x_1^c, x_1, P_{x_1y}, y, y^c, P_{y^cv}, v)$ can therefore be found(see Figure 34(a)).

(1.2) $|N_{AQ_n-F}(x)\cap \{u, v\}| = 0$. By Lemma 3.5, three disjoint paths $P_{ux^h}$, $P_{x^cx_1^c}$, $P_{y^cv}$ exist in $R$ with $V(P_{ux^h})\cup V(P_{x^cx_1^c})\cup V(P_{y^cv}) = V(R)$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux^h}, x^h, x, x^c, P_{x^cx_1^c}, x_1^c, x_1, P_{x_1y}, y, y^c, P_{y^cv}, v)$ can therefore be found(see Figure 34(b)).

(2) There is a vertex $x_1$ incident to vertex $x$ in $L-F^L$. Choose a vertex $y\in V(L)-\{x, x_1, v^h, v^c, u^h, u^c\}$ with $(x_1, y)$ is a normal vertex-pair in $L-F^L_1$, then $u, v\notin \{y^h, y^c\}$. By induction hypothesis, a Hamiltonian path $P_{x_1y}$ exists in $L-F^L_1$. There is a vertex $x^g\in \{x^h, x^c\}$ with $x^g\neq \{u, v\}$. By Lemma 3.4, two disjoint paths $P_{ux^g}$, $P_{y^cv}$ exist in $R$ with $V(P_{ux^g})\cup V(P_{y^cv}) = V(R)$. An error-free Hamiltonian path $P_{uv} = (u, P_{ux^g}, x^g, x, x_1, P_{x_1y}, y, y^c, P_{y^cv}, v)$ can therefore be found(see Figure 34(c)).

Combining the above cases, we completed the proof of the Theorem 4.1.

5.   Conclusions

This paper studied the Hamiltonian path in $n$-dimensional augmented cube $AQ_n$ with a set $F$ of up to $2n-3$ faulty elements. We have proved that for arbitrary vertex-pair $(u, v)$ in $AQ_n-F$, there exists a fault-free Hamiltonian path that joins vertices $u$ and $v$ with the exception of $(u, v)$, which is a weak vertex-pair in $AQ_n-F$($n\geq4$). It is worth pointing out that we also proved that if there is a weak vertex-pair in $AQ_n-F$, there is at most one pair. This paper improved the current result that $AQ_n$ is $2n-4$ fault-tolerant Hamiltonian connected. Since the degree of each vertex is $2n-1$ in $AQ_n$, our result is optimal and sharp under the condition of no restriction to each vertex.

The result of the paper can be further improved. One possible research is the Hamiltonian connectivity when the correct degree of each vertex is restricted and the fault-tolerant bound of $AQ_n$ may be improved; another is the issue of finding the shorter path under the current optimal fault-tolerant bound in which when $|F|\leq2n-3$, any correct two vertices $u, v$ in $AQ_n-F$ have a path of each length from $d$-rank to $2^n-f_v-2$ connecting them, where $d$ is the distance of $u, v$ and $f_v$ is the number of faulty vertices in $AQ_n$.

Acknowledgments

The work was supported by NNSF of China (No.61170303, 61472465, 61562066) and the National Key R & D Program of China (No. 2018YFC0910500, No.2020AAA0108004).

Conflict of interest

The authors declare that they have no competing interests.