Is there a link between depression, neurochemical asymmetry and cardiovascular function?

AB Segarra; I Prieto; M Martínez-Cañamero; Manuel Ramírez-Sánchez; AB Segarra; I Prieto; M Martínez-Cañamero; Manuel Ramírez-Sánchez

doi:10.3934/Neuroscience.2020022

AIMS Neuroscience

2020, Volume 7, Issue 4: 360-372. doi: 10.3934/Neuroscience.2020022

Previous Article Next Article

Review Topical Sections

Is there a link between depression, neurochemical asymmetry and cardiovascular function?

Department of Health Sciences, University of Jaén, Jaén, Spain

Received: 21 July 2020 Accepted: 23 September 2020 Published: 28 September 2020

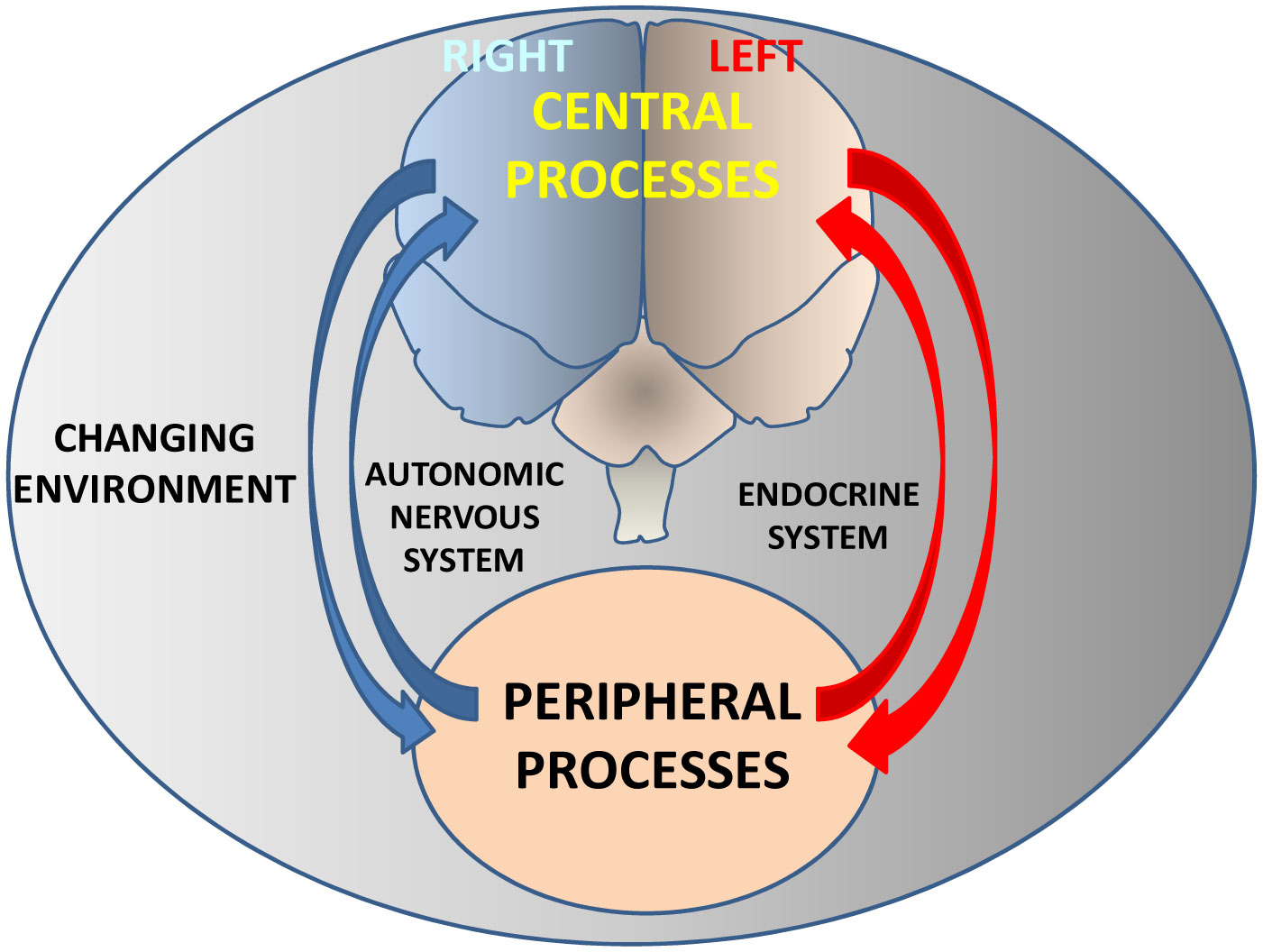
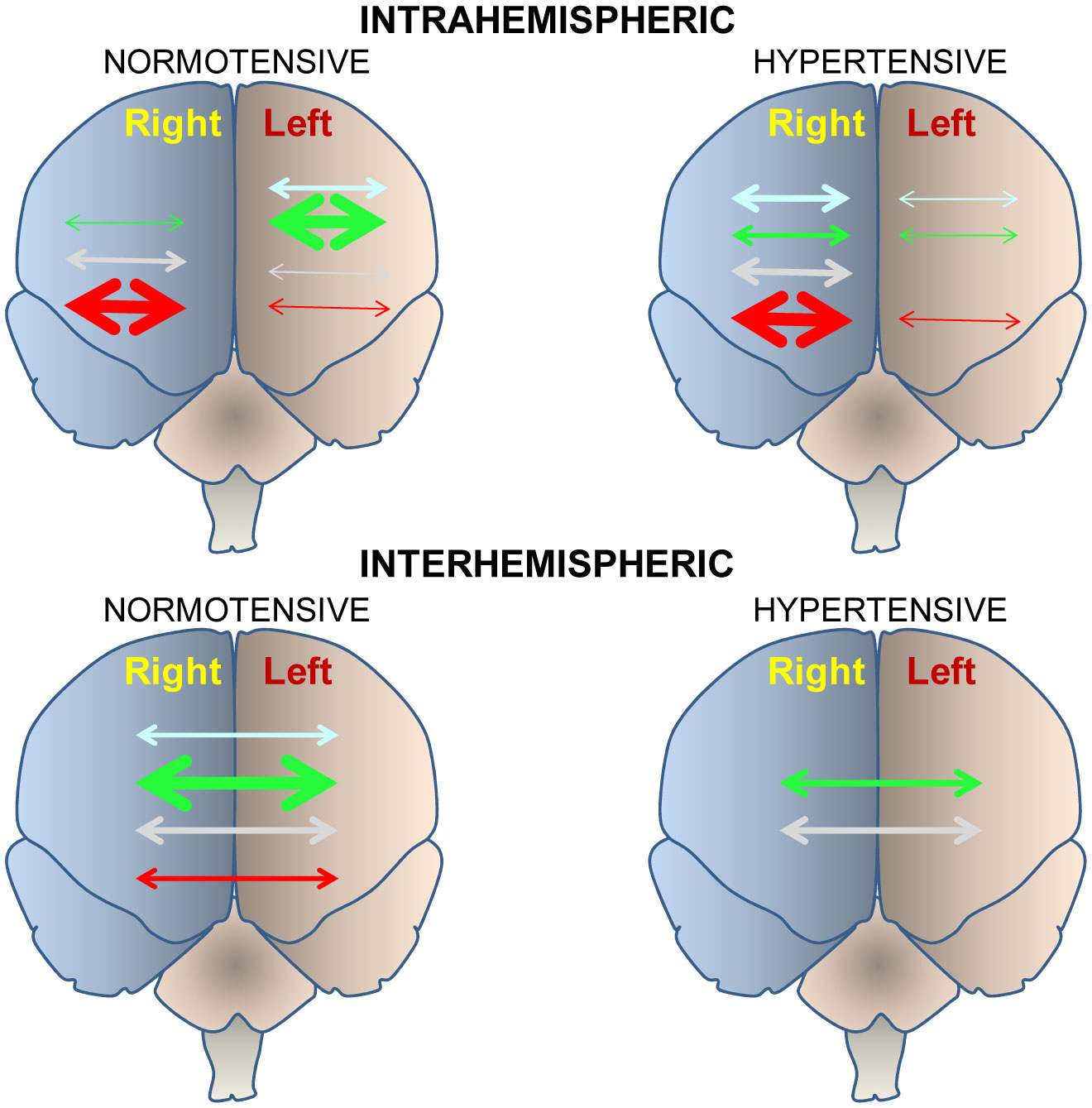
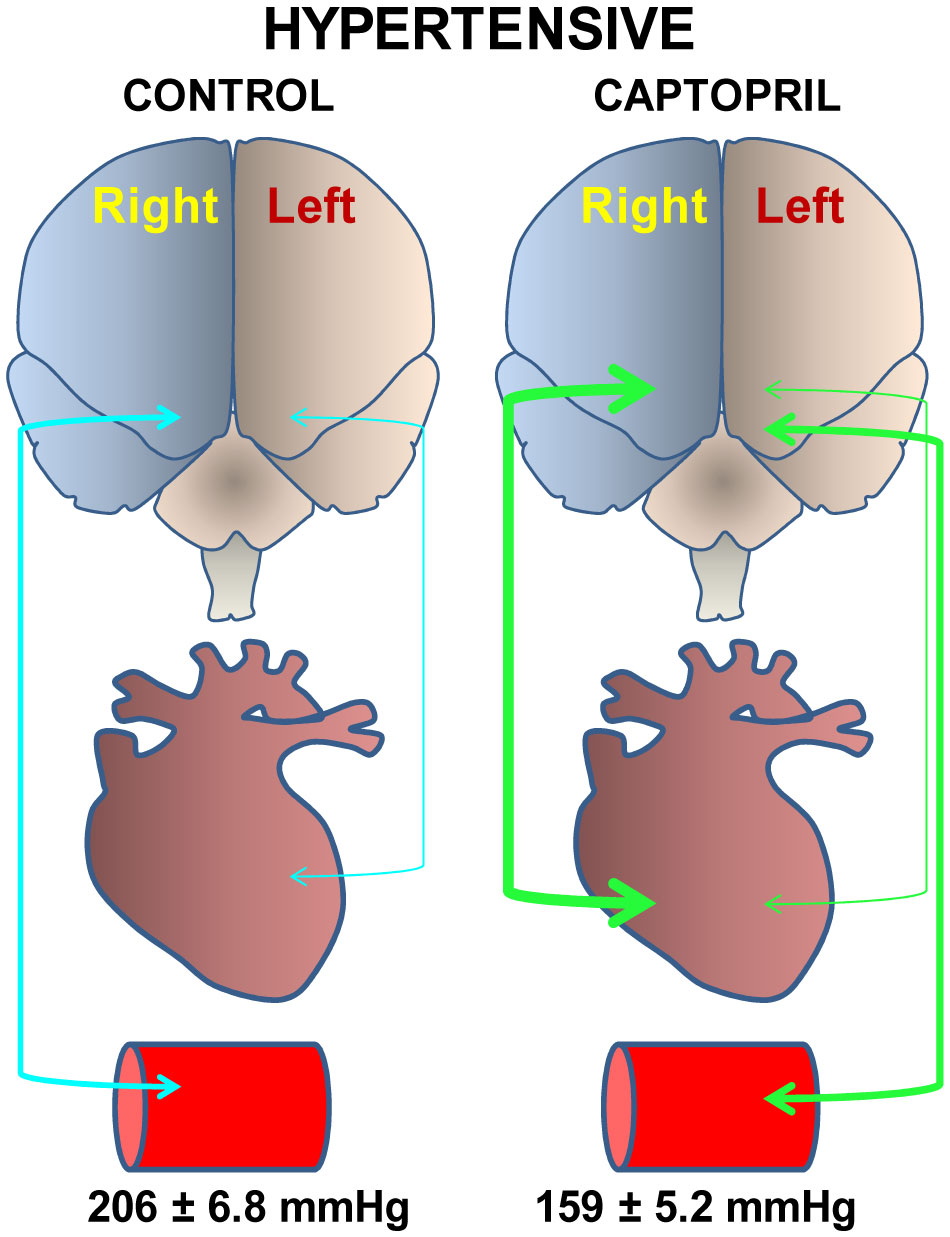
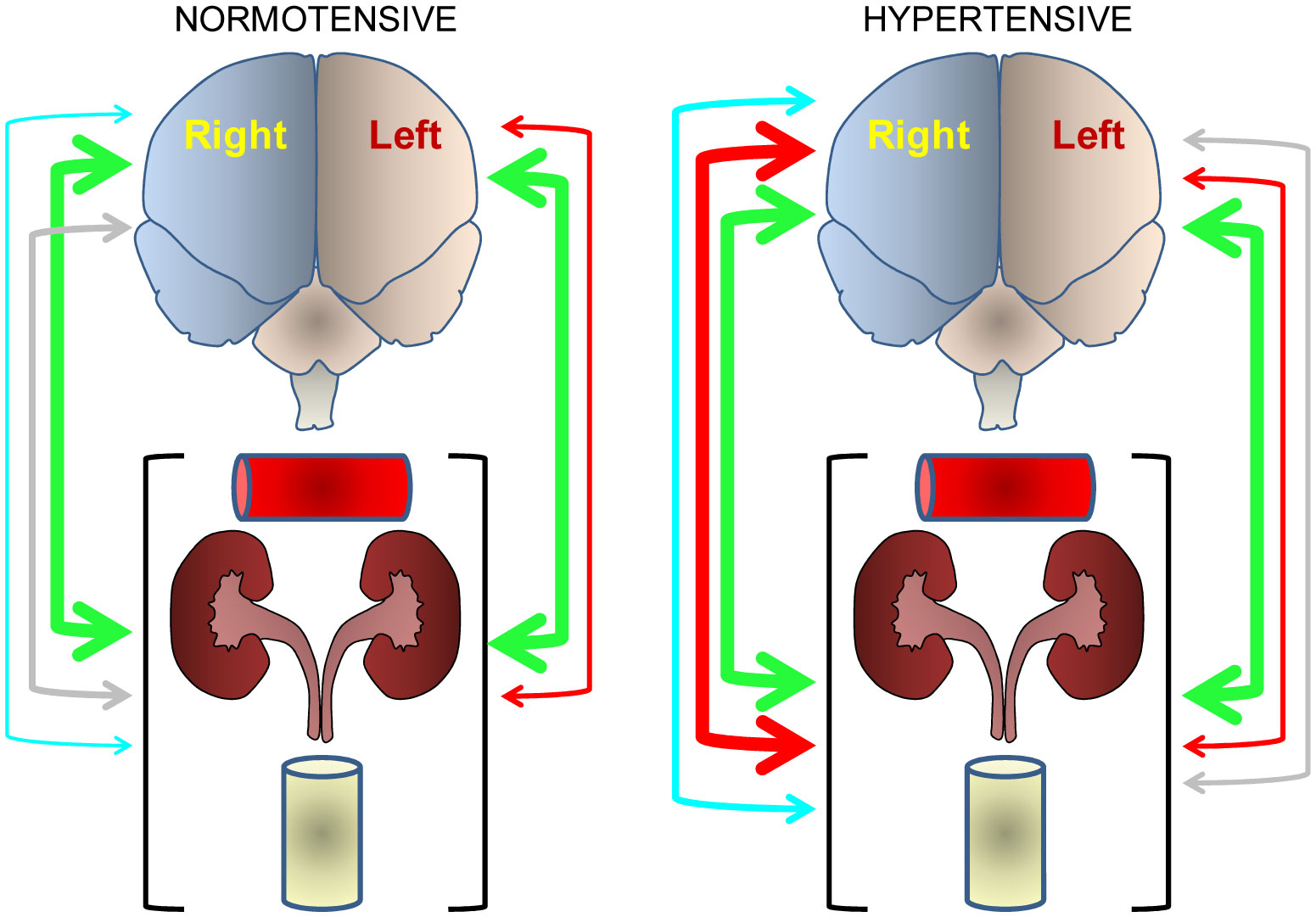
Although at present depression is one of the most disabling disorders in our social environment, the understanding of its pathogenesis and the resources for its treatment are still unsatisfactory. The importance of brain asymmetry in the pathogenesis of disorders in brain function, including mood disorders such as depression, is a highly unexplored, sometimes underrated, and even ignored topic. It is important to note that the basal and pathological functional lateralization must have an underlying neurochemical substrate. It is also necessary to indicate that the brain asymmetry extends to a neurovisceral integration whose behavior may also be lateralized. One of the most studied axis from the functional point of view is the brain-heart connection, in whose operation there are observations that suggest an asymmetric behavior in basal conditions that is modified by central and peripheral changes, as well as by pharmacological treatments. There are evidences that connect cardiovascular function, neurochemical asymmetries, and depression. A deep understanding of the bilateral behavior of the brain following pathophysiological changes in blood pressure as well as pharmacologically induced, can provide us with therapeutic suggestions for the treatment of depression. In this article, we analyze remarkable results of some representative selected contributions, with which we discuss our proposal on the relationship between hypertension, depression and neurochemical asymmetry.

Keywords:

Citation: AB Segarra, I Prieto, M Martínez-Cañamero, Manuel Ramírez-Sánchez. Is there a link between depression, neurochemical asymmetry and cardiovascular function?[J]. AIMS Neuroscience, 2020, 7(4): 360-372. doi: 10.3934/Neuroscience.2020022

Related Papers:

[1]	Daphiny Pottmaier, Marcello Baricco . Materials for hydrogen storage and the Na-Mg-B-H system. AIMS Energy, 2015, 3(1): 75-100. doi: 10.3934/energy.2015.1.75
[2]	Daido Fujita, Takahiko Miyazaki . Techno-economic analysis on the balance of plant (BOP) equipment due to switching fuel from natural gas to hydrogen in gas turbine power plants. AIMS Energy, 2024, 12(2): 464-480. doi: 10.3934/energy.2024021
[3]	Daido Fujita . The prospects of clean hydrogen utilization in power generation industry. AIMS Energy, 2023, 11(5): 991-1011. doi: 10.3934/energy.2023047
[4]	Peter Majewski, Fatemeh Salehi, Ke Xing . Green hydrogen. AIMS Energy, 2023, 11(5): 878-895. doi: 10.3934/energy.2023042
[5]	Vui Thi Hoang, Diem Huong Hoang, Ngoc Duc Pham, Hanh My Tran, Ha Thi Viet Bui, Tien Anh Ngo . Hydrogen production by newly isolated Clostridium species from cow rumen in pure- and co-cultures on a broad range of carbon sources. AIMS Energy, 2018, 6(5): 846-865. doi: 10.3934/energy.2018.5.846
[6]	Dheeraj Rathore, Anoop Singh, Divakar Dahiya, Poonam Singh Nigam . Sustainability of biohydrogen as fuel: Present scenario and future perspective. AIMS Energy, 2019, 7(1): 1-19. doi: 10.3934/energy.2019.1.1
[7]	Kharisma Bani Adam, Jangkung Raharjo, Desri Kristina Silalahi, Bandiyah Sri Aprilia, IGPO Indra Wijaya . Integrative analysis of diverse hybrid power systems for sustainable energy in underdeveloped regions: A case study in Indonesia. AIMS Energy, 2024, 12(1): 304-320. doi: 10.3934/energy.2024015
[8]	Patrick Moriarty, Damon Honnery . When will the hydrogen economy arrive?. AIMS Energy, 2022, 10(6): 1100-1121. doi: 10.3934/energy.2022052
[9]	Lifita N. Tande, Valerie Dupont . Autothermal reforming of palm empty fruit bunch bio-oil: thermodynamic modelling. AIMS Energy, 2016, 4(1): 68-92. doi: 10.3934/energy.2016.1.68
[10]	Lawrence Moura, Mario González, Jéssica Silva, Lara Silva, Izaac Braga, Paula Ferreira, Priscila Sampaio . Evaluation of technological development of hydrogen fuel cells based on patent analysis. AIMS Energy, 2024, 12(1): 190-213. doi: 10.3934/energy.2024009

Abstract

1. Introduction

Fractional calculus (FC) is a subject that dates back to 1695 and is regarded to be as old as ordinary calculus. Ordinary calculus made it impossible to model nonlinear real-world phenomenon in nature, hence fractional calculus became popular among researchers. The fractional derivative is the derivative of arbitrary order in applied mathematics and mathematical analysis. In the nineteenth century, Riemann Liouville ^[1] implemented the fractional derivative when simulating real-world problems. Some of the Nobel contributions of mathematicians are listed here, Caputo ^[2], Kemple and Beyer ^[3], Abbasbandy ^[4], Jafari and Seifi ^{[5, 6]}, Miller and Ross ^[7], Podlubny ^[8], Kilbas and Trujillo ^[9], Diethelm et al. ^[10], Hayat et al. ^[11], Debanth ^[12], Momani and Shawagfeh ^[13], etc. Fractional calculus has become one of the fascinating science and engineering research areas in recent years. Viscoelasticity and damping, diffusion and wave propagation, electromagnetism and heat transfer, biology, signal processing, robotics system classification, physics, mechanics, chemistry, and control theory are the most important scientific fields that use fractional calculus at the moment.

Researchers are interested in FC because of its wide applications in physics, engineering, and real-life sciences. Fractional differential equations accurately represent these physical facts. Fractional differential equations are significantly greater generalizations of integer-order differential equations. Fractional differential equations (FDEs) have generated much interest in recent years. As a result of their frequent appearance in diverse applications, such as quantum mechanics ^[14], chaotic dynamics ^[15], plasma physics ^{[16, 17]}, theory of long-range interaction ^[18], mechanics of non-Hamiltonian systems ^[19], physical kinetics ^[20], anomalous diffusion and transport theory ^[21], mechanics of fractional media ^[22], astrophysics ^[23], and so on. FDEs have been the subject of numerous investigations. Many works have been dedicated to developing efficient methods for solving FDEs, but it is important to remember that finding an analytical or approximate solution is difficult, therefore, accurate methods for obtaining FDE solutions are still being researched. In the literature, there are several analytical and numerical approaches for solving FDEs. For example, the generalized differential transform method (GDTM) ^[24], adomian decomposition method (ADM) ^[25], homotopy analysis method (HAM) ^[26], variational iteration method (VIM) ^[27], homotopy perturbation method (HPM) ^[28], Elzaki transform decomposition method (ETDM) ^[29], iterative Laplace transform method (ILTM) ^[30], fractional wavelet method (FWM) ^{[31, 32]}, residual power series method (RPSM) ^{[33, 34]}.

In this paper, we used two powerful techniques with the aid of the Antagana-Baleanu fractional derivative operator and Laplace transform for solving time fractional NWSEs. The two well-known methods that we implement are LTDM and VITM. The suggested techniques give series form solutions having quick convergence towards the exact solutions. Four non-linear NWSEs case study issues are resolved using the given methodology. Newell and Whitehead ^[35] developed the non-linear NWSE. The diffusion term's influence interacts with the reaction term's nonlinear effect in the Newell-Whitehead-Segel equation model. The fractional NWSE is written in the following way:

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = kD_{\xi}^{2}\mu(\xi, \tau)+g\mu-h\mu^{r}, \end{equation}$

(1.1)

where $r$ is a positive integer and $g, h$ are real numbers with $k > 0$ . The first term $D_{\tau}^{\Im}\mu(\xi, \tau)$ on the left hand side in (1.1) shows the deviations of $\mu(\xi, \tau)$ with time at a fixed location, while the right hand side first term $D_{\xi}^{2}\mu(\xi, \tau)$ shows the deviations with spatial variable $\xi$ of $\mu(\xi, \tau)$ at a specific time and the right hand side remaining terms $g\mu-h\mu^{r},$ is the source terms. $\mu(\xi, \tau)$ is a function of the spatial variable $\xi$ and the temporal variable $\tau$ in (1.1), with $\xi\in R$ and $\tau\geq0$ . The function $\mu(\xi, \tau)$ might be considered the (nonlinear) temperature distribution in an infinitely thin and long rod or as the fluid flow velocity in an infinitely long pipe with a small diameter. Many researchers find the analytical solution of NWSEs ^{[36, 37]} due to their wide range of applications in mechanical and chemical engineering, ecology, biology, and bioengineering.

2. Preleminaries

Some basic definitions related to fractional calculus are expressed here in this section.

Definition 2.1. The Caputo fractional-order derivative is given as

$\begin{equation} ^{LC}D^{\Im}_{{\tau}}\{{g}({{\tau}})\} = \frac{1}{(n-{\Im})}\int_{0}^{{{\tau}}}({{\tau}}-k)^{{n}-{\Im}-1}{g}^{{n}}(k)dk, \end{equation}$

(2.1)

where ${n} < {\Im} \leq {n}+1.$

Definition 2.2. The Caputo fractional-order derivative via Laplace transformation $^{LC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}$ is defined as

$\begin{equation} \mathbb{L}\{^{LC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}\}({\omega}) = \frac{1}{{\omega}^{{n}-{\Im}}}\left[{\omega}^{n}\mathbb{L}\{{g}(\xi, {{\tau}})\}({\omega})-{\omega}^{{n}-1}{g}(\xi, 0)-\cdots-{g}^{{n}-1}(\xi, 0)\right]. \end{equation}$

(2.2)

Definition 2.3. The Atangana-Baleanu derivative in Caputo manner is given as

$\begin{equation} ^{ABC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{A({\Im})}{1-{\Im}}\int_{a}^{{{\tau}}}{g}^{'}(k)E_{{\Im}}\left[-\frac{{\Im}}{1-{\Im}}(1-k)^{{\Im}}\right]dk, \end{equation}$

(2.3)

where $A({\gamma})$ is a normalization function such that $A(0) = A(1) = 1, {g}\in H^1(a, b), b > a, {\Im}\ \in[0, 1]$ and $E_{{\gamma}}$ represent the Mittag-Leffler function.

Definition 2.4. The Atangana-Baleanu derivative in Riemann-Liouville manner is given as

$\begin{equation} ^{ABC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{A({\Im})}{1-{\Im}}\frac{d}{d{{\tau}}}\int_{a}^{{{\tau}}}{g}(k)E_{{\Im}}\left[-\frac{{\gamma }}{1-{\Im}}(1-k)^{{\Im}}\right]dk. \end{equation}$

(2.4)

Definition 2.5. The Laplace transform connected with the Atangana-Baleanu operator is define as

$\begin{equation} ^{AB}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}({\omega}) = \frac{A({\gamma}){\omega}^{{\Im}}\mathbb{L}\{{g}({{\tau}})\}({\omega})-{\omega}^{{\Im}-1}{g}(0)}{(1-{\Im})\left({\omega}^{{\Im}}+\frac{{\Im}}{1-{\gamma}}\right)}. \end{equation}$

(2.5)

Definition 2.6. Consider $0 < {\Im} < 1$ , and ${g}$ is a function of ${\Im}$ , then the fractional-order integral operator of ${\Im}$ is given as

$\begin{equation} ^{ABC}I^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{1-{\Im}}{A({\Im})}{g}({{\tau}})+\frac{{\Im}}{A({\Im})\Gamma({\Im})}\int_{a}^{{{\tau}}}{g}(k)({{\tau}}-k)^{{\Im}-1}dk. \end{equation}$

(2.6)

3. The idea of LTDM

The solution by LTDM for partial differential equations having fractional-order is described in this section.

$\begin{equation} D_\tau^\Im{\mu(\xi, \tau)}+\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau) = \mathcal{F}(\xi, \tau), \quad 0 < \Im \leq 1, \end{equation}$

(3.1)

with some initial sources

$\mu(\xi, 0) = \xi(\xi)\quad\rm{and}\quad\frac{\partial}{\partial\tau}\mu(\xi, 0) = \zeta(\xi),$

where $D_\tau^\Im = \frac{\partial^\Im}{\partial \tau^\Im}$ is the fractional-order $AB$ operator having order $\Im, \mathcal{\bar{G}}_1$ is linear operator and $\mathcal{N}_1$ is non-linear and $\mathcal{F}(\xi, \tau)$ indicates the source term.

Employing the Laplace transform to (3.1), and we acquire

$\begin{equation} L[D_\tau^\Im{\mu(\xi, \tau)}+\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)] = L[\mathcal{F}(\xi, \tau)]. \end{equation}$

(3.2)

By the virtue of Laplace differentiation property, we have

$\begin{equation} L[\mu(\xi, \tau)] = \Theta(\xi, \omega)-\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)], \end{equation}$

(3.3)

where

$\Theta(\xi, \omega) = \frac{1}{\omega^{\Im+1}}[\omega^{\Im}g_{0}(\xi)+\omega^{\Im-1}g_{1}(\xi)+\cdots+g_{1}(\xi)]+\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}\mathcal{F}(\xi, \tau).$

Now, applying inverse Laplace transform yields (3.3) into

$\begin{equation} \mu(\xi, \tau) = \Theta(\xi, \omega)-L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)]\right\}, \end{equation}$

(3.4)

where $\Theta(\xi, \omega)$ demonstrates the terms occurring from source factor. LTDM determines the solution of the infinite sequence of $\mu(\xi, \tau)$

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau). \end{equation}$

(3.5)

and decomposing the nonlinear operator $\mathcal{N}_1$ as

$\begin{equation} \mathcal{N}_1(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mathcal{A}_m, \end{equation}$

(3.6)

where $\mathcal{A}_m$ are Adomian polynomials given as

$\begin{equation} \mathcal{A}_m = \frac{1}{m!}\left[\frac{\partial^m}{\partial\ell^m}\left\{\mathcal{N}_1\left(\sum\limits_{k = 0}^{\infty}\ell^k\xi_k, \sum\limits_{k = 0}^{\infty}\ell^k\tau_k\right)\right\}\right]_{\ell = 0}. \end{equation}$

(3.7)

Putting (3.5) and (3.7) into (3.4), gives

$\sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \Theta(\xi, \omega)-L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\sum\limits_{m = 0}^{\infty}\xi_m, \sum\limits_{m = 0}^{\infty}\tau_m)+\sum\limits_{m = 0}^{\infty}\mathcal{A}_m]\right\}.$

(3.8)

The following terms are described:

$\begin{align} \mu_0(\xi, \tau)& = \Theta(\xi, \omega) \end{align}$

(3.9)

$\begin{align} \mu_1(\xi, \tau)& = L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi_0, \tau_0)+\mathcal{A}_0]\right\}. \end{align}$

(3.10)

Thus all components for $m\geq1$ are calculated as

$\begin{equation} \mu_{m+1}(\xi, \tau) = L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi_m, \tau_m)+\mathcal{A}_m]\right\}. \end{equation}$

(3.11)

4. VITM formulation

The VITM solution for FPDEs is defined in this section.

$\begin{equation} D_{\tau}^{\Im}{\mu(\xi, \tau)}+\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau) = 0, \quad m-1 < {\Im} \leq m, \end{equation}$

(4.1)

with initial source

$\begin{equation} \mu(\xi, 0) = g_1(\xi), \end{equation}$

(4.2)

where $D_\mathfrak{\tau}^{\Im} = \frac{\partial^{\Im}}{\partial \mathfrak{\tau}^{\Im}}$ is stand for fractional-order $AB$ operator, $\mathcal{M}$ is a linear operator and $\mathcal{N}$ is nonlinear term and $\mathcal{P}$ indicates the source term.

The Laplace transform is applied to Eq (4.1), we have

$\begin{equation} L[D_{\tau}^{\Im}{\mu(\xi, \tau)}]+L[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)] = 0. \end{equation}$

(4.3)

By the property of $LT$ differentiation, we get

$\begin{equation} L[{\mu(\xi, \tau)}] = \frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\Im)}L\left[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)\right]. \end{equation}$

(4.4)

The iteration technique for (4.4) as

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)+\Im(s)\left[\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\Im)}L\left[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)\right]\right], \end{equation}$

(4.5)

where $\Im(s)$ is Lagrange multiplier and

$\begin{equation} \Im(s) = -\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}, \end{equation}$

(4.6)

with the application of inverse Laplace transform, (4.5) series form solution is given by

$\begin{align*} \mu_{0}(\xi, \tau)& = \mu(0)+L^{-1}\left[\Im(s)L[-\mathcal{P}(\xi, \tau)]\right]\\ \mu_{1}(\xi, \tau)& = L^{-1}\left[\Im(s)L[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)]\right]\\ &\;\;\vdots\\ \mu_{n+1}(\xi, \tau)& = L^{-1}\left[\Im(s)L\left[\mathcal{M}\left[\mu_{0}(\xi, \tau)+\mu_{1}(\xi, \tau)+\cdots+\mu_{n}(\xi, \tau)\right]\right]\right.\\ &\quad\left.+\mathcal{N}\left[\mu_{0}(\xi, \tau)+\mu_{1}(\xi, \tau)+\cdots+\mu_{n}(\xi, \tau)\right]\right]. \end{align*}$

5. Convergence analysis

Here we discuss uniqueness and convergence analysis.

Theorem 5.1. The result of (3.1) is unique for $LTDM_{ABC}$ , when

$0 < (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{\mu}}{\Gamma(\mu+1)}\right) < 1.$

Proof. Let $H = (C[J], ||.||)$ with the norm $||\phi(\tau)|| = \max_{\tau\in J}|\phi(\tau)|$ be the Banach space, for all continuous function on $J.$ Let $I: H\rightarrow H$ is a non-linear mapping, where

$\mu^{C}_{l+1} = \mu^{C}_{0}+L^{-1}[p({{\Im}}, {{\upsilon}}, {\omega})L[\mathcal{L}(\mu_{l}(\xi, \tau))+\mathbb{N}(\mu_{l}(\xi, \tau))]], \quad l\geq0.$

Suppose that $|\mathcal{L}(\mu)-\mathcal{L}(\mu^{*})| < \theta_{1}|\mu-\mu^{*}|$ and $|\mathbb{N}(\mu)-\mathbb{N}(\mu^{*})| < \theta_{2}|\mu-\mu^{*}|$ , where $\mu: = \mu(\xi, \tau)$ and $\mu^{*}: = \mu^{*}(\xi, \tau)$ are two different function values and $\theta_{1}, \theta_{2}$ are Lipschitz constants.

$\begin{align} ||I\mu-I\mu^{*}||&\leq \max\limits_{t\in J}|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L[\mathcal{L}(\mu)-\mathcal{L}(\mu^{*})]+q({{\Im}}, {{\upsilon}}, {\omega})L[\mathbb{N}(\mu)-\mathbb{N}(\mu^{*})]|\right]\\ &\leq \max\limits_{t\in J}\left[\theta_{1}L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[|\mu-\mu^{*}|]]+\theta_{2}L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[|\mu-\mu^{*}|]]\right]\\ &\leq \max\limits_{t\in J}(\theta_{1}+\theta_{2})\left[L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L|\mu-\mu^{*}|]\right]\\ &\leq(\Im_{1}+\theta_{2})\left[L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L||\mu-\mu^{*}||]\right]\\ & = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma{{{\Im}}+1}}\right)||\mu-\mu^{*}||, \end{align}$

(5.1)

where $I$ is contraction as

$0 < (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma{{{\Im}}+1}}\right) < 1.$

From Banach fixed point theorem, the result of (3.1) is unique.

Theorem 5.2. The $LTDM_{ABC}$ result of (3.1) is convergent.

Proof. Let $\mu_{m} = \sum_{r = 0}^{m}\mu_{r}(\xi, \tau)$ . To show that $\mu_{m}$ is a Cauchy sequence in $H$ . For $n\in\mathbb{N}$ , let

$\begin{align} ||\mu_{m}-\mu_{n}||& = \max\limits_{\tau\in J}|\sum\limits_{r = n+1}^{m}\mu_{r}|\\ &\leq \max\limits_{\tau\in J} \left|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L\left[\sum\limits_{r = n+1}^{m}(\mathcal{L}(\mu_{r-1})+\mathbb{N}(\mu_{r-1}))\right]\right]\right|\\ & = \max\limits_{\tau\in J} \left|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L\left[\sum\limits_{r = n+1}^{m-1}(\mathcal{L}(\mu_{r})+\mathbb{N}(u_{r}))\right]\right]\right|\\ &\leq \max\limits_{\tau\in J}\left|L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[(\mathcal{L}(\mu_{m-1})-\mathcal{L}(\mu_{n-1})+\mathbb{N}(\mu_{m-1})-\mathbb{N}(\mu_{n-1}))]]\right|\\ &\leq\theta_{1}\max\limits_{\tau\in J}\left|L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[(\mathcal{L}(\mu_{m-1})-\mathcal{L}(\mu_{n-1}))]]\right|\\ &\quad+\theta_{2}\max\limits_{\tau\in J}\left|L^{-1}[p({{\Im}}, {{\upsilon}}, {\omega})L[(\mathbb{N}(\mu_{m-1})-\mathbb{N}(\mu_{n-1}))]]\right|\\ & = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma({{\Im}}+1)}\right)||\mu_{m-1}-\mu_{n-1}||. \end{align}$

(5.2)

Let $m = n+1$ , then

$\begin{equation} ||\mu_{n+1}-\mu_{n}||\leq \theta||\mu_{n}-\mu_{n-1}||\leq \theta^{2}||\mu_{n-1}\mu_{n-2}||\leq \cdots \leq \theta^{n}||\mu_{1}-\mu_{0}||, \end{equation}$

(5.3)

where

$\theta = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma({{\Im}}+1)}\right).$

Similarly, we have

$\begin{align} ||\mu_{m}-\mu_{n}||&\leq ||\mu_{n+1}-\mu_{n}||+||\mu_{n+2}\mu_{n+1}||+\cdots+||\mu_{m}-\mu_{m-1}||\\ &\leq (\theta^{n}+\theta^{n+1}+\cdots+\theta^{m-1})||\mu_{1}-\mu_{0}||\\ &\leq \theta^{n}\left(\frac{1-\theta^{m-n}}{1-\theta}\right)||\mu_{1}||. \end{align}$

(5.4)

As $0 < \theta < 1$ , we get $1-\theta^{m-n} < 1$ . Therefore, we have

$\begin{equation} ||\mu_{m}-\mu_{n}||\leq \frac{\theta^{n}}{1-\theta}\max\limits_{t\in J}||\mu_{1}||. \end{equation}$

(5.5)

Since $||\mu_{1}|| < \infty$ and $||\mu_{m}-\mu_{n}||\rightarrow 0$ , when $n \rightarrow \infty$ . As a result, $\mu_m$ is a Cauchy sequence in $H$ , implying that the series $\mu_m$ is convergent.

6. Applications

Four cases of nonlinear NWSEs are presented to demonstrate the suggested technique's capability and reliability.

Example 1. The NWSE has given in (1.1) for $g = 2, h = 3, k = 1$ and $r = 2$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2} (\xi, \tau), \quad 0 < \theta\leq 1, \end{equation}$

(6.1)

with initial source $\mu(\xi, 0) = \Upsilon.$

Applying Laplace transform to (6.1), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2}(\xi, \tau)\right]. \end{equation}$

(6.2)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \Upsilon+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2}(\xi, \tau)\right]\right]. \end{equation}$

(6.3)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.4)

where $\mu^{2} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.3) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \Upsilon+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.5)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as

$\begin{equation} \mathcal{A}_0 = \mu_{0}^2, \quad\mathcal{A}_1 = 2\mu_{0}\mu_{1}, \quad\mathcal{A}_2 = 2\mu_{0}\mu_{2}+(\mu_{1})^{2}. \end{equation}$

(6.6)

Thus, on comparing both sides of (6.5)

$\begin{equation*} \mu_0(\xi, \tau) = \Upsilon. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = 2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we have

$\begin{align*} \mu(\xi, \tau)& = \Upsilon+\Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \mu(\mu, \tau) = \frac{-\frac{2}{3}\Upsilon\exp({2\tau})}{-\frac{2}{3}+\Upsilon-\Upsilon\exp({2\tau})}. \end{equation}$

(6.7)

The analytical results by VITM:

The iteration formulas for (6.1), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+2\mu_{m}(\xi, \tau)-3\mu_{m}^{2}(\xi, \tau)\right\}\right], \end{equation}$

(6.8)

where $\mu_0(\xi, \tau) = \Upsilon.$

For $m = 0, 1, 2, \ldots$ , we have

(6.9)

(6.10)

Therefore, we obtain

$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \Upsilon+\Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.11)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figure 1 and Table 1.

$\begin{equation} \ \mu(\xi, \tau) = \frac{-\frac{2}{3}\Upsilon\exp({2\tau})}{-\frac{2}{3}+\Upsilon-\Upsilon\exp({2\tau})}. \end{equation}$

(6.12)

Figure 1. The solution graph of Example 1, the exact solution and the analytical solution at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 1.

$\mu(\xi, \tau)$ Comparison of the exact solution, our methods solution and absolute error (AE) of Example 1.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\Upsilon}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.000000000000000	0.000000000000000	0.0000000000E+00	0.0000000000E+00	0.0000000000E+00
0.1	0.100000170000000	0.100000100000000	7.0000000000E-08	2.4390000000E-07	1.5317000000E-06
0.2	0.200000280000000	0.200000200000000	8.0000000000E-08	5.4790000000E-07	3.1233000000E-06
0.3	0.300000330000000	0.300000300000000	3.0000000000E-08	9.1180000000E-07	4.7750000000E-06
0.4	0.400000320000000	0.400000400000000	8.0000000000E-08	1.3357000000E-06	6.4866000000E-06
0.5	0.500000250000000	0.500000500000000	2.5000000000E-07	1.8197000000E-06	8.2582000000E-06
0.6	0.600000120000000	0.600000600000000	4.8000000000E-07	2.3636000000E-06	1.0089700000E-05
0.7	0.699999930000000	0.700000700000000	7.7000000000E-07	2.9675000000E-06	1.1981300000E-05
0.8	0.799999680000000	0.800000800000000	1.1200000000E-06	3.6315000000E-06	1.3932800000E-05
0.9	0.899999370000000	0.900000900000000	1.5300000000E-06	4.3554000000E-06	1.5944400000E-05
1.0	0.999999000000000	1.000001000000000	2.0000000000E-06	5.1390000000E-06	1.8016000000E-05

| Show Table

DownLoad: CSV

Example 2. The NWSE has given in (1.1) for $g = 1, h = 1, k = 1$ and $r = 2$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau)), \quad 0 < \Im\leq1, \end{equation}$

(6.13)

with initial source

$\begin{equation*} \mu(\xi, 0) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}. \end{equation*}$

Applying Laplace transform to (6.13), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau))\right]. \end{equation}$

(6.14)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau))\right]\right]. \end{equation}$

(6.15)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.16)

where $\mu^{2} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.15) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.17)

Applying the proposed analytical approach and the nonlinear terms can be obtained with the aid of Adomian's polynomials stated in (3.7), we acquire

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{5}{3}\frac{\exp\left({\frac{\xi}{\sqrt{6}}}\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = \frac{25}{18}\left(\frac{\exp\left({\frac{\xi}{\sqrt{6}}}\right)\left(-1+2\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \frac{1}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{2}}+\frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]+\frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{4}}\right)\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \mu(\mu, \tau) = \left(\frac{1}{1+\exp\left(\frac{\xi}{\sqrt{6}}-\frac{5}{6}\tau\right)}\right)^{2}. \end{equation}$

(6.18)

The analytical results by VITM:

The iteration formulas for (6.13), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+\mu_{m}(\xi, \tau)(1-\mu_{m}(\xi, \tau))\right\}\right], \end{equation}$

(6.19)

where

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+\mu_{0}(\xi, \tau)(1-\mu_{0}(\xi, \tau))\right\}\right]\\ \mu_1(\xi, \tau)& = \frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right] \end{align}$

(6.20)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+\mu_{1}(\xi, \tau)(1-\mu_{1}(\xi, \tau))\right\}\right]\\ \mu_2(\xi, \tau)& = \frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right] \\\;\;\vdots\notag \end{align}$

(6.21)

Therefore, we obtain

$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{2}}+\frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.22)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 2, 3 and Table 2.

$\begin{equation} \mu(\xi, \tau) = \left(\frac{1}{1+\exp\left(\frac{\xi}{\sqrt{6}}-\frac{5}{6}\tau\right)}\right)^{2}. \end{equation}$

(6.23)

Figure 2. The exact solution and analytical solution of Example 2 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The two and three dimensional different fractional order graphs of

$\Im$ example 2.

DownLoad: Full-Size Img PowerPoint

Table 2.

$\mu(\xi, \tau)$ Comparison of exact solution, our methods solution and Absolute Error (AE) of Example 2.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.250020833800000	0.250020833700000	1.0000000000E-10	3.3580800000E-05	1.2032390000E-04
0.1	0.239919747900000	0.239919747800000	5.0941566800E-11	3.2881658260E-05	1.1781851670E-04
0.2	0.230035072700000	0.230035072600000	8.1583004800E-11	3.2156851240E-05	1.1522127190E-04
0.3	0.220374241800000	0.220374241700000	1.3295068340E-10	3.1408781520E-05	1.1254074080E-04
0.4	0.210943948200000	0.210943948100000	1.7637132220E-10	3.0639941880E-05	1.0978578190E-04
0.5	0.201750129200000	0.201750129000000	1.5669454130E-10	2.9852894210E-05	1.0696543270E-04
0.6	0.192797956100000	0.192797956000000	1.0301314750E-10	2.9050141560E-05	1.0408873760E-04
0.7	0.184091829000000	0.184091828700000	2.3924337590E-10	2.8234000470E-05	1.0116457590E-04
0.8	0.175635376500000	0.175635376200000	2.9445508530E-10	2.7407274000E-05	9.8202291510E-05
0.9	0.167431461100000	0.167431460800000	3.1297190840E-10	2.6572425380E-05	9.5210825130E-05
1.0	0.159482188800000	0.159482188600000	2.6399135400E-10	2.5731952810E-05	9.2199048510E-05

| Show Table

DownLoad: CSV

Example 3. The NWSE has given in (1.1) for $g = 1, h = 1, k = 1$ and $r = 4$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\mu^{4}(\xi, \tau), \quad 0 < \Im\leq1 \end{equation}$

(6.24)

with initial source

$\begin{equation*} \mu(\xi, 0) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

Applying Laplace transform to (6.24), we get

(6.25)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\mu^{4}(\xi, \tau)\right]\right]. \end{equation}$

(6.26)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.27)

where $\mu^{4} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.26) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.28)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as

$\begin{equation} \mathcal{A}_0 = \mu_{0}^4, \quad\mathcal{A}_1 = 4\mu_{0}^{3}\mu_{1}, \quad\mathcal{A}_2 = 4\mu_{0}^{3}\mu_{2}+6\mu_{0}^{2}\mu_{1}^{2}. \end{equation}$

(6.29)

Thus, on comparing both sides of (6.30)

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = \frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+\frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \ \mu(\xi, \tau) = \frac{1}{2}\tanh\left(-\frac{3}{2\sqrt{10}}\left(\xi-\frac{7}{\sqrt{10}}\tau\right)\right). \end{equation}$

(6.30)

The analytical results by VITM:

The iteration formulas for (6.24), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+\mu_{m}(\xi, \tau)-\mu_{m}^{4}(\xi, \tau)\right\}\right], \end{equation}$

(6.31)

where

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+\mu_{0}(\xi, \tau)-\mu_{0}^{4}(\xi, \tau)\right\}\right], \\ \mu_1(\xi, \tau)& = \frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right], \end{align}$

(6.32)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+\mu_{1}(\xi, \tau)-\mu_{1}^{2}(\xi, \tau)\right\}\right], \\ \mu_2(\xi, \tau)& = \frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp^{\frac{3}{\sqrt{10}}\xi}}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \\ \;\;\vdots\notag \end{align}$

(6.33)

Therefore, we obtain

$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau)\\ & = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+\frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.34)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 4, 5 and Table 3.

$\begin{equation} \mu(\xi, \tau) = \frac{1}{2}\tanh\left(-\frac{3}{2\sqrt{10}}\left(\xi-\frac{7}{\sqrt{10}}\tau\right)\right). \end{equation}$

(6.35)

Figure 4. The exact solution and analytical solution graph of Example 3 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The error graph of Example 3 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 3.

$\mu(\xi, \tau)$ Comparison of exact solution, our methods solution and Absolute Error (AE) of Example 3.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.630004621400000	0.630004623000000	1.6000000000E-09	7.1080200000E-05	2.5467930000E-04
0.1	0.609938405400000	0.609938406700000	1.3721312690E-09	7.2077200130E-05	2.5825129220E-04
0.2	0.589628520300000	0.589628521400000	1.1413782460E-09	7.2815436450E-05	2.6089584380E-04
0.3	0.569148496800000	0.569148497700000	8.7201231790E-10	7.3288425700E-05	2.6259010230E-04
0.4	0.548573070400000	0.548573071000000	6.9266503090E-10	7.3494089020E-05	2.6332630440E-04
0.5	0.527977019100000	0.527977019700000	5.8687018460E-10	7.3434320340E-05	2.6311129590E-04
0.6	0.507434030100000	0.507434030300000	1.9085441870E-10	7.3114619290E-05	2.6196573810E-04
0.7	0.487015628200000	0.487015628200000	1.4619007300E-11	7.2545024110E-05	2.5992429560E-04
0.8	0.466790202200000	0.466790202100000	1.0115621760E-10	7.1738176370E-05	2.5703268760E-04
0.9	0.446822151300000	0.446822151000000	3.7765613140E-10	7.0709457140E-05	2.5334660600E-04
1.0	0.427171171700000	0.427171171200000	5.2356035770E-10	6.9477036140E-05	2.4893040880E-04

| Show Table

DownLoad: CSV

Example 4. The NWSE has given in (1.1) for $g = 3, h = 4, k = 1$ and $r = 3$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau) , \ \ 0 < \Im\leq1, \end{equation}$

(6.36)

with initial source

$\begin{equation*} \mu(\xi, 0) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

Applying Laplace transform to (6.36), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau)\right]. \end{equation}$

(6.37)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau)\right]\right]. \end{equation}$

(6.38)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.39)

where $\mu^{3} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.38) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.40)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as,

$\begin{equation} \mathcal{A}_0 = \mu_{0}^3, \quad\mathcal{A}_1 = 3\mu_{0}^{2}\mu_{1}, \quad\mathcal{A}_2 = 3\mu_{0}^{2}\mu_{2}+3\mu_{0}\mu_{1}^{2}. \end{equation}$

(6.41)

Thus, on comparing both sides of (6.40)

$\begin{equation*} \mu_0(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{align*} \mu_2(\xi, \tau)& = \frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{align*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}+\frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \ \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi-\frac{9}{2}\tau\right)}. \end{equation}$

(6.42)

The analytical results by VITM:

The iteration formulas for (6.36), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+3\mu_{m}(\xi, \tau)-4\mu_{m}^{3}(\xi, \tau)\right\}\right], \end{equation}$

(6.43)

where

$\begin{equation*} \mu_0(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+3\mu_{0}(\xi, \tau)-4\mu_{0}^{3}(\xi, \tau)\right\}\right], \\ \mu_1(\xi, \tau)& = \frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right], \end{align}$

(6.44)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+3\mu_{1}(\xi, \tau)-4\mu_{1}^{3}(\xi, \tau)\right\}\right], \\ \mu_2(\xi, \tau)& = \frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \\\;\;\vdots\notag \end{align}$

(6.45)

Therefore, we obtain

$\begin{align} &\mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}\\ &\quad+\frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.46)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 6, 7 and Table 4.

$\begin{equation} \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi-\frac{9}{2}\tau\right)}. \end{equation}$

(6.47)

Figure 6. The exact solution and analytical solution graph of Example 4 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The error graph of Example 4 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 4.

$\mu(\xi, \tau)$ Comparison of Exact solution, Our methods solution and Absolute Error (AE) of example 4.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.433022444800000	0.433022445000000	1.7320508080E-10	7.9386816730E-06	2.2292879540E-05
0.1	0.459505816600000	0.459505816600000	3.2194421390E-11	7.9089032580E-06	2.2209048130E-05
0.2	0.485791725000000	0.485791725200000	1.6732056440E-10	7.8207979170E-06	2.1961331750E-05
0.3	0.511688623000000	0.511688622800000	2.1377960370E-10	7.6762722350E-06	2.1556125910E-05
0.4	0.537016284000000	0.537016284300000	3.7853826310E-10	7.4809626080E-06	2.1006564010E-05
0.5	0.561610593500000	0.561610593600000	1.3316432970E-10	7.2385076780E-06	2.0326137420E-05
0.6	0.585327390000000	0.585327389900000	4.4316889200E-11	6.9562540670E-06	1.9533837800E-05
0.7	0.608045207500000	0.608045207500000	4.4341099960E-11	6.6414869210E-06	1.8649762960E-05
0.8	0.629666845500000	0.629666845900000	4.6131349780E-10	6.3016518320E-06	1.7694707350E-05
0.9	0.650119804000000	0.650119803700000	7.6816056310E-10	5.9421274000E-06	1.6687344050E-05
1.0	0.669355693000000	0.669355693500000	4.9676049840E-10	5.5740946070E-06	1.5651582380E-05

| Show Table

DownLoad: CSV

7. Results and discussion

, show the behavior of the exact and proposed methods solution at $\Im = 1$ in (AB fractional derivative) manner of Example 1. The comparison of the exact and analytical solution of Example 2 is shown Figure 2, whereas the graphical view for various fractional orders is demonstrated with the help of figures. In Figure 3, the two and three dimensional different fractional order graphs of Example 2. The figures show that our solution approaches the exact solution as the fractional order goes towards the integer-order. Figure 4, demonstrate the layout of the exact and analytical solution while Figure 5 shows the error comparison of the exact and analytical results of Example 3. The error confirms the efficiency of the suggested techniques. The graphical view of Example 4 for exact and our solution can be seen in , however, shows the error comparison of both results. Furthermore, the behavior of the exact and proposed method solution with the aid of absolute error at different orders of $\Im$ is shown in Tables 1–4. Finally, it is clear from the figures and tables that the proposed methods have a sufficient degree of accuracy and quick convergence towards the exact solution.

8. Conclusions

The LTDM and VITM were used for solving time fractional Newell-Whitehead-Segel equation. The solution we obtained is a series that quickly converges to exact solutions. Four cases are studied, which shows that the proposed methods solutions strongly agree with the exact solution. It is found that the suggested techniques are easy to implement and need a small number of calculations. This shows that LTDM and VITM are very efficient, effective, and powerful mathematical tools easily applied in finding approximate analytic solutions for a wide range of real-world problems arising in science and engineering.

Acknowledgements

This research received funding support from the National Science, Research and Innovation Fund (NSRF), Thailand.

Conflict of interest

The authors declare that they have no competing interests.

Conflict of interest

The authors declare no conflicts of interest.

References

[1]	Kaltenboeck A, Harmer C (2018) The neuroscience of depressive disorders: A brief review of the past and some considerations about the future. Brain Neurosci Adv 2: 239821281879926. doi: 10.1177/2398212818799269
[2]	Prieto I, Segarra AB, Martinez-Canamero M, et al. (2017) Bidirectional asymmetry in the neurovisceral communication for the cardiovascular control: New insights. Endocr Regul 51: 157-167. doi: 10.1515/enr-2017-0017
[3]	Segarra AB, Prieto-Gomez I, Banegas I, et al. (2019) Functional and neurometabolic asymmetry in SHR and WKY rats following vasoactive treatments. Sci Rep 9: 16098. doi: 10.1038/s41598-019-52658-9
[4]	Madison A, Kiecolt-Glaser JK (2019) Stress, depression, diet, and the gut microbiota: human-bacteria interactions at the core of psychoneuroimmunology and nutrition. Curr Opin Behav Sci 28: 105-110. doi: 10.1016/j.cobeha.2019.01.011
[5]	Harmer CJ, Duman RS, Cowen PJ (2017) How do antidepressants work? New perspectives for refining future treatment approaches. Lancet Psychiatry 4: 409-418. doi: 10.1016/S2215-0366(17)30015-9
[6]	Prieto I, Segarra AB, De Gasparo M, et al. (2016) Neuropeptidases, Stress and Memory—A Promising Perspective. AIMS Neurosci 3: 487-501. doi: 10.3934/Neuroscience.2016.4.487
[7]	Bogdan R, Pizzagalli DA (2006) Acute stress reduces reward responsiveness: implications for depression. Biol Psychiatry 60: 1147-1154. doi: 10.1016/j.biopsych.2006.03.037
[8]	Barber BA, Kohl KL, Kassam-Adams N, et al. (2014) Acute stress, depression, and anxiety symptoms among English and Spanish speaking children with recent trauma exposure. J Clin Psychol Med Settings 21: 66-71. doi: 10.1007/s10880-013-9382-z
[9]	Broca MP (1861) Remarques sur le siége de la faculté du language articulé, suivies d'une observation d'aphémie (perte de la parole). Bull Soc Anat (París) VI: 330-357.
[10]	Corballis MC (2014) Left brain, right brain: facts and fantasies. PLoS Biol 12: e1001767. doi: 10.1371/journal.pbio.1001767
[11]	Hellige JB (1993) Hemispheric asymmetry: what's right and what's left London: Harvard University Press.
[12]	Rogers LJ, Vallortigara G, Andrew RJ (2013) Divided Brains. The biology and behaviour of brain asymmetries Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511793899
[13]	Gazzaniga MS (2015) Tales from both sides of the brain. A life in neuroscience New York: Harper Collins.
[14]	Zimmerberg B, Glick SD, Jerussi TP (1974) Neurochemical correlate of a spatial preference in rats. Science 185: 623-625. doi: 10.1126/science.185.4151.623
[15]	Oke A, Keller R, Mefford I, et al. (1978) Lateralization of norepinephrine in human thalamus. Science 200: 1411-1413. doi: 10.1126/science.663623
[16]	Bernard C (1878) Etude sur la physiologie du coeur. La Sci Exp 316-366.
[17]	Domínguez-Vías G, Aretxaga G, Prieto I, et al. (2020) Asymmetrical influence of a standard light/dark cycle and constant light conditions on the alanyl-aminopeptidase activity of the left and right retinas in adult male rats. Exp Eye Res 198: 108149. doi: 10.1016/j.exer.2020.108149
[18]	Segarra AB, Prieto I, Banegas I, et al. (2012) Asymmetrical effect of captopril on the angiotensinase activity in frontal cortex and plasma of the spontaneously hypertensive rats: expanding the model of neuroendocrine integration. Behav Brain Res 230: 423-427. doi: 10.1016/j.bbr.2012.02.039
[19]	Segarra AB, Prieto I, Banegas I, et al. (2013) The brain-heart connection: frontal cortex and left ventricle angiotensinase activities in control and captopril-treated hypertensive rats—a bilateral study. Int J Hypertens 2013: 156179. doi: 10.1155/2013/156179
[20]	Prieto I, Segarra AB, Villarejo AB, et al. (2019) Neuropeptidase activity in the frontal cortex of Wistar-Kyoto and spontaneously hypertensive rats treated with vasoactive drugs: a bilateral study. J Hypertens 37: 612-628. doi: 10.1097/HJH.0000000000001884
[21]	Henriques JB, Davidson RJ (1991) Left frontal hypoactivation in depression. J Abnorm Psychol 100: 535-545. doi: 10.1037/0021-843X.100.4.535
[22]	Ramírez M, Prieto I, Vives F, et al. (2004) Neuropeptides, neuropeptidases and brain asymmetry. Curr Protein Pept Sci 5: 497-506. doi: 10.2174/1389203043379350
[23]	Cohen BE, Edmondson D, Kronish IM (2015) State of the Art Review: Depression, Stress, Anxiety, and Cardiovascular Disease. Am J Hypertens 28: 1295-1302. doi: 10.1093/ajh/hpv047
[24]	Liguori I, Russo G, Curcio F, et al. (2018) Depression and chronic heart failure in the elderly: an intriguing relationship. J Geriatr Cardiol 15: 451-459.
[25]	Testa G, Cacciatore F, Galizia G, et al. (2011) Depressive symptoms predict mortality in elderly subjects with chronic heart failure. Eur J Clin Invest 41: 1310-1317. doi: 10.1111/j.1365-2362.2011.02544.x
[26]	Agustini B, Mohebbi M, Woods RL, et al. (2020) The association of antihypertensive use and depressive symptoms in a large older population with hypertension living in Australia and the United States: a cross-sectional study. J Hum Hypertens 30.
[27]	Eze-Nliam CM, Thombs BD, Lima BB, et al. (2010) The association of depression with adherence to antihypertensive medications: a systematic review. J Hypertens 28: 1785-1795. doi: 10.1097/HJH.0b013e32833b4a6f
[28]	Bautista LE, Vera-Cala LM, Colombo C, et al. (2012) Symptoms of depression and anxiety and adherence to antihypertensive medication. Am J Hypertens 25: 505-511. doi: 10.1038/ajh.2011.256
[29]	Braszko JJ, Karwowska-Polecka W, Halicka D, et al. (2003) Captopril and enalapril improve cognition and depressed mood in hypertensive patients. J Basic Clin Physiol Pharmacol 14: 323-343. doi: 10.1515/JBCPP.2003.14.4.323
[30]	Cacciatore F, Amarelli C, Maiello C, et al. (2020) Effect of Sacubitril-Valsartan in reducing depression in patients with advanced heart failure. J Affect Disord 272: 132-137. doi: 10.1016/j.jad.2020.03.158
[31]	Rotenberg VS (2008) Functional brain asymmetry as a determinative factor in the treatment of depression: theoretical implications. Prog Neuropsychopharmacol Biol Psychiatry 32: 1772-1777. doi: 10.1016/j.pnpbp.2008.08.011
[32]	Banegas I, Prieto I, Segarra AB, et al. (2011) Blood pressure increased dramatically in hypertensive rats after left hemisphere lesions with 6-hydroxydopamine. Neurosci Lett 500: 148-150. doi: 10.1016/j.neulet.2011.06.025
[33]	Segarra AB, Banegas I, Prieto I, et al. (2016) Brain asymmetry and dopamine: beyond motor implications in Parkinson's disease and experimental hemiparkinsonism. Rev Neurol 63: 415-421.
[34]	Banegas I, Prieto I, Segarra AB, et al. (2019) Angiotensin II, dopamine and nitric oxide. An asymmetrical neurovisceral interaction between brain and plasma to regulate blood pressure. AIMS Neurosci 6: 116-127. doi: 10.3934/Neuroscience.2019.3.116
[35]	Banegas I, Segarra AB, Prieto I, et al. (2019) Asymmetrical response of aminopeptidase A in the medial prefrontal cortex and striatum of 6-OHDA-unilaterally-lesioned Wistar Kyoto and spontaneously hypertensive rats. Pharmacol Biochem Behav 182: 12-21. doi: 10.1016/j.pbb.2019.05.007
[36]	Guo SX, Kendrick KM, Zhang J, et al. (2013) Brain-wide functional inter-hemispheric disconnection is a potential biomarker for schizophrenia and distinguishes it from depression. Neuroimage Clin 2: 818-826. doi: 10.1016/j.nicl.2013.06.008
[37]	Xu K, Jiang WY, Ren L, et al. (2013) Impaired interhemispheric connectivity in medication-naive patients with major depressive disorder. J Psychiatry Neurosci 38: 43-48. doi: 10.1503/jpn.110132
[38]	Ben-Shimol E, Gass N, Vollmayr B, et al. (2015) Reduced connectivity and inter-hemispheric symmetry of the sensory system in a rat model of vulnerability to developing depression. Neuroscience 310: 742-750. doi: 10.1016/j.neuroscience.2015.09.057
[39]	Bohlender J, Imboden H (2012) Angiotensinergic neurotransmission in the peripheral autonomic nervous system. Front Biosci (Landmark Ed) 17: 2419-2432. doi: 10.2741/4062
[40]	Foster PS, Harrison DW (2006) Magnitude of cerebral asymmetry at rest: covariation with baseline cardiovascular activity. Brain Cogn 61: 286-297. doi: 10.1016/j.bandc.2006.02.004
[41]	Swislocki AL, LaPier TL, Khuu DT, et al. (1999) Metabolic, hemodynamic, and cardiac effects of captopril in young, spontaneously hypertensive rats. Am J Hypertens 12: 581-589. doi: 10.1016/S0895-7061(99)00012-6
[42]	Thayer JF, Lane RD (2009) Claude Bernard and the heart-brain connection: further elaboration of a model of neurovisceral integration. Neurosci Biobehav Rev 33: 81-88. doi: 10.1016/j.neubiorev.2008.08.004
[43]	Holzer P, Farzi A (2014) Neuropeptides and the microbiota-gut-brain axis. Adv Exp Med Biol 817: 195-219. doi: 10.1007/978-1-4939-0897-4_9
[44]	Prieto I, Hidalgo M, Segarra AB, et al. (2018) Influence of a diet enriched with virgin olive oil or butter on mouse gut microbiota and its correlation to physiological and biochemical parameters related to metabolic syndrome. PLoS One 13: e0190368. doi: 10.1371/journal.pone.0190368
[45]	Hidalgo M, Prieto I, Abriouel H, et al. (2018) Changes in Gut Microbiota Linked to a Reduction in Systolic Blood Pressure in Spontaneously Hypertensive Rats Fed an Extra Virgin Olive Oil-Enriched Diet. Plant Foods Hum Nutr 73: 1-6. doi: 10.1007/s11130-017-0650-1
[46]	Fujiwara Y, Kubo M, Kohata Y, et al. (2011) Association between left-handedness and gastrointestinal symptoms. Digestion 84: 114-118. doi: 10.1159/000324680
[47]	Morris DL, Montgomery SM, Galloway ML, et al. (2001) Inflammatory bowel disease and laterality: is left handedness a risk? Gut 49: 199-202. doi: 10.1136/gut.49.2.199
[48]	Denny K (2009) Handedness and depression: evidence from a large population survey. Laterality 14: 246-255. doi: 10.1080/13576500802362869
[49]	Işcen S, Özenç S, Tavlasoglu U (2014) Association between left-handedness and cardiac autonomic function in healthy young men. Pacing Clin Electrophysiol 37: 884-888. doi: 10.1111/pace.12365
[50]	Vagena E, Ryu JK, Baeza-Raja B, et al. (2019) A high-fat diet promotes depression-like behavior in mice by suppressing hypothalamic PKA signaling. Transl Psychiatry 9: 141. doi: 10.1038/s41398-019-0470-1
[51]	Sarris J, Murphy J, Mischoulon D, et al. (2016) Adjunctive Nutraceuticals for Depression: A Systematic Review and Meta-Analyses. Am J Psychiatry 173: 575-587. doi: 10.1176/appi.ajp.2016.15091228
[52]	Segarra AB, Ramirez M, Banegas I, et al. (2008) Dietary fat influences testosterone, cholesterol, aminopeptidase A, and blood pressure in male rats. Horm Metab Res 40: 289-291. doi: 10.1055/s-2008-1046800
[53]	Vancassel S, Aïd S, Pifferi F, et al. (2005) Cerebral asymmetry and behavioral lateralization in rats chronically lacking n-3 polyunsaturated fatty acids. Biol Psychiatry 58: 805-811. doi: 10.1016/j.biopsych.2005.04.045
[54]	Tryon MS, Stanhope KL, Epel ES, et al. (2015) Excessive Sugar Consumption May Be a Difficult Habit to Break: A View From the Brain and Body. J Clin Endocrinol Metab 100: 2239-2247. doi: 10.1210/jc.2014-4353
[55]	Redondo-Useros N, Nova E, González-Zancada N, et al. (2020) Microbiota and Lifestyle: A Special Focus on Diet. Nutrients 12: E1776. doi: 10.3390/nu12061776

This article has been cited by:

1.	Bharati Panigrahy, K. Narayan, B. Ramachandra Rao, Green hydrogen production by water electrolysis: A renewable energy perspective, 2022, 67, 22147853, 1310, 10.1016/j.matpr.2022.09.254
2.	Richard Cartland, Al-Mas Sendegeya, Jean de Dieu Khan Hakizimana, Performance Analysis of a Hybrid of Solar Photovoltaic, Genset, and Hydro of a Rural-Based Power Mini-Grid: Case Study of Kisiizi Hydro Power Mini-Grid, Uganda, 2023, 11, 2227-9717, 175, 10.3390/pr11010175
3.	Harpreet Singh, Chengxi Li, Peng Cheng, Xunjie Wang, Qing Liu, A critical review of technologies, costs, and projects for production of carbon-neutral liquid e-fuels from hydrogen and captured CO2, 2022, 1, 2753-1457, 580, 10.1039/D2YA00173J
4.	Josmar B. Cristello, Jaehyun M. Yang, Ron Hugo, Youngsoo Lee, Simon S. Park, Feasibility analysis of blending hydrogen into natural gas networks, 2023, 03603199, 10.1016/j.ijhydene.2023.01.156
5.	Pasquale Marcello Falcone, Editorial to the 'Special Issue—Energy transition in a circular economy perspective' of AIMS Energy, 2022, 10, 2333-8334, 582, 10.3934/energy.2022029
6.	Patrick Moriarty, Damon Honnery, When will the hydrogen economy arrive?, 2022, 10, 2333-8334, 1100, 10.3934/energy.2022052
7.	Franz Teske, Jano Schubert, Adrian Fehrle, Felix Funk, Jörg Franke, Techno-economic analysis of battery storage systems and hydrogen-based storage systems as an alternative to grid expansion in the medium voltage grid in Germany, 2023, 11, 2333-8334, 358, 10.3934/energy.2023019
8.	Marino Burba, Eleonora Pargoletti, Frank Marken, Neil B. McKeown, Mariolino Carta, Alberto Vertova, Alessandro Minguzzi, Polymer of Intrinsic Microporosity as Binders for both Acidic and Alkaline Oxygen Reduction Electrocatalysis, 2024, 11, 2196-0216, 10.1002/celc.202300481
9.	Inês Rolo, Vítor A. F. Costa, Francisco P. Brito, Hydrogen-Based Energy Systems: Current Technology Development Status, Opportunities and Challenges, 2023, 17, 1996-1073, 180, 10.3390/en17010180
10.	Pedro Fernandes, Pedro D. Gaspar, Pedro D. Silva, Peltier Cell Integration in Packaging Design for Minimizing Energy Consumption and Temperature Variation during Refrigerated Transport, 2023, 7, 2411-9660, 88, 10.3390/designs7040088
11.	Hasan Ozcan, Rami S. El-Emam, Selahattin Celik, Bahman Amini Horri, Recent advances, challenges, and prospects of electrochemical water-splitting technologies for net-zero transition, 2023, 8, 27727823, 100115, 10.1016/j.clce.2023.100115
12.	Andrea Navarro Jiménez, Huaili Zheng, Fueling Costa Rica’s green hydrogen future: A financial roadmap for global leadership, 2024, 51, 17550084, 100651, 10.1016/j.ref.2024.100651
13.	Eugeniusz Mokrzycki, Lidia Gawlik, The Development of a Green Hydrogen Economy: Review, 2024, 17, 1996-1073, 3165, 10.3390/en17133165
14.	Juan Gabriel Segovia-Hernández, Advancing E-fuels production through process intensification: overcoming challenges and seizing opportunities for a sustainable energy future - A critical review, 2025, 208, 02552701, 110107, 10.1016/j.cep.2024.110107
15.	Jianxin Wang, Xianying Hao, Hui Zhang, Zhiguang Chen, Chaokui Qin, Simulation and experimental investigation on the static mixer of natural gas mixed with hydrogen, 2025, 99, 03603199, 1, 10.1016/j.ijhydene.2024.12.045
16.	Hancheng Lu, Baoling Guo, Jingxin Yao, Yufeng Yan, Xinhui Chen, Zilong Xu, Baoqing Liu, CFD analysis on leakage and diffusion of hydrogen-blended natural gas pipeline in soil-brick gutter coupling space, 2025, 100, 03603199, 33, 10.1016/j.ijhydene.2024.12.280
17.	Laveet Kumar, Ahmad K. Sleiti, Wahib A. Al-Ammari, Thermo-economic analysis of blending hydrogen into natural gas pipeline with gaseous inhibitors for sustainable hydrogen transportation, 2025, 311, 00092509, 121619, 10.1016/j.ces.2025.121619

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Neuroscience

3.1 4.2

Metrics

Article views(4536) PDF downloads(93) Cited by(5)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(4) / Tables(1)

AIMS Neuroscience

Is there a link between depression, neurochemical asymmetry and cardiovascular function?

Related Papers:

Abstract

1. Introduction

2. Preleminaries

3. The idea of LTDM

4. VITM formulation

5. Convergence analysis

6. Applications

7. Results and discussion

8. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Neuroscience

Is there a link between depression, neurochemical asymmetry and cardiovascular function?

Related Papers:

Abstract

1. Introduction

2. Preleminaries

3. The idea of LTDM

4. VITM formulation

5. Convergence analysis

6. Applications

7. Results and discussion

8. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog