Making a case for a Non-standard frequency axial-flux permanent-magnet generator in an ultra-low speed direct-drive hydrokinetic turbine system

1.   Introduction

Hydropower is one of many renewable energy sources. The widely used form of hydropower is obtained from potential energy stored in water behind dams, but due to their adverse effects on forests ^[1] and public perception, they are now rarely built. However, there are other forms of hydropower called hydrokinetic power: wave, tidal and stream ^[1]. Hydrokinetic power turbines extract kinetic energy from a flowing mass of water, which is akin to wind turbines. However, because water is denser than air, there is more energy to be extracted from the same swept area. This idea has received a lot of interest from researchers due to its lower costs and minimal civil constructions. Turbines can be installed in rivers or channels where water flows. Rivers with high water velocity are suitable locations, but they are usually in remote areas. Therefore, the systems must be durable and simple to maintain by local people. Hydrokinetic turbines have 4 major components; a turbine rotor, a transmission shaft, a gearbox and a generator. The generator is normally of the radial-flux type, which operates at above 1500 RPM ^[2], but the turbine rotor spins at a much lower speed. Thus a gearbox is required. As a result, there is an approximately 10% ^[3] loss of energy. Hydrokinetic Darrieus turbines produce mechanical power at lower rotational speeds compared to Darrieus wind turbines. A Darrieus wind turbine wind tunnel test ^[4] showed that the turbine starts to produce power at over 60 RPM while a simulated Darrieus hydrokinetic turbine works at 70 RPM and below ^[5]. As a result, applying a direct-drive system to it would be a challenging task. The said turbine is 4 m in diameter, however, if the diameter is 2 m, the rotational speed becomes 140 RPM. There is a narrow window of peak power output at each water velocity, where the generator must be designed to operate within.

If a direct-drive system could be implemented, it would eliminate the friction loss at the gearbox, but the generator speed would become too low for power generation. In such a system, the Darrieus rotor drives a permanent magnet rotor, while the armature coil stator is stationary ^[6]. Directly-driven axial-flux generators have been tested with wind turbines and hydrokinetic turbines. Table 1 shows the performances such as water velocity (V), turbine radius (R_T), rotational speed (n_i) and electrical power output (P_e) of hydrokinetic turbine systems. Davila-Vilchis and Mishra (2014) ^[2] tested a generator at 420 RPM, where it produced 47 W of P_e. Bannon et al. (2013) ^[7] designed a similar generator at a speed as low as 22 RPM, and the P_e was estimated to be 6.9–803.6 W (at 22–92.3 RPM).

Table 1.  Operational parameters of low-speed hydrokinetic turbine systems.

Performance	3-blade rotor [8]	4-blade rotor [9]	3-blade rotor [10]	5-blade rotor [11]	3-blade rotor [12]
V (m/s)	1.1	0.6	0.3–2.5	1	0.6–1
RT (m)	0.8	0.45	0.3–0.6	1.2	0.35
ni (RPM)	525	110	132–202	65	100–500
Pe (W)	620	150- 190	240–1140	750	50–80

---

 | Show Table

DownLoad: CSV

The main factors influencing the voltage and current outputs are the relative speed between magnets and coils and the generator torque, respectively. The former is also directly proportional to the number of turns of copper in the armature coils. A group of researchers ^[13,14,15] have illustrated that it is possible for a generator to produce P_e at low n_i. They conducted an experiment with a direct-drive permanent-magnet generator (PMG) in a wind turbine system that was operated at 127 RPM. However, direct-drive hydrokinetic turbines operate at a much lower speed ^[16]. Firstly, the Darrieus rotor has to operate at its designated tip speed ratio (λ) ^[17,18], corresponding to the maximum power coefficient (C_P), while the generator has to produce a sufficient voltage. The problem arises when the Darrieus rotor diameter is large, which forces the n_i to drop. As a result, the generator diameter must also be increased to maintain the relative speed between magnets and coils. However, the impacts of the turbine rotor and generator sizes on n_i and P_e have not been fully explored. This research project seeks to provide a solution and supporting data that would allow engineers to keep the generator size compact, while making sure that the system could provide sufficient voltage.

The objective of this project was to study the parametric relationship between rotor and generator sizes of a direct-drive hydrokinetic turbine system and to investigate a way to reduce the generator size while possessing the capability to produce sufficient voltage at an ultra-low RPM. The system used a 3-blade Darrieus rotor to drive an axial-flux permanent-magnet generator directly. Simulation programs were constructed in MATLAB to compute parameters of the Darrieus rotor and the generator. The Darrieus rotor simulation program obtained hydrodynamic parameters such as forces on the turbine blade, n_i, torque (τ) and C_P. The data were then input into the axial-flux permanent-magnet generator simulation program and the output voltage and P_e delivered calculated. The performances of the system at various rotor and generator diameters are reported in this paper. A suggestion on generator electrical frequency is put forward, which would facilitate a novel and more suitable generator for this application.

2.   Research methodology

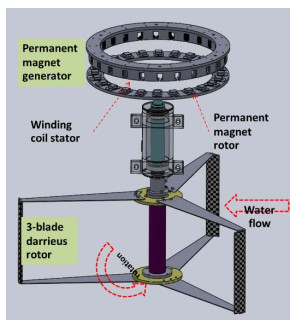
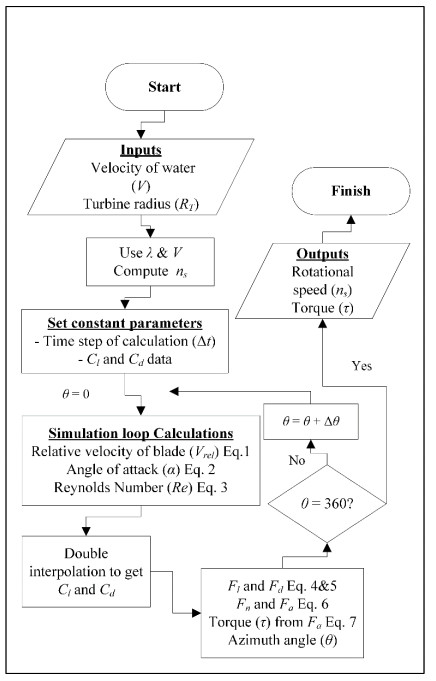
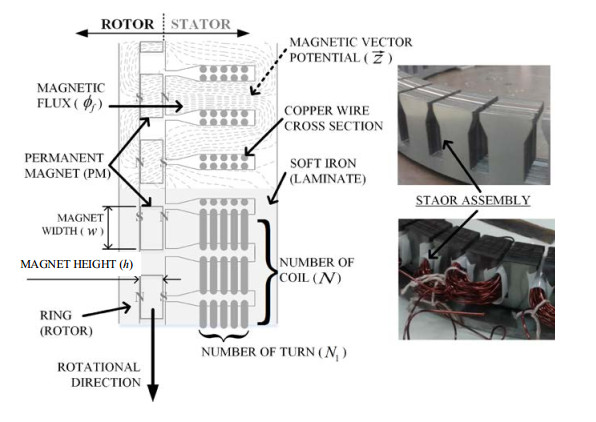
The direct-drive hydrokinetic turbine system consists of a 3-blade Darrieus rotor and an axial-flux permanent-magnet generator (Figure 1). The Darrieus rotor has a shaft that is connected to the permanent-magnet rotor of the generator. The armature coil stator is fixed. The numerical simulation was divided into 2 parts: Darrieus rotor simulation and axial-flux permanent-magnet generator simulation. The former provided inputs for the latter; those inputs being n_i and τ. The simulation programs were written in MATLAB. This investigation performed analyses on rotors at a constant n_i. It assumed that the rotors were started and brought up to speed by a mechanism. The energy associated with the process would be very small compared to the total energy production.

Figure 1.  The direct-drive hydrokinetic turbine system, where a 3-blade Darrieus rotor drives the permanent-magnet rotor of the axial-flux permanent-magnet generator.

DownLoad: Full-Size Img PowerPoint

2.1.   Darrieus rotor simulation

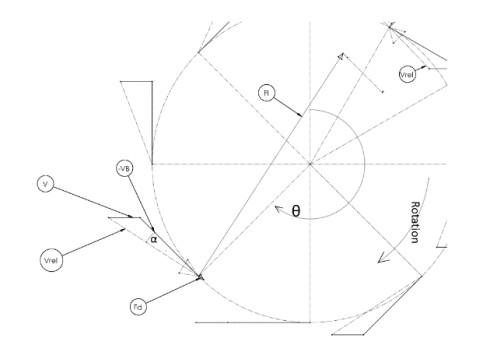
The Darrieus rotor simulation program calculated the hydrodynamic parameters at several values of R_T and V. The λ used is approximately 6 ^[19] and hence its nominal speed (n_s) at each V was determined. As the rotor turned at the speed of n_s, the blades were at various angles of attack (α). The vector of relative velocity (V_rel) and α changed constantly, which was used to find the lift (C_l) and drag coefficients (C_d) ^[20]. These blade data belong to the NACA 0018 blade profile and were built into the program ^[21]. The program calculated lift (F_l), drag (F_d) (Figure 2) and resultant forces (F_r) on the blades. The normal (F_n) and tangential (F_a) forces led to the τ produced by the rotor. The outputs of the Darrieus rotor simulation program were n_s and τ at various conditions (Figure 3).

Figure 2.  Force diagram of a Darrieus rotor, while water is flowing from left to right and the turbine is spinning in the clockwise direction.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Flowchart illustrating the design of the Darrieus rotor simulation program in MATLAB.

DownLoad: Full-Size Img PowerPoint

At a given θ and n_i, the V_B was calculated using Eq 1.

Vectors of V and V_B were provided to obtain V_rel and α using Eqs 2 and 3, respectively.

The vector of V_rel and α changed constantly, which was used to find the C_l and C_d. The instantaneous Re was computed according to Eq 4. The written program used this data to interpolate for C_l and C_d from the NACA 0018 data file ^[21] before calculating the F_l and F_d using Eqs 5 and 6.

Lastly, F_a was obtained using Eq 7, where it is responsible for τ, which was obtained for every blade using Eq 8. The next instantaneous θ was computed after Δt had passed and so the iteration proceeded (Figure 3). The outputs of the Darrieus rotor simulation program were n_s and τ at various conditions.

2.2.   Axial-flux permanent-magnet generator simulation

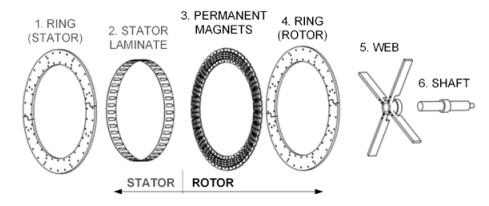
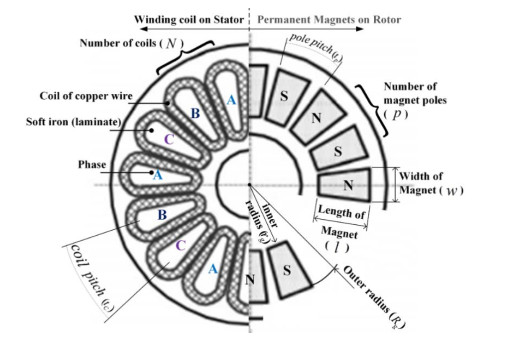
The basic design of the generator is shown in Figure 4, where the permanent-magnet rotor is connected to the Darrieus rotor via a shaft. The magnet size was fixed and the number of magnets varied with generator radius (R_g). The stator had laminate sheets packed together to produce the core for the coils. The rotor and stator were assembled with an air gap of 1 mm. Detailed dimensions of common parts (Figures 5 and 6) were specified before calculations took place. A mathematical model of the axial-flux permanent-magnet generator was built, where n_s was the primary input. Even though n_s is dictated by the turbine, it directly affects p of the generator. R_g was varied (Table 2), which directly affected the number of slots (N). The stator winding was of the concentrated winding type. Therefore, the key parameters of the generator were n_s and R_g.

Figure 4.  Exploded view of the axial-flux permanent-magnet generator.

DownLoad: Full-Size Img PowerPoint

Figure 5.  2D drawing of the stator and rotor.

DownLoad: Full-Size Img PowerPoint

Figure 6.  2D sectional view of the stator’s copper coils (left) and rotor’s magnets (right).

DownLoad: Full-Size Img PowerPoint

Table 2.  The initial design parameters of the axial-flux permanent-magnet generator.

Parameter	Rg	f	Magnet	Load	N/p
Values	0.2, 0.4 and 0.6	50	Neodymium	Resistive wire	3/2

---

 | Show Table

DownLoad: CSV

The coil to pole ratio (N/p) was kept constant. The electromagnetic potential (E_f) for each case was computed and compared.

The generator has to produce power at electrical frequency (f) = 50 Hz, which means the number of pole pairs (p) was computed using Eq 9 ^[22]. n_s from each R_T was obtained from the hydrokinetic rotor analysis.

Then E_f was estimated using Eq 10 ^[22], which clearly states that it is proportional to n_s, while keeping N₁ as 1.

where N₁ is the number of turns in series per phase, k_w1 is the winding factor and ϕ_f is the Magnetic flux/pole.

Moreover, k_w1 and ϕ_f must also be obtained using Eqs 11 & 12 ^[22].

(11)

(12)

where m₁ is the number of phases, β is the coil pitch to pole pitch ratio, q₁ is the slot per pole per phase, B_avg is the averaged flux density and r_g is the generator inner radius.

The generator produces a 3-phase AC voltage which has to be converted into a DC voltage (V_dc) using a full-wave rectifier. Equation 13 ^[22] represents the AC-DC electrical conversion. This voltage can be applied to loads such as a resistive heater, a battery charger or a DC-to-AC inverter.

3.   Results

3.1.   Darrieus rotor hydrodynamic performance

For each V, R_T was varied and n_s was obtained while keeping the λ at 6. The Darrieus rotor simulation program solved for n_s and τ, which were needed for the generator simulation program. It has to be noted that the rotors in all the cases have the same solidity. This entails that rotors with small R_T would have blades with short chord lines and vice versa. The data show that τ is directly proportional to V and R_T (Table 3), which means a fast moving stream and large rotor are desirable for a hydrokinetic power application in general. However, large rotors will spin even slower with low n_s. The relationship between R_T and n_s is dictated by the need to have a constant λ, which corresponds to the maximum C_p.

Table 3.  The initial design parameters of the axial-flux permanent-magnet generator.

Parameter	V	CP	τ	λ	ns
					RT = 0.4	RT = 0.5	RT = 0.6
Results	0.5	0.25–0.26	1.7–3.6	6	72	57	48
	1.0	0.26–0.28	6.6–16.5		143	115	96
	1.5	0.28–0.31	16.2–39.5		215	172	143
	2.0	0.30–0.33	31–75		287	229	191

---

 | Show Table

DownLoad: CSV

At the same water velocity, C_p improved only slightly with R_T. For instance, rotors with R_T = 0.6 m produced more τ and better C_p, whereas higher water velocity did help in C_p gain by as much as 20% from V = 0.5 to V = 2.0 m/s. In the deployment of the turbine system, we would measure the water velocity and then proceed with a rotor design. A rotor configuration with R_T = 0.6 m would be chosen, but we run the risk of not being able to find a PMG design that produces usable voltage due to the ensuing low n_s.

3.2.   Axial-flux permanent-magnet generator performances

The generator simulation yielded E_f when R_g was varied. At each V, R_T and R_g were essentially redesigned to find a set up that gives E_f at a usable level. It was found that E_f rises in proportion to R_g. At R_g = 0.2 m, E_f was 1.26 V/turn/coil/phase. When R_g is 3 times larger (at the same V), E_f went up by approximately the same factor (Table 4). The total voltage per phase becomes E_f multiplied by the number of turns in series per phase (N₁). The value of N₁ will increase when there is a higher number of coils and larger slot to accommodate conductors.

Table 4.  Estimated E_f of the direct-drive hydrokinetic turbine system.

Parameter	Values
V	0.5	1.0	1.5	2.0	0.5	1.0	1.5	2.0	0.5	1.0	1.5	2.0
Rg	0.2				0.4				0.6
RT	0.4				0.5				0.6
ns	72	143	215	286	57	115	171	229	48	95	143	191
N (/phase)	125	63	42	31	158	78	53	39	188	95	63	47
Ef (/phase)	1.26				2.63				3.99

---

 | Show Table

DownLoad: CSV

In addition, E_f became independent of V and R_T because f was fixed at 50 Hz. In other words, an installation with high V will deliver improved power production, while a larger R_T gives higher τ, but the consequential system configuration contributes no change to E_f compared to another configuration installed at a lower V. However, N was directly affected, the reason being that as n_s changed with V and R_T, N must be adjusted to keep f at 50 Hz.

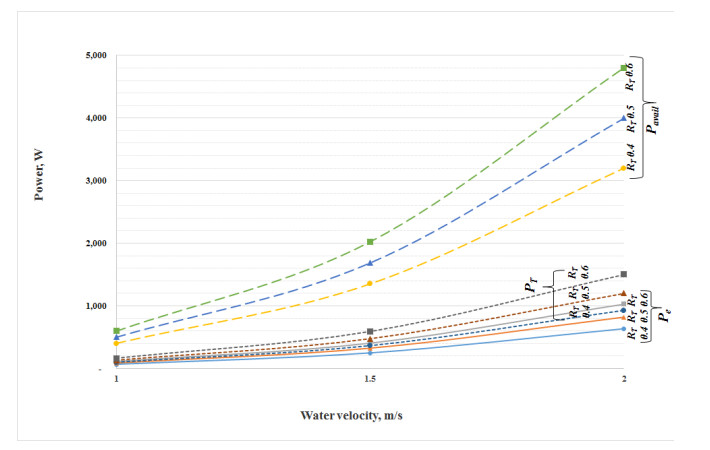
Moreover, P_e was strongly influenced by R_T and V. For instance, at V = 1 m/s and R_T = 0.6 m, the available power in the water (P_avail) was 600 W but P_e was 112 W (Figure 7). However, at double the water velocity (V = 2 m/s), the turbine system was predicted to produce P_e = 1,028 W. Likewise, when R_T was lowered to 0.4 m, P_e dropped to 636 W.

Figure 7.  Comparisons between P_e and P_avail as V increases at various R_T.

DownLoad: Full-Size Img PowerPoint

The estimated P_e and the required N₁ were obtained (Table 5) from the generator numerical model, which assumed resistive wires as a load. The overall output of the system could be raised by increasing R_T. It was also found that a generator with small R_g required more turns of conductor to produce the same level of usable voltage. The findings suggest that to have sufficient power, the system should be installed in rivers with V of at least 1.5 m/s.

Table 5.  Suggested configurations of the direct-drive hydrokinetic turbine system and their estimated P_e.

Configuration	1	2	3
Rg	0.2	0.4	0.6
N1	22	11	7
RT	0.4	0.5	0.6
Pe @ V = 1.5 m/s	250	325	405
Pe @ V = 2.0 m/s	636	821	1028

---

 | Show Table

DownLoad: CSV

Not all PMG designs from this analysis are suitable for production. For a practical reason, putting 125 slots/phase (Table 4) into a generator with R_g of 0.2 m may be challenging. A more attainable number of slots is 31 slots/phase, and hence the voltage per phase per turn is 39.06 V_rms or 35.18 V_dc (Eq 13). This level of voltage is usable for battery charging applications, and so the design character is desirable.

A direct-drive hydrokinetic turbine system has an inherent low voltage output due to its low n_s. It would be novel to be able to produce more voltage when a location with high water velocity is available, in addition to an improved power production. However this is currently not the case because f is strictly maintained at 50 (or 60) Hz. In such a case where high water velocity is available, the turbine unit would be redesigned specifically for the site. The rotor would be able to produce more mechanical power and the generator to output more electricity, albeit at the same E_f.

We want to be able to redesign the turbine unit to take advantage of the increased water velocity in all dimensions. A solution would allow engineers to either design a generator that produces higher voltage at a given V and n_s or a generator with smaller R_g at a given E_f.

For illustration, the current generator designs have high n_s at higher V. Fixing f at 50 Hz gives N = 31 at V = 2.0 m/s (Table 4). If we assume that at R_g = 0.2 m, there is enough space on the circumference to put in more slots. According to equation 8, it is possible to have f = 100 Hz and 62 slots/phase rather than 31 slots/phase. As a result, the voltage per phase per turn is 78.12 V_rms or 70.36 V_dc. The actual number of slots that R_g could accommodate must be investigated further.

On the other hand, if high E_f is not needed, R_g could be halved. It is also possible for the generator to output almost the same level of E_f as before by having R_g equal to 0.1 m while keeping f = 100 Hz and 31 slots/phase. Although the voltage per phase per turn may not be as straightforward as before, the generator could be made more compact. The complication comes from the compounding effects of a lower number of slots and the relative speed between the permanent magnets and the armature coils.

This study found that there is a need to design a generator whose electrical frequency is anything rather than 50 Hz. By allowing the frequency to increase, the generator could be producing higher usable voltage at the same diameter or the same voltage at a smaller diameter. At the current state of generator design, an off-the-shelve PMG is not suitable for the direct-drive hydrokinetic turbine system, because it cannot fully utilize the benefit of increased water velocity.

4.   Conclusions

This research project formed numerical models of a hydrokinetic Darrieus rotor and an axial-flux permanent-magnet generator. The outputs of the rotor model were n_s and τ, which were then fed into the generator model. The combined system became a direct-drive hydrokinetic turbine system, where a transmission system was left out and hence friction loss was eliminated. To produce sufficient voltage and power, R_g was enlarged. The design parameters of the rotor and generator are presented. The study particularly indicates R_g and N₁ values necessary for the generator to produce usable outputs. Turbine system configurations were obtained, for which estimated power outputs were also compared.

It was found that E_f became independent of V and R_T because f was fixed at 50 Hz. As a result, this study made a case for designing a generator with electrical frequency other than the standard frequency, where it would be novel to be able to produce more voltage when a location with high water velocity is available, in addition to an improved power production.

This investigation used models with moderate complexity to prove the idea of a direct-drive hydrokinetic turbine system. It presented key parameters for an experiment which will be carried out in the near future. In the meantime, the models must be developed further to cover all aspects of operation. For example, the rotor model should have hydrodynamic data from a 3-D rotor simulation and experimental data. Moreover, the generator model could be improved by having 2-D magnetic flux simulation data. All models would be integrated into a single model, which should help to design a direct-drive hydrokinetic turbine system to suit a wide range of flow conditions.

The rotor sizes (R_T) are 0.4–0.6 m because they dictate n_s to be 72–191 RPM. The literature review shows that there was only one study at 65 RPM among many low-speed hydrokinetic turbine systems (Table 1). This study performed analyses at these speeds before attempting to lower n_s in the future. Although, R_T could be smaller, this would result in the blades being too thin (if the solidity is to be kept constant) and fail during operation. On the other hand, R_g should be as large as possible but since this research team had built a test generator whose dimensions were restricted by the available machineries and tools in the laboratory. This study took the test generator as the reference.

Acknowledgments

This research was sponsored by the National Research Council of Thailand (NRCT), Thailand through Research and Technology Transfer Affairs, KKU. Grant number 600038.

Conflict of interest

The authors declare no conflict of interest.