Citation: Michael Z. Hu, Peng Lai. Substrate effect on nanoporous structure of silica wires by channel-confined self-assembly of block-copolymer and sol-gel precursors[J]. AIMS Materials Science, 2015, 2(4): 346-355. doi: 10.3934/matersci.2015.4.346
| [1] | Xiaoxu Peng, Heming Jia, Chunbo Lang . Modified dragonfly algorithm based multilevel thresholding method for color images segmentation. Mathematical Biosciences and Engineering, 2019, 16(6): 6467-6511. doi: 10.3934/mbe.2019324 |
| [2] | Wenqi Ji, Xiaoguang He . Kapur's entropy for multilevel thresholding image segmentation based on moth-flame optimization. Mathematical Biosciences and Engineering, 2021, 18(6): 7110-7142. doi: 10.3934/mbe.2021353 |
| [3] | Shikai Wang, Heming Jia, Xiaoxu Peng . Modified salp swarm algorithm based multilevel thresholding for color image segmentation. Mathematical Biosciences and Engineering, 2020, 17(1): 700-724. doi: 10.3934/mbe.2020036 |
| [4] | Nilkanth Mukund Deshpande, Shilpa Gite, Biswajeet Pradhan, Ketan Kotecha, Abdullah Alamri . Improved Otsu and Kapur approach for white blood cells segmentation based on LebTLBO optimization for the detection of Leukemia. Mathematical Biosciences and Engineering, 2022, 19(2): 1970-2001. doi: 10.3934/mbe.2022093 |
| [5] | Shenghan Li, Linlin Ye . Multi-level thresholding image segmentation for rubber tree secant using improved Otsu's method and snake optimizer. Mathematical Biosciences and Engineering, 2023, 20(6): 9645-9669. doi: 10.3934/mbe.2023423 |
| [6] | Hong Qi, Guanglei Zhang, Heming Jia, Zhikai Xing . A hybrid equilibrium optimizer algorithm for multi-level image segmentation. Mathematical Biosciences and Engineering, 2021, 18(4): 4648-4678. doi: 10.3934/mbe.2021236 |
| [7] | Yating Fang, Baojiang Zhong . Cell segmentation in fluorescence microscopy images based on multi-scale histogram thresholding. Mathematical Biosciences and Engineering, 2023, 20(9): 16259-16278. doi: 10.3934/mbe.2023726 |
| [8] | Yu Li, Meilong Zhu, Guangmin Sun, Jiayang Chen, Xiaorong Zhu, Jinkui Yang . Weakly supervised training for eye fundus lesion segmentation in patients with diabetic retinopathy. Mathematical Biosciences and Engineering, 2022, 19(5): 5293-5311. doi: 10.3934/mbe.2022248 |
| [9] | Jiande Zhang, Chenrong Huang, Ying Huo, Zhan Shi, Tinghuai Ma . Multi-population cooperative evolution-based image segmentation algorithm for complex helical surface image. Mathematical Biosciences and Engineering, 2020, 17(6): 7544-7561. doi: 10.3934/mbe.2020385 |
| [10] | Ran Zhou, Yanghan Ou, Xiaoyue Fang, M. Reza Azarpazhooh, Haitao Gan, Zhiwei Ye, J. David Spence, Xiangyang Xu, Aaron Fenster . Ultrasound carotid plaque segmentation via image reconstruction-based self-supervised learning with limited training labels. Mathematical Biosciences and Engineering, 2023, 20(2): 1617-1636. doi: 10.3934/mbe.2023074 |
At the nanoscale, materials have distinctly different characteristics from their corresponding one at macroscopic scale. This is one of the main causes of the fast growth of research studies on nanomaterials in recent years. However, the key to achieving their applications for devices is the integration of the nanomaterials on desired locations of the devices. The two major strategies in coupling nanomaterials on surfaces are through the formation of multilayer of nanomaterials or through the formation of vertically nanostructures, such as nanopillars, i.e., nanowires standing on surfaces. In recent years, fabrication and applications of nanopillars have attracted more and more attention. There are two principle approaches to nanopillar fabrication: top-down approaches such as lithography and etching, and bottom-up growth techniques. Bottom-up fabrication methods of nanopillars include chemical vapor deposition (CVD) [1], physical vapor deposition (PVD) [2], template synthesis [3,4], and self-assembled methods. In this mini-review, we intend to summarize fabrication methods, formation mechanisms, factors controlling characteristics, and applications of nanopillars based on the bottom-up, self-assembly approach, with more attention being focused on the factors that affect the growth of the nanopillars. Top-down fabrications [5,6], including lithography based on templated methods [7,8], are not included in this short review. It is noteworthy that although, to a certain extent, CVD and PVD belong to the self-assembled class of approaches and have been widely used to make nanopillars, such as nanopillars of ZnO, CdS, etc., we will only briefly summarize the reports which mentioned the concept of self-assembly. The purpose of this review is to provide new researchers in this area with a quick overview on the body of work containing self-assembled nanopillars. For reviews on nanopillars from CVD or PVD, readers are suggested to read other recent reviews [9,10,11,12].
The self-assembly approach offers a simple and efficient method for growth aligned nanostructures. This includes:
a. Self-assembled inorganic nanopillars in the gas phase by deposition of aerosol, and pulsed laser deposition (PLD).
b. Self-assembled inorganic nanopillars in solutions by hydrothermal + polymer assisted template.
c. Self-assembled organic compounds in solution on surfaces through liquid evaporation.
Both horizontal and vertical films can be formed on a substrate by deposition of aerosol in the gas phase. The vertical nanopillared films offer advantages over the horizontal ones when a larger surface area is required [13,14].
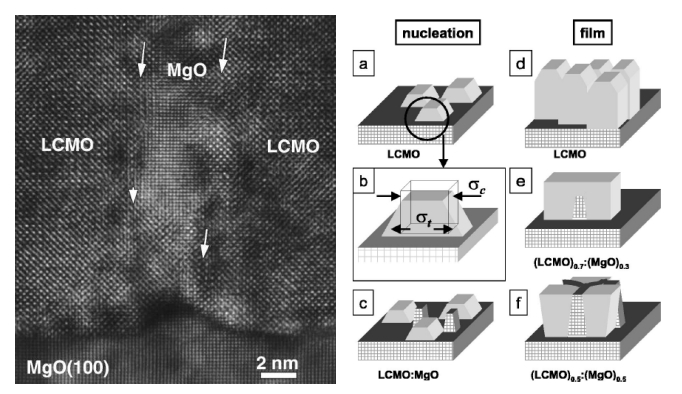
Lebedev et al. reported [15] nanopillared (La0.67Ca0.33MnO3)1−x:(MgO)x (LCMO) composite films on a MgO substrate. The films were prepared via the deposition of metal organic aerosols on the MgO substrate. The magneto-transport responses of the film depend on the percentage of (100) MgO in the composite (0 < x < 0.8) (Figure 1 left). The resistivity of the film increased dramatically when x > 0.3 due to its unique structure. The film was made of LCMO materials, with epitaxial nanopillars of MgO embedded in the LCMO film. The formation mechanism was proposed as shown in Figure 1 right.
Figure 1. Left: Cross-section electron microscopy image of the interface (La0.67Ca0.33MnO3)1−x–(MgO)x/MgO(100) for x = 0.5. Right: Schematic representation of the growth mechanism of the composite film at different stages: (a) Nucleation of the LCMO film on the MgO substrate. (b) Enlargement of one LCMO island on the MgO substrate. Close to the interface the LCMO region is under a two-dimensional tensile stress; the upper part of the LCMO island is under a two-dimensional compressive stress. The shape of LCMO becomes pyramidal. (c) Nucleation of the (LCMO)1−x:(MgO)x composite film on the MgO substrate. (d) The columnar structure of the LCMO film on the MgO substrate. (e) Structure of the (LCMO)1−x:(MgO)x film for x = 0.33. Intergrowth of the MgO islands in between LCMO domains occurs. (f) Structure of the (LCMO)1−x:(MgO)x film for x = 0.5. Every LCMO grain is surrounded by MgO through the complete film thickness. Figure from Ref [15] reprinted with permission from the American Physics Society.In a later work, Moshnyaga et al. further confirmed the formation of vertical nanopillars made of a composition of (La0.7Ca0.3MnO3)1−x:(MgO)x [16]. Again, the magneto-transport properties of the nanopillared films could be tuned via the MgO components.
In later reports, the pulsed laser deposition (PLD) method becomes the most popular method in this area and it has been successfully used in the fabrication of ceramic materials with nanopillars embedded in films. PLD is a thin film deposition technique. The energy of laser beam is high enough to vaporize a material into a plasma and deposits the plasma on a substrate to form a thin film. A variety of materials, such as La2O3, MnCO3, SrCO3, ZnO, Bi2O3, Fe2O3 and Sm2O3, BiFeO3:Sm2O3, BiFeO3:NiFe2O4, BaTiO3:CoFe2O4, La0.5Sr0.5CoO3:Ce0.9Gd0.1O1.95, etc, have been deposited on substrates to form vertical pillars with unique functionalities [17]. To name a few examples, Li et al. [18] prepared self-assembled PbTiO3–CoFe2O4 epitaxial nanostructures on SrTiO3 single crystals from a composite 0.67PbTiO3–0.33CoFe2O4 target by using the PLD approach. The nanostructures on the SrTiO3 surface is composed of vertical columns of CoFe2O4 embedded in a PbTiO3 film. In their later work [19], they also demonstrated multiferroic xCoFe2O4–(1−x)PbTiO3 films on the same substrates.
It has generally been accepted that the formation of the vertical nanostructures in films is due to the immiscibility of the two materials that requires the minimization of the interfacial and elastic strain energies between them. The morphology and the size of vertical nanopillars are related to the lattice misfit with the substrate [20]. By choosing two appropriate materials, nanopillar array can form in the epitaxial films. The properties of the films are related to the morphology and structure of the nanostructures and the interface. The two requirements for self-assembled two-phase nanocomposites are 1) the similarity of the crystal lattice parameters between the two materials; and 2) the low solubility or miscibility of the two materials. In the above paper, Li et al. [18] also showed orientation and morphology of the nanostructures could be controlled by the epitaxial stress of the substrates. The platelet-like column is parallel to the [110] and [111] planes for the [001] and [110] directions, respectively (Figure 2).
Figure 2. TEM images of the PbTiO3–CoFe2O4 nanostructures grown on (001) SrTiO3 (a) cross section, (b) plane view of the structures on (110) SrTiO3. (c) cross section, (d) plane view the structures on (110) SrTiO3. The image shown in (b) is a bright field image recorded near the [001] orientation parallel to the surface normal. In all the images, the CoFe2O4 phase appears as bright regions. Figure from Ref [18] reprinted with permission from the American Physics Society.Deng et al. [21] developed self-assembled (CoFe2O4)0.3–(BaTiO3)0.7 (CFO–BTO) feather-like nanopillars by using a cost-effective method that combined a hydrothermal reaction and a polymer-assisted fabrication. The crystalline CFO nanopillars were implanted in the BTO film. The mixed film showed unique ferromagnetic and ferroelectric properties. The proposed mechanism may be used for growing other perovskite-spinel nanomaterials.
By using a pulsed laser deposition method, Kim et al. prepared a three component self-assembled core-shell-matrix nanocomposite that was made of Cu nanorods that were covered by a shell of SrO embedded in a Sr(Ti, Cu)O3−δ perovskite matrix on SrTiO3 substrates [22]. After etching of Cu nanorods, the porous SrO pillars in the nanocomposite can be refilled with CoFeO4 pillars in a BiFeO3 perovskite matrix that showed unique magnetic properties.
Ji et al. have recently developed a novel, surface-assisted self-assembly approach to harvest vertically aligned single-crystalline organic nanopillar semiconductors from a solution of organic chemicals [23]. In these experiments, when cyanuric acid (CA) and melamine (M) are mixed at lower concentrations on a gold surface, an array of nearly 100% hexagonal nanopillars of the CA·M complex was obtained (scanning electron microscopy (SEM) images in Figure 3). The nanopillar is composed of a cyclic CA3M3 rosette assembly [24] (Figure 3 left). CA3M3 rosette molecular assemblies are hierarchically stacked or coordinated into insoluble nano-or micro-structures in 3D space due to hydrogen bonding, π–π stacking, hydrophobic interactions, and van der Waals interactions. They showed that the CA·M complexes nucleate as a thin, hexagonal plate on the gold surface at the onset stage, and grow wider and taller after more solvent evaporates. The unique aspect of this result is that this assembly is the first of such well-defined self-assembled nanopillars made of small organic molecules. It is expected that arrays of pillars can be developed from several other complexes. The nanopillars prepared by this method can be made in large quantities at a low cost due to the facile self-assembling method. By using the same method, the group reported two self-assembled metal-organic micropillar arrays on Au surfaces: Cu/BTC prepared from Cu2+ and 1, 3, 5-benzenetricarboxylic acid (TBC), and Zn/ADC from Zn2+ and 9, 10-anthracenedicarboxylic acid (ADC) [25,26].
Figure 3. Molecular structures (left) and SEM images of 1:1 CA·M hexagonal nanopillars on a gold surface. Figure from Ref [23] reprinted with permission from the American Chemical Society.Another organic nanopillar was prepared from a self-assembled mixture of copper phthalocyanine (CuPc) and 3, 4, 9, 10-perylene-tetracarboxylic-dianhydride (PTCDA by using a thermal gradient sublimation technique [27,28]. The CuPc/PTCDA nanopillars may be used for developing organic photovoltaic cells and near-IR photodetectors. It is also interesting that polymers could form well-defined nanopillars by using a spin-casting process. These polymers should have large coplanar segments and strong attraction between polymers in order to self-assembling into nanopillars [29].
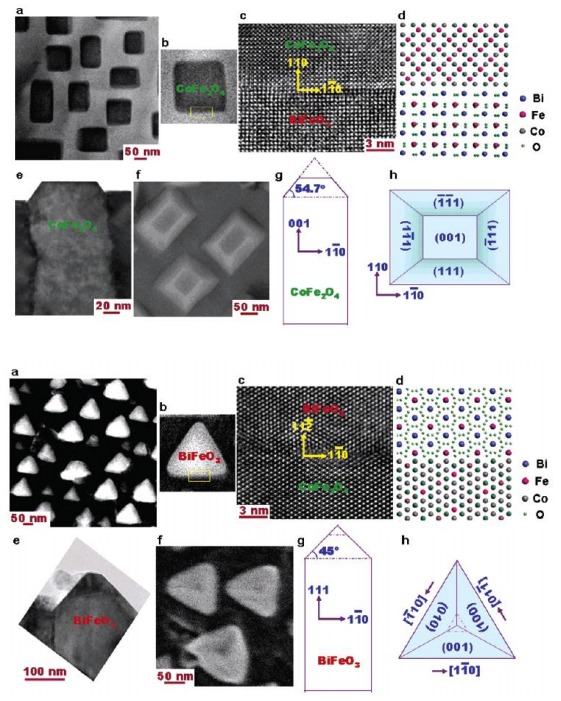
The property of surfaces is the main factor that controls the formation and characteristics of nanopillars. For the nanopillars from the pulsed laser deposition method, it has been believed that the growth of vertical nanopillars was due to the mismatch between the evaporated material and the substrate. This mismatch caused an in-plane compressive strain that limited the lateral growth of the material on the substrate [30]. The evaporated materials and substrates should have a similar structure and chemistry at their interface to facilitate the nucleation. This mechanism suggests that it is possible to design new nanostructures with desired properties by choosing appropriate substrates. For example, Zheng et al. [31] reported that the morphologies of self-assembled perovskite-spinel nanostructures were different on substrates with different orientations; rectangular CoFe2O4 nanopillars on a (001) and triangular BiFeO3 nanopillars on a (111) substrate (Figure 4).
Figure 4. Morphologies of the BiFeO3–CoFe2O4 nanostructures grown on a (001)-oriented (top) and a (111)-oriented (bottom) SrTiO3 substrate. (a) Z-contrast image from a TEM sample. (b) A TEM image of a single CoFe2O4 pillar embedded in a BiFeO3 matrix (top). A TEM image of a single BiFeO3 pillar embedded in a CoFe2O4 matrix (bottom). (c) A high-resolution TEM image from the interface region marked by the rectangle in b. (d) Structural model of the interface between CoFe2O4 and BiFeO3 showing that the interfaces are {110} planes (top) or {112} planes (bottom), both along $\left\langle {110} \right\rangle $ directions. (e) Cross-sectional TEM image of a single CoFe2O4 pillar (top) or BiFeO3 pillar (bottom). (f) SEM image of the CoFe2O4 pillars (top) and BiFeO3 pillars (bottom). (g) A schematic of a CoFe2O4 pillar (top) or a BiFeO3 pillar (bottom). (h) A schematic of a CoFe2O4 pillar (top) or a BiFeO3 pillar (bottom) showing three crystal facets. Figure from Ref [31] reprinted with permission from the American Chemical Society.More morphologies of nanopillars based on rational selections of substrates have been demonstrated by Liao et al. [32]. They showed that in the BiFeO3/CoFe2O4 system, CoFe2O4 nanopillars are in pyramid, roof, and triangular shapes on the (001), (011), and (111) surfaces, respectively (Figure 5). The magnetic anisotropies of these CoFe2O4 are different as well.
Figure 5. AFM topography of BiFeO3–CoFe2O4 films. (a–c) 2D (3 μm × 3 μm) and 3D (500 nm × 500 nm) images of the films grown on different substrates. Figure from Ref [32] reprinted with permission from the American Chemical Society.The substrates play a major role in the growth of the CA·M nanopillars [21]. The density of the CA·M hexagonal nanopillars was approximately 30 per μm2 on a glass or silicon surface, which was much greater than the density of 0.1 per μm2 found on the gold surface. The CA·M nanopillars on a glass or silicon surface were shorter and smaller in diameter than those made on the gold surface.
In another work, Jayaramulu demonstrated that the surface of highly fluorinated graphene oxide (HFGO) had an orientation-directing property that guided the selective nucleation of zeolite imidazole framework (ZIF-8) nanostructures between HFGO layers. This HFGO/ZIF-8 composite may be used for separation of oil from water [33].
Other than substrate surfaces, factors to control the structure and subsequent properties of nanopillars include the following:
a) Vertical strain within layered heterostructures. It was recently shown that the vertical strain also controls the characteristics of the nanopillar films. Macmanus-Driscoll et al. [34] demonstrated that ordered nanostructures were produced from La0.70Sr0.3MnO3/ZnO (LSMO/ZnO) and BiFeO3/Sm2O3 (BFO/SmO) on a single-crystal SrTiO3 (STO). Vertical strain dominated the strain state in the films. Yang et al. [35] suggested that the leakage current, the lattice parameters, the strain state of the two phases, and dielectric properties can be affected by the vertical interface. In another reports, Varanasi [36]and Zhu [37] showed that in YBa2Cu3O7−x (YBCO)/BaSnO3 (BSO) nanocomposite thin films, the lattice BSO nanopillars was rather tuned by YBCO, but not the substrate.
b) Temperature. For example, the average diameter of CoFe2O4 pillars in a system were 9 and 70 nm at 750 and 950 ℃, respectively [17].
c) Deposition frequency. Chen et al. [38] observed that the morphology and properties of (La0.7Sr0.3MnO3)0.5:(ZnO)0.5 (LSMO:ZnO) nanostructures on SrTiO3 (STO) (001) substrates can be tuned with the deposition frequency.
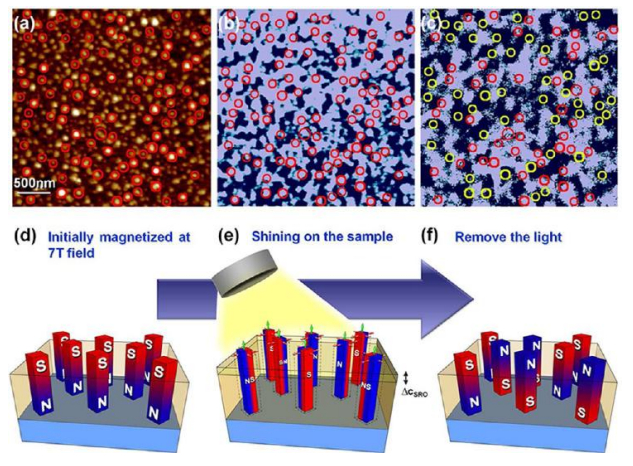
d) Light. For instance, Liu et al. [39] demonstrated that light could induce a fast change in magnetization of self-assembled CoFe2O4 nanopillars in a photostrictive SrRuO3 (SRO) film (Figure 6).
Figure 6. (a) AFM topology and (b) MFM image at the same area of a nanostructured CFO–SRO sample that has been magnetized by applying a large out-of-plane magnetic field before being illuminated. (c) MFM image at the same area after being illuminated. We randomly selected 100 nanopillars to conveniently observe the change in magnetic direction. The red circles in (b) are the nanopillars in (a) with downward magnetization, and half these pillars flipped upward in (c) are presented in yellow circles, suggesting a "liberation" in magnetization during illumination. (d–f) Schematic illustration of the process of magnetic domain flipping during the illumination by ultrafast Ti:sapphire laser pulses. (d) Application of a large out-of-plane magnetic field (7T) to magnetize all nanopillars downward. (e) Introduction of light on the nanostructured thin film to expand the lattice of SRO and release the vertical compressive strain of CFO. (f) Removal of light, resulting in the magnetization of the CFO nanopillars becoming either upward or downward for the energetically preferred state. Figure from Ref [39] reprinted with permission from the American Chemical Society.Self-assembled vertical nanostructures have new functionalities. Some applications of these nanopillars are briefly summarized as follows:
The nanopillar-embedded films hold potential as an excellent magnetoelectric materials. Magnetoelectric materials are materials that exhibit a coupling effect between the magnetic and the electric properties. The unique two-phase nanostructures that combine the vertically aligned nanopillars in a uniform film offers the potential to fabricating new magnetoelectric devices with stronger magnetoelectric responses.
Zheng et al. [13,17] prepared self-assembled epitaxial CoFe2O4–BaTiO3 ferroelectromagnetic nanopillars on SrTiO3 (001) substrates by using the pulsed laser deposition method (Figure 7). CoFe2O4 is magnetic and BaTiO3 is ferroelectric. The size of the hexagonal CoFe2O4 nanopillars was from 20 to 30 nanometers. This nanocomposite showed strong magnetoelectric coupling.
Figure 7. Left: Schematic illustration of a self-assembled nanostructured thin film formed on the substrate. Middle: AFM topography image of the film showing a quasi-hexagonal arrangement of the CoFe2O4 nanopillars. Right: TEM planar view image showing the CoFe2O4 nanostructures in the BaTiO3 matrix. Figure from Ref [13] reprinted with permission from the AAAS.Zavaliche et al. [40] also reported a similar epitaxial nanostructure with a thickness of ~200 nm. They presented direct evidence on magnetization reversal at room temperature. Stratulat et al. demonstrated a large area of highly ordered CoFe2O4-nanopillar/BiFeO3 composite [41]. Further proof of enhanced ferromagnetic coupling can be found from Chen's work [42].
These nanopillar-embedded films may also be used as ferroelectric materials for energy harvesting to high-power electronic transducing. The ferroelectricity and ferroelectric Curie temperature Tc can be affected from the strain in the oxide films.
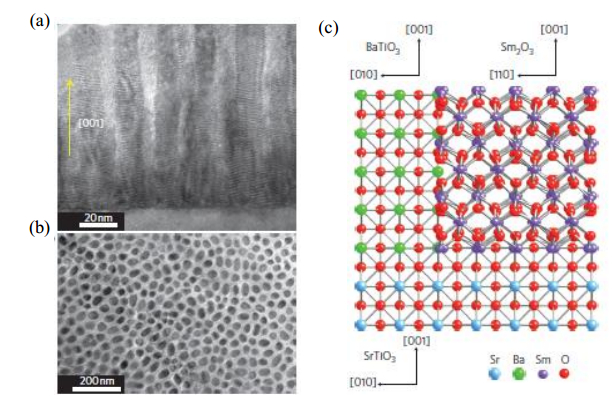
In BiFeO3:Sm2O3, an improvement in dielectric properties and reduced leakage were achieved when the vertical strain increased [34,35]. Harrington et al. [43] reported ferroelectric materials based on micrometer-thick films of BaTiO3 (BTO), which were embedded with vertical pillars of Sm2O3 throughout the film (Figure 8). Sm2O3 is used to control the strain because 1) it does not dissolve in BTO; 2) its elastic modulus (125 GPa) is larger than that of BTO (67 GPa), and 3) it is an insulating material. The Curie temperature of the film was 330 ℃, and the phase transition temperature was higher than 800 ℃, indicating it is a high-temperature ferroelectric material. The results also suggested that vertical nanopillars can be used to control strains in thicker films [44,45,46].
Figure 8. Self-assembled vertical nanostructure. TEM images of a 600-nm-thick BaTiO3:Sm2O3 film on SrTiO3: cross-section (a); plan view (b). Sm2O3 shows a darker contrast compared with BaTiO3. Yellow arrow represents c-axis direction. (c) Crystallographic model of interface matching. Figure from Ref [43] reprinted with permission from the Nature Publishing Group.The introduction of nanopillars in membranes may also be a promising approach for optimizing high-temperature superconductors (HTSs). This is due to an increase in their critical current density Jc and a reduction of their anisotropy. The introduction of nanostructures may pin magnetic flux vortices and oppose vortex motion induced by the Lorentz force.
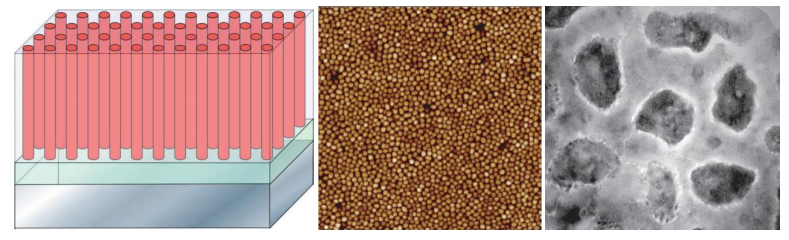
Wee et al. prepared [47] Ba2YNbO6 (BYNO) nanopillars in YBa2Cu3O7−δ (YBCO) films via a laser ablation method. The YBCO + BYNO films exhibited a superior Jc performance. Wee et al. [48] also reported another material with a structure of Ba2RETaO6.
Zhang et al. [30] reported a BaFeO2 nanopillars-embedded superconducting BaFe2As2 thin film. The nanopillars provided effective flux pinning centers and high critical current density in the film (Figure 9). The use of self-assembled nanopillars as correlated defects for strong vortex pinning provides an efficient method for increasing Jc without any apparent film thickne0ss dependence or need for post-processing.
Figure 9. A high angle annular dark field (Z-contrast) image showing the atomic structure of an epitaxial nanopillar in the Ba-122 film. Figure from Ref [30] reprinted with permission from the American Chemical Society.Several other pinning materials including Y2BaCuO5, BaZrO3, BaIrO3, Nd2O3, YSZ, Y2O3, and BaSnO3 have also been investigated. Kang et al. [49] found that short segments of a superconducting wire and annopillar arrays in thicker films (3 mm) may be used for large-scale applications that require a high supercurrent.
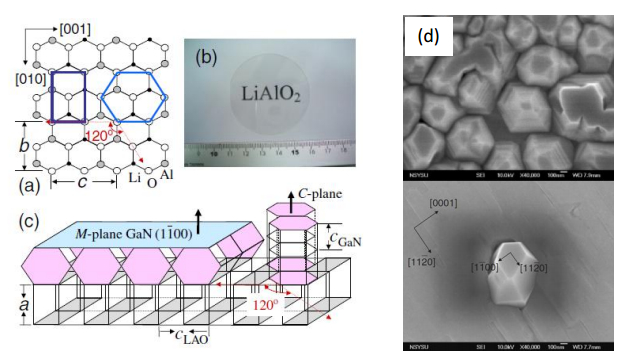
GaN-based quantum wells (QWs) are a promising candidate for optoelectronic devices, such as spin-polarized field effect transistors (spin-polarized FETs) [50]. When light-polarized M-plane GaN (Figure 10) and spin-polarized C-plane GaN are fabricated on the same substrate (e.g., γ-LiAlO2), two-phase GaN provides an opportunity to combine optoelectronics and spintronics to an optically controlled spin-polarized FET by the coupling of polarized light and the polarized spin of 2DEG [51]. Hsieh et al. showed that the formation of GaN nanopillars is through nucleation on hexagonal anionic bases of LiAlO2. This heterostructure might be used in optically controlled spintronic devices.
Figure 10. (a) Lattice structure of LAO (100). (b) High quality LAO wafer. (c) Schematic diagram of two-phase growth mode. (d) A 3D c-plane GaN nanopillar and a 2D M-plane GaN film are simultaneously grown on a γ-LiAlO2 substate, forming a 120o angle between them. Figure from Ref [51] reprinted with permission from the Japan Society of Applied Physics.The self-assembled nanopillars hold great promises for developing novel electronic devices. The nanostructures can form over a large area, either as an array or embedded in a matrix, and the vertical interfaces have a significant effect on the property of the film. In a two-phase film, the materials exhibit coupling effect of the two materials. Investigations which are ongoing in this field include the optimization of ordered structures and the design of two-phase systems for better parameter coupling, such as metallic-nnaopillar/semiconductors [52] and metallic-nanopillars/ceramic composites [53]. More applications of the these structures are expected—for instance, recently, SRO/SrTiO3 [54] and SRO/Pb(Zr, Ti)O3 [55] were demonstrated to be photosensitive materials; Co-BaZrO3 nanocomposite may be used for high density recording [56]. More applications in the energy field are expected. Furthermore, similar two phase systems have not been achieved in organic based materials since self-assembled nanopillars are still in their infancy. Realization of organic based two-phase, vertical nanocomposites may lead to new nanostructures with new electric or optical properties for multifunctional applications.
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
| [1] |
Sanchez C, Julian B, Belleville P, et al. (2005) Applications of hybrid organic-inorganic nanocomposites. J Mater Chem 15: 3559-3592. doi: 10.1039/b509097k
|
| [2] |
Wu Y, Livneh T, Zhang YX, et al. (2004) Templated Synthesis of Highly Ordered Mesostructured Nanowires and Nanowire Arrays. Nano Lett 4: 2337-2342. doi: 10.1021/nl048653r
|
| [3] |
Kresge CT, Leonowicz ME, Roth WJ, et al. (1992) Ordered mesoporous molecular sieves synthesized by a liquid-crystal template mechanism. Nature 359: 710-712. doi: 10.1038/359710a0
|
| [4] |
Göltner CG, Antonietti M (1997) Mesoporous materials by templaling of liquid crystalline phases. Adv Mater 9: 431-436. doi: 10.1002/adma.19970090516
|
| [5] |
Wang J, Tsung CK, Hayward RC, et al. (2005) Single-crystal mesoporous silica ribbons. Angew Chem 117:332-336. doi: 10.1002/ange.200461623
|
| [6] |
Brinker CJ, Lu Y, Sellinger A, et al. (1999) Evaporation-induced self-assembly: Nanostructures made easy. Adv Mater 11: 579-585. doi: 10.1002/(SICI)1521-4095(199905)11:7<579::AID-ADMA579>3.0.CO;2-R
|
| [7] |
Kickelbick G (2005) Formation of Hexagonal Mesoporous Silica in Submicrometer Channels. Small 1: 168-170. doi: 10.1002/smll.200400098
|
| [8] | Ku AY, Taylor ST, Loureiro SM (2005) Mesoporous silica composites containing multiple regions with distinct pore size and complex pore organization. J Am Chem Soc 127: 6934-6935. |
| [9] |
Platschek B, Petkov N, Bein T (2006) Tuning the Structure and Orientation of Hexagonally Ordered Mesoporous Channels in Anodic Alumina Membrane Hosts: A 2D Small-Angle X-ray Scattering Study. Angew Chem Int Ed 45: 1134-1138. doi: 10.1002/anie.200503301
|
| [10] |
Yao BD, Fleming D, Morris MA, et al. (2004) Structural Control of Mesoporous Silica Nanowire Arrays in Porous Alumina Membranes. Chem Mater 16: 4851-4855. doi: 10.1021/cm0487425
|
| [11] |
Cott DJ, Petkov N, Morris MA, et al. (2006) Preparation of oriented mesoporous carbon nano-filaments within the pores of anodic alumina membranes. J Am Chem Soc 128: 3920-3921. doi: 10.1021/ja058441b
|
| [12] |
Wu Y, Cheng G, Katsov K, et al. (2004) Composite mesostructures by nano-confinement. Nature Mater 3: 816-822. doi: 10.1038/nmat1230
|
| [13] |
Liang Z, Susha AS (2004) Mesostructured Silica Tubes and Rods by Templating Porous Membranes. Chem Eur J 10: 4910-4914. doi: 10.1002/chem.200400005
|
| [14] | Lai P, Hu MZ, Shi D, et al. (2008) STEM characterization on silica nanowires with new mesopore structures by space-confined self-assembly within nano-scale channels. Chem Comm 2008: 1338-1340. |
| [15] | Hu MZ, Shi D, Blom DA (2014) Nanostructured Mesoporous Silica Wires with Intrawire Lamellae via Evaporation-Induced Self-Assembly in Space-Confined Channels. J Nanomater 2014, Article ID 932160. |
| [16] | Israelachvili JN (1992) Intermolecular & Surface Forces (second edition), Academic Press: San Diego, USA. |
| [17] |
Lu Y, Ganguli R, Drewien CA, et al. (1997) Continuous formation of supported cubic and hexagonal mesoporous films by sol-gel dip-coating. Nature 389: 364-368. doi: 10.1038/38699
|
| [18] |
Yamaguchi A, Uejo F, Yoda T, et al. (2004) Self Assembly of Silica-Surfactant Nanocomposite in Porous Alumina Membrane. Nature Mater 3: 337-341. doi: 10.1038/nmat1107
|
| [19] |
Soni SS, Brotons G, Bellour M, et al. (2006) Quantitative SAXS Analysis of the P123/Water/Ethanol Ternary Phase Diagrams. J Phys Chem B 110: 15157-15165. doi: 10.1021/jp062159p
|
| [20] |
Yu CZ, Fan J, Tian BZ, et al. (2003) Synthesis of mesoporous silica from commercial poly(ethylene oxide)/poly(butylene oxide) copolymers: Toward the rational design of ordered mesoporous materials. J Phys Chem B 107: 13368-13375. doi: 10.1021/jp027046u
|
| [21] |
Holmqvist P, Alexandridis P, Lindman B (1998) Modification of the microstructure in block copolymer-water-“oil” systems by varying the copolymer composition and the “oil” type: Small-angle X-ray scattering and deuterium-NMR investigation. J Phys Chem B 102: 1149-1158. doi: 10.1021/jp9730297
|
| [22] |
Xiang H, Shin K, Kim T, et al. (2005) The influence of confinement and curvature on the morphology of block copolymers. J Poly Sci Part B-Poly 43: 3377-3383. doi: 10.1002/polb.20641
|
| 1. | Jinhua You, Heming Jia, Di Wu, Honghua Rao, Changsheng Wen, Qingxin Liu, Laith Abualigah, Modified Artificial Gorilla Troop Optimization Algorithm for Solving Constrained Engineering Optimization Problems, 2023, 11, 2227-7390, 1256, 10.3390/math11051256 | |
| 2. | Rong Zheng, Abdelazim G. Hussien, He-Ming Jia, Laith Abualigah, Shuang Wang, Di Wu, An Improved Wild Horse Optimizer for Solving Optimization Problems, 2022, 10, 2227-7390, 1311, 10.3390/math10081311 | |
| 3. | Honghua Rao, Heming Jia, Di Wu, Changsheng Wen, Shanglong Li, Qingxin Liu, Laith Abualigah, A Modified Group Teaching Optimization Algorithm for Solving Constrained Engineering Optimization Problems, 2022, 10, 2227-7390, 3765, 10.3390/math10203765 | |
| 4. | Shikai Wang, Honghua Rao, Changsheng Wen, Heming Jia, Di Wu, Qingxin Liu, Laith Abualigah, Improved Remora Optimization Algorithm with Mutualistic Strategy for Solving Constrained Engineering Optimization Problems, 2022, 10, 2227-9717, 2606, 10.3390/pr10122606 | |
| 5. | Di Wu, Honghua Rao, Changsheng Wen, Heming Jia, Qingxin Liu, Laith Abualigah, Modified Sand Cat Swarm Optimization Algorithm for Solving Constrained Engineering Optimization Problems, 2022, 10, 2227-7390, 4350, 10.3390/math10224350 | |
| 6. | Di Wu, Shuang Wang, Qingxin Liu, Laith Abualigah, Heming Jia, Navid Razmjooy, An Improved Teaching-Learning-Based Optimization Algorithm with Reinforcement Learning Strategy for Solving Optimization Problems, 2022, 2022, 1687-5273, 1, 10.1155/2022/1535957 | |
| 7. | Laith Abualigah, Khaled H. Almotairi, Mohamed Abd Elaziz, Multilevel thresholding image segmentation using meta-heuristic optimization algorithms: comparative analysis, open challenges and new trends, 2022, 0924-669X, 10.1007/s10489-022-04064-4 | |
| 8. | Rong Zheng, Heming Jia, Laith Abualigah, Qingxin Liu, Shuang Wang, An improved arithmetic optimization algorithm with forced switching mechanism for global optimization problems, 2022, 19, 1551-0018, 473, 10.3934/mbe.2022023 | |
| 9. | Jie Xing, Hanli Zhao, Huiling Chen, Ruoxi Deng, Lei Xiao, Boosting Whale Optimizer with Quasi-Oppositional Learning and Gaussian Barebone for Feature Selection and COVID-19 Image Segmentation, 2023, 20, 1672-6529, 797, 10.1007/s42235-022-00297-8 | |
| 10. | Shuang Wang, Abdelazim G. Hussien, Heming Jia, Laith Abualigah, Rong Zheng, Enhanced Remora Optimization Algorithm for Solving Constrained Engineering Optimization Problems, 2022, 10, 2227-7390, 1696, 10.3390/math10101696 | |
| 11. | Arti Tiwari, Kamanasish Bhattacharjee, Millie Pant, Jana Nowakova, Vaclav Snasel, 2022, Chapter 27, 978-3-030-84909-2, 253, 10.1007/978-3-030-84910-8_27 | |
| 12. | Rong Zheng, Heming Jia, Laith Abualigah, Shuang Wang, Di Wu, An improved remora optimization algorithm with autonomous foraging mechanism for global optimization problems, 2022, 19, 1551-0018, 3994, 10.3934/mbe.2022184 | |
| 13. | Jie Xing, Xinsen Zhou, Hanli Zhao, Huiling Chen, Ali Asghar Heidari, Elite levy spreading differential evolution via ABC shrink-wrap for multi-threshold segmentation of breast cancer images, 2023, 82, 17468094, 104592, 10.1016/j.bspc.2023.104592 | |
| 14. | Essam H. Houssein, Doaa A. Abdelkareem, Marwa M. Emam, Mohamed Abdel Hameed, Mina Younan, An efficient image segmentation method for skin cancer imaging using improved golden jackal optimization algorithm, 2022, 149, 00104825, 106075, 10.1016/j.compbiomed.2022.106075 | |
| 15. | Hongmin Chen, Zhuo Wang, Heming Jia, Xindong Zhou, Laith Abualigah, Hybrid Slime Mold and Arithmetic Optimization Algorithm with Random Center Learning and Restart Mutation, 2023, 8, 2313-7673, 396, 10.3390/biomimetics8050396 | |
| 16. | D. Rasi, M. AntoBennet, P. N. Renjith, M. R. Arun, D. Vanathi, YOLO Based Deep Learning Model for Segmenting the Color Images, 2023, 11, 2347-470X, 359, 10.37391/ijeer.110217 | |
| 17. | Yijie Zhang, Yuhang Cai, Adaptive dynamic self-learning grey wolf optimization algorithm for solving global optimization problems and engineering problems, 2024, 21, 1551-0018, 3910, 10.3934/mbe.2024174 | |
| 18. | Laith Abualigah, Ali Diabat, Cuong-Le Thanh, Samir Khatir, Opposition-based Laplacian distribution with Prairie Dog Optimization method for industrial engineering design problems, 2023, 414, 00457825, 116097, 10.1016/j.cma.2023.116097 | |
| 19. | Shuang Wang, Heming Jia, Abdelazim G Hussien, Laith Abualigah, Guanjun Lin, Hongwei Wei, Zhenheng Lin, Krishna Gopal Dhal, Boosting aquila optimizer by marine predators algorithm for combinatorial optimization, 2024, 11, 2288-5048, 37, 10.1093/jcde/qwae004 | |
| 20. | Achraf Ben Miled, Mohammed Ahmed Elhossiny, Marwa Anwar Ibrahim Elghazawy, Ashraf F. A. Mahmoud, Faroug A. Abdalla, Enhanced Chaos Game Optimization for Multilevel Image Thresholding through Fitness Distance Balance Mechanism, 2024, 14, 1792-8036, 14945, 10.48084/etasr.7713 | |
| 21. | Xianwen Wang, Yingyuan Yang, Minhang Nan, Guanjun Bao, Guoyuan Liang, Optimum Multilevel Thresholding for Medical Brain Images Based on Tsallis Entropy, Incorporating Bayesian Estimation and the Cauchy Distribution, 2025, 15, 2076-3417, 2355, 10.3390/app15052355 |
Figures(7)
Michael Z. Hu, Peng Lai. Substrate effect on nanoporous structure of silica wires by channel-confined self-assembly of block-copolymer and sol-gel precursors[J]. AIMS Materials Science, 2015, 2(4): 346-355. doi: 10.3934/matersci.2015.4.346
DownLoad: 