Interstitial Pressure And Fluid Motion In Tumor Cords

1.   Introduction

Laboratory experiments have revealed that the intracellular bacterium Wolbachia, deliberately introduced in Aedes aegypti female mosquitoes (the major transmitters of dengue and other vector-borne infections), is capable of suppressing or even blocking the development of the dengue virus inside the mosquito ^[1,2,3,4]. This naturally entails the reduced rate of the virus transmission towards human hosts and leads to a considerable reduction of the dengue morbidity in human populations.

Wolbachia is transmitted maternally from the female insect to her offspring and grants a reproductive advantage to its carriers relative to wild insects that are Wolbachia-free. The reproductive advantage of Wolbachia-carrying insects is attributed to the phenotype of cytoplasmic incompatibility (CI, see Table 1), according to which the cross-mating between Wolbachia-carrying males and wild females renders inviable eggs thus reducing the non-Wolbachia offsprings and favoring the invasion of the bacterium in wild insect populations.

Wolbachia-based biocontrol of dengue has recently emerged as a novel method for prevention this viral disease, and it operates by releases of Wolbachia-infected mosquitoes targeting to crush the wild populations ^[5,6]. The releases of Wolbachia-infected Ae. aegypti mosquitoes have the potential to ultimately annihilate the local circulation of the dengue virus by a combination of three basic mechanisms:

$–$ direct reduction and/or blocking of mosquito's ability to transmit the virus;

$–$ reduction of the vectorial density by suppressing mosquito populations;

$–$ shortening the mosquito lifespan so that she cannot mature the viral infection and dies before becoming infectious.

Depending on the Wolbachia strain employed for biocontrol, a stronger or weaker impact on the dengue transmissibility can be expected. In particular, wMelPop strain of Wolbachia confer stronger inhibition of dengue virus replication in mosquitoes than wMel strain does ^[3,5,7,8].

On the other hand, Wolbachia infection caused by wMelPop strain imposes higher fitness costs than does wMel strain on transinfected insects, such as increased adult mortality, lower fecundity, lengthened larval development time, and reduced survival of quiescent eggs in diapause ^[5,6]. Due to the lower comparative fitness, wMelPop Wolbachia invasion of the natural mosquito population is harder to achieve, sustain, and protect from occasional immigration of wild insects. Nonetheless, the wMelPop strain can reduce the total size of Ae. aegypti population to a greater extent, and the impact of wMelPop-based biocontrol can be seen earlier than in the case of wMel-based biocontrol.

Regardless of the strain, Wolbachia-based biocontrol is aimed at replacing the wild mosquitoes, which are capable of transmitting dengue, with Wolbachia-carrying insects, whose capacity of the disease transmission is very low. To achieve the population replacement, considerable quantities of transinfected insects are mass-reared in a destined facility and then the field releases are performed. This general methodology raises various pertinent questions of different nature, and some of them can be answered by applying the mathematical modeling approach.

In the present study, we have tried to assess the impact of two Wolbachia strains, wMelPop and WMel, on dengue prevention and control and to produce some useful recommendations for Wolbachia-based biocontrol from the standpoint of mathematical modeling and dynamic optimization. Our main intention was to bring forth a methodology capable of providing quantitative estimations of the three key metrics of Wolbachia-based biocontrol when the initial size of the wild mosquito population to be replaced can be fairly assessed. The proposed methodology stems from the dynamic optimization approach and allows to design the strain-dependent optimal release programs that can be characterized by the following three quantifications: (a) optimal time of effective releases; (b) a total number of Wolbachia-carrying insects to be mass-reared, and (c) the estimated number of human infections to be prevented.

The quantitative outcomes of our study have resulted unbiased in the sense that we refrain from recommending univocally one particular strain for Wolbachia-based biocontrol given that each of them exhibits advantages and drawbacks. Nonetheless, our qualitative arguments can be accounted for when the ultimate choice of an appropriate strain should be taken by the decision-makers.

This paper is organized as follows. In Section 2 we introduce a dengue transmission model that is designed on the basis of the sex-structured population dynamics model involving Wolbachia proposed by Campo-Duarte et al. ^[9]. This epidemiological model of agrees with other dengue transmission models accounting for Wolbachia-carrying vectors in the sense of having four possible outcomes: with or without Wolbachia and with or without dengue ^[10,11,12]. To reach the desired outcome (with Wolbachia and without dengue), we propose to employ the dynamic optimization approach based on the optimal control and described in Section 3. Major results related to the design and evaluation of the strain-based optimal release programs are engrossed in Section 4, while the practical recommendations are recapitulated in Section 5.

2.   Dengue transmission model involving Wolbachia

Epidemiological models describing dengue transmission dynamics traditionally include Susceptible-Infected-Recovered (SIR) compartments for human hosts and Susceptible-Infected (SI) compartments for female mosquitoes or vectors, which act as transmitters of the dengue virus ^[13]. If the vector population is subdivided into two competing groups of mosquitoes – one consisting of wild insects and another comprising Wolbachia-carriers – each group of vectors must be also divided into Susceptible-Infected compartments. Furthermore, these two groups of vectors compete for the same food resources, breeding sites, and mating opportunities. These aspects should be depicted in the population dynamics model describing mosquitoes' growth.

In this section, we outline the sex-structured model depicting the population dynamics of wild and Wolbachia-carrying mosquitoes that was proposed and examined by Campo-Duarte et al. ^[9] (Subsection 2.1). Further on, this model is laid into the basis of the vector-host model describing the dengue transmission dynamics (Subsection 2.2), which is then analyzed in Subsection 2.3.

2.1.   Population dynamics of wild and Wolbachia-carrying mosquitoes

Let $M_n(t), F_n(t)$ and $M_w(t), F_w(t)$ denote, respectively, the densities of wild and Wolbachia-infected male and female mosquitoes present in the target locality at the day $t$. Recently, Campo-Duarte et al. ^[9] have proposed the following sex-structured mathematical model without pair formation that describes the interaction of wild and Wolbachia-carrying mosquito population:

The recruitment rates of new individuals (i.e., the positive terms in the right-hand sides of (2.1)) are modeled using the so-called "harmonic form" of the birth function, that is, $\mathcal{H}(M, F): = \dfrac{M F}{M+F}$ where $M$ and $F$ denote the densities of adult male and female individual that are available for mating. Notably, Caswell & Weeks ^[14] have provided solid arguments that the harmonic form is a fitting choice for modeling the birth functions, as it fulfils a number of criteria for sexual reproduction. In particular, $\mathcal{H}(M, F)$ is non-negative and increasing with respect to male and female densities, and $\mathcal{H}(M, F) \to 0$ whenever $M \to 0$ or $F \to 0$.

In the dynamical system (2.1), the subindexes $\{n, w \}$ indicate that the key parameters $\epsilon, \rho, \mu, \delta > 0$ belong to either uninfected or Wolbachia-infected mosquitoes, respectively. Namely, $\epsilon_{\{n, w \}}/(1-\epsilon_{\{n, w \}})$ express the adult sex ratio in offspring; $\rho_{\{n, w \}}$ stands for the number of viable eggs laid by one female mosquito in average per day, while $\mu_{\{n, w \}}$ and $\delta_{\{n, w \}}$ are sex-specific mortality rates for males and females. There is evidence ^[15] that mating females have higher longevity than mating males; therefore, it is assumed that

The exponential term in the recruitment part of all four equations of (2.1) expresses the survival of eggs to adulthood through larvae and pupae stages and the parameter $\sigma > 0$ regulates the larval development under density dependence and competition. Thus, higher values of $\sigma$ imply stronger competition and fewer breeding sites, while its lower values permit that a larger fraction of eggs survives to adulthood.

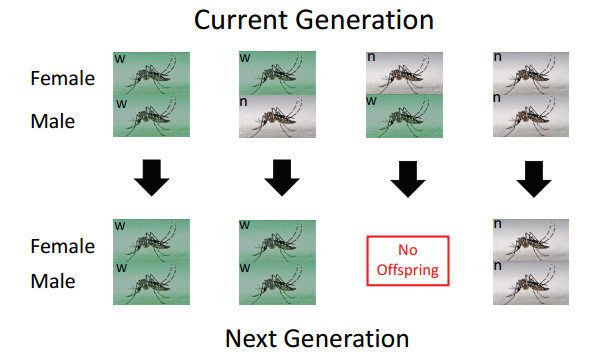
Equations (2.1a)-(2.1b) basically state that wild males and females are progenies of wild mosquitoes, $M_n$ and $F_n$. On the other hand, equations (2.1c)-(2.1d) reflect the reproductive phenotype of cytoplasmic incompatibility induced by Wolbachia together with its maternal transmission ^[5,16]. Namely, Wolbachia-infected males and females are produced by Wolbachia-carrying females $F_w$ after their successful matings with either wild or Wolbachia-carrying males, $M_n$ and $M_w$ (see Table 1).

Survival and persistence of both mosquito sub-populations are guaranteed by the following conditions ^[9] imposed on the parameters of the model (2.1):

where the quantities $\mathcal{Q}_n$ and $\mathcal{Q}_w$ are referred to as basic offspring numbers of uninfected and Wolbachia-infected mosquitoes, respectively. Conditions (2.2) are quite natural and simply imply that, in the absence of density dependence, mosquitoes' birth rates $\rho_n, \rho_w$ are always greater than the sum of their death rates, weighted by a possible sex-ratio distortion.

Note that system (2.1) is neither strictly mutualistic nor competitive in a general sense. However, uninfected males and females do exhibit obligatory mutualism induced by the CI-phenotype (see Eqs. (2.1a)-(2.1b) and Table 1), while the presence of Wolbachia-infected males is facultative (not obligatory) for survival and persistence of Wolbachia-carriers, both males and females. In essence, Eqs. (2.1c)-(2.1d) state that Wolbachia-infected offsprings result from successful mating of Wolbachia-carrying females with either infected or uninfected males. Figure 1 clearly illustrates the reproductive preeminence of Wolbachia-carrying mosquitoes granted by the CI-phenotype and maternal transmission: every posterior generation has a greater share of Wolbachia-carriers than the previous one.

On the other hand, the prime advantage of wild mosquitoes with respect to Wolbachia-carriers consists in their unaltered individual fitness since Wolbachia reduces the individual fitness of its hosts ^[5]. Namely, wild females are more fertile than Wolbachia-infected ones, and wild mosquitoes (both males and females) live longer than their Wolbachia-infected coevals. The latter is expressed by the following conditions imposed on the mosquito-related parameters of the model (2.1):

Model (2.1) expresses that wild mosquitoes $M_n, F_n$ compete with Wolbachia-carriers for "better mating options", and they tend to decrease their densities for higher densities of $M_w, F_w$. The latter is attested by the following relationships:

for all positive $M_n, F_n, M_w, F_w$. Alternatively, Wolbachia-carriers $M_w$ and $F_w,$ despite bearing reduced fitness, tend to increase their density for lower densities of wild females in the sense that

for all positive $M_n, F_n, M_w, F_w$. Therefore, model (2.1) captures the frequency-dependence and exhibits the property of bistability, which is inherent to other models describing Wolbachia invasion either in terms of the infection frequencies ^[17,18,19] or competitive population dynamics ^{[20,21,22,23,24,25,26]}. The bistability property of Wolbachia invasion in wild insect populations fully agrees with the principle of competitive exclusion ^[27] according to which only one of two species competing for the same resources should ultimately survive. This property and other characteristic features of the system (2.1) have been established by Campo-Duarte et al. ^[9] and we state here some cardinal results that are necessary for further inferences.

Proposition 1 (^[9]). Under the conditions (2.2), (2.3) and for any nonzero initial condition $\big(M_n(0), F_n(0), M_w(0), F_w(0) \big) \in \mathbb{R}^4_+$ the ODE system (2.1) has a unique nonnegative and bounded solution that exists for all $t > 0$ and admits the following estimate:

Additionally, the ODE system (2.1) has three nonnegative steady states in $\mathbb{R}^4_+$ and exhibits bistability in the following sense:

1. A Wolbachia-free equilibrium

that is locally asymptotically stable in $\mathbb{R}_{+}^{4}$ (nodal attractor) and is reachable at low frequencies of Wolbachia-carriers.

2. A Wolbachia-invasion equilibrium

that is locally asymptotically stable in $\mathbb{R}_{+}^{4}$ (nodal attractor) and is reachable at high frequencies of Wolbachia-carriers.

3. A strictly positive coexistence equilibrium $E^c = \big(M_n^c, F_n^c, M_w^c, F_w^c \big)$ with coordinates

that is unstable (saddle point) and exists only if

It was also proved ^[9] that relationships (2.8) hold under the conditions (2.3). Furthermore, the quantity $\mathcal{R}_0^w$ can be viewed as the basic reproductive ratio of Wolbachia infection among the mosquito population. Indeed, the numerator of $\mathcal{R}_0^w$ in (2.8) expresses an average number of Wolbachia-carrying female mosquitoes produced by one Wolbachia-infected female mosquito during her lifespan while the denominator of $\mathcal{R}_0^w$ stands for an average number of wild female mosquitoes produced by one wild female mosquito during her lifespan. Thus, $\mathcal{R}_0^w < 1$ fully agrees with the reduced individual fitness of Wolbachia-carrying mosquitoes.

In the next section we propose a dengue transmission model where the ODE system (2.1) describes the population dynamics of two interacting Ae. aegypti sub-populations – wild and Wolbachia-carrying mosquitoes.

2.2.   Vector-host model with Wolbachia

The dengue virus (DENV) is transmitted from an infectious human individual to a female mosquito during her blood-feeding. The virus then replicates inside the mosquito and can be transmitted to a susceptible human host during subsequent blood-feeding. It should be emphasized that male mosquitoes never become infected with DENV or other arboviruses since they do not ingest human blood. There is solid evidence that wMel Wolbachia strain induces resistance to dengue virus in Ae. aegypti females ^[1,3,5], while a more virulent strain wMelPop Wolbachia is even capable of blocking the dengue virus ^[4,5,7]. These factors should reduce the dengue incidence among the human population since Wolbachia detains or inhibits the replication of DENV within the mosquito that minifies the number of effective contacts (through infectious bites) between the human hosts and Ae. aegypti females.

Let us suppose that at the day $t \geq 0$ there are two populations present in some target locality: the mosquito population $N_m(t)$ defined in (2.4) with time-variable size, and the population of human individuals $N_h$ that is assumed essentially invariant in time, i.e.,

In the above expression, three disjoint compartments $S(t), I(t),$ and $R(t)$ represent, respectively, the numbers of susceptible, infectious, and recovered human individuals.

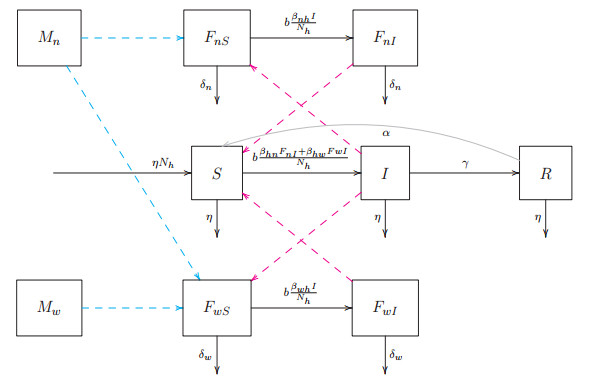
To develop the modeling framework of dengue transmission accounting for wild and Wolbachia-carrying vectors, we suppose that each group of female mosquitoes $F_n$ and $F_w$ is further subdivided into two disjoint compartments:

where the subscript $S$ indicates the female mosquitoes uninfected with dengue (both Wolbachia-carrying and wild insects), whereas the subscript $I$ indicates the dengue-infected female mosquitoes (both Wolbachia-carrying and wild vectors) that are capable of transmitting the DENV virus to the human hosts.

In order to keep our model mathematically tractable, we introduce the following general assumptions:

(ⅰ) Both populations $N_h$ and $N_m$ are well-mixed and homogeneous in terms of attraction, susceptibility, and exposure to the dengue virus.

(ⅱ) Virus incubation periods in mosquitoes and human hosts are disregarded.

(ⅲ) There is no mortality due to the dengue disease for human hosts.

(ⅳ) Recovered human hosts may become infected only with heterologous DENV serotypes after losing their temporary cross-immunity.

(ⅴ) Transovarial or vertical DENV transmission by female mosquitoes is ignored.

Remark 1. Assumptions (i)–(iii) are quite typical for many dengue transmission models ^[13,28]. Assumption (iv) is plausible if there are different DENV serotypes circulating in the environment ^[29]. Furthermore, assumption (v) stays in line with the review performed by Grunnill & Boots ^[30] according to which vertical transmission of DENV is infrequent in Ae. aegypti females; therefore, the importance of transovarial transmission is insignificant for epidemiological persistence of dengue at a local or regional level.

Using the idea of Cardona-Salgado et al. ^[10], the dynamics of dengue transmission between human hosts and two mosquito populations can be described by the following ODE system:

Equations (2.10a)-(2.10c) refer to the traditional framework of SIR-models for the human population (Susceptible-Infectious-Recovered individuals) and verify the relationship (2.9). In these equations, $\eta > 0$ denotes the rate of demographic inflow and outflow (birth/death rates) of the human population, while $\alpha \geq 0$ expresses the rate of loss of the temporary cross-immunity by human hosts. Equation (2.10c) states that human individuals recover from the disease after $1/\gamma$ days and then become susceptible to heterologous DENV serotypes after $1/\alpha$ days. If there are different DENV serotypes circulating simultaneously in the environment, then we set $\alpha > 0$ and thus open the possibility of re-infection after the loss of cross-immunity. On the other hand, the dominance of one particular DENV serotype implies that $\alpha = 0$. In other words, recovered human hosts become completely immune to homologous DENV serotype. The detailed rationale of this modeling approach is attributed to Barrios et al. ^[29] (see Remark 1 in that work).

Our principal attention will be centered on the dynamics of human DENV infections represented in the model (2.10) by the class $I$. It is worthwhile to point out that the evolution of human infections exhibits much faster dynamics than the demographic changes in the human population. This was the reason for assuming the total size of the human population essentially invariant in time (cf. the relationship (2.9)). However, the duration of DENV infections in humans is in the range of days or weeks, so it is comparable to the lifespan of mosquitoes. Therefore, the measures of external control intervention applied to the mosquito population (such as the releases of Wolbachia-carrying insects) should be reflected on the dynamics of infectious people bearing a similar (or a bit faster) timescale with the dynamics of mosquitoes.

The core parameter related to the disease transmission is the biting rate $b > 0$ that expresses the number of successful bites (or blood meals) that one female mosquito takes on average per day in order to mature her eggs. It is worthwhile to note that the presence of DENV within mosquitoes does not affect their biting habits ^[31], while Wolbachia infection does not alter the host-seeking abilities of female mosquitoes ^[32,33]. Therefore, we can assume the same biting rate $b$ for all effective contacts between female mosquitoes and human hosts, namely, the bites received by human hosts, and the bites taken by either wild or Wolbachia-carrying female mosquitoes.

Susceptible human hosts become infected with dengue virus after receiving bites from infectious female mosquitoes $F_{nI}$ and $F_{wI}$ with effective contact rates $\beta_{hn}$ and $\beta_{hw}$, respectively (see equations (2.10a)-(2.10b)). Here we assume that a human host becomes infected with the same probability after being bitten by an infectious vector (with or without Wolbachia) since there is no evidence attesting otherwise. However, there is sufficient evidence that the DENV pathogen is passed from infectious human hosts to susceptible female mosquitoes $F_{nS}$ and $F_{wS}$ with different effective contact rates $\beta_{nh}$ and $\beta_{wh}$ (cf. equations (2.10f)-(2.10i)), because Wolbachia reduces or even blocks the DENV replication within mosquito and thus suppresses the development of viral load sufficient for transmission ^[1,3,4,5,7]. Therefore, we introduce the following relationships:

Another important feature regarding the virus transmission probabilities $\beta_{hn}, \beta_{hw}$ and $\beta_{nh}, \beta_{wh}$ is that they denote the so-called effective contact rates. In other words, they account only for infectious bites, i.e., those leading to new infections when the viral load becomes sufficient for transmission after the extrinsic and intrinsic virus incubation in mosquitoes and human hosts, respectively. This particular way of defining the virus transmission probabilities ($\beta_{hn}, \beta_{hw}, \beta_{nh}, \beta_{wh}$) compensates the omission of the virus incubation periods in the model (2.10) (see Assumption (ⅱ) on page 2959).

After taking a bite on an infectious human individual, a small share of wild mosquitoes and the majority of Wolbachia-carriers cannot develop the viral load sufficient for transmitting the virus to other human hosts. In this sense, such female mosquitoes remain latent or non-infectious during their lifetime and do not contribute to the disease propagation. Only the females that do develop the viral infection are considered capable of producing new infections in the human population. Likewise, some human individuals, after receiving a bite from an infectious mosquito, may not develop the viral load sufficient for becoming infectious. These features are contemplated in the definitions of $\beta_{hn}, \beta_{hw}, \beta_{nh},$ and $\beta_{wh}$ as effective contact rates, i.e., those really leading to the appearance of new infections.

It is easy to check that by summing up the equations (2.10f) and (2.10g) we obtain the equation (2.1b), while the sum of (2.10h) and (2.10i) results in (2.1d). Figure 2 exhibits the flowchart diagram of the vector-host model (2.10) where solid lines indicate transitions from one compartment to another, dashed blue-colored lines depict successful matings (resulting in viable offspring), and dashed red-colored lines highlight the pathogen transmission.

Taking into account the properties of the model (2.1) summarized in Proposition 1, it is easy to see that state variables

of the model (2.10) are defined over the closed and bounded domain $\Omega_{\bf{X}} \subset \mathbb{R}_+^9$ given by

This domain is invariant in the sense that all trajectories of (2.10) engendered by an initial condition ${\bf{X}}(0) \in \Omega_{\bf{X}}$ remain in $\Omega_{\bf{X}}$ for all $t > 0$. Therefore, it is safe to affirm that the epidemiological ODE system (2.10) is mathematically well-posed.

The asymptotic behavior of trajectories of the dengue transmission model is addressed in the next subsection section, where we also derive the basic reproductive number and calculate locally stable equilibria of the ODE system (2.10).

2.3.   Local analysis of the vector-host model

One of the core metrics in epidemiology is the so-called basic reproduction number $\mathscr{R}_{0}$ that expresses the expected number of secondary infections produced, in a completely susceptible population, by one infective individual during his/her entire period of infectiousness ^[34]. In other words, $\mathscr{R}_{0}$ characterizes the speed with which an infection propagates through a host population.

For compartmental epidemiological models, such as the model (2.10), the basic reproductive number $\mathscr{R}_{0}$ can be obtained as the largest eigenvalue (or spectral radius) of the next-generation matrix evaluated at the disease-free steady state ^[35]. However, due to the bistable nature of mosquito population dynamics (2.1), the epidemiological system (2.10) has two disease-free equilibria. One of them corresponds to the persistence of wild mosquitoes $(M_n, F_n)$ and another complies with the population replacement and survival of Wolbachia-carriers $(M_w, F_w)$. Using the conventional approach developed by Cardona-Salgado et al. ^[10], both disease-free steady states of (2.10) can be written in a closed form as

where $\phi \in \{ 0, 1 \}$ is an auxiliary binary variable.

The application of the next-generation method ^[35] to the symbolic form of ${\bf{E}}^0$ given by (2.14), renders the closed form of the basic reproductive number also parameterized by $\phi \in \{ 0, 1 \}:$

Meticulous details regarding the calculation of $\mathscr{R}_{0}$ are omitted here; however, interested readers may consult a step-by-step procedure applied to a vector host model involving only female mosquitoes and developed by Cardona-Salgado et al. ^[10] (see Appendix A in that work). It is worth pointing out that in the case of vector-borne diseases, there are two stages involved in the pathogen transmission from one human host to another (human-to-vector and vector-to-human), and that $\mathscr{R}_{0}$ given by (2.15) stands the expected number of secondary human infections produced, in a completely susceptible human population, by one infective human individual during his/her entire period of infectiousness.

From the closed form (2.15) it follows that, in the absence of Wolbachia-infected mosquitoes ($\phi = 1$), we directly obtain the basic reproductive number for traditional dengue transmission models of SIR(S)-SI type ^[28,34], that is,

Here, $\dfrac{F^{\sharp}_n}{N_h}$ stands for the so-called "vector density" that expresses the average number of wild female mosquitoes per one human host. The numerator of (2.15) contains parameters referring to the disease transmission, while its denominator contains parameters related to the disease transition.

Similarly, in the absence of wild mosquitoes ($\phi = 0$), we obtain from (2.15)

where $\dfrac{F^{\sharp}_w}{N_h}$ expresses the average number of Wolbachia-carrying female mosquitoes per one human host (i.e., vector density with respect to Wolbachia-carriers). In virtue of the relationships (2.3) and (2.11) it holds that

Let us also recall that $\mathscr{R}_{0}$ acts as a threshold value for determination of stability of the disease-free and endemic equilibria for dengue transmission models ^[11,34], in the following sense:

● $\mathscr{R}_{0} < 1$ implies that an infectious human individual induces, on average, less than one secondary infection during his/her period of infectiousness, and the disease will eventually disappear.

● $\mathscr{R}_{0} > 1$ implies that an infective human individual induces, on average, more than one secondary infection, and the disease will persists in the host population.

Our dengue transmission model (2.10) inherits bistability from the model (2.1) that describes the population dynamics of two groups of vectors capable of transmitting the DENV pathogen to human individuals and vice versa. Therefore, besides having two disease-free equilibria, it is also expected to have two disjoint endemic equilibria ${\bf{E}}^{\sharp}_{n}$ and ${\bf{E}}^{\sharp}_{w}$ corresponding to the persistency of either wild or Wolbachia-infected mosquito population. Thus, the evolution of the dengue transmission system (2.10) essentially depends on the ultimate survival or extinction of either wild or Wolbachia-carrying mosquito population.

Let us suppose that wild mosquitoes persist in the target locality and Wolbachia-carrying mosquitoes eventually become extinct, that is, $\phi = 1$, meaning that

In this case, the dengue transmission system (2.10) evolves towards one of the following equilibria:

● A disease-free equilibrium ${\bf{E}}^{0}_{n} = \big(N_h, 0, 0, M_n^{\sharp}, 0, F_n^{\sharp}, 0, 0, 0 \big)$ if $\mathscr{R}_{0} = \mathscr{R}^{n}_{0} < 1.$

● An endemic equilibrium ${\bf{E}}^{\sharp}_{n} = \big(S_{n}^{\sharp}, I_{n}^{\sharp}, R_{n}^{\sharp}, M_{n}^{\sharp}, 0, F_{nS}^{\sharp}, F_{nI}^{\sharp}, 0, 0 \big)$ if $\mathscr{R}_{0} = \mathscr{R}^{n}_{0} > 1$.

The coordinates $M_n^{\sharp}$ and $F_n^{\sharp}$ of ${\bf{E}}^{0}_{n}$ are defined by (2.5), while the coordinates of ${\bf{E}}^{\sharp}_{n}$ are positive solutions of the nonlinear system composed by six algebraic equations:

This system can be solved by applying the stylized method presented by Cardona-Salgado et al. ^[10] (see Appendix B in that work), and we display here the final outcomes:

where $F_n^{\sharp}$ and $\mathscr{R}^{n}_{0}$ are given by (2.5) and (2.16) in terms of the model's parameters, while the new quantity

is introduced in (2.18b), (2.18e), (2.18f) to express the average number of infectious bites $b \beta_{nh}$ taken by a susceptible wild female mosquito (not infected with DENV) on infectious human hosts during her lifespan $1/\delta_n$. It should be noted that the coordinates $I_n^{\sharp}, M_n^{\sharp}$ are directly expressed in terms of the model's parameters, whereas other components of ${\bf{E}}^{0}_{n}$ are given in function of $I_n^{\sharp}$, which stays positive while $\mathscr{R}^{n}_{0} > 1$. Furthermore, it is easy to check that it holds

Let us now suppose that Wolbachia-carrying mosquitoes persist in the target locality and wild mosquitoes eventually become extinct, that is, $\phi = 0$, meaning that

In this case, the dengue transmission system (2.10) evolves towards one of the following equilibria:

● A disease-free equilibrium ${\bf{E}}^{0}_{w} = \big(N_h, 0, 0, 0, M_w^{\sharp}, 0, 0, F_w^{\sharp}, 0 \big)$ if $\mathscr{R}_{0} = \mathscr{R}^{w}_{0} < 1.$

● An endemic equilibrium ${\bf{E}}^{\sharp}_{w} = \big(S_{w}^{\sharp}, I_{w}^{\sharp}, R_{w}^{\sharp}, 0, M_{w}^{\sharp}, 0, 0, F_{wS}^{\sharp}, F_{wI}^{\sharp} \big)$ if $\mathscr{R}_{0} = \mathscr{R}^{w}_{0} > 1$.

The components $M_w^{\sharp}$ and $F_w^{\sharp}$ of ${\bf{E}}^{0}_{n}$ are defined by (2.6), while the coordinates of ${\bf{E}}^{\sharp}_{w}$ are positive solutions of the following nonlinear system:

Using the same method attributed to Cardona-Salgado et al. ^[10] we can calculate the components of ${\bf{E}}^{\sharp}_{w}$ and then display them in a similar way to (2.18):

Here $F_w^{\sharp}$ and $\mathscr{R}^{w}_{0}$ are given by (2.6) and (2.17) in terms of the model's parameters and we have introduced in (2.20b), (2.20e), (2.20f) a resembling quantity

that expresses the average number of infectious bites $b \beta_{wh}$ taken by a susceptible Wolbachia-carrying female mosquito (not infected with DENV) on infectious human hosts during her lifespan $1/\delta_w$. Likewise the previous case with $\phi = 1$, the coordinates $I_w^{\sharp}, M_w^{\sharp}$ are directly expressed in terms of the model's parameters, whereas other components of ${\bf{E}}^{0}_{w}$ are given in function of $I_w^{\sharp}$, which stays positive while $\mathscr{R}^{w}_{0} > 1$. Again, one can easily check the validity of the following relationships:

Thus, we finally have four possible equilibria of the vector-host model (2.10) that includes two mosquito populations: ${\bf{E}}^{0}_{n}, {\bf{E}}^{\sharp}_{n}, {\bf{E}}^{0}_{w}$ and ${\bf{E}}^{\sharp}_{w}$. To analyze the local stability of these four equilibria, the standard procedure consists in the calculation of eigenvalues of the Jacobian matrices of the right-hand sides of (2.10) evaluated at each equilibrium. However, this procedure is rather knotty and cumbersome from the computational standpoint. As an alternative, we propose to use the Monte Carlo method ^[36,37], adopted for population and epidemiological models ^[9,10,23].

To implement the Monte Carlo method, let us recall that the coordinates of all four steady states can be expressed explicitly in terms of seventeen positive parameters

related to the dengue transmission model (2.10). The baseline numerical values of these seventeen parameters, as well as their referenced ranges, are provided in Tables 3 and 4 (see Section 4 below).

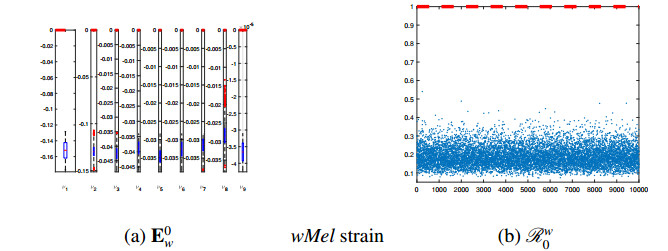
The first step was to define a sampling pool $\mathbb{S} = \prod \limits_{i = 1}^{17} P_i \in \mathbb{R}^{17}_+$ as a Cartesian product of seventeen closed intervals of the form $P_i = [p_i - \theta p_i, p_i + \theta p_i ]$ where each $p_i, i = 1, \ldots, 17$ stands for the baseline value of one single parameter (see Tables 3 and 4) and $\theta > 0$ defines the range of variation. Our sampling embraced $10^{4}$ assorted scenarios $S = (s_1, \ldots, s_{17}) \in \mathbb{S}$ where each $s_i \in P_i, i = 1, \ldots 17$ was chosen in random for $\theta = 0.15$ (that is, with $15$% deviation from the baseline values) under uniform distribution with no correlation between parameters. The result of numerical simulations are displayed by Figures 3, 4, and 5 with explanation given below.

We have conducted the simulations for a larger number of trials but to keep the graphical presentation cleaner the results displayed in Figure 3 correspond to the total of $10^4$ attested trials. The well-posedness of this approach was guaranteed by verifying repeatedly the following conditions before each trial:

For numerical simulations, we have considered two Wolbachia strains, wMelPop and wMel, using their underlying parameter values from Table 4, and each trial $k = 1, 2, \ldots, 10^4$ comprised the accomplishment of three consecutive actions:

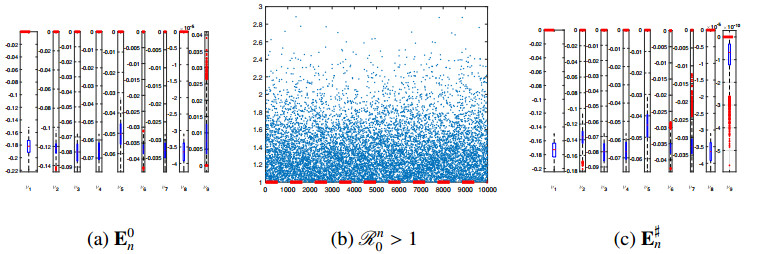
1. The values of $\mathscr{R}^{n}_{0}$ and $\mathscr{R}^{w}_{0}$ were computed by formulas (2.16) and (2.17) for each strain and then plotted versus the trial number $k = 1, 2, \ldots, 10^4$ (see Figure 3(b) for $\mathscr{R}^{n}_{0}$ and Figures 4(b), 5(b) for $\mathscr{R}^{w}_{0}$ corresponding to wMelPop and wMel Wolbachia strains, respectively).

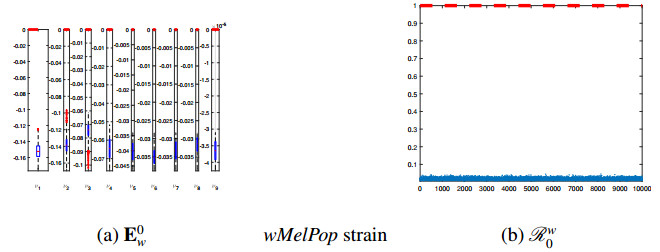
2. For each Wolbachia strain, the real parts of nine eigenvalues of the Jacobian matrices of (2.10) have been evaluated in the disease-free steady states, ${\bf{E}}^0_{n}$ and ${\bf{E}}_w^{0}$, and then their distributions were plotted (see Figure 4(a) for ${\bf{E}}^0_{n}$ and Figures 4(a), 5(a) corresponding to wMelPop and wMel Wolbachia strains, respectively).

3. For each Wolbachia strain, the components of endemic steady states ${\bf{E}}^{\sharp}_{n}$ and ${\bf{E}}^{\sharp}_{w}$ were calculated according to formulas (2.18) and (2.20) and then tested for positiveness. Only for attested points, the Jacobian of (2.10) was evaluated, the real parts of its eigenvalues were computed, and then their distributions were plotted in Figure 3(c).

It is worthwhile to point out that the components of ${\bf{E}}^{\sharp}_{w}$ completely failed the positiveness test for all trials and for both Wolbachia strains. Only the components of ${\bf{E}}^{\sharp}_{n}$ have been attested. This outcome was quite expectable since all trials revealed that $\mathscr{R}^{w}_{0} < 1$ for wMelPop and wMel strains.

Considering the simulation results for the disease-free equilibrium ${\bf{E}}_n^{0}$ (see Figure 3(a)), we detect that there is one eigenvalue ($\nu_9$) with strictly positive real part, while the rest of eigenvalues ($\nu_i, i = 1, \ldots, 8$) exhibit strictly negative real parts. Thus, we conclude that the disease-free equilibrium ${\bf{E}}_n^{0}$ is unstable (saddle point). On the other hand, for the endemic equilibrium ${\bf{E}}_n^{\sharp}$, all eigenvalues have strictly negative real parts (see Figure 3(c)), so we conclude that ${\bf{E}}_n^{\sharp}$ is locally asymptotically stable (nodal attractor). In other words, persistence of wild mosquitoes ($M_w(t) + F_{wS}(t) + F_{wI}(t) \to 0$ as $t \to \infty$) implies the persistence of the disease and the dengue transmission system (2.10) evolves toward the endemic equilibrium ${\bf{E}}_n^{\sharp}$. This outcome is validated in Figure 3(b) that displays $\mathscr{R}_{0}^{n} > 1$ for all trials $k = 1, \ldots, 10^{4}$.

The simulation results for the disease-free equilibria ${\bf{E}}_w^{0}$ (corresponding to both Wolbachia strains, wMelPop and wMel, see Figures 4(a) and 5(a), respectively) display that all eigenvalues of the Jacobian evaluated at ${\bf{E}}_w^{0}$ exhibit strictly negative real parts. Additionally, the coordinates of ${\bf{E}}_w^{0}$ failed the positiveness test for all trials $k = 1, 2, \ldots, 10^4$ due to the fact that $\mathscr{R}_{0}^{w} < 1$ (cf. Figures 4(b) and 5(b)). Thus, we can conclude that for both Wolbachia strains, the disease-free equilibria ${\bf{E}}_w^{0}$ are locally asymptotically stable (nodal attractors). Therefore, if the insects carrying either wMelPop or wMel strain of Wolbachia can ultimately manage to invade and conquer the grounds (meaning that $M_n(t) + F_{nS}(t) + F_{nI}(t) \to 0$ as $t \to \infty$), there will be no endemic equilibria and the solutions of the dengue transmission system (2.10) will evolve towards the disease-free steady state ${\bf{E}}_w^{0}$.

From the above conclusions, it becomes clear that the reduction of the dengue morbidity and eventual disease eradication in the target locality can be reached by replacing the wild population of mosquitoes by Wolbachia-carriers. The latter is known as "Wolbachia-based biocontrol", a novel method that persuades two principal objectives:

1. Establishment and persistence of Wolbachia-infected mosquitoes within the target locality (or population replacement of wild mosquitoes by Wolbachia-infected mosquitoes).

2. Reduction of human morbidity and the incidence of dengue in the target locality.

The major issue here consists in finding an appropriate and efficient way to achieve both objectives by an external intervention capable of moving the system (2.10) from its habitual endemic steady state ${\bf{E}}_n^{\sharp}$ to the desired disease-free equilibrium ${\bf{E}}_w^{0}$.

In the following section, we sketch out the method that enables the design of optimal programs for releases of Wolbachia-carrying insects in order to cope simultaneously with both objectives in minimum time.

3.   Optimal control technique for design of release policies

An external intervention aimed at the population replacement can be modeled by introducing an exogenous time-dependent variable that mimics the releases of Wolbachia-carrying mosquitoes. For example, Campo-Duarte et al. ^[9] had studied the population dynamics model (2.1) with an exogenous (or control) variable that denoted the rate of release of Wolbachia-carrying mosquitoes. Under such an approach, the release size for each day $t$ was proportional to the number of Wolbachia-infected insects present in the target locality on the same day $t$. However, that approach needed faithful assessments of the population sizes and did not account for the limited capacities for the rearing of Wolbachia-carrying insects. Other studies were conducted by considering the population dynamics of only female mosquitoes ^[23,25] as well as its combination with dengue transmission ^[10], while supposing the presence of sufficient males for successful matings. In those studies, the control variable expressed the number of Wolbachia-infected female mosquitoes to be released daily in the target locality. The major limitation of that approach was an a priori knowledge of the Allee threshold (minimum viable population size) of the wild female mosquitoes that was explicitly included in the mosquito population dynamics.

It is worthwhile to point out that such a limitation has no place for the sex-structured mosquito population dynamics described by (2.1) since the Allee threshold related to wild and Wolbachia-infected populations can be identified by the components of the coexistence equilibrium $E^c = \big(M_n^c, F_n, M_w^c, F_w^c \big)$ computable through the model's parameters (see formulas (2.7)). In particular, Campo-Duarte et al. ^[9] have shown that if for some $T > 0$ a point $\big(M_n(T), F_n(T), M_w(T), F_w(T) \big) \in \mathbb{R}^4_+$ satisfies the conditions

then this point belongs to the attraction basin of the steady state $E_w^{\sharp} = \big(0, 0, M_w^{\sharp}, F_w^{\sharp} \big)$ and the Wolbachia invasion eventually occurs, that is, $\big(M_n(t), F_n(t), M_w(t), F_w(t) \big) \to E_w^{\sharp}$ for $t > T$ and $t \to \infty$.

In this paper, we propose to define the control variable in a different way in order to express the releases of both male and female insects transinfected with Wolbachia.

Let $u(t): [0, T] \mapsto [0, u_{\max}]$ denote the number of Wolbachia-carrying to be released at the day $t$ in the target locality. Here, $u_{\max} > 0$ is the maximal number of Wolbachia-carriers available for a single daily release, and this number is defined by the production capacity of a facility where these Wolbachia-carrying insects are reared. Let us suppose that the overall time $T > 0$ of control intervention is finite but is left free.

In mathematical terms, the main goal of control intervention consists in driving the population dynamics system (2.1) to the "secure region" of the attraction basin corresponding to the desired steady state $E^{\sharp}_w$ (defined by (2.6)) where the relationships (3.1) will remain valid for all successive times $t > T$. The latter can be done by deliberately increasing the densities of Wolbachia-infected males and females, $M_w(t)$ and $F_w(t)$ through an external input defined by $u(t)$, and thus suppressing the densities $M_n(t)$ and $F_n(t)$ of wild mosquitoes below their minimum viable population sizes $M_n^c$ and $F_n^c$. It is also clear that under sustained reduction of the female population, the size of the male population will undergo an inevitable reduction since the wild males are progenies of mating between wild males and wild females.

Therefore, it is useful from the practical standpoint to replace the conditions (3.1) by equality-type constraints:

where $0 < \varepsilon < 1$ is some value assigned by the decision-makers. Other objectives of the control intervention include:

● minimization of the total number of dengue infections in human hosts acquired during the intervention, that is, $\int \limits_{0}^{T} I(t) dt;$

● minimization of the total time $T: = \int \limits_{0}^{T} dt$ of control intervention;

● minimization of the cumulative control effort over the period $[0, T]$ that refers to the rearing of Wolbachia-carrying insects and that can be expressed ^[10] as $\int \limits_{0}^{T} \dfrac{1}{2} u^2(t) dt.$

All indicated goals of the control intervention can be recapped by the objective functional

where the scalar function

replaces the endpoint constraint (3.2) with $A_1 > 0$ denoting the penalty for violation of this constraint, and other nonnegative coefficients $A_i, i = 2, 3, 4$ should be adequately chosen in order to reflect the desired priorities of decision-making. It is worthwhile to note that the global minimum of $\Phi: \ \mathbb{R}^2_+ \mapsto \mathbb{R}_+$ is zero and it is attained exactly at $t = T$ that fulfills the endpoint constraint (3.2).

Remark 2. In accordance with other studies ^[9,10,23,28], we assume no linear relationship between the coverage of control interventions and their respective costs. However, we do assume that the marginal cost of control action, i. e. $A_4 u(t)$, is proportional to the control effort at each $t \in [0; T]$ which, in its turn, is expressed by the number of Wolbachia-carriers to be released on the same day $t$. This is the reason why the integrand in (3.3) is assumed quadratic with respect to the control variable $u$. Furthermore, under such assumption, the costs associated with a certain release program $u(t), t \in [0, T]$ can be assessed through the cumulative number of Wolbachia-carrying insects (NWC) released during the whole campaign:

Thus, we seek to design an optimal release program $u^{*}(t) \in [0, u_{\max}], t \in [0, T^{*}]$ and to find the minimum time $T^{*} \in (0, \infty)$ that jointly minimize the objective functional (3.3) subject to the dengue-transmission dynamics (2.10) amended by the control intervention. To cope with this task, we formulate the following optimal control problem:

subject to

with initial conditions

satisfying the relationships

The optimal control problem (3.6)-(3.8) possesses the core properties that are sufficient to assure the existence of its solution ^[38] when $u_{\max}$ is large enough. Namely,

● the control domain $[0, u_{\max}]$ is closed, bounded, and convex in $\mathbb{R};$

● the trajectories of (3.7) are bounded for all admissible $u(t) \in [0, u_{\max}]$;

● the right-hand sides of (3.7) are linear in the control variable $u$;

● the terminal-state function (3.4) is continuous in its variable and bounded from below;

● the integrand of (3.6) is convex in $u$ and satisfies the coercivity condition

with $\mathcal{K}_1 = \dfrac{1}{2} A_4 > 0, \ \alpha = 2 > 1,$ and $\mathcal{K}_2 = 0$.

Formal solution of the optimal control problem (3.6)-(3.8) can be achieved by applying the Pontryagin maximum principle that constitutes the necessary condition for optimality of $\big(u^{*}, T^{*} \big)$. Here, we are interested in the particular variant of maximum principle that is applicable to optimal control problems with free terminal time ^[39].

To formulate the Pontryagin maximum principle, we define the so-called Hamiltonian function $H({\bf{X}}, u, \boldsymbol{\lambda}): \: \Omega_{\bf{X}} \times [0, u_{\max}] \times \mathbb{R}^9 \mapsto \mathbb{R}$ associated with the optimal control problem (3.6)-(3.8)

where ${\bf{X}}$ is the vector of state variables defined by (2.11), $\mathbb{F} ({\bf{X}}, u) : = \big(\mathcal{F}_1({\bf{X}}, u), \ldots, \mathcal{F}_9({\bf{X}}, u) \big)$ denotes the right-hand sides of the system (3.7), and $\boldsymbol{\lambda}: = \big(\lambda_{1}, \ldots, \lambda_9 \big)$ can be viewed as a vector of Lagrange multipliers linked to the differential constraints (3.7).

On the other hand, $\lambda_{i} = \lambda_{i}(t), i = 1, \ldots, 9$ are time-varying real adjoint functions that express the marginal variations in the value of objective functional $\mathcal{J}(u, T)$ induced by changes in the current values of state variables ${\bf{X}}$ (in the "component-by-component" sense). Thus, the current values of $\lambda_{i} = \lambda_{i}(t), i = 1, \ldots, 9$ reflect additional benefits or costs associated with changes in the vector of states ${\bf{X}}$ and they are the necessary elements of the Pontryagin maximum principle ^[39], which is formulated as follows.

Let $\big(u^{*}, T^{*} \big)$ be an optimal pair in the sense that $u^{*}(t)$ is a piecewise continuous real function with domain $[0, T^{*}]$ and range $[0, u_{\max}]$ and

for all other controls $u$ and times $T$. Let ${\bf{X}}^{*}(t) = {\bf{X}} \big(t, u^{*}(t) \big)$ be the corresponding vector of states defined for all $t \in[0, T^{*}]$. Then, there exists a piecewise differentiable adjoint vector function $\boldsymbol{\lambda}: \ [0, T^{*}] \mapsto \mathbb{R}^9$ satisfying the adjoint system of differential equations

with transversality condition

and $0 < T^{*} < \infty$ fulfills the time-optimality condition

The Pontryagin maximum principle converts the problem of finding a control that minimizes the objective functional (3.6) subject to the ODE system (3.7) with initial conditions (3.8) into the pointwise maximization of the Hamiltonian with respect to the control variable. Effectively, the Hamiltonian (3.9) is concave with respect to $u$ since we have $\dfrac{\partial^2 H}{ \partial u^{2}} = - A_4 < 0$, and hence it holds that

for all admissible controls $u(t): [0, T^{*}] \mapsto [0, u_{\max}]$ and almost for all $t \in [0, T^{*}]$. Relationship (3.13) implies that $H({\bf{X}}^{*}, u, \boldsymbol{\lambda})$ attains its maximum with respect to $u$ exactly at $u = u^{*}$ in the pointwise sense, and we can rewrite this relationship in a more convenient and explicit ^[39] form:

It is easy to check that

and we can obtain the compact form of (3.14)

which is also known as the characterization of optimal control.

Remark 3. Relationships (3.14) and (3.15) have an interesting interpretation regarding the costs and benefits of control strategies. It stems from (3.15) that, under the optimal release program $u^{*}$, the marginal cost of control action (expressed by the term $A_4 u(t)$) is equal to its marginal benefit (given by the term $\epsilon_w \lambda_5 + (1-\epsilon_w) \lambda_8$). It also follows from (3.14) that it will be optimal to use all available resources, i.e., to set $u^{*}(t) = u_{\max}$ if the marginal cost of $u^{*}$ drops below its marginal benefit (that is, if $\dfrac{\partial H}{\partial u} > 0$ in (3.14)). Moreover, no release will be needed ($u^{*}(t) = 0$) if the marginal cost of $u^{*}(t)$ exceeds its marginal benefit (that is, if $\dfrac{\partial H}{\partial u} < 0$ in (3.14)).

Using the closed form of $u^{*}(t)$, the original optimal control problem (3.6)-(3.8) can be reduced to a two-point boundary value problem that consists of eighteen differential equations with eighteen endpoint conditions specified at $t = 0$ and $t = T^{*}$. This boundary value problem is often referred to as optimality system, and its entries are:

● nine direct differential equations (3.7) where $u(t)$ is replaced by its characterization (3.16);

● nine adjoint differential equations (3.10) where $u(t)$ is replaced by its characterization (3.16);

● nine initial conditions (3.8) specified at $t = 0$;

● nine transversality conditions (3.11) specified at $t = T^{*}$.

Here, it is essential to recall that the optimal time $0 < T^{*} < \infty$ must be determined from the time-optimality condition (3.12).

Due to non-linearity and high dimension, the optimality system described above does not admit a closed-form solution, and it can only be solved numerically. Traditional techniques for solving two-point boundary value problems for ODE systems (such as forward-backward sweep methods, shooting techniques, and collocation methods) require an a priori knowledge of both endpoints; therefore, they are unable to guarantee the convergence of numerical algorithm when the final time $T^{*}$ is left free.

As an alternative, we propose to employ the GPOPS-Ⅱ Next-Generation Optimal Control Software ^[40,41] designed for MATLAB platform, which is capable of dealing with time-optimal control problems. Note that the GPOPS-Ⅱ manual with detailed descriptions is downloadable from http://gpops2.com/, while its concise description can be found in the work by Campo-Duarte et al. ^[9] (see Appendix B in that paper).

This solver does not rely on numerical integration and implements an adaptive combination of two collocation techniques (direct and orthogonal collocation) known as Radau pseudospectral method ^[42], which is capable of dealing with free terminal time $T$. The main limitation of the GPOPS-Ⅱ package is that it requires the Hamiltonian to be twice continuously differentiable in all its variables. However, the Hamiltonian (3.8) meets this condition.

4.   Numerical results and discussion

Our numerical simulations will be carried out for two Wolbachia strains, and our ultimate goal is to conduct an epidemiological assessment of these two strains. Several studies have pointed out that wMelPop strain of Wolbachia, despite its high fitness cost, possesses the best features for prevention and control of arboviral infections ^[3,6,8]. On the other hand, many scholars have claimed that wMel strain of Wolbachia, despite its lower potential for the virus inhibition, have better perspectives for a faster invasion into wild mosquito populations due to its lower fitness cost ^[2,4,5]. The latter implies that the population replacement will be easier to achieve by releasing the insects carrying wMel strain.

From the mathematical standpoint, reaching the population replacement means moving the dengue transmission system (3.7) from its habitual state (e.g., endemic equilibrium ${\bf{E}}^{\sharp}_{n}$) characterized by the disease persistence with $\mathscr{R}_{0} = \mathscr{R}_{0}^{n} > 1$, to the desirable disease-free equilibrium ${\bf{E}}^{0}_{w}$ where $\mathscr{R}_{0} = \mathscr{R}_{0}^{w} < 1$. Whilst the system is being moved from its initial state to ${\bf{E}}^{0}_{w}$ by external releases $u(t)$ of Wolbachia-carrying insects, new dengue infections among human hosts are still expected. Our interest lies in comparing the number of human infections that can be averted by releasing the insects carrying each Wolbachia strain (wMelPop versus wMel) until the population replacement is achieved, and also in assessing the underlying costs of intervention in terms of the overall time of the release campaign and the total number of mosquitoes needed for its successful accomplishment.

4.1.   Preliminary settings

To make our simulations more meaningful and realistic, let $N_h$ express the total size of Santiago de Cali, which is one of the largest Colombian cities regarded as "endemic" with respect to dengue morbidity ^[43,44].

Our numerical simulations will be focused on the "worst" scenario, that is, supposing that the wild mosquitoes have equilibrium densities just before the control intervention ($t = 0$), while Wolbachia-carrying insects are not present in the target locality. Therefore, the initial conditions assigned to the dengue transmission system (2.10) are taken equal to the endemic equilibrium (2.18) for all numerical simulations (see Table 2).

The values of parameters of the dynamical system (2.10) related to the human inhabitants are specified in Table 3 and those related to the vector-host virus transmission and to the population dynamics of three mosquitoes species (wild and transinfected with either wMelPop or wMel strains of Wolbachia) are given in Table 4. It is worthwhile to point out that previous studies ^[28,29,45] have revealed that the average vector density of Ae. aegypti in Cali, Colombia is about $1.5$ female insects per one human inhabitant. Therefore, we have fitted the parameter $\sigma$ to satisfy the relationship $\dfrac{F_n^{\sharp}}{N_h} \approx 1.5$ where $F_n^{\sharp} = F_{nS}^{\sharp}+F_{nI}^{\sharp}$ is given by (2.5).

In the absence of Wolbachia-carrying mosquitoes and using the parameters values from Tables 3 and 4, the basic reproductive number is calculated according to (2.15) and is $\mathscr{R}_{0} = \mathscr{R}^{n}_{0} = 1.14631 > 1$. This stays in line with the existence of endemic equilibrium ${\bf{E}}_n^{\sharp}$.

The ultimate goal of control intervention consist in moving the dynamical system (2.10) from its endemic equilibrium ${\bf{E}}^{\sharp}_n$ to the disease-free steady state ${\bf{E}}^0_n$ by releasing a reasonable number of male and female mosquitoes infected with Wolbachia $u(t) = \epsilon_w u(t) + (1-\epsilon_w) u(t) \leq u_{\max}$ at each day $t \in [0, T^{*}]$ in the target locality. Here, $u_{\max} > 0$ denotes the maximum capacity of daily releases that should match the daily output of the mass-rearing facility where Wolbachia-carrying insects are bred.

The daily output of the mass-rearing facility should be sufficiently high so the daily releases allow reaching the frequency of Wolbachia that ensures its invasion and ultimate persistence in the target locality. From the mathematical standpoint, this will also guarantee the existence of the solution to the optimal control problem (3.6)-(3.8) which, otherwise, would possess no feasible solution. In effect, if $u_{\max}$ is not high enough, then the releases of Wolbachia-carriers may go on forever without achieving the frequencies ensuring their definitive invasion. The latter is attributed to the reduced individual fitness of Wolbachia-carriers at high frequencies of wild coevals and it has been addressed in several studies encompassing the population dynamics of Wolbachia invasion ^{[9,20,21,22,23,24,25,26]}.

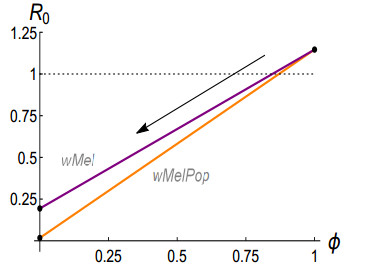
As Wolbachia-carrying mosquitoes are being released in the target locality, they will gradually replace the wild mosquitoes, especially wild females, that are capable of transmitting dengue and other infections. Therefore, it is expected that the dengue incidence would also slow down, and a lesser number of secondary infections would be entailed by each infective human host. As a consequence, the basic reproductive number $\mathscr{R}_{0}$ given by (2.15) will be gradually reduced from $\mathscr{R}_{0}^{n} = 1.1431 > 1$ (when $\phi = 1$) to either $\mathscr{R}_{0}^{w} = 0.1937 < 1$ or $\mathscr{R}_{0}^{w} = 0.01719 < 1$ depending on the Wolbachia strain that is used to mosquito transinfection during mass-rearing (when $\phi = 0$). Figure 6 illustrates schematically such a situation where the binary variable $\phi \in \{ 0, 1 \}$ is deliberately allowed to take on intermediate values from a continuous domain $[0, 1]$.

When the population of wild females drops below its minimum viable population size $F_{n}^{c}$ (see Eq. (2.7a)) and the overall number of Wolbachia-carrying females exceeds its minimum viable population size $F_{w}^{c}$ (given by (2.7b)), the releases can be suspended ($u(t) = 0$) and the epidemiological system (3.7) will still evolve towards the disease-free steady state ${\bf{E}}_{w}^{0}$. In this case, the population replacement will eventually occur leading to the local extinction of the disease. This is exactly the desirable outcome to be sought by solving the optimal control problem (3.6)-(3.8). Moreover, we expect to achieve this outcome in the minimum time and using the least possible number of Wolbachia-carrying mosquitoes.

All entries of the objective functional (3.3), (3.6) are measured in different units. In order to make them more comparable, their underlying weight coefficients $A_i, i = 1, 2, 3, 4$ must account for proper scaling. In this study, we adopt the following scaling:

where $F_n^{\sharp} = F_{nS}^{\sharp}+F_{nI}^{\sharp}$ and $I_n^{\sharp}$ refer to the coordinates of the endemic equilibrium (2.18), time is scaled to years ($= 365$ days), and the control effort is normalized by the maximal release capacity $u_{\max}$. In the gauged values (4.1), the coefficients $\mathcal{P}_i, i = 1, 2, 3, 4$ define "pure" priorities of the decision-making, which are dimensionless.

Our top priority should be to seek for replacement of wild mosquitoes (capable of transmitting the virus to human individuals) by Wolbachia-carrying insects whose vectorial capacity is drastically reduced by the Wolbachia bacterium ^{[1,2,3,4,5,7]}. Therefore, the largest value must be assigned to $\mathcal{P}_1$ thus seeking to fulfill the endpoint condition (3.2) and to obtain that $\Phi \big(F_{nS}(T), F_{nI}(T)\big) = 0$ in (3.3), (3.6). On the other hand, the lowest priority can be assigned to $\mathcal{P}_4$ that stands for the rearing (unit) cost of Wolbachia-carrying mosquitoes.

Previous studies ^[10] revealed that time to reach the population replacement is more important than reduction of the overall number of human infections, and the latter has rather explicit explanation based on the rational choice. Namely, the longer wild mosquitoes remain in the system, the higher number of human infections they produce. Therefore, it is prudent to consider that $\mathcal{P}_2 < \mathcal{P}_3$.

In view of the above rationale, we have assigned the following "pure" priorities in all numerical simulations presented in Subsection 4.2:

Another issue to address is the choice of $\varepsilon \in (0, 1)$ in the terminal part of the objective functional (3.3), (3.6). In this context, it is useful to recall that Campo-Duarte et al. ^[9] have disclosed an interesting feature related to the fulfillment of the terminal condition $F_n(T^{*}) = 10^{-k}, k = 2, 4$ by the optimal release strategies. If such very small values of $F_n(T^{*})$ are sought, the optimal release strategy indicates suspension of active releases just several days after that $F_n(t)$ drops below the threshold of minimum viable population size $F_{n}^{c}$ and this occurs well before the terminal constraint become active. Therefore, it seems reasonable to consider sufficiently large values for $\varepsilon \in (0, 1)$ in the terminal part $\Phi$ of the objective functional (3.3), (3.6). Thus, we set $\varepsilon = 0.9$ for all numerical simulations presented in Subsection 4.2.

It follows from the formulation of the optimal control problem (3.6)-(3.8) that $T^{*}$ will be delivered by the numerical algorithm together with underlying optimal release program $u^{*}(t)$ defined on $[0, T^{*}]$. However, if we consider different scenarios (such as two Wolbachia strains and contrasting maximum rearing capacities $u_{\max}$), the value of $T^{*}$ is expected to be dissimilar for each scenario. Therefore, we have to determine an "equable" observation interval $[0, \hat{T}]$ with $\hat{T}$ exceeding any other $T^{*}$ obtained for each considered scenario.

Furthermore, the optimal release programs $u^{*}(t)$ defined on $[0, T^{*}]$ for each particular $T^{*}$ can be overspread to the equable observation interval $[0, \hat{T}]$ by a simple transformation:

To justify such an extension, it is worthwhile to recall that each optimal release program $u^{*}(t)$ gets effectively suspended when the endpoint constraint (3.2) becomes active (i.e., the terminal function $\Phi$ in $J(u, T)$ achieves its global minimum equal to zero), and this occurs exactly at $t = T^{*}$.

Moreover, all optimal state trajectories: $\big(S^{*}(t), I^{*}(t), R^{*}(t), M_n^{*}(t), M_n^{*}(t), F_{nS}^{*}(t), F_{nI}^{*}(t), F_{wS}^{*}(t), F_{wI}^{*}(t) \big)$ are delivered by the numerical algorithm as real functions defined for $t \in [0, T^{*}]$, and they can also be overspread to the equable interval $[0, \hat{T}]$ by running the controlled system (3.7) with $\hat{u}^{*}(t)$ defined by (4.3).

To compare the effects of the optimal release programs on dengue transmission under different scenarios, it is also appropriate to evaluate their outcomes over the equable interval $[0, \hat{T}]$, that is, during and after the control intervention. To assess the benefits of optimal release strategies under different scenarios, it is convenient to employ an auxiliary variable known as cumulative incidence and defined as

where $I(\cdot)$ stands for the state profile of the system (2.10) without control intervention ($u(t) = 0$). Formula (4.4) states that $\mathcal{I}_c(t)$ sums up all new infections acquired by human individuals during the period $[0, t]$ without taking into account their posterior recovery. In a similar way, we can also define

where $I^{*}(\cdot)$ stands for the state profile of the controlled system (3.7) under the optimal release program $\hat{u}^{*}(t)$ expressed by (4.3). Here, $\mathcal{I}_c^{*}(t)$ expresses the total number of human infections acquired during the period $[0, t]$ under the optimal release program $\hat{u}^{*}(t)$.

In effect, the current values of $\mathcal{I}_c(t)$ and $\mathcal{I}_c^{*}(t)$ can be obtained by complementing the systems (2.10) and (3.7) with an additional differential equation and its underlying initial condition

and then by solving numerically these systems composed by ten ODEs with corresponding initial conditions.

Formulas (4.4) and (4.5) then allow us to quantify the benefit of each optimal release program $\hat{u}^{*}(t)$. The latter can be expressed by the total number of human infections that are averted or prevented under the action of $\hat{u}^{*}(t)$ during the whole observation interval $[0, \hat{T}]$. Let us denote by $\text{AHI} \big(\hat{u}^{*} \big)$ the number of averted human infections during the period $[0, \hat{T}]$ and express it as

On the other hand, to assess the cost of each optimal release program $\hat{u}^{*}(t)$ one can use two quantities: the overall time of the control intervention $T^{*}$ and the total number of Wolbachia-carrying insects to be mass-reared for releases, $\text{NWC}(u^{*})$ which was introduce in Remark 2, formula (3.5).

Thus, for each scenario, the optimal release program $\hat{u}^{*}(t)$ extended to the equable observation period $[0, \hat{T}]$ will be characterized by three quantities: $\text{AHI} \big(\hat{u}^{*} \big), T^{*},$ and $\text{NWC}(u^{*})$.

Several scenarios encompassing two Wolbachia strains (wMelPop and wMel) are presented and analyzed in the following subsection. Our core interest stands in determining which strain of Wolbachia exhibits better potentials for dengue prevention in the long-term perspective.

4.2.   Numerical results for wMelPop and wMel strains

Empirical evidence suggests that two Wolbachia strains, wMelPop and wMel, affect to a greater or lesser extent the individual fitness of their carriers ^[2,4,5] and also have different capacities for virus inhibition ^[3,6,8]. These features are reflected by the values of parameters borrowed from existent literature (see Table 4, columns 3 and 4), which will be used for numerical solutions of the optimal control problem (3.6)-(3.8).

Many scholars point out that, due to more severe fitness loss induced by wMelPop strain in Ae. aegypti mosquitoes, more intense and sophisticated release programs are needed in order to achieve the population replacement. Therefore, it is reckoned that the costs of control intervention will be considerably higher for wMelPop than for wMel. On these grounds, it is reasonable to concede greater values of $u_{\max}$ (i.e., maximum daily capacity of the mass-rearing facility where Wolbachia-carrying insects are artificially bred) for wMelPop strain and lesser values of $u_{\max}$ for wMel strain. Furthermore, it is not difficult to foreknow that the optimal time $T^{*}$ of active releases will be shorter for wMel strain than for wMelPop.

On the other hand, the benefits of employing the wMelPop strain, quantified by the overall number of averted human infections, are also expected to be higher by comparison with the wMel strain.

To illustrate such predictions and to derive other interesting insights regarding the Wolbachia-based biocontrol, we have explored the following six scenarios:

It was established by numerical simulations that the optimal control problem (3.6)-(3.8) does not have feasible solution if the values for $u_{\max}$ are chosen below those set for Cases A in (4.8).

For each scenario, the optimal control problem (3.6)-(3.8) has been solved numerically, and its underlying solutions have been extended to the equable interval of $500$ days, that is, we have set $\hat{T} = 500$ in order to assure that $[0, \hat{T}]$ be longer than $[0, T^{*}]$ for any $T^{*}$ obtained as optimal solution for each particular scenario. To quantify the benefits of all scenarios, we have also assessed by the formula (4.4) the cumulative incidence without control intervention and obtained $\mathcal{I}_c(\hat{T}) = 4.3486 \times 10^4$, meaning that $43 486$ new dengue cases are expected during $500$ days without performing the releases.

As mentioned in the end of Section 3, we have employed the GPOPS-Ⅱ Next-Generation Optimal Control Software ^[40,41] which is an advance solver that handles all internal computations by scaling an input interval $[0, T]$ (given as an initial guess) to the interval $[-1, 1]$. This operation mode allows this solver to deal with time-optimal problems, and to obtain $T^{*}$ as an output only if the time-optimality condition (3.12) is satisfied within the limits of prescribed accuracy. For our calculations, we have assumed the standard numerical tolerance of $10^{-5}$ with respect to scaling and we also acknowledge that for all six scenarios the numerical algorithm had effectively found the optimal solution.

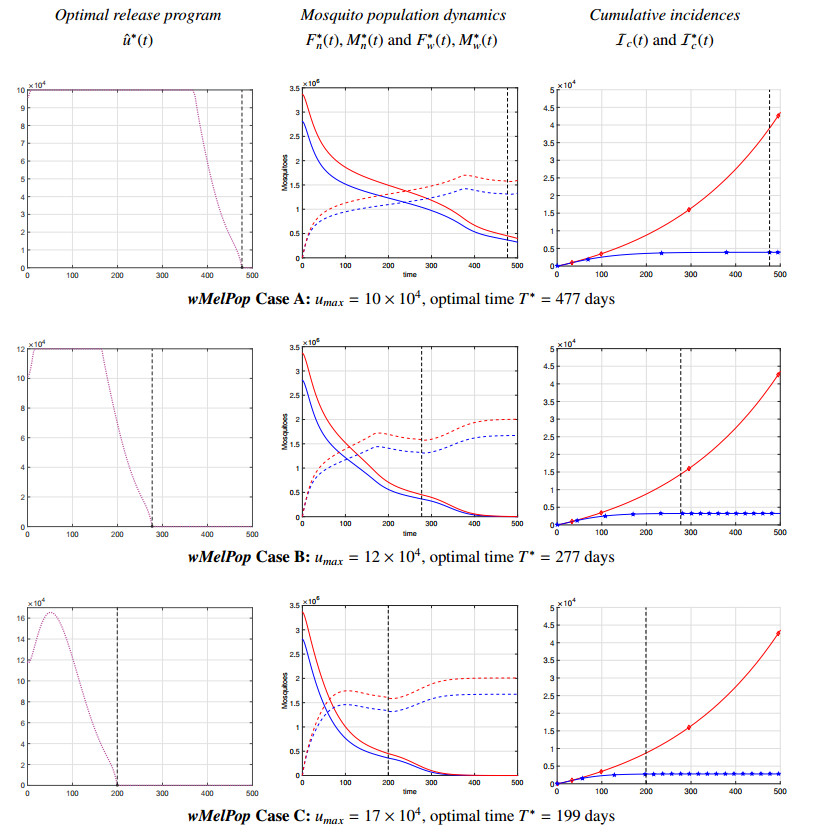
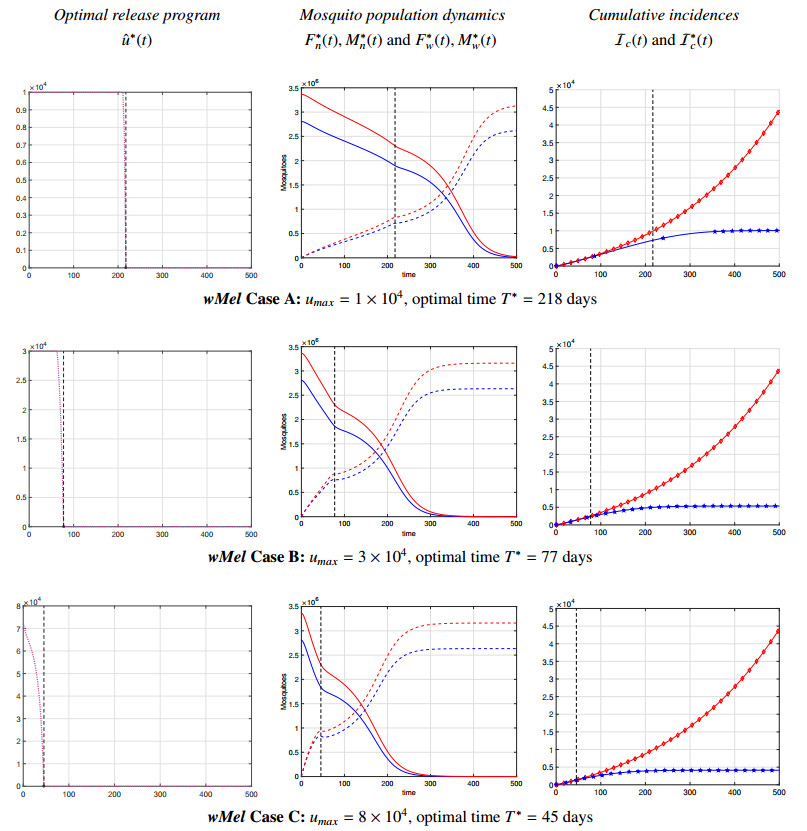
The results of numerical solutions of the optimal control problem (3.6)-(3.8) with the weigh coefficients (4.1), (4.2) and initial conditions given in Table 2 are displayed in Figures 7 (for wMelPop strain) and 8 (for wMel strain). In these two figures, each row contains three charts corresponding to each scenario described in (4.8) for different values of $u_{\max}$. In all charts, the vertical dashed line $t = T^{*}$ indicates the optimal time at which the boundary condition (3.2) is met and after which the releases are suspended.

Charts in the left columns of Figures 7 and 8 display the optimal release programs $\hat{u}^{*}(t)$ extended to the equable interval $[0, \hat{T}] = [0,500]$, and their positive parts denote the optimal controls $u^{*}(t), t \in [0, T^{*}]$, i.e., solutions to the optimal control problems (3.6)-(3.8) corresponding to each particular scenarios from (4.8).

Charts in the central columns of both figures present the population dynamics (optimal state profiles) of wild mosquitoes (solid curves) and Wolbachia-carrying mosquitoes (dashed curves) on the extended interval $[0, \hat{T}] = [0,500]$. The profiles of male insects $M_n^{*}(t)$ and $M_w^{*}(t)$ are plotted in blue color, and the state trajectories $F_n^{*}(t) = F_{nS}^{*}(t) + F_{nI}^{*}(t)$ and $F_w^{*}(t) = F_{wS}^{*}(t) + F_{wI}^{*}(t)$ are drawn in red color.

Finally, the charts in the right columns of Figures 7 and 8 show the cumulative incidences in absence of control intervention ($\mathcal{I}_c (t)$, red curves) and under the corresponding optimal release program $\hat{u}^{*}(t)$ ($\mathcal{I}^{*}_c (t)$, blue curves), both extended to $[0, \hat{T}] = [0,500]$.

Table 5 summarizes the key metrics of all six scenarios: optimal time $T^{*}$ of effective releases, expected benefits expressed via $\text{AHI} \big(\hat{u}^{*} \big)$, the total number of human infections prevented by the corresponding optimal release strategy during the equable interval of $\hat{T} = 500$ days, and the overall number of Wolbachia-carrying insects $\text{NWC}(u^{*})$ that are needed for implementation of the optimal release program $u^{*}(t), t \in [0, T^{*}].$

Looking at the left column of Figure 7, we observe that, when using the wMelPop Wolbachia strain, all optimal release programs $u^{*}(t)$ exhibit a somewhat "bell-shaped" structure. Such an outcome stays in concordance with previous results obtained for this particular strain ^[9,10,23]. On the other hand, the optimal release programs $u^{*}(t)$ designed for wMel Wolbachia strain (see left column of Figure 8) exhibit a monotone decreasing structure. However, the optimal release programs $u^{*}(t)$ designed for both Wolbachia strains possess common characteristics: higher values of $u_{\max}$ ensure shorter optimal time $T^{*}$ of effective releases.

Furthermore, the charts in the left lower corners of Figures 7 and 8 indicate that the maximum daily release capacities $u_{\max} = 17 \times 10^4$ and $u_{\max} = 8 \times 10^4$ (for wMelPop and wMel strains, respectively) are not achieved during the implementations of the optimal release programs.

This reveals the existence of a certain tradeoff between the initial size of the targeted wild population to be replaced and the daily productivity of the mass-rearing facilities where Wolbachia-carrying mosquitoes are artificially bred. Thus, if the initial size of the targeted wild population remains the same, any increase in $u_{\max}$ above a certain "top level" is unnecessary: it neither alters the structure of $u^{*}(t)$ nor it reduces the optimal time $T^{*}$. Such an important feature should be taken into account when the production capacity of the mass-rearing facilities is determined.

Inspecting the central columns of Figures 7 and 8, it is easy to see that the underlying optimal release programs $u^{*}(t)$ induce steady decline of the wild mosquito populations $M_n^{*}(t)$ and $F_n^{*}(t) = F_{nS}^{*}(t) + F_{nI}^{*}(t)$ (solid curves), which becomes more pronounced for higher values of $u_{\max}$ and still continues even when the release program is suspended (that is, when the vertical line $t = T^{*}$ gets crossed). It is essential to recall that $u^{*}(t)$ is suspended exactly at $t = T^{*}$ (cf. formula (4.3)), that is, when the current sizes of all four mosquito populations meet the conditions (3.1) and the end-point constraint (3.2) becomes active.

By comparison of the results presented in the central columns of Figures 7 and 8, one can easily detect the striking dissimilarities between two sets of charts with regards to the current sizes of the wild and Wolbachia-infected mosquito populations at which the releases get effectively suspended (see the intersections of the vertical line $t = T^{*}$ with the state profiles in the indicated charts). Such a disparity has a very natural explanation that stems from the different level of fitness loss induced by the wMelPop and wMel strains in transinfected mosquitoes (cf. parameter values given in Table 4 for these two strains). The latter entails different values of the minimum viable population sizes determined by the coexistence equilibrium $E_c = \big(M_n^c, F_n^c, M_w^c, F_w^c \big)$ of the population dynamics model (2.1). Namely, using formulas (2.7) together with the parameter values from Table 4 for each Wolbachia strain, we can obtain the minimum viable population sizes corresponding to both strains:

As a result, the right columns of Figures 7 and 8, as well as the estimations of the total number of averted infections, $\text{AHI}(\hat{u}^{*})$ (see the last column of Table 5) clearly highlight a better performance of wMelPop strain for short- and long-term prevention and control of human infections. Indeed, the wMelPop strain, being a stronger blocker of the virus in mosquitoes, outperforms the more suitable for mass-rearing wMel strain thanks to this important feature; albeit, this is not the only reason.

By revisiting the charts in the central columns of Figures 7 and 8 (in particular, those located in the upper rows), it is detected that around $t = 250$ (the mid-point of $[0, \hat{T}]$) the population of wild females $F^{*}(t) = F_{nS}^{*}(t) + F_{nI}^{*}(t)$, fully capable of transmitting the virus, is reduced by more than $50\%$ for wMelPop-based biocontrol and by less the $30\%$ in case of wMel-based biocontrol. In other words, when wMel strain is employed, wild females remain in the locality at higher frequencies and for a longer time. As a result, more human infections are expected during and after the releases of wMel-carrying insects compared to the releases of wMelPop-infected mosquitoes.

Another important characteristic in favor of the wMelPop strain is exactly the drastically reduced individual fitness it induces in mosquitoes. Scientific evidence ^[5,7,8,16] asserts that the lifespan of wMelPop-infected females is $50\%$ shorter than that of the wild females, and about $40-45\%$ shorter than of wMel-infected females. Therefore, even if some wMelPop-carrying females manage to acquire the virus (with a small probability of about $5\%$ ^[5]), it is unlikely they live enough to develop a viral load sufficient for its transmission to human hosts.

Moreover, the reduced individual fitness of wMelPop-infected mosquitoes decreases their saturation density expressed by the steady-state values $M_w^{\sharp}$ and $F_w^{\sharp}$. The latter can be identified by examining once again the charts in the central columns of Figures 7 and 8 and also calculating these steady-state values for both strains:

Thus, when the population replacement of wild mosquitoes by wMelPol-carriers is finally achieved, the average vectorial density (that is, the average number of female mosquitoes per one human individual) in the target locality will be considerably lower than in case of population replacement by wMel-carriers. Since Wolbachia-carrying females still need to ingest human blood for maturing their eggs, human inhabitants would get bitten more often (on average) by wMel-carrying females than by wMelPop-carrying females, once the invasion of either strain is ultimately attained in the target locality.

These two last features of wMelPop strain (reduced lifespan and vectorial density at saturation level) are not accounted for by the quantitative metrics given in Table 5 but they should be taken into consideration by the healthcare entities in order to decide which strain to choose for Wolbachia-based biocontrol.

5.   Conclusions

In this paper, we have presented a dengue transmission model that accounts for the sex-structured population dynamics of wild and Wolbachia-carrying mosquitoes, of which only the female insects are capable of transmitting the DENV pathogen to human individuals. The presence of male mosquitoes (that do not transmit the virus) in the model facilitated to mimic more explicitly the reproductive phenotype of cytoplasmic incompatibility, induced by Wolbachia and was also helpful for modeling the releases of entire cohorts of Wolbachia-carrying insects thus avoiding their sex-separation during mass-rearing and saving the corresponding costs. It is worthwhile to emphasize that the inclusion of male mosquitoes into the dengue transmission system constitutes the contextual difference of the present study from the one accomplished by Cardona-Salgado et al. ^[10] that was entirely focused on releasing only female mosquitoes transinfected with wMelPop strain of Wolbachia.

The principal goal of this paper was to analyze the performance of two Wolbachia strains, wMelPop and wMel, that are recommended for dengue prevention and control. Our approach, stemming from the fusion of mathematical modeling, analysis of the dynamical systems, and dynamic optimization via optimal control, has rendered rather interesting results and has also given rise to a set of recommendations for the practical implementation of Wolbachia-based biocontrol.

Using the optimal control approach, we have considered several scenarios and designed underlying programs for optimal releases of transinfected mosquitoes carrying either wMelPop or wMel strain while varying the daily capacities of releases and keeping the same decision-making priorities.

In our study, we have deliberately focused on the "worst possible option" by supposing that, at the beginning of all release programs, the wild mosquitoes have equilibrium densities. This situation is the most compatible with the climatic conditions of the city of Cali, Colombia. This city, located very close to the equator, provides the ideal environment all year round for fast reproduction, abundant perseverance, and persistence of Ae. aegypti mosquitoes due to frequent intermittent rainfalls combined with the absence of seasonal temperature variations.

On the other hand, wild mosquito populations may exhibit seasonal size variations in other tropical and sub-tropical regions ^[50,51], and our methodology for the design of optimal release strategies can be naturally adapted to match diverse initial values of the wild population. Indeed, given the bistable nature of the population dynamics model (2.1) and regardless of the strain used for Wolbachia-based biocontrol, all three key metrics of the optimal release programs ($T^{*}, \text{NWC}(u^{*}),$ and $\text{AHI}(\hat{u}^{*})$) can be greatly improved by taking lower initial values of wild mosquitoes. In such a case, the shorter overall time of effective releases can be expected, the smaller total number of Wolbachia-carrying insects would be needed, and the greater number of human infections can be avoided.

In this context, the best timing for implementation of Wolbachia-based biocontrol by either wMel or wMelPop strain will be the periods of relatively low mosquito abundance. Such periods usually correlate with cooler and windier seasons in tropical and sub-tropical regions ^[50,51] or arise after carefully planned and thoroughly implemented vector control measures ^{[28,45,52,53]}.

Concerning the simulation results obtained in this study, they have revealed rather interesting and potentially useful insights regarding the performance of two Wolbachia strains for dengue prevention and control. Let us now highlight the advantages and disadvantages of each strain by comparison.

Advantages of wMel-based biocontrol:

1. Artificial breeding of wMel-carrying insects requires a lower daily production capacity of a mass-rearing facility than does the cultivation of wMelPop-carriers.

2. Release programs designed for wMel strain require for mass-rearing of smaller overall quantities of transinfected insects than wMelPop-based release programs.

3. Shorter time of effective daily releases is needed for wMel-based biocontrol than for wMelPop-based biocontrol.

4. After the population replacement is achieved, the wMel-infected population will be more robust and less vulnerable to the possible massive immigrations of wild mosquitoes than the wMelPop-infected population. This is explained by a wide gap between the minimum viable population sizes of wild mosquitoes $M_n^c$ and $F_n^c$ that favors the carriers of wMel strain (see relationships (4.10))

Advantages of wMelPop-based biocontrol:

1. wMelPop-based release strategies ensure a faster decline of wild female mosquitoes, capable of transmitting the virus, and thus guarantee an earlier reduction in the overall number of human infections than the release strategies based on wMel strain.

2. Among Wolbachia-carrying females that somehow manage to become DENV-infected, the wMel-carriers have a higher probability to develop the virus load sufficient for transmission than those transinfected with wMelPop strain whose lifespan is a lot shorter.

3. In general terms, optimal release programs designed for wMelPop strain exhibit better outcomes for short- and long-term dengue prevention and control than those designed for wMel strain.

4. After the population replacement is achieved, the wMelPop-carrying population will exhibit lower average vectorial density at saturation level than the wMel-infected population, and the human inhabitants would receive a fewer number of mosquito bites.

From the foregoing arguments, it is rather hard to univocally conclude which Wolbachia strain is more appropriate and beneficial, but each of them has the potential to ultimately annihilate the local circulation of the dengue virus and bring the system to the disease-free steady state. Unfortunately, we do not have any reliable information about the possible differences in the costs of mass cultivation of insects transinfected with each strain, nor about the relationship between such costs and expenses associated with traditional vector control measures (insecticides or larvicides spraying), nor with costs intended for the prevention of human dengue infections. Our arguments have the quantifying nature but other aspects and potential hazards of releasing Wolbachia-carrying insects, as well as the societal acceptance of such releases, must be carefully evaluated by other specialists (biologists, ecologists, healthcare managers, etc.). Also, we do believe that the outcomes of this study will be helpful and informative to local authorities in countries affected by dengue and motivate them for more responsible decision-making.

Acknowledgments

This research was financed by the National Fund for Science, Technology, and Innovation (Autonomous Heritage Fund Francisco José de Caldas) by way of the Research Program No. 1106-852-69523, Contract: CT FP 80740-439-2020 (Colombian Ministry of Science, Technology, and Innovation – Minciencias), Grant IDs: CI-71241 (Universidad del Valle), 20 INTER 356 (Universidad Autonoma de Occidente).

Daiver Cardona-Salgado and Olga Vasilieva also appreciate the endorsement obtained from the STIC AmSud Program for regional cooperation (20-STIC-05 NEMBICA project, international coordinator: Pierre-Alexandre Bliman, INRIA – France). Mikhail Svinin acknowledges partial support by the Japan Science and Technology Agency, through the JST Strategic International Collaborative Research Program under Project 18065977.

Conflict of interest

The authors have no conflict of interest.