1. Introduction

Aedes aegypti, Aedes albopictus, and Anopheles stephensi, are the primary vectors of some life-threatening mosquito-borne diseases such as dengue, malaria, and Zika. Since there are no effective vaccines available for these diseases, current controls mostly rely on environmental management by destructing vector breeding sites physically or chemically. Unfortunately, the chemical method of spraying pesticides causes severe environmental pollution and induces mosquito's insecticide resistance.

The study on the interaction of Wolbachia and mosquitoes has flourished due to the groundbreaking work [1,2,37,38,39,40], which paved an avenue for a biologically safe method of mosquito-borne disease control [5,10,17,18]. As expected, Wolbachia can block the replication of viruses such as dengue and Zika inside the mosquitoes [1,37,38,39,40] and confer resistance to the human malaria parasite Plasmodium falciparum [2]. In mosquitoes, maternally transmitted Wolbachia is associated with cytoplasmic incompatibility (CI), i.e., the reduced hatch rate of embryos produced from fertilization of uninfected ova by sperm from Wolbachia infected males. Infected females therefore have a reproductive advantage, allowing Wolbachia to spread in polymorphic populations [4,9,14].

An appealing strategy is to release a large number of Wolbachia infected males in the natural area so that the CI mechanism can drive all the mated females sterile and the whole population can be suppressed. However, a complete population suppression requires a nearly perfect separation of males from infected females, which exerts tremendous challenges in extending this technology over large areas. An alternative strategy to meet the challenge is to seed the natural population with infected mosquitoes, both male and female, so the reproductive advantage for infected females induced by CI and the high maternal transmission rate can drive Wolbachia infected mosquitoes to replace the wild population. For the success of population replacement, it is critical to identify the release threshold: above which Wolbachia will invade all mosquitoes, but below which it will be wiped out [4,9,12,34].

Some earlier mathematical models making use of difference equations have played an instrumental role in determining the release threshold for Wolbachia fixation in non-overlapping populations in laboratory [4,9]. Inspired by its great potential to eliminate the mosquito-borne diseases, modeling Wolbachia spread dynamics parameterized by laboratory or field data [7,11,14,23,27,36] has emerged as a hot topic for extensive studies. There have been models of ordinary [8,22,29], delayed differential equations [41] built to explore the subtle relations between Wolbachia invasion and important parameters. Such parameters include: (Infection peak versus the rate at which protective susceptible individuals forget) the maternal transmission rate ($1-\mu$, where $\mu$ is the rate of uninfected ova produced by infected females); (ⅱ) the intensity of CI ($s_h$, the reduced egg-hatch produced by matings between infected males and uninfected females), (ⅲ) the fecundity cost/benefit of infected females relative to uninfected females. More recent models have also considered the impact of environmental heterogeneity and mosquito diffusion in space by stochastic equations [19] and reaction-diffusion equations [20,21].

In most of the current theoretical studies on Wolbachia spreading dynamics in mosquitoes, it was assumed that maternal transmission is perfect ($\mu=0$), and CI is complete ($s_h=1$) which are supported by recent findings in mosquitoes. For example, maternal transmission loss was not observed for both the WB1 in Aedes aegypti and the wAlbA, wAlbB in Aedes albopictus together with complete CI [1,37,38,39,40]: examinations from crosses of uninfected Waco females and infected WB1 males showed that no egg hatch resulted from $>$3800 eggs [39]. In 2013, the LB1 infection was successfully established in an important malaria vector, Anopheles stephensi [2]. Again, of 8087 eggs resulting from crosses between LB1 females and the naturally uninfected LIS males, only $1.2%$ hatched, and the 100$%$ maternal transmission efficiency was confirmed by fluorescence in situ hybridization (FISH) in self-crossing LB1 mosquitoes, while the data on maternal transmission efficiency in outcrossing (LB1 females $\times$ LIS males) is absent.

However, imperfect maternal transmission $(\mu>0$) has been repeatedly documented in nature with respect to the wRi, wRu infection in Drosophila simulans [3,23,24,32], and the wMel in Drosophila melanogaster [14]. In D. simulans, data indicates that uninfected ova produced by the wRi infected females are susceptible to CI. However, the wRu in D. simulans and the wMel in D. melanogaster cause weak or non-CI. Hence, among-female variation of Wolbachia deposition in ova seems to be generally associated with among-male variation in the effect of Wolbachia on sperm in Drosophila. For systematic studies on Wolbachia spreading in D. simulans, we refer the readers to Hoffmann and Turelli's work since 1990s [15,16,30,31,32,33,34] in which both Wolbachia infidelity and partial CI were identified.

It was predominantly believed that the maternal transmission of Wolbachia in mosquitoes is perfect. However, a very recent study [28] demonstrates that high temperatures (26-37${}^{\circ}\mathrm{C}$) can induce both imperfect maternal transmission and incomplete CI of Wolbachia in Aedes aegypti, the primary vector of dengue. Imperfect maternal transmission was also observed in a recent study on the spread of Wolbachia strain LB1 in Anopheles stephensi, along with a confirmed complete CI in [2]. The findings in [2] show that self-crossing LB1 produces significantly lower hatching ($\sim$52.4$%$) than the outcrossing of LB1 females with uninfected males ($\sim$80$%$) and uninfected self-crossing ($\sim$90$%$), see Fig.1(B) in [2]. With the potential of a Wolbachia-based intervention for vector control on mosquito-borne diseases, we develop a model with complete CI and imperfect maternal transmission, and present a detailed mathematical analysis on the dynamics of Wolbachia spread. The main purpose of this manuscript is to dissect the effect of imperfect maternal transmission on Wolbachia spreading, which has not been studied in the existing literature.

To proceed, we divide the mosquitoes into four classes: uninfected females $U_F$, infected females $I_F$, uninfected males $U_M$, and infected males $I_M$. Assume that $U_F: U_M=I_F:I_M$ and hence the population can be formally considered hermaphroditic. Let $I$ and $U$ denote the total numbers of infected, and uninfected mosquitoes, respectively, i.e., $I=I_F+I_M$ and $U=U_F+U_M$. Let $\mu\in (0, 1)$ be the proportion of uninfected ova produced by an infected female. Following [22,41], we let $b_U$ denote the average number of offspring produced by one uninfected female. Let $\delta_U$ denote the constant death rate for uninfected mosquitoes. For generality, we introduce $b_I$ and $\delta_I$ as the corresponding parameters for infected mosquitoes as Wolbachia infection usually modifies the fitness and the longevity [25,35] of the host. CI arises when an uninfected ova, born from infected females or uninfected females, is fertilized by the sperm from an infected male. Then, with complete CI between $I_M$ and $U_F$ [1,2,35,39] and random mating, no uninfected adult progeny will be observed from the crossing of $I_F\times I_M$. Uninfected adult progeny still arise from the crossing $I_F\times U_M$ due to imperfect transmission. With random mating, the chance of a female crossing with $U_M$ is $U_M/(I_M+U_M)=U/(I+U)$, and the chance of a female crossing with $I_M$ is $I_M/(I_M+U_M)=I/(I+U)$. The latter one is also the probability of CI-occuring. Our model takes the form

$\frac{dI}{dt}= b_I I\cdot\frac{I}{I+U}+ b_I(1-\mu)I\cdot\frac{U}{I+U} -\delta_II (I+U),\label{I}\\ $

(1)

$\frac{dU}{dt}= b_I \mu I\cdot\frac{U}{I+U}+b_U\cdot U\cdot\Big (1-\frac{I}{ I+U }\Big)-\delta_U U (I+U).\label{U}$

(2)

In (2), the first term accounts for the birth of uninfected progeny from infected mothers, and the second term accounts for the birth from uninfected mothers, who have a probability $I/(I+U)$ to mate with infected males, and a contribution to the birth reduced by a factor $1-I/(I+U)=U/(I+U)$ due to complete CI.

If we apply the rescaling

$x=\frac{\delta_U}{b_U} I, y= \frac{\delta_U}{b_U} U, s= b_U \, t, \beta= \frac{b_I}{b_U}, \delta=\frac{\delta_I}{\delta_U},$

(3)

and rewrite $d\cdot/ds$ as $d\cdot/dt$, then we can transform (1)-(2) into

$\frac{dx}{dt}=\beta \frac{x^2}{x+y}+\beta(1-\mu)\frac{xy}{x+y} -\delta x (x+y):=f(x, y),\label{7}$

(4)

$\frac{dy}{dt}= \beta\mu \frac{xy}{x+y}+ \frac{ y^2}{x+y}- y(x+y):=g(x, y).\label{8}$

(5)

In [41], we studied the case of perfect maternal transmission (i.e., $\mu=0$), and included the average waiting time $\tau$ from parent mating to the emergence of reproductive progeny as a time delay in the model. We proved that when $\delta=1$, i.e., the infection does not alter the mean life span, Wolbachia can spread into the whole population as long as the infection frequency stays strictly above a threshold value for a period no less than the reproductive period $\tau$. Interestingly, we also found that such a threshold value of infection frequency cannot be well defined for $\delta\ne 1$. For the reduced system without maturation delay, we obtained sharp estimates on a threshold curve determined by the population sizes of both infected and uninfected mosquitoes. This is different from a differential equation for the fraction of Wolbachia-infected mosquitoes [29], with the assumptions of constant population size and perfect maternal transmission of Wolbachia, where the threshold infection frequency is unique.

The remaining part of this paper is divided into three sections. In Section 2, we prove invariance and boundedness of solutions to system (4)-(5), and present two useful identities together with additional preliminary results. These help us study the global dynamics in Section 3 and prove that the system can exhibit monomorphic, bistable, and polymorphic dynamics, and give sufficient and necessary conditions for each case. Imperfect maternal transmission could lead to infinitely many polymorphic states, see Theorem 3.1. Also, our discussions in Section 4 highlights some challenges associated with the release of $\it{w}$MelPop.

---

2. Preliminaries

---

2.1. Invariance and boundedness

Noticing that $f(x, y)\to 0$ and $g(x, y)\to 0$ as $(x, y)\to (0, 0)$, we can extend the domain of system (4)-(5) to including $(0, 0)$ by defining $f(0, 0)=g(0, 0)=0$. Then the system has the origin $E_0=(0, 0)$ as an equilibrium point. It is obvious that the $x$-axis, the $y$-axis, the first quadrant $\mathbb{R}_+^2:=\{(x, y): x\ge 0,\ y\ge 0\}$ and its interior set $\mathbb{R}_{+0}^2:=\{(x, y): x>0, y>0\}$ are all invariant sets of (4)-(5). For application purpose, we restrict our discussion on the first quadrant $\mathbb{R}_+^2$ only.

Lemma 2.1. Every solution of (4)-(5) initiated from the first quadrant is bounded. Moreover, for each $(x_0, y_0)$ with $x_0\ge 0$ and, $y_0\ge 0$,

$\omega(x_0, y_0)\subset \{(x, y): 0\leq x\leq \beta(2-\mu)/\delta,\ 0\leq y\leq\beta\mu+1\},$

(6)

where $\omega(x_0, y_0)$ is the set of limit points of solutions of (4)-(5) initiated from $(x_0, y_0)$.

Proof. Let $x(t)$ and $y(t)$ be solutions of (4)-(5) with $x_0\ge 0$, $y_0\ge 0$. It is seen that

$x'(t)<\beta x+\beta(1-\mu)x-\delta x^2 =\delta x\Big[\frac{\beta(2-\mu)}{\delta}-x\Big]$

Hence $x'(t)<0$ when $x(t)>\beta(2-\mu)/\delta$, implying immediately that

$\limsup\limits_{t\to\infty} x(t)\le \beta(2-\mu)/\delta.$

Similarly, if $y(t)>\beta\mu+1$, then

$y'(t)<(\beta\mu+1)y-y^2=y(\beta\mu+1-y)<0,$

and so $\limsup_{t\to\infty} y(t)\le \beta\mu+1$ and (6) is verified.

---

2.2. The equilibrium points

Besides $E_0$, system (4)-(5) always admits a Wolbachia-fixation equilibrium point $E_1=(\beta/\delta, 0)$ and a Wolbachia-free equilibrium point $E_2=(0, 1)$. Interior equilibria $(x, y)$, if any, are the intersections of the $x$-nullcline $f(x, y)=0$ and the $y$-nullcline $g(x, y)=0$, that is

$\Gamma_x: \beta x+\beta (1-\mu)y=\delta (x+y)^2,$

(7)

$\Gamma_y: \beta\mu x+y=(x+y)^2\label{Gamma(y)}.$

(8)

Multiplying (8) by $\delta$ and then comparing the resulting equation with (7), we see that $\Gamma_x$ and $\Gamma_y$ coincide if and only if

$(C1): \;\;\;\; \mu\delta=1, \;\;\text{and}\;\; \beta(1-\mu)=\delta.$

When (C1) is not satisfied, we subtract (7) by the product of (8) with $\delta$ and obtain

$\beta(1-\mu\delta)x=\big[\delta-\beta(1-\mu)\big]y.$

(9)

Lemma 2.2. System (4)-(5) admits interior equilibrium points if and only if one of the following conditions holds:

(C2): $\mu\delta>1, \;\;\text{and}\;\; \beta(1-\mu)>\delta;$

(C3): $\mu\delta<1, \;\;\text{and}\;\; \beta(1-\mu)<\delta$.

In this case, there is exactly one interior equilibrium point given by $E^*=(x^*, y^*)$ with

$x^*= \frac{\beta\mu+k}{(1+k)^2}, y^*= \frac{k(\beta\mu+k)}{(1+k)^2},$

(10)

where

$k:=\frac{\beta(1-\mu\delta)}{\delta-\beta(1-\mu)}.$

(11)

Proof. If the system admits interior equilibrium point $(x, y)$, then (9) implies $k>0$, so one of (C2) and (C3) must hold. On the other hand, either (C2) or (C3) gives $k>0$ and (9) becomes $y=kx$. By inserting it into (8) we derive the expressions of $x^*$ and $y^*$ as in (10).

If none of (C1)-(C3) holds, then system (4)-(5) does not admit any interior equilibrium point. For convenience of later discussion, we classify the remaining cases as the following 6 cases.

(C4): $\mu\delta<1, \;\;\text{and}\;\; \beta(1-\mu)>\delta$;

(C5): $\mu\delta<1, \;\;\text{and}\;\; \beta(1-\mu)=\delta;$

(C6): $\mu\delta=1, \;\;\text{and}\;\; \beta(1-\mu)>\delta$;

(C7): $\mu\delta>1, \;\;\text{and}\;\; \beta(1-\mu)<\delta;$

(C8): $\mu\delta>1, \;\;\text{and}\;\; \beta(1-\mu)=\delta$.

(C9): $\mu\delta=1, \;\;\text{and}\;\; \beta(1-\mu)<\delta.$

---

2.3. The Jacobian matrix and two auxiliary functions

As $f(x,y)>0$ and $g(x,y)>0$ when both $x>0$ and $y>0$ are sufficiently small, $E_0(0,0)$ is a repeller. To determine the stability of other equilibria, we first compute the determinant and the trace of the Jacobian matrix [13] of system (4)-(5):

$\mathbf{J}=\left(\begin{array}{ccccc} \displaystyle\beta-\beta\mu\cdot\frac{y^2}{(x+y)^2}-\delta(2x+y)&\displaystyle -\beta\mu\cdot\frac{x^2}{(x+y)^2}-\delta x\\ \\ \displaystyle (\beta\mu-1)\cdot \frac{y^2}{(x+y)^2}-y&\displaystyle \beta\mu\cdot \frac{x^2}{(x+y)^2}+\frac{y(2x+y)}{(x+y)^2}-(x+2y)\\ \end{array}\right).$

(12)

At $E_1(\beta/\delta, 0)$ and $E_2(0, 1)$, direct calculations give

$\mathbf{J}(E_1)= \left(\begin{array}{ccccc} -\beta -\beta(\mu+1)\\ 0 \beta(\mu\delta-1)/\delta\\ \end{array}\right), \mathbf{J}(E_2)=\left(\begin{array}{ccccc} \beta(1-\mu)-\delta 0\\ \beta\mu-2 -1\\ \end{array}\right)$

and at $E^*(x^*, y^*)$ by using $y^*=kx^*$ we find

$\mathbf{J}(E^*)=\left(\begin{array}{ccccc} \displaystyle \beta-\frac{\beta\mu k^2}{(k+1)^2}-\delta(2+k)x^* \displaystyle-\frac{\beta\mu}{(k+1)^2}-\delta x^*\\ \\ \displaystyle (\beta\mu-1)\cdot \frac{ k^2}{(k+1)^2} -kx^* \displaystyle\frac{\beta\mu}{(k+1)^2}+\frac{k(k+2)}{(k+1)^2}-(1+2k)x^*\end{array}\right).$

Lemma 2.3. (i) At $E^*$, we have

${\rm det}\; J(E^*) = \frac{\beta k}{(k+1)^2}\Big[\frac{\beta(1-\mu)}{\delta}\cdot\mu\delta-1\Big].$

(13)

(ii) The trace of $J$ at $E^*$ is

$tr\;J(E^*)=\frac{-k^2+(1-\beta)k-\beta}{(k+1)^2}.$

(14)

Proof. Write $J(E^*)=(J_{ij})_{2\times 2}$. By using the definition of $x^*$ we obtain

$J_{11}=\beta-\frac{\beta\mu k^2}{(k+1)^2}-\delta(2+k)\frac{\beta\mu+k}{(1+k)^2} \\\;\;\;\;\;=\frac{1}{(k+1)^2}\Big[\beta(k+1)^2-\beta\mu k^2-\delta (2+k)(\beta\mu+k)\Big]\\\;\;\;\;\;= \frac{1}{(k+1)^2}\Big[(\beta(1-\mu)-\delta)k^2+(2\beta-\beta\mu\delta-2\delta)k+\beta(1-2\mu\delta)\Big].$

By the definition of $k$ in (11), we have the identity

$\big[\beta(1-\mu)-\delta\big]k=-\beta(1-\mu\delta),$

and hence $J_{11}$ can be further reduced to

$J_{11}=\frac{1}{(k+1)^2}\Big[-\beta(1-\mu\delta)k+(2\beta-\beta\mu\delta-2\delta)k+\beta(1-2\mu\delta)\Big]\\ =\frac{1}{(k+1)^2}\Big[(\beta-2\delta)k+\beta(1-2\mu\delta)\Big].$

The other three entries $J_{12}$, $J_{21}$ and$J_{22}$ can be simplified similarly, and $J(E^*)$ is reduced to

$J(E^*)=\frac{1}{(k+1)^4}\left(\begin{array}{ccccc} (\beta-2\delta)k+\beta(1-2\mu\delta) -\delta k-\beta\mu(1+\delta)\\ k\big[(\beta\mu-2)k-\beta\mu\big] k\big[-k+(1-2\beta\mu)\big]\end{array}\right).$

(i) For notation simplicity, instead of calculating ${\rm det}\;J(E^*)$, we compute

$\bar{J}:=\frac{(k+1)^4}{k}{\rm det}\;J(E^*),$

and then

$\begin{align*} \bar{J}&=\big[(\beta-2\delta)k+\beta(1-2\mu\delta)\big]\cdot \big[-k+(1-2\beta\mu)\big]\\&+\big[\delta k+\beta\mu(1+\delta)\big]\cdot \big[(\beta\mu-2)k-\beta\mu\big]\\&=-\beta(1-\mu\delta)k^2+\big[(\beta\mu)^2\delta+(\beta\mu)^2+3\beta\mu\delta-2\beta^2\mu-2\beta\mu-2\delta\big]k\\& +3(\beta\mu)^2\delta+\beta-(\beta\mu)^2-2\beta^2\mu-2\beta\mu\delta.\end{align*}$

Note that (11) is equivalent to each of the following two identities

$\delta k=\beta(1-\mu) k+\beta(1-\mu\delta),$

(15)

$\beta\mu\delta=\beta+\big[\beta(1-\mu)-\delta\big]k,$

(16)

which help us simplify $\bar{J}$ to the following

$\begin{align*} \frac{1}{\beta}\bar{J}&=-(1-\mu\delta)k^2+\Big\{\beta\mu+\mu\big[\beta(1-\mu)-\delta\big]k+\beta\mu^2+3\mu\delta-2\beta\mu-2\mu\Big\}k\\&-2(1-\mu)k-2(1-\mu\delta)+3\mu\Big\{\beta+\big[\beta(1-\mu)-\delta\big]k\Big\}\\&+1-\beta\mu^2-2\beta\mu-2\mu\delta\\&= (\beta\mu-\beta\mu^2-1)k^2+2(\beta\mu-\beta\mu^2-1)k+(\beta\mu-\beta\mu^2-1)\\&= (\beta\mu-\beta\mu^2-1)(k+1)^2= \Big[\frac{\beta(1-\mu)}{\delta}\cdot\mu\delta-1\Big](k+1)^2.\end{align*}$

Therefore

${\rm det}\;J(E^*)=\frac{k}{(k+1)^4}\bar{J}= \frac{\beta k}{(k+1)^2}\Big[\frac{\beta(1-\mu)}{\delta}\cdot\mu\delta-1\Big].$

(ii) Again, by using of (15), $\text{tr}J^*$ can be simplified to

$\begin{align*} \text{tr}J^*&=J_{11}+J_{22}\\&= \frac{1}{(k+1)^2}\Big[(\beta-2\delta)k+\beta(1-2\mu\delta)-k^2+(1-2\beta\mu)k\Big] \\&= \frac{1}{(k+1)^2}\Big[-k^2+(\beta-2\delta+1-2\beta\mu)k+\beta(1-2\mu\delta)\Big] \\&= \frac{1}{(k+1)^2}\Big[-k^2+(\beta+1-2\beta\mu)k-2\delta k+\beta(1-2\mu\delta)\Big]\\&= \frac{1}{(k+1)^2} \Big[-k^2+(\beta+1-2\beta\mu)k-2\beta(1-\mu)k\\&-2\beta(1-\mu\delta)+\beta(1-2\mu\delta)\Big]\\&= \frac{1}{(k+1)^2} \Big[ -k^2+(1-\beta)k-\beta\Big]. \end{align*}$

This completes the proof.

Lemma 2.4. Assume that $\gamma(t)=(x(t), y(t))$ is a solution of (4)-(5) in $\mathbb{R}_{+0}^2$, let

${zt} z(t)=\ln \left(x^{1/\delta}(t)y^{-1}(t)\right)$

(17)

Then the derivative of $z(t)$ satisfies

${z'(t)} z'(t) =\frac{\beta}{\delta}(1-\mu\delta)\frac{x}{x+y}+\Big[\frac{\beta(1-\mu)}{\delta}-1\Big]\frac{y}{x+y}.$

(18)

Proof. By rewriting $z(t)=(1/\delta)\ln x(t) -\ln y(t)$ and taking derivatives, we find

$\begin{align*} z'(t)&= \frac {f(x, y)}{\delta x}-\frac {g(x,y)}{y}\\ &=\frac{\beta}{\delta} \frac{x}{x+y}+\frac{\beta(1-\mu)}{\delta} \frac{y}{x+y}-\frac{\beta\mu x}{x+y}-\frac{y}{x+y} \\ &=\frac{\beta}{\delta}(1-\mu\delta)\frac{x}{x+y}+\Big[\frac{\beta(1-\mu)}{\delta}-1\Big]\frac{y}{x+y}.\end{align*}$

This completes the proof.

For fixed constant $c>0$, we denote by $L_c$ the ray $y=cx, \, x> 0$. Also for a solution $\gamma(t)=(x(t), y(t))$ of (4)-(5) in $\mathbb{R}_{+0}^2$, let $l_c(t)=cx(t)-y(t).$ Obviously, if $\gamma(t)=(x(t), y(t))\in L_c$, then $l_c(t)=0$. Moreover, we have

Lemma 2.5. For fixed constant $c>0$ and any solution $(x(t), y(t))$ of (4)-(5) in $\mathbb{R}_{+0}^2$, we have

${lc'(t)} l'_c(t)|_{L_c}=y \Big[ (\delta-1) \frac{f(x, y)}{\delta x}+z'(t)\Big].$

(19)

proof. By interchanging $cx$ with $y$ when necessary, we obtain from (4)-(5) that

$\begin{align*} &l'_c(t)|_{L_c}\\&= c\Big[\frac{\beta x^2}{x+y}+\beta(1-\mu)\frac{x y}{x+y}-\delta x(x+y)\Big]-\Big[\beta\mu\frac{x y}{x+y}+\frac{y^2}{x+y}-y(x+y)\Big]\\ &= y\Big[\frac{\beta x}{x+y}+\beta(1-\mu)\frac{y}{x+y}-\delta(x+y)-\beta\mu\frac{x}{x+y}-\frac{y}{x+y}+(x+y)\Big]\\ &= y\Big[\beta(1-\mu)-\frac{y}{x+y}-(\delta-1)(x+y)\Big]\\ &= y\Big\{(\delta-1)\Big[\frac{\beta}{\delta}-\frac{\beta\mu}{\delta}\frac{y}{x+y}-(x+y)\Big]+\beta(1-\mu)-\frac{y}{x+y}\\&+\frac{\beta\mu(\delta-1)}{\delta}\frac{y}{x+y}-\frac{\beta(\delta-1)}{\delta}\Big\}\\ &= y \Big\{(\delta-1)\Big[\frac{\beta}{\delta}-\frac{\beta\mu}{\delta}\frac{y}{x+y}-(x+y)\Big]\\&+\Big[\frac{\beta}{\delta}-\frac{\beta\mu}{\delta}\frac{y}{x+y}-\beta\mu\frac{x}{x+y}-\frac{y}{x+y}\Big]\Big\}\\&=y \Big\{(\delta-1)\Big[\frac{\beta}{\delta}-\frac{\beta\mu}{\delta}\frac{y}{x+y}-(x+y)\Big]+ \frac{\beta}{\delta}(1-\mu\delta)\frac{x}{x+y}\\&+\Big[\frac{\beta(1-\mu)}{\delta}-1\Big]\frac{y}{x+y}\Big\}.\end{align*}$

By applying the relation (18) and

$\frac{\beta}{\delta}-\frac{\beta\mu}{\delta}\frac{y}{x+y}-(x+y)=\frac{f(x, y)}{\delta x},$

the proof is completed.

---

3. Stability of equilibria

$E_0(0, 0)$ is always a repeller since $f(x, y)>0$ and $g(x, y)>0$ when both $x>0$ and $y>0$ are sufficiently small. In this section, we shall analyze the stability of equilibria and the global dynamics of system (4)-(5). The primary tool in our proof is (13) and (14) in Lemma 2.3, differential identities (18) in Lemma 2.4, and (19) in Lemma 2.5.

---

3.1. The degenerate case (C1)

Assume that (C1) holds. Then both $E_1$ and $E_2$ are degenerate since $J(E_1)$ and $J(E_2)$ have zero as their eigenvalues. Furthermore, system (4)-(5) is reduced to

$\frac{dy}{dx}= \frac{y}{\delta x},$

(20)

and the two nullclines defined in (7) and (8) are identical. All points on this coincident nullcline in $\mathbb{R}_{+0}^2$, including $E_1$ and $E_2$ on the boundary, are equilibrium points.

Theorem 3.1. Let (C1) hold. Let $(x(t), y(t))$ be the solution of (4)-(5) initiated from $(x_0, y_0)\in \mathbb{R}_{+0}^2\setminus \Gamma_y$. Then

$y=y_0\Big(\frac{x}{x_0}\Big)^{1/\delta},$

(21)

and $(x(t), y(t))\to (x_+, y_+)$ as $t\to +\infty$, where $(x_+, y_+)\in \mathbb{R}_{+0}^2$ is the only intersecting point of $(21)$ and the coincident nullcline $\Gamma_y$.

Proof. The relation (21) is easily derived by solving (20) with the initial condition. The only non-trivial part in the proof of the remaining conclusions is to show that $(21)$ intersects the nullcline $\Gamma_y$ (or $\Gamma_x$ as they are identical) exactly once at $(x_+, y_+)\in \mathbb{R}_{+0}^2$.

Let $(x, y)\in\Gamma_y\cap \mathbb{R}_{+0}^2$. Since

$\beta(1-\mu)=\delta=\frac{1}{\mu} \Longrightarrow \beta\mu=\frac{1}{1-\mu}>1,$

it holds that

$x+y<\beta \mu x+y=(x+y)^2<\beta \mu x+\beta \mu y, 1<x+y<\beta \mu.$

Now if $\beta\mu\leq 2$, by taking derivative with respect to $x$ on both sides of (8), we have

$\frac{dy}{dx}=-\frac{2(x+y)-\beta\mu}{2(x+y)-1}<0.$

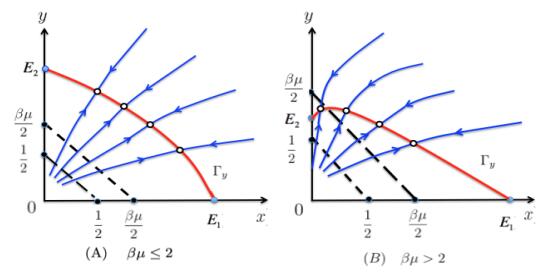
Hence $y$ decreases in $x$ along $\Gamma_y$ in $\mathbb{R}_{+0}^2$, and the increasing curve (21) intersects it exactly once for $x_+\in (0, \beta\mu)$, see Figure 1-(A).

If $\beta\mu>2$, then $E_2$ lies between $(0, \beta\mu/2)$ and $(0, 1/2)$, and $\Gamma_y$ increases from $E_2$ until hitting the straight line $x+y=\beta\mu/2$, then decreases until reaching $E_1$ (See Figure 1-(B)). We only need to prove that if (21) cuts $\Gamma_y$ within $1/2<x+y<\beta\mu/2$, then it can cut only once. To the end, it suffices to prove that the slope of the tangent line to the curve (21) is always greater than the slope of the tangent line to $\Gamma_y$ at possible intersecting points when $1/2<x+y<\beta\mu/2$, i.e.,

$\frac{y}{\delta x}>\frac{\beta\mu-2(x+y)}{2(x+y)-1} .$

(22)

Actually, by using $\mu\delta=1$ and the expression of $\Gamma_y$, we have

$\begin{align*} (22)&\Leftrightarrow y\big[2(x+y)-1\big]>\delta x\big[\beta\mu-2(x+y)\big] \\&\Leftrightarrow 2y(x+y)-y>\beta x-2\delta x(x+y) \\&\Leftrightarrow 2(x+y)(y+\delta x)>\beta x+y \\&\Leftrightarrow 2(x+y)^2(y+\delta x)>(\beta x+y)(x+y) \\&\Leftrightarrow 2(y+\beta\mu x)(y+\delta x)>(y+\beta x)(y+x) \\&\Leftrightarrow y^2+\big[2\delta +2\beta\mu-\beta-1\big]xy+\beta x^2>0. \end{align*}$

The last inequality always holds for case (C1) due to

$\beta=\frac{\delta}{1-\mu}=\frac{1}{\mu(1-\mu)}>1,$

and hence

$2\delta +2\beta\mu-\beta-1=2\beta(1-\mu)+2\beta\mu-\beta-1=\beta-1>0.$

This completes the proof.

---

3.2. Polymorphism and bistability

The following theorem shows that Condition (C2) leads to a polymorphic scenario.

Theorem 3.2. Let (C2) hold. Then both $E_1$ and $E_2$ are saddle points, and the interior equilibrium point $E^*(x^*,y^*)$ is globally asymptotically stable: for each point $(x,y)\in \mathbb{R}_{+0}^2$, $\omega(x,y)=E^*$.

Proof.Both $E_1$ and $E_2$ are saddle points since their Jacobian matrix have one positive and one negative eigenvalue. By (13), ${\rm det}\;J(E^*)>0$. Meanwhile, we have

$\mu\delta>1 \Rightarrow \delta>1 \Rightarrow \beta(1-\mu)>\delta>1 \Rightarrow \beta>\frac{1}{1-\mu}>1, \label{delta>1}$

(23)

and hence,

$tr J(E^*)=\frac{-k^2+(1-\beta)k-\beta}{(k+1)^2}<0.$

Thus $E^*$ is locally asymptotically stable. To prove its global stability, it suffices to show that there is no closed orbits. Take

$B(x, y)= 1/(xy^2)>0$

(24)

in $\mathbb{R}_{+0}^2$. The divergence of the vector field $(Bf, Bg)$ satisfies

$\begin{align*} &\nabla \cdot(Bf, Bg)\\&=\frac{\partial}{\partial x}\Big[\frac{\beta x}{y^2(x+y)}+\frac{\beta(1-\mu)}{y(x+y)}-\frac{\delta(x+y)}{y^2}\Big]\\&+\frac{\partial}{\partial y}\Big[\frac{\beta\mu}{y(x+y)}+\frac{1}{x(x+y)}-\frac{x+y}{xy}\Big]\\ &=\frac{\beta}{y(x+y)^2}-\frac{\beta(1-\mu)}{y(x+y)^2}-\frac{\delta}{y^2}-\beta\mu\frac{x+2y}{y^2(x+y)^2}-\frac{1}{x(x+y)^2}+\frac{1}{y^2}\\ &=-\beta\mu\Big[\frac{x}{y^2(x+y)^2}+\frac{1}{y(x+y)^2}\Big]-\frac{1}{x(x+y)^2}+\frac{1-\delta}{y^2}<0\end{align*}$

which declares nonexistence of closed orbits in $\mathbb{R}_{+0}^2$ by the Dulac's criterion [13].

The following theorem indicates that (C3) corresponds to a bistable scenario.

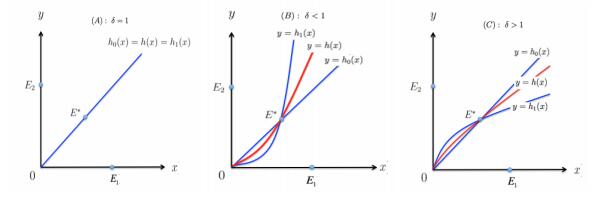
Theorem 3.3. Assume that (C3) holds. Then the unique interior equilibrium point $E^*(x^*, y^*)$ is a saddle point, and $E_1$ and $E_2$ are locally asymptotically stable. Moreover, denoting by $y=h(x)$ the stable manifold of $E^*$, $h(x)$ is continuous and increasing, and is the separatrix that defines the basins of attraction of $E_1$ and $E_2$ in $\mathbb{R}_{+0}^2$, and it lies between $h_0(x)$ and $h_1(x)$, where

$h_0(x)=\frac{y^*}{x^*}x, h_1(x)=y^*\Big(\frac{x}{x^*}\Big)^{1/\delta}.$

(25)

Proof.Condition $\mu\delta<1$ (resp. $\beta(1-\mu)<\delta$) in (C3) implies that $J(E_1)$ (resp. $J(E_2)$) has two negative eigenvalues, and hence both $E_1$ and $E_2$ are locally asymptotically stable under (C3). Moreover, ${\rm det}\;J(E^*)<0$ by (13), and hence $E^*$ is a saddle point.

Noticing that along $y=cx$, (18) implies that

$z'(t)|_{y=cx} =\frac{\beta(1-\mu\delta)-\big[\delta-\beta(1-\mu)\big] c}{\delta (1+c)}.$

(26)

We have

$z'(t)|_{y=cx}=0 \Leftrightarrow c=k; z'(t)|_{y=cx}<0 \Leftrightarrow c>k; z'(t)|_{y=cx}>0 \Leftrightarrow c<k.$

(27)

By (19), we have

$l'_k(t)|_{L_k}=y(\delta-1) \frac{f(x, y)}{\delta x}.$

There are three cases to consider.

(i) $\delta=1$. Then $l'_{k}(t)|_{L_k}\equiv 0$, implying that $L_k: y=kx$ consists of solution curves of system (4)-(5), which also serves as the stable manifold of $E^*$.

(ii) $\delta>1$. Consider the domain

$\mathcal{D}_{1}=\big\{(x,y): \, 0<x<x^*,\ h_0(x)<y<h_1(x)\big\}.$

We claim that $\mathcal{D}_{1}$ is negatively invariant with respect to the dynamics of (4)-(5). In fact, on its upper boundary where $y=h_1(x)$, (27) implies that $z'(t)<0$. On its lower boundary $y=h_0(x)$,

$\displaystyle l'_k(t)|_{L_k}=y(\delta-1) \frac{f(x, y)}{\delta x}>0.$

It follows that solutions of system (4)-(5) initiated within $\mathcal{D}_{1}$ other than the origin and $E^*$ will leave this region in finite time and stay outside thereafter.

Similarly, consider

$\mathcal{D}_{2}=\big\{(x,y): \, x>x^*,\, h_1(x)<y<h_0(x)\big\}.$

Then we have $l'_k(t)|_{L_k}<0$ on its upper boundary $y=h_0(x)$, and $z'(t)> 0$ on the lower boundary $y=h_1(x)$. Consequently, the stable manifold of $E^*$ must locate inside $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ and (2) is verified.

(iii) $\delta<1$. By using the same argument as above, the negative invariance of

$\mathcal{D}_{3}=\big\{(x,y): \, 0<x<x^*,\, h_1(x)<y<h_0(x)\big\}$

and

$\mathcal{D}_{4}=\big\{(x,y): \, x>x^*,\, h_0(x)<y<h_1(x)\big\}$

could be proved by dissecting the sign of $l'_k(t)|_{L_k}$ and $z'(t)$ on the boundaries.

---

3.3. Monomorphism

Theorem 3.4. Assume that one of the Conditions (C4), (C5) and (C6) holds. Then $E_1$ is globally asymptotically stable: for each point $(x,y)\in \mathbb{R}_{+0}^2$, $\omega(x,y)=E_1$.

Proof.From (18), $z'(t)>0$ always holds for these 3 cases, showing that (4)-(5) does not have any non-trivival periodic solution. We claim that $E_2$ could not be the $\omega$-limit set of the trajectory $(x(t), y(t))$ initiated from $\mathbb{R}_{+0}^2$. For cases (C4) and (C6), it is trivial since $E_2$ is a hyperbolic saddle point with the stable manifold on the $y$-axis. However, $E_2$ becomes non-hyperbolic for case (C5), whose local stability cannot be determined by the Jacobian matrix approach. In this case, since $z'(t)>0$, it holds that $z(t)>z(0)$ for all $t>0$, and so $E_2$ cannot be an $\omega$-limit point. Hence, $\omega(x,y)=E_1$ by the classical Poincar$\acute{e}$-Bendixson theorem [13].

Theorem 3.5. Assume that one of the Conditions (C7), (C8) and (C9) holds. Then $E_2$ is globally asymptotically stable in the sense that for each point $(x,y)\in \mathbb{R}_{+0}^2$, $\omega(x,y)=E_2$.

Proof.It is easily seen that $z'(t)<0$ for all cases, which again implies that (4)-(5) does not have non-trivial periodic solution. The equilibrium point $E_1$ could not be the $\omega$-limit set of any trajectory $(x(t), y(t))$ in $\mathbb{R}_{+0}^2$ for cases (C7) and (C8) since it is a hyperbolic saddle point with the stable manifold on the $x$-axis. For case (C9), since $z'(t)<0$, it holds that $z(t)<z(0)$ for all $t>0$, and so $E_1$ cannot be an $\omega$-limit point. Hence, $\omega(x,y)=E_2$ by the classical Poincar$\acute{e}$-Bendixson theorem [13].

---

4. Discussion

---

4.1. Polymorphism, bistability and monomorphism

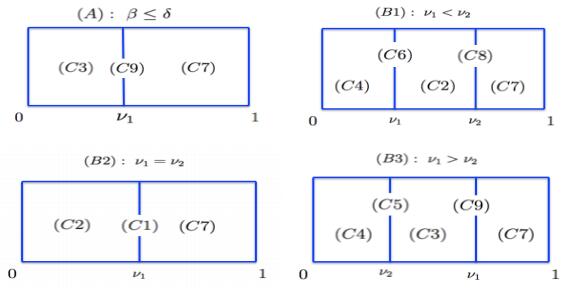
The asymptotic behavior of the Wolbachia spreading dynamics in a mixed population of infected and uninfected mosquitoes depends strongly on the life parameters modified by the Wolbachia infection. We classify the system parameters into Cases (C1) to (C9) and identify their correspondence to three different scenarios:

Polymorphism: Theorems 3.1 and 3.2 show that the mixed population remains polymorphic for which both infected and uninfected mosquitoes coexist when (C1) or (C2) holds. If the degenerate case (C1) occurs, then the ultimate coexistent state may change with the initial infection level. When (C2) occurs, the asymptotic population size is independent of the initial value and the infection frequency at the steady-state is $x^*/(x^*+y^*)$.

Bistability: For case (C3), Theorem 3.3 offers a sharp threshold given by the separatrix $y=h(x)$ on the initial values for successful Wolbachia invasion. If Wolbachia does not alter the longevity of the mosquito, i.e., $\delta=1$, then the stable manifold of $E^*$ coincides with $h_0(x)\equiv h_1(x)$, see Figure 2-(A). If $\delta\neq 1$, then $y=h(x)$ is nested by the straight line $y=h_0(x)$ and the curve $y=h_1(x)$, see Figure 2-(B) ($\delta<1$) and Figure 2-(C) ($\delta>1$). For these three cases, the solution initiated below $y=h(x)$ approaches Wolbachia fixation equilibrium point $E_1$, while the solution initiated above $y=h(x)$ approaches Wolbachia free equilibrium point $E_2$.

Monomorphism: Theorem 3.4 implies that under either (C4) or (C5) or (C6), for any initial positive release, the Wolbachia infected mosquitoes will eventually replace the wild ones. Theorem 3.5 shows that under either (C7) or (C8) or (C9), Wolbachia infection will fail to establish, regardless of the number of initial release.

With perfect maternal transmission rate, i.e., $\mu_1=\mu_2=0$, system (4)-(5) is reduced to

$\frac{dx}{dt}=\beta x -\delta x (x+y),$

(28)

$\frac{dy}{dt}=\frac{ y^2}{x+y}- y(x+y)$

(29)

When $\beta/\delta \ge 1$, the environment is more favorable (or at least equally favorable) for infected mosquitoes, and we say that Wolbachia infection has a fitness benefit. In this case, system (28)-(29) only admits the Wolbachia free equilibrium point $E_2$ and the Wolbachia replacement equilibrium point $E_1$. Theorem 3.4 for Cases (C4) or (C5) shows that successful Wolbachia spreading is ensured from any initial release above 0 for the fitness benefit case. When $\beta<\delta$, we say that the infection has a fitness cost, and besides $E_1$ and $E_2$, there is a unique interior equilibrium point of system (28)-(29) which is a saddle point. Theorem 3.3 for Case (C3) displays bistable dynamics for the fitness cost case. These results are in line with the results in [41] which also include the corresponding results in [41] as special cases.

Comparing to perfect maternal transmission, the imperfect maternal transmission generates richer dynamics. To see this, we fix $\beta$ and $\delta$ and consider separately the fitness cost case (i): $\beta\leq \delta$, and the benefit case (ii): $\beta>\delta.$ We explore the impact of $\mu>0$ in terms of its relation with two critical values

$\nu_1=\frac{1}{\delta}, \nu_2=1-\frac{\delta}{\beta}.$

The detailed outcomes in different cases are shown in Figure 3. For example, in the fitness cost case (i), small $\mu$ corresponds to the bistable case (C3). However, increasing $\mu$ leads to (C9) and (C7), for which all solutions are attracted to $E_2$, and Wolbachia will be eventually wiped out, no matter how many infected mosquitoes are initially released. Thus, we see a transition from the bistable state to the monomorphic state $E_2$ as $\mu$ increases. In the fitness benefit case (ii) with $\nu_1<\nu_2$, small $\mu$ corresponds to (C4) and (C6), for which all solutions converge to $E_1$: Wolbachia infected mosquitoes will eventually replace the wild ones, as long as $\mu<\nu_1$. But when $\mu$ is large, (C4) is replaced by (C2), (C8) and (C7) consecutively, which again implies the failure of the release because all solutions converge to $E_2$. Thus, there is also a transition of convergences to equilibria when $\mu>0$ is increased: transition from convergence to the replacement equilibrium $E_1$ to convergence to $E^*$ (the unique positive equilibrium, giving a unique polymorphic outcome), and finally to the failure equilibrium $E_2$. This is in contrast to the transition in (i) which is a transition from the bistable state to the monomorphic state $E_2$.

---

4.2. Success or failure: Review on some recent releases

We consider two Wolbachia strains, the benign $\it{w}$Mel and the virulent $\it{w}$MelPop, of Aedes aegypti in Australia. It was found that $\it{w}$Mel caused only 10% longevity reduction and no significant fecundity cost [35], but $\it{w}$MelPop decreased the longevity of infected female mosquitoes by $\sim$50% and resulted in a fecundity cost of $\sim$56% [25]. By using the laboratory data in [25,35], we estimated the birth rates $b_I$ and $b_U$ from the oviposition rate, egg hatching rate and survival rate of larvae to adults, as well as the death rates $\delta_I$ and $\delta_U$ from the half-life of adults [41]. We found that $b_U=0.3976$ and $\delta_U=8.5034\times 10^{-6}$, and for the benign Wolbachia strain $\it{w}$Mel: $b_I=0.3976$, $\delta_I=9.4482\times 10^{-6},$ and for the virulent Wolbachia strain $\it{w}$MelPop: $b_I=0.2154$, $\delta_I=1.4172\times 10^{-5}.$ These parameter values lead to

$\beta=\frac{0.3976}{0.3976}=1, \delta=\frac{9.4482\times 10^{-6}}{8.5034\times 10^{-6}}\approx 1.1111$

for the benign $\it{w}$Mel, and

$\beta=\frac{0.2154}{0.3976}\approx 0.5418, \delta=\frac{1.4172\times 10^{-5}}{8.5034\times 10^{-6}}\approx1.6667$

for the virulent $\it{w}$MelPop.

In 2011, the Wolbachia strain $\it{w}$Mel was introduced into Aedes aegypti populations in some northern Australian field sites [17] and had almost completely replaced wild mosquitoes for more than 3 years [10,18]. Since September 2014, the $\it{w}$Mel mosquitoes were released in two neighborhoods in Brazil [5]: Tubiacanga in Rio de Janeiro (2014-2015) and Jurujuba in Niteroi (2015) to reduce dengue transmission. Successful or ongoing field trials also include the $\it{w}$Mel release in January 2014 in Indonesia, and in May 2015 in Colombia. Achievements of these field trials have been so encouraging that the strategy is becoming a worldwide plan to combat Zika and other mosquito-borne viruses.

In contrast to the effective and sustainable invasion of the $\it{w}$Mel release in Australia, the 2013 $\it{w}$MelPop trial in central Vietnam (Tri Nguyen, Hon Mieu Island) [26] was a failure: $\it{w}$MelPop could be established transiently, but not persistently, in any of the two sites. The failure was largely attributed to the virulent property of the $\it{w}$MelPop that causes the infected mosquitoes to have a shorter lifespan ($\delta=1.6667>1$) and produce fewer offspring than the wild ones ($\beta=0.5418<1$).

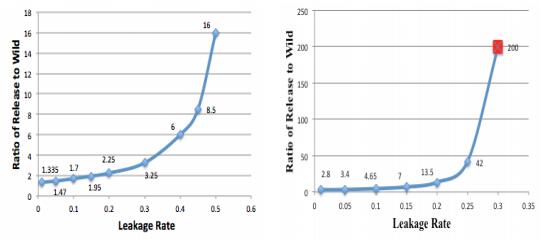
We can claim that maternal transmission leakage even makes a transient establishment of Wolbachia in the wild mosquito population a big challenge. Consider again the $\it{w}$MelPop strain as an example. Given the uninfected mosquito's density $y_0$ and the leakage rate $\mu$, if the maternal transmission leakage occurs, then (4)-(5) determines a unique Wolbachia release threshold $x_0=x_0(y_0, \mu)$. We plot the ratio $x_0/y_0$ against the leakage rate in the left panel in Figure 4. It displays a steep elevation of the threshold ratio $x_0/y_0$ for a successful Wolbachia invasion as the leakage $\mu$ increases from 0.3 to 0.5, and reaches as high as 16 when $\mu=0.5$. Furthermore, should the leakage is accompanied by incomplete CI as shown in [28], the scenario is even more discouraging. It was shown in [28] that, among 1848 eggs from the crossing of uninfected females and $w$MelPop-infected males, 301 (16.31%) hatched. This leads to a reduction of the CI intensity $s_h$ from $s_h=1$ in (4)-(5) to $s_h=0.8369$. With the incorporation of incomplete CI, the model is modified to

$\frac{dx}{dt}=\beta \frac{x^2}{x+y}+\beta(1-\mu)\frac{xy}{x+y} -\delta x (x+y),$

(30)

$\frac{dy}{dt}= \beta\mu \frac{xy}{x+y}+ y\cdot\Big(1-s_h\cdot\frac{ x}{x+y}\Big)- y(x+y).$

(31)

Again, we can determine the unique threshold value $x_0=x_0(y_0, \mu, s_h)$. In this case, a small increase on the leakage rate could bring a catastrophic failure of Wolbachia release. As shown in the right panel in Figure 4, the threshold ratio is as large as 7 when $\mu=0.15$. Further increase of the leakage rate from 0.15 to 0.25 results in an augment of 6-fold on the threshold ratio. If $\mu=0.3$, we found that even if the ratio is as large as 200, Wolbachia will be wiped out. Our example highlights some challenges associated with releasing $\it{w}$MelPop, which is in line with the results in [26,28].

---

5. Acknowledgments

This work was supported by National Natural Science Foundation of China (11631005,11626246,11571084), Program for Changjiang Scholars and Innovative Research Team in University (IRT_16R16), and National Research and Development Plan of China (2016YFC1200500). We thank the anonymous reviewers for their careful reading of our manuscript and stimulating comments.

---