Our investigation is motivated by the need to design bilayer membranes with tunable interfacial and mechanical properties for use in a range of applications, such as targeted drug delivery, sensing and imaging. We draw inspiration from biological cell membranes and focus on their principal constituents. In this paper, we present our results on the role of molecular architecture on the interfacial, structural and dynamical properties of bio-inspired membranes. We focus on four lipid architectures with variations in the head group shape and the hydrocarbon tail length. Each lipid species is composed of a hydrophilic head group and two hydrophobic tails. In addition, we study a model of the Cholesterol molecule to understand the interfacial properties of a bilayer membrane composed of rigid, single-tail molecular species. We demonstrate the properties of the bilayer membranes to be determined by the molecular architecture and rigidity of the constituent species. Finally, we demonstrate the formation of a stable mixed bilayer membrane composed of Cholesterol and one of the phospholipid species. Our approach can be adopted to design multi-component bilayer membranes with tunable interfacial and mechanical properties. We use a Molecular Dynamics-based mesoscopic simulation technique called Dissipative Particle Dynamics that resolves the molecular details of the components through soft-sphere coarse-grained models and reproduces the hydrodynamic behavior of the system over extended time scales.
Citation: Koufos Evan, Muralidharan Bharatram, Dutt Meenakshi. Computational Design of Multi-component Bio-Inspired Bilayer Membranes[J]. AIMS Materials Science, 2014, 1(2): 103-120. doi: 10.3934/matersci.2014.2.103
| [1] | Michael Sebastiano, Xiaolei Chu, Fikret Aydin, Leebyn Chong, Meenakshi Dutt . Interactions of Bio-Inspired Membranes with Peptides and Peptide-Mimetic Nanoparticles. AIMS Materials Science, 2015, 2(3): 303-318. doi: 10.3934/matersci.2015.3.303 |
| [2] | Martin O. Steinhauser . Multiscale modeling, coarse-graining and shock wave computer simulations in materials science. AIMS Materials Science, 2017, 4(6): 1319-1357. doi: 10.3934/matersci.2017.6.1319 |
| [3] | P. Di Pietro, G. Forte, L. D’Urso, C. Satriano . The hybrid nanobiointerface between nitrogen-doped graphene oxide and lipid membranes: a theoretical and experimental study. AIMS Materials Science, 2017, 4(1): 43-60. doi: 10.3934/matersci.2017.1.43 |
| [4] | Shaohua Chen, Yaopengxiao Xu, Yang Jiao . Modeling solid-state sintering with externally applied pressure: a geometric force approach. AIMS Materials Science, 2017, 4(1): 75-88. doi: 10.3934/matersci.2017.1.75 |
| [5] | Grujicic Mica, Ramaswami S., S. Snipes J., Yavari R. . Multi-Scale Computation-Based Design of Nano-Segregated Polyurea for Maximum Shockwave-Mitigation Performance. AIMS Materials Science, 2014, 1(1): 15-27. doi: 10.3934/matersci.2014.1.15 |
| [6] | Ravipati Praveena, Gottapu. Varaprasada Rao, Karna Balasubrahmanyam, M. Ghanashyam Krishna, Vinjanampati Madhurima . Optical and water repellant properties of Ag/SnO2 bilayer thin films. AIMS Materials Science, 2016, 3(1): 231-244. doi: 10.3934/matersci.2016.1.231 |
| [7] | Gérrard Eddy Jai Poinern, Nurshahidah Ali, Xuan Le, Derek Fawcett . Nano-hardness and elastic modulus of anodic aluminium oxide based Poly (2-hydroxyethylmethacrylate) composite membranes. AIMS Materials Science, 2014, 1(3): 159-173. doi: 10.3934/matersci.2014.3.159 |
| [8] | Serguei Chiriaev, Nis Dam Madsen, Horst-Günter Rubahn, Shuang Ma Andersen . Helium Ion Microscopy of proton exchange membrane fuel cell electrode structures. AIMS Materials Science, 2017, 4(6): 1289-1304. doi: 10.3934/matersci.2017.6.1289 |
| [9] | Charles Defor, Shih-Feng Chou . Electrospun polytetrafluoroethylene (PTFE) fibers in membrane distillation applications. AIMS Materials Science, 2024, 11(6): 1179-1198. doi: 10.3934/matersci.2024058 |
| [10] | Kengo Sawai, Keiya Sugiura, Toshio Ogawa, Ta-Te Chen, Fei Sun, Yoshitaka Adachi . Analysis of tensile properties in tempered martensite steels with different cementite particle size distributions. AIMS Materials Science, 2024, 11(5): 1056-1064. doi: 10.3934/matersci.2024050 |
Our investigation is motivated by the need to design bilayer membranes with tunable interfacial and mechanical properties for use in a range of applications, such as targeted drug delivery, sensing and imaging. We draw inspiration from biological cell membranes and focus on their principal constituents. In this paper, we present our results on the role of molecular architecture on the interfacial, structural and dynamical properties of bio-inspired membranes. We focus on four lipid architectures with variations in the head group shape and the hydrocarbon tail length. Each lipid species is composed of a hydrophilic head group and two hydrophobic tails. In addition, we study a model of the Cholesterol molecule to understand the interfacial properties of a bilayer membrane composed of rigid, single-tail molecular species. We demonstrate the properties of the bilayer membranes to be determined by the molecular architecture and rigidity of the constituent species. Finally, we demonstrate the formation of a stable mixed bilayer membrane composed of Cholesterol and one of the phospholipid species. Our approach can be adopted to design multi-component bilayer membranes with tunable interfacial and mechanical properties. We use a Molecular Dynamics-based mesoscopic simulation technique called Dissipative Particle Dynamics that resolves the molecular details of the components through soft-sphere coarse-grained models and reproduces the hydrodynamic behavior of the system over extended time scales.
Biological cell membranes are dynamic, adaptive, stimuli-responsive multi-component soft materials which separate the cytosol from the extracellular environment, and participate in vital functions, for example intracellular and extracellular traffic, sensing and cell signaling [1]. Soft materials are mesoscopic supramolecular structures assembled from the self-organization of nanoscopic building blocks such as lipid molecules whose predominant behavior occurs at room temperature. In addition to molecular-scale interactions between the nanoscopic units, the kinetics and thermodynamics of the structure, dynamics and function of cell membranes is dictated by hydrodynamic interactions which are predominant at the mesoscopic length scales. The complex interplay between these key factors across multiple scales determines the structure of the membrane and thereby the entire cell, and its responses to changes in the external environment such as temperature, pH and presence of ions, or binding or catalytic events at the membrane interface. The dynamic nature of this multi-component smart active biomaterial enables the modulation of membrane tension and thereby, its mechanical properties to facilitate various physiological processes. The molecular geometry and rigidity of the species will determine their packing and organization in the bilayer membrane [2,3], thereby influencing the mechanical and the interfacial properties of the membrane. Different types of cell membranes can be characterized by the composition of their constituent amphiphilic lipid or sterol species [4]. Hence, the innate responsive nature of cell membranes can inspire the design of robust soft materials with highly adaptive mechanical and interfacial properties. In addition, the ability to target certain cells by way of their specific membranes has lead to the development of new areas of medical research for applications in drug delivery, sensing and imaging [4,5,6,7,8]. Based on the surface chemistry of the cell membrane, nano-sized particles with active payloads can target specific cell membranes [9]. Therefore, there is a critical need to underst and the effect of the molecular geometry of the constituent species on the properties and functions of cell membranes.
There are challenges to using experimental approaches such as X-ray diffraction, NMR spectroscopy, and neutron diffraction to study the interactions of nano-sized particles with cell membranes [10], and the role of the individual molecular species on the interaction process. Computer simulations [11] can be used to elucidate the role of the membrane composition on the interaction between foreign particles and cell membranes, or the response of cell membranes to changes in external cues, through the use of suitable models and techniques. Earlier computational studies on lipid bilayers have adopted techniques such as Monte Carlo [12,13,14], and Molecular Dynamics [15,16,17,18,19,20]. Given the importance of hydrodynamic interactions on the properties of cell membranes, we adopt a Molecular Dynamics-based mesoscopic simulation technique which bridges the atomistic and continuum scales, and captures the hydrodynamic behavior of the system over extended time scales. This method is entitled Dissipative Particle Dynamics [10,20,21,22,23,24,25,26,27,28,29,30,31] and uses soft-repulsive core interaction models between the various particles which are coarse-grained representations of a group of atoms. This approach enables the study of complex dynamical and structural properties, and biological processes [32,33] which are not easily resolved by Molecular Dynamics [15,16,17]. In addition, DPD has been used to demonstrate the dependence of the phase behavior, the mechanical and interfacial properties of a lipid membrane on the membrane composition, hydrocarbon tail saturation, head group architecture, and hydrocarbon chain length [9,34,35]. Other investigations have examined the response of bilayer membranes to external stimuli [21,25,36]. Therefore, this approach can aid in the design and development of bio-inspired cells composed of phospholipid vesicles for targeted delivery of therapeutic compounds [11,37,38,39,40,41,42]. We would like to note that the DPD method has been used to provide insight into the interactions between nanoparticles and block copolymers [43,44].
Via the Dissipative Particle Dynamics (DPD) approach, we will investigate the role of the architecture of amphiphilic lipids on the interfacial, structural and dynamical properties of lipid bilayer membranes [21,25,26,27,28,29]. We focus on four lipid architectures with differing molecular geometries. The first lipid model represents DPPC (Dipalmitoylphosphatidylcholine) which is a cylindrical-shaped molecule with a large head group and two hydrocarbon tails [20,25,26,27,28,29,31]. The other three lipid models represent DMPC (Dimyristoyl-sn-glycero-3-phosphocholine) which is an inverted wedge-shaped molecule with a small head group and two-hydrocarbon tails [45]. The three models of DMPC have different hydrocarbon tail lengths. In addition, we have investigated a coarse-grained model for Cholesterol which has a small head group and a single rigid hydrocarbon tail with a steroid ring [46]. We have examined the interfacial properties of the Cholesterol molecule as a function of the inter-molecular spacing. Finally, we demonstrate the design of a stable mixed bilayer membrane composed of DPPC and cholesterol molecules using their average area per molecule corresponding to a tensionless bilayer. Our approach can be adopted for the conception and design of multi-component bilayer membranes with tunable mechanical and interfacial properties.
DPD is a mesoscopic MD-based simulation technique that uses soft-sphere coarse-grained (CG) models to capture both the molecular details of the system components and their supramolecular organization while simultaneously resolving the hydrodynamics of the system over extended time scales [9,10,11,21,47,48]. In order to capture the dynamics of the soft spheres, the DPD technique integrates Newton’s equation of motion via the use of similar numerical integrators used in other deterministic particle-based simulation methods [21,22]. The force acting on a soft sphere i due to its interactions with a neighboring soft sphere j (j ¹i) has three components: a conservative force, a dissipative force and a r and om force, which operate within a certain cut-off distance rc from the reference particle i. These forces are pairwise additive and yield the total force acting of particle i, which is given by Fi=∑j≠iFc,ij+Fd,ij+Fr,ij. The soft spheres interact via a soft-repulsive force (Fc,ij=aij(1−rij╱rc)rij, for rij < rc and and Fc,ij=0 , for rij ≥ rc), a dissipative force (Fd,ij=−γωd(rij)(ˆrij∙vij)ˆrij) and a random force (Fr,ij=−σωr(rij)θˆrij), where wd (r) =[wr (r) ]2= (1-r) 2 (for r<1) , and σ2=2γkBT. aij is the maximum repulsion between spheres i and j, vij = vi - vj is the relative velocity of the two spheres, rij = ri - rj, rij = |ri - rj|, ˆrij= rij/rij, r = rij/rc, γ is viscosity related parameter used in the simulations, qij (t) is a r and omly fluctuating variable from Gaussian statistics, wd and wr are the separation dependent weight functions which become zero at distances greater than or equal to the cutoff distance r c. Each force conserves linear and angular momentum. Since the local momentum is conserved by all of these three forces, even the small systems exhibit hydrodynamic behavior [21]. The constraints imposed on the r and om and dissipative forces by certain relations ensure that the statistical mechanics of the system conforms to the canonical ensemble [21,22]. The relation between the pair repulsion parameter aij and the Flory interaction parameter c for a bead number density r = 3 is given by [48].
As shown in Figure 1 (a) - (e), the individual lipid and cholesterol molecules are represented by bead-spring models. Two consecutive beads in a chain are connected via a bond that is described by the harmonic spring potential Ebond=Ebond ((r-b)/rc)2, where Kbond is the bond constant and b is the equilibrium bond length. The constants, Kbond and b are assigned to the values of 64 and 0.5, respectively [20,24,25,26,27,28,29,85,49,50]. For the lipid molecules, a weaker bond is inserted (K’bond = 16) between the first beads on the two tails to ensure that the tails are positioned in the same direction. The three-body stiffness potential along the lipid tails has the form Eangle=Kangle (1+cosθ) where % θis the angle formed by three adjacent beads. The coefficient Kangle is set to be 20 in our simulations. This stiffness term increases the stability and bending rigidity of the bilayers [47].
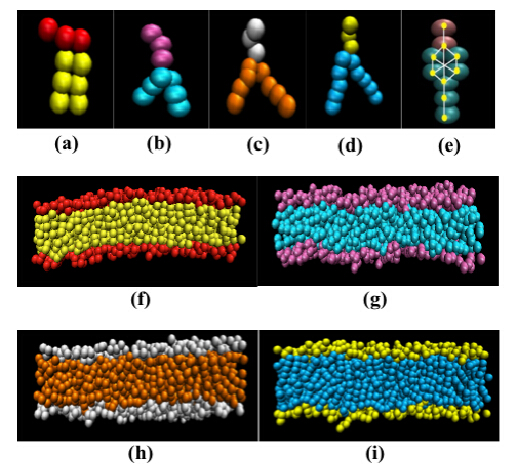 Figure 1. Coarse-grained bead-spring models of (a) DPPC; DMPC with respectively, (b) 3, (c) 4, and (d) 5 beads in each hydrocarbon tail, and (e) Cholesterol. Images of a tensionless lipid bilayer membrane for phospholipid models (f) A, (g) B, (h) C and (i) D.
Figure 1. Coarse-grained bead-spring models of (a) DPPC; DMPC with respectively, (b) 3, (c) 4, and (d) 5 beads in each hydrocarbon tail, and (e) Cholesterol. Images of a tensionless lipid bilayer membrane for phospholipid models (f) A, (g) B, (h) C and (i) D.The soft repulsive pair potential parameters for the lipid and cholesterol hydrophilic and hydrophobic beads were selected to capture their amphiphilic nature. The interaction parameters between the like components, aij, are based on the property of water [21]. The repulsion parameter between two beads of the same type is set at aii = 25 (measured in units of kBT) which is based upon the compressibility of water at room temperature [21] for a bead density of r = 3. The soft repulsive interaction parameter aij between hydrophobic and hydrophilic beads is set at aij=100, and is determined by using the Flory-Huggins interaction parameters, c, as aij=aii+3.496χ, for r = 3.
The soft repulsive interaction parameters between the head (h), tail (t) beads of lipid molecules, and the solvent (s) beads are assigned the following values: ass = 25, ahh = 25, att = 25, ahs = 25, ats = 100 and aht = 100. The values of the inter-lipid species head-head ah1h2 and tail-tail at1t2 soft repulsive interaction parameters will mimic mixtures of lipid species with different head or tail groups. The physical properties of the lipid molecules are summarized in Table 1. These parameters are selected to model the effective distinct chemistry of the molecular species, thereby capturing the differences in the melting temperature of the individual species [13,51,52]. This approach enables us to develop a simple representation of mixtures composed of lipids with two hydrocarbon tails.
| Lipid A | Lipid B | Lipid C | Lipid D | |
| Experimental Area (nm2) | 0.645 | 0.664 | 0.664 | 0.664 |
| rc (nm) | 0.732 | 0.714 | 0.707 | 0.718 |
| t (ns) | 7.90 | 7.46 | 7.38 | 7.42 |
| Experimental Lateral Diffusion Coefficient (m2/s) | 5.00 | 1.30 | 5.00 | 5.00x10-3 |
| Transverse Diffusion Coefficient (m2/s) | 4.07x10-2 | 8.20x10-2 | 4.19x10-2 | 3.47x10-2 |
| Transitions Temperature (℃) | 41 | 23 | 23 | 23 |
In our simulations, the respective characteristic length and energy scales are rc and kBT. We run our simulations at a reduced temperature T = 1 which corresponds to the temperature at which the DPPC bilayer is in the fluid state. The transition temperatures for pure DPPC and DMPC bilayers are respectively, 41°C and 23°C [53,54], as shown in Table 1. As a result, our characteristic time scale can be described as t=√mr2c/kbT. Finally, σ = 3 and Δt = 0.02τ are used in the simulations along with the total bead number density of ρ = 3 and a dimensionless value of rc = 1 [24].
To develop a correspondence between the reduced and physical units, we relate the experimental measurements of the area per lipid [54] for a tensionless membrane and the diffusion coefficient of a lipid molecule in a membrane in the fluid state [55,56]. We obtain the characteristic length scale for our model through the comparison of experimental measurements of the interfacial area per lipid of the corresponding bilayer with similar measurements from our simulations. To compute the average area per lipid, the vesicle is divided into many small rectangular patches so that each patch can be treated as a bilayer membrane. By summing the areas of all the patches and then averaging them over the systems total number of lipid molecules in the whole system, the average area per lipid for the vesicle bilayer is computed. The diffusion coefficient of the lipid molecule in the simulations can be found by tracking the mean squared displacements of 10 lipid molecules in a vesicle bilayer. We use the re lation ∂⟨r2(t)⟩∂t=2dDto relate the diffusion coefficient D to the mean square displacement of a particle in a time intervalt [23]. The variable d is the dimensionality of the system that is given to be 3 for our system. We calculate the diffusion coefficient D using the slope of the time evolution of the mean square displacement. Table 1 lists the physical correspondence of the reduced units for the four lipidmodels. We note that the lipid model A is based upon the DPPC molecule and lipid model B represents the DMPC molecule.
We explore the effect of the lipid molecular architecture in the bilayer properties. We study four models of double-tail lipids with variations in the molecular packing parameter and the hydrocarbon chain length [2]. The molecular packing parameter for each lipid architecture depends upon its area per lipid, hydrocarbon chain volume, and the chain length [2]. Lipid model A has a cylindrical shape with a packing parameter around 1, and is comprised of three head group beads (which are hydrophilic in nature) and two hydrocarbon tails with three hydrophobic beads each (see Figure 1). Lipid models B, C and D have an inverted wedge shape and a molecular packing parameter greater than 1, with successively longer hydrocarbon chain lengths (see Figure 1) The head group architectures for models B, C and D are identical and are comprised of three hydrophilic beads. Each hydrocarbon tail is comprised of three, four and five hydrophobic beads respectively, for lipid models B, C and D. In summary, lipid models A and B differ in their head architecture; lipid models A, C and D differ in their head and tail architectures, and lipid models B, C and D differ in their hydrocarbon tail length.
The cholesterol molecule is modeled by two hydrophilic head beads and seven hydrophobic beads that are organized in a ring and a short tail (see Figure 1) To model the sterol ring, we introduce bonds between diametrically opposite beads encompassing the ring, in addition to the bonds between successive beads at the periphery of the ring. A schematic of the bond topology of the molecule is overlaid on the coarse-grained representation (see Figure 1.) For simplicity, we have maintained the harmonic bond potential Kbond = 64 and equilibrium bond length r0 = 0.5. The angle potential energy between three consecutively bonded beads is set at Kangle = 20.
We use a cubic simulation box of dimension 20rc with periodic boundary conditions along all three directions, with 24, 000 beads. We begin with a preassembled lipid bilayer membrane with a predetermined average area per lipid [32,57], equilibrate the membrane for a time interval of 102, 000t, and measure interfacial properties over a duration of 20, 000t. We repeat this process for each of the molecular models. Following the equilibration phase, we measured the interfacial properties for the lipid bilayer membranes as a function of the area per lipid. We measure contributions to the interfacial properties by computing the pair, bond and angle energies of the lipid bilayer membranes composed of the different models. The enthalpic component of the free energy of a bilayer in solution encompasses contributions from the inter-head, head-tail, inter-tail, head-solvent, and the tail-solvent pair interaction energies. We would like to note that the pair, bond and angle energies presented in the paper are averaged over the total number of beads in the system. An increase in the inter-lipid spacing or area per lipid is accompanied by a growth of voids in the hydrophobic regions in the membrane. The response of the bilayer to this increasing number of voids in the hydrophobic region of the membrane is determined by the shape of the lipids. Our measurements of the interfacial tension of the bilayers composed of lipids B, C and D demonstrate lower sensitivity to the increased inter-lipid spacing or area per lipid. The lipid molecules are able to increase the splaying of their hydrocarbon tails with the area per lipid, thereby filling in the voids in the hydrophobic region with minimal decrease in the inter-head, head-tail, and inter-tail enthalpic interactions, as shown in Figure 2. We attribute this response to the smaller head groups of the lipids and the splayed hydrocarbon tails. We would like to note that longer hydrocarbon tail lengths might contribute to tighter packing of the lipid molecules, and thereby increase the inter-head interactions. Furthermore, the differences in the inter-tail energies are attributed to the architecture and the tail length of the lipid molecule, and increases with the packing of the hydrocarbon tails and their length. Lipid A has a cylindrical shape with straight hydrocarbon tails and larger-sized head groups which span the lateral area (with respect to the bilayer normal) of the hydrocarbon tails. Hence, the bilayer composed of lipid A has higher inter-head and head-tail interfacial energies, and smaller head-solvent and tail-solvent interfacial energies (see Figure 3) Our measurements of the head-solvent and tail-solvent interactions energies also highlight the differences in the molecular architectures of the different lipid models. The protruding head groups of lipids B, C and D are responsible for the higher head-solvent and tail-solvent interaction energies, in comparison to similar measurements for lipid A. However, both the head-solvent and tail-solvent interactions decrease with chain length due to the higher inter-head interactions resulting from the tighter packing between the lipid molecules. The bond and angle energies highlight the role of the molecule shape and hydrocarbon tail length, as shown in Figure 4. We observe the cylindrical shaped lipid architecture to have higher bond and angle energies. In addition, there is an increase in these energies with the hydrocarbon tail length.
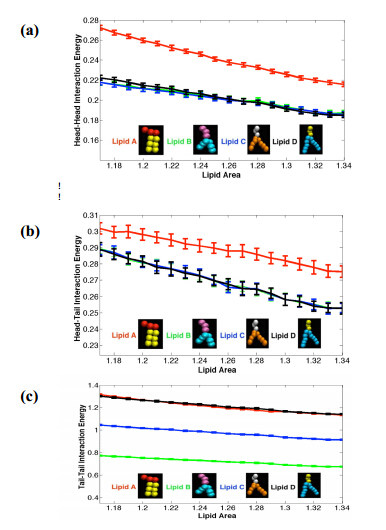 Figure 2. Plot of the (a) head-head, (b) head-tail and (c) tail-tail interaction energies as a function of the area per lipid, for each lipid model.
Figure 2. Plot of the (a) head-head, (b) head-tail and (c) tail-tail interaction energies as a function of the area per lipid, for each lipid model.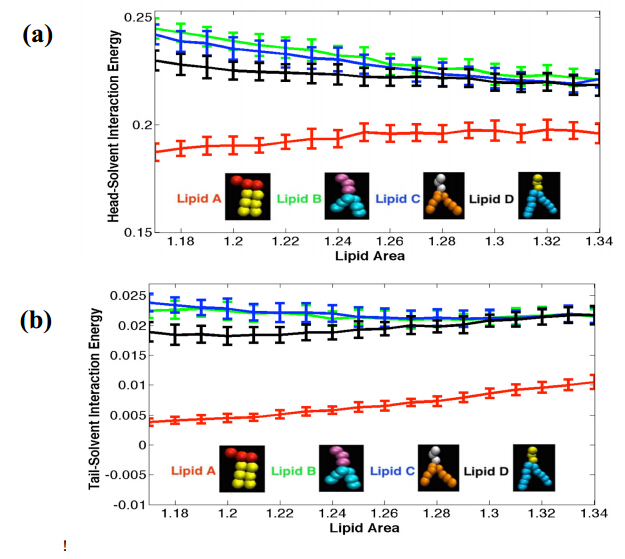 Figure 3. Plot of the (a) head-solvent and (b) tail-solvent interaction energies as a function of the area per lipid, for each lipid model.
Figure 3. Plot of the (a) head-solvent and (b) tail-solvent interaction energies as a function of the area per lipid, for each lipid model.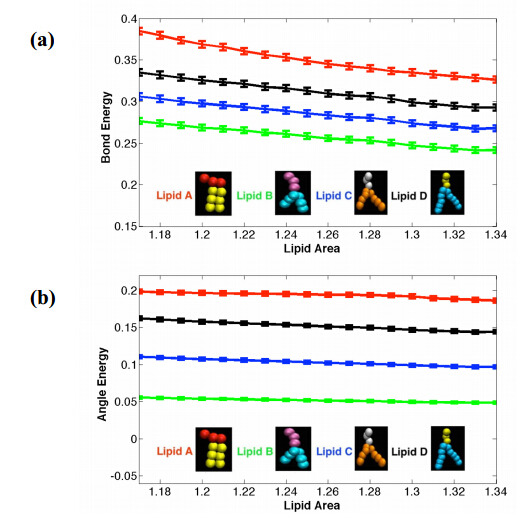 Figure 4. Plot of the (a) bond and (b) angle energies as a function of the area per lipid, for each lipid model.
Figure 4. Plot of the (a) bond and (b) angle energies as a function of the area per lipid, for each lipid model.The pair interaction, bond and angle energies between the different components of the system will determine the interfacial tension of the bilayer. We utilize the principle pressure components Pxx, Pyy, and Pxx to compute the interfacial tensionusing the following relation σr2/kbT=(Lz×(Pxx−12Pyy−12Pzz))[14] where is the dimension of the cubic simulation box [40]. The average value of the interfacial tension was computed via the box averaging. In this techniq ue, five consecutive measurements of the interfacial tension are averaged. This process is repeated on the subsequent average values until there is one final value of tension, as opposed to computing one singular average. This technique is useful because it demonstrates a reduction in st and ard deviation (in comparison to experimental results) while maintaining fixed the total number of measurements of the interfacial tension. A similar approach was adopted by [58,59]. The errors bars for the interfacial tension measurements are computed using the st and ard deviation. From Figure 5, we can determine the areas per lipid corresponding to the tensionless bilayers for models A, B, C and D that are respectively, 1.205 rc2 (664 lipids), 1.303 rc2 (582 lipids), 1.328 rc2 (560 lipids) and 1.287 rc2 (584 lipids.) These results are also shown in Table 1. We surmise that the cylindrical shape of lipid A prevents the lipid tails from splaying with increase in the spacing between the lipid molecules, thereby resulting in a lower area per lipid corresponding to a tensionless membrane. Using the molecular shape argument, one would expect the area per lipid corresponding to a tensionless membrane to decrease with the hydrocarbon tail length. However, we note that the head- and tail-solvent interaction energies decrease with hydrocarbon chain length on account of the tighter packing of the lipids in the bilayers. Therefore, we hypothesize that the interplay between inter-tail, head- and tail-solvent interactions will also determine the area per lipid corresponding to a tensionless bilayer membrane.
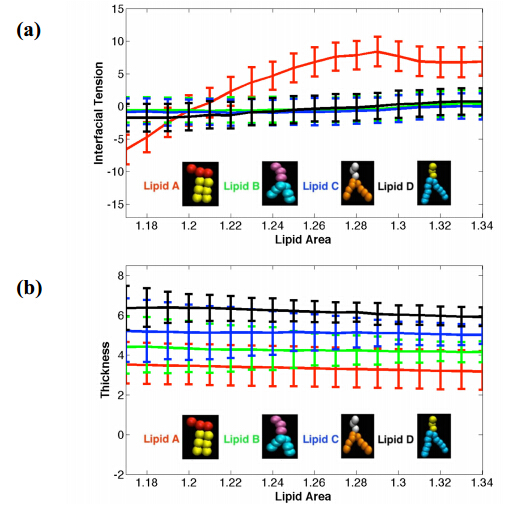 Figure 5. Plot of the (a) interfacial tension and (b) bilayer thickness as a function of the area per lipid, for each lipid model.
Figure 5. Plot of the (a) interfacial tension and (b) bilayer thickness as a function of the area per lipid, for each lipid model.We measured the thickness of the bilayer membranes associated with each lipid model. The average thickness of each tensionless lipid model was calculated by dividing the bilayer membrane into many patches, measuring the width of the patch at multiple sites (using the lipid head bead positions), and averaging over all the measurements. These measurements were done for a range of average area per lipid ranging from 1.17 to 1.34, for each lipid model. Figure 5 shows the bilayer thickness measurements for the different lipid architectures, and shows theaverage thickness for the tensionless membranes for models A, B, C and D to respectively be, 3.439 rc, 4.181rc , 5.018rc and 6.080rc. We expect that the combination of a large head group and the cylindrical shape of lipid model A to favor tight hydrocarbon chain packing in the hydrophobic region of the membrane, and not exhibit interdigitation of the lipid tails. Interdigitation is known to occur in bilayers composed of the inverted wedge-shaped lipids where the hydrocarbon tails of lipids in opposing monolayers interlock with each other leading to a lower bilayer thickness [2]. Our calculation of the membrane thickness does not demonstrate significant variation with the area per lipid. However, we do observe the membrane thickness to increase with the hydrocarbon tail length on a proportional scale. This proportional increase is quite surprising since it does not show any signs of interdigitation. One plausible explanation for this could be the fact that these simulations were run above the lipid’s transition temperature. In agreement with earlier studies, if the temperature of the system is above the lipid’s transition temperature the tails will not remain straight and are therefore unable to interdigitate [60].
We have also investigated the role of molecular architecture on the lateral and transverse diffusion of lipids in a bilayer membrane. Earlier theoretical studies [61,62,63,64,65,66] suggest that the lateral diffusion of lipids in a bilayer membrane depends upon the mean free volume as well as area per lipid, chain length, and lipid packing. Recent results from atomistic simulations and quasi-elastic neutron scattering experiments have shown that the theory of mean free volume is not sufficient for predicting the lateral diffusion of lipid molecules [61,62,63,64,67,68,69]. Experimental studies [3,62,70,71] have shown the area per lipid and hydrocarbon chain length to affect the lateral diffusion coefficient. Changes in the area per lipid and hydrocarbon chain length can influence the packing of the lipid molecules in the bilayer, and hence determine the lateral diffusion coefficient [3,62,70,71].
The transverse diffusion, or flip-flop, of lipids is the movement of a lipid molecule from one monolayer to another, across the hydrophobic region of the bilayer. Studies on the transverse diffusion have related the interaction energies of the lipids with the requirement of an activation energy barrier that has to be overcome for a flip-flop event to occur [72]. Furthermore, lipid molecules constituting bilayer membranes with lower inter-head interactions energy are more suitable to participate in transverse diffusion. We measure the lateral and transverse diffusion coefficient of the lipid molecules, for the different lipid models [73], and provide them in Table 1.
En route to building a mixed phospholipid-cholesterol membrane, we investigated the interfacial properties of a pure cholesterol bilayer membrane. Where as pure cholesterol bilayers are not found in nature, we use the bilayer to determine the area per cholesterol molecule corresponding to a tensionless membrane. We repeat the process detailed earlier to build a pure cholesterol bilayer membrane with an average area per molecule varying from 1.00 to 1.15 rc2. Our measurements of the interfacial tension (as shown in Table 2) demonstrate the area per molecule corresponding to a tensionless cholesterol bilayer membrane to be 1.045 rc2. We note that the average area per molecule corresponding to a tensionless bilayer is smaller for cholesterol than for the different phospholipid models. We surmise that the relative higher rigidity of the cholesterol molecule, on account of its sterol ring, prevents conformational changes to fill in the voids created in the hydrophobic region of the bilayer while under positive tension. Hence, the inter-molecular spacing between the cholesterol molecules at which the membrane attains a tensionless state is smaller than for its phospholipid counterparts.
| Area Per Lipid | Interfacial Tension |
| 1.00 | -0.349 |
| 1.01 | -0.316 |
| 1.02 | -0.356 |
| 1.03 | -0.281 |
| 1.04 | -0.113 |
| 1.05 | 0.148 |
| 1.06 | 0.463 |
| 1.07 | 0.531 |
| 1.08 | 0.993 |
| 1.09 | 1.210 |
| 1.10 | 1.492 |
| 1.11 | 1.535 |
| 1.12 | 1.584 |
| 1.13 | 1.551 |
| 1.14 | 1.729 |
| 1.15 | 1.833 |
Human cell membranes have been found to have a 50 % concentration of cholesterol that plays an important role in regulating the fluidity in a membrane, as well as several other key functions [1]. We build a mixed bilayer membrane comprised of DPPC and cholesterol en route to designing a bio-inspired membrane. We use the area per molecule corresponding to tensionless bilayers for both molecules, and vary the relative concentration of cholesterol from 10 % to 50 %. Given the total lateral area of the simulation box we can determine the number of Cholesterol and DPPC molecules, for a given concentration of each of the species. Using an identical simulation box to the earlier investigations, we place the DPPC and cholesterol molecules in the pre-assembled bilayer and equilibrate the system for a duration of 20, 000t. Given that the tensionless area per molecule of cholesterol is smaller than that for the DPPC molecule, we observe the mixed bilayers to have negative tension, resulting in excess area of the membrane. To obtain a tensionless mixed membrane, we gradually stretch the membrane by 1% of its original area (while preserving the simulation box volume) until we get a tensionless mixed bilayer. Figure 6 shows images of a stable mixed 1:1 DPPC:Cholesterol membrane (a) before and (b) after stretching. Our approach has demonstrated the formation of a stable tensionless mixed lipid bilayer, and can be used for generating multi -component bilayers composed of other species of surfactant molecules.
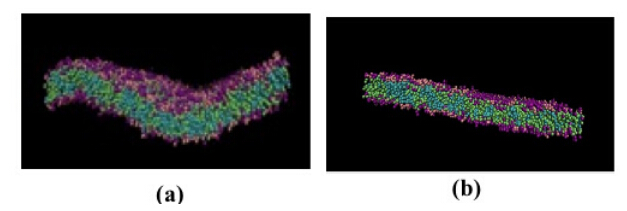 Figure 6. Images of a 1:1 DPPC:Cholesterol bilayer membrane (a) before stretching and (b) after stretching.
Figure 6. Images of a 1:1 DPPC:Cholesterol bilayer membrane (a) before stretching and (b) after stretching.
In summary, we explore the role of molecular geometry of phospholipid molecules on the properties of lipid bilayer membranes as a function of inter-lipid spacing through the characterization of the interfacial tension, the interaction energies, diffusivity of the molecules and the membrane thickness. We have shown how both the molecular shape and the hydrocarbon tail length can determine properties of the lipid bilayer membranes. In addition, we have examined the properties of a pure cholesterol bilayer and found the molecular stiffness to be responsible for a relatively smaller average area per molecule. We have further demonstrated the design of stable mixed bilayers composed of DPPC and cholesterol using their average area per lipid corresponding to tensionless bilayer membranes. Our results can be potentially used to design bio-inspired membranes for probing the interactions between therapeutic peptides or delivery vehicles and the biological cell membranes, for applications in biomedicine, sensing and imaging.
| [1] | Alexeev A, Uspal WE, Balazs AC (2008) Harnessing janus nanoparticles to create controllable pores in membranes.ACS Nano 2: 1117-1122. |
| [2] | Israelachvili JN (2010) Intermolecular and Surface Forces, 3 Eds..Waltham: Elsevier Science . |
| [3] | Almeida P, Vaz W (1995) Lateral diffusion in membranes.Handb Biol Phys 1: 305-357. |
| [4] | Monticelli L, Salonen E, Ke PC, et al. (2009) Effects of carbon nanoparticles on lipid membranes: a molecular simulation perspective.Soft Mat 5: 4433-4445. |
| [5] | Albanese A, Tang PS, Chan WCW (2012) The effect of nanoparticle size, shape, and surface chemistry on biological systems.Annu Rev Biomed Eng 14: 1-16. |
| [6] | Ding H, Ma Y (2012) Role of physicochemical properties of coating ligands in receptor-mediated endocytosis of nanoparticles.Biomaterials 33: 5798-5802. |
| [7] | Balme S, Janot J, Berado L, et al. (2011) New bioinspired membrane made of a biological ion channel confined into the cylindrical nanopore of a solid-state polymer.Nano Lett 11: 712-716. |
| [8] | Zhao L, Feng SS (2004) Effects of lipid chain length on molecular interactions between paclitaxel and phospholipid within model biomembranes.J Colloid Interface Sci 274: 55-68. |
| [9] | Baszkin A, Norde W (1999) Physical Chemistry of Biological Interfaces, 1 Eds..Boca Raton: CRC Press . |
| [10] | Hoogerbrugge PJ, Koelman J (1992) Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics.Europhys Lett 19: 155-160. |
| [11] | Lin CM, Li CS, Sheng YJ, et al. (2012) Size-dependent properties of small unilamellar vesicles formed by model lipids.Langmuir 28: 689-700. |
| [12] | Schmid F, Schick M (1994) Monte Carlo study of interfacial properties in an amphiphilic system.Phys Rev E 49: 494-500. |
| [13] | Laradji M, Kumar P (2011) Advances in Planar Lipid Bilayers and Liposomes.In: Iglic A, 1 ed., Waltham: Elsevier Science . |
| [14] | Farago O (2008) Mode excitation Monte Carlo simulations of mesoscopically large membranes.J Chem Phys 128: 184105. |
| [15] | Klein ML, Shinoda W (2008) Large-scale molecular dynamics simulations of self-assembling systems.Science 321: 798-800. |
| [16] | Heller H, Schaefer M, Schulten K (1993) Molecular dynamics simulation of a bilayer of 200 lipids in the gel and in the liquid crystal phase.J Phys Chem 97: 8343-8360. |
| [17] | Wang Y, Jiang W, Yan T, et al. (2007) Understanding ionic liquids through atomistic and coarse-grained molecular dynamics simulations.Acc Chem Res 40: 1193-1199. |
| [18] | Cooke IR, Deserno M (2006) Coupling between lipid shape and membrane curvature.Biophys J 91: 487-495. |
| [19] | Brown FLH (2011) Continuum simulations of biomembrane dynamics and the importance of hydrodynamic effects.Q Rev Biophys 44: 391-432. |
| [20] | Aydin F, Dutt MIn Preparation. |
| [21] | Groot RD, Warren PB (1997) Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation.J Chem Phys 107: 4423. |
| [22] | Gao L, Shillcock J, Lipowsky R (2007) Improved dissipative particle dynamics simulations of lipid bilayers.J Chem Phys 126: 01510. |
| [23] | Gullingsrud J, Schulten K (2004) Lipid bilayer pressure profiles and mechanosensitive channel gating.Biophys J 86: 3496-3509. |
| [24] | Dickson CJ, Rosso L, Betz RM, et al. (2012) GAFFlipid: a General Amber Force Field for the accurate molecular dynamics simulation of phospholipid.Soft Mat 8: 9617. |
| [25] | Dutt M, J. Nayhouse M, Kuksenok O, et al. (2011) Interactions of End-functionalized Nanotubes with Lipid Vesicles: Spontaneous Insertion and Nanotube Self-Organization.Curr Nanosci 7: 699-715. |
| [26] | Dutt M, Kuksenok O, Nayhouse MJ, et al. (2011) Modeling the self-assembly of lipids and nanotubes in solution: forming vesicles and bicelles with transmembrane nanotube channels.ACS Nano 5: 4769-4782. |
| [27] | Dutt M, Kuksenok O, Little SR, et al. (2011) Forming transmembrane channels using end-functionalized nanotubes.Nanoscale 3: 240-250. |
| [28] | Dutt M, Kuksenok O, Balazs AC (2012) Designing Tunable Bio-nanostructured Materials via Self-Assembly of Amphiphilic Lipids and Functionalized Nanotubes.MRS Proc 1464: mrss12-1464-rr08-09. |
| [29] | Dutt M, Kuksenok O, Balazs AC (2013) Nano-pipette directed transport of nanotube transmembrane channels and hybrid vesicles.MRS Proc 5: 9773-9784. |
| [30] | Frenkel D, Smit B (2002) Understnading Molecular Simulation: From Algorithms to Applications, 2 Eds..San Diego: Academic Press . |
| [31] | Alexeev A, Balazs AC (2007) Designing smart systems to selectively entrap and burst microcapsules.Soft Mat 3: 1500. |
| [32] | Orsi M, Essex JW (2013) Physical properties of mixed bilayers containing lamellar and nonlamellar lipids: insights from coarse-grain molecular dynamics simulations.Faraday Discuss 161: 249-272. |
| [33] | Schulz M, Olubummo A, Binder WH (2012) Beyond the lipid-bilayer: interaction of polymers and nanoparticles with membranes.Soft Mat 8: 4849-4864. |
| [34] | Lai K, Wang B, Zhang Y, et al. (2013) Computer simulation study of nanoparticle interaction with a lipid membrane under mechanical stress.Phys Chem Chem Phys 15: 270-278. |
| [35] | Deserno M (2009) Mesoscopic membrane physics: concepts, simulations, and selected applications.Macromol Rapid Commun 30: 752-757. |
| [36] | Bennun SV, Hoopes MI, Xing C, et al. (2009) Coarse-grained modeling of lipids.Chem Phys Lipids 159: 59-66. |
| [37] | Boal DH (2012) Mechanics of the Cell, 2 Eds..Cambridge: Cambridge University Press . |
| [38] | Zhong OY, Helfrich W (1987) Instability and Deformation of a Spherical Vesicle by Pressure.Phys Rev Lett 59: 2486-2488. |
| [39] | Lipowsky R (1991) The conformation of membranes.Nature 349: 475-478. |
| [40] | McIntosh TJ, Simon SA (2006) Roles of bilayer material properties in function and distribution of membrane proteins.Annu Rev Biophys Biomol Struct 35: 177-198. |
| [41] | Garcia ML (2004) Ion channels: gate expectations.Nature 430: 153-155. |
| [42] | Lin CM, Li CS, Sheng YJ, et al. (2012) Size-dependent properties of small unilamellar vesicles formed by model lipids.Langmuir 28: 689-700. |
| [43] | Chen H, Ruckinstein E (2011) Aggregation of nanoparticles in a block copolymer bilayer.J Coll Int Sci 363: 573-578. |
| [44] | Chen H, Ruckinstein E (2011) Nanoparticle aggregation in a block copolymer.J Chem Phys 131: 244904. |
| [45] | Venturoli M, Smit B, Sperotto MM (2005) Simulation studies of protein-induced bilayer deformations, and lipid-induced protein tilting, on a mesoscopic model for lipid bilayers with embedded proteins.Biophys J 88: 1778-1798. |
| [46] | de Meyer F, Smit B (2009) Effect of cholesterol on the structure of a phospholipid bilayer.Proc Natl Acad Sci 106: 3654-3658. |
| [47] | Koelman J, Hoogerbrugge PJ (1993) Dynamic Simulations of Hard-Sphere Suspensions Under Steady Shear.Europhys Lett 21: 363-368. |
| [48] | Venturoli M, Maddalena SM, Kranenburg M, et al. (2006) Mesoscopic models of biological membranes.Phys Rep 437: 1-54. |
| [49] | Koufos E, Dutt M (2013) Designing Nanostructured Hybrid Inorganic-biological Materials via the Self-assembly.MRS Proc 1569: mrss13-1569-ll02-03. |
| [50] | Kuksenok O, Balazs A (2007) Modeling multicomponent reactive membranes.Phys Rev E 75: 051906. |
| [51] | Zan GH, Tan C, Deserno M, et al. (2012) Hemifusion of giant unilamellar vesicles with planar hydrophobic surfaces: a fluorescence microscopy study.Soft Mat 8: 10877. |
| [52] | Weikl TR, Groves JT, Lipowsky R (2002) Pattern formation during adhesion of multicomponent membranes.Europhys Lett 59: 916-922. |
| [53] | Plimpton S (1995) Fast Parallel Algorithms for Short-Range Molecular Dynamics.J Comput Phys 117: 1-19. |
| [54] | Kučerka N, Nieh MP, Katsaras J (2011) Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature.Biochim Biophys Acta 1808: 2761-2767. |
| [55] | Smith KA, Jasnow D, Balazs AC (2007) Designing synthetic vesicles that engulf nanoscopic particles.J Chem Phys 127: 084703. |
| [56] | Illya G, Lipowsky R, Shillcock JC (2005) Effect of chain length and asymmetry on material properties of bilayer membranes.J Chem Phys 122: 24490. |
| [57] | Goetz R, Lipowsky R (1998) Computer simulations of bilayer membranes: Self-assembly and interfacial tension.J Chem Phys 108: 7397-7409. |
| [58] | Cooke I, Kremer K, Deserno M (2005) Tunable generic model for fluid bilayer membranes.Phys Rev E 72: 011506. |
| [59] | Feller SE, Pastor RW (1999) Constant surface tension simulations of lipid bilayers: The sensitivity of surface areas and compressibilities.J Chem Phys 111: 1281-1287. |
| [60] | Smit B, Kranenburg M, Sperotto MM, et al. (2006) Computer Simulations in Condensed Matter: From Materials to Chemical Biology, Ferrario M, Ciccotti G, Binder K, 1 Eds..Berlin: Springer . |
| [61] | Turnbull D, Cohen MH (1970) On the Free-Volume Model of the Liquid-Glass Transition.J Chem Phys 52: 3038-3041. |
| [62] | Grest GS, Cohen MH (1981) Liquids, Glasses, and the Glass Transition: A Free-Volume Approach, Prigogine I, Rice SA.Adv Chem Phys 48: 455-525. |
| [63] | Almeida PFF, Vaz WLC, Thompson TE (1992) Lateral diffusion in the liquid phases of dimyristoylphosphatidylcholine/cholesterol lipid bilayers: a free volume analysis.Biochemistry 31: 6739-6747. |
| [64] | Turnbull D, Cohen MH (1961) Free-Volume Model of the Amorphous Phase: Glass Transition.J Chem Phys 34: 120-124. |
| [65] | Filippov A, Orädd Gäin model membranes studied by pulsed-field gradient-NMR: the role of lipid polyunsaturation.Biophys J 93: 3182-3190. |
| [66] | Bernardino de la Serna J, Orädd G, Bagatolli LA, et al. (2009) Segregated phases in pulmonary surfactant membranes do not show coexistence of lipid populations with differentiated dynamic properties.Biophys J 97: 1381-1389. |
| [67] | Falck E, Róg T, Karttunen M, et al. (2008) Lateral diffusion in lipid membranes through collective flows.J Am Chem Soc 130: 44-45. |
| [68] | Busch S, Smuda C, Pardo LC, et al. (2010) Molecular mechanism of long-range diffusion in phospholipid membranes studied by quasielastic neutron scattering.J Am Chem Soc 132: 3232-3233. |
| [69] | Apajalahti T, Niemela P, Govindan P, et al. (2010) Concerted diffusion of lipids in raft-like membranes.Faraday Discuss 144: 411-430. |
| [70] | Allen P, Tildesley DJ (1987) Computer Simulation of Liquids, 1 Eds..New York: Oxford University Press . |
| [71] | Vaz WLC, Clegg RM, Hallmann D (1985) Translational diffusion of lipids in liquid crystalline phase phosphatidylcholine multibilayers.A comparison of experiment with theory. Biochemistry 24: 781-786. |
| [72] | Egberts E, Berendsen HJC (1988) Molecular dynamics simulation of a smectic liquid crystal with atomic detail.J Chem Phys 89: 3718-3732. |
| [73] | Keffer D (2001) The Working Man's Guide to Obtaining Self Diffusion Coefficients from Molecular Dynamics Simulations.Available from: http://www.cs.unc.edu/Research/nbody/pubs/external/Keffer/selfD.pdf. . |
| 1. | Michael Sebastiano, Xiaolei Chu, Fikret Aydin, Leebyn Chong, Meenakshi Dutt, Interactions of Bio-Inspired Membranes with Peptides and Peptide-Mimetic Nanoparticles, 2015, 2, 2372-0484, 303, 10.3934/matersci.2015.3.303 | |
| 2. | Xiaolei Chu, Fikret Aydin, Meenakshi Dutt, Modeling Interactions between Multicomponent Vesicles and Antimicrobial Peptide-Inspired Nanoparticles, 2016, 10, 1936-0851, 7351, 10.1021/acsnano.5b08133 | |
| 3. | Xinghua Shi, Falin Tian, Multiscale Modeling and Simulation of Nano‐Carriers Delivery through Biological Barriers—A Review, 2019, 2, 2513-0390, 1800105, 10.1002/adts.201800105 | |
| 4. | Fikret Aydin, Paul Ludford, Meenakshi Dutt, Phase segregation in bio-inspired multi-component vesicles encompassing double tail phospholipid species, 2014, 10, 1744-683X, 6096, 10.1039/C4SM00998C |
| Lipid A | Lipid B | Lipid C | Lipid D | |
| Experimental Area (nm2) | 0.645 | 0.664 | 0.664 | 0.664 |
| rc (nm) | 0.732 | 0.714 | 0.707 | 0.718 |
| t (ns) | 7.90 | 7.46 | 7.38 | 7.42 |
| Experimental Lateral Diffusion Coefficient (m2/s) | 5.00 | 1.30 | 5.00 | 5.00x10-3 |
| Transverse Diffusion Coefficient (m2/s) | 4.07x10-2 | 8.20x10-2 | 4.19x10-2 | 3.47x10-2 |
| Transitions Temperature (℃) | 41 | 23 | 23 | 23 |
| Area Per Lipid | Interfacial Tension |
| 1.00 | -0.349 |
| 1.01 | -0.316 |
| 1.02 | -0.356 |
| 1.03 | -0.281 |
| 1.04 | -0.113 |
| 1.05 | 0.148 |
| 1.06 | 0.463 |
| 1.07 | 0.531 |
| 1.08 | 0.993 |
| 1.09 | 1.210 |
| 1.10 | 1.492 |
| 1.11 | 1.535 |
| 1.12 | 1.584 |
| 1.13 | 1.551 |
| 1.14 | 1.729 |
| 1.15 | 1.833 |
| Lipid A | Lipid B | Lipid C | Lipid D | |
| Experimental Area (nm2) | 0.645 | 0.664 | 0.664 | 0.664 |
| rc (nm) | 0.732 | 0.714 | 0.707 | 0.718 |
| t (ns) | 7.90 | 7.46 | 7.38 | 7.42 |
| Experimental Lateral Diffusion Coefficient (m2/s) | 5.00 | 1.30 | 5.00 | 5.00x10-3 |
| Transverse Diffusion Coefficient (m2/s) | 4.07x10-2 | 8.20x10-2 | 4.19x10-2 | 3.47x10-2 |
| Transitions Temperature (℃) | 41 | 23 | 23 | 23 |
| Area Per Lipid | Interfacial Tension |
| 1.00 | -0.349 |
| 1.01 | -0.316 |
| 1.02 | -0.356 |
| 1.03 | -0.281 |
| 1.04 | -0.113 |
| 1.05 | 0.148 |
| 1.06 | 0.463 |
| 1.07 | 0.531 |
| 1.08 | 0.993 |
| 1.09 | 1.210 |
| 1.10 | 1.492 |
| 1.11 | 1.535 |
| 1.12 | 1.584 |
| 1.13 | 1.551 |
| 1.14 | 1.729 |
| 1.15 | 1.833 |