Estimation of $P(X < Y)$ for Fréchet, reversed Weibull and Weibull distributions: Analytical expressions, simulations and applications

1.   Introduction

Let $X_1, X_2, \cdots$ be a sequence of random variables (RVs), independent and identically distributed (iid) with a common distribution $G(\cdot)$. The extreme value theory (EVT) ^[1] proposes asymptotic distribution functions $F(\cdot)$ for partial maximum $M_n = \max \{X_j; j = 1, \cdots, n\}$. The derivation of extreme distributions is based on the asymptotic approximation of the normalized partial maximum. More specifically,

where $a_n > 0$, $b_n\in\mathbb{R}$, $F(\cdot)$ is a nondegenerate distribution function and $\overset{d}{\rightarrow }$ denotes convergence in distribution.

Fisher and Tippet theorem ^[2,3] guarantees us that there are three extreme values distributions $F(\cdot)$ satisfying Eq (1.1). These distributions are known as Fréchet, reversed Weibull, and Gumbel. Note that $\min\{X_1, \cdots, X_n \} = - \max\{X_1, \cdots, X_n\}$ results presented for the maximum can be converted to the minimum. The conditions on the distribution function $G(\cdot)$ for Eq (1.1) to hold true are well-documented and can be referenced in ^[1,3,4]. Applications of EVT are found in finance, natural catastrophes, and equipment failures, among others ^[5].

In order to study extreme value distributions in a stress-strength framework, lets assume that a random stress $Y$ is applied to a random strength $X$ and both are independent and possess the same extreme distribution, but with different parameters. Then the stress-strength probability (or reliability) is defined as $R = P(X < Y)$, where $X$ is the strength and $Y$ is the stress. The probability of stress-strength relationships for extreme value distributions such as the Fréchet and Weibull (which are the possible limiting distributions of partial minima) distributions has been extensively explored in the literature. Nadarajah ^[6] examined the class of extreme value distributions and derived their corresponding reliability forms, expressed in terms of special functions. Krishnamoorthy and Lin ^[7] presented confidence limits for reliability ($R$) incorporating Weibull models. Kundu and Raqab ^[8] introduced a modified maximum likelihood estimator for $R$ and established the asymptotic distribution of these estimators, which was then used to construct confidence intervals for $R$. Nojosa and Rathie ^[9] extended previous findings on $R$ for the Weibull distribution by expressing it in terms of $H$-functions ^[10]. Bayesian estimation of $R$ for both the Fréchet and Weibull distributions was carried out by ^[11,12].

The stress-strength theory is naturally extended to a multicomponent system that consists of $k$ strength components with common stress, and the system functions when at least $s$ $(1\leq s\leq k)$ components simultaneously survive. Estimation of reliability in a multicomponent stress-strength model was done by several authors (e.g., ^[13,14]).

In real-world data modeling, a fundamental step after selecting an appropriate model family is estimating the parameters involved. Several estimation methods for stress-strength probability and multicomponent stress-strength have been proposed in the literature. When paired datasets are available, nonparametric or copula search methods can be employed (cf. ^[15]). If $X$ and $Y$ are independent, a common approach is to model each variable separately. In this case, maximum likelihood procedures or Bayesian methods can be used to estimate the parameters of the distributions (cf. ^[16]). Then, estimates of $R = P(X < Y)$ are obtained using the marginal fits of $X$ and $Y$ applied to possible analytical expressions of $R$.

In this paper, we consider the problem of deriving new analytical expressions to the stress–strength reliability $R = P(X < Y)$ when $X$ and $Y$ are independent Fréchet, Weibull, or reversed Weibull random variables. Our main contributions are:

● to derive $R$ analytically in terms of the extreme value $\mathbb{H}$-function recently introduced in ^[17], which also allowed for fewer parameter restrictions comparing to previous results in the literature;

● to validate the maximum likelihood estimation procedure for $R$ via a simulation study and

● to apply the theoretical results in real dataset modeling.

Our Theorems 3.1–3.3 show that for Fréchet, reversed Weibull, and Weibull distributions, respectively, the stress-strength probability $R$ is written in terms of the $\mathbb{H}$-function (recently introduced in ^[17]) with the advantage that we do not use transformations in the dataset and its expression requires fewer parameter restrictions as possible. Also, some additional parameter restrictions lead us to expressions in terms of the $H$-function or even closed-form expressions can be obtained in terms of elementary functions. These new results generalize the previous work of ^[6] for Fréchet and Weibull distributions by removing parameters' restrictions. Parametric estimation of $R$—based on estimating location, scale, and shape parameters of extreme distributions—and nonparametric estimation—based only on empirical information—are also addressed (cf. Algorithms 1 and 2).

Applications of our theoretical results are presented (cf. Section 5). First, we analyze the statistical behavior of financial assets' returns, showing how $P(X < Y)$ can be used to build an interesting approach to perform asset selection as previously illustrated by Rathie and Ozelim ^[18]. Estimates are obtained by both maximum likelihood and nonparametric procedures, while confidence intervals for each estimator are obtained by the Bootstrap method. Second, minimum monthly flows of water are analyzed. Finally, we obtain stress-strength measures to compare failure voltage levels of two types of electrical cable insulation.

The paper is organized as follows: In Section 2, we define the $\mathbb{H}$-function, $H$-function and the extreme distributions (Fréchet, reversed Weibull and Weibull). Section 3 deals with the derivation of $R$ when $X$ and $Y$ are independent extreme RVs. The maximum likelihood estimation and a nonparametric estimation procedure for $R$ are addressed in Section 4. Section 5 presents Monte-Carlo simulations for the estimation of $R$ and also deals with three real situations. The last section presents concluding remarks.

2.   Preliminaries

In this section, we present definitions and results on which our contributions are based.

2.1.   Special functions

Let us consider the extreme-value $\mathbb{H}$-function, recently defined in ^[17]. This function, hereby denoted as $\mathbb{H}$, can be defined as

where $\Re (a_1), \Re (a_2), \Re (a_4) \in\mathbb{R}_+, a_3, a_5\in\mathbb{C}$, not both $\Re (a_1)$ and $\Re (a_2)$ can be equal to zero at the same time, $\Re (a_6) > -1$ when $a_1 \neq 0$ or $a_1 = 0$ and $\text{sign} (a_3) = \text{sign} (a_5)$, $\Re (a_6) < -1$ when $a_1 = 0$ and $\text{sign} (a_3) \neq \text{sign} (a_5)$. In this paper, $\mathbb{R}$, $\mathbb{C}$, and $\Re$ denote the real numbers, complex numbers, and the real part of a complex number, respectively.

Note that Eq (2.5) generalizes some important cases of the $H$-function (cf. ^[10]) defined by

where $0 \leq m \leq q$, $0 \leq n \leq p$ (not both $m$ and $n$ simultaneously zero), $A_j > 0$ ($j = 1, \cdots, p$), $B_k > 0$ ($k = 1, \cdots, q$), and $a_j$ and $b_k$ are complex numbers such that no poles of $\Gamma (b_k + B_k s)$ ($k = 1, \cdots, m)$ coincide with poles of $\Gamma (1-a_j - A_j s)$ ($j = 1, \cdots, n)$. $L$ is a suitable contour $w -i \infty$ to $w + i \infty$, $w\in\mathbb{R}$, separating the poles of the two types mentioned above. For more details, see ^[10].

An important special case of Eq (2.5) is obtained by taking $a_4 = 0$, which represents an upper (or lower) bound for its value depending on the sign of $a_5$. This case is, therefore, an extreme value of the function and can be written in terms of the $H$-function as ^[17]

when $\text{sign} (a_3) = \text{sign} (a_5)$ and

otherwise.

In this work, we are interested in the case $a_6 = 0$. Thus, we omit such a parameter from the representation and denote only

where $a_1, a_2 \in\mathbb{R}_+, \; a_3, a_4, a_5\in\mathbb{R}$. Another interested special case of the extreme value $\mathbb{H}$-function, taking $a_1 = 1$ and $a_4 = 0$, we have that $\mathbb{H}(1, a_2, a_3, 0, a_5)$ can be rewritten as

and when $a_3a_5 = 1$, Eq (2.6) reduces to explicit form

In the following sections, we generalize the results of ^[6] proving that all stress-strength probabilities involving Fréchet, reversed Weibull, and Weibull distributions can be written as $\mathbb{H}-$functions, with as few parameter restrictions as possible.

2.2.   Three-parameter distributions

Next, we describe the cumulative distribution function (CDF) and the probability density function (PDF) of Fréchet, reversed Weibull and Weibull models. The parameters $\mu, \sigma$, and $\alpha$ denote the location, scale, and shape of the CDFs.

We say that a random variable $X$ has three-parameter Fréchet distribution, and denote by $X\sim$ Fréchet$(\mu, \sigma, \alpha)$ with $\mu\in\mathbb{R}, \sigma, \alpha\in\mathbb{R}_+$, if $X$ has CDF and PDF, respectively, given by

and

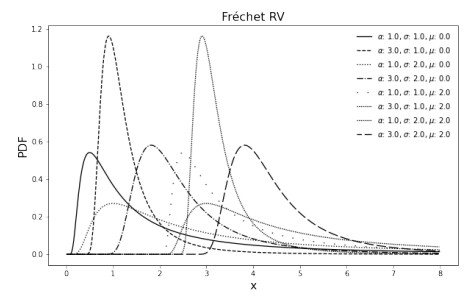
where $1_A$ denotes the indicator function on the set $A$. Figure 1 shows the behavior of Fréchet PDFs when parameters vary.

We say that a random variable $X$ has three-parameter reversed Weibull distribution, and denote by $X\sim$ RWeibull$(\mu, \sigma, \alpha)$ with $\mu\in\mathbb{R}, \sigma, \alpha\in\mathbb{R}_+$, if $X$ has CDF and PDF, respectively, given by

and

Figure 2 shows the behavior of reversed Weibull PDFs when parameters vary.

Finally, we say that a random variable $X$ has three-parameter Weibull distribution, and denote by $X\sim$ Weibull$(\mu, \sigma, \alpha)$ with $\mu\in\mathbb{R}, \sigma, \alpha\in\mathbb{R}_+$, if $X$ has CDF and PDF, respectively, given by

and

Figure 3 presents Weibull PDFs generated using different parameter sets. When compared to Figure 2, PDFs with the same $\alpha$ and $\sigma$ but opposite $\mu$ are symmetric with respect to the ordinate axis.

3.   Stress-strength probability

Table 1 presents references that worked with the Fréchet and Weibull models to calculate and estimate $R$, as well as the respective parameter restrictions adopted. The results that we present in the following subsections are obtained without such restrictions, allowing greater freedom in application to real dataset modeling, as presented in Section 5.

3.1.   Fréchet distribution

Theorem 3.1. Let $X\sim$ Fréchet$(\mu_2, \sigma_2, \alpha_2)$ and $Y\sim$ Fréchet$(\mu_1, \sigma_1, \alpha_1)$ be independent random variables, with $\mu_j\in\mathbb{R}, \sigma_j, \alpha_j\in \mathbb{R}_+$, $j = 1, 2$. Then,

In particular, if $\mu_1 = \mu_2$, then

When $\alpha = \alpha_1 = \alpha_2$, $R$ can be written explicitly by

Proof. Denote $M = \max\{\mu_1, \mu_2\}$. Then,

Substituting $y = \left(\frac{x-\mu_1}{\sigma_1} \right)^{-\alpha_1}$ and taking $M = \mu_1$, we can rewrite Eq (3.4) as

Hence, for the case $\mu_1\geq\mu_2$, Eq (3.1) follows from Eqs (2.5) and (3.5). For the case $\mu_1 < \mu_2$, it suffices to notice that $P(X < Y) = 1-P(Y < X)$ and interchange subindices of Eq (3.5). In addition, applying Eq (2.6) with $\mu_1 = \mu_2$, we obtain Eq (3.2). In the case where $\alpha = \alpha_1 = \alpha_2$, we have the explicit form Eq (3.3).

3.2.   Reversed Weibull distribution

Theorem 3.2. Let $X\sim$ RWeibull$(\mu_2, \sigma_2, \alpha_2)$ and $Y\sim$ RWeibull$(\mu_1, \sigma_1, \alpha_1)$ be independent random variables, with $\mu_j\in\mathbb{R}, \sigma_j, \alpha_j\in \mathbb{R}_+$, $j = 1, 2$. Then,

In particular, if $\mu_1 = \mu_2$, then

When $\alpha = \alpha_1 = \alpha_2$, $R$ can be written explicitly by

Proof. Denote $m = \min\{\mu_1, \mu_2\}$. Then,

Substituting $y = \left(\frac{\mu_1-x}{\sigma_1} \right)^{\alpha_1}$ and taking $m = \mu_1$, we can rewrite Eq (3.4) as

Hence, the first equation in (3.6) follows from Eqs (2.5) and (3.10). For the second case, it suffices to notice that $P(X < Y) = 1-P(Y < X)$ and interchange subindices of Eq (3.10). In addition, applying Eq (2.6) with $\mu_1 = \mu_2$, we obtain Eq (3.7). In the case where $\alpha = \alpha_1 = \alpha_2$, we have the explicit form Eq (3.8).

3.3.   Weibull distribution

Theorem 3.3. Let $X\sim$ Weibull$(\mu_2, \sigma_2, \alpha_2)$ and $Y\sim$ Weibull$(\mu_1, \sigma_1, \alpha_1)$ be independent random variables, with $\mu_j\in\mathbb{R}, \sigma_j, \alpha_j\in \mathbb{R}_+$, $j = 1, 2$. Then,

In particular, if $\mu_1 = \mu_2$, then

When $\alpha = \alpha_1 = \alpha_2$, $R$ can be written explicitly by

Proof. Denote $M = \max\{\mu_1, \mu_2\}$. Then,

Substituting $y = \left(\frac{x-\mu_1}{\sigma_1} \right)^{\alpha_1}$ and taking $M = \mu_1$, we can rewrite Eq (3.14) as

Hence, the first equation in (3.11) follows from Eqs (2.5) and (3.15). Second equation in (3.11) follows by noticing that $P(X < Y) = 1-P(Y < X)$ and interchanging subindices of Eq (3.15). In addition, applying Eq (2.6) with $\mu_1 = \mu_2$, we obtain Eq (3.12). In the case where $\alpha = \alpha_1 = \alpha_2$, we have the explicit form Eq (3.13).

We finish this section by noting that Theorems 3.1 and 3.2 can be generalized to random samples of a given CDF $G(\cdot)$ that is in the domain of attraction of Fréchet or reversed Weibull distributions (see ^[3] for a complete characterization of the domains of attraction of these CDFs). We describe below these generalizations.

Let $Y$ be an RV with PDF $f_Y(\cdot; \alpha_1, \beta_1, \gamma_1)$ given in Eq (2.7) or (2.8). Let $X_1, \cdots, X_n$ be a random sample from some CDF $G(\cdot)$, independent of $Y$, and assume that there exist sequences of real numbers $\{a_n\}$ and $\{b_n\}$ with $a_n > 0, b_n\in\mathbb{R}$ such that Eq (1.1) holds for $F_Y(\cdot; \mu_2, \sigma_2, \alpha_2)$. That means,

for all $x$ continuity points of $F_Y$, where $M_n = \max\{X_1, \cdots, X_n\}$. Set $\tilde{M}_n = \frac{M_n-b_n}{a_n}$. Then, Eq (3.16) implies

Using the corresponding Theorem 3.1 or 3.2, Eq (3.18) can be obtained in terms of the $\mathbb{H}$-function.

Remark 3.4. Especially concerning the Fréchet distribution, one can arrive at the same conclusion as in Eq (3.18) without relying on the assumption of iid RVs $X_1, \cdots, X_n$. Refer to Theorem 3.1 in ^[20] for a broader application of Eq (3.16).

4.   Estimation

This section deals with parameter estimation for $R = P(X < Y)$ given two independent random variables $X$ and $Y$ following the distribution Fréchet, Weibull, or reversed Weibull. The literature presents maximum likelihood estimators (MLEs) for $R$ considering explicit forms of $R$ obtained after severe parameter restrictions on extreme value distributions (such as ^[8,11,12]). Those approaches require the estimation of the parameters to be done jointly in the two samples. In our case, such restrictions are not required since we worked with expressions of $R$ in terms of extreme value $\mathbb{H}$-functions.

Consider a random sample ${\bf X} = (X_1, \cdots, X_n)$ from a Fréchet distribution with parameter $\boldsymbol{\theta} = (\mu, \sigma, \alpha)$. The likelihood function is given by the following:

where $1_A$ denotes the indicator function on the set $A$.

Analogously, the likelihood function of the Weibull and reversed Weibull distributions are given, respectively, by

and

Note that the location parameter $\mu$ in the support of the distributions makes the three likelihood functions non-regular.

Let $X\sim \text{Fréchet}(\mu_x, \sigma_x, \alpha_x)$ and $Y\sim \text{Fréchet}(\mu_y, \sigma_y, \alpha_y)$ be independent random variables. Theorem 3.1 indicates that $R = R(\boldsymbol{\theta}_x, \boldsymbol{\theta}_y)$, where we denote $\boldsymbol{\theta}_x = (\mu_x, \sigma_x, \alpha_x)$ and $\boldsymbol{\theta}_y = (\mu_y, \sigma_y, \alpha_y)$. Thus, let ${\bf X} = (X_1, \cdots, X_n)$ be a random sample of $X$ and consider an independent random sample ${\bf Y} = (Y_1, \cdots, Y_m)$ of $Y$. Let $\hat{\boldsymbol{\theta}}_x = (\hat{\mu}_x, \hat{\sigma}_x, \hat{\alpha}_x)$ and $\hat{\boldsymbol{\theta}}_y = (\hat{\mu}_y, \hat{\sigma}_y, \hat{\alpha}_y)$ be the estimates of $\boldsymbol{\theta}_x$and $\boldsymbol{\theta}_y$. Then, we consider the natural estimator of $R$ simply as $\hat{R} = R(\hat{\boldsymbol{\theta}}_x, \hat{\boldsymbol{\theta}}_y)$. Similarly, we estimate $R$ in the distributions reversed Weibull (Theorem 3.2) and Weibull (Theorem 3.3).

In this work, we concentrate on estimating $\boldsymbol{\theta}_x$ and $\boldsymbol{\theta}_y$ through maximum likelihood. Thus, we denote the estimator of $R$ by

In future work, we aim to employ alternative parameter estimation techniques, including Bayesian acceptance and rejection methods (e.g., ^[16]).

In the next sections, we will compare the results of $\hat{R}_{MLE}$ with an empirical (nonparametric) estimator denoted as $\hat{R}_{E}$, which is defined as:

To illustrate the suitability of the analytical closed-form expressions hereby derived, a simulation study and real-world applications are carried out in the next section.

5.   Applications

We present Monte-Carlo simulations for the distribution families under study in Section 5.1 as well as the modeling of three real datasets involving financial records, minimum river flows, and insulation failure voltages in Section 5.2.

5.1.   Simulation study

Departing from Theorems 3.1–3.3, we assessed the consistency of results using Monte-Carlo simulations to get an estimate $\hat{R}_{MC}$. The expressions for $R$ in Eqs (3.5), (3.10), and (3.15) were evaluated numerically.

For each distribution family $F(x; \mu, \sigma, \alpha)$, we took a pair of RVs $X_1$ and $X_2$ to compare $R$ to $\hat{R}_{MC}$. A Monte-Carlo simulation consists of 1000 draws, from which we evaluate $\hat{R}_{MC}$ and its confidence interval at the 95% significance level. In each Monte-Carlo draw, we take 10,000 samples from each distribution $F(x_1; \mu_1, \sigma_1, \alpha_1)$ and $F(x_2; \mu_2, \sigma_2, \alpha_2)$ and evaluate $R = P(X_2 < X_1)$ by nonparametric approaches.

The results for the family of Fréchet distributions are shown on Table 2. The bias and the RMSE (root mean squared error) between $\hat{R}_{MC}$ and $R$ are also presented and indicate an accurate estimation procedure with bias values below $4\times10^{-4}$ in absolute value.

Tables 3 and 4 present results for the families of reversed Weibull and Weibull distributions respectively. The bias values remained below $4\times10^{-4}$ in absolute value for the same Monte-Carlo simulation parameters, which indicates good accuracy on the estimation procedure. It should be noted that Theorems 3.2 and 3.3 require minor restrictions regarding the order of $\mu_1$ and $\mu_2$, which can be achieved by means of simple RV swapping. Due these restrictions for each family, the simulations yielded $R\geq0.5$ for reversed Weibull distributions meanwhile $R\leq0.5$ for Weibull distributions. Despite results from Table 2 showing $R > 0.4$, $R$ can assume any value in the interval $\lbrack0, 1\rbrack$ for Fréchet distributions.

5.2.   Real datasets

Real datasets are modeled according Theorems 3.1–3.3 and discussed in Sections 5.2.4 and 5.2.5. Besides providing $R$ by applying Eqs (3.5), (3.10) and (3.15) directly on estimated parameters distribution, we used the Bootstrap method ^[21] to evaluate confidence intervals of $R$ according to two different approaches: a parametric estimation $\hat{R}_{P}$ and an empirical estimation $\hat{R}_{E}$. $\hat{R}_{P}$ is a parametric estimation in a sense that we first fit distribution from data to later apply the results from Eqs (3.5), (3.10), and (3.15). The empirical approach $\hat{R}_{E}$ relies on the relative counts of samples such that $X < Y$.

5.2.1.   Bootstrap Parametric estimation

Algorithm 1 provides an estimation $\hat{R}_{P}$ of $R$ and its confidence intervals.

5.2.2.   Bootstrap Empirical estimation

The empirical (nonparametric) estimation $\hat{R}_{E}$ of $R$ and its confidence intervals are computed according to Algorithm 2.

In the Sections 5.2.4 and 5.2.5, $\hat{R}_E$ and $\hat{R}_P$ were computed using $M = 10,000$ Bootstrap draws in Algorithms 2 and 1, respectively.

5.2.3.   Asset selection

The proposed framework can be used to orient financial asset selection when managing a portfolio. So, instead of relying on the conventional approach of solely comparing expected values of $X$ and $Y$, which is based on modern portfolio theory, we investigate the application of the reliability measure $P(X < Y)$ as an alternative parameter for assessing returns.

The real dataset under analysis is composed by RVs $X_1, X_2, X_3$, and $X_4$, which are the stock price log-returns from tickers^* BBAS3.SA (Banco do Brasil S.A.), ITUB4.SA (Itaú Unibanco Holding S.A.), VALE3.SA (Vale S.A.) and VIIA3.SA (Via Varejo S.A.), respectively. The daily closing prices between 2022-01-01 and 2023-04-30 were retrieved from Yahoo! Finance, providing samples of length $n = 331$. From now on, we will omit the.SA suffixes present on the four tickers under analysis. To model stock prices log-returns and compare them in a reliability sense, we assume that the log-returns are independent ^[22].

^*Traded on BOVESPA, São Paulo Stock Exchange.

In order to start the investigation, a first step is to test for the best distribution fit between Fréchet, Weibull, and reversed Weibull distributions. Summary statistics for the datasets $X_1, X_2, X_3$, and $X_4$ are presented in Table 5 and Figure 4 to show the boxplots from the RVs, revealing certain symmetry of log-returns around zero and greater variability for $X_4$.

Theorems 3.1–3.3 constrain the reliability measure $P(X < Y)$ to a scenario when the RVs belong to the same distribution family. Thus, besides some evidence of independence between RVs, the same PDF should model the RVs under comparison. One way to choose the most suitable family of distributions for modeling each dataset is by comparing their information criteria such as the akaike information criterion (AIC), bayesian information criterion (BIC), and efficient determination criterion (EDC). For each of RVs $X_1$ to $X_4$, Table 6 shows the estimated parameters and information criteria for the PDFs Fréchet, Weibull, and reversed Weibull.

Reversed Weibull emerged as the best candidate distribution to model all the RVs $X_1$ to $X_4$, as supported by the information criteria AIC, BIC, and EDC and the histograms and CDFs shown in Figures 5 and 6. This choice was also supported by the Kolmogorov-Smirnov tests, whose p-values were $0.564$, $0.662$, $0.596$, and $0.410$, for $X_1$ to $X_4$, respectively, indicating that we could not reject the null hypothesis that the RVs follow a reversed Weibull distribution. The Weibull distribution provided the worst fit both in terms of information criteria as well as in terms of the severe impairment observed on Figures 5 and 6.

The estimation of probabilities of the type $R = P(X < Y)$ according Theorems 3.1–3.3 requires $X$ and $Y$ to be independent RVs. In this sense, we analyzed the dependency structures of $X_1, \cdots, X_4$ using the Pearson, Kendal, and Spearman correlation matrices. Table 7 suggests that the suitable pairs to be compared are $X_3$–$X_1$, $X_3$–$X_2$, and $X_3$–$X_4$.

Reliability measures of the type $R = P(X < Y)$ can orient the decision process of an investor. In summary, when $X$ and $Y$ represent return RVs and $R < 1/2$, it is advisable that the investor chooses the variable $X$. If $R > 1/2$, the opposite occurs. The case $R = 1/2$ is inconclusive. Thus, knowing how to evaluate $R$ accurately is important to support the decision process. In this sense, Table 8 presents the estimates of $P(X_3 < X_1)$, $P(X_3 < X_2)$ and $P(X_3 < X_4)$ and the $95\%$ Bootstrap confidence intervals (CI). The estimates $\hat{R}_{MLE}$ (4.1), $\hat{R}_{P}$ (Algorithm 1) and $\hat{R}_{E}$ (Algorithm 2) are compared.

Using Theorem 3.2 on the parameters of Table 6, we get estimates of $R$ that indicate that within the analyzed time period, BBAS3 and ITUB4 would be preferred over VALE3, while VALE3 would be preferred over VIIA3. Both the parametric $\hat{R}_P$ and nonparametric $\hat{R}_E$ estimates yielded consistent values belonging to overlapping CIs at 95% significance level.

An impairment is observed on the assessment of $R$ for $X_3$–$X_4$, whose nonparametric $\hat{R}_E$ estimate performed better than $\hat{R}_P$ in a sense of shorter CIs and smaller bias. Figure 4 has already shown that VIIA3 ($X_4$) has the greater volatility on the time period, which reveals a heavy tailed RV as supported by the highest shape parameter on Table 6. The $\hat{R}_P$ estimation procedure seems to be more sensitive to the Bootstrap sampling strategy when dealing with a heavy tailed RV: heavy tailed RVs carry information on their tails ^[23] and removing some extreme samples resulted in distribution parameters estimations far from the parameters obtained from the complete dataset for RV $X_4$. On the other hand, the Bootstrap CI estimates indicate that only the case $P(X_3 < X_4)$ has less uncertainty because the CI for $\hat{R}_E$ includes $0.5$ on its upper bound.

5.2.4.   Minimum monthly flows of water

Ramos et al. ^[24] presented five real datasets related to minimum monthly flows of water ($m^3/s$) on the Piracicaba River, located in São Paulo state, Brazil. The datasets were provided by the Department of Water Resources and Power of the agency responsible for managing the water resources of the state of São Paulo from 1960 to 2014. Their study concluded that Fréchet distribution fitted the data better than the Weibull, Gamma, Lognormal, Gumbel, and Generalized Exponential distributions.

We model $R = P(X < Y)$ using the Theorem 3.1, taking the flows from May ($X$) and September ($Y$). Data from May ($X$) and September ($Y$) minimum monthly flows of water are presented below:

Descriptive statistics for $X$ and $Y$ are presented in Table 9. The boxplot shown in Figure 7 shows that $X$ looks slightly greater than $Y$, and its maximum is more than 2 times the greatest observed sample for $Y$. Computing the value of the statistic $R$ is important to probabilistically measure such a difference observed in the datasets.

Figure 8 shows the fit of distributions to datasets meanwhile the estimated parameters are presented in Table 10. The findings of ^[24] demonstrate the suitability of zero-mean Fréchet distributions^† in modeling the minimum monthly flow of water. By modeling datasets using 3-parameter Fréchet distributions, we extend previous results ^[6,11,12,19] on stress-strength reliability analysis. Results from the KS test indicate that 3-parameter Fréchet distribution provides an adequate model for the datasets: the distance between the fitted and the empirical distribution functions for $X$ and $Y$ were 0.0917 and 0.0833 with the corresponding p-values 0.9806 and 0.9933, respectively.

^†2-parameter Fréchet distributions.

Using Theorem 3.1 on the parameters of Table 10, we obtain $\hat{R}_{MLE} = 0.2993$ from the fitted distributions and $\hat{R}_{P} = 0.2996$, whose CI is $(0.1928, 0.4258)$ at $95\%$ significance level. That indicates a low probability that the minimum monthly flows of September will be superior to May minimum monthly flows. By its turn, $\hat{R}_{E} = 0.3166$ in the CI $(0.175, 0.45)$ at $95\%$ significance level. The results from the empirical evaluation $\hat{R}_{E}$ were consistent with the results from the parametric evaluation $\hat{R}_{P}$, however the CI was larger for the empirical approach. The greater uncertainty is justified by the small number of samples available on the dataset when compared to the amount of samples suitable to provide accurate relative frequencies computation.

5.2.5.   Failure voltage levels of two types of electrical cable insulation

As an application involving Weibull distributions, we take a dataset of voltage levels (stress) at which dielectric ruptures were observed. The rupture is a failure on the insulation of electrical cables and can be provoked by subjecting cables specimens to increasing voltage levels. In a laboratory test reported by ^[25], two types of cable insulation (TypeS Ⅰ and Ⅱ) were tested. From each type, twenty specimens were selected and the failure voltages (in kilovolts per millimeter) were recorded as follows:

Descriptive statistics for $X$ (Type Ⅰ Insulation) and $Y$ (Type Ⅱ Insulation) are presented in Table 9. The boxplot shown in Figure 9 shows that $Y$ looks greater than $X$. Computing the value of the statistic $R$ is important to probabilistically measure such a difference observed in the datasets.

Figure 10 shows the fit of distributions to datasets meanwhile the estimated parameters are show in Table 12. Engineering experience suggests that failure voltages for the two types of cable could be suitably represented by Weibull distributions ^[25]. By modeling datasets using 3-parameter Weibull distributions, we extend previous results ^[6,7,8,9] on stress-strength reliability analysis. Results from the KS test indicate that 3-parameter Weibull distribution provides a reasonable model for the datasets: the distance between the fitted and the empirical distribution functions for $X$ and $Y$ were 0.1833 and 0.3000 with the corresponding p-values 0.6670 and 0.1214, respectively.

Using Theorem 3.3 on the parameters of Table 12, we obtain $\hat{R}_{MLE} = 0.8808$ from the fitted distributions and $\hat{R}_{P} = 0.8811$, whose CI is $(0.7393, 0.9734)$ at $95\%$ significance level. That indicates that the Type Ⅱ insulation specimens are more robust to dielectric ruptures when stressed under increasing voltage levels. By its turn, $\hat{R}_{E} = 0.8807$ in a CI of $(0.7000, 1.000)$ at $95\%$ significance level. The results from the empirical evaluation $\hat{R}_{E}$ of $R$ were consistent to results from the parametric evaluation $\hat{R}_{P}$, however the former CI was larger. As elucidated on Section 5.2.4, the greater uncertainty is justified by the small number of samples available on the dataset. Besides uncertainty involved in the modeling and up to our best knowledge, results are in accordance with the most recent work ^[9] regarding the dataset.

6.   Conclusions

In this paper, we studied the stress-strength reliability $R$ for 3 families of EVT-distributions: Fréchet, reversed Weibull, and Weibull. To the best of our knowledge, novel exact expressions for $R$ have been obtained in terms of the extreme-value $\mathbb{H}-$function with the least parameter restrictions to date. Monte-Carlo simulations and applications in real datasets were carried out to show the performance of the proposed estimators $\hat{R}_{MC}$ (cf. Tables 2–4), $\hat{R}_{MLE}$, $\hat{R}_{P}$ and the nonparametric $\hat{R}_{E}$ estimator. The modeling on real datasets was extensive in a sense that all distribution families were evaluated in Sections 5.2.3 and 5.2.4, and demonstrated coherency between parametric and nonparametric (empirical) estimators. Furthermore, we expanded upon earlier analyses involving comparable study cases, demonstrating that the novel expressions offer more versatile modeling alternatives. In summary, compared to previous studies, the findings of this paper enable a more accurate representation of the statistical behavior of real-world datasets.

The framework we explored in this work can be generalized to derive closed-form expressions for multicomponent system reliability with components following Fréchet, Weibull, or reversed Weibull distributions. Another possibility for future studies is the modeling of other datasets. For example, these distributions can successfully model data involving wind speeds.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Authors contributions

All authors contributed equally to the development of this work.

Acknowledgments

The authors would like to thank the editor and anonymous referees for their useful comments which helped us improve the manuscript. We also acknowledge the support provided by the University of Brasilia (Edital DPI/DPG/BCE Nº 01/2024).

Conflict of interest

The authors declare there is no conflict of interest.