Rigorous derivation of discrete fracture models for Darcy flow in the limit of vanishing aperture

1.   Introduction

Porous media with fractures or other thin heterogeneities, such as membranes, occur in a wide range of applications in nature and industry including carbon sequestration, groundwater flow, geothermal engineering, oil recovery, and biomedicine. Fractures are characterized by an extreme geometry with a small aperture but a significantly larger longitudinal extent, typically by several orders of magnitude. Therefore, it is often computationally unfeasible to represent fractures explicitly in full-dimensional numerical methods, especially in the case of fracture networks, as this results in thin equi-dimensional domains that require a high resolution. However, the presence of fractures can have a crucial impact on the flow profile in a porous medium with the fractures acting either as major conduits or as barriers. Moreover, in order to obtain accurate predictions for the flow profile, generally, one also has to take into account the geometry of fractures, i.e., curvature and spatially varying aperture ^[1,2].

In the following paragraph, we provide a brief overview on modeling approaches for flow in fractured porous media with a focus on discrete fracture models. For details on modeling and discretization strategies, we refer to the review article ^[3] and the references therein. Conceptually, one can distinguish between models with an explicit representation of fractures and models that represent fractures implicitly by an effective continuum. For the latter category, there is a distinction between equivalent porous medium models ^[4,5], where fractures are modeled by modifying the permeability of the underlying porous medium, and multi-continuum models ^[6,7], where the fractured porous medium is represented by multiple superimposed interacting continua---in the simplest case by a fracture continuum and a matrix continuum. In contrast, discrete fracture models represent fractures explicitly as interfaces of codimension one within a porous medium. In comparison with implicit models, there is an increase in geometrical complexity but no upscaled description based on effective quantities. Besides, there are also hybrid approaches for fracture networks, where only dominant fractures are represented explicitly ^[8,9]. The most popular method for the derivation of discrete fracture models is vertical averaging ^{[10,11,12,13,14,15,16,17]}, where the governing equations inside the fracture are integrated in normal direction. This leads to a description based on averaged fracture quantities on an interface of codimension one. However, the integration in normal direction provides no relation between the resulting interfacial model and the bulk flow model. Thus, using this approach, the resulting mixed-dimensional model is typically closed by making assumptions on the flow profile inside the fracture, which eventually renders the model derivation formal. Most commonly, averaged discrete fracture models are based on the conception of a planar fracture geometry with constant aperture. However, there are also works that consider curved fractures and fractures with spatially varying aperture ^[1,18]. Moreover, there are papers that take a fully mathematically rigorous approach for the derivation of discrete fracture models by applying weak compactness arguments to prove (weak) convergence towards a mixed-dimensional model in the limit of vanishing aperture ^{[19,20,21,22,23,24,25]}. This is also the approach that we follow here. In this case, in contrast to the method of vertical averaging, the width-to-length ratio of a fracture serves as a scaling parameter $\varepsilon$ and one has to specify how the model parameters, such as the hydraulic conductivity, scale with respect to $\varepsilon$ in the limit $\varepsilon \rightarrow 0$. Depending on their scaling, one can identify different regimes with fundamentally different limit problems as $\varepsilon \rightarrow 0$. Similar to the idea of homogenization theory, in the first place, this approach provides insight on the behavior of the system in the limit of vanishing width-to-length ratio $\varepsilon \rightarrow 0$ but the resulting limit models can be also be viewed as a computationally efficient approximation for real fractures with positive width-to-length ratio $0 < \varepsilon \ll 1$. Further, we mention ^[26,27], where formal asymptotic expansions are employed to obtain limit models for the Richards equation and two-phase Darcy flow in the limit of vanishing aperture, and ^[28], where a rigorous asymptotic approximation is presented for a convection-diffusion problem in a thin graph-like network. Besides, rigorous error estimates for classical solutions of discrete fracture models are obtained in ^[29,30]. In particular, in ^[30], an asymptotic expansion based on a Fourier transform is used to obtain the reduced model for one particular scaling of the fracture hydraulic conductivity with respect to the fracture aperture. Further, the authors in ^[31] have developed a mixed-dimensional functional analysis, which is utilized in ^[32] to obtain a poromechanical discrete fracture model using a formal "top-down" approach. In addition, we also mention phase-field models ^[33], which are convenient to track the propagation of fractures and can be combined with discrete fracture models ^[34].

In this paper, we consider single-phase fluid flow in a porous medium with an isolated fracture. Here, the term fracture refers to a thin heterogeneity inside the bulk porous medium which may itself be described as another porous medium with a distinctly different permeability, e.g., a debris- or sediment-filled crack inside a porous rock. We assume that the flow is governed by Darcy's law in both bulk and fracture. Further, we introduce the characteristic width-to-length ratio $\varepsilon > 0$ of the fracture as a scaling parameter. Given that the ratio ${{K_ {\mathrm{f}}}}^\star / {{K_\mathrm{b}}}^\star$ of characteristic hydraulic conductivities in the fracture and bulk domain scales with $\varepsilon^\alpha$, we obtain five different limit models as $\varepsilon \rightarrow 0$ depending on the value of the parameter $\alpha \in \mathbb{R}$. As the mathematical structure of the limit models is different in each case and reaches from a simple boundary condition to a PDE on the interfacial limit fracture, the different cases require different analytical approaches. Aside from delicate weak compactness arguments, the convergence proofs rely on tailored parameterizations and a novel coordinate transformation with controllable behavior with respect to the scaling parameter $\varepsilon$. Besides, we show the wellposedness of the limit models and strong convergence.

The limit of vanishing width-to-length ratio $\varepsilon\rightarrow 0$ is also considered in some of the works mentioned above for systems with simple geometries and constant hydraulic conductivities. In particular, for more simple systems, this is discussed in ^[20,22] for the case $\alpha = -1$ and in ^[25] for the case $\alpha = 1$. Moreover, our approach is related to the approach in ^[21], where Richards equation is considered for $\alpha < 1$. However, while their focus is on dealing with the nonlinearity and time-dependency of unsaturated flow, our focus is on the derivation of limit models for general fracture geometries and spatially varying tensor-valued hydraulic conductivities for the whole range of parameters $\alpha \in \mathbb{R}$. This aspect is not considered in ^[21]. In particular, in our case, the presence of off-diagonal elements in the hydraulic conductivity matrix inside the fracture complicates the analysis in the cases $\alpha = -1$ and $\alpha = 1$. Moreover, one of the limit models ($\alpha = -1$) will explicitly depend on these off-diagonal components.

The structure of this paper is as follows. In Section 2, we define the full-dimensional model problem of Darcy flow in a porous medium with an isolated fracture and introduce the characteristic width-to-length ratio $\varepsilon$ of the fracture as a scaling parameter. Section 3 deals with the derivation of a-priori estimates for the family of full-dimensional solutions parameterized by $\varepsilon > 0$. Further, in Section 4, depending on the choice of parameters, we identify the limit models as $\varepsilon \rightarrow 0$ and provide rigorous proofs of convergence. A short summary of the geometric background is given in Appendix A.

2.   Full-dimensional model and geometry

First, in Section 2.1, we define the geometric setting and introduce the full-dimensional model problem of single-phase Darcy flow in a porous medium with an isolated fracture in dimensional form. Then, in Section 2.2, dimensional quantities are rescaled by characteristic reference quantities to obtain a non-dimensional problem. Section 2.3 discusses the dependence of the domains and parameters on the width-to-length ratio $\varepsilon$ of the fracture, which is introduced as a scaling parameter. Further, given an atlas for the surface that represents the fracture in the limit $\varepsilon \rightarrow 0$, Section 2.4 introduces suitable local parameterizations for the bulk and fracture domains, which, in Section 2.5, allow us to transform the weak formulation of the non-dimensional problem from Section 2.2 into a problem with $\varepsilon$-independent domains.

2.1.   Full-dimensional model in dimensional form

In the following, dimensional quantities are denoted with a tilde to distinguish them from the non-dimensional quantities that are introduced in Section 2.2. Constant reference quantities are marked by a star.

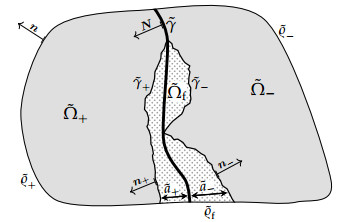
Let $n\in\mathbb{N}$ with $n\ge 2$ denote the spatial dimension of a porous medium. Of pratical interest are the cases $n \in \{2, 3\}$ but we also allow $n > 3$. First, we introduce a technical domain ${\tilde{{G}}} \subset \mathbb{R}^n$, which we suppose to be bounded with $\partial {\tilde{{G}}} \in \mathcal{C}^2$ (see Figure 2). We write ${\mathit{\boldsymbol{{N}}}} \in \mathcal{C}^1 (\partial {\tilde{{G}}}; \mathbb{R}^n)$ for the outer unit normal field on $\partial{\tilde{{G}}}$. Subsequently, we will consider the limit of vanishing width-to-length ratio for an isolated fracture in a porous medium such that $\overline{{\tilde{{\gamma}}}}$ represents the closure of the interfacial fracture in the limit model. It has to satisfy $\emptyset \not = \overline{{\tilde{{\gamma }}}} \subset \partial {\tilde{{G}}}$ as a compact and connected $\smash{\mathcal{C}^{0, 1}}$-submanifold with boundary $\smash{\partial \overline{{\tilde{{\gamma}}}}}$ and dimension $n-1$. The interior of $\smash{\overline{{\tilde{{\gamma}}}}}$ is denoted by $\smash{{\tilde{{\gamma}}}}$. We remark that ${\tilde{{\gamma}}} \subset \partial {\tilde{{G}}}$ is in fact a $\mathcal{C}^2$-submanifold without boundary, while $\smash{\overline{{\tilde{{\gamma}}}}}$ as a submanifold with boundary is only required to be of class $\mathcal{C}^{0, 1}$ (i.e., $\smash{\overline{{\tilde{{\gamma}}}}}$ can have corners for example). The domain ${\tilde{{G}}}$ plays a purely technical role: It induces an orientation on ${\tilde{{\gamma}}}$. Besides, the domain ${\tilde{{G}}}$ (or rather its boundary $\partial {\tilde{{G}}}$) allows to us to directly apply geometrical results for (compact) manifolds without boundary without worrying about $\smash{\overline{{\tilde{{\gamma}}}}}$ as a manifold with boundary. In particular, $\partial {\tilde{{G}}}$ is endowed with a signed distance function $\smash{d_\leftrightarrow^{\partial {\tilde{{G}}}}}$. Moreover, $\smash{\partial{\tilde{{G}}}}$ has bounded curvature. Thus, there exists a neighborhood of $\smash{\partial {\tilde{{G}}}}$ where the orthogonal projection $\smash{\mathcal{P}^{\partial {\tilde{{G}}}}}$ and the signed distance function $\smash{d_\leftrightarrow^{\partial {\tilde{{G}}}}}$ are well-defined and differentiable. We refer to Appendix A.1 for the relevant geometric background.

In the following, we define the geometry of the full-dimensional model. Given aperture functions $\smash{{\tilde{{a}}}_i \in \mathcal{C}^{0, 1} \bigl(\overline{{\tilde{{\gamma }}} }\bigr)}$ for $i \in \{ +, - \}$ such that the total aperture ${\tilde{{a}}} : = {\tilde{{a}}}_+ + {\tilde{{a}}}_- \ge 0$ is non-negative, we define the fracture domain $\smash{{\tilde{{\Omega}}}_\mathrm{f}}$ and its boundary segments $\smash{{\tilde{{\gamma}}}_\pm}$ by

Here and subsequently, we use the index $\pm$ as an abbreviation to simultaneously refer to two different quantities or domains on the inside ($-$) and outside ($+$) of the domain $\smash{{\tilde{{G}}}}$. Further, we distinguish between the parts of the fracture interface $\smash{{\tilde{{\gamma}}}}$ and the boundary segments $\smash{{\tilde{{\gamma}}}_\pm}$ with non-zero and zero aperture $\smash{{\tilde{{a}}}}$, i.e., $\smash{{\tilde{{\gamma}}} = {\tilde{{\Gamma }}} \; \dot{\cup} \; \smash{{\tilde{{\Gamma}}}}_0^0}$ and $\smash{{\tilde{{\gamma}}}_\pm = {\tilde{{\Gamma}}}_\pm \; \dot{\cup} \; {\tilde{{\Gamma}}}_0}$, where

We assume that $\smash{{\tilde{{\Omega}}}_\mathrm{f}}$ is connected with $\smash{\lambda_n ({\tilde{{\Omega}}}_\mathrm{f}) > 0}$, where $\lambda_n$ denotes the $n$-dimensional Lebesgue measure. In addition, we assume that the aperture functions ${\tilde{{a}}}_\pm$ are sufficiently small such that $\smash{{\tilde{{\Omega}}}_\mathrm{f} \subset \operatorname{unpp}(\partial {\tilde{{G}}})}$ with $\smash{\operatorname{unpp}(\partial {\tilde{{G}}}) \subset \mathbb{R}^n}$ as defined in Definition A.2. Besides, we denote by $\smash{ {\tilde{{\Omega}}}_\pm \subset \mathbb{R}^n}$ two disjoint and bounded Lipschitz domains such that $\smash{{\tilde{{\Omega}}}_\pm \cap {\tilde{{\Omega}}}_\mathrm{f} = \emptyset}$ and $\smash{\partial {\tilde{{\Omega}}}_\pm \cap \partial {\tilde{{\Omega}}}_\mathrm{f} = \overline{{\tilde{{\gamma}}}}_\pm}$. $\smash{{\tilde{{\Omega}}}_+}$ and $\smash{{\tilde{{\Omega}}}_-}$ are bulk domains adjacent to the fracture domain $\smash{{\tilde{{\Omega}}}_\mathrm{f}}$. Further, we define the total domain

which we assume to be a Lipschitz domain. Moreover, we write

for the external boundaries of the bulk domains ${\tilde{{\Omega}}}_i \subset {\tilde{{\Omega}}}$, $i \in \{ +, -, \mathrm{f}\}$, which are composed of disjoint Dirichlet and Neumann segments $\smash{{\tilde{{ \varrho}}}_{i, \mathrm{D}}}$ and $\smash{{\tilde{{ \varrho}}}_{i, \mathrm{N}}}$. The resulting geometric configuration is sketched in Figure 1. Besides, the position of the technical domain ${\tilde{{G}}}$ is sketched in Figure 2.

Now, let $\smash{{\tilde{{\mathbf{{K}}}}}_\pm \in L^\infty ({\tilde{{\Omega}}}_\pm; \mathbb{R}^{n\times n})}$ and $\smash{{\tilde{{\mathbf{{K}}}}}_\mathrm{f} \in L^\infty ({\tilde{{\Omega}}}_\mathrm{f}; \mathbb{R}^{n\times n})}$ be symmetric and uniformly elliptic hydraulic conductivity matrices. Further, for $i \in \{ +, -, \mathrm{f} \}$, let $\smash{{\tilde{{p}}}_i}$ denote the pressure head in $\smash{{\tilde{{\Omega}}}_i}$. Then, given the source terms $\smash{{\tilde{{q}}}_\pm \in L^2 ({\tilde{{\Omega}}}_\pm)}$ and $\smash{{\tilde{{q}}}_\mathrm{f} \in L^2 ({\tilde{{\Omega}}}_\mathrm{f})}$, we consider the following problem of Darcy flow in $\smash{{\tilde{{\Omega}}}}$.

Find $\smash{{\tilde{{p}}}_\pm \colon {\tilde{{\Omega}}}_\pm \rightarrow \mathbb{R}}$ and $\smash{{\tilde{{p}}}_\mathrm{f} \colon {\tilde{{\Omega}}}_\mathrm{f} \rightarrow \mathbb{R}}$ such that

Here, ${\mathit{\boldsymbol{{n}}}}$ is the outer unit normal on $\partial{\tilde{{\Omega}}}$ and ${\mathit{\boldsymbol{{n}}}}_\pm$ denotes the unit normal on ${\tilde{{\gamma}}}_\pm$ pointing into $\smash{{\tilde{{\Omega}}}_\pm}$. We remark that the choice of homogeneous boundary conditions in Eq (2.5) is only made for the sake of simplicity. The extension to the inhomogeneous case is straightforward.

2.2.   Full-dimensional model in non-dimensional form

We write $\smash{{{L}}^\star} \; \text{[m]}$ and $\smash{{{a}}^\star} \; \text{[m]}$ for the characteristic values of the length and aperture of the fracture given by

Here, $\smash{\lambda_{\partial{\tilde{{G}}}}}$ denotes the Riemannian measure on the submanifold $\partial{\tilde{{G}}} \subset \mathbb{R}^n$ (cf. Appendix A.3). Then, we define $\varepsilon : = {{{a}}^\star} / {{{L}}^\star} > 0$ as the characteristic width-to-length ratio of the fracture. Subsequently, in Sections 3 and 4, we will treat $\varepsilon$ as scaling parameter and analyze the limit behavior as $\varepsilon \rightarrow 0$.

Next, let ${{K}}^\star_\mathrm{b} \; \text{[m/s]}$ and ${{K}}^\star_\mathrm{f} \; \text{[m/s]}$ be characteristic values of the hydraulic conductivities ${\tilde{{\mathbf{{K}}}}}_\pm$ and ${\tilde{{\mathbf{{K}}}}}_\mathrm{f}$ in the bulk and fracture. In addition, we define the non-dimensional position vector $\smash{{\mathit{\boldsymbol{{x}}}} : = {\tilde{{{\mathit{\boldsymbol{{x}}}}}}} / {{L}}^\star}$. The non-dimensionalization of the position vector ${\mathit{\boldsymbol{{x}}}}$ results in a rescaling of spatial derivative operators, e.g., $\nabla = {{L}}^\star {\tilde{{\nabla}}}$. Besides, it necessitates the definition of non-dimensional domains (and boundary interfaces), which will be denoted without tilde, e.g., $\smash{\Omega : = {\tilde{{\Omega}}} / {{L}}^\star}$. If a domain or interface depends on the width-to-length $\varepsilon$ of the fracture, this is indicated by an additional index, e.g., $\smash{\Omega_+^ \varepsilon : = {\tilde{{\Omega}}}_+ / {{L}}^\star}$. Moreover, we define

We require $\smash{\lambda_{\partial\Omega } (\varrho_{\mathrm{b}, \mathrm{D}}^ \varepsilon) > 0 }$. Besides, we sometimes require the stronger assumption

i.e., both bulk domains $\Omega_+^ \varepsilon$ and $\Omega_-^ \varepsilon$ have a boundary part with Dirichlet conditions (and not possibly only one of them). This is subsequently referred to as "assumption $(\mathbb{A})$". Further, we define the non-dimensional quantities

where ${{p}}^\star_\mathrm{b} : = {{L}}^\star$, ${{p}}^\star_\mathrm{f} : = {{L}}^\star$, and ${{q}}^\star_\mathrm{b} : = {{K}}^\star_\mathrm{b} / {{L}}^\star$. We assume that there exist parameters $\alpha \in \mathbb{R}$ and $\beta \ge -1$ such that the characteristic fracture quantities ${{K}}^\star_\mathrm{f}$ and ${{q}}^\star_\mathrm{f}$ scale like

The dimensional Darcy system in Eq (2.5) now corresponds to the following non-dimensional problem.

Find $\smash{p_\pm^ \varepsilon \colon \Omega_\pm^ \varepsilon \rightarrow \mathbb{R}}$ and $\smash{p_\mathrm{f}^ \varepsilon \colon \Omega_\mathrm{f}^ \varepsilon \rightarrow \mathbb{R}}$ such that

In Eq (2.10), $\smash{{\mathit{\boldsymbol{{n}}}}}$ is the outer unit normal on $\smash{\partial\Omega}$ and $\smash{{\mathit{\boldsymbol{{n}}}}_\pm^ \varepsilon}$ denotes the unit normal on $\smash{\gamma_\pm^ \varepsilon}$ pointing into $\smash{\Omega^ \varepsilon_\pm}$. The geometry of the non-dimensional problem (2.10) with full-dimensional fracture $\smash{\Omega_ {\mathrm{f}}^ \varepsilon}$, as well as the limit geometry as $\varepsilon \rightarrow 0$, are sketched in Figure 3.

Next, we define the space

where the equalities on $\smash{\Gamma_0^ \varepsilon }$ and $\smash{\Gamma_\pm^ \varepsilon}$ are to be understood in the sense of traces. Then, a weak formulation of the system in Eq (2.10) is given by the following problem.

Find $\bigl(p_+^ \varepsilon, p_-^ \varepsilon, p_\mathrm{f}^ \varepsilon \bigr) \in \Phi^ \varepsilon$ such that, for all $\bigl(\varphi_+^ \varepsilon, \varphi_-^ \varepsilon, \varphi_\mathrm{f}^ \varepsilon \bigr) \in \Phi^ \varepsilon$,

As a consequence of the Lax-Milgram theorem, the Darcy problem (2.12) admits a unique solution $\smash{\bigl(p_+^ \varepsilon, p_-^ \varepsilon, p_\mathrm{f}^ \varepsilon \bigr) \in \Phi^ \varepsilon }$.

2.3.   Scaling of domains and parameters with respect to $\varepsilon$

Let $\smash{\kappa_k \in \mathcal{C}^0 (\partial G) }$, $k \in \{ 1, \dots, n-1\}$, denote the principal curvatures on $\partial G$ and set

Then, we have $\smash{\kappa_{\max} < \infty }$ due to the compactness of $\smash{\overline{\gamma}}$. Further, we define

with $\smash{\operatorname{reach}(\partial G) }$ as defined in Definition A.2. In the following, we require $\varepsilon \in (0, \hat{ \varepsilon}]$. In Eq (2.14), the condition $\smash{\hat {\hat \varepsilon} \le 1}$ ensures that $\smash{\hat {\hat \varepsilon}}$ is finite and the condition $\smash{\hat {\hat \varepsilon} < [3 \kappa_{\max}]^{-1}}$ guarantees the invertibility of certain $\varepsilon$-perturbed identity operators on the tangent space ${\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}}\Gamma$ (cf. Lemma 2.2 below). Besides, the condition $\smash{\hat {\hat \varepsilon} < \operatorname{reach}(\partial G)}$ allows us to use the results from Appendix A.1 on the regularity and wellposedness of the orthogonal projection $\smash{\mathcal{P}^{\partial G}}$ and the signed distance function $\smash{d_\leftrightarrow^{\partial G}}$.

The dependence of the non-dimensional domains and quantities on the width-to-length ratio $\varepsilon$ of the fracture is made explicit in the notation. For the non-dimensional fracture domain $\Omega_\mathrm{f}^ \varepsilon$, the $\varepsilon$-dependence is evident. Specifically, we have

Accordingly, the hydraulic conductivity $\smash{\mathbf{{K}}_\mathrm{f}^ \varepsilon}$ and the source term $\smash{q_\mathrm{f}^ \varepsilon}$ scale like

where the transformation $\smash{{\mathit{\boldsymbol{{T}}}}_\mathrm{f}^ \varepsilon \colon \Omega_\mathrm{f}^ \varepsilon \rightarrow \Omega_\mathrm{f}^{\hat{ \varepsilon}} }$ is given by

Further, we define

Note that only the inner region $\smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon}$ of the bulk domain $\smash{\Omega_\pm^ \varepsilon}$ depends on the scaling parameter $\varepsilon$, while the outer region $\smash{\Omega_{\pm, \mathrm{out}}}$ does not. For the inner region $\smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon}$, we impose a linear deformation in normal direction with decreasing $\varepsilon$, i.e., the hydraulic conductivity $\smash{\mathbf{{K}}_\pm^ \varepsilon}$ and the source term $\smash{q_\pm^ \varepsilon}$ satisfy

for $\smash{{\mathit{\boldsymbol{{x}}}} \in \Omega_{\pm, \mathrm{in}}^ \varepsilon }$, where the transformation $\smash{ {\mathit{\boldsymbol{{T}}}}^ \varepsilon_\pm \colon \Omega_{\pm, \mathrm{in}}^ \varepsilon \rightarrow \Omega_{\pm, \mathrm{in}}^0 }$ is given by

It is now easy to see that the following lemma holds.

Lemma 2.1. Let $\varepsilon \in (0, \hat{ \varepsilon}]$. Then, $\smash{{\mathit{\boldsymbol{{T}}}}_\mathrm{f}^ \varepsilon \colon \Omega_ {\mathrm{f}}^ \varepsilon \rightarrow \Omega_ {\mathrm{f}}^{\hat{ \varepsilon}}}$ is a $\smash{\mathcal{C}^1}$-diffeomorphism. Besides, $\smash{{\mathit{\boldsymbol{{T}}}}_\pm^ \varepsilon \colon \Omega_{\pm, \mathrm{in}}^ \varepsilon \rightarrow \Omega_{\pm, \mathrm{in}}^0 }$ is bi-Lipschitz. The inverses $\smash{ \underline {{{\mathit{\boldsymbol{{T}}}}}}_ {\mathrm{f}}^ \varepsilon : = ({\mathit{\boldsymbol{{T}}}}^ \varepsilon_ {\mathrm{f}})^{-1}}$ and $\smash{ \underline {{{\mathit{\boldsymbol{{T}}}}}}_\pm^ \varepsilon : = ({\mathit{\boldsymbol{{T}}}}_\pm^ \varepsilon)^{-1}}$ are given by

2.4.   Local parameterization

Subsequently, beginning with an atlas for the fracture interface $\Gamma$, we develop a suitable local parameterization of the fracture domain $\smash{\Omega_ {\mathrm{f}}^ \varepsilon}$ and the interior bulk domains $\Omega_{\pm, \mathrm{in}}^ \varepsilon$. Further, we will introduce transformations onto $\varepsilon$-independent domains and characterize how they depend on the scaling parameter $\varepsilon$. Eventually, in Section 2.5, this will allow us to reformulate the Darcy problem (2.10) in terms of $\varepsilon$-independent domains. In the following, we use the definitions and notations from Appendix A.3.

We observe that $\Gamma \subset \partial G$ is open so that $\Gamma \subset \mathbb{R}^n$ is itself a $\mathcal{C}^2$-submanifold of dimension $n-1$. Besides, $\smash{\overline{\Gamma} \subset \mathbb{R}^n}$ is a $\smash{\mathcal{C}^{0, 1}}$-submanifold with boundary. Now, let $\smash{\{ (U_j, {\mathit{\boldsymbol{{\psi}}}}_j, V_j) \}_{j\in{ J }}}$ be a $\mathcal{C}^2$-atlas for $\Gamma$ consisting of charts ${\mathit{\boldsymbol{{\psi}}}}_j \colon U_j \rightarrow V_j$, where $U_j \subset \Gamma$ and $V_j \subset \mathbb{R}^{n-1}$ are open. Then, for $j \in J$ and $\varepsilon \in (0, \hat{ \varepsilon}]$, we write $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j : = {\mathit{\boldsymbol{{\psi}}}}_j^{-1}}$ for the inverse charts and define

for $\varepsilon \in (0, \hat{ \varepsilon}]$, as well as

for $\varepsilon \in [0, \hat{ \varepsilon}]$. In the following, we will also think of the subdomains $\smash{\Omega_\mathrm{f}^ \varepsilon}, \ \smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon} \subset \mathbb{R}^n$ as $n$-dimensional $\mathcal{C}^{0, 1}$-submanifolds. With the given atlas for $\Gamma$, we can construct a $\mathcal{C}^{0, 1}$-atlas $\smash{\{ (U_{\mathrm{f}, j}^ \varepsilon, {\mathit{\boldsymbol{{\psi}}}}_{\mathrm{f}, j}^ \varepsilon, V_{\mathrm{f}, j }) \}_{j\in J }}$ for $\smash{\Omega_\mathrm{f}^ \varepsilon}$ for $\varepsilon \in (0, \hat{ \varepsilon}]$, as well as $\mathcal{C}^{0, 1}$-atlases $\smash{\{(U_{\pm, j}^ \varepsilon, {\mathit{\boldsymbol{{\psi}}}}_{\pm, j}^ \varepsilon, V_{\pm, j }) \}_{j\in J }}$ for $\smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon}$ for $\varepsilon \in [0, \hat{ \varepsilon}]$. For $j \in J$, the charts $\smash{{\mathit{\boldsymbol{{\psi}}}}_{\mathrm{f}, j}^ \varepsilon }$ and $\smash{{\mathit{\boldsymbol{{\psi}}}}_{\pm, j}^ \varepsilon }$, as well as their inverses $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{ {\mathrm{f}}, j}^ \varepsilon}$ and $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^ \varepsilon }$, are given by

Further, we introduce the product-like $n$-dimensional $\mathcal{C}^2$-submanifold

Then, $\smash{\Gamma_a }$ is the interior of the following $\smash{\mathcal{C}^{0, 1}}$-manifolds with boundary.

Besides, we write

for the external boundary segment of $\smash{\overline{\Gamma}_a^par}$ with Dirichlet conditions. A $\mathcal{C}^2$-atlas of $\Gamma_a$ is given by $\smash{\{ (U_j^a, {\mathit{\boldsymbol{{\psi}}}}_j^a, V_{ {\mathrm{f}}, j }) \}_{j\in J}}$, where

Further, for $f \in H^1 (\Gamma_a)$, we decompose the gradient $\smash{\nabla_{\! \Gamma_a }} f$ into a tangential and a normal component, i.e.,

Next, we write $\smash{\mathbf{{S}}^{{\mathit{\boldsymbol{{\psi}}}}_j} ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime) \in \mathbb{R}^{(n-1)\times (n-1)}}$ for the matrix representation of the shape operator $\smash{\mathcal{S}_{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime)}}$ of $\Gamma$ at $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j({\mathit{\boldsymbol{{ \vartheta}}}}^\prime) }$ with respect to the basis

Details on the shape operator $\smash{\mathcal{S}_{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime)}}$ can be found in Appendix A.2. In addition, for $j \in J$ and $\smash{{\mathit{\boldsymbol{{ \vartheta}}}} = ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime, \vartheta_n) \in V_{ {\mathrm{f}}, j}}$ or $\smash{V_{\pm, j}}$, we introduce the abbreviations

where $\smash{\mathbf{{I}}_{n-1} \in \mathbb{R}^{(n-1)\times (n-1)}}$ is the identity matrix. Besides, we define the operators

for all $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$ and $\smash{{\mathit{\boldsymbol{{x}}}}\in \Omega_{\pm, \mathrm{in}}^0}$ by

The operators in Eq (2.34) will appear when considering gradients of yet to be introduced transformations "$\Omega_{\pm, \mathrm{in}}^ \varepsilon \rightarrow \Omega_{\pm, \mathrm{in}}^0$" and "$\Omega_ {\mathrm{f}}^ \varepsilon \rightarrow \Gamma_a$" onto $\varepsilon$-independent domains (cf. Eq (2.45) and Lemma 2.4 (iii) and (iv) below). Moreover, the operators in Eq (2.34) have the following properties. In particular, we can characterize their behavior as $\varepsilon \rightarrow 0$.

Lemma 2.2. (i) The operators $\smash{ \underline {{\mathcal{R}}}_ {\mathrm{f}}^ \varepsilon }$ and $\smash{ \underline {{\mathcal{R}}}_\pm^ \varepsilon }$ exist for all $\varepsilon \in (0, \hat{ \varepsilon}]$.

(ii) For all $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a}$ and $\smash{{\mathit{\boldsymbol{{x}}}} \in \Omega^0_{\pm, \mathrm{in}}}$, the operators

are self-adjoint for $\smash{ \varepsilon \in (0, \hat{ \varepsilon}]}$. In particular, for $i \in \{ +, -, {\mathrm{f}} \}$, it is

(iii) For $j\in J$ and $\smash{ \varepsilon \in (0, \hat{ \varepsilon}]}$, the matrix representations of the operators

with respect to the basis (2.32) are given by $\smash{\bigl[\mathbf{{R}}_{ {\mathrm{f}}, j}^ \varepsilon ({\mathit{\boldsymbol{{ \vartheta }}}}) \bigr]^{-1}}$, $\smash{\bigl[\mathbf{{R}}_{\pm, j}^ \varepsilon ({\mathit{\boldsymbol{{ \vartheta }}}}) \bigr]^{-1}}$, and $\smash{\mathbf{{R}}_{\pm, j}^0 ({\mathit{\boldsymbol{{ \vartheta }}}}) }$.

(iv) As $\varepsilon \rightarrow 0$, we have

for $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$ and $\smash{{\mathit{\boldsymbol{{x}}}}\in \Omega^0_{\pm, \mathrm{in}}}$.

Proof. (i) Using Eq (2.14) and the self-adjointness of $\smash{\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}}}$, we find

Thus, the operator $\smash{ \underline {{\mathcal{R}}}_ {\mathrm{f}}^ \varepsilon \bigr\vert_{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n)}}$ exists for all $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$ and $\varepsilon \in (0, \hat{ \varepsilon }]$.

Further, with Eq (2.14) and the self-adjointness of $\smash{\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}}}$, we have

for all $\smash{{\mathit{\boldsymbol{{x}}}} \in \Omega_{\pm, \mathrm{in}}^0}$ so that $\smash{\mathcal{R}^0_\pm \bigr\vert_{\mathit{\boldsymbol{{x}}}}}$ is invertible with

Besides, it is

where we have used that $\smash{0 \le {{ }\vert {\hat {\hat \varepsilon}^{-1} d_\leftrightarrow^{\partial G} ({\mathit{\boldsymbol{{x}}}}) \pm 1} { }\vert} \le \frac{3}{2}}$. Consequently, the operator

exists for all $\smash{{\mathit{\boldsymbol{{x}}}} \in \Omega_{\pm, \mathrm{in}}^0}$ and $\smash{ \varepsilon \in (0, \hat{ \varepsilon }]}$.

(ii) The result follows directly from the self-adjointness of the shape operator.

(iii) We have

for $i \in \{ 1, \dots, n-1\}$, where $\smash{{\mathit{\boldsymbol{{e}}}}_i \in \mathbb{R}^{n-1}}$ denotes the $i$th unit vector, and hence

The result for $\smash{ \underline {{\mathcal{R}}}^ \varepsilon_\pm }$ follows analogously. The result for $\smash{\mathcal{R}_\pm^0}$ is trivial.

(iv-a) Using (ii), we find

Here, $\smash{\kappa_k \in \mathcal{C}^0 (\partial G) }$, $k \in \{ 1, \dots, n-1 \}$, denote the principal curvatures on $\partial G$, which are bounded due to the compactness of $\partial G$.

(iv-b) Using Eq (2.14) and the self-adjointness of $\smash{\mathcal{S}_{\mathcal{P}^{\partial G} ({\mathit{\boldsymbol{{x}}}})}}$, we find

Thus, we can express $\smash{ \underline {{\mathcal{R}}}_\pm^ \varepsilon \bigr\vert_{{\mathit{\boldsymbol{{x}}}}}}$ as a Neumann series and obtain

where $\smash{ \underline {{t}}_\pm^ \varepsilon \bigl(\mathcal{P}^{\partial G } ({\mathit{\boldsymbol{{x}}}}), - d_\leftrightarrow^{\partial G} ({\mathit{\boldsymbol{{x}}}}) \bigr) + d_\leftrightarrow^{\partial G} ({\mathit{\boldsymbol{{x}}}}) = \mathcal{O}(\varepsilon)}$. □

Further, for $j \in J$, the Jacobians of the inverse charts $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{ {\mathrm{f}}, j}^ \varepsilon}$, $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^ \varepsilon}$ are given by

where

Consequently, with $\smash{\bigl[\mathbf{{D}} \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime) \bigr]^ \mathrm{t} {\mathit{\boldsymbol{{N}}}} \bigl(\underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime) \bigr) = {\mathit{\boldsymbol{{0}}}} }$, we find that the metric tensors of $\smash{\Omega_ {\mathrm{f}}^ \varepsilon }$ and $\smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon }$ in coordinates of the charts $\smash{{\mathit{\boldsymbol{{\psi}}}}_{ {\mathrm{f}}, j}^ \varepsilon}$ and $\smash{{\mathit{\boldsymbol{{\psi}}}}_{\pm, j}^ \varepsilon}$, $j \in J$, are given by

where $\smash{{\mathit{\boldsymbol{{e}}}}_n \in \mathbb{R}^n}$ is the $n$th unit vector and $\smash{{\mathbf{{g}}}\vert^{{\mathit{\boldsymbol{{\psi}}}}_{j} } }$ denotes the metric tensor on $\Gamma$ in coordinates of the chart $\smash{{\mathit{\boldsymbol{{\psi}}}}_j}$. Subsequently, for $j \in J$, we will use the notation

Moreover, we have the following result on the metric tensors.

Lemma 2.3. Let $\varepsilon \in (0, \hat{ \varepsilon}]$ and $j\in J$. As $\varepsilon \rightarrow 0$, we have

The prefactors on the right-hand side of Eq (2.42) do not depend on $j \in J$.

Proof. Given the principal curvatures $\smash{\kappa_k \in \mathcal{C}^0 (\partial G) }$ on $\partial G$, $k\in\{ 1, \dots, n-1\}$, which are bounded on the compact submanifold $\partial G$, we have

for $j\in J$, where $\smash{ \underline {{t}}_\pm^ \varepsilon \bigl(\underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime), \vartheta_n \bigr) = \underline {{t}}_\pm^0 \bigl(\underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime), \vartheta_n \bigr) + \mathcal{O}(\varepsilon) }$. This yields

so that Eq (2.42a) follows. Moreover, as a consequence of Sylvester's determinant theorem, the relation

holds true for any invertible matrix $\smash{\mathbf{{A}} \in \mathbb{R}^{n\times n}}$ and ${\mathit{\boldsymbol{{c}}}}, {\mathit{\boldsymbol{{d}}}}, {\mathit{\boldsymbol{{e}}}}, {\mathit{\boldsymbol{{f}}}} \in \mathbb{R}^n$. Thus, with Eq (2.43b), we find

□

Next, given a partition of unity $\smash{\{ \chi_j \}_{j\in J }}$ of $\Gamma$ that is subordinate to the covering $\smash{\{ U_j \}_{j\in J }}$, we define the partitions of unity

● $\smash{\{ \chi^ \varepsilon_{\pm, j }\}_{j\in J }}$ on $\smash{\Omega_{\pm, \mathrm{in}}^ \varepsilon}$ subordinate to $\smash{ \{ U_{\pm, j}^ \varepsilon \}_{j\in J }}$ by $\smash{\chi^ \varepsilon_{\pm, j} : = \chi_j \circ \mathcal{P}^{\partial G}\bigr\vert_{\Omega_{\pm, \mathrm{in}}^ \varepsilon }}$,

● $\smash{\{ \chi^ \varepsilon_{\mathrm{f}, j} \}_{j\in J }}$ on $\smash{\Omega_\mathrm{f}^ \varepsilon}$ subordinate to $\smash{ \{ U_{\mathrm{f}, j}^ \varepsilon \}_{j\in J }}$ by $\smash{\chi^ \varepsilon_{\mathrm{f}, j} : = \chi_j \circ\mathcal{P}^{\partial G}\bigr\vert_{\Omega_ {\mathrm{f}}^ \varepsilon }}$,

● $\smash{\{ \chi^a_j \}_{j\in J }}$ on $\smash{\Gamma_a}$ subordinate to $\smash{ \{ U_j^a \}_{j\in J }}$ by $\smash{\chi^a_{ j} ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) : = \chi_j ({\mathit{\boldsymbol{{\pi}}}}) }$.

Further, for $\varepsilon \in (0, \hat{ \varepsilon}]$, we define the transformations $\smash{\mathcal{Y}^ \varepsilon_\pm \colon L^2 (\Omega_\pm^0) \rightarrow L^2 (\Omega_\pm^ \varepsilon)}$ and $\smash{\mathcal{Y}^ \varepsilon_\mathrm{f} \colon L^2 (\Gamma_a) \rightarrow L^2 (\Omega_\mathrm{f}^ \varepsilon)}$ by

The inverse maps $\smash{ \underline {{\mathcal{Y}}}_\pm^ \varepsilon : = (\mathcal{Y}_\pm^ \varepsilon)^{-1}}$ and $\smash{ \underline {{\mathcal{Y}}}_ {\mathrm{f}}^ \varepsilon : = (\mathcal{Y}^ \varepsilon_ {\mathrm{f}})^{-1} }$ are given by

Moreover, we define the product map

and write $\smash{ \underline {{\mathcal{Y}}}^ \varepsilon : = (\mathcal{Y}^ \varepsilon)^{-1}}$ for its inverse. Then, the following result for the asymptotics of the transformations $\smash{\mathcal{Y}^ \varepsilon_\pm}$, $\smash{\mathcal{Y}_ {\mathrm{f}}^ \varepsilon}$ between the final domains $\smash{\Omega_\pm^0}$, $\smash{\Gamma_a}$ and the $\varepsilon$-dependent original domains $\smash{\Omega_\pm^ \varepsilon}$, $\smash{\Omega_ {\mathrm{f}}^ \varepsilon}$ holds true as $\varepsilon \rightarrow 0$.

Lemma 2.4. There is an $\bar{ \varepsilon} > 0$ such that the following results hold for all $\varepsilon \in (0, \bar{ \varepsilon}]$.

(i) $\mathcal{Y}_ {\mathrm{f}}^ \varepsilon \colon L^2 (\Gamma_a) \rightarrow L^2 (\Omega_ {\mathrm{f}}^ \varepsilon)$ defines an isomorphism with

for all $\smash{ \varphi_ {\mathrm{f}} \in L^2 (\Gamma_a) }$.

(ii) $\mathcal{Y}_\pm^ \varepsilon \colon L^2 (\Omega_\pm^0) \rightarrow L^2 (\Omega_\pm^ \varepsilon)$ defines an isomorphism with

for all $\smash{ \varphi_\pm \in L^2 (\Omega_\pm^0) }$.

(iii) ${\mathcal{Y}_ {\mathrm{f}}^ \varepsilon \bigr\vert_{H^1 (\Gamma_a) } \colon H^1 (\Gamma_a) \rightarrow H^1 (\Omega_ {\mathrm{f}}^ \varepsilon) }$ is an isomorphism. In particular, we have

for $\varphi_ {\mathrm{f}} \in H^1 (\Gamma_a)$ and a.a. $({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a$ and hence

(iv) ${\mathcal{Y}_\pm^ \varepsilon \bigr\vert_{H^1 (\Omega_\pm^0) } \colon H^1 (\Omega_\pm^0) \rightarrow H^1 (\Omega_\pm^ \varepsilon) }$ is an isomorphism. In particular, we have

for $\smash{ \varphi_\pm \in H^1 (\Omega_\pm^0)}$ and a.a. ${\mathit{\boldsymbol{{x}}}} \in \Omega_{\pm, \mathrm{in}}^0$, where

Besides, it is

where $\smash{\mathbf{{I}}_n \in \mathbb{R}^{n\times n }}$ denotes the identity matrix. Thus, we obtain

Proof. (i) It is easy to see that $\smash{\mathcal{Y}_ {\mathrm{f}}^ \varepsilon }$ is linear and bijective with inverse $\smash{ \underline {{\mathcal{Y}}}_ {\mathrm{f}}^ \varepsilon}$. Moreover, with Lemma 2.3, we have

(ii) $\smash{\mathcal{Y}_\pm^ \varepsilon }$ is clearly linear and bijective with inverse $\underline {{\mathcal{Y}}}_\pm^ \varepsilon$. Further, we have

Then, by using Lemma 2.3 and $\smash{{\mathit{\boldsymbol{{T}}}}_\pm^ \varepsilon \circ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^ \varepsilon = \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^0 }$, we find

(iii) Let $\smash{ \varphi_ {\mathrm{f}} \in H^1 (\Gamma_a)}$ and $\smash{ \varphi_ {\mathrm{f}}^ \varepsilon : = \mathcal{Y}_ {\mathrm{f}}^ \varepsilon \varphi_ {\mathrm{f}}}$. Then, by using the Eqs (2.38a), (2.40a) and Lemma 2.2 (ii) and (iii), we find

for $j \in J$ and a.a. $\smash{{\mathit{\boldsymbol{{ \vartheta}}}} = ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime, \vartheta_n) \in V_{ {\mathrm{f}}, j}}$. Thus, with Lemma 2.2 (iv), we have

for a.a. $({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a$ so that Eq (2.51) follows with Lemma 2.3.

(iv) Equation (2.52) follows by applying the chain rule. Now, let $\smash{ \varphi_\pm \in H^1 (\Omega_\pm^0})$ and $\smash{ \varphi_\pm^ \varepsilon : = \mathcal{Y}_\pm^ \varepsilon \varphi_\pm }$. Then, by using that $\smash{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^ \varepsilon = \underline {{{\mathit{\boldsymbol{{T}}}}}}_\pm^ \varepsilon \circ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^0}$, the chain rule yields

With Eq (2.38b) and the Sherman-Morrison formula, we obtain

where $\smash{\mathbf{{I}}_n \in \mathbb{R}^{n\times n}}$ is the identity matrix and

Consequently, with Lemma 2.2 (ii), we find

where we have used the abbreviation

Thus, using that

we find

for all $\smash{{\mathit{\boldsymbol{{z}}}}\in\mathbb{R}^n }$, where

denotes the orthogonal projection onto $\smash{ {\mathrm{T}}_{ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_j ({\mathit{\boldsymbol{{ \vartheta}}}}^\prime) } \Gamma }$. Further, it is easy to see that

Thus, the result follows with Lemma 2.2 (iv). □

2.5.   Full-dimensional problem with $\varepsilon$-independent domains

Subsequently, we will rewrite the integrals in the weak formulation (2.12) on $\smash{\Omega_{\pm }^ \varepsilon}$ and $\smash{\Omega_\mathrm{f}^ \varepsilon}$ as integrals on $\smash{\Omega_{\pm }^0}$ and $\smash{\Gamma_a}$ by using the results on the transformations $\smash{\mathcal{Y}_\pm^ \varepsilon}$ and $\smash{\mathcal{Y}_ {\mathrm{f}}^ \varepsilon}$ from Lemma 2.4. In this way, we avoid working with $\varepsilon$-dependent domains and can more easily identify the dominant behavior for vanishing $\varepsilon$.

Let $\bar{ \varepsilon} > 0$ be as in Lemma 2.4. Then, for $\varepsilon\in (0, \bar{ \varepsilon}]$, we define the solution and test function space

As a consequence of Lemma 2.4 (iii) and (iv), the space $\Phi$ does not depend on $\varepsilon$ (cf. Lemma 3.2). In addition, we define

Next, for $\varepsilon \in (0, \bar{ \varepsilon}]$, let $\smash{(\varphi_+, \varphi_-, \varphi_\mathrm{f}) \in \Phi}$ and set

Further, given the unique solution $(p_+^ \varepsilon, p_-^ \varepsilon, p_\mathrm{f}^ \varepsilon) \in \Phi^ \varepsilon$ of Eq (2.12), we define

Then, with Lemma 2.3, we have

In the same way, by additionally using Lemma 2.4 (iii), we obtain

Moreover, it is

where we have used that $\smash{ {\mathit{\boldsymbol{{T}}}}_\pm^ \varepsilon \circ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j}^ \varepsilon = \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_{\pm, j }^0 }$ for $j \in J$ and hence, with Lemma 2.3,

Analogously, by additionally using Lemma 2.4 (iv), we obtain

Thus, by combining the Eqs (2.60)–(2.64), we find that, if $\smash{(p^ \varepsilon_+, p^ \varepsilon_-, p^ \varepsilon_ {\mathrm{f}}) \in \Phi^ \varepsilon}$ solves the weak formulation (2.12), then $\smash{(\hat{p}^ \varepsilon_+, \hat{p}^ \varepsilon_-, \hat{p}^ \varepsilon_ {\mathrm{f}}) \in \Phi}$ satisfies

for all $\smash{ \varphi = (\varphi_+, \varphi_-, \varphi_\mathrm{f}) \in \Phi}$ as $\varepsilon \rightarrow 0$. The bilinear forms $\smash{\mathcal{A}_\pm \colon \Omega_\pm^0 \times \Omega_\pm^0 \rightarrow \mathbb{R}}$ and $\smash{\mathcal{A}_\mathrm{f}^ \varepsilon \colon \Gamma_a \times \Gamma_a \rightarrow \mathbb{R}}$ are given by

3.   A-priori estimates and weak convergence

In this section, we obtain a-priori estimates for the solution $(\hat{p}_+^ \varepsilon, \hat{p}_-^ \varepsilon, \hat{p}_ {\mathrm{f}}^ \varepsilon) \in \Phi$ of the transformed weak formulation (2.65) and, consequently, can identify a weakly convergent subsequence as $\varepsilon \rightarrow 0$. The main results are developed in Section 3.3. They build on trace inequalities from Section 3.1 and Poincaré-type inequalities from Section 3.2.

First, we introduce useful functions spaces on $\Gamma$ and $\Gamma_a$, as well as averaging operators on $\smash{\Gamma_a}$. Given a $\smash{\lambda_\Gamma}$-measurable, non-negative weight function $w \colon \Gamma \rightarrow \mathbb{R}$, we define the weighted Lebesgue space $L^2_w (\Gamma)$ as the $L^2$-space on $\Gamma$ with measure $w\lambda_\Gamma$. Further, we define the weighted Sobolev space $H^1_a (\Gamma)$ as the completion of

with respect to the norm ${\left\Vert {f} \right\Vert}_{H^1_a (\Gamma) }^2 : = {\left\Vert {f} \right\Vert}_{L^2_a (\Gamma) }^2 + {\left\Vert { \nabla_{\!\Gamma} f} \right\Vert}^2_{{\mathit{\boldsymbol{{L}}}}^2_a (\Gamma) }$. Besides, we define the space $\smash{H^1_{{\mathit{\boldsymbol{{N}}}}} (\Gamma_a) \subset L^2 (\Gamma_a)}$ as the closure of the space

with respect to the norm ${\left\Vert {f} \right\Vert}_{H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a) }^2 : = {\left\Vert {f} \right\Vert}_{L^2 (\Gamma_a) }^2 + {\left\Vert { \nabla_{\!{\mathit{\boldsymbol{{N}}}}} f} \right\Vert}_{{\mathit{\boldsymbol{{L}}}}^2 (\Gamma_a) }^2$. Moreover, we introduce the averaging operators

3.1.   Trace inequalities

We begin by introducing a trace operator $\smash{\mathfrak{T}_\pm}$ on $\smash{H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a) }$ for the lateral boundaries of $\smash{\overline{\Gamma}_a^perp}$.

Lemma 3.1. There exists a uniquely defined bounded linear operator

such that, for all $\smash{f \in \mathcal{C}^{0, 1} (\overline{\Gamma}_a^perp)}$, we have

Proof. W.l.o.g., we consider $\smash{\mathfrak{T}_+}$. The operator $\smash{\mathfrak{T}_-}$ can be treated analogously.

Let $\smash{ f \in \mathcal{C}^{0, 1} (\overline{\Gamma}_a^perp) }$. Then, for all $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$, we have

An integration over $\smash{\Gamma_a }$ yields

By applying Hölder's inequality, we obtain

The result now follows from the fact that $\smash{\mathcal{C}^{0, 1} (\overline{ \Gamma}_a^perp) }$ is dense in $\smash{H^1_{\mathit{\boldsymbol{{N}}}}(\Gamma_a) }$. □

Besides, we obtain the following characterization of the space $\Phi$.

Lemma 3.2. We have

In particular, for $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi}$, it is

Proof. Using that $\smash{\mathcal{C}^{0, 1} (\overline{\Omega_\pm^0 }) \subset H^1 (\Omega_\pm^0)}$ and $\smash{\mathcal{C}^{0, 1} (\overline{\Gamma}_a^perp) \subset H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a) }$ are dense, we find

almost everywhere for any $\smash{ \varepsilon \in (0, \bar{ \varepsilon}]}$ for all $\varphi_\pm \in H^1 (\Omega_\pm^0)$ and $\varphi_ {\mathrm{f}} \in H^1 (\Gamma_a)$. Thus, it is easy to see that

where $\smash{\Phi^\prime}$ denotes the space on the right-hand side of Eq (3.6). Besides, Eq (3.7) is a consequence of the trace inequality in $\smash{\Omega_\pm^0}$. □

Further, it is easy to see that the following lemma holds, which introduces a trace operator on the weighted Sobolev space $H^1_a (\Gamma)$.

Lemma 3.3. Let ${\mathfrak{T}_{\overline{\Gamma}_a^par } \colon H^1 (\overline{\Gamma}_a^par) \rightarrow L^2 (\partial \overline{\Gamma}_a^par) }$ denote the trace operator on $\smash{\overline{\Gamma}_a^par }$ from Lemma A.3. Further, we introduce the constant extension operator

Then, the trace operator $\smash{\mathfrak{T}_par^a \colon H^1_a (\Gamma) \rightarrow L^2_a (\partial \overline{\Gamma })}$ defined by

is bounded and satisfies

3.2.   Poincaré-type inequalities

We obtain two Poincaré-type inequalities for functions in $\smash{H^1_{\mathit{\boldsymbol{{N}}}}(\Gamma_a) }$.

Lemma 3.4. Let $i\in\{ +, -\}$ and $f \in H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a)$. Then, we have

Proof. We prove the inequality (3.11) for $i = +$ and $\smash{f \in \mathcal{C}^{0, 1} (\overline{\Gamma}_a^perp)}$. The case $i = -$ is analogous. The general case follows from a density argument. We now have

□

Lemma 3.5. Let $i\in\{ +, -\}$ and $f \in H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a)$. Then, we have

Proof. Subsequently, we prove the inequality (3.12) for $i = +$ and $\smash{f \in \mathcal{C}^{0, 1} (\overline{\Gamma}_a^perp)}$. Then, the desired inequality is obtained from a density argument. The case $i = -$ follows by analogy. Now, let $\smash{ ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$. Then, we have

and hence, by using Hölder's inequality,

Consequently, we obtain

An additional integration on $\Gamma$ yields

Further, we have $\smash{{\left\Vert {f (\cdot, a_+(\cdot)) } \right\Vert}_{L^2 (\Gamma_a)} = {\left\Vert {\mathfrak{T}_+ f} \right\Vert}_{L^2_a (\Gamma) }}$ so that the result follows by applying the reverse triangle inequality in Eq (3.13). □

We can now combine Poincaré's inequality and the Lemmas 3.2 and 3.5 to obtain the following estimate for function triples $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi}$, which fits the setting of the coupled Darcy problem in Eq (2.65).

Lemma 3.6. Let $\smash{ (\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi }$.

(i) There exists an $\smash{ \varepsilon^\ast > 0}$ such that, for all $\smash{ \varepsilon \in (0, \varepsilon^\ast]}$ and $\nu \ge 0$, we have

(ii) Let $\nu \ge 0$ and $\varepsilon \in [0, 1]$. Given additionally the assumption $(\mathbb{A})$, we have

Proof. (i) Let $(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi$ and, for $\varepsilon \in (0, \bar{ \varepsilon}]$, define $\smash{ \varphi^ \varepsilon \in H^1_{0, \varrho_\mathrm{D}^ \varepsilon } (\Omega)}$ by

Then, with Lemma 2.4 (ii) and Poincaré's inequality, we have

if $\varepsilon > 0$ is sufficiently small. Moreover, Lemma 2.4 (iii) and (iv) yield

By using Poincaré's inequality and the Lemmas 3.2 and 3.5, we obtain

(ii) Follows directly from Poincaré's inequality and the Lemmas 3.2 and 3.5. □

3.3.   Results

Using Lemma 3.6, we can obtain the following a-priori estimates for the solution $\smash{(\hat{p}_+^ \varepsilon, \hat{p}_-^ \varepsilon, \hat{p}_ {\mathrm{f}}^ \varepsilon) \in \Phi}$ of the transformed Darcy problem (2.65).

Proposition 3.7. Let $\beta \ge -1$. Besides, let either $\alpha \le 0$ or, given the assumption $(\mathbb{A})$, let $\smash{ 2\beta \ge\alpha - 3}$. Further, let $2\nu \ge \max \{ 0, \alpha - 1 \}$. Then, there exists $\varepsilon^\ast > 0$ such that, for all $\varepsilon \in (0, \varepsilon^\ast]$, the solution $(\hat{p}^ \varepsilon_+, \hat{p}^ \varepsilon_-, \hat{p}^ \varepsilon_\mathrm{f}) \in \Phi$ of the transformed Darcy problem (2.65) satisfies

Proof. We use the solution $\smash{ (\hat{p}^ \varepsilon_+, \hat{p}^ \varepsilon_-, \hat{p}^ \varepsilon_\mathrm{f}) \in \Phi }$ as a test function in the transformed weak formulation Eq (2.65). The uniform ellipticity of the hydraulic conductivity $\smash{\mathbf{{K}}_\pm^0}$ yields

Here, we have used that, as a consequence of Lemma 2.3 and Lemma 2.4 (iv), it is

Besides, by using Lemma 2.2 (iv) and the uniform ellipticity of $\smash{\hat{\mathbf{{K}}}_ {\mathrm{f}}}$, we obtain

By applying Hölder's inequality on the right-hand side of Eq (2.65), we find

if $\varepsilon > 0$ is sufficiently small. Thus, the inequality (3.16a) follows after applying Lemma 3.6 on the right-hand side of Eq (3.17). Then, the inequality in Eq (3.16b) follows from Eq (3.16a) and Lemma 3.6. □

As a consequence of Proposition 3.7, the solution families $\smash{\{ \hat{p}_i^ \varepsilon \}_{ \varepsilon \in (0, \hat{ \varepsilon}]}}$, $i \in \{ +, -, {\mathrm{f}} \}$, have weakly convergent subsequences in the following sense as $\smash{ \varepsilon \rightarrow 0}$.

Proposition 3.8. Let $\beta \ge -1$. Besides, let either $\alpha \le 0$ or, given the assumption $(\mathbb{A})$, let $\smash{ 2\beta \ge\alpha - 3}$. Then, there exists a sequence $\{ \varepsilon_k\}_{k\in\mathbb{N}} \subset (0, \hat{ \varepsilon}]$ with $\varepsilon_k \searrow 0$ as $k \rightarrow \infty$ such that

In particular, we have $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}^\ast_ {\mathrm{f}}) \in \Phi}$ if $\alpha \le -1$ and $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}^\ast_ {\mathrm{f}}) \in \Phi^\ast }$ if $\alpha \le 1$, where $\smash{\Phi^\ast}$ denotes the closure of $\Phi$ in $\smash{H^1 (\Omega_+^0) \times H^1 (\Omega_-^0) \times H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a)}$.

Proof. The weak convergence statements (3.18a), (3.18b), (3.18c), and (3.18d) are a direct consequence of the estimates in Proposition 3.7 and the Rellich-Kondrachov theorem. Further, the weak convergence (3.18e) follows from Proposition 3.7 and

Besides, we have $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}^\ast_ {\mathrm{f}}) \in \Phi}$ if $\alpha \le -1$ since $\Phi$ is convex and closed in $\smash{H^1 (\Omega_+^0)} \times \smash{H^1 (\Omega_-^0)} \times \smash{H^1 (\Gamma_a) }$. Further, $\smash{\Phi^\ast}$ is convex and closed in $\smash{H^1 (\Omega_+^0)} \times \smash{H^1 (\Omega_-^0)} \times \smash{H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a) }$ and hence $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}^\ast_ {\mathrm{f}}) \in \Phi^\ast}$ if $\alpha \le 1$. □

Using Proposition 3.7, we can conclude that the limit solution $\smash{\hat{p}_ {\mathrm{f}}^\ast}$ in $\smash{\Gamma_a}$ is constant in $\vartheta_n$-direction if $\alpha < 1$ and completely constant if $\alpha < -1$.

Proposition 3.9. Let $\beta \ge -1$. Besides, let either $\alpha \le 0$ or, given the assumption $(\mathbb{A})$, let $\smash{ 2\beta \ge\alpha - 3}$.

(i) Let $\alpha < -1$. Then, for a.a. $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$, the limit function $\smash{\hat{p}_\mathrm{f}^\ast \in H^1 (\Gamma_a)}$ from Proposition 3.8 satisfies

(ii) Let $\alpha < 1$. Then, for a.a. $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$, the limit function $\smash{\hat{p}_\mathrm{f}^\ast \in H^1_{{\mathit{\boldsymbol{{N}}}}} (\Gamma_a)}$ from Proposition 3.8 satisfies

Proof. The results follow from the Propositions 3.7 and 3.8. □

If $\alpha < 1$, we obtain continuity of the limit solution across the interface $\Gamma$.

Proposition 3.10. Let $\beta \ge -1$. Besides, let either $\alpha \le 0$ or, given the assumption $(\mathbb{A})$, let $\smash{ 2\beta \ge\alpha - 3}$. Then, if $\alpha < 1$, the limit functions $\smash{\hat{p}^\ast_\pm \in H^1 (\Omega^0_\pm)}$ and $\smash{\hat{p}^\ast_\mathrm{f} \in H^1_{{\mathit{\boldsymbol{{N}}}}}(\Gamma_a)}$ from Proposition 3.8 satisfy

Proof. Let $\zeta \in L^2_a (\Gamma)$. Then, we have

Using a version of the Sobolev trace inequality [35, Thm. II.4.1], we obtain

where, with Proposition 3.8, the first term vanishes as $k \rightarrow \infty$ and the second term is bounded. Besides, by using the Lemmas 3.2 and 3.4 and Proposition 3.7, we find

Further, the last term on the right-hand side of Eq (3.22) vanishes due to the weak convergence (3.18e) in Proposition 3.8 as $k\rightarrow \infty$. □

4.   Limit models

In the following, we present the convergence proofs and resulting limit models for vanishing $\varepsilon$. Depending on the value of the parameter $\alpha \in \mathbb{R}$, we obtain five different limit models. We distinguish between the following cases that are discussed in separate subsections.

● Section 4.1 discusses the case $\alpha < - 1$ of a highly conductive fracture, where the limit pressure head inside the fracture becomes completely constant.

● In Section 4.2, we discuss the case $\alpha = - 1$ of a conductive fracture, where the fracture pressure head in the limit model solves a PDE of effective Darcy flow on the interface $\Gamma$.

● In Section 4.3, we examine the case $\alpha \in (- 1, 1)$, where the fracture disappears in the limit model, i.e., we have both the continuity of pressure and normal velocity across the interface $\Gamma$ without any effect of the fracture conductivity.

● Section 4.4 is concerned with the case $\alpha = 1$, where the fracture turns into a permeable barrier with a pressure jump across the interface $\Gamma$ that scales with an effective conductivity.

● Section 4.5 discusses the case $\alpha > 1$, where the fracture acts like a solid wall in the limit model.

The parameter $\alpha\in\mathbb{R}$ determines the conductivity of the fracture in the limit $\varepsilon \rightarrow 0$. In particular, in accordance with Proposition 3.10, and in agreement with the models in ^[21,26,27], the pressure will be continuous across the fracture interface $\Gamma$ for $\alpha < 1$, which is indicative for a conductive fracture. Besides, for $\alpha > -1$, the normal velocity will be continuous across $\Gamma$, which is indicative for an obstructing fracture. Further, the parameter $\beta \ge -1$ controls the presence of a source term for the fracture in the limit model. For $\beta = -1$ a fracture source term will remain in the limit $\varepsilon \rightarrow 0$, while, for $\beta > -1$, the source term will vanish. The role of the parameters $\alpha \in \mathbb{R}$ and $\beta \ge -1$ and the corresponding limit model regimes are briefly summarized in Table 1.

Each subsection is structured as follows. First, we state the strong formulation of the respective limit model and introduce a corresponding weak formulation. Then, we prove weak convergence towards the limit model for the subsequence $\smash{\{ \varepsilon_k\}_{k\in\mathbb{N}}}$ as $k\rightarrow \infty$ and express the limit solution in terms of the limit functions from Proposition 3.8. In a second step, we show strong convergence for the whole sequence $\smash{\{ \varepsilon\}_{ \varepsilon \in (0, \hat{ \varepsilon}]}}$ as $\varepsilon \rightarrow 0$ and discuss the wellposedness of the limit model.

Further, for $\smash{f_\pm \colon \Omega_\pm^0 \rightarrow \mathbb{R}}$ and $\smash{{\mathit{\boldsymbol{{F}}}}_\pm \colon \Omega_\pm^0 \rightarrow \mathbb{R}^n}$ with well-defined (normal) trace on $\Gamma$, we define the jump operators

Besides, regarding the convergence of the bulk solution, we obtain the following result that will be useful for all cases.

Lemma 4.1. Let $\beta \ge -1$. Besides, let either $\alpha \le 0$ or, given the assumption $(\mathbb{A})$, let $\smash{ 2\beta \ge\alpha - 3}$. Then, for all $\smash{ \varphi_\pm \in H^1 (\Omega^0_\pm)}$, we have

as $k\rightarrow \infty$, where $\smash{\hat{p}_\pm^\ast \in H^1 (\Omega_\pm^0)}$ denote the limit functions from Proposition 3.8.

Proof. For all $\smash{ \varphi_\pm \in H^1 (\Omega^0_\pm) }$, we find

As $k \rightarrow \infty$, the first two terms on the right-hand side vanish due to Lemma 2.4 (iv), the third term due to Proposition 3.8. Thus, the result follows with Proposition 3.8. □

As a consequence of Lemma 4.1, the bulk part of the limit problem as $\varepsilon \rightarrow 0$ will have the following structure in all of the cases.

Find $p_\pm \colon \Omega^0_\pm \rightarrow \mathbb{R}$ such that

Here, the functions $p_\pm$ can be identified as the limit functions $\smash{\hat{p}_\pm^\ast}$ from Proposition 3.8. The bulk problem (4.3) is incomplete and has to be supplemented with a fracture problem or suitable conditions on the fracture interface $\Gamma$, which will depend on the choice of the parameter $\alpha \in \mathbb{R}$.

4.1.   Case I: $\alpha < - 1$

If $\alpha < -1$, the fracture conductivity is much larger than the bulk conductivity. As a result, the pressure head $\smash{\hat{p}_ {\mathrm{f}}^ \varepsilon}$ inside the fracture becomes constant as $\varepsilon \rightarrow 0$, i.e., pressure fluctuations in the fracture are instantaneously equilibrated. This matches with the models obtained in ^[21,27] for Richards equation for $\alpha < - 1$. The range of achievable constants for the fracture pressure head in the limit model may be constrained by the choice of Dirichlet conditions at the external fracture boundary. For this reason, we define the set

of admissible constants for the limit pressure head in the fracture. Then, the set $W$ can be characterized as follows.

Remark 4.2. (i) It is either $W = \mathbb{R}$ or $W = \{ 0 \}$.

(ii) If $\smash{\lambda_{\partial\Omega } (\varrho^{\hat{ \varepsilon}}_{ {\mathrm{f}}, \mathrm{D}}) > 0}$, then we have $W = \{ 0 \}$.

(iii) If $\smash{\lambda_{\partial \Omega }(\varrho_{ {\mathrm{f}}, \mathrm{D}}^{\hat{ \varepsilon}}) = 0 }$ and $\smash{ \lambda_{\partial \Omega } (\varrho_{\mathrm{b}, \mathrm{D}}^0 \cap U_\delta (\Gamma)) = 0}$ for a constant $\smash{\delta > 0}$, then we have $W = \mathbb{R}$.

The strong formulation of the limit problem for $\alpha < -1$ and $\beta \ge -1$ as $\varepsilon \rightarrow 0$ now reads as follows.

Find $p_\pm \colon \Omega^0_\pm \rightarrow \mathbb{R}$ and $p_\Gamma \in W$ such that

and the bulk problem (4.3) is satisfied. Moreover, if $W = \mathbb{R}$, the model is closed by the condition

Here, $A\in\mathbb{R}$ and $\smash{\overline{q_\Gamma}} \in \mathbb{R}$ are defined by

A weak formulation of the system in the Eqs (4.3) and (4.5) is given by the following problem.

Find $(p_+, p_-, p_\Gamma) \in \Phi^0_\mathrm{I}$ such that, for all $(\varphi_+, \varphi_-, \varphi_\Gamma) \in \Phi^0_\mathrm{I}$,

Here, the space $\Phi^0_\mathrm{I}$ is given by

Further, we obtain the following weak convergence result.

Theorem 4.3. Let $\alpha < - 1$ and $\beta \ge -1$. Then, $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\mathrm{f} \hat{p}_\mathrm{f}^\ast) \in \Phi_\mathrm{I}^0}$ is a weak solution of problem (4.7), where $\smash{\hat{p}^\ast_\pm\in H^1(\Omega^0_\pm)}$, $\smash{\hat{p}^\ast_\mathrm{f} \in H^1 (\Gamma_a)}$ denote the limit functions from Proposition 3.8. Moreover, we have $\smash{\hat{p}_\mathrm{f}^\ast ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) = \mathfrak{A}_\mathrm{f} \hat{p}^\ast_\mathrm{f} \in W}$ for a.a. $\smash{ ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$.

Proof. Take a test function triple $\smash{ (\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi}$ with $\smash{ \varphi_ {\mathrm{f}} \equiv \varphi_\Gamma \in W}$. By inserting $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) }$ into the transformed weak formulation (2.65), we obtain

Thus, by letting $k \rightarrow \infty$ and using Lemma 4.1, we find that the limit solution $\smash{ (\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\mathrm{f} \hat{p}_\mathrm{f}^\ast)}$ satisfies Eq (4.7). Besides, with the Propositions 3.8 and 3.9, it is $\smash{(\hat{p}^\ast_+, \hat{p}_-^\ast, \hat{p}_ {\mathrm{f}}^\ast) \in \Phi}$ with $\smash{ \hat{p}_ {\mathrm{f}}^\ast \equiv \mathfrak{A}_ {\mathrm{f}} \hat{p}_ {\mathrm{f}}^\ast }$ and hence $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \mathfrak{A}_ {\mathrm{f}} \hat{p}_ {\mathrm{f}}^\ast) \in \Phi_\mathrm{I}^0}$. □

Moreover, we obtain strong convergence in the following sense.

Theorem 4.4. Let $\alpha < -1$ and $\beta \ge -1$. Then, for the whole sequence $\smash{ \{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $\smash{i\in\{ +, -, \mathrm{f}\}}$, we have strong convergence

as $\varepsilon \rightarrow 0$. Further, $\smash{ (\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\mathrm{f} \hat{p}_\mathrm{f}^\ast) \in \Phi_\mathrm{I}^0}$ is the unique weak solution of problem (4.7).

Proof. The solution of Eq (4.7) is unique as a consequence of the Lax-Milgram theorem. Thus, the weak convergence (3.18a) and (3.18c) in Proposition 3.8 hold for the whole sequence $\smash{ \{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $\smash{i\in\{ +, -, \mathrm{f}\}}$. This follows from Proposition 3.7 and the fact that every weakly convergent subsequence has the same limit.

Now, in order to show the strong convergence (4.9), we define the norm $\smash{{\left\vert\left\vert\left\vert {\cdot } \right\vert\right\vert\right\vert}}$ on $\Phi \subset \smash{ H^1 (\Omega_+^0) \times H^1 (\Omega_-^0) \times H^1 (\Gamma_a)}$ by

Then, with Lemma 3.6, it is easy to see that the norm $\smash{{\left\vert\left\vert\left\vert {\cdot } \right\vert\right\vert\right\vert}}$ on the space $\Phi$ is equivalent to the natural product norm of $\smash{ H^1 (\Omega_+^0) \times H^1 (\Omega_-^0) \times H^1 (\Gamma_a)}$. Moreover, with analogous arguments as in Lemma 4.1, we find

The uniform ellipticity of $\smash{\hat{\mathbf{{K}}}_ {\mathrm{f}}}$ and Proposition 3.7 yield

Thus, with $\smash{\mathcal{A}_\mathrm{f}^ \varepsilon (\hat{p}_\mathrm{f}^ \varepsilon, \hat{p}_\mathrm{f}^ \varepsilon) \ge 0}$ and Eq (2.65), we have

With Proposition 3.8 and Theorem 4.3, we find

Consequently, with the weak lower semicontinuity of the norm, we obtain

□

4.2.   Case II: $\alpha = -1$

For $\alpha = -1$ and $\beta \ge -1$, the fracture pressure head in the limit models fulfills a Darcy-like PDE on the interface $\Gamma$ with an effective hydraulic conductivity matrix $\smash{\mathbf{{K}}_\Gamma}$. The inflow from the bulk domains into the fracture is modeled by an additional source term on the right-hand side of the interfacial PDE. The bulk and interface solution are coupled by the continuity of the pressure heads across the interface $\Gamma$, which corresponds to the case of a conductive fracture in accordance with the choice of the parameter $\alpha = -1$. We remark that the effective conductivity matrix $\smash{\mathbf{{K}}_\Gamma}$ for the limit fracture in Eq (4.13) below explicitly depends on the off-diagonal entries of the full-dimensional conductivity matrix $\smash{\hat{\mathbf{{K}}}_ {\mathrm{f}}}$, which is not accounted for in previous works with equivalent scaling of bulk and fracture conductivities ^[20,21,22].

The resulting limit model for $\alpha = -1$ resembles discrete fracture models for Darcy flow that are derived by averaging methods ^[1,15]. The averaging approach leads to a Darcy-like PDE on the fracture interface $\Gamma$ as in Eq (4.11a) below. However, the choice of coupling conditions between bulk and interface solution does not occur naturally in this case, especially if the averaged model aspires to describe both conductive and blocking fractures. Therefore, coupling conditions in averaged models are typically obtained by making formal assumptions on the flow profile inside the fracture and usually include a jump of pressure across the fracture interface. Here, only the conductive case corresponding to $\alpha = -1$ is considered. In particular, as a consequence of Proposition 3.10, the pressure is continuous across the fracture interface $\Gamma$ in the limit model.

The strong formulation of the limit problem for $\alpha = -1$ and $\beta \ge -1$ now reads as follows.

Find $\smash{p_\pm \colon \Omega_\pm^0 \rightarrow \mathbb{R}}$ and $\smash{p_\Gamma \colon \Gamma \rightarrow \mathbb{R}}$ such that

and the bulk problem (4.3) is satisfied. Here, $\smash{q_\Gamma \in L^2_a (\Gamma)}$ and $\smash{\mathbf{{K}}_\Gamma \in L^\infty (\Gamma; \mathbb{R}^{n\times n})}$ in Eq (4.11a) are given by

In Eq (4.13), the application of the operator $\smash{\mathfrak{A}_\Gamma}$ is to be understood componentwise. We remark that $\mathbf{{K}}_\Gamma$ agrees with $\mathbf{{K}}_ {\mathrm{f}}$ on $\mathbf{{T}}\Gamma$ if $\mathbf{{K}}_ {\mathrm{f}}$ is constant and ${\mathit{\boldsymbol{{N}}}}$ is an eigenvector of $\mathbf{{K}}_ {\mathrm{f}}$, which is in agreement with the models in ^[21,22]. The boundary parts $\smash{\partial\Gamma_\mathrm{D}}$, $\smash{\partial\Gamma_\mathrm{N}}$ in the Eqs (4.11d) and (4.11c) are given by

Generally, in particular, we have $\smash{\partial \Gamma_\mathrm{N} \setminus \partial \Omega \not = \emptyset}$, i.e., we also have a homogeneous Neumann condition at closing points of the fracture inside the domain.

A weak formulation of the system in the Eqs (4.3) and (4.11) is given by the following problem.

Find $({p}_+, p_-, p_\Gamma) \in \Phi^0_\mathrm{II}$ such that, for all $(\varphi_+, \varphi_-, \varphi_\Gamma) \in \Phi^0_\mathrm{II}$,

Here, the space $\Phi^0_\mathrm{II}$ is defined by

We now have the following weak convergence result.

Theorem 4.5. Let $\alpha = -1$ and $\beta \ge - 1$. Then, $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\Gamma \hat{p}_\mathrm{f}^\ast) \in \Phi_\mathrm{II}^0}$ is a weak solution of problem (4.15), where $\smash{\hat{p}^\ast_\pm\in H^1(\Omega^0_\pm)}$, $\smash{\hat{p}^\ast_\mathrm{f} \in H^1 (\Gamma_a)}$ denote the limit functions from Proposition 3.8. Further, for a.a. $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$, we have $\smash{\hat{p}_\mathrm{f}^\ast ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) = (\mathfrak{A}_\Gamma \hat{p}^\ast_\mathrm{f}) ({\mathit{\boldsymbol{{\pi}}}})}$.

Proof. According to Proposition 3.7, we have $\smash{{\left\Vert { \varepsilon^{-1} \nabla_{\!{\mathit{\boldsymbol{{N}}}}} \hat{p}_\mathrm{f}^ \varepsilon} \right\Vert}_{{\mathit{\boldsymbol{{L}}}}^2 (\Gamma_a)} \lesssim 1}$. Thus, there exists $\smash{\zeta^\ast \in L^2 (\Gamma_a)}$ such that

as $k\rightarrow \infty$. By multiplying the transformed weak formulation (2.65) by $\smash{ \varepsilon_k}$ and taking the limit $k\rightarrow \infty$, we find

for any test function triple $\smash{ (\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi}$, where we have used Lemma 2.2 (iv). A solution for $\smash{\zeta^\ast \in L^2 (\Gamma_a) }$ is now clearly given by

Moreover, suppose that $\smash{\bar{\zeta}^\ast \in L^2 (\Gamma_a)}$ is another solution of Eq (4.18). Then, with Eq (4.18), we find

Thus, by choosing $\smash{ \varphi_ {\mathrm{f}} \in H^1_{\mathit{\boldsymbol{{N}}}}(\Gamma_a)}$ as

we obtain $\smash{\zeta^\ast = \bar{\zeta}^\ast}$ a.e. in $\Gamma_a$, i.e., $\zeta^\ast$ is uniquely determined by Eq (4.19).

Next, we define the space

and take a test function triple $\smash{ (\varphi_+, \varphi_-, \varphi_\mathrm{f}) \in \Phi}$ with $\varphi_\mathrm{f} \in \Phi_\mathrm{f}$. Then, there is a function $\smash{ \varphi_\Gamma \in H^1_a (\Gamma)}$ with $\smash{ \varphi_\mathrm{f} ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n)} = \smash{ \varphi_\Gamma ({\mathit{\boldsymbol{{\pi}}}})}$ a.e. in $\smash{\Gamma_a }$. With Proposition 3.8, Lemma 4.1, and Eq (4.17), we obtain

as $k\rightarrow \infty$. Here, we have used that

for all $\smash{ \varphi_ {\mathrm{f}} \in H^1 (\Gamma_a)}$, where the first two terms on the right-hand side vanish according to Lemma 2.2 (iv) as $k\rightarrow \infty$ and the third terms tends to zero with Proposition 3.8. Moreover, with Eq (4.19) and Proposition 3.9 (ii), we have

where $\smash{\mathbf{{K}}_\Gamma}$ is defined by Eq (4.13). Thus, by inserting $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}})}$ into the transformed weak formulation (2.65) and letting $k\rightarrow \infty$, it follows that the limit solution $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\Gamma \hat{p}^\ast_\mathrm{f}) }$ satisfies Eq (4.15). Besides, with Lemma 3.3 and Proposition 3.10, we have $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\Gamma \hat{p}^\ast_\mathrm{f}) \in \Phi_\mathrm{II}^0}$. □

The effective hydraulic conductivity matrix $\smash{\mathbf{{K}}_\Gamma}$ has the following properties.

Lemma 4.6. (i) The effective hydraulic conductivity matrix $\smash{\mathbf{{K}}_\Gamma}$ from Eq (4.13) is symmetric and positive semidefinite. In addition, for all ${\mathit{\boldsymbol{{\pi}}}} \in \Gamma$ and ${\mathit{\boldsymbol{{\xi}}}} \in {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}}\Gamma$, we have $\smash{{\mathit{\boldsymbol{{\xi}}}} \cdot \mathbf{{K}}_\Gamma ({\mathit{\boldsymbol{{\pi}}}}) \, {\mathit{\boldsymbol{{\xi}}}} > 0}$.

(ii) If $\smash{\hat{\mathbf{{K}}}_ {\mathrm{f}} \in \mathcal{C}^0 (\overline{\Gamma}_a^par; \mathbb{R}^{n\times n }) }$, then $\smash{\mathbf{{K}}_\Gamma }$ is uniformly elliptic on ${\mathrm{T}} \Gamma$, i.e., for all ${\mathit{\boldsymbol{{p }}}}\in \Gamma$ and ${\mathit{\boldsymbol{{\xi}}}}\in {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}}\Gamma$, we have $\smash{{\mathit{\boldsymbol{{\xi}}}} \cdot \mathbf{{K}}_\Gamma ({\mathit{\boldsymbol{{\pi}}}}) \, {\mathit{\boldsymbol{{\xi}}}} \gtrsim {\left\vert {{\mathit{\boldsymbol{{\xi}}}}} \right\vert}^2 }$.

Proof. (i) $\smash{\mathbf{{K}}_\Gamma}$ is symmetric by definition. Moreover, for ${\mathit{\boldsymbol{{\xi}}}} \in \mathbb{R}^n$, we have

With the Cauchy-Schwarz inequality, we obtain

with strict inequality if ${\mathit{\boldsymbol{{N}}}} \perp {\mathit{\boldsymbol{{\xi}}}}$.

(ii) Suppose that, for all $k\in \mathbb{N}$, there exist ${\mathit{\boldsymbol{{\pi}}}}_k \in \Gamma$ and $\smash{ {\mathit{\boldsymbol{{\xi}}}}_k \in {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}_k}\Gamma }$ such that

W.l.o.g., we assume $\smash{{\left\vert {{\mathit{\boldsymbol{{\xi}}}}_k} \right\vert} = 1}$ for all $k \in \mathbb{N}$. Then, with the Bolzano-Weierstraß theorem, there exists a subsequence such that

as $l \rightarrow \infty$. In particular, we have

as $l \rightarrow \infty$, which is a contradiction to (i). □

Further, the following strong convergence result holds true.

Theorem 4.7. Let $\alpha = -1$ and $\beta \ge -1$. Then, we have strong convergence

as $k\rightarrow \infty$, where $\smash{\zeta^\ast \in L^2 (\Gamma_a) }$ is given by Eq (4.19). Moreover, if $\smash{\mathbf{{K}}_\Gamma}$ is uniformly elliptic on ${\mathrm{T}}\Gamma$, $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\Gamma \hat{p}_\mathrm{f}^\ast) \in \Phi_\mathrm{II}^0}$ is the unique weak solution of the problem in Eq (4.15) and the strong convergence in Eq (4.20) holds for the whole sequence $\smash{ \{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $\smash{i\in\{ +, -, \mathrm{f}\}}$.

Proof. First, we define the norm

on $\smash{\Phi \times L^2 (\Gamma_a)}$. Then, with Lemma 3.6, it is easy to see that the norm $\smash{{\left\vert\left\vert\left\vert {\cdot} \right\vert\right\vert\right\vert}}$ is equivalent to the product norm on $\smash{\Phi \times L^2 (\Gamma_a) \subset H^1 (\Omega_+^0) \times H^1 (\Omega_-^0) \times H^1 (\Gamma_a) \times L^2 (\Gamma_a) }$. With Lemma 2.2 (iv), Proposition 3.7, and the Eqs (2.65) and (4.10), we find

Thus, with the Proposition 3.8 and Theorem 4.5, we obtain

Additionally, with the Eqs (4.13) and (4.19) and Proposition 3.9, it is

Thus, with Proposition 3.9, we have

Now, let $\smash{\mathbf{{K}}_\Gamma}$ be uniformly elliptic on ${\mathrm{T}} \Gamma$ and $\smash{ (\varphi_+, \varphi_-, \varphi_\Gamma) \in \Phi_\mathrm{II}^0}$. Then, we have

Hence, we obtain coercivity on $\smash{\Phi_\mathrm{II}^0}$ by applying Lemma 3.6. Thus, as a consequence of the Lax-Milgram theorem, $\smash{ (\hat{p}^\ast_+, \hat{p}^\ast_-, \mathfrak{A}_\Gamma \hat{p}_\mathrm{f}^\ast) \in \Phi_\mathrm{II}^0}$ is the unique weak solution of the problem in Eq (4.15). Further, this implies the convergence of the whole sequence $\smash{ \{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $\smash{i\in\{ +, -, \mathrm{f}\}}$, as $\varepsilon\rightarrow 0$ since every convergent subsequence has the same limit. □

4.3.   Case III: $\alpha \in (-1, 1)$

For $\alpha \in (-1, 1)$ and $\beta \ge -1$, the hydraulic conductivities in bulk and fracture are of similar magnitude such that the fracture disappears in the limit $\smash{ \varepsilon \rightarrow 0}$. No effect of the fracture conductivity is visible in the limit model and pressure and normal velocity are continuous across the interface $\Gamma$ (except for source terms if $\beta = -1$). This fits the models derived in ^[21,27] for $\alpha \in (-1, 1)$, where Richards equation is considered. The strong formulation of the limit problem reads as follows.

Find $\smash{p_\pm \colon \Omega^0_\pm \rightarrow \mathbb{R}}$ such that

and the bulk problem (4.3) is satisfied, where $\smash{ q_\Gamma \in L^2_a (\Gamma) }$ is defined as in Eq (4.12).

A weak formulation of the system in the Eqs (4.3) and (4.21) is given by the following problem.

Find $\smash{(p_+, p_-) \in \Phi^0_\mathrm{III}}$ such that, for all $\smash{ (\varphi_-, \varphi_+) \in \Phi_\mathrm{III}^0}$ with $\smash{ \varphi_\Gamma : = \varphi_\pm\bigr\vert_{\Gamma}}$,

Here, the space $\Phi^0_\mathrm{III}$ is given by

We now obtain the following convergence results.

Theorem 4.8. Let $\alpha \in (-1, 1)$ and $\beta \ge -1$. Besides, let either $\alpha \le 0$ or assume that $(\mathbb{A})$ holds. Then, given the limit functions $\smash{\hat{p}^\ast_\pm\in H^1(\Omega^0_\pm)}$ and $\smash{\hat{p}^\ast_\mathrm{f} \in H^1_{{\mathit{\boldsymbol{{N}}}}} (\Gamma_a)}$ from Proposition 3.8, we find that $\smash{ (\hat{p}^\ast_+, \hat{p}^\ast_-) \in \Phi_\mathrm{III}^0}$ is a weak solution of Eq (4.22). Moreover, we have $\smash{\hat{p}^\ast_\pm = \mathfrak{A}_\Gamma \hat{p}_\mathrm{f}^\ast}$ on $\Gamma$ and $\smash{\hat{p}_\mathrm{f}^\ast ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) = (\mathfrak{A}_\Gamma \hat{p}^\ast_\mathrm{f}) ({\mathit{\boldsymbol{{\pi}}}})}$ for a.a. $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$.

Proof. Take a test function triple $\smash{(\varphi_+, \varphi_-, \varphi_\mathrm{f}) \in \Phi}$ such that $\smash{ \varphi_\mathrm{f} ({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) = \varphi_\Gamma ({\mathit{\boldsymbol{{\pi}}}})}$ a.e. in $\smash{\Gamma_a }$. Then, by inserting $\smash{(\varphi_+, \varphi_-, \varphi_\mathrm{f})}$ into the transformed weak formulation (2.65), we obtain

Further, with Lemma 2.2 (iv) and Proposition 3.7, we have

if $\varepsilon$ is sufficiently small. Thus, by using Proposition 3.8 and Lemma 4.1 and letting $k\rightarrow \infty$ in Eq (4.24), it follows that the limit solution pair $(\hat{p}^\ast_+, \hat{p}^\ast_-)$ satisfies the weak formulation (4.22). Besides, with Proposition 3.10, we have $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast) \in \Phi^0_\mathrm{III}}$. □

Theorem 4.9. Let $\alpha \in (-1, 1)$ and $\beta \ge -1$. Then, given the assumption $(\mathbb{A})$, we have strong convergence

as $\varepsilon \rightarrow 0$ for the whole sequence $\smash{\{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $i \in \{ +, -, \mathrm{f}\}$. Besides, $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast) \in \Phi_\mathrm{III}^0}$ is the unique weak solution of Eq (4.22).

Proof. As consequence of the Lax-Milgram theorem, the problem in Eq (4.22) has a unique weak solution. Thus, the weak convergence (3.18a) holds for the whole sequence $\smash{\{ \hat{p}^ \varepsilon_\pm \}_{ \varepsilon \in (0, \hat{ \varepsilon}]}}$. This follows from Proposition 3.7 and the fact that every weakly convergent subsequent has the same limit. Besides, with the Propositions 3.7, 3.9, and 3.10, the weak convergence (3.18d) is satisfied for the whole sequence $\smash{\{ \hat{p}_\mathrm{f}^\ast \}_{ \varepsilon \in (0, \hat{ \varepsilon}]} }$.

Next, we equip the space $\smash{\Phi^\ast}$ with the norm $\smash{{\left\vert\left\vert\left\vert {\cdot} \right\vert\right\vert\right\vert}}$ defined by

which, as a consequence of Lemma 3.6, is equivalent to the usual product norm on $\smash{ \Phi^\ast \subset H^1(\Omega_+^0) \times H^1 (\Omega_-^0) \times H^1_{{\mathit{\boldsymbol{{N}}}}} (\Gamma_a)}$. Besides, with Proposition 3.7, we have

Thus, using the Eqs (2.65) and (4.10) and $\smash{\mathcal{A}_ {\mathrm{f}}^ \varepsilon (\hat{p}^ \varepsilon_ {\mathrm{f}}, \hat{p}_ {\mathrm{f}}^ \varepsilon) \ge 0}$, we find

Further, Theorem 4.8 yields

With the weak lower semicontinuity of the norm, we now have

□

4.4.   Case IV: $\alpha = 1$

For $\alpha = 1$ and $\beta \ge -1$, the fracture becomes a permeable barrier in limit $\varepsilon \rightarrow 0$ with a jump of pressure heads across the interface $\Gamma$ but continuous normal velocity (except for source terms).

In the following, we will derive two different limit models for $\alpha = 1$ and $\beta \ge -1$. First, in Section 4.4.1, we obtain a coupled limit problem, where the pressure head $\smash{\hat{p}_ {\mathrm{f}}^\ast}$ in the fracture satisfies a parameter-dependent Darcy-type ODE inside the full-dimensional fracture domain $\Gamma_a$. The ODE is formulated with respect to the normal coordinate $\vartheta_n$, while the tangential coordinate ${\mathit{\boldsymbol{{\pi}}}}$ acts as a parameter. This resembles the limit problem in ^[27] for Richards equation with the respective scaling of hydraulic conductivities. However, in Section 4.4.2, it then turns out that the bulk problem can be solved independently from the fracture problem. This is akin to the limit model in ^[25], where the Laplace equation is considered. In the decoupled bulk limit problem, the jump of pressure heads across the interface $\Gamma$ scales with an effective hydraulic conductivity, that is defined as a non-trivial mean value of the fracture conductivity in normal direction and reminds of a result from homogenization theory. In particular, if one is still interested in the fracture solution, it is possible to first solve the decoupled bulk limit problem in Section 4.4.2, which will then provide the boundary conditions to solve the ODE for the fracture pressure head in Section 4.4.1.

4.4.1.   Coupled limit problem

The strong formulation of the coupled limit problem for $\alpha = 1$ and $\beta \ge -1$ reads as follows.

Find $\smash{p_\pm \colon \Omega^0_\pm \rightarrow \mathbb{R}}$ and $\smash{p_ {\mathrm{f}} \colon \Gamma_a \rightarrow \mathbb{R}}$ such that

and the bulk problem (4.3) is satisfied. Here, $\smash{\hat{q}^\ast_ {\mathrm{f}} \in L^2 (\Gamma_a) }$ and $\smash{\hat{K}_ {\mathrm{f}}^\perp \in L^\infty (\Gamma_a) }$ are defined by

A weak formulation of the system in the Eqs (4.3) and (4.27) is given by the following problem.

Find $\smash{ (p_+, p_-, p_ {\mathrm{f}}) \in \Phi^\ast}$ such that, for all $\smash{ (\varphi_+, \varphi_-, \varphi_\mathrm{f}) \in \Phi^\ast}$,

We obtain the following convergence results.

Theorem 4.10. Let $\alpha = 1$ and $\beta \ge -1$. Then, given the assumption $(\mathbb{A})$, the triple $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}_ {\mathrm{f}}^\ast) \in \Phi^\ast }$ is a weak solution of problem (4.30), where $\smash{\hat{p}_\pm^\ast \in H^1 (\Omega_\pm^0) }$ and $\smash{\hat{p}_ {\mathrm{f}}^\ast \in H^1_{\mathit{\boldsymbol{{N}}}} (\Gamma_a) }$ denote the limit functions from Proposition 3.8.

Proof. According to Proposition 3.7, we have

and hence

as $k\rightarrow \infty$. As a result, we have

where, as $k\rightarrow \infty$, the first term vanishes with Lemma 2.2 (iv) and the second term with Eq (4.31). Thus, with the Propositions 3.7 and 3.8 and the Lemmas 2.2 (iv) and 4.1, we conclude that $\smash{(\hat{p}^\ast_+, \hat{p}_-^\ast, \hat{p}_\mathrm{f}^\ast) \in \Phi^\ast}$ solves Eq (4.30) by taking the limit $\smash{k \rightarrow \infty}$ in the transformed weak formulation (2.65). □

Theorem 4.11. Let $\alpha = -1$ and $\beta \ge -1$. Then, given the assumption $(\mathbb{A})$, we have strong convergence

as $\varepsilon \rightarrow 0$ for the whole sequence $\smash{\{ \hat{p}_i^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $i \in \{ +, -, \mathrm{f}\}$. Besides, we find that $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast, \hat{p}_ {\mathrm{f}}^\ast) \in \Phi^\ast}$ is the unique weak solution of the problem in Eq (4.30).

Proof. Clearly, the bilinear form of the weak formulation (4.30) is continuous and coercive with respect to the norm defined by Eq (4.26). Thus, with the Lax-Milgram theorem, we obtain that $\smash{(\hat{p}^\ast_+, \hat{p}^\ast_-, \hat{p}^\ast_\mathrm{f}) \in \Phi^\ast}$ is the unique solution of Eq (4.30). As a result, every weakly convergent subsequence has the same limit and hence, with Proposition 3.7, the weak convergence statements (3.18a) and (3.18d) in Proposition 3.8 hold for the whole sequence $\smash{\{ \hat{p}_i^ \varepsilon\}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$, $i\in\{ +, -, \mathrm{f}\}$.

Further, we define the space

and equip the product space $\smash{\Phi^\ast \times {\mathit{\boldsymbol{{L}}}}^2_\Gamma (\Gamma_a) }$ with the norm

Then, with Lemma 3.6, it is easy to see that the norm $\smash{{\left\vert\left\vert\left\vert { \cdot } \right\vert\right\vert\right\vert} }$ is equivalent to the standard product norm on $\smash{\Phi^\ast \times {\mathit{\boldsymbol{{L}}}}^2_\Gamma (\Gamma_a) }$. Moreover, with Lemma 2.2 (iv) and the Eq (2.65) and (4.10), we have

Thus, with Proposition 3.8 and Theorem 4.10, we find

□

4.4.2.   Decoupled limit problem

Starting from the coupled limit problem (4.30), we will subsequently derive a decoupled limit problem for the bulk solution only. The strong formulation of the decoupled bulk limit problem reads as follows.

Find $\smash{p_\pm \colon \Omega^0_\pm \rightarrow \mathbb{R}}$ such that

and the bulk problem (4.3) is satisfied, where $\smash{q_\Gamma \in L^2_a (\Gamma)}$ is given by Eq (4.12). $\smash{Q_\Gamma \in L^2 (\Gamma)}$ and the effective hydraulic conductivity $\smash{K_\Gamma^\perp \colon \Gamma \rightarrow \mathbb{R}}$ with $\smash{a K_\Gamma^\perp \in L^\infty(\Gamma)}$ are defined by

A weak formulation of the system in the Eqs (4.3) and (4.33) is given by the following problem.

Find $(p_+, p_-) \in \Phi^0_\mathrm{IV}$ such that, for all $\smash{(\varphi_+, \varphi_-) \in \Phi_\mathrm{IV}^0}$,

Here, the space $\Phi^0_\mathrm{IV}$ is given by

We require the following auxiliary result.

Lemma 4.12. The map

defines a continuous embedding $\smash{\Phi^\ast \hookrightarrow \Phi_\mathrm{IV}^0}$.

Proof. With Lemma 3.2, we have

for a.a. $\smash{({\mathit{\boldsymbol{{\pi}}}}, \vartheta_n) \in \Gamma_a }$. Thus, an additional integration on $\Gamma$ yields

□

We now obtain the following convergence result.

Theorem 4.13. Let $\alpha = 1$ and $\beta \ge -1$. Then, given that the assumption $(\mathbb{A})$ holds true, $\smash{ (\hat{p}_+^\ast, \hat{p}_-^\ast) \in \Phi^0_\mathrm{IV}}$ is the unique solution of problem (4.36), where $\smash{\hat{p}_\pm^\ast \in H^1(\Omega^0_\pm)}$ denote the limit functions from Proposition 3.8.

Proof. Let $\smash{(\varphi_+, \varphi_-) \in \Phi^0_\mathrm{IV}}$. We define $\varphi_\mathrm{f} \in H_{{\mathit{\boldsymbol{{N}}}}}^1 (\Gamma_a)$ by

where $\smash{K_\Gamma^\perp \in L^\infty_a (\Gamma)}$ is given by Eq (4.35). It is easy to check that $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) \in \Phi^\ast}$. In particular, we have

Thus, by inserting the test function triple $\smash{(\varphi_+, \varphi_-, \varphi_ {\mathrm{f}}) }$ into the weak formulation (4.30) and by using that

we find that $\smash{ (\hat{p}_+^\ast, \hat{p}_-^\ast) }$ satisfies Eq (4.36). With Lemma 4.12, we have $\smash{(\hat{p}_+^\ast, \hat{p}_-^\ast) \in \Phi_\mathrm{IV}^0}$. The uniqueness of the solution follows from the Lax-Milgram theorem. □

4.5.   Case V: $\alpha > 1$

For $\alpha > 1$ and $2 \beta \ge \alpha - 3$, the fracture becomes a solid wall as $\varepsilon \rightarrow 0$, i.e., the interface $\Gamma$ is an impermeable barrier with zero flux across $\Gamma$. This matches the formally derived limit model in ^[27] in the case $\alpha > 1$, where the Richards equation is considered. The strong formulation of the limit problem reads as follows.

Find $\smash{p_\pm \colon \Omega_\pm^0 \rightarrow \mathbb{R}}$ such that

and the bulk problem (4.3) is satisfied. A weak formulation of the system in the Eqs (4.3) and (4.39) is given by the following problem.

Find $(p_+, p_-) \in \Phi^0_\mathrm{V}$ such that, for all $(\varphi_+, \varphi_-) \in \Phi_\mathrm{V}^0$,

Here, the space $\Phi^0_\mathrm{V}$ is given by

We now have the following convergence results.

Theorem 4.14. Let $\alpha > 1$ and $2 \beta \ge \alpha - 3$. Then, given the assumption $(\mathbb{A})$, $\smash{ (\hat{p}^\ast_+, \hat{p}^\ast_-) \in \Phi_\mathrm{V}^0}$ is a weak solution of problem (4.40), where $\smash{\hat{p}^\ast_\pm\in H^1(\Omega^0_\pm)}$ denote the limit functions from Proposition 3.8.

Proof. With Proposition 3.7, we have

Thus, with the Lemmas 2.2 (iv) and 4.1, the result follows by letting $k\rightarrow \infty$ in the transformed weak formulation (2.65). □

Theorem 4.15. Let $\alpha > -1$ and $2 \beta \ge \alpha - 3$. Then, given the assumption $(\mathbb{A})$, we have strong convergence

as $\varepsilon \rightarrow 0$ for the whole sequence $\smash{\{ \hat{p}_\pm^ \varepsilon \}_{ \varepsilon\in (0, \hat{ \varepsilon}]}}$. Moreover, $\smash{ (\hat{p}_+^\ast, \hat{p}_-^\ast) \in \Phi_\mathrm{V}^0}$ is the unique weak solution of the problem in Eq (4.40).

Proof. The result follows with analogous arguments as in the cases above. □

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–project number 327154368–SFB 1313, and under Germany's Excellence Strategy–EXC 2075 – 390740016. The authors also were supported by the Stuttgart Center for Simulation Science (SimTech).

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix A.   Geometric background

In the following, we summarize useful definitions and results related to the geometry of Euclidean submanifolds.

Definition A.1. Let $n \in \mathbb{N}$ and $m \in \mathbb{N}_0$ with $m \le n$. Besides, let $k \in \mathbb{N} \cup \{ \infty \}$ and $l \in [0, 1]$. Then, $M \subset \mathbb{R}^n$ is called an $m$-dimensional submanifold of class $\mathcal{C}^{k, l}$ if, for all ${\mathit{\boldsymbol{{\pi}}}}\in M$, there exists $U \subset \mathbb{R}^n$ open with ${\mathit{\boldsymbol{{\pi}}}} \in U$ and a $\mathcal{C}^{k, l}$-diffeomorphism ${\mathit{\boldsymbol{{h}}}} \colon U \rightarrow V$, where $V = {\mathit{\boldsymbol{{h}}}}(U) \subset \mathbb{R}^n$ open, such that

Here, ${\mathit{\boldsymbol{{0}}}}_{n-m} \in \mathbb{R}^{n-m}$ denotes the zero vector.

A.1.   Orthogonal projection and signed distance function

We introduce the orthogonal projection and (signed) distance function of a set and state selected properties and regularity results. For details, we refer to ^[36].

Definition A.2. Let $\emptyset \not = M \subset \mathbb{R}^n$.

(i) We write $\smash{d^M \colon \mathbb{R}^n \rightarrow [0, \infty)}$, $\smash{d^M ({\mathit{\boldsymbol{{x}}}}) : = \inf_{{\mathit{\boldsymbol{{\pi}}}}\in M} {\left\vert {{\mathit{\boldsymbol{{x}}}} - {\mathit{\boldsymbol{{\pi}}}}} \right\vert}}$ for the distance function of $M$. If $M = \partial A \not = \emptyset$ for a set $A \subset \mathbb{R}^n$, we can define the signed distance function of $M$ by

(ii) A set $A \subset \mathbb{R}^n$ is said to have the unique nearest point property with respect to $M$ if, for all ${\mathit{\boldsymbol{{x}}}}\in A$, there exists a unique ${\mathit{\boldsymbol{{\pi}}}} \in M$ such that $\smash{d}^M ({\mathit{\boldsymbol{{x}}}}) = {\left\vert {{\mathit{\boldsymbol{{x}}}} - {\mathit{\boldsymbol{{\pi}}}}} \right\vert}$. We write $\mathrm{unpp}(M)$ for the maximal set with this property.

(iii) We define the orthogonal projection onto $M$ by

(iv) Let $\delta > 0$. Then, we define the $\delta$-neighborhood of $M$ by

For ${\mathit{\boldsymbol{{x}}}} \in \mathbb{R}^n$, we also write $U_\delta ({\mathit{\boldsymbol{{x}}}}) : = U_\delta (\{ {\mathit{\boldsymbol{{x}}}} \})$.

(v) We define the reach of $M$ by

Let $M \subset \mathbb{R}^n$ be a $\mathcal{C}^k$-submanifold, $k\in \mathbb{N}$. Then, the orthogonal projection $\mathcal{P}^M$ is $\mathcal{C}^{k-1}$-differentiable on $\mathrm{unpp}(M)^\circ$ [36, Thm. 2]. If $k\ge 2$, we have $\mathcal{P}^M ({\mathit{\boldsymbol{{\pi}}}} + {\mathit{\boldsymbol{{n}}}}) = {\mathit{\boldsymbol{{\pi}}}}$ for ${\mathit{\boldsymbol{{\pi}}}}\in M$ and ${\mathit{\boldsymbol{{n}}}} \perp {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}}M$ with ${\mathit{\boldsymbol{{\pi}}}} + {\mathit{\boldsymbol{{n}}}} \in \mathrm{unpp}(M)^\circ$ [36, Prop. 2]. Besides, if $M$ is compact and $k\ge 2$, we have $\mathrm{reach} (M) > 0$ [36, Prop. 6]. Moreover, if $M = \partial A$ for a set $A \subset \mathbb{R}^n$ of class $\mathcal{C}^k$, $k \ge 2$, the signed distance function $d_\leftrightarrow^{\partial A}$ is $\mathcal{C}^k$-differentiable on $\mathrm{unpp}(\partial A)^\circ$ (cf. [37, Thm. 7.8.2] and [36, Thm. 2]).

A.2.   Shape operator

Let $2 \le k \in \mathbb{N}$ and $M \subset \mathbb{R}^n$ be an $(n-1)$-dimensional $\mathcal{C}^k$-submanifold with a global unit normal vector field ${\mathit{\boldsymbol{{N}}}}\in \mathcal{C}^{k-1} (M; \mathbb{R}^n)$. We define the shape operator $\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}}$ of $M$ at ${\mathit{\boldsymbol{{\pi}}}}\in M$ for each ${\mathit{\boldsymbol{{v}}}} \in {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}}M$ as the negative directional derivative $\smash{\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}} ({\mathit{\boldsymbol{{v}}}}) : = -\nabla_{\!{\mathit{\boldsymbol{{v}}}}} {\mathit{\boldsymbol{{N}}}}({\mathit{\boldsymbol{{\pi}}}})}$. Then, for each ${\mathit{\boldsymbol{{\pi}}}} \in M$, the shape operator $\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}}$ is a self-adjoint linear operator $\smash{\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}} \colon {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}} M \rightarrow {\mathrm{T}}_{{\mathit{\boldsymbol{{\pi}}}}} M}$. The eigenvalues $\kappa_1 ({\mathit{\boldsymbol{{\pi}}}}), \dots, \kappa_{n-1} ({\mathit{\boldsymbol{{\pi}}}})$ of the shape operator $\mathcal{S}_{{\mathit{\boldsymbol{{\pi}}}}}$ are called the principal curvatures of $M$ at ${\mathit{\boldsymbol{{\pi}}}} \in M$. In particular, we have $\kappa_1, \dots, \kappa_{n-1} \in \mathcal{C}^{k-2} (M)$.

A.3.   Function spaces on manifolds

Let $M \subset \mathbb{R}^n$ be an $m$-dimensional $\smash{\mathcal{C}^{0, 1} }$-submanifold with boundary $\partial M$. We denote charts for $M$ as triples $\smash{(U, {\mathit{\boldsymbol{{\psi}}}}, V) }$, i.e., $U \subset M$ and $\smash{V \subset \mathbb{R}^m}$ (or $V \subset \mathbb{R}^{m-1} \times [0, \infty)$ for charts with boundary) are open and ${\mathit{\boldsymbol{{\psi }}}}\colon U \rightarrow V$ is bi-Lipschitz. For the inverse chart $\smash{{\mathit{\boldsymbol{{\psi}}}}^{-1}}$, we also use the symbol $\underline {{{\mathit{\boldsymbol{{\psi}}}}}}$. Besides, we write $\smash{\mathbf{{g}}\vert^{{\mathit{\boldsymbol{{\psi}}}}}}$ for the metric tensor in coordinates of the chart $\smash{{\mathit{\boldsymbol{{\psi}}}} }$, i.e., $\smash{\mathbf{{g}}\vert^{{\mathit{\boldsymbol{{\psi}}}} } ({\mathit{\boldsymbol{{ \vartheta}}}}) = [\mathbf{{D}} \underline {{{\mathit{\boldsymbol{{\psi}}}}}} ({\mathit{\boldsymbol{{ \vartheta }}}})]^ \mathrm{t} \mathbf{{D}} \underline {{{\mathit{\boldsymbol{{\psi}}}}}} ({\mathit{\boldsymbol{{ \vartheta }}}}) \in \mathbb{R}^{m\times m }}$. For $p \in [1, \infty]$, we write $L^p (M)$ for the Lebesgue space on $M$ with respect to the Riemannian measure $\lambda_M$. Moreover, we define $\smash{{\mathit{\boldsymbol{{L}}}}^p (M) : = L^p (M)^m}$. Following ^[38], we define the first-order Sobolev space $H^1 (M)$ as the completion of

with respect to the norm $\smash{{\left\Vert {f} \right\Vert}_{H^1(M)}^2 : = {\left\Vert {f} \right\Vert}_{L^2 (M) }^2 + {\left\Vert {\nabla_{\! M} f} \right\Vert}^2_{{\mathit{\boldsymbol{{L}}}}^2 (M) }}$, where $\smash{\nabla_{\! M} f}$ denotes the gradient of $f$. In local coordinates, we have

Besides, $\smash{H^1 (M)}$ is a reflexive Hilbert space. For the more general case of Sobolev spaces $\smash{W^{k, p}(M)}$ of arbitrary order $k\in\mathbb{N}$ and $1 \le p < \infty$ on Riemannian manifolds, we refer to ^[38]. Further, if $M$ is compact, we can alternatively define the Sobolev space $\smash{H^1 (M)}$ by using local coordinates ^[39]. Given a finite atlas $\smash{\{(U_i, {\mathit{\boldsymbol{{\psi}}}}_i, V_i) \}_{i\in I}}$ of $M$ and a subordinate partition of unity $\smash{\{ \chi_i \}_{i\in I }} \subset \mathcal{C}^{0, 1} (M)$, we define the space

with the norm $\smash{{\left\Vert {f} \right\Vert}_{H^1(M) }^2 : = \sum_{i \in I } {\left\Vert {(\chi_i f) \circ \underline {{{\mathit{\boldsymbol{{\psi}}}}}}_i } \right\Vert}_{H^1 (V_i) }^2 }$. It is easy to check that the two definitions for $\smash{H^1 (M)}$ are equivalent. Consequently, it is $\smash{ H^1 (M) = H^1 (\operatorname{Int} (M))}$, where $\operatorname{Int}(M)$ denotes the interior of $M$. Moreover, with analogous arguments as in [40,§11], one can prove the following trace theorem.

Lemma A.3. Let $\partial M$ be compact. Then, there exists a unique bounded linear operator $\smash{\mathfrak{T}_M \colon H^1(M) \rightarrow L^2 (\partial M) }$ such that $\smash{\mathfrak{T}_M f = f\vert_{\partial M } }$ for all $\smash{f \in H^1 (M) \cap \mathcal{C}^0 (M)}$.