1.
Introduction
In this paper, we are interested in the Vlasov-Poisson-Fokker-Planck (VPFP) system with multi-dimensional random inputs. The VPFP system describes the Brownian motion of a large system of particles in a surrounding bath, with a wide range of applications in plasma physics [4]. The physical system usually contains uncertainty, which can not be precisely described by deterministic partial differential equations. In this paper, we will mainly focus on the system with random initial input due to measurement errors or random impurity of the environment, and study how the randomness will affect the physical system. The uncertainty is modeled by multi-dimensional independent random variables with given probability density functions. We first study how the random initial data propagate in time, as well as the long-time behavior of the solution. We also study the stability and the convergence rate of the numerical method to the VPFP system with uncertainty, specifically, the generalized Polynomial Chaos stochastic Galerkin (gPC-SG) method. Both problems need an understanding of the regularity of the solution in the random space.
There are plenty of developments regarding the solution of elliptic or parabolic equations with uncertainty [2,5,6], while the regularity of the solution in the random space to kinetic equations has seldom studied until recently [9,15,13,16,19,17]. Kinetic equations give a uniform description of both mesoscopic and macroscopic physical quantities in terms of the Knudsen number $ \epsilon $. When $ \epsilon\to0 $, the microscopic kinetic model approaches to the macroscopic hydrodynamic models[3]. Numerical and analytical difficulties increase when $ \epsilon $ is small. In the numerical aspect, one efficient multiscale paradigm is the Asymptotic-Preserving schemes, which mimic the asymptotic transitions from kinetic equations to their diffusion or hydrodynamic limits in the numerically discrete space [12]. [14] extended this concept to random kinetic equations by stochastic Asymptotic-Preserving (sAP) methods. [13] gives the first result of uniform-in-$ \epsilon $ regularity in the random space for linear transport equation, [15] gives the first result on uniform regularity for a nonlinear system, the Vlasov-Poisson-Fokker-Planck system. There are also some other uniform regularity results, we mention some of them here [16,22,10,17,19,17].
Depending on different scales, the VPFP system possesses two distinguished asymptotic limits, the high field limit, and the parabolic limit [1]. For the deterministic VPFP system without scaling parameters, [8,18,20] studied the convergence of the weak solution to its asymptotic limits, while [11] gave regularity results for classical solution near the global Maxwellian. For the VPFP system with uncertainty and scaling parameters, [15] get an exponential decay of the perturbative solution independent of the small parameter $ \epsilon $ under some mild initial condition, which leads to a uniform regularity of the solution in the random space for both high field and parabolic limits.
This paper studies the same VPFP system as [15], but in more physically interesting setup. Space and velocity variables are in $ \mathbb R^3 $, and the random variable is $ d $-dimensional. As to the long-time behavior, the first improvement compared to [15] is a much sharper decay rate to the global Maxwellian under a more general condition on initial data. The upper bound for the decay of the random perturbative solution near the global Maxwellian in a suitable Sobolev norm is $ O(e^{-t/\epsilon}) $ in [15], which is improved to $ O(e^{-t/\epsilon^{1+a}}) $, where $ a = 1 $ for parabolic regime and $ a = 0 $ for high field regime, under the condition that the initial perturbation is smaller than $ O(\epsilon^{-(1+a)}) $. This implies that for both regimes, as $ \epsilon $ goes to $ 0 $, The range of the initial perturbation that will decay exponentially becomes larger. While in [15], only small random perturbation will decay exponentially in high field regime. Other than obtaining a sharp estimate when $ \epsilon $ is small, getting rid of the bad dependency on large $ M $ in the initial condition for solutions in Sobolev norm $ H^M_{\mathbf{z}}(L^2_{{\mathbf{x}}, {\mathbf{v}}}) $ is another improvement in this paper. [15] mentioned briefly about eliminating the dependency on $ M $ for the one-dimensional case at Appendix, we generate it in detail for multi-dimension. Why a sharp estimation on $ H^M_{\mathbf{z}}(L^2_{{\mathbf{x}}, {\mathbf{v}}}) $ in terms of small $ \epsilon $ and large $ M $ is not trivial and how we overcome the difficulties is stated in Section 2.3.
We treat the high field regime and the parabolic regime in a unified framework in this paper. The regularity of the solution in the random space comes from the study of the sensitivity of the perturbation near the global Maxwellian. With carefully designed energy norms, we combine the microscopic energy estimate and the macroscopic one to get the proper Lyapunov-type inequalities, which allows us to obtain the uniform regularity in the random space in terms of the scaling parameter $ \epsilon $. Under some mild conditions on the initial data, we find that the solution will decay exponentially to the global Maxwellian in a rate independent of $ \epsilon $. Our results also reveal that the solution becomes less sensitive to the initial random perturbation as $ \epsilon $ goes to $ 0 $, in which we call it decreasing sensitivity to the initial perturbation. Moreover, we complete the proof of the spectral convergence for the gPC-SG method. When approximating the numerical solution by the $ K $-th order polynomial chaos basis, the error of the approximation solution in $ H^M_{\mathbf{z}} $ is $ O(K^{-M}) $, which means that the gPC-SG method enjoys spectral accuracy.
This paper is organized as follows. In Sections 2 and 3, we study the analytic solution of the VPFP system. In Sections 2.1 and 2.2, we introduce the VPFP system with uncertainty we are interested in this paper and its perturbative solution around the steady state. The main result Theorem 2.1 on the sensitivity of the VPFP system under random perturbation is stated in Section 2.3. The difficulties and the techniques in the proof of the sensitivity analysis are also included in Section 2.3. In the following Section 3, we give the complete proof of Theorem 2.1. In Sections 4, 5, 6, we study the numerical method we use to approximate the solution in the random space, that is, the gPC-SG method. We study the stability and convergence rate of this method. In Section 4.1, we review the gPC-SG method and apply it to the VPFP system. We give the main results Theorems 4.1 and 4.2 on the numerical method and the key techniques of the proof in Section 4.2. Finally, we give the complete proof of Theorems 4.1 and 4.2 in Sections 5 and 6 respectively.
2.
The Model and Asymptotic Preserving Scaling
2.1. The VPFP system with uncertainty
Consider the Vlasov-Poisson-Fokker-Planck (VPFP) System with initial random perturbation around the global Maxwe- llian. The density distribution function $ f(t, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $ under the action of an self-consistent electrical potential $ \phi(t, {\mathbf{x}}, {\mathbf{z}}) $ satisfies,
with initial data
Here the distribution function $ f(t, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $ depends on time $ t $, position $ {\mathbf{x}} $, velocity $ {\mathbf{v}} $ and random variable $ {\mathbf{z}} $. The density function $ \rho(t, {\mathbf{x}}, {\mathbf{z}}) $ is defined as,
The collision operator $ \mathcal{F} $ describes the Brownian motion of the particles,
where $ \mathcal{M} $ is the global Maxwellian,
In the dimensionless system, $ \delta $ represents the reciprocal of the scaled thermal velocity, while $ \epsilon $ is the scaled thermal mean free path [20]. We will introduce two different regimes for this system [1]. One is the high field regime, where $ \delta = 1 $. Another is the parabolic regime, where $ \delta = \epsilon $. We will study the two different scalings in a unified framework, where we assume,
The random perturbation introduced by the initial data is characterized by a $ d $-dimensional random variable $ {\mathbf{z}} \in I_{\mathbf{z}}\subset \mathbb R^d $. It is in a properly defined probability space $ (\Sigma, \mathbb{A}, \mathbb P) $, whose event space is $ \Sigma $ and is equipped with $ \sigma- $algebra $ \mathbb{A} $ and probability measure $ \mathbb P $. Define $ \pi({\mathbf{z}}): I_{\mathbf{z}} \to \mathbb R^+ $ as the probability density function of the random variable $ {\mathbf{z}}(\omega), \omega\in \Sigma $. So one has a corresponding weighted $ L^2 $ space in the measure of
We further define
according to the dependent variables of $ {\mathbf f} $ and here $ \left\lVert\cdot \right\rVert^2_2 $ is the regular Euclidean norm for vector function $ {\mathbf f} $; and $ \left\langle {\mathbf f} , {\mathbf g} \right\rangle_\mu $ is the corresponding inner product.
2.2. The perturbative solution
It is easy to check that the global Maxwellian is a stationary solution to the VPFP system. We further introduce the perturbative solution $ h(t, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $, perturbative density $ \sigma(t, {\mathbf{x}}, {\mathbf{v}}) $, perturbative flux $ {\mathbf{u}}(t, {\mathbf{x}}, {\mathbf{z}}) $, near the the global Maxwellian,
The perturbative solution $ h $ satisfies,
where $ \mathcal{L} $ is the so-called linearized Fokker-Planck operator,
It is straightforward to see that multiplying $ 1, {\mathbf{v}} $ to (4), then integrating it over $ {\mathbf{v}} $ gives
We call (4)-(5) the microscopic system, and (7)-(8) the macroscopic system. Moreover we define the projection onto the null space of $ \mathcal{L} $, $ \mathcal{N}(\mathcal{L}) = \text{Span}\{\sqrt{\mathcal{M}}\} $ as,
and one can check that,
One important property of the linearized Fokker Planck operator $ \mathcal{L} $ is its local coercivity, which can be stated in the following Proposition.
Proposition 1. Define
then the linearized Fokker-Planck operator defined in (6) satisfies
This is first introduced in [7], and [15] expanded it into the random space, and specified that $ \lambda = \frac{1}{7} $ in this case.
2.3. Main result on the sensitivity analysis
We are interested in studying how the perturbation $ h $ evolves in time in terms of the following norm,
Here $ \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\alpha}}} = \partial_{z_1}^{\alpha_1} \partial_{z_2}^{\alpha_2} \cdots\partial_{z_d}^{\alpha_d} $ for $ d $-dimensional variables $ {\mathbf{z}} $ and $ d $-dimensional vector $ {\mathit{\boldsymbol{\alpha}}} $.
There are mainly two reasons why we are interested in this norm. The first is that this norm indicates the sensitivity of the perturbation in the random space, so we can understand how the initial randomness affects the system by studying the evolution of this norm. Second, this norm reveals the regularity of the solution to the VPFP system in the random space, which is important to prove the spectral accuracy of the gPC-SG method introduced in Section 4.
However, how to get a sharp estimate of $ \left\lVert h \right\rVert^2_{H^M_{\mathbf{z}}} $ in terms of small $ \epsilon $ and large $ M $ is not trivial. First, we will explain why direct energy estimation on $ \left\lVert h \right\rVert_\mu^2 $ couldn't give a sharp estimate in small $ \epsilon $ and how we obtain an estimate that is sharp in $ \epsilon $ by designing a new Lyapunov functional. Later we will explain the issue with large $ M $.
We define $ \left\lVert \cdot \right\rVert^2 $ as the regular $ L^2 $ norm in $ {\mathbf{x}}, {\mathbf{v}} $. If we do regular energy estimation in $ {\mathbf{x}}, {\mathbf{v}} $ to (4), we will have
where $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^2_{\mathbf{x}}} $ comes from the Sobolev Embedding of $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{L^\infty_{\mathbf{x}}} $ for $ {\mathbf{x}} \in \mathbb R^3 $. First notice that the regularity in $ {\mathbf{x}} $ for $ \nabla_{\mathbf{x}}\phi $ is different on both sides. The RHS is two order higher than the LHS. In order to balance the norm on both sides, we do energy estimation on
and then we have
From the above inequality, we find that the only dissipative term $ \left\lVert (1-\Pi) h \right\rVert^2_{H^3_{\mathbf{x}}(L^2_\nu)} $ from the linearized Fokker Planck operator can not balance the nonlinear term $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^3_{\mathbf{x}}} \left\lVert h \right\rVert_{H^3_{\mathbf{x}}(L^2_\nu)}^2 = \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^3_{\mathbf{x}}}( \left\lVert (1-\Pi)h \right\rVert_{H^3_{\mathbf{x}}(L^2_\nu)}^2 + \left\lVert \Pi h \right\rVert_{H^3_{\mathbf{x}}(L^2_\nu)}^2) $ on the RHS. We need dissipation of $ \left\lVert \Pi h \right\rVert^2_{H^3_{\mathbf{x}}} = \left\lVert \sigma \right\rVert^2_{H^3_{\mathbf{x}}} $ and $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert^2_{H^3_{\mathbf{x}}} $ to balance the nonlinear term. So we design a new Lyapunov functional:
The first two terms of the above functional also appears in (11), so it comes from energy estimation of (4), while the third and fourth terms are obtained by multiplying $ \nabla_{\mathbf{x}}\phi $ to (8) and its corresponding derivatives. Therefore, the evolution of this Lyapunov functional can be estimated by doing energy estimation on both the microscopic equation (4) and the macroscopic equation (8). By involving the macroscopic equation, we can completely control the nonlinear term on the RHS of (11) because the dissipative terms $ \left\lVert \sigma \right\rVert_{H^3_{\mathbf{x}}}^2 $ can be obtained by $ \sum_{|{\mathit{\boldsymbol{\alpha}}}|\leq 3}\left\langle \partial_x^{\mathit{\boldsymbol{\alpha}}} \nabla_{\mathbf{x}} \sigma, \partial_x^{\mathit{\boldsymbol{\alpha}}} \nabla_{\mathbf{x}}\phi \right\rangle $ and $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^3_{\mathbf{x}}}^2 $ can be obtained from the last term on the LHS of (8). Combine this two dissipative terms with $ \left\lVert (1-\Pi)h \right\rVert^2_{H^3_{\mathbf{x}}(L^2_\nu)} $ from (11), we can entirely control the nonlinear term $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^3_{\mathbf{x}}} \left\lVert h \right\rVert_{H^3_{\mathbf{x}}(L^2_\nu)}^2 $ and end up with the following inequality,
where
Since
$ \mathcal{E} $ defined in (12) is equivalent to $ E $ defined in (14). If one applies continuity argument to (13), as long as initially
then the perturbation will exponentially decay in time as follows,
Integrating the above two equations over $ d\mu({\mathbf{z}}) $ gives a sharp estimates in terms of small $ \epsilon $ on $ \left\lVert h \right\rVert^2_\mu $.
Second issue is how to get a sharp estimate on $ \left\lVert h \right\rVert_{H^M_{\mathbf{z}}} $ in terms of large $ M $. First notice that integrating $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M}\left\lVert \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h \right\rVert^2 $ over $ d\mu({\mathbf{z}}) $ directly gives an estimation on $ \left\lVert h\right\rVert^2_{H^M_{\mathbf{z}}} $, so we only need to do estimation on $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M}\left\lVert \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h \right\rVert^2 $. However, a sharp estimation on $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M}\left\lVert \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h \right\rVert^2 $ is not trivial. This is because if we take partial derivative of order $ {\mathit{\boldsymbol{\beta}}} $ with respect to $ {\mathbf{z}} $ and do energy estimation, then the nonlinear term $ \nabla_{\mathbf{x}}\phi h $ becomes
Here for $ d $-dimensional variable $ {\mathit{\boldsymbol{\beta}}}, {\mathbf{i}} $, the notations $ \binom{{\mathit{\boldsymbol{\beta}}}}{{\mathbf{i}}}, |{\mathit{\boldsymbol{\beta}}}|\leq M, {\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}} $, $ [{\mathit{\boldsymbol{\beta}}}/2] $ represent
$ - $ $ \binom{{\mathit{\boldsymbol{\beta}}}}{{\mathbf{i}}} = \binom{\beta_1}{i_1}\binom{\beta_2}{i_2}\cdots\binom{\beta_d}{i_d}, \text{ where }\binom{\beta}{i} \text{ is the binomial coeffiecient} $;
$ - $ $ \left\{|{\mathit{\boldsymbol{\beta}}}|\leq M\right\} = \left\{{\mathit{\boldsymbol{\beta}}}: \sum_{i = 1}^d\beta_i \leq M \right\};\quad \left\{{\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}}\right\} = \left\{{\mathbf{i}}: i_j\leq \beta_i, \text{ for } 1\leq j\leq d \right\} $;
$ - $ $ [{\mathit{\boldsymbol{\beta}}}/2] = {\mathbf{i}} $, where $ i_j $ is the smallest integer larger or equal to $ \beta_j/2 $.
Since we need to do energy estimation on $ \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h $ for all $ |{\mathit{\boldsymbol{\beta}}}| \leq M $, we add up all the nonlinear terms,
When one does energy estimation to another nonlinear term $ \nabla_{\mathbf{x}}\phi\partial_{\mathbf{v}} h $ in the microscopic equation and the nonlinear term $ -\nabla_{\mathbf{x}}\phi\sigma $ in the macroscopic equation, one will have similar results. So the energy estimation on the corresponding Lyapunov functional
becomes
where
Applying the continuity argument to (16) implies that only if initially
the random perturbation will exponentially decay in time. This assumption is not reasonable because stronger assumption is required on smoother initial random perturbation. Therefore, the estimate on $ \left\lVert h \right\rVert^2_{H^M_{\mathbf{z}}} $ is not sharp enough for large $ M $. We will overcome this difficulty by adding a weight to $ \partial_{\mathbf{z}}^Mh $ as follows,
where $ q_{\mathit{\boldsymbol{\beta}}} $ is defined as,
here $ d $ is the dimension of random variable $ {\mathbf{z}} $. The weight $ q_{\mathit{\boldsymbol{\beta}}} $ is used to eliminate $ \left[\#\{|{\mathit{\boldsymbol{\beta}}}|\leq M\}\right]^{-1} $, while the weight $ \frac{1}{{\mathit{\boldsymbol{\beta}}}!} $ is used to absorb $ \left[\max_{|{\mathit{\boldsymbol{\beta}}}|\leq M}\binom{{\mathit{\boldsymbol{\beta}}}}{[{\mathit{\boldsymbol{\beta}}}/2]}^2\right]^{-1} $.
To sum up, we obtain a sharp estimate in both small $ \epsilon $ and large $ M $ on
by doing energy estimation in $ {\mathbf{x}}, {\mathbf{v}} $ on $ \mathcal{E}^{M, N} $,
then integrate the final result over $ d\mu({\mathbf{z}}) $ to get Theorem 2.1.
Before we present the main theorem on the sensitivity analysis, we first introduce some constants that will be used frequently later.
Notation. $ - $ $ C_S $: For $ \forall h \in H^2_{\mathbf{x}}(L^2_{\mathbf{v}}) $, by Sobolev embedding
for $ \forall h \in H^r_{\mathbf{z}}(H^2_{\mathbf{x}}) $ with r the smallest constant strictly larger than $ \frac{d}{2} $, by Sobolev embedding,
$ - $ $ A $: For $ d- $dimensional vector $ {\mathbf{i}} $,
where $ q_{\mathbf{i}} $ is defined in (19). See Appendix A for the boundedness of the constant $ A $.
$ - $ $ C_N $:
Theorem 2.1. (Sensitivity under the initial perturbation) For $ \forall N\geq 3, M\geq 0 $, if the initial energy satisfies
then the analytic solution $ (h, \nabla_{\mathbf{x}}\phi) $ decays in time as follows,
Here all the constants are independent of $ \epsilon $ and $ M $, where $ C_0 = (\frac{1}{5AC_NC_S})^2 $, $ \xi = \frac{16+4\lambda }{\lambda} $, $ \lambda, C_S, A, C_N $ are defined in (10), (20), (22), (23) respectively.
Remark 1. This theorem implies two things about the VPFP system with uncertainty.
1. The random perturbation around the steady state will exponentially decay. As $ \epsilon\to0 $, the VPFP system becomes less sensitive to the random perturbation.
2. The regularity of the solution to the VPFP system in the random space is preserved. Furthermore, the regularity result is uniform in $ \epsilon $.
3.
Sensitivity analysis for the solution with initial random perturbation
In this section, we will prove Theorem 2.1. Theorem 2.1 is about the energy in $ H^M_{\mathbf{z}}(H^N_{\mathbf{x}}(L_{\mathbf{v}}^2)) $, however, we will first prove the energy in $ H^N_{\mathbf{x}}(L_{\mathbf{v}}^2) $ for $ \{\partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h\}_{|{\mathit{\boldsymbol{\beta}}}| \leq M} $, and then one just need to do another integral over $ \mu({\mathbf{z}}) $ to $ E^{M, N}_h $.
For fixed $ {\mathbf{z}} $, we define the weighted energy as,
where $ q_{\mathit{\boldsymbol{\beta}}} $ is defined in (19). Accordingly, we define the dissipation terms as,
The main strategy is to do energy estimates on the following micro-macro systems. By taking $ \partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} $, $ |{\mathit{\boldsymbol{\beta}}}|\leq M $ to (4) - (5) and (7) - (8), one has the micro-macro system,
and,
If one does energy estimates on (26), one obtains estimates on $ E^{M, N}_h + \frac{1}{\epsilon^{1-a}}E^{M, N}_\phi $ as in Lemma 3.4, and further by doing estimates on (28), one obtains estimates on $ G^{M, N} $ as in Lemma 3.5, where
Combine the two energy estimates in Lemma 3.4 and 3.5 in a proper way, one can obtain a Lyapunov-type inequality as in Lemma 3.6 for
which is exactly the energy we want to estimate. Finally apply the continuity argument to Lemma 3.6, one can obtain the sensitivity result in Theorem 2.1.
To get the optimal estimates, one needs to carefully deal with the two nonlinear terms in (26) and (27), that is $ \sum\limits_{{\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}}} \binom{{\mathit{\boldsymbol{\beta}}}}{{\mathbf{i}}}\partial^{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi \cdot (\nabla_{\mathbf{v}}\partial_{\mathbf{z}}^{\mathbf{i}} h - \frac{{\mathbf{v}}}{2} \partial_{\mathbf{z}}^{\mathbf{i}} h) $ and $ \sum\limits_{{\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}}} \binom{{\mathit{\boldsymbol{\beta}}}}{{\mathbf{i}}}\partial^{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi\partial^{\mathbf{i}}_{\mathbf{z}}\sigma $, so we list the estimates for this two terms in Lemma 3.2, 3.3 respectively.
Lemma 3.1. For $ d- $dimensional vector $ {\mathit{\boldsymbol{\beta}}} $ and $ q>d+1 $, one has
Proof. See Appendix A.
Lemma 3.2. For $ N\geq 3 $, $ M\geq 0, $ the following inequality holds,
where $ q $, $ C_S $, $ A $, $ C_N $ are constants defined in (19), (20), (22), (23).
Proof. First note,
So break $ \partial^{\mathit{\boldsymbol{\alpha}}}_{\mathbf{x}}\partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h = \partial^{\mathit{\boldsymbol{\alpha}}}_{\mathbf{x}}\partial^{\mathit{\boldsymbol{\beta}}}_{\mathbf{z}}\sigma\sqrt{\mathcal{M}} + (1-\Pi)\partial^{\mathit{\boldsymbol{\alpha}}}_{\mathbf{x}}\partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h $, one has,
where the first inequality comes from the Sobolev embedding (20) and
While the last inequality is true for $ \forall N\geq3 $. Therefore,
for $ e = \frac{1-a}{2} $. One obtains the last inequality by using Young's inequality and $ \frac{q_{\mathit{\boldsymbol{\beta}}}}{q_{\mathbf{i}} q_{{\mathit{\boldsymbol{\beta}}} - {\mathbf{i}}}} \leq \frac{2^q}{q_{{\mathit{\boldsymbol{\beta}}} - {\mathbf{i}}}} + \frac{2^q}{q_{\mathbf{i}}} $.
Let $ \left\lVert \frac{q_{{\mathit{\boldsymbol{\beta}}} - {\mathbf{i}}}}{({\mathit{\boldsymbol{\beta}}}-{\mathbf{i}})!} \partial^{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi \right\rVert^2_{H^N_{\mathbf{x}}} = a_{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}} $, $ \left\lVert \frac{q_{\mathbf{i}}}{{\mathbf{i}}!}\partial_{\mathbf{z}}^{\mathbf{i}} h \right\rVert^2_{H^N_{\mathbf{x}}} = b^2_{\mathbf{i}} $, $ \left\lVert \frac{q_{\mathit{\boldsymbol{\beta}}}}{{\mathit{\boldsymbol{\beta}}}!}(1-\Pi)\partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h\right\rVert^2_{H^N_{\mathbf{x}}(L^2_{{\mathbf{v}}, \nu})} $ $ = c_{\mathit{\boldsymbol{\beta}}}^2 $, then the last second term of (32) can be bounded by $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M} \sum_{{\mathbf{i}}\leq{\mathit{\boldsymbol{\beta}}}} \frac{a_{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}}{q_{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}} (b_{\mathbf{i}}^2 $ $ +c_{\mathit{\boldsymbol{\beta}}}^2) \leq(\sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M}\frac{a_{\mathit{\boldsymbol{\beta}}}}{q_{\mathit{\boldsymbol{\beta}}}})(\sum_{|{\mathbf{i}}|\leq M} b_{\mathbf{i}}^2) + (\sum_{|{\mathbf{i}}|\leq M}\frac{a_{\mathbf{i}}}{q_{\mathbf{i}}})( \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M}c_{\mathit{\boldsymbol{\beta}}}^2) $. One can do similar estimates to the last term. Therefore, applying Lemma 3.1 to (32) and breaking $ \left\lVert\partial_{\mathbf{z}}^{\mathbf{i}} h \right\rVert_{H^N_{\mathbf{x}}}^2 \leq \left\lVert \partial^{\mathbf{i}}_{\mathbf{z}}\sigma \right\rVert^2_{H^N_{\mathbf{x}}} + \left\lVert (1-\Pi) \partial_{\mathbf{z}}^{\mathbf{i}} h\right\rVert^2_{H^N_{\mathbf{x}}(L^2_{{\mathbf{v}}, \nu})} $ gives,
Lemma 3.3. For $ N\geq 3 $, $ M\geq0 $, the following inequality holds,
where $ q $, $ C_S $, $ A $, $ C_N $ are constants defined in (19), (20), (22), (23).
Proof. We first sum over $ |{\mathit{\boldsymbol{\alpha}}}|\leq N $,
Noticing by changing $ {\mathbf{j}} $ and $ {\mathit{\boldsymbol{\alpha}}}-{\mathbf{j}} $, $ {\mathbf{i}} $ and $ {\mathit{\boldsymbol{\beta}}} - {\mathbf{i}} $, the following equality holds,
Therefore, (36) shows that the first term and second term in (35) can be cancelled out when summing over $ |{\mathit{\boldsymbol{\beta}}}|\leq M $, $ {\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}} $. Therefore one just needs to prove the bounds for
We first sum over $ \sum_{|{\mathit{\boldsymbol{\alpha}}}|\leq N}\sum_{{\mathbf{j}} \leq {\mathit{\boldsymbol{\alpha}}}} $, similar to (31), one separates $ \left\{{\mathbf{j}} \leq {\mathit{\boldsymbol{\alpha}}}\right\} $ into $ \left\{|{\mathbf{j}}| \leq \frac{|{\mathit{\boldsymbol{\alpha}}}|}{2}\right\} $ and $ \left\{|{\mathbf{j}}| > \frac{|{\mathit{\boldsymbol{\alpha}}}|}{2}\right\} $, then using the Sobolev Embedding on $ \left\lVert\partial_{\mathbf{x}}^{\mathbf{j}}\partial^{\mathbf{i}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi\right\rVert_{L^\infty_{\mathbf{x}}} $ or $ \left\lVert \partial_{\mathbf{x}}^{{\mathit{\boldsymbol{\alpha}}}-{\mathbf{j}}}\partial^{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi\right\rVert_{L^\infty_{\mathbf{x}}} $, to bound them by $ \left\lVert\partial_{\mathbf{x}}^{\mathbf{j}}\partial^{\mathbf{i}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi\right\rVert_{H^2_{\mathbf{x}}} $ or $ \left\lVert \partial_{\mathbf{x}}^{{\mathit{\boldsymbol{\alpha}}}-{\mathbf{j}}}\partial^{{\mathit{\boldsymbol{\beta}}}-{\mathbf{i}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi\right\rVert_{H^2_{\mathbf{x}}} $ respectively. Then one ends up with the following bound,
Afterwards, for $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq M} \sum_{{\mathbf{i}}\leq {\mathit{\boldsymbol{\beta}}}} $, similar to (33)-(34), it is straightforward to get,
for $ d = \frac{1-a}{2} $.
The following is some equalities and inequalities that will be frequently used later.
Proposition 2..
(a) $ \left\langle {\mathbf{v}}\sqrt{\mathcal{M}} \nabla_{\mathbf{x}}\phi , h \right\rangle = \frac{\epsilon^a}{2} \partial_t\left\lVert \nabla_{\mathbf{x}}\phi \right\rVert^2 $.
(b) $ \left\lvert \left\langle {\mathbf{u}}, \partial_t\nabla_{\mathbf{x}}\phi \right\rangle\right\rvert \leq \frac{1}{\epsilon^a}\left\lVert {\mathbf{u}} \right\rVert^2 $.
(c) $ \left\langle \nabla_{\mathbf{x}}\sigma, \nabla_{\mathbf{x}}\phi \right\rangle = \left\lVert \sigma\right\rVert^2 $.
(d) $ \left\langle {\mathbf{u}}, \nabla_{\mathbf{x}}\phi \right\rangle = \frac{\epsilon^a}{2}\partial_t\left\lVert \nabla_{\mathbf{x}}\phi \right\rVert^2 $.
(e) $ \left\langle \nabla_{\mathbf{x}}\cdot \int {\mathbf{v}}\otimes{\mathbf{v}}\sqrt{\mathcal{M}} (1-\Pi) h d{\mathbf{v}}, \nabla_{\mathbf{x}}\phi\right\rangle \leq \frac{3\gamma}{2} \left\lVert(1-\Pi)h \right\rVert_\nu^2 + \frac{1}{2\gamma}\left\lVert \sigma \right\rVert^2 $, for any positive constant $ \gamma $.
Proof. $ \text{(a)} $ By the definition of $ {\mathbf{u}} $ in (3), the continuity equation (7), the Poisson equation (5), one has,
$\text{(b)} $ By (7), (5) and $ L^2 $ boundedness of $ \nabla\Delta^{-1}\nabla $ (See Riesz potential [21]),
$ \text{(c)} $ By (5),
$ \text{(d)} $ By (7), (5),
$ \text{(e)} $ By Young's inequality,
Lemma 3.4. The Microscopic energy estimate is
where $ q $, $ C_S $, $ A $, $ C_N $ are constants defined in (19), (20), (22), (23).
Proof. If one takes $ \partial_{\mathbf{x}}^{\mathit{\boldsymbol{\alpha}}} $ and multiplies $ (\frac{q_{\mathit{\boldsymbol{\beta}}}}{{\mathit{\boldsymbol{\beta}}} !})^2\partial_{\mathbf{x}}^{\mathit{\boldsymbol{\alpha}}}\partial_{\mathbf{z}}^{\mathit{\boldsymbol{\beta}}} h $ to (26), then integrates it over $ {\mathbf{x}}, {\mathbf{v}} $, sums over $ |{\mathit{\boldsymbol{\alpha}}}|\leq N $, $ |{\mathit{\boldsymbol{\beta}}}|\leq M $, by Proposition 2 (a), Proposition 1 and Lemma 3.2, it is straightforward to get the above Lemma.
Lemma 3.5. The Macroscopic energy estimate is
where $ q $, $ C_S $, $ A $, $ C_N $ are constants defined in (19), (20), (22), (23), $ G^{M, N} $ is defined in (29).
Proof. If one takes $ \partial_{\mathbf{x}}^{\mathit{\boldsymbol{\alpha}}} $ and multiplies $ (\frac{q_{\mathit{\boldsymbol{\beta}}}}{{\mathit{\boldsymbol{\beta}}} !})^2\partial_{\mathbf{x}}^{\mathit{\boldsymbol{\alpha}}}\partial^{\mathit{\boldsymbol{\beta}}}_{\mathbf{z}}\nabla_{\mathbf{x}}\phi $ to (28), then integrates it over $ {\mathbf{x}} $, finally sums it over $ |{\mathit{\boldsymbol{\alpha}}}|\leq N $, $ |{\mathit{\boldsymbol{\beta}}}|\leq M $, by Lemma 3.3, and Proposition 2 (c), (d), it is straightforward to get,
Then by Proposition 2 (b), (e), one has,
Let $ \gamma = 2\epsilon^a $, by the fact that $ \epsilon^a \leq \frac{1}{\epsilon^a} $, one completes the proof.
Lemma 3.6. The micro-macro energy estimate is
where $ q $, $ C_S $, $ A $, $ C_N $ are constants defined in (19), (20), (22), (23). $ \mathcal{E}^{M, N} $ is equivalent to $ E^{M, N} = E^{M, N}_h + \frac{1}{\epsilon^2}E^{M, N}_{\nabla_{\mathbf{x}}\phi} $ in the sense of,
Proof. (39) $ + \frac{\lambda}{8\epsilon} $ (40) gives,
where $ \mathcal{E}^{M, N} = (E^{M, N}_h + \frac{1}{\epsilon^{1-a}}E^{M, N}_{\nabla_{\mathbf{x}}\phi})+\frac{2\lambda}{8\epsilon}G^{M, N} $. By definition of $ G^{M, N} $ in (29) and the fact that $ \left\lVert {\mathbf{u}} \right\rVert^2 \leq \left\lVert h \right\rVert^2 $, one can bound $ G^{M, N} $ by
Thus one can bound $ \mathcal{E}^{M, N} $ by,
Therefore, (43) becomes,
By Lemma 3.6 and the continuity argument, if initially,
then for $ t>0 $, the RHS of $ (42) \leq \frac{\lambda}{4\epsilon^{1+a}}D^{M, N}_{h_1} + \frac{\lambda}{64\epsilon^{1+a}}D^{M, N}_\sigma + \frac{\lambda}{16\epsilon^2}D^{M, N}_{\nabla_{\mathbf{x}}\phi} $, therefore,
Because of the fact that $ D^{M, N}_{h_1} + D^{M, N}_\sigma \geq E^{M, N}_h $ and $ D^{M, N}_{\nabla_{\mathbf{x}}\phi} = E^{M, N}_{\nabla_{\mathbf{x}}\phi} $, one has,
If one integrates (48) over time, and uses the equivalent relationship between $ \mathcal{E}^{M, N} $ and $ E^{M, N} $ in (45), (48) implies,
So one ends up with two inequalities for $ E^{M, N}_h $ and $ E^{M, N}_{\nabla_{\mathbf{x}}\phi} $ respectively,
By Grownwall's inequality, one has the decay rates for $ E^{M, N}_h $ and $ E^{M, N}_{\nabla_{\mathbf{x}}\phi} $,
However, we want to estimate $ h $ and $ \nabla_{\mathbf{x}}\phi $ in the random space, that is, $ \left\lVert h \right\rVert_{H^{M, N}} $, $ \left\lVert \nabla_{\mathbf{x}}\phi \right\rVert_{H^{M, N}} $. Actually, this norm can be bounded by $ \int {} E^{M, N} d\mu({\mathbf{z}}) $ up to a constant. So by integrating (47) over $ \mu({\mathbf{z}}) $, the initial constrain becomes,
In addition, since $ \beta_1! \cdots \beta_d! \leq (\beta_1+\cdots + \beta_d)! $, hence $ \min\limits_{|{\mathit{\boldsymbol{\beta}}}|\leq M} \left\{ (\frac{q_{\mathit{\boldsymbol{\beta}}}}{{\mathit{\boldsymbol{\beta}}}!})^2 \right\} \geq (\frac{1}{M!})^2 $, so $ \left\lVert h (t)\right\rVert_{H^{M, N}} \leq (\frac{1}{M!})^2\int E^{M, N}_h(t)d\mu({\mathbf{z}}) $, $ \left\lVert \nabla_{\mathbf{x}}\phi(t) \right\rVert_{H^{M, N}}\leq\int {} E^{M, N}_{\nabla_{\mathbf{x}}\phi}(t)d\mu({\mathbf{z}}) $. Therefore, under the condition of (49),
which completes the proof of Theorem 2.1.
4.
The gPC-SG Method
4.1. The numerical method
In this section, we will review a numerical method gPC-SG and apply to the VPFP system with uncertainty. We will prove the stability and the spectral accuracy of the method.
For random variable $ {\mathbf{z}} = (z_1, \cdots, z_d) $, if $ z_i $, $ 1\leq i \leq d $ are independent of each other and the probability density function of $ z_i $ is $ \pi_i(z_i) $, then
Therefore, let $ \{\Phi^i_k\}_{k = 0}^\infty $ be the corresponding orthogonal polynomial basis with respect to $ \pi_i(z_i)dz_i $, then the orthogonal polynomial basis for $ \mu({\mathbf{z}}) $ can be written as,
where $ {\mathbf{i}} = (i_1, \cdots, i_d) $. $ \{\Phi_{\mathbf{i}}\}_{|{\mathbf{i}}|\geq0} $ satisfies the orthogonal condition under the measure $ \mu({\mathbf{z}}) $,
The $ K $-th order subspace is therefore spanned by $ \{\Phi_{\mathbf{i}}\}_{|{\mathbf{i}}|\leq K} $.
As a popular numerical method, the generalized Polynomial Chaos stochastic Galerkin (gPC-SG) method is to find the approximate solution in the truncated $ K $-th order subspace. Insert the approximate solution $ ({\hat{f}^K}, {\hat{\phi}^K}) $ in the form of,
into (1) and then project it onto the subspace, one has the system for the approximate solution,
where $ {\mathit{\boldsymbol{\Phi}}}^K({\mathbf{z}}) = \{\Phi_{\mathbf{i}}\}_{|{\mathbf{i}}|\leq K} $ is the vector function that contains all basis functions up to $ K $-th order. Similarly the approximation for the perturbative solution $ h(t, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $ is defined as,
and correspondingly the approximation for the perturbative density and flux,
where $ {\hat{\mathbf{h}}^K}(t, {\mathbf{x}}, {\mathbf{v}}), {\hat{\mathit{\boldsymbol{\sigma}}}^K}(t, {\mathbf{x}}, {\mathbf{v}}), {\hat{\mathbf{u}}^K}(t, {\mathbf{x}}, {\mathbf{v}}) $ are deterministic vector functions. Therefore $ ({\hat{h}^K}, \nabla_{\mathbf{x}}{\hat{\phi}^K}) $ satisfies,
or equivalently, the deterministic coefficients of $ {\hat{h}^K} $, i.e. the vector function $ ({\hat{\mathbf{h}}^K}, $ $ {\hat{\mathit{\boldsymbol{\phi}}}^K}) $ $ = ({\hat{h}}_{\mathit{\boldsymbol{\beta}}}(t, {\mathbf{x}}, {\mathbf{v}}), \nabla_{\mathbf{x}}{\hat{\phi}}_{\mathit{\boldsymbol{\beta}}}(t, {\mathbf{x}}, {\mathbf{v}}))_{|{\mathit{\boldsymbol{\beta}}}|\leq K} $ satisfies the following deterministic system,
where
Theorem 4.1 and Theorem 4.2 about the approximate solution by gPC-SG are based on the following condition of the basis functions $ \Phi_{\mathit{\boldsymbol{\beta}}}({\mathbf{z}}) $.
Condition 1. The basis functions $ \Phi_{\mathit{\boldsymbol{\beta}}}({\mathbf{z}}) $ satisfy,
where $ c_{\mathit{\boldsymbol{\beta}}} $ is a function of $ {\mathit{\boldsymbol{\beta}}} $ satisfying,
(a) If $ |{\mathit{\boldsymbol{\beta}}}| \leq |\mathit{\boldsymbol{\gamma}}| $, then $ c_{\mathit{\boldsymbol{\beta}}} \leq c_\mathit{\boldsymbol{\gamma}} $;
(b) $ c_{\lambda {\mathit{\boldsymbol{\beta}}}} \leq C(\lambda ) c_{\mathit{\boldsymbol{\beta}}} $, for any constant $ \lambda $. Specifically, we define
Remark 2. For example, if the basis functions $ \Phi_i(z_i) $ satisfy
then the basis functions $ \Phi_{\mathit{\boldsymbol{\beta}}}({\mathbf{z}}) $ satisfy
Remark 3. This is a generalization of the condition given in [19]. The i.i.d normalized Legendre polynomials, which corresponds to Uniform distribution in $ [-1, 1]^d $ with pdf $ \pi(z_i) = \frac{1}{2^d} $, and the Chebyshev polynomials, which corresponds to the random variable with pdf $ \pi(z_i) = \frac{2}{\pi\sqrt{1-z_i^2}} $ satisfy this condition. Specifically, for the normalized Legendre polynomials, $ c_{\mathit{\boldsymbol{\beta}}} = \prod_{i = 1}^d(\beta_i + 1)^{1/2} $, while for the Chebyshev polynomials, $ c_{\mathit{\boldsymbol{\beta}}} = 1 $.
4.2. Main results on stability and accuracy of the gPC-SG method
We want to estimate the error of the approximation $ {\hat{h}^K} $ obtained by the gPC-SG method. We first decomposed the error into two parts,
where $ \bar{h}^K $ is the projection of $ h $ onto $ {\mathit{\boldsymbol{\Phi}}}^K $,
The first part of the error $ h^K_p $ is caused by the gPC projection, which is related to the smoothness of the solution in the random space, which has been studied in Section 2 and 3. On the other hand, the second part of the error $ h^K_e $ is caused by the stochastic Galerkin, which is related to the stability of the gPC-SG method.
The difficulty in the proof of the stability of the gPC-SG method is to get a sharp estimate on $ \left\lVert {\hat{h}^K} \right\rVert^2 $ in terms of large $ K $. If we directly estimate $ \left\lVert {\hat{h}^K} \right\rVert^2 $, then similar to the sensitivity analysis in (15), the nonlinear term on the RHS of $ (51) $ will be as large as
so only when the initial data is as small as
the gPC method is stable. Actually, there is a much sharper estimates in terms of large $ K $. Under Condition 1, we introduce a weight to $ {\hat{h}}_{\mathit{\boldsymbol{\beta}}} $ as follows,
where
Here the weight $ c_{\mathit{\boldsymbol{\beta}}} $ is used to eliminate $ \left[\max_{|{\mathit{\boldsymbol{\kappa}}}|, |\mathit{\boldsymbol{\gamma}}|, |{\mathit{\boldsymbol{\beta}}}|\leq K}E_{{\mathit{\boldsymbol{\kappa}}}\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\beta}}}} \right]^{-1} $, while $ q_{\mathit{\boldsymbol{\beta}}} $ is used to eliminate $ K^{-1} $ in (54).
Before we come to the final results on the stability and accuracy of the gPC-SG method, we will first define some constants that will be frequently used later.
Notation. $ - $ $ \hat{A} $:
with $ C_2 $ defined in (53), $ q $ defined in (19).
$ - $ $ D $: $ \bar{h} = (\int h(0) {\mathit{\boldsymbol{\Phi}}}^K d\mu({\mathbf{z}})) \cdot {\mathit{\boldsymbol{\Phi}}}^K $ is the projection of $ h\in H^{M, 0} $ onto $ {\mathit{\boldsymbol{\Phi}}}^K $, where $ {\mathit{\boldsymbol{\Phi}}}^K $ are orthonormal bases under $ d\mu({\mathbf{z}}) $, then by classical approximation theorem,
Theorem 4.1. (Stability of the gPC-SG method) Let
under Condition 1, for $ \forall N\geq 3 $, if initially,
then the approximation solution $ ({\hat{h}^K}, \nabla_{\mathbf{x}}{\hat{\phi}^K}) $ obtained by gPC-SG method decays in time as follows,
Here all the constants are independent of $ \epsilon $ and $ K $, where $ \hat{A}, \xi, C_N, C_S $ are the same constants in Thoerem 2.1.
Remark 4. The above theorem tells us that the gPC-SG method is stable under a mild condition on the initial randomness.
Remark 5. Notice there is another sufficient initial condition directly on $ (h(0, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}), $ $ \nabla_{\mathbf{x}}\phi(0, {\mathbf{x}}, {\mathbf{z}})) $ to guarantee the stability of the gPC-SG method, which has been derived in Remark 7.
Based on the regularity of the solution in the random space as in Theorem 2.1 and the stability of the gPC-SG method as in Theorem 4.1, one has the following Theorem about the spectral convergence of the gPC-SG method.
Theorem 4.2. (Spectral convergence of the gPC-SG method) Under Condition 1, for $ \forall M, K $, if initially,
then the error decays in time as follows,
Here $ r $ is the smallest integer strictly larger than $ \frac{d}{2} $,
and $ \xi $ are the same constants as in Theorem 2.1, $ \lambda, C_3, C_S, A, \hat{A}, D $ are defined in (20) - (57).
Remark 6. The above Theorem tells us as long as the initial data $ (h, \nabla_{\mathbf{x}}\phi) $ has enough regularity in the random space, and the initial perturbation around the global Maxwellian is smaller than $ O(\frac{1}{\epsilon^{1+a}}) $, then the gPC-SG method enjoys spectral accuracy.
5.
Stability of the gPC-SG method
In this section, we will prove Theorem 4.1. We will study the stability of the gPC-SG method in terms of $ \hat{E}^{K, N}_h $, $ \hat{E}^{K, N}_{\nabla_{\mathbf{x}}\phi} $ defined as follows,
where $ {\hat{h}}_{\mathit{\boldsymbol{\beta}}} $ is the $ {\mathit{\boldsymbol{\beta}}} $-th component of the vector function $ {\hat{\mathbf{h}}^K}(t, {\mathbf{x}}, {\mathbf{v}}) $, same for $ {\hat{\phi}}_{\mathit{\boldsymbol{\beta}}} $. Also $ \hat{D}^{K, N}_{h_1}, \hat{D}^{K, N}_\sigma $, $ \hat{D}^{K, N}_{\nabla_{\mathbf{x}}\phi} $ are the corresponding dissipations of $ (1-\Pi){\hat{\mathbf{h}}^K}, {\hat{\mathit{\boldsymbol{\sigma}}}^K}, \nabla_{\mathbf{x}}{\hat{\mathit{\boldsymbol{\phi}}}^K} $ in the norm of $ \left\lVert \cdot \right\rVert_{H^N_\omega} $. One needs to do energy estimation on (51) to get the estimates for $ \hat{E}^{K, N}_h $ and $ \hat{E}^{K, N}_{\nabla_{\mathbf{x}}\phi} $. Actually, if one compares (51) with (26), one finds the only difference is the nonlinear term. Therefore, one can use the same proof strategy to estimates $ \hat{E}^{K, N}_h + \frac{\hat{E}^{K, N}_{\nabla_{\mathbf{x}}\phi}}{\epsilon^2} $, except we need to re-estimate the nonlinear term again.
Before we estimate the nonlinear term, we first define a characterized function $ \chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $,
which implies,
Here the first inequality comes from the orthogonality of the basis. The second one is because of the first property of $ \left\lVert \Phi_\mathit{\boldsymbol{\gamma}} \right\rVert_{L^\infty_{\mathbf{z}}} $ in Condition 1. Moreover, from the definition of $ \chi $, one has the following Lemma.
Lemma 5.1. For any multi-dimensional vectors $ {\mathit{\boldsymbol{\beta}}}, {\mathit{\boldsymbol{\kappa}}}, \mathit{\boldsymbol{\gamma}} $, positive integer $ K $ and functions $ h_\mathit{\boldsymbol{\gamma}}, g_{\mathit{\boldsymbol{\kappa}}}, f_{\mathit{\boldsymbol{\beta}}} $, the following inequality holds,
where $ \hat{A} $ defined in (56).
Proof. First, notice $ \frac{c_\mathit{\boldsymbol{\gamma}}}{\omega_\mathit{\boldsymbol{\gamma}}} = \frac{1}{q_\mathit{\boldsymbol{\gamma}}} $ by the definition of $ \omega_\mathit{\boldsymbol{\gamma}} $ in (55); Besides that, since $ \chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $ is nonzero only when $ |{\mathit{\boldsymbol{\beta}}}|\leq |\mathit{\boldsymbol{\gamma}}|+|{\mathit{\boldsymbol{\kappa}}}| \leq 2|{\mathit{\boldsymbol{\kappa}}}| $, and the first property in Condition 1, so $ \frac{\omega_{\mathit{\boldsymbol{\beta}}}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}}}{\omega_{\mathit{\boldsymbol{\kappa}}}} \leq \frac{c_{2{\mathit{\boldsymbol{\kappa}}}}q_{2{\mathit{\boldsymbol{\kappa}}}}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}}}{c_{\mathit{\boldsymbol{\kappa}}} q_{\mathit{\boldsymbol{\kappa}}}} $; Finally, by the second property in Condition 1 and the definition of $ q_{\mathit{\boldsymbol{\kappa}}} $ in(19), one has, $ \frac{\omega_{\mathit{\boldsymbol{\beta}}}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}}}{\omega_{\mathit{\boldsymbol{\kappa}}}} \leq C_22^q\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $. Therefore, one has,
The second inequality is because that by the definition of $ \chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $, for fixed $ |\mathit{\boldsymbol{\gamma}}|\leq|{\mathit{\boldsymbol{\kappa}}}| $, it is not zero only when $ |{\mathit{\boldsymbol{\kappa}}}| - |\mathit{\boldsymbol{\gamma}}| \leq |{\mathit{\boldsymbol{\beta}}}|\leq |{\mathit{\boldsymbol{\kappa}}}| + |\mathit{\boldsymbol{\gamma}}| $, so the first term $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq K}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} \leq 2|\mathit{\boldsymbol{\gamma}}| $; while the second term is similar. The last inequality comes from the definition of $ A $ in (22).
Now based on Lemma 5.1, and the bound for $ E_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $ in (62), one can bound the two nonlinear terms as stated in the following Lemma.
Lemma 5.2. Under Condition 1, for $ N\geq 4 $, one can bound the nonlinear term as
where $ \hat{A} $, $ C_N, C_S $ are constants defined in (56), (23), (20).
Proof. Similar to (30) - (33), one has,
Then summing over $ |{\mathit{\boldsymbol{\beta}}}|, |\mathit{\boldsymbol{\gamma}}|, |{\mathit{\boldsymbol{\kappa}}}| \leq K $, one has,
where the first inequality comes from (62), while the second inequality comes from Young's inequality. Then by Lemma 5.1, one completes the proof of (64). The proof for (65) is similar to it, so we omit it here.
Compare Lemma 5.2 with Lemma 3.2 and 3.3, one notes that the estimates for the two nonlinear terms are similar, so one ends up with the similar energy estimates for $ \hat{E}^{K, N} $ in Theorem 4.1.
Remark 7. Here we derive a sufficient condition on the initial data $ (h(0, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $, $ \nabla_{\mathbf{x}}\phi(0, {\mathbf{x}}, {\mathbf{z}})) $. We require
in Theorem 4.1, where $ C_0 = (\frac{1}{5\hat{A}C_NC_S})^2\frac{1}{\epsilon^{1+a}} $. Since $ {\hat{h}^K}(0) = (\int h(0) {\mathit{\boldsymbol{\Phi}}}^K d\mu({\mathbf{z}})) \cdot {\mathit{\boldsymbol{\Phi}}}^K $ is the projection of $ h $ onto $ {\mathit{\boldsymbol{\Phi}}}^K $, where $ {\mathit{\boldsymbol{\Phi}}}^K $ are orthonormal bases under $ d\mu({\mathbf{z}}) $, so one has,
where $ {\hat{h}}_{\mathit{\boldsymbol{\beta}}}(0) = \int h(0) \Phi_{\mathit{\boldsymbol{\beta}}} d\mu({\mathbf{z}}) $. By the classical approximation theorem, we know that for $ h \in H^{M, N} $,
for some constant $ D $ depending on the measure $ \mu({\mathbf{z}}) $. Plug (67) into (68), one gets,
Similarly, one can get the bound for $ \nabla_{\mathbf{x}}{\hat{\phi}}_{\mathit{\boldsymbol{\beta}}} $,
Therefore the condition (66) becomes,
hence a sufficient initial condition for the stability of the gPC-SG method is,
If $ c_{\mathit{\boldsymbol{\beta}}} $ grows algebraically, then there exists an positive integer $ p $, such that, $ c_{\mathit{\boldsymbol{\beta}}} \lesssim (|{\mathit{\boldsymbol{\beta}}}|+1)^p $ up to a constant, which implies that as long as $ M > \frac{d}{2}+q+p $, then 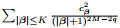 can be bounded by a finite constant $ A $ (the proof is the same as Appendices A).
can be bounded by a finite constant $ A $ (the proof is the same as Appendices A).
To sum up, another sufficient condition to enjoy the stability of gPC-SG method as in (25) is that firstly the bound of the basis $ \Phi_{\mathit{\boldsymbol{\beta}}} $ grows algebraically as $ \left\lVert \Phi_{\mathit{\boldsymbol{\beta}}} \right\rVert_{L^\infty_{\mathbf{z}}} \lesssim (|{\mathit{\boldsymbol{\beta}}}|+1)^p $, and initially
for $ N\geq3 $, $ M > \frac{d}{2}+q+p $.
6.
Spectral convergence of the gPC-SG method
In this section, we will prove Theorem 4.2. Let us define the projection of the analytic perturbative solution $ h $ onto the subspace $ {\mathit{\boldsymbol{\Phi}}}^K = \{ \Phi_{\mathit{\boldsymbol{\beta}}}\}_{|{\mathit{\boldsymbol{\beta}}}|\leq K} $ as,
Then we can decompose the error of the approximation solution $ ({\hat{h}^K}, \nabla{\hat{\phi}^K}) $ in the subspace $ {\mathit{\boldsymbol{\Phi}}}^K $ into two parts,
where $ (h^K_p, \nabla_{\mathbf{x}}\phi^K_p) $ represents for the projection error, $ (h^K_e, \nabla_{\mathbf{x}}\phi^K_e) $ are errors from the stochastic Gelarkin. Define vector functions, energy and dissipation terms for error as follows,
Here is the proof sketch of the spectral convergence of the gPC-SG method. Project the microscopic system for the perturbative solution (4)-(5) onto the truncated subspace $ \{ {\mathit{\boldsymbol{\Phi}}}^K\} $, and then subtract the approximate perturbative system (50) from it, one has the following microscopic error system,
If one does energy estimate to the above system, one has microscopic error estimates as in Lemma 6.1. If one multiplies $ v\sqrt{\mathcal{M}} $, and integrate over $ v $ to (72), then one has the following macroscopic system of error,
If one does energy estimate to it, one will obtain estimates as Lemma 6.2. If one combines the microscopic and macroscopic error estimates in a proper way as in Lemma 6.3, and then based on Corollary 1, one can obtain the spectral convergence of the gPC-SG method.
From Theorems 2.1 and 4.1, one can derive the following Corollary.
Corollary 1. Under the same condition in Theorems 2.1 and 4.1, if $ (h(0, {\mathbf{x}}, {\mathbf{v}}, {\mathbf{z}}) $, $ \nabla_{\mathbf{x}}\phi(0, {\mathbf{x}}, {\mathbf{z}})) \in H^{M+r, 3} $, then the following inequalities hold,
where $ \xi = \frac{16+4\lambda}{\lambda}, D_r = (r!)^2\xi, D_M = (M!)^2\xi $, $ D $ is a constant defined in (57)
Proof. (75) and (76) is a direct corollary from Theorems 2.1 and 4.1 respectively. (77) comes from the classical approximation theorem of orthogonal basis. For $ h \in H^{M+r, 2}_{\mathbf{z}} $,
where the second inequality comes from Theorem 2.1, similar bounds can be obtained for $ \left\lVert \nabla_{\mathbf{x}}\phi^K_p \right\rVert_\mu^2 $.
Lemma 6.1. The microscopic error estimate is
Proof. If one multiplies $ h_{e, {\mathit{\boldsymbol{\beta}}}} $ to the $ {\mathit{\boldsymbol{\beta}}}- $th row of (72), integrates it over $ {\mathbf{x}}, {\mathbf{v}} $, and sums over $ |{\mathit{\boldsymbol{\beta}}}|\leq K $, one has,
By (30) and integral by parts, the nonlinear term becomes,
First notice that
For $ I $, one can use the definition of $ \omega_{\mathit{\boldsymbol{\beta}}} $ in (55) and the bound for $ E_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $ in (62), bound it in a similar way as in Lemma 5.2.
where the second inequality is because of $ \frac{E_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}}}{\omega_\mathit{\boldsymbol{\gamma}}} \leq \frac{c_\mathit{\boldsymbol{\gamma}}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}}}{c_\mathit{\boldsymbol{\gamma}} q_\mathit{\boldsymbol{\gamma}}} $. The first term of the last second inequality is because that for fixed $ \mathit{\boldsymbol{\gamma}}, {\mathit{\boldsymbol{\kappa}}} $, by the definition of $ \chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} $ in (61), it is nonzero only if $ |{\mathit{\boldsymbol{\kappa}}}| - |\mathit{\boldsymbol{\gamma}}| \leq |{\mathit{\boldsymbol{\beta}}}| \leq |{\mathit{\boldsymbol{\kappa}}}| +|\mathit{\boldsymbol{\gamma}}| $, so $ \sum_{|{\mathit{\boldsymbol{\beta}}}|\leq K} \chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} \leq 2|\mathit{\boldsymbol{\gamma}}| $; while the second term is because that for fixed $ \mathit{\boldsymbol{\gamma}} $, $ {\mathit{\boldsymbol{\beta}}} $, $ \sum_{|{\mathit{\boldsymbol{\kappa}}}|\leq K}\chi_{\mathit{\boldsymbol{\gamma}}{\mathit{\boldsymbol{\kappa}}}{\mathit{\boldsymbol{\beta}}}} \leq 2|\mathit{\boldsymbol{\gamma}}| $, A is defined in (22).
For II, by the Sobolev embedding (21), one has,
where $ r $ is the smallest constant strictly larger than $ \frac{d}{2} $. So one can bound the second part of the nonlinear term by,
Combine (81) and (82), one has,
for $ \delta_1 = \frac{\lambda}{6\sqrt{5}A\epsilon^a} $, $ \delta_2 = \frac{30\epsilon^a}{\lambda} $, which completes the proof.
Lemma 6.2. The macroscopic error estimate is
where $ G_e = \left\langle u^K_e, \nabla_{\mathbf{x}}\phi^K_e\right\rangle + \frac{1}{2\epsilon}\tilde{E}_{\nabla_{\mathbf{x}}\phi^K_e} $.
Proof. Multiplying $ \nabla_{\mathbf{x}}\phi_{e, {\mathit{\boldsymbol{\beta}}}} $ to the $ {\mathit{\boldsymbol{\beta}}} $-th row of (74), integrating it over $ {\mathbf{x}}, {\mathbf{v}} $, and summing over $ |{\mathit{\boldsymbol{\beta}}}|\leq K $, since the linear part of (74) is similar to the linear part of (28), it is straightforward to get the LHS of (84) and the first term on the RHS. For the nonlinear term, we use the same method as in Lemma 6.1. Similar to (81) - (83), one can bound the nonlinear term by,
for $ \delta_3 = 10A $, $ \delta_4 = \frac{1}{5} $, $ \delta_5 = \frac{1}{5} $. In order to get a sharp estimate, we need to carefully deal with $ \left\langle \sigma\nabla_{\mathbf{x}}\phi^K_e, \nabla_{\mathbf{x}}\phi^K_e\right\rangle $. Using (5) and integration by parts,
for $ \delta_6 = \frac{1}{10} $, which completes the proof.
Combine Lemma 6.1, Lemma 6.2 in a proper way, one has the following Lemma.
Lemma 6.3. Under the condition of
one has micro-macro error estimates,
where $ \tilde{C}_0 $ is the same as defined in Theorem 4.2 and
Proof. (78) $ +\frac{\lambda}{8\epsilon} $ (84) gives
where $ E_e = \tilde{E}_{h^K_e} + \frac{1}{\epsilon^{1-a}}\tilde{E}_{\nabla_{\mathbf{x}}\phi^K_e} + \frac{\lambda}{4\epsilon} G_e $. Moreover, similar to (44) - (46), $ E_e $ is equivalent to $ \tilde{E}_{h^K_e} +\frac{1}{\epsilon^2}\tilde{E}_{\nabla_{\mathbf{x}}\phi^K_e} $ in the sense of
By Corollary 1, one has,
In order to control the RHS of (86) by the dissipation terms on the LHS, we require $ II\leq \frac{\lambda}{4\epsilon^{1+a}} $, $ III \leq \frac{\lambda}{64\epsilon^{1+a}} $, $ IV \leq \frac{3\lambda}{32\epsilon^2} $, so $ \hat{E}^{K, N}(0) $, $ E^{r, 3}_q(0) $ has to be bounded by,
Under the above initial condtion, (86) becomes,
which completes the proof.
Based on the micro-macro error estimates and the fact that $ \tilde{E}_{h^K_e}(0) + \frac{1}{\epsilon^2}\tilde{E}_{\nabla_{\mathbf{x}}\phi}(0) = 0 $, one obtains,
By Grownwall's inequality, one has,
Then by (70), (71), one can bound the error of the approximation solution $ ({\hat{h}^K}, {\hat{\phi}^K}) $ by
Hence, under the condition of
one can obtain
where
Note that the initial condition (59) in Theorem 4.2 is a sufficient condition to (87).
Appendices
A. The proof of Lemma 3.1
First, notice that
where $ A = \sum_{ |{\mathbf{j}}| = 0}^\infty \frac{|{\mathbf{j}}|}{(|{\mathbf{j}}| + 1)^{q}} $. Since
by changing variables,
one has,
Since,
by simple calculation, $ \int_0^\pi (\sin\theta_1)^{d-2}\, d\theta_1\cdots\int_0^\pi\sin\theta_{d-2} \, d\theta_{d-2} \leq 11 $, then one has,
which completes the proof.
Acknowledgments
The author would like to express her special thanks to her Ph.D. advisor, Shi Jin, for his useful discussions and constant encouragement, and also for Renjun Duan for a helpful discussion.









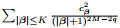 can be bounded by a finite constant
can be bounded by a finite constant 


 DownLoad:
DownLoad: