Traveling fronts guided by the environment for reaction-diffusion equations

1.   Introduction

The mathematical modelling of biological problems always gains the interest of many researchers. The birth-death process introduced by Yule ^[1], Feller ^[2] and Kendall ^[3], represents a natural theoretical framework of different biological studies. Such studies have various applications as population dynamics, genome evolution and etc.. In this paper, I am interested in studying the asexual reproduction of like-individual (organisms, cells, genome, etc.). Beginning by the classical branching process that describes a large population that consists initially of $ N_e $ like haploid individuals. In each succeeding generation with assuming non-overlapping, the population produces asexually like individuals with number $ N(t) $. Each one of them may give birth to $ 0, 1, 2, \cdots $, individuals with corresponding probabilities $ p_0, p_1, p_2, \cdots $ such that $ \sum\limits_k p_k = 1 $. The individuals of any generation are independent identically distributed random (i.i.d.r.) numbers. The number of individuals in the n-th generation is denoted by a random variable (r.v.) of a Markov-Type. Kolmogorov ^[4] mathematically formulated this model in the form of the Fokker-Planck equation, namely

where the indepenedent random variable $ x $ represents the size and $ u(x, t) $ is a probability density function being subjected to the initial condition $ u(x, 0) = \delta(x) $, and there is no boundary conditions imposed on it. $ a(x) $ is the expected number of individuals and $ b(x) $ is its variance. Kolmogorov assumed in his derivation of (1.1) that the only restriction imposed on the number of the population size $ N_e $ is that it is fixed at any generation.

Later, Feller ^[5], assumed that the density function $ u(x, t) $ is independent of on the total population size $ N_e $ and formulated his exponential growth equation as

where $ \alpha $ and $ \gamma $ are initially assumed to be constants. This equation is called by Feller ^[5], the exponential population growth because its expected population size is obtained as

That means $ M(t) $ is growing up exponentially. $ \alpha $ represents the actual rate of population increase and can be written as $ \alpha = \frac{1}{t} ln(\frac{M(t)}{ N_e}) $. The variance could be written as

Then according to Feller, the mean and the variance are necessarily proportional to the instantaneous population size $ N(t) $. As $ \alpha > 0 $ the population average increases, as $ \alpha < 0 $ the population decreases. Feller stated that the analytic unique solution of Eq (1.2) could be written in terms of the Bessel function $ I_1 $, see for more details ^[5]. According to Feller, the probability that the population dies out before time $ t $ is

and on the long run, i.e., as $ t\to \infty $, the probability that there is no individual exists is given as

For more details about the difference views between the pioneers of the population genetics researchers and the modern studies, see Ewens ^[6]. Dutykh ^[7], give an approximate solution of the classical Feller's Eq (1.2) after replacing the drift term $ (a(x) u(x, t))_{x} $ by $ ((ax +c u(x, t)))_{x} $. The author reformulated the equation by the so called Lagrangian or material variables, to avoid the unbounded of its variable coefficients. Masoliver ^[8] studied the non-stationary classical Feller process with time-varying coefficients. The author obtained the exact probability distribution and prove as Ross proved that the probability density function approaches the Gamma distribution on the long run. Recently, Giorno et al. ^[9] studied the time-inhomogeneous Feller-Type diffusion process in the population dynamics. The authors calculated the expectation, the moment generating function and the periodicity of the density function of the classical diffusion of the birth-death process with immigration.

The discrete birth-death process or the so called $ M/M/1 $ exponential model, represents a system in which an individual (customer) joins a system for having a specific service with rate $ \lambda $ and the service (leaving or death) rate is $ \mu $ with $ \frac{ \lambda}{ \mu} < 1 $. The server is serving only one customer at each time instant. The probability of finding $ m $ (customers) at any time $ n $ at the system has the same meaning of the asexual production being studied by Fokker-Planck and is mathematically formulated by Eq (1.1).

In this paper, I am interested in proving that the discrete birth-death process, with random birth rate $ \lambda $ and with random death rate $ \mu $ is mathematically formulated by the same Eq (1.1) as the birth and death rats are linearly growth. I am interested also in studying the approximate solution of Eq (1.1), for many cases. The first case, is to assume that the number of individuals is fixed at any generation. The second case is to assume that the number of individuals are randomly vary from a generation to generation. Finally is to add the memory effects on the diffusion process Eq (1.1) by extending the first order time derivative to the Caputo time-derivative, namely

I prefer to call this equation the time-fractional linear population growth equation. This is allowed as Eq (1.1) represents a solution of a stochastic process and $ u(x, t) \to 0, \, x^{n} u(x, t) \to 0 $ as $ x \to \infty $ for all $ n \in \mathbb{N}_{0} $, see reference ^[12] for more details about the extension of partial differential equation to fractional differential equation.

For this aim, I implement two numerical methods. The first method is the finite difference method and the second is the fourth order compact finite difference method. The Grünwald-Letnikov scheme is utilized to find the the discrete scheme of the Caputo time-fractional operator. Abdel-Rehim, see for example ^[10,11,12], has successfully used the Grünwald-Letnikov scheme to simulate many time-fractional diffusion equations. Talib et al. ^[13] used another numerical method based on the operational matrices to find the numerical solutions of time-fractional differential equations. The authors used the Caputo and the Riemann-Liouville of two-parametric orthogonal shifted Jaccobi polynomials. Talib et al. ^[14] has recently generalized the existing operational matrix method to operational matrix of mixed partial derivative terms in Caputo sense. In this improvement, the authors used the orthogonal shifted Legendre polynomials.

It is worth to say that Polito et al.^[15] studied a fractional birth-death process. The authors presented in their paper a subordination relationship connected the fractional birth-death process with the classical birth-death process. Later Polito ^[16] studied the generalized Yule models. Recently, Ascion et al. ^[17] studied some non-local diffusion-differential equations related to the birth-death processes and are appeared as discrete approximations of Pearson diffusions. The authors in these papers used the branching processes and the stochastic processes tools to discuss theoretically the fractional birth-death process.

To this aim, the paper is organized as follows. Section $ 1 $ is devoted to the introduction. Section $ 2 $ is to derive the diffusion equation of the linear birth-death discrete exponential model. Section $ 3 $, is to derive the approximate discrete solutions of the classical (Markov) and non-classical (Non-Markov) linear birth-death process by the finite difference method. Section $ 4 $, is for driving the approximate solutions by the fourth order compact finite difference method. Finally, section $ 5 $, is to present and to discuss the numerical results.

2.   The diffusion equation of the linear birth-death process

The birth death process is a stochastic process being defined as $ \{ X(t) = n \, , t \ge 0 \} $, where its states $ X(0) = 0, X(1) = 1, X(2) = 2, \cdots $ represent the number of customers or the number of (similar individuals) exist in the system at any time $ t $, $ n \in \mathbb{N}_{0} $. Now suppose two time instants $ t, t+\tau $ with $ \tau\to 0 $ and two non negative integers $ i, j $ that represent the number of individuals ^[18]. Define the continuous time Markov chain's transition probability from the state $ X(t) $ with $ i $ number of individuals to its neighbour $ X(t+\tau) $ with $ j $ number of individuals as

or in other words, the process in the sate $ X(t+\tau) $, depends only in the previous state $ X(t) $, and not on all the previous states, i.e., the the process has no memory. The Bays formula for the continuous time Markov chain

The Kolmogorov's forward equation of the discrete Markov chain reads

Subtract $ P_{ij} $ from both sides, where for small $ \tau $, one can set $ P_{ij}(t) = (1-P_{ii} (\tau)) P_{ij}(t) $. So far, one gets

where $ P_{ii}\ne0\, , \forall i\ge 0 $, i.e., there is no absorbing states and $ \sum\limits_{j} P_{ij} = 1 $. If $ P_{ii}(\tau) $ is the probability that the process is in state $ i $ and will stay in $ i $ at the time $ \tau $, the $ 1-P_{ii} $ is the probability that the process is no longer in state $ i $. Now divide both sides by $ \tau $ and take the limit as $ \tau \to 0 $, to get

where $ C_i = \underset{\tau \to 0} {lim}\frac{ P_{ik} }{ \tau} $, and $ D_i = \underset {\tau \to 0}{ \lim} \frac{ 1-P_{ii} }{ \tau} $ are constants. For the birth-death process with birth rate $ \lambda_i $ and death rate $ \mu_i $, see ^[18], and for $ j = 0 $, i.e. the system is empty, one has

This equation represents also the exponential queueing model $ M/M/1 $ in which there is only one customer in the system and is being served and no one joins the queue. The only restriction for the the queueing system is that $ \frac{\lambda}{\mu} < 1 $, to ensure that all the customers will be served. For $ j\ge 1 $, one has

$ \lambda_{j}, (1- (\lambda_j + \mu_j)), \mu_{j} $ are the possible transition probabilities from the state $ X_j $ at the time instant $ t_n $ to the sates $ X_{j+1}, X_{j}, X{j-1} $, respectively, at the time instant $ t_{n+1} $, where $ X_j = jh $. This equation represents the $ M/M/1 $ queue in which customers arrive according to Poisson process with arrival rate $ \lambda_{j} $ and the customer is served with rate $ \mu_j $ and the time of serving is an exponential random variable.

This equation represents also the first order time derivative of the transition probability $ P_{ij} $ at any time instant $ t_n $, $ n\ge 0 $. For simplicity write $ P_{ij} = P_{j} $, $ \forall i $, and the same for the birth and death rates. The solution of Eq (2.4) represents the probability of finding $ j $ individuals at the system at any time $ t $. Now suppose the number of customers in the system, the number of individuals exists at the colony, or the queueing system, are very large. or in other words $ j\to \infty $, and for mathematical convenience replace $ j $ by $ x $. Then one can write $ \lambda_{j-1} P_{j-1} = \lambda(x-h) P(x-h) $, with $ h\to 0 $, $ (\lambda_{j}+ \mu_j) P_{j} = (\lambda(x)+ \mu(x)) P(x) $, and $ \mu_{j+1} P_{j+1} = \mu(x+h) P(x+h) $, where $ h $ is the space instant and $ h\to 0 $. Now, Eq (2.4), could be rewritten as

and now the Taylor's expansion can be used to expand the terms $ \lambda(x-h) P(x-h) $ and $ \mu(x+h) P(x+h) $, to get

The functions $ \lambda(x) $ and $ \mu(x) $ could be any smooth convergent functions. For linear birth-death process, one has to choose $ \lambda(x) = \lambda x $ and $ \mu(x) = \mu x $, and henceforth Eq (2.6) is rewritten as

Let $ R $ be the number of $ x $ steps and put $ h = 1/R $, and define the coefficients

then Eq (2.7), with Eq (2.8) is identical with Eq (1.2), and is called the linear birth-death process. The linear birth-death process is a stochastic exponential model with random birth rate, rate of arrivals, $ \lambda \in (0, 1) $ and random death rate $ \mu \in (0, 1) $, rate of departure or rate of service. The right hand side of Eq (2.7) is a special the form of the Fokker-Planck operator $ L_{fp} $, see ^[12]. So far I prefer to write the linear birth-death process as

The waiting time between any two successive arrivals (birth) and departures (death) are exponentially distributed as $ e^{-\lambda t} $ and $ e^{-\mu t} $, respectively. The values of $ \lambda $ and $ \mu $ could be fixed random number at all the next generations and could be computed as exponential random variables at each generation. The expected population size Eq (1.3) of Eq (2.7) is obtained as

As $ \lambda > \mu $, the population increases and as $ \lambda < \mu $, the population decreases. In the next section, I am going to derive the discrete approximate solution of Eq (1.2), with its $ \alpha $ and $ \gamma $ are calculated by Eq (2.8), by the explicit finite difference method (fdm).

3.   The approximate solution of the classical and non-classical birth death process by the finite difference method

I am beginning the discussion of the approximate solution by the common rules of the explicit fdm as the basic of all the numerical methods. Define the $ n^{th} $-time step as

Introduce the clump $ y^{(n)} $ as

where $ y^{(n)} = y(t_n) $ represents the discrete probability column vector to find $ m $ individual at the generation $ t_n $ or at the time instant $ t_n $. To solve the partial differential Eq (1.2) and its equivalent Eq (2.7), the initial value $ y^{(0)} $ has to satisfy $ \sum \limits_{j = 1}^{R-1} y_j^{(0)} = 1 $, $ \, \forall n\in \mathbb{N}_0 $. The proper choice is $ u(x, 0) = \delta(x) $, hence fourth

The discrete scheme of Eq (2.7), reads

where $ n \ge 0 $. Define the scaling relation $ \eta = \frac{ \tau}{h^2} $, and solve for $ y_{j}^{(n+1)} $, to get

where $ n\ge 0 $ and $ y_{j}^{(n+1)} $ represents the discrete probability density function of finding the system at the time instant $ t_{n+1} $ with $ m $ individuals. Summing the coefficients of the $ y_{j-1}^{(n)}, y_{j}^{(n)}, y_{j+1}^{(n)} $, one can easily find $ \sum\limits_{j = 1}^{R-1} y_{j}^{(n+1)} = 1 $. The difference scheme (3.5) is stable and convergent if the scaling relation $ \eta $ satisfies the following condition

and for the suitable choice as $ j = \frac{ R}{2} $, one gets $ \eta \le \frac{1}{ \gamma } $. The difference scheme (3.5), could be written in a matrix form as

where the matrix $ P = P_{ij} $ is $ R-1\times R-1 $ and is defined as

For proving the stability of this approximate solution, define the two column vectors $ \Lambda $ and $ 0 $, with length $ R-1 $ as

The matrix $ P $ is stable if it satisfies the two equal conditions

or

Since $ P $ is a stochastic matrix, and $ P^T. \Lambda = \Lambda $, i.e., the sum over all its rows is $ 1 $. The matrix $ P $ satisfies the both stability conditions. The greatest eigenvalue of $ P $ is $ 1 $, then its spectral radius being defined as

where $ \{ \zeta_i \} $ is the set of the eigenvalues of $ P^T $. Then for this case $ \rho (P^T) \le || P^T||_{ \infty} = 1 $, see ^[19] for more details about the stability of the explicit difference methods of the diffusion convection equations. Now for the purpose of computation, it is better to take the transpose of Eq (3.7) and rewrite it as

where $ z^{(n)} = (y^{(n)})^T $, I is the unit matrix. $ H1^T $ is the matrix that satisfies $ H1^T. \Lambda = 0 $, i.e., the sum over all its rows is zero, and being defined as

The transition probabilities at Eq (3.5), constitute a Markov chain. Therefore, the waiting time between every two random events, arrivals of a new individual, is $ \approx e^{-t} $, i.e., is exponentially distributed. That means this stochastic process at the time instant $ t_{n+1} $, depends only on the time instant $ t_n $, and neither nor all its previous history. In Reality, this is not correct and the history of the process has to be considered. In other words the number of individuals at the time instants $ t_{n-1} $, $ t_{n-2} $, $ \cdots, t_0 $, should be known.

3.1.   The approximation of the time-fractional linear growth equation

Now, to find the approximate solution of the time-fractional linear growth defined in Eq (1.6). The Caputo time fractional operator of order $ \beta $ is defined for a smooth function $ f(t) $ as

where

The kernel $ K_{\beta} (t-\tau) $ represents the memory function, and it reflects the memory effects of many physical, biological and etc. processes, see ^[22] and ^[23].

Before going on our descretization of the Caputo fractional operator, I give a quick review about the advantages of using this operator on modelling the read–world problems. to do so, recall the definition the Riemann-Liouville fractional integral operator, denoted by $ J^{\beta} $, as

For completeness, one sets $ J^{0} f(t) = f(t) $. This means $ J^{0} $ is an identity operator. The Riemann-Liouville fractional derivative operator, for a sufficiently smooth function $ f(t) $ given in an interval $ [0, \infty) $, is defined as (see for example:^[25] and ^[24])

and

From the definitions (3.15) and (3.16), we can define the Riemann-Liouville fractional derivative $ D^{\beta} $ as the left inverse of $ J^{\beta} $, $ \beta \ge 0 $. Therefore some authors prefer to write the Riemann-Liouville fractional integral operator $ J^{\beta} $ as $ D^{- \beta} $ (e.g. ^[25,26,27]). For completeness, we have $ D^{0} = I $. One can deduce from the two definitions (3.14) and (3.16) that both the operators are non local but both have different kernels. The definition of Caputo is restrictive than Eq (3.16) because it requires that $ f^{(m)}(t) $ exists. therefore, Caputo is more convenience for the mathematical manipulations. For completeness, we have $ D^{0} = I $.

The Riemann-Liouville fractional derivative of the power function $ t^{\mu} $, gives

This means the Riemann-Liouville fractional derivative of a non-zero constant is different from zero. In fact

This is the main disadvantage of this operator. But $ \underset{0\; \; t}{^{ \rm C}{D}^{\beta}} f(t) = I $ as $ \beta = 0 $. The Caputo operator with the Riemann-Liouville satisfies the relation

Caputo can also be defined through its image in the Laplace transform domain, which is

The Caputo fractional derivative of order, in the special case $ 0 < \beta \le 1 $ satisfies also

and

we can deduce that

This is the second difference between the Caputo and the Riemann Liouville derivatis. In other words, the Caputo depends on the initial condition of the function $ f(t) $. Recently Diethelm ^[29] stated in his book "The Main Disadvantage of the Riemann-Liouville Fractional Derivative is that it Fails to Model the Real World Phenomena of Fractional Differential Equation.".

For discretizing the Caputo time-fractional derivative, I utilize the Grünwald- Letnikov scheme being reads

where

To find the average number of individuals of this memory-dependent process $ M(t) $ defined in Eq (1.3), it is important to write Eq (1.6) in terms of the Fokker-Planck operator $ L_{fp} $ and the Riemann-Liouville fractional derivative operator $ \underset{0\; \; t}{D}^{\beta} $, as

See reference ^[24]. This equation can also be written as

where $ \underset{0\; \; t}{D}^{-\beta} = J^{ \beta} $, is the Riemann-Liouville fractional. Now multiply both sides of Eq (3.22) by $ x $ and integrate over $ x \in [0, \infty) $, with regarding the initial condition $ u(x, 0) = \delta (x) $, and by using the natural properties of $ u(x, t) $ as probability density function, namely $ u(x, t) \to 0 $, $ x \frac{ \rm \partial u }{\rm \partial x} \to 0 $ and $ x \frac{ \rm \partial^2 u }{ \rm \partial x^2} \to 0 $ as $ x \to \infty $, to get

This equation has the solution

which is a special form of the so called Mittag-Leffler function. In the special case as $ \beta = 1 $, it is identical to the exponential function $ e^{ - \alpha t} $, for its simulation see reference ^[12]. That means the special case as $ \beta $ gives the same exponential average of individuals defined in Eq (2.10) but as $ 0 < \beta < 1 $, the average $ M(t) $ exhibits proportionally as the power function $ \alpha t^{- (\beta+1)} $. Abdel-Rehim ^[38] has recently simulated the asymptotic behaviour of the Mittag-Leffler function and compared the results with the exponential function $ e^{-t} $ and Hypergeometric1F1$[1+n, 2+n, -t] $ function, for different values of $ t $, $ \beta $ and $ n $. Now the discrete scheme of the time-fractional population growth Eq (1.6) reads

where its error is of order $ O(h^2+\tau^{\beta}) $. For convenience, recall the following coefficients

which are introduced by Gorenflo et al. ^[28]. These coefficients satisfy that $ b_{0} = c_{1} = \beta $, all $ c_{k}\ge 0 $, $ b_{n}\ge 0 $, $ \sum\limits_{k = 1}^{\infty}c_{k} = 1 $, and finally satisfy the relation

Assuming the new scaling relation as $ \eta = \frac{ \tau^{ \beta }}{h^2} $, rearranging the terms of Eq (3.25) and solving for $ y_j^{(n+1)} $, to get

where $ n\ge 1 $. For computing $ y_j^{(n+1)} $, the values of $ y_j^{(n)} $, $ y_j^{(n-1)} $, $ y_j^{(n-2)} $, $ \cdots, y_j^{(0)} $, should be known. That means the diffusion process for $ n\ge 1 $, depends on all the history, the process has a memory. That what is called the Non-Markov process. The difference scheme (3.27), is convergent if the coefficient of $ y_j^{(n)} $, is positive and that requires that the scaling relation of this non-classical case should satisfy

and again by choosing $ j = R/2 $, one gets a suitable condition for the scaling relation $ \eta $. The difference scheme (3.27) could be written in the matrix form as

Again the difference scheme (3.27) is stable as the matrix $ (\beta I+ \eta. H1)^T. \Lambda = \beta \, \Lambda $, then $ || (\beta I+ \eta. H1)^T ||_{ \infty} = \beta $ with $ 0 < \beta < 1 $. That satisfies the stability condition (3.9), and hence forth the second condition (3.10) is satisfied. The maximum eigenvalue of the matrix $ (\beta I+ \eta. H1)^T $ is $ \beta < 1 $, therefore the spectral radius being defined as of this difference scheme is $ \rho (\beta I+ \eta. H1)^T < 1 $. Then this difference scheme is stable and the scaling relation condition (3.28) ensures its convergence. Abdel-Rehim ^[20] proved that the waiting time between every two arrivals (events) on the time-fractional diffusion processes is the Mittag-Leffler function, see also ^[21] and the references therein for more details about the job of the Mittag-Leffler function on the continuous time random walk.

For $ n = 0 $, this is the first state after the initial state. By returning back to Eq (3.25), we find that $ y^{(1)} $ represents the probability of finding the system at the state $ X(1) $. Therefore, the approximate solution as $ n = 0 $, is computed according to Eq (3.12) as

and in this case, the transitions could be described as a Markov chain. In the following section, I use the fourth order compact finite difference method (focfd) to derive the stable difference scheme of studied models to be compared with the results obtained by fdm.

4.   The approximate solution of the classical and non-classical birth death process by the fourth order compact finite difference method

The finite difference method used in the above section has many advantages such as: it is computationally efficiency, requires simple code structures and it maintain the mass conservation. Its only disadvantage is that it is irregular geometric matching. To interpret this sentence suppose that $ f(x) $ is a smooth continuous function and its derivative $ f_{x} = \frac{df(x)}{dx} $ exists. define the truncation error by $ O $. Define also $ x_i = ih $, $ x_{i+1 = x+h} $, and $ x_{i-1} = x-h $. Then one deduce

and

In general

That means to obtain a truncation error of order $ O(h^{n}) $, one needs to use $ 2n+1 $ values of $ f(x) $ to approximate $ f_x (x_i) $. Therefore, the fdm is inconvenience for solving the partial differential equations with variable coefficients near the boundaries.

The focfd did overcome this trouble by adding more nodes with few grid points smaller mesh sizes, in order to obtain a higher order of truncation error.

The focfd has been proved and implemented by many authors. It has been proved that the obtained approximate solution is approximately consistent with the exact solution, especially of the advection convection equations, than by using the common fdm rules.

Turkel and Singer ^[30], introduced limited grid sizes to make the high-order compact finite difference schemes produce more accurate solutions. Later ^[33], the focfd is improved by eliminating the convection term to make it more easier to implement the central difference schemes to solve convection-diffusion equations efficiently. For more details about the advantages and the disadvantages of the compact finite difference methods, see ^{[31,32,34,35,36]}. One can deduce from these references that the main advantage of the focfd is the high accuracy.

It is known that the first $ \delta_x y_j^{(n)} $ and the second $ \delta_x^2 y_j^{(n)} $ classical spatial discrete central finite difference operators are defined as

where the clump $ y^{(n)} $, for this method, is defined as

To implement the focfd one has to use 1^st derivative operator that is defined as, see references ^[33,34],

and the 2^nd derivative operator is defined as

First apply the focfd method on the classical case (2.7), to get

and use the same scaling relation of the classical Markov case $ \eta = \frac{ \tau}{ h^2} $, one gets after some manipulations

As we see from this difference scheme $ y_{j}^{(n+1)} $ is the probability of finding $ m $ individuals at the time instant $ t_{n+1} $, i.e., at the states while it may be at one of the states $ X_{j-2}(t_n), X_{j-1}(t_n), X_{j}(t_n), X_{j+1}(t_n), X_{j+2}(t_n) $. This difference scheme could be written in the matrix form as

where the matrix $ K $ is defined as

It is clear that the sum over all its elements is one. The matrix $ H $ has the form

where it is easy to prove that the sum over all its elements is zero. Now take the transpose of each sides of Eq (4.7) and multiply each sides by $ K^{-1} $, to get

where $ z^{n} $ is the transpose of the clump defined in Eq (4.2). Again the obtained approximate solution is stable as $ (I+ \eta. H. K^{-1})^T. \Lambda = \Lambda $, and the two stability conditions (3.9) and (3.10) are satisfied. Again the scheme is also convergent the scaling relation $ \eta $ satisfies the following condition.

Now, I seek to find the approximate solution of the time fractional linear birth-death (linear growth) large population Eq (1.6). Therefore apply the 1^nd and the 2^nd derivative operators, to get

Regarding the initial condition $ u(x, 0) = \delta(x) $ and its discrete clump (3.3), one gets after some mathematical manipulations.

where the matrices $ K $ and $ H $ are defined in Eqs (4.8) and (4.9) respectively. Again this discrete difference scheme is convergent if the scaling relation $ \eta = \frac{ \tau^{ \beta}}{ h^2} $, satisfies the positivity condition

The stability of the matrix $ (\beta I+ \eta H. K^{-1}) $ has been previously proven. The case as $ n = 0 $, is calculated similar to the classical Markov case as

In the next section, the time evolutions of the obtained approximate solutions will be simulated with different values of the fractional order $ \beta $ and $ t $, to show how the memory affects on the randomly number of individuals existing on the birth-death queueing system (the number of asexually like produced individuals at any colony).

5.   Numerical results

Feller ^[5], assumed in his paper that $ \gamma = 1 $, and $ \alpha $ may has one the three values $ 0, 1, -1 $. Galton-Watson assumed that $ \alpha $ and $ \gamma $ are proportional to the initial size of individuals $ N_e $, see ^[37]. The authors at ^[37], fix the expected population size as $ M(t) = M(0) = M_0 \to N_e $, from Eq (1.3) then $ -\alpha = \frac{1}{t} ln \frac{ N_e} {M_0} $, for $ \lambda < \mu $ and substitute on the analytic solution derived by Feller. The authors fix also $ \sigma^2 = \gamma $ to be one or two.

In this paper, I give numerical results for the cases corresponding to $ \lambda > \mu $ and $ \lambda < \mu $. To grantee the stability of the difference schemes, the scaling relation $ \eta $, should satisfy the stability relations (3.6) and (3.28). Further more for better approximate solutions, one has to choose $ 0 < \eta < < \frac{R}{2j \gamma} $ for the classical case and $ 0 < \eta < < \frac{ \beta R}{2j \gamma} $ for the non-classical case.

The first group of Figures 1–8 are devoted for the case $ \lambda < \mu $. I choose $ \lambda = 0.1 $ and $ \mu = 0.3 $, i.e., $ \alpha = -0.02 $ and $ \gamma = 0.002 $, and $ \frac{\lambda}{\mu} = \frac{1}{3} $.

First the numerical results by the finite difference method: Figure 1, represents the time evolution of the approximate solutions of the classical and time-fractional linear birth death equations, for small values of $ t $.

Figure 2 represents the time evolution of their $ y^{(n)} $, for different values of $ t $. The figure shows that the diffusion of the time-fractional growth is slower than the classical one.

It is worth to say that all the approximate solutions behave likely for small values of $ t $. The difference on the $ y- $axis becomes larger as $ t $ increases.

The comparison of the approximate solutions by the finite difference method are given in Figure 3. The figure shows also that the classical case diffuses faster than the fractional case.

Second the numerical results by the fourth order compact finite difference:

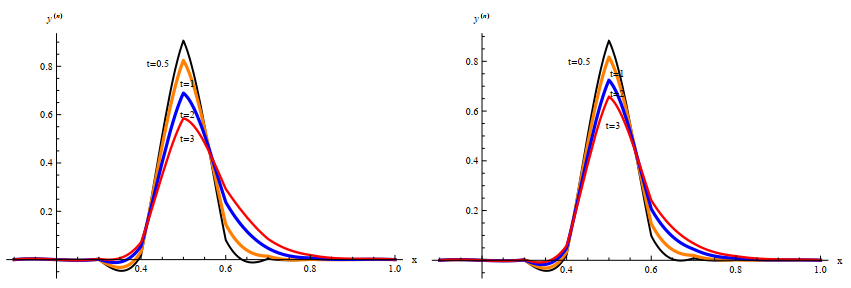
Figure 4 shows the time evolution of the classical case. The figure shows the diffusion is much faster as $ \beta = 1 $ than by using the fdm for both small and large values of $ t $.

Figure 5 represents the time evolution of the classical and non-classical for different values of $ \beta $ and $ t $. The fractional growth is more slower than the classical as it diffuses near its initial condition but the classical diffuses far away than its initial value.

Figure 6 represents the comparison of the approximate solutions of the classical and non classical. The figure shows that the power growth is slower than the exponential growth.

Now, I compare the results obtained by the finite difference and the fourth order compact finite difference at Figures 7 and 8. The figures show that the difference between the two methods is very big at small values of $ t $ as the focfd diffuses faster. But at $ t $ increases the difference becomes smaller.

The focfd has to imitate the exact solution. it has to be more accurate than the fdm. One can that the behavior is different near $ x = 0 $ and $ x = 1 $.

The second group of Figures 9–12 are for the case $ \lambda > \mu $. I choose $ \lambda = 0.3 $ and $ \mu = 0.1 $, i.e., $ \alpha = 0.02 $ and $ \gamma = 0.002 $, and $ \frac{\lambda}{\mu} = 3 $.

I begin this group the approximate solutions by the finite difference method. Figure 9 represents the approximate solutions of the discussed cases for different values of $ \beta $ and $ t $. It is obvious that the growth diffuses faster than the first group of figures, namely as $ \lambda < \mu $.

Figure 10 shows the comparison of the solutions for fixed time and different values of $ \beta $. I used here the fourth order compact finite difference method. One can see that power growth is faster than exponential growth.

Figure 11 represents the time evolution of the discrete schemes for different values of $ t $ by using the fdm. The time fractional is also slower than the classical.

The comparison of the results obtained by the fourth order compact finite difference for different values of $ \beta $ is shown at Figure 12.

Now, I compare the numerical results of the finite difference and the fourth order compact finite difference methods at the Figures 13 and 14. The results show that the effect of the drift on the diffusion process is obvious as $ \lambda > \mu $. Also the results show that the classical case always diffuses faster than the classical case.

The comparison between the results of fd and focfd shows that the difference is bigger at the earlier time and the difference becomes smaller on the long run. The difference is also bigger in the classical case than the non-classical case.

6.   Conclusions

In this paper, I derived the classical birth-death equation. This equation represents the exponential growth of large similar population. Then I extent it to the time fractional birth-death equation as a non-classical partial differential equation. It formulates the power growth of the large similar population. I fix the number of individuals and choose suitable values for the rate of birth and the rate of death to be consistent with the international rates of growth and death. I used the finite difference method and the fourth order compact finite difference method to obtain the approximate solutions of the studied equations. I give numerical results for the rate of birth is bigger than the rate of death and vice versa.

In general the numerical results show that the time-fractional approximate solution diffuses slower than than the classical one. The power and the exponential growth are faster as $ \lambda > \mu $ than as $ \lambda < \mu $. Another important note, is that the time-fractional birth-death process diffuses near its initial values more than the classical case which diffuses far away than it. Finally, The behaviours of the plot near the lateral points are different in both methods and this is consistent with main advantage of the focfd, which is it is more accurate more than the fd especially near the boundaries.

Conflict of interest

The author declares there is no conflicts of interest.