Gaussian estimates on networks with applications to optimal control

1.   Introduction

The paper deals with a phase transition model (PT model for short) that takes into account the presence along a unidirectional road of obstacles that hinder the flow of vehicles, such as speed bumps, traffic lights, construction sites, toll booths, etc. More precisely, the traffic away from these inhomogeneities of the road is described by the PT model introduced in [9], whereas the effects of these inhomogeneities are described by considering one of the two constrained Riemann solvers introduced in Section 3.

Traffic models based on differential equations can mainly be divided in three classes: microscopic, mesoscopic and macroscopic. The present PT model belongs to the class of macroscopic traffic models. We defer to the surveys [8,36,39] and to the books [27,29,42] as general references on macroscopic models for vehicular traffic. Among these models, two of most noticeable importance are the LWR model by Lighthill, Whitham [35] and Richards [40]

and the ARZ model by Aw, Rascle [7] and Zhang [43]

Theses two models aim to predict the evolution in time $t$ of the density $\rho$ and of the (average) speed $v$ of vehicles moving along a homogeneous road with no entries or exits and parametrized by the coordinate $x \in {\mathbb{R}}$.

Both of these models have their drawbacks. In fact, the LWR model assumes that the velocity is a function of the density alone. However empirical studies show that the density-flux diagram can be approximated by a curve only at low densities, whereas at high densities it has a multivalued structure. Hence, it is more reasonable to describe the traffic in a congested phase by a second order model, such as the ARZ model. On the other hand the ARZ model is not well-posed near the vacuum: in general the solution does not depend continuously on the initial data when the density is close to zero.

This motivated the introduction in [32] of a PT model that couples LWR and ARZ models to describe the free-flow and the congested phases, respectively. The coupling is achieved via phase transitions, namely discontinuities that separate two states belonging to different phases and satisfying the first of the Rankine-Hugoniot conditions (RH) corresponding to the conservation of the number of vehicles. The resulting model has the advantage of correcting the aforementioned drawbacks of the LWR and ARZ models taken separately.

We recall that the macroscopic two-phase approach was first introduced by Colombo in [17,18], where the free-flow phase is governed by the LWR model and the congested phase by a $2\times2$ system of conservation laws expressing the conservation of both the number of vehicles and of the linearized momentum. From the analytical point of view, in [21] this model is proved to be globally well posed for any initial datum with bounded total variation; in [13,14] a new version of Godunov scheme is proposed in order to compute numerically its solutions. In [16,20,33] this model has been generalized to the case of a network.

The macroscopic two-phase approach was then exploited and investigated by other authors in subsequent papers, see for instance [9,10,23,24,30,31,37,38] and the references therein.

A couple of mathematical difficulties have to be highlighted. First, one difficulty is that the curves in the $(t,x)$-plane dividing two regimes are not given a priori. The model cannot be reduced therefore into solving two different systems in two distinct regions with prescribed boundary conditions. Another difficulty is the possibility that two phase transitions may interact with each other and cancel themselves. In fact, for instance, it is perfectly reasonable to consider a traffic characterized by a single congested region $\bf C$, with vehicles emerging at the front end of $\bf C$ and moving into a free-flow phase region with a velocity higher than the tail of the queue at the back end of $\bf C$, so that after a certain time the congested region disappears and the whole traffic is in a free-flow phase. For this reason a global approach for the study of the corresponding Cauchy problem can not be applied, as it would require a priori knowledge of the phase transition curves; it is instead preferable to apply the wave-front tracking algorithm [11,34], as it allows to track the positions of the phase transitions.

The present article deals with the constrained version of the PT model introduced in [9], that can be regarded as a generalization of the one given in [32]. We aim to study the PT model introduced in [9] equipped with a local point constraint on the flow, so that at the interface $x=0$ the flow of the solution must be lower than a given constant quantity $Q_0$. This models, for instance, the presence of a toll gate across which the flow of the vehicles cannot exceed its capacity $Q_0$. The additional difficulty that this adds to the mathematical modelling of the problem is that this time one can start with a traffic that is initially completely in the free-flow phase, but congested phases arise in a finite time in the upstream of $x=0$, as it is perfectly reasonable in the case of a toll gate with a very limited capacity. We establish two constrained Riemann solvers for this model and study their properties. These two Riemann solvers may be used in a wave-front tracking scheme to study the resulting Cauchy problem.

Before concluding this introduction, let us briefly summarize the literature on conservation laws with point constraint on the flow recalling that:

● the LWR model with a local point constraint is studied analytically in [19,41] and numerically in [5,12,15,22];

● the LWR model with a non-local point constraint is studied analytically in [1,3] and numerically in [2];

● the ARZ model with a local point constraint is studied analytically in [4,25,26] and numerically in [6].

To the best of our knowledge, the present model is the first PT model with a point constraint.

The paper is organized as follows. In Section 2 we state carefully the model and introduce the needed notations and assumptions. In Section 3 we define four Riemann solvers. More precisely, beside the Riemann solver already presented in [9] and here denoted by $\mathcal{R}_1$, we propose a further Riemann solver $\mathcal{R}_2$. We then construct the two constrained Riemann solvers $\mathcal{R}^{\rm c}_1$ and $\mathcal{R}^{\rm c}_2$ corresponding to $\mathcal{R}_1$ and $\mathcal{R}_2$, respectively. In Section 4 we study their basic properties. Finally, in the last section we apply these Riemann solvers to simulate an heterogeneous traffic in the upstream of a toll booth.

2.   The phase transition model

In this section, we briefly recall the PT model treated in [9].

2.1.   Notations and main assumptions

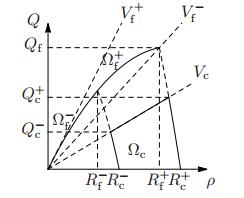
In this subsection we collect some useful notations, see Figure 1, and the main assumptions on parameters and functions used throughout the paper. First, at any time $t \ge 0$ and in any position $x \in \mathbb{R}$ along the road, the traffic is described by the vector

where $\rho$ is the density and $v$ is the (average) speed. The vector $u$ belongs to

where $\Omega_{\rm f}$ and $\Omega_{\rm c}$ are respectively the domains of free-flow and congested phases, whose rigorous definitions are given below after the introduction of necessary parameters and functions. First, we fix two threshold densities $R_{\rm f}^+ > R_{\rm f}^- > 0$. Let $V \in {\mathbf{C^{2}}}([0,R_{\rm f}^+];{\mathbb{R}}_+)$ be the speed map and $p \in {\mathbf{C^{2}}}([R_{\rm f}^-,\infty);{\mathbb{R}})$ be the pressure map such that

where the prime stands for the derivative with respect to the density $\rho$.

A typical choice for $V$ and $p$ is

where $R$, $\gamma$, $v_{\rm ref}$ and $\rho_{\max}$ are strictly positive parameters, that can be chosen so that (H1), (H2) and (H3) are satisfied, see [9] for the details.

We then introduce also the following constants:

By (H2) the map $p^{-1} \colon [W_{\rm c}^- - V(R_{\rm f}^-),W_{\rm c}^+] \to [R_{\rm f}^-,R_{\rm c}^+]$ is increasing and

The above constants have the following physical meaning: $V_{\rm f}^+$ and $V_{\rm f}^-$ are the maximal and minimal speeds in the free-flow phase, respectively, $W_{\rm c}^+$ and $W_{\rm c}^-$ are the maximal and minimal Lagrangian markers in the congested phase, respectively, so that $1/R_{\rm c}^+$ and $1/R_{\rm c}^-$ are the minimal and maximal length of a vehicle, respectively.

Finally, denoted by $V_{\rm c} \in (0, V_{\rm f}^-)$ the maximal velocity in the congested phase, we can define the free-flow and congested domains

respectively. Observe that $\Omega_{\rm f}$ and $\Omega_{\rm c}$ are invariant domains for the LWR and the ARZ models, respectively. Let us also introduce

Clearly, $Q_{\rm c}^-$ is the flow of the state in $\Omega_{\rm c}$ with lowest density, $Q_{\rm c}^+$ is the maximal flow in $\Omega_{\rm c}$ and $Q_{\rm f}$ is the maximal flow in $\Omega_{\rm f}$ (hence in $\Omega$).

2.2.   The phase transition model and its main properties

The traffic is governed by the PT model [9,32]

where the flux map $Q \colon \Omega \to [0,Q_{\rm f}]$ and the Lagrangian marker map $W \colon \Omega \to [W_{\rm c}^-,W_{\rm c}^+]$ (extended to $\Omega_{\rm f}$) are defined by

with

In the following table we collect the informations on the system governing the congested phase:

Above $r_i$ is the $i$-th right eigenvector, $\lambda_i$ is the corresponding eigenvalue and the graph of the map $\mathcal{L}_i(\,\cdot\,;u_0)$ gives the $i$-Lax curve passing through $u_0$. By the assumptions (H1) and (H2) the characteristic speeds are bounded by the velocity, i.e. $\lambda_{\rm f}(u) \le v$ and $\lambda_1(u) \leq \lambda_2(u) = v$, $\lambda_1$ is genuinely non-linear, i.e. $\nabla\lambda_1 \cdot r_1(u) \neq0$, and $\lambda_2$ is linearly degenerate, i.e. $\nabla\lambda_2 \cdot r_2(u) =0$.

In the subsequent definitions of the Riemann solvers we make use of the functions

defined as follows

These maps have a clear geometrical interpretation; indeed, roughly speaking, $u_{\rm c}(w)$ and $u_{\rm f}(w)$ are the intersections of the 1-Lax curve $\{u \in \Omega\colon W(u) = w\}$ with the line $\{u \in \Omega\colon v= V_{\rm c}\}$ and with $\Omega_{\rm f}$, respectively. Obviously $R_{\rm f}^\pm = \rho_{\rm f}(W_{\rm c}^\pm)$.

3.   The Riemann solvers

In this section we propose two Riemann solvers ${\mathcal{R}_1}$, ${\mathcal{R}_2}$ for the Riemann problem of the PT model (1), namely for the Cauchy problem of (1) with an initial datum of the form

where $u_\ell,u_r \in \Omega$ are given constants. We then construct two constrained Riemann solvers ${\mathcal{R}_1^{\rm c}}$, ${\mathcal{R}_2^{\rm c}}$ for the Riemann problem (1), (3) coupled with a pointwise constraint on the flux

where $Q_0 \in (0,Q_{\rm f})$ is a fixed constant.

For notational simplicity we let

Furthermore, for any $u_-,u_+ \in \Omega$ with $\rho_-\neq\rho_+$ we let

to be the speed of propagation of any discontinuity between $u_-$ and $u_+$. Observe that the first Rankine-Hugoniot condition (RH) is satisfied with $s=\sigma(u_-,u_+)$, therefore the number of vehicles is conserved across any discontinuity.

In the following we denote by $\mathcal{R}_{\rm LWR}$ and $\mathcal{R}_{\rm ARZ}$ the Riemann solvers for LWR and ARZ models, respectively.

3.1.   The Riemann solvers $\mathcal{R}_1$ and $\mathcal{R}_1^{\rm c}$

In this subsection we first recall the Riemann solver for (1), (3) introduced in [9], here denoted by $\mathcal{R}_1$, and then construct the corresponding constrained Riemann solver $\mathcal{R}^{\rm c}_1$ for (1), (3), (4).

Definition 3.1. The Riemann solver $\mathcal{R}_1 \colon \Omega^2 \to \mathbf{L}^\infty({\mathbb{R}};\Omega)$ is defined as follows:

(R₁.a) If $u_\ell, u_r \in \Omega_{\rm f}$, then $\mathcal{R}_1[u_\ell,u_r] \doteq\mathcal{R}_{\rm LWR}[u_\ell,u_r]$.

(R₁.b) If $u_\ell, u_r \in \Omega_{\rm c}$, then $\mathcal{R}_1[u_\ell,u_r] \doteq\mathcal{R}_{\rm ARZ}[u_\ell,u_r]$.

(R₁.c) If $(u_\ell, u_r) \in \Omega_{\rm f} \times \Omega_{\rm c}$, then we let $u_m \doteq (p^{-1}(w_\ell - v_r), v_r) \in \Omega_{\rm c}$ and

(R₁.d) If $(u_\ell, u_r) \in \Omega_{\rm c} \times \Omega_{\rm f}$, then

In general, $[(t,x) \mapsto \mathcal{R}_1[u_\ell,u_r](x/t)]$ does not satisfy the point constraint (4). For this reason we introduce the sets

and for any $(u_\ell,u_r) \in \mathcal{N}_1$, we replace the self-similar weak solution $[(t,x) \mapsto \mathcal{R}_1[u_\ell,u_r](x/t)]$ by a self-similar map $[(t,x) \mapsto \mathcal{R}_1^{\rm c}[u_\ell,u_r](x/t)]$ satisfying (3), (4) and obtained by juxtaposing maps constructed by means of $\mathcal{R}_1$. It is easy to see that

where

and

Definition 3.2. The constrained Riemann solver ${\mathcal{R}_1^{\rm c}} \colon \Omega^2 \to \mathbf{L}^\infty({\mathbb{R}};\Omega)$ is defined as follows:

(R₁^ca) If $(u_\ell,u_r) \in \mathcal{C}_1$, then we let ${\mathcal{R}_1^{\rm c}}[u_\ell,u_r] \doteq \mathcal{R}_1[u_\ell,u_r]$.

(R₁^cb) If $(u_\ell,u_r) \in \mathcal{N}_1$, then we let

where $\hat{u}_1 = \hat{u}_1(w_\ell,Q_0) \in \Omega_{\rm c}$ and $\check{u}_1 = \check{u}_1(w_\ell,v_r,Q_0) \in \Omega$ satisfy

Observe that according to the second condition in (8) we have that $\check{u}_1 \in \Omega_{\rm c}$ if and only if $u_r \in \Omega_{\rm c}$ and $Q_0 \ge p^{-1}(W_{\rm c}^- - v_r) \, v_r$, otherwise $\check{u}_1 \in \Omega_{\rm f}$.

In the following proposition we show that ${\mathcal{R}_1^{\rm c}}$ is well defined, namely that for any $(u_\ell,u_r) \in \mathcal{N}_1$ there exists a unique couple in $(\hat{u}_1,\check{u}_1)$ in $\Omega^2$ satisfying (7), (8). For notational simplicity we let

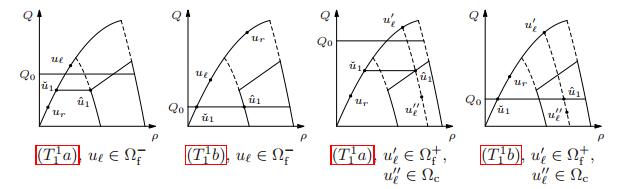
Proposition 1. For any $(u_\ell,u_r) \in \mathcal{N}_1$, we have that $(\hat{u}_1, \check{u}_1) \in \Omega_{\rm c} \times \Omega$ is uniquely selected by (7), (8) as follows:

(T₁¹) If $(u_\ell, u_r) \in \mathcal{N}^{\rm f,f} \cup \mathcal{N}^{\rm c,f}$, then we distinguish the following cases:

(T₁¹a) If $Q_0 > Q(u_{\rm c}(w_\ell))$, then $\hat{u}_1 = u_{\rm c}(w_\ell)$, $\check{q}_1 = \hat{q}_1$ and $\check{u}_1 \in \Omega_{\rm f}$.

(T₁¹b) If $Q_0 \le Q(u_{\rm c}(w_\ell))$, then $\hat{w}_1 = w_\ell$, $\hat{q}_1 = \check{q}_1 = Q_0$ and $\check{u}_1 \in \Omega_{\rm f}$.

(T₁²) If $(u_\ell, u_r) \in \mathcal{N}^{\rm c,c} \cup \mathcal{N}_1^{\rm f,c}$, then we distinguish the following cases:

(T₁²a) If $Q_0 \ge p^{-1}(W_{\rm c}^- - v_r) \, v_r$, then $\hat{w}_1 = w_\ell$, $\hat{q}_1 = \check{q}_1 = Q_0$ and $\check{v} = v_r$.

(T₁²b) If $Q_0 < p^{-1}(W_{\rm c}^- - v_r) \, v_r$, then $\hat{w}_1 = w_\ell$, $\hat{q}_1 = \check{q}_1 = Q_0$ and $\check{u}_1 \in \Omega_{\rm f}^-$.

In particular, ${\mathcal{R}_1^{\rm c}}$ is well defined in $\Omega^2$.

The proof of the above proposition is straightforward and is therefore omitted, see Figure 2 and Figure 3. Let us just underline that if $(u_\ell,u_r) \in \mathcal{N}_1$, then $\hat{u}_1$ and $\check{u}_1$ must be distinct otherwise, by the consistency of $\mathcal{R}_1$ proved in [9,Proposition 4.2], we would have that $\mathcal{R}_1^{\rm c}[u_\ell,u_r]$ coincides with $\mathcal{R}_1[u_\ell,u_r]$, and this gives a contradiction. Moreover, if $(u_\ell,u_r) \in \mathcal{N}_1$, then (7), (8) imply that $\mathcal{R}_1[u_\ell,\hat{u}_1]$ contains only waves with negative speeds and $\mathcal{R}_1[\check{u}_1,u_r]$ contains only waves with positive speeds; consequently ${\mathcal{R}_1^{\rm c}}[u_\ell,u_r](0^-) = \hat{u}_1$, ${\mathcal{R}_1^{\rm c}}[u_\ell,u_r](0^+) = \check{u}_1$ and $[(t,x) \mapsto \mathcal{R}_1^{\rm c}[u_\ell,u_r](x/t)]$ satisfies (4) because $Q(\check{u}_1) = Q(\hat{u}_1) \le Q_0$.

3.2.   The Riemann solvers $\mathcal{R}_2$ and $\mathcal{R}_2^{\rm c}$

Differently from any other constrained Riemann solver available in the literature, see [1,3,4,19,24,25,26], it may well happen that $(u_\ell,u_r) \in \mathcal{N}_1$ but $Q({\mathcal{R}_1^{\rm c}}[u_\ell,u_r](0^\pm)) \neq Q_0$, see the case (T₁¹a) described in Proposition 1. Moreover, for any fixed $(u_\ell,u_r) \in \mathcal{N}_1$, among the self-similar maps $u$ of the form (6), namely

with $(\hat{u},\check{u}) \in \Omega^2$ eventually distinct from $(\hat{u}_1,\check{u}_1)$ but satisfying the minimal requirements

$\mathcal{R}_1^{\rm c}[u_\ell,u_r]$ is the only one that maximizes the flow through ${x=0}$, namely

with the equality holding if and only if $u = \mathcal{R}_1^{\rm c}[u_\ell,u_r]$. For these reasons in this subsection we introduce a further Riemann solver $\mathcal{R}_2$ for (1), (3), that allows to construct a second constrained Riemann solver ${\mathcal{R}^{\rm c}_2}$ for (1), (3), (4) such that $Q({\mathcal{R}_2^{\rm c}}[u_\ell,u_r](0^\pm)) = Q_0$ for all $(u_\ell,u_r) \in \mathcal{N}_1$, at least in the case $Q_0 \leq Q_{\rm c}^+$.

Definition 3.3. The Riemann solver $\mathcal{R}_2 \colon \Omega^2 \to \mathbf{L_{\rm{loc}}^1}({\mathbb{R}};\Omega)$ is defined by letting

for any $(u_\ell,u_r) \in \Omega_{\rm f} \times \Omega_{\rm c}$ with $\rho_\ell \ne 0$ and $w_\ell < w_r$, and by letting $\mathcal{R}_2[u_\ell,u_r] \doteq \mathcal{R}_1[u_\ell,u_r]$ in all the remaining cases.

In analogy to the previous subsection we introduce the sets

and for any $(u_\ell,u_r) \in \mathcal{N}_2$, we replace $[(t,x) \mapsto \mathcal{R}_2[u_\ell,u_r](x/t)]$ by a self-similar map $[(t,x) \mapsto \mathcal{R}_2^{\rm c}[u_\ell,u_r](x/t)]$ satisfying (3), (4) and obtained by juxtaposing maps constructed by means of $\mathcal{R}_2$. It is easy to see that

where

Definition 3.4. The Riemann solver ${\mathcal{R}^{\rm c}_2} \colon \Omega^2 \to \mathbf{L}^\infty({\mathbb{R}};\Omega)$ is defined as follows:

(R₂a) If $(u_\ell,u_r) \in \mathcal{C}_2$, then we let ${\mathcal{R}^{\rm c}_2}[u_\ell,u_r] \doteq \mathcal{R}_2[u_\ell,u_r]$.

(R₂b) If $(u_\ell,u_r) \in \mathcal{N}^{\rm c,f}$ and $Q_0 > Q(u_{\rm c}(w_\ell))$, then we let

(R₂c) If $(u_\ell,u_r) \in \mathcal{N}^{\rm c,f}$ and $Q_0 \le Q(u_{\rm c}(w_\ell))$ or $(u_\ell,u_r) \in \mathcal{N}_2 \setminus \mathcal{N}^{\rm c,f}$, then we let

In both cases (R₂b) and (R₂c), $\hat{u}_2 = \hat{u}_2(w_\ell,v_r,Q_0)$ and $\check{u}_2 = \check{u}_2(v_r,Q_0)$ are implicitly defined by

Observe that according to the second condition in (10) we have that $\check{u}_2 \in \Omega_{\rm c}$ if and only if $u_r \in \Omega_{\rm c}$ and $Q_0 \ge p^{-1}(W_{\rm c}^- - v_r) \, v_r$, otherwise $\check{u}_2 \in \Omega_{\rm f}$.

In the following proposition we show that ${\mathcal{R}^{\rm c}_2}$ is well defined. For notational simplicity we let

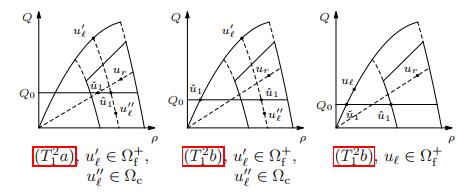
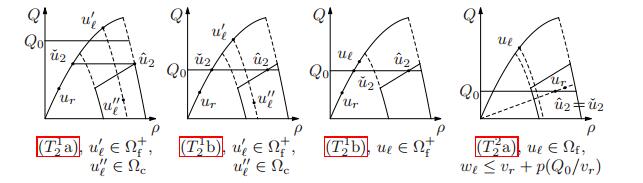
Proposition 2. For any $(u_\ell,u_r) \in \mathcal{N}_2$, $(\hat{u}_2, \check{u}_2) \in \Omega_{\rm c} \times \Omega$ is uniquely selected by (9), (10) as follows:

(T₂¹) If $(u_\ell, u_r) \in \mathcal{N}^{\rm f,f} \cup \mathcal{N}^{\rm c,f}$, then we distinguish the following cases:

(T₂¹a) If $Q_0 > Q_{\rm c}^+$, then $\hat{q}_2 = \check{q}_2 = Q_{\rm c}^+$ and $\check{u}_2 \in \Omega_{\rm f}$.

(T₂¹b) If $Q_0 \leq Q_{\rm c}^+$, then $\hat{w}_2 = \max\left \{w_\ell, V_{\rm c}+p\left (Q_0/V_{\rm c}\right )\right \}$, $\hat{q}_2 = \check{q}_2 = Q_0$ and $\check{u}_2 \in \Omega_{\rm f}$.

(T₂²) If $(u_\ell, u_r) \in \mathcal{N}^{\rm c,c} \cup \mathcal{N}_2^{\rm f,c}$, then we distinguish the following cases:

(T₂²a) If $Q_0 \ge p^{-1}(W_{\rm c}^- - v_r) \, v_r$, then $\hat{w}_2 = \max\{w_\ell,v_r+p(Q_0/v_r)\}$, $\hat{q}_2 = \check{q}_2 = Q_0$ and $\check{v} = v_r$.

(T₂²b) If $Q_0 < p^{-1}(W_{\rm c}^- - v_r) \, v_r$, then $\hat{w}_2 = w_\ell$, $\hat{q}_2 = \check{q}_2 = Q_0$ and $\check{u}_2 \in \Omega_{\rm f}^-$.

In particular, ${\mathcal{R}_2^{\rm c}}$ is well defined in $\Omega^2$.

The proof of the above proposition is straightforward and is therefore omitted, see Figure 4. Let us just underline that, despite (T₂²a) and (T₂²b) are apparently the same as (T₁²a) and (T₁²b), respectively, they differ because $\mathcal{N}_1^{\rm f,c} \ne \mathcal{N}_2^{\rm f,c}$ as shown in the following Example 1. Let us also underline that $\hat{u}_1 \ne \check{u}_1$ for all $(u_\ell,u_r) \in \mathcal{N}_1$, whereas in the case (T₂²a) with $w_\ell \le v_r + p(Q_0/v_r)$ we have $\hat{u}_2 = \check{u}_2$, see the last picture in Figure 4; this occurs because $\mathcal{R}_1$ is consistent whereas $\mathcal{R}_2$ is not, see Proposition 5. Clearly the map $[(t,x) \mapsto \mathcal{R}_2^{\rm c}[u_\ell,u_r](x/t)]$ satisfies (4).

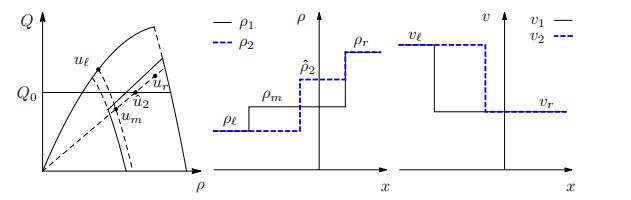
Example 1. Fix $(u_\ell,u_r) \in \Omega_{\rm f}^+ \times \Omega_{\rm c}$ with $w_\ell<w_r$ and $p^{-1}(w_\ell-v_r) \, v_r < Q_0 < q_r < q_\ell$, see Figure 5. In this case $Q(\mathcal{R}_1[u_\ell,u_r](0)) = Q(u_m) < Q_0$, where $u_m \doteq (p^{-1}(w_\ell-v_r) , v_r)$, and therefore $(u_\ell,u_r) \in \mathcal{C}_1^{\rm f,c}$. As a consequence $\mathcal{R}_1^{\rm c}[u_\ell,u_r]$ coincides with $\mathcal{R}_1[u_\ell,u_r]$ and performs a phase transition from $u_\ell$ to $u_m$, followed by a contact discontinuity from $u_m$ to $u_r$. On the other hand, $Q(\mathcal{R}_2[u_\ell,u_r](0^\pm)) = q_r > Q_0$ and therefore $(u_\ell,u_r) \in \mathcal{N}_2^{\rm f,c}$. By (T₂²a) we have that $\hat{u}_2 = \check{u}_2 = (p^{-1}(Q_0/v_r),v_r)$. Hence $\mathcal{R}_2^{\rm c}[u_\ell,u_r]$ performs a phase transition from $u_\ell$ to $\hat{u}_2$, followed by a contact discontinuity from $\hat{u}_2$ to $u_r$.

4.   Main properties of the Riemann solvers

In this section we expose the main properties of the Riemann solvers constructed in the previous sections. This study may be useful to compare the difficulty of applying one of these Riemann solvers in a wave-front tracking scheme [11,34]. In particular, we introduce their invariant domains and discuss their consistency and $\mathbf{L_{\rm{loc}}^1}$-continuity. In this regard, we recall the following definition.

Definition 4.1. Let $\mathcal{S} \colon \Omega^2 \to \mathbf{L}^\infty({\mathbb{R}};\Omega)$ be a Riemann solver.

● $\mathcal{I} \subseteq \Omega$ is an invariant domain for $\mathcal{S}$ if $\mathcal{S}[\mathcal{I},\mathcal{I}](\mathbb{R}) \subseteq \mathcal{I}$.

● $\mathcal{S}$ is $\mathbf{L_{\rm{loc}}^1}$-continuous in $\mathcal{D} \subseteq \Omega$ if for any $\nu_1, \nu_2 \in \mathbb{R}$ and for any sequences $u_\ell^n, u_r^n \subset \mathcal{D}$ converging to $u_\ell, u_r \in \mathcal{D}$:

● $\mathcal{S}$ is consistent in an invariant domain $\mathcal{I} \subseteq \Omega$ if for any $u_\ell, u_m, u_r \in \mathcal{I}$ and $\underline{\nu} \in {\mathbb{R}}$:

We recall that the consistency is a necessary condition for the well-posedness in $\mathbf{L^1}$ of the Cauchy problem.

In the following proposition we show that a constrained Riemann solver cannot be consistent in $\Omega$ because it cannot satisfy (Ⅰ) of Definition 4.1 in $\Omega$. As a consequence, none of the constrained Riemann solvers $\mathcal{R}_1^{\rm c}$ and $\mathcal{R}_2^{\rm c}$ is consistent in $\Omega$ and in the forthcoming propositions we consider in $\Omega$ only (Ⅱ).

Proposition 3. Let $\mathcal{S} \colon \Omega^2 \to \mathbf{L}^\infty({\mathbb{R}};\Omega)$ be a Riemann solver satisfying (4). If $\mathcal{I}$ is an invariant domain for $\mathcal{S}$ and $Q_0 < \max_{u\in \mathcal{I}}Q(u)$, then $\mathcal{S}$ does not satisfy (Ⅰ) of Definition 4.1 in $\mathcal{I}$.

Proof. By assumption there exist $u_\ell, u_r \in \mathcal{I}$ such that $q_r >Q_0$. By the finite speed of propagation of the waves there exists $\underline{\nu} >0$ such that $\mathcal{S}[u_\ell,u_r](\underline{\nu}) = u_r$. Let $u_m \doteq u_r$. Then the property $\mathcal{S}[u_m,u_r](\nu) = u_m$ for any $\nu < \underline{\nu}$ required in (Ⅰ) cannot be satisfied. Indeed, if by contradiction $\mathcal{S}[u_m,u_r](\nu) = u_m$ for any $\nu < \underline{\nu}$, then $Q(\mathcal{S}[u_m,u_r](0^\pm)) = q_r > Q_0$ and this gives a contradiction because by assumption $(t,x) \mapsto \mathcal{S}[u_m,u_r](x/t)$ satisfies (4).

4.1.   Main properties of ${\mathcal{R}_1}$ and ${\mathcal{R}_2}$

In the following propositions we collect the main properties of ${\mathcal{R}_1}$ and ${\mathcal{R}_2}$.

Proposition 4 (Invariant domains). For any $\rho_{\min}, \rho_{\max} \in [0, R_{\rm f}^+]$, $v_{\min} , v_{\max} \in [0, V_{\rm c}]$ and $w_{\min} , w_{\max} \in [W_{\rm c}^- , W_{\rm c}^+]$ such that $\rho_{\min} < \rho_{\max}$, $v_{\min} < v_{\max}$ and $w_{\min} < w_{\max}$, we have that

are invariant domains for both $\mathcal{R}_1$ and $\mathcal{R}_2$. If moreover $\rho_{\min}<R_{\rm f}^-$, then

is a further invariant domain for both $\mathcal{R}_1$ and $\mathcal{R}_2$.

The proof is straightforward and is therefore omitted.

Proposition 5. $\mathcal{R}_1$ is $\mathbf{L_{\rm{loc}}^1}$-continuous and consistent in $\Omega$; whereas $\mathcal{R}_2$ is $\mathbf{L_{\rm{loc}}^1}$-continuous but not consistent in $\Omega$.

Proof. In [9,Proposition 4.2] we already proved that $\mathcal{R}_1$ is $\mathbf{L_{\rm{loc}}^1}$-continuous and consistent. By taking $u_\ell,\ u_m$ and $u_r$ as in the Example 1, see Figure 5, we have that $\mathcal{R}_2$ does not satisfy (Ⅱ) of Definition 4.1, hence it is not consistent. Finally proceeding as in [9,Proposition 4.2] it can be proved that $\mathcal{R}_2$ is $\mathbf{L_{\rm{loc}}^1}$-continuous.

4.2.   Main properties of ${\mathcal{R}_1^{\rm c}}$

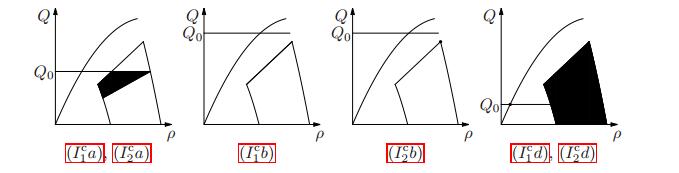
In the following propositions we collect the main properties of ${\mathcal{R}_1^{\rm c}}$. We start by studying the invariant domains of ${\mathcal{R}_1^{\rm c}}$, see Figure 6. Clearly, $\Omega$ is an invariant domain for both ${\mathcal{R}_1}$ and ${\mathcal{R}_1^{\rm c}}$. Moreover, $\Omega_{\rm f}$ and $\Omega_{\rm c}$ are invariant domains for ${\mathcal{R}_1}$ but not for ${\mathcal{R}_1^{\rm c}}$. For this reason we look for minimal (with respect to the inclusion) invariant domains for ${\mathcal{R}_1^{\rm c}}$ containing $\Omega_{\rm f}$ or $\Omega_{\rm c}$.

Proposition 6 (Invariant domains of ${\mathcal{R}_1^{\rm c}}$).

(I₁^ca) If $Q_0 < Q_{\rm c}^+$, then $\Omega_{\rm f} \cup \{u \in \Omega_{\rm c} \colon Q(u) \leq Q_0 \le p^{-1}(W_{\rm c}^+-v) \, v \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_1}$ containing $\Omega_{\rm f}$.

(I₁^cb) If $Q_0 \ge Q_{\rm c}^+$, then $\Omega_{\rm f} \cup \{ u \in \Omega_{\rm c} \colon v = V_{\rm c} \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_1}$ containing $\Omega_{\rm f}$.

(I₁^cc) If $Q_0 \geq Q_{\rm c}^-$, then $\Omega_{\rm c}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_1}$ containing $\Omega_{\rm c}$.

(I₁^cd) If $Q_0 < Q_{\rm c}^-$, then $\Omega_{\rm c} \cup \{ u \in \Omega_{\rm f}^- \colon Q(u) = Q_0 \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_1}$ containing $\Omega_{\rm c}$.

Proof. (I₁^ca) In order to prove that if $Q_0 < Q_{\rm c}^+$, then the smallest invariant domain containing $\Omega_{\rm f}$ is $\mathcal{I}_0 \doteq \Omega_{\rm f} \cup \{u \in \Omega_{\rm c} \colon Q(u) \leq Q_0 \le p^{-1}(W_{\rm c}^+-v) \, v \}$ it suffices to observe that $\mathcal{I}_0$ is an invariant domain and that if $\mathcal{I}$ is an invariant domain containing $\Omega_{\rm f}$, then

where the last inclusion holds because

(I₁^cb) In order to prove that if $Q_0 \ge Q_{\rm c}^+$, then the smallest invariant domain containing $\Omega_{\rm f}$ is $\mathcal{I}_0 \doteq \Omega_{\rm f} \cup \{ u \in \Omega_{\rm c} \colon v = V_{\rm c} \}$ it suffices to observe that $\mathcal{I}_0$ is an invariant domain and that if $\mathcal{I}$ is an invariant domain containing $\Omega_{\rm f}$, then

where the last inclusion holds because

(I₁^cc) In order to prove that if $Q_0 \geq Q_{\rm c}^-$, then the smallest invariant domain containing $\Omega_{\rm c}$ is $\Omega_{\rm c}$ it suffices to prove that $\Omega_{\rm c}$ is an invariant domain. Since $\Omega_{\rm c}$ is an invariant domain for $\mathcal{R}_{\rm ARZ}$ we immediately have that ${\mathcal{R}_1^{\rm c}}[\mathcal{C}^{\rm c,c}]({\mathbb{R}}) = \mathcal{R}_{\rm ARZ}[\mathcal{C}^{\rm c,c}]({\mathbb{R}}) \subseteq \Omega_{\rm c}$. Moreover, if $(u_\ell,u_r) \in \mathcal{N}^{\rm c,c}$, then $\hat{u}_1, \check{u}_1 \in \Omega_{\rm c}$ because $Q_0 \geq Q_{\rm c}^- \ge p^{-1}(W_{\rm c}^-v_r) \, v_r$, see (T₁²a). As a consequence ${\mathcal{R}_1^{\rm c}}[u_\ell,u_r]({\mathbb{R}}) = \mathcal{R}_{\rm ARZ}[u_\ell,\hat{u}]({\mathbb{R}}) \cup \mathcal{R}_{\rm ARZ}[\check{u},u_r]({\mathbb{R}}) \subseteq \Omega_{\rm c}$.

(I₁^cd) In order to prove that if $Q_0 < Q_{\rm c}^-$, then the smallest invariant domain containing $\Omega_{\rm c}$ is $\mathcal{I}_0 \doteq \Omega_{\rm c} \cup \{ u_0 \}$, where $u_0$ is the unique element of $\{ u \in \Omega_{\rm f}^- \colon Q(u) = Q_0 \}$, it suffices to observe that $\mathcal{I}_0$ is an invariant domain and that if $\mathcal{I}$ is an invariant domain containing $\Omega_{\rm c}$, then $\mathcal{I} \supseteq {\mathcal{R}_1^{\rm c}}[\mathcal{N}^{\rm c,c}]({\mathbb{R}}) \supseteq \{u_0\}$, where the last inclusion holds because by (T₁²) we have that for any $(u_\ell, u_r) \in \mathcal{N}^{\rm c,c}$ either $\check{u}_1 \in \Omega_{\rm c}$ or $\check{u}_1 = u_0$.

Proposition 7 (Consistency of ${\mathcal{R}_1^{\rm c}}$).

(C₁^ca) ${\mathcal{R}_1^{\rm c}}$ satisfies (Ⅱ) of Definition 4.1 in $\Omega$.

(C₁^cb) ${\mathcal{R}_1^{\rm c}}$ is consistent in the invariant domain $\mathcal{I}_1 \doteq \{u \in \Omega \colon Q(u) \leq Q_0 \}$; moreover it is not consistent in any other invariant domain containing $\mathcal{I}_1$.

Proof. (C₁^ca) Since ${\mathcal{R}_1}$ satisfies (Ⅱ), it suffices to consider the cases where at least one among $(u_\ell,u_m)$, $(u_m,u_r)$ and $(u_\ell,u_r)$ belongs to $\mathcal{N}_1$. We observe that ${\mathcal{R}^{\rm c}_1}[u_\ell,u_m]$ cannot perform any contact discontinuity, otherwise it would not be possible to juxtapose ${\mathcal{R}^{\rm c}_1}[u_\ell,u_m]$ and ${\mathcal{R}^{\rm c}_1}[u_m,u_r]$. For the same reason $(u_\ell,u_m)$ cannot belong to $\mathcal{C}^{\rm f,f}$. Moreover, $(u_\ell,u_m)$ cannot belong to $\mathcal{C}^{\rm c,f}$, because in this case ${\mathcal{R}^{\rm c}_1}[u_\ell,u_m]$ and ${\mathcal{R}^{\rm c}_1}[u_m,u_r]$ can be juxtaposed if and only if $u_m = u_{\rm f}(w_\ell) \in \Omega_{\rm f}^+$ (hence $Q(u_m) \le Q_0$ because $(u_\ell,u_m) \in \mathcal{C}^{\rm c,f}$) and $u_r \in \Omega_{\rm f}$, but then also $(u_\ell,u_r)$ and $(u_m,u_r)$ belong to $\mathcal{C}_1$. We are then left to consider the following cases.

● Let $(u_\ell,u_m) \in \mathcal{N}^{\rm f,f}$ and $u_m = \check{u}_1(w_\ell,v_m,Q_0)$, namely $q_\ell > Q_0 \ge Q(u_m)$. We have then that either $u_r \in \Omega_{\rm c}$ and $p^{-1}(W_{\rm c}^- - v_r) \, v_r > Q_0$ or $u_r \in \Omega_{\rm f}$.

● Let $u_\ell, u_m \in \Omega_{\rm c}$. In this case, we have either $(u_\ell,u_m) \in \mathcal{N}^{\rm c,c}$ or $(u_\ell,u_m) \in \mathcal{C}^{\rm c,c}$ and $w_\ell = W(u_m)$. In the first case, whether $u_m = \check{u}_1(w_\ell,v_m,Q_0) \in \Omega_{\rm c}$ and $W(u_m) < w_\ell$ or $\check{u}_1(w_\ell,v_m,Q_0) \in \Omega_{\rm f}$ and $Q(u_m) > Q_0$, we have that $v_r = v_m$. In the latter case, we have $Q(u_m) = Q_0$, $v_r > v_m$ and $(u_m,u_r) \in \mathcal{N}^{\rm c,f} \cup \mathcal{N}^{\rm c,c}$.

● Let $(u_\ell,u_m) \in \mathcal{N}^{\rm c,f}$ and $u_m=\check{u}_1(w_\ell,v_m,Q_0)$. Then either $u_r \in \Omega_{\rm c}$ satisfies $p^{-1}(W_{\rm c}^- - v_r) \, v_r > Q_0$ or $u_r \in \Omega_{\rm f}$.

● Let $(u_\ell,u_m) \in \Omega_{\rm f}^- \times \Omega_{\rm c}$. In this case, we have $W(u_m) = W_{\rm c}^-$ and either $Q(u_m) = Q_0 < q_\ell$ and $v_r > v_m$ or $Q(u_m) > Q_0$ and $v_r = v_m$.

● Let $(u_\ell,u_m) \in \Omega_{\rm f}^+ \times \Omega_{\rm c}$. In this case, we have $Q(u_m) = Q_0 < q_\ell$ and either $\hat{v}_1(u_\ell,Q_0) < v_m = v_r$ or $\hat{v}_1(u_\ell,Q_0) = v_m \le v_r$.

For each of the above cases it is easy to conclude.

(C₁^cb) By (C₁^ca) it is sufficient to prove that ${\mathcal{R}_1^{\rm c}}$ satisfies (Ⅰ) in $\mathcal{I}_1$. Fix $u_\ell, u_m, u_r \in \mathcal{I}_1$ and $\underline{\nu} \in {\mathbb{R}}$ such that ${\mathcal{R}_1^{\rm c}}[u_\ell,u_r](\underline{\nu}) = u_m$. If $(u_\ell,u_r) \in \mathcal{C}_1 \cap \mathcal{I}_1^2$, then also $(u_\ell,u_m), (u_m,u_r) \in \mathcal{C}_1$ and (Ⅰ) comes from the consistency of $\mathcal{R}_1$. On the other hand, if $(u_\ell,u_r) \in \mathcal{N}_1 \cap \mathcal{I}_1^2 \subseteq \mathcal{N}^{\rm c,c} \cup \mathcal{N}^{\rm c,f}$ and $\underline{\nu} \leq 0$ (the case $\underline{\nu} \geq 0$ is analogous), then $ u_m = {\mathcal{R}_1^{\rm c}}[u_\ell,u_r](\underline{\nu}) = \mathcal{R}_1[u_\ell,\hat{u}_1(w_\ell, Q_0)](\underline{\nu})$, $W(u_m) = w_\ell$ and by exploiting the consistency of $\mathcal{R}_1$ we have

and

We conclude the proof by observing that the maximality of $\mathcal{I}_1$ follows directly from Proposition 3.

Proposition 8 (Continuity of ${\mathcal{R}_1^{\rm c}}$).

(L₁^ca) $\mathcal{R}_1^{\rm c}$ is $\mathbf{L_{\rm{loc}}^1}$-continuous in $\Omega^2$ if and only if $Q_0 \le Q_{\rm c}^-$.

(L₁^cb) If $Q_0 > Q_{\rm c}^-$, then $\mathcal{R}_1^{\rm c}$ is $\mathbf{L_{\rm{loc}}^1}$-continuous in $\Omega^2 \setminus(\mathcal{C}_1 \cap \overline{\mathcal{N}^{\rm f,f}})$ and is not $\mathbf{L_{\rm{loc}}^1}$-continuous in any point of $\mathcal{C}_1 \cap \overline{\mathcal{N}^{\rm f,f}}$.

Proof. Assume that $Q_0 > Q_{\rm c}^-$ and take $(u_\ell,u_r) \in \mathcal{C}_1 \cap \overline{\mathcal{N}^{\rm f,f}}$, namely $u_\ell,u_r \in \Omega_{\rm f}$ with $Q(u_\ell) = Q_0$. Let $u_\ell^n \in \Omega_{\rm f}$ with $Q(u_\ell^n) = Q_0+1/n$. Then $u_\ell^n$ converges to $u_\ell$ but $\mathcal{R}_1^{\rm c}[u_\ell^n,u_r]$ does not converge to $\mathcal{R}_1^{\rm c}[u_\ell,u_r]$ in $\mathbf{L_{\rm{loc}}^1}({\mathbb{R}};\Omega)$. Indeed, $\mathcal{R}_1^{\rm c}[u_\ell,u_r] \equiv u_\ell$ in ${\mathbb{R}}_-$ and by (T₁¹a) the restriction of $\mathcal{R}_1^{\rm c}[u_\ell^n,u_r]$ to ${\mathbb{R}}_-$ converges to

It remains to prove that if $Q_0 > Q_{\rm c}^-$ and $(u_\ell,u_r) \in \Omega^2 \setminus (\mathcal{C}_1 \cap \overline{\mathcal{N}^{\rm f,f}})$ or $Q_0 \le Q_{\rm c}^-$ and $(u_\ell,u_r) \in \Omega^2$, then $\mathcal{R}_1^{\rm c}[u_\ell^n,u_r^n]$ converges to $\mathcal{R}_1^{\rm c}[u_\ell,u_r]$ in $\mathbf{L_{\rm{loc}}^1}({\mathbb{R}};\Omega)$ for all $(u_\ell^n,u_r^n) \in \Omega^2$ converging to $(u_\ell,u_r)$. Since we already know that $\mathcal{R}_1$ is $\mathbf{L_{\rm{loc}}^1}$-continuous in $\Omega^2$, we can assume that $(u_\ell^n,u_r^n) \in \mathcal{N}_1$. Thus, by Definition 3.2, completing the proof is a matter of showing that $\mathcal{R}_1[u^n_\ell,\hat{u}_1(w_\ell^n,Q_0)] \to \mathcal{R}_1^{\rm c}[u_\ell,u_r]$ pointwise in $\{x<0\}$, $\mathcal{R}_1[\check{u}_1(w_\ell^n,v^n_r,Q_0),u^n_r] \to \mathcal{R}_1^{\rm c}[u_\ell,u_r]$ pointwise in $\{x>0\}$, and applying the dominated convergence theorem of Lebesgue. For this, it suffices to observe that either $\hat{u}_1(w_\ell^n,Q_0) \to \mathcal{R}_1[u_\ell,u_r](0^-)$ and the result follows then by the $\mathbf{L_{\rm{loc}}^1}$-continuity of $\mathcal{R}_1$, or $\sigma(u^{n}_\ell, \hat{u}_1(w_\ell^n,Q_0)) \to 0$, $\mathcal{R}_1[u_\ell,u_r] \equiv u_\ell$ in $\{x <0\}$ and therefore $\mathcal{R}_1[u^n_\ell,\hat{u}_1(w_\ell^n,Q_0)] \to \mathcal{R}_1[u_\ell,u_r]$ pointwise in $\{x<0\}$. A similar analysis proves that $\mathcal{R}_1[\check{u}_1(w_\ell^n,v^n_r,Q_0),u^n_r] \to \mathcal{R}_1[u_\ell,u_r]$ pointwise in $\{x>0\}$.

4.3.   Main properties of ${\mathcal{R}^{\rm c}_2}$

The following proposition deals with the minimal invariant domains for ${\mathcal{R}^{\rm c}_2}$ containing $\Omega_{\rm f}$ or $\Omega_{\rm c}$, see Figure 6; its proof is analogous to that of Proposition 6 and is therefore omitted.

Proposition 9 (Invariant domains for ${\mathcal{R}^{\rm c}_2}$).

(I₂^ca) If $Q_0 < Q_{\rm c}^+$, then $\Omega_{\rm f} \cup \{u \in \Omega_{\rm c} \colon Q(u) \leq Q_0 \le p^{-1}(W_{\rm c}^+-v) \, v \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_2}$ containing $\Omega_{\rm f}$.

(I₂^cb) If $Q_{\rm c}^+ \leq Q_0$, then $\Omega_{\rm f} \cup \{ (V_{\rm c},W_{\rm c}^+) \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_2}$ containing $\Omega_{\rm f}$.

(I₂^cc) If $Q_0 \geq Q_{\rm c}^-$, then $\Omega_{\rm c}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_2}$ containing $\Omega_{\rm c}$.

(I₂^cd) If $Q_0 < Q_{\rm c}^-$, then $\Omega_{\rm c} \cup \{ u \in \Omega_{\rm f}^- \colon Q(u) = Q_0 \}$ is the smallest invariant domain for ${\mathcal{R}^{\rm c}_2}$ containing $\Omega_{\rm c}$.

Concerning ${\mathcal{R}^{\rm c}_2}$, in general no significant positive result for consistency can be expected because $\mathcal{R}_2$ is not consistent, see Proposition 5.

Proposition 10 (Consistency of ${\mathcal{R}_2^{\rm c}}$).

(C₂^ca) ${\mathcal{R}^{\rm c}_2}$ does not satisfy (Ⅱ) of Definition 4.1 in $\Omega$.

(C₂^cb) ${\mathcal{R}^{\rm c}_2}$ does not satisfy (Ⅱ) of Definition 4.1 in any invariant domain containing $\mathcal{I}_1 \doteq \{u \in \Omega \colon Q(u) \leq Q_0 \}$.

Proof. (C₂^ca) Clearly, (Ⅱ) is not satisfied by ${\mathcal{R}^{\rm c}_2}$ because we already know by Proposition 5 that it is not satisfied by ${\mathcal{R}_2}$.

(C₂^cb) It is easy to see that $\mathcal{I}_1$ is an invariant domain if and only if $Q_0 \le Q_{\rm c}^-$. In any case, by taking $\underline{\nu}<0$ sufficiently close to zero, $u_\ell$ as the unique element of $\{ u \in \Omega_{\rm f} \colon Q(u) = Q_0\}$ and $u_m, u_r \in \Omega_{\rm c}$ such that $v_m = 0 = v_r$, $W(u_m) = w_\ell$ and $w_r = W_{\rm c}^+$, we have that $u_\ell,u_m,u_r \in \mathcal{I}_1$ but $\mathcal{R}^{\rm c}_2$ does not satisfy (Ⅱ).

Proposition 11 (Continuity of ${\mathcal{R}_2^{\rm c}}$). ${\mathcal{R}^{\rm c}_2}$ is $\mathbf{L_{\rm{loc}}^1}$-continuous in $\Omega^2$.

Proof. ● If $u_\ell,u_r \in \Omega_{\rm f}$, then the $\mathbf{L_{\rm{loc}}^1}$-continuity of ${\mathcal{R}^{\rm c}_2}$ follows from the continuity of $\sigma(u_\ell,\hat{u})$, $\sigma(\check{u},u_r)$ with respect to $(u_\ell,u_r)$ and from the continuity of $\mathcal{R}_{\rm LWR}$.

● If $u_\ell,u_r \in \Omega_{\rm c}$ or $(u_\ell, u_r) \in \Omega_{\rm c} \times \Omega_{\rm f}$ and $Q(u_{\rm c}(w_\ell)) > Q_0$, then ${\mathcal{R}^{\rm c}_2}[u_\ell,u_r] = {\mathcal{R}_1^{\rm c}}[u_\ell,u_r]$ and the continuity follows from Proposition 8.

● If $(u_\ell, u_r) \in \Omega_{\rm c} \times \Omega_{\rm f}$ and $Q(u_{\rm c}(w_\ell)) < Q_0$, then the continuity follows from the continuity of $u_{\rm c}(w_\ell)$, $u_{\rm f}(w_\ell)$, $\sigma(u_{\rm f}(w_\ell), \hat{u})$ with respect to $u_\ell$ and Proposition 8.

● If $(u_\ell, u_r) \in \Omega_{\rm c} \times \Omega_{\rm f}$ and $Q(u_{\rm c}(w_\ell)) = Q_0$, then it suffices to consider for $n$ sufficiently large $u_\ell^n$ defined by $v_\ell^n \doteq v_\ell$ and $w_\ell^n \doteq w_\ell - 1/n$. Clearly $u_\ell^n \to u_\ell$ and $Q(u_{\rm c}(w_\ell^n)) < Q_0$. Moreover, ${\mathcal{R}^{\rm c}_2}[u_\ell^n,u_r]$ has two phase transitions, one from $u_{\rm c}(w_\ell^n)$ to $u_{\rm f}(w_\ell^n)$ and one from $u_{\rm f}(w_\ell^n)$ to $\hat{u}$, that are not performed by ${\mathcal{R}^{\rm c}_2}[u_\ell,u_r]$. Since both $\sigma(u_{\rm c}(w_\ell^n),u_{\rm f}(w_\ell^n))$ and $\sigma(u_{\rm f}(w_\ell^n), \hat{u})$ converge to $\sigma(u_{\rm f}(w_\ell), \hat{u})$, also in this case we have that ${\mathcal{R}^{\rm c}_2}[u_\ell^n, u_r] \to {\mathcal{R}^{\rm c}_2}[u_\ell, u_r]$ in $\mathbf{L_{\rm{loc}}^1}$.

● If $(u_\ell, u_r) \in \Omega_{\rm f} \times \Omega_{\rm c}$, then the continuity comes from the continuity of $\sigma(u_\ell,u_r)$, $\sigma(u_\ell,\hat{u})$, $\sigma(\check{u},u_r)$ and ${\mathcal{R}_1^{\rm c}}$ with respect to $(u_\ell,u_r)$.

4.4.   Total variation estimates

In this subsection we consider the total variation of the two constrained Riemann solvers in the Riemann invariant coordinates $(v,w)$. We provide two examples showing that in general the comparison of their total variations can go in both ways. This suggests that the total variation is not a relevant selection criteria for choosing a wave-front tracking algorithm based on one or the other constrained Riemann solver.

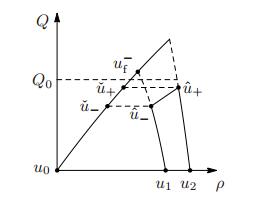
Example 2. With reference to Figure 7, let $Q_0 \in \bigl(Q_{\rm c}^-, Q_{\rm c}^+\bigr)$ and $u_0 \in \Omega_{\rm f}^+$ with $Q(u_0) \in ( Q_0, Q_{\rm f})$ be such that there exist $\check{u}_1, \check{u}_2 \in \Omega_{\rm f}$ and $\hat{u}_1, \hat{u}_2 \in \Omega_{\rm c}$ satisfying

Then ${\mathrm{TV}}(V \circ {\mathcal{R}_1^{\rm c}}[u_0,u_0])= 2[V(\check{u}_1) - V_{\rm c}] > {\mathrm{TV}}(V \circ {\mathcal{R}^{\rm c}_2}[u_0,u_0]) = 2[V(\check{u}_2) - V_{\rm c}]$. If we further assume that

then ${\mathrm{TV}}(W \circ {\mathcal{R}_1^{\rm c}}[u_0,u_0])= 2[W(u_0) - W(\check{u}_1)] > {\mathrm{TV}}(W \circ {\mathcal{R}^{\rm c}_2}[u_0,u_0]) = 2[W(\hat{u}_2) - W(\check{u}_2)]$.

Example 3. If there exist $(u_\ell , u_r) \in \Omega_{\rm c} \times \Omega_{\rm f}$ and $Q_0$ such that $v_\ell = V_{\rm c}$ and $q_\ell = q_r < Q_0 < Q(u_{\rm f}(w_\ell))$, then ${\mathrm{TV}}(V \circ {\mathcal{R}_1^{\rm c}}[u_\ell,u_r]) =$$ v_r - V_{\rm c}<{\mathrm{TV}}(V \circ {\mathcal{R}^{\rm c}_2}[u_\ell,u_r]) = $$v_r + 2 V(u_{\rm f}(w_\ell)) - 3 V_{\rm c} $ and ${\mathrm{TV}}(W \circ {\mathcal{R}_1^{\rm c}}[u_\ell,u_r]) = w_\ell - w_r < {\mathrm{TV}}(W \circ {\mathcal{R}^{\rm c}_2}[u_\ell,u_r]) =$$ 2 \hat{w}_2 - w_\ell - w_r $, where $\hat{w}_2 \doteq V_{\rm c} + p\left(Q_0/V_{\rm c}\right)$.

4.5.   Conservativeness

For any fixed $u_\ell,u_r \in \Omega$, let us consider $u_i \doteq \mathcal{R}_i[u_\ell,u_r]$, $i=1,2$. Since both $\mathcal{R}_1$ and $\mathcal{R}_2$ coincide with $\mathcal{R}_{\rm ARZ}$ in $\Omega_{\rm c}^2$, all the possible discontinuities of $u_1$ and $u_2$ in $\Omega_{\rm c}$ satisfy the Rankine-Hugoniot conditions. This means that if $u_1$ or $u_2$ performs a discontinuity from $u_- \in \Omega_{\rm c}$ to $u_+ \in \Omega_{\rm c}$ with speed of propagation $s \in \mathbb{R}$, then $\rho_- \ne \rho_+$ and

By the first condition in (RH) we immediately have that $s = \sigma(u_-,u_+)$, with $\sigma$ defined in (5). We recall that the first and second conditions in (RH) express the conservation across the discontinuity of the number of vehicles and the linearized momentum, respectively. As a consequence, both the number of vehicles and the linearized momentum are conserved across discontinuities in $\Omega_{\rm c}$ performed by $u_1$ or $u_2$.

By the assumption (H3), the 1-Lax curves defined in $\Omega_{\rm c}$ can be extended in a natural way up to reach $\Omega_{\rm f}^+$. Any point of the curve $\Omega_{\rm f}^+$ is reached by exactly one extended 1-Lax curve. Hence, since the Lagrangian marker is constant along the 1-Lax curves, there is a natural way to define the Lagrangian marker in $\Omega_{\rm f}^+$, see the definition of $W$ given in (2). It is then easy to see that also all the possible phase transitions between $\Omega_{\rm f}^+$ and $\Omega_{\rm c}$ performed by $u_1$ satisfy (RH), whereas those performed by $u_2$ satisfy in general only the first condition in (RH). In fact, this is the case if $u_2$ performs a phase transition from $u_- \in \Omega_{\rm f}^+$ to $u_+ \in \Omega_{\rm c}$ with $W(u_-) < W(u_+)$.

The extension to $\Omega_{\rm f}^-$ of the Lagrangian marker given in (2) ensures that any phase transition away from the vacuum performed by $u_1$ satisfies (RH). Now, since the extended Lagrangian marker is defined in $\Omega_{\rm f}$, we can question whether the shocks between states in $\Omega_{\rm f}$ satisfy (RH) or not. It is easy to see that the answer is positive if and only if $V_{\rm f}^- = V_{\rm f}^+$, however this contradicts our assumption (H1).

In conclusion, we have that both $\mathcal{R}_1$ and $\mathcal{R}_2$ conserve the number of vehicles but not the (extended) linearized momentum; consequently also $\mathcal{R}_1^{\rm c}$ and $\mathcal{R}_2^{\rm c}$ do so. This is in the same spirit of the Riemann solvers introduced for traffic through locations with reduced capacity in [24,25,26] and for traffic at junctions in [28].

Let us finally underline that, even if we generalize our model to the case $V_{\rm f}^- = V_{\rm f}^+$ as done in [24] and consider only solutions away from the vacuum so that $\mathcal{R}_1$ conserves also the linearized momentum, the corresponding constrained Riemann solver $\mathcal{R}_1^{\rm c}$ would not conserve it.

5.   Numerical example

In this section we apply the Riemann solvers introduced in Section 3 to simulate the traffic across a toll gate placed in $x=0$ and with capacity $Q_0 \in (Q_{\rm c}^+, Q(u_{\rm f}(W_{\rm c}^-)))$, see Figure 8. We consider two types of vehicles: the 1-vehicles and the 2-vehicles. Fix $x_1<x_2<0$ and assume that initially the 1-vehicles and the 2-vehicles are stopped in $(x_1,x_2)$ and $(x_2,0)$, respectively, and have Lagrangian markers $W_{\rm c}^-$ and $W_{\rm c}^+$, respectively. Then we are led to consider the Cauchy problem for (1) with initial datum

where $u_0 \doteq (0,V(0))$ belongs to $\Omega_{\rm f}$ and $u_1 \doteq (R_{\rm c}^-,0),\ u_2 \doteq (R_{\rm c}^+,0)$ belong to $\Omega_{\rm c}$.

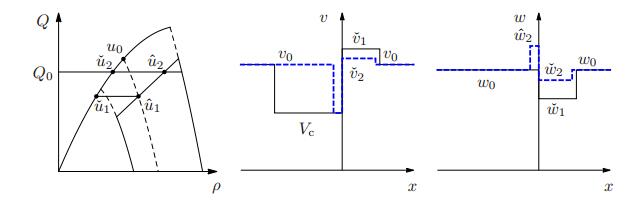
In subsections 5.1 and 5.2 we construct the solutions obtained by applying the wave-front tracking method [11,34] based on the Riemann solvers $\mathcal{R}_1,\ \mathcal{R}_1^{\rm c}$ and $\mathcal{R}_2,\ \mathcal{R}_2^{\rm c}$, respectively. The simulations presented in Figure 9 are obtained by the explicit analysis of the wave-fronts interactions with computer-assisted computation of the interaction times and front slopes and correspond to the following choice of the parameters

We use in this section the following notation

Observe that by definition we have $\hat{u}_- = \hat{u}_1(W_{\rm c}^-,Q_0)$ and $\hat{u}_+ = \hat{u}_1(W_{\rm c}^-,Q_0) = \hat{u}_2(W_{\rm c}^-,V(0),Q_0) = \hat{u}_2(W_{\rm c}^+,V(0),Q_0)$, see Figure 8.

5.1.   The numerical solution corresponding to $\mathcal{R}_1$ and $\mathcal{R}_1^{\rm c}$

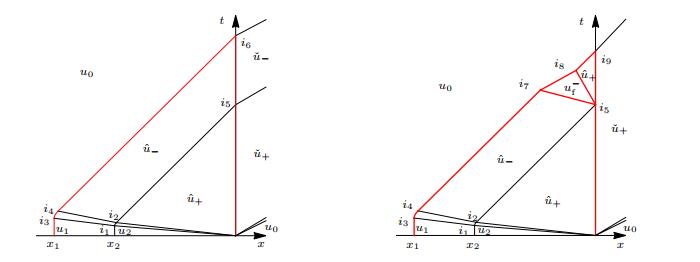
In this subsection we apply the Riemann solver $\mathcal{R}_1$ away from $x = 0$ and the constrained Riemann solver $\mathcal{R}_1^{\rm c}$ at $x = 0$ to construct the solution to the Cauchy problem (1), (11). The first step consists in solving the Riemann problems at the points $(x,t) = (x_1,0),(x_2,0),(0,0)$.

● The Riemann problem at $(x_1,0)$ is solved by a stationary phase transition $\mathsf{PT}_1$ from $u_0$ to $u_1$.

● The Riemann problem at $(x_2,0)$ is solved by a stationary contact discontinuity $\mathsf{C}_1$ from $u_1$ to $u_2$.

● The Riemann problem at $(0,0)$ is solved by a rarefaction $\mathsf{R}_1$ from $u_2$ to $\hat{u}_+$, followed by a stationary undercompressive phase transition $\mathsf{U}_1$ from $\hat{u}_+$ to $\check{u}_+$ and then by another rarefaction $\mathsf{R}_2$ from $\check{u}_+$ to $u_0$.

To prolong then the solution we have to consider the Riemann problems arising at each interaction $i_* \in [x_1,0]\times(0,\infty)$ as follows.

● First, $\mathsf{C}_1$ starts to interact with $\mathsf{R}_1$ at $i_1$. The result of this interaction is a contact discontinuity $\mathsf{C}_2$, which accelerates during its interaction with $\mathsf{R}_1$. $\mathsf{C}_2$ stops to interact with $\mathsf{R}_1$ once it reaches $i_2$. Then, a contact discontinuity $\mathsf{C}_3$ from $\hat{u}_-$ to $\hat{u}_+$ starts from $i_2$.

● The result of the interaction between $\mathsf{C}_3$ and $\mathsf{U}_1$ at $i_5$ is a stationary undercompressive phase transition $\mathsf{U}_2$ from $\hat{u}_-$ to $\check{u}_-$ followed by a shock $\mathsf{S}_1$ from $\check{u}_-$ to $\check{u}_+$.

● Each point of $\mathsf{C}_2$ is the center of a rarefaction appearing on its left. Let $\mathsf{R}_3$ be the juxtaposition of these rarefactions. Then $\mathsf{PT}_1$ starts to interact with $\mathsf{R}_3$ at $i_3$. The result of this interaction is a phase transition $\mathsf{PT}_2$, which accelerates during its interaction with $\mathsf{R}_3$. $\mathsf{PT}_2$ stops to interact with $\mathsf{R}_3$ once it reaches $i_4$. Then, a phase transition $\mathsf{PT}_3$ from $u_0$ to $\hat{u}_-$ starts from $i_4$.

● Finally, the result of the interaction between $\mathsf{PT}_3$ and $\mathsf{U}_2$ at $i_6$ is a shock $\mathsf{S}_2$ from $u_0$ to $\check{u}_-$.

The constructed solution is qualitatively represented in Figure 9, left, see also Figure 10 for a quantitative representation.

5.2.   The numerical solution corresponding to $\mathcal{R}_2$ and $\mathcal{R}_2^{\rm c}$

In this subsection we apply the Riemann solver $\mathcal{R}_2$ away from $x = 0$ and the constrained Riemann solver $\mathcal{R}_2^{\rm c}$ at $x = 0$ to construct the solution to the Cauchy problem (1), (11). The solution coincides with that constructed in Subsection 5.1 up to the interaction $i_5$. The result of the interaction at $i_5$ is now a phase transition $\mathsf{PT}_4$ from $\hat{u}_-$ to $ u_{\rm f}^-$, followed by another phase transition $\mathsf{PT}_5$ from $ u_{\rm f}^-$ to $\hat{u}_+$ and then by a stationary undercompressive phase transition $\mathsf{U}_3$ from $\hat{u}_+$ to $\check{u}_+$.To prolong then the solution it is sufficient to observe that:

● the result of the interaction at $i_7$ between $\mathsf{PT}_3$ and $\mathsf{PT}_4$ is a shock $\mathsf{S}_3$ from $u_0$ and $ u_{\rm f}^-$;

● the result of the interaction at $i_8$ between $\mathsf{S}_3$ and $\mathsf{PT}_5$ is a phase transition $\mathsf{PT}_6$ from $u_0$ and $\hat{u}_+$;

● the result of the interaction at $i_9$ between $\mathsf{PT}_6$ and $\mathsf{U}_3$ is a shock $\mathsf{S}_3$ from $u_0$ and $\check{u}_+$.

The constructed solution is qualitatively represented in Figure 9, right, see also Figure 10 and Figure 11 for a quantitative representation.

Aknowledgments

The authors thank Boris Andreianov, Edda Dal Santo and Carlotta Donadello for very helpful discussions. The first author thanks the Faculty of Mathematics, Physics and Computer Science of Maria Curie-Sklodowska-University (UMCS), for the hospitality during the preparation of this paper. The first author also thanks the Gran Sasso Science Institute (GSSI), with a special mention to Pierangelo Marcati, for the support they brought during the time this work was accomplished. The last author was also supported by the INdAM -GNAMPA Project 2017 "Equazioni iperboliche con termini nonlocali: teoria e modelli".