Three-dimensional physics-based earthquake ground motion simulations for seismic risk assessment in densely populated urban areas

1.   Introduction

In the last few decades, losses induced by natural disasters have shown a dramatic increase on a worldwide scale. The reasons are manifold and include the increase in world population, together with the development of new mega-cities with population larger than 2 millions, as well as the development of highly exposed regions and high vulnerability of modern societies and technologies ^[1]. Many of these densely populated areas are located in seismic prone areas. The destructive earthquakes of the last decade, such as Chile (Haiti 2010), New Zealand (Canterbury 2010 - 2011), Japan (Tohoku 2011, Kunamoto 2016) and Italy (L'Aquila 2009, Po Plain 2012, Norcia 2016), have caused a very high number of victims with losses estimated of the order of several billion dollars. For example, the Haiti earthquake (2010) counts 159.000 fatalities, whereas the overall economic losses caused by the Tohoku 2011 earthquake were estimated to be about 210 billion US dollars with about 15.500 victims ($\mathtt{https://natcatservice.munichre.com}$).

The assessment of seismic risk at portfolio, urban or regional scale is a key element for the definition of risk mitigation strategies to lessen the adverse economic and social effects of earthquakes, the planning and management of emergency response in the aftermath of a disaster event and for the definition of earthquake insurance schemes for risk transfer objectives. A variety of methodologies, tools and applications dealing with different components of seismic risk assessment have been proposed, see, e.g., the overview in ^[2]. In general, the chain of seismic risk assessment involves first the quantification of seismic hazard, then its combination with suitable vulnerability models of structures and facilities and, finally, the measurement of expected losses by incorporating the exposure information. Seismic hazard models provide a quantification of the expected earthquake shaking in a given area in terms of various ground motion Intensity Measure ($IM$), such as Peak Ground Acceleration ($PGA$) or acceleration response spectra ordinates ($SA$). For a structural typology, the direct physical damage can be determined using suitable fragility/vulnerability relationships providing the probability of damage/loss, conditioned on the level of $IM$. Eventually, economic (direct and indirect) and social (casualties) losses can be estimated as a function of physical damage estimates.

Among the many challenges that a reliable seismic risk assessment pose, we focus on the characterization of earthquake ground motion. The goal is to produce estimates of the probability distribution of ground motion $IM$ as a function of explanatory variables, such as magnitude, source-to-site distance and site conditions, amongst others. An extensive body of approaches exists for this purpose, ranging from Ground Motion Prediction Equations (GMPEs), Empirical Green Functions and stochastic methods, to three-dimensional (3D) numerical simulations, see review in ^[3]. These approaches differ essentially for the amount and detail of input information, as regards both the seismic source and propagation path from the source to the site, and the levels of output, either in terms of peak values of ground motion or an entire time history.

GMPEs are statistical regressions on instrumental observations from past earthquakes. They still represent the most commonly used approach for ground motion prediction, see ^[4]. Nonetheless, GMPEs suffer from some major limitations, especially when used for earthquake ground motion prediction at urban or regional scale. Indeed they are poorly calibrated in the near-source region of moderate to large earthquakes ^[5] and, as a consequence of ergodic assumption ^[6], they cannot account for region-, path- and site- specific effects related to the earthquake source, recording site conditions (e.g., complex site effects in case of large sedimentary basins) and source-to-site path. Moreover GMPEs alone cannot provide reliable estimates of the spatial correlation of ground motion, which may be crucial for seismic risk assessment of large urban areas with spatially distributed portfolios or infrastructural systems, see e.g., ^[7,8,9].

In recent years, boosted by the continuous development of numerical methods together with computational power facilities, there has been an increasing research of numerical methods for the simulation of seismic wave propagation ^[10]. Hence, 3D physics-based simulations (referred to as PBS hereafter) have emerged as a powerful and effective tool for earthquake ground motion prediction ^[11]. Typically, PBS are based on finite difference (FD) methods, finite element (FE) methods and spectral element (SE) methods that approximate the solution of the (visco)elastodynamics equation ^{[11,12,13,14,15,16,17,18]}. The output of PBS consists of ground motion time histories reflecting the physics of the seismic wave propagation problem as a whole, from the fault rupture to the propagation path and local site response. SE methods are among the most popular methods used in computational seismology due to their intrinsic capability of providing highly accurate solutions. In ^[19] Discontinuous Galerkin SE (DGSE) methods have been proposed and analyzed to further enhance the flexibility of SE methods, see also ^{[11,16,17,18,20,21,22,23]}. Indeed, DGSE methods are well suited for capturing local variations of the physical solution since they feature comparable accuracy of SE methods by keeping the numerical dispersion and dissipation errors low, cf. ^[24]. Moreover, they are more flexible than SE methods, because they allow for non-conforming simplicial/hexahedral grids and locally varying polynomial approximation orders ^[19].

In recent years, PBSs have achieved a substantial maturity in the scientific community, so that they can now be embedded within simulation-based seismic hazard assessment frameworks ^{[11,25,26,27]} and in the generation of large scale simulation-based seismic risk assessments ^[28,29]. The HayWired Earthquake scenario ^[30,31] is an example of cutting-edge evaluation of scenario-based seismic risk from 3D simulations. The physics-based ground shaking scenario of a hypothetical $M_w$ 7 earthquake on the Hayward Fault (San Francisco Bay area, California) provides an estimate of the expected physical and environmental damages resulting from the earthquake shaking. From this scenario it is also possible to obtain insights into social and economic consequences, planning of emergency responses and policy considerations. Recently, Smerzini and Pitilakis ^[29] combined 3D physics-based simulations with the capacity spectrum method to estimate the damage to reinforced concrete buildings in the city of Thessaloniki during the destructive $M_w$ 6.5 1978 earthquake and to compare it with available post-earthquake damage observations.

In this paper we propose a comprehensive methodological approach for seismic risk assessment to yield physics-based damage scenarios, which employs, on the one hand, a rigorous numerical model for the prediction of near-source earthquake ground motion, and on the other, a suitable set of fragility functions for prescribed building typologies to quantify a probabilistic expected buildings damage. 3D physics-based earthquake scenarios, that are the key ingredients of our approach, exploit the DGSE method proposed in ^[19] and implemented in the open source code SPEED ($\mathtt{http://speed.mox.polimi.it}$, cf. also ^[22]). The proposed approach based on PBSs is expected to provide more accurate, site-specific estimates of earthquake ground motion and, then, of the resulting damage, especially when the coupling of near-field effects and complex site amplification in sedimentary basins may play a key role.

The paper is organized as follows. In Section 2 the proposed methodological approach for seismic risk assessment combining PBSs scenarios with fragility models is presented. The three methodological pillars of this approach, i.e., the DGSE method for physics-based numerical simulation of earthquakes, the ground motion intensity measure $IM$ and the fragility functions for the vulnerability model, are discussed in Sections 3, 4 and 5, respectively. Finally, in Sections 6 and 7, we present an application of the proposed approach focusing on the metropolitan area of Beijing (China). The city of Beijing is located in the proximity of a well-known mapped fault system capable of triggering severe earthquakes of magnitude up to 7.3 $M_w$. Based on employing our model, we produce maps of seismic damage focusing on the specific class of high-rise buildings, accounting for a wide set of fault rupture realizations with magnitude in the range 6.5-7.3 $M_w$.

2.   A methodological approach for seismic risk assessment based on 3D physics-based numerical simulations and fragility functions

For a specific asset, seismic risk is computed by convolution of hazard with vulnerability. Conventionally, the probability of damage is estimated on the basis of the total probability theorem, as follows:

where $P(DS\ge d_s|IM = \mathtt{im})$ represents the probability of exceeding a certain damage level (or state) conditioned on the intensity measure $IM = \mathtt{im}$, i.e., the fragility function expressing the complementary cumulative distribution function for $DS$ conditional to $IM$, while $f_{IM}({\tt im})$ is the probability density function of the given $IM$. In the most comprehensive context of performance-based earthquake engineering, $f_{IM}({\tt im})$ is derived from the seismic hazard curve at a site (given the annual probability of exceedance as a function of the given $IM$) computed through a Probabilistic Seismic Hazard Assessment (PSHA), and (2.1) allows to compute the annual probability of exceedance of a given loss metric (e.g., monetary losses or damage state, the latter being related to losses through correlations of damage with repair or replacement costs). In deterministic risk calculations, the risk is computed for a single ground shaking scenario without computing the convolution integral of (2.1).

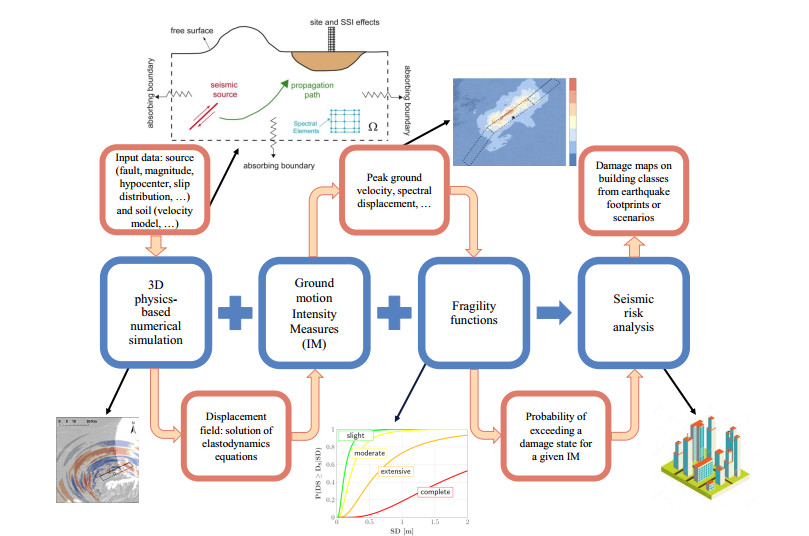
The key element of the comprehensive methodological approach proposed in this paper (see Figure 1 for a schematic representation) is the characterization of seismic ground shaking and of its spatial variability through 3D physics-based numerical models of earthquakes. These earthquake scenarios are based on solving approximately a differential problem modeling the displacement of a (visco)elastic medium subjected to an external excitation source. The numerical method employed to approximate the displacement field is the DGSE method proposed in ^[19] and implemented in the open source code SPEED ($\mathtt{http://speed.mox.polimi.it}$, cf. also ^[22]). Besides being verified in a number of benchmarks, see ^[22,23], SPEED has been proven successful to simulate real earthquakes, such as the 2009 April 6th L'Aquila, Central Italy ^[32], the 2011 February 22nd Christchurch, New Zealand ^[33], the 2012 May 29th Po Plain, Northern Italy ^[17], the 1978 June 20th Volvi, Northern Greece ^[34], the 1915 January 15th Marsica ^[18].

Each numerical simulation provides as output, at any site of interest, the full waveform of ground motion compatible with the source rupture process (causative fault, magnitude $M_w$, hypocenter location, fault slip distribution, etc.), the source-to-site path and the local geological conditions. Note that, for a given magnitude $M_w$, multiple realizations are simulated to account for the aleatory uncertainty associated with the fault rupture process, in terms of slip distribution, hypocenter location and kinematic source parameters (e.g., rupture velocity and rise time). For the sake of clarity, in the following the term scenario will be used to refer to a set of earthquakes on a given fault characterized by a prescribed magnitude $M_w$, while footprint is used to denote the specific realization (i.e., in terms of co-seismic slip distribution across the fault and hypocenter location) within a given scenario. From the synthetic waveform, the associated ground motion $IM$ can be computed, depending on the class of structures/infrastructures at risk, provided that the simulated ground motion is broadband, i.e., it is sufficiently accurate in a broad frequency range of interest for the seismic response of structures. Once the selected $IM$ is computed, it is used as input to the fragility functions for the target class of structures to compute the probability of exceedance of a given damage state.

The methodological approach implemented in this work allows to compute seismic risk estimates at two different levels.

$(1).$ At the first level ($L1$), deterministic seismic risk estimates, i.e., $P(DS\ge d_s|IM = \mathtt{im})$, are provided for representative earthquake footprints computed through a single numerical simulation.

$(2).$ At the second level ($L2$), based on Eq (2.1), seismic risk estimates are computed for a given earthquake scenario with prescribed magnitude $M_w$, i.e., $P(DS\ge d_s|scenario)$, exploiting a statistically significant set of earthquake footprints, from which the probability distribution of ground motion can be computed. This implies that, for any site of interest, the probability distribution of earthquake shaking, i.e., the term $f_{IM}({\tt im})$ in (2.1) can be computed from the $N$ footprints of the given earthquake scenario.

For the latter approach, in order to evaluate $P(DS\ge d_s)$, we have to compute the integral in (2.1). This can be evaluated numerically by means of Gaussian quadrature formula. Note that under specific hypothesis it is possible to calculate analytically the value of the integral in (2.1). In our case, for the mathematical description of $P(DS\ge d_s|IM = \mathtt{im})$ we refer to Section 5 (see (5.1)), whereas we assume that $IM$ is log-normally distributed with probability density function given by

where $\mu_{im}$ and $\sigma_{im}$ are the median and logarithmic standard deviation.

In this paper, we are mainly interested in the methodological chain for seismic risk assessment via PBS, so that we do not explicitly account for specific exposure models of the region under study. This means that, as output, we provide risk estimates for any site of the model that contains a prescribed building typology. Furthermore, only physical damage predictions are provided, overlooking the computation of economic and/or social losses. In the three following sections we will focus our attention on the three main ingredients of the methodological approach of Figure 1, i.e., a rigorous numerical model for the prediction of near-source earthquake ground motion (Section 3), a quantification of ground motion intensity measures (Section 4) and suitable fragility functions for prescribed building typologies (Section 5).

3.   DGSE methods for ground motion prediction

Our mathematical model for earthquake scenarios consists in the dynamic equation in a portion of soil that we identify (at rest) with the three-dimensional region $\Omega \subset \mathbb{R}^3$ in the temporal interval $(0, T]$. The linear momentum equation is given by

where $\rho$ is the medium density, $\xi > 0$ is a suitable decay factor proportional to the inverse of time, $\mathbf{u}$ is the unknown displacement field, $\mathit{\boldsymbol{\sigma}}$ is the stress tensor and $\mathbf{f}$ represents the seismic source. Here $t = 0$ conventionally represents the time instant of the earthquake origin. To simplify the notation, we implicitly assume the dependency in space and time of the quantities $\mathbf{u}$, $\mathit{\boldsymbol{\sigma}}$ and $\mathbf{f}$, whereas $\rho$ and $\xi$ only have the space dependency. Eq (3.1) is supplemented with a constitutive relation that express the stress tensor as a function of the displacement. Here, we consider the Hooke's law, i.e.,

where ${\mathcal D}$ is a fourth-order tensor encoding the material properties of the medium depending on the first and second Lamé parameters $\lambda$ and $\mu$, $\mathit{\boldsymbol{\varepsilon}}$ is the symmetric gradient. The constitutive equation (3.1) is supplemented with suitable boundary and initial conditions of the form

respectively, where $\mathbf{n}$ is the outward normal vector to the boundary of the domain $\partial\Omega$. We assume that the boundary is split into two disjoint portions $\Gamma_N$, where surface loads $\mathbf{t} = \mathbf{t}(\mathbf{x}, t)$ are imposed, and $\Gamma_{NR}$, where non-reflecting boundary conditions are prescribed. In order to model transparent boundaries, we consider a fictitious traction field $\mathbf{t}^* = \mathbf{t}^*(\mathbf{x}, t)$ introduced to avoid unphysical reflections on the artificial boundaries, see ^[35,36]. The exact expression of $\mathbf{t}^*$ can be found in ^[36]. Moreover $\mathbf{u}_0$ and $\mathbf{u}_1$ represent given initial displacement and velocity fields, respectively.

Hereafter, we will use the symbols $v_p$ and $v_s$ to denote the characteristic compressional and shear wave speeds of the medium, defined as $v_p = \sqrt{(\lambda+2\mu)/\rho}$ and $v_s = \sqrt{\mu/\rho}$.

The seismic source $\mathbf{f}$ in (3.1) is described through a kinematic finite-fault model expressed in terms of a distribution of double-couple point sources. Its mathematical representation is based on the seismic moment tensor $m(\mathbf{x}, t)$ defined for $0\le t < T$ as in ^[37],

where $\mathit{\boldsymbol{\nu}}$ and $\mathbf{s}$ are the fault normal and the unit slip vector along the fault, respectively. In (3.4) $M_0(\mathbf{x}, t)$ is the time history of the moment release at the source point $\mathbf{x}$ inside the elementary volume $V$. Finally, the body force distribution $\mathbf{f}$ is given by the relation $\mathbf{f}(\mathbf{x}, t) = -\nabla\cdot m(\mathbf{x}, t)$, cf. ^[14]. Following ^[19], see ^[36] for a review, we introduce the DGSE space discretization to problem (3.1)–(3.3) based on a domain decomposition approach. At the first level, we subdivide $\Omega$ into $K$ non-overlapping regions $\Omega_k$, $k = 1, \dots, K$, such that $\Omega = \cup_{k = 1}^K \Omega_k$, and we denote by $\mathcal{S}$ the collection of the interfaces between subdomains. Note that this (macro) decomposition can be geometrically non-conforming. Then problem (1) is solved in each $\Omega_k$ together with transmission conditions at the interface between the sub-domains that are encoded in the scheme. Then, within each subdomain $\Omega_k$, we construct a grid $\mathcal{T}_{h_k}$ made of hexahedral elements $E_k^l$, with diameter $h_k^l$, and assign a polynomial approximation degree $N_k\geq1$. We suppose that each $E_k^l\in\Omega_k$ is the image through the map $\mathbf{F}_k^l:\hat{E}\to E_k^l$ of the unit reference hexahedron $\hat{E}$. Notice that mesh generation is performed independently on each subdomain and also the local polynomial degree $N_k$ can vary subdomainwise. We define $\mathcal{T}_h$ to be the union of the (independently generated) grids $\mathcal{T}_{h_k}$, and collect all the element faces (here a face is the non empty interior of the intersection of two neighboring hexahedral elements that belong to $\mathcal{T}_{h}$) that lie on the interface $\mathcal{S}$ in the set ${\mathcal F}_h$. Problem (3.1)–(3.3) is then discretized on each subdomain $\Omega_k$ with a SE method of degree $N_k$ and at the interfaces ${\mathcal F}_h$ the DG paradigm is employed. We introduce the space $\mathbf{V}_{h_k}^{N_k}(\Omega_k) = \{\mathbf{v}\in\mathbf{C}^0(\overline{\Omega}_k):\mathbf{v}|_{E_k^l}\circ\mathbf{F}_k^l\in[\mathbb{Q}^{N_k}(\hat{E})]^3 \quad \forall E_k^l\in\mathcal{T}_{h_k} \}$, where $\mathbb{Q}^{N_k}(\hat{E})$ is the space of polynomials of degree $N_k$ in each coordinate direction on $\hat{E}$. Then, denoting by ${\mathbf V}_{DG}$ the discrete space of function that are piecewise continuous polynomials of degree $N_k$ in each coordinate direction on each subdomain $\Omega_k$, i.e., $\mathbf{V}_{DG} = \{\mathbf{v}\in\mathbf{L}^2(\Omega):\mathbf{v}|_{\Omega_k}\in\mathbf{V}_{h_k}^{N_k}(\Omega_k), \, k = 1, \ldots, K\}$, and that can be discontinuous at the interface $\mathcal{S}$, the semi-discrete DGSE formulation reads as follows: for any $t \in (0, T]$, find $\mathbf{u}_h = \mathbf{u}_h(t) \in {\mathbf V}_{DG}$ such that

for any $\mathbf{v} \in {\mathbf V}_{DG}$, where

For any two neighbouring regions $\Omega_{k^\pm}$ that share a face $F\in\mathcal{F}_h$ we denote with $\mathbf{v}^\pm$ and $\mathit{\boldsymbol{\tau}}^\pm$ the traces of (regular enough) vector- and tensor-valued functions $\mathbf{v}$ and $\mathit{\boldsymbol{\tau}}$ on $\Omega_{k^\pm}$, respectively. We also denote with $\mathbf{n}^\pm$ the unit normal vector to $F$ pointing outward to $\Omega_{k^\pm}$. We define the averages $\{{\cdot}\}$ and jumps $[\![{\cdot}]\!]$ operators (see ^[36,38]) as

where $\mathbf{a}\otimes\mathbf{b}\in\mathbb{R}^{3\times3}$ is the tensor with entries $(\mathbf{a}\otimes\mathbf{b})_{ij} = a_ib_j$, $i, j = 1, 2, 3$, for all $\mathbf{a}, \mathbf{b}\in\mathbb{R}^3$. On each face $F \in {\mathcal F}_h$ shared by two elements $E^+\subset \Omega_{k^+}$ and $E^-\subset \Omega_{k^-}$ the penalty parameter $\eta_{F}$ is defined as

where $\{q\}_A = 2q^+q^-/(q^++q^-)$ is the harmonic average of the quantity $q$ across $F$, $\alpha$ is a (large enough) positive constant to be properly chosen ^[38,39,40], and $\mathtt{N}$ and $\mathtt{h}$ are defined on each face $F\in {\mathcal F}_h$ as $\mathtt{N} = \max\{N_{k^+}, N_{k^-}\}$ and $\mathtt{h} = \min\{h_{k^+}, h_{k^-}\}$. Error bounds and stability estimates for formulation (3.5) can be found for instance in ^{[19,21,23,41,42]}. The algebraic version of (3.5) can be obtained by: (ⅰ) introducing a basis $\{\mathit{\boldsymbol{\Psi}}\}_{i = 1, ..., N_{h}}$ for the finite element space ${\mathbf V}_{DG}$; (ⅱ) expressing $\mathbf{u} \in {\mathbf V}_{DG}$ as linear combination of the shape functions, i.e., $\mathbf{u}(\mathbf{x}, t) = \sum_{i = 1}^{N_h} \mathtt{U}_j(t)\mathit{\boldsymbol{\Psi}}_j(\mathbf{x})$; and (ⅲ) choosing $\mathbf{v} = \mathit{\boldsymbol{\Psi}}_i$ for any $i = 1, ..., N_{h}$. The resulting system has the following structure

together with initial conditions ${ \mathtt{U}}(0) = \hat{ \mathbf{u}}_0$ and $\dot{ \mathtt{U}}(0) = \hat{ \mathbf{u}}_1$, being $\hat{ \mathbf{u}}_0$ and $\hat{ \mathbf{u}}_1$ suitable approximation in ${\mathbf V}_{DG}$ of the initial data ${ \mathbf{u}}_0$ and ${ \mathbf{u}}_1$. In (3.6), the vector $\mathtt{U}(t) \in \mathbb{R}^{N_h}$ contains the unknown expansion coefficients in the chosen basis, i.e., $\mathtt{U}_j(t) = \mathbf{u}(\mathbf{x}_j, t)$. The mass, damping, and stiffness matrices are defined as

respectively. Finally, the right-hand side $\mathtt{F}(t)$ has the following expression

Notice that the choice of the basis functions $\{ \mathit{\boldsymbol{\Psi}}_i \}$ for the spectral element space ${\mathbf V}_{DG}$ reflects on the structure of system (3.6). To span the discrete space we consider tensor product nodal Lagrangian functions associated to the tensor product of the Gauss-Legendre-Lobatto (GLL) interpolating points ^[43]. This in turn gives a diagonal structure to the matrices $\mathtt{M}$ and $\mathtt{C}$ that can be effectively exploited for the time integration scheme. Indeed, to integrate (3.6) in time we proceed as follows. We subdivide the time interval $(0, T]$ into $N_T$ time slabs of length $\Delta t = T/N_T$ and we denote by $\mathtt{U}^k$ the approximation of $\mathtt{U}$ at time $t^k = k \Delta t$, i.e., $\mathtt{U}^k\approx \mathtt{U}(t_k)$, $k = 0, ..., N_T$. Given $\mathtt{U}^0 = \mathtt{U}(0)$ and $\mathtt{V}^0 = \dot{ \mathtt{U}}(0)$, to solve system (3.6) we use the leap-frog scheme:

with

By taking advantage of the structure of $\mathtt{M}$ and $\mathtt{C}$ we can easily invert the system $\mathtt{M} + \frac{\Delta t}{2} \mathtt{C}$ in (3.7). We recall that the leap-frog scheme (3.7) is explicit and second order accurate, therefore to ensure the numerical stability the Courant-Friedrichs-Lewy (CFL) condition has to be satisfied, see e.g., ^[44,45].

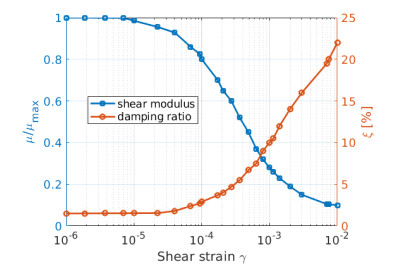
We remark that the algorithm presented above can be straightforwardly generalized to the case of a nonlinear soil model as the one we are going to consider for the application in Section 6, cf. ^[46,47]. The latter is a 3D generalization of the classical $\mu-\gamma$ and $\xi-\gamma$ curves used within 1D linear-equivalent approaches, see, e.g., ^[48], where $\gamma$ is the 1D shear strain.

At each time step of the analysis the shear modulus $\mu$ and the viscous damping $\xi$ are updated on the basis of the maximum deformation achieved at each element of the model. In particular, referring to the Mohr's circle, the maximum shear deformation $\gamma_{max}$ is evaluated at each grid node from the principal strains $\epsilon_I$, $\epsilon_{II}$ and $\epsilon_{III}$, as follows

This value, averaged on each mesh element, defines update shear modulus $\mu$ and damping ratio $\xi$ at each time step, following a material stress-strain ($\mu-\gamma$) and a damping-strain ($\xi-\gamma$) curve, respectively. In practice, at the generic position x and generic instant of time $t$ a scalar measure of shear strain amplitude $\gamma$ is computed, then this value is introduced in the $\mu-\gamma$ and $\xi-\gamma$ curves, and finally the corresponding parameters are updated for the following timestep. Therefore, unlike the classical linear-equivalent approach, the initial values of the dynamic soil properties are recovered at the end of the excitation, i.e., when the displacement wave field, and consequently $\gamma_{max}$, is close to zero. An example of $\mu-\gamma$ and $\xi-\gamma$ curves used for the shallow soil materials are reported in Figure 5.

4.   Ground motion intensity measures

The ground motion intensity measure $IM$ provides a quantification of the seismic event. Typical choices to quantify the $IM$ are the Peak Ground Acceleration ($PGA$), the Peak Ground Velocity ($PGV$), the Spectral Acceleration ($SA$), the Spectral Displacement ($SD$), or an integral measure of ground shaking, such as the Housner intensity ($I_H$) ^[49,50].

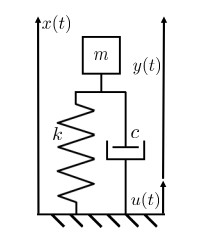
The Peak Ground measures are computed through their maximum absolute value w.r.t. time. For example, the Peak Ground Velocity ($PGV$) is defined as $PGV = \max_t|v(t)|$, where $v(t)$ is the velocity time history. In a similar way the Peak Ground Displacement ($PGD$) or the Peak Ground Acceleration ($PGA$) can be described. Spectral quantities are defined through the solution of the vibratory motion of the damped single-degree-of-freedom given by

where $x(t)$ and $u(t)$ are the absolute displacements of the oscillator and of the support, respectively, and $y(t)$ represents the relative displacement of the oscillator w.r.t. the support, see Figure 2. The parameters $m$, $c$ and $k$ denote the mass, elasticity constant and damping of the system, respectively. The system depends on the natural period $T = 2\pi/\omega$ and damping ratio $\zeta = c/(2m\omega)$, where $\omega = \sqrt{k/m}$ is the circular frequency of the oscillator.

Then the spectral displacement is defined as the maximum relative displacement response $y(t)$, subjected to a prescribed acceleration $\ddot{u}(t)$ at the base, for a given vibration period $T$ and damping ratio $\zeta$, i.e., $SD(T, \zeta) = \max_t|y(t)|$. With similar arguments we can introduce the velocity and acceleration response spectral ordinates, that are Spectral Velocity ($SV$) and Spectral Acceleration ($SA$), respectively. $SV$ and $SA$ are defined as the maximum relative velocity and maximum absolute acceleration, respectively, i.e., $SV(T, \zeta) = \max_t|\dot{y}(t)|$ and $SA(T, \zeta) = \max_t|\ddot{x}(t)|$. Moreover the spectral values introduced are related by the period of interest, that is $SV = (T/2\pi)SD$ and $SA = (T/2\pi)^2 SD$. As natural consequence of the spectral values, we introduce the Housner intensity defined as the integral of the elastic velocity spectrum between $0.1s$ and $2.5s$, i.e.:

where $T, \zeta$ are the parameters of the structure and $SV$ is the spectral velocity spectrum.

In our application, cf. Sections 6 and 7, we will consider the Peak Ground Velocity ($PGV$) and the Spectral Displacement ($SD$). They are computed by considering their 2D generalization by means of the geometric mean of their horizontal components, i.e., the intensity measure is computed as $IM = \sqrt{IM_{x_1}IM_{x_2}}$ where $IM_{x_k}$, $k = 1, 2$, represent the 1D-intensity measure $IM = SD, PGV$ associated to each horizontal component.

5.   Fragility models

The fragility function is a key component of the chain for seismic risk assessment, as it measures the probability of exceeding certain performance (or design) criteria as a function of the level of seismic input intensity, see (2.1). In general, the fragility function is defined as the conditional probability of a given damage state (or measure) $DS$ exceeding a threshold $d_s$, given a value of the ground motion intensity measure $IM = \mathtt{im}$, i.e.,

where $P(A|B)$ is the conditional probability of $A$ given $B$, cf. ^[51,52].

The most common form of a seismic fragility function is the log-normal cumulative distribution function ^[53,54], given by

where $\phi$ is the standard Gaussian cumulative distribution function, $\mu_s$ is the median value of the distribution and $\sigma_s$ is its logarithmic standard deviation for each damage state $d_s$, $s = 1, \ldots, N$. The log-normal distribution is typically used because: (ⅰ) it fits a variety of structural component failure data, as well as non-structural failure data and building collapse by Incremental Dynamic Analyses performed on numerical structural models, see ^[55]; (ⅱ) it has a strong theoretical basis, being positive definite and fully defined by measures of the first and second statistical moments. The parameters $\mu_s$ and $\sigma_s$ can be evaluated with the use of the maximum likelihood estimation ^{[51,53,56,57]} or with the linear regression method ^{[51,58,59,60]}.

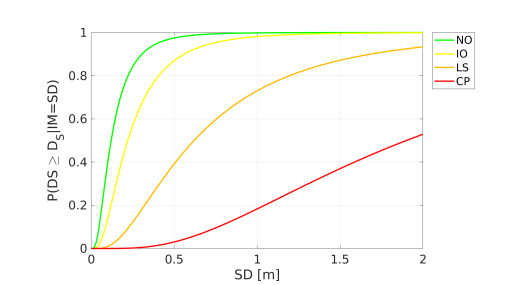
As an illustrative example, in Figure 3, we show the family of fragility functions for high-rise buildings (height below 200 $m$ and low seismic design code) developed by Wu et al. ^[61] as a function of spectral displacement $SD$, cf. Section 4.

In Figure 3 fragility functions are given for the following damage states: Normal Operation ($d_1 = \rm{NO}$), Immediate Occupancy ($d_2 = \rm{IO}$), Life Safe ($d_3 = \rm{LS}$), Collapse Prevention ($d_4 = \rm{CP}$). Each function is represented by a log-normal probability distribution, see Eq (5.1), therefore it is fully described, for each damage state $d_s$, by the pair $(\mu_s, \sigma_s)$ reported in Table 1.

6.   Earthquake ground motion prediction in the metropolitan area of Beijing

To apply the methodological approach described in Section 2, we consider the metropolitan area of Beijing. Beijing is situated on a large sedimentary basin and, with its more than 20 million inhabitants and strong urbanization, is one of the many megacities around the world highly exposed to the seismic threat. From an historical point of view Beijing was severely affected by seismic events ^[62], such as the Sanhe-Pinggu earthquake in 1679, with an estimated magnitude 8. In this work, we are interested in investigating the potential rupture of two relevant, well-known seismogenic structures, namely, the Shunyi-Qianmen-Liangxiang and the Nanyuan-Tongxian faults, crossing the metropolitan area of Beijing. Being capable to generate earthquakes up to magnitude 7.3, these faults represent, in fact, a significant threat to the city.

The proximity to these faults along with the complex geological configuration makes the large urban area of Beijing an interesting case study, where non-standard approaches are needed for a more accurate characterization of strong ground motion. To this end, a 3D physics-based numerical model of the Beijing metropolitan area was constructed to simulate a large set of earthquake scenarios originating along these faults with magnitude varying from 6.5 to 7.3. Then, seismic risk estimates were obtained by combining these earthquake ground shaking scenarios with fragility functions for high-rise buildings, the latter ones being an important component of the entire building stock of the city.

Even if some studies adopted physics-based numerical simulation ^[63] or tried to explicitly model in full 3D the detailed shape of the alluvial basin of Beijing ^[64], to our knowledge, none of the previous investigations have considered a large number of earthquake scenarios occurring along the two aforementioned faults. Furthermore, in those studies, no attempt was made to use synthetic ground motion scenarios to generate seismic damage scenarios for specific building typologies existing in this hazardous area.

As already pointed out by Xiong et al. ^[65], our synthetic seismograms obtained via wave propagation simulation might be used as input for dynamic response history analyses of buildings requiring the entire time history rather than $IM$ values, as recently done by Xu et al. and Lu et al. ^[66,67].

6.1.   Set-up of the 3D numerical model

The 3D computational domain for the Beijing area was set up considering the following input data: (ⅰ) the topography model, (ⅱ) the seismic fault whose rupture is modelled using a kinematic representation, (ⅲ) the 3D subsoil structure accounting for the variable thickness of the sedimentary basin and the 3D velocity profiles, cf. ^[36]. The topography model was built from freely-available digital elevation dataset of CGIAR-CSI for the Beijing area (downloaded from the website $\mathtt{http://srtm.csi.cgiar.org}$). The data have a resolution of approximately $90\times90$ $m$, for north-south and east-west directions.

Among the relevant seismic sources (i.e., Shunyi-Qianmen-Liangxian, SQL, and Nanyuan-Tongxian, NT, faults), for sake of presentation, herein we investigate earthquake rupture scenarios occurring only along the SQL fault system which crosses the central Beijing area. It is a normal quasi-vertical (the dip angle is about $80^\circ$) fault consisting of three main segments with different strike angles. The total fault length is about 90 $km$ and it can produce events up to $M_w$ 7.3. In Table 2 we report the parameters of the SQL fault, as implemented in our computational model.

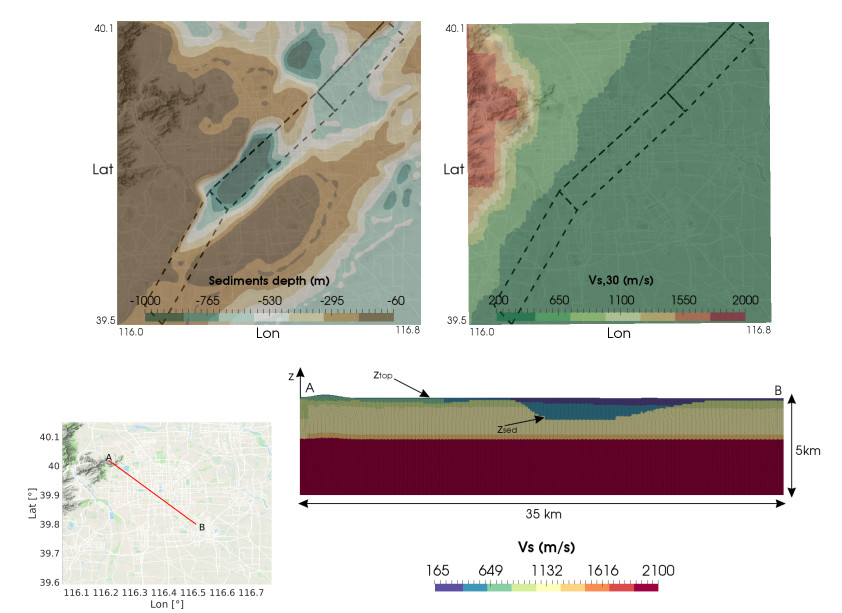
As regards the 3D soil model, it was constructed by merging data regarding both the geologic structure of the alluvial basin, see Figure 4 (top left), and the spatial distribution of $V_{s, 30}$ (weighted average shear wave velocity in the top 30 $m$), cf. Figure 4 (top right) and ^[68]. The former was derived from the digitalization of the model proposed in ^[64], while the latter was adapted from $\mathtt{https://earthquake.usgs.gov/data/vs30}$. In particular, given $z_{top}$ and $z_{sed}$, that represent the projection of a generic point with coordinate $z$ into the surface and the sediment base, respectively, we have considered for the first layer (0 to 2 $km$ depth) the following properties, cf. Figure 4 (bottom),

where the velocity profiles are in $m/s$. Similarly, we defined the soil density in $kg/m^3$ as follows

In addition, we consider a non-linear soil behaviour of the soft soil deposits ($V_{s, 30}\le400$ $m/s$ and $z_{top} - 300\le z\le z_{top}$ $m$), as described in Section 3, based on the modulus reduction and damping curves shown in Figure 5.

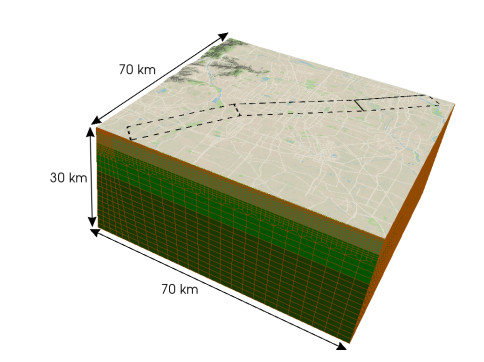
Dynamic properties for the underlying bedrock layers (depth $> 2$ $km$), assumed to be horizontally stratified, have been assigned in accordance with ^[64], see Table 3. The computational domain was built by considering all the information above and extends over an area of $70 \times 70$ $km^2$ down to 30 $km$ depth (see Figure 6).

In order to correctly simulate by SPEED the earthquake ground motion up to a maximum frequency $f = 1.5\; Hz$, we built a conforming mesh with size of 150 $m$ on the top surface, of 600 $m$ at 4 $km$ depth and reaching 1800 $m$ in the underlying layers. In particular the model consists of 859.677 hexahedral elements and, by using a fourth order polynomial approximation degree $N = 4$, it has approximately 160 million degrees of freedom. Then we fixed the total observation time $T = 30$ $s$ and we used a time step $\Delta t = 0.001$ $s$. The walltime for each simulation is around 12 hours on 512 cores on the Marconi cluster at CINECA, Italy ($\mathtt{http://www.cineca.it/en/content/marconi}$).

To capture the variability of earthquake ground motion resulting from different fault ruptures along the SQL fault, a set of 30 footprints was performed by varying the moment magnitude $M_w$, from a minimum of 6.5 up to a maximum of 7.3, the location of the hypocenter, the kinematic slip distribution on the fault and the rupture area location. A summary of the simulated seismic footprints, grouped according to the three magnitude levels (i.e., scenario), is provided in Table 4.

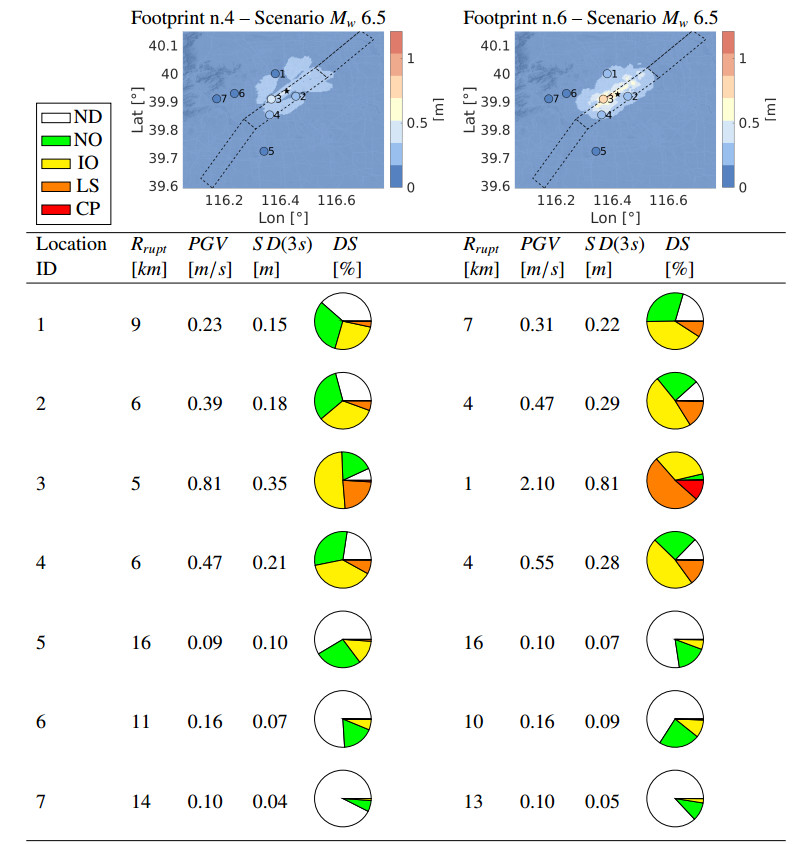
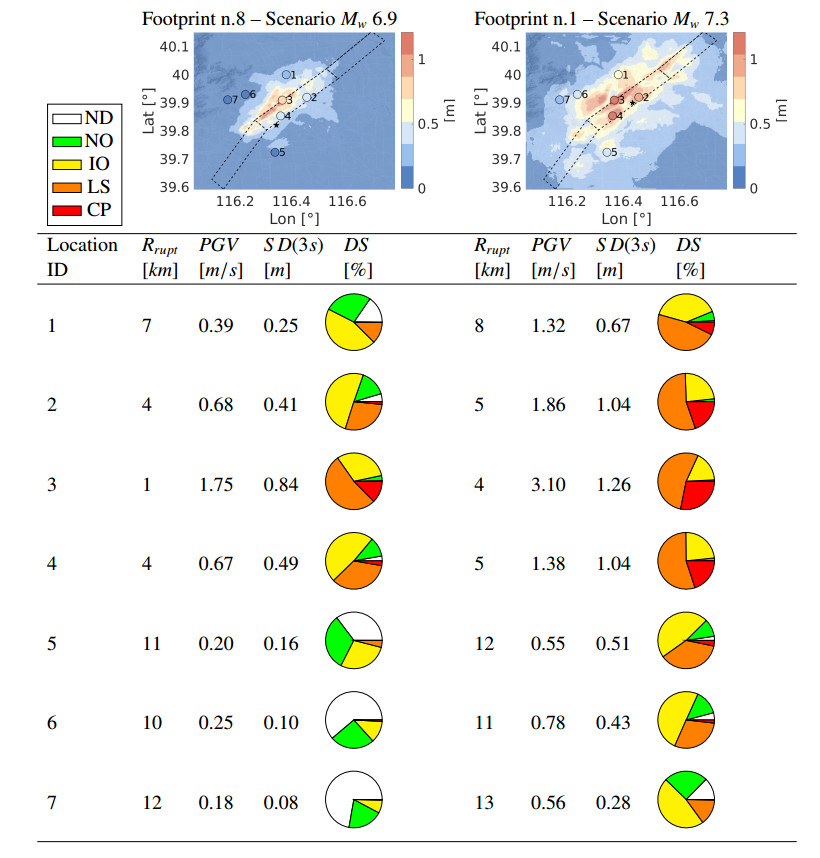
The main kinematic parameters of the slip distributions for a given fault and a given earthquake magnitude were chosen by considering probability distributions ensuring that the resulting scenario variability is not affected by systematic bias in the input parameters. In order to produce a number of random slip distributions, a pre-processing Matlab toolboox was defined: given a fault type and a target magnitude $M_w$, the program computes the fault length ($L$), the fault width ($W$), the maximum displacement (MD) and the average displacement (AD) of the slip distribution according to the Wells and Coppersmith ^[69] relations. Moreover, the hypocenter position is defined at run-time randomly, using a Gaussian distribution with mean depth equal to $10$ km and standard deviation equal to $2$ km. Then, the relative position of the rupture fault is obtained by assuming a Weibull distribution with parameters defined according to ^[70]. For each scenario kinematic slip distribution, rupture time and rise time are directly generated by the model of Schmedes et al. ^[71]. The resulting outputs are then read by the SPEED code and at run-time applied to the discretization nodes. In the following we will consider different rupture realizations for four selected footprints, namely n.4 and n.6 for scenario $M_w$ 6.5, n.8 for scenario $M_w$ 6.9 and n.1 for scenario $M_w$ 7.3.

6.2.   Results of 3D PBS and comparison with GMPE

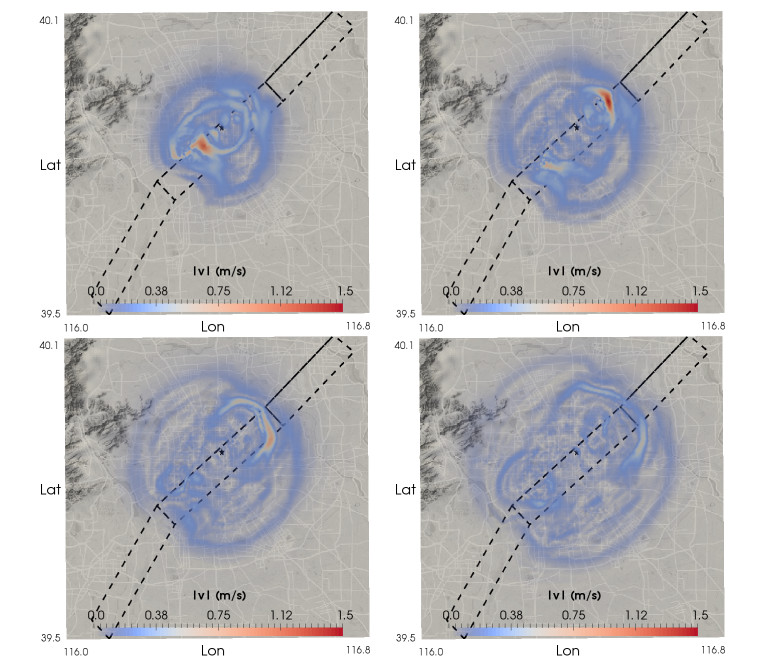
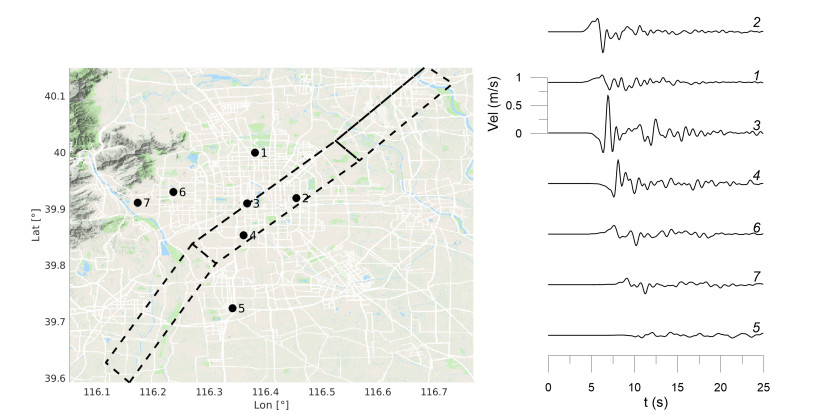
In the following, some representative results of the 3D physics-based numerical simulations will be discussed with emphasis on the characterization of earthquake ground motion. Figure 7 shows some snapshots of the velocity wave field (modulus of horizontal components) for the footprint n.4 – scenario $M_w$ 6.5. Interestingly, two large pulses, pointing south-west and north-east with respect to the epicenter and almost aligned along the surface projection of the top segment of the fault, are clearly visible. These pulses can be observed also in the velocity time histories, East-West (EW) component, illustrated in Figure 8 for 7 representative sites, more specifically at stations 2, 3 and 4, lying above the surface projection of the fault.

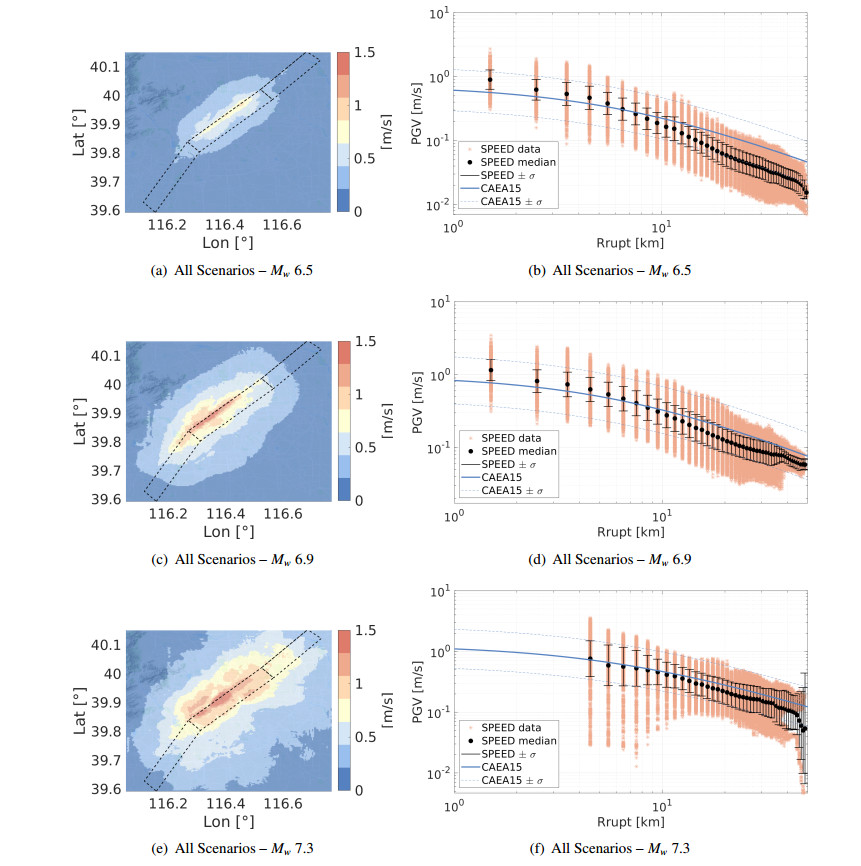
As already proposed by Villani et al. ^[16], for each scenario the first statistical moments obtained for the relevant ground motion parameters from the population of synthetic signals (at the sites of interest) can be computed, and used in the same way as one would use the median and the standard deviation of a classical GMPE. Figure 9 (left column) shows the map of the median values (first statistical moment) of the peak ground velocity (maximum absolute value w.r.t. time of velocity, $PGV$, geometric mean of horizontal components, cf. Section 4), computed from all set of simulated footprints for each scenario magnitude: $M_w$ 6.5 (top), $M_w$ 6.9 (middle) and $M_w$ 7.3 (bottom), cf. Table 4. The right column of Figure 9 compares the median $PGV$, obtained by the numerical simulation against the one based on the GMPE proposed by Cauzzi et al. ^[72], referred to as CAEA15 hereafter. For simplicity, the GMPE was calculated assuming an average $V_{s, 30}$ equal to 235 $m/s$, being this value relatively constant throughout the whole metropolitan area of Beijing. Consistently to the chosen GMPE, the metric adopted for the comparison is the closest distance to the fault rupture ($R_{rupt}$). Note that, for scenario $M_w$ 7.3, the minimum rupture distances are larger than the ones for other scenarios, because of the larger depth of the rupture area.

It is worth to highlight that the results obtained by PBS present an overall good agreement with the prediction of the GMPE. However, PBS produce median peak ground values systematically higher at short distances from the fault (typically for $R_{rupt}$ less than around 5 km) and generally lower at longer distances. Furthermore, the standard deviation computed from our site-specific simulations tends to be smaller than the corresponding one obtained based on employing CAEA15, as the latter is increased because of the ergodic assumption, applied to site-generic applications of earthquake ground motion modeling.

7.   Seismic risk assessment for high-rise buildings

In this section the numerical simulations obtained in Section 6 are coupled with fragility functions to generate seismic damage scenarios for the buildings in the urban area of Beijing. In this work, we focus on a special class of buildings: the so-called super high-rise buildings with height over 100 $m$, cf. ^[73,74]. For this purpose, the results of PBS, introduced in previous Section, are combined with the fragility functions developed by Wu et al. ^[61] specifically for Chinese high-rise buildings. For simplicity, results will be only provided in terms of seismic damage assessment, while the extension to comprehensive seismic risk evaluation including fatality and/or loss assessment is beyond the scope of this work.

Starting from the published data regarding more than 50 high-rise buildings, Wu et al. ^[61] developed regression analyses between the maximum storey drift ratios and the response spectral displacement for high-rise buildings located in China. Fragility functions were then proposed for different categories of high-rise buildings, depending on the building height (above 200 $m$ and below 200 $m$) and the level of seismic design code (low, moderate and high), and for the following damage states: Normal Operation (NO), Immediate Occupancy (IO), Life Safe (LS), Collapse Prevention (CP). These four classes can be described in terms of damage levels as follows: NO = very light, IO = light, LS = moderate and CP = severe, cf. FEMA273 ^[75]. In our analysis, without loss of generality, we focus on the category of high-rise buildings with height below 200 $m$ and low prescriptions levels for seismic design, see Figure 3 and Table 1 in Section 5.

Considering buildings with height of approximately 100 $m$, for which, on average, a fundamental period of vibration of 3$s$ can be defined based on statistical analysis of vibration properties of Chinese high-rise buildings ^[76], spectral displacement ($SD$) at 3$s$ with damping ratio $5\%$ was assumed as a ground motion proxy for the fragility functions. In our framework $SD$ is the maximum relative displacement response w.r.t. time of the building w.r.t. the ground. It is computed as geometric mean of the spectral displacement associated to each horizontal component, cf. Section 4.

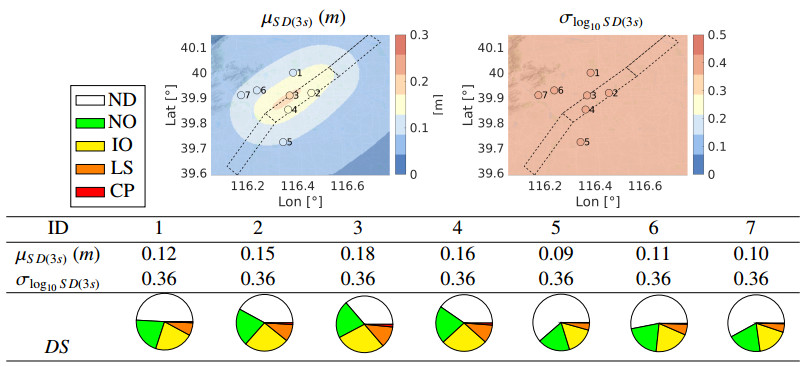
Given the location of the Shunyi-Qianmen-Liangxiang fault, a rather large portion of the metropolitan area of Beijing falls in this near-field range. In Tables 5 and 6, for the four selected footprints, the probability associated to each performance level is depicted as a pie chart where the different colors denote the damage states, specifically, white – No Damage (ND), green – Normal Operation (NO), yellow – Immediate Occupancy (IO), orange – Life Safe (LS) and red – Collapse Prevention (CP). We observe the following: starting from footprint n.4 ($M_w$ 6.5) the dominating effects are null and slight damages (colors white and green), while footprint n.1 ($M_w$ 7.3) shows a predominance of significant and severe damages up to collapse (colors yellow, orange and red). Furthermore, comparing results obtained for the different sites, it is evident that sites 2, 3 and 4, located on the surface projection of the fault, show, across all footprints, the most dangerous damage estimates.

So far, seismic risk scenarios were generated for specific earthquake footprints in a deterministic way ($L1$ risk analysis), focusing on the analysis of the damage distribution as a function of the distance from the causative fault. Finally, to shed light on the potential use of 3D PBS within probabilistic frameworks for seismic risk assessment, the conditional probability $P(DS\ge d_s|scenario)$ was computed by the convolution integral of Eq (2.1) according to the procedure proposed in Section 2 ($L2$ risk analysis).

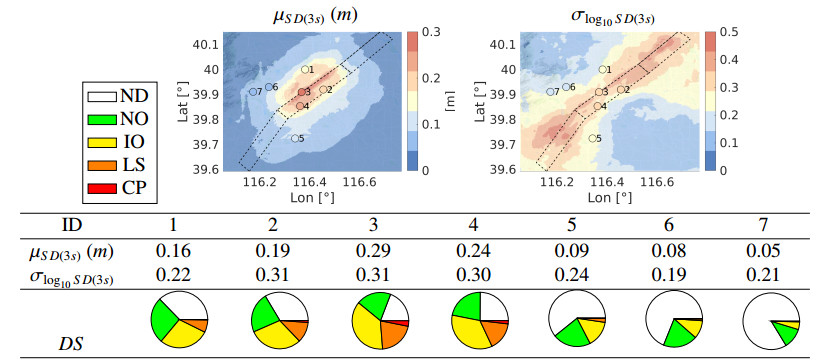
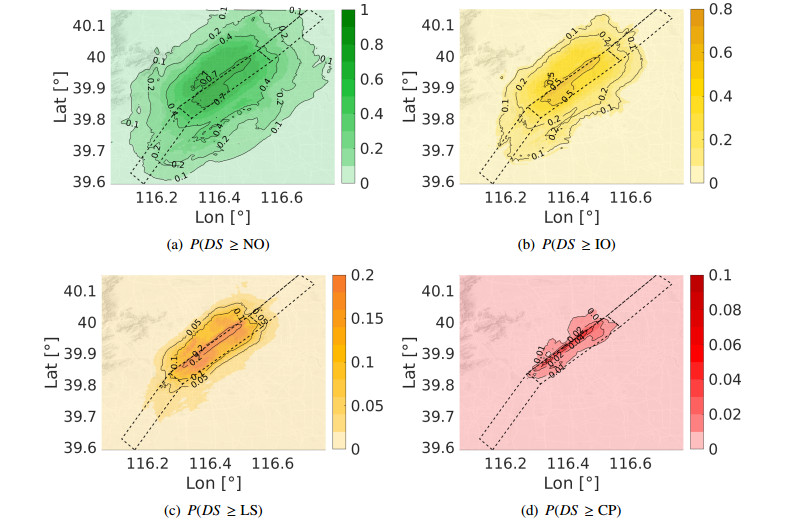
For the sake of brevity, we focus here on the earthquake scenario with magnitude $M_w$ 6.5, for any site of the model, the probability of different damage states was derived by taking into account all 15 earthquake footprints simulated for this scenario (see Table 4). This means that, under the assumption of a log-normal probability density function for $SD(3s)$ (see equation (2.2)), $\mu_{SD(3s)}$ and $\sigma_{SD(3s)}$ are estimated, for the selected scenario, from the corresponding set of footprints by using the maximum likelihood method. Then, in order to be able to compare PBS and CAEA15 results, we need to attribute $\mu_{SD(3s)}$ and $\sigma_{SD(3s)}$ to a log-normal base 10 distribution. The median $\mu_{SD(3s)}$ does not change, whereas $\sigma_{SD(3s)}$ becomes $\sigma_{\log_{10}{SD(3s)}}$. The computed results along with the SQL fault obtained at the 7 sites under consideration are shown in Table 7 in terms of $\mu_{SD(3s)}$, $\sigma_{\log_{10}{SD(3s)}}$ and $P(DS = d_s| M_w\:6.5)$ for the different damage states. Figure 10 illustrates the spatial distribution of damage probabilities $P(DS\ge d_s| M_w\:6.5)$ obtained by means of PBS. In order to highlight the differences that may arise adopting GMPEs, Table 8 shows the analogous results obtained using CAEA15 for the same scenario earthquake. Note that top rows of both Tables 7 and 8 illustrate the map of $\mu_{SD(3s)}$, $\sigma_{\log_{10}{SD(3s)}}$ from PBS and CAEA15, respectively. From the comparison of these maps, it is clear that: (ⅰ) median values from PBS show a steep gradient of the ground motion predicted in the proximity of the fault due to the coupling of source rupture effects with complex site effects in the Beijing basin; (ⅱ) $\sigma$ values from PBS tend to be smaller, on average, than the ones from CAEA15 as the former are site-specific (i.e., ergodic assumption is removed, see ^[6]); furthermore, PBS produce dispersion values characterised by a strong spatial dependency, which cannot, or can only partially, be accounted for in GMPEs.

8.   Conclusions

In this work we have introduced a simple and effective approach for seismic risk assessment which couples 3D physics-based scenarios (PBSs) and fragility functions in order to obtain risk estimate. This approach uses PBSs as an alternative to standard empirical approaches, based on Ground Motion Prediction Equations (GMPEs). The latter may provide inaccurate results, especially in the near-field of an earthquake, because the number of records might be not sufficient to satisfactorily constrain the expected site-specific ground motion spatial distribution, including peculiar effects, such as directivity or spatial correlation of the ground motion. For this reason, instead of GMPEs, we proposed a mathematical framework that exploits PBSs by solving the wave propagation problem. Once a relatively large set of synthetic scenarios was generated, we combined suitable ground motion intensity measures with classical fragility functions in order to finally evaluate the seismic risk for any specific class of buildings. As a case study of the proposed approach, the large metropolitan area of Beijing was considered, the seismic hazard of which is governed by the Shunyi-Qianmen-Liangxiang and Nanyuan-Tongxian faults. For this purpose, a set of PBSs was obtained with magnitudes ranging from a minimum of 6.5 $M_w$ up to a maximum of 7.3 $M_w$; the location of hypocenter, the slip patterns and other parameters have been systematically varied, aiming at covering, as much as possible, the variability of seismic shaking, associated with the different ruptures that might realistically take place in the future. The potential consequences of such scenarios have been investigated, focusing on the structural response of the high-rise building class, particularly relevant in Beijing. To this end, we adopted fragility functions explicitly calibrated for the Chinese building stock.

Our analysis suggest that PBSs can be successfully adopted for seismic risk assessment purposes. The comparison of our results with similar ones obtained by GMPEs highlighted that systematic differences take place especially in the near-field region. Considering the fact that GMPEs tend to lack of calibration data in this area and that PBSs are intrinsically physically constrained, we conclude that the PBS methodology may be complementary to GMPEs when the seismogenic structure that governs local seismic hazard is known and a sufficiently accurate 3D model of the local geology may be constructed.

Acknowledgments

Paola F. Antonietti, Ilario Mazzieri and Laura Melas have been partially supported by SIR (Scientific Independence of young Researchers) starting grant n. RBSI14VT0S funded by the Italian Ministry of Education, Universities and Research (MIUR). Paola F. Antonietti acknowledges the financial support of PRIN grant n. 201744KLJL funded by MIUR. Paola F. Antonietti and Ilario Mazzieri have been also partially funded by INdAM-GNCS. This work was also partially supported by Munich RE.

We acknowledge the CINECA HPC supporting under the ISCRA initiative for the availability of high performance computing resources and support. The authors would like also to thank Maria Infantino for her valuable help with post-processing analysis of 3D physics-based scenarios.

Conflict of interest

The authors declare no conflict of interest.