Shape derivative for obstacles in crowd motion

1.   Introduction

Modeling crowd behavior has been a very active field of applied mathematics these last years, and its importance in real life applications is straightforward, besides its connections with many other phenomena coming for example from activities of human beings, biology (cell migration, tumor growth, pattern formations in animal populations, etc.), particle physics and economics. We cite for instance few classical studies in the mathematical analysis of crowd models, such as ^[7,10], but also the more recent ^[17,23] which will be closer to the models used in our paper.

In all these models congestion phenomena are the crucial issue which rules the movement of the crowd. When these models are applied to the study of the evacuation of a crowd (see ^[6]), a natural question concerns the role played by obstacles. It is classical but shocking folklore that in some cases obstacles can indeed fluidify the evacuation, because they tend to reduce congestion (people move on the two sides of the obstacle, instead on concentrating in the middle). We refer, for instance, to ^[24] for an applied study of this phenomenon. Numerically, simulations have been run on the Hughes model with and without obstacles, in order to compare the different performances with and without obstacles (^[26]). Yet, a theoretical and general mathematical study of this question (which is in some sense also related to the so-called Braess paradox in traffic networks, ^[3]) is, to the best of our knowledge, still lacking.

In this work, our goal is to perform an analysis using the notion of shape derivative (see ^[8,21]). This is a standard tool in shape optimization: whenever a domain $\Omega$ has to be chosen, under possible constraints, so as to minimize a functional $J(\Omega)$ - whose value depends on the solution $u_\Omega$ of a PDE set on $\Omega$, with boundary conditions on $\partial\Omega$ - one wonders how to compute $\frac{d}{d\varepsilon} J(\Omega_ \varepsilon)$, where $V$ is a given smooth vector field and $\Omega_ \varepsilon: = (id+\varepsilon V)(\Omega)$. This allows to program descent algorithms and/or to study the optimality conditions by imposing that these derivatives should vanish. The main result of the whole theory is to compute the above derivative under the form $\int_{\partial\Omega} F\, V\cdot n$, where $F$ can be computed in terms of the solutions of some PDEs on $\Omega$ (and not on $\Omega_ \varepsilon$; moreover, it is important that $F$ does not depend on $V$). It is not surprising that only the scalar product $V\cdot n$ appears, since tangential deformation of a domain do not change it. Several formulae and techniques are provided in order to compute $F$, which allows, for instance, to prepare a descent method by choosing $V = -Fn$ on the boundary.

In our case, one has first to choose a model for the evolution of the crowd density $\rho$, which follows a PDE taking care of the spontaneous direction of the crowd (we will concentrate on evacuation scenarios, where the crowd spontaneously moves towards the exits) and of the congestion effects, and then define the target functional, which will be chosen in this study to be equal to the average exit time. Several choices for the PDE model are natural, and in particular the density-constrained formulation given in ^[12]. This PDE is the gradient flow in the Wasserstein space (see ^[2,11] and ^[18,25] for a general introduction to optimal transport) of the functional

where $\mathcal D$ is the distance function to the exit, and we set $f(s) = 0$ for $s\leq 1$ and $f(s) = +\infty$ for $s > 1$. Yet, this choice is very singular and lets several difficulties arise, and a simpler analysis can be performed in the case where one uses $f(s) = (s^m-s)/(m-1)$ (using $f(s) = s\log s$ for $m = 1$), which approximates the previous choice as $m\to\infty$ (see ^[1]). This gives as a state equation the PDE

complemented with Dirichlet boundary conditions on the exit $\Gamma\subset\partial\Omega$ and no-flux conditions on $\partial\Omega\setminus\Gamma$. In particular, even if this is far from approximating the crowd motion model with density constraints of ^[12], for $m = 1$ one has a very simple (and linear) Fokker-Planck equation. The potential $\mathcal D$ is taken to be the geodesic distance, inside $\Omega$, to the exit $\Gamma$. This means that, if $\Omega$ varies, the solution $\rho$ varies both because the domain where the PDE is solved changes, but also because the potential $\mathcal D$ depends upon $\Omega$.

In the present paper we compute and exploit the shape derivative of the average exit time functional, which can be written as $\int dt\int_\Omega d\rho_t$, with respect to variations of an obstacle $O$, setting $\Omega = R\setminus O$. The exit $\Gamma$ is located on the fixed part on the boundary, i.e., $\Gamma\subset \partial\Omega\setminus O$. For simplicity, the initial state $\rho_0$ is supposed to be supported far from $O$.

We insist that the goal of this paper is to provide tools, in the form of shape derivatives, to handle possible optimization problems on the form of obstacles in crowd evacuation models. Among the question that one could consider there is confirming or not the general idea that obstacles could sometimes be profitable to the evacuation time: a possible way to check this consists in computing the shape derivative starting from a given obstacle and seeing whether it suggests to enlarge or reduce it (at least via a numerical procedure). Other questions could involve the optimization in restricted class (for instance imposing that the obstacle is a disk, as for columns, or imposing volume or mechanical constraints). Even if the main goal of computing the shape derivative that we provide is to use it so as to perform numerical investigations, this paper is neither a paper in numerical analysis nor in PDEs. It is rather a piece of applied mathematics and modeling, and it is not our goal to provide fine numerical results, nor to take care of the necessary regularity that we should need to justify the derivatives we compute. The main goal is indeed to provide ready-to-use formulas which require a certain analysis and a certain background in order to be retrieved.

The paper is organized as follows: the first section after the introduction is devoted to the position of the problem together with its modeling. Then arrives Section 3, where the aim is to prepare the computations necessary to obtain the shape derivatives. The section starts with various preliminary results (Section 3.1) and then presents the core output of the paper, i.e., the shape derivative of the gradient of the geodesic distance (3.2). Section 4, instead, contains the main results of the paper, i.e., the delicate computations of the shape derivative of the average exit time when the crowd is ruled by the Fokker-Planck equation (section 4.1) and the adaptations to be performed to deal with other diffusion cases, including the Porous-Medium case (4.2).

2.   Models for crowd motion, approximation, and position of the problem

The model introduced in ^[12,13] (also look at ^[17], at ^[14,23] for a microscopic counterpart, and at ^[15] for the case with diffusion) considers in a domain $\Omega$ the evolution of a probability measure $\rho_t$ in $\Omega$, with the additional constraint that $\rho_t$ is absolutely continuous with respect to the Lebesgue measure and its density is less or equal to $1$ (which stands for the fact that $\rho_t$ represents a crowd, and people cannot concentrate too much). The idea is that individuals follow a spontaneous velocity field of the form $-\nabla \mathcal D$ where $\mathcal D$ is the distance function to their destination, but have to adapt their velocity to the congestion constraint. The main assumption of such a model is that the actual velocity is the projection of the vector field $-\nabla \mathcal D$ onto the set of velocity fields preserving at an infinitesimal level such a constraint (i.e., those fields which have positive divergence on the region $\{\rho_t = 1\}$; see also ^[20] for a general presentation of this theory). The destination here is an exit $\Gamma$, considered as a subset of $\partial\Omega$. This PDE model was presented in ^[12] as a gradient flow in the Wasserstein space (see ^[2,19]) but this a priori requires conservation of the mass. We let the reader adapt the modeling in ^[12,13] to see that, formally, allowing the mass to exit through $\Gamma$, provides the following PDE system

with the following boundary conditions:

● on $\partial\Omega\setminus\Gamma$, we have the no-flux condition $\rho_t(-\nabla \mathcal{D} - \nabla p_t)\cdot n = 0$;

● on $\Gamma$, we have the Dirichlet condition $p_t = 0$.

Then, the flux on $\Gamma$ is not zero, and equals $\rho_t(-\nabla \mathcal{D} - \nabla p_t)\cdot n$. Note that the mass only exits through $\Gamma$ (and never comes back), since both $\mathcal D$ and $p$ vanish on $\Gamma$ and are positive inside. It means that

is the amount of mass which is exiting at time $t$. It is then possible to compute the average exit time $J$ of the crowd as

where the last equality comes from an integration by parts first in time, and then in space (but one can also retrieve the same result considering that $\int_\Omega \rho_t dx$ is the amount of mass still in $\Omega$ at time $t$, and applying Cavalieri's principle). However, for numerical reasons, we will set our PDE on $[0, T]\times \Omega$ with $T < +\infty$ and use

which corresponds to computing the average of the minimum between the exit time and $T$.

Remark 2.1. It is also possible to replace the factor $t$ in the first integral in (2) with $t^q$, in order to obtain the $L^q$ norm of the exit time. For large $q$, this can also approximate the maximum time. Yet, the simplest and most natural case to consider is $q = 1$.

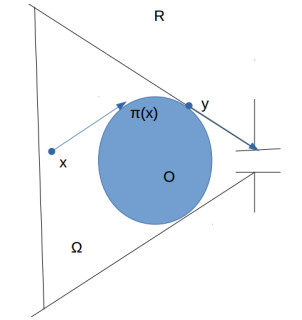
We will assume that for every $\rho_0$ the solution to (1) exists and is unique (for existence we refer to ^[19]; uniqueness has not been proven in all situations, but it is true if $\mathcal D$ is semi-convex or if we add diffusion, as in ^[5,15]). In this case, the average exit time is a quantity depending on $\rho_0$, on the domain $\Omega$, and on the potential $\mathcal D$. We will choose $\mathcal D$ to be the geodesic distance to $\Gamma$ inside $\Omega$ (as in Figure 1), i.e.,

and in this way $J$ will only depend on $\rho_0$ and $\Omega$, since $\mathcal D$ depends on $\Omega$ as well.

As for the choice of the domain $\Omega$, we will consider $\Omega: = R\setminus O$, where $R$ is a given large room and $O$ an obstacle, which will be later the unknown of our model. The obstacle $O$ is supposed to be far from $\partial R$, so that $\partial\Omega = \partial R\cup\partial O$ and the exit $\Gamma$ is considered to be a subset of $\partial R = \partial \Omega\setminus O$. Note that in general $\mathcal D$ is not semi-convex as soon as $\Omega$ is not convex, and of course with obstacles we lose convexity. However, the possible lack of uniqueness for Eq (1) is not a problem for the scientific purposes of this paper: indeed, we do not perform directly shape derivative computations on this limit model with density constraints, but only on less singular approximations, where the diffusion guarantees uniqueness. However, we do believe that uniqueness also holds for more general distance functions $\mathcal D$ than semi-convex ones, but we are aware that this is a difficult question.

Our goal will be to consider a moving density $\rho_t(\Omega)$ of crowd or particles in a domain $\Omega = R\setminus O\subset \mathbb{R}^d$ ($\Omega$ is supposed to be smooth, $O$ is an obstacle and $d\geq 2$). As said before the PDE we are looking is (1). We would like to compute the shape derivative of (2) with respect to the obstacle $O$.

Unfortunately, analyzing this very model is quite difficult. We should compute the shape derivative of the pressure, which is out of reach, since it is not given as a differentiable function of $\rho$, but only defined in an implicit way (a formal computation would let two different equations appear in the zone where $\rho = 1$ and $\rho < 1$, a system for which existence is not clear). Fortunately enough, as we said in the introduction, the approximation described in ^[1] and using a porous-medium type equation is available. Indeed, in ^[1], the authors consider the relationship between Hele-Shaw evolution and the porous media equation with drift and the congested crowd motion model originally proposed by ^[12,13], and they showed that the solutions of the porous media equations

converge to the Hele-Shaw solution as $m \rightarrow \infty$ provided the drift potential is strictly sub-harmonic (note that, if we take $m = 1$, we obtain the Fokker-Planck equation, which is linear and much easier to study).

Using the gradient flow structure of both the porous media equation (see ^[16]) and the crowd motion model, they proved also that the solutions of the porous media equations solutions also converge to the congested crowd motion as $m \rightarrow \infty$.

Even if the convergence result proved in ^[1] requires $\Delta \mathcal D\geq 0$, the convergence is also expected in general, as a consequence of the $\Gamma$-convergence of the associated functionals. Yet, passing from $\Gamma$-convergence of the functionals to the convergence of the gradient flows is a delicate matter, and the reader can refer to ^[22], where additional assumptions are required in order to perform the proofs.

In this paper, following what said above, we consider the case where the moving density $\rho_t$ is driven by a porous media equation and compute the shape derivative of (2). We start from the case $m = 1$, and then we show how to adapt to the case of more general diffusion equations $\partial_t\rho-\Delta(h(\rho))-\nabla\cdot(\rho\nabla\mathcal D) = 0$, which include the porous medium equation.

3.   Shape derivatives tools for the average exit time

In this section we are going at first to give some fundamental results on shape derivatives. Then, we shall present a preliminary key result for the computation of the shape derivative of the gradient of the geodesic distance $\mathcal D$.

3.1.   Preliminary results

For all shape derivative tools we refer to for instance ^[4,8,9] and references therein. We remind here just few results that we are going to use such as the so called differentiation formula for the integrals on variable domains and some elements of tangential calculus.

Theorem 3.1. [differentiation formula] Let $\Omega$ be a measurable set and $E > 0.$ Let $\Phi: [0, E)\rightarrow W^{1, \infty}(\mathbb{R}^d),$ be a family of diffeomorphisms which is differentiable w.r.t. $\epsilon$ at $\epsilon = 0$, such that $\Phi(0) = I$ is the identity map in $\mathbb{R}^d$ and $\Phi'(0) = V$. Let $f: \epsilon \in [0, E) \mapsto f(\epsilon)\in L^1(\mathbb{R}^d)$ be differentiable map at $\epsilon = 0$ with its derivative noted $f'(0)$. We suppose in addition that $f(0)\in W^{1, 1}(\mathbb{R}^d)$. Then the function $\epsilon\mapsto I(\epsilon) = \int_{\Omega_\epsilon}f(\epsilon)$ is differentiable at $\epsilon = 0$ and we have

Furthermore, if $\Omega$ is an smooth enough open set, then we also have

Before proceeding further let us give the definitions of the tangential gradient of a function $g \in \mathcal C^1 (\partial \Omega)$ and of the tangential divergence of a vector field $W$ belonging to $\mathcal C^1 (\partial \Omega, \mathbb{R}^d).$

Definition 3.1. Given $g \in \mathcal C^1 (\partial \Omega),$ the tangential gradient is defined by

where $\tilde{g} \in \mathcal C^{1}(\mathbb{R}^d)$ is any extension of $g.$

Definition 3.2. Given $\ W \in \mathcal C^1 (\partial \Omega, \mathbb{R}^d),$ the tangential divergence $W$ is defined by

where $\tilde{W}\in \mathcal C^1 (\mathbb{R}^d), \mathbb{R}^d)$ is any extension of $W$ and $D \tilde{W}$ its Jacobian matrix (we use the notation $Dz[v]$ to denote the Jacobian of a vector-valued function $z$ applied to the direction $v$, i.e., $\partial z/\partial v$: in case $z$ is scalar this coincides with $z\cdot v$).

Remark 3.1. These definitions also extend by density to the whole space $W^{1, 1 }(\partial \Omega): = \overline{\mathcal C^1 (\partial \Omega)}^{\|.\|_{1, 1}},$ $\|g\|_{1, 1} = \int_{\partial \Omega}|g|+ |\nabla_{\tau} g|$, and to $W^{1, 1}(\mathbb{R}^d, \mathbb{R}^d).$

Remark 3.2. The above definitions do not depend on the choice of the extensions of $g$ and $W.$

Proposition 3.2. Let $\Omega$ be an open set of class $C^2$ in $\mathbb{R}^d$ and $u:\bar{\Omega}\rightarrow \mathbb{R}$ of class $C^2$. Then

where $\Delta_{\tau}u = div_{\tau}(\nabla_{\tau} u)$ is the Laplace-Beltrami operator.

Let $f\in W^{1, 1}(\partial \Omega), \ W\in W^{1, 1}(\partial \Omega, \mathbb{R}^d)$. Then

where $\kappa$ is the mean curvature of $\partial \Omega, \nabla_\tau f$ the tangential gradient of $f$ and $div_{\tau} = \nabla_{\tau}.$ the tangential divergence. $W_{\tau}$ stands for the tangential component of $W$ (i.e. the orthogonal projection of W on the tangent hyperplane defined as $W_{\tau}: = W - (W.n)n$).

Furthermore we have:

Since the obstacle is perturbed and we have no-flux boundary conditions on it, we have to understand how this condition is perturbed.

First we need to compute the normal direction to $\Omega_\epsilon$. This can be done through the following easy computation.

Proposition 3.3. Let $\Omega$ be of class $C^1.$ Let $n\in \mathcal C^1 (\mathbb{R}^d, \mathbb {R}^d)$ be an extension of the unit normal vector to $\partial \Omega.$ Then

is normal to $\partial \Omega_{\epsilon}$ and $\epsilon \mapsto n_{\epsilon}$ is in $\mathcal C (\mathbb{R}^d, \mathbb {R}^d)$ and is differentiable at $0.$

The above result can be exploited in a very simple way. Since our goal is to study boundary conditions of the form $z\cdot n = 0$, the normalization of $w_\epsilon$ is not really important. Moreover, if we take a point $x\in \partial \Omega$ we can find a point on $\partial\Omega_\epsilon$ by taking $\Phi(\epsilon)(x)$. In particular, if we have a PDE on $\Omega_\epsilon$ where a certain vector-valued function $z_\epsilon$ satisfies a no-flux boundary condition, we can write it as

We want to differentiate this condition, and using $\Phi(\epsilon) = Id+\epsilon V$ we obtain

Differentiating in terms of $\epsilon$ hence provides

We can re-write this expression in a more convenient way. First, we treat separately the normal and tangential components of $V$, thus getting

Then we observe that, differentiating the relation $z\cdot n = 0$ tangentially in the direction of $V_{\tau}$ on $\partial\Omega_0$, we obtain $(Dz [V_\tau])\cdot n = -z\cdot (Dn [V_\tau])$. This allows to write

Finally, we replace the term $Dn [V_\tau] +(DV)^t [n]$ with $\nabla (V\cdot n)$ (let us see in a while why this is possible) and then with $\nabla_\tau (V\cdot n)$ (this last transformation is possible because we take the scalar product with $z$, which has no normal component since we have $z\cdot n = 0)$. In order to see that we have $Dn [V_\tau] +(DV)^t [n] = \nabla (V\cdot n)$ we first observe that $Dn$ is a symmetric matrix (since $n$ can be extended out of $\partial \Omega$ as the gradient of the signed distance function to $\partial\Omega$, hence $Dn$ is a Hessian matrix); then, the fact that $n$ is a unit vector implies $n\cdot Dn = 0$, but because of symmetry we also have $Dn[n] = 0$. Hence we deduce $Dn [V_\tau] = Dn [V]$. Computing $\nabla (V\cdot n) = n\cdot DV+V\cdot Dn$, we are just left to check that we have $Dn[V]+(DV)^t[n] = n\cdot DV+V\cdot n$, which can be done componentwise, using again the symmetry of $Dn$.

Hence we finally obtain the following result, whose proof is just a consequence of the above considerations.

Proposition 3.4. Let $\Omega$ be an open set of class $C^1$, $(\Phi(\varepsilon))$ a smooth family of diffeomorphisms with $\Phi(0) = Id$ and $\Phi'(0) = V$, and set $\Omega_\epsilon = (\Phi(\varepsilon))(\Omega)$. Let $(z_\epsilon)_\epsilon$ be a smooth family of vector fields satisfying $z_\epsilon\cdot n_\epsilon = 0$ on $\partial\Omega_\epsilon$, where $n_\epsilon$ is the normal to $\partial\Omega_\epsilon$. Let us call $n$ the unit normal vector to $\partial\Omega$.

Then we have

Note that when $z$ is a gradient, the term $Dz [n]\cdot n$ is a second derivative in the normal direction.

3.2.   Shape derivative of the geodesic distance gradient

Let us now state results related to the shape derivative of the geodesic distance. Since we only need the gradient of the geodesic distance, we will not compute the derivative $\mathcal D'$, but directly $(\nabla\mathcal D)'$, that we denote $\mathcal D'$.

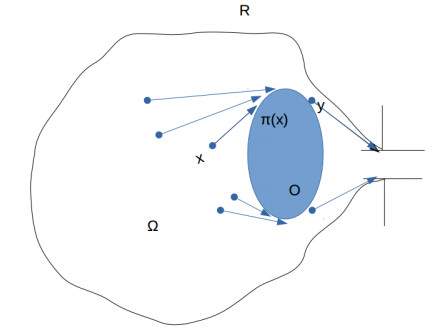
Proposition 3.5. Let $\Omega = R\setminus O \in\mathbb{R}^d$ be a $C^2$ open set as above. Let us call $K_O$ the set of points $x\in\Omega$ such that the geodesic from $x$ to $\Gamma$ inside $\overline\Omega$ is unique and touches the obstacle $O$. For every $x\in K_O$ we call $\pi(x)$ the first contact point of such a geodesic with $O$ (see Figure 2). Let $\mathcal{D}:x\in\Omega\mapsto dist(x, \Gamma)$ be the geodesic distance to $\Gamma$. Then the shape derivative of the gradient of $\mathcal{D}$ is given by

while for $x\notin K_O$ we have $\nabla \mathcal{D}'(x) = 0$.

Proof. First of all we note that $\nabla \mathcal{D}'(x) = 0$ for $x\notin K_O$ is straightforward, as a small perturbation of the obstacle will not change $\mathcal D$ locally around $x$.

In order to compute the derivative for points of $K_O$, more sophisticated computations are needed. We suppose that the boundary of $O$ is parameterized by a smooth curve $\gamma$ with unit speed. After performing a shape variation, the obstacle will become $O_ \varepsilon: = \Phi_ \varepsilon(O)$, with $\Phi_ \varepsilon(x) = x+ \varepsilon V(x)$, and the boundary is now parameterized by the curve $s\mapsto \gamma(s)+ \varepsilon V(\gamma(s))$ (which is no more parameterized by unit speed, but this is not important). The geodesic curve from $x$ to $\Gamma$ inside $\Omega_ \varepsilon$ will touch the obstacle $O_ \varepsilon$ is a point $\pi_ \varepsilon(x)$ which will be of the form $\pi_ \varepsilon(x) = \gamma(s(\varepsilon))+ \varepsilon V(\gamma(s(\varepsilon)))$, and the choice of the parameter $s(\varepsilon)$ is done such that the tangent to the boundary of $O_ \varepsilon$ at $\pi_ \varepsilon(x)$ is parallel to the vector $\pi_ \varepsilon(x)-x$. Also, the vector $-\nabla \mathcal D_ \varepsilon(x)$ is the unit vector oriented exactly as $\pi_ \varepsilon(x)-x$ and also as the tangent line to $\partial O_ \varepsilon$ at $\pi_ \varepsilon(x)$. We can arrange the parameterization so that $s(0) = 0$ and that $\gamma$ is orientated so that the exterior normal vector $n$ on points of $\partial O$ (exterior to $\Omega$, i.e., entering $O$) is of the form $n = R\gamma'$ where $R$ is a fixed $90^{o}$ rotation, say the clockwise one, and that $x-\pi(x)$ is of opposite direction w.r.t. $\gamma'(0)$.

Hence, if we denote by $N$ the normalization map $z\mapsto z/|z|$ defined on $\mathbb{R}^2\setminus\{0\}$ we have

Our goal is to differentiate this vector w.r.t. to $\varepsilon$ and find $\nabla \mathcal D'(x)$. It is possible by suitable applications of the implicit function theorem, provided the curvature of $O$ does not vanish, which provided injectivity of the tangent, to prove that all these quantities are indeed smooth and differentiable.

If we differentiate at $\varepsilon = 0$, we get

Since $DN[z] = (I-\hat z\otimes \hat z)/|z|$ and $|\gamma'(0)| = 1$, this means that $DN[\gamma'(0)]$ is the projection onto the orthogonal component to $\gamma'(0)$, i.e., the projection onto the $n(\pi(x))$-component. Hence, if we set $w: = \gamma''(0)s'(0)+DV(\gamma(0))\cdot\gamma'(0)$, we just need to prove

and the claim is proven.

If we write the condition

and we differentiate it w.r.t. $\varepsilon$ at $\varepsilon = 0$ we get, using $\gamma(0) = \pi(x)$:

We can re-write this using $\gamma(0) = \pi(x)$, $R\gamma'(0) = n(\pi(x))$ and simplifying the term $\gamma'(0)\cdot R\gamma'(0) = 0$ as follows

Using $R(x-\pi(x)) = -|x-\pi(x)|n(\pi(x))$ the result follows.

4.   Shape derivative of the average exit time

We are going now to compute the shape derivative of the average exit time. Let us recall that we consider the following shape functional

We want to compute its variation around a certain fixed domain $\Omega = R\setminus O \in \mathbb{R}^d$. For that we are going to consider all the perturbations of $\Omega$ given by a diffeomorphism $\Phi(\epsilon):\mathbb{R}^d\rightarrow \mathbb{R}^d$ defined for every $\epsilon\in [0, E], E\in\mathbb{R}$, with $\Phi(0)(y): = \Phi(0, y) = y$ for every $y\in \Omega$ (see ^[8] and ^[9] Chapter $5$ for more details). Notice that we only perturb $O$ (we can consider $V = 0$ far from $O$), so that $\Omega_\epsilon = R\setminus O_\epsilon$ as $\Omega = R\setminus O$. Moreover, we will assume that the support of $\rho_0$ is far from $O$. We set as usual $V(0) = \frac{\partial \Phi}{\partial \epsilon}(\epsilon)_{|_{\epsilon = 0}}$ and we define the following function

where $\rho^\epsilon: = \rho_t^{\epsilon}$ is the solution of (1) defined in $\Omega_\epsilon$, with initial datum $\rho_0$ (which does not depend on $\epsilon$ and it is extended to $0$ outside the original domain $\Omega_0$).

Let us note that $\Omega_0 = \Omega,$ and in the sequel we are going to use any of these two notations.

4.1.   The linear diffusion case

We will start from considering the case where the moving density $\rho_t$ is ruled by the Fokker-Planck equation (case $m = 1$). We associate with such a density, as it is said in the previous section, the shape functional (10). We consider small perturbations of the domain $\Omega_0$ by using the diffeomorphism $\Phi(\epsilon)$ defined above, and we look at the new system which rules $\rho_t^\epsilon$, the new evolution of the density in the perturbed domain $\Omega_\epsilon$.

where $\Gamma_2 = \partial R \backslash \Gamma, \Omega_{\epsilon} = R\backslash O_{\epsilon}, O_0: = O.$

The derivation of the boundary condition ruling $\rho'$ is stated here below, and is a consequence of the computations of Section 3.1.

Lemma 4.1. Let us consider the following boundary condition

that we will use for $m = 1$ or $m > 1$. Perturbating $O$ via the diffeomorphism $\Phi (\epsilon),$ we get the following boundary shape derivative condition

Proof. It suffices to apply the computation rules in Proposition 3.4 to the case $z = \rho\nabla\mathcal D+\nabla(\rho)$.

We then come into the core of the computations with the following result.

Theorem 4.2. Let $\Omega_0$ be a $C^2$ open set of $\mathbb{R}^d, \ d\geq 2$. Let $\rho_t$ be the solution of the Eq (12). The shape derivative of the average exit time (10) is then given by

where $\psi$ is a adjoint state characterized by

Proof. The shape derivative of (10) is given by

where $\rho'$ is the shape derivative of $\rho^\epsilon$, characterized by

We make use of the adjoint state $\psi$ defined by (15).

If we multiply by $\rho'$ the first equation in the system (15) and integrate by parts we obtain

Before considering the boundary term we observe that, using the equation defining $\rho'$, we may transform the above integral on $\Omega_0$ into

Let us now consider the boundary terms. The terms after integrating by parts in time vanish, because $\psi(T) = 0$ and $\rho'(0) = 0$. We only need to consider the boundary terms in space, i.e.,

Let us note, in the spirit of Proposition 3.4, $z: = \rho \nabla \mathcal D+\nabla \rho$. These boundary terms can hence be written as

We will distinguish what happens on the three parts of $\partial\Omega_0$, i.e., $\partial O, \Gamma_2$ and $\Gamma.$ Since $\rho' = 0$ on $\Gamma$ and $\nabla\psi\cdot n = 0$ on $\partial O\cup \Gamma_2$ the last term vanishes. We are then left to consider $\int_0^T\int_{\partial \Omega_0}\psi z' \cdot n$. This integral reduces to $\partial O\cup \Gamma_2$, since $\psi = 0$ on $\Gamma$. On $\partial O\cup \Gamma_2$ we have no-flux boundary conditions, and we can hence apply Proposition 3.4:

We first note that, due to the presence of $V\cdot n$, we can now reduce the integral to $\partial O$ since $V = 0$ on $\Gamma_2$. We integrate by parts the term with $\nabla_\tau$ on the boundary $\partial O$ using (6), thus obtaining

yet the term with $\kappa$ vanishes since we have $z\cdot n = 0$ on $\partial O$. We then use the formula for $\nabla_\tau\cdot$ coming from Definition (2) and we get

We now use $\partial_t \rho = \nabla\cdot z$ and $\nabla \psi\cdot n = 0$ on $\partial O$ in order to finally obtain

We then obtain the claim by putting together all the above computations.

The next computation, based on Proposition 3.5, will be restricted to the two-dimensional case.

Lemma 4.3. Suppose $O\subset R\subset \mathbb{R}^2$ is a smooth obstacle. Let us call $K_O$ the set of points $x\in\Omega$ such that the geodesic from $x$ to $\Gamma$ inside $\overline\Omega$ is unique and touches the obstacle $O$. Then, for every $x\in K_O$ we call $\pi(x)$ the first contact point of such a geodesic with $O$ and for every $y\in \partial O$ set $S(y): = \pi^{-1}(y)$. The set $S(y)$ is a segment starting from $y$ and parallel to the tangent to $\partial O$ at $y$, and is reduced to a point for every $y$ where $\partial O$ has negative curvature $\kappa(y) < 0$. For every vector field $v:\Omega\to \mathbb{R}^2$, set $W_{v}(y): = \int_{S(y)} v$, the integral being performed w.r.t. the usual length measure on the segment $S(y)$. Then, we have

Proof. We will make use of the formula for $\nabla \mathcal D'$ computed in Proposition 3.5 and of a change-of-variable. First, we note that for every $x\in\Omega\setminus K_O$ we have $\nabla \mathcal D'(x) = 0$, then the integral on the left-hand side may be restricted to $K_O$. Then, we parametrize $\partial O$ with a smooth arc-length curve $\gamma$ (in case $\partial O$ is not connected, this will be done locally). Every point in $K_O$ can be written in a unique way as $\gamma(\theta)+\ell \gamma'(\theta)$ (up to choosing, again locally, the direction of the parametrization $\gamma$) and we want to integrate in $(\theta, \ell)$ instead of integrating in $x$. If we write, by abuse of notation, $n(\theta)$ and $V(\theta)$ instead of $n(\gamma(\theta))$ and $V(\gamma(\theta))$, we have

an equality which is based on Proposition 3.5. The change of variable $x = \gamma(\theta)+\ell \gamma'(\theta)$ provides, via the computation of the determinant, $dx = |(\gamma'(\theta)+\ell \gamma''(\theta))\wedge \gamma'(\theta)|d\ell d\theta = |\ell \gamma''(\theta)\wedge \gamma'(\theta)|d\ell d\theta = \ell\kappa(\theta)d\ell d\theta$. We then have

which provides the desired result since integrating on $[0, L(\theta)]$ w.r.t. $d\ell$ is the same as integrating on $S(y)$ for $y = \gamma(\theta)$.

As a consequence, we can give a formula for the shape derivative that we are looking for. Let $F:\partial O\to \mathbb{R}$ be given via

We can then summarize our results as follows

Theorem 4.4. With the notations of Theorem 4.2, we have

4.2.   Adaptation to more general diffusion equations

We will explain the slight modifications that have to be performed if one wants to consider the case where the moving density $\rho_t$ is actually ruled by the Porous Media equation or by a more general diffusion equation of the form

The average exit time is again given by (10). In this case we define

where $\psi$ is again the solution of an adjoint equation, this time chosen as

The equation satisfied by the shape derivative $\rho'$ is now

where the shape derivative of the boundary condition is now

We note that

● The Fokker-Planck case corresponds to $h(s) = s$ and the Porous Medium case to $h(s) = s^m$.

● The gradient flow of $\mathcal F(\rho): = \int \mathcal D d\rho+\int f(\rho(x))dx$ provides a PDE of this form, for $h(s) = sf'(s)-f(s)$.

● For ellipticity (parabolicity, actually) reasons, one needs $h$ to be non-decreasing.

● The case where $h(s) = s^m+\nu s$ provides, at the limit $m\to\infty$, an approximation of the crowd motion model with density constraints endowed with diffusion, as studied in ^[5,15], which corresponds to the system

● Using $h(s) = s^m+\nu s$ with $\nu > 0$ is a reasonable choice, because the equation is less degenerate and in particular in the adjoint Eq (18) the coefficient in front of $\Delta\psi$ does not vanish, which makes the equation solvable.

Acknowledgments

This work was supported by NLAGA Project (Non Linear Analysis, Geometry and Applications Project) and by Institut Universitaire de France (IUF) via the second author's fundings. The kind hospitality of Laboratoire de Mathématiques d'Orsay during a three months visit of the first author to the second is also warmly acknowledged.

Conflict of interest

The authors declare no conflict of interest.