Foreword to the special issue "Contemporary PDEs between theory and modeling"

1.   Introduction

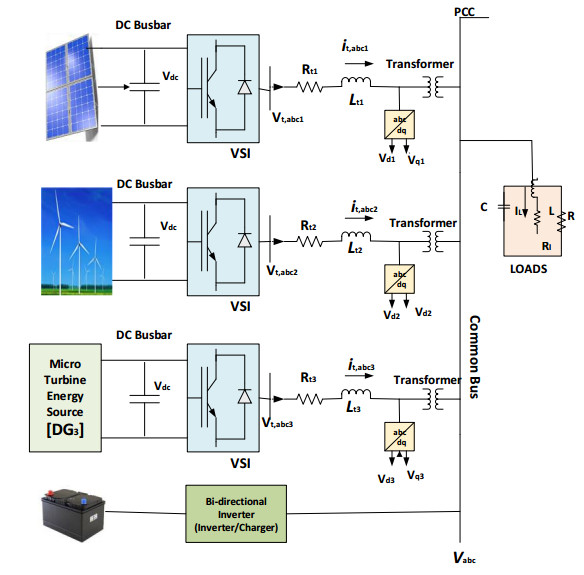
The increasing penetration of renewable energy sources (RES) into the main electricity grid is a profitable development. With the high penetration of RES, dependence on fossil fuel-based energy sources is reduced significantly. Thus, the concern for the impacts of greenhouse gas emission on the environment could be reduced by the large scale implementation of RES-based microgrids ^[1,2,3,4]. A microgrid (MG) which is a fraction of the main electric grid, is a small electrical network that can independently generate electricity when it is disconnected from the main electricity grid owing to faults, disturbance of the power flow of the main grid or when the main grid is non-existent ^[5,6,7,8]. Two modes of operations are possible with microgrids; the grid-connected or autonomous mode of operation. When operating in the grid-connected mode, the microgrid is directly connected to and is controlled by the main grid. While in autonomous or islanded mode, the frequency and voltage of the microgrid are controlled locally and independent of the main grid. Shown in Figure 1 are three DGs of an islanded system of microgrids with heterogeneous RES: the solar PV system, the wind generator and the microturbine. The RES serves as the prime mover for the microgrid system, without which there will be no output from the microgrid. A three-phase voltage source inverter (VSI) is connected to change the energy generated to its AC equivalent. The output of the VSI is connected to the microgrid system's main bus via a line impedance and a transformer. The energy storage system serves to store generated energy for later use. The load to be powered is connected to the main bus of the microgrid.

A microgrid has one or more DG sources which could be non-renewable energy-based or renewable energy-based. Common renewable energy sources are solar photovoltaic systems, small hydro turbines, wind turbines, and fuel cells etc. Unlike synchronous generator rich in inertial, RES-based DG microgrids have very low inertial and random output values. Therefore, microgrid uses intelligent electronic devices (IEDs) and communication networks for its smooth operation. Although, some methods, such as the droop-based techniques, used control methods that are not dependent on the communication network. Power converters and electronic control units are essential for the interconnected DG systems for appropriate working. Communication networks are indispensable for the exchange of information in the MG. System operation and control information upon which the power inverters' smooth operation must be shared via the installed communication networks ^[9].

Distributed systems in the microgrid are interconnected with communication networks. The electrical energy produced flows along the microgrid, while energy management data, billing and control data are transmitted through the communications networks which could be wireline or wireless ^[10,11,12]. The use of communications networks for information sharing gives rise to delays in the delivery of system operation information and power control information or even a complete loss of vital information during the signal transmission. Signal interference is likewise a common problem because communication channel is shared with other users. Some previous work considered information delay a constant value to simplify the design. In other studies, the communication delay is regarded as negligible. It is vital to give attention to communications delays and packet loss during transmission while designing a load sharing control system for the DGs to have appropriate and synchronized output values from all the inverters ^[13,14]. Most communication networks are prone to delay. Wireless communication networks such as ZigBee (802.15.4), Wi-Fi (802.11), and WiMAX (802.16) proposed for microgrid communication experience time-varying delay. The observations mentioned above make the study of time-varying communication delay very crucial for power inverters control in MG.

Several methods have been proposed to mitigate communication network-induced impairments in microgrids. In ^[15], an investigation on the effects of wireless communication on MG control was carried out. A constant delay was maintained for all transfer routes using a unified Smith predictor approach. The approach was unsuccessful in mitigating the time-varying delay, which generally results when different routes are involved. Y. Xu et al. ^[16] studied smart grid wireless network, communication delay analysis was carried out. Results provided from the work set-theoretical delay bounds that could be employed in designing wireless networks for smart grids. Results also suggest the applicability of wireless mesh networks for microgrids. However, the possibility of communication failure when packet loss occurs was not considered. An optimal design scheme was proposed by ^[17] for directed network topology. A small signal dynamic model of an MG was derived to investigate the effects of delay on MG stability. Real-time hardware-in loop simulations were used to verify the proposed method's effectiveness.

In ^[18] master-slave communication model between generating sources in the MG was used. Lyapunov-Krasovskii was employed in the calculation of allowable delay that ensures system stability. The system was modelled as a time delay system that uses wireless communication between inverters in the MG. Although master-slave depicts good performance in load sharing among inverters, it suffers from a single point of failure. If the master cluster fails to function, the whole system will collapse. G. Chen et al. ^[19] proposed Lyapunov-Krasovskii functions for the analysis of the stability of a distributed secondary control of an MG under communication delays. The control protocol is implemented using a sparse communication network. The performance of the method was not tested under varying load characteristics. G. Lou et al. ^[14] worked on a distributed cooperative scheme to achieve frequency synchronization from different distributed generations in the MG. Time-varying communication delays were taken into consideration in the design. Delay boundary that ensures stable system operation of the system was presented. However, signal failure was not accounted for in this design.

A series of research conducted by ^[20,21,22] on MG control use different approaches for DC and AC MG control. Distributed adaptive droop control and distributed cooperative control of DC MG was investigated. Also, a droop-free distributed control for AC MGs was investigated. In all these works, neighbouring inverters share control information using wireless communication. A sparse communication graph that connected the inverters in the MG was used. The ability of the methods to handle disturbances originating from communication networks was presented. However, delay caused by communication network was treated as a constant value. Q. Shafiee et al. ^[23] defined packet loss and packet latency as important communication network parameters to analyze control effects in microgrids. In this article, the review of communication induced impairments in microgrids and how they are modelled is carried out. The impacts of communication impairments on microgrids operation, the mitigation methods employed for communication impairments reduction and findings from the work are analyzed.

2.   Related review articles

Secondary control in microgrids requires communication networks for smooth operation ^[24]. The impairments induced by the use of communication networks in secondary control of microgrids should be mitigated. Efforts to achieve optimum secondary control have been reviewed, some of the related review articles are presented in this section. In ^[13], the impact of communication failure on distributed control methods in AC microgrids was the review's focus. A comparison of methods used to reduce communication latency, data packet dropout, and channel noise on distributed controllers was presented. Also discussed is the distinctiveness of distributed control systems and their challenges. An analysis of the influence of wireline and wireless communications on microgrid performance was carried out in ^[25], the review aimed at determining the network requirements for a successful operation of microgrids. The review in ^[26] is focused on hierarchical control in microgrids. The discussion is on the optimum active and reactive power-sharing, and eliminating the effects of communication delays using hierarchical control of microgrids. The review article by ^[27] highlights the control strategies and techniques used to stabilise DC microgrids. Stability analysis tools for smooth system operation was also presented. A survey of primary controllers used for distributed generation synchronization was carried out by ^[28], the control scheme for centralized architecture and master/slave control technique was presented. To avoid communication link challenges, droop control was intended for use where the system's stability is considered critical. The review however does not include secondary control methods. The review's focus carried out by ^[29,30] is to describe various techniques employed for autonomous AC microgrid control. Attention was given to the level of communication required by the secondary control methods discussed. ^[31,32] reviewed control methods used in DC microgrids, while ^[32] carried out a general review of the methods, ^[31] presented a review describing hierarchical control issues such as power-sharing, voltage regulation and stabilization methods. ^[33] review operation of smart inverters with a specific interest in plug and play, self-awareness, cooperativeness and adaptability of the inverters as reasons for categorizing them as smart. The work also discusses the possibility of inverters communicating over a long-range to empower various control schemes. The survey in ^[34] discussed the cyber security of smart microgrids. Attacks on data integrity, availability and confidentiality were discussed. Also reviewed are the economic impacts of cyber-attacks on microgrids installations and the detection and defensive strategies employed against false data injection attacks. Adaptive protection of microgrids was the focus of the review in ^[35]. It was pointed out that the reliability of the communication network and protection against cyber-attacks remains a big challenge in the implementation of reliable schemes based on adaptive protection.

In all these review articles, no attention was given to how communication impairments are modelled, and none has considered cyber-attacks on microgrids installations as impairment induced because of the increasing use of wireless communication networks.

From the viewpoint of the previously mentioned research gaps, this review investigates communication induced impairments in autonomous microgrids. The study contributions are described as follows:

(1) Impairment models and mitigation approaches were described for data packet dropouts and communication network induced delay in autonomous microgrids.

(2) Cyber-attacks resulting from using communication networks in the microgrid network, especially wireless communications, were discussed.

(3) The review presented and discussed cyber-attack detection techniques, impacts of attacks on system operations, and attack mitigation techniques.

The paper is arranged thus: Section Ⅰ presents the introduction to the review, related reviews are presented in section Ⅱ. Communication technologies employed in microgrid operations were discussed in section Ⅲ, while the focus of section Ⅳ is the specific communication induced impairments studied in the literature, their impacts on microgrid operations and how they are modelled for further investigation of their nature. Section Ⅴ deals with mitigation approaches and control methods used in islanded microgrid control. Ⅵ and Ⅶ discuss mitigation approaches and control methods used in islanded microgrids control. In section Ⅷ, a conclusion to the review was drawn.

3.   Communication technologies employed in microgrid communication

For wireless technologies, the advantages of lower installation cost, suitability for deployment in rural areas and flexibility future expansion make its applications more desirable than their wired counterparts. Wired communication technologies can give higher bandwidth, and are more reliable, but the installation cost is high, and they are not as flexible when there is a need for expansion ^[25]. Suitable wired communication technologies for microgrids applications include power-line communication (PLC), Ethernet and Fibre Optics, while Bluetooth, Wi-Fi, ZigBee, Cellular, LoRa, and WiMax are commonly used wireless communication technologies.

3.1.   Functionality of the communication technologies

All wired transmission media have a physical connection from the signal source to the sink where the transmitted signal is received. Power Line Communication (PLC) technology enables the transmission of data over existing power cables. This implies that, with this technology, power cables that initially can only carry power to devices can now simultaneously control the device and even retrieve data from it. In Narrow Band Power Line Communication (NB-PLC) technology, data transmission is achieved through a narrow frequency band and at a low bit rate. The technologies emanating from NB-PLC had the focus on enhancing smart grid applications and building automation. A data transfer speed of between 10-500kbps is achievable with this technology. The Broad Band Power Line Communication (BB-PLC) can operate at a higher speed, reaching hundreds of Mbps. It was designed to have the capability for applications that require internet access ^[36].

Ethernet communication provides the means of connecting various electronic devices and computers in a physical network often referred to as the local area network (LAN). The idea makes efficient sharing of data, files, and information possible between computers and electronic devices. The most common deployment of Ethernet cables is connecting a Wi-Fi modem or router to the entry port of the internet. Ethernet connections are faster and more reliable than its wireless counterpart. Fibre optics technology involves using thin strands of glass drawn carefully to a diameter similar to that of human hair. Bundles of the glass strands are put together in optical cables. Data transmission is by light. At the source, the data information is used to encode the light signals which is effectively decoded to retrieve the data at the receiving end. The optical fibre is essentially a transmission medium.

Bluetooth technology is widespread for wireless voice and data communications within a short range. Bluetooth devices employ short-range radio waves for pairing with devices within range. Each Bluetooth device is equipped with a tiny computer chip that broadcast its signal to detect and connect. Wi-Fi technology is comparable to Bluetooth since it also utilizes radio waves for conveying data at a high-speed over short ranges wirelessly. By breaking the entire signal into small units, transmitting the pieces over multiple radio frequencies. Wi-Fi can achieve transmission at lower power per individual frequencies. This technique also makes possible the use of multiple devices on the same Wi-Fi transmitter. Another technology for the connection of smart devices over the wireless link is the ZigBee, which was built upon the IEEE 802.15.4 standard. The technology promises to be cost-effective and energy efficient compared to Bluetooth and Wi-Fi technologies. Unlike Bluetooth, which operate on point-to-point communication, ZigBee operates in a mesh network. Its connections are spread among the nodes of the wireless network. The nodes are capable of communicating with one another and sharing networks over a large area ^[25]. The operation of WiMAX is close to Wi-Fi except that the speed of operation is higher and the range and numbers of users are much larger. LoRa (Long Range), a wireless technology, combines two desirable characteristics; ultra-low power consumption and effective long-range. Long Range Wide Area Network (LoRaWAN) represents the communication protocol and system architecture for LoRa network. However, the range is dependent on the topology of the environment. A typical LoRa operates within a range of 13 Km and 15 Km. Lora radios are equipped with chirp spread spectrum (CSS) modulation method to realize an advantageous long range of communication while sustaining a low power consumption capability.

Global System for Mobile Communications (GSM) come with a combination of Time Division Multiple Access (TDMA) and Frequency Division Multiple Access (FDMA). In FDMA GSM, a 25 MHz frequency band is divided into 124 carrier frequencies with a 200 KHz space between each carrier. The same frequency channel is allotted to different subscribers; this is done by dividing the frequency band into multiple time slots. This arrangement makes sharing the same transmission space by multiple stations possible. While GSM is still in use, upgrades of the basic system are already available in Universal Mobile Telecommunications System (UTMS), the Long Term Evolution (LTE) and the emerging 5G networks wireless standards.

Table 1 compares microgrids communication technologies, giving attention to coverage, data rate, frequency and specific usage of the technologies considered in microgrids applications with given references.

Optical fibre and Ethernet are suitable for primary control purposes in the microgrids. They have the required data rate, which ensures low latency for optimal operation of the primary controllers. They have been applied for information communication between DGs in ^[37], and monitoring and control of energy meters in ^[38]. In ^[39], optical fibre was used for metering communication. PLC may not be suitable for primary control purposes given its low data rate. GSM networks are primarily designed for machine to human communications and operate in the licensed radio frequencies. Operating such networks for microgrid will be expensive and can reduce the gains derived from microgrid installations. Bluetooth, Wi-Fi, and ZigBee/6LoWPAN technologies are appropriate and cost-effective in applying microgrids. They have been applied for information sensing and data communications ^[40,41,42]. Bluetooth technology, however, is limited in coverage range. While the likes of WiMAX, LoRa and SIGFOX technologies offer a wider coverage range. They are essentially designed for communication over a long distance.

4.   Impacts of communication network induced impairments on microgrids operation

The inclusion of communication networks in the microgrid network can lead to several challenges that must be addressed to avoid degrading the performance of the microgrid operation. In this section, the impacts of communication networks induced impairments are discussed. Communication induced impairments in microgrids mostly investigated in pieces of literature are packet latency or delay, packet loss, noise, jitter and cyberattacks.

A data packet is considered lost if it is not delivered at the expected receiving end after transmission due to communication link failure or expiration of the delay limit while queuing at the point of reception ^[48]. Time-varying delays naturally result because of the asymmetry of interactions, congestion, bandwidth, and transmission speed. Packet latency or delay can be estimated by the total time taken from the time the last bit is transmitted at the transmitting end, and the time the last bit is received at the targeted receiving end ^[49,50,51]. Communication noise is another practical impairment that plagues the microgrid operation. It is stochastic and dependent on the characteristics of the medium of communication. Channel noise in communication among several agents was considered in ^[52], while investigating the impact of communication noise among multi-agent systems using consensus protocol was the focus in ^[53,54,55]. Cyber-attack is not inherent impairment, but the network is exposed to such attacks that come mainly external to the microgrid system because the wireless communication network is integrated in the system operation.

For microgrid operations and management, data packet losses, information packet delay and cyber-attacks have the most devastating effects and are primarily investigated. The effects of communication network delay and packet loss are inherent in a wireless communication network; they generally reduce the performance of the control algorithm in microgrids. In ^[24] it was shown that latency affects the speed and stability of the system control. ^[56] used Smith Predictor based on information of delayed packets. The results show that time-varying delay affects both the amplitude and frequency of the entire system. It also shows that power loss also increased when there is no mitigation of packet latency. In ^[57], the algorithm for state estimation of microgrids was presented. The least mean square was used for the implementation of the algorithm. In the simulation, predefined values were set for the Gaussian noise and packet loss. The results show that the proposed state estimation converges rapidly without packet loss. In a similar work, ^[9] made a simulation with four sensing stations sending information in a broadcast fashion and using predefined, time-invariant parameters for the entire system. The results also showed that packet loss increase system instability.

Communication delay was calculated in ^[42], ^[58] based on the number of DGs, controller location and wireless network used. The work sought to improve load sharing performance, regulate the frequency and voltage of microgrid containing multiple DGs. Results show that voltages of the system are subjected to substantial oscillations when communication delay is lower than that required for processing by the converter. It also shows that the lower the communication bandwidth, the more significant the delay becomes. Varying communication latencies were tested by ^[23,59,60], in attempts to regulate voltage, stabilize frequency and share power in islanded microgrids. Close-loop system response tends to oscillate also; results indicate oscillations increases with delays and convergence speed is proportional to communication delay.

Distributed secondary control rely on communication networks for operation. Although many advantages could be derived from the application of distributed systems, it is, however, vulnerable to malicious attacks. In ^[61], individual DERs were the subjects of cyber-attacks while the link between DERs was targeted in ^[62] to corrupt data transfer. When false data injection is capable of corrupting data transfer, and as a result, the integrity of the data can be compromised. Using a centralized control structure, ^[63] proposed detection and mitigation schemes to correct cyber-attacks in DC power systems.

4.1.   Mathematical modelling of packet loss probability

Data packet transmission between two agents or nodes is illustrated in Figure 2. The problem of packet loss is most significant when wireless communication networks such as Wi-Fi, Bluetooth, LoRa, ZigBee and WiMAX are used for data communication. The mathematical model for the description of data packet loss is explained thus: Given two nodes m and n as shown in Figure 2; the information packet ${J}_{k}$ arrives at node m, packet waits in the queue at node m after which it is transmitted to node n, via link (m, n). Following the requirement of power inverters for optimal performance in the microgrid system, a delay limit ${\tau }_{limit}$ is set for each packet. A packet arriving outside this ${\tau }_{limit}$ is discarded and considered lost. However, a packet lost during transmission within ${\tau }_{limit}$ will be retransmitted as long as the ${\tau }_{limit}$ is not exceeded until it is successfully delivered or eventually lost due to exceeding ${\tau }_{limit}$. The total packet loss probability ${G}_{l}^{\left(m, n\right)}$ by packet ${J}_{k}$ is dependent on two factors:

1. the probability of packet drop ${G}_{d}^{\left(m\right)}$ due to expiration of delay limit while queueing at node m, and

2. the probability of packet loss ${G}_{l}^{\left(m\right)}$ over the link (m, n), which is a function of packet error probability ${G}_{e}^{\left(m\right)}$ due to signal fading over the link (m, n).

4.1.1.   Packet loss probability due to signal fading

Determining packet loss probability over communication link affected by signal fading requires the knowledge of the packet error probability ${\mathrm{G}}_{\mathrm{e}}^{\left(\mathrm{m}\right)}$ which depends on the specific channel conditions of the link (m, n) and the applied transmission schemes. The packet error probability ${\mathrm{G}}_{\mathrm{e}}^{\left(\mathrm{m}\right)}$ for packet ${\mathrm{J}}_{\mathrm{k}}$ can be modelled by the sigmoid function as ^[64]:

where γ is the channel status information parameters in terms of the detected link SINR, ζ and δ are constants corresponding to the used modulation and coding schemes for a given packet of length L. In a wireless network such as Wi-Fi, the packet collision probability ${G}_{c}^{\left(m\right)}$ due to contention access to the medium is also included in the estimation of the link's packet loss probability. Packet collision probability ${G}_{c}^{\left(m\right)}$ can be determined from:

where τ is the probability that node m transmits in a randomly chosen slot time, and x is the number of contending nodes. Therefore, packet loss probability over the link (m, n) can be written as ^[15,64]:

However, Bernoulli distribution was used to represent the packet loss model in ^[9,65], the probability representation used for packet loss is given in Eq 4 as:

where ${\mathrm{\lambda }}^{a}$ is the average packet arrival rate at node m. The model shown in Eq 4 is simple yet effective, therein packet loss is measured based on whether the signal is successfully delivered at the receiving point or not.

4.1.2.   Packet loss probability due to expiration of delay limit

Packet loss due to expiration of delay limit is affected by the bandwidth, available throughput and transmission rate. If ${b}_{\left(m, n\right)}$ is the bandwidth of link (m, n). Then, the available throughput over the link (m, n) is directly determined by the transmission rate ${r}_{\left(m, n\right)}\left({b}_{\left(m, n\right)}\right)$. The effective transmission rate is given by:

To derive the packet drop probability, ${G}_{d}^{\left(m\right)}$ due to the packet delay limit expiration during the wait in the queue of node m, it is important to analyze the queueing model of the packet ${J}_{k}$ at that node. Let ${\tau }_{crt}$ be the current delay incurred by packet ${J}_{k}$ when the packet arrives at node m and enters the queue of that node. The maximum retransmission limit ${\tau }_{max}^{\left(m, n\right)}$ for packet ${J}_{k}$ over the link (m, n) based on the delayed deadline ${\tau }_{limit}$ can be expressed as ^[66]:

Considering service time ${X}_{\left(m, n\right)}^{t}$ for packet ${J}_{k}$ over the link (m, n), by queuing analysis, the mean time spent waiting for packet ${J}_{k}$ at node m can be shown as in ^[15,64]:

where ${\mathrm{\lambda }}^{a}$ is the average packet arrival rate at node m.

Research work on microgrid communication that investigates mitigation techniques used to reduce the impacts of packet loss is discussed here. Frequency and voltage restoration in an islanded microgrid is the focus of the research conducted in ^[23]. Each agent in the network calculates a new average of data after the reception of information from other agents in the network. Bernoulli random process was used to model packet losses to give a probability of 0 or 1 when investigating the impact of data packet dropout on the system. The control method uses the previously measured value at intervals when the information packet is lost to prevent performance degradation. Thus, the distributed secondary control method restored frequency and voltage to normal values for optimum operation of the microgrid. Estimation of packet loss on the microgrid was carried out by ^[9,65], Bernoulli distribution was used for modelling packet loss. Information data were transmitted over a sparse communication graph as reported in ^[67,68]; the graph was designed with a minimum redundancy to prevent a breakdown of operation when data packets are not delivered as a result of link breakdown. Results demonstrated the capability of a well-designed sparse communication graph in mitigating link failure. Distributed cooperative control method was used in ^[48] for microgrid voltage control. Communication link failure causes a time-varying communication graph which could degrade system performance. The DG that lost communication operates in the network based on the droop controller and the latest control command received. Results from work show that the output of the DG with communication link failure is not synchronized with the other DGs in the network. Presented in Table 2 are the description of packet loss and the mitigation approaches employed in pieces of literature.

4.2.   Latency/Delay

Latency or delay is inherent in the communication systems. In some applications, the communication delay is negligible when the delay is within an acceptable range for the normal operation of that system. A comprehensive link delay includes four components: the processing delay, the time interval from the time packet is received, and the time it is assigned for transmission. The propagation delay occurs between the time the last bit is transmitted and received from the head node and the link's tail node, respectively ^[49,50,51]. Other components are the queueing delay which signifies the time a packet is transmitted and the actual time reception. Delay as a result of transmission is the time interval between the transmission of the first and last bits of the packet.

The inherent communication delay of the channels of each DG can be measured using the packet round trip time (RTT) method ^[14]. Suppose $\tau \left(t\right)$ represent RTT when node i received acknowledgement, for the corresponding link i, let: ${d}_{p, i}\left(t\right)$ be processing delay, ${d}_{g, i}\left(t\right)$ the propagation delay, ${d}_{q, i}\left(t\right)$ stand for the delay due to queueing and ${d}_{t, i}\left(t\right)$ be the transmission delay. Given that the network end-to-end connection has K nodes, then ^[69]:

The microgrids communication network connection is expected to be constant or fixed during a session. The propagation and processing delay can be safely treated as a constant value, denoted here as X. Delay dynamics will then be limited to the evolving state of transmission and queueing along the path. Thus, total delay due to packet transmission via link (m, n) when the acknowledgement is received at node n can be calculated using:

where ${q}_{i}^{(m, n)}\left(t\right)$ dynamics of queue length, and it is given by Eq 7.

In ^[70] voltage regulation was the main focus of the research. Distributed controller, which mimics harmonic voltage sources together with virtual impedance, thus lower voltage distortion in the network. Communication delay was quantified as time addition of time set for point generation and the inverter to receive set point from neighbours. Results from the work indicate that current sharing errors increase with communication delay. The method employed reduced communication congestion and established current sharing performance is highly dependent on delay. To regulate voltage and achieve accurate power-sharing in DC MGs, ^[71], a secondary control technique handles power-sharing via a distributed strategy, while dc bus voltage restoration was achieved using a decentralized technique. Communication delay was represented by ${e}^{-{\tau }_{d}s}$, transient response damping becomes lower under delay, however, it becomes stable and oscillating around consensus values with the application of the control method. Disturbance-observer based method for frequency regulation in a MG with low inertia was carried out by researchers in ^[72]. Communication delay was taken to vary randomly from 0.05 to 0.15 sec. Uniform distribution was assumed. The delay led to high-frequency transients in the system frequency. The magnitude of oscillations was significantly reduced using the method proposed.

Using a fixed communication delay of 0.01 to 1 sec ^[68] investigated the performance of a consensus-based cooperative droop control to achieve enhanced reactive power-sharing, in the technique used, the droop slope gain was adaptively adjusted. Laboratory results show that the system remains stable as the eigenvalues remain in the left half complex plane. Also, simulated power-sharing at a delay of 1 second is moderate. In the research by ^[73], precise load sharing is affected through the droop control technique. A low-speed communication; control area network (CAN) was used to obtain voltage regulation. A time delay of 0, 20, 60 and 100μs were used to test the impacts of communication delay. Stability analysis revealed that communication delay forces the closed-loop system poles to draw closer to the imaginary axis.

4.3.   Cyber security issues

Microgrid installations become prone to cyber-attacks, especially when a wireless communication network is used for information sharing. Such attacks seek to gain unauthorized access to user data to deny intended users access to the network, change consumer data for economic reasons, or disturb the smooth operation of the entire system. Common attacks experienced because of the use of wireless communication networks in MGs are discussed in this section.

4.3.1.   Denial of service (DOS)

This type of malicious attack is carried out to prevent authorized user access to the network. In synchronization floods DOS attack, the attacker transmits spoofed synchronization requests continuously to the IED. This attack can distort the connection between the intended user and the network. In buffer overflow DOS, a malicious code is transmitted to initiate a large data size, resulting in buffer overflow ^[35,74]. The focus of the research in ^[75] is to investigate the impacts of denial of service attacks on the security of cyber-physical MGs and analyze the system stability while under such an attack. Simulation results revealed DoS attacks on MGs can result in communication delay and eventual system instability. In ^[76] mitigation of DoS attacks was carried out by splitting the data plane from the network control plane. Then, an exchange of control plane overpower bus was implemented. In this way, the configuration of the data plane was made possible. Each DER are treated as either active or passive agent in the network. The operating mode of each agent is determined by software-defined MG control. Using a distributed secondary control framework, researchers in ^[77] were able to detect DoS attacks on energy storage systems of an MG. The detection mechanism was based on an acknowledgement-based strategy. For paralyzed communication graphs, a communication recovery technique was proposed. Experimental results show the applicability of the approach.

4.3.2.   Data manipulation attack (DMA)

An attacker intends to compromise the password and manipulate data to gain undue advantage and access to a system's network or IEDs. Upon gaining such unauthorized access, a false signal could be sent across the network, resulting in system collapse and disengagement from the targeted part, thereby disrupting regular system operation. The approach used in ^[78], ^[79] relies on information theory precisely Kullback-Liebler divergence-based criterion in detecting and mitigating data manipulation attacks on secondary control of frequency and voltage in an AC microgrid distributed system. Individual DER can detect compromise in the integrity of the information received from its neighbour in the distributed network and discard such malicious information. The approach was operated on communication graph connectivity.

4.3.3.   False data injection attack (FDIA)

In a false data injection attack, an attacker alters the system mode by injecting malicious data into each of the network agents ^[80]. ^[81] investigate false data injection attacks aimed at depriving users of MG network services paid for. The study results suggest that an attack signal may be optimized to balance energy demand with supply. Such false data injection attacks could be detected when differences in earnings are calculated for similar energy trading. In similar research, researchers in ^[80] used Hilbert-Huang transform and blockchain-based approach to secure data exchange to detect false data injection attack. Simulation results showed that the approach could detect and prevent attackers from penetrating the network of DC MGs. To detect and quantify the impact of false data injection attacks of DC MG network, ^[82] use signal temporal logic-based detection approach. The effectiveness of the approach was verified using a hardware-in-loop experiment. Preliminary results indicate the method can be applied for detection of both DoS and false data injection attacks on MG networks. Researchers in ^[83] use the mitigation approach relies on a weighted mean subsequence reduced algorithm for a multi-microgrid system. Individual MG acting as agents is programmed to reject unusual traffic coming from an agent under attack in the network, and thus system desired performance could be maintained. In Table 3, a description of cyber-attack featuring; attack detection techniques, impacts on microgrid installations and mitigation approaches is presented.

5.   Communication impairments mitigation strategies

Communication induced impairments in microgrids could be handled using two methods, which are:

ⅰ. the use of high-speed communication networks such as fibre optics, 5G cellular network, or non-industrial, scientific, and medical (ISM) frequency bands (Non-ISM bands).

ⅱ. development of smart control solutions and mechanisms incorporated into the microgrids controllers that make the microgrids resilient against communication impairments, thus reducing the resultant effects of communication impairments on the general operation of the system ^[25].

In this review, attention will be given to secondary control solutions employed to mitigate communication impairments in microgrids. Apart from the lack of interoperability of specialized high-speed communication networks, the cost of operating one could render the microgrid itself cost-ineffective. Therefore, researchers tend to use inexpensive but effective control methods for impairments mitigation. However, new communication technologies are emerging that can bridge the gap between the two alternatives.

6.   Microgrid control

The hierarchical control structure is the bedrock for the microgrid control framework. The primary, secondary and tertiary control structures are the three levels of hierarchical control in microgrid ^[25]. Voltage and frequency stability maintenance after the islanding process is handled by the primary control. The autonomous operation of MG using only the primary control layer results in deviations in operating frequency and voltage. The corresponding adverse effects on the general performance and operations of the MG demands a secondary control that will effectively mitigate the anomaly introduced by the primary control method ^[59]. As a follow-up of primary control, the secondary control compensates for the inadequacies created by the primary control. Voltage and frequency synchronization are restored at this level of control. The tertiary control manages the power flow between the main grid and the microgrid. The economical and optimal operation of the grid is a responsibility of the tertiary control level. Microgrids hierarchical control structure and the function of each control stage is shown in Figure 3. In Primary control, instantaneous control of frequency and voltage is a requirement to ensure system stability. This implies the operation of the controllers are time-critical and, thus, should not rely on the communication network. The effects of communication impairments are chiefly felt in the secondary control. Communication induced impairments such as latency, data packet dropout and noise could degrade the performance of the microgrids. Information shared in the tertiary control layer are not time critical and cannot affect system performance, since data shared at this level are related to business aspect of the microgrid. An exception to this is when the system comes under malicious attacks seeking to compromise the integrity, authenticity and intension of the data shared.

6.1.   Centralized communication dependent control (CCDC)

Mitigation strategies that rely on the CCDC schemes exchange information such as control commands, operation and sensors' information between a centralized controller and the local controllers in the DERs. The centralized controller is responsible for processing the information after which the control commands are related to the individual local controllers. The drawback of the CCDC is related to its dependence on the communication network used. It also has reliability concerns because it is subject to a single point of failure. Once there is a problem with the central control, the entire system collapses. In Figure 4, all the local controllers take information from the central controller for their operation. The performance of the local controllers is directly dependent on the central controller.

6.2.   Distributed communication dependent control (DCDC)

Distributed communication dependent control scheme uses a framework where each DG can communicate directly with each other ^[85]. Local controllers achieve control but status information is shared so that synchronization can be ensured at the common bus of the microgrid. DCDC scheme is more reliable than centralized control since there is no single point of failure that can result in a complete system collapse in a situation where one link of the system failed. However, communication latency and packet dropout between the links could degrade the system's performance. Local controllers must operate at a faster rate compared to the secondary controller to prevent system instability. The architecture of a distributed communication dependent controller is shown in Figure 5. Each controller shares information with its neighbour via the communication network installed. The individual controller can operate independently. However, under normal operating conditions, the neighbour's reference signals are used by the local controller to update its output so that synchronization can be achieved at the common bus where the output of the microgrid is connected to the load.

6.3.   Communication-free control: droop/primary control of microgrid

The droop control method is used at the primary level of control because at this level, the operation of the controllers is time-critical. Long latency will result in system instability since instantaneous control of frequency and voltage is required to ensure system instability. Hence, control at this level is not reliant on communication networks whose major impairment is a delay. However, the anomaly that results from primary control methods is corrected by the secondary control methods.

Imbalance line impedance degrades the performance of the conventional droop method. Poor load sharing and voltage regulation is the drawback of the method ^[86,87]. Voltage regulation via secondary control techniques is a common approach used in combatting the menace of voltage deviations or mismatch among distributed inverters in islanded microgrids. The conventional voltage and frequency droop control is given as ^[88]:

where E is the amplitude of DG output voltage (RMS value), ${E}^{*}$ is the rated RMS voltage of the inverter, ${\omega }^{*}$ is the rated system line frequency, $\omega$ is the measured system line frequency, ${n}_{q}$ and ${m}_{p}$ are the droop coefficients. Artificial droop is introduced in the inverter frequency to share real power among the multi-inverters, ^[32]. If $\omega$ is inverter frequency which is set by ${m}_{p}$ and the phase is set by integrating the frequency. Droop characteristics introduced in the voltage magnitude is responsible for reactive power sharing among multiple inverters. A voltage set point say $\delta {e}_{i}^{2}$ and frequency set point of $\delta {\omega }_{i}^{2}$ is assigned to the inverters attached to primary controllers in order to reach a global voltage regulation. The set point is responsible for adjusting the voltage to the nominal value. The droop equation then takes the form:

For simplicity and ease of understanding, the diagram shown in Figure 6 depicts an equivalent circuit representing islanded microgrid with n DGs connected in parallel. Although the DGs are of similar power ratings, disparities in the impedances results in varying voltage magnitude and frequency at the common AC bus. Considering DG1 and DG2, given that ${Z}_{1} > {Z}_{2}$, the E-Q droop characteristics are shown in Figure 7, while the P-ω droop characteristics are represented in Figure 8.

6.3.1.   E-Q conventional droop control

(a) Voltage restoration: The E-Q characteristics representing voltage restoration is depicted in Figure 7a, E₁ and Q₁ gives the voltage magnitude and reactive power due to DG₁, respectively, while DG₂ injected E₂ and Q₂ into the microgrid network. The voltage and reactive power responses with the conventional droop control are represented by K (E_1, Q₁) and M (E₂, Q₂); the solid black line. The different values of reactive power is an indication that it is not being shared accurately. ΔQ1 gives the reactive power deviation at this point. The point L (E*, Q'₁) and N (E*, Q'₂) represent the points when the secondary method is used to restore the voltage to the rated value E* at which point the reactive power deviation is larger and it is given by ΔQ₂.

(b) Reactive power-sharing: A similar scenario is depicted in Figure 7b, which represents reactive power-sharing. Points M (E'_1, Q') and N (E'_2, Q') which represent the new values of voltages from the secondary reactive power sharing control, from the initial values of K (E₁, Q1) and L(E₂, Q2) when the conventional droop was applied. With the improvement in reactive power-sharing at Q', the magnitude of voltage deviation increases from ΔE₁ to ΔE₂. Obviously, achieving voltage restoration comes at the cost of degrading reactive power-sharing. So, there is a trade-off between the two objectives ^[26].

6.3.2.   ω-P conventional droop control

(a) Frequency restoration: The ω-P characteristics representing frequency restoration is shown in Figure 8a, ω₁ and P₁ gives the magnitude of frequency and active power due to DG₁, respectively, while DG₂ injected ω₂ and P₂ into the microgrid network. The frequency and active power curves with the conventional droop control are represented by K (ω_1, P₁) and M (ω₂, P₂); the solid black line. The active power is shared according to the power ratings of each DGs. The active power deviation at this point is given by ΔP₁. The point L (ω*, P'₁) and N (E*, Q'₂) represent the points when the secondary method is used to restore the frequency to the rated value ω* at which point the active power deviation is larger and it is given by ΔP₂.

(b) Active power-sharing: Following the same narration, depicted in Figure 8b is active power sharing characteristics. Points M (ω'_1, P') and N (ω'_2, P') which are the new values of frequency from the secondary active power sharing control, from the initial values of K (ω₁, P1) and L (ω₂, Q2) when the conventional droop control was employed. The active power sharing improvement can be seen in the fact that the two DG sources shared a common value P'. However, the magnitude of frequency deviation increases from ΔP₁ to ΔP₂. The analysis shows that a trade-off must be made between frequency stability and active power-sharing while using the secondary droop control technique for islanded microgrids.

To enhance the stability of voltage and frequency using droop control, voltage and frequency are drooped based on the active (P) and reactive (Q) power as the control level demanded. ^[86] proposed an improved droop method for reactive power-sharing, low-bandwidth synchronization signals is used for error reduction and voltage restoration operations. The technique used improved reactive power-sharing and general performance of the microgrid system. Also, in ^[89], the analysis of the line impedance difference between various inverters on power-sharing with the traditional droop control method was presented. ^[90] proposed a control strategy for harmonic power-sharing in an islanded microgrid in another droop-based method. In work by ^[91], a strategy that employs an adaptive voltage droop control to achieve accurate reactive power-sharing was investigated. Droop-based methods are usually low cost, take measurement locally and apply to both grid-connected and islanded mode. A drawback of the control method in the islanded mode is that microgrid voltage and frequency vary with load change. Therefore, a mechanism must restore the system frequency and voltage to nominal values after a load change. The performance is also poor in MG with high penetration of RES.

Various modifications of the conventional droop control method have been used to reduce the disadvantages of the method. In the adjustable load sharing method, the active and reactive power control can be achieved without impacting the frequency and voltage of the DG source. The voltage active power droop/ frequency reactive power boost (VPD/FQB) approach, alternate consideration of VPD/FQB characteristics for improvement in the control was employed. Another modification is the virtual frame transformation technique. This method transfers the active and reactive powers to a different reference frame where the effects of line impedance do not impact power generated. The adjustable load sharing control and adaptive voltage droop methods are the most effective for voltage control. The droop control is generally weak in handling nonlinear loads and most times accurate voltage regulation is not guaranteed. The droop techniques offer local controls independent of any communication infrastructures. The pros and cons of the conventional droop control technique and its modifications indicate the need for the secondary control level for improved control and operation of the microgrid system ^[30].

7.   Secondary control methods for communication network impairments mitigation

The droop control technique is a conventional method used for primary control and power-sharing in islanded microgrids. However, the secondary control methods mitigate the anomalies introduced by using the droop control. The restoration of voltage and frequency synchronization takes place at this level. The need for information sharing to achieve system stability makes secondary control communication dependent. The impacts of communication impairments are chiefly felt in the secondary control. Communication induced impairments such as latency, data packet dropout and noise could degrade the performance of the microgrids. Secondary control in AC MGs is essential for frequency and voltage regulation, active and reactive load power-sharing, islanded microgrid synchronization, and power quality matters.

7.1.   Multi-agent-based methods

Agent-based methods have appeared recently in distributed control of islanded MG. In a multi-agent system, each essential component is represented by an intelligent, independent agent. Control is achieved with a sparse communication graph that is considered a basic component that gives a rational and computationally feasible solution. Multi-agent systems control can give a mechanism that is efficient for coordination and communication of protocol for the individual component in the system. Control schemes are rested on the output characteristics of individual power sources. The technique also includes control approaches to optimize the trade-off between performance of the system and cost of operation ^[14], ^[92], ^[93].

A directed graph (digraph) can be used for DGs topology representation to achieve distributed control. It describes the topology between agents in a microgrid. Given $G = (v, \varepsilon, A)$ is a weighted digraph of order n, with the set of nodes $v = \left\{{v}_{1, }\dots.{v}_{n}\right\}$, set of edges $\varepsilon \subseteq v \times v$, and a weighted adjacency matrix $A = \left[{{a_{ij}}} \right]$ having nonnegative adjacency elements ${a_{ij}}$. The nodes of the digraph represent each DG agent in a microgrid. The edges denote communication links between DGs. Each edge ${e_{ij}} = ({v_i}, {v_j})$ implies that the agent ${DG}_{i}$ receives information from agent ${DG}_{j}$ ^[94], ^[95]. For a digraph, an agent ${DG}_{i}$ only receives information from its neighbours Ni. ${a_{ij}}$ is the weight of edge ${e_{ij}} = ({v_i}, {v_j})$ and ${a_{ij}}$ = 1 if $\left({V}_{i}, {V}_{j}\right)ϵ\varepsilon$, otherwise ${a_{ij}}$ = 0. The set of neighbours of node ${v_i}$is denoted by ^[96], ^[97]:

Smart control issue for an islanded microgrid for secure voltages and maximum economic and environmental benefits ^[98]. ^[99] worked on decentralized multi-agent system-based cooperative frequency control for autonomous MGs with communication constraints. In ^[93], an agent-based secondary control strategy for an islanded MG consisting of a two-layer control structure was proposed. ^[100] presented a distributed control structure for implementing the frequency control of an islanded MG. Multi-agent based methods rely on communication networks and are directly affected by the performance of the installed communication system. Although a very advantageous distributed secondary control technique, the design of multi-agent control must be built with resilience for communication link failure in mind.

7.2.   Consensus-based methods

Consensus-based methods seek to converge values from different RES in a MG to a single value. Using the communication links between adjacent RES, an optimal global value for all the distributed agents can be attained for voltage and frequency control in AC MGs ^[13], ^[29]. Consensus problems in a network of continuous-time integrator agents, when the topology is switching, and communication delay is negligible, can be solved using the consensus protocol given as:

where the set of neighbours ${N_i} = {N_i}(G)$ of the node ${v_i}$is variable in networks with switching topology. However, a fixed topology $G = (v, \varepsilon, A)$ and communication time-delay ${\tau _{ij}} > 0$corresponding to the edge ${e_{ij}} \in \varepsilon$ the following linear time-delayed consensus protocol is used:

The consensus-based method was used in ^[101] to investigate reactive power-sharing among DGs. The proposed method can improve system reliability and flexibility. In ^[94], to achieve accurate reactive power sharing, not being bothered by the effects of line impedance mismatched. A method that employs both consensus and control was used to determine the reactive power mismatch among DG units. Also, in related research by ^[102], a containment and consensus-based distributed coordination control was presented to achieve both bounded voltage and accurate reactive power sharing regulation in islanded AC MG'. ^[103] presented a paper to address distributed noise in the communication links between DGs in MGs. The consensus-based control methods, just like its counterpart, the multi-agent-based methods, require a communication network for operation. Its performance is closely related to the performance of the communication network used for the sharing of its coordination and control information.

7.3.   Model predictive control (MPC)-based methods

MPC is a control method used in the process industries. It has also found applications in error tracking based on dynamic models in power systems. The MPC approach can take future prediction and an effective control action. When current plant measurement, process variables, and system dynamic state are available, the MPC method can be used to determine future events. The cost function that has been predetermined is used to calculate optimal values for future control objectives ^[104], ^[105]. For example, to enhance operation efficiency, RES implementation and reducing energy storage system depletion. The optimization problem can be implemented using an objective cost function C given as:

where ${J}_{bt}\left(i\right)$, ${J}_{pv}\left(i\right)$, ${J}_{w}\left(i\right)$, and ${J}_{dpg}\left(i\right)$ represent the cost term relating to battery, PV generation system, wind generation, and amount of dispatchable generation used, respectively.

A model predictive control method used in secondary control of microgrid frequency by ^[87] output signals from the control unit is transmitted via the communication channel to the generation sources to achieve frequency control. The performance of the MPC method is better when compared with the smith predictor based method. ^[105], ^[106] used MPC to assess energy management in an autonomous microgrid, which relies on PV generation and a hybrid energy storage system composed of a fuel cell, battery and supercapacitor. In ^[106] MPC approach was applied for operations optimization in microgrids to improve economic efficiency. The performance of MPC was compared with the heuristic-based method, and results indicate the MPC method improves the performance of islanded microgrid. Model Predictive Control (MPC) was proposed by ^[107] for frequency stabilization in a microgrid under solar penetration and load fluctuation. In addition, ^[108] designed a robust model predictive controller for grid voltage control of an islanded microgrid. ^[109] used MPC for distributed secondary control for both voltage and frequency regulation in islanded microgrids. MPC method for MG control was robust, but it could be very complex to implement.

7.4.   Linear quadratic regulator (LQG)-based methods

LQG controllers can track the performance of islanded microgrids. It gives large gain at low frequency. Considering the state pace representation of system (microgrids) dynamics and noise as:

where $x$, is the state vector, $u$, represent the system input, and $y$ measured output. $v$ and $w$, are the input and output Gaussian white noise, respectively. ${A}_{1}$, is the matrix of the system state while ${B}_{1}$, and ${C}_{1}$ are the input and output matrix, respectively. Finding a control input $u$ that will optimize the cost function is the objective of the LQG controller. The cost function for the LQG controller can be represented as ^[110], ^[111]:

when the time horizon becomes infinity, the term ${x}^{T}\left(T\right)Fx\left(T\right)$ becomes negligible. E is the expected value, the term ${x}^{T}Qx$ represent the state minimization, while ${u}^{T}Ru$ describe control input minimization. Though this controller has a significant gain at low frequency, it suffers from the lack of robustness against the changes in plant dynamics ^[111], ^[112].

The voltage oscillation controller designed for microgrids control in ^[110] is based on integral LQG, in the approach used, the system output is augmented to attain integral action. The LQG controller can also track grid voltage when the microgrid is operating in grid-connected mode. A comparison with LQR and LQG controllers shows that the integral LQG performs better in damping voltage oscillations in microgrid networks. The method used in ^[113] utilizes an H-infinity controller to modify the droop control method. MG voltage control using linear quadratic regulator (LQR) method based on linearization techniques designed to attain fast and accurate response was proposed ^[111].

7.5.   Proportional-integral-derivative (PID)-based control methods

Proportional-Integral-Derivative (PID) takes the leading role among many other controllers being implemented in industrial applications today ^[104]. The transfer function of PID controller consisting of Proportional, Integral and Derivative structures in a single package is represented by:

where U(s) is the control variable, E(s) the error, and Kp, KI, and KD are proportional, integral, and differential gains. The P-term is proportional to the error, the Ⅰ-term is proportional to the integral of the error, and the D-term is proportional to the derivative of the error. The system's transient response is enhanced via proportional gain; the integral gain minimises the steady-state error, while the derivative gain of the PID controller degrades the overshoot of the system.

The benefits of using PID controllers for voltage control in islanded microgrids are investigated in ^[114]. In the analysis, both theoretical and experimental approaches were employed. The analysis shows cascade control is a possibility in islanded microgrid control, and employing measured current in the control information enhances the system performance. Frequency regulation in AC microgrids was the focus of ^[115], multi-verse optimized fractional order PID controller, an adaptation of the PID controller. Also, in similar research, ^[116] used fractional order PID with parameter optimization done by the multi-verse optimizer for frequency regulation in AC microgrids. PID and Combined Proportional-Integral (PI) controllers have been proposed to improve the limitation of H-infinity controller by ^[117]. Furthermore, ^[7] designed a modified adaptive PID controller for voltage and current control of islanded microgrid.

7.6.   H-infinity (H-∞) based methods

The general problem of the H∞ is to realize compensator K such that the close-loop controller is stabilized and minimized following the H∞ norm. H-infinity controller was developed by ^[118] to achieve a robust microgrid performance against unmolded load and uncertainties. ^[119], in their work use H∞ and μ-synthesis approach to developing the secondary frequency control in islanded MG. The work by ^[120] presents a robust virtual inertial control of an islanded MG with high penetration of RESs. The design of H-infinity depends on the norms minimization and order of the system. As a result, a high order system needs a high order controller that may require advanced digital signal processing to control the microgrid's performance.

Presented in Table 4 is the summary of some of the control methods used for mitigating impairments induced by communication network on the smooth operation of the microgrid. As discussed under section 6.3, the droop based methods are independent of communication network and are not affected by the impairments they introduced. It is conventionally use at the primary control level of the microgrids. The weaknesses and strengths of some of the secondary control methods used are presented in the table.

8.   Discussion

The need for reliable, sustainable and clean energy coupled with the demand for optimal operation of renewable energy-based autonomous microgrids requires developing its control system. The mitigation of the communication induced impairments in islanded microgrids will improve the overall performance of the control system and the microgrid at large. Exchanging information between microgrid components is faced with challenges, as highlighted in this paper. literature does not fully address communication-induced impairments such as latency, packets dropouts, and cyber security challenges. Smart control techniques are emerging that can reduce the impacts of the impairments on the performance of the microgrid system. Smart control techniques are preferable to developing new communication technology because of the cost and difficulties new communication infrastructure would require before eventual deployment.

The primary control units of microgrids do not require communication infrastructures, and as a result, does not suffer severe degradation because of malfunction induced by the presence of a communication network. Mitigation efforts for communication induced impairments are not required at this level. But the secondary layer depends on communication networks and are directly affected by their performance. Control techniques must be smart enough to guarantee the microgrid operation's performance. Consensus protocol and multi-agent-based control techniques are being applied to microgrid control. The results in ^[121], ^[122] have shown robustness against communication failure and cyber-attacks.

Existing wireless communication technology such as Wi-Fi, WiMAX, LoRa, and the emerging 5G cellular network can be deployed for microgrid control applications. Wireless communication is flexible, meaning future expansion will not be problematic. Deployment in rural communities will also be comparatively easy compared to its wired counterpart. The comparison of both wired and wireless networks given in this paper could guide while making choices. Depending on the specific application targeted by the user and the range required, choices could be made for the most suitable technology.

GSM technology was originally designed for machine to human communication. Its application to a microgrid system, a machine to machine communication, is still undergoing development. Fibre optics communication will be most appropriate in time-critical applications where large delay cannot be tolerated. However, if flexibility becomes an issue, the emerging 5G network could be considered for deployment. Some inverters available for installation come with Wi-Fi technology for information sharing between individual inverters in the microgrid network. However, using Ethernet cables for connection rather than the wireless Wi-Fi connection proved more effective for most of the products. Future products should come with more reliable wireless infrastructure in order to enjoy all the benefits derivable from wireless connection. Most microgrid controllers follow the IEEE 2030.7-2017 standard for microgrid controllers. It provides microgrid operation based on the microgrid internal controller and SCADA. The products enhance the integration of renewable energy to the main grid and can autonomous control of microgrid when operating in islanded mode. Most of the available controllers operate with the droop controller in the primary level of control.

9.   Conclusion and future direction

This paper presents a comprehensive review of mitigation strategies for communication induced impairments in autonomous microgrid control. Three major communication network induced impairments were mostly researched in literature: data packet dropouts, information packet delay/latency and cyber-attacks induced by using communication networks, especially the wireless networks for information sharing among DGs in the microgrid networks. The approach used in the literature rely mainly on smart control solutions rather than using high-speed communication networks for impairment mitigation. High-speed communication network could be costly to use, and incorporating one in the microgrid system can render the system too expensive to operate. It can therefore be seen that smart control solutions integrated with microgrid control are the way to go in the mitigation of impairments induced as a result of using communication networks in microgrid operation. The review also shows the following:

(ⅰ) Bernoulli random process is very effective for modelling data packet dropouts; it yields an output of 1 or 0 for successful data delivery or communication failure, respectively. The probability of data packet drops when queuing time exceeds the delay limit can also be explored to measure and quantify data packet dropout and delay.

(ⅱ) If propagation and processing delay are treated as a constant value, delay dynamics can be limited to the evolving transmission state and queueing along the signal path.

(ⅲ) Common cyber-attacks directed against microgrid installations are denial of service, false data injection, and data manipulation attacks. Therefore, advanced effort is required to effectively combat these evolving attacks on microgrid installations.

(ⅳ) A sparse communication graph is a basis for communication topology design for distributed secondary control in the microgrid. The fixed and shifting topology should be further investigated to engender optimal topology design.

The need for further investigation on effective integration of communication networks in the microgrid is presented in this paper. The use of communication networks in the microgrids network is indispensable. Current trends in the development of the smart grid suggest that the incorporation of communication networks will continue to increase.

Conflict of interest

The authors declare that there is no conflict of interest.