Soluble Fas ligand, soluble Fas receptor, and decoy receptor 3 as disease biomarkers for clinical applications: A review

1.   Introduction

Regression is the most frequently employed technique in nonparametric statistics to examine the association between two variables $X$ and $Y$. In this context, $Y$ represents the response variable, while $X$ is a random vector of predictors (covariates) that can assume values in the real number space $\mathbb{R}$. The regression function at a point $x\in\mathbb{R}$ is the conditional expectation of $Y$ given $X = x$, denoted as

Various techniques can be employed to estimate a regression function, including kernel estimators, regression spline methods, and others. Nevertheless, these methods lack robustness as they are highly susceptible to outliers. Given that outliers are commonly observed in various fields, such as finance, it is essential to handle outliers properly to emphasize a dataset's unique features. Robust regression is a statistical technique used to address the issue of lack of robustness in regression models. It ensures that the model remains stable and resistant to the influence of outliers.

Robust regression holds significant importance within the realm of statistics. It is employed to overcome certain constraints of non-robust regression, specifically when the data exhibit heteroscedasticity or include outliers. The earliest significant outcome in this field can be traced back to Huber's work in ^[1]. The regression estimation method mentioned has been extensively researched. For empirical data, notable studies include Robinson ^[2], Collomb and H$\ddot{a}$rdle ^[3], Boente and Fraiman ^[4,5], and Fan et al. ^[6] for earlier findings. Recent advancements and references can be found in Laib and Ould-Saïd ^[7] and Boente and Rodriguez ^[8]. Traditional kernel estimators often exhibit significant bias near boundaries because the kernel's support can extend beyond them, resulting in inaccurate estimates. Being supported on the entire interval, Bernstein estimators do not suffer from this boundary bias, leading to more accurate estimations near the edges.

The Bernstein polynomial is widely acknowledged as a valuable tool for interpolating functions on a closed interval, rendering it suitable for approximating density functions within that interval.

The use of Bernstein polynomials as density estimators for variables with finite support has been proposed in several articles. Vitale ^[9] first introduced this concept, followed by Petrone ^[10,11]. Further studies on this topic were conducted by Babu, et al. ^[12], Petrone and Wassermann^[13], and Kakizawa ^[14].

Recently, Ouimet ^[15] studied some asymptotic properties of Bernstein cumulative distribution function and density estimators on the d-dimensional simplex and studied their asymptotic normality and uniform strong consistency. Belalia et al. ^[16] introduced a two-stage Bernstein estimator for conditional distribution functions. Various other statistical topics related to the Bernstein estimator have been treated; for more references, see Ouimet ^[15]. Khardani ^[17] investigated various asymptotic properties (bias, variance, mean squared error, asymptotic normality, uniform strong consistency) for Bernstein estimators of quantiles and cumulative distribution functions when the variable of interest is subject to random right-censoring.

It is essential to mention that several authors have devised Bernstein-based methodologies for addressing non-parametric function estimation problems. Priestley and Chao^[18] first proposed the potential application of Bernstein polynomials for regression problems. Tenbusch ^[19], Brown and Chen ^[20], Choudhuri, Ghosal, and Roy ^[21], Chang, Hsiung, Wu, and Yang ^[22], Kakizawa ^[23], and Slaoui and Jmaei ^[24] have all conducted research on various non-parametric function estimation problems.

In this paper, our contribution is to find asymptotic expressions for the bias, variance, and mean squared error (MSE) for the Bernstein robust regression function estimator defined in (2.4) and (2.3) and also prove their asymptotic normality and convergence. We deduce the asymptotically optimal bandwidth parameter $m$ using the expression for the MSE as well. The results provided by our Bernstein approach for the robust regression function are better than those of the traditional kernel estimators. In future work, using some kernels, such as Dirichlet, Wishart, and inverse Gaussian kernels, and the robust function will be investigated in other spaces, such as the simplex, the space of positive definite matrices, and half-spaces, etc.

The subsequent sections of the paper are structured in the following manner. In the next section, we will introduce our model. Section 3 presents notations, assumptions, and investigates various asymptotic properties of the proposed estimator. Section 4 presents a simulation study that evaluates the proposed approach's performance compared to the Bernstein-Nadaraya-Watson estimator and the Nadaraya-Watson estimator. Section 5 discusses a real data application, while the proofs of the results are provided in the Appendix.

2.   Robust estimation with Bernstein polynomial

Let $(X, Y), \left(X_{1}, Y_{1}\right), \ldots, \left(X_{n}, Y_{n}\right)$ be independent, identically distributed pairs of random variables with joint density function $g(x, y)$, and let $f$ denote the probability density of $X$, which is supported on $[0, 1]$. Let $x$ be a fixed element of $\mathbb{R}$, and let $\rho$ a real-valued Borel function that satisfies specific regularity conditions outlined below. The robust method used to study the links between $X$ and $Y$ belongs to the class of M-estimates introduced by Huber ^[1]. The robust nonparametric parameter studied in this work, denoted by $\theta_x$, is implicitly defined as the unique minimizer w.r.t. $t$ of

that is

This definition covers and includes many important nonparametric models, for example, $\rho(t) = t^2$ yields the non-robust regression, $\rho(t) = |t|$ leads to the conditional median function $m(x) = \text{med}(Y \mid X = x)$, and the $\alpha-$th conditional quantile is obtained by setting $\rho(t) = |t| + (2\alpha - 1)(t)$. We return to Stone ^[25] for other examples of the function $\rho$.

We utilize the techniques outlined in Vitale ^[9] and Leblanc ^[26,27] for distribution and density estimation. Additionally, we refer to the work of Slaoui ^[28] and Tenbusch ^[19,29] for non-robust regression. Our objective is to establish a Bernstein estimator for robust regression, defined as

with at a given point $x \in[0, 1]$ such that $f(x) \neq 0$ and

where $B_{k}(m, x) = \left(\begin{array}{c}m \\ k\end{array}\right) x^{k}(1-x)^{m-k}$ is the Bernstein polynomial of order $m$. This estimator can be viewed as a generalization of the estimator proposed in Slaoui and Jmaei ^[28], with

where $f_n$ is Vitale's estimator of the density $f$ defined, for all $x \in[0, 1]$, by

with $F_n$, the empirical distribution function of the variable $X$.

This paper will use the following notations:

Moreover, we denote by $o$ the pointwise bound in $x$ (i.e., the error is not uniform in $x\in [0, 1]$).

Remark 2.1. Robust regression is advantageous in real data settings where outliers, non-normal errors, or heteroscedasticity are present, making it a more flexible and resilient choice.

3.   Assumptions and main results

To state our results, we will need to gather some assumptions to make reading our results easier. In what follows, we will assume that the following assumptions hold:

Throughout the paper, $C_{1}, C_{2}, C_{3}$ represent positive constants, while $C$ denotes a generic constant independent of $n$. Let $I_{0}: = \{x \in [0, 1] \; : \; f(x) > 0\}$ and $S$ be a compact subset of $I_{0}$.

H1: $m_{n}\geq2$, $m_{n}\underset{n \rightarrow +\infty}\longrightarrow\infty$ and $m_{n} / n \underset{n \rightarrow +\infty}\longrightarrow0.$

H2: $g(s, t)$ is twice continuously differentiable with respect to $s$.

H3: For $q \in\{0, 1, 2\}, s \mapsto \int_{\mathbb{R}} t^q g(s, t) d t$ is a bounded function continuous at $s = x$.

H4: For $q > 2, s \mapsto \int_{\mathbb{R}}|t|^{-q} g(s, t) d t$ is a bounded function.

H5: The function $\rho(.)$ is a bounded, monotone, differentiable function. Its derivative is bounded.

H6: The functions $r$ and $f$ are continuous and admit twice continuous and bounded derivatives such that $| \frac{\partial r}{\partial x}(x, t)|\geq C > 0,$ $\forall x \in \mathbb{R}$.

H7: $r(x, .)$ is of class $\mathcal{C}^{1}$ on $\left[ \theta_{x}-\tau, \theta_{x}+\tau\right]$ and satisfies $\inf_{\left[ \theta_{x}-\tau, \theta_{x}+\tau\right]}\left| \frac{\partial r}{\partial t}(x, .) \right| > C_{3}$ and uniformly continuous.

The assumptions we make are typical for this type of framework. Assumption (H1) is a technical requirement imposed to make proofs more concise. Assumptions (H2)–(H4) are necessary conditions for the estimation of the regression function in the couple $(X, Y)$, as outlined in the works of Nadaraya ^[30], Watson ^[31], and Slaoui and Jmaei ^[28]. These assumptions pertain to the regularity of the density function. The condition (H5) controls the robustness properties of our model. It maintains the same conditions on the function $\rho^{\prime}$ as those provided by Collomb and Härdle ^[3] and Boente and Rodriguez ^[8] in the multivariate case. Assumptions (H6) and (H7) deal with some regularity of the function $r(., .)$. Note that condition (H6) is used to get the asymptotic normality of our estimator, and condition (H7) is somewhat less restrictive compared to that presented in the literature (see Boente and Fraiman ^[32], L. Aït Hennani, M.Lemdani, and E. Ould Saïd ^[33], Attouch et al.^[34,35]), needed for the consistency result.

Proposition 3.1. Under Assumptions (H1)–(H5), and for $x\in \left[0, 1 \right]$ such that $f(x) > 0$, we have

To minimize the $MSE$ of $\widehat{r}_{n}$, for $x \in[0, 1]$ such that $f(x) > 0$, the order $m_{n}$ must be equal to

Then,

Theorem 3.1. Under conditions of Proposition 3.1, we have

Proposition 3.2. Let Assumptions (H1)–(H7) hold.

1) For $x \in(0, 1)$, we have:

i) If $n m_{n}^{-5 / 2} \underset{n \rightarrow +\infty}{\longrightarrow} c$ for some constant $c \geq 0$, then

ii) If $n m_{n}^{-5 / 2} \underset{n \rightarrow +\infty}{\longrightarrow} \infty$, then

2) For $x = \{0, 1\}$, we have:

i) If $n m_{n}^{-3} \underset{n \rightarrow +\infty}{\longrightarrow} c$ for some constant $c \geq 0$, then

ii) If $n m_{n}^{-3} \underset{n \rightarrow +\infty}{\longrightarrow} \infty$, then

where $\underset{n \rightarrow +\infty}{\stackrel{\mathcal{D}}{\rightarrow }}$ denotes the convergence in distribution, $\mathcal{N}$ the Gaussian distribution, and $\underset{n \rightarrow +\infty}{\stackrel{\mathbb{P}}{\rightarrow }}$ the convergence in probability.

Theorem 3.2. (The Mean Integrated Squared Error (MISE) of $\widehat{r}_{n}$).

Let Assumptions (H1)–(H7) hold. Then, we have

Hence, the asymptotically optimal choice of $m$ is

for which we get

Theorem 3.3. Assume that (H1)–(H7) hold. If $\Gamma(x, \theta_{x}) = \mathbb{E}\left[ \rho^{\prime} (Y-\theta_{x}) \rvert\, X = x\right]\neq 0$, then $\widehat{\theta}_{x}$ exists and is unique with great probability, and we have:

i) when $x \in(0, 1)$ and $m_{n}$ is chosen such that $n m_{n}^{-5 / 2} \rightarrow 0$, then

ii) when $x\in [0, 1]$ and $m_{n}$ is chosen such that $n m_{n}^{-3} \rightarrow 0$, then

where

$\underset{n \rightarrow +\infty}{\stackrel{\mathcal{D}}{\rightarrow }}$ denotes the convergence in distribution, and $\mathcal{N}$ the Gaussian distribution.

The following corollary directly follows from the previous theorem and provides the weak convergence rate of the estimator $\widehat{\theta}_{x}$ for $x\in [0, 1]$, where $f(x) > 0$. This is specifically for the case when $m_{n}$ is chosen such that $nm_{n}^{-5/2}\rightarrow0$ for $x\in (0, 1)$ and $nm_{n}^{-3}\rightarrow0$ for $x\in [0, 1]$.

Corollary 3.1. When $x \in(0, 1)$ and $m_{n}$ is chosen such that $n m_{n}^{-5 / 2} \rightarrow 0$, then

When $x\in [0, 1]$ and $m_{n}$ is chosen such that $n m_{n}^{-3} \rightarrow 0$, then

where

4.   Simulation and real data application

This section is divided into two parts: the first shows our estimate's behavior for some particular conditional regression functions, and the second deals with asymptotic normality.

4.1.   Consistency

Consider the regression model

where $\varepsilon \sim \mathcal{N}(0, 1)$.

A simulation was conducted to compare the proposed estimators $\widehat{\theta}_{x}$ (robust Bernstein polynomial estimator) with $\widehat{r}^{BNW}_{n}(x)$ (Bernstein-Nadaraya-Watson estimator) introduced by Slaoui and Jmaei ^[28] and defined by

where $B_{k}(m, x) = \left(\begin{array}{c}m \\ k\end{array}\right) x^{k}(1-x)^{m-k}$ is the Bernstein polynomial of order $m$, and $\widehat{r}^{NW}_{n}(x)$ (Nadaraya-Watson estimator) is defined, for $x\in \mathbb{R}$ such that $f(x)\neq 0$, by

where $K:\mathbb{R}\rightarrow \mathbb{R}$ is a nonnegative, continuous, bounded function satisfying $\int_{\mathbb{R}} K(z)dz = 1, \int_{\mathbb{R}} z K(z)dz = 1$ and $\int_{\mathbb{R}} z^{2}K(z)dz < \infty$ and $h = (h_{n})$ is a sequence of positive real numbers that goes to zero.

When using the estimator $\widehat{r}^{NW}_{n}(x)$, we choose the Gaussian kernel $K(x) = (2 \pi)^{-1 / 2} \exp \left(-x^2 / 2\right)$ and the bandwidth equal to $\left(h_n\right) = m_n^{-1}$.

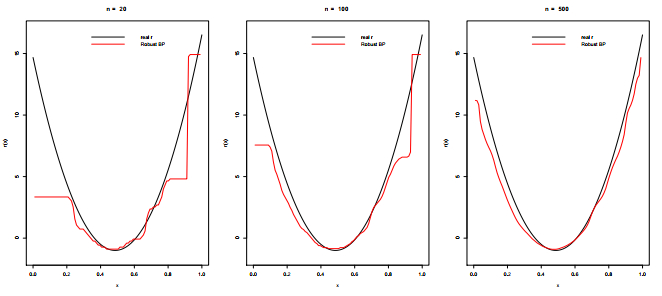
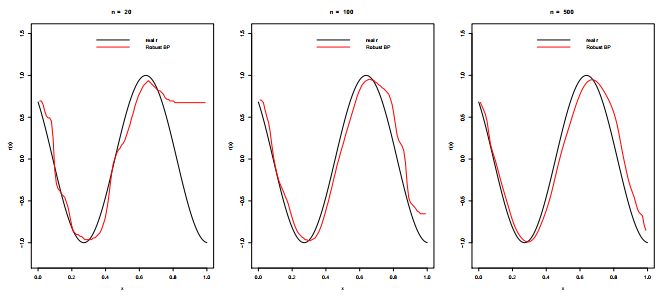
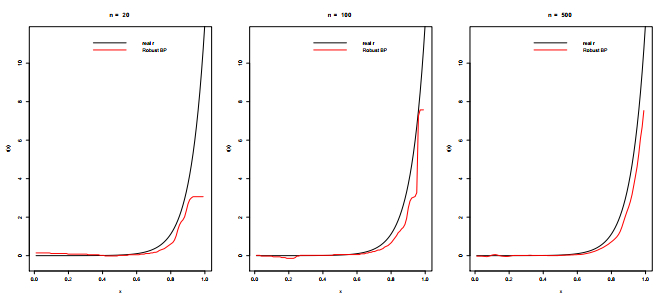
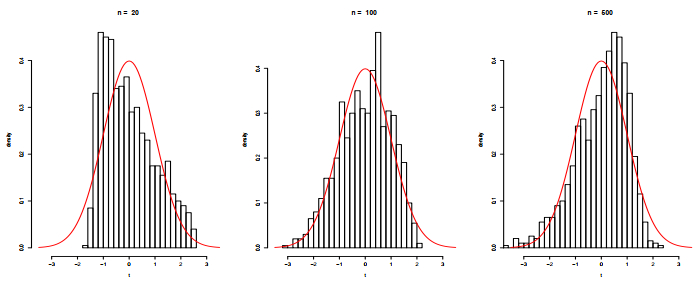
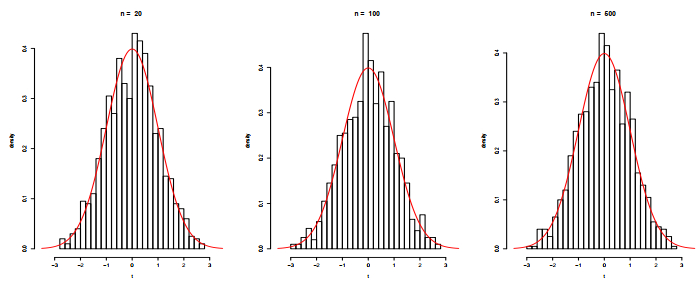
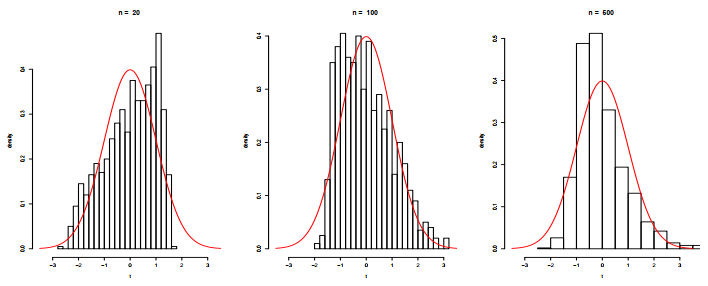
We consider three sample sizes $n = 20, n = 100$, and $n = 500$, four regression functions

and three densities of $X$: the truncated standard normal density $\mathcal{N}_{[0, 1]}(0, 1)$ ($X\in [0, 1]$), the exponential density $Exp(2)$ ($X\in [0, \infty)$), and the standard normal density $\mathcal{N}(0, 1)$ ($X\in (-\infty, \infty)$). It is also possible to use the transformations $\widetilde{X} = \frac{X}{1 + X}$ or $\widetilde{X} = \frac{1}{2} + \frac{1}{\pi} \tan^{-1}(X)$ to cover the cases of random variables $X$ with support $\mathbb{R}_+$ and $\mathbb{R}$, respectively. These transformations allow for the application of Bernstein polynomials to smooth the empirical distribution function.

The simulation consists of four parts. In the first three parts, the estimators are compared by their average integrated squared error $\overline{AISE}$. Every $\overline{AISE}$ is calculated by a Monte-Carlo simulation with $N = 1000$ repetitions of sample size $n$,

where $\bar{r}_k$ is the estimator ($\widehat{\theta}_{x}$ or $\widehat{r}^{BNW}_{n}(x)$ or $\widehat{r}^{NW}_{n}(x)$) computed from the $k^{\text {th }}$ sample, and

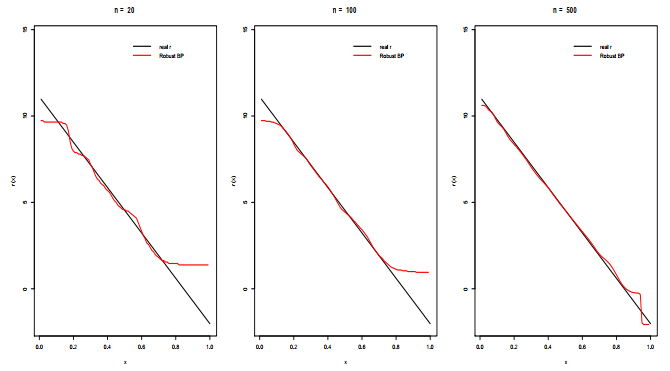
According to Figures 1–4, it is evident that the robust Bernstein polynomial estimation converges when $n$ is large. This is observed in all cases.

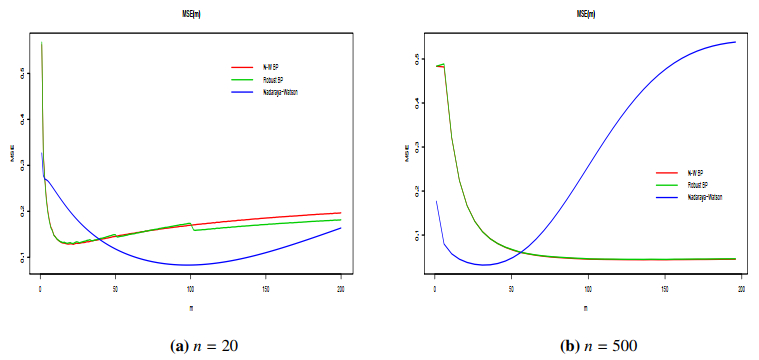
The $\overline{AISE}$ of three estimators is graphed in Figure 5 for different parameter values ranging from 1 to 200. The estimators are evaluated for two sample sizes, $n = 20$ and $n = 500$. The outcomes are highly comparable when outlier values are not present. Nevertheless, the analysis of Tables 1–4 demonstrates that both the kernel estimator and the Bernstein-Nadaraya-Watson estimator exhibit significant sensitivity towards outlier values. This heightened sensitivity leads to substantial inaccuracies in predictions. In contrast, our robust Bernstein polynomial estimator consistently sustains its performance irrespective of the quantity of outlier values.

4.2.   Asymptotic normality

The objective is to demonstrate the property of asymptotic normality in the context of the sine regression model. The equation is

Next, let $r(x)$ be defined as the sine function with a coefficient of $\frac{3}{2}$. The data provided is the same as in the previous subsection. The procedure consists of the following steps: We approximate the regression function $r(x)$ using $\widehat{\theta}_{x_0}$ and compute the normalized deviation between this approximation and the theoretical regression function (refer to Theorem 3.3) for $x_0 = 0, \; 0.5\; \text{and}\; 1$. Under this scheme, we generate $N$ separate sets of $n$ samples that are not influenced by each other. Next, we analyze the form of the estimated density (with normalized deviation) and compare it to the shape of the standard normal density in the context of the sine regression model. The following figures and table present the density of $\widehat{\theta}_{x_0}$ as well as the $p-$value by the Shapiro-Wilk normality test. We examine various values of $n$, specifically $n = 20$, $n = 100$, and $n = 500$.

Figures 6–8 and Table 5 demonstrate the advantageous characteristics of our asymptotic law compared to the standard normal distribution.

5.   Real data application

Air pollution significantly affects the lives of individuals in developed nations. The source of this issue is increased levels of smoke produced by industries or vehicles, prompting authorities to search for more efficient methods to regulate air quality in real-time. London is experiencing a significant problem with air pollution exceeding legal and World Health Organisation limits. An example of this is the incident in 2010 when air pollution caused various health problems in the city, leading to a financial cost of around £3.7 billion.

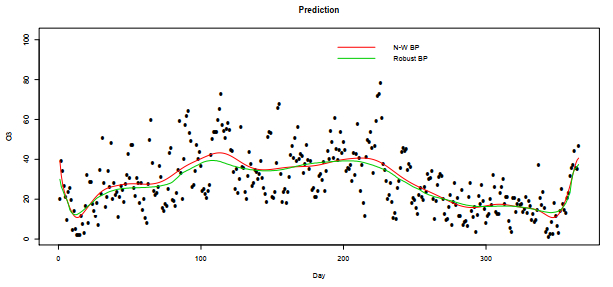
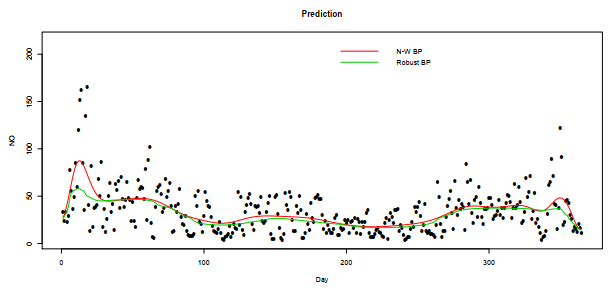
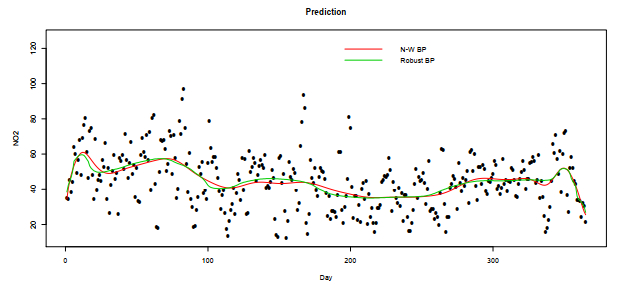
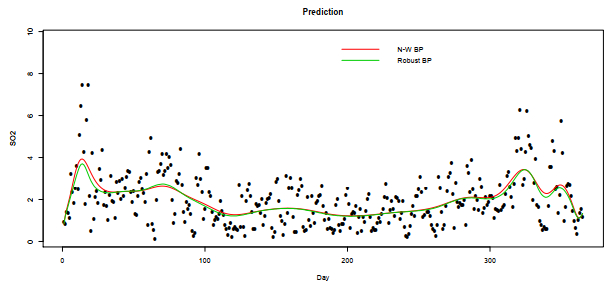
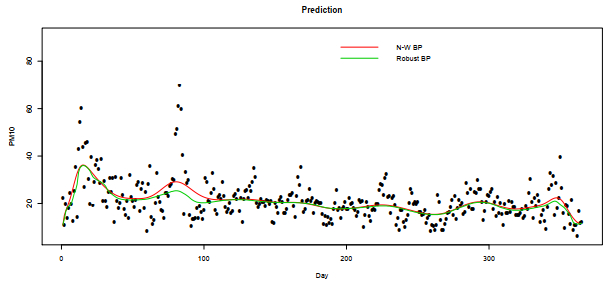
This segment analyzes the mean daily levels of gases detected at the Marylebone Road monitoring station in London. The dataset includes the average daily measurements recorded throughout 2022 for five important variables: Ozone ($O_3$), Nitric Oxides ($NO$), Nitrogen Dioxide ($NO_2$), Sulphur Dioxide ($SO_2$), and Particulate Matter ($PM_{10}$). The main objective of our research is to determine the most practical forecasting models for air pollutant concentration. The data used in this analysis was obtained from the specified website: https://www.airqualityengland.co.uk/site/data?site_id = MY1.

To ensure clarity, let us delineate the mathematical expression representing our prediction objective. Let us consider predicting the daily air pollutant concentration, represented by the variable $Y$, for 365 days, denoted by $X$. Formally, we assume that the output variable $Y$ and the input variable $X$ are connected by the following equation:

A dependable data-dependent rule for order selection is crucial when estimating an unknown regression function in any practical scenario. A widely used and effective method is cross-validation:

where $\bar{r}_{-i}$ is the regression estimate without the data point $\left(X_i, Y_i\right)$.

In practice, choosing the right degree $m$ for a Bernstein polynomial requires balancing between the complexity of the model and how well it fits the data. A useful method for this is cross-validation, where the dataset is divided into training and validation sets.

Then, the smoothing parameter is chosen by minimizing

For convenience, we assume that the minimum of days is 1 and the maximum is 365 (the day data are such that $\min _i\left(X_i\right) = 1$ and $\max _i\left(X_i\right) = 365$). Finally, we used the cross-validation method to obtain the results in Figures 9–13 and Table 6.

Based on the analysis of Figures 9 to 13, it is evident that the two estimators are nearly identical, except for the scenario depicted in Figure 10. In this case, non-robust estimator $\widehat{r}^{BNW}_{n}(x)$ is found to be sensitive to outliers, which provides evidence of the efficiency of our estimator.

Based on the information in Table 6, we can infer that the parameter $m$ can be adjusted. It does not need to be equal to $n$. Instead, we can choose a lower-degree polynomial to achieve a more favorable outcome.

6.   Conclusions

In this paper, we proposed a new robust regression estimator based on the Bernstein polynomials. Our contribution extends the work of Slaoui and Jmaei ^[28] to the case of robust regression. The asymptotic properties of this estimator were established. Afterward, we validated the effectiveness of the proposed method through a simulation study and applied it to real data on air pollution,

We found that, in all three models, the average ISE of our robust regression estimator $\widehat{\theta}_{x}$, defined in 2.4, was the smallest. We also noted that the robust regression provided better results than the non-robust method when outliers were present, in the sense that, even if the sample size increases, the average ISE decrease. To conclude, the use of the robust regression estimator with Bernstein polynomials successfully addressed the edge problem, yielding results comparable to those of non-robust and Nadaraya-Watson estimators in the absence of outliers.

We believe our research provides a foundational step that can be further developed and expanded. It sets the stage for future work to extend our robust regression estimator using the Bernstein polynomial by considering the interest random variable to be truncated. We also plan to work on the robust regression estimation using Lagrange polynomials.

Author contributions

Sihem Semmar: Conceptualization, data curation, formal analysis, investigation, methodology, software, validation, writing original draft, writing – review & editing; Omar Fetitah, Salah Khardani and Mohammad Kadi Attouch: Conceptualization, supervision, writing–review & editing; Mohammed Kadi Attouch and Ibrahim M. Almanjahie: Resources, validation, writing–review & editing. All authors have read and approved the final version of the manuscript for publication.

Data availability

The real data used in this application can be found at this link: https://www.airqualityengland.co.uk/site/data?site_id = MY1

Acknowledgments

The authors thank and extend their appreciation to the funder of this work. This work was supported by the Deanship of Scientific Research and Graduate Studies at King Khalid University through the Large Research Groups Project under grant number R.G.P. 2/338/45.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

A.   Appendix

In this section, we present proofs for the results in Section 3. First, we recall a series of results, which are proven in Leblanc ^[26], linked to different sums of Bernstein polynomial, defined by

These results are given in the following lemma.

Lemma A.1. We have

(i) $0 \leq S_{m_{n}}(x) \leq 1, \forall x \in[0, 1]$.

(ii) $S_{m_{n}}(x) = m^{-1 / 2}\left[\psi(x)+o_x(1)\right], \forall x \in(0, 1)$.

(iii) $S_{m_{n}}(0) = S_{m_{n}}(1) = 1$.

(iv) Let $g$ be any continuous function on $[0, 1]$. Then, $m_{n}^{1 / 2} \int_0^1 g(x) S_{m_{n}(x)}dx = \int_0^1 g(x) \psi(x) d x+o(1)$.

Proof. The proof of this lemma is in Leblanc ^[26] and Babu et al. ^[12]. □

A.1.   Proof of Proposition 3.1

Lemma A.2.

Proof.

Using a Taylor expansion, we have

and since $N(x, t) = r(x, t)f(x)$, we obtain

where $T_{j, m_{n}-1}(x)$ are the central moments of the Binomial distribution of order $j\in \mathbb{N}$, defined as

Note that it is easy to obtain

Then, we have

□

Lemma A.3. We have

Proof. We have

where

So, we have

and

Using Lemma A.1 (ⅱ) and (ⅲ), we obtain

□

Lemma A.4.

Proof. We have

Using Lemma A.1 (ⅱ) and (ⅲ), we get

To obtain the bias of $\widehat{r}_{n}(x, t)$, we let $h(x, y) = \frac{u}{v}$. Using a Taylor expansion, we have

Then, we have

We set $\left(u, v\right) = \left(N_{n}(x, t), f_{n}(x)\right)$ and $(u_{0}, v_{0}) = (N(x, t), f(x))$. Therefore, we infer that

Hence, we set $\left(u, v\right) = \left(f_{n}(x), N_{n}(x, t)\right)$ and $(u_{0}, v_{0}) = (f(x), N(x, t))$ to obtain

Then,

Use Vitale's estimator $f_{n}$, we get

and

To obtain (3.1) of Proposition 3.1, we use (A.6) and (A.2) to obtain

Now for the variance of $\widehat{r}_{n}(x, t)$, we have

which ensures that

So, for $x = (0, 1)$, we have $f$,

and, for $x \in {0, 1}$, we have

which gives the proof of Proposition 3.1. □

A.2.   Proof of Theorem 3.1

Without loss of generality we can suppose that $\rho(Y-.)$ is increasing, with the decreasing case being obtained by considering $-\rho(Y-.)$. As $\rho(Y-.)$ is increasing, then for all $\epsilon > 0$,

Proposition 3.1 shows that

for all real $t \in[\theta_{x}-\tau, \theta_{x}+\tau]$. As $r(x, \theta_{x}) = 0$, for sufficiently large $n$ and for all $\epsilon \leq \tau,$ this implies

Since $\widehat r(x, \widehat \theta_{x}) = 0$, and by the continuity of $\widehat r(x,$.$)$ on $[\theta_{x}-\tau, \theta_{x}+\tau]$, we deduce that

On the other hand, since $\theta_{x}$ and $\hat{\theta_{x}}$ are solutions of $r(x, t)$ and $\widehat{r}(x, t)$, respectively, then we have

Under (H7), and by a Taylor expansion of $r(x,$.$)$ of order one around $\hat\theta_{x}$, we have

where $\xi_{n}$ is between $\theta_{x}$ and $\hat{\theta_{x}}$. Hence,

which yields

and the rest of the proof is a sequence of Proposition 3.1.

A.3.   Proof of Proposition 3.2

From (2.4), we adopt the decomposition stated as

Lemma A.5. Under Assumptions (H1)–(H3), and for $x \in[0, 1]$ such that $f(x) > 0$, we have

Proof. We have by the results of Lemmas A.2 and A.3, that

and

Hence,

□

Lemma A.6. Under Assumptions (H1)–(H4), and for $x \in(0, 1)$ such that $f(x) > 0$, we have:

i) if $m_n$ is chosen such that $n m_n^{-5 / 2} \rightarrow c$ for some constant $c \geq 0$, then

ii) if $m_n$ is chosen such that $n m_n^{-5 / 2} \rightarrow \infty$, then

Proof. By Lemmas A.2 and A.8, we have:

i) if $n m_n^{-5 / 2} \rightarrow c$ for some constant $c \geq 0$, then

ii) if $n m_n^{-5 / 2} \rightarrow \infty$, then

□

Lemma A.7. Under Assumptions (H1)–(H4), and for $x \in(0, 1)$ such that $f(x) > 0$, we have

Proof. We write

where

The proof of this lemma is based on the Lyapunov central limit theorem (FELLER, W.^[36]) on $L_i(x)$, i.e., it suffices to show, for some $\delta > 0$, that

Clearly,

Hence,

Therefore, to complete the proof of this lemma, it is enough to show that the numerator of (A.12) converges to 0. For this, we use the $C_r$-inequality (cf. Loève ^[37], page 155) to show that

Recall that, because of Assumption (H4) and Lemma A.1 (ⅱ), we have

Similarly, for the second term $\left(\sum_{i = 1}^n\left|\mathbb{E}\left[L_i(x)\right]\right|^{2+\delta}\right)$, we get

Finally, (A.9) in Lemma A.6, Lemma A.7, and Slutsky's theorem complete the proof of part 3.4 of Proposition 3.2. □

Now, if $n m_n^{-5 / 2} \rightarrow \infty$, we have

Since we have $n^{-1 / 2} m_n^{5 / 4} \rightarrow 0,$ A.10 in Lemma A.6, Lemma A.7, and Slutsky's theorem complete the proof of part 3.5. Proposition 3.2 follows from (A.11) when $x \in\{0, 1\}$.

Lemma A.8. Under Assumptions (H1)–(H4), and for $x \in\{0, 1\}$ such that $f(x) > 0$, we have:

i) if $m_n$ is chosen such that $n m_n^{-3} \rightarrow c$ for some constant $c \geq 0$, then

ii) if $m_n$ is chosen such that $n m_n^{-3} \rightarrow \infty$, then

Proof. The proof of this lemma is analogous to Lemma A.6. □

Lemma A.9. Under Assumptions (H1)–(H4), and for $x \in\{0, 1\}$ such that $f(x) > 0$, we have

Proof. We write

where

The proof of this lemma is based on the Lyapounov central limit theorem (FELLER, W.^[36]) on $L_i(x)$. Clearly,

Hence,

Therefore, to complete the proof of this lemma, we follow the same steps as in the proof Lemma A.7, and find that

Finally, (A.13) in Lemma A.8, Lemma A.9, and Slutsky's theorem complete the proof of part 3.6 of Proposition 3.2. Now, if $n m_n^{-3} \rightarrow \infty$, we have

Since we have $n^{-1 / 2} m_n^{3 / 2} \rightarrow 0,$ A.14 in Lemma A.8, Lemma A.9, and Slutsky's theorem completes the proof of part 3.7 of Proposition 3.2 follows from (A.15). □

A.4.   Proof of Theorem 3.2

First, we have

Moreover, we have

Then,

First, we have

where $f_{m}^{2}(x) = \mathbb{E}^{2}\left[f_{n}(x)\right] = f^{2}(x)+O\left(m_{n}^{-1}\right)$, and

for $x \in[0, 1]$ and $m_{n} \geq 2$, where

Note that this error term is not uniform. For this, we use the Cauchy-Schwarz inequality to write

for all $m_{n} \geq 1$ and $x \in[0, 1]$, since $0 \leq B_k\left(m_n, x\right) \leq 1$ and

Then, starting from Eq (A.17) and applying Jensen's inequality and Lemma A.1 (ⅳ), we have

Then, we infer that

and, using Lemma A.1 (ⅳ), we have

Second, we have

Then, using the same argument for $H_{mn-1}(x)$ as previously, we obtain

Third, we have

Then,

Finally, substituting (A.18), (A.19), and (A.20) into (A.16), we obtain

Then, we obtain

A.5.   Proof of Theorem 3.3

Using a Taylor expansion of order one around $\theta$, we get

with $\xi_{n} \in(\widehat{\theta_{x}}, \theta_{x})$. Because of the definition of $\widehat{\theta}$, we have

We will prove that the numerator is asymptotically normal, whereas the denominator converges in probability to $\Gamma(x, \theta_{x})$; for that, we will use the following decompositions:

i) When $x\in (0, 1)$ and $m_{n}$ is chosen such that $n m^{-5/2}\rightarrow c$, then

ii) When $x\in \{0, 1\}$ and $m_{n}$ is chosen such that $n m^{-3}\rightarrow c$, then

So, we state asymptotic normality by Slutsky's Theorem, and by Proposition 3.2 with $t = \theta$. We show that the numerator suitably normalized is asymptotically normally distributed. Then, it suffices to show that the denominator converges in probability to $\Gamma(x, \theta_{x})$ (see Lemma A.10).

Lemma A.10. Under Assumptions (H1)–(H3), and for $x \in[0, 1]$ where $f(x) > 0$, we have

Proof. We explore the following decomposition:

For $J_{1}(x)$, we write

Because $\frac{\partial \rho(y-t)}{\partial t}$ is continuous at $\theta$ uniformly, the use of Theorem 3.1 and the convergence in probability of $f_{n}(x)$ to $f(x)$ show that the first term of (A.21) converges in probability to 0. However, the limit of the second term is obtained by evaluating, separately, the bias and the variance terms of $\frac{\partial \widehat{r}}{\partial t}\left(x, \theta_{x} \right)$. Clearly, a similar argument to those invoked for proving (3.1) can be used to obtain that

□