During the outbreak of new infectious diseases, media information and medical resources play crucial roles in shaping the dynamics of disease transmission. To investigate the combined impact of media information and limited medical resources on disease spread, we proposed a two-group compartmental model. This model divided the population into two groups based on their ability to receive information. We derived the basic reproduction number, analyzed the local stability of the disease-free equilibrium, and examined the conditions under which disease extinction or persistence occured. For control strategies, we explored both constant and optimal control approaches under the constraint of limited media resources. Numerical simulations indicated that enhancing the population's responsiveness to media and medical resources helped reduce the infection rate. The model also exhibited complex dynamical behaviors, such as backward bifurcation, forward-backward bifurcation, and homoclinic bifurcation, which presented significant challenges for disease control. Furthermore, we conducted numerical simulations of the optimal control problem to validate and support our theoretical findings. In the case of constant control, as the disparity between the two populations increases, media resources should be increasingly allocated to the information-insensitive group. For optimal control, we employed the forward-backward sweep method, where media resources were increasingly allocated to information-insensitive groups as population heterogeneity rises. This study established an empirical framework for optimizing media-driven public health communication strategies, offering critical insights into the strategic allocation of limited media resources across heterogeneous populations.
Citation: Zehan Liu, Daoxin Qiu, Shengqiang Liu. A two-group epidemic model with heterogeneity in cognitive effects[J]. Mathematical Biosciences and Engineering, 2025, 22(5): 1109-1139. doi: 10.3934/mbe.2025040
| [1] | Boli Xie, Maoxing Liu, Lei Zhang . Bifurcation analysis and optimal control of SEIR epidemic model with saturated treatment function on the network. Mathematical Biosciences and Engineering, 2022, 19(2): 1677-1696. doi: 10.3934/mbe.2022079 |
| [2] | Xinyu Liu, Zimeng Lv, Yuting Ding . Mathematical modeling and stability analysis of the time-delayed $ SAIM $ model for COVID-19 vaccination and media coverage. Mathematical Biosciences and Engineering, 2022, 19(6): 6296-6316. doi: 10.3934/mbe.2022294 |
| [3] | Aili Wang, Yanni Xiao, Huaiping Zhu . Dynamics of a Filippov epidemic model with limited hospital beds. Mathematical Biosciences and Engineering, 2018, 15(3): 739-764. doi: 10.3934/mbe.2018033 |
| [4] | Wenjie Qin, Jiamin Zhang, Zhengjun Dong . Media impact research: a discrete SIR epidemic model with threshold switching and nonlinear infection forces. Mathematical Biosciences and Engineering, 2023, 20(10): 17783-17802. doi: 10.3934/mbe.2023790 |
| [5] | Tao Chen, Zhiming Li, Ge Zhang . Analysis of a COVID-19 model with media coverage and limited resources. Mathematical Biosciences and Engineering, 2024, 21(4): 5283-5307. doi: 10.3934/mbe.2024233 |
| [6] | Toshikazu Kuniya, Taisuke Nakata, Daisuke Fujii . Optimal vaccine allocation strategy: Theory and application to the early stage of COVID-19 in Japan. Mathematical Biosciences and Engineering, 2024, 21(6): 6359-6371. doi: 10.3934/mbe.2024277 |
| [7] | Pengfei Liu, Yantao Luo, Zhidong Teng . Role of media coverage in a SVEIR-I epidemic model with nonlinear incidence and spatial heterogeneous environment. Mathematical Biosciences and Engineering, 2023, 20(9): 15641-15671. doi: 10.3934/mbe.2023698 |
| [8] | Wei Ding, Li Ding, Zhengmin Kong, Feng Liu . The SAITS epidemic spreading model and its combinational optimal suppression control. Mathematical Biosciences and Engineering, 2023, 20(2): 3342-3354. doi: 10.3934/mbe.2023157 |
| [9] | Cunjuan Dong, Changcheng Xiang, Wenjin Qin, Yi Yang . Global dynamics for a Filippov system with media effects. Mathematical Biosciences and Engineering, 2022, 19(3): 2835-2852. doi: 10.3934/mbe.2022130 |
| [10] | Sarita Bugalia, Jai Prakash Tripathi, Hao Wang . Mathematical modeling of intervention and low medical resource availability with delays: Applications to COVID-19 outbreaks in Spain and Italy. Mathematical Biosciences and Engineering, 2021, 18(5): 5865-5920. doi: 10.3934/mbe.2021295 |
During the outbreak of new infectious diseases, media information and medical resources play crucial roles in shaping the dynamics of disease transmission. To investigate the combined impact of media information and limited medical resources on disease spread, we proposed a two-group compartmental model. This model divided the population into two groups based on their ability to receive information. We derived the basic reproduction number, analyzed the local stability of the disease-free equilibrium, and examined the conditions under which disease extinction or persistence occured. For control strategies, we explored both constant and optimal control approaches under the constraint of limited media resources. Numerical simulations indicated that enhancing the population's responsiveness to media and medical resources helped reduce the infection rate. The model also exhibited complex dynamical behaviors, such as backward bifurcation, forward-backward bifurcation, and homoclinic bifurcation, which presented significant challenges for disease control. Furthermore, we conducted numerical simulations of the optimal control problem to validate and support our theoretical findings. In the case of constant control, as the disparity between the two populations increases, media resources should be increasingly allocated to the information-insensitive group. For optimal control, we employed the forward-backward sweep method, where media resources were increasingly allocated to information-insensitive groups as population heterogeneity rises. This study established an empirical framework for optimizing media-driven public health communication strategies, offering critical insights into the strategic allocation of limited media resources across heterogeneous populations.
In recent years, infectious diseases such as Dengue Fever (1979), severe acute respiratory syndromes (SARS) (2003), influenza a (H1N1) (2009), and Corona virus disease 2019 (COVID-19) (2019) have spread globally. The impact of these infectious diseases extends beyond the health sector, severely threatening the lives and health of people worldwide [1,2,3,4,5]. In the age of information, the spread of infectious diseases is often accompanied by the rapid dissemination of information. On the one hand, information related to diseases can raise public awareness, providing details about transmission routes, infectiousness, and possible preventive measures, thereby enabling individuals to take effective protective actions. On the other hand, disease-related information can also cause panic, leading to negative behaviors. As a result, the spread of disease-related information can induce changes in individual behavior, which, in turn, significantly impacts the transmission of the disease [6,7,8].
With the continuous rise of social media, news channels, scientific research, and other information sources, public understanding and responses to infectious diseases are undergoing profound changes. Media information not only serves as a carrier of knowledge, but also plays a pivotal role in disease prevention and control. Many ordinary differential equation models were used to analyze the impact of individual behavioral changes, such as wearing masks, maintaining social distancing, etc., in response to the spread of disease-related information. Generally, studies examining the dissemination of disease-related information can be classified into two main approaches: one assumes that behavioral changes lead to a reduction in infection or contact rates. This approach typically models infection rates as a function of the number of infected individuals [9,10,11,12] or the number of news items [13,14,15,16], treating news items as a separate compartment. For example, Luo and Liu [17] studied an susceptible-vaccinated susceptible-exposed-infected-quarantined-recovered (SSvEIQR) model with nonlinear contact rate, isolation rate and vaccination rate driven by media coverage. The sufficient conditions to prove the global stability of the endemic equilibrium were obtained by applying the geometric method into the four-dimensional system. They obtained some measures to control the spread of the disease, such as reducing contact, strengthening isolation, and vaccination. The second approach divides the population into two categories: those who are sensitive to disease-related information and those who are not. Individuals sensitive to such information may subconsciously take protective measures, thus reducing exposure rates. This method introduces a heterogeneous modeling solution, which inevitably increases the system's dimensionality and complicates theoretical analysis [18,19,20]. For instance, Li and Xiao [21] proposed a two-group model that simulates both disease and information propagation, incorporating saturated recovery rates. By applying fast-slow theory and analyzing the system dynamics directly, they identified the existence and stability of potential equilibrium points and the occurrence of backward bifurcation. Consequently, considering heterogeneous models becomes crucial, as variations in information sensitivity present significant challenges in controlling and eliminating infectious diseases.
In the early stages of emerging infectious diseases, the most significant challenge is the limitation of medical resources, a threat faced by nearly all countries. For instance, during the initial outbreak of COVID-19 in mainland China in early 2020, the shortage of detection kits, hospital beds, and ventilators emerged as the most pressing issue. The need to ensure an adequate supply of medical resources to effectively respond to outbreaks has become increasingly emphasized. In this context, Cui et al. [22,23] developed an epidemiological model incorporating saturated recovery in infected individuals, demonstrating that saturated recovery can lead to bistability and periodicity. To analyze the impact of medical conditions, Wang [24] proposed an Ebola epidemic model that incorporates limited medical resources, immunity loss, and the tracking and quarantining of susceptible individuals. The study explores bifurcation phenomena and conducts sensitivity analysis, revealing a strong correlation between the control reproduction number and the incineration or burial rate of dead bodies. Asamoah et al. [25] introduced a mathematical model to describe the nonlinear recovery rate in bacterial meningitis, offering a framework for controlling disease transmission in resource-limited settings, and identifying both forward and backward bifurcations. Li and Xiao [26] proposed an epidemic SEIM model incorporating saturated media growth and a saturated recovery rate. The theoretical results suggest that only nonlinear recovery models may exhibit backward bifurcation under specific conditions. Through numerical simulations, their model revealed a rich array of dynamical behaviors, including forward and backward bifurcations, Hopf bifurcations, saddle-node bifurcations, homoclinic bifurcations, and unstable limit cycles. Thus, the limitations of medical resources give rise to complex dynamics, posing significant challenges in the elimination and control of infectious diseases.
As discussed in [21,26,27], during the outbreak of emerging infectious diseases, medical resources are often in short supply, and leveraging media information to control disease transmission proves to be a highly effective strategy. Consequently, it is essential to incorporate the limitations of medical resources into epidemiological modeling. While existing research on mathematical models incorporating media information is relatively well-developed, few studies have considered the heterogeneity of different population groups or examined how media-influenced infection rates and limited medical resources interact to impact disease dynamics. Furthermore, the challenge of formulating more effective and targeted control strategies under conditions of limited media resources remains an area of concern. In light of these issues, this paper aims to explore the heterogeneity in population responses to media and the constraints posed by limited medical resources. Specifically, we focus on how these two factors influence disease transmission and control strategies within a two-group model, taking into account the limitations of media resources.
The structure of this paper is organized as follows. Section 2 presents the model formulation for heterogeneous infectious diseases. In Section 3, we analyze the well-posedness of the model, calculate the basic reproduction number, and investigate the local stability of the disease-free equilibrium. Additionally, we establish the conditions for disease extinction and persistence in the absence of medical resource constraints. In Section 4, we formulate a control problem that considers media information allocation and solve the corresponding optimal control problem with control variables. Section 5 is dedicated to numerical simulations, where we explore the sensitivity of the model to parameter changes, the bifurcation structure, and the effectiveness of two types of control strategies. Finally, Section 6 provides a summary of the findings and an outlook for future research.
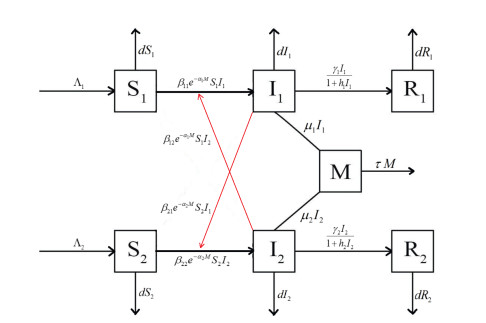
We use a classical SIR model to describe the dynamics of disease transmission, where S, I, and R represent the susceptible, infectious, and removed (recovered or deceased) individuals, respectively. To account for individual responses to the information they receive, we divide the total population into two groups: information-sensitive groups (S1, I1, R1) and information-insensitive groups (S2, I2, R2) [21]. We assume that the transmission rate between group j and group i is given by βij, where i,j=1,2. Due to the limitations of medical resources, infectious individuals enter the removed compartment with a recovery rate that follows a saturation function, γi1+hiIi, where i=1,2. Here, Λi (for i=1,2) represents the immigration rates, and d is the natural mortality rate for all individuals.
To simulate the impact of media reports and information on disease transmission, we consider the number of media reports related to the epidemic as an independent variable, denoted as M(t). To capture the effect of media reports in reducing the effective contact between susceptible and infected individuals, we introduce an exponential decay factor, as proposed in [26], represented by e−α1M and e−α2M, which describes the declining coefficient of incidence for the susceptible and infected groups, respectively. Parameters μ1 and μ2 represent the response rates of infected individuals who are sensitive and insensitive to information, respectively. Finally, τ denotes the natural disappearance rate of media reports. Based on this framework, we consider the following model of differential equations:
| {dS1dt=Λ1−β11e−α1MS1I1−β12e−α1MS1I2−dS1,dI1dt=β11e−α1MS1I1+β12e−α1MS1I2−γ1I11+h1I1−dI1,dR1dt=γ1I11+h1I1−dR1,dS2dt=Λ2−β21e−α2MS2I1−β22e−α2MS2I2−dS2,dI2dt=β21e−α2MS2I1+β22e−α2MS2I2−γ2I21+h2I2−dI2,dR2dt=γ2I21+h2I2−dR2,dMdt=μ1I1+μ2I2−τM, | (2.1) |
The model flow diagram is shown in Figure 1, and all parameters are nonnegative constants, and their descriptions, values, and sources are provided in Table 1. Since the equations for R1 and R2 can be decoupled from the other equations in model (2.1), we exclude these equations from further consideration in this work. Therefore, we focus on discussing the following simplified model,
| {dS1dt=Λ1−β11e−α1MS1I1−β12e−α1MS1I2−dS1,dI1dt=β11e−α1MS1I1+β12e−α1MS1I2−γ1I11+h1I1−dI1,dS2dt=Λ2−β21e−α2MS2I1−β22e−α2MS2I2−dS2,dI2dt=β21e−α2MS2I1+β22e−α2MS2I2−γ2I21+h2I2−dI2,dMdt=μ1I1+μ2I2−τM. | (2.2) |
| Parameters | Descriptions | Values | Units | Sources |
| Λ1 | Immigration into the compartment of sensitive susceptible population | 3 | day−1 | [21] |
| Λ2 | Immigration into the compartment of insensitive susceptible population | 4 | day−1 | [21] |
| β11 | Contact rate of susceptible and infected individuals in group 1 | 0.00003 | personsday−1 | [26] |
| β12 | Contact rate of susceptible individuals in group 1 and infected individuals in group 2 | 0.00005 | personsday−1 | [26] |
| β21 | Contact rate of susceptible individuals in group 2 and infected individuals in group 1 | 0.00006 | personsday−1 | [26] |
| β22 | Contact rate of susceptible and infected individuals in group 2 | 0.00009 | personsday−1 | [26] |
| α1 | Reaction of susceptible individuals to the media in group 1 | 0.0033 | - | [26] |
| α2 | Reaction of susceptible individuals to the media in group 2 | 0.0028 | - | Assumed |
| γ1 | Recovery rate in group 1 | 0.2 | day−1 | [26] |
| γ2 | Recovery rate in group 2 | 0.15 | day−1 | Assumed |
| h1 | The parameter that measures the effect of medical resource limitation in group 1 | 0.29 | - | [26] |
| h2 | The parameter that measures the effect of medical resource limitation in group 2 | 0.029 | - | Assumed |
| μ1 | Response rate of infected individuals in group 1 | 0.4 | day−1 | [26] |
| μ2 | Response rate of infected individuals in group 2 | 0.2 | day−1 | Assumed |
| d | Natural mortality rate | 0.001345 | day−1 | [26] |
| τ | Natural disappearance rate of media reports | 0.08 | day−1 | [26] |
We first prove the nonnegativity and boundedness of the solutions of model (2.2) to show the the biological feasibility of it.
Theorem 3.1. Model (2.2) has a bounded solution for all time t≥0 with initial condition lying in domain
| Ω={(S1,I1,S2,I2,M)∈R5+:0≤S1+I1+S2+I2≤Λ1+Λ2d,0≤M≤μ1Λ1+μ2Λ2τd}. |
Moreover, the compact set Ω is positively invariant with respect to model (2.2).
Proof. Since the vector field described by the righthand sides of model (2.2) is Lipschitz continuous in Ω, a unique solution exists when t≥0. Note that S1=0⇒S′1≥0, I1=0⇒I′1≥0, S2=0⇒S′2≥0, I2=0⇒I′2≥0, and M=0⇒M′≥0. Therefore, all solutions of model (2.2) starting from Ω remain in Ω, and model (2.2) is mathematically and epidemiological well-posed in Ω.
The total population is represented by N=S+I+R. Depending on the difference of groups, the total population N is divided into two parts, N1 and N2, to represent the total population number of two groups. To demonstrate the boundedness of the solutions of model (2.1), we add all equations of model (2.1):
| N′1=Λ1−dN1⇒N1≤Λ1d,N′2=Λ2−dN2⇒N2≤Λ2d,N=N1+N2≤Λ1+Λ2d. |
The above inequality implies that N is bounded above as well as below. Now we prove the boundedness of M through the equation of M in (2.1). By some calculations as,
| M′+τM=μ1I1+μ2I2≤μ1Λ1+μ2Λ2d. |
Thus 0≤M≤μ1Λ1+μ2Λ2τd, which indicates that the feasible region for the model (2.2) is
| Ω={(S1,I1,S2,I2,M)∈R5+:0≤S1+I1+S2+I2≤Λ1+Λ2d,0≤M≤μ1Λ1+μ2Λ2τd}. |
We now demonstrate that model (2.2) has a disease-free equilibrium (DFE) given by
| E0=(S01,I01,S02,I02,M0)=(Λ1d,0,Λ2d,0,0). |
Additionally, we determine the basic reproduction number (R0), which serves as a critical threshold in epidemiological models. R0 represents the average number of secondary infections generated by an infectious individual in a population of susceptible individuals during the infectious period. To calculate R0, we use the next-generation matrix approach [28] and rewrite the equations for the infectious compartments as follows:
| F=(β11e−α1MS1I1+β12e−α1MS1I20β21e−α2MS2I1+β22e−α2MS2I200) |
and
| V=(γ1I11+h1I1+dI1−Λ1+β11e−α1MS1I1+β12e−α1MS1I2+dS1γ2I21+h2I2+dI2−Λ2+β21e−α2MS2I1+β22e−α2MS2I2+dS2−μ1I1−μ2I2+τM). |
Then we calculate the Jacobian matrices F and V at the E0, which are given as
| F=(β11Λ1d0β12Λ1d0000000β21Λ2d0β22Λ2d000000000000),V=(γ1+d0000β11Λ1ddβ12Λ1d0000γ2+d00β21Λ2d0β22Λ2dd0−μ10−μ50τ). |
The basic reproduction number is derived by computing the spectral radius of the next-generation matrix, FV−1,
| R0=ρ(FV−1)=k1+k2+√(k1−k2)2+4k1k22, |
where
| k1=β11Λ1d(d+γ1),k2=β22Λ2d(d+γ2),k3=β12Λ1d(d+γ2),k4=β21Λ2d(d+γ1). |
Next, we examine the dynamical behavior of model (2.2) around the DFE E0, and identify the basic reproduction number R0 as a crucial threshold parameter that governs the disease's extinction or persistence. To begin, we analyze the local stability of the E0, by evaluating the sign of the eigenvalues of the Jacobian matrix at the E0.
Theorem 3.2. The DFE E0 of model (2.2) is locally asymptotically stable (LAS) when R0<1, and it becomes unstable when R0>1.
Proof. The Jacobian matrix at E0 is given by:
| J(E0)=(−d−β11Λ1d0−β12Λ1d00β11Λ1d−γ1−d0β12Λ1d00−β21Λ2d−d−β22Λ2d00β21Λ2d0β22Λ2d−γ2−d00μ10μ2−τ). |
It is clear that the eigenvalues −d, −d, and −τ are three negative eigenvalues of J(E0). Therefore, the local stability of the DFE, E0, depends on the remaining eigenvalue of J(E0). The sign of the remaining eigenvalues is determined by the rest of the Jacobian matrix, denoted as J1(E0). The eigenvalues of J1(E0) are obtained by solving the characteristic equation:
| |λE−J1(E0)|=|λ−(β11Λ1d−γ1−d)−β12Λ1d−β21Λ2dλ−(β22Λ2d−γ2−d)|=0. |
Thus, the characteristic equation is:
| λ2−[β11Λ1−d(d+γ1)d+β22Λ2−d(d+γ2)d]λ+[β11Λ1−d(d+γ1)][β22Λ2−d(d+γ2)]d2−β12β21Λ1Λ2d2=0. |
In the light of Routh-Hurwitz criterion, we need to prove
| λ1λ2=[β11Λ1−d(d+γ1)][β22Λ2−d(d+γ2)]−β12β21Λ1Λ2d2>0, |
and
| λ1+λ2=β11Λ1−d(d+γ1)d+β22Λ2−d(d+γ2)d<0. |
When R0 is less than 1, we can get k1+k2+√(k1−k2)2+4k3k4<2. Upon further simplification, this leads to the condition
| k3k4<(1−k1)(1−k2). |
After substitution, we can get
| β12Λ1d(d+γ2)⋅β21Λ2d(d+γ1)<(1−β11Λ1d(d+γ1))(1−β22Λ2d(d+γ2)), |
which yields
| [β11Λ1−d(d+γ1)][β22Λ2−d(d+γ2)]>β12β21Λ1Λ2. |
Thus, we have λ1λ2>0. Next, we demonstrate that λ1+λ2<0. Since R0>0, we deduce that k1+k2+√(k1−k2)2+4k3k4>0, which implies that k3k4>k1k2. Substituting into the specific expressions, we obtain β12β21>β11β22. Furthermore, from the inequality
| [β11Λ1−d(d+γ1)][β22Λ2−d(d+γ2)]>β12β21Λ1Λ2, |
we substitute β12β21>β11β22 into the above inequality to obtain the result:
| [β11Λ1−d(d+γ1)][β22Λ2−d(d+γ2)]>β11β22Λ1Λ2, |
After simplification, we get β11Λ1d(d+γ1)+β22Λ2d(d+γ2)<1, which implies β11Λ1d(d+γ1)<1 and β22Λ2d(d+γ2)<1, and this can be further written as β11Λ1<d(d+γ1) and β22Λ2<d(d+γ2). Therefore, we have
| λ1+λ2=β11Λ1−d(d+γ1)d+β22Λ2−d(d+γ2)d<0. |
Through the calculation, when R0 is less than 1, we can get tr(J(E0))<0 and det(J(E0))>0. Therefore, according to the Routh-Hurwitz criterion, we complete the proof.
Note that model (2.2) has high nonlinearity, which makes the analysis of the model's dynamics challenging. Therefore, we consider a special case:
| {dS1dt=Λ1−β11e−α1MS1I1−β12e−α1MS1I2−dS1,dI1dt=β11e−α1MS1I1+β12e−α1MS1I2−γ1I1−dI1,dS2dt=Λ2−β21e−α2MS2I1−β22e−α2MS2I2−dS2,dI2dt=β21e−α2MS2I1+β22e−α2MS2I2−γ2I2−dI2,dMdt=μ1I1+μ2I2−τM, | (3.1) |
This special case only includes the factor of contact rate influenced by information, i.e., h1=0 and h2=0. Then, we proceed to theoretically analyze the conditions for the extinction or persistence of the disease in the special case.
Theorem 3.3. Assume model (3.1) satisfies R0<1, then E0 is globally asymptotically stable in Ω given there exist two positive constant ρ1 and ρ2 with
| ρ1<β11Λ12β21Λ2,max{β11Λ1d(γ1+d),β21Λ2d(γ1+d)}<ρ1<1 |
and
| ρ2<β22Λ22β12Λ1,max{β12Λ1d(γ2+d),β22Λ2d(γ2+d)}<ρ2<1. |
Proof. In model (3.1), we can continue to use the conditions of the Routh-Hurwitz criterion in Section 3.2, because when h1 = 0 and h2 = 0, the conditions are interlinked. We use the method of constructing the Lyapunov function to prove the disease extinction of model (3.1). The Lyapunov function is given by:
| L=S1−S01−S01lnS1S01+S2−S02−S02lnS2S02+I1+I2. |
It is straightforward that L is a positive definite function. Along the trajectories of model (3.1), we have
| dLdt=(1−S01S1)dS1dt+(1−S02S2)dS2dt+dI1dt+dI2dt=(1−S01S1)(Λ1−β11e−α1MS1I1−β12e−α1MS1I2−dS1)+(1−S02S2)(Λ2−β21e−α2MS2I1−β22e−α2MS2I2−dS2)+β11e−α1MS1I1+β12e−α1MS1I2−γ1I1−dI1+β21e−α2MS2I1+β22e−α2MS2I2−γ2I2−dI2=Λ1(2−S1S01−S01S1)+Λ2(2−S2S02−S02S2)+(β11e−α1MS01+β21e−α2MS02−γ1−d)I1+(β12e−α1MS01+β22e−α2MS02−γ2−d)I2≤Λ1(2−S1S01−S01S1)+Λ2(2−S2S02−S02S2)+(β11S01+β21S02−γ1−d)I1+(β12S01+β22S02−γ2−d)I2. |
Note that the first and second terms are clearly nonpositive, and the sign of the derivative of the Lyapunov function is primarily determined by the latter two terms. Specifically, we focus on the expression inside the parentheses of the third term,
| β11S01+β21S02−γ1−d=β11Λ1d+β21Λ2d−γ1−d=(γ1+d)[β11Λ1d(γ1+d)+β21Λ2d(γ1+d)−1]. |
Therefore, if β11Λ1d(γ1+d)≤12 and β21Λ2d(γ1+d)≤12 are satisfied, it can be demonstrated that the third term is nonpositive. To achieve this, we assume that there exists 0<ρ1<1, such that 0<β11Λ1d(γ1+d)<ρ1. Due to β21Λ2d(γ1+d)=β11Λ1d(γ1+d)⋅β21Λ2β11Λ1, we can rewrite the expression as β21Λ2d(γ1+d)=β11Λ1d(γ1+d)⋅β21Λ2β11Λ1<ρ1⋅β21Λ2β11Λ1. To ensure that β21Λ2d(γ1+d)≤12, it is sufficient to have ρ1⋅β21Λ2β11Λ1<12, which implies ρ1<β11Λ12β21Λ2. Thus, it is enough to require that max{β11Λ1d(γ1+d),β21Λ2d(γ1+d)}<ρ1<1 in order to guarantee that the third term is nonpositive. The treatment of the last term follows a similar approach. We can conclude that there exists 0<ρ2<1, and it is sufficient to require that ρ2<β22Λ22β12Λ1 and max{β12Λ1d(γ2+d),β22Λ2d(γ2+d)}<ρ2<1. These conditions ensure that the last term is also nonpositive.
Hence, together with conditions, we have dLdt≤0. Then, dLdt=0, if S1=S01,I1=I01,S2=S02,I2=I02. Therefore, the largest invariant set contained in {(S1,I1,S2,I2)|dLdt=0} is (S01,I01,S02,I02). According to the Lasalle's invariance principle [29], the DFE is globally asymptotically stable.
When R0>1, E0 becomes unstable. Therefore, it is reasonable to assume that in this case, the infected population I1(t) and I2(t) will remain continuous. In fact, the following theorem holds.
Theorem 3.4. Model (3.1) is uniformly persistent when R0>1 if, and only if, there exists a nonnegative constant η>0, such that all solutions of model (3.1) satisfy:
| liminft→∞I1(t)>η,liminft→∞I2(t)>η. |
Proof. We will apply Theorem 3.4 in [30] to prove the uniform persistence of model (3.1). Set
| X={(S1(t),I1(t),S2(t),I2(t),M(t))∈R5+:I1(0)≥0,I2(0)≥0},X0={(S1(t),I1(t),S2(t),I2(t),M(t))∈X:I1(0)>0,I2(0)>0},∂X0=Ω∖X0={(S1(t),0,S2(t),0,0)∈X:I1(0)=0orI2(0)=0}, |
which is relatively closed in X.
Let Φ(t):X→X be the solution flow associated with model (3.1), that is, Φ(t)(A0)=A(t). According to the positivity, it is easy to know when S1(0)≥0,I1(0)≥0,S2(0)≥0,I2(0)≥0,M(0)≥0, Φ(t) is positively invariant about X, so for ∀t>0, then S1(t)>0,I1(t)>0,S2(t)>0,I2(t)>0,M(t)>0. Now we prove that X0 is positive invariant for Φ(t). According to the second and fourth equations of model (3.1), we get that
| dI1(t)dt≥−(γ1+d)I1(t),∀t>0,dI2(t)dt≥−(γ2+d)I2(t),∀t>0. |
If I1(0)≥0,I2(0)≥0, according to the above two equations, we can get
| I1(t)≥I1(0)e−(γ1+d)t,I2(t)≥I2(0)e−(γ2+d)t,∀t>0. |
Therefore, X0 is positive invariant for Φ(t). Moreover, model (3.1) has the ultimate upper boundary, thus we obtain X is point dissipative for Φ(t). We set M∂={A0∈∂X0,∀t≥0}. We claim that M∂={(S1,0,S2,0,0)}.
Hypothesize that A(t)∈M∂,∀t≥0, and it suffices to show that I1(t)=I2(t)=0,∀t≥0. If it is not true, then there exists t0≥0 such that either (a) I1(t0)>0,I2(t0)=0; or (b) I1(t0)=0,I2(t0)>0.
For case (a), from the fourth equation of model (3.1), we have
| dI2(t)dt|t=t0=β21e−α2M(t0)S2(t0)I1(t0)>0. |
Hence, there is an ε0>0 such that I2(t)>0, ∀t∈(t0,t0+ε0). On the other hand, from I1(t0)>0, there exists an ε1 (0<ε1<ε0) such that I1(t)>0, ∀t∈(t0,t0+ε1). Thus, we have I1(t)>0,I2(t)>0,∀t∈(t0,t0+ε1), which contradicts the assumption that {S1(t),I1(t),S2(t),I2(t),M(t)∈M∂,∀t≥0}. Similarly, we can obtain a contradiction for case (b). This proves the claim.
Let A=∩x∈Abω(x), where Ab is the global attractor of model (3.1) restricted to ∂X0. We show that A=E0. In fact, from A⊆M∂ and the first and third equations of model (3.1), we have
| limt→∞S1(t)=Λ1+εd,limt→∞S2(t)=Λ2+εd. |
Thus, E0 is the isolated invariant set in X.
Next we show that Ws(E0)∩X0=∅. If it is not true, then there exists a solution (S1(t),I1(t),S2(t),I2(t),M(t))∈X0 such that
| limt→∞(S1(t),I1(t),S2(t),I2(t),M(t))=(Λ1d,0,Λ2d,0,0). |
Therefore, for any sufficiently small constant ξ>0, there exists a positive constant T1=T1(ξ) such that we have the following inequalities for all t≥T1:
| Λ1−ξd≤S1(t)≤Λ1+ξd,Λ2−ξd≤S2(t)≤Λ2+ξd,0≤I1(t)≤ξ,0≤I2(t)≤ξ,0≤M(t)≤ξ. |
Consider the following auxiliary system with the above constant ξ:
| dI1(t)dt=β11e−α1M(t)S1(t)I1(t)+β12e−α1M(t)S1(t)I2(t)−γ1I1(t)1+h1I1(t)−dI1(t)≥[β11e−α1ξΛ1−ξd−(γ1+d)]I1(t)+β12e−α1ξΛ1−ξdI2(t),dI2(t)dt=β21e−α2M(t)S2(t)I1(t)+β22e−α2M(t)S2(t)I2(t)−γ2I2(t)1+h2I2(t)−dI2(t)≥β21e−α2ξΛ2−ξdI1(t)+[β22e−α2ξΛ2−ξd−(γ2+d)]I2(t). |
Considering the following comparing system, where ˜I1(0)=I1(0),˜I2(0)=I2(0):
| {d˜I1(t)dt=[β11e−α1ξΛ1−ξd−(γ1+d)]I1(t)+β12e−α1ξΛ1−ξdI2(t),d˜I2(t)dt=β21e−α2ξΛ2−ξdI1(t)+[β22e−α2ξΛ2−ξd−(γ2+d)]I2(t). |
Then, the nonnegative matrix ˜F and the non-singular M-matrix ˜M, represented as new-infection and transition matrices severally, for the model (3.1), are provided by
| ˜F=(β11e−α1ξ(Λ1−ξ)dβ12e−α1ξ(Λ1−ξ)dβ21e−α2ξ(Λ2−ξ)dβ22e−α2ξ(Λ2−ξ)d),˜M=(γ1+d00γ2+d). |
Denote
| ˜J(ξ)=˜F˜M−1=(β11e−α1ξ(Λ1−ξ)d(γ1+d)β12e−α1ξ(Λ1−ξ)d(γ2+d)β21e−α2ξ(Λ2−ξ)d(γ1+d)β22e−α2ξ(Λ2−ξ)d(γ1+d)). |
According to Lemma 2.1 in [31], as long as R0>1, when ξ and s(˜J(0))>0, s(˜J(ξ)) is continuous. We can select such sufficiently small ξ>0 that we obtain s(˜J(ξ))>0, and this can explain that the positive solutions of the lower comparing system increase exponentially. By contrasting to the standard comparing system, as t→∞, the solutions I1(t) and I2(t) of model (3.1) are infinite, which are opposite to the truth that the solutions of the model (3.1) are bounded. Thus, Ws(E0)∩X0=∅. Clearly, every orbit in M∂ converges to E0. Thus, by Theorem 3 in [32], we have
| liminft→∞(I1(t),I2(t))>(η,η),η>0. |
By Theorem 4.3 and Remark 4.3 in [33], we conclude that model (3.1) is uniformly persistent with respect to (X0,∂X0). From Theorem 2.4 in [34], model (3.1) has at least one equilibrium (S∗1,I∗1,S∗2,I∗2,M∗)∈X0, with I∗1≫0 and I∗2≫0. Accordingly, there is at least one an endemic equilibrium in model (3.1). The proof of the theorem is complete.
In this section, we use optimal control techniques to study the model (2.1). In order to minimize the cost of implementing control strategies, it is necessary to find time-dependent control strategies. Most of the control strategies used in daily life are considering continuous control. In fact, this problem is a typical optimal control problem. If public health institutions want to eradicate a disease, maintaining a high level of control is crucial. However, this often incurs significant economic costs, so it is necessary to develop a time-dependent control strategy. The control strategy we adopt focuses on the allocation of media resources. Specifically, the total media resource allocation for two groups of infected individuals sums to 1. Let the media resource allocation rate for the sensitive infected individuals be denoted as u(t), while the allocation rate for the insensitive infected individuals is 1−u(t). Our primary objective is to minimize both the total number of infections and the costs associated with adjusting media coverage intensity.
Another key issue is the limitation of media resources when using media information to control infectious diseases. In particular, during emergencies, media resources are often constrained, as platforms such as television, radio, and social media have limitations in terms of coverage area, transmission frequency, and target audience. Therefore, communicators must prioritize the delivery of essential information and avoid excessive or redundant details. In the optimal control problem we consider, we assume a limited media resource, denoted as V. Optimal control problem with minimizing objective function
| J(u(t))=∫tf0[AI1(t)+BI2(t)+C2u2(t)]dt |
subject to
| {dS1dt=Λ1−β11e−α1MS1I1−β12e−α1MS1I2−dS1,dI1dt=β11e−α1MS1I1+β12e−α1MS1I2−γ1I11+h1I1−dI1,dR1dt=γ1I11+h1I1−dR1,dS2dt=Λ2−β21e−α2MS2I1−β22e−α2MS2I2−dS2,dI2dt=β21e−α2MS2I1+β22e−α2MS2I2−γ2I21+h2I2−dI2,dR2dt=γ2I21+h2I2−dR2,dMdt=V[u(t)μ1I1+(1−u(t))μ2I2]−τM, | (4.1) |
where the initial condition is the same as that of model (2.1). The coefficients A, B and C/2 are positive. A, B represent the weight of the two groups of infected people respectively. Here we assume that C/2 is the weight associated with control u(t). Note that u(t) is a Lebesgue measurable function on a finite interval [0,tf], where 0<u(t)<1. To start, we prove the existence of an optimal control for the model (4).
Theorem 4.1. There exists an optimal control u∗(t) such that
| J(u∗(t))=min{∫tf0(AI1(t)+BI2(t)+C2u∗2(t))dt} |
subject to the control model (4.1).
Proof. By the result in [35], we prove the existence of an optimal control. Note that the control and the state variable are nonnegative values. In this minimizing problem, the necessary convexity of the objective functional in u(t) is satisfied. Meanwhile, u(t) belongs to the control set U, where
| U={u(t):[0,tf]→R∣u(t) is a Lebesgue measure on [0,1]}. |
The boundedness of the optimal system ensures the compactness required for the existence of an optimal control. In addition, the integrand in the objective function is convex on the control set U. Also, we can see that there exist a constant ρ>1 and positive numbers ω1,ω2 such that
| J(u(t))≥ω1|u1(t)|ρ−ω2, |
because the state variables are bounded, which completes the existence of an optimal control.
In order to find the optimal solution, we use Pontryagin's maximum principle as follows [36]. Define the Hamiltonian H for the control problem:
| H=(S1,I1,R1,S2,I2,R2,M,u,λS1,λI1,λR1,λS2,λI2,λR2,λM,t)=AI1+BI2+C2u21(t)+λS1dS1dt+λI1dI1dt+λR1dR1dt+λS2dS2dt+λI2dI2dt+λR2dR2dt+λMdMdt. |
Then, the adjoint equations are given:
| dλS1dt=−∂H∂S1=(β11e−α1MI1+β12e−α1MI2)(λS1−λI1)+λS1d,dλI1dt=−∂H∂I1=−A+β11e−α1MS1(λS1−λI1)+β21e−α2MS2(λS2−λI2)+γ1(λI1−λR1)(1+h1I1)2+λI1d−λMμ1Vu(t),dλR1dt=−∂H∂R1=λR1d,dλS2dt=−∂H∂S2=(β21e−α2MI1+β22e−α2MI2)(λS2−λI2)+λS2d,dλI2dt=−∂H∂I2=−B+β12e−α1MS1(λS1−λI1)+β22e−α2MS2(λS2−λI2)−γ2(λI2−λR2)(1+h2I2)2+λI2d−λMμ2V(1−u(t)),dλR2dt=−∂H∂R2=λR2d,dλMdt=−∂H∂M=(β11α1e−α1MS1I1+β12α1e−α1MS1I2)(λI1−λS1)+(β21α2e−α2MS2I1+β22α2e−α2MS2I2)(λI2−λS2)+λMτ. |
By the optimality conditions, we have
| ∂H∂u(t)=Cu(t)+λMV(μ1I1−μ2I2)=0⇒u∗(t)=λMV(μ2I2−μ1I1)C, |
Note that the boundness is placed on the control variable u(t), then the optimality condition is changed to
| u∗(t)=max{min{λMV(μ2I2−μ1I1)C,1},0}, |
which is the optimal control.
First, we study the impact of the reaction of susceptible individuals to the media, α1 and α2, on the number of sensitive infected individuals, insensitive infected individuals, and total infected individuals at steady state, which are given in Figure 2. Figure 2(a) shows that I1 decreases with the increase of α1, however, the impact of α2 remains negligible. Figure 2(b) illustrates that a higher value of α2 leads to a more significant reduction in the number of insensitive infected individuals. Figure 2(c) indicates that increases in both α1 and α2 contribute to a decrease in the total number of infected individuals. Figure 3 shows the impact of the response rate of infected individuals, μ1 and μ2, on the number of sensitive infected individuals, insensitive infected individuals, and total infected individuals at steady state. As shown in Figure 3(a), both an increase in μ1 and μ2 lead to a decrease in I1, with the effect of μ2 being more pronounced. Figure 3(b) demonstrates that an increase in μ2 reduces I2, while μ1 has a negligible impact. Figure 3(c) indicates that both μ1 and μ2 contribute to a reduction in the total number of infected individuals, although the effect of μ2 is more pronounced. The effect of the impaction of limited medical resources, h1 and h2, on the numbers of sensitive infected individuals, insensitive infected individuals, and total infected individuals at steady state is shown in Figure 4. As shown in Figure 4(a), a decrease in h1 and an increase in h2 both lead to a reduction in I1. Figure 4(b) indicates that I2 decreases as h2 decreases, while h1 has almost no impact. Figure 4(c) demonstrates that reductions in both h1 and h2 contribute to a decrease in the total number of infected individuals. In general, while the impact of different parameters varies, increasing the influence of media information and medical resources contributes to a reduction in the total number of infected individuals.
Next, we examine the impact of several key parameters on the total number of infections and model stability, as shown in Figure 5. It is evident from the figure that variations in these key parameters significantly influence both the changes in and the stability of the total number of infected individuals. Then, we analyze the relationship between changes in key parameters and stability through the following bifurcation diagrams.
Figures 6 and 7 are Hopf bifurcation diagrams of I1 and I2 caused by parameters. As shown in Figure 6(a), for the range of the reaction of sensitive susceptible individuals to the media, 0<α1≤0.0102, the disease is asymptotically stable. For 0.0102<α1≤0.043, the periodic oscillations (limit cycle) will appear, i.e., the disease outbreak will occur repeatedly. However, for a higher value of α1, i.e., for α1>0.043, the periodic solutions disappear and the disease again becomes stable. For Figure 6(b), when 0<α2≤0.014, the disease is asymptotically stable. When alpha2>0.014, periodic oscillation (limit cycle) will occur, that is, disease outbreaks will occur repeatedly. For Figure 6(c), when 0<μ1<1, there will always be periodic oscillation (limit cycle), and the disease will break out repeatedly. In Figure 6(d), when 0<μ2≤0.16, the disease will remain stable, while when 0.16<μ2≤1, the disease will occur in periodic outbreaks. In Figure 6(e), when 0<h1<4, the disease will occur periodic outbreaks. The situation of the Figure 6(f) is similar to that of Figure 6(a). When 0<h2≤0.006, the disease is stable, while when 0.006<h2≤0.068, the disease is unstable and periodic oscillation occurs, and when h2 is increased again, the disease will become stable.
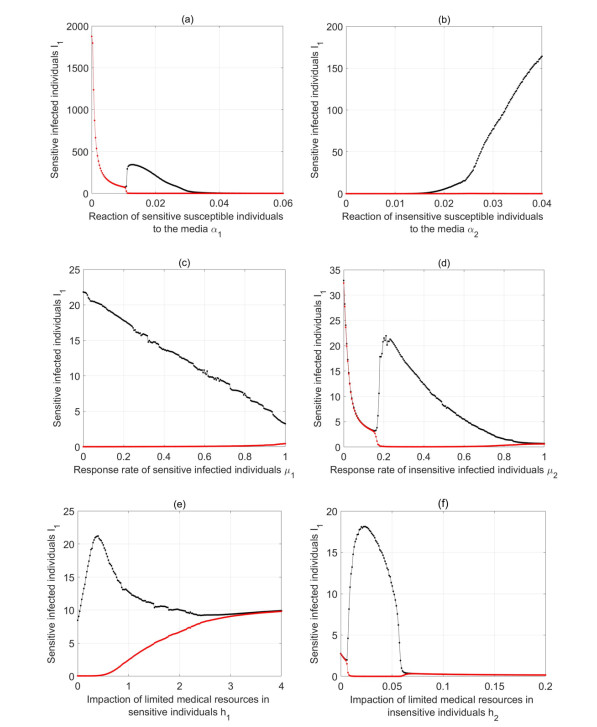
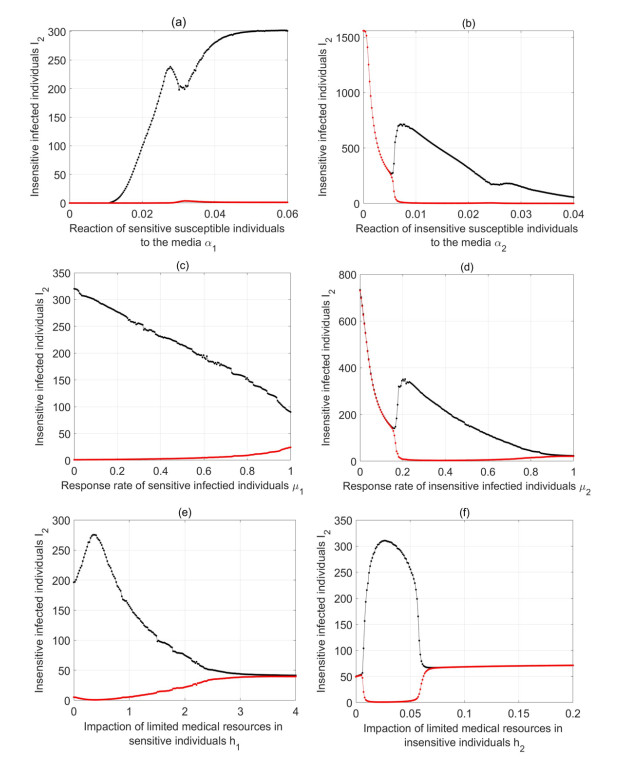
Figure 7(a)–(f) analytical methods parallel to those employed for Figure 6. There are also several situations caused by parameter changes, such as from stable to unstable, unstable to stable, unstable in the whole stage, and from stable to unstable and then to stable. Therefore, media information and medical resources play crucial roles in inducing complex dynamics in model (2.2).
Due to computational challenges, we use the MATCONT package to perform numerical simulations and analyze the dynamical behaviors and bifurcations of model (2.2) under various conditions. We shall illustrate forward bifurcation, backward bifurcation, and forward-backward bifurcation in the following.
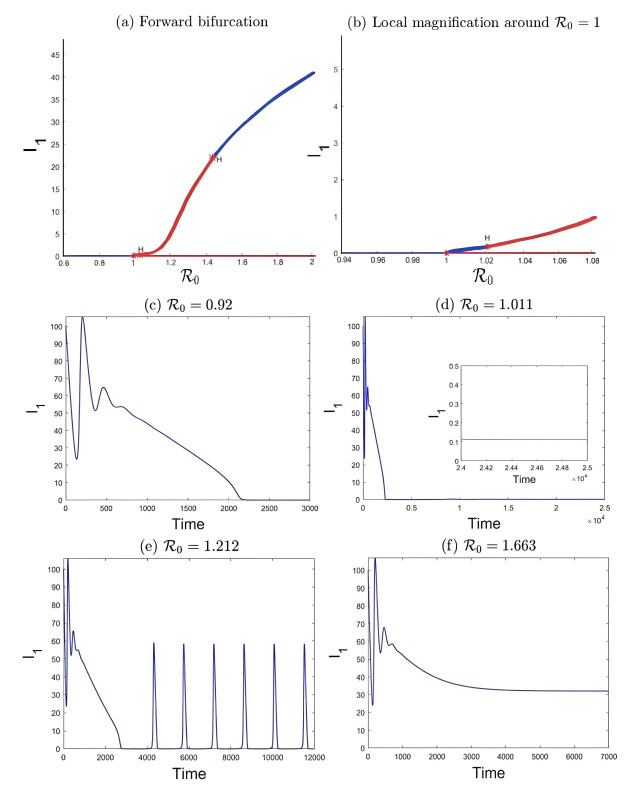
A forward bifurcation is illustrated in Figure 8, and Figure 8(a) gives variation in equilibrium level of sensitive infected individuals with the basic reproduction number (associated with parameter Λ1) and corresponding bifurcations, say, when R0=1.0214, the model (2.2) undergoes Hopf bifurcation. Figure 8(b) is a partial enlarged view of Figure 8(a) near R0=1. Figure 8(c)–(f) illustrates the time series of the model (2.2) with different parameters Λ1 which stabilize to either the disease-free equilibrium or endemic state or bifurcated periodic solution. The first Lyapunov coefficients at both Hopf points are negative, which means that the Hopf bifurcation is supercritical and the periodic orbits are born stably, that is to say, the model exists a stable limit cycle when 1.0214<R0<1.413. Also, we can see that when R0<1, the model (2.2) only has the DFE, which is globally asymptotically stable, shown in Figure 8(c); when 1<R0<1.0214 and R0>1.413, the model (2.2) has an unstable DFE and a globally stable endemic equilibrium, shown in Figure 8(d),(f); when 1.0214<R0<1.413, the model (2.2) has an unstable DFE and an unstable endemic equilibrium, but has a bifurcated periodic solution around this unstable endemic equilibrium, shown in Figure 8(e).
A backward bifurcation is shown in Figure 9, and Figure 9(a) illustrates the saddle-node bifurcation at R0=0.585 and backward bifurcation at R0=1. Figure 9(b)–(d) are time serious diagrams corresponding to different R0 of backward bifurcation diagram. When R0<0.585, model (2.2) has a unique stable DFE, shown in Figure 9(b). As R0 increases, the E0 coexists with a stable endemic state E∗ for 0.585<R0<1, shown Figure 9(c), and further increasing R0 leads to model (2.2) stabilizing to the stable endemic equilibrium for R0>1, shown in Figure 9(d).
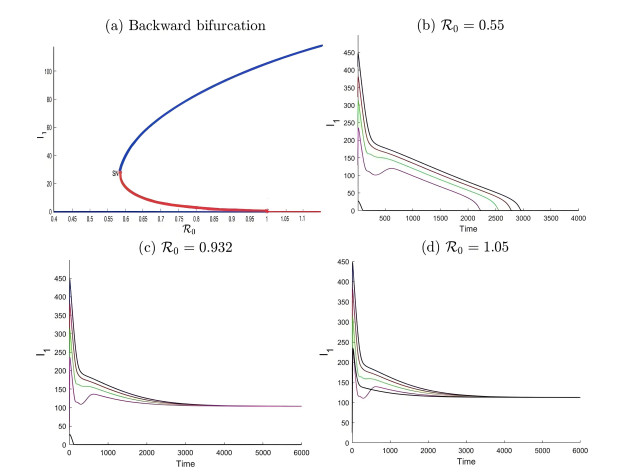
The forward-backward bifurcation is illustrated in Figure 10(a) where saddle-node bifurcation occurs for R0>1 and Hopf bifurcation may also occur, and Figure 10(b) is a local magnification of Figure 10(a) around R0=1. We find two Hopf bifurcation points at R0=0.6451 and R0=1.0092528 and two saddle-node bifurcation points at R0=0.617 and R0=1.0288. The first Lyapunov coefficients at those two Hopf points are both positive, which means that the Hopf bifurcations are subcritical and the bifurcated periodic orbits are born unstable. To further analyze how periodic orbits change, we plot local bifurcation diagrams (Figure 10(c),(d)) and the variation in period of cycles versus R0 (Figure 10(e),(f)). Figure 10(c),(d) show that once the periodic orbit appears, the minimum value of I(t) of the periodic orbit is infinitely close to the value of I(t) at the unstable saddle point (or DFE) at R0=0.6534 and R0=1.009208. Figure 10(e),(f) shows that the periods eventually go to infinity at R0=0.6534 and R0=1.009208, at which the homoclinic bifurcations occur and the limit cycle is replaced by a homoclinic orbit.
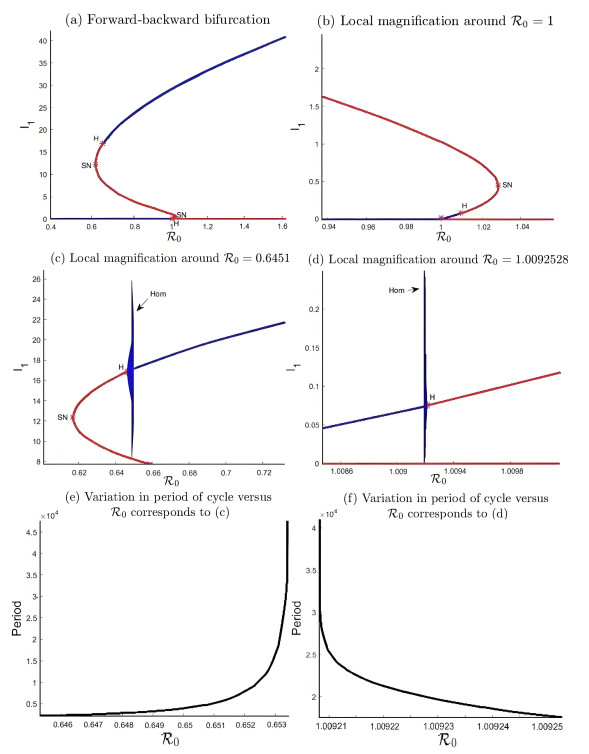
In summary, the numerical bifurcation diagrams reveal the occurrence of forward bifurcation, Hopf bifurcation, backward bifurcation, forward-backward bifurcation, and homoclinic bifurcation. During the initial phase of an emerging infectious disease outbreak, intensifying public awareness campaigns and implementing containment measures can effectively reduce the initial number of infections. This reduction enables the system to stabilize the infection count at a lower endemic equilibrium, thereby mitigating long-term public health burdens.
To investigate the information allocation between two populations with different information reception capabilities, numerical simulations will be conducted to determine the total number of infections and the constant media resource allocation rate u under the constraint of limited media resources. Subsequently, a time-varying optimal allocation rate u(t) control strategy will be proposed to minimize both the total number of infections and the cost associated with media information allocation. In this section, we use the media resource data from [38] as the parameter values for V. In their study, the daily news data from Xinhuanet (news.cn) ranged approximately between 5 to 45 articles per day. Therefore, we also adopted this data range in our analysis, where 5 articles per day indicate insufficient media coverage (limited resources), and 45 articles per day represent sufficient media coverage (abundant resources).
First, Figure 11 illustrates the relationship between the constant allocation rate (u) of model (4.1) and the total number of infected individuals across varying resource levels, considering two groups with three different types of heterogeneity. From Figure 11(a), it can be observed that when heterogeneity is low and V≤25, media resources should be allocated to the group with higher information sensitivity. However, when V>25, resources should be allocated to the insensitive group. Figure 11(b) indicates that when the heterogeneity between the two groups is moderate, the allocation strategy shifts at V=25, with resources now being allocated to the insensitive group. In cases of high heterogeneity between the two groups, as shown in Figure 11(c), media resources should also be allocated to the insensitive group when V=15. Therefore, the allocation of media resources is closely related to the heterogeneity between the two groups. As heterogeneity increases, resources are more frequently allocated to the insensitive group.
Next, to gain a deeper understanding of the optimal media allocation strategy for minimizing infections and associated costs, we simulated the optimal control in model (4.1) and derived the corresponding optimal control. In the context of three different levels of group heterogeneity, we use the same parameter values, except for the values of α1 and α2, and apply the forward-backward sweep method to solve the control problem. We numerically calculated optimal control strategies based on the iterative method used in [39]. This algorithm addresses the optimal control problem by simulating the system dynamics through Ordinary Differential Equation Solvers and updating the control strategy using adjoint equations. During each iteration, the objective is to minimize the cost function by adjusting the control variables. After every iteration, the control variables are updated and the system states are recalculated until the convergence criteria are satisfied. The specific steps are as follows:
1) Parameter initialization:
● Set global variables such as λ1, λ2, β11, α1, etc., which are parameters related to the model.
● Initialize control variables, iteration parameters, such as u, u(t) (current and previous iteration control variables), and initial system states y0.
2) Model definition:
● Define different models corresponding to different control strategies.
● These models describe the system state evolution over time with control inputs affecting the system dynamics.
3) Objective function definition:
● The objective function J is used to evaluate the effectiveness of the current control strategy. It is computed by summing the cost at each time point, which usually involves factors such as infection rates and control cost.
● During each iteration, calculate the new objective function and compare it with the previous iterations value to check for convergence.
4) Control input calculation:
● Update control input u based on the adjoint equation (Lagrange multiplier) and the current state y.
● Control input u is updated using the adjoint variable λS1,λI1,λR1,λS2,λI2,λR2,λM and the system state y.
● Ensure the control input is within a specified range, and update the control variable using a step size.
5) Adjoint equation solution:
● Solve the adjoint equation to update the adjoint variables λS1,λI1,λR1,λS2,λI2,λR2,λM. This step is necessary in optimal control problems.
● In the backward step, starting from the terminal time, the adjoint equations (typically linked to the Lagrange multiplier equations of the optimization problem) are solved to update the adjoint variables.
6) Optimization iteration:
● Iterate multiple times, updating the control variable u at each step until the objective function changes by less than a threshold or the maximum number of iterations is reached.
● After each iteration, print the current control variables u and state variables y, and update the objective function values.
7) Visualization:
● During the iterations, plot various graphs, such as the infection rate change and the evolution of control strategies.
● Display the results for different control strategies.
As shown in Figure 12(a),(c),(e), the optimal control strategy is implemented from the onset of the epidemic. Initially, media resources are gradually allocated to sensitive groups. As the disease progresses, all media resources must be allocated to sensitive groups. However, as the infection rate within the population declines, media resources should gradually be shifted toward less sensitive groups. The key distinction across varying levels of population heterogeneity is that, as heterogeneity increases, the timing of the transition in media resource allocation occurs progressively earlier.
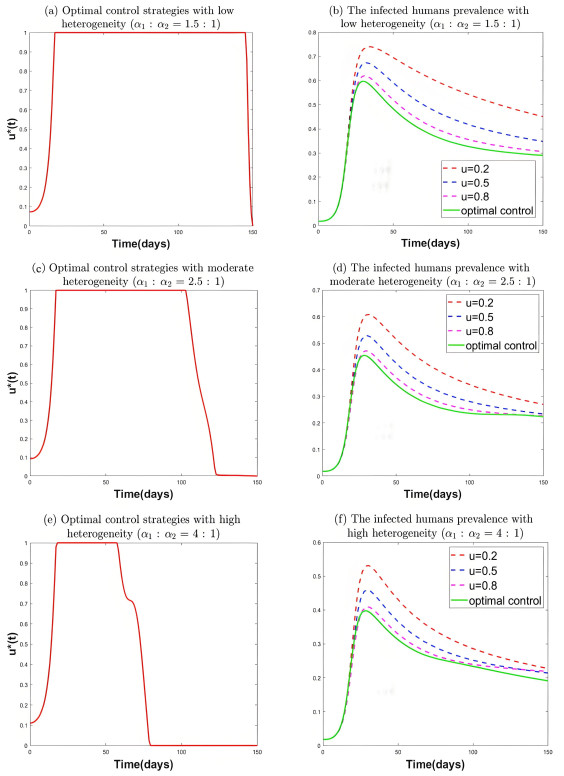
Figure 12(b),(d),(f) presents the infected humans prevalence, where the red dashed line represents the infection rate with a control strategy of 0.2, the blue dashed line represents the infection rate with a control strategy of 0.5, the purple dashed line represents the infection rate with a control strategy of 0.8, and the green solid line indicates the infection rate under the optimal control strategy. It is evident that under optimal control, the infected humans prevalence is minimized. However, the overall difference in the effectiveness of infection prevalence control across the three types of heterogeneous populations is minimal. Only in groups with high heterogeneity does controlling the infected humans prevalence below 20% lead to slightly more effective control compared to the other two strategies. Thus, the distribution of media resources follows a heterogeneity-dependent allocation paradigm: under low heterogeneity conditions, priority is given to information-responsive groups, whereas higher heterogeneity triggers a proportional reallocation to demographic segments exhibiting limited responsiveness to media interventions.
In this study, we proposed an improved infectious disease SIR model that divides the population into two distinct groups: the information-sensitive group and the information-insensitive group. This model incorporates two nonlinear functions to examine the impact of media coverage and limited medical resources on disease transmission. It more accurately reflects the actual dynamics of infectious disease transmission under varying heterogeneity conditions. We analyze the well-posedness of the original model, but due to its high nonlinearity, we focused on the case where only media information influences and investigated the conditions for disease extinction and persistence. Numerical simulations were conducted on media and medical resource parameters. The bifurcation analysis revealed various dynamic behaviors, including forward bifurcation, backward bifurcation, Hopf bifurcation, saddle-node bifurcation, and homoclinic bifurcation. In the control problem, we further considered the allocation of limited media resources and explored the issue from both constant and optimal control perspectives. Under constant control, we simulated the changes in the number of infected individuals for different types of population heterogeneity, considering varying media allocations and limited media resources. In the case of optimal control, we applied optimal control theory to explore the problem related to information allocation and derived optimal control strategy. In addition, we validated the effectiveness of the proposed control strategy by simulating the optimal media resource allocation for different types of population heterogeneity, and compared the similarities and differences in control strategies and effects among different types of groups.
Our model incorporates factors such as media coverage and medical resource limitations, particularly in the early stages of a pandemic, where these factors significantly influence disease transmission. It also captures the variations in media responses across different populations, which is essential for developing targeted public health policies. By analyzing simplified conditions for disease extinction and persistence, we provide theoretical insights into epidemic dynamics. However, media coverage and medical resource limitations do not affect the threshold conditions for disease extinction or persistence. Numerical simulations of media and medical resource parameters illustrate their impact on the number of infected individuals. Overall, increasing public responsiveness to media and medical resources helps reduce infections, and both factors influence the stability. Bifurcation analysis reveals complex dynamics under varying parameters, highlighting the challenges of controlling disease spread. Two control methods were simulated with limited media resources. Under constant control, resources tend to be allocated to insensitive groups as population heterogeneity increases. In optimal control, a key distinction across varying levels of heterogeneity is that as heterogeneity increases, resources gradually shift toward insensitive groups.
Compared to [21] and [26], our work extends the model by jointly considering the effects of media coverage and medical resources, and explores control strategies for populations with varying heterogeneity. Our research suggests that during the early stages of an emerging infectious disease outbreak, public health organizations can reduce the initial number of infections and stabilize the infected population at a lower level through measures such as quarantine controls or intensified disease awareness campaigns. Furthermore, the allocation of media resources is closely tied to population heterogeneity: when heterogeneity is low, resources are predominantly allocated to information-sensitive groups, while as heterogeneity increases, resources gradually shift toward insensitive groups. Thus, our study may contribute to advancing their work in this area. However, certain limitations remain, particularly in the theoretical analysis, where the high nonlinearity of the model constrained us to focus on the extinction and persistence conditions of a simplified model. Additionally, our current framework does not account for the heterogeneity of media information, such as its veracity (truthfulness vs. misinformation) and practical relevance (actionable guidance vs. speculative content), which are critical factors requiring explicit consideration in real-world public health communication strategies. This aspect can be further refined in future research.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors are very grateful to the editor and the anonymous reviewers for their careful review and valuable advice, which helped to improve the presentation of the paper. The authors sincerely thank Dr Xiulei Jin, Ning Wang, and Wei You for their valuable contributions to the numerical simulation section of this paper, which significantly improved the quality of this work. The authors acknowledge support from the National Natural Science Foundation of China (No.12271401, W2421101) and the Natural Science Foundation of Tianjin, China (No.22JCYBJC00080).
The authors declare there is no conflict of interest. Shengqiang Liu is a guest editor for Mathematical Biosciences & Engineering and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.
| [1] | M. Benzeval, C. L. Booker, J. Burton, T. F. Crossley, A. Jackle, M. Kumari, et al., Briefing Note COVID-19 Survey: Health and Caring, Understanding Society Working Paper Series, 2020. |
| [2] |
F. S. Dawood, S. Jain, L. Finelli, M. W. Shaw, S. Lindstrom, R. J. Garten, et al., Emergence of a novel swine-origin influenza a (H1N1) virus in humans, N. Eng. J. Med., 360 (2009), 2605–2615. https://doi.org/10.1056/NEJMoa0903810 doi: 10.1056/NEJMoa0903810

|
| [3] |
R. D. Smith, Responding to global infectious disease outbreaks: Lessons from SARS on the role of risk perception, communication and management, Soc. Sci. Med., 63 (2006), 3113–3123. https://doi.org/10.1016/j.socscimed.2006.08.004 doi: 10.1016/j.socscimed.2006.08.004

|
| [4] |
W. Kawohl, C. Nordt, COVID-19, unemployment, and suicide, Lancet Psychiatry, 7 (2020), 389–390. https://doi.org/10.1016/S2215-0366(20)30141-3 doi: 10.1016/S2215-0366(20)30141-3

|
| [5] |
W. W. Thompson, D. K. Shay, E. Weintraub, L. Brammer, N. Cox, L. J. Anderson, et al., Mortality associated with influenza and respiratory syncytial virus in the United States, J. Am. Med. Assoc., 289 (2003), 179–186. https://doi.org/10.1001/jama.289.2.179 doi: 10.1001/jama.289.2.179

|
| [6] |
H. Li, L. Pan, W. Chen, The influence of media information sources on preventive behaviors in China: After the outbreak of COVID-19 pandemic, Math. Method. Appl. Sci., 42 (2023). https://doi.org/10.1155/2023/4941436 doi: 10.1155/2023/4941436

|
| [7] |
G. Qian, M. Ada, N. Yang, A COVID-19 transmission within a family cluster by presymptomatic infectors in China, Clin. Infect. Dis., 71 (2020), 15. https://doi.org/10.1093/cid/ciaa316 doi: 10.1093/cid/ciaa316

|
| [8] |
Z. Niu, Z. Qin, P. Hu, T. Wang, Health beliefs, trust in media sources, health literacy, and preventive behaviors among high-risk Chinese for COVID-19, Health Promot. Int., 37 (2022), 1004–1012. https://doi.org/10.1080/10410236.2021.1880684 doi: 10.1080/10410236.2021.1880684

|
| [9] |
A. Wang, Y. Xiao, A Filippov system describing media effects on the spread of infectious diseases, Nonlinear Anal. Hybri., 11 (2013), 84–97. https://doi.org/10.1016/j.nahs.2013.06.005 doi: 10.1016/j.nahs.2013.06.005

|
| [10] |
M. L. Diagne, F. B. Agusto, H. Rwezaura, J. M. Tchuenche, S. Lenhart, Optimal control of an epidemic model with treatment in the presence of media coverage, Sci. Afr., 24 (2024), e02138. https://doi.org/10.1016/j.sciaf.2024.e02138 doi: 10.1016/j.sciaf.2024.e02138

|
| [11] |
Y. Xiao, S. Tang, J. Wu, Media impact switching surface during an infectious disease outbreak, Sci. Rep., 5 (2015), 7838. https://doi.org/10.1038/srep07838 doi: 10.1038/srep07838

|
| [12] |
J. Xie, H. Guo, M. Zhang, Dynamics of an SEIR model with media coverage mediated nonlinear infectious force. Math. Biosci. Eng., 20 (2023), 14616–14633. https://doi.org/10.3934/mbe.2023654 doi: 10.3934/mbe.2023654

|
| [13] |
W. Zhou, Y. Xiao, J. M. Heffernan, Optimal media reporting intensity on mitigating spread of an emerging infectious disease, PLoS One, 14 (2019), e0213898. https://doi.org/10.1371/journal.pone.0213898 doi: 10.1371/journal.pone.0213898

|
| [14] |
L. Hu, L. Nie, Stability and Hopf bifurcation analysis of a multi-delay Vector-Borne disease model with presence awareness and media effect, Fractal Fract., 7 (2023), 831. https://doi.org/10.3390/fractalfract7120831 doi: 10.3390/fractalfract7120831

|
| [15] |
K. K. Pal, R. K. Rai, P. K. Tiwari, Impact of psychological fear and media on infectious diseases induced by carriers, Chaos, 34 (2024), 123168. https://doi.org/10.1063/5.0217936 doi: 10.1063/5.0217936

|
| [16] |
N. Wang, L. Qi, M. Bessane, M. Hao, Global Hopf bifurcation of a two-delay epidemic model with media coverage and asymptomatic infection, J. Differ. Equations, 369 (2023), 1–40. https://doi.org/10.1016/j.jde.2023.05.036 doi: 10.1016/j.jde.2023.05.036

|
| [17] | Y. Luo, P. Liu, T. Zheng, Z. Teng, Dynamic analysis of an SSvEIQR model with nonlinear contact rate, isolation rate and vaccination rate dependent on media coverage, Int. J. Biomath., (2024), 2450011. https://doi.org/10.1142/S1793524524500116 |
| [18] |
H. Zang, S. Liu, Y. Lin, Evaluations of heterogeneous epidemic models with exponential and non-exponential distributions for latent period: The Case of COVID-19, Math. Biosci. Eng., 20 (2023), 12579–12598. https://doi.org/10.3934/mbe.2023560 doi: 10.3934/mbe.2023560

|
| [19] |
H. Zang, Y. Lin, S. Liu, Global dynamics of heterogeneous epidemic models with exponential and nonexponential latent period distributions, Stud. Appl. Math., 152 (2024), 1365–1403. https://doi.org/10.1111/sapm.12678 doi: 10.1111/sapm.12678

|
| [20] | Y. Lin, H. Zang, S. Liu, Final size of an n-group SEIR epidemic model with nonlinear incidence rate, Int. J. Biomath., 11 (2024). https://doi.org/10.1142/S1793524524500086 |
| [21] |
T. Li, Y. Xiao, Linking the disease transmission to information dissemination dynamics: An insight from a multi-scale model study, J. Theor. Biol., 526 (2021), 110796. http://doi.org/10.1016/j.jtbi.2021.110796 doi: 10.1016/j.jtbi.2021.110796

|
| [22] |
J. Cui, X. Mu, H. Wan, Saturation recovery leads to multiple endemic equilibria and backward bifurcation, J. Theor. Biol., 254 (2008), 275–283. https://doi.org/10.1016/j.jtbi.2008.05.015 doi: 10.1016/j.jtbi.2008.05.015

|
| [23] |
X. Zhou, J. Cui, Analysis of stability and bifurcation for an SEIR epidemic model with saturated recovery rate, Commun. Nonlinear Sci., 16 (2011), 4438–4450. http://dx.doi.org/10.1016/j.cnsns.2011.03.026 doi: 10.1016/j.cnsns.2011.03.026

|
| [24] |
X. Wang, J. Li, S. Guo, M. Liu, Dynamic analysis of an Ebola epidemic model incorporating limited medical resources and immunity loss, J. Appl. Math. Comput., 69 (2023), 4229–4242. https://doi.org/10.1007/s12190-023-01923-2 doi: 10.1007/s12190-023-01923-2

|
| [25] |
J. K. Asamoah, F. Nyabadza, Z. Jin, E. Bonyah, M. A. Khan, M. Y. Li, et al., Backward bifurcation and sensitivity analysis for bacterial meningitis transmission dynamics with a nonlinear recovery rate, Chaos Solitons Fractals, 140 (2020), 110237. https://doi.org/10.1016/j.chaos.2020.110237 doi: 10.1016/j.chaos.2020.110237

|
| [26] |
T. Li, Y. Xiao, Complex dynamics of an epidemic model with saturated media coverage and recovery, Nonlinear Dyn., 107 (2022), 2995–3023. https://doi.org/10.1007/s11071-021-07096-6 doi: 10.1007/s11071-021-07096-6

|
| [27] |
Y. Hao, Y. Luo, Z. Teng, Role of limited medical resources in an epidemic model with media report and general birth rate, Infect. Dis. Modell., 10 (2025), 522–535. https://doi.org/10.1016/j.idm.2025.01.001 doi: 10.1016/j.idm.2025.01.001

|
| [28] |
P. Dreessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 doi: 10.1016/S0025-5564(02)00108-6

|
| [29] | J. P. L. Salle, The stability of dynamical systems, in CBMS-NSF Regional Conference Series in Applied Mathematics, (1976). https://doi.org/10.1137/1.9781611970432 |
| [30] |
H. Thieme, R. Horst, Persistence under relaxed point-dissipativity (with application to an endemic model), SIAM J. Math. Anal., 24 (2006), 407–435. https://doi.org/10.1137/0524026 doi: 10.1137/0524026

|
| [31] |
W. Wang, X. Zhao, An epidemic model in a patchy environment, Math. Biosci., 19 (2004), 97–112. https://doi.org/10.1016/j.mbs.2002.11.001 doi: 10.1016/j.mbs.2002.11.001

|
| [32] |
H. L. Smith, X. Zhao, Robust persistence for semidynamical systems, Nonlinear Anal., 47 (2001), 6169–6179. https://doi.org/10.1016/S0362-546X(01)00678-2 doi: 10.1016/S0362-546X(01)00678-2

|
| [33] |
M. W. Hirsch, H. L. Smith, X. Zhao, Chain transitivity, attractivity, and strong repellors for semidynamical systems, J. Dyn. Differ. Equations, 13 (2001), 107–131. https://doi.org/10.1023/A:1009044515567 doi: 10.1023/A:1009044515567

|
| [34] | X. Zhao, Uniform persistence and periodic coexistence states in infinite-dimensional periodic semiflows with applications, Can. Appl. Math., 3 (1995), 473–495. |
| [35] | W. Fleming, R. Rishel, Deterministic and Stochastic Optimal Control, 1st edition, Springer-Verlag, New York, 1975. |
| [36] | L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze, E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience Publishers John Wiley and Sons, Inc., New York-London, 1962. |
| [37] |
H. Zhang, Z. Yang, K. A. Pawelek, S. Liu, Optimal control strategies for a two-group epidemic model with vaccination-resource constraints, Appl. Math. Comput., 371 (2020), 124956. https://doi.org/10.1016/j.amc.2019.124956 doi: 10.1016/j.amc.2019.124956

|
| [38] |
Q. Yan, S. Tang, S. Gabriele, J. Wu, Media coverage and hospital notifications: Correlation analysis and optimal media impact duration to manage a pandemic, J. Theor. Biol., 390 (2016), 1–13. https://doi.org/10.1016/j.jtbi.2015.11.002 doi: 10.1016/j.jtbi.2015.11.002

|
| [39] |
K. W. Blayneh, A. B. Gumel, S. Lenhart, T. Clayton, Backward bifurcation and optimal control in transmission dynamics of west nile virus, B. Math. Biol., 72 (2010), 1006–1028. https://doi.org/10.1007/s11538-009-9480-0 doi: 10.1007/s11538-009-9480-0

|
| Parameters | Descriptions | Values | Units | Sources |
| Λ1 | Immigration into the compartment of sensitive susceptible population | 3 | day−1 | [21] |
| Λ2 | Immigration into the compartment of insensitive susceptible population | 4 | day−1 | [21] |
| β11 | Contact rate of susceptible and infected individuals in group 1 | 0.00003 | personsday−1 | [26] |
| β12 | Contact rate of susceptible individuals in group 1 and infected individuals in group 2 | 0.00005 | personsday−1 | [26] |
| β21 | Contact rate of susceptible individuals in group 2 and infected individuals in group 1 | 0.00006 | personsday−1 | [26] |
| β22 | Contact rate of susceptible and infected individuals in group 2 | 0.00009 | personsday−1 | [26] |
| α1 | Reaction of susceptible individuals to the media in group 1 | 0.0033 | - | [26] |
| α2 | Reaction of susceptible individuals to the media in group 2 | 0.0028 | - | Assumed |
| γ1 | Recovery rate in group 1 | 0.2 | day−1 | [26] |
| γ2 | Recovery rate in group 2 | 0.15 | day−1 | Assumed |
| h1 | The parameter that measures the effect of medical resource limitation in group 1 | 0.29 | - | [26] |
| h2 | The parameter that measures the effect of medical resource limitation in group 2 | 0.029 | - | Assumed |
| μ1 | Response rate of infected individuals in group 1 | 0.4 | day−1 | [26] |
| μ2 | Response rate of infected individuals in group 2 | 0.2 | day−1 | Assumed |
| d | Natural mortality rate | 0.001345 | day−1 | [26] |
| τ | Natural disappearance rate of media reports | 0.08 | day−1 | [26] |
| Parameters | Descriptions | Values | Units | Sources |
| Λ1 | Immigration into the compartment of sensitive susceptible population | 3 | day−1 | [21] |
| Λ2 | Immigration into the compartment of insensitive susceptible population | 4 | day−1 | [21] |
| β11 | Contact rate of susceptible and infected individuals in group 1 | 0.00003 | personsday−1 | [26] |
| β12 | Contact rate of susceptible individuals in group 1 and infected individuals in group 2 | 0.00005 | personsday−1 | [26] |
| β21 | Contact rate of susceptible individuals in group 2 and infected individuals in group 1 | 0.00006 | personsday−1 | [26] |
| β22 | Contact rate of susceptible and infected individuals in group 2 | 0.00009 | personsday−1 | [26] |
| α1 | Reaction of susceptible individuals to the media in group 1 | 0.0033 | - | [26] |
| α2 | Reaction of susceptible individuals to the media in group 2 | 0.0028 | - | Assumed |
| γ1 | Recovery rate in group 1 | 0.2 | day−1 | [26] |
| γ2 | Recovery rate in group 2 | 0.15 | day−1 | Assumed |
| h1 | The parameter that measures the effect of medical resource limitation in group 1 | 0.29 | - | [26] |
| h2 | The parameter that measures the effect of medical resource limitation in group 2 | 0.029 | - | Assumed |
| μ1 | Response rate of infected individuals in group 1 | 0.4 | day−1 | [26] |
| μ2 | Response rate of infected individuals in group 2 | 0.2 | day−1 | Assumed |
| d | Natural mortality rate | 0.001345 | day−1 | [26] |
| τ | Natural disappearance rate of media reports | 0.08 | day−1 | [26] |