Figure 1.
Location of AWS and manual weather observation equipment at Stamar Paotere Makassar.
Protein functions are closely related to their subcellular locations. At present, the prediction of protein subcellular locations is one of the most important problems in protein science. The evident defects of traditional methods make it urgent to design methods with high efficiency and low costs. To date, lots of computational methods have been proposed. However, this problem is far from being completely solved. Recently, some multi-label classifiers have been proposed to identify subcellular locations of human, animal, Gram-negative bacterial and eukaryotic proteins. These classifiers adopted the protein features derived from gene ontology information. Although they provided good performance, they can be further improved by adopting more powerful machine learning algorithms. In this study, four improved multi-label classifiers were set up for identification of subcellular locations of the above four protein types. The random k-labelsets (RAKEL) algorithm was used to tackle proteins with multiple locations, and random forest was used as the basic prediction engine. All classifiers were tested by jackknife test, indicating their high performance. Comparisons with previous classifiers further confirmed the superiority of the proposed classifiers.
Citation: Lei Chen, Ruyun Qu, Xintong Liu. Improved multi-label classifiers for predicting protein subcellular localization[J]. Mathematical Biosciences and Engineering, 2024, 21(1): 214-236. doi: 10.3934/mbe.2024010
| [1] | Farman Ali Shah, Kamran, Dania Santina, Nabil Mlaiki, Salma Aljawi . Application of a hybrid pseudospectral method to a new two-dimensional multi-term mixed sub-diffusion and wave-diffusion equation of fractional order. Networks and Heterogeneous Media, 2024, 19(1): 44-85. doi: 10.3934/nhm.2024003 |
| [2] | Rong Huang, Zhifeng Weng . A numerical method based on barycentric interpolation collocation for nonlinear convection-diffusion optimal control problems. Networks and Heterogeneous Media, 2023, 18(2): 562-580. doi: 10.3934/nhm.2023024 |
| [3] | Yaxin Hou, Cao Wen, Yang Liu, Hong Li . A two-grid ADI finite element approximation for a nonlinear distributed-order fractional sub-diffusion equation. Networks and Heterogeneous Media, 2023, 18(2): 855-876. doi: 10.3934/nhm.2023037 |
| [4] | Narcisa Apreutesei, Vitaly Volpert . Reaction-diffusion waves with nonlinear boundary conditions. Networks and Heterogeneous Media, 2013, 8(1): 23-35. doi: 10.3934/nhm.2013.8.23 |
| [5] | Min Li, Ju Ming, Tingting Qin, Boya Zhou . Convergence of an energy-preserving finite difference method for the nonlinear coupled space-fractional Klein-Gordon equations. Networks and Heterogeneous Media, 2023, 18(3): 957-981. doi: 10.3934/nhm.2023042 |
| [6] | Yinlin Ye, Hongtao Fan, Yajing Li, Ao Huang, Weiheng He . An artificial neural network approach for a class of time-fractional diffusion and diffusion-wave equations. Networks and Heterogeneous Media, 2023, 18(3): 1083-1104. doi: 10.3934/nhm.2023047 |
| [7] | Yves Achdou, Victor Perez . Iterative strategies for solving linearized discrete mean field games systems. Networks and Heterogeneous Media, 2012, 7(2): 197-217. doi: 10.3934/nhm.2012.7.197 |
| [8] | Xiaoqian Gong, Alexander Keimer . On the well-posedness of the "Bando-follow the leader" car following model and a time-delayed version. Networks and Heterogeneous Media, 2023, 18(2): 775-798. doi: 10.3934/nhm.2023033 |
| [9] | Kexin Li, Hu Chen, Shusen Xie . Error estimate of L1-ADI scheme for two-dimensional multi-term time fractional diffusion equation. Networks and Heterogeneous Media, 2023, 18(4): 1454-1470. doi: 10.3934/nhm.2023064 |
| [10] | Li-Bin Liu, Limin Ye, Xiaobing Bao, Yong Zhang . A second order numerical method for a Volterra integro-differential equation with a weakly singular kernel. Networks and Heterogeneous Media, 2024, 19(2): 740-752. doi: 10.3934/nhm.2024033 |
Protein functions are closely related to their subcellular locations. At present, the prediction of protein subcellular locations is one of the most important problems in protein science. The evident defects of traditional methods make it urgent to design methods with high efficiency and low costs. To date, lots of computational methods have been proposed. However, this problem is far from being completely solved. Recently, some multi-label classifiers have been proposed to identify subcellular locations of human, animal, Gram-negative bacterial and eukaryotic proteins. These classifiers adopted the protein features derived from gene ontology information. Although they provided good performance, they can be further improved by adopting more powerful machine learning algorithms. In this study, four improved multi-label classifiers were set up for identification of subcellular locations of the above four protein types. The random k-labelsets (RAKEL) algorithm was used to tackle proteins with multiple locations, and random forest was used as the basic prediction engine. All classifiers were tested by jackknife test, indicating their high performance. Comparisons with previous classifiers further confirmed the superiority of the proposed classifiers.
Since 2014, Badan Meteorologi Klimatologi dan Geofisika (BMKG) or the Indonesian Meteorology, Climatology and Geophysics Agency has determined that it will switch weather observations from manual to automatic in the entire BMKG weather observation network. One of the obstacles to improving the quality of data spatially and temporally is the limited capacity of human resources (untrained) and the difficulty of reaching certain locations [1,2]. Automation is one solution to improve the quality and quantity of BMKG observation data, both spatially and temporally. This modernization is very important to keep up with the digital era as well as to increase the quantity and quality of weather data so as to produce fast, precise, and accurate meteorological, climatological and geophysical information which is the current vision of the BMKG [3]. The problem that arises from the transition from manual to automatic weather observations is the suitability of the automatic observation data and the previous manual data [4]. This alignment effort requires parallel testing of these two data types. Meteorological observations manually (OBS) in the BMKG environment are generally obtained with standards, such as measuring instruments, observation method, time of observation, reporting, location, and equipment park [5]. But as technology advances, many things become recorded, digitized, and automated. Even in the 2020 era, there are demands for memorization, which inevitably BMKG also has to adjust.
The term automatic weather observation according to the World Meteorological Organization (WMO) is weather observations obtained from weather equipment that can record and transmit data automatically [6]. This collection of equipment that measures several weather parameters is known as an automatic weather station. In contrast to manual weather observations, which are weather observations using a tool whose observations are recorded manually. One way to maintain the quality of observational data is to conduct measurement alignment automatically and manually within a minimum period of a year or two years and check for differences [7]. However, the WMO suggests that it is necessary to parallelize automatic weather observations over a certain period [8]. This process requires data from AWS to meet quality control (QC) requirements with statistical methods. The results of this quality control are very important in producing realistic and validated data that can be used as a basis for claiming that the data on the spot is a continuation of the previous manual observation.
A comparison of automatic and manual data in China found that there were variations in rainfall and air temperature, although they were still within tolerable limits [9]. However, this difference could be caused by a change in the tools used [10] or the data is not homogeneous [11]. The difference between these two types of measurement may be quite significant in the long run [12]. According to the research report in the Indonesian region, it shows that bias occurs during extreme conditions [13]. The difference between these two measurements is also influenced by location, where these two types of data are not normally distributed and are not homogeneous [14].
The coastal area which is the border of the sea and land is influenced by diurnal circulation in the form of sea breezes and land breezes. Likewise, Makassar City, which borders the Makassar Strait and the Java Sea, is significantly influenced by monsoon circulation and local wind circulation on land and sea [15]. The monsoon cycle can be seen from the nature of the rain that changes every half year, while the presence of land-sea winds can be detected by the dominant changes in westerly and southeasterly winds almost throughout the year in this city. If the estimation of rainfall using satellites that are very far away is quite good in this place compared to other places in South Sulawesi, are the measurements using AWS also less different than manual data [16,17,18]. Considering that weather observations will be transferred automatically and most of Indonesia's population is located in coastal areas, this change should not reduce the accuracy of meteorological data. Parallel comparison between these two measurements becomes very important to do. Therefore, the purpose of this study is to calculate and analyze the parallel measurement bias between manual parameter observations and automatic measurement data in coastal areas with monsoon patterns.
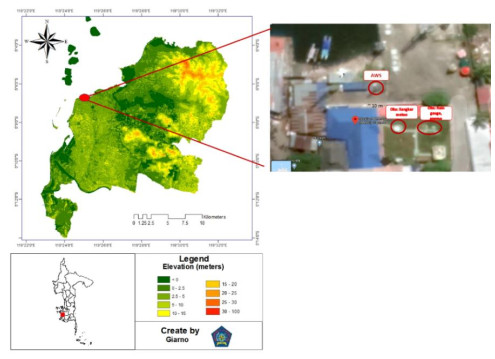
This study uses weather observation data in Makassar City, to be precise at the Paotere maritime meteorology station. As a city that has a strategic position because it is at the crossroads of trade traffic lanes, Makassar is a city that is developing very rapidly both in terms of economy and population dynamics. Makassar City is located at coordinates 1190BT and 5.80LS with an elevation of 1–32 meters above sea level. This tropical city is always warm all year round with air temperatures ranging from 20 ℃ to 39 ℃. The weather observation location is located in Paotere, which is the heritage port of the Gowa Sultanate—Tallo Perahu which is located in Ujung Tanah District, Makassar, South Sulawesi. This port is ± 5 km from Makassar City Square (Karebosi Field). Paotere is one of the most historic heritage folk harbors that still survives and is a testament to the legacy of the Gowa-Tallo Sultanate since the XIV century, where the 2nd King of Tallo Karaeng Same ri Liukang once dispatched 200 Phinisi Boat fleets to Malacca. Currently, Paotere Harbor is still normally used as a place for people's boats to dock, such as the phinisi and lambo. This place is also a trading center for fisherme's catch, which can be seen along the road in the harbor lined with shops selling various types of dried fish, and fishing equipment, as well as several seafood restaurants. According to Baharuddin, who works as a supervisor at Paotere Harbor, the word Paotere comes from the word Otere, which is a rope used in ships that dock. The location of the AWS equipment and manuals is near the Paotere fish auction as shown in Figure 1. Recorded in the last 10 years, the maximum annual rainfall reached 3693 mm in 2017 and the highest rainfall intensity in an hour reached 110 mm on December 16, 2014.
The location of manual observation equipment is in the world standard meteorological instrument park [15]. Manual equipment consists of various types, for example a digital barometer which is recorded every hour by the brand Vaisala, a digital anemometer produced by RM Young 26800, a manual rainfall meter which is measured every 3 hours and air temperature using a Schneider mercury thermometer. While, automatic weather station is produced by Vaisala and is located close to the Makassar Strait waters than the tool park. Unlike the manual rain gauge, the AWS rain gauge is a tipping bucket type with a sensitivity of 0.5 mm. The distance of the automatic weather system to the meteorology cage in the tool park is about 10 meters as shown in Figure 1. The anemometer elevations of these two types of tools are the same height, which is about 10 meters, while the temperature and humidity sensors are 50 cm apart. The data used in this study is data on all-weather parameters obtained by both types of observations. Humidity, air pressure, average, minimum, and maximum temperature, rainfall and wind direction and speed. January was chosen to represent the difference between observations using AWS and manual when there was a lot of rain, while June was to represent the dry season. The temporal resolution of AWS is very high, where data can be degenerated in 10 minutes, while the highest manual observation data can only be every hour. Both types of observations use the world standard time of the UTC universal time coordinate so that comparisons can be made directly.
In general, automatic and manual measurements of weather data generally have an abnormal distribution, but the homogeneity test generally shows that both are homogeneous [14,19,20,21,22]. The value of the difference between these two measurements is visible when using the calculation of the root mean square error, and correlation [13,23,24,25]. The difference between automatic and manual measurements in this study uses six methods, namely homogeneity analysis, statistical comparison of values and visually using wind rose for wind direction. The wind variable is a vector quantity that is very difficult to distinguish using only numbers. Visualization in this research uses wind rose because it is easy to analyze and can describe the distribution of wind distribution very clearly. Meanwhile, to calculate the difference between automatic and manual measurement results, correlation, root mean square error (RMSE), and mean absolute error (MAE) were formulated using Eqs (1)–(3).
| r=∑Ni=1(Oi−−O)(Mi−−M)√∑Ni=1(Oi−−O)2√∑Ni=1(Mi−−M)2, | (1) |
| RMSE=√∑Ni=1(Mi−Oi)2N, | (2) |
| MAE=∑Ni=1|Mi−Oi|N, | (3) |
where N is the number of observations, O is the value of the weather parameter in the automatic tool, M is the value of the weather parameter in the manual, −O is the average value of the weather parameter in the automatic tool, −M is the average value of the weather parameter in the manual.
Correlation (r) measures the strength and direction of the relationship between variables [26]. The correlation value ranges between −1 and 1, where a value of 1 indicates a strong relationship between variables and is considered to have no relationship if the correlation is 0. A positive sign indicates a change in the direction of the variable in the same direction, while a negative sign indicates a change in the opposite direction. Much of the literature on correlation statistics is divided into 5 classes, namely uncorrelated (0.00–0.20), weak (0.21–0.40), moderate (0.41–0.60), strong (0.61–0. 80) and very strong if the value is > 0.80. Karaseva et al. and Prasetia et al. divide the correlation, which is strongly correlated if the value of r ≥ 0.50 [1,27]. Although there are also many evaluations of remote sensing rainfall estimates, the category of strong and weak correlation is not stated [28,29,30,31,32].
RMSE and MAE values are measures of deviation between automatic and manual tools. If each deviation is added up and divided by the amount of data, then the average size of the deviation is obtained. But the direct addition will cause each other to cancel the value of the deviation if there are positive and negative values. In contrast to the use of absolute values which will reduce the nature of mutually canceling deviations. This calculation is known as the mean absolute error or MAE. The weakness of the negating nature of the number of deviations can also be eliminated using the root mean square error or RMSE because each deviation is squared which automatically results are all positive. It's just that RMSE is sensitive to the value of outliers or outliers [31]. In contrast to the homogeneity test, which is a test of whether or not the variances of two or more distributions are equal. The homogeneity test that will be discussed in this paper is the homogeneity test of variance. The statistical homogeneity test was carried out to determine whether the data in the automatic weather variable O and manual M were homogeneous or not using varied data [33]. Equation (4) is the variance formulation which is applied to the results of manual and automatic observations.
| Varo=√∑Ni=1(Oi−−O)2n(n−1),VarM=√∑Ni=1(Mi−−M)2n(n−1). | (4) |
To test for homogeneity, the F test was used.
| F=VaroVarM. | (5) |
The F value is obtained from Fisher's statistical table. Equation (5) is used if the automatic variance is greater than the manual one. If the opposite happens, Eq (5) must be reversed with the automatic variance as a divisor, so that the result is that the F value is always greater than or equal to 1. While the test hypothesis H0: Varo=VarM, H1: Varo≠VarM.
Besides statistical calculations and homogeneity tests, wind rose diagrams are also used. This is because the direction variable cannot be directly tested using numerical calculations.
Based on the homogeneity test, it was found that not always these two types of measurements are homogeneous. The amount of rainfall and its value greatly affect the homogeneity of AWS measurements and manual observations. In January only the results of temperature and pressure measurements were homogeneous as can be seen in Table 1. The F test values for wind speed, humidity and rainfall were greater than the F table values, which means that the AWS and manual data for these parameters were not homogeneous.
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.660 | 2.699 | 12.876 | 75.470 | 27.213 |
| Variance-OBS | 5.914 | 2.675 | 9.133 | 66.170 | 73.364 |
| Fcount | 1.045 | 1.009 | 1.410 | 1.141 | 2.696 |
| FTabel | 1.128 | 1.128 | 1.128 | 1.128 | 1.233 |
| Decision | Homogeneous | Homogeneous | Non-homogeneous | Non-homogeneous | Non-homogeneous |
DownLoad:
CSV
Different results were obtained from the calculation in June 2020, where in this month the rainfall was very rare. Based on the homogeneity test, only rainfall that is not homogeneous from the two types of measurements is obtained. The least amount of rainfall affects the homogeneity of AWS measurements and manual observations. This month only the results of rainfall measurements are not homogeneous as can be seen in Table 2. The F test values for wind speed, humidity and rainfall parameters are smaller than the F table values, which means that AWS and manual data for these parameters are homogeneous. The statistical comparison between AWS and manual using Correlation, RMSE and MAE in January and June can be seen in Tables 3 and 4. Except for rainfall, the correlation between the two types of data is generally strong to very strong. Measurements of temperature, pressure, and humidity are very strong with a correlation of more than 0.9, in contrast to wind speeds of only 0.76 to 0.81. While the rainfall in the two measurements is very weak correlation. AWS and manual deviations for temperature, wind speed and rainfall bias values are higher during the rainy season compared to when there is no or infrequent rain. Meanwhile, at the same time, the pressure and humidity values are usually higher during the dry season.
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.131 | 1.581 | 4.101 | 95.616 | 0.192 |
| Variance-OBS | 5.189 | 1.561 | 3.544 | 96.718 | 0.320 |
| Fcount | 1.011 | 1.013 | 1.157 | 1.011 | 1.664 |
| FTable | 1.131 | 1.131 | 1.365 | 1.131 | 1.237 |
| Decision | Homogeneous | Homogeneous | Homogeneous | Homogeneous | Non-homogeneous |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.980 | 0.810 | 0.940 | −0.100 |
| RMSE | 1.430 | 0.340 | 2.090 | 3.430 | 10.560 |
| MAE | −1.320 | 0.000 | 0.180 | 1.590 | −1.590 |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.970 | 0.760 | 0.920 | 0.900 |
| RMSE | 1.540 | 0.370 | 1.410 | 4.400 | 0.250 |
| MAE | −1.450 | 0.180 | −0.340 | 2.080 | −0.010 |
DownLoad:
CSV
The homogeneity test resulted in significant differences in wind and humidity values from January and June, both of which were not homogeneous in January and became homogeneous in June. In the wind, in addition to the wind speed component, there is a wind direction component that should be a comparison. The comparison of the wind and its direction is carried out using wind rose as shown in Figure 2 for January and Figure 3 for June.
In the rainy season, the dominant wind direction comes from the west, but the east wind is the second most common in Makassar. This condition is a consequence of Makassar's location on the seafront, so that the influence of land-sea winds is evident, both AWS and manual data. The influence of the land sea breeze is always there in the rainy season months such as January, as well as in the dry season in June. In the dry season, where the east wind is dominant, it is seen in June, but the wind is both westerly. There are always east and west winds due to the location of the city of Makassar facing west on the ocean, which can be seen in the emergence of land-sea wind circulation. When viewed from the deviation of the wind speed, it seems that the magnitude of the wind speed in January has an effect on the homogeneity test.
The difference in measurement results between AWS and manual can also be seen from the boxplot graph that describes the quantile distribution. Data with high disparity means the quantile value will be very different from data with low distribution. The distribution of quantile values for each AWS and manual parameter can be seen in Figures 6 to 13.
The pressure values in January between AWS and manual are almost the same as in Figure 4, while there are slightly different in June. Manually measuring pressure results in slightly lower values than using AWS. The range of automatic measurement is also slightly higher than that of manual measurement as shown in Figure 5.
Temperatures in January and June on measurements using AWS and manual have almost the same pattern as in Figure 6. The results of manual measurements are slightly higher than those of automatic measurements. The median and first and third quantile values in manual observations tend to be higher than AWS, both in January and June.
A different pattern was found in wind speed measurements, where in January, AWS data showed a very high disparity compared to manual observations. Meanwhile, in June this measurement disparity is smaller compared to January which has a lot of rain as shown in Figure 6. The rainfall homogeneity test resulted in a non-homogeneous conclusion in January and June. The difference will be clearer by comparing the two measurements using a plot series of rainfall data as shown in Figures 7 and 8. Generally, the manual measurement results were much higher in the month where rainfall fell a lot, namely January which was seen in Figure 7. When the rainfall value is 30 mm/hour, AWS records a smaller value than the manual. Even in the event of rain with an intensity of more than 60mm/hour, the AWS value is very small compared to the manual rainfall rate.
Rain detection on AWS and manual looks better in the dry season in June. Only when it rains below 1 mm/hour, where manual equipment does not record rain, AWS is more sensitive to recording rainfall. However, it seems that the sensitivity of AWS equipment in the dry season is reduced when the rainfall is more than 4 mm/hour. When the rainfall has high intensity, AWS slow records the rainwater that enters the device. This may be because the tipping bucket movement did not record rainfall. However, if you look at the amount of rain the next day, it seems that the lack of rainfall on AWS will be recorded the next day as shown in Figure 8.
The conditions are different compared to June where the rainfall is not too much. This month the boxplot chart shows a higher variance in the AWS measurements than the manual, although in fact the rainfall values may be almost the same. In June, the intensity of rain fell is low, this makes it somewhat sensitive to variance so that the homogeneity test shows that it is not homogeneous. The boxplot results on humidity are almost the same as the temperature boxplot, where the manual data pattern is lower than AWS as shown in Figure 9.
The results of manual measurements and AWS produce data that is partially homogeneous, but sometimes also not homogeneous. In the rainy season, the difference between the two types of measurements is greater than in the dry season. Based on the boxplot graph, it shows changes in variability due to the magnitude of the measured parameter values, where humidity and rain are very sensitive to the disparity of measured values.
In January the pressure on AWS was about the same as the manual. In addition, based on the homogeneity test and boxplot graphs, it is shown that the two measurements are very similar. However, this condition changes during the dry season, where the pressure on AWS is higher than the manual results. Based on the temperature boxplot graph which shows the higher AWS temperature disparity compared to manual, it is suspected that it will have an effect on the air density at the location where the equipment is installed. Due to the air density affecting the pressure, automatically in June this air pressure also experienced a disparity in value between AWS and manual. Rapid changes in air are caused by the lack of water vapor content that can store latent heat which results in rapid changes in air pressure. However, this change is not too much value at temperature and pressure. The quantiles of temperature and pressure during the dry season are around the average.
In contrast to humidity, which during the rainy season tends to be very high in value or wetter when it rains, and then decreases when it is sunny, the disparity during the rainy season is higher than during the dry season. As a result, the homogeneity test during the rainy season, AWS and manual homogeneity tests concluded that it was not homogeneous. The location and elevation of the AWS sensors near the sea may have an effect on the rapid changes in air properties around the seaside compared to areas that are further away such as in the tool park, especially between the tool park and the AWS sensor there is a separator that is sufficient to block the wind. Both AWS and manual observations show that the influence of land-sea winds in Makassar is very strong. During the rainy season, where the dominant wind direction should only be from the west or around the west, but the easterly wind appears to be the second most common in Makassar. Both AWS and manual observations show the same result. This is reinforced during the dry season, where the east wind or around the east should be very dominant, but the results of the analysis show that in June the dominant wind is both westerly winds. There are always east and west winds due to the location of the city of Makassar facing west on the ocean, which can be seen in the emergence of land-sea wind circulation. When viewed from the deviation of the wind speed, it seems that the magnitude of the wind speed in January has an effect on the homogeneity test.
Precipitation is the most consistently different weather parameter between manual measurement and automatic observation or AWS. Both in January and June obtained the homogeneity test resulted in a non-homogeneous conclusion. In both rainy and low-rainy months, manual measurement is higher than automatic measurement. The disparity between the two types of measurement results in an inhomogeneous between AWS and manual. Based on the properties of these two types of measurements, it is possible to distort the results of observations. The first is time resolution, where AWS records every 10 minutes while manual observations every hour. In manual measurements, rain is even recorded every three hours so that the temporal resolution is very different. The AWS rain gauge type is tipping bucket, while manual observation is capped using gauge degrees. The second, according to the technician, there is a possibility that the electric current will weaken so that the rainfall record will be disrupted when the intensity of rainfall starts to increase. However, the comparison in this research uses data every 3 hours so that the AWS and manual rainfall values should not be much different. But given the inhomogeneity of the two and the obvious differences there are likely AWS tools to look out for.
Based on the comparative analysis of AWS and manual measurements, the homogeneity of these two types of measurements can change at any time with the following details:
1) During the rainy season, only pressure and temperature are identical and homogeneous. Meanwhile, in the dry season, apart from these two parameters, humidity and wind speed are also homogeneous and rainfall is an unstable parameter in January and June. The homogeneity test is very sensitive to very different values, where humidity and rainfall are very sensitive to the disparity of measured values.
2) Both AWS and manual observations show that the influence of land-sea winds in Makassar is very strong. During the rainy season, where the dominant wind direction should only be from the west or around the west, but the easterly wind appears to be the second most common in Makassar.
3) Both AWS and manual observations show the same result. This is reinforced during the dry season, where the east wind or around the east should be very dominant, but the results of the analysis show that in June the dominant wind is both westerly winds.
4) There are always east and west winds due to the location of Makassar city which faces west on the ocean, it can be seen in the emergence of land-sea wind circulation. The homogeneity test is very sensitive to very different values, where humidity and rainfall are very sensitive to the disparity of measured values.
AWS and manual observations show that the influence of land-sea winds in Makassar is very strong. During the rainy season, where the dominant wind direction should only be from the west or around the west, however, the easterly wind appears to be the second most common in Makassar. This is reinforced during the dry season, where the east wind or around the east should be very dominant, but the results of the analysis show that in June the dominant wind is both westerly winds. There are always east and west winds due to the location of Makassar city which faces west on the ocean, it can be seen in the emergence of land-sea wind circulation.
All authors declare no conflicts of interest in this paper.
| [1] |
K. C. Chou, H. B. Shen, Recent progress in protein subcellular location prediction, Anal. Biochem., 370 (2007), 1–16. https://doi.org/10.1016/j.ab.2007.07.006 doi: 10.1016/j.ab.2007.07.006
|
| [2] | R. F. Murphy, M. V. Boland, M. Velliste, Towards a systematics for protein subcellular location: quantitative description of protein localization patterns and automated analysis of fluorescence microscope images, in Proceedings International Conference on Intelligent System Molecular Biology, 8 (2000), 251–259. |
| [3] |
J. Cao, W. Liu, J. He, H. Gu, Mining proteins with non-experimental annotations based on an active sample selection strategy for predicting protein subcellular localization, PLoS One, 8 (2013), e67343. https://doi.org/10.1371/journal.pone.0067343 doi: 10.1371/journal.pone.0067343
|
| [4] |
H. B. Shen, J. Yang, K. C. Chou, Methodology development for predicting subcellular localization and other attributes of proteins, Expert Rev. Proteomics, 4 (2007), 453–463. https://doi.org/10.1586/14789450.4.4.453 doi: 10.1586/14789450.4.4.453
|
| [5] |
A. Reinhardt, T. Hubbard, Using neural networks for prediction of the subcellular location of proteins, Nucleic Acids Res., 26 (1998), 2230–2236. https://doi.org/10.1093/nar/26.9.2230 doi: 10.1093/nar/26.9.2230
|
| [6] |
J. Cedano, P. Aloy, J. A. Perez-Pons, E. Querol, Relation between amino acid composition and cellular location of proteins, J. Mol. Biol., 266 (1997), 594–600. https://doi.org/10.1006/jmbi.1996.0804 doi: 10.1006/jmbi.1996.0804
|
| [7] |
Y. X. Pan, Z. Z. Zhang, Z. M. Guo, G. Y. Feng, Z. D. Huang, L. He, Application of pseudo amino acid composition for predicting protein subcellular location: stochastic signal processing approach, J. Protein Chem., 22 (2003), 395–402. https://doi.org/10.1023/a:1025350409648 doi: 10.1023/a:1025350409648
|
| [8] |
J. Y. Shi, S. Zhang, Q. Pan, G. Zhou, Using pseudo amino acid composition to predict protein subcellular location: approached with amino acid composition distribution, Amino Acids, 35 (2008), 321–327. https://doi.org/10.1007/s00726-007-0623-z doi: 10.1007/s00726-007-0623-z
|
| [9] |
H. Lin, H. Ding, F. Guo, A. Zhang, J. Huang, Predicting subcellular localization of mycobacterial proteins by using Chou's pseudo amino acid composition, Protein Pept. Lett., 15 (2008), 739–744. https://doi.org/10.2174/092986608785133681 doi: 10.2174/092986608785133681
|
| [10] |
K. Chou, Prediction of protein cellular attributes using pseudo-amino acid composition, Proteins, 43 (2001), 246–255. https://doi.org/10.1002/prot.1035 doi: 10.1002/prot.1035
|
| [11] |
T. Liu, X. Zheng, C. Wang, J. Wang, Prediction of subcellular location of apoptosis proteins using pseudo amino acid composition: an approach from auto covariance transformation, Protein Pept. Lett., 17 (2010), 1263–1269. https://doi.org/10.2174/092986610792231528 doi: 10.2174/092986610792231528
|
| [12] |
Y. Shen, J. Tang, F. Guo, Identification of protein subcellular localization via integrating evolutionary and physicochemical information into Chou's general PseAAC, J. Theor. Biol., 462 (2019), 230–239. https://doi.org/10.1016/j.jtbi.2018.11.012 doi: 10.1016/j.jtbi.2018.11.012
|
| [13] |
Y. H. Yao, Z. X. Shi, Q. Dai, Apoptosis protein subcellular location prediction based on position-specific scoring matrix, J. Comput. Theor. Nanos., 11 (2014), 2073–2078. https://doi.org/10.1166/jctn.2014.3607 doi: 10.1166/jctn.2014.3607
|
| [14] |
T. Liu, P. Tao, X. Li, Y. Qin, C. Wang, Prediction of subcellular location of apoptosis proteins combining tri-gram encoding based on PSSM and recursive feature elimination, J. Theor. Biol., 366 (2015), 8–12. https://doi.org/10.1016/j.jtbi.2014.11.010 doi: 10.1016/j.jtbi.2014.11.010
|
| [15] |
S. Wang, W. Li, Y. Fei, An improved process for generating uniform PSSMs and its application in protein subcellular localization via various global dimension reduction techniques, IEEE Access, 7 (2019), 42384–42395. https://doi.org/10.1109/ACCESS.2019.2907642 doi: 10.1109/ACCESS.2019.2907642
|
| [16] |
X. Cheng, X. Xiao, K. C. Chou, pLoc-mHum: predict subcellular localization of multi-location human proteins via general PseAAC to winnow out the crucial GO information. Bioinformatics, 34 (2018), 1448–1456. https://doi.org/10.1093/bioinformatics/btx711 doi: 10.1093/bioinformatics/btx711
|
| [17] |
X. Cheng, S. Zhao, W. Lin, X. Xiao, K. Chou, pLoc-mAnimal: predict subcellular localization of animal proteins with both single and multiple sites, Bioinformatics, 33 (2017), 3524–3531. https://doi.org/10.1093/bioinformatics/btx476 doi: 10.1093/bioinformatics/btx476
|
| [18] |
X. Cheng, X. Xiao, K.C. Chou, pLoc-mGneg: Predict subcellular localization of Gram-negative bacterial proteins by deep gene ontology learning via general PseAAC, Genomics, 110 (2017), 231–239. https://doi.org/10.1016/j.ygeno.2017.10.002 doi: 10.1016/j.ygeno.2017.10.002
|
| [19] |
X. Cheng, X. Xiao, K. C. Chou, pLoc-mEuk: Predict subcellular localization of multi-label eukaryotic proteins by extracting the key GO information into general PseAAC, Genomics, 110 (2018), 50–58. https://doi.org/10.1016/j.ygeno.2017.08.005 doi: 10.1016/j.ygeno.2017.08.005
|
| [20] |
K. Chou, Y. Cai, A new hybrid approach to predict subcellular localization of proteins by incorporating gene ontology, Biochem. Biophys. Res. Commun., 311 (2003), 743–747. https://doi.org/10.1016/j.bbrc.2003.10.062 doi: 10.1016/j.bbrc.2003.10.062
|
| [21] |
S. Wan, M. Mak, S. Kung, GOASVM: A subcellular location predictor by incorporating term-frequency gene ontology into the general form of Chou's pseudo-amino acid composition, J. Theor. Biol., 323 (2013), 40–48. https://doi.org/10.1016/j.jtbi.2013.01.012 doi: 10.1016/j.jtbi.2013.01.012
|
| [22] |
S. Wan, M. Mak, S. Kung, mGOASVM: Multi-label protein subcellular localization based on gene ontology and support vector machines, BMC Bioinf., 13 (2012), 290. https://doi.org/10.1186/1471-2105-13-290 doi: 10.1186/1471-2105-13-290
|
| [23] |
K. C. Chou, Y. D. Cai, Using functional domain composition and support vector machines for prediction of protein subcellular location, J. Biol. Chem., 277 (2002), 45765–45769. https://doi.org/10.1074/jbc.M204161200 doi: 10.1074/jbc.M204161200
|
| [24] |
K. Chou, H. Shen, A new method for predicting the subcellular localization of eukaryotic proteins with both single and multiple sites: Euk-mPLoc 2.0, PLoS One, 5 (2010), e9931. https://doi.org/10.1371/journal.pone.0009931 doi: 10.1371/journal.pone.0009931
|
| [25] |
Y. Cai, K. Chou, Nearest neighbour algorithm for predicting protein subcellular location by combining functional domain composition and pseudo-amino acid composition, Biochem. Biophys. Res. Commun., 305 (2003), 407–411. https://doi.org/10.1016/s0006-291x(03)00775-7 doi: 10.1016/s0006-291x(03)00775-7
|
| [26] |
K. Chou, Y. Cai, Predicting subcellular localization of proteins by hybridizing functional domain composition and pseudo-amino acid composition, J. Cell. Biochem., 91 (2004), 1197–1203. https://doi.org/10.1002/jcb.10790 doi: 10.1002/jcb.10790
|
| [27] |
X. Pan, L. Chen, M. Liu, Z. Niu, T. Huang, Y. Cai, Identifying protein subcellular locations with embeddings-based node2loc, IEEE/ACM Trans. Comput. Biol. Bioinf., 19 (2022), 666–675. https://doi.org/10.1109/TCBB.2021.3080386 doi: 10.1109/TCBB.2021.3080386
|
| [28] |
X. Pan, H. Li, T. Zeng, Z. Li, L. Chen, T. Huang, et al., Identification of protein subcellular localization with network and functional embeddings, Front. Genet., 11 (2021), 626500. https://doi.org/10.3389/fgene.2020.626500 doi: 10.3389/fgene.2020.626500
|
| [29] |
H. Liu, B. Hu, L. Chen, Identifying protein subcellular location with embedding features learned from networks, Curr. Proteomics, 18 (2021), 646–660. https://doi.org/10.2174/1570164617999201124142950 doi: 10.2174/1570164617999201124142950
|
| [30] | R. Wang, L. Chen, Identification of human protein subcellular location with multiple networks, Curr. Proteomics, 19 (2022), 344–356. |
| [31] |
R. Su, L. He, T. Liu, X. Liu, L. Wei, Protein subcellular localization based on deep image features and criterion learning strategy, Briefings Bioinf., 22 (2020), bbaa313. https://doi.org/10.1093/bib/bbaa313 doi: 10.1093/bib/bbaa313
|
| [32] |
M. Ullah, F. Hadi, J. Song, D. Yu, PScL-DDCFPred: an ensemble deep learning-based approach for characterizing multiclass subcellular localization of human proteins from bioimage data, Bioinformatics, 38 (2022), 4019–4026. https://doi.org/10.1093/bioinformatics/btac432 doi: 10.1093/bioinformatics/btac432
|
| [33] |
M. Ullah, K. Han, F. Hadi, J. Xu, J. Song, D. Yu, PScL-HDeep: image-based prediction of protein subcellular location in human tissue using ensemble learning of handcrafted and deep learned features with two-layer feature selection, Briefings Bioinf., 22 (2021), bbab278. https://doi.org/10.1093/bib/bbab278 doi: 10.1093/bib/bbab278
|
| [34] | G. Tsoumakas, I. Vlahavas, Random k-Labelsets: An ensemble method for multilabel classification, in Machine Learning: ECML 2007, (2007), 406–417. https://doi.org/10.1007/978-3-540-74958-5_38 |
| [35] |
L. Breiman, Random forests, Mach. Learn., 45 (2001), 5–32. https://doi.org/10.1023/A:1010933404324 doi: 10.1023/A:1010933404324
|
| [36] |
K. C. Chou, Z. C. Wu, X. Xiao, iLoc-Hum: using the accumulation-label scale to predict subcellular locations of human proteins with both single and multiple sites, Mol. Biosyst., 8 (2012), 629–641. https://doi.org/10.1039/c1mb05420a doi: 10.1039/c1mb05420a
|
| [37] |
H. B. Shen, K. C. Chou, A top-down approach to enhance the power of predicting human protein subcellular localization: Hum-mPLoc 2.0, Anal. Biochem., 394 (2009), 269–274. https://doi.org/10.1016/j.ab.2009.07.046 doi: 10.1016/j.ab.2009.07.046
|
| [38] |
W. Z. Lin, J. Fang, X. Xiao, K. Chou, iLoc-Animal: a multi-label learning classifier for predicting subcellular localization of animal proteins, Mol. Biosyst., 9 (2013), 634–644. https://doi.org/10.1039/c3mb25466f doi: 10.1039/c3mb25466f
|
| [39] |
H. B. Shen, K. C. Chou, Gneg-mPLoc: a top-down strategy to enhance the quality of predicting subcellular localization of Gram-negative bacterial proteins, J. Theor. Biol., 264 (2010), 326–333. https://doi.org/10.1016/j.jtbi.2010.01.018 doi: 10.1016/j.jtbi.2010.01.018
|
| [40] |
X. Xiao, Z. C. Wu, K. C. Chou, A multi-label classifier for predicting the subcellular localization of gram-negative bacterial proteins with both single and multiple sites, PLoS One, 6 (2011), e20592. https://doi.org/10.1371/journal.pone.0020592 doi: 10.1371/journal.pone.0020592
|
| [41] |
G. Tsoumakas, I. Katakis, Multi-label classification: An overview, Int. J. Data Warehouse. Min., 3 (2007), 1–13. https://doi.org/10.4018/jdwm.2007070101 doi: 10.4018/jdwm.2007070101
|
| [42] | S. Al-Maadeed, Kernel collaborative label power set system for multi-label classification, in Qatar Foundation Annual Research Forum Volume 2013 Issue 1, Hamad bin Khalifa University Press, 2013 (2013). https://doi.org/10.5339/qfarf.2013.ICTP-028 |
| [43] |
J. P. Zhou, L. Chen, Z. H. Guo, iATC-NRAKEL: An efficient multi-label classifier for recognizing anatomical therapeutic chemical classes of drugs, Bioinformatics, 36 (2020), 1391–1396. https://doi.org/10.1093/bioinformatics/btz757 doi: 10.1093/bioinformatics/btz757
|
| [44] |
J. P. Zhou, L. Chen, T. Wang, M. Liu, iATC-FRAKEL: A simple multi-label web-server for recognizing anatomical therapeutic chemical classes of drugs with their fingerprints only, Bioinformatics, 36 (2020), 3568–3569. https://doi.org/10.1093/bioinformatics/btaa166 doi: 10.1093/bioinformatics/btaa166
|
| [45] |
X. Li, L. Lu, L. Chen, Identification of protein functions in mouse with a label space partition method, Math. Biosci. Eng., 19 (2022), 3820–3842. https://doi.org/10.3934/mbe.2022176 doi: 10.3934/mbe.2022176
|
| [46] |
H. Li, S. Zhang, L. Chen, X. Pan, Z. Li, T. Huang, et al., Identifying functions of proteins in mice with functional embedding features, Front. Genet., 13 (2022), 909040. https://doi.org/10.3389/fgene.2022.909040 doi: 10.3389/fgene.2022.909040
|
| [47] |
L. Chen, Z. Li, T. Zeng, Y. Zhang, H. Li, T. Huang, et al., Predicting gene phenotype by multi-label multi-class model based on essential functional features, Mol. Genet. Genomics, 296 (2021), 905–918. https://doi.org/10.1007/s00438-021-01789-8 doi: 10.1007/s00438-021-01789-8
|
| [48] |
Y. Zhu, B. Hu, L. Chen, Q. Dai, iMPTCE-Hnetwork: a multi-label classifier for identifying metabolic pathway types of chemicals and enzymes with a heterogeneous network, Comput. Math. Methods Med., 2021 (2021), 6683051. https://doi.org/10.1155/2021/6683051 doi: 10.1155/2021/6683051
|
| [49] |
J. Che, L. Chen, Z. Guo, S. Wang, Aorigele, Drug target group prediction with multiple drug networks, Comb. Chem. High Throughput Screen., 23 (2020), 274–284. https://doi.org/10.2174/1386207322666190702103927 doi: 10.2174/1386207322666190702103927
|
| [50] |
H. Wang, L. Chen, PMPTCE-HNEA: Predicting metabolic pathway types of chemicals and enzymes with a heterogeneous network embedding algorithm, Curr. Bioinf., 18 (2023), 748–759. https://doi.org/10.2174/1574893618666230224121633 doi: 10.2174/1574893618666230224121633
|
| [51] | J. Read, P. Reutemann, B. Pfahringer, MEKA: A multi-label/multi-target extension to WEKA, J. Mach. Learn. Res., 17 (2016), 1–5. |
| [52] |
B. Ran, L. Chen, M. Li, Y. Han, Q. Dai, Drug-Drug interactions prediction using fingerprint only, Comput. Math. Methods Med., 2022 (2022), 7818480. https://doi.org/10.1155/2022/7818480 doi: 10.1155/2022/7818480
|
| [53] |
M. Onesime, Z. Yang, Q. Dai, Genomic island prediction via chi-square test and random forest algorithm, Comput. Math. Methods Med., 2021 (2021), 9969751. https://doi.org/10.1155/2021/9969751 doi: 10.1155/2021/9969751
|
| [54] |
L. Chen, K. Chen, B. Zhou, Inferring drug-disease associations by a deep analysis on drug and disease networks, Math. Biosci. Eng., 20 (2023), 14136–14157. https://doi.org/10.3934/mbe.2023632 doi: 10.3934/mbe.2023632
|
| [55] |
P. Chen, T. Shen, Y. Zhang, B. Wang, A sequence-segment neighbor encoding schema for protein hotspot residue prediction, Curr. Bioinf., 15 (2020), 445–454. https://doi.org/10.2174/1574893615666200106115421 doi: 10.2174/1574893615666200106115421
|
| [56] |
Z. B. Lv, J. Zhang, H. Ding, Q. Zou, RF-PseU: A random forest predictor for rna pseudouridine sites, Front. Bioeng. Biotechnol., 8 (2020), 134. https://doi.org/10.3389/fbioe.2020.00134 doi: 10.3389/fbioe.2020.00134
|
| [57] |
F. Huang, Q. Ma, J. Ren, J. Li, F. Wang, T. Huang, et al., Identification of smoking associated transcriptome aberration in blood with machine learning methods, Biomed. Res. Int., 2023 (2023), 445–454. https://doi.org/10.1155/2023/5333361 doi: 10.1155/2023/5333361
|
| [58] |
F. Huang, M. Fu, J. Li, L. Chen, K. Feng, T. Huang, et al., Analysis and prediction of protein stability based on interaction network, gene ontology, and kegg pathway enrichment scores, Biochim. Biophys. Acta. Proteins Proteom., 1871 (2023), 140889. https://doi.org/10.1016/j.bbapap.2023.140889 doi: 10.1016/j.bbapap.2023.140889
|
| [59] |
J. Ren, Y. Zhang, W. Guo, K. Feng, Y. Yuan, T. Huang, et al., Identification of genes associated with the impairment of olfactory and gustatory functions in COVID-19 via machine-learning methods, Life (Basel), 13 (2023), 798. https://doi.org/10.3390/life13030798 doi: 10.3390/life13030798
|
| [60] |
K. C. Chou, C. T. Zhang, Prediction of protein structural classes, Crit. Rev. Biochem. Mol. Biol., 30 (1995), 275–349. https://doi.org/10.3109/10409239509083488 doi: 10.3109/10409239509083488
|
| [61] |
K. C. Chou, Z. C. Wu, X. Xiao, iLoc-Euk: A multi-label classifier for predicting the subcellular localization of singleplex and multiplex eukaryotic proteins, PLoS One, 6 (2011), e18258. https://doi.org/10.1371/journal.pone.0018258 doi: 10.1371/journal.pone.0018258
|
| [62] | S. Tang, L. Chen, iATC-NFMLP: Identifying classes of anatomical therapeutic chemicals based on drug networks, fingerprints and multilayer perceptron. Curr. Bioinf., 17 (2022), 814–824. |
| [63] |
H. Zhao, Y. Li, J. Wang, A convolutional neural network and graph convolutional network-based method for predicting the classification of anatomical therapeutic chemicals, Bioinformatics, 37 (2021), 2841–2847. https://doi.org/10.1093/bioinformatics/btab204 doi: 10.1093/bioinformatics/btab204
|
| [64] |
W. Chen, H. Yang, P. Feng, H. Ding, H. Lin, iDNA4mC: identifying DNA N4-methylcytosine sites based on nucleotide chemical properties, Bioinformatics, 33 (2017), 3518–3523. https://doi.org/10.1093/bioinformatics/btx479 doi: 10.1093/bioinformatics/btx479
|
| [65] |
L. Wei, P. Xing, R. Su, G. Shi, Z. S. Ma, Q. Zou, CPPred-RF: A sequence-based predictor for identifying cell-penetrating peptides and their uptake efficiency, J. Proteome Res., 16 (2017), 2044–2053. https://doi.org/10.1021/acs.jproteome.7b00019 doi: 10.1021/acs.jproteome.7b00019
|
| [66] |
S. R. Safavian, D. Landgrebe, A survey of decision tree classifier methodology, T-SMCA, 21 (1991), 660–674. https://doi.org/10.1109/21.97458 doi: 10.1109/21.97458
|
| [67] |
C. Cortes, V. Vapnik, Support-vector networks, Mach. Learn., 20 (1995), 273–297. https://doi.org/10.1007/BF00994018 doi: 10.1007/BF00994018
|
 mbe-21-01-010-supplementary.pdf |
 |
| 1. | Dingwen Deng, Zhu-an Wang, Zilin Zhao, The maximum norm error estimate and Richardson extrapolation methods of a second-order box scheme for a hyperbolic-difference equation with shifts, 2024, 1607-3606, 1, 10.2989/16073606.2024.2385424 | |
| 2. | V. G. Pimenov, A. B. Lozhnikov, Richardson Method for a Diffusion Equation with Functional Delay, 2023, 321, 0081-5438, S204, 10.1134/S0081543823030173 |
Lei Chen, Ruyun Qu, Xintong Liu. Improved multi-label classifiers for predicting protein subcellular localization[J]. Mathematical Biosciences and Engineering, 2024, 21(1): 214-236. doi: 10.3934/mbe.2024010
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.660 | 2.699 | 12.876 | 75.470 | 27.213 |
| Variance-OBS | 5.914 | 2.675 | 9.133 | 66.170 | 73.364 |
| Fcount | 1.045 | 1.009 | 1.410 | 1.141 | 2.696 |
| FTabel | 1.128 | 1.128 | 1.128 | 1.128 | 1.233 |
| Decision | Homogeneous | Homogeneous | Non-homogeneous | Non-homogeneous | Non-homogeneous |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.131 | 1.581 | 4.101 | 95.616 | 0.192 |
| Variance-OBS | 5.189 | 1.561 | 3.544 | 96.718 | 0.320 |
| Fcount | 1.011 | 1.013 | 1.157 | 1.011 | 1.664 |
| FTable | 1.131 | 1.131 | 1.365 | 1.131 | 1.237 |
| Decision | Homogeneous | Homogeneous | Homogeneous | Homogeneous | Non-homogeneous |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.980 | 0.810 | 0.940 | −0.100 |
| RMSE | 1.430 | 0.340 | 2.090 | 3.430 | 10.560 |
| MAE | −1.320 | 0.000 | 0.180 | 1.590 | −1.590 |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.970 | 0.760 | 0.920 | 0.900 |
| RMSE | 1.540 | 0.370 | 1.410 | 4.400 | 0.250 |
| MAE | −1.450 | 0.180 | −0.340 | 2.080 | −0.010 |
DownLoad:
CSV
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.660 | 2.699 | 12.876 | 75.470 | 27.213 |
| Variance-OBS | 5.914 | 2.675 | 9.133 | 66.170 | 73.364 |
| Fcount | 1.045 | 1.009 | 1.410 | 1.141 | 2.696 |
| FTabel | 1.128 | 1.128 | 1.128 | 1.128 | 1.233 |
| Decision | Homogeneous | Homogeneous | Non-homogeneous | Non-homogeneous | Non-homogeneous |
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Variance-AWS | 5.131 | 1.581 | 4.101 | 95.616 | 0.192 |
| Variance-OBS | 5.189 | 1.561 | 3.544 | 96.718 | 0.320 |
| Fcount | 1.011 | 1.013 | 1.157 | 1.011 | 1.664 |
| FTable | 1.131 | 1.131 | 1.365 | 1.131 | 1.237 |
| Decision | Homogeneous | Homogeneous | Homogeneous | Homogeneous | Non-homogeneous |
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.980 | 0.810 | 0.940 | −0.100 |
| RMSE | 1.430 | 0.340 | 2.090 | 3.430 | 10.560 |
| MAE | −1.320 | 0.000 | 0.180 | 1.590 | −1.590 |
| Parameter | Temperature | Pressure | Speed wind | Humidity | Rainfall |
| Correlation | 0.970 | 0.970 | 0.760 | 0.920 | 0.900 |
| RMSE | 1.540 | 0.370 | 1.410 | 4.400 | 0.250 |
| MAE | −1.450 | 0.180 | −0.340 | 2.080 | −0.010 |
