The purpose of this paper is to give some sufficient conditions for the existence of periodic oscillation of a class of in-host MERS-Cov infection model with cytotoxic T lymphocyte (CTL) immune response. A new technique is developed to obtain a lower bound of the state variable characterizing CTL immune response in the model. Our results expand on some previous works.
Citation: Tuersunjiang Keyoumu, Ke Guo, Wanbiao Ma. Periodic oscillation for a class of in-host MERS-CoV infection model with CTL immune response[J]. Mathematical Biosciences and Engineering, 2022, 19(12): 12247-12259. doi: 10.3934/mbe.2022570
| [1] | K. M. S. Y. Konara, M. L. Kolhe, Arvind Sharma . Power dispatching techniques as a finite state machine for a standalone photovoltaic system with a hybrid energy storage. AIMS Energy, 2020, 8(2): 214-230. doi: 10.3934/energy.2020.2.214 |
| [2] | Aaron St. Leger . Demand response impacts on off-grid hybrid photovoltaic-diesel generator microgrids. AIMS Energy, 2015, 3(3): 360-376. doi: 10.3934/energy.2015.3.360 |
| [3] | Sulabh Sachan . Integration of electric vehicles with optimum sized storage for grid connected photo-voltaic system. AIMS Energy, 2017, 5(6): 997-1012. doi: 10.3934/energy.2017.6.997 |
| [4] | Surender Reddy Salkuti . Sustainable energy technologies for emerging renewable energy and electric vehicles. AIMS Energy, 2024, 12(6): 1264-1270. doi: 10.3934/energy.2024057 |
| [5] | Syed Sabir Hussain Rizvi, Krishna Teerth Chaturvedi, Mohan Lal Kolhe . A review on peak shaving techniques for smart grids. AIMS Energy, 2023, 11(4): 723-752. doi: 10.3934/energy.2023036 |
| [6] | Tilahun Nigussie, Wondwossen Bogale, Feyisa Bekele, Edessa Dribssa . Feasibility study for power generation using off- grid energy system from micro hydro-PV-diesel generator-battery for rural area of Ethiopia: The case of Melkey Hera village, Western Ethiopia. AIMS Energy, 2017, 5(4): 667-690. doi: 10.3934/energy.2017.4.667 |
| [7] | François KREMER, Stéphane RAEL, Matthieu URBAIN . 1D electrochemical model of lithium-ion battery for a sizing methodology of thermal power plant integrated storage system. AIMS Energy, 2020, 8(5): 721-748. doi: 10.3934/energy.2020.5.721 |
| [8] | Faris Elmanakhly, Andre DaCosta, Brittany Berry, Robert Stasko, Michael Fowler, Xiao-Yu Wu . Hydrogen economy transition plan: A case study on Ontario. AIMS Energy, 2021, 9(4): 775-811. doi: 10.3934/energy.2021036 |
| [9] | Mohamed Hamdi, Hafez A. El Salmawy, Reda Ragab . Optimum configuration of a dispatchable hybrid renewable energy plant using artificial neural networks: Case study of Ras Ghareb, Egypt. AIMS Energy, 2023, 11(1): 171-196. doi: 10.3934/energy.2023010 |
| [10] | Dalong Guo, Chi Zhou . Potential performance analysis and future trend prediction of electric vehicle with V2G/V2H/V2B capability. AIMS Energy, 2016, 4(2): 331-346. doi: 10.3934/energy.2016.2.331 |
The purpose of this paper is to give some sufficient conditions for the existence of periodic oscillation of a class of in-host MERS-Cov infection model with cytotoxic T lymphocyte (CTL) immune response. A new technique is developed to obtain a lower bound of the state variable characterizing CTL immune response in the model. Our results expand on some previous works.
Nomenclature: EV: Electric Vehicle; PV: Photovoltaic plants; RES: Renewable Energy Sources; GTEP: Generation and Transmission Expansion Planning; MV: Medium-Voltage; LV: Low-Voltage; HV: High-Voltage; EHV: Extra-High-Voltage; HP: Heat Pumps; BCS: The Business, Commerce and Services industry
The German energy supply is to become less dependent on fossil energy sources to reduce greenhouse gas emissions and raw material imports. In terms of electricity production, this means a change in generation technologies. It is envisioned that at least 80% of gross electricity will come from renewable energy sources (RES) [1]. While the share of RES generation was only 3.4% in 1990, it has steadily increased since then. In the years from 2010 to 2020, the share increased from 17.1% to 45.2%. In 2020,251 TWh were generated by RES, such as hydropower, biomass, wind plants or photovoltaics (PVs) [2]. To achieve the targets, the expansion must be further increased significantly. Accordingly, increases in the expansion paths of wind power plants and PVs as well as an acceleration of planning and approval procedures are planned [1].
Residential PV systems are a cost-efficient way to reduce electricity costs and make a relevant contribution to the environment in many parts of the world [3,4]. In Germany, the subsidy for PV electricity for systems below 10 kW was only 6.06 cents per kWh in September 2022 [5]. Coupled with falling storage prices, more and more PV systems are being combined with home storage systems. In April 2022 there were around 500,000 home storage systems in Germany, and this number increases constantly [6]. With the help of these storage systems, owners of a PV system can store self-generated, climate-friendly electricity and consume it later. In this way, self‑consumption and security of supply are increased, and the feed-in can be made more constant. This reduces the loads to the power grid.
While home storage systems stabilize the feed‑in and purchase of a household or building by storing PV electricity, this concept can also be transferred to entire grid areas using large-scale storage systems. This serves to even out the fluctuating generation of RES, to absorb load and generation peaks and by that to reduce grid loads and contribute to grid stability [7]. In addition to battery storage, hydrogen-based storage systems are particularly suitable as large-scale storage systems. In this context, these storage systems can reduce carbon emissions, increase the penetration of stochastic RES in the power grid and increase supply reliability, thus making a significant contribution to meeting energy demand and decarbonizing the energy industry [8]. However, hydrogen-based storage systems in small-scale designs, such as home storage, have significant cost disadvantages compared to battery storage [9]. Therefore, hydrogen-based storage systems, as implemented in this paper, are mainly interesting as large-scale storage systems.
The impact of a high share of generation from volatile RES on the power system can be addressed in different ways. For example, optimized generation expansion planning can be undertaken to minimize the negative technical and economic impacts on the power system when RES are expanded [10]. This formulation of the problem can be extended to include investment and operating costs as well as generation and transmission capacity. This problem formulation is integrated in the generation and transmission expansion planning (GTEP). In most cases, a multi-stage planning model for power distribution systems is implemented for this purpose. In this process alternatives can be compared to determine an efficient grid adjustment, as in [11], for example. These alternatives include the expansion or construction of new substations, deployment of distributed energy resources possible changes in grid topology and replacement of power lines. With respect to multiple interconnected grid levels, the GTEP was considered in [12]. There, the value of coordinated microgrid decision-making in terms of investment and operating costs is determined. It was demonstrated that coordinated expansion planning adds economic value. In [13], a planning model of microgrids was presented as an alternative to co-optimization of GTEP. To minimize costs, the expected cost of undelivered energy is integrated along with the investment and operating costs of generators and transmission lines. In contrast to the holistically designed integrated GTEP approach, this paper focuses on the techno‑economic analysis of electricity storage as an alternative to grid expansion.
In [14], the storage requirements for increasing electricity generation from RES in Germany were analyzed. These include determining the need for storing electricity in the distribution grid as an alternative to grid expansion, in the transmission grid for balancing generation and in both grid levels for providing system services. The study concludes that electricity storage is not needed until RES penetration is very high and that other flexibility options are more favorable. At the same time, however, it highlights that storage can already provide some system services cost-efficiently and that grid expansion in the distribution grid can also be averted cost-efficiently by grid-serving storage in the distribution grid.
In [15], battery storage systems were modeled in a German distribution grid with aging effects being taken into account. The use cases (1) grid support, (2) industrial use and (3) parallel operation with PV systems or wind turbines were examined for their economic efficiency. For the grid support application, economic viability is considered in relation to the provision of primary control power. The paper concludes that the operation of battery storage systems in these use cases is barely economically viable, as returns are rather low.
In [16], battery storage, vehicle-to-grid and flexible demand were integrated in an energy management framework to investigate the welfare of the energy community with the use of different control strategies. It is highlighted that the examined uncertainties like demand, renewable generation or energy pricing have a high influence on the operational cost of the system. Nevertheless, a suitable energy management can lead to improved grid operation.
In [17], battery storage systems, smart energy management and energy flexibility enhancement were examined in energy sharing districts. Therefore, several control strategies were implemented. Afterwards, a multi-objective optimization was performed to integrate the objectives of the different stakeholders like prosumers, utility grid companies or policymakers. It is stated that the provided energy sharing system provides an optimized operation of the battery storage system taking the dynamic depreciation into account.
In [18], different use cases of LV and MV battery storage systems were investigated with respect to the impact on electricity costs, grid security and externalities in Germany. Examples of use cases were grid-serving applications by distribution grid operators, provision of balancing energy and optimized applications. As a result, the cost of electricity is reduced in the first two use cases. In the optimized application, the evaluation depends on many factors such as battery costs, grid expansion, and grid topology, so no unambiguous answer can be given. In terms of grid security, the use cases have a positive effect, except for the application provision of control energy, which is neutral. Regarding the provision of control energy, automatic frequency restoration reserve and frequency containment reserve were considered.
Reference [19] investigated different grid configurations of the Swiss power grid and whether the use of grid-serving battery storage systems can lead to a financial advantage compared to conventional grid expansion, curtailment or more innovative measures. The study concludes that neither in the year 2017 nor in the year 2035 battery storage can achieve a cost advantage over the alternatives. The result stays the same if an additional market-oriented use of storage is allowed. However, it is stated that the use of storage systems can reduce the loads at higher grid levels and thus possibly also avoid grid expansion costs.
In [20], applications of battery storage systems in Germany were examined for their economic viability and technical feasibility. The use of battery storage at different grid levels compared to avoided grid expansion clearly showed that the latter was not economical under the given conditions. For further consideration, the multi-purpose use of storage systems was investigated. Nevertheless, these did not represent economic applications in the consideration in 2016. However, it was assumed that the significant reduction in the investment costs of battery storage systems will increase their use in the future.
In [21], it was stated that by storing electricity, grid expansion in Germany can be avoided or delayed. To achieve this, storage plants should contribute to stabilizing the voltage in the low-voltage (LV) and MV grid, compensate for reduced feed‑ins from RES and provide support in situations of grid overload. Storage plants are technically capable of solving the studied use cases. However, the alternatives of grid expansion measures, load management, power to heat and high-dynamic power plants were identified as more economical options, which additionally ensure higher supply security.
In [22,23,24], several positive effects on the power supply in Austria were demonstrated for battery storage systems. In addition to avoiding and delaying the expansion of the grid, they enable a more efficient use of grid capacities, reduce the load on operating resources and prevent grid bottlenecks. Furthermore, they can serve as flexibility options, contribute to voltage stability and smoothing of power peaks and support reactive power management. For this purpose, five grid storage systems were installed at a transformer station in Vienna to provide grid services.
In [25], various use cases of battery storage systems in Germany were investigated. These included the avoidance of grid expansion measures and the provision of primary control power. Based on the year 2015, the use of storage for the provision of primary control power was assessed as economical. The use case of avoiding grid expansion measures examined the costs of battery storage deployment, conventional grid expansion with line installing or reinforcement, the deployment of controllable local grid transformers and the targeted curtailment of RES, especially PV. With the assumptions made, battery storage turned out to be uneconomic in both the LV and MV grids.
In [26], the optimal use of storage systems for power grid flexibility in Germany was investigated on the basis of various use cases. In the context of that work, the application of grid expansion reduction in the MV grid by the grid operator and the use of on-site storage in the MV grid were of particular interest. In the first case, a MV grid with limit violations due to PV and wind power feed-ins is analyzed. The conventional options of the grid operator were compared with the use of battery storage. In the result, the costs for storage were significantly higher than for grid expansion. To be profitable, the cost of the storage systems would have to fall by 95% if market revenues are not considered. In the case of on-site storage, a PV park, which is located in a fully loaded MV grid, was equipped with battery storage. With the present dimensioning, the storage cannot contribute to fulfill the limits of the grid. Thus, the economic operation of battery storage as an alternative to grid expansion was rejected here.
In [27], conventional grid expansion in the distribution grid in Germany was compared with various flexibility options. The options included two control strategies for the reactive power of PV systems as well as a home storage system and two large-scale battery storage systems. The focus was on the consideration of increasing PV penetration and the associated grid loads. It was shown that the flexibility options increase the absorption capacity for PV systems within the grid area, and in this way an alternative to conventional grid expansion is created. At the same time, the flexibility options show a cost-saving potential compared to grid expansion.
In [28], the reduction of grid expansion through the use of storage in the distribution grid was investigated using the example of grid reinforcement of a grid in Germany. A high-voltage (HV) grid was considered, and for that a possible storage dimensioning was determined. From a technical point of view, the use of storage to reduce grid expansion is possible, but the costs are four to eight times higher than with conventional grid expansion measures. In addition, distributed storage in the MV grid were being considered to relieve grid bottlenecks in the HV grid. This requires significantly higher total powers and capacities than central storage plants in the HV grid.
There are several international publications that analyze the optimal dimensioning and positioning of storage in a microgrid. However, in most cases, only the costs of the power grid are investigated without considering the technical aspects of the grid design. The storage systems are mostly seen as an alternative to other generators, so a minimum of power supply costs is sought. The publications [29,30,31,32] are to be mentioned at this point. In [33], on the other hand, the optimal dimensioning and positioning in an independent microgrid were considered. The costs were not considered, but the storage system was designed to cover generation and consumption.
In [34], the operation of distributed energy storage systems in a MV and a LV grid in Australia was optimized. The optimization was done considering the costs for the distribution grid and the battery storage. In particular, the applications of voltage stability, loss reduction and peak reduction were investigated. In both considered grids, storage can be used to reduce voltage fluctuations, as well as losses and the maximum power.
In [35], a storage system with 300 kW power and a capacity of 300 kWh was analyzed for voltage stability in two exemplary MV grids. The IEEE 33- and 69-bus MV grids were used. A correlation between the centrality of the storage and the voltage fluctuations was established. It was found that the more decentralized positioning of the storage unit leads to lower voltage differences and is therefore to be preferred.
In [36], the costs for grid reinforcement and storage systems for voltage stability were determined for PV penetrations of 50% and 80%, respectively. It considered a LV grid in Germany, in which both the storage systems are optimally distributed over the grid via an algorithm and the grid expansion requirement is determined automatically via another algorithm. Depending on the application, the storage units were positioned at different grid nodes. The limit of 3% and the limit of 5% were analyzed as permissible voltage deviations. As a result, battery storage was the more favorable alternative to grid expansion.
In [37], the positioning and dimensioning of energy storage systems were optimized on the basis of two reference grids. For this purpose, different scenarios took seasonal differences into account. It was shown that, using storage, voltage deviations, line loads, and total operating costs can be reduced by an optimal storage design, so that grid expansion measures can be postponed. However, it did not consider the impact of increasing RES generation, increasing electricity consumption or decreasing storage costs.
In [38], grid reinforcement was compared to storage deployment. The IEEE 33 bus model with a total load of 3.7 MW and different cases of storage positioning were examined, with no RES generation considered. The time frame considered was 20 years, and the load was increased by 3% per year, so different lines needed to be reinforced at different times depending on the case. The use of storage led to a cost reduction compared to the reference case without storage. The use of multiple storage units turned out to be more advantageous than a single storage unit. It was recommended to continue the investigations under consideration of the expected cost degression of the storage.
In [39], different storage systems, including battery storage and a hydrogen-based storage system, were compared with each other in terms of costs and technical parameters when used as grid storage. Fixed power levels and storage durations were assumed, and different points in time were investigated. It was indicated that compressed air storage is the most cost-efficient alternative, with battery storage becoming increasingly competitive as development progresses. Hydrogen storage often has cost disadvantages due to lower efficiencies.
In [40], battery and hydrogen grid storage systems were compared with respect to their energy efficiencies during construction and operation. Hydrogen storage systems have significant disadvantages compared to battery storage systems, particularly in the operating phase, due to their poorer efficiency.
In [41], the focus was on the investigation of hydrogen storage systems for stabilizing the grid in the event of increased generation from RES. Hydrogen storage systems were compared with battery storage systems, pumped storage power plants and compressed air storage systems regarding their costs, and a method for dimensioning RES generation technologies as well as the individual components of hydrogen storage systems was developed. In terms of cost, hydrogen storage was evaluated to have disadvantages compared to the other storage systems. However, it was highlighted that increased penetration of RES generation can be implemented through hydrogen storage.
In [42], a battery and a hydrogen storage system were compared as storage for a grid-connected PV system of a multi-party rental building. A pessimistic and an optimistic cost scenario were investigated, and different operating strategies were considered. In the pessimistic scenario, battery storage resulted in lower costs, while in the optimistic scenario, comparable results were achieved.
The previously presented literature shows a broad scientific foundation in the evaluation of battery storage in the distribution grid as an alternative to grid expansion. From a technical point of view, it is possible to use battery storage to avoid grid expansion measures. In [21], it was presented that storage can stabilize the voltages in the grid by balancing fluctuating generation and in situations of grid congestion. The sources [22,23,24,27,28] also assumed that battery storage systems can avoid or postpone grid expansion from a technical point of view. In this context, the technical grid parameters can be optimized by appropriate storage sizing and positioning. In [33], optimization was performed in a stand-alone microgrid, whereas in [34], a MV and LV grid was considered. As a result, the parameters of voltage stability, loss reduction and peak reduction could be improved by using battery storage. In [35], it was indicated that a more decentralized positioning of the storage system can contribute more to voltage stability. Reference grids were used in [37] and [38] to investigate positioning and dimensioning, which is why a reference grid, which is explained in more detail in section 3.2, is also used for this study. To reflect the growing demands on the grids, the effects of increasing PV penetration were investigated in [36] by using scenarios. Increasing loads were also assumed in [38] and in [19], the year 2035 is investigated in addition to the year 2017. Accordingly, scenarios 2022 and 2050 are investigated in this paper to be able to consider the increasing demands on the power grids. These are explained in section 4.
Regarding the economic efficiency of a grid-serving use of battery storage, different results were given, whereby a large part of the literature assumed that the use of storage is uneconomical. Examples of this are [20,21,25,26]. The author of [15] considered that economic operation is only possible at very low interest rates. In [14], it was found that some system services can already be provided cost‑efficiently. In the result of [38], battery storage deployment was more economical than grid expansion. Among other things, the assumed expansion of RES, the revenue potentials in addition to the grid expansion and the grid levels considered differed. While in [20] and [21] examination was limited to one year, in [19] also a scenario in 2035 was considered, and in [36] increasing PV penetration was assumed. Thus, although future developments in terms of loads, generation or storage costs were partly included, this was mostly limited to one parameter and leaves out the combined investigation of future developments. Furthermore, it must be considered that some works did not investigate the MV grid, but instead a storage use in the LV or HV grid, whereby it is not guaranteed that the results can be exactly transferred to the MV level. While in [28] the focus was put on the HV grid, in [35] the MV grid was considered, and in [36] the LV grid. The authors of [18] included various applications of LV and MV battery storage in the analyses. In [25] and [26], different applications at LV and MV level were studied. Moreover, the evaluation approaches to economic viability differed. While in [20] a multi‑purpose use was considered in addition to the use for grid expansion avoidance, in [19] d the possibility of grid expansion reduction at higher grid levels was cited without considering this in the analysis.
The literature overview reveals the following research gaps:
● Overall, hydrogen storage systems have been underrepresented in considerations of the use of storage to compensate for grid expansion needs, although they should play a significant role in a decarbonized energy system of the future [8].
● The existing literature lacks a holistic comparative analysis. While in [39] cost and technical parameters of battery and hydrogen grid storage systems were compared, in [40] a comparison of them in terms of energy efficiency was performed, in [41] a methodology for sizing the hydrogen storage component was developed, and in [42] battery and hydrogen storage were examined as alternative PV storage systems. None of these publications considers the impact of hydrogen storage on the power grid or compares it to grid expansion and battery storage.
● Furthermore, the literature lacks additional revenue potentials that have not been considered so far. These include arbitrage trading, heat extraction and grid expansion compensation in superimposed grid levels. This enables a better comparison of battery and hydrogen storage.
This paper therefore examines, considering the research gaps, whether and which electricity storage system can most efficiently reduce the need for grid expansion in a future energy system. In this context, a battery storage system and a hydrogen storage system will be compared to the classical grid expansion from a technical and economic point of view. Furthermore, other revenue potentials of the selected storage systems are considered and included in the analysis. The approach to classical grid expansion used here is taken from [43]. Other technical options for increasing the power quality in the grid, such as enhanced dynamic voltage restorer [44], are not considered due to the focus on electricity storage. The focus is on the time-structured control of the active power of the electricity storage systems. The possibilities to control the active and reactive power of the converter are neglected [45] to ensure the comparability of the scenarios.
Thus, the main contributions in this paper are:
1.) Development of two representative configurations of a selected MV grid topology for the year 2022 based on current data and for the year 2050 based on forecasts for the expansion of distributed RES and flexible distributed consumers in Germany. This allows to determine a cost-efficient alternative in a low RES and a high-RES grid with respect to Germany without having to change relevant parameters such as the grid topology.
2.) A holistic techno-economic comparison of selected alternatives to reduce grid expansion in the assumed scenarios. In addition, both hydrogen and battery storage were modeled in the simulation, allowing a comparison between storage solutions. To consider, the additional application possibilities of the individual storage systems for the economic analysis, heat extraction, arbitrage from electricity transactions and compensation for grid expansion at higher grid levels are considered as additional economic parameters. Thus, to the best of the authors' knowledge, this paper provides a unique and relevant analysis of this research area.
This paper is structured as follows: The following section presents the methodology of the technical analysis of the work presented here. Then, section 4 provides an overview of the MV grid, storage options and their control algorithms. Section 5 describes the methodology and background for the economic analysis. Before conclusions are given in the last section, the results are presented and discussed.
In this section, the methodology of the technical analysis is explained. First, the Python open‑source tool for power system modeling (pandapower) is presented. Then, the methodology used to determine the cost-efficient solution is described in detail. Finally, the exogenous data sets used are explained. This section of the data basis is divided into two subsections: first, the general data basis, which is the same for each scenario, and then the data basis, which changes in the scenarios. This section thus demonstrates the robustness of the results through realistic input data and a robust methodology. The modeling approach is therefore well suited for a technical-economic comparison of the three alternatives for ensuring electrical supply security in the future German electricity system.
The tool pandapower from [46] and [47] is a Python-based open-source power grid analysis tool. It is intended for the automated analysis of static or quasi-static power system states or the optimization of balanced power systems. The basic functionalities are load flow calculation, power flow optimization, topological grid search and short circuit calculations according to IEC 60909. pandapower uses an element-based model for the implementation of electrical grids. The individual elements, such as lines, transformers, switches, generators or loads, are connected to grid nodes. Furthermore, relevant parameters must be defined for the individual elements. These include, for example, the nominal voltage and the voltage deviation for the nodes, the active power and reactive power for the loads and generators and the rated power and the short-circuit power for the transformer. Lines can be parameterized via the line length, the resistance, or the reactance and some other parameters. The line current is calculated at both ends of the line, and the percentage load indicates the ratio between the actual current and the thermally maximal permissible current. In addition, an external grid can be included in the grid modeling as a voltage source. The grids chosen here and described in the next sections are already included in pandapower.
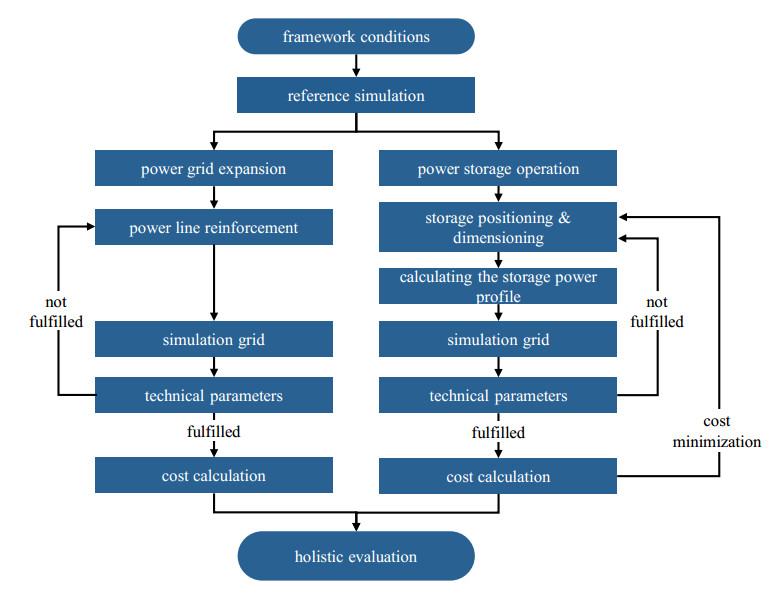
The goal of the simulation is the economic comparison of alternatives to solve challenges in the grid area. These technical challenges are basically the thermal overload of power cables and the violation of voltage bands. The background and definition of the grid parameters are explained in detail in the section on power grids in subsection 4.1.3. These challenges arise from the transformation of the energy system by the expansion of RES (PV and wind plants) as well as decentralized flexible consumers (HPs, EV). For this reason, two reference points are chosen: the energy system in 2022 and the energy system in 2050. The detailed description and parameters of these scenarios are presented in the next subsection. The challenges resulting from the transformation can be solved in this work either by grid expansion in the sense of installing power cables in parallel or by installing and operating a grid storage system. Methodically, the procedure is the same for both battery and hydrogen storage alternatives. The following description of the methodological procedure for the deterministic and iterative approach to determining the cost-optimal solution for each alternative can be taken visually from Figure 1.
The simulation starts with the definition of the framework conditions, which are presented in detail in section 3.3. The simulations can be carried out for the framework conditions of the selected MV grid in 2022 and 2050. In addition to the framework conditions, there is a reference simulation. This reference simulation is a simulation of the selected grid without grid expansion and storage. It is run once for 2022 and 2050, respectively, and is intended to quantify current and future challenges in the power grid. In the case of grid expansion, the overloaded lines are gradually reinforced until the required conditions derived from the reference simulation are met. The procedure can be seen on the left in Figure 1. The reference simulation has already identified the overloaded lines. For the next passes of the simulation, an additional line is installed in parallel in this line section. For each simulation run, if two overloaded lines are present, only the most heavily loaded line is reinforced. This iterative procedure is carried out until the technical restrictions are met. Since only the overloaded sections are reinforced, and the number of parallel lines is only ever increased by one, the result can be considered the most cost‑efficient solution.
For the solution variants by means of storage positioning, shown on the right-hand side of the sequence in Figure 1, a similar procedure is followed. Here, as in the case of the grid expansion, the cost-optimal solution is to be found for each storage scenario. First, the storage units are positioned both at the transformer to the HV grid and at the nodes of the overloaded lines. For the initial dimensioning, a sufficiently large capacity and power are assumed, which in any case, if correctly positioned, will lead to compliance with the grid parameters. Therefore, if this positioning still does not provide a solution, alternative positioning must be checked. If compliance with the grid parameters is achieved, the technical parameters are to be reduced, comparable to grid expansion, until the grid parameters are no longer complied with. Thus, the cost‑optimal dimensioning of the storage for this positioning can be determined iteratively. To determine that this combination of positioning and sizing represents the global minimum of consideration, alternative positionings are to be examined. To do this, each node is run at least once to clearly identify the global minimum.
Table 1 provides a summary of how many simulations are run for each scenario. For grid expansion in 2022, a total of 4 simulations with different configurations were carried, and 8 simulations were carried out for 2050. To achieve suitable positioning and dimensioning, considering cost minimization, 79 simulations were carried out for battery storage in 2022 and 283 simulations in 2050. The higher number of simulations required is a result of the complexity caused by increased grid loads. For hydrogen storage, a total of 56 simulations were performed in scenario 2050 to find a cost-optimal solution. The scope of the simulations is lower than for the battery storage since unfavorable positioning was already known from the battery storage simulation.
| Scenario | Grid expansion | Battery storage | Hydrogen storage |
| 2022 | 4 | 79 | 3 |
| 2050 | 8 | 283 | 56 |
As described in the previous section, the simulation was implemented in Python and the grid expansion, and the validation of the grid parameters was carried out with the help of pandapower. The power grid as well as the generation and load profiles are exogenously given and will be explained in detail in the following subsection.
To be able to derive statements from the simulations that are as robust as possible, a representative exogenous data basis must be selected. Since the load flow simulation is carried out in 15-minute time intervals, the power values for each consumer or generator are required for the period under consideration in a 15-minute resolution. In the following, these are briefly explained, and the consumers, generators and storage plants are discussed. Several LV reference grids are connected to the simulated MV reference grid. This consists of 146 residential buildings, including 97 one-family houses, 24 two-family houses and 25 multi‑family houses. The distribution is based on [48]. Furthermore, the household size is based on [49], so that the basic consumption of the households can be scaled using the annual electricity consumption from [50]. The standard load profile H0 from [51] is varied according to [51] and [52]. For the simulation of the LV grids, different penetration levels of relevant technologies, including PVs, home storage, HPs and EVs, are assumed for each of the two observation dates 2022 and 2050. These are based on [53] and can be taken from Table 2.
| 2022 | 2050 | |
| PV | 26% | 76% |
| Home storage | 2% | 29% |
| HP | 4% | 52% |
| EV | 0.6% | 39% |
Since the standard load profile H0 only represents private consumption without special applications, heat pumps (HPs) must be considered separately. For this purpose, the standardized load profile WP0 [54] is used. To determine the associated quarter-hourly power values, further calculations must be made, which are based on the load forecast procedures from [54,55,56,57]. The respective required daily mean temperature over the course of the year is given for the German city Erlangen in [58]. In the context of the simulation, the values for the year 2021 are used. For scaling to electricity consumption, the average living space per person of 45.1 m² from [59] and the space heating energy demand of 131 kWh/m² according to [53] and [60] are used. Modernization and new construction can be expected to reduce this value. As an average value from [61,62,63], 85 kWh/m² is used for 2050. In addition, the hot water energy demand from [64] and an annual performance factor of HPs of 3.5 according to [65] are used. To simulate the charging profile of the EVs, the profile from [66] is used on the one hand, and on the other hand, an individual load profile is created for the individual EVs using the average charging capacities from [67] and the restart times from [68]. The electricity consumption is determined using the average annual mileage from [69] and the electricity consumption of an EV per 100 km from [70]. For business, commerce, services industry (BCS) and industry, the standard load profile from [52,71], which gives the weighted average of the total group studied, is used. Here, the electricity consumption of commerce, trade, services and industry is calculated using the sector net electricity consumption from [72,73] and the consumption of the simulated households. The synthetic feed‑in profile from [74] is used as the generation profile. The peak powers of the simulated PV systems in the LV and MV grid are based on the values from [75]. Likewise, the expected output in MWh of the PV system is based on the source just mentioned. Using the installed capacity from [76] and the population level from [77], an expected output for the grid area can be determined. For the year 2050, the forecast from [78] is used. For the simulation of wind power, the generic feed‑in time series from [79] are used. These provide normalized feed‑in profiles for onshore wind power for the base years 2020 and 2050. The normalized profile must be multiplied by the installed capacity of the wind turbine to obtain a corresponding generation profile. The turbine capacity is determined by the wind capacity installed in Bavaria from [80,81,82] as well as the population of Bavaria from [77] and the inhabitants of the considered grid area. For the year 2050, the forecast from [78] is applied. The following Tables 3 and 4 show how the connected LV grids, consumers and generators are distributed over the MV reference grid. The main difference here is the increasing generation from RES for the year under consideration 2050.
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 140 | ||
| 4 | 3 | 500 | 260 | ||
| 5 | 1 | 1,300 | 1,950 | ||
| 6 | 2 | 700 | 240 | ||
| 7 | 2,200 | 1,360 | |||
| 8 | 1 | 900 | 350 | ||
| 9 | 900 | 440 | |||
| 10 | 1 | 1,000 | 3,100 | 150 | |
| 11 | 2 | 810 | 190 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 410 | ||
| 4 | 3 | 500 | 750 | ||
| 5 | 1 | 1,300 | 3,200 | ||
| 6 | 2 | 700 | 500 | ||
| 7 | 2,200 | 3,000 | |||
| 8 | 1 | 900 | 3,500 | ||
| 9 | 900 | 800 | |||
| 10 | 1 | 1,000 | 3,100 | 2,100 | |
| 11 | 2 | 810 | 550 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
In this section, the technical systems used for this analysis are presented and described. For this purpose, the CIGRE MV grid used is introduced first, followed by the relevant economic parameters of the grid expansion for the economic analysis. For the technical analysis, the grid restrictions (voltage band and current carrying capacity) are described here, which must be ensured in the simulations by both the grid expansion and the storage systems. After this overview of the power grids, the storage systems are introduced, and the control algorithm, as well as the technical and economic parameters, are described. A comprehensive presentation of these values is necessary to be able to fully compare the storage systems with the grid expansion economically and technically in the selected reference power grid. Peak shaving was selected as the operating mode of the storage systems that can be used as an alternative for grid expansion. Depending on the storage type, peak shaving is either daily (battery) or seasonal (hydrogen).
This section describes the characteristics of the power grids used. The topology, the grid parameters, and the economic parameters of the grid expansion are discussed. It is assumed that the power grids described here belong to a grid operator who is faced with the challenge of managing them cost‑efficiently. This means that the grid parameters described here are adhered to and the costs incurred are to be minimized. The grid operator has an existing grid structure on which they can build. Anticipating the expansion of RES and decentralized flexible consumers, the grid operator should now analyze whether to reinforce the power lines or install the described storage plants and operate them in a grid‑serving manner.
The CIGRE reference grid [83,84] is used as the MV grid. The CIGRE grids have no reference to Germany. However, there is insufficient data for selected and representative German medium-voltage grids to allow for both meaningful results and simple processing in the model presented here. For this reason, the CIGRE grids were used. These grids were developed to investigate the economic, robust and environmentally friendly grid integration of decentralized energy technologies. Based on these reference grids, which represent actual integration challenges, methods and smart grid technologies are to be analyzed and validated for their quality and advantages. For this purpose, HV, MV and LV grids were developed in sufficient detail. Figure 2 shows the CIGRE MV grid used here with the integration of PVs and wind power plants. The CIGRE MV reference grid is basically composed of 15 lines and 15 nodes connected to an external HV grid through two transformers. There are 18 loads distributed across the grid and eight switches exist to control power flows. This grid is supplemented by nine generators to consider PV and wind, which are composed of eight PV systems and one wind turbine. As an additional extension, home fuel cells, two battery storage units, one combined heat and power unit and one fuel cell each can be integrated, so that three CIGRE grids are available for analysis in pandapower. Unlike the original CIGRE reference grids, pandapower uses a HV of 110 kV instead of 220 kV to ensure sound transformer data.
In general, grid bottlenecks are to be eliminated by the grid operator using the "NOVA" principle [85]. This means that grid optimization is carried out first before the grid is strengthened or expanded. In doing so, an attempt is made to fully utilize the potential in the grid at each level and only then resort to the next level. In the context of the simulation, it is assumed that the MV grid is strengthened by installing power lines in parallel at congested points. The service life of power cables in the MV grid is usually given as 40 years [25,86]. The cost of installing MV cables ranges from 80,000 EUR/km to 140,000 EUR/km [87], with costs usually varying between 100,000 EUR/km and 120,000 EUR/km [25,86,88,89]. Accordingly, a value of 110,000 EUR/km is used in the simulation. As detailed breakdowns of project costs, e.g., by population density or line length, are not available, these costs are used for all cables in the reference grid. Furthermore, this value is valid for the two years of consideration 2022 and 2050, since depending on the source, an increase or reduction in costs is assumed and therefore these effects are excluded. The operating costs of power grids are one percent of the investment sum per year [86]. The simulation continues to use an equity interest rate of 5.64% [80,90].
To assess whether the simulated grid expansion or the installed and operated power storage is sufficient to maintain the power quality in the grid, a load flow calculation is performed. It is also checked whether the voltage band has been violated or whether the thermal load capacity of the power lines has been exceeded [91]. For the requirement of permissible load flow, it is necessary to investigate whether the feeders, transfer powers and loads result in a permissible grid condition [91]. For this purpose, the requirement for the continuous thermal load must be fulfilled. This means that the load current is always below the thermally permissible operating current, and the currents occurring in the grid are permissible for all equipment. This criterion is particularly relevant for power cables, since a temperature rise in these can lead to thermal breakdown because of increased losses due to heating [91]. In addition, the voltage must lie within a defined voltage band. For the medium and LV grid, the permissible deviation is defined in DIN EN 50160 as 10%. It should be noted that the permissible deviation is usually divided between the medium and LV levels, since these are usually rigidly coupled via unregulated local transformers [91]. Therefore, the limit value for voltage deviation in the MV grid is usually only 4% [14,87]. A remedy for this problem is provided, for example, by controllable local grid transformers, which allow the permissible ten percent to be utilized in both the LV and MV grids [14,92]. Especially in the transmission system, the transmission system operator has some possibilities to influence the voltage. These include voltage regulation in power plants, the use of compensating reactors in lines, adjustable ratios and corrective switching. However, the grid customer, such as large industrial companies, can also compensate for voltage fluctuations, for example, with flywheel storage [91,93].
This section describes the assumed installation and operation of the storage systems. In the first subsection, the technical and economic parameters of the storage systems are presented and described. After that, the control of the storage systems is described. Before the description, the most important parameters are briefly and concisely summarized in the following Tables 5 and 6.
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 120 | 300 | 2.5 | 15 | 90 |
| H2 electrolysis | 1,200 | 5 | 15 | 70 | |
| H2 fuel cell | 1,700 | 5 | 15 | 50 | |
| H2 storage | 6 | 5 | 30 | 100 | |
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 50 | 160 | 2.5 | 20 | 93 |
| H2 electrolysis | 650 | 5 | 20 | 75 | |
| H2 fuel cell | 600 | 5 | 20 | 55 | |
| H2 storage | 1 | 5 | 30 | 100 | |
In the state of the art, lithium‑ion technology is a widely used storage technology, so it is considered in this work. For the state of the art of battery storage, efficiency data varies between 84% and 95% depending on the source [21,94,95,96,97,98], which is why 90% is assumed as the average value in the simulation. As development progresses, an increase in efficiency can be assumed. This is also reflected in the future efficiencies of 88% to 97% given in the sources [21,39,96,98], so 93% is taken as the efficiency for the year 2050. Regarding efficiency, it is important to note that the stated efficiency refers to charging and discharging processes. The lifetime of a battery storage system is estimated to be 15 years at the time of writing in 2022, since the majority of sources assume lifetimes between ten and 20 years [14,21,28,39,96] or directly state 15 or 16 years [26,99] as lifetimes. For the year 2050, the range of lifetimes increases to up to 30 years [21,28,96], which is why the lifetimes assumed in the simulation are raised to 20 years.
The economic evaluation of storage systems requires consideration of both investment and operating costs. For the former, the sources again provide a wide range of cost assumptions. The total cost is determined by the power and capacity of the storage system. Depending on the source, sometimes only power or capacity related costs are given, with the feed-out period having a large influence on the parameters in this respect. Other sources give the total cost as a combination of power and capacity costs. This type of cost is much more suitable for modelling the storage systems in the simulation, as the storage systems can be dimensioned flexibly, and resilient costs can be determined. For the state of the art, according to [15,21,28,95], capacity related costs range from 70 EUR/kW to 150 EUR/kW. So a value of 120 EUR/kW is considered realistic. The capacity-related costs vary mainly between 200 EUR/kWh and 800 EUR/kWh [15,21,28,38,94,95,96,99,100], using 300 EUR/kWh for the simulation. The costs assumed in the simulation are compared with other sources based on a storage tank with a discharge time of four hours and are found to be reasonable. For the 2050 values, a similar approach is chosen, resulting in a power-related cost of 50/kW and a capacity-related cost of 160 EUR/kWh [21,28,94,96,99,101]. Operating costs are sometimes given as a value based on production and electricity sales [39,94]. Alternatively, it can be determined as a percentage of the investment costs required annually for operation. Sources give values between 2% and 3% [14,99], so the simulation is calculated at 2.5%.
Regarding the efficiency parameters for hydrogen storage, a distinction must be made between feed‑ins by means of an electrolyzer and feed‑outs by means of a fuel cell. Both electrolyzers and fuel cells are based on the alkaline or the proton exchange membrane process. Accordingly, the efficiencies are similar but slightly different, with an average value used in the simulation. For the electrolyzer, the source data on the state of the art range from 44% to 86% [102,103]. However, in most cases the efficiency is around 70% [104,105,106], so this value is used for the simulation in 2022. The efficiency will increase so that 75% [104,105] is considered realistic for 2050. Fuel cell efficiencies are somewhat lower overall. In the state of the art, sources indicate 32% to 60% [102], so an efficiency of 50% [104] is used for the simulation. The sources also assume an improvement in efficiency for the fuel cell. Therefore, the value for the year 2050 is 55% [104]. The storage losses of the hydrogen storage are very low, so the efficiency is assumed to be 100%. Thus, the overall power-to-power efficiency for the year 2050 is 45% and is also in a source‑based range [107].
The lifetime of the subsystems electrolyzer and fuel cell are simulated with 15 years at the state of the art and with 20 years in 2050, since these values can be regarded as realistic average values [102,107,108]. The lifetime of the actual hydrogen storage system is 30 years [39,107]. For the electrolyzer, the investment costs at the state of the art are mostly between 1,000 EUR/kW and 1,500 EUR/kW [102,104,105,109,110,111,112], which is why a value of 1,200 EUR/kW is used in the simulation. For the fuel cell, prices tend to be somewhat higher, so a value of 1,700 EUR/kW seems realistic [102]. The actual hydrogen storage has only low marginal costs of 6 EUR/kWh due to the mostly high storage volume [107,108], so the total costs of the storage are in line with the source data of about 3,000 EUR/kW [39,108]. By 2050, this value will drop to about 1,300 EUR/kW [39,108], with a split between electrolyzer costs of 650 EUR/kW [105,111,112], fuel cell costs of 600 EUR/kW [105,110] and storage costs of 1 EUR/kWh [97,107,109]. The operating costs for hydrogen storage are generally higher than for battery storage. Taking this fact into account in the simulation, an annual share of the investment costs of 5% is assumed, so that the procedure is the same as for battery storage [39,94,102,107].
Grid operators in Germany already have various operating resources to ensure their supply tasks. For example, compensation coils are used to maintain the quality of the supply of reactive power. For this reason, it is a valid use case to use large battery storage and hydrogen storage to maintain voltage quality. Therefore, we consider here the technically economical grid‑serving use of large battery and hydrogen storage favorably positioned in the grid by the grid operator. In order to implement grid‑friendly control for both storage systems, a grid‑friendly charging and discharging strategy widely used in the literature is employed, i.e., valley filling or peak shaving [113,114]. This means that for each day, the storage mitigates the consumption peaks by discharging the storage at these times. Depending on the generation capacity of the RES, which achieves high outputs especially in the summer months due to PV feed‑in, the storage is either charged at times of maximum feed‑in from RES or at times of minimum grid draw, should the feed‑in not exceed the consumption at any time of the day. In this way, peaks are reduced in terms of both maximum consumption and maximum feed‑in, and overall grid interchange is equalized. Figure 3 shows an example of this charging and discharging behavior.

Hydrogen storage and battery storage can perform this control equally. Battery storage is better suited for compensating intraday fluctuations, while hydrogen storage excels at compensating seasonal fluctuations. However, hydrogen storage systems have a significantly lower efficiency during storage and retrieval since hydrogen generation in electrolysis or electricity generation from hydrogen in fuel cells is associated with higher losses. Still, due to the high capacities that can be realized, it is possible to use them as long-term or seasonal storage. In this case, generation surpluses from RES are stored in the summer months and released again in the winter, mainly at peak load times. In this way, power generation and consumption can be balanced throughout the year. This behavior is implemented via a corresponding functionality in the simulation. The power determination of the battery storage systems for band regulation is performed in the simulation using the logic shown in Figure 4.
Based on the power profile at the respective grid node where the battery storage system is installed, the maximum and minimum grid power values are determined for each day of the year. Upper and lower daily power limits are then defined for each day. For each time interval of the day, the actual grid power is determined. If the actual power is above the upper daily power limit, the discharge power of the battery storage is set to the difference between the actual grid power and the upper daily power limit. Accordingly, if the grid power is below the lower daily power limit of the battery storage, the charge power of the battery storage is set to the difference between the actual grid power and the lower daily power limit. If the grid power is between the lower and upper daily power limit, the battery storage power is set to zero. In this process, the capacity, power and state of charge of the battery storage must be considered, as no further charging is possible in the case where the battery storage is fully charged, no further discharging is possible in the case where the battery storage is fully discharged, and the discharging and charging power cannot exceed the defined power of the battery storage system. After setting a battery storage power for each time interval of the day, the power profile of the storage system can be derived. It is then checked whether the resulting grid powers at the node are within the set power limits. If this is not the case, the upper and lower daily power limits are shifted. If the resulting grid power exceeds the upper daily power limit, it must be set to a higher value, as the technical parameters of the storage cannot guarantee that the grid power will remain within the set daily limits. Accordingly, if the resulting grid power falls below the set lower daily power limit, the daily power limit is lowered. This process is carried out iteratively until appropriate power limits are found for the day in question that use most of the available power and capacity of the storage system. The determination of the feasibility of the grid state follows Figure 1, and therefore an iterative convergence to the optimal dimensioning of the battery storage is also performed. The simulation methodology for hydrogen storage differs from that for battery storage because the focus is on seasonal storage. The simulation methodology is shown in Figure 5.
The power profile of the hydrogen grid storage is also determined based on the grid power profile. Here, maximum and minimum grid power values can be determined over the year. The hydrogen storage is charged when there is a power surplus in the grid, and there would be a feed-in to the higher grid level in a certain time interval. Under certain circumstances, electrolysis must take place at partial load if the power surplus is less than the maximum electrolysis power of the hydrogen storage system. Otherwise, it is a feed-in to the higher grid level if the feed-in grid power exceeds the maximum electrolysis power of the hydrogen storage system. Thus, a charging profile of the hydrogen storage tank can be determined. If the grid power is above the annual discharge limit, power is discharged via the fuel cell to comply with the upper annual power limit. Following the methodology of the battery storage the discharge power of the hydrogen storage is set to the difference between the actual grid power and upper annual power limit. The main difference between the power limits of the storage technologies lies in the applicability of the limits. In the case of the battery storage, an individual power limit is set for each day of the year. For the hydrogen storage, the power limit is set for the whole year. After setting the charge and discharge powers for each time interval, a hydrogen storage power profile can be derived. The final step is to check whether the resulting grid power profile is within the set annual power limits. If the resulting grid power exceeds the set upper power limit due to limiting technical parameters of the hydrogen storage, the upper power limit is set to a higher value. The dimensioning of the hydrogen storage system to ensure a feasible grid state follows the methodology in Figure 1.
In addition to the unconditional compliance with the grid restrictions, the various alternatives are to be compared economically. Here, storage systems offer further advantages above grid expansion measures, as they can generate additional revenue from arbitrage, heat extraction and avoidance of grid expansion in superimposed grid levels. After these revenue options have been presented in the following subsections, the last subsection discusses how these cash flows with different payment horizons are transferred into a common valuation unit. In this way, the investment costs mentioned in the previous sections can be added to the operating costs and revenue potentials based on the different depreciation periods and thus compared across measures.
This section explains arbitrage trading for revenue generation of storage systems and the associated electricity price assumptions. Fluctuations in electricity prices can be used for arbitrage trading. In this process, electricity is purchased at times of low prices, stored, fed out and sold at a later time at higher prices [18,20]. Accordingly, the simulation assumes the possibility of participation in the spot market. It is assumed that the average price minus the standard deviation can be realized as the purchase price and the average price plus the standard deviation of the respective electricity price scenario as the sales price. To show the effects of fluctuating electricity prices, three price scenarios are used to determine the realizable revenues.
From 2018 to 2020, the average wholesale electricity prices on the European Power Exchange ranged from 30.5 EUR/MWh to 44.5 EUR/MWh, and the average standard deviation ranged from 9.0 EUR/MWh to 9.8 EUR/MWh [116]. In 2021, there was a sharp price jump that raised the average wholesale price to 96.9 EUR/MWh [117]. Price fluctuations also increased significantly, resulting in a standard deviation of 24.5 EUR/MWh for 2021 [116]. The maximum price was 620 EUR/MWh [117]. Previous forecasts have predicted such electricity prices and price fluctuations only for the year 2030 or even 2050, assuming increasing prices and fluctuations overall [118]. In this context, an electricity price of 70 EUR/MWh to 100 EUR/MWh and a standard deviation of about 25 EUR/MWh are given for the year 2050 [119,120,121,122]. Therefore, three price scenarios are considered in the simulation, which, however, are not to be assigned to any years due to the current price situation but only serve as a cost comparison. A price of 60 EUR/MWh and a standard deviation of 15 EUR/MWh are assumed as the low‑price scenario. In the mid‑price scenario, the previous forecasts are incorporated, so that a price of 85 EUR/MWh and a standard deviation of 20 EUR/MWh are used. In the high‑price scenario, a price of 100 EUR/MWh and a standard deviation of 25 EUR/MWh are assumed to reflect current prices and on the assumption that prices will tend to rise.
In the process of the hydrogen storage, major losses occur both in the generation of hydrogen by electrolysis and in the conversion of hydrogen back into electricity by means of a fuel cell. These occur mainly in the form of waste heat, which can be used for heating in winter and cooling in summer [123]. Due to the power class of the hydrogen storage system, it is assumed that the waste heat will be fed into an existing district heating grid and that a sufficient heat sink and pipe sizes are available. In this way, revenues can be generated by selling the heat. The economic value of heat is 92 EUR/MWh [124]. This price is constant because the heat is mostly sold to residential customers who have long‑term contracts at fixed prices.
By balancing generation and consumption locally, grid expansion at higher grid levels can be avoided or reduced [125]. Since the MV grid is considered in this simulation, there is a reduced need for expansion in the HV and extra‑high‑voltage (EHV) grid. To specify this, the maximum feed‑in and powers of the reference grid are used and compared with the maximum powers of the solution alternatives. In this way, a difference can be determined that indicates the extent of the reduction. The costs of the "SuedLink" route are used to estimate the savings. Investment costs of around 10 billion EUR are estimated for this, with a transmission capacity of 4 GW to be realized [126,127,128]. This results in investment costs of 2.5 million EUR per MW of transmission capacity. This value is used for the simulation to map the cost avoidance in the HV and EHV grid. Subsequently, the avoided investment costs are annualized.
To be able to compare the costs and revenues of the alternatives on a uniform valuation basis, they are determined for one year in each case. The associated methodology is explained in this subsection. The investment costs of grid expansion at the various levels and of storage systems are annualized using (4.1). This is done by considering service life and equity interest rate [88].
| Ca = CI* r(1-(1 + r)-L) | (4.1) |
Ca = Annualized costs [EUR/a]
CI = Investment costs [EUR]
r = Equity interest rate [%]
L = Lifetime [a]
The operating costs are given as an annual percentage of the investment costs and can accordingly be easily calculated as annual operating costs. The revenues from arbitrage trading relate in each case to the energy handled in a year by means of the storage systems, so that annual revenues can be determined with the price assumptions used. The same applies to the revenues from waste heat utilization, which are also determined on an annual basis, using the feed-ins and feed-outs of the hydrogen storage system over the course of the year. In the case of cost avoidance in the HV and EHV grid, investment costs can be determined, which in turn are converted to annualized costs via (4.1) to obtain the valuation basis of one year.
In this section, the results of the reference simulations are first explained to show the initial situation in the two scenarios investigated. Based on this, the identified alternative solutions for grid expansion, battery storage and hydrogen storage are presented and finally compared in the last subsection. The first subsection shows the situation in 2022, which represents little stress for the power grid. In contrast, the next subchapter for the scenario in 2050 shows the massive impacts because of the energy system transition in Germany. Then, in the next three subsections, the alternatives are presented and compared with each other. In the following subsection, it is shown that battery storage, in contrast to grid expansion, can generate revenues and is therefore the more economical alternative. Hydrogen storage, on the other hand, is significantly more expensive than grid expansion.
The parameters of the simulation of the reference scenario 2022 were presented in section 3.3. This reference scenario is used to represent a current grid load and the resulting search for the most cost-efficient solution to remedy the violation of grid restrictions. The grid load of this scenario is shown in Figure 6 as the minimum and maximum power per day.
As can be seen in the figure, the grid supply from the HV grid and the consumption power correlate. In winter, both values are at their maximum, as this is when the highest electricity consumption for households, EVs and HPs occurs due to the temperature. At the same time, PV-based power generation is the lowest here. Therefore, especially in winter, to supply all consumers, electricity must be drawn particularly strongly from the HV grid and distributed within the MV grid. In this process, line overloads occur, which are shown in the following Figure 7. There are slight violations of the maximum load capacity of the line in winter.
The seasonality of the line load is also reflected in the voltage curve in Figure 8. The voltage drops are triggered by consumption, whereas the voltage increases result from generation and feed‑in. Accordingly, the voltage drops are significantly higher in winter than in summer since this is also when the maximum consumption of power occurs.
The parameters of the simulation of the reference scenario 2050 are presented in section 3.3. This reference scenario is used to represent a future grid load based on the projected expansion of RES and flexible consumption devices and the resulting search for the most cost-efficient solution to address the anticipated violations of grid constraints. The grid load of this scenario is presented in Figure 9 as the minimum and maximum power per day.
As for the shape of the graphs, they are comparable to the reference scenario 2022. However, the curves are significantly more pronounced, i.e., the maximum and minimum values are significantly increased. This, in turn, ensures a significantly more frequent and stronger violation of the grid parameters, as can be seen for the power line overload in Figure 10 and the voltage band in Figure 11.
In this subsection, the results for the solution alternative grid expansion are presented. First, the simulations for the year 2022 and then for the year 2050 are discussed. In the reference simulation 2022, line 0 emerged as the line with the highest load. Accordingly, only this line is initially reinforced via a parallel line. In this way, line overload can be avoided. After that, line 1, which connects grid nodes 1 and 2, proves to be the most loaded line. The maximum voltage increases at node 7 and is also reduced from 2.3% to 1.9%, although this is never in an impermissible range. The feed‑in and reference values are not affected, apart from slightly lower line losses. To install a cable along line 0, which has a length of 2.82 km, investment costs of 310,200 EUR are incurred according to the cost assumptions from section 4.1.2. Annualizing these costs over a service life of 40 years [86] results in annualized costs of 19,689 EUR. In addition, annual operating costs of 3,102 EUR arise, so in total additional annual costs of 22,790 EUR are to be expected to ensure grid stability in the MV grid under consideration for scenario 2022. By increasing the maximum feed‑in capacity it cannot be assumed that grid expansion costs in the HV and EHV grid can be avoided.
Since line 1 is the most heavily loaded line in the reference simulation of the 2050 scenario, it is reinforced in the first step, as shown in Figure 12 as an example. However, in this way, an overload occurs in line 0, so this line also must be reinforced. This means that line overload no longer occurs in the simulated reference grid. However, the voltage increase at node 7 on one day in summer is 4.7% and thus outside the permissible range. Therefore, additional reinforcement of line 9, which connects node 3 with node 8, takes place. This reduces the maximum voltage increase at node 7 to 4.3%, but the limit is still violated. Therefore, line 1, which is again the most loaded line in this case, is reinforced by another parallel line. In this way, all grid conditions can be met. Overall, lines 0, 1 and 9 will be reinforced, with line 1 being reinforced twice. This will result in investment costs of 1,425,600 EUR. Supplemented by the operating costs of 14,356 EUR, the grid expansion of the power lines results in additional annual costs of 104,739 EUR. This value is almost five times higher than the value for scenario 2022. The feed‑in capacity also increases in scenario 2050, so that there is no avoidance of expansion costs in the HV and EHV grid.
This section summarizes the results of the battery storage solution alternative. To ensure grid security in the scenario 2022, two storage positions are investigated. On the one hand, smaller storage systems are distributed and simulated across all grid nodes, and on the other hand, a central battery storage system is investigated. For the battery storage scenario 2022, it is shown that to fulfill the stability criteria within the grid area by means of distributed storage, a storage system with 0.15 MW power and 0.45 MWh storage capacity must be built at each grid node. For the central storage positioned at node 3, different dimensions are investigated until the storage system with the lowest cost is found that ensures grid stability. For this purpose, the storage is gradually reduced in size. A suitable storage dimensioning results in a power of 0.8 MW and a capacity of 2.4 MWh. A further reduction of the capacity or the power leads to the fact that the grid conditions are no longer fulfilled.
When comparing the battery storage alternatives for scenario 2022, the positioning of storage at node 3 is shown to be a better solution compared to the distributed storage plants, as significantly lower investment costs are incurred. This is particularly because the storage capacity and power required in the grid area are significantly lower than for distributed storage. At the same time, all relevant stability criteria are fulfilled by both alternatives, and the occurring losses are lower due to the smaller amount of stored electricity. This is particularly relevant because the electricity often must be drawn from the HV grid. This can be explained by the fact that there is rarely a power surplus in the grid area. The mentioned storage at node 3 causes investment costs of 816,000 EUR. Annualization and consideration of the operating costs of 20,400 EUR result in annual costs of 102,453 EUR. Assuming arbitrage trading, which exploits price differences, annual revenues of between 18,881 EUR and 31,469 EUR can be realized, depending on the cost scenario. In addition, annual costs of 76,032 EUR can be avoided by reducing the need for expansion in the HV grid because of the low purchase and feed-in capacities. If the costs are also examined under the cost assumptions for the year 2050, the values are slightly better, since the investment costs would, because of cost degression, be reduced to 424,000 EUR.
For the battery storage scenario 2050, it is shown that a single, centrally positioned storage cannot contribute to keeping the grid parameters within an acceptable range. This is true regardless of the positioning and dimensioning chosen. The storage cannot compensate for voltage fluctuations to the extent necessary to meet grid conditions. Therefore, a solution using distributed storage is developed for scenario 2050. If the storages are to be of the same size at each grid node, the power of the storage system would have to be 1.18 MW and the capacity 8 MWh. However, this is not the optimal solution in terms of cost, since the storage systems can be significantly smaller in some cases, or the storage systems at nodes 12 to 14 can be dispensed with completely. The technical parameters of the distributed storage systems are based on the power of the respective node, so that the power of the distributed storage systems is between 0.4 MW and 1.3 MW, and the capacity is between 1.2 MWh and 6.0 MWh. In this way, the grid parameters can be kept within the permissible limits using peak shaving. This storage configuration incurs an investment cost of 6,298,000 EUR, which can be annualized to an annual cost of 533,151 EUR. The annual operating costs amount to 157,450 EUR, resulting in total annual costs of 690,601 EUR. The storage systems allow arbitrage trading, which can generate annual revenues of between 180,899 EUR and 301,498 EUR. In addition, annual costs of 568,591 EUR are avoided in the HV and EHV grid.
This section presents the results of the alternative solution of hydrogen storage. In addition to the positioning at the grid node to the HV grid, the positioning at a central node within the grid area is also examined. For the hydrogen storage scenario 2022, it is shown that hydrogen storage is not to be considered useful, since only 29.7 MWh is fed into the HV grid, and almost all the 5,260 MWh fed into the MV grid is consumed at the time of generation. Under these circumstances, there are no generation surpluses in the summer months that can be stored, so seasonal hydrogen storage is not practical. Winter loads could indeed be mitigated somewhat by storing RES generated electricity in the summer. However, this would significantly increase the amount of power drawn from the HV grid in the summer months. Due to the low efficiency of hydrogen storage system, additional energy would be lost in this way. Therefore, the construction of a seasonal hydrogen storage system is not examined in detail in scenario 2022.
For the hydrogen storage scenario 2050, it is shown that positioning at the node to the HV grid does not make sense, since the grid parameters within the MV grid do not improve in this way. Instead, the hydrogen storage system must be positioned at a central node within the MV grid. By means of simulations (for methodology, see section 3.2), it is determined that node 8 is best suited for this, since a hydrogen storage system can be dimensioned smallest at this node. Larger storage systems would be needed at other nodes to meet grid parameters. The hydrogen storage system at node 8 must have an electrolysis capacity of 4.5 MW, a fuel cell capacity of 2.8 MW and a storage capacity of 3.5 GWh. This means that the grid parameters considered are kept within the permissible limits, so that security of supply is guaranteed.
The investment costs for this hydrogen storage system amount to 8,105,000 EUR. This results in annual costs of 1,039,636 EUR, of which 405,250 EUR is accounted for by operating costs. Annual revenues from the use of waste heat of 218,571 EUR can be realized. In addition, annual costs of 498,401 EUR are avoided in the HV and EHV grid. Arbitrage trading leads to additional costs between 11,243 EUR and 21,802 EUR due to the low efficiencies of the hydrogen storage system. Therefore, participation in arbitrage trading does not appear to make sense for the hydrogen storage system.
In this section, the results for the three scenarios considered are compared for 2022 and 2050. Scenario 2022 shows that the costs for grid expansion are significantly lower than for battery storage. However, a positive contribution margin for the battery storage system can be generated via additional revenues. At 310,200 EUR, the investment costs for the grid expansion solution are significantly lower than for the battery storage system, which requires 816,000 EUR. The operation of hydrogen storage system does not make sense in this scenario, as explained in section 5.5. The annual operating costs are 3,102 EUR for the grid expansion and 20,400 EUR for the battery storage system. This results in the lowest total annual costs of 22,790 EUR for the grid expansion, followed by the battery storage system with 102,453 EUR. This shows that state of the art storage systems incurs higher investment and operating costs to meet critical grid conditions than conventional grid expansion.
However, the battery storage system can be used for arbitrage trading and thus generate income and avoid costs for the expansion of the HV and EHV grid by balancing the grid supply and mitigating the feed‑in and feed‑out peaks. The revenue from arbitrage trading here depends on the electricity price scenario used, so that this is generated for the battery storage system for the low‑price scenario 18,881 EUR, for the mid‑price scenario 24,776 EUR and the high‑price scenario 31,469 EUR. The cost avoidance in the higher grid levels amounts to 76,032 EUR for the battery storage, so in this way the incurred costs of the battery storage are covered in most cost scenarios. In total, this results in annual costs of 22,790 EUR for the grid expansion, whereas the annual result of the battery storage is between −7,540 EUR and 5,048 EUR. Thus, battery storage represents an economic alternative to conventional grid expansion. In Table 7, the economic parameters of the solution alternatives are presented.
| Parameter | Grid expansion | Battery storage | Hydrogen storage | |
| Investment costs [EUR] | 310,200 | 816,000 | - | |
| Operating costs [EUR/a] | 3,102 | 20,400 | - | |
| Overall costs [EUR/a] | 22,790 | 102,453 | - | |
| Revenue arbitrage trading [EUR/a] | - | 18,881–31,469 | - | |
| Revenues from heat [EUR/a] | - | - | - | |
| Cost avoidance HS grid [EUR/a] | - | 76,032 | - | |
| Result [EUR/a] | −22,790 | −7,540–5,048 | - | |
For scenario 2050, the costs are again lowest for grid expansion, but the battery storage systems can be operated economically via additional revenue and cost avoidance. As in scenario 2022, the investment costs for grid expansion are the lowest at 1,425,600 EUR. This is followed by battery storage at 6,298,000 EUR and hydrogen storage at 8,105,000 EUR. This also affects the operating costs, which in the same order are 14,256 EUR, 157,450 EUR and 405,250 EUR. This results in annual costs of 104,739 EUR for the grid expansion, 690,601 EUR for battery storage and 1,039,636 EUR for hydrogen storage.
Revenue can be generated through arbitrage trading of the storage units, the avoidance of grid expansion at higher grid levels and the waste heat utilization of the hydrogen storage. For the solution alternative grid expansion, no grid expansion costs at higher levels can be avoided, leaving annual costs of 104,739 EUR for grid expansion in the MV grid. In the case of battery storage, it can be assumed that economic operation is possible for all cost scenarios. This is achieved through arbitrage revenues of 180,899 EUR to 301,498 EUR, depending on the price scenario, and the avoidance of grid expansion at higher grid levels of 568,591 EUR per year. Thus, the total result for battery storage is between 58,889 EUR and 179,488 EUR. Due to the low efficiencies of the hydrogen storage system, it incurs annual costs of 11,243 EUR to 21,802 EUR through arbitrage trading. However, there are annual revenues from the use of waste heat of 218,571 EUR, and the grid expansion avoidance at higher grid levels is monetized by 498,401 EUR per year. This leaves annual costs for hydrogen storage between 333,907 EUR and 344,466 EUR. Overall, it must be emphasized the advantage of storage for balancing consumption and generation. Its importance increases with the increasing penetration of RES and thus fluctuating power generation. Hydrogen storage is also a way to store surplus electricity in the summer months and reuse it in the high‑consumption winter months. In Table 8, the economic parameters of the solution alternatives in 2050 are presented.
| Parameter | Grid expansion | Battery storage | Hydrogen storage |
| Investment costs [EUR] | 1,425,600 | 6,298,000 | 8,105,000 |
| Operating costs [EUR/a] | 14,256 | 157,450 | 405,250 |
| Overall costs [EUR/a] | 104,739 | 690,601 | 1,039,636 |
| Revenue arbitrage trading [EUR/a] | - | 180,899–301,498 | −21,802–−11,243 |
| Revenues heat [EUR/a] | - | - | 218,571 |
| Cost avoidance HS grid [EUR/a] | - | 568,591 | 498,401 |
| Result [EUR/a] | −56,639 | 58,889–179,488 | −344,466–−333,907 |
In this work, different scenarios are simulated in two different configurations of a MV grid. These MV power grids were developed and published specifically for research into the economic, robust and environmentally friendly grid integration of distributed energy technologies. However, power grids represent a very complex system in which almost every MV grid has a different configuration and different connections to HV and LV grids. These interconnected higher and lower grid levels were not fully modeled in this work, which meant that interactions with them could not be considered in this work. Furthermore, the results are highly dependent on the framework and assumptions used. Therefore, this work considers profiles at high levels of aggregation and averages. These do not represent extreme scenarios, which means that further simulations are necessary to answer the question for these scenarios. RES deployment can also vary significantly by region within Germany. The modeling of generation capacities carried out here is based on average values and therefore, comparable to the grid topology, cannot be used to describe extreme scenarios.
Furthermore, this work is limited to the investigation of storage systems as an alternative to grid expansion. However, there are several other possibilities to reduce grid loads and thus contribute to a more cost-efficient solution. These include, for example, the regulation of generation surpluses or local energy markets. However, there are also several additional technical and regulatory alternatives. In most cases, combinations of the individual options are also implemented, which could not be depicted here due to the focus on storage systems. Furthermore, the grid parameters voltage band and thermal load capacity of the power lines were mainly investigated here. In the power grid, however, there are other technical constraints that could be included in the simulation. Therefore, this analysis is to be related to the technical challenges during RES expansion. To provide comparability of results, daily (battery storage) or seasonal (hydrogen storage) peak shaving was implemented for the storage systems. However, there are other algorithms for optimizing the feed-ins and feed-outs of the storage systems. In further work, it is therefore appropriate to perform a similar analysis on this trade-off, designing a control algorithm for the storages that produces the desired grid relief at the lowest possible cost.
This article has shown that storage systems need additional revenue sources to be economically superior to grid expansion. For this purpose, heat extraction, arbitrage and compensation of grid expansion in higher grid levels were used. This list is not exhaustive, which means that by incorporating further potentials, the storage plants should further improve economically. To date, no scientific basis exists to rank the additional revenue sources of storage. Other work may therefore reach different conclusions if different exogenous price time series and transmission projects are used as the economic basis. Also, if other revenue sources, such as power balancing services, are used, there could be discrepancies in the overall analysis. To ensure that the results presented here are robust, scenarios for these economic parameters were therefore used to show the sensitivities of the influences.
In this work, a techno-economic analysis of different storage systems as an alternative to classical grid expansion was carried out in a selected MV grid with representative RES data from Germany. The technical part of the analysis shows that both grid expansion and storage systems, when properly placed and sized, can ensure compliance with grid constraints and thus provide reliable supply at high penetration levels of RES. Based on scenarios investigated here, consisting of reference grids and selected consumers and generators, it could also be shown that grid expansion represents the cost‑optimal solution, provided that additional revenue potentials of storage systems are neglected. This corresponds to the results of the literature reviewed in chapter 1.2. However, most literature lacks in integrating additional revenue potentials. If heat extraction, the avoidance of grid expansion at higher grid levels, and arbitrage trading on the electricity market are integrated into the economic analysis, battery storage technologies are economically superior to grid expansion. The direct comparison of hydrogen storage and battery storage is one of the main contributions of this analysis. In both scenarios with low penetration and high penetration from RES, battery storage is economically superior to hydrogen storage. Grid expansion is more economical than hydrogen storage in any scenario. In the case of hydrogen storage, arbitrage trading is considered uneconomic since no positive contribution margin can be generated due to the low efficiencies. The present analysis has thus shown that it is economically preferable to replace grid expansion with battery storage. This contrasts with the literature review which states that battery storage is uneconomical to avoid grid expansion according to the state of the art. To achieve this, however, the regulation of the electricity grids must first be changed in such a way that there is no longer any obligation to expand the grid, but instead battery storage systems are encouraged to behave in a way that serves the grid, or grid operators are allowed to compensate for grid expansion with battery storage systems. Additional potential for the use of electricity storage systems must also be developed or permitted by regulation. Only when battery storage systems exploit their full potential, they can represent a more cost-efficient alternative to grid expansion and thus contribute to an economically efficient energy system. Without exploiting these use cases, the classic grid expansion is the cost‑efficient alternative.
The authors declare that there is no conflict of interest in publishing this paper.
Franz Teske handled the conception, structuring and methodology of the study, researched, supervised the research in its execution and wrote to all sections. Jano Schubert researched, performed simulations, and wrote on all sections of the paper. Adrian Fehrle supervised the research, handled the organization, and provided critical revision of the article. Felix Funk has critically revised the article and optimized the linguistic aspects. Jörg Franke supervised the research, provided critical revision of the article, and provided final approval of the version to be published.
| [1] |
A. M. Zaki, S. van Boheemen, T. M. Bestebroer, A. D. M. E. Osterhauset, R. A. M. Fouchier, Isolation of a novel coronavirus from a man with pneumonia in saudi arabia, N. Engl. J. Med., 367 (2012), 1814–1820. https://doi.org/10.1056/NEJMoa1211721 doi: 10.1056/NEJMoa1211721

|
| [2] |
A. M. Alnuqaydan, A. G. Almutary, A. Sukamaran, B. T. W. Yang, X. T. Lee, W. X. Lim, et al., Middle East Respiratory Syndrome (MERS) virus-pathophysiological axis and the current treatment strategies, AAPS PharmSciTech, 22 (2021), 173. https://doi.org/10.1208/s12249-021-02062-2 doi: 10.1208/s12249-021-02062-2

|
| [3] |
J. Lee, G. Chowell, E. Jung, A dynamic compartmental model for the Middle East respiratory syndrome outbreak in the Republic of Korea: A retrospective analysis on control interventions and superspreading events, J. Theor. Biol., 408 (2016), 118–126. https://doi.org/10.1016/j.jtbi.2016.08.009 doi: 10.1016/j.jtbi.2016.08.009

|
| [4] |
Q. Lin, A. P. Chiu, S. Zhao, D. He, Modeling the spread of Middle East respiratory syndrome coronavirus in Saudi Arabia, Stat. Methods Med. Res., 27 (2018), 1968–1978. https://doi.org/10.1177/0962280217746442 doi: 10.1177/0962280217746442

|
| [5] |
T. Sardar, I. Ghosh, X. Rodó, J. Chattopadhyay, A realistic two-strain model for MERS-CoV infection uncovers the high risk for epidemic propagation, PLoS Negl. Trop. Dis., 14 (2020), e0008065. https://doi.org/10.1371/journal.pntd.0008065 doi: 10.1371/journal.pntd.0008065

|
| [6] |
I. Ghosh, S. S. Nadim, J. Chattopadhyay, Zoonotic MERS-CoV transmission: Modeling, backward bifurcation and optimal control analysis, Nonlinear Dyn., 103 (2021), 2973–2992. https://doi.org/10.1007/s11071-021-06266-w doi: 10.1007/s11071-021-06266-w

|
| [7] |
K. S. Kim, K. Ejima, S. Iwanami, Y. Fujita, H. Ohashi, Y. Koizumi, et al., A quantitative model used to compare within host SARS-CoV-2, MERS-CoV, and SARS-CoV dynamics provides insights into the pathogenesis and treatment of SARS-CoV-2, PLoS Biol., 19 (2021), e3001128. https://doi.org/10.1371/journal.pbio.3001128 doi: 10.1371/journal.pbio.3001128

|
| [8] |
S. Tang, W. Ma, P. Bai, A novel dynamic model describing the spread of the MERS-CoV and the expression of dipeptidyl peptidase 4, Comput. Math. Methods Med., 2017 (2017), 5285810. https://doi.org/10.1155/2017/5285810 doi: 10.1155/2017/5285810

|
| [9] |
M. A. Nowak, C. R. M. Bangham, Population dynamics of immune responses to persistent viruses, Science, 272 (1996), 74–79. https://doi.org/10.1126/science.272.5258.74 doi: 10.1126/science.272.5258.74

|
| [10] |
A. U. Neumann, N. P. Lam, H. Dahari, D. R. Gretch, T. E. Wiley, T. J. Layden, et al., Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-α therapy, Science, 282 (1998), 103–107. https://doi.org/10.1126/science.282.5386.103 doi: 10.1126/science.282.5386.103

|
| [11] |
A. S. Perelson, P. W. Nelson, Mathematical analysis of HIV-1 dynamics in vivo, SIAM Rev., 41 (1999), 3–44. https://doi.org/10.1137/S0036144598335107 doi: 10.1137/S0036144598335107

|
| [12] |
T. Keyoumu, W. Ma, K. Guo, Existence of positive periodic solutions for a class of in-host MERS-CoV infection model with periodic coefficients, AIMS Math., 7 (2021), 3083–3096. https://doi.org/10.3934/math.2022171 doi: 10.3934/math.2022171

|
| [13] | R. E. Gaines, J. L. Mawhin, Coincidence Degree and Nonlinear Differential Equations, Springer-Verlag, Berlin, 1977. https://doi.org/10.1007/BFb0089537 |
| [14] |
C. Egami, Bifurcation analysis of the Nowak-Bangham model in CTL dynamics, Math. Biosci., 221 (2009), 33–42. https://doi.org/10.1016/j.mbs.2009.06.005 doi: 10.1016/j.mbs.2009.06.005

|
| [15] |
J. Pang, J. Cui, J. Hui, The importance of immune responses in a model of hepatitis B virus, Nonlinear Dyn., 67 (2012), 723–734. https://doi.org/10.1007/s11071-011-0022-6 doi: 10.1007/s11071-011-0022-6

|
| [16] |
F. Li, W. Ma, Z. Jiang, D. Li, Stability and Hopf bifurcation in a delayed HIV infection model with general incidence rate and immune impairment, Comput. Math. Method Med., 2015 (2015), 206205. https://doi.org/10.1155/2015/206205 doi: 10.1155/2015/206205

|
| [17] |
J. Li, K. Men, Y. Yang, D. Li, Dynamical analysis on a chronic hepatitis C virus infection model with immune response, J. Theoret. Biol., 365 (2015), 337–346. https://doi.org/10.1016/j.jtbi.2014.10.039 doi: 10.1016/j.jtbi.2014.10.039

|
| [18] |
A. M. Elaiw, N. H. AlShamrani, Stability of HIV/HTLV-I co-infection model with delays, Math Meth Appl Sci., 45 (2022), 238–300. https://doi.org/10.1002/mma.7775 doi: 10.1002/mma.7775

|
| [19] |
G. Li, Y. Fan, Y. Lai, T. Han, Z. Li, P. Zhou, et al., Coronavirus infections and immune responses, J. Med. Virol., 92 (2020), 424–432. https://doi.org/10.1002/jmv.25685 doi: 10.1002/jmv.25685

|
| [20] |
F. Chen, D. Sun, J. Shi, Periodicity in a food-limited population model with toxicants and state dependent delays, J. Math. Anal. Appl., 288 (2003), 136–146. https://doi.org/10.1016/S0022-247X(03)00586-9 doi: 10.1016/S0022-247X(03)00586-9

|
| [21] |
M. Fan, Y. Kuang, Dynamics of a nonautonomous predator-prey system with the Beddington-DeAngelis functional response, J. Math. Anal. Appl., 295 (2004), 15–39. https://doi.org/10.1016/j.jmaa.2004.02.038 doi: 10.1016/j.jmaa.2004.02.038

|
| [22] |
K. Zhao, Y. Li, Four positive periodic solutions to two species parasitical system with harvesting terms, Comput. Math. Appl., 59 (2010), 2703–2710. https://doi.org/10.1016/j.camwa.2010.01.038 doi: 10.1016/j.camwa.2010.01.038

|
| [23] |
A. Muhammadhaji, Z. Teng, Global attractivity of a periodic delayed N-species model of facultative mutualism, Discrete Dyn. Nat. Soc., 2013 (2013), 580185. https://doi.org/10.1155/2013/580185 doi: 10.1155/2013/580185

|
| [24] |
C. Celik, N. T. Ozarslan, Existence of periodic solution for a tumor growth model with vaccine interaction, Topol. Methods Nonlinear Anal., 55 (2020), 37–49. https://doi.org/10.12775/TMNA.2019.083 doi: 10.12775/TMNA.2019.083

|
| [25] |
K. Guo, K. Song, W. Ma, Existence of positive periodic solutions of a delayed periodic Microcystins degradation model with nonlinear functional responses, Appl. Math. Lett., 131 (2022), 108056. https://doi.org/10.1016/j.aml.2022.108056 doi: 10.1016/j.aml.2022.108056

|
| [26] |
J. Yang, R. Xu, H. Sun, Dynamics of a seasonal brucellosis disease model with nonlocal transmission and spatial diffusion, Commun. Nonlinear Sci. Numer. Simul., 94 (2021), 105551. https://doi.org/10.1016/j.cnsns.2020.105551 doi: 10.1016/j.cnsns.2020.105551

|
| [27] |
C. Li, J. Xu, J. Liu, Y. Zhou, The within-host viral kinetics of SARS-CoV-2, Math. Biosci. Eng., 17 (2020), 2853–2861. https://doi.org/10.3934/mbe.2020159 doi: 10.3934/mbe.2020159

|
| Scenario | Grid expansion | Battery storage | Hydrogen storage |
| 2022 | 4 | 79 | 3 |
| 2050 | 8 | 283 | 56 |
| 2022 | 2050 | |
| PV | 26% | 76% |
| Home storage | 2% | 29% |
| HP | 4% | 52% |
| EV | 0.6% | 39% |
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 140 | ||
| 4 | 3 | 500 | 260 | ||
| 5 | 1 | 1,300 | 1,950 | ||
| 6 | 2 | 700 | 240 | ||
| 7 | 2,200 | 1,360 | |||
| 8 | 1 | 900 | 350 | ||
| 9 | 900 | 440 | |||
| 10 | 1 | 1,000 | 3,100 | 150 | |
| 11 | 2 | 810 | 190 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 410 | ||
| 4 | 3 | 500 | 750 | ||
| 5 | 1 | 1,300 | 3,200 | ||
| 6 | 2 | 700 | 500 | ||
| 7 | 2,200 | 3,000 | |||
| 8 | 1 | 900 | 3,500 | ||
| 9 | 900 | 800 | |||
| 10 | 1 | 1,000 | 3,100 | 2,100 | |
| 11 | 2 | 810 | 550 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 120 | 300 | 2.5 | 15 | 90 |
| H2 electrolysis | 1,200 | 5 | 15 | 70 | |
| H2 fuel cell | 1,700 | 5 | 15 | 50 | |
| H2 storage | 6 | 5 | 30 | 100 | |
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 50 | 160 | 2.5 | 20 | 93 |
| H2 electrolysis | 650 | 5 | 20 | 75 | |
| H2 fuel cell | 600 | 5 | 20 | 55 | |
| H2 storage | 1 | 5 | 30 | 100 | |
| Parameter | Grid expansion | Battery storage | Hydrogen storage | |
| Investment costs [EUR] | 310,200 | 816,000 | - | |
| Operating costs [EUR/a] | 3,102 | 20,400 | - | |
| Overall costs [EUR/a] | 22,790 | 102,453 | - | |
| Revenue arbitrage trading [EUR/a] | - | 18,881–31,469 | - | |
| Revenues from heat [EUR/a] | - | - | - | |
| Cost avoidance HS grid [EUR/a] | - | 76,032 | - | |
| Result [EUR/a] | −22,790 | −7,540–5,048 | - | |
| Parameter | Grid expansion | Battery storage | Hydrogen storage |
| Investment costs [EUR] | 1,425,600 | 6,298,000 | 8,105,000 |
| Operating costs [EUR/a] | 14,256 | 157,450 | 405,250 |
| Overall costs [EUR/a] | 104,739 | 690,601 | 1,039,636 |
| Revenue arbitrage trading [EUR/a] | - | 180,899–301,498 | −21,802–−11,243 |
| Revenues heat [EUR/a] | - | - | 218,571 |
| Cost avoidance HS grid [EUR/a] | - | 568,591 | 498,401 |
| Result [EUR/a] | −56,639 | 58,889–179,488 | −344,466–−333,907 |
| Scenario | Grid expansion | Battery storage | Hydrogen storage |
| 2022 | 4 | 79 | 3 |
| 2050 | 8 | 283 | 56 |
| 2022 | 2050 | |
| PV | 26% | 76% |
| Home storage | 2% | 29% |
| HP | 4% | 52% |
| EV | 0.6% | 39% |
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 140 | ||
| 4 | 3 | 500 | 260 | ||
| 5 | 1 | 1,300 | 1,950 | ||
| 6 | 2 | 700 | 240 | ||
| 7 | 2,200 | 1,360 | |||
| 8 | 1 | 900 | 350 | ||
| 9 | 900 | 440 | |||
| 10 | 1 | 1,000 | 3,100 | 150 | |
| 11 | 2 | 810 | 190 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
| Node | LV grid(s) | BCS [MWh/a] | Industry [MWh/a] | PV [MW] | Wind [MW] |
| 1 | 1 | 600 | 1,500 | ||
| 2 | 3,600 | ||||
| 3 | 1 | 1,700 | 410 | ||
| 4 | 3 | 500 | 750 | ||
| 5 | 1 | 1,300 | 3,200 | ||
| 6 | 2 | 700 | 500 | ||
| 7 | 2,200 | 3,000 | |||
| 8 | 1 | 900 | 3,500 | ||
| 9 | 900 | 800 | |||
| 10 | 1 | 1,000 | 3,100 | 2,100 | |
| 11 | 2 | 810 | 550 | ||
| 12 | 2 | 1,600 | 1,800 | ||
| 13 | 830 | ||||
| 14 | 1 | 1,100 | 2,900 |
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 120 | 300 | 2.5 | 15 | 90 |
| H2 electrolysis | 1,200 | 5 | 15 | 70 | |
| H2 fuel cell | 1,700 | 5 | 15 | 50 | |
| H2 storage | 6 | 5 | 30 | 100 | |
| Component | Investment cost | Operating cost | Lifetime | Efficiency | |
| EUR/kW | EUR/kWh | %/a | a | % | |
| Battery storage | 50 | 160 | 2.5 | 20 | 93 |
| H2 electrolysis | 650 | 5 | 20 | 75 | |
| H2 fuel cell | 600 | 5 | 20 | 55 | |
| H2 storage | 1 | 5 | 30 | 100 | |
| Parameter | Grid expansion | Battery storage | Hydrogen storage | |
| Investment costs [EUR] | 310,200 | 816,000 | - | |
| Operating costs [EUR/a] | 3,102 | 20,400 | - | |
| Overall costs [EUR/a] | 22,790 | 102,453 | - | |
| Revenue arbitrage trading [EUR/a] | - | 18,881–31,469 | - | |
| Revenues from heat [EUR/a] | - | - | - | |
| Cost avoidance HS grid [EUR/a] | - | 76,032 | - | |
| Result [EUR/a] | −22,790 | −7,540–5,048 | - | |
| Parameter | Grid expansion | Battery storage | Hydrogen storage |
| Investment costs [EUR] | 1,425,600 | 6,298,000 | 8,105,000 |
| Operating costs [EUR/a] | 14,256 | 157,450 | 405,250 |
| Overall costs [EUR/a] | 104,739 | 690,601 | 1,039,636 |
| Revenue arbitrage trading [EUR/a] | - | 180,899–301,498 | −21,802–−11,243 |
| Revenues heat [EUR/a] | - | - | 218,571 |
| Cost avoidance HS grid [EUR/a] | - | 568,591 | 498,401 |
| Result [EUR/a] | −56,639 | 58,889–179,488 | −344,466–−333,907 |