Synchronization and chimera states in the network of electrochemically coupled memristive Rulkov neuron maps

1.   Introduction

The study of neural behaviors has become one of the hottest issues for many years ^[1]. Neurons are the fundamental parts of the brain's neural system ^[2]. Therefore, the investigation of these vital elements has not been limited to medicine, and many mathematical models have been introduced to study neuronal behavior and its structure. Some of these models are flow-based ^[3,4], and some others are map-based ^[5,6]. Recently, map-based neuronal models have received much attention due to their computational efficiency, flexibility, simplicity, and high speed ^[1,7].

A memristor is an electrical component that can describe the impacts of electromagnetic induction in neurons by coupling the membrane potential and the magnetic flux ^[8,9]. Therefore, some researchers have tried to present memristive neuronal models based on the original non-memristive ones ^[10,11]. For example, Usha and Subha ^[12] presented the memristive Hindmarsh-Rose neuronal model. Also, they have investigated the behavior of single and two coupled memristive Hindmarsh-Rose neurons. Hu and Liu ^[13] presented the memristive version of the well-known Hodgkin-Huxley neuronal model. Another example is the memristive map-based neuronal model, which was introduced by Li et al. ^[9]. Employing the Rulkov model, a two-dimensional map-based neuronal model, they introduced the m-Rulkov model. Besides, the idea of employing discrete memristors was also used by Bao et al. ^[14] and Li et al. ^[15]. In these studies, some memristor-based maps were introduced.

The investigation of the collective behaviors of neurons in a complex network is another exciting field of study ^[16,17]. A complex network of neurons can be constructed by two independent kinds of synapses, namely chemical and electrical synapses. In fact, these synapses, which can independently exist, are the pathways for transferring information among neurons ^[18]. Many researchers have explored the different behaviors of diverse neuronal models in an interacting network. For example, Sun and Cao ^[19] studied the synchronization states of two electrically coupled Rulkov maps. They announced that the Rulkov model cannot get completely synchronized through electrical synaptic couplings. However, Hu and Cao ^[20] revealed that two chemically coupled Rulkov maps can get synchronized completely. Moreover, Rakshit et al. ^[21] investigated the different behaviors of two coupled Rulkov neuronal models with both electrical and chemical synapses. They showed that a Rulkov map could be synchronized through electrical and chemical synapses, and the increments of chemical coupling strength can enhance the synchronization. Rulkov model, a two-dimensional map-based neuronal model, has been employed in many other studies. For instance, the effect of Gaussian noise on the collective behaviors of the Rulkov model in a $128\times 128$ grid network was studied by Perc ^[22]. In this study, the second derivative was considered to couple neighboring neurons. Another study conducted by Sun et al. ^[23] elaborated on the impact of noise correlation by adding Gaussian noise to the network of electrically coupled Rulkov models. They found a slight impact of noise correlation on the mean firing rate changes and a significant influence of noise intensity on population coherence. Also, Wang et al. ^[24] studied delay-induced synchronization to show the critical effect of delays in synchronization. This study employed the Rulkov model with additive Gaussian noise in a scale-free network of 200 nodes.

One of the essential collective behavior of neurons is synchronization ^[25]. Synchronization is a phenomenon or process that occurs in a network consisting of more than one dynamic unit in interaction ^[26,27]. This phenomenon is present everywhere in nature, and its traces can be observed in many fields, including biology ^[26]. For example, Fell and Axmacher ^[28] approved the leading role of synchronization in memory processes in the brain. Their study indicated that phase synchronization plays an essential role in both working memory and long-term memory. Also, as declared by Arnulfo et al. ^[29], phase synchronization is present in the human brain's cortex. More specifically, they found phase synchronization between the brain's regions in high frequencies by recording and studying local-field potential signals. Moreover, some other studies have shown the presence of synchronization and its prominent role in attention and cognition ^[30,31]. Also, some other researchers have discussed the relation of synchronization and some diseases like epilepsy ^[32] and Parkinson's ^[33].

Another important collective behavior in complex networks is the chimera state ^[34]. Chimera refers to the state in which some oscillators of the network are synchronous while others are asynchronous ^[35]. So, chimera can denote partial synchronization in complex networks ^[36,37]. Chimera was first observed in a network of phase oscillators ^[38]. However, this state has been found in chemical ^[39], electrical ^[40], neuronal ^[41,42,43] systems, etc. Chimeras are highly dependent on initial conditions ^[44] and the network's topology ^[45]. Moreover, different types of chimera, such as amplitude chimera ^[46], traveling chimera ^[47], chimera death ^[46], spiral wave chimera ^[48], etc., have been reported in the literature. For instance, traveling chimera is a phenomenon in which the displacement of coherent oscillators with a constant pace over time can be observed ^[34]. This phenomenon which was reported by Simo et al. ^[49], was observed in a network of Hindmarsh-Rose neuronal models. In another study conducted by Simo et al. ^[50], the emergence of traveling chimera was detected in a Hindmarsh-Rose neuron network under the electrical field.

As mentioned above, the collective behavior of two electrically, chemically, and electrochemically coupled non-memristive Rulkov models have been investigated. In this paper, the collective behavior of the memristive Rulkov model is investigated by considering two coupled m-Rulkov models and a network of 100 m-Rulkov models in a ring topology. In both conditions, the neurons are connected via electrical synapses, chemical synapses, and both of them. The effects of these synapses and their coupling strengths are under consideration. The paper is organized as follows: The m-Rulkov model and its network are described and detailed in Section 2. Section 3 presents the obtained results for different considered cases. The conclusion of the findings is declared in Section 4.

2.   Memristive Rulkov neuronal network

Rulkov model is basically a two-dimensional map-based neural model which was theoretically designed by Rulkov ^[5]. In this paper, the memristive version of the Rulkov map, which was presented by Li et al. ^[9], is employed. The m-Rulkov model is able to present different neuronal behaviors like spiking, bursting, etc., in different parameters' values and initial conditions. The discrete m-Rulkov model is described as follows:

where $x\left(n\right)$, $y\left(n\right)$, and $\varphi \left(n\right)$ are respectively the excitatory (represents action potential), recovery, and flux (represents electromagnetic induction) variables. Moreover, the term $\gamma \mathit{tanh}\left(\varphi \left(n\right)\right)x\left(n\right)$ denotes the electromagnetic induction impact on the excitatory variable with the strength of $\gamma$. In addition, $\varepsilon$ determines the time scale when electromotive force is generated, and $\mu$ is the control parameter. Also, the discontinuous nonlinear $F\left(x\left(n\right), y\left(n\right)\right)$ is defined as below:

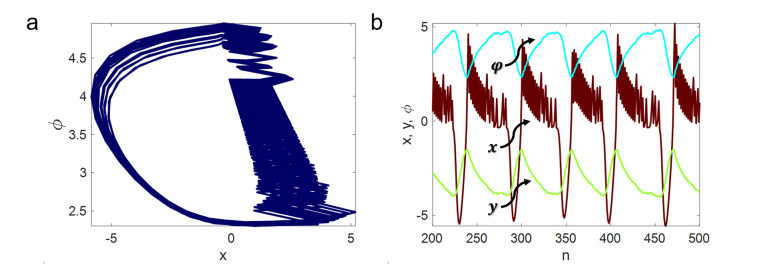
here, $\alpha$ is the control parameter. In fact, the $\alpha$ parameter determines the system regime in different conditions like resting, spiking or bursting. Considering $\alpha = 5, \mu = \varepsilon = 0.05,$ and $\gamma = 0.55$, the phase diagram and the time series of System (1) are shown in Fig. 1. The parameters are set in a way that the system exhibits chaotic bursting, as mentioned in ^[9]. The initial conditions are randomly selected for $x$ and $y$ variables in the range $\left[-1 ~~1\right]$ and the initial value of the $\varphi$ variable is set to zero.

Figure 1.  a) The phase diagram in the $x-\varphi$ plane and b) the time-series of $x$ (dark red), $y$ (green), and $\varphi$ (cyan) variables of System (1) for $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55$. In this set of parameters, the system shows chaotic bursting.

DownLoad: Full-Size Img PowerPoint

To investigate the behavior of the neuronal networks, the map-based memristive Rulkov is employed as the dynamical behavior of each node of the network. The general form of the neuronal network, considering both electrical and chemical synaptic coupling functions, can be formulated as follows:

where $ϵ\sum _{j = 1}^{N}{G}_{ij}^{1}f\left({x}_{j}\left(n\right), {y}_{j}\left(n\right)\right)$ denotes the electrical synaptic coupling with the strength of $ϵ$, and ${g}_{c}\left({v}_{s}-{x}_{i}\left(n\right)\right)\sum _{j = 1}^{N}{G}_{ij}^{2}\mathrm{\Gamma }\left({x}_{j}\left(n\right)\right)$ refers to the chemical synaptic coupling with the strength of ${g}_{c}$. Also, $\Gamma \left({x}_{j}\right) = \frac{1}{1+{e}^{\left(-\beta \left({x}_{j}-{\Theta }_{s}\right)\right)}} ~~~~$ and $f\left({x}_{i}\left(n\right), {y}_{i}\left(n\right)\right) = F\left({x}_{i}\left(n\right), {y}_{i}\left(n\right)\right)+\gamma \mathit{tanh}\left({\varphi }_{i}\left(n\right)\right){x}_{i}\left(n\right)$. The parameter ${v}_{s}$ is the synaptic reversal potential, ${\Theta }_{s}$ is the threshold of synaptic firing, and $\beta$ is the sigmoid slope. Note that the value of $d = {v}_{s}-{x}_{i}\left(n\right)$ can determine whether the synapse is excitatory or inhibitory. If $d>0$, the synapse is excitatory, otherwise the synapse is inhibitory. In this study, the parameter values are set at ${v}_{s} = {\Theta }_{s} = -1.4, ~~and~~\beta = 50$ as described in ^[21].

3.   Results

To study the synchronized behaviors of m-Rulkov models, we first consider $N = 2$, i.e., two coupled m-Rulkov maps. Then, considering $N = 100$, we study the different patterns of the network, including synchronization and chimera states. In both cases, the initial conditions are randomly selected between $-1$ to $1$, except the flux variables which are set to zero. In order to determine the synchronous state, the averaged synchronization error, as described in Eq (4), is employed as the synchronization criterion for the neurons' action potentials.

where $N$ is the number of network nodes, and $n$ is the number of samples for each node. Note that all results are obtained for $n = 1, \dots, 1000$, and the normalized values of error are presented.

3.1.   Two-coupled neurons

In this subsection, the synchronization of two coupled m-Rulkov models is investigated under different couplings with considering $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4,$and $\beta = 50$. As declared in ^[19], two non-memristive Rulkov models cannot get synchronized through the electrical synapses. However, using chemical synaptic couplings, they can be fully synchronized ^[20]. Moreover, considering electrochemical synapses, it was proved in ^[21] that two non-memristive Rulkov models could be synchronized. Here, firstly, the synchronization error of the action potential signal is calculated by assuming ${g}_{c} = 0$ for different electrical synaptic strengths ($ϵ$). The result is represented in Figure 2(a). Similarly, considering $ϵ = 0$, the synchronization error is calculated for different values of chemical synaptic strength (${g}_{c}$), which is shown in Figure 2(b). As represented in Figure 2(a), two coupled m-Rulkov models can be synchronized through electrical synapses for $0.3\le ϵ\le 0.5$. Similarly, Figure 2(b) indicates that two m-Rulkov models can be synchronized via chemical synapses for $0.36\le {g}_{c}\le 1$. However, in this range, the neurons reach an amplitude death state, not a synchronous oscillation. Therefore, in contrast to the result of coupled non-memristive Rulkov models ^[19], the network consisting of two memristive Rulkov models can get synchronized even without chemical synapses.

Figure 2.  Normalized synchronization error of two m-Rulkov models coupled via a) electrical and b) chemical synapses. The two coupled m-Rulkov models are able to be synchronized through each electrical or chemical synaptic couplings. The parameters are $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4, and~~\beta = 50$.

DownLoad: Full-Size Img PowerPoint

Then, the behavior of two coupled m-Rulkov maps is studied by calculating the normalized synchronization error considering the variation of both electrical ($ϵ$) and chemical (${g}_{c}$) strengths, which is shown in Figure 3. As demonstrated in Figure 3, two coupled m-Rulkov neurons can be synchronized in the presence of both electrical and chemical synapses. The dark blue regions in Figure 3 determine the states in which the neurons are synchronized, so the synchronization error is almost zero. Furthermore, by varying the electrical and chemical coupling strengths, i.e., $ϵ$ and ${g}_{c}$, different firing patterns can be observed, which are shown in Figure 4. As it can be seen in Figure 4, two coupled m-Rulkov models can be synchronized in different spiking, bursting, and resting states.

Figure 3.  Normalized synchronization error of two m-Rulkov models coupled via both electrical and chemical synapses. The two coupled m-Rulkov models are able to be synchronized through both electrical and chemical synaptic couplings. The parameters are $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4,$ and $\beta = 50$.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Different firing patterns of two coupled m-Rulkov neuronal models in synchronization state. Two coupled m-Rulkov maps can be synchronized through electrical, chemical, and both electrical and chemical couplings. The parameters are $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4, \beta = 50$ and a) $ϵ = 0.42$ and ${g}_{c} = 0$, b) $ϵ = 0.3$ and ${g}_{c} = 0.3$, c) $ϵ = 0.28$ and ${g}_{c} = 0.27$, d) $ϵ = 0.22$ and ${g}_{c} = 0.3$, e) $ϵ = 0.4$5 and ${g}_{c} = 0.5$, and f) $ϵ = 0.5$ and ${g}_{c} = 1$.

DownLoad: Full-Size Img PowerPoint

3.2.   N-coupled neurons

For deeper investigation, this section considers a ring network of 100 m-Rulkov models coupled via both electrical and chemical synapses to study the different collective behaviors of the memristive Rulkov model in a large network. Similar to the previous section, first, the effect of electrical synapses (assuming ${g}_{c} = 0$), then the effect of chemical synapses (assuming $ϵ = 0$), and finally, the effect of both electrical and chemical synapses are investigated. To this purpose, by setting $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4, and~~\beta = 50$, the synchronization error is calculated for each condition. More specifically, Figure 5(a), (b) respectively show the normalized synchronization error for electrical (${g}_{c} = 0$) and chemical ($ϵ = 0$) synapses.

Figure 5.  Normalized synchronization error of a ring of 100 m-Rulkov models coupled via a) electrical synapses and b) chemical synapses. The neurons are not able to be synchronized through electrical synaptic couplings. Furthermore, the zero error region in the chemical coupling case represents the amplitude death condition. The parameters are $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4,~~ and~~\beta = 50$.

DownLoad: Full-Size Img PowerPoint

According to Figure 5(a), the neurons cannot get synchronized when the coupling is only via electrical synapses. In the previous subsection, it was shown that the two coupled neurons could reach synchronization. While, for $N = 100$, increasing the electrical coupling leads to instability of the oscillators. Thus, it can be inferred that the synchronization of electrically coupled neurons depends on the number of neurons in the network. To represent this issue, Figure 6 is presented. This figure shows the parameter plane of the network corresponding to the variation of the coupling strength $ϵ$ and the network size ($N$). The yellow, green, dark magenta, and gray colors in this figure represent the regions of synchronization, amplitude death, asynchronization, and instability. In order to determine different regions, the synchronization error for the N electrically coupled m-Rulkov models is calculated. The asynchronous state is determined by non-zero errors, while zero error represents the synchronization and amplitude death regions. To distinguish synchronization state from amplitude death state, the difference between the mean of some of the last samples is calculated. Besides, in the instability region, the error is an undefined value. It is observed that synchronization is only possible in small networks. Furthermore, increasing the strength of the couplings in small networks leads to the neurons being unstable. As the number of the oscillators increases, by strengthening the electrical coupling, the network's behavior changes from asynchronization to instability.

Figure 6.  The regions of different behaviors of the ring network consisting of electrically coupled m-Rulkov neuron models in the parameter plane of the network's size and electrical coupling strength. The yellow, cyan, dark magenta, and gray regions indicate the synchronization state, amplitude death, asynchronous state, and neurons instability state, respectively. M-Rulkov neuron models cannot get synchronized as the network size increases.

DownLoad: Full-Size Img PowerPoint

When the neurons are coupled with chemical synapses, based on Figure 5(b), the error of synchrony becomes zero for $0.187\le {g}_{c}\le 0.712$. However, in this case, the pattern is amplitude death state, and the neurons reach a common resting state. In other words, after an asynchronous spike, all neurons stay in their resting state with no oscillation. Also, For ${g}_{c}>0.712$, the neurons become unstable.

Figure 7 represents the normalized synchronization error obtained for a specific interval of $ϵ$ and ${g}_{c}$, with assuming $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4, and~~\beta = 50$. In this figure, the dark blue regions represent the almost zero value of synchronization error. Nevertheless, similar to the chemical coupling in all of these conditions, the coupled neurons evolve into amplitude death, not synchronous firing.

Figure 7.  Normalized synchronization error of a ring of 100 coupled m-Rulkov models via both electrical and chemical synapses. One hundred coupled m-Rulkov maps cannot get synchronized through electrical couplings; however, in some chemical and both electrical and chemical coupling strengths, the synchronization error becomes zero since the neurons reach the resting state. The parameters are $\alpha = 5, \mu = \varepsilon = 0.05, \gamma = 0.55, {v}_{s} = {\Theta }_{s} = -1.4,$and $\beta = 50$.

DownLoad: Full-Size Img PowerPoint

3.2.1.   Chimera patterns

As mentioned above, assuming ${g}_{c} = 0$ or, in other words, with only considering electrical synapses, the neurons in large networks cannot get synchronized. However, in the asynchronous region, different patterns can be observed, some of which are shown in Figure 8. The figures represent the formation of the non-stationary chimera state since the position of asynchronous neurons changes in time. It can be seen that the increase in coupling strength $ϵ$ from $0.07$ (Figure 8(a)) to $0.11$ (Figure 8(b)) results in more asynchrony in the pattern. But further increments of $ϵ$ to $0.22$ leads to a more synchronous pattern. Although the neurons never get synchronized completely, they represent a sine-like synchronization state which can be seen in Figure 8(c). Note that for $ϵ>0.445$, the neuron gets unstable, and no complete synchronization can be observed.

Figure 8.  Different patterns (the spatiotemporal patterns (top panel) and snapshots (bottom panel)), observed in a network of 100 m-Rulkov neuronal models setting in a ring topology connected through electrical synapses (${g}_{c} = 0$) with the strength of a) $ϵ = 0.07$, b) $ϵ = 0.11$, and c) $ϵ = 0.22$. All snapshots are plotted in the last sample ($n = 1000$). Non-stationary chimera and sine-like synchronization states can be observed for some electrical coupling strengths.

DownLoad: Full-Size Img PowerPoint

To investigate the effect of the chemical synapses, $ϵ = 0$ is considered, and different behavior of the network is studied for different values of ${g}_{c}$. By varying ${g}_{c}$, two main patterns are observed, which are illustrated in Figure 9. For $0187\le {g}_{c}\le 712$, the neurons reach the same resting state as shown in Figure 9(a). Before this state, in some values of coupling strength ${g}_{c}$, the chimera patterns can be observed, as represented in Figure 9(b).

Figure 9.  Different patterns (the spatiotemporal patterns (top panel) and snapshots (bottom panel)), observed in a network of 100 m-Rulkov neuronal models setting in a ring topology connected through chemical synapses ($ϵ = 0$) with the strength of a) ${g}_{c} = 0.2$, and b) ${g}_{c} = 0.18$. The snapshots are plotted in the last sample ($n = 1000$). Amplitude death and chimera states can be observed for some chemical coupling strengths.

DownLoad: Full-Size Img PowerPoint

In the existence of both electrical and chemical synaptic couplings, more different patterns can be noticed. For instance, Figure 10 illustrates four different patterns of the network. Traveling chimera in $ϵ = 0.11$ and ${g}_{c} = 0.8$, and lagged-phase synchronization in $ϵ = 0.1$ and ${g}_{c} = 0.5$ are respectively represented in Figure 10(a), (b). Moreover, other patterns of chimera state are formed, which can have a different level of synchrony. More specifically, larger synchronous clusters can be seen in Figure 10(c), compared with the synchronous clusters in Figure 10(d). In other words, for $ϵ = 0.13$ and ${g}_{c} = 0.15$, more local neurons are synchronized in comparison with the number of locally synchronized neurons for $ϵ = 0.08$ and ${g}_{c} = 0.16$.

Figure 10.  Different patterns (the spatiotemporal patterns (top panel) and snapshots (bottom panel)), observed in a network of 100 m-Rulkov neuron models setting in a ring topology connected through electrical and chemical synapses with the strength of a) $ϵ = 0.11, {g}_{c} = 0.$8, b) $ϵ = 0.1, {g}_{c} = 0.5$, c) $ϵ = 0.13, {g}_{c} = 0.15$, and d) $ϵ = 0.08, {g}_{c} = 0.16$. The snapshots are respectively plotted in $n = 900$, $n = 850$, $n = 1000$, and $n = 1000$. Different chimera patterns and lagged-phase synchronization can be observed for some electrochemical coupling strengths.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

In the presented paper, different collective behaviors of the memristive version of the Rulkov map, namely, the m-Rulkov map were studied in two main parts. First, the synchronous behavior of two coupled m-Rulkov models was on the focus. Then, considering a network of 100 m-Rulkov models in the ring topology, different collective behaviors were explored. In both cases, the effects of each electrical synapse and chemical synapse, along with the effects of their simultaneous presence, were investigated. The results indicated that two coupled m-Rulkov maps could be synchronized through electrical synaptic coupling; while, as mentioned in ^[19], two electrically coupled non-memristive Rulkov neurons cannot get synchronized. Besides, similar to ^[20], two chemically coupled maps could reach the same resting state. In contrast, no other synchronous patterns were recognized through chemical synaptic couplings. Compared with the results expressed in ^[21], two coupled m-Rulkov neurons could be synchronized, and different synchronization patterns were noticed through electrical and chemical synapses. This synchronization was dependent on the size of the network and was only observed in small networks. Investigation on the ring network of 100 m-Rulkov models, by calculating the synchronization error, indicated that the neurons could not get synchronized via electrical synapses. Nevertheless, non-stationary chimera and sine-like synchronization have been found in electrically coupled neurons. Also, the neurons were attracted by the same fixed point when they were coupled through chemical synapses. However, some chimera patterns could also be found before reaching the resting state. In both cases, the neurons became unstable for high coupling strengths. The presence of both electrical and chemical synaptic couplings could lead to different collective behaviors such as traveling chimera, non-stationary chimera, lagged-phase synchronization, and amplitude death state.

Acknowledgments

This work is partially funded by Centre for Nonlinear Systems, Chennai Institute of Technology, India vide funding number CIT/CNS/2021/RD/064.

Conflict of interest

The authors declare that they have no conflict of interest.