Dynamics of a density-dependent predator-prey biological system with nonlinear impulsive control

1.   Introduction

Lotka-Volterra predator-prey system, which is one of the most successful models used to explain the interactions between two biological species in the early stage of biology. The Volterra principle shows that a disturbance to the predator-prey system (harvesting or killing part of the prey and predator population in proportion) will increase the average amount of the prey ^[1,2]. The classical Lotka-Volterra model assumes that the relative growth rate of two populations are linear functions, these assumption conditions are limited in describing the interaction of two species. Taking into account the saturation factor of the predator to the prey, based on the experiments and analysis, the ecologist C.S.Holling proposed three types of functional response functions adapted to different organisms in 1965 ^[3], which made the classical Lotka-Volterra system more realistic.

Lotka-Volterra model and its extended models are widely used in fishery resources, pest control and other fields ^{[4,5,6,7,8,9,10]}. The integrated pest management (IPM) ^{[11,12,13,14]}, which is based on the theoretical knowledge and experimental data of biological population dynamics, pesticide science, economics, combined with physical, chemical and biological technologies, is a dynamic management system. A series of integrated pest control models based on the Lotka-Volterra system can be used effectively for analyzing the changing laws of biological populations, discovering the advantages and disadvantages of treatment measures, and revealing biological principles for the pest management ^{[15,16,17,18,19,20,21]}. Tang and Chen developed the Lotka-Volterra model by introducing a proportion poisoning for the pests and releasing a constant number of predators at each impulsive event, and analyzed the impulsive differential system at fixed moments and unfixed moments respectively, which laid the foundation for the development of integrated pest control model ^[15]. In paper ^[21], the authors proposed a planar impulsive Holling II prey-predator model and provided a comprehensive qualitative analysis of global dynamics for whole parameter space.

In many previous IPM models, the number of natural enemies (predators) to be released at each impulsive event is a constant, the killing rate is proportional to the density of the pest population (preys) ^{[21,22,23,24,25,26,27,28,29]}, which means that the control strategy is not closely tied to the related observational data of predators and preys in the field. However, the implementation of control strategy should be closely combined with the data of biological population, economic threshold, and biological resources ^[30,31,32]. For example, the number of natural enemies to be released should be guided by the density of the current natural enemies. In addition, in the process of biological evolution, the predator will kill the prey to maintain the reproduction and continuation of the population, and the prey will also gradually form a set of anti-predator strategies to deal with foreign predators and self-defense ^[33,34]. Many experiments shows that some adult preys may attack vulnerable young predators ^[35,36]. Therefore, the anti-predator behavior should be reflected in the predator-prey models.

Actually, with the development of technology, the automation and intelligence of real-time monitoring and pre-warning system on insect pests provides convenience for observing the populations of the pests and the natural enemies, offers the basis for accurate and effective spraying of pesticides and releasing the natural enemies, and also provides a platform for the development and research of the IPM. Therefore, in order to study how the density dependent control actions affect the dynamic behavior of the biological system under the disturbance of external environment, we propose the following mathematical model:

where $x(t)$ and $y(t)$ represent the densities of the prey (pest) and predator populations (natural enemies), respectively. $a$ denotes the intrinsic growth rate of the prey, and the prey is hunted by the predator at a rate $bxy$. $\frac{cx}{1+\omega x}$ denotes Holling II functional response function, and the digestibility of the predator to the prey gradually slows down with the increase of the density of the prey. The anti-predator behavior is reflected in $qxy$, i.e., the prey also attack the predator to improve the chances of survival, and the predator declines at a rate $dy$ ^{[16,17,27,37]}.

Throughout this paper we assume that the initial density of the pest population is less than the economic threshold $E_T$, i.e., $x(0^+) < E_T$, and the initial densities of the natural enemy populations $y(0^+) > 0$. If the pest's population density reaches the economic threshold $E_T$ at time $t$, then controlling strategies are applied immediately and the numbers of the pest and its natural enemy are updated to $(1-\frac{\delta x(t)}{x(t)+\beta})x(t)$ and $y(t)+\frac{\tau}{1+\theta y(t)}$ (i.e., $x(t^+)$ and $y(t^+)$), respectively. The third and fourth equations reflect the density dependence of the implementation of the control strategy, $\delta > 0$ is the maximal killing rate and $\beta > 0$ denotes the half saturation constant. We employ a nonlinear releasing term $\frac{\tau}{1+\theta y(t)}$ to describe the releasing strategy, which is a decreasing function of $y(t)$, thus $\tau > 0$ is the maximum number of the predator released, and $\theta > 0$ is a shape parameter.

The main purpose of the paper is to investigate the global dynamical behavior of the density dependent nonlinear control model (1.1) and to reveal that how the main parameters of the model (1.1) affect the dynamics of the system. In Section 2, we first analyze the exact impulsive sets and the exact phase sets of system (1.1), the analytical expression of the Poincaré map is defined, and the properties of Poincaré map have been discussed in more detail. Moreover, in Section 3, the existence, stability and uniqueness of order-1 periodic solution, and the existence of order-$k$ ($k\geq 2$) periodic solution will be addressed. Finally, the theoretical conclusions and biological significance are presented.

2.   Analytical formula and properties for the Poincaré map

In order to discuss the effect of impulsive control strategies on the dynamic behavior of prey and predator populations, we need some preliminary knowledge of system (1.1) without any impulses, i.e., the corresponding ordinary differential equation (ODE) model of (1.1) should be analyzed. Many scholars have studied this ODE model, improved and extended the ODE model by taking into more realistic factors, which have been applied in many domains, such as control of insect pests, treatment of immunogenic tumours and HIV virus-guided therapy ^{[27,37,38,39,40,41]}.

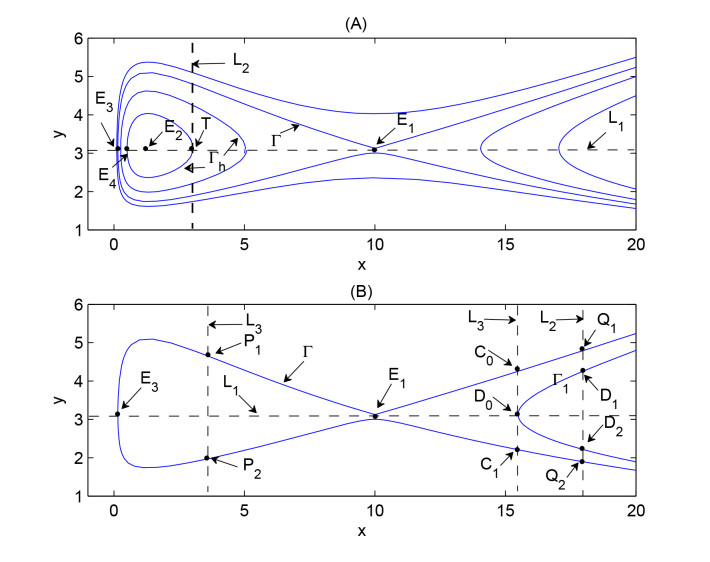
The main results of model (1.1) without any impulses that we will use are as follows, and the primary trend of solution trajectories, useful points and lines are as shown in Figure 1.

(1) There is a trivial equilibrium $O(0, 0)$; If the inequalities $c-q-d\omega > 0$, $(c-q-d\omega)^2 > 4qd\omega$ hold, then there are two interior equilibria: $E_1(x_1^\ast, y_1^\ast)$ is a saddle point, $E_2(x_2^\ast, y_2^\ast)$ is a center. Note that $x_i^\ast(i = 1, 2)$ is the roots of the equation $q\omega x^2+(q-c+d\omega)x+d = 0$, $y_i^\ast = \frac{a}{b}$;

(2) The family of closed orbits is

where $h_i = a{\rm ln}(\frac{ae^{-1}}{b})-\frac{c}{\omega}{\rm ln}(1+\omega x_i^\ast)+d{\rm ln}x_i^\ast+qx_i^\ast, i = 1, 2;$ $\Gamma_h$ converts to the homoclinic cycle (denoted by $\Gamma$) as $h\rightarrow h_1$; $\Gamma_h$ converges to the equilibrium $E_2(x_2^\ast, y_2^\ast)$ as $h\rightarrow h_2$.

(3) Denote the point $E_3(x_3^\ast, y_3^\ast)$ as the left intersection point of the homoclinic cycle $\Gamma$ with the line $y = \frac{a}{b}$ (denoted by $L_1$). Point $E_2$ is located in inside of the trajectory $\Gamma_h$, which is denoted by $E_2$$\in$ Int$\Gamma_h$, the right side of $\Gamma_h$ is tangent to the line $x = E_T$ (denoted by $L_2)$ at point $T(E_T, \frac{a}{b})$, and the left side of $\Gamma_h$ meets the line $L_1$ at point $E_4(x_4^\ast, y_4^\ast)$, as shown in Figure 1(A).

(4) The first integral is

where $h$ is a constant.

To investigate the dynamics of system (1.1), we need to know whether the trajectories of the system (1.1) reach the impulsive set or not, and if the trajectories reach the impulsive set, whether the system (1.1) exists periodic solutions. Firstly we will discuss the domains of the impulsive set and phase set, which provide a basis for defining the Poincaré map.

2.1.   Impulsive set

From the first equation of system (1.1) we know that there exists a isocline $L_1$: $y = \frac{a}{b}$, which means that $[0, \frac{a}{b}]$ is the maximum interval for the vertical components of impulsive set, and any solution of system (1.1) either can't arrive at $L_2$ or reaches $L_2$ and the lower intersection point is located at or below point $(E_T, \frac{a}{b})$. Therefore, the basic impulsive set $\mathcal{M}$ can be determined as follows:

According to the impulsive function $I: (E_T, y)\in\mathcal{M}\rightarrow (x^+, y^+) = \left((1-\frac{\delta E_T}{E_T+\beta})E_T, y+\frac{\tau}{1+\theta y}\right)$, the phase set $\mathcal{N}$ which corresponding to the basic impulsive set $\mathcal{M}$ is:

where $Y_{\mathcal{M}} = \{y^+\mid\ y^+ = y+\frac{\tau}{1+\theta y}, 0\leq y\leq \frac{a}{b}\}$.

Base on the value of economic threshold $E_T$ and the position of line $x = \left(1-\frac{\delta E_T}{E_T+\beta}\right)E_T$ (denoted by $L_3$, as shown in Figure 1(B)) where the phase set is located on, we will obtain the conclusions about the exact domains of the impulsive set for the following different cases:

where $P_{E_T} = \frac{\delta E_T}{E_T+\beta}.$

Moreover, the Lambert W function ^[42] and three quantities $A_0$, $A_1$ and $A_2$ are useful throughout the analysis of impulsive set and phase set. For ease of discussion, we denote the Lambert W function by W, and $A_0$, $A_1$ and $A_2$ are defined as

Lemma 2.1. The corresponding impulsive sets of the system (1.1) in different cases are as follows:

$(A): \mathcal M_2,$ $(B): \left\{\begin{array}{l} (B_{11}): \mathcal M_2, \\ (B_{12}): \mathcal M, \end{array}\right.$ $(C): \left\{\begin{array}{l} (C_{11}): \mathcal M_1, \\ (C_{12}): \mathcal M_2, \\ (C_{13}): \mathcal M_2, \end{array}\right.$

where

and

Proof. Firstly, for case $(C)(C_{11})$, i.e., $E_T\geq x_1^*$ and $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, according to the trend of solution trajectory of (1.1), it is easy to know that the right branch of homoclinic cycle $\Gamma$ intersects with line $L_2$ at two points $Q_1$ and $Q_2$, as shown in Figure 1(B). The vertical components of $Q_1$ and $Q_2$ can be solved by the first integral (2.2).

Any solution initiating from the initial point $(x_0, y_0)$ satisfies the following equation:

where $h_0 = a{\rm {\rm ln}}y_0-by_0-\frac{c}{\omega}{\rm ln}(1+\omega x_0)+d{\rm ln}x_0+qx_0$.

Thus, the equation of homoclinic cycle which crosses the point $(x_1^\ast, \frac{a}{b})$ can be determined as:

Substituting $x = E_T$ into Eq 2.8 yields

i.e., $a{\rm {\rm ln}}y-by = a{\rm ln}\frac{a}{b}-a-A_0$. Solving Eq 2.9 with respect to $y$, the solutions of Eq 2.9 are the vertical components of points $Q_i\; (i = 1, 2)$.

By using some properties of the Lambert W function, if $A_0\geq0$, then the roots of (2.9) are as follows:

therefore, the intersection points of $\Gamma$ and $L_2$ are $Q_1(E_T, Y_{Is})$ and $Q_2(E_T, Y_{is})$. It is easy to know that if $E_T\geq x_1^*$, $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, then any solution starting from $(x_0^+, y_0^+)\in\mathcal{N}$ either can't reach $L_2$ or arrives at the basic impulsive set $\mathcal{M}$ and the intersection point is located at or below the point $Q_2$, which means that the exact domain of the impulsive set for case $(C)(C_{11})$ is $\mathcal M_1 = \{(x, y)\in R_+^2\mid x = E_T, 0\leq y\leq Y_{is}\}$.

Next, we will discuss the case $(C)(C_{12})$. As shown in Figure 1(B), if $(1-P_{E_T})E_T > x_1^*$, then there is a orbit $\Gamma_1$ which tangents to the line $L_3$, the coordinates of the tangent point (denoted by $D_0$) are $((1-P_{E_T})E_T, \frac{a}{b})$, and $\Gamma_1$ intersects $L_2$ at two points $D_1, D_2$. By the similar method used for case $(C)(C_{11})$, we can obtain the vertical components of points $D_1$ and $D_2$. Substituting the point $((1-P_{E_T})E_T, \frac{a}{b})$ into Eq 2.7 yields the equation of orbital curve which crosses point $D_0$:

If $A_1 < 0$, then letting $x = E_T$ and solve Eq 2.11 with respect to $y$, we have

Therefore, the intersection points of $\Gamma_1$ and $L_2$ are $D_1(E_T, Y_{IS}^1)$ and $D_2(E_T, Y_{is}^1)$. If $E_T\geq x_1^*$ and $(1-P_{E_T})E_T > x_1^*$, then any solution starting from $(x_0^+, y_0^+)\in\mathcal{N}$ arrives at the basic impulsive set $\mathcal{M}$ and the intersection point is located at or below the point $D_2$, and then the exact domain of impulsive set for case $(C)(C_{12})$ is $\mathcal M_2 = \{(x, y)\in R_+^2\mid x = E_T, 0\leq y \leq Y_{is}^1\}$.

For case $(A), (B)(B_{11}), (C)(C_{13})$, according to the vector field of system (1.1), it's easy to know that there exists an orbital curve tangents to the line $L_3$, and this orbital curve intersects $L_2$ at two points $D_1$ and $D_2$. Therefore, by taking advantage of the similar method, all of the impulsive sets for these cases are $\mathcal M_2$.

Finally, for case $(B)(B_{12})$. If $x_2^* < E_T < x_1^*$ and $(1-P_{E_T})E_T > x_4^*$, then the closed orbit $\Gamma_h$ intersects with $L_3$ at two points, tangents to the line $L_2$ at the point $T(E_T, \frac{a}{b})$, and any solution starting from the phase set can reach the set $\{(x, y)|x = E_T, 0\leq y\leq\frac{a}{b}\}$. Therefore, the impulsive set of system (1.1) for this case is $\mathcal M$. This completes the proof.

Due to the nonlinear term and the diversity of threshold $E_T$ of system (1.1), the dynamic behavior of system (1.1) might be very complex, next we will focus on two representative cases $(C)(C_{11})$ and $(C)(C_{12})$ for a comprehensive analysis.

2.2.   Phase set

In order to discuss the exact domains of the phase set of the system (1.1), it is necessary to ensure the conditions under which the trajectory starting from $(x_0^+, y_0^+)\in\mathcal{N}$ is free from pulse effects. By analyzing the dynamics of trajectories, the conclusions can be obtained as follows.

Lemma 2.2. For case $(C)(C_{11})$, any solution starting from the point $(x_0^+, y_0^+)\in\mathcal{N}$ with $y_0^+\in[Y_{\rm min}, Y_{\rm max}]$ will be free from pulse effects, where

Moreover, $x_3^* < (1-P_{E_T})E_T < x_1^*$ $\Leftrightarrow$ $A_2 > 0$; If $(1-P_{E_T})E_T = x_1^*$ or $(1-P_{E_T})E_T = x_3^*$, then $A_2 = 0$.

Proof. If $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, then the homoclinic cycle $\Gamma$ intersects with line $L_3$. Substituting $x = (1-P_{E_T})E_T$ into Eq 2.8 yields

i.e.,

Note that if $A_2\geq0$, then Eq 2.15 with respect to $y$ can be solved. Next we will discuss the value of $A_2$. Denote $A(x) = \frac{c}{\omega}{\rm ln}\left(\frac{1+\omega x_1^\ast}{1+\omega x}\right)-d{\rm ln}\left(\frac{x_1^\ast}{x}\right)-q(x_1^\ast-x)$, then $A_2 = A((1-P_{E_T})E_T)$. Due to the left intersection point of $\Gamma$ and $L_1$ is $E_3(x_3^\ast, \frac{a}{b})$, then substituting the coordinates of $E_3$ into Eq 2.8 yields $A(x_3^\ast) = A(x_1^\ast) = 0$. Moreover, solving $A'(x) = 0$ with respect to $x$, we have $x = x_1^\ast$ and $x = x_2^\ast$, which means that the abscissa of two interior equilibrium satisfy the equation, i.e., $A'(x_1^\ast) = A'(x_2^\ast) = 0$. Note that ${\lim_{x \to 0^+}} A(x) = -\infty$, base on the monotonicity and continuity of the function $A(x), x\in(0, +\infty)$, we can obtain that $A(x) > 0$ for $x\in(x_3^\ast, x_1^\ast)\cup(x_1^\ast, +\infty)$. Therefore, for case $(C)(C_{11})$, if $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, then $A_2\geq0$. The two roots of Eq (2.15) with respect to $y$ are as follows:

As shown in Figure 1(B), if $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, then the intersection points of homoclinic cycle $\Gamma$ and $L_3$ are $P_1 = ((1-P_{E_T})E_T, Y_{\max})$ and $P_2 = ((1-P_{E_T})E_T, Y_{\min})$. Any solution initiating from the point $(x_0^+, y_0^+)$ ($y_0^+\in[Y_{\rm min}, Y_{\rm max}]$) will not reach at the impulsive set $\mathcal M_1$, on the contrary, any solution initiating from the set $(x_0^+, y_0^+)$ ($y_0^+\in Y_0 = [0, Y_{\rm min})\cup(Y_{\rm max}, +\infty)$) can arrive at the impulsive set $\mathcal M_1$ and then experiences impulsive effects.

If $(1-P_{E_T})E_T\in (x _3^*, x_1^*)$, then $A_2 = A((1-P_{E_T})E_T) > 0$; Conversely, $(1-P_{E_T})E_T\in (x _3^*, x_1^*)$ once $A_2 > 0$. If $(1-P_{E_T})E_T = x_1^*$ or $(1-P_{E_T})E_T = x_3^*$, then $A_2 = 0$. This completes the proof.

Next, we will discuss the exact phase sets for case $(C)(C_{11})$ and $(C)(C_{12})$, respectively. First of all, it is necessary to analyze the properties of impulsive function $y(t^+) = y(t)+\frac{\tau}{1+\theta y(t)}$. Obviously, the monotonicity of function $y(t^+)$ is related to the value of $y(t)$. Letting $F(y) = y+\frac{\tau}{1+\theta y}$, $y\in[0, \frac{a}{b}]$, it is easy to know $F'(y) = 0$ at $y = \frac{\sqrt{\tau\theta}-1}{\theta}$. In view of $\theta > 0$, we know that if $\frac{\sqrt{\tau\theta}-1}{\theta}\leq0$, i.e., $\sqrt{\tau\theta}-1\leq0$, then $F'(y)\geq0$ for $y\in[0, +\infty)$; If $\sqrt{\tau\theta}-1 > 0$, then $F'(y)\leq0$ for $y\in[0, \frac{\sqrt{\tau\theta}-1}{\theta}]$ and $F'(y) > 0$ for $y\in[\frac{\sqrt{\tau\theta}-1}{\theta}, +\infty)$.

For case $(C)(C_{11})$, we can discuss the exact domains of the phase sets for three cases: $(\rm i)$ $\sqrt{\tau\theta}-1\leq0$; $(\rm ii)$ $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}$; $(\rm iii)$ $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$.

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then the impulsive function $F(y)$ is increasing on $[0, Y_{is}]$, $F(y)\in\left[\tau, Y_{is}+\frac{\tau}{1+\theta Y_{is}}\right]$, denote $Y_{11} = \left[\tau, Y_{is}+\frac{\tau}{1+\theta Y_{is}}\right]$. As any solution initiating from $(x_0^+, y_0^+)$ ($y_0^+\in[Y_{\rm min}, Y_{\rm max}]$) can not arrive at the impulsive set $\mathcal M_1$, the phase set which corresponds to the impulsive set $\mathcal M_1$ is

where $Y_{11}^0 = Y_{11}\cap Y_0$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}$, then the impulsive function $F(y)$ is decreasing on $[0, Y_{is}]$, and $F(y)\in\left[Y_{is}+\frac{\tau}{1+\theta Y_{is}}, \tau\right]$, denote $Y_{12} = \left[Y_{is}+\frac{\tau}{1+\theta Y_{is}}, \tau\right]$. It is similar to the case $(\rm i)$, any solution initiating from $(x_0^+, y_0^+)$ ($y_0^+\in[Y_{\rm min}, Y_{\rm max}]$) can not arrive at the impulsive set $\mathcal M_1$, then the phase set which corresponds to the impulsive set $\mathcal M_1$ is

where $Y_{12}^0 = Y_{12}\cap Y_0$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$, then according to the monotonicity of the impulsive function $F(y)$, we can show that $F'(y)\leq0$, $F(y)\in\left[\frac{2\sqrt{\tau\theta}-1}{\theta}, \tau\right]$ for all $y\in[0, \frac{\sqrt{\tau\theta}-1}{\theta}]$, and $F'(y) > 0$, $F(y)\in(\frac{2\sqrt{\tau\theta}-1}{\theta}, Y_{is}+\frac{\tau}{1+Y_{is}\theta}]$ for all $y\in(\frac{\sqrt{\tau\theta}-1}{\theta}, Y_{is}]$. Denote $Y_{13} = \left[\frac{2\sqrt{\tau\theta}-1}{\theta}, \tau\right]$, $Y_{13}^0 = Y_{13}\cap Y_0$, $Y_{14} = \left(\frac{2\sqrt{\tau\theta}-1}{\theta}, Y_{is}+\frac{\tau}{1+Y_{is}\theta}\right]$ and $Y_{14}^0 = Y_{14}\cap Y_0$. The phase set which corresponds to the impulsive set $\mathcal M_1$ = $\mathcal M_{11}\cup\mathcal M_{12}$ is $\mathcal N_{13}\cup\mathcal N_{14}$, where

For case $(C)(C_{12})$, if $(1-P_{E_T})E_T > x_1^*$, then $\Gamma$ intersects with $L_3$ at two points, in order to distinguish this case from case $(C)(C_{11})$, these two intersection points denoted by $C_0(x_{C_0}, y_{C_0}) = ((1-P_{E_T})E_T, Y_{\rm max})$ and $C_1(x_{C_1}, y_{C_1}) = ((1-P_{E_T})E_T, Y_{\rm min})$. Considering the characteristics of the homoclinic cycle $\Gamma$, the trajectory which initiating from $C_0$ will be close to the point $E_1$ infinitely, but not reach the impulsive set $\mathcal M_2$. By the similar method used in case $(C)(C_{11})$, we can discuss the exact phase sets for the following three cases: $(\rm i)$ $\sqrt{\tau\theta}-1\leq0$; $(\rm ii)$ $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}^1$; $(\rm iii)$ $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$.

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then the impulsive function $F(y)$ is increasing on $[0, Y_{is}^1]$, and $F(y)\in\left[\tau, Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}\right]$, denote $Y_{21} = \left[\tau, Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}\right]$. As the solution initiating from $C_0$ will not reach the impulsive set $\mathcal M_2$, the phase set which corresponds to the impulsive set $\mathcal M_2$ is

where $Y_{21}^0 = \left\{y^+|\tau \leq y^+\leq Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}, y^+\neq Y_{\rm max}\right\}$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}^1$, then the impulsive function $F(y)$ is decreasing on $[0, Y_{is}^1)$, and $F(y)\in\left[Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}, \tau \right]$, denote $Y_{22} = \left[Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}, \tau \right]$. The phase set which corresponds to the impulsive set $\mathcal M_2$ is

where $Y_{22}^0 = \left\{{y^+| Y_{is}^1+ \frac{\tau}{1+\theta Y_{is}^1}}\right. \left.{\leq y^+\leq\tau, y^+\neq Y_{\rm max}}\right\}$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, then on the basis of the monotonicity of $F(y)$, it is easy to know $F(y)\in\left[\frac{2\sqrt{\tau\theta}-1}{\theta}, \tau\right]$ for all $y\in[0, \frac{\sqrt{\tau\theta}-1}{\theta}]$, and $F(y)\in\left(\frac{2\sqrt{\tau\theta}-1}{\theta}, Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}\right]$ for all $y\in(\frac{\sqrt{\tau\theta}-1}{\theta}, Y_{is}^1]$. Denote $Y_{23}^0 = \left\{y^+| \frac{2\sqrt{\tau\theta}-1}{\theta} \leq y^+\leq\tau, y^+\neq Y_{\rm max}\right\}$ and $Y_{24}^0 = \left\{{y^+| \frac{2\sqrt{\tau\theta}-1}{\theta} < y^+\leq Y_{is}^1+\frac{\tau}{1+\theta Y_{is}^1}, y^+\neq }\right. \left.{Y_{\rm max}}\right\}$. The phase set which corresponds to the impulsive set $\mathcal M_2$ = $\mathcal M_{11}\cup\mathcal M_{21}$ is $\mathcal N_{23}\cup\mathcal N_{24}$, where

In conclusion, we list all the exact domains of the impulsive sets and phase sets in different parameter spaces for case $(C)(C_{11})$ and $(C)(C_{12})$ in Table 1, it can be seen that the changes of key parameters such as economic threshold ET affect the dynamic behaviors of the system (1.1).

2.3.   Poincaré map

Base on the impulsive sets and phase sets we discussed above, the main theorems of Poincaré map can be obtained.

Theorem 1. The Poincaré map of model (1.1) for cases $(C)(C_{11})$ and $(C)(C_{12})$ can be defined as:

Case$(C)(C_{11})$ : $E_T\geq x_1^*$, $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$

Case$(C)(C_{12})$: $E_T\geq x_1^*$, $(1-P_{E_T})E_T > x_1^*.$

Where

Proof. Assuming that any solution initiating from $z_0^+ = (x_0^+, y_0^+)\in\mathcal{N}$ will experience finite or infinite pulse effects. Denote $p_i = (E_T, y_i)\in\mathcal{M}$, and $p_i^+ = ((1-P_{E_T})E_T, y_i^+)\in\mathcal{N}$, $(i = 1, 2, 3\cdots)$, $p_i^+$ is the point which corresponds to $p_i$ in the phase set after a pulse effect. If $p_i^+$ and $p_{i+1}$ lie in the same trajectory, then the corresponding coordinates of these two points satisfy the following equation:

For case $(C)(C_{11})$, from the analysis of Lemma 2.2 we know that if the initial point $p_0^+ = ((1-P_{E_T})E_T, y_0^+)$ lies on the homoclinic cycle $\Gamma$ or in the interior of $\Gamma$, the trajectory starting from $p_0^+$ will not arrive at the impulsive set $\mathcal M_1$, and we can see $A_2\geq0$ for $x_3^\ast\leq(1-P_{E_T})E_T\leq x_1^\ast$. Moreover, for case $(C)(C_{12})$, the trajectory initiating from $C_0$ can not arrive at $\mathcal M_2$, and $A_1 < 0$ for $(1-P_{E_T})E_T > x_1^\ast$ holds.

Next, we rearrange (2.19) yields

By using the properties of the Lambert W function, we can solve the Eq 2.20 with respect to $y_{i+1}$:

Therefore, we have

Note that the analytical formula of $\mathcal {P}(y_i^+)$ is related to the Lambert W function, according to the definition of the Lambert W function, the analytical equation of $\mathcal {P}(y_i^+)$ can be analysed as follows.

For $A_1\leq0$, it is easy to know $-\frac{b}{a}y_i^+{\rm exp}(-\frac{b}{a}y_i^+ +\frac{A_1}{a})\in[-e^{-1}, 0)$, and the Eq 2.22 is well defined. From Eq 2.12 we know that $A_1 < 0$ for case $(C)(C_{12})$. Therefore, Eq 2.17 is true for different value range of $\frac{\sqrt{\tau\theta}-1}{\theta}$.

For $A_1 > 0$, we need to ensure that $-\frac{b}{a}y_i^+{\rm exp}(-\frac{b}{a}y_i^+ +\frac{A_1}{a})\geq-e^{-1}$, i.e., the following inequality holds:

By employing the properties of Lambert W function, it is easy to know that the inequality (2.23) holds for $y_i^+\in(0, Y_{\rm min}^1]\cup[Y_{\rm max}^1, \infty)$, where

From the proof of Lemma 2.2 we know that $A(x_1^\ast) = 0$, and $A(x) > 0$ for all $x\in(x_3^\ast, x_1^\ast)\cup(x_1^\ast, +\infty)$. Thus, $A(E_T)\geq0$ for $E_T\geq x_1^\ast$, i.e.,

Therefore, if $E_T\geq x_1^\ast$, then $A_2\geq A_1$. According to the monotonicity of Lambert W function, if $A_2\geq A_1 > 0$, then we have $-\frac{a}{b}W(-e^{-1-\frac{A_2}{a}})\leq -\frac{a}{b}W(-e^{-1-\frac{A_1}{a}})$, and $-\frac{a}{b}W(-1, -e^{-1-\frac{A_2}{a}})\geq -\frac{a}{b}W(-1, -e^{-1-\frac{A_1}{a}})$, i.e., $Y_{\rm min}\leq Y_{\rm min}^1$, $Y_{\rm max}\geq Y_{\rm max}^1$. Furthermore, $[Y_{\rm min}^1, Y_{\rm max}^1]\subseteq[Y_{\rm min}, Y_{\rm max}]$, which means that if $A_1 > 0$, then Eq 2.23 is true for case $(C)(C_{11})$. By combining with the conclusion that $-\frac{b}{a}y_i^+{\rm exp}(-\frac{b}{a}y_i^+ +\frac{A_1}{a})\geq-e^{-1}$ for $A_1\leq0$, we know that the Poincaré map can be given by (2.16). This completes the proof.

As we can see from the above discussion, the varieties of parameters will produce complex effects on the determining of the Poincaré map. The relations among the key parameters, the signs of $A_1, A_2$ and the domains of the Poincaré map as shown in Table 2.

It follows from Lemma 2.1 and Lemma 2.2 that if $E_T\geq x_1^*$, $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$, then $\Gamma$ intersects with $L_3$ at points $P_1$ and $P_2$, $\Gamma$ intersects with $L_2$ at points $Q_1$ and $Q_2$. Moreover, $Q_2^+((1-P_{E_T})E_T, Y_{is}+\frac{\tau}{1+\theta Y_{is}})$ is the pulse point of $Q_2$ after a singer impulsive effect, which lies on the line $L_3$. If $E_T\geq x_1^*$, $(1-P_{E_T})E_T > x_1^*$, then $\Gamma$ intersects with $L_3$ at points $C_0$ and $C_1$, $\Gamma_1$ intersects with $L_2$ at points $D_1$ and $D_2$. Furthermore, denote $Q(x_Q, y_Q) = (E_T, \frac{\sqrt{\tau\theta}-1}{\theta})$ in view of the particularity of $\frac{\sqrt{\tau\theta}-1}{\theta}$, and if the trajectory of system (1.1) arrives at the point $Q$ and experiences impulsive effects, then $Q^+((1-P_{E_T})E_T, y_Q^+)$ is the pulse point of $Q$. For case $(C)(C_{11})$ and case $(C)(C_{12})$, we can obtain the following monotonicity of Poincaré map in the interval related to these above-mentioned intersection points.

Theorem 2. For case $(C)(C_{11})$: $E_T\geq x_1^*$, $x_3^*\leq(1-P_{E_T})E_T\leq x_1^*$,

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then the Poincaré map $\mathcal{P}(y_i^+)$ is increasing on $[0, Y_{\rm min})$, and decreasing on $(Y_{\rm max}, +\infty)$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, Y_{\rm min})$, and increasing on $(Y_{\rm max}, +\infty)$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{m_2}]$ and $(Y_{\rm max}, y_{m_1}]$, and increasing on $[y_{m_2}, Y_{\rm min})$ and $[y_{m_1}, +\infty)$, where $y_{m_2} = min\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}, y_{m_1} = max\{y^+ :\mathcal{P}(y^+) = y_{Q^+}\}$.

Proof. Without loss of generality, assuming $p_i^+$ is the impulsive point which is located in the phase set, if the trajectory initiating from $p_i^+$ intersects with $L_2$ at $p_{i+1}$, then there exists a corresponding relationship between the two points $p_i^+$ and $p_{i+1}$. Denote a mapping about the ordinate of two points by $y_{i+1} = g(y_i^+)$.

Based on the proof of Lemma 2.2, we can see that any solution of system (1.1) initiating from $(x_0^+, y_0^+)$ with $y_0^+\in[Y_{\rm min}, Y_{\rm max}]$ will be free from impulsive effects. when the trajectory passes through the point $p_i^+$ and arrive at $L_2$, then the function $g(y_i^+)$ is increasing on $[0, Y_{\rm min})$ and decreasing on $(Y_{\rm max}, +\infty)$ according to the uniqueness of solution of system. Moreover, we have discussed the monotonicity of impulsive function $F(y) = y+\frac{\tau}{1+\theta y}$, $y\in[0, \frac{a}{b}]$ for case $(C)(C_{11})$, and the Poincaré map $\mathcal{P}(y_i^+)$ can be regarded as a composite function of $g$ and $F$. On the basis of the monotonicity of function $g$ and $F$, we have the following conclusions.

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then $\mathcal{P}(y_i^+)$ is increasing on $[0, Y_{\rm min})$, and decreasing on $(Y_{\rm max}, +\infty)$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}$, then $\mathcal{P}(y_i^+)$ is decreasing on $[0, Y_{\rm min})$, and increasing on $(Y_{\rm max}, +\infty)$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$, then the solution which passes through the points $m_1((1-P_{E_T})E_T, y_{m_1})$ and $m_2((1-P_{E_T})E_T, y_{m_2})$ intersects with $L_2$ at the point $Q(E_T, \frac{\sqrt{\tau\theta}-1}{\theta})$, where $y_{m_2} = min\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}, y_{m_1} = max\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}$, $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{m_2}]$ and $(Y_{\rm max}, y_{m_1}]$, and increasing on $[y_{m_2}, Y_{\rm min})$ and $[y_{m_1}, +\infty)$. This completes the proof.

Theorem 3. For case $(C)(C_{12})$: $E_T\geq x_1^*$, $(1-P_{E_T})E_T > x_1^*$,

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then the Poincaré map $\mathcal{P}(y_i^+)$ is increasing on $[0, y_{D_0}]$ $($$y_{D_0}$ is the ordinate of $D_0$$)$, and decreasing on $(y_{D_0}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}^1$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{D_0}]$, and increasing on $(y_{D_0}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, there are three cases for the monotonicity of $\mathcal{P}(y_i^+)$ as follows.

If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{M_2}]$, $[\frac{a}{b}, Y_{\rm max})$, and $(Y_{\rm max}, y_{M_1}]$, and increasing on $[y_{M_2}, \frac{a}{b})$ and $[y_{M_1}, +\infty)$, where $y_{M_2} = min\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}, y_{M_1} = max\{y^+ :\mathcal{P}(y^+) = y_{Q^+}\}$.

If $Y_{is} < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{M_2}]$, $[\frac{a}{b}, y_{M_1})$, and increasing on $[y_{M_2}, \frac{a}{b}]$, $[y_{M_1}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$, where $y_{M_2} = min\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}, y_{M_1} = max\{y^+ :\mathcal{P}(y^+) = y_{Q^+}\}$.

If $Y_{is} = \frac{\sqrt{\tau\theta}-1}{\theta}$, then the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{\rm min}]$ and $(\frac{a}{b}, Y_{\rm max})$, and increasing on $[y_{\rm min}, \frac{a}{b}]$ and $(Y_{\rm max}, +\infty)$.

Proof. It is similar to the Theorem 2, we define the $Q(E_T, \frac{\sqrt{\tau\theta}-1}{\theta})$ is the intersection point of $L_2$ and a trajectory which pass through the points $M_1((1-P_{E_T})E_T, y_{M_1})$ and $M_2((1-P_{E_T})E_T, y_{M_2})$, where $y_{M_2} = min\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}$, $y_{M_1} = max\{y^+: \mathcal{P}(y^+) = y_{Q^+}\}$. According to the vector field of the solution trajectory, it is easy to see that $g(y_i^+)$ is increasing on $[0, y_{D_0}]$, and decreasing on $[y_{D_0}, y_{C_0})$ and $(y_{C_0}, +\infty)$ (here $y_{D_0} = \frac{a}{b}$, $y_{C_0} = Y_{\rm max})$. Furthermore, we have discussed the monotonicity of impulsive function $F(y)$ for case $(C)(C_{12})$ in the previous subsection. Therefore, we can obtain the following conclusions of $\mathcal{P}(y_i^+)$ by combining with the monotonicity of functions $g$ and $F$.

$(\rm i)$ If $\sqrt{\tau\theta}-1\leq0$, then $\mathcal{P}(y_i^+)$ is increasing on $[0, \frac{a}{b}]$, and decreasing on $(\frac{a}{b}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$.

$(\rm ii)$ If $\frac{\sqrt{\tau\theta}-1}{\theta}\geq Y_{is}^1$, then $\mathcal{P}(y_i^+)$ is decreasing on $[0, \frac{a}{b}]$, and increasing on $(\frac{a}{b}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$.

$(\rm iii)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, then according to the value of $\frac{\sqrt{\tau\theta}-1}{\theta}$ and $Y_{is}$, the monotonicity of $\mathcal{P}(y_i^+)$ can be discussed for the following three cases:

$(a)$ If $0 < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}$, then the point $M_2$ lies below the point $C_1$, and the point $M_1$ lies above the point $C_0$, the coordinates relationship of these points is: $y_{M_2} < Y_{\rm min} < \frac{a}{b} < Y_{\rm max} < y_{M_1}$. Base on the monotonicity of the functions $g$ and $F$, we infer that $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{M_2}]$, $[\frac{a}{b}, Y_{\rm max})$ and $(Y_{\rm max}, y_{M_1}]$, and increasing on $[y_{M_2}, \frac{a}{b})$ and $[y_{M_1}, +\infty)$.

$(b)$ If $Y_{is} < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, then the point $C_1$ lies below the point $M_2$, and the point $C_0$ lies above the point $M_1$, the coordinates relationship of these points is: $Y_{\rm min} < y_{M_2} < \frac{a}{b} < y_{M_1} < Y_{\rm max}$. It is easy to know $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{M_2}]$ and $[\frac{a}{b}, y_{M_1})$, and increasing on $[y_{M_2}$, $\frac{a}{b}]$, $[y_{M_1}, Y_{\rm max})$ and $(Y_{\rm max}, +\infty)$.

$(c)$ If $Y_{is} = \frac{\sqrt{\tau\theta}-1}{\theta}$, then the points $Q$ and $Q_2$ coincide, i.e., $Q = Q_2$, the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{\rm min}]$ and $(\frac{a}{b}, Y_{\rm max})$, and increasing on $[y_{\rm min}, \frac{a}{b}]$ and $[Y_{\rm max}, +\infty)$. This completes the proof.

3.   Existence and stability of the periodic solutions

Note that the fixed point of Poincaré map $\mathcal {P}(y_i^+)$ corresponds to the periodic solution of system (1.1). Based on the impulsive sets, phase sets and Poincaré map $\mathcal {P}(y_i^+)$ were investigated in the previous sections, we will discuss the existence and stability of the periodic solutions of system (1.1) for some cases.

3.1.   Order-1 periodic solution for $\tau=0$

Theorem 4. If $\tau = 0$ and $A_1 = 0$, then any $y_i^+$ in the phase set is a fixed point of Poincaré map $\mathcal{P}(y_i^+)$. If $\tau = 0$ and $A_1\neq0$, then $y_i^+ = 0$ is a unique fixed point of Poincaré map $\mathcal{P}(y_i^+)$.

Proof. The analytical formula of Poincaré map $\mathcal {P}(y_i^+)$ has been analyzed, and the special case of $\mathcal {P}(y_i^+)$ for $\tau = 0$ can be defined as follows:

By using the properties of Lambert W function, it is easy to know that $y_i^+ = -\frac{a}{b}W\left[-\frac{b}{a}y_i^+{\rm exp}(-\frac{b}{a}y_i^+)\right]$ is true. Therefore, if $\tau = 0$ and $A_1 = 0$, then any $y_i^+$ in the phase satisfies $\mathcal{P}(y_i^+) = y_i^+$, i.e., any $y_i^+$ in the phase set is a fixed point of $\mathcal{P}(y_i^+)$, which means that any solution which initiating from $((1-P_{E_T})E_T, y_i^+)$ is an order-1 periodic solution for system (1.1). Moreover, if $\tau = 0$ and $A_1\neq0$, it follows from equality (3.1) that $\mathcal{P}(y_i^+) = y_i^+$ holds if and only if $y_i^+ = 0$, then $y_i^+ = 0$ is a unique fixed point of $\mathcal{P}(y_i^+)$, which corresponds to a unique boundary order-1 periodic solution with initial point $((1-P_{E_T})E_T, 0)$ for system (1.1). This completes the proof.

3.2.   Order-1 periodic solution for $\tau > 0$

Theorem 5. For case $(C)(C_{11})(\rm i)$, if $\tau > Y_{\rm max}$ or $y_{Q_2^+} < Y_{\rm min}$ $($where $y_{Q_2^+}$ is the vertical component of point $Q_2^+$, $y_{Q_2^+} = Y_{is}+\frac{\tau}{1+\theta Y_{is}}$$)$, then there exists an order-1 periodic solution for system (1.1).

Proof. For case $(C)(C_{11})(\rm i)$, if $\tau > Y_{\rm max}$ or $y_{Q_2^+} < Y_{\rm min}$, then any solution of system (1.1) will map to the phase set with $y^+\in[\tau, y_{Q_2^+}]$ after a single impulsive effect. The point $Q_2^+$ is the pulse point of $Q_2$, and it is the highest impulsive point, the solution which crosses $Q_2^+$ will reach $L_2$ and experiences impulsive effects, and the pulse point will be located below the point $Q_2^+$. Thus we have

Moreover, the point $P_\tau((1-P_{E_T})E_T, \tau)$ is the lowest impulsive point, the solution which crosses $P_\tau$ will reach $L_2$ and experiences impulsive effects, and the pulse point will be located above $P_\tau$, we will obtain

On the basis of the continuity of $\mathcal{P}(y_i^+)$, it follows from the inequalities (3.2) and (3.3) that there exists at least one fixed point $y^\ast\in(\tau, y_{Q_2^+})$, i.e., $\mathcal{P}(y^\ast) = y^\ast$, which corresponds to an order-1 periodic solution for system (1.1). This completes the proof.

Theorem 6. For case $(C)(C_{11})(\rm ii)$, if $\tau < Y_{\rm min}$ or $y_{Q_2^+} > Y_{\rm max}$, then there exists an order-1 periodic solution for system (1.1).

Proof. For case $(C)(C_{11})(\rm ii)$, we have known that $F(y)$ is decreasing on $[0, Y_{is})$. If $\tau < Y_{\rm min}$ or $y_{Q_2^+} > Y_{\rm max}$\rm, then any solution of system (1.1) will map to the phase set with $y^+\in[y_{Q_2^+}, \tau]$ after a single impulsive effect. Thus, the point $P_\tau((1-P_{E_T})E_T, \tau)$ is the highest impulsive point, which indicated that

Furthermore, the point $Q_2^+$ is the lowest impulsive point. Then, the solution which initiating from $Q_2^+$ will satisfy the following relationship:

It follows from the inequalities (3.4) and (3.5) that there exists at least one fixed point $y^\ast\in(y_{Q_2^+}, \tau)$, i.e., there exists an order-1 periodic solution for system (1.1).

Theorem 7. For case $(C)(C_{11})(\rm iii)$, if $y_{Q_2^+} < Y_{\rm min}$ or $y_{Q^+} > Y_{\rm max}$, and the phase set of system (1.1) is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{Q_2^+}\right\}$ or $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq\tau\right\}$, then there exists an order-1 periodic solution for the system (1.1).

Proof. For case $(C)(C_{11})(\rm iii)$, if $y_{Q_2^+} < Y_{\rm min}$, and the trajectories of system (1.1) map to the phase set with $y^+\in[y_{Q^+}, y_{Q_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects, then we can discuss the existence of the fixed point of $\mathcal {P}(y_i^+)$ for the following two cases:

$(1)$ $y_{Q_2^+} > \tau$. It has been proved that the impulsive function $F(y)$ is decreasing on $[0, y_Q]$ and increasing on $(y_Q, Y_{is}]$ for case $(C)(C_{11})(\rm iii)$. Then, if $y_{Q_2^+} > \tau$, then the point $Q_2^+$ is the highest impulsive point and the point $Q^+$ is the lowest one, where $Q^+((1-P_{E_T})E_T, y_{Q^+})$ is the pulse point of $Q(E_T, y_Q)$. Moreover, any solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{Q_2^+}]$ after a single impulsive effect. Due to the uniqueness of any two solutions, the inequality $\mathcal{P}(y_{Q_2^+}) < y_{Q_2^+}$ (3.2) and the following inequality is true:

Therefore, it follows from (3.2) and (3.6) that there exists at least one fixed point $y^\ast\in[y_{Q^+}, y_{Q_2^+})$, which corresponds to an order-1 periodic solution of system (1.1).

$(2)$ $y_{Q_2^+} < \tau$. For this case, the trajectory of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, \tau]$ after impulsive effects, $P_\tau$ is the highest impulsive point and $Q^+$ is the lowest one. It is easy to know that the inequalities (3.4) and (3.6) are true, then there exists at least one fixed point $y^\ast\in[y_{Q^+}, \tau)$, which is indicated that there exists an order-1 periodic solution for system (1.1).

For case $(C)(C_{11})(\rm iii)$, if $y_{Q^+} > Y_{\rm max}$, and the trajectories of system (1.1) map to the phase set with $y^+\in[y_{Q^+}, y_{Q_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects, the same conclusions can be proved by using the similar methods. This completes the proof.

Theorem 8. If $y_{Q_2^+} < Y_{\rm min}$ for case $(C)(C_{11})(\rm i)$ $($or if $y_{Q_2^+} > Y_{\rm max}$ for case $(C)(C_{11})(\rm ii)$$)$, then the fixed point $y^\ast$ is globally stable provided that it is unique.

Proof. From Theorem 5 we know that if $y_{Q_2^+} < Y_{\rm min}$ for case $(C)(C_{11})(\rm i)$, then there exists a fixed point $y^\ast\in(\tau, y_{Q_2^+})$. Assuming it is unique, next we will discuss the global stability of the $y^\ast$. For one thing, we have proved that $\mathcal {P}(y_i^+)$ is increasing on $[0, Y_{\rm min})$, then $y_i^+ < \mathcal{P}(y_i^+) < y^\ast$ for any $y_i^+\in[0, y^\ast]$, which indicated that $\mathcal{P}^k(y_i^+)$ is monotonically increasing as $k$ increase, and we have ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$ for $y_i^+\in[0, y^\ast)$; Moreover, $y^\ast < \mathcal{P}(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, Y_{\rm min})$, which means that $\mathcal{P}^k(y_i^+)$ is monotonically decreasing as $k$ increase, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$ for $y_i^+\in[y^\ast, Y_{\rm min})$. For another, $\mathcal{P}(y_i^+)\in[\tau, y_{Q_2^+}]$ for any $y_i^+\in(Y_{\rm max}, +\infty)$ is true, then we have ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{k+1}(y_i^+) = y^\ast}$ for $y_i^+\in(Y_{\rm max}, +\infty)$. In conclusion, if $y_{Q_2^+} < Y_{\rm min}$ for case $(C)(C_{11})(\rm i)$, then the fixed point $y^\ast$ is globally stable provided that it is unique.

If $y_{Q_2^+} > Y_{\rm max}$ for case $(C)(C_{11})(\rm ii)$, the conclusions can be proved by using the similar methods. This completes the proof.

Theorem 9. For case $(C)(C_{11})(\rm ii)$, if $\tau < Y_{\rm min}$, and $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in[0, y^\ast)$ $($or for case $(C)(C_{11})(\rm i)$, if $\tau > Y_{\rm max}$, and $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in(Y_{\rm max}, y^\ast)$$)$, then there exists an unique fixed point $y^\ast$, and it is globally stable.

Proof. From Theorem 6 we know that if $\tau < Y_{\rm min}$ for case $(C)(C_{11})(\rm ii)$, then any solution of system (1.1) will map to the phase set with $y^+\in[y_{Q_2^+}, \tau]$ after a single impulsive effect, and there exists a fixed point $y^\ast\in(y_{Q_2^+}, \tau)\subset[0, Y_{\rm min})$. Moreover, as Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, Y_{\rm min})$, therefore, $y^\ast$ is the unique fixed point of $\mathcal{P}(y_i^+)$.

The global stability of $y^\ast$ can be discussed as follows. Firstly, $\mathcal{P}(y_i^+) > y^\ast$ for $y_i^+\in[0, y^\ast)$ due to the monotonicity of $\mathcal{P}(y_i^+)$, and if $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in[0, y^\ast)$, then the inequality $y_i^+ < \mathcal{P}^2(y_i^+) < y^\ast$ holds true. By induction, we conclude that $\mathcal{P}^{2(k-1)}(y_i^+) < \mathcal{P}^{2k}(y_i^+) < y^\ast$, $k\geq1$. It means that $\mathcal{P}^{2k}(y_i^+)$ monotonically increasing as $k$ increases, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k}(y_i^+) = y^\ast}, y_i^+\in[0, y^\ast)$. Secondly, according to the analytic expression of $\mathcal{P}(y_i^+)$ and the properties of Lambert W function, it's not hard to deduce ${\lim\limits_{\substack{y_i^+\rightarrow +\infty}}\mathcal{P}(y_i^+) = \tau}$, which indicated that if $\tau < Y_{\rm min}$, then $\mathcal{P}(y_i^+)\in(0, y^\ast]$ or $\mathcal{P}^2(y_i^+)\in(0, y^\ast)$ is true for any $y_i^+\in(y^\ast, Y_{\rm min})\cup(Y_{\rm max}, +\infty)$, combined with the above analysis, we infer that ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{j+2k}(y_i^+) = y^\ast}$ ($j = 1$ or 2). In summary, the unique fixed point $y^\ast$ is globally stable.

For case $(C)(C_{11})(\rm i)$, if $\tau > Y_{\rm max}$, and $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in(Y_{\rm max}, y^\ast)$, the conclusions can be proved by employing the same methods. This completes the proof.

Theorem 10. For case $(C)(C_{11})(\rm iii)$, if there exists a unique fix point $y^\ast$ for the the Poincaré map $\mathcal{P}(y_i^+)$, then we can draw the following conclusions:

$(1)$ If $y_{Q^+} > Y_{\rm max}$, and the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{Q_2^+}\right\}$ or $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq\tau\right\}$, then the fixed point $y^\ast$ is globally stable provided that one of the following three conditions is satisfied, $(a)$ $y^\ast > y_{m_1}$; $(b)$ $y^\ast = y_{m_1}$; $(c)$ $y^\ast < y_{m_1}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{m_1}]$.

$(2)$ If $y_{Q_2^+} < Y_{\rm min}$, and the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{Q_2^+}\right\}$ or $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq\tau\right\}$, then the fixed point $y^\ast$ is globally stable provided that one of the following three conditions is satisfied, $(a)$ $y^\ast > y_{m_2}$; $(b)$ $y^\ast = y_{m_2}$; $(c)$ $y^\ast < y_{m_2}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{m_2})$.

Proof. $(1)$ It follows from Theorem 7 that for case $(C)(C_{11})(\rm iii)$, if $y_{Q^+} > Y_{\rm max}$, and any solution of system (1.1) will map to the phase set with $[y_{Q^+}, y_{Q_2^+}]$ or $[y_Q^+, \tau]$ after impulsive effects, then there exists at least one fixed point $y^\ast$ for $\mathcal{P}(y_i^+)$, and $y^\ast > y_{Q^+} > Y_{\rm max}$. Assuming the fixed point $y^\ast$ is unique, the global stability of $y^\ast$ can be discussed for the following three situations according to the value of $y^\ast$ and $y_{m_1}$:

$(a)$ $y^\ast > y_{m_1}$. In this situation, there must be $y_Q^+ > y_{m_1}$ based on the uniqueness of $y^\ast$. It's easy to see $\mathcal{P}(y_i^+)$ is increasing on $[y_{m_1}, y^\ast)$, and $y_i^+ < \mathcal{P}(y_i^+) < y^\ast$ for any $y_i^+\in[y_{m_1}, y^\ast)$, by induction, we know $\mathcal{P}^k(y_i^+)$ is monotonically increasing as $k$ increase, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$; For any $y_i^+\in(y^\ast, +\infty)$, $y^\ast < \mathcal{P}(y_i^+) < y_i^+$, $\mathcal{P}^k(y_i^+)$ is monotonically decreasing as $k$ increase, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$. Furthermore, there must be $\mathcal{P}(y_i^+)\in(y_{m_1}, +\infty)$ for any $y_i^+\in[0, Y_{\rm min})\cup(Y_{\rm max}, y_{m_1})$, ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{1+k}(y_i^+) = y^\ast}$ is true.

$(b)$ $y^\ast = y_{m_1}$. From the conclusion of case $(a)$ we know that $y^\ast\leq\mathcal{P}(y_i^+) < y_i^+$ for any $y_i^+\in[y_{m_1}, +\infty)$, $\mathcal{P}^k(y_i^+)$ is monotonically decreasing as $k$ increase, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$. For $y_i^+\in[0, Y_{\rm min})\cup(Y_{\rm max}, y_{m_1})$, there must be $\mathcal{P}(y_i^+)\in(y_{m_1}, +\infty)$, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{k+1}(y_i^+) = y^\ast}$ is true.

$(c)$ $y^\ast < y_{m_1}$. For this case, we know that $y^\ast\subset[y_{Q^+}, y_{m_1})\subset(Y_{\rm max}, y_{m_1})$, and the Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $(y^\ast, y_{m_1}]$. If $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{m_1}]$, then $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$, and $\mathcal{P}^{2k}(y_i^+)$ is monotonically decreasing as $k$ increase, it means that ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k}(y_i^+) = y^\ast}$. Moreover, for any $y_i^+\in[0, Y_{\rm min})\cup(Y_{\rm max}, y^\ast)\cup(y_{m_1}, +\infty)$, there exists a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in[y^\ast, y_{m_1}]$, and we have ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{l+2k}(y_i^+) = y^\ast}$.

In summary, the results shown in case $(1)$ are true. For case $(2)$, the conclusions can be proved in a similar way. This completes the proof.

Theorem 11. For case $(C)(C_{12})(\rm i)$, if $y_{D_0} < y_{D_2^+} < y_{C_0}$ or $y_{D_2^+} < y_{D_0}$ or $\tau > y_{C_0}$, $($where $y_{D_0}$, $y_{D_2^+}$ and $y_{C_0}$ are the vertical component of points $D_0$, $D_2^+$ and $C_0$, respectively$)$, then there exists an order-1 periodic solution for system (1.1).

Proof. For case $(C)(C_{12})(\rm i)$, the solution which passes through the point $D_0$ intersects with $\mathcal M_2$ at two points, the lower intersection point is $D_2$, and $D_2^+$ is the resetting point of $D_2$, i.e., $\mathcal{P}(y_{D_0}) = y_{D_2^+}$. If $y_{D_0} < y_{D_2^+} < y_{C_0}$, then the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, \tau\leq y^+\leq y_{D_2^+}\right\}$, $P_\tau$ is the lowest impulsive point and $D_2^+$ is the highest one, therefore, we have the inequalities (3.3): $\mathcal{P}(\tau) > \tau$, and

It follows from (3.3) and (3.7) that there exists at least one fixed point $y^\ast\in(\tau, y_{D_2^+})$, i.e., there exists an order-1 periodic solution for system (1.1). If $y_{D_2^+} < y_{D_0}$ or $\tau > y_{C_0}$ for case $(C)(C_{12})(\rm i)$, the conclusions can be proved by using the similar methods. This completes the proof.

Theorem 12. For case $(C)(C_{12})(\rm ii)$, if $\tau < y_{C_0}$ or $y_{D_2^+} > y_{C_0}$, then there exists an order-1 periodic solution for system (1.1).

Proof. It has been proved that the impulsive function $F(y)$ is decreasing on $[0, Y_{is}^1)$ for case $(C)(C_{12})(\rm ii)$. If $\tau < y_{C_0}$ or $y_{D_2^+} > y_{C_0}$, then the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{D_2^+}\leq y^+\leq \tau\right\}$, $P_\tau$ is the highest impulsive point and $D_2^+$ is the lowest one. Therefore, we have the inequalities (3.4): $\mathcal{P}(\tau) < \tau$, and

In conclusion, there exists at least one fixed point $y^\ast\in(y_{D_2^+}, \tau)$, which indicated that there exists an order-1 periodic solution for system (1.1). This completes the proof.

Theorem 13. For case $(C)(C_{12})(\rm iii)$, there exists an order-1 periodic solution for system (1.1) if either of the following conditions is satisfied.

$(1)$ $y_{D_2^+} > \tau$, and $y_{D_2^+} < y_{C_0}$ $($or $y_{Q^+} > y_{C_0}$$)$.

$(2)$ $y_{D_2^+} < \tau$, and $\tau < y_{C_0}$ $($or $y_{Q^+} > y_{C_0}$ or $y_{D_2^+} < y_{D_0}$$)$.

Proof. $(1)$ For case $(C)(C_{12})(\rm iii)$, if $\tau < y_{D_2^+} < y_{C_0}$ (or $y_{D_2^+} > \tau$ and $y_{Q^+} > y_{C_0}$), then the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{D_2^+}\right\}$, the point $D_2^+$ is the highest impulsive point and $Q^+$ is the lowest one. Therefore, the inequalities (3.7): $\mathcal{P}(y_{D_2^+}) < y_{D_2^+}$ and

are true. In summary, there exists at least one fixed point $y^\ast\in[y_{Q^+}, y_{D_2^+})$.

$(2)$ If $y_{D_2^+} < \tau$, and $\tau < y_{C_0}$ or $y_{Q^+} > y_{C_0}$, it is easy to know that the solution of system (1.1) will map to the phase set with $y^+\in[y_Q^+, \tau]$ after impulsive effects, $P_\tau$ is the highest impulsive point and $Q^+$ is the lowest one. Therefore, the two inequalities (3.4): $\mathcal{P}(\tau) < \tau$, and (3.9): $\mathcal{P}(y_{Q^+})\geq y_{Q^+}$ are true, which indicated that there exists at least one fixed point $y^\ast\in[y_{Q^+}, \tau)$.

If $y_{D_2^+} < y_{D_0}$, i.e., $\mathcal{P}(y_{D_0}) < y_{D_0}$, then combined with the inequality (3.9) we can infer that there exists at least one fixed point $y^\ast\in[y_{Q^+}, y_{D_0})$.

In conclusion, the results shown in Theorem 13 are true. This completes the proof.

Theorem 14. For case $(C)(C_{12})$, if $y_{D_2^+} = y_{D_0}$, then the trajectory $\widehat{D_0D_2}$ is an order-1 periodic solution of system (1.1).

Proof. For case $(C)(C_{12})$, if $y_{D_2^+} = y_{D_0}$, i.e., $\mathcal{P}(y_{D_0}) = y_{D_0}$, then the fixed point $y^\ast = y_{D_0}$, the trajectory $\widehat{D_0D_2}$ is an order-1 periodic solution for system (1.1). This completes the proof.

Theorem 15. For case $(C)(C_{12})(\rm i)$, if there exists a fixed point $y^\ast$ of Poincaré map $\mathcal{P}(y_i^+)$ for the system (1.1), the stability of $y^\ast$ is as follows:

$(1)$ If the fixed point $y^\ast$ is unique, then it is globally stable provided either of the following conditions is true.

$(a)$ $\mathcal{P}(y_{D_0}) < y_{D_0}$;

$(b)$ $y_{D_0} < \mathcal{P}(y_{D_0}) < y_{C_0}$, and $\mathcal{P}^2(y_i^+) > y_i^+$ for any $y_i^+\in[y_{D_0}, y^\ast)$.

$(2)$ If $\tau > y_{C_0}$, then the fixed point $y^\ast$ is unique, and $y^\ast$ is globally stable provided that $\mathcal{P}^2(y_i^+) > y_i^+$ for any $y_i^+\in[\tau, y^\ast)$.

Proof. $(1)$ $(a)$: It follows from Theorem 11 that if $\mathcal{P}(y_{D_0}) < y_{D_0}$ for case $(C)(C_{12})(\rm i)$, there exists a fixed point $y^\ast$, and $y^\ast\in(\tau, y_{D_2^+})\subset(0, y_{D_0})$. Assuming the fixed point $y^\ast$ of $\mathcal{P}(y_i^+)$ is unique, then we have $y_i^+ < \mathcal{P}(y_i^+) < y^\ast$ for any $y_i^+\in[\tau, y^\ast)$ according to the monotonicity of $\mathcal{P}(y_i^+)$, it means that $\mathcal{P}^{k_1}(y_i^+)$ is monotonically increasing as $k_1$ increase, and ${\lim\limits_{\substack{k_1\rightarrow +\infty}}\mathcal{P}^{k_1}(y_i^+) = y^\ast}$; Moreover, $y^\ast < \mathcal{P}(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{D_2^+}]$, $\mathcal{P}^{k_2}(y_i^+)$ is monotonically decreasing as $k_2$ increase, and ${\lim\limits_{\substack{k_2\rightarrow +\infty}}\mathcal{P}^{k_2}(y_i^+) = y^\ast}$ is also true. In summary, if $\mathcal{P}(y_{D_0}) < y_{D_0}$, and the fixed point $y^\ast$ is unique, then it is globally stable.

$(1)$ $(b)$: It has been proved that $\mathcal{P}(y_i^+)$ is decreasing on $[y_{D_0}, y_{C_0})$ for case $(C)(C_{12})(\rm i)$. If $y_{D_0} < \mathcal{P}(y_{D_0}) < y_{C_0}$, then the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, \tau\leq y^+\leq y_{D_2^+}\right\}$, and it is easy to know $\mathcal{P}^{2}(y_{D_0}) < \mathcal{P}(y_{D_0})$, i.e., $\mathcal{P}(y_{D_2^+}) < y_{D_2^+}$. Therefore, the fixed point $y^\ast\in(y_{D_0}, y_{D_2^+})\subset[\tau, y_{D_2^+}]$. Assuming the fixed point $y^\ast$ is unique, the stability of $y^\ast$ will be discussed in three subinterval: $[y_{D_0}, y^\ast)$, $(y^\ast, y_{D_2^+})$, $[\tau, y_{D_0}]$.

First of all, according to the monotonicity of $\mathcal{P}(y_i^+)$, we have $\mathcal{P}(y_{D_0})\geq \mathcal{P}(y_i^+) > y^\ast$ and $\mathcal{P}^2(y_{D_0})\leq \mathcal{P}^2(y_i^+) < y^\ast$ for any $y_i^+\in[y_{D_0}, y^\ast)$, combined with the inequality $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in[y_{D_0}, y^\ast)$, we will obtain that $y_i^+ < \mathcal{P}^2(y_i^+) < y^\ast$. By induction, it is easy to know $\mathcal{P}^{2(k-1)}(y_i^+) < \mathcal{P}^{2k}(y_i^+) < y^\ast$, which means that $\mathcal{P}^{2k}(y_i^+)$ is monotonically increasing and tends to $y^\ast$ as $k$ increase, $\mathcal{P}^{2k+1}(y_i^+)$ is monotonically decreasing and tends to $y^\ast$ as $k$ increase. Secondly, we know $\mathcal{P}(y_i^+)\in(y^\ast, y_{D_2^+}]$ for any $y_i^+\in[y_{D_0}, y^\ast)$, base on the conclusion of the former part, ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k}(y_i^+) = y^\ast}$ or ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k+1}(y_i^+) = y^\ast}$ for any $y_i^+\in(y^\ast, y_{D_2^+}]$ is true. Thirdly, it follows from the monotonicity of $\mathcal{P}(y_i^+)$ that there must exist a positive integer $n$ such that $\mathcal{P}^n(y_i^+)\in[y_{D_0}, y^\ast]$ or $(y^\ast, y_{D_2^+})$ for any $y_i^+\in[\tau, y_{D_0})$. In conclusion, for case $(C)(C_{12})(\rm i)$, the fixed point $y^\ast$ is globally stable provided the conditions $(1)b$ are satisfied.

$(2)$ If $\tau > y_{C_0}$, from Theorem 11 we know that there exists a fixed point $y^\ast$, and the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, \tau\leq y^+\leq y_{D_2^+}\right\}$. It means that $y^\ast\in[\tau, y_{D_2^+}]\subset[y_{C_0} +\infty)$. We have proved that $\mathcal{P}(y_i^+)$ is decreasing on $(y_{D_0}, y_{C_0})\cup(y_{C_0}, +\infty)$, then the fixed point $y^\ast$ is unique, obviously.

As for the stability of $y^\ast$, for one thing, based on the monotonicity of $\mathcal{P}(y_i^+)$, $y_i^+ < y^\ast < \mathcal{P}(y_i^+)$ for any $y_i^+\in[\tau, y^\ast)$ is true, combined with $\mathcal{P}^2(y_i^+) > y_i^+$, we have $y^\ast > \mathcal{P}^2(y_i^+) > y_i^+$, by induction, $y^\ast > \mathcal{P}^{2k}(y_i^+) > \mathcal{P}^{2(k-1)}(y_i^+)$ or $y^\ast < \mathcal{P}^{2k+1}(y_i^+) < \mathcal{P}^{2k-1}(y_i^+)$ is true, $\mathcal{P}^k(y_i^+)$ is monotone increasing and tends to $y^\ast$ as $k$ increase. For another, $\mathcal{P}(y_i^+)\in(\tau, y^\ast)$ for $y_i^+\in(y^\ast, y_{D_2^+}]$, therefore, it can be inferred that ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^k(y_i^+) = y^\ast}$. In conclusion, if $\tau > y_{C_0}$ for case $(C)(C_{12})(\rm i)$, the fixed point $y^\ast$ of system (1.1) is unique, and $y^\ast$ is globally stable provided that $\mathcal{P}^2(y_i^+) > y_i^+$ for $y_i^+\in[\tau, y^\ast)$. This completes the proof.

Theorem 16. For case $(C)(C_{12})(\rm ii)$, if there exists a unique fix point $y^\ast$ for the Poincaré map $\mathcal{P}(y_i^+)$, then $y^\ast$ is globally stable provided that one of the following three conditions is satisfied.

$(1)$ $\tau < y_{C_0}$ and $y_{D_0} < y_{D_2^+}$;

$(2)$ $\tau < y_{C_0}$, $y_{D_2^+} < y_{D_0}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{D_0}]$;

$(3)$ $y_{D_2^+} > y_{C_0}$.

Proof. $(1)$ If $\tau < y_{C_0}$ and $y_{D_0} < y_{D_2^+}$, it follows from Theorem 12 that any solution of system (1.1) will map to the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{D_2^+}\leq y^+\leq\tau\}$ after impulsive effects, and there exists a fixed point $y^\ast\in(y_{D_2^+}, \tau)\subset(y_{D_0}, y_{C_0})$, assuming it is unique. It has been proved that $\mathcal{P}(y_i^+)$ is increasing on $(y_{D_0}, y_{C_0})$. Therefore, we can infer that $\mathcal{P}^{k_1}(y_i^+)$ is monotone increasing and tends to $y^\ast$ as $k_1$ increase for any $y_i^+\in[y_{D_2^+}, y^\ast)$, and $\mathcal{P}^{k_2}(y_i^+)$ is monotone decreasing and tends to $y^\ast$ as $k_2$ increase for any $y_i^+\in(y^\ast, \tau]$. In summary, the fixed point $y^\ast$ is globally stable provided it is unique.

$(2)$ According to the monotonicity of the impulsive function $F(x)$, if $y_{D_2^+} < y_{D_0}$, i.e., $\mathcal{P}(y_{D_0}) < y_{D_0}$, then we have $\mathcal{P}(y_{D_2^+}) > y_{D_2^+}$, which indicated that $y^\ast\in(y_{D_2^+}, y_{D_0})$. Assuming the fixed point is unique, from Theorem 3 we know that $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{D_0}]$, therefore, $\mathcal{P}(y_i^+) < y^\ast < y_i^+$ for any $y_i^+\in(y^\ast, y_{D_0}]$ is true; If $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{D_0}]$, it is easy to know $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$. By induction, we can infer that $y^\ast < \mathcal{P}^{2k}(y_i^+) < \mathcal{P}^{2(k-1)}(y_i^+)$, and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k}(y_i^+) = y^\ast}$ for $y_i^+\in(y^\ast, y_{D_0}]$. Moreover, on the basis of $\tau < y_{C_0}$ and${\lim\limits_{\substack{y_i^+\rightarrow +\infty}}\mathcal{P}(y_i^+) = \tau}$, there must exist a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in[y^\ast, y_{D_0}]$ and ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k+l}(y_i^+) = y^\ast}$ for any $y_i^+\in[0, y^\ast)\cup(y_{D_0}, y_{C_0})\cup(y_{C_0}, +\infty)$. In conclusion, if $\tau < y_{C_0}$ and $y_{D_2^+} < y_{D_0}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{D_0}]$, then the unique fixed point $y^\ast$ is globally stable.

$(3)$ For this case, if $y_{D_2^+} > y_{C_0}$, then any solution of system (1.1) will map to the phase set $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{D_2^+}\leq y^+\leq\tau\}$ after impulsive effects, and there exists a fixed point $y^\ast\in(y_{D_2^+}, \tau)\subset(y_{C_0}, +\infty)$. Assuming the fixed point is unique, according to the monotonicity of $\mathcal{P}(y_i^+)$, it is easy to see that $\mathcal{P}^{k_1}(y_i^+)$ is increasing and tends to $y^\ast$ as $k_1$ increase for any $y_i^+\in[y_{D_2^+}, y^\ast)$, and $\mathcal{P}^{k_2}(y_i^+)$ is decreasing and tends to $y^\ast$ as $k_2$ increase for any $y_i^+\in(y^\ast, \tau]$. In summary, if $y_{D_2^+} > y_{C_0}$, then the unique fixed point $y^\ast$ is globally stable. This completes the proof.

Theorem 17. For case $(C)(C_{12})(\rm iii)$, if there exists a unique fix point $y^\ast$ for the Poincaré map $\mathcal{P}(y_i^+)$, and $Y_{is} < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$, then $y^\ast$ is globally stable provided that one of the following four conditions is satisfied.

$(a)$ $\mathcal{P}(y_{M_i}) > y_{C_0}\; (i = 1, 2)$;

$(b)$ $\mathcal{P}(y_{M_1}) < y_{M_1}$, $\mathcal{P}(y_{M_2}) > y_{M_2}$, $y_{D_0} < \mathcal{P}(y_{D_0}) < y_{C_0}$, $\tau < y_{C_0}$, and $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_1}]$;

$(c)$ $\mathcal{P}(y_{M_1}) < y_{M_1}$, $\mathcal{P}(y_{M_2}) > y_{M_2}$, $\mathcal{P}(y_{D_0}) < y_{D_0}$, $\tau < y_{C_0}$;

$(d)$ $\mathcal{P}(y_{M_i}) < y_{M_i} (i = 1, 2)$, $\tau < y_{C_0}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_2}]$.

Proof. For case $(C)(C_{12})(\rm iii)$, $Y_{is} < \frac{\sqrt{\tau\theta}-1}{\theta} < Y_{is}^1$ means that the point $Q$ is located between the points $Q_2$ and $D_2$, and the coordinates relationship of $M_1$ and $M_2$ is: $0 < y_{M_2} < y_{D_0} < y_{M_1} < y_{C_0}$.

$(a)$ If $\mathcal{P}(y_{M_i}) = y_{Q^+} > y_{C_0}\; (i = 1, 2)$, then from the Theorem 13 we know that there exists a fixed point $y^\ast$, and the solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{D_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects. Assuming $y^\ast\in[y_{Q^+}, \tau]$ and it is unique, it has been proved that $\mathcal{P}(y_i^+)$ is increasing on $[y_{Q^+}, \tau]$, therefore, $y_i^+ < \mathcal{P}(y_i^+) < y^\ast$ for any $y_i^+\in[y_{Q^+}, y^\ast)$ is true, and we conclude that $\mathcal{P}^{k_1}(y_i^+)$ is increasing and tends to $y^\ast$ as $k_1$ increase; Moreover, $y^\ast < \mathcal{P}(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, \tau]$ is true, and $\mathcal{P}^{k_2}(y_i^+)$ is decreasing and tends to $y^\ast$ as $k_2$ increase. In summary, if $\mathcal{P}(y_{M_i}) > y_{C_0}$, then the unique fixed point $y^\ast$ is globally stable. The analysis methods can also be used for $y^\ast\in[y_{Q^+}, y_{D_2^+}]$.

$(b)$ If $\tau < y_{C_0}$, and $y_{D_0} < \mathcal{P}(y_{D_0}) < y_{C_0}$ i.e., $y_{D_0} < y_{D_2^+} < y_{C_0}$, then any solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{D_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects. From $\mathcal{P}(y_{D_0}) > y_{D_0}$ and $\mathcal{P}(y_{M_1}) < y_{M_1}$ we know that the fixed point $y^\ast\in(y_{D_0}, y_{M_1})$. Assuming the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{D_2^+}\}$ and $y^\ast$ is unique. It is easy to know $y_{Q^+}\in[y_{D_0}, y^\ast)$ follows from $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_1}]$, which means $y^\ast\in(y_{Q^+}, y_{M_1})\subset(y_{D_0}, y_{M_1})$. According to the monotonicity of $\mathcal{P}(y_i^+)$, we infer that $y^\ast < \mathcal{P}^{2k}(y_i^+) < \mathcal{P}^{2(k-1)}(y_i^+)$ for any $y_i^+\in(y^\ast, y_{M_1}]$, it means that $\mathcal{P}^{2k}(y_i^+)$ is decreasing and tends to $y^\ast$ as $k$ increase, or $\mathcal{P}^{2k+1}(y_i^+)$ is increasing and tends to $y^\ast$ as $k$ increase; Moreover, we have $\mathcal{P}(y_i^+)\in(y^\ast, y_{M_1})$ for any $y_i^+\in[y_{Q^+}, y^\ast)$; If $y_{D_2^+} > y_{M_1}$, for any $y_i^+\in(y_{M_1}, y_{D_2^+}]$, there must exist a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in[y^\ast, y_{M_1}]$; In conclusion, ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{k}(y_i^+) = y^\ast}$ for $y_i^+\in[y_{Q^+}, y_{D_2^+}]$ is true, and the unique fixed point $y^\ast$ is globally stable. If the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq \tau\}$, the conclusions can be proved by using the similar analysis methods.

$(c)$ For this case, the solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{D_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects. $Q^+$ is the lowest pulse point, then $\mathcal{P}(y_{Q^+}) > y_{Q^+}$ is true, combined with the inequality $\mathcal{P}(y_{D_0}) < y_{D_0}$, we know that the fixed point $y^\ast$ is located in the interval $(y_{Q^+}, y_{D_0})$, assuming it is unique. If the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{D_2^+}\}$, then $y^\ast\in(y_{Q^+}, y_{D_2^+})$ $\subset(y_{Q^+}, y_{D_0})$. According to the monotonicity of $\mathcal{P}(y_i^+)$, it is easy to infer that $\mathcal{P}^k(y_i^+)$ is increasing and tends to $y^\ast$ as $k$ increase for any $y_i^+\in[y_{Q^+}, y^\ast)$, and $\mathcal{P}^k(y_i^+)$ is decreasing and tends to $y^\ast$ as $k$ increase for any $y_i^+\in(y^\ast, y_{D_2^+}]$, thus the fixed point $y^\ast$ is globally stable. If the phase set is $\left\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq \tau\right\}$ and $y_{D_0}\geq\tau$, the conclusions can be proved in a similar way; Moreover, if $y_{D_0} < \tau < y_{C_0}$, there must exist a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in[y_{Q^+}, y_{D_2^+}]$ for $y_i^+\in(y_{D_2^+}, \tau]$. In conclusion, the unique fixed point $y^\ast$ is globally stable.

$(d)$ For this case, $Q^+$ is the lowest pulse point, then $\mathcal{P}(y_{Q^+}) > y_{Q^+}$ is true, then combined with $\mathcal{P}(y_{M_2}) < y_{M_2}$, we can infer that the fixed point $y^\ast\in(y_{Q^+}, y_{M_2})$, assuming it is unique. If $\mathcal{P}(y_{M_i}) < y_{M_i} (i = 1, 2)$ and $\tau < y_{C_0}$, it is easy to know $\mathcal{P}(y_{D_0}) < y_{D_0}$ follows from the monotonicity of $\mathcal{P}(y_i^+)$ and uniqueness of $y^\ast$, and $y^+ < y_{C_0}$ is true for the point ($x^+, y^+$) of phase set. According to the monotonicity of $\mathcal{P}(y_i^+)$ on $(y^\ast, y_{M_2}]$ and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_2}]$, we can speculate that $\mathcal{P}^{2k}(y_i^+)$ is decreasing and tends to $y^\ast$ as $k$ increase. Furthermore, $\mathcal{P}(y_i^+)\in(y^\ast, y_{M_2})$ for $y_i^+\in[y_{Q^+}, y^\ast)$ is true, and there must exist a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in(y^\ast, y_{M_2}]$ for any $y_i^+\in[y_{M_2}, y_{C_0})$. Therefore, for the point $(x^+, y^+$) of phase set, ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{k}(y^+) = y^\ast}$ is true. In conclusion, the unique fixed point $y^\ast$ is globally stable if the conditions of the theorem are satisfied. This completes the proof.

Theorem 18. For case $(C)(C_{12})(\rm iii)$, if there exists a unique fix point $y^\ast$ for the Poincaré map $\mathcal{P}(y_i^+)$, and $0 < \frac{\sqrt{\tau\theta}-1}{\theta}\leq Y_{is}$, then $y^\ast$ is globally stable provided that one of the following four conditions is satisfied.

$(a)$ $\mathcal{P}(y_{M_i}) > y_{M_i}\; (i = 1, 2)$;

$(b)$ $\mathcal{P}(y_{M_1}) < y_{M_1}$, $\mathcal{P}(y_{M_2}) > y_{M_2}$, $y_{Q^+} > y_{C_0}$, and $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_1}]$;

$(c)$ $\mathcal{P}(y_{M_1}) < y_{M_1}$, $\mathcal{P}(y_{M_2}) > y_{M_2}$, $\mathcal{P}(y_{D_0}) < y_{D_0}$, and $\tau < y_{C_0}$;

$(d)$ $\mathcal{P}(y_{M_i}) < y_{M_i}\; (i = 1, 2)$, $\tau < y_{C_0}$, and $\mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_2}]$.

Proof. For case $(C)(C_{12})(\rm iii)$, $0 < \frac{\sqrt{\tau\theta}-1}{\theta}\leq Y_{is}$ means that the point $Q$ is located below the point $Q_2$, the coordinates relationship of $M_1$ and $M_2$ is: $0 < y_{M_2} < y_{D_0} < y_{C_0} < y_{M_1}$.

$(a)$ If $\mathcal{P}(y_{M_i}) > y_{M_i}\; (i = 1, 2)$, then any solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{D_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects. If the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq \tau\}$, then $P_\tau$ is the highest impulsive point and $Q^+$ is the lowest one, it follows from $\mathcal{P}(y_{Q^+}) > y_{Q^+}$ and $\mathcal{P}(\tau) < \tau$ that the fixed point $y^\ast\in(y_{Q^+}, \tau)\subset(y_{M_1}, +\infty)$, assuming it is unique. Because the Poincaré map $\mathcal{P}(y_i^+)$ is increasing on $[y_{M_1}, +\infty)$, it is easy to know that $\mathcal{P}^k(y_i^+)$ is increasing and tends to $y^\ast$ as $k$ increase for any $y_i^+\in[y_{Q^+}, y^\ast)$, and $\mathcal{P}^k(y_i^+)$ is decreasing and tends to $y^\ast$ as $k$ increase for any $y_i^+\in(y^\ast, \tau]$, which indicated that the unique fixed point $y^\ast$ is globally stable. If the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, y_{Q^+}\leq y^+\leq y_{D_2^+}\}$, the conclusions can be proved by using the similar methods.

$(b)$ If $\mathcal{P}(y_{M_1}) = \mathcal{P}(y_{M_2}) = y_{Q^+} > y_{C_0}$, then any pulse point will be located above the point $C_0$, and the solution of system (1.1) will map to the phase set with $y^+\in[y_{Q^+}, y_{D_2^+}]$ or $[y_{Q^+}, \tau]$ after impulsive effects, $Q^+$ is the lowest impulsive point. It follows from $\mathcal{P}(y_{Q^+}) > y_{Q^+}$ and $\mathcal{P}(y_{M_1}) < y_{M_1}$ that the fixed point $y^\ast\in(y_{Q^+}, y_{M_1})$, assuming it is unique. It is has been proved that $\mathcal{P}(y_i^+)$ is decreasing on $[y_{Q^+}, y_{M_1}]$ and increasing on $(y_{M_1}, +\infty)$, if $y^\ast < \mathcal{P}^2(y_i^+) < y_i^+$ for any $y_i^+\in(y^\ast, y_{M_1}]$, then we can infer that $y^\ast < \mathcal{P}^{2k}(y_i^+) < \mathcal{P}^{2(k-1)}(y_i^+)$, which means ${\lim\limits_{\substack{k\rightarrow +\infty}}\mathcal{P}^{2k}(y^+) = y^\ast}$ for $y_i^+\in(y^\ast, y_{M_1}]$. Furthermore, $\mathcal{P}(y_i^+)\in(y^\ast, y_{M_1})$ for any $y_i^+\in(y_{Q^+}, y^\ast)$ is true, and there must exist a positive integer $l$ such that $\mathcal{P}^l(y_i^+)\in[y^\ast, y_{M_1}]$ for any $y_i^+\in(y_{M_1}, y_{D_2^+}]$ or $(y_{M_1}, \tau]$. In summary, the unique fixed point $y^\ast$ is globally stable.

For case $(c)$ and case $(d)$, it can be noticed that the conditions of Theorem 18 are the same as Theorem 17 for these two cases, respectively. Therefore, the global stability of the fixed point $y^\ast$ can be proved by taking advantage of the similar method. This completes the proof.

3.3.   Order-k periodic solution for $\tau > 0$

In the previous subsection, we have analyzed the existence and global stability of order-1 periodic solutions. The existence of order-$k$($k\geq2$) periodic solutions of system (1.1) will be discussed as follows.

Theorem 19. If one of the following conditions is satisfied, then there only exists order-1 periodic solutions for system (1.1).

$(1)$ For case $(C)(C_{11})(\rm i)$, $y_{Q_2^+} < Y_{\rm min}$;

$(2)$ For case $(C)(C_{11})(\rm ii)$, $y_{Q_2^+} > Y_{\rm max}$;

$(3)$ For case $(C)(C_{12})(\rm i)$, $y_{D_2^+} < y_{D_0}$;

$(4)$ For case $(C)(C_{12})(\rm ii)$, $y_{D_2^+} > y_{C_0}$;

$(5)$ For case $(C)(C_{12})(\rm ii)$, $\tau < y_{C_0}$ and $y_{D_2^+} > y_{D_0}$.

Proof. From the analysis of previous subsection we know that there exists an order-1 periodic solution for system (1.1) if one of the five conditions of Theorem 19 is satisfied.

For case $(C)(C_{11})(\rm i)$, it has been proved that Poincaré map $\mathcal{P}(y_i^+)$ is increasing on $[0, Y_{\rm min})$. If $y_{Q_2^+} < Y_{\rm min}$, then the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, \tau\leq y^+\leq y_{Q_2^+}\}$. Assuming the order-1 periodic solution passes through the points $P(E_T, \eta_0)$ and $P^+((1-P_{E_T})E_T, \eta_0^+)$, which are located on the line $L_2$ and $L_3$, respectively. The trajectory initiating from point $Q_2^+$ intersects with line $L_2$ at point $Q_3$, the point $Q_3$ is located below the point $Q_2$ according to the disjointness of any two trajectories. Moreover, we have proved that the pulse function $F$ is increasing on $[0, Y_{is}]$, then the pulse point $Q_3^+$ will lie below the point $Q_2^+$, by induction, the relationship of the series of pulse points is: $Y_{\rm min} > y_{Q_2^+} > y_{Q_3^+} > y_{Q_4^+} > \cdots > y_{Q_i^+} > \cdots > \eta_0^+ > \cdots > \tau$. It means that the series of pulse points $Q_i^+$ is decreasing as $i$ increase, a periodic solution with order-$k(k\geq2)$ does not exist for system (1.1).

For case $(C)(C_{12})(\rm ii)$, it has been proved that Poincaré map $\mathcal{P}(y_i^+)$ is decreasing on $[0, y_{D_0}]$, and increasing on $(y_{D_0}, Y_{\rm max})$. If $\tau < y_{C_0}$ and $y_{D_2^+} > y_{D_0}$, then the solution of system (1.1) will map to the phase set with $y^+\in[y_{D_2^+}, \tau]$ after impulsive effects, $[y_{D_2^+}, \tau]\subset(y_{D_0}, Y_{\rm max})$. The solution initiating from point $D_2^+$ intersects with line $L_2$ at $D_3$ and then experiences impulsive effects, $D_3^+$ is the pulse point of $D_3$, it is obviously that $D_3$ lies below $D_2$, and $D_3^+$ lies above $D_2^+$, by induction, the relationship about the coordinate of pulse points is: $y_{D_0} < y_{D_2^+} < y_{D_3^+} < \cdots < \eta_0^+ < \cdots < \tau$, where $\eta_0^+$ is the fixed point of $\mathcal{P}(y_i^+)$. Therefore, an order-$k(k\geq2)$ periodic solution does not exist for system (1.1) in the view of this relationship of the pulse points.

If $y_{Q_2^+} > Y_{\rm max}$ for case $(C)(C_{11})(\rm ii)$ or if $y_{D_2^+} < y_{D_0}$ for case $(C)(C_{12})(\rm i)$ or if $y_{D_2^+} > y_{C_0}$ for case $(C)(C_{12})(\rm ii)$, the conclusions can also be proved by using the same methods. This completes the proof.

Theorem 20. If one of the following conditions is satisfied, then there only exists order-1 or order-2 periodic solutions for system (1.1).

$(1)$ For case $(C)(C_{11})(\rm i)$, $\tau > Y_{\rm max}$;

$(2)$ For case $(C)(C_{11})(\rm ii)$, $\tau < Y_{\rm min}$;

$(3)$ For case $(C)(C_{12})(\rm i)$, $\tau > y_{C_0}$ $($or $y_{D_0} < y_{D_2^+} < y_{C_0}$ and $y_{D_3^+}\geq y_{D_0}$$)$.

Proof. For case $(C)(C_{11})(\rm i)$, if $\tau > Y_{\rm max}$, then the phase set is $\{(x^+, y^+)\in R_+^2|x^+ = \left(1-P_{E_T}\right)E_T, \tau\leq y^+\leq y_{Q_2^+}\}$. The solution which initiating from the point $Q_2^+$ intersects with line $L_2$ at $Q_3$, then map to $Q_3^+$ after a single impulsive effect. According to the monotonicity of the pulse function $F(y)$ on $[0, Y_{is}]$, it is easy to see the pulse point $Q_3^+$ lies below the point $Q_2^+$; Moreover, the solution which passes through the point $Q_3^+$ intersects with line $L_2$ at $Q_4$, then the pulse point $Q_4^+$ lies between $Q_2^+$ and $Q_3^+$. By induction, we infer that the relationship about the vertical component of these pulse points is: $Y_{\rm max} < \tau < y_{Q_3^+} < y_{Q_5^+} < \cdots < y_{Q_{2i-1}^+} < y_{Q_{2i+1}^+} < \cdots < y_{Q_{2i+2}^+} < y_{Q_{2i}^+} < \cdots < y_{Q_4^+} < y_{Q_2^+}$. From this relationship we see that there are two series of pulse point: ${y_{Q_{2i+1}^+}}$ and $y_{Q_{2i}^+}$, the series ${y_{Q_{2i+1}^+}}$ is increasing as $i$ increase and the series $y_{Q_{2i}^+}$ is decreasing as $i$ increase. Therefore, we have ${\lim\limits_{\substack{i\rightarrow +\infty}}y_{Q_{2i+1}^+} = y_1^\ast}$, ${\lim\limits_{\substack{i\rightarrow +\infty}}y_{Q_{2i}^+} = y_2^\ast}$, and the limit value $y_1^\ast = y_2^\ast$ or $y_1^\ast\neq y_2^\ast$, which means that there exists an order-1 or order-2 periodic solution for the system (1.1), and an order-$k(k\geq3)$ periodic solution does not exist.

If $\tau < Y_{\rm min}$ for case $(C)(C_{11})(\rm ii)$ or if $\tau > y_{C_0}$ for case $(C)(C_{12})(\rm i)$, or if $y_{D_0} < y_{D_2^+} < y_{C_0}$ and $y_{D_3^+}\geq y_{D_0}$ for case $(C)(C_{12})(\rm i)$, the conclusions can also be proved by using the same methods. This completes the proof.

4.   Conclusions

The IPM strategy based on chemical and biological techniques promotes the development of a series of impulsive predator-prey models ^{[17,18,19,20,21,22,23,24,25,26,27,28,29]}. The research of the models not only promoted the theoretical development of impulsive dynamical system, but also provided an effective foundation for control of pests. In order to control pests effectively and reduce the environmental pollution caused by the excessive use of chemical pesticides, the IPM strategy should be more realistic for practical environment. Considering the wide application of pest real-time monitoring technology in agriculture, we propose a predator-prey model concerning density guided releasing natural enemies and spraying pesticide with nonlinear state-dependent feedback control strategy. The main purpose of this paper is to explore the complex dynamic behavior of the model, and to reveal whether the pests can be effectively controlled under the interference of external environment and control measures, and research how the key factors affect the dynamic behaviors.

Firstly, we summarize the basic conclusions of the corresponding ODE system of (1.1) in the case of no external interference. Secondly, in order to study the dynamics of model (1.1) under impulsive disturbance, we make a qualitative analysis for the model (1.1) by using the basic theory of impulsive semi-dynamic system: a basic pulse set $\mathcal{M}$ and the corresponding basic phase set $\mathcal{N}$ are defined according to the isoline. Due to the fact that there is a saddle point and a center in the system, the judgment of the exact impulsive and phase sets needs to be classified and discussed according to the position relationship between the saddle point, the center and the line where the impulsive set and the phase set are located in. We obtain the coordinates of important points on the solution trajectory by using the first integral and Lambert W function. The exact impulsive sets under different conditions with pulse interference are determined, and the exact phase sets of two representative cases $(C)(C_{11})$ and $(C)(C_{12})$ are discussed, as shown in Table 1. We analysed the conditions about the solution of system (1.1) will be free from impulsive effects, and the analytic expression of Poincaré map $\mathcal {P}(y_i^+)$ for the sequence of impulsive points is defined. Table 2 shows the relationship between the domain of Poincaré map and some important parameters. According to the value range of the key parameter $\frac{\sqrt{\tau\theta}-1}{\theta}$, we study the properties of Poincaré map, such as the monotonicity of $\mathcal {P}(y_i^+)$. On the basis of these analysis, the existence, uniqueness, stability of the order-1 periodic solutions of system (1.1) in case $(C)(C_{11})$ and $(C)(C_{12})$ and the existence of order-$k (k\geq2)$ periodic solutions have been provided.

Compared with the IPM model that has been studied before, we have consider more practical elements, such as the anti-predator behavior which can reflect the interaction between pests and natural enemies^{[16,21,24,29]}, the killing rate of pests and the amount of natural enemies to be released are depend on the real-time density of them. In particular, the natural enemy density regulatory factor $\theta$ in the model not only reflecting the application of real-time monitoring and early warning technology for plant diseases and insect pests in agriculture, but also brings new research subjects and challenges for the nonlinear impulsive prey-predator model. The discussion of the definition and properties of Poincaré map, the existence and stability of periodic solutions fully reflects the complexity of the dynamic behavior of the density-dependent nonlinear model.

The theoretical analysis results of the article show that the effective control of pests depends on the initial density of pests and natural enemies, and the implementation of control methods. The dynamic behavior of the system is affected by the maximum killing rate of pests, the half-saturation constant, the maximum amount of natural enemies to be released and regulatory factor in the nonlinear term of the system, and all these factors will determine whether the pests can be controlled. It can be seen that under some conditions, there exists a unique globally asymptotically stable order-1 periodic solution for the system, which means that the pests and natural enemies can coexist. As long as the pest monitoring technology is fully utilized, spraying insecticides and releasing natural enemies reasonably, the pests can be controlled economically and effectively without destroying the ecological balance. The theoretical analysis of the article verifies that the model is meaningful for the research of IPM strategies, and it promotes the further development of nonlinear state-dependent feedback control system. Due to the complexity of the system, we only selected two representative case $(C)(C_{11})$ and case $(C)(C_{12})$ for discussion in the analysis of the exact phase set and Poincaré map. Therefore, the novel analytical techniques should be developed in near future, and more generalized models with complex nonlinear impulsive control effects could be investigated.

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China (NSFCs: 12031010, 11631012, 61772017, 11961024), and by the Scientific Research Foundation of the Education Department of Hubei Province B2018091, and by Doctorial Foundation of Hubei Minzu University MD2020B020.

Conflict of interest

All authors declare that they have no competing interests.